Złożoność problemów automatowych

Zaprojektować algorytm, który dla wyrażenia regularnego \(\beta\) i słowa \(w\in\Sigma^{*}\) odpowiada na pytanie, czy \(w\) należy do języka opisywanego przez \(\beta\)
1. w czasie \({\cal O}(|\Sigma|\cdot|\beta|^{2}\cdot|w|)\),
2. w czasie \({\cal O}(|\beta|\cdot|w|)\),
Wskazówka. Skonstruować automat niedeterministyczny równoważny wyrażeniu \(\beta\) i obliczyć zbiór stanów osiągalnych po słowie \(w\). Dla oszacowania w punkcie ?? użyć automatu z \(\epsilon\)-przejściami (por. zadanie ??.?? ), w grafie którego z każdego stanu wychodzą co najwyżej dwie krawędzie.
Rozważamy pytanie ,,\(w\in L[\beta]\) ?” jak w zadaniu ??, ale dla uogólnionego wyrażenia regularnego, tj. takiego, w którym dopuszczamy również operacje teorio–mnogościowe \(\cap\) i \(-\). Zaprojektować algorytm, który rozstrzyga to pytanie w czasie wielomianowym od \(|\beta|+|w|\).

Wskazówka. Zastosować metodę programowania dynamicznego:

dla \(1\leq i\leq j\leq|w|\) sukcesywnie obliczać zbiór podwyrażeń

\(\alpha\) wyrażenia \(\beta\) takich, że \(w[i..j]\in L[\alpha]\).
Konstrukcję automatu z zadań ??.?? i ??.?? , który dla danego \(w\) rozpoznaje język \(\Sigma^{*}w\), można przeprowadzić za pomocą następującego algorytmu. Niech \(m=|w|\).

Najpierw obliczamy pomocniczą tablicę \(F[0..m]\), taką, że \(F[0]=0\) oraz \(F[i]\) jest długością najdłuższego prefiksu właściwego \(w[1..i]\) będącego jednocześnie sufiksem \(w[1..i]\), dla \(i=1,\ldots,m\).

\(F[0]:=F[1]:=0\); \(i:=0\);

for \(j:=2\) to \(m\) do

begin \((*\, i=F[j-1]\,*)\)

while \(w_{j}\neq w_{{i+1}}\) \(\wedge\) \(i>0\) do \(i:=F[i]\);

if \(w_{j}=w_{{i+1}}\) then \(i:=i+1\);

\(F[j]:=i\)

end

W konstrukcji automatu przyjmujemy, że stany są liczbami \(0,1,\ldots,m\) (które można utożsamić z prefiksami \(w\) o odpowiednich długościach). Funkcję przejścia \(\delta\) określamy przez
1. \(\delta(0,w_{1})=1\), \(\delta(0,a)=0\), dla \(a\neq w_{1}\),
2. \(\delta(j,w_{{j+1}})=j+1\), \(\delta(j,a)=\delta(F[j],a)\), dla \(a\neq w_{{j+1}}\)
Dowieść, że powyższy algorytm oblicza żądany automat w czasie liniowym względem długości \(w\) (zależnym od alafabetu).
Niech \(A\) będzie ustalonym automatem deterministycznym. Zaprojektować algorytm, który dla danej liczby \(n\) znajduje w czasie \({\cal O}(n)\) liczbę słów długości \(n\) akceptowanych przez \(A\).
Podać przykład świadczący o tym, że najkrótsze słowo, jakiego nie akceptuje automat niedeterministyczny o \(n\) stanach może mieć długość \(2^{{\Omega(n)}}\).

Wskazówka. Rozważyć automat akceptujący wszystko za wyjątkiem słowa

\((\ldots((a_{0}^{2}a_{1})^{2}a_{2})^{2}a_{3}\ldots a_{{n-1}})^{2}a_{n}.\)
Dowieść, że jeśli dwa stany \(n\)–stanowego automatu deterministycznego nie są równoważne (tzn. \(L(A,q)\neq L(A,p)\)), to istnieje słowo długości nie większej niż \(n\) akceptowane z dokładnie jednego z nich.

Wskazówka. Rozważyć zstępujący ciąg relacji równoważności na zbiorze stanów: \(R_{i}(p,q)\) o ile stany \(p\) i \(q\) są nierozróżnialne słowami długości \(\leq i\).
Podać algorytm rozstrzygający równoważność dwóch automatów deterministycznych.

Uwaga. Zastosowanie idei zadania prowadzi do efektywniejszego algorytmu niż testowanie niepustości automatu produktowego.
Czy dla słów \(u,v\) takich, że \(|u|< |v|=n\) istnieje automat deterministyczny spełniający: \(u\in L(A)\ \wedge v\notin L(A)\) i mający \({\cal O}(\log n)\) stanów?
1. Wykazać, że dla dowolnego automatu niedeterministycznego o \(n\) stanach można skonstruować równoważne wyrażenie regularne długości \(2^{{{\cal O}(n)}}\).
2. (**) Podać przykład świadczący o tym, że najkrótsze wyrażenie regularne równoważne danemu automatowi deterministycznemu o \(n\) stanach może mieć długość \(2^{{\Omega(n)}}\).
  
  Wskazówka. Rozważyć automat, którego graf jest pełnym grafem o \(n\) wierzchołkach, a każda krawęd”z ma inną etykietę. Stosując indukcję po \(n\), skonstruować pętlę, która ,,wymusza” eksponencjalną długość wyrażenia regularnego.
Eksplozja stanów w produkcie automatów. Niech \(\Sigma=\{ 0,1,\ldots,k\}\) i niech dla \(i=1,\ldots,k\), \(L_{i}\) będzie zbiorem słów \(v\) nad \(\Sigma\) o następującej własności:
\(i\) występuje w \(v\), ale przed pierwszym i pomiędzy kaźdymi dwoma kolejnymi wystąpieniami \(i\), \(i-1\) występuje co najmniej dwa razy.

Nietrudno jest skonstruować deterministyczny automat o 4 stanach rozpoznający \(L_{i}\). Dowieść, że każdy (nawet niedeterministyczny) automat rozpoznający język \(L_{1}\cap\ldots\cap L_{k}\) musi mieć co najmniej \(2^{{k+1}}-1\) stanów.

Wskazówka. Oszacować od dołu długość najkrótszego słowa w tym języku.
Dowieść, że jakikolwiek automat niedeterministyczny rozpoznający język \(\{ xcy:\, x,y\in\{ a,b\}^{*}\,\wedge\, x[1..k]=y[1..k]\}\) ma \(2^{{\Omega(k)}}\) stanów.
Zakładając, że następujący automat deterministyczny \(A_{n}\) ma \(n\) stanów (\(n\geq 2\), na rysunku \(n=6\)), dowieść, że jakikolwiek automat deterministyczny rozpoznający lustrzane odbicie języka \(L(A_{n})\) ma co najmniej \(2^{n}\) stanów (por. zadanie ?? na str. ?? ).
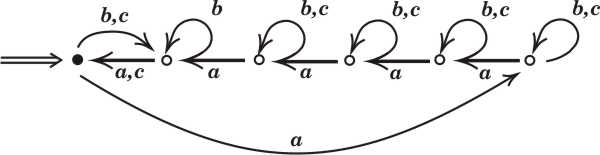
Słowo synchronizujące. Mówimy, że słowo \(w\) synchronizuje stany automatu deterministycznego, jeśli istnieje taki stan \(q_{0}\), że startując z dowolnego stanu i czytając słowo \(w\), automat dojdzie zawsze do stanu \(q_{0}\), tzn.
\((\forall q\in Q)\, q\stackrel{w}{\rightarrow}q_{0}\).
1. Znaleźć słowo synchronizujące dla automatu nad alfabetem \(\{ a,b\}\) o zbiorze stanów \(\{ 0,1,\ldots,k-1\}\) i funkcji przejścia
  
  \(i\stackrel{a}{\rightarrow}i+1\;\;(\textrm{mod}k)\)
  dla \(i=0,1,\ldots,k-1\)
  
  \(i\stackrel{b}{\rightarrow}i\)
  dla i = 0,1, …, k-2
  
  \(k-1\stackrel{b}{\rightarrow}0\)
  
  Wskazówka. Dla k=5 słowem synchronizującym (najkrótszym) jest \(w=\left(ba^{4}\right)^{3}b\)
2. Zaprojektować algorytm, który dla automatu o \(n\) stanach rozstrzyga w czasie \({\cal O}(n^{3})\), czy istnieje słowo synchronizujące i w pozytywnym przypadku znajduje takie słowo (długości \(\leq(n-1)^{3}\)).
  
  Wskazówka. Dla każdej pary stanów sprawdzamy, czy istnieje słowo synchronizujące dla tej pary. Szukamy ścieżki w grafie
  par od danej pary do pary o identycznych składowych. Wystarczy jeden taki graf dla wszystkich par.
  Graf ma rozmiar kwadratowy. Zatem pare można zsynchronizować słowem długości kwadratowej.
  Zaczynamy od zbioru wszystkich stanów. Stosując słowo do jednej pary sklejamy je w jeden stan. Teraz mamy juz tylko n-1
  stanów. Znowu bierzemy parę róznych słów. Dla niej liczymy słowo synchronizujące
  (w czasie kwadratowym) i sklejamy te stany. Kontynuujemy aż skleimy wszystkie stany do jednego stanu.
3. (*) Znaleźć najkrótsze słowo synchronizujące dla automatu z punktu ().
Uwaga. Licząca już 40 lat hipoteza Černego, zobacz www.liafa.jussieu.fr/\(\sim\)jep/Problemes/Cerny.html , głosi, że najkrótsze słowo synchronizujące, o ile istnieje, ma długość \((n-1)^{2}\).
Podać wielomianowy algorytm sprawdzania, czy dany skończony zbiór słów \(C\subseteq\Sigma^{*}\) jest kodem (por. rozdz. ?? , ?? zadanie ).
Wskazówka. Skonstruować automat skończony, rozpoznający hipotetyczne słowa posiadające dwie różne faktoryzacje.
Podać algorytmy rozwiązujace następujące dwa problemy (złożoność moze być duża).
1. Dany jest (poprzez automat skończony) język regularny \(L\) nad skończonym alfabetem \(\Sigma\), sprawdzić czy zachodzi
  
  \(\forall\ (x\in L)\ \forall\ (r,\ s\in\Sigma\ )\ \# _{{r}}(x)=\# _{{s}}(x).\)
2. Dany jest (poprzez automat skończony) język regularny \(L\) nad skończonym alfabetem \(\Sigma\), sprawdzić czy dla wszystkich słów \(x\in L\) poza skończoną ilością zachodzi
  
  \(\forall\ (r,\ s\in\Sigma\ )\ r\ne s\ \Rightarrow\ \# _{{r}}(x)\ \ne\ \# _{{s}}(x).\)