Grupy i ciała

Grupy

Przez strukturę algebraiczną rozumie się zbiór składający się ze skończonej liczby zbiorów i ze skończonej liczby odwzorowań iloczynów kartezjańskich tych zbiorów w te zbiory. Odwzorowania te nazywa się działaniami.

Zaczniemy od rozważenia najprostszych struktur.

Niech \(G\) będzie zbiorem niepustym. Działaniem wewnętrznym w zbiorze \(G\) nazywamy odwzorowanie \(d:G\times G\longrightarrow G\). Działanie \(d\) jest łączne, jeśli dla każdych \(a,b,c\in G\) zachodzi równość


\(d(a, d(b,c))=d(d(a,b),c).\)


Mówimy, że działanie \(d\) jest przemienne, jeśli dla każdych elementów \(a,b\in G\) zachodzi równość


\(d(a,b)=d(b,a).\)


Element \(e\in G\) nazywa się elementem neutralnym ze względu na działanie \(d\), jeśli dla każdego elementu \(a\in G\) mamy


\(a= d(e,a)=d(a,e).\)


Łatwo widać, że jeśli istnieje element neutralny, to element taki jest jedyny w \(G\). Istotnie, niech \(e\) i \(e'\) będą elementami neutralnymi ze względu na \(d\). Zachodzą następujące równości


\(e'=d(e,e')=e.\)


Działania oznacza się najczęściej znakiem plus, tzn. \(+\), lub znakiem kropki, która zwykle jest w zapisie pomijana. Oczywiście są też inne sposoby oznaczania działań, np. kółkiem, gwiazdką, etc. Działanie oznaczane znakiem \(+\) nazywa się dodawaniem, działanie oznaczane kropką nazywa się mnożeniem. Jeśli działanie oznaczone jest plusem, to łączność oznacza, że dla każdych \(a,b,c\in G\) mamy \(a+(b+c)= (a+b) +c\). A zatem zapis \(a+b+c\) ma sens. Podobnie dla działania zapisywanego multyplikatywnie, czyli kropką, łączność oznacza, że \(a(bc)=(ab)c\) dla każdych \(a,b,c\in G\), a zapis \(abc\) ma sens. Oczywiście, łączność dodawania oznacza, że zapis \(a_1+...+a_n\) ma sens dla dowolnego \(n\in \mathbb N\), zaś w przypadku mnożenia, zapis \(a_1\cdot ...\cdot a_n\) ma sens dla dowolnego \(n\in \mathbb N\).

Jeśli działanie zapisywane jest w sposób addytywny, tzn. za pomocą znaku \(+\), to element neutralny (o ile istnieje) nazywany jest zerem i oznaczany przez \(0\). W przypadku zapisu multyplikatywnego, element neutralny nazywany jest często jedynką i oznaczany cyfrą \(1\).

Załóżmy, że działanie \(d\) w zbiorze \(G\) ma element neutralny \(e\). Załóżmy najpierw, że działanie to jest zapisywane addytywnie. Mówimy, że element \(a\in G\) ma element przeciwny, jeśli istnieje element \(a'\in G\) taki, że \(a+a'=a'+a=e\). Jeśli działanie zapisywane jest multyplikatywnie, to mówimy, że element \(a\in G\) ma element odwrotny w \(G\), jeśli istnieje element \(a'\in G\), taki że \(aa'=a'a=e\).

Zauważmy, że jeśli działanie jest łączne, ma element neutralny i element \(a\in G\) ma element odwrotny (przeciwny), to element taki jest jedyny. Mianowicie, jeśli \(a'\) i \(a''\) są elementami odwrotnymi do \(a\), to (stosując zapis multyplikatywny) mamy następujące równości


\(a'=a'e=a'(aa'')=(a'a)a''=ea''=a''.\)


Jeżeli działanie zapisywane jest w sposób addytywny i element \(a\) ma dokładnie jeden element przeciwny, to element ten oznaczamy przez \(-a\). Ponadto, jeśli \(b\in G\), to przyjmujemy oznaczenie


\(b-a=b+(-a).\)      (1.1)


Jeśli działanie zapisywane jest w sposób multyplikatywny i element \(a\) ma dokładnie jeden element odwrotny, to oznaczamy go przez \(a^{-1}\). Przyjmujemy także oznaczenie


\(ab^{-1}= {a\over b}\, .\)


Definicja 1.1 [Grupa]

Mówimy, że zbiór niepusty \(G\) z działaniem wewnętrznym jest grupą, jeśli działanie to jest łączne, ma element neutralny i każdy element \(G\) ma element odwrotny (przeciwny).

Grupę nazywamy przemienną, lub abelową, jeśli jej działanie jest przemienne.

Załóżmy, że \(G'\) jest niepustym podzbiorem grupy \(G\). Mówimy, że \(G'\) jest podgrupą grupy \(G\), jeśli działanie grupy \(G\) zawężone do \(G'\times G'\) ma wartości w \(G'\) oraz dla każdego elementu \(a\in G'\) jego element odwrotny \(a^{-1}\) również należy do \(G'\).

Łatwo można sprawdzić, że podgrupa z zawężonym działaniem jest grupą.


Ciała

Rozważymy teraz zbiory wyposażone w dwa działania - dodawanie i mnożenie. Przyjmiemy następującą definicję.

Definicja 2.1 [Ciało]

Ciałem (dokładniej mówiąc - ciałem przemiennym) nazywamy zbiór \(\mathbb K\) wyposażony w dwa działania wewnętrzne - dodawanie i mnożenie, które spełniają następujące warunki:

C1) \(\mathbb K\) z dodawaniem jest grupą przemienną,

C2) mnożenie w \(\mathbb K\) jest przemienne i zbiór \(\mathbb K\setminus \{0\}\) z mnożeniem jest grupą,

C3) \(a(b+c)=ab+ac\) dla każdych elementów \(a,\, b,\, c\in \mathbb K\) (prawo rozdzielności mnożenia względem dodawania).

Udowodnimy najbardziej podstawowe własności ciał.

Twierdzenie 2.2 [Własności Ciała]

W ciele zachodzą następujące warunki:

  1. \(1\ne 0\),
  2. \(0\cdot a= a\cdot 0=0,\)
  3. \((-1)\cdot a =-a,\)
  4. jeżeli \(ab=0\), to \(a=0\) lub \(b=0\),
  5. jeżeli \(a\ne 0\) i \(b\ne 0\), to \((ab)^{-1}=b^{-1}a^{-1}\)

dla każdych \(a,\, b \in \mathbb K\).

Dowód

Wiemy, że zbiór \(\mathbb K \setminus \{0\}\) jest grupą ze względu na mnożenie, a więc \(1\in \mathbb K\setminus \{0\}\). Stąd mamy pierwszą własność.

Dla udowodnienia drugiej własności zauważmy, że


\(0\cdot a +0\cdot a =(0+0)a=0\cdot a.\)


Dodając do obydwu stron \(-(0\cdot a)\) dostajemy żądaną równość. Korzystając z przemienności mnożenia w całym \(\mathbb K\) dostajemy równość \(a\cdot 0=0\) dla każdego \(a\in \mathbb K\). Stąd i założonej łączności mnożenia w \(\mathbb K\setminus\{0\}\) wynika już łączność mnożenia w całym zbiorze \(\mathbb K\).

Korzystając z drugiej własności dostajemy teraz


\(0=0\cdot a=(1+(-1))a=a +(-1)a.\)


Ponieważ dodawanie w \(\mathbb K\) jest przemienne, dostajemy równość \((-1)a +a=0\). Oznacza to, że \((-1)a\) jest elementem przeciwnym do \(a\), co dowodzi trzeciej własności.

Dla dowodu czwartej własności przypuśćmy, że \(a\ne 0\). Wtedy, wykorzystując już udowodnioną własność (2) dostajemy


\(b=(a^{-1}a)b=a^{-1}(ab)=a^{-1}0=0.\)


Własność ta wynika też z aksjomatu C2), bo w aksjomacie tym implicite założono, że \(\mathbb K\setminus \{0\}\) jest zamknięty ze względu na mnożenie.

Własność ostatnia wynika z następujących równości


\((b^{-1}a^{-1})(ab)= b^{-1}(a^{-1}a)b= b^{-1}b=1.\)


Konsekwencją trzeciej własności i wcześniejszej umowy (1.1) jest równość następująca:


\(a(b-c)=ab-ac\)


dla każdych \(a,\, b,\, c\in \mathbb K\).

Wprowadzimy teraz pojęcie charakterystyki ciała.

Definicja 2.3 [Charakterystyka ciała]

Niech \(\mathbb K\) będzie ciałem. Jeżeli istnieje liczba naturalna \(n\) taka, że


\(1+...+1 =0,\)


gdzie jedynka w powyższej sumie występuje \(n\) razy, to najmniejszą taką liczbę \(n\) nazywamy charakterystyką ciała. Jeśli taka liczba naturalna nie istnieje, mówimy, że charakterystyka ciała równa jest \(0\).

Ponieważ \(1\ne 0\), więc charakterystyka ciała, jeśli nie jest równa \(0\), musi być większa lub równa \(2\). Ciałem o charakterystyce 2 jest tzw. ciało zero-jedynkowe, które można wprowadzić tak. W zbiorze \(\{0,\, 1\}\) wprowadzamy działania


\(0+0=0,\ \ \ 0+1=1+0=1,\ \ \ 1+1=0,\)
\(0\cdot 0=0,\ \ \ 0\cdot 1=1\cdot 0=0,\ \ \ 1\cdot 1=1.\)


Łatwo widać, że spełnione są wszystkie warunki definiujące ciało i ciało to ma charakterystykę równą 2.

Ciałami są zbiór liczb wymiernych i zbiór liczb rzeczywistych ze zwykłymi działaniami. Są to oczywiście ciała o charakterystyce \(0\). Ciała te oznaczamy symbolami \(\mathbb Q\) i \(\mathbb R\) odpowiednio.


Ciało liczb zespolonych

Niech \(\mathbb C\) będzie zbiorem \(\mathbb R\times \mathbb R\) wyposażonym w dwa następujące działania:


\((a,b)+(c,d)=(a+c, b+d),\)


\((a,b)\cdot (c,d)=(ac-bd, ad+bc).\)
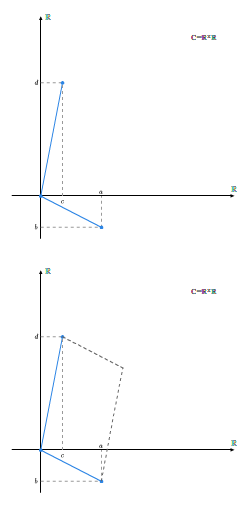
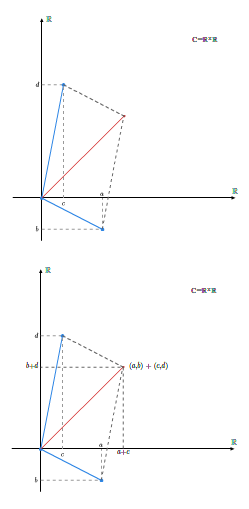Dodawanie liczb zespolonychDodawanie liczb zespolonych


Sprawdzenie, że tak zdefiniowana struktura jest ciałem jest kwestią bezpośredniego rachunku. Elementem neutralnym ze względu na dodawanie (zerem w \(\mathbb C\)) jest element \((0,0)\), zaś elementem neutralnym ze względu na mnożenie jest element \((1,0)\). Elementem przeciwnym do elementu \((a,b)\) jest element \((-a,-b)\).

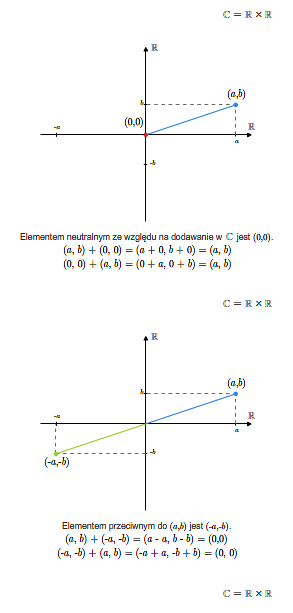
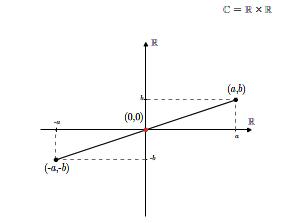
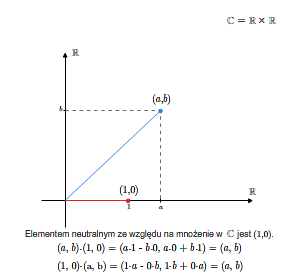
Element neutralny i elementy przeciwne w \((\mathbb C,+)\)
Element neutralny w \((\mathbb C, \cdot )\)


Elementem odwrotnym do niezerowego elementu \((a,b)\) jest element


\((a,b)^{-1}=\left({a\over {a^2+b^2}} ,- {b\over{a^2+b^2}}\right).\)


Ciało liczb zespolonych ma charakterystykę 0.

Element \((0,1)\) oznaczamy przez \(\mathbf i\). Liczbę rzeczywistą \(a\) utożsamiamy z liczbą zespoloną \((a,0)\). Dokładniej mówiąc, odwzorowanie


\(\mathbb R \ni a \longrightarrow (a, 0)\in \mathbb C\)


jest injekcją, czyli zbiór liczb rzeczywistych można uważać za podzbiór


\(\{(a,0)|\ a\in \mathbb R\}\)


zbioru liczb zespolonych. Co więcej, według powyższych formuł definiujących dodawanie i mnożenie w ciele liczb zespolonych, zwykłe dodawanie i mnożenie liczb rzeczywistych jest zawężeniem dodawania i mnożenia (odpowiednio) z ciała liczb zespolonych. Mówimy, że ciało \(\mathbb R\) jest podciałem ciała \(\mathbb C\).

Liczba zespolona \(\mathbf i =(0,1)\) ma tę własność, że \(\mathbf i ^2=-1\). W związku z tym, liczbę tę zapisywano jako \(\sqrt {-1}\). Oznaczenie to używane było już w XVI wieku, jako formalny symbol, do obliczania pierwiastków wielomianów. Współczesna teoria i symbolika liczb zespolonych pochodzi z XIX wieku.


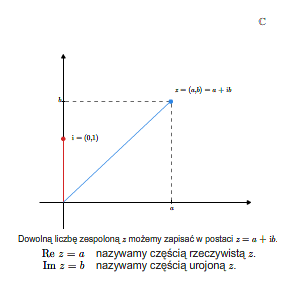
Postać algebraiczna liczby zespolonej

Liczbę \(\mathbf i\) nazywamy jednostką urojoną i zgodnie z przyjętymi wyżej definicjami i ustaleniami, każdą liczbę zespoloną \((a,b)\) możemy zapisać jako \(a+b\mathbf i\). Liczbę rzeczywistą \(a\) nazywamy częścią rzeczywistą (z łac. realis) liczby zespolonej \(z=a+b\mathbf i\) i oznaczamy ją \(\Re\, z\), zaś liczbę rzeczywistą \(b\) nazywamy częścią urojoną ( z łac. imaginalis) liczby zespolonej \(z\) i oznaczamy ją przez \(\Im\, z\).

Liczby zespolone, jako elementy zbioru \(\mathbb R ^2\), możemy identyfikować z punktami na płaszczyźnie wyposażonej w prostokątny układ współrzędnych. Dokładniej mówiąc, liczbę zespoloną \(z=(a,b)\) przedstawiamy na płaszczyźnie jako punkt o współrzędnych \((a,b)\) lub jako wektor o początku w początku układu współrzędnych (w punkcie o współrzędnych \((0,0)\)) i końcu w punkcie o współrzędnych \((a,b)\). Przyjmując tę geometryczną interpretację liczby zespolonej, zbiór wszystkich liczb zespolonych nazywamy płaszczyzną liczb zespolonych. Dodawaniu liczb zespolonych odpowiada dodawanie wektorów zaczepionych w początku układu współrzędnych.

Dla liczby zespolonej wprowadzamy pojęcie modułu i argumentu. Modułem liczby zespolonej \(z=a+b\mathbf i\) nazywamy liczbę rzeczywistą \(|z|\) określoną wzorem


\(|z| =\sqrt {a^2+b^2}.\)


Biorąc pod uwagę geometryczną interpretację liczb zespolonych, widzimy, że moduł liczby \(z= a+b\mathbf i\) jest odległością punktu \((a,b)\) od początku układu współrzędnych lub długością wektora reprezentującego tę liczbę zespoloną. Moduł liczby zespolonej jest równy zeru wtedy i tylko wtedy, gdy liczba ta jest równa zeru.

Argumentem różnej od zera liczby zespolonej \(z=a+b\mathbf i\) nazywamy każdą liczbę rzeczywistą \(\varphi\) spełniającą układ równań


\(\begin{array} {l} \cos \varphi ={a\over {|z|}},\\ \sin\varphi ={b\over {|z|}}. \end{array}\)


Umawiamy się, że dla liczby zespolonej \(z=0\) argumentem jest każda liczba rzeczywista. Argumentem głównym liczby zespolonej \(z\ne 0\) nazywamy ten argument, który leży w przedziale \([0,2\pi)\). Argument główny liczby zespolonej (niezerowej) oznaczmy przez \(\arg z\).

Argument główny jest kątem nachylenia wektora \(z\) do dodatniej półosi odciętych. Liczbę zespoloną \(z=a+b\mathbf i\) różną od \(0\) możemy teraz zapisać jako


\(z=|z|(\cos\arg z +\mathbf i \sin\arg z ).\)


Każdą liczbę zespoloną możemy zapisać jako


\(z=|z|(\cos\varphi +\mathbf i \sin\varphi )\)


dla pewnego argumentu \(\varphi\). Zapis ten nazywamy trygonometryczną postacią liczby zespolonej.


]
Postać trygonometryczna liczby zespolonej


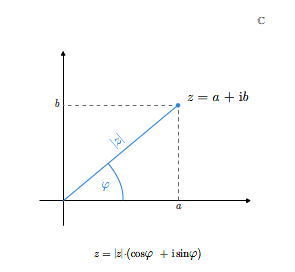
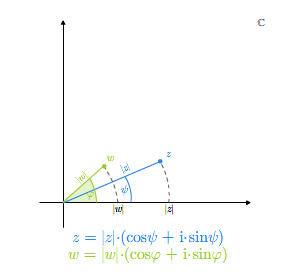
Można przeliczyć, stosując znane ze szkoły wzory trgonometryczne, że jeśli \(z_1=|z_1|( \cos\varphi _1 +\mathbf i \sin\varphi _1)\) i \(z_2 = |z_2|(\cos\varphi _2 +\mathbf i \sin\varphi _2)\), to


\(z_1z_2= |z_1||z_2|(\cos (\varphi _1 +\varphi _2) +\mathbf i\sin(\varphi _1 +\varphi_2)).\)


Mnożenie liczb zespolonych

Jeśli przyjmiemy, że \(z^n = z\cdot ...\cdot z\), gdzie \(z\) powtarza się \(n\) razy, to posługując się ostatnim wzorem na mnożenie liczb zespolonych w postaci trygonometrycznej, dostajemy natychmiast tzw. wzory de Moivre'a na \(n\)-tą potęgę liczby zespolonej


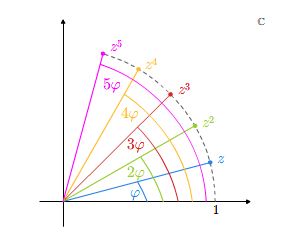
Potęgowanie liczb zespolonych

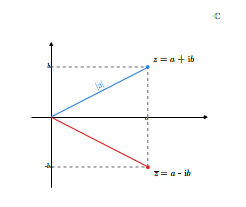
\([|z|(\cos\varphi +\mathbf i \sin\varphi )]^n=|z|^n(\cos n\varphi +\mathbf i \sin n\varphi).\)


Dla liczby zespolonej \(z=a+b\mathbf i\) definiujemy tak zwaną liczbę sprzężoną \(\overline z\) do liczby \(z\). Mianowicie, definiujemy


\(\overline z = a-b\mathbf i .\)


Jeśli \(z=|z|(\cos\varphi +\mathbf i \sin \varphi )\), to


\(\overline z=|z|(\cos (- \varphi) +\mathbf i \sin (-\varphi)).\)


Wobec tego liczba sprzężona \(\overline z\) jest obrazem przez odbicie symetryczne względem osi odciętych liczby \(z\), gdzie \(z\) traktujemy jako punkt płaszczyzny lub wektor.

Moduł i sprzężenie liczby zespolonej

Na koniec tego wykładu przytoczymy, bez dowodu, bardzo ważną cechę ciała liczb zespolonych, której to cechy nie ma ciało liczb rzeczywistych. Najpierw wprowadźmy następującą definicję

Definicja 3.1 [Algebraiczna domkniętość]

Mówimy, że ciało \(\mathbb K\) jest algebraicznie domknięte, jeśli każdy wielomian jednej zmiennej o współczynnikach z ciała \(\mathbb K\) ma w ciele \(\mathbb K\) miejsce zerowe.

Jak wiadomo, ciało liczb rzeczywistych nie ma takiej własności, bo np. wielomian \(x^2 +1\) nie ma miejsc zerowych w \(\mathbb R\).

W przypadku liczb zespolonych zachodzi następujące twierdzenie, nazywane zasadniczym twierdzeniem algebry


Twierdzenie 3.2

Ciało liczb zespolonych jest algebraicznie domknięte.

Z twierdzenia tego wynika, że każdy wielomian o współczynnikach z ciała \(\mathbb C\) jest rozkładalny na czynniki stopnia 1 o współczynnikach z ciała \(\mathbb K\).