Przestrzenie wektorowe

Definicja przestrzeni wektorowej

Na początku tego wykładu wprowadzimy pojęcie przestrzeni wektorowej - najważniejszej struktury, którą zajmuje się algebra liniowa.

Definicja 1.1 [Przestrzeń wektorowa]

Niech \(V\) będzie zbiorem niepustym wyposażonym w działanie wewnętrzne - dodawanie. Dane jest także ciało \(\mathbb K\) oraz działanie zewnętrzne, tak zwane mnożenie zewnętrzne z lewej strony, będące odwzorowaniem zbioru \(\mathbb K \times V\) w zbiór \(V\). Wartość tego odwzorowania na parze \((\lambda ,v)\in \mathbb K\times V\) oznaczamy przez \(\lambda\cdot v\). Występującą tu kropkę najczęściej pomijamy.

Mówimy, że struktura składająca się ze zbioru \(V\), ciała \(\mathbb K\) oraz dwóch powyższych działań jest przestrzenią wektorową, jeśli spełnionych jest pięć poniższych warunków, zwanych aksjomatami przestrzeni wektorowej:

V1) Zbiór \(V\) z dodawaniem jest grupą przemienną,

V2) Dla każdych \(\lambda\, \mu \in \mathbb K\) i dla każdego \(v\in V\) zachodzi równość \(\lambda(\mu v)=(\lambda\mu )v\).

V3) Dla każdych \(\lambda\, \mu \in \mathbb K\) i dla każdego \(v\in V\) zachodzi równość \((\lambda +\mu )v=\lambda v +\mu v\).

V4) Dla każdego \(\lambda \in \mathbb K\) i każdych \(v,w\in V\) zachodzi równość \(\lambda (v+w)= \alpha v +\alpha w\).

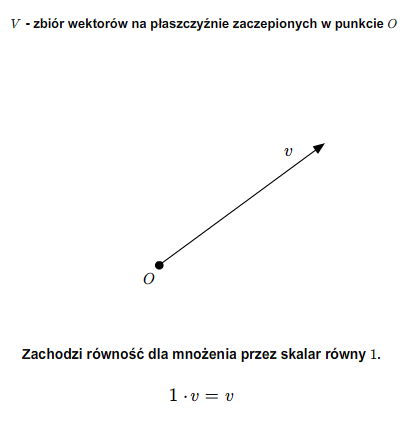
V5) Dla każdego \(v\in V\) zachodzi równość \(1\cdot v= v\).

W pierwszym aksjomacie najczęściej żąda się, tak jak to zrobiliśmy, aby grupa była przemienna, choć przemienność tej grupy jest konsekwencją pozostałych warunków. Proponujemy, aby czytelnik sam sprawdził ten fakt. Aksjomaty V2)- V5) są w definicji niezbędne. Proponujemy, aby czytelnik sprawdził to, znajdując przykład struktury, dla której spełnione są wszystkie warunki oprócz V2), następnie przykład struktury, dla której spełnione są wszystkie warunki oprócz warunku V3), etc. Własność V3) nazywa się łącznością mieszaną, własność V4) - rozdzielnością mnożenia zewnętrznego względem dodawania w ciele i wreszczcie własność V4) - rozdzielnością mnożenia zewnętrznego względem dodawania wewnętrznego.

Jeśli spełnione są wszystkie powyższe aksjomaty, to mówimy także, że \(V\) jest przestrzenią wektorową nad ciałem \(\mathbb K\). Elementy przestrzeni \(V\) nazywamy wektorami, zaś elementy ciała \(\mathbb K\) nazywamy skalarami.

Zauważmy najpierw pewne elementarne własności przestrzeni wektorowych.

Twierdzenie 1.2

Niech \(V\) będzie przestrzenią wektorową nad ciałem \(\mathbb K\). Wtedy dla każdego \(v\in V\) i każdego \(\lambda \in \mathbb K\) zachodzą równości:


\(0\cdot v=0,\)


\(\lambda \cdot 0=0,\)


\((-1)v=-v,\)


\(\lambda \cdot v= 0 \Longrightarrow \lambda =0 \ \rm {lub}\ v=0.\)

Uwaga 1.3

W pierwszej z powyższych równości \(0\) z lewej strony jest zerem w ciele, zaś \(0\) z prawej strony jest zerem w przestrzeni wektorowej. W drugiej równości oba \(0\) są zerami w przestrzeni wektorowej.

Dowód

Dowód trzech pierwszych z powyższych własności jest analogiczny do odpowiednich części dowodu Twierdzenia 2.2. z Wykładu 1. Dla dowodu czwartej własności załóżmy, że \(\lambda \ne 0\) i \(\lambda v=0\). Pomnóżmy obie strony przez \(\lambda ^{-1}\). Otrzymujemy stąd równość \(v=0\).

Podamy teraz kilka przykładów przestrzeni wektorowych.

Przykład 1.4

Dowolny zbiór jednoelementowy jest przestrzenią wektorową nad dowolnym ciałem. Jedyny element takiego zbioru jest zerem w tej przestrzeni. Taką przestrzeń nazywamy przestrzenią zerową.

Przykład 1.5

Każde ciało jest przestrzenią wektorową nad samym sobą.

Ogólniej, jeśli \(\mathbb K\) jest ciałem, to iloczyn kartezjański \(\mathbb K ^n\), \(n\in \mathbb N\), ma naturalną strukturę przestrzeni wektorowej nad ciałem \(\mathbb K\). Dodawanie w \(\mathbb K ^n\) definiujemy następująco


\((a_1,...,a_n) +(b_1,...,b_n) =(a_1+b_1,..., a_n +b_n),\)


zaś mnożenie zewnętrzne dane jest formułą


\(\lambda (a_1,...,a_n)=(\lambda a_1,...,\lambda a_n).\)


Bezpośrednim i łatwym rachunkiem można sprawdzić, że tak zdefiniowana struktura na \(\mathbb K ^n\) jest przestrzenią wektorową nad ciałem \(\mathbb K\).

W kolejnym przykładzie zdefiniujemy strukturę przestrzeni wektorowej na iloczynie kartezjańskim dowolnych przestrzeni wektorowych.

Przykład 1.6

Niech \(V\), \(W\) będą przestrzeniami wektorowymi nad ciałem \(\mathbb K\). Wtedy iloczyn kartezjański \(V\times W\) ma naturalną strukturę przestrzeni wektorowej nad ciałem \(\mathbb K\). Istotnie, jeśli zdefiniujemy dodawanie formułą


\((v_1,w_1)+(v_2,w_2)=(v_1+v_2, w_1+w_2),\)


dla \(v_1, v_2\in V\) i \(w_1, w_2\in W\), a mnożenie zewnętrzne formułą


\(\lambda (v,w)=(\lambda v, \lambda w)\)


dla \(\lambda \in\mathbb K\) i \(v\in V\), \(w\in W\), to otrzymujemy strukturę przestrzeni wektorowej (nad ciałem \(\mathbb K\)) na \(V\times W\).

Przykład 1.7

Załóżmy, że dana jest przestrzeń wektorowa \(V\) nad ciałem \(\mathbb K\) i \(X\) jest dowolnym zbiorem niepustym. Weźmy zbiór wszystkich odwzorowań \(f:X\longrightarrow V\). Oznaczmy ten zbiór przez \(V^X\). W zbiorze \(V ^X\) wprowadzamy dodawanie


\((f+g)(x)=f(x)+g(x)\)


dla każdych \(f,g\in V^X\) i dla każdego \(x\in X\). Mnożenie zewnętrzne definiujemy formułą


\((\lambda f)(x)=\lambda (f(x))\)


dla \(\lambda \in\mathbb K\), \(f\in V\) i \(x\in X\).

Tak określone działania definiują , co łatwo sprawdzić, strukturę przestrzeni wektorowej na \(V^X\) nad \(\mathbb K\).

Jako szczególny przypadek możemy wziąć zbiór wszystkich ciągów nieskończonych o wartościach w dowolnej przestrzeni wektorowej \(V\). Zbiorem \(X\) jest tutaj zbiór liczb naturalnych \(\mathbb N\).

Jeśli za \(X\) weźmiemy zbiór \(\{1,...,n\}\), a \(V\) jest dowolną przestrzenią wektorową, to otrzymamy przestrzeń ciągów o długości \(n\) i wyrazach w \(V\).

Jeśli za \(X\) przyjmiemy pewien przedział w zbiorze liczb rzeczywistych, to zbiór wszystkich funkcji określonych na tym przedziale i o wartościach w zbiorze liczb rzeczywistych jest przestrzenią wektorową.

Przykład 1.8

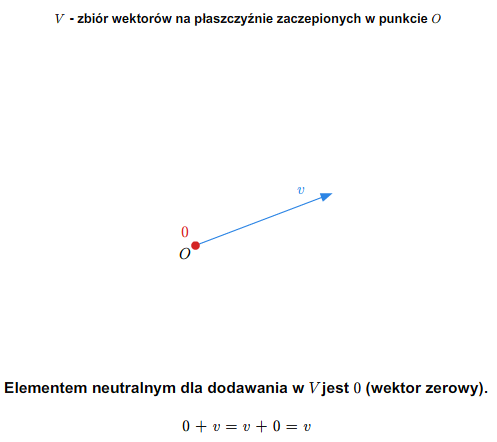
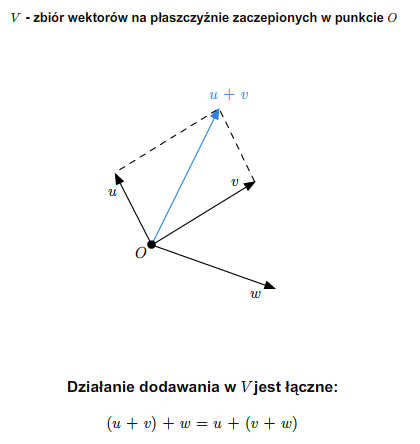
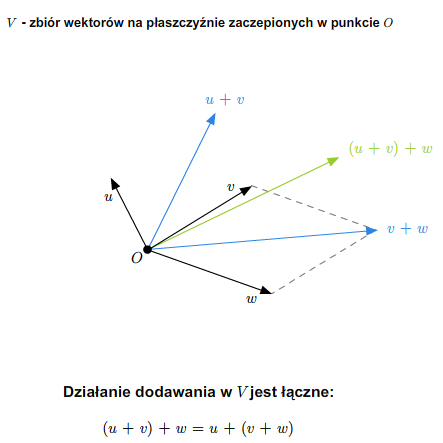
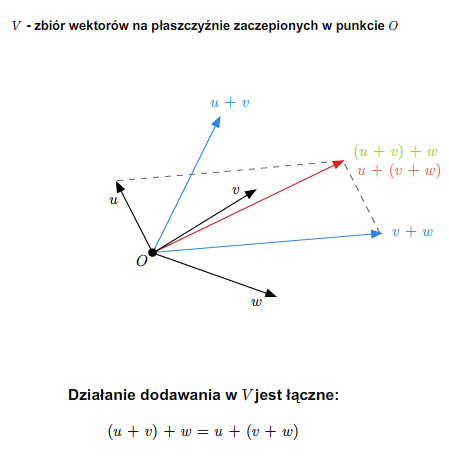
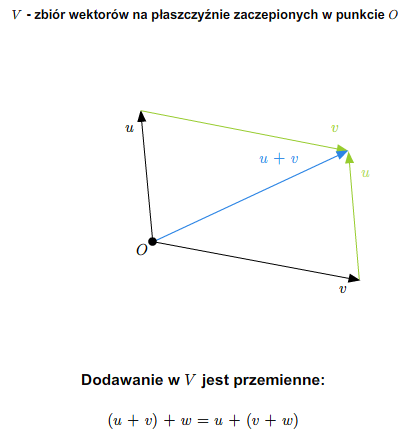
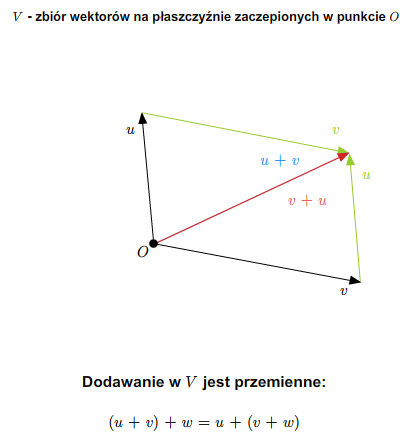
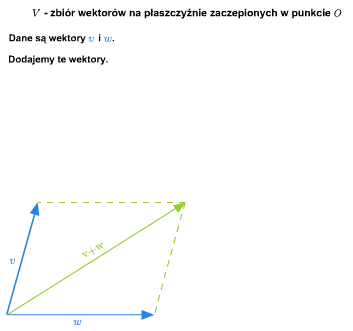
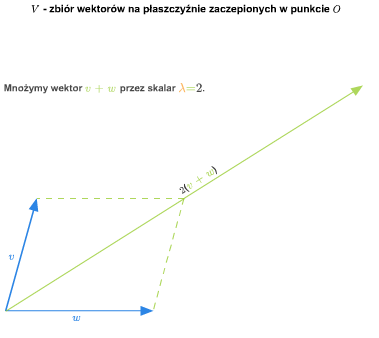
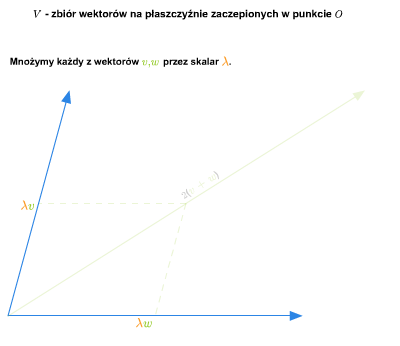
W szkole wprowadza się pojęcie wektora swobodnego na płaszczyźnie. Zbiór wszystkich takich wektorów ze znanymi ze szkoły dodawaniem (przez zastosowanie reguły równoległoboku) i mnożeniem wektorów przez liczby rzeczywiste stanowi przykład przestrzeni wektorowej nad ciałem \(\mathbb R\). Podobnie ma się rzecz ze zbiorem wektorów swobodnych w trójwymiarowej przestrzeni fizycznej.

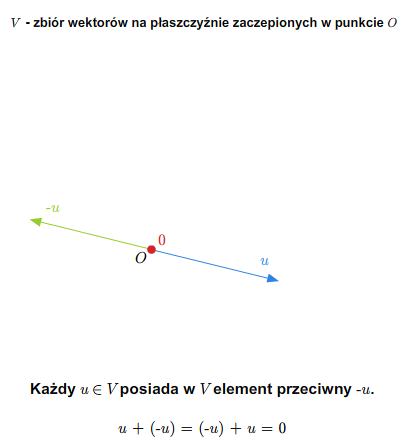
Można też rozumować tak (pomijając pojęcie wektora swobodnego). Rozważmy płaszczyznę (lub trójwymiarową przestrzeń) z ustalonym punktem (np. początkiem pewnego układu współrzędnych). Bierzemy zbiór wszystkich wektorów zaczepionych w tym punkcie. Wprowadzamy dodawanie wektorów i mnożenie przez liczbę rzeczywistą tak, jak się to robi w szkole. Tak otrzymana struktura jest przestrzenią wektorową nad \(\mathbb R\).

Jeśli płaszczyzna (lub trójwymiarowa przestrzeń fizyczna) jest wyposażona w układ współrzędnych, to tak otrzymaną przestrzeń wektorów można utożsamiać z \(\mathbb R ^2\) (w przypadku płaszczyzny) lub z \(\mathbb R ^3\) (w przypadku trójwymiarowej przestrzeni fizycznej).

Aksjomat V1 przestrzeni wektorowej

Aksjomat V2 przestrzeni wektorowej

Aksjomat V3 przestrzeni wektorowej

Aksjomat V4 przestrzeni wektorowej

Aksjomat V5 przestrzeni wektorowej


Przestrzeń wektorową \(V\) nad ciałem liczb zespolonych nazywamy przestrzenią wektorową zespoloną. Przestrzeń wektorową nad ciałem liczb rzeczywistych nazywamy przestrzenią wektorową rzeczywistą. Każda przestrzeń wektorowa zespolona jest automatycznie przestrzenią wektorową rzeczywistą (z mnożeniem zewnętrznym będącym zawężeniem do \(\mathbb R\times V\) mnożenia zewnętrznego przez liczby zespolone).


Podprzestrzenie wektorowe

Definicja 2.1

Niech \(V\) będzie przestrzenią wektorową nad ciałem \(\mathbb K\). Załóżmy, że \(W\) jest niepustym podzbiorem zbioru \(V\). Podzbiór \(W\) nazywamy podprzestrzenią wektorową przestrzeni \(V\), jeśli dla każdych \(v,w\in W\) i \(\lambda\in\mathbb K\) mamy


\(v+w\in W,\)


\(\lambda v\in W.\)


Innymi słowy, podprzestrzeń wektorowa \(W\) przestrzeni \(V\) jest niepustym podzbiorem przestrzeni \(V\) zamkniętym ze względu na działania w \(V\). Jest jasne, że jeśli \(W\) jest podprzestrzenią \(V\), to dla każdych \(\lambda _1,...,\lambda _k \in \mathbb K\) i dla każdych wektorów \(v_1,..., v_k \in W\) wektor równy \(\lambda _1v_1+...+\lambda _kv_k\) należy do podprzestrzeni \(W\).

Jeżeli \(W\) jest podprzestrzenią wektorową przestrzeni \(V\) i \(v\in W\), to \(-v=(-1) v\) również należy do \(W\). A zatem \(0=v+(-1)v \in W\), czyli do każdej podprzestrzeni wektorowej \(W\) musi należeć zero przestrzeni \(V\).

Ponieważ własności działań przestrzeni wektorowej \(V\) zawarte w aksjomatach dziedziczą się łatwo na podzbiór zamknięty ze względu na te działania, więc podprzestrzeń wektorowa jest przestrzenią wektorową (nad tym samym ciałem co przestrzeń \(V\)).

Podamy kilka najważniejszych przykładów podprzestrzeni wektorowych. Oczywiście cała przestrzeń \(V\), a także podzbiór \(\{0\}\subset V\) są podprzestrzeniami wektorowymi \(V\). Są to tak zwane podprzestrzenie trywialne.

Kolejny przykład będzie odgrywać ważną rolę w naszym wykładzie

Przykład 2.2

Jeśli \(a_1,...a_n\) są ustalonymi elementami ciała \(\mathbb K\), to zbiór opisany równaniem liniowym \(a_1x_1+...+a_nx_n=0\), tzn. zbiór


\(\{ (x_1,...x_n)\in \mathbb K ^n|\ a_1x_1 +...+a_nx_n=0\},\)


jest podprzestrzenią wektorową przestrzeni \(\mathbb K ^n\). Uogólnimy teraz ten przykład. Jednorodnym układem równań liniowych nazywamy układ równań

\(\begin{cases} & a_{11}x_1+...+a_{1n}x_n=0,\\ & .\\ & .\\ & .\\ & a_{m1}x_1+...+a_{mn}x_n=0, \end{cases}\)      (2.2)

gdzie \(a_{ij}\) dla \(i=1,...,m\), \(j=1,...,n\), są dowolnymi ustalonymi skalarami. Jest to układ \(m\) równań z \(n\) niewiadomymi \(x_1,...x_n\). Zbiór wszystkich rozwiązań tego układu, czyli zbiór wszystkich ciągów \((x_1,....,x_n)\in \mathbb K ^n\) spełniających (2.2), jest podprzestrzenią wektorową przestrzeni \(\mathbb K ^n\).}

Wróćmy teraz do Przykładu 1.7.

Przykład 2.3

Niech dany będzie przedział \((a,b)\subset \mathbb R\). Niech \(V=\mathbb R ^{(a,b)}\) będzie przestrzenią wszystkich funkcji określonych na \((a,b)\) i mających wartości rzeczywiste. Weźmy podzbiór składający się ze wszystkich funkcji ciągłych lub podzbiór składający się ze wszystkich funkcji różniczkowalnych w tym przedziale. Łatwo widać (posługując się wiedzą ze szkoły np. o tym, że suma funkcji ciągłych jest funkcją ciągłą), że podzbiory te są podprzestrzeniami przestrzeni \(V\).

Inny przykład wywodzący się z Przykładu 1.7 jest taki. Weźmy przestrzeń \(V=\mathbb R ^{\mathbb N}\) wszystkich nieskończonych ciągów o wyrazach rzeczywistych. Weźmy podzbiór składający się ze wszystkich ciągów zbieżnych do liczb rzeczywistych. Podzbiór ten jest podprzestrzenią \(V\).

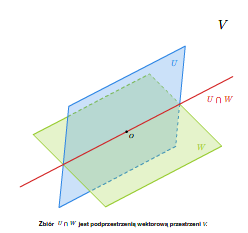
Jeżeli \(W\) i \(U\) są podprzestrzeniami wektorowymi przestrzeni \(V\), to ich iloczyn mnogościowy jest też podprzestrzenią wektorową przestrzeni \(V\). Istotnie, \(0\) należy do \(U\) i \(V\), a zatem \(U\cap W\) jest niepusty. Dalej, jeśli \(v, w\in U\cap W\), to obydwa te wektory należą do \(U\), a więc ich suma należy do \(U\), a także należą do \(W\), a więc ich suma należy do \(W\). Czyli \(v+w\in U\cap W\). Podobnie, jeśli \(\lambda \in\mathbb K\) i \(v\in U\cap W\), to \(\lambda v\) należy zarówno do \(U\) jak i do \(W\). Wobec tego \(\lambda v\in U\cap W\).

Równie łatwo można stwierdzić, że jeśli mamy dowolną niepustą rodzinę podprzestrzeni \({W_t}_{\{t\in T\}}\) przestrzeni \(V\), to ich iloczyn mnogościowy \(\bigcap _{t\in T} W_t\) jest podprzestrzenią wektorową.

Iloczyn mnogościowy podprzestrzeni wektorowych

Dodawanie mnogościowe podprzestrzeni wektorowych nie jest dobrą operacją, tzn. suma mnogościowa podprzestrzeni wektorowych na ogól nie jest podprzestrzenią wektorową. Zachodzi następujące twierdzenie, którego dowód proponujemy czytelnikowi

Twierdzenie 2.4

Suma mnogościowa dwóch podprzestrzeni wektorowych \(U\), \(W\) przestrzeni \(V\) jest podprzestrzenią wektorową przestrzeni \(V\) wtedy i tylko wtedy, gdy \(U\subset W\) lub \(W\subset U\).

Zamiast sumy mnogościowej podprzestrzeni rozważa się sumę algebraiczną podprzestrzeni.

Mianowicie, niech \(U\), \(W\) będą podprzestrzeniami wektorowymi przestrzeni \(V\). Definiujemy zbiór


\(U+W= \{u+w|\, u\in U, w\in W\}.\)


Łatwo sprawdzić, że zbiór ten spełnia warunki podprzestrzeni wektorowej. Sumę tę można uogólnić na skończoną liczbę składników. Jeśli \(W_1,...,W_k\) są podprzestrzeniami wektorowymi przestrzeni \(V\), to


\(W_1+...+W_k=\{w_1+...+w_k|\ w_1\in W_1,...,w_k\in W_k\}.\)


Zbiór ten jest podprzestrzenią wektorową przestrzeni \(V\).

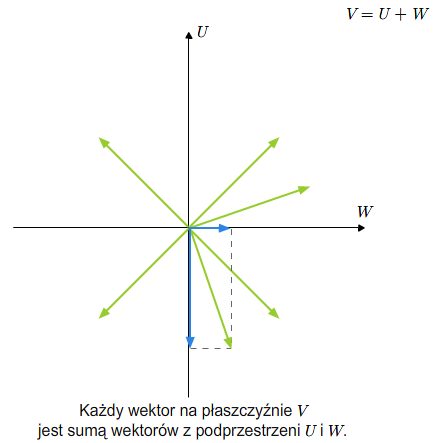
Suma algebraiczna podprzestrzeni wektorowych

Bardzo ważnym pojęciem dotyczącym sumy algebraicznej podprzestrzeni jest pojęcie sumy prostej podprzestrzeni.

Definicja 2.5 [Suma prosta]

Mówimy, że \(V\) jest sumą prostą swoich podprzestrzeni \(U\) i \(W\), jeśli \(V=U +W\) oraz \(U\cap W=\{0\}\). Piszemy \(V=U\oplus W\).

Jednym z podstawowych powodów, dla których sumy proste są ważne, jest następujące twierdzenie

Twierdzenie 2.6

Jeżeli \(V=U\oplus W\), to każdy wektor \(v\in V\) można jednoznacznie przedstawić jako sumę wektorów przestrzeni \(U\) i \(W\).


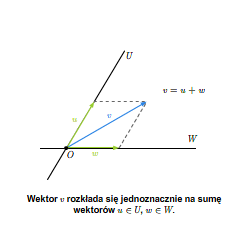
Suma prosta podprzestrzeni wektorowych

Dowód

Do pokazania jest jednoznaczność. Niech \(v=u+w\), gdzie \(u\in U\) i \(w\in W\) oraz \(v=u'+w'\), gdzie \(u'\in U\) i \(w'\in W\). Wtedy \(u'-u=w-w'\). Po lewej stronie równości mamy wektor z przestrzeni \(U\), po prawej - z przestrzeni \(W\). A zatem oba należą do \(U \cap W\), czyli muszą być równe zeru.

Mając sumę prostą \(V=U\oplus W\) możemy zdefiniować rzutowania. Mianowicie, niech \(v\in V\). Wtedy \(v\) rozkłada się jednoznacznie na sumę \(v=u+w\), gdzie \(u\in U\) i \(v\in V\). Odwzorowanie \(P_U: V\longrightarrow V\), które wektorowi \(v\) przyporządkowuje \(u\) z powyższego rozkładu, nazywamy rzutowaniem na podprzestrzeń \(U\) w kierunku podprzestrzeni \(W\) (lub rzutowaniem na \(U\) równoległym do \(W\)). Podobnie definiuje się rzutowanie \(P_W\) na \(W\) w kierunku \(U\).

Jeżeli \(V=U\oplus W\), to \(W\) nazywamy dopełnieniem algebraicznym do \(U\). Oczywiście \(U\) jest wtedy dopełnieniem algebraicznym do \(W\).