Macierze
Definicja macierzy, podstawowe pojęcia
Niech ustalone będzie ciało \(\mathbb K\) i dwie liczby naturalne \(m\), \(n\).
Macierzą o wyrazach z ciała \(\mathbb K\) i wymiarach \(m\) na \(n\) nazywamy każdą funkcję
Macierz taką zapisujemy w postaci tabelki
\(A= \left [\begin{array} {crclc} \ a_{11} &\cdot&\cdot &\cdot & a_{1n}\\ \ \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot \ \ \ & \cdot \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot\ \ \ & \cdot \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot \ \ \ & \cdot \\ \ \\ \ a_{m1}&\cdot&\cdot &\cdot & a_{mn} \end{array} \right ]\) (1.1)
Macierz zapisujemy również na wiele innych sposobów, w zależności od tego jaką jej cechę chcemy wziąć pod uwagę lub podkreślić. I tak, możemy zapisać macierz jako \(A_{m\times n}\) (określono wymiary macierzy), \([a_{ij}]\) (oznaczono wyrazy macierzy), \(A=A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array}}\), (nazwano wyrazy, określono wymiary) lub po prostu \(A\) (dokładniejsze informacje są niepotrzebne lub wynikają z kontekstu).
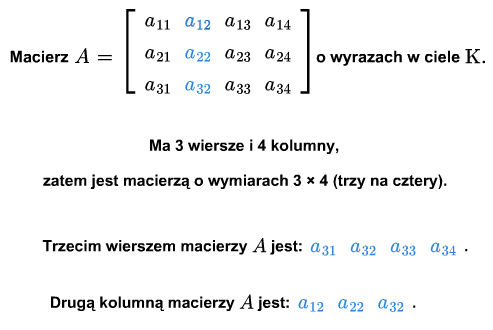
Ciąg \(a_{i1},..., a_{in}\), \(i=1,...,m\) nazywamy \(i\)-tym wierszem macierzy (1.1). Ciąg \(a_{1j},...,a{mj}\), \(j=1,...,n\), nazywamy \(j\)-tą kolumną macierzy (1.1).
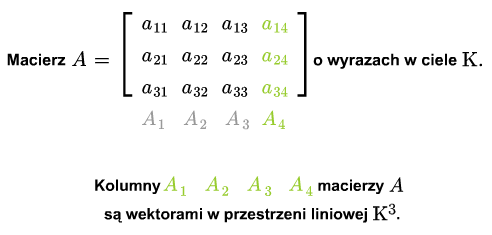
Niech \(A_1,...,A_n\) będą kolumnami macierzy \(A\). Jest to ciąg wektorów z \(\mathbb K ^m\). Rząd układu kolumn \(A_1,...,A_m\) nazywamy rzędem macierzy i oznaczamy \( rk A\).

Mamy następujący lemat przydatny w rachunku macierzy
Lemat 1.1
Niech dany będzie układ wektorów \(w_1,...,w_k\), \(k>1\), przestrzeni wektorowej \(V\). Wtedy \( rk \{w_1,...,w_k\}= rk \{ u_1, w_2,...,w_k\}\), gdzie \(u_1 =w_1 +\lambda _2w_2+...+\lambda_kw_k\) i \(\lambda _2,...,\lambda _k\) są dowolnymi skalarami.
Dowód
Pokażemy, że \( lin \{w_1,...,w_k\}= lin \{u_1,w_2,...,w_k \}\). Oczywiście prawa strona zawiera się w lewej. Ponieważ \(w_1=u_1-\lambda _2w_2-...-\lambda _k w_k\), więc lewa strona zawiera się w prawej.
Mówimy krótko, że rząd układu wektorów nie zmieni się, jeśli do któregoś z jego wektorów dodamy kombinacją liniową wektorów pozostałych.
A zatem rząd układu kolumn nie zmieni się, jeśli do którejś kolumny dodamy kombinację liniową pozostałych kolumn.
Oczywiście, jeśli spermutujemy kolumny, to, choć macierz najczęściej istotnie się zmieni, jej rząd się nie zmieni.
Jeśli którąkolwiek z kolumn macierzy \(A\) pomnożymy przez niezerowy skalar, to rząd macierzy nie zmieni się.
Wszystkie wymienione wyżej operacje na macierzy, tj. dodanie do danej kolumny kombinacji liniowej pozostałych kolumn, pomnożenie kolumny przez niezerowy skalar, permutowanie kolumn, nazywamy operacjami dopuszczalnymi (ze względu na rząd macierzy).
Macierz \(A_{m\times n}\) nazywamy kwadratową, jeśli \(m=n\).
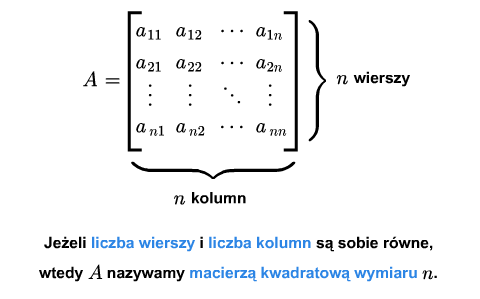
W przeciwnym wypadku mówimy, że macierz jest prostokątna (dla podkreślenia, że nie jest kwadratowa). Dla macierzy kwadratowej podaje się jeden wymiar.
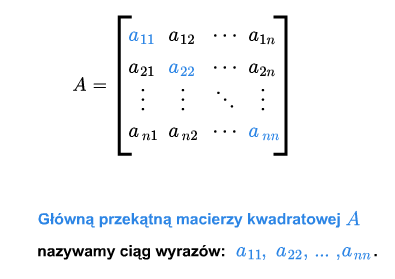
Dla macierzy kwadratowej \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le n\\ 1\le j\le n \end{array} }\) definiujemy główną przekątną jako ciąg \(a_{11},..., a_{nn}\).
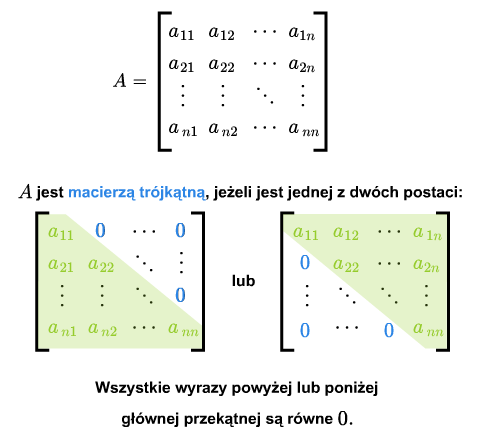
W macierzy kwadratowej można wyróżnić wyrazy leżące ponad przekątną i wyrazy leżące poniżej przekątnej. Macierz kwadratowa nazywa się macierzą trójkątną, jeśli wszystkie jej wyrazy leżące ponad główną przekątną lub wszystkie wyrazy leżące poniżej głównej przekątnej są zerami.
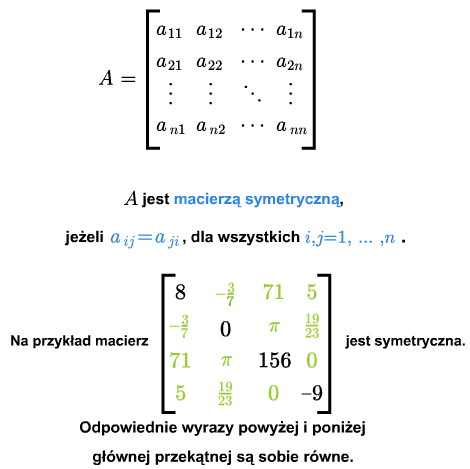
Macierz kwadratową \(A={[a_{ij}]}_{1\le i,j\le n}\) nazywa się symetryczną, jeśli \(a_{ij} =a_{ji}\) dla każdych \(i,j=1,...,n\).
Macierz \(A\) nazywa się antysymetryczną (lub skośnie symetryczną), jeśli \(a_{ij}=-a_{ji}\) dla każdych \(i,j=1,...,n\). W macierzy skośnie symetrycznej wszystkie wyrazy leżące na głównej przekątnej są równe zeru.
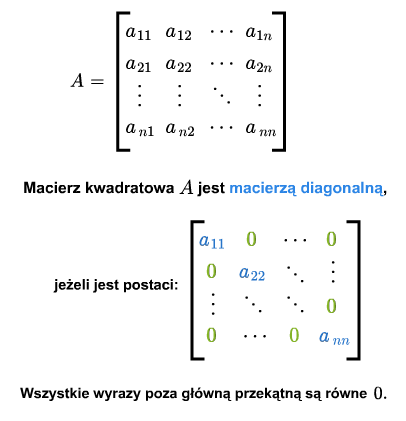
Macierz kwadratowa nazywa się diagonalną, jeśli wszystkie jej wyrazy poza główną przekątną są zerami.
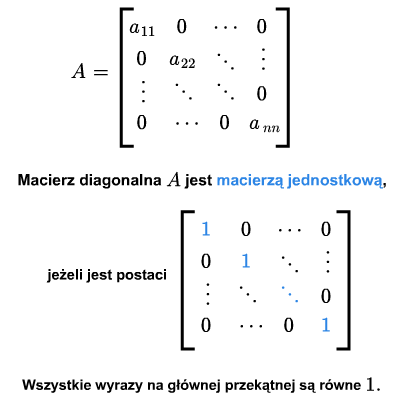
Macierz kwadratowa nazywa się jednostkową, jeśli jest diagonalna a na jej głównej przekątnej są same jedynki. Macierz tę oznaczać będziemy przez \(I\) lub \(I_{n\times n}\).
Oznaczyliśmy już(w Wykładzie 3.) przez \(I\) odwzorowanie identycznościowe danej przestrzeni wektorowej. Okaże się wnet, że nie ma tu wielkiej kolizji oznaczeń.
Operacje na macierzach
Zbiór wszystkich macierzy o wymiarach \(m\) na \(n\) i wyrazach z \(\mathbb K\) oznaczmy przez \(M(m,n;\mathbb K)\). Zbiór ten jest podprzestrzenią przestrzeni \(\mathbb K ^X\), gdzie \(X=\{1,..., m\}\times \{1,...,n\}\) (porównaj Przykład 7. Wykładu 2.)
W szczególności, działania w \(M(m,n;\mathbb K)\) są określone następująco. Niech
Sumą macierzy \(A\) i \(B\) jest macierz następująca
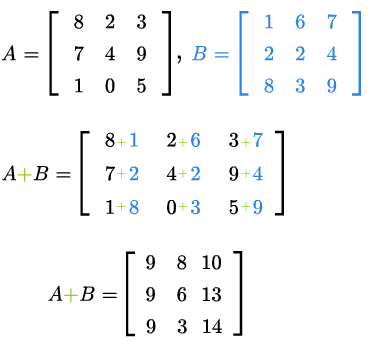
Jeśli \(\lambda\in\mathbb K\), to macierz \(\lambda A\) jest
zdefiniowana tak

Z Przykładu 7. Wykładu 2. wiemy, że dodawanie w \(M(m,n;\mathbb K)\) jest łączne, przemienne, ma element neutralny (który jest macierzą składająca się z samych zer) i każda macierz ma macierz przeciwną. Macierzą przeciwną do macierzy (1.1) jest macierz
Ustalimy teraz jaki jest wymiar przestrzeni \(M(m,n;\mathbb K)\). Rozważmy odwzorowanie
Z grubsza mówiąc, odwzorowanie to polega na przepisaniu kolejnych wierszy jeden po drugim w jednym ciągu. Oczywiście odwzorowanie to jest bijekcją.
Ponadto, łatwo widać, że odwzorowanie to jest liniowe. Zatem odwzorowanie to jest izomorfizmem. Mamy więc
Wniosek 2.1
Zachodzi równość \(\dim M(m,n;\mathbb K)=mn\).
Załóżmy teraz, że mamy dwie macierze: \(A=A_{m\times k}\) i \(B=B_{k\times n}\). Możemy zdefiniować iloczyn tych macierzy \(A B\) według następującego przepisu. Jeżeli \(\displaystyle A= [a_{il}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le l\le k \end{array} }\) i \(\displaystyle B=[b_{lj}]_ {\tiny\begin{array} {l} 1\le l\le k\\ 1\le j\le n \end{array} }\), to \(AB\) jest macierzą \(C=[c_{ij}]\) o wymiarach \(m\) na \(n\), której wyrazy określone są formułą
dla wszystkich wskaźników \(i,j\), gdzie \(i=1,...,m\) oraz \(j=1,..., n\).
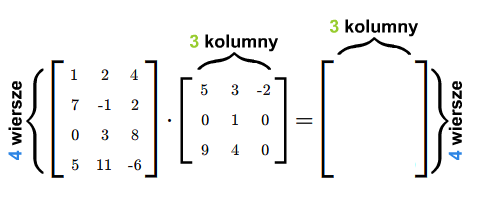
Podkreślmy mocno, że możemy wykonać mnożenie \(AB\) tylko takich macierzy \(A\), \(B\), dla których liczba kolumn macierzy \(A\) jest równa liczbie wierszy macierzy \(B\). W rezultacie mnożenia otrzymujemy macierz, która ma tyle wierszy co macierz \(A\) i tyle kolumn co macierz \(B\).
Mnożąc macierze najpierw sprawdzamy, czy możemy je pomnożyć, następnie ustalamy wymiary iloczynu macierzy. Potem wyliczamy wyrazy iloczynu (w dowolnej kolejności), być może tylko te, które chcemy znać.
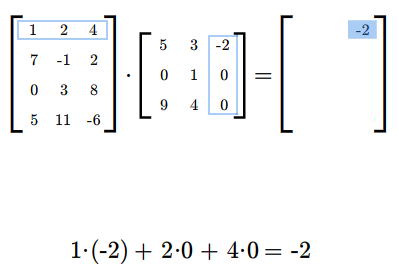
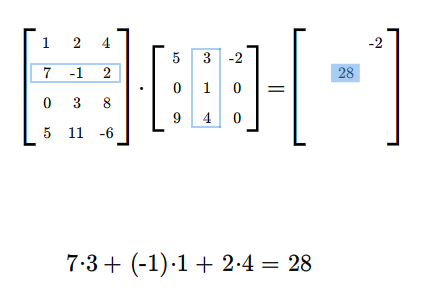
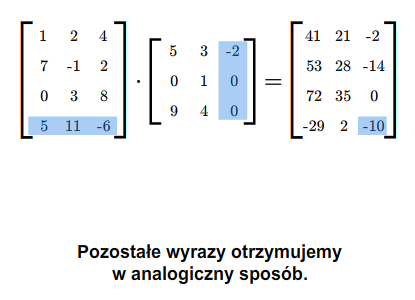
Mnożenie macierzy jest łączne, tzn. jeśli \(A,B,C\) są takie, że można wykonać mnożenia \(AB\) i \(C(AB)\), to można też wykonać mnożenia \(CA\) i \((CA)B\) oraz \(C(AB)=(CA)B\). Można tę własność bezpośrednio przerachować. W następnym wykładzie pokażemy, że łączność ta jest konsekwencją łączności składania odwzorowań.
Zachodzi też następująca własność rozdzielności mnożenia macierzy względem dodawania macierzy. Jeśli \(A, B\in M(k,n;\mathbb K)\) i \(C\in M(m,k;\mathbb K)\), to \(C(A+B)=CA+CB\). Podobnie można sformułować prawo rozdzielności \((A+B)C\). Objaśnimy tę własność w następnym wykładzie. Można też te własności bezpośrednio sprawdzić.
Nietrudno sprawdzić, że jeśli \(A=A_{m\times n}\) oraz \(I=I_ n\times n}\), to \(AI=A\). Podobnie, jeśli \(A=A_{m\times n}\) oraz \(I=I_{m\times m}\), to \(IA=A\).
Przez \(n\)-tą potęgę \(A^n\) macierzy kwadratowej \(A\) rozumiemy iloczyn \(n\) egzemplarzy macierzy \(A\).
Przykład 2.2
Dowolna potęga macierzy diagonalnej jest macierzą diagonalną. Jeśli
to
Przykład 2.3
Niech
Indukcyjnie można udowodnić, że
gdzie
Przykład 2.4
Jeśli
to stosując indukcję można stwierdzić, że
gdzie \(\{a_m\}\) jest ciągiem Fibonacciego, czyli ciągiem zdefiniowanym wzorem rekurencyjnym
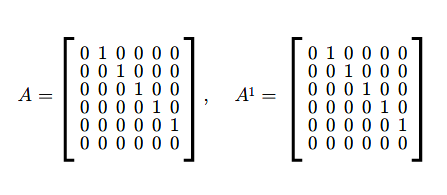
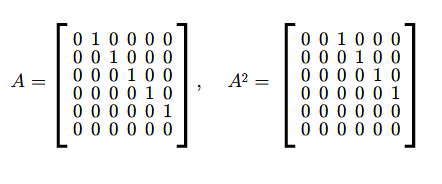
Przykład 2.5
Niech \(A\in M(n,n;\mathbb K)\)
\(A=\left [\begin{array} {lcccccr} \ 0 &1& & & & 0\\ \ 0& 0& 1& & & 0\\ \ .&. & .& .& .& .\\ \ 0 & & & 0 & 1 & 0\\ \ 0 & & & & 0 & 1\\ \ 0 & & & & &0 \end{array} \right ]\) (2.2)
Łatwo sprawdzić, że \(A^{n}=0\).
Jeżeli dany jest wielomian \(W(t)=a_0 +a_1t+....+a_r t^r\) jednej zmiennej \(t\) o współczynnikach z ciała \(\mathbb K\) i \(A\) jest macierzą kwadratową, to przez \(W(A)\) rozumiemy macierz
gdzie \(I\) jest macierzą jednostkową takiego samego wymiaru co macierz \(A\). Każdy wielomian \(W(t)\), dla którego \(W(A)=0\), nazywa się anihilatorem macierzy \(A\).
Ogólna grupa liniowa
Rozważmy teraz przestrzeń macierzy kwadratowych \(M(n,n;\mathbb K)\). Każde dwie macierze \(A,B\in M(n,n;\mathbb K)\) można pomnożyć w obydwu kolejnościach, tzn. można znaleźć zarówno iloczyn \(AB\) jak i \(BA\). Na ogół macierze \(AB\) i \(BA\) są różne. Na przykład weźmy następujące macierze (istniejące dla każdego ciała \(\mathbb K\))
Mamy
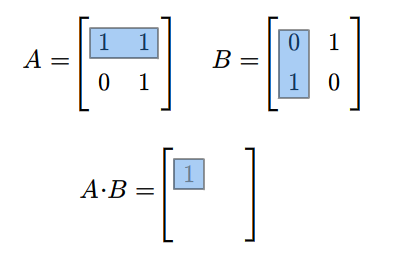
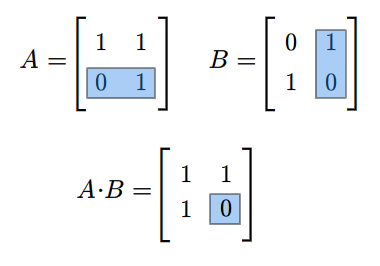
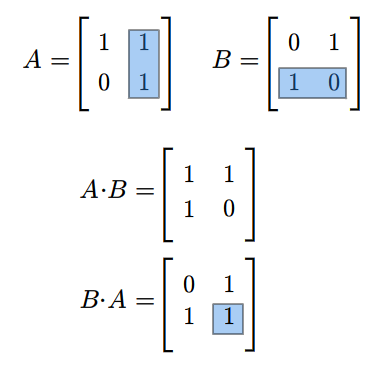
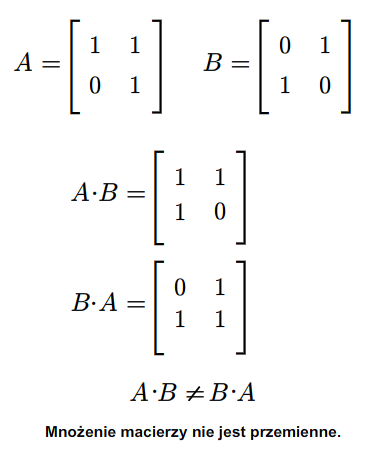
Macierz kwadratową \(A\in M(n,n:\mathbb K)\) nazywamy odwracalną, jeśli istnieje macierz \(B\in M(n,n;\mathbb K)\) taka, że
\(AB=BA=I.\) (3.3)
Macierz \(B\) spełniająca (3.3) jest jedyna.
Przypuśćmy, że \(AB'=B'A=I\). Pomnóżmy równość \(AB=I\) obustronnie z lewej strony przez \(B'\). Mamy następujące równości \(B'(AB)=B'\). Korzystając z łączności mnożenia macierzy otrzymujemy
\(B'=(B'A)B=IB=B\). A zatem \(B=B'\). Mogliśmy również skorzystać z pierwszego wykładu, z fragmentu poprzedzającego definicję grupy.
Macierz \(B\) spełniającą warunek (3.3) nazywamy macierzą odwrotną do \(A\). Oznaczamy tę macierz przez \(A^{-1}\).
Zbiór macierzy \(A\in M(n,n;\mathbb K)\) odwracalnych stanowi grupę. Grupa ta, poza przypadkiem \(n=1\), jest nieprzemienna. Grupę tę oznaczamy \(GL(n;\mathbb K)\) i nazywamy ogólną grupą liniową nad ciałem \(\mathbb K\).
Niech będzie daną macierzą. Macierzą dualną (lub transponowaną) do macierzy \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} }\) nazywamy macierz \(A^*= [a_{ji}]_ {\tiny\begin{array} {l} 1\le j\le n\\ 1\le i\le m \end{array} }\). A zatem macierz \(A^*\) powstaje z macierzy \(A\) przez zamianę wierszy na kolumny.
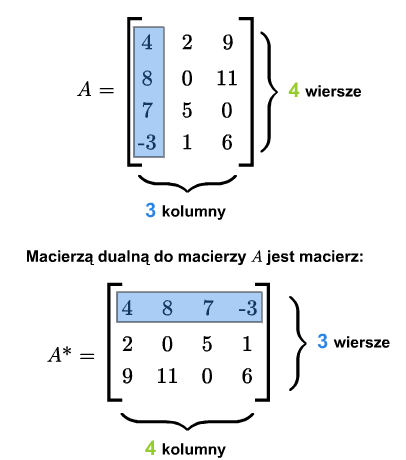
Macierz dualna do macierzy \(A^*\) jest macierzą \(A\), czyli \((A^*)^*=A\). Macierz kwadratowa \(A\) jest symetryczna wtedy i tylko wtedy, gdy \(A^*=A\). Macierz kwadratowa \(A\) jest skośnie symetryczna wtedy i tylko wtedy, gdy \(A^*=-A\).