Macierze a odwzorowania liniowe

W niniejszym wykładzie wszystkie rozważane przestrzenie są skończenie wymiarowe a bazy są uporządkowane.


Macierz odwzorowania liniowego


Niech dane będą przestrzenie wektorowe \(V\) i \(W\) nad ciałem \(\mathbb K\) oraz odwzorowanie liniowe \(f:V\longrightarrow W\).

Niech \(e_1,...,e_n\) będzie bazą przestrzeni wektorowej \(V\), zaś \(e'_1,...,e'_m\) bazą przestrzeni \(W\). Dla odwzorowania liniowego \(f\) mamy


\(\begin{array} {rcl} &&f(e_1) =a_{11}e'_1+... +a_{m1}e'_m,\\ &&\ \ \ .\\ &&\ \ \ .\\ &&\ \ \ .\\ &&f(e_n)= a_{1n}e'_1+...+a_{mn}e'_m. \end{array}\)      (1.1)


dla pewnych skalarów \(a_{ij}\), \(i=1,...,m\), \(j=1,...,n\). Inaczej zapisując


\(\displaystyle f(e_j)=\sum _{i=1}^ma_{ij}e'_i\)


dla każdego \(j=1,...,n\).

Macierz odwzorowania liniowego

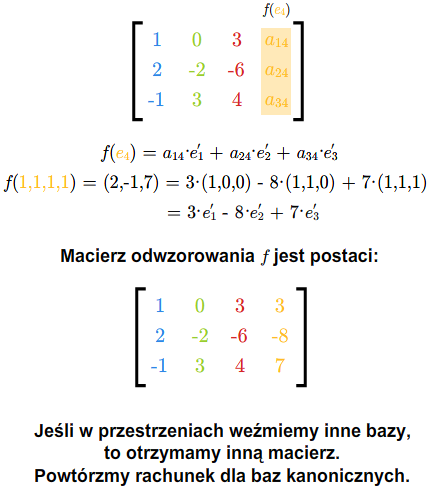
Otrzymaliśmy więc macierz \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} }\), która całkowicie opisuje odwzorowanie liniowe \(f\). Istotnie, jeśli znamy wartości odwzorowania liniowego na bazie, to znamy to odwzorowanie. Macierz tę nazywamy macierzą odwzorowania \(f\) przy bazach \(e_1,...,e_n\) i \(e'_1,...,e'_m\).

Jeśli mamy daną macierz \(A\), ustalone bazy w przestrzeniach \(V\), \(W\), to macierz ta jest macierzą odwzorowania liniowego \(f:V\longrightarrow W\). Odwzorowanie to jest dane formułą (1.1).

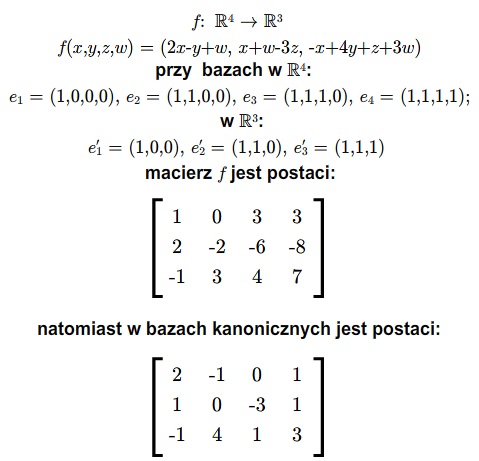
Wygodnie jest myśleć o macierzach jako o odwzorowaniach liniowych. Jeśli żadne szczególne przestrzenie nie są wyróżnione, to macierz \(A=A_{m\times n}\) możemy traktować jako odwzorowanie liniowe \(f:\mathbb K ^n\longrightarrow \mathbb K^m\) dane przepisem (1.1), gdzie \(e_1,...,e_n\) jest bazą kanoniczną przestrzeni \(\mathbb K ^n\), zaś \(e'_1,...,e'_m\) jest bazą kanoniczną przestrzeni \(\mathbb K ^m\).

Jeśli \(A\) jest macierzą odwzorowania \(f:V\longrightarrow W\) i przez \(A_1,..., A_n\) oznaczymy kolumny macierzy \(A\), to każda kolumna \(A_j\) jest ciągiem współrzędnych wektora \(f(e_j)\) w bazie \(e'_1,..., e'_m\). Oznacza to, że układ kolumn macierzy \(A\) można uważać za wektory (wyrażone we współrzędnych w bazie \(e_1,...,e_n\)) \(f(e_1),...,f(e_n)\). Rząd odwzorowania \(f\) jest więc rzędem układu wektorów \(A_1,..., A_n\) macierzy \(A\).

Mamy więc


Twierdzenie 1.1

Jeśli \(A\) jest macierzą odwzorowania \(f:V\longrightarrow W\) przy pewnych bazach przestrzeni \(V\) i \(W\), to \( rk A= rk f\).

Niech \(f,h :V\longrightarrow W\) będą dwoma odwzorowaniami liniowymi. Wiemy, że suma tych odwzorowań jest odwzorowaniem liniowym. Przy danych bazach \(e_1,...,e_n\), \(e'_1,...,e'_m\) przestrzeni \(V\) i \(W\) odpowiednio, macierz odwzorowania \(f+h\) jest sumą macierzy \(A_f+A_h\), gdzie \(A_f\) jest macierzą odwzorowania \(f\) a \(A_h\) macierzą odwzorowania \(h\). A zatem dodawanie macierzy odpowiada dodawaniu odwzorowań liniowych. Podobnie mnożeniu macierzy przez skalar odpowiada mnożenie odwzorowania liniowego przez skalar.

Załóżmy teraz, że mamy trzy przestrzenie wektorowe \(V\), \(W\), \(U\). Załóżmy ponadto, że \(e_1,...,e_n\) jest bazą \(V\), \(e'_1,...,e'_k\) jest bazą \(W\) i \(e''_1,...,e''_m\) jest bazą \(U\). Niech \(f:V\longrightarrow W\) i \(h:W\longrightarrow U\) będą odwzorowaniami liniowymi. Oznaczmy przez


\(A= [a_{lj}]_ {\tiny\begin{array} {l} 1\le l\le k\\ 1\le j\le n \end{array} },\ \ \ B= [b_{il}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le l\le k \end{array} }, \ \ \ \ C= [c_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} },\)


macierze odwzorowania \(f\), \(h\) i \(h\circ f\) odpowiednio, przy danych bazach. Zachodzą następujące równości


\(\displaystyle f(e_j)=\sum _{l=1}^k a_{lj}e'_l,\ \ \ \ h(e'_l)=\sum _{i=1}^m b_{il}e''_i,\ \ \ \ \ (h\circ f)(e_j)= \sum _{i=1}^m c_{ij}e''_i.\)


Z drugiej strony


\(\begin{aligned}(h \circ f)(e_j)= h(f(e_j))&=h(\sum _{l=1}^k a_{lj}e'_l)=\sum _{l=1}^k a_{lj}h(e'_l) \\ &=\sum _{l=1}^k a_{lj}\left(\sum _{i=1}^m b_{il}e''_i\right)\\ &=\sum _{i=1}^m \left(\sum _{l=1}^kb_{il}a_{lj}\right )e''_i . \end{aligned}\)


Zatem


\(\displaystyle c_{ij}=\sum _{l=1}^kb_{il}a_{lj}.\)


Oznacza to, że


\(C=BA.\)


Krótko mówiąc, mnożenie macierzy odpowiada składaniu odwzorowań liniowych. Ponieważ składanie odwzorowań jest łączne, więc mnożenie macierzy jest łączne. Wspomnieliśmy już tę własność w poprzednim wykładzie. Teraz uzasadniliśmy jej prawdziwość.

Zauważmy także, że jeśli \(h_1, h_2: W\longrightarrow U\), to \((h_1+h_2)\circ f= h_1\circ f +h_2\circ f\). Jeśli \(f_1, f_2:V\longrightarrow W\), to \(h\circ (f_1+f_2)=h\circ f_1 +h\circ f_2\). W języku macierzy oznacza to, że \((B_1 +B_2)A=B_1A+B_2A\) oraz \(B(A_1+A_2)=BA_1+BA_2\) (jeśli występujące tu dodawania i mnożenia macierzy można wykonać). Te własności rachunku macierzy również wymieniliśmy w poprzednim wykładzie.


Macierz dualna i odwzorowanie dualne

Niech \(e^*_1,..., e^*_n\) będzie bazą dualną do bazy \(e_1,...,e_n\) przestrzeni \(V\) i \(e'^*_1,...,e'^*_m\) bazą dualną do bazy \(e'_1,...,e'_m\) przestrzeni \(W\). Rozważmy odwzorowanie dualne \(f^*:W^* \longrightarrow V^*\). Chcemy znaleźć macierz \(f^*\) przy wyróżnionych właśnie bazach dualnych. Oznaczmy poszukiwaną macierz przez \(B=[b_{ji}]_ {\tiny\begin{array} {l} 1\le j\le n\\ 1\le i\le m \end{array} }\), czyli


\(\displaystyle f^*(e'^*_i)=\sum _{j=1}^n b_{ji}e^*_j.\)


Po obydwu stronach powyższej równości mamy wektory z \(V^*\), czyli odwzorowania liniowe określone na \(V\) i o wartościach w \(\mathbb K\). Obliczymy wartość tych odwzorowań na wektorach bazy \(e_1,..., e_n\). Otrzymujemy


\(\begin{aligned}\left( f^*(e'^*_i)\right)(e_s)&=\left((e'^*_i)\circ f\right)(e_s) =e'^*_i\left(\sum _{l=1}^m a_{ls}e'_l\right) \\ &=\sum _{l=1}^m a_{ls}\left(e'^*_i(e'_l) \right)\\ &=\sum _{l=1}^m a_{ls}\delta _{il} =a_{is}. \end{aligned}\)


Z drugiej strony


\(\displaystyle \left( \sum _{j=1}^n b_{ji}e^*_j\right)(e_s)= \sum _{j=1}^n b_{ji}(e^*_j(e_s))= \sum _{j=1}^n b_{ji}\delta _{js}=b_{si} .\)


A zatem \(a_{is}=b_{si}\), co oznacza, że macierz \(B\) jest macierzą dualna do macierzy \(A\).

Macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego, jeśli w przestrzeniach dualnych wybierzemy bazy dualne.

Stąd, że dla odwzorowań liniowych zachodzi formuła \((f \circ h)^* = h^* \circ f^*\), otrzymujemy analogiczną formułą dla macierzy.


Twierdzenie 2.1

Jeśli iloczyn \(AB\) jest wykonalny, to wykonalny jest iloczyn \(B^* A^*\) oraz


\((AB)^* = B^* A^*.\)


Udowodnimy teraz następujące twierdzenie


Twierdzenie 2.2

Rząd odwzorowania dualnego do \(f\) jest równy rzędowi odwzorowania \(f\).


Dowód

Wiemy, że

\( rk f^*=\dim W^*-\dim ker f^*=\dim W-\dim\ker f^*.\)      (2.2)


Przyjrzyjmy się więc przestrzeni \(\ker f^*\). Mamy


\(\ker f^*=\{\beta \in W^*|\ \beta\circ f=0\}=\{\beta \in W^*|\ \beta _{| im f}=0\}.\)


Weźmy bazę \(w_1,...,w_k\) przestrzeni \( im f\). Jeśli \( im f= W\), to \( rk f=\dim W\) i \(\ker f^*= \{0\}\). Twierdzenie w tym przypadku jest prawdziwe..

Jeśli \( im f\ne W\), to układ \(w_1,...,w_k\) rozszerzmy do bazy


\(w_1,...,w_k, w_{k+1},...,w_m\)


przestrzeni \(W\). Przestrzeń \(U\) rozpięta na wektorach \(w_{k+1},...,w_m\) jest dopełnienieniem algebraicznym do \( im f\) w \(W\), czyli \(W=U\oplus im f\). Zauważmy, że odwzorowanie


\(\phi : \ker f^*\ni \beta\longrightarrow \beta _{|U}\in U^*\)


jest izomorfizmem. Oczywiście odwzorowanie \(\phi\) jest liniowe. Jeśli \(\phi(\beta)=0\), to \(\beta_{|U}\) i \(\beta _{| im f}\) są odwzorowaniami zerowymi. A zatem, \(\beta\) jest odwzorowaniem zerowym na całym \(W\). Odwzorowanie \(\phi\) jest więc monomorfizmem.

Jest też epimorfizmem. Jeśli bowiem \(\gamma :U\longrightarrow \mathbb K\) jest liniowe, to odwzorowanie liniowe \(\beta: W\longrightarrow \mathbb K\) zdefiniowane na bazie przestrzeni \(W\) następująco: \(\beta (w_i)=0\) dla \(i=1,...,k\),\(\beta (w_i)=\gamma (w _i)\) dla \(i=k+1,..., m\), jest takie, że \(\phi (\beta)=\gamma\).

Ponieważ \(\phi\) jest izomorfizmem, więc \(\dim\ker f^* = \dim U ^* =\dim U =m-k =\dim W- rk f\). Porównując tę równość z równością z pierwszego zdania tego dowodu otrzymujemy żądaną tezę.

Z powyższego twierdzenia i stąd, że macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego wynika następujący wniosek


Wniosek 2.3

Dla dowolnej macierzy \(A\) zachodzi równość \( rk A= rk A^*\).

Przypomnijmy sobie teraz operacje dopuszczalne na macierzy (ze względu na rząd macierzy). Korzystając z równości \({rk} A={rk} A^*\) dostajemy natychmiast kilka kolejnych operacji dopuszczalnych, tzn. nie zmieniających rzędu macierzy. Mianowicie, dodając do danego wiersza macierzy \(A\) kombinację liniową pozostałych wierszy tej macierzy, nie zmieniamy jej rzędu. Mnożąc dowolny wiersz przez niezerowy skalar nie zmieniamy rzędu macierzy. I wreszczcie, permutując wiersze macierzy nie zmieniamy jej rzędu.

Tak jak w dowodzie twierdzenia o istnieniu bazy z Wykładu 2. możemy stwierdzić, że rząd skończonego układu wektorów jest równy maksymalnej liczbie wektorów liniowo niezależnych, które można wybrać z danego układu wektorów.

A zatem mamy następujące twierdzenie


Twierdzenie 2.4 [Rząd macierzy]

Niech \(A\in M(m,n;\mathbb K)\).

  1. Rząd macierzy A jest równy maksymalnej liczbie kolumn liniowo niezależnych, które można wybrać z macierzy \(A\).
  2. Rząd macierzy A jest równy maksymalnej liczbie wierszy liniowo niezależnych, które można wybrać z macierzy \(A\).

Macierz odwrotna, ogólna grupa liniowa

Załóżmy teraz, że \(V=W\) i \(f:V\longrightarrow V\) jest endomorfizmem. Wybieramy jedną bazę, tzn. bazę \(e_1,...,e_n\) przestrzeni \(V\), i definiujemy macierz kwadratową \(A=[a_{ij}]_ {\small 1\le i,j\le n}\) formułą


\(\begin{array} {rcl} &&f(e_1) =a_{11}e_1+... +a_{n1}e_n,\\ &&\ \ \ .\\ &&\ \ \ .\\ &&\ \ \ .\\ &&f(e_n)= a_{1n}e_1+...+a_{nn}e_n. \end{array}\)      (3.3)


Ponieważ mnożenie macierzy odpowiada składaniu odwzorowań, więc odwracalność macierzy \(A\) jest równoważna izomorficzności odwzorowania \(f\). Ponadto macierz odwrotna \(A^{-1}\) do macierzy \(A\) jest macierzą odwzorowania odwrotnego \(f^{-1}\).

Ogólną grupę liniową \(GL(n;\mathbb K)\) możemy traktować jako grupę wszystkich izomorfizmów liniowych \(f:\mathbb K^n\longrightarrow\mathbb K^n\), z działaniem będącym składaniem odwzorowań. Pamiętamy, że grupa ta dla \(n>1\) jest nieprzemienna. Zauważyliśmy już, że macierz kwadratowa \(A\) jest odwracalna wtedy i tylko wtedy, gdy jest macierzą izomorfizmu. Odwzorowanie liniowe \(f:\mathbb K ^n\longrightarrow \mathbb K^n\) jest izomorfizmem wtedy i tylko wtedy, gdy \( rk f=n\). Oznacza to, że prawdziwe jest następujące twierdzenie


Twierdzenie 3.1

Macierz kwadratowa \(A=A_{n\times n}\) jest odwracalna wtedy i tylko wtedy, gdy \( rk A=n\).


Macierz przejścia

Niech \(e_1,...,e_n\) będzie bazą przestrzeni \(V\) i niech \(e'_1,..., e'_n\) będzie inną bazą tej samej przestrzeni. Istnieją jednoznacznie określone skalary \(p_{ij}\), \(1\le i,j\le n\), takie, że


\(\displaystyle e'_j=\sum _{i=1}^n p_{ij}e_i,\)      (4.4)


dla \(j=1,...n\). Macierz \(P=[p_{ij}]_{1\le i, j\le }\) nazywa się macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\). Macierz przejścia jest macierzą izomorfizmu przestrzeni \(V\), który przekształca bazę \(e_1,...,e_n\) na bazę \(e'_1,...,e'_n\) i macierz ta jest utworzona przy bazie \(e_1,...,e_n\). W szczególności, macierz przejścia jest macierzą odwracalną.

Zamieńmy rolami dane bazy. Istnieją jednoznacznie wyznaczone skalary \(q_{ij}\), \(1\le i,j\le n\), takie, że


\(\displaystyle e_i=\sum _{j=1}^n q_{ji}e'_j.\)


Macierz \([q_{ij}]\) oznaczmy przez \(Q\).

Otrzymujemy więc następujące równości


\(\displaystyle e_i=\sum _{j=1}^n q_{ji}e'_j=\sum _{j=1} ^n q_{ji}\sum _{l=1}^n p_{lj}e_l=\sum _{l=1}^n \left ( \sum _{j=1}^n p_{lj}q_{ji}\right )e_l\)


dla każdego \(i=1,...,n\). Oznacza to, że \(\displaystyle \sum _{j=1}^n p_{lj}q_{ji}=\delta _{li}\) i, w konsekwencji, macierze \(P\) i \(Q\) są wzajemnie odwrotne.

Niech teraz \(f:V\longrightarrow V\) będzie odwzorowaniem liniowym. Niech \(A\) będzie macierzą tego odwzorowania przy bazie \(e_1,...,e_n\) i \(B\) będzie macierzą tego samego odwzorowania \(f\) przy bazie \(e'_1,...,e'_n\). Chcemy ustalić związek między macierzami \(A\) i \(B\).

Mamy następujące równości


\(\displaystyle f(e'_i)=\sum _{j=1}^n b_{ji}e'_j = \sum _{j=1}^n\sum _{l=1}^n p_{lj}b_{ji}e_l=\sum _{l=1}^n \left (\sum _{j=1}^n p_{lj}b_{ji}\right ) e_l.\)


Z drugiej strony


\(\begin{aligned} f(e'_i ) = f\left (\sum _{j=1} ^n p_{ji}e_j\right )= \sum _{j=1} ^np_{ji} f(e_j)&= \sum _{j=1} ^n p_{ji}\left (\sum _{l=1}^n a_{lj} e_l \right )\\&= \sum _{j=1}^n\sum _{l=1}^n a_{lj} p_{ji}e_l =\sum _{l=1}^n\left (\sum _{j=1}^n a_{lj} p_{ji}\right )e_l. \end{aligned}\)


Otrzymaliśmy równość \(AP=PB\). A zatem udowodniliśmy następujące twierdzenie


Twierdzenie 4.1

Jeżeli \(A\) jest macierzą endomorfizmu \(f\) przy bazie \(e_1,..., e_n\) i \(B\) jest macierzą tego samego endomorfizmu przy bazie \(e'_1,..., e'_n\), to


\(B=P^{-1}AP,\)


gdzie \(P\) jest macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\).