Zastosowania wyznacznika. Układy równań liniowych
Minory i rząd macierzy. Macierz odwrotna
Ponieważ w wykładzie tym intensywnie będziemy korzystać z poprzedniego wykładu, musimy dokonać tych samych wstępnych ustaleń, a mianowicie, zakładamy, że wszystkie rozważane przestrzenie są skończenie wymiarowe nad ciałem \(\mathbb K\) o charakterystyce różnej od \(2\).
Niech dana będzie macierz \(A=[a_{ij}]\in M(m,n;\mathbb K )\). Wiemy, że rząd tej macierzy jest równy rzędowi układu kolumn \(A_1,..., A_n\in \mathbb K ^m\) tej macierzy. Jest też równy rzędowi układu wierszy tej macierzy, bo rząd macierzy \(A\) jest równy rzędowi macierzy dualnej. Wiemy też, że rząd układu wektorów jest równy maksymalnej liczbie wektorów liniowo niezależnych, które można wybrać z tego układu wektorów.
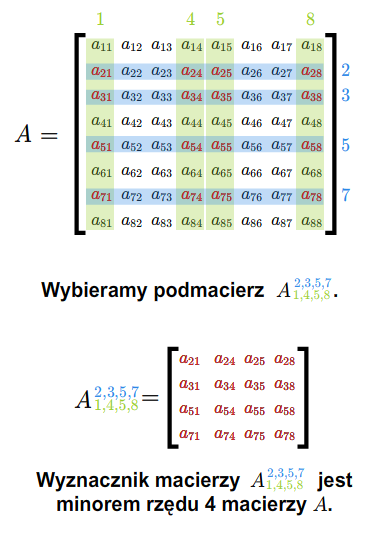
Wprowadzimy teraz pojęcie minora macierzy. Niech \(k\) będzie pewną liczbą naturalną nie większą od \(m\) i \(n\). Ustalmy ciągi wskaźników \(1\le i_1<...<i_k\le m\), \(1\le j_1<...<j_k\le n\). Oznaczmy przez
macierz powstałą przez wybór wyrazów stojących na przecięciu wierszy o numerach \(i_1,...,i_k\) i kolumn o numerach \(j_1,..., j_k\). Otrzymujemy macierz kwadratową o wymiarach \(k\) na \(k\). Wyznacznik tak otrzymanej macierzy nazywamy minorem rzędu \(k\) macierzy \(A\).
Następujący lemat będzie przydatny w dalszych rozumowaniach.
Lemat 1.1
Kolumny \(A_{j_1},..., A_{j_k}\) są liniowo niezależne wtedy i tylko wtedy, gdy istnieją takie wskaźniki \(1\le i_1<...<i_k\le m\), że \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\).
Dowód
Załóżmy najpierw, że kolumny \(A_{j_1},...,A_{j_k}\) są liniowo niezależne. Wtedy macierz \(A_{j_1,...,j_k}=[A_{j_1},...,A_{j_k}]\) składająca się tylko z tych kolumn ma rząd równy \(k\). Ponieważ rząd macierzy danej jest równy rzędowi macierzy dualnej, więc wsród wierszy macierzy \(A_{j_1,...,j _k}\) istnieje \(k\) liniowo niezależnych wektorów. Niech będą to wiersze o numerach \(1\le i_1<...<i_k\le m\). Oznacza to, że w macierzy \(A^{i_1,...,i_k}_{j_1,...,j_k}\) wiersze o numerach \(i_1,...,i_k\) są liniowo niezależne, czyli rząd tej macierzy jest równy \(k\). A zatem \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\).
Załóżmy teraz, że \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\). Wtedy wiersze tej macierzy są liniowo niezależne. A zatem rząd macierzy \([A_1,...,A_k]\) jest równy \(k\) (bo nie może być większy). Oznacza to, że \(k\) kolumn tej macierzy stanowi układ liniowo niezależny.Z powyższego lematu wynika natychmiast następujące twierdzenie.
Twierdzenie 1.2
Dla dowolnej macierzy \(A\) jej rząd jest równy \(k\) wtedy i tylko wtedy, gdy istnieje niezerowy minor rządu \(k\) tej macierzy i każdy minor rzędu większego od \(k\) jest zerowy.
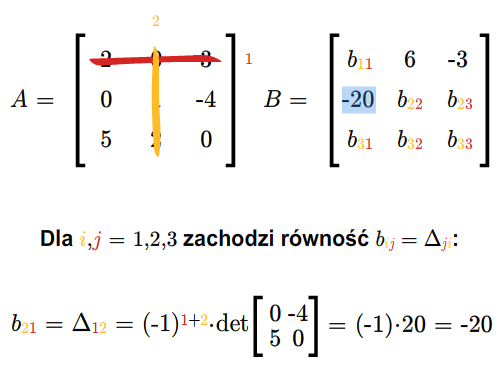
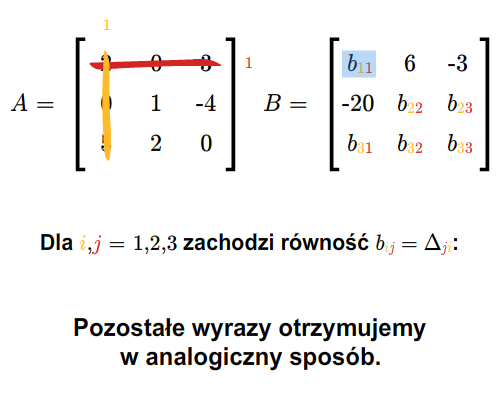
Przed udowodnieniem kolejnego twierdzenia przypomnijmy, że dla macierzy \(A=[a_{ij}]\) wprowadziliśmy wielkości \(\Delta _{ij}=(-1)^{i+j} \det A_{ij}\), gdzie \(A_{ij}\) jest macierzą otrzymaną z macierzy \(A\) przez wykreślenie \(i\)-tego wiersza i \(j\)-tej kolumny.
Twierdzenie 1.3
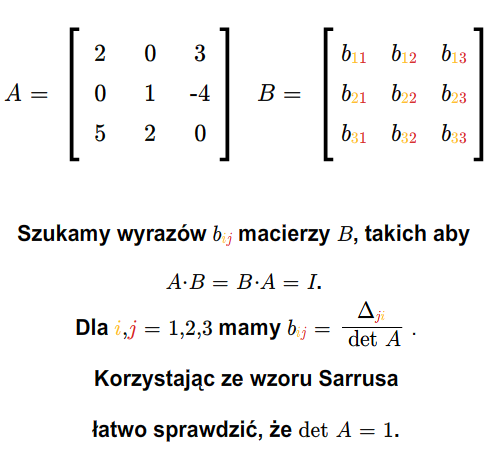
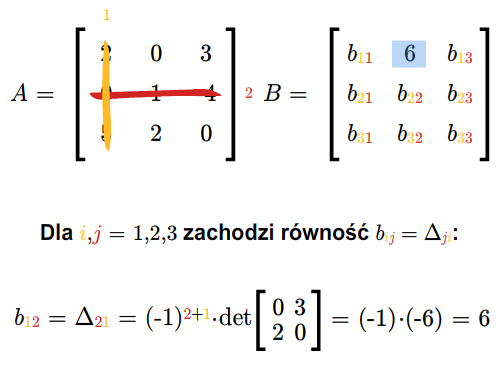
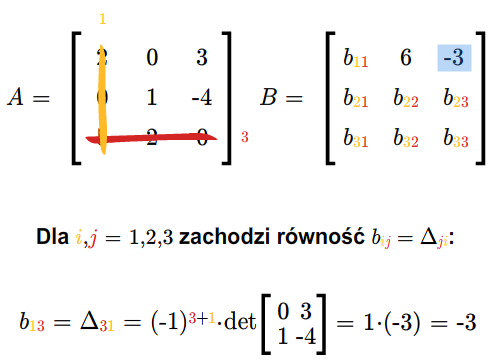
Niech \(A\in M(n,n;\mathbb K)\) będzie macierzą odwracalną i niech \(B=[b_{ij}]\) oznacza jej macierz odwrotną. Wtedy
Dowód
Wystarczy sprawdzić, że \(AB=I\). Niech \(C= AB\) i \(C=[c_{ij}]\). Korzystając z rozwinięcia Laplace'a otrzymujemy
gdzie \(D\) jest macierzą powstałą z macierzy \(A\) przez zastąpienie \(j\)-tego wiersza \(i\)-tym wierszem. Jeśli \(i=j\), to macierz \(A\) jest równa macierzy \(D\). Jeśli \(i\ne j\), to w macierzy \(D\) są dwa takie same wiersze. A zatem \(c_{ij}=\delta _{ij}\) i w konsekwencji \(C=I\).

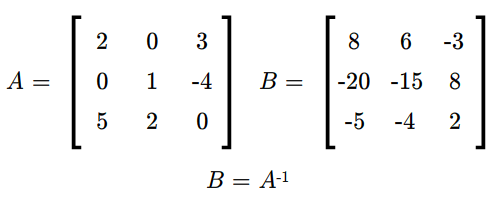

Układy równań liniowych
Układem równań liniowych nazywamy układ równań
\(\left\{ \begin{array} {lr} \ a_{11}x_1+...+a_{1n}x_n =b_1\\ .........................................\\ \ a_{m1}x_1+...+a_{mn}x_n=b_m, \end{array} \right .\) (2.1)
gdzie \(x_1,..., x_n\) są niewiadomymi, zaś \(a_{ij}\), \(b_i\), gdzie \(i=1,...,m\); \(j=1,....n\) są skalarami z pewnego ciała \(\mathbb K\). Rozwiązaniem tego układu nazywamy każdy ciąg \((x_1,...,x_n)\in \mathbb K ^n\), który spełnia (2.1). Skalary \(a_{ij}\) nazywają się współczynnikami układu równań. Skalary \(b_1,...,b_m\) nazywają się wyrazami wolnymi układu (2.1). Jeżeli wszystkie wyrazy wolne są równe zeru, układ równań (2.1) nazywa się jednorodnym. Układ taki rozważaliśmy już w Wykładzie II. W przeciwnym wypadku mówimy, że układ jest niejednorodny. Współczynniki układu (2.1) stanowią macierz \(A=[a_{ij}]\) o \(m\) wierszach i \(n\) kolumnach. Wyrazy wolne
układamy w jednokolumnową macierz
Podobnie, niewiadome ułożymy w jednokolumnową macierz
Układ równań (2.1) można teraz zapisać w postaci macierzowej
\(Ax=b.\) (2.2)
Jeżeli w układzie równań (2.1) zastąpimy wyrazy wolne zerami, to otrzymujemy tzw. układ jednorodny skojarzony z (2.1)
\(\left\{ \begin{array} {lr} \ a_{11}x_1+...+a_{1n}x_n =0\\ .........................................\\ \ a_{m1}x_1+...+a_{mn}x_n=0 \end{array} \right .\) (2.3)
Traktując macierz \(A\) jako odwzorowanie
\(A:\mathbb K ^n\ni x\longrightarrow Ax\in \mathbb K^m,\) (2.4)
widzimy, że jądrem tego odwzorowania jest zbiór rozwiązań układu jednorodnego
(2.3). A zatem zbiór rozwiązań układu jednorodnego jest podprzestrzenią wektorową \(\mathbb K^n\). Na podstawie twierdzenia opisującego relację wymiaru jądra i wymiaru obrazu danego odwzorowania liniowego wiemy, że wymiar tej przestrzeni jest równy \(n - rk A\). Oznaczmy tę przestrzeń przez \(V_o\). Niech teraz \(x_o=({x_o}_1,...,{x_o}_n)\) będzie pewnym rozwiązaniem układu (2.1). Niech \((v_1,...,v_n)\) będzie dowolnym rozwiązaniem układu skojarzonego (2.3). Wtedy
jest również rozwiązaniem układu (2.1).
Jeśli teraz mamy dwa rozwiązania \(({x_o}_1,..., {x_o}_n)\), \(({x}_1,..., {x}_n)\) układu (2.1), to ciąg \((x_1-{x_o}_1,... ,x_n-{x_o}_n)\) jest rozwiązaniem układu (2.3). Udowodniliśmy następujące twierdzenie
Twierdzenie 2.1
Jeżeli układ równań (2.1) ma rozwiązanie oraz
jest pewnym rozwiązaniem (2.1), to zbiór wszystkich rozwiązań układu (2.1) jest równy zbiorowi
gdzie \(V_o\) jest zbiorem wszystkich rozwiązań układu jednorodnego
(2.3). Przestrzeń \(V_o\) jest \((n-k)\)-wymiarowa, gdzie
\(k= rk A\).
W twierdzeniu powyższym zakłada się, że istnieje rozwiązanie układu równań (2.1). O ile układ jednorodny zawsze posiada rozwiązanie, bo, na przykład, ciąg \((0,...,0)\) jest rozwiązaniem takiego układu, o tyle układ niejednorodny niekoniecznie ma rozwiązanie. Proste kryterium rozwiązywalności układu niejednorodnego daje następujące twierdzenie Kroneckera-Capellego.
Twierdzenie 2.2
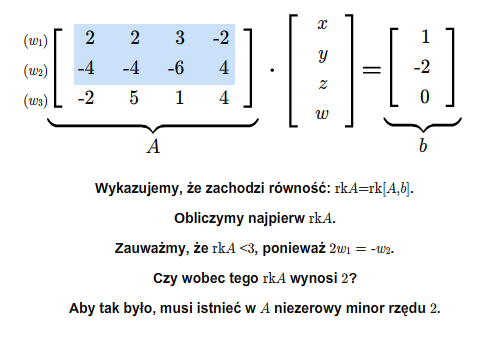
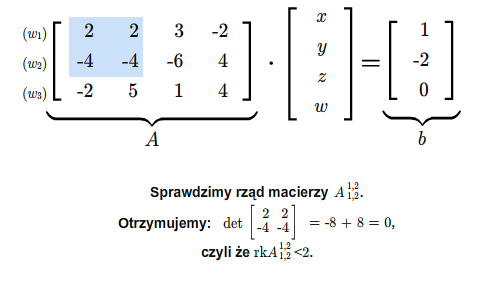
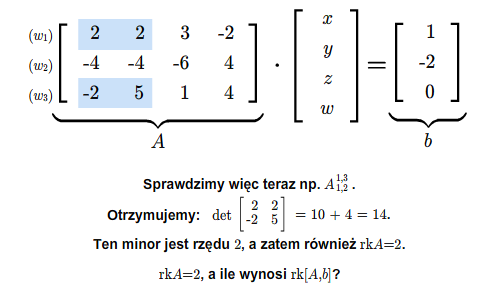
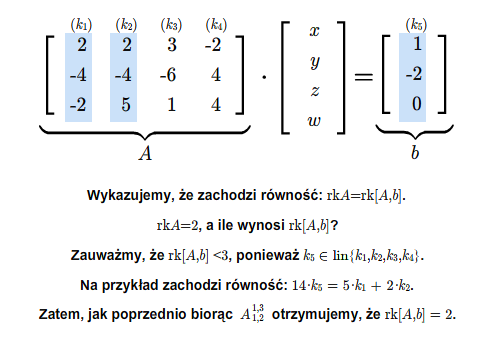
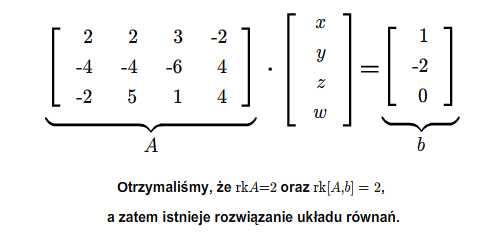
Układ równań (2.1) ma rozwiązanie wtedy i tylko wtedy, gdy
gdzie \([A,b]\) jest macierzą utworzoną z macierzy \(A\) przez dopisanie do niej kolumny wyrazów wolnych.
Dowód
\(x_1A_1+...+x_nA_n=b.\) (2.5)
Macierz \([A,b]\), o której mówi się w powyższym twierdzeniu, nazywa się macierzą rozszerzoną układu (2.1).
Twierdzenie Kroneckera-Capellego dotyczy każdego układu równań, tzn. liczba równań i liczba niewiadomych mogą być dowolne. Kolejne twierdzenie, twierdzenie Cramera, dotyczy tylko tych układów, w których liczba równań jest równa liczbie niewiadomych.
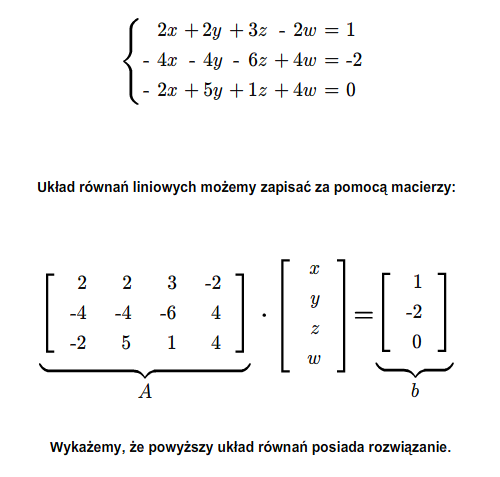
Twierdzenie 2.3
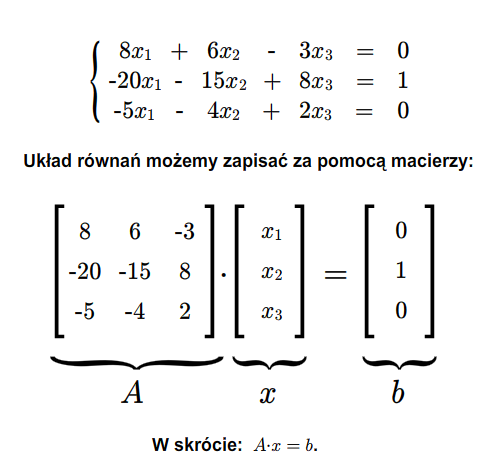
\(\left\{\begin{array} {l} \ a_{11}x_1+...+a_{1n}x_n=b_1 \\ \ .......................................\\ \ a_{n1}x_1+...+a_{nn}x_n=b_n \end{array} \right .\) (2.6)
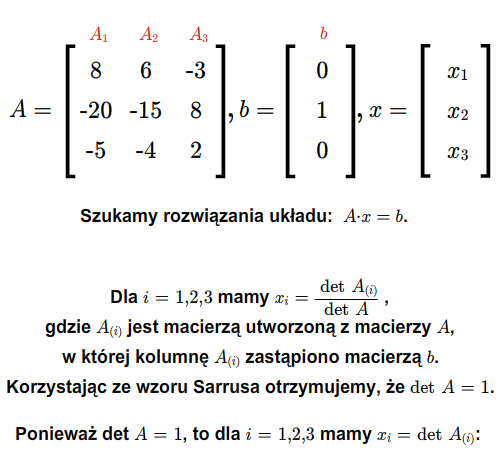
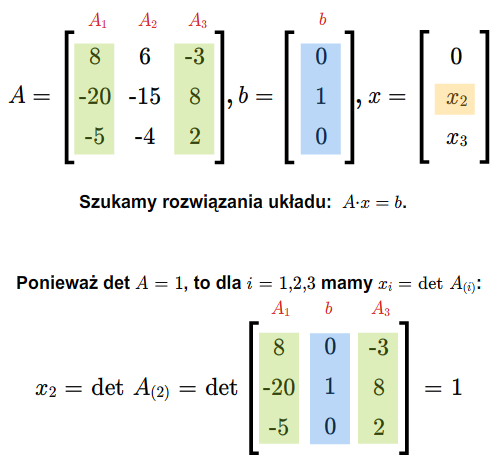
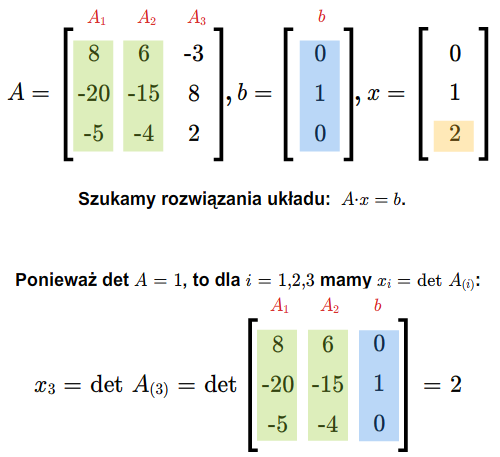
taki, że \(\det A\ne 0\). Wtedy układ (2.6) ma dokładnie jedno rozwiązanie i rozwiązanie to jest dane wzorami
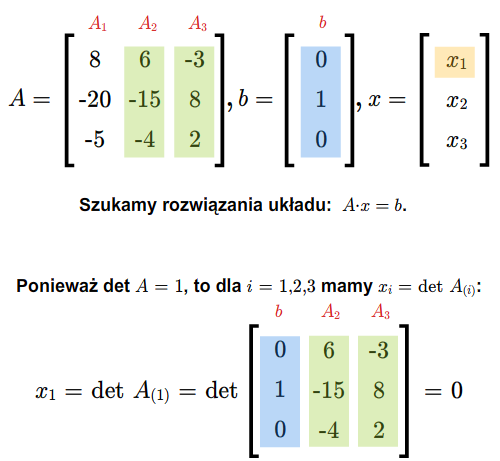
\(x_i= {{\det A_{(i)}\over \det A}},\) (2.7)
dla \(i=1,...,n\), gdzie \(A_{(i)}\) jest macierzą otrzymaną z macierzy \(A\) przez zastąpienie \(i\)-tej kolumny kolumną wyrazów wolnych.
Dowód
Rozważmy postać macierzową układu (2.6). Mamy więc równanie macierzowe \(Ax=b.\). Obłóżmy obustronnie to równanie przez \(A^{-1}\). Ponieważ \(\det A\ne 0\), macierz odwrotna \(A^{-1}\) istnieje. Mamy więc
Wykorzystamy teraz wzory na wyrazy macierzy odwrotnej. Oznaczmy wyrazy tej macierzy przez \(c_{ij}\). A zatem \(c_{ij}= (-1)^{i+j}{{\det A_{ji}}\over{\det A} }\).
Mamy następujące równości
Ostatnia równość wynika z rozwinięcia Laplace'a wyznacznika. W ten sposób udowodniliśmy istnienie rozwiązania, jego jedyność i wzory(2.7), które nazywają się wzorami Cramera.
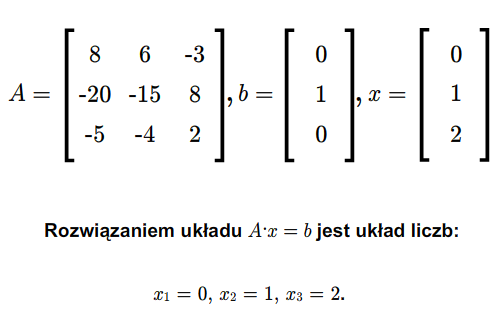
Ustalmy jeszcze, jakie operacje można wykonać na układzie równań, aby otrzymać układ równoważny, tzn. taki, który ma dokładnie taki sam zbiór rozwiązań. Na pewno można równania permutować. Poza tym do danego równania można dodać kombinację liniową pozostałych równań. Każde równanie można pomnożyć przez niezerowy skalar. Wymienione operacje służą do rozwiązywania układów równań liniowych tzw. metodą Gaussa, która będzie omówiona na ćwiczeniach.