Zaawansowane CPP
Forma zajęć
Wykład (30 godzin) + laboratorium (30 godzin)
Opis
Celem przedmiotu jest zapoznanie studentów z zaawansowanymi technikami programowania obiektowego w C++.
Sylabus
Autorzy
- Piotr Białas - Uniwersytet Jagielloński, Wydział Fizyki, Astronomii i Informatyki Stosowanej,
- Wojciech Palacz - Uniwersytet Jagielloński, Wydział Fizyki, Astronomii i Informatyki Stosowanej,
Wymagania wstępne
- Programowanie Obiektowe
- Znajomość C++
Szablony I
Szablony funkcji
Funkcje uogólnione
W praktyce programowania często spotykamy się z funkcjami (algorytmami), które można zastosować do szerokiej klasy typów i struktur danych. Typowym przykładem jest funkcja obliczająca maksimum dwu wartości. Ten trywialny, aczkolwiek przydatny kod można zapisać np. w postaci:
int max(int a,int b) { return (a>b)?a:b; };
Przykład 1.1
Funkcja max wybiera większy z dwu int-ów, ale widać, że kod będzie identyczny dla argumentów dowolnego innego typu pod warunkiem, iż istnieje dla niego operator porównania i konstruktor kopiujący. W językach programowania z silną kontrolą typów, takich jak C, C++ czy Java definiując funkcję musimy jednak podać typy przekazywanych parametrów oraz typ wartości zwracanej. Oznacza to, że dla każdego typu argumentów musimy definiować nową funkcję max:
int max(int a, int b) {return (a>b)?a:b;}; double max(double a,double b) {return (a>b)?a:b;}; string max(string a,string b) {return (a>b)?a:b;}; <i>skorzystaliśmy tu z dostępnej w C++ możliwości przeładowywania funkcji</i><br /> main() { cout<< max(7,5) <<end; cout<< max(3.1415,2.71) <<endl; cout<< max("Ania","Basia") <<endl; }
Przykład 1.2
Takie powtarzanie kodu, poza oczywistym zwiększeniem nakładu pracy, ma inne niepożądane efekty, związane z trudnością zapewnienia synchronizacji kodu każdej z funkcji. Jeśli np. zauważymy błąd w kodzie, to musimy go poprawić w kilku miejscach. To samo dotyczy optymalizacji kodu. W powyższym przykładzie kod jest wyjątkowo prosty, ale taki sam problem dotyczy np. funkcji sortujących. Rozważmy prosty algorytm sortowania bąbelkowego:
inline void swap(double &a,double &b) { double tmp=a;a=b;b=tmp; } void buble_sort(double *data,int N) { for(int i=n-1;i>0;--i) for(int j=0; j < i;++j) if(data[j]>data[j+1]) swap(data[j],data[j+1]); }
Powyższa funkcja sortuje tablicę zawierającą wartości typu double, ale widać, że znów kod będzie identyczny, jeśli zamiast double użyjemy dowolnego innego typu, którego wartości możemy porównywać za pomocą funkcji operator>() i dla którego zdefiniowany jest operator przypisania. Co więcej, kod nie zmieni się jeśli zamiast tablicy użyjemy dowolnej innej struktury danych, umożliwiającej indeksowany dostęp do swoich składowych, np. std::vector ze Standardowej Biblioteki Szablonów STL. W tym przypadku kod jest już bardziej skomplikowany i kłopoty związane z jego powielaniem będą większe. Przykłady takie można mnożyć, istnieje bowiem wiele takich funkcji czy algorytmów uogólnionych. Ich kod może być znacznie bardziej skomplikowany niż w podanych przykładach, a zależność od typu argumentów nie musi ograniczać się do sygnatury, ale występować również we wnętrzu funkcji, jak np. w przypadku zmiennej tmp w funkcji swap. Powielanie takiego kodu dla różnych typów parametrów może łatwo prowadzić do błędów, utrudnia ich wykrywanie, a konieczność edycji każdego egzemplarza kodu zniechęca do wprowadzania ulepszeń.
Funkcje uogólnione bez szablonów
Jak radzili, a właściwie jak radzą sobie programiści bez możliwości skorzystania z szablonów? Tradycyjne sposoby rozwiązywania tego typu problemów to między innymi makra:
#define max(a,b) ( (a>b)?a:b) )lub używanie wskaźników typów ogólnych, takich jak void *, jak np. w funkcji qsort ze standardowej biblioteki C:
void qsort (void *base, size_t nmemb, size_t size, int(*compar)(const void *, const void *));
Mimo iż użyteczne, żadne z tych rozwiązań nie może zostać uznane za wystarczająco ogólne i bezpieczne.
Można się również pokusić o próbę rozwiązania tego problemu za pomocą mechanizmów programowania obiektowego. W sumie jest to bardziej wyrafinowana odmiana rzutowania na void *. Polega na zdefiniowaniu ogólnego typu dla obiektów, które mogą być porównywane:
class GreaterThanComparable { public: virtual bool operator>(const GreaterThanComparable &) const = 0; };
następnie zdefiniowaniu funkcji max w postaci:
const GreaterThanComparable & max(const GreaterThanComparable &a, const GreaterThanComparable &b) { return (a>b)? a:b; }
( Źródło: max_oop.cpp)
i używaniu jej np. w następujący sposób:
class Int:public GreaterThanComparable { int val; public: Int(int i <nowiki>=</nowiki> 0):val(i) {}; operator int() {return val;}; virtual bool operator>(const GreaterThanComparable &b) const { return val > static_cast<const Int&>(b).val; } }; main() { Int a(1),b(2); Int c; c = (const Int &)::max(a,b); cout<<(int)c<<endl; }
( Źródło: max_oop.cpp)
Widać więc wyraźnie, że to podejście wymaga sporego nakładu pracy, a więc w szczególności w przypadku tak prostej funkcji jak max jest wysoce niepraktyczne. Ogólnie rzecz biorąc ma ono następujące wady:
- Wymaga dziedziczenia z abstrakcyjnej klasy bazowej GreaterThanComparable, czyli może być zastosowane tylko do typów zdefiniowanych przez nas. Inne typy, w tym typy wbudowane, wymagają kopertowania w klasie opakowującej, takiej jak klasa Int w powyższym przykładzie.
- Ponieważ potrzebujemy polimorfizmu funkcja operator>() musi być funkcją wirtualną, a więc musi być funkcją składową klasy i nie może być typu inline. W przypadku tak prostych funkcji niemożność rozwinięcia ich w miejscu wywołania może prowadzić do dużych narzutów w czasie wykonania.
- Funkcja max zwraca zawsze referencje do GreaterThanComparable, więc konieczne jest rzutowanie na typ wynikowy (tu Int).
Szablony funkcji
Widać, że podejście obiektowe nie nadaje się najlepiej do rozwiązywania tego szczególnego problemu powielania kodu. Dlatego w C++ wprowadzono nowy mechanizm: szablony. Szablony zezwalają na definiowanie całych rodzin funkcji, które następnie mogą być używane dla różnych typów argumentów.
Definicja szablonu funkcji max, odpowiadającej definicji 1.1 wygląda następująco:
template<typename T> T max(T a,T b) {return (a>b)?a:b;};
( Źródło: max_template.cpp)
Przyjrzyjmy się jej z bliska. Wyrażenie template
int i,j,k; k=max<int>(i,j);
Takie użycie szablonu spowoduje wygenerowanie identycznej funkcji jak 1.1. W powyższym przypadku za T podstawiamy int. Oczywiście możemy podstawić za T dowolny typ i używając szablonów program 1.2 można zapisać następująco:
template<typename T> T max(T a,T b) {return (a>b)?a:b;} main() { cout<<::max<int>(7,5)<<endl; cout<<::max<double>(3.1415,2.71)<<endl; cout<<::max<string>("Ania","Basia")<<endl; }
( Źródło: max_template.cpp)
W powyższym kodzie użyliśmy konstrukcji ::max(a,b). Dwa dwukropki oznaczają, że używamy funkcji max zdefiniowanej w ogólnej przestrzeni nazw. Jest to konieczne aby kod się skompilował, ponieważ szablon max istnieje już w standardowej przestrzeni nazw std. W dalszej części wykładu będziemy te podwójne dwukropki pomijać.
Oczywiście istnieją typy których podstawienie spowoduje błędy kompilacji, np.
complex<double> c1,c2; max<complex<double> >(c1,c2); //brak operatora >
( Źródło: max_template.cpp)
lub
class X { private: X(const X &){}; }; X a,b; max<X>(a,b); //prywatny (niewidoczny) konstruktor kopiujący
( Źródło: max_template.cpp)
Ogólnie rzecz biorąc, każdy szablon definiuje pewną klasę typów, które mogą zostać podstawione jako jego argumenty.
Dedukcja argumentów szablonu
Użyteczność szablonów funkcji zwiększa istotnie fakt, że argumenty szablonu nie muszą być podawane jawnie. Kompilator może je wydedukować z argumentów funkcji. Tak więc zamiast
int i,j,k; k=max<int>(i,j);
możemy napisać
int i,j,k; k=max(i,j);
i kompilator zauważy, że tylko podstawienie int-a za T umożliwi dopasowanie sygnatury funkcji do parametrów jej wywołania i automatycznie dokona odpowiedniej konkretyzacji.
Może się zdarzyć, że podamy takie argumenty funkcji, że dopasowanie argumentów wzorca będzie niemożliwe, otrzymamy wtedy błąd kompilacji. Trzeba pamiętać, że mechanizm automatycznego dopasowywania argumentów szablonu powoduje wyłączenie automatycznej konwersji argumentów funkcji. Podanie jawnie argumentów szablonu (w nawiasach ostrych za nazwą szablonu) jednoznacznie określa sygnaturę funkcji, a więc umożliwia automatyczną konwersję typów. Ilustruje to poniższy kod:
template<typename T> T max(T a,T b) {return (a>b)?a:b;} main() { cout<<::max(3.14,2)<<endl; // błąd: kompilator nie jest w stanie wydedukowac argumentu szablonu, bo typy // argumentów (double,int) nie pasują do (T,T) cout<<::max<int>(3.14,2)<<endl; // podając argument jawnie wymuszamy sygnaturę int max(int,int), a co za tym // idzie automatyczną konwersję argumentu 1 do int-a cout<<::max<double>(3.14,2)<<endl; // podając argument szablonu jawnie wymuszamy sygnaturę // double max(double,double) // a co za tym idzie automatyczną konwersję argumentu 2 do double-a int i; cout<<::max<int *>(&i,i)<<endl; //błąd: nie istnieje konwersja z typu int na int*
( Źródło: max_template.cpp)
Może warto zauważyć, że automatyczna dedukcja parametrów szablonu jest możliwa tylko wtedy, jeśli parametry wywołania funkcji w jakiś sposób zależą od parametrów szablonu. Jeśli tej zależności nie ma, z przyczyn oczywistych dedukcja nie jest możliwa i trzeba parametry podawać jawnie. Wtedy istotna jest kolejność parametrów na liście. Jeżeli parametry, których nie da się wydedukować, umieścimy jako pierwsze, wystarczy, że tylko je podamy jawnie, a kompilator wydedukuje resztę. Ilustruje to poniższy kod:
template<typename T,typename U> T convert(U u) { return (T)u; }; template<typename U,typename T> T inv_convert(U u) { return (T)u; }; fukcje różnią się tylko kolejnością parametrów szablonu main() { cout<<convert(33)<<endl; błąd: kompilator nie jest w stanie wydedukować pierwszego parametru szablonu, bo nie zależy on od parametru wywołania funkcji cout<<convert<char>(33)<<endl; w porządku: podajemy jawnie argument T, kompilator sam dedukuje argument U z typu argumentu wywołania funkcji cout<<inv_convert<char>('a')<<endl; błąd: podajemy jawnie argument odpowiadający parametrowi U. Kompilator nie jest w stanie wydedukować argumentu T, bo nie zależy on od argumentu wywołania funkcji cout<<inv_convert<int,char>(33)<<endl; w porządku: podajemy jawnie oba argumenty szablonu }
( Źródło: convert.cpp)
Używanie szablonów
Z użyciem szablonów wiąże się parę zagadnień niewidocznych w prostych przykładach. W językach C i C++ zwykle rozdzielamy deklarację funkcji od jej definicji i zwyczajowo umieszczamy deklarację w plikach nagłówkowych *.h, a definicję w plikach źródłowych *.c, *.cpp itp. Pliki nagłówkowe są w czasie kompilacji włączane do plików, w których chcemy korzystać z danej funkcji, a pliki źródłowe są pojedynczo kompilowane do plików “obiektowych” *.o. Następnie pliki obiektowe są łączone w jeden plik wynikowy (zob. rysunek 1.1). W pliku korzystającym z danej funkcji nie musimy więc znać jej definicji, a tylko deklarację. Na podstawie nazwy funkcji konsolidator powiąże wywołanie funkcji z jej implementacją znajdującą się w innym pliku obiektowym. W ten sposób tylko zmiana deklaracji funkcji wymaga rekompilacji plików, w których z niej korzystamy, a zmiana definicji wymaga jedynie rekompilacji pliku, w którym dana funkcja jest zdefiniowana.
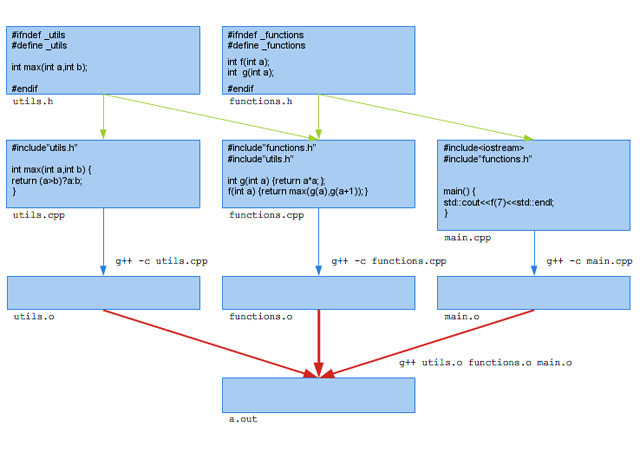 Rysunek 1.1. Przykład organizacji kodu C++ w przypadku użycia zwykłych funkcji.
Rysunek 1.1. Przykład organizacji kodu C++ w przypadku użycia zwykłych funkcji.
Taka organizacja umożliwia przestrzeganie "reguły jednej definicji" (one definition rule), wymaganej przez C++. Osobom nieobeznanym z programowaniem w C/C++ zwracam uwagę na konstrukcję
#ifndef _nazwa_pliku_ #define _nazwa_pliku_ ... #endif
uniemożliwiajacą podwójne włączenie tego pliku do jednej jednostki translacyjnej.
Podobne podejście do kompilacje szablonów się nie powiedzie (zob. rysunek 1.2).
Powodem jest fakt, że w trakcie kompilacji pliku utils.cpp
kompilator nie wie jeszcze, że potrzebna będzie funkcja max
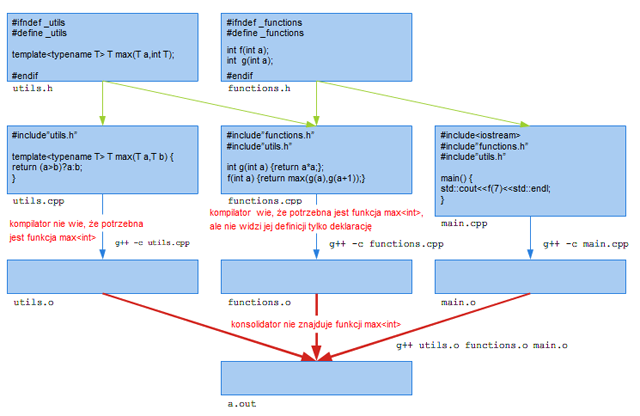 Rysunek 1.2. Przykład błędnej organizacji kodu w przypadku użycia szablonów.
Rysunek 1.2. Przykład błędnej organizacji kodu w przypadku użycia szablonów.
Istnieją różne rozwiązania tego problemu. Najprościej chyba jest zauważyć, że opisane zachowanie jest analogiczne do zachowania podczas kompilacji funkcji rozwijanych w miejscu wywołania (inline), których definicja również musi być dostępna w czasie kompilacji. Podobnie więc jak w tym przypadku możemy zamieścić wszystkie deklaracje i definicje szablonów w pliknu nagłówkowym, włączanym do plików, w ktorych z tych szablonów korzystamy (zob. rysunek 1.3). Podobnie jak w przypadku funkcji inline reguła jednej definicji zezwala na powtarzanie definicji/deklaracji szablonów w różnych jednostkach translacyjnych, pod warunkiem, że są one identyczne. Stąd konieczność umieszczania ich w plikach nagłówkowych.
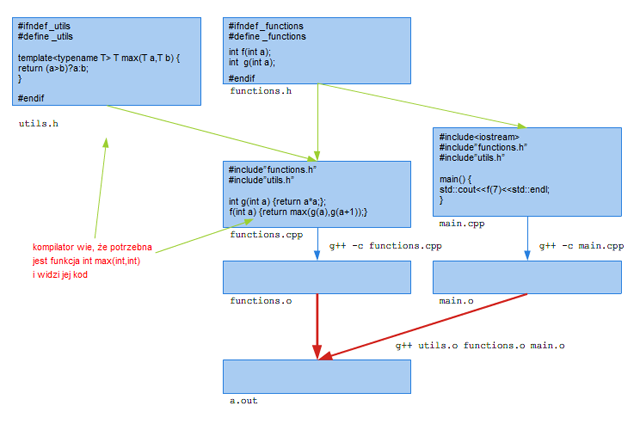 Rysunek 1.3. Przykład organizacji kodu z szablonami, wykorzystującego strategię włączania.
Rysunek 1.3. Przykład organizacji kodu z szablonami, wykorzystującego strategię włączania.
Ten sposób organizacji pracy z szablonami, nazywany modelem włączenia, jest najbardziej uniwersalny. Jego główną wadą jestkonieczność rekompilacji całego kodu korzystającego z szablonów przy każdej zmianie definicji szablonu. Również jeśli zmienimy coś w pliku, w którym korzystamy z szablonu, to musimy rekompilować cały kod szablonu włączony do tego pliku, nawet jeśli nie uległ on zmianie. Jeśli się uwzględni fakt, że kompilacja szablonu jest bardziej skomplikowana od kompilacji "zwykłego" kodu, to duży projekt intensywnie korzystający z szablonów może wymagać bardzo długich czasów kompilacji.
Możemy też w jakiś sposób dać znać kompilatorowi, że podczas kompilacji
pliku utils.cpp powinien wygenerować kod dla funkcji
max
template<typename T> T max(T a,T b) {return (a>b)?a:b;} template int max<int>(int ,int); <i>konkretyzacja jawna</i>
Używając konkretyzacji jawnej musimy pamiętać o dokonaniu konkretyzacji każdej używanej funkcji, tak że to podejście nie skaluje się zbyt dobrze. Ponadto w przypadku szablonów klas (omawianych w następnym module) konkretyzacja jawna pociąga za sobą konkretyzację wszystkich metod danej klasy, a konkretyzacja “na żądanie” - jedynie tych używanych w programie.
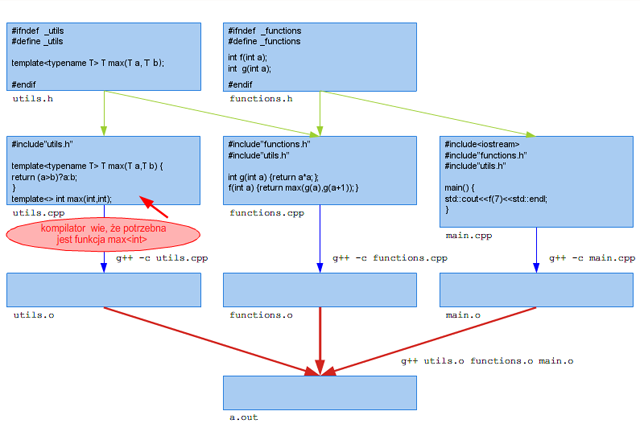 Rysunek 1.4. Przykład organizacji kodu z szablonami, wykorzystującego jawną konkretyzację.
Rysunek 1.4. Przykład organizacji kodu z szablonami, wykorzystującego jawną konkretyzację.
Pozatypowe parametry szablonów
Poza parametrami określającymi typ, takimi jak parametr T w dotychczasowych przykładach, szablony funkcji mogą przyjmować również parametry innego rodzaju. Obecnie mogą to być inne szablony, co omówię w następnym podrozdziale lub parametry określające nie typ, ale wartości. Jak na razie (w obecnym standardzie) te wartości nie mogą być dowolne, ale muszą mieć jeden z poniższych typów:
- typ całkowitoliczbowy bądź typ wyliczeniowy
- typ wskaźnikowy
- typ referencyjny.
Takie parametry określające wartość nazywamy parametrami pozatypowymi. W praktyce z parametrów pozatypowych najczęściej używa się parametrów typu całkowitoliczbowego. Np.
template<size_t N,typename T> T dot_product(T *a,T *b) { T total=0.0; for(size_t i=0;i<N;++i) total += a[i]*b[i] ; return total; };
( Źródło: dot_product.cpp)
Po raz drugi zwracam uwagę na kolejność parametrów szablonu na liście parametrów. Dzięki temu, że niededukowalny parametr N jest na pierwszym miejscu wystarczy podać jawnie tylko jego, drugi parametr typu T zostanie sam automatycznie wydedukowany na podstawie przekazanych argumentów wywołania funkcji:
main() { double x[3],y[3]; dot_product<3>(x,y); }
( Źródło: dot_product.cpp)
Parametry pozatypowe są zresztą "ciężko dedukowalne". Właściwie jedynym sposobem na przekazania wartości stałej poprzez typ argumentu wywołania jest skorzystanie z parametrów będących szablonami klas (zob. następny podrozdział).
Używając pozatypowych parametrów szablonów musimy pamiętać, że odpowiadające im argumenty muszą być stałymi wyrażeniami czasu kompilacji. Stąd jeżeli używamy typów wskaźnikowych, muszą to być wskaźniki do obiektów łączonych zewnętrznie, a nie lokalnych. Ponieważ jednak jeszcze ani razu nie używałem pozatypowych parametrów szablonów innych niż typy całkowite, to nie będę podawał żadnych przykładów takich paremtrów na tym wykładzie.
Szablony parametrów szablonu
Jak już wspomniałem w poprzednim podrozdziale, parametrami szablonu funkcji mogą być również szablony klas (zob. następny podrozdział). Szablony parametrów szablonu umożliwiają przekazanie nazwy szablonu jako argumentu szablonu funkcji. Więcej o nich napiszę w drugiej części wykładu. Tutaj tylko pokażę jako ciekawostkę w jaki sposób można dedukować wartości pozatypowych argumentów szablonu.
template< template<int N> class C,int K> <i>taka definicja oznacza, że parametr C określa szablon klasy posiadający jeden parametr typu <tt>int</tt>. Parametr N służy tylko do definicji szablonu C i nie może być użyty nigdzie indziej</i> void f(C<K>){ cout<<K<<endl; };<br /> template<int N> struct SomeClass {};<br /> main() { SomeClass<1> c1; SomeClass<2> c2;<br /> f(c1); <i>C=SomeClass K=1</i> f(c2); <i>C=SomeClass K=2</i> }
( Źródło: deduce_N.cpp)
Szablony metod
Jak na razie definiowaliśmy szablony zwykłych funkcji. C++ umożliwia również definiowanie szablonów metod klasy np.:
struct Max { template<typename T> T max(T a,T b) {return (a>b)?a:b;} }; main() { Max m; m.max(1,2); }
( Źródło: max_method.cpp)
Szablonów metod składowych dotyczą takie same reguły jak szablonów funkcji.
Szablony klas
Typy uogólnione
Uwagi na początku poprzedniego rozdziału odnoszą się w tej samej mierze do klas, jak i do funkcji. I tutaj mamy do czynienia z kodem, który w niezmienionej postaci musimy powielać dla różnych typów. Sztandarowym przykładem takiego kodu są różnego rodzaju kontenery (pojemniki), czyli obiekty służące do przechowywania innych obiektów. Jest oczywiste, że kod kontenera jest w dużej mierze niezależny od typu obiektów w nim przechowywanych. Jako przykład weźmy sobie stos liczb całkowitych. Możliwa definicja klasy stos może wyglądać następująco, choć nie polecam jej jako wzoru do naśladowania w prawdziwych aplikacjach:
class Stack { private: int rep[N]; size_t top; public: static const size_t N=100; Stack():_top(0) {}; void push(int val) {_rep[_top++]=val;} int pop() {return rep[--top];} bool is_empty {return (top==0);} }
Ewidentnie ten kod będzie identyczny dla stosu obiektów dowolnego innego typu, pod warunkiem, że typ ten posiada zdefiniowany operator=() i konstruktor kopiujący.
W celu zaimplementowania kontenerów bez pomocy szablonów możemy probować podobnych sztuczek jak te opisane w poprzednim rozdziale. W językach takich jak Java czy Smalltalk, które posiadają uniwersalną klasę Object, z której są dziedziczone wszystkie inne klasy, a nie posiadają (Java już posiada) szablonów, uniwersalne kontenery są implementowane właśnie poprzez rzutowanie na ten ogólny typ. W przypadku C++ nawet to rozwiązanie nie jest praktyczne, bo C++ nie posiada pojedynczej hierarchii klas.
Szablony klas
Rozwiązaniem są znów szablony, tym razem szablony klas. Podobnie jak w przypadku szablonów funkcji, szablon klasy definiuje nam w rzeczywistości całą rodzinę klas. Szablon klasy Stack możemy zapisać następująco:
template<typename T> class Stack { public: static const size_t N=100; private: T _rep[N]; size_t _top;<br> public: Stack():_top(0) {}; void push(T val) {_rep[_top++]=val;} T pop() {return _rep[--_top];} bool is_empty {return (_top==0);} };
( Źródło: stack.cpp)
Tak zdefiniowanego szablonu możemy używać podając jawnie jego argumenty.
Stack<string> st ; st.push("ania"); st.push("asia"); st.push("basia"); while(!st.is_empty() ){ cout<<st.pop()<<endl; }
( Źródło: stack.cpp)
Dla szablonów klas nie ma możliwości automatycznej dedukcji argumentów szablonu, ponieważ klasy nie posiadają argumentów wywołania, które mogłyby do tej dedukcji posłużyć. Jest natomiast możliwość podania argumentów domyślnych, np.
template<typename T = int> Stack { ... }
( Źródło: stack.cpp)
Wtedy możemy korzystać ze stosu bez podawania argumentów szablonu i wyrażenie
Stack s;
będzie równoważne wyrażeniu:
Stack<int> s;
Dla domyślnych argmentów szablonów klas obowiązują te same reguły, co dla domyślnych argumentów wywołania funkcji.
Należy pamiętać, że każda konkretyzacja szablonu klasy dla różniących się zestawów argumentów jest osobną klasą:
Stack<int> si;
Stack<double> sd;
sd=si; //błąd: to są obiekty różnych klas a nie zdefiniowano przypisania( Źródło: stack.cpp)
Okazuje się, że próba zdefiniowania operatora przypisania, który np. przypisywałby do siebie stosy różnych typów, nie jest łatwa, ponieważ dwa takie stosy nie widzą swoich reprezentacji.
Pozatypowe parametry szablonów klas
Zestaw możliwych parametrów szablonów klas jest taki sam jak dla szablonów funkcji. Podobnie najczęściej wykorzystywane są wyrażenia całkowitoliczbowe. W naszym przykładzie ze stosem możemy ich użyć do przekazania rozmiaru stosu:
template<typename T = int , size_t N = 100> class Stack { private: T rep[N]; size_t top; public: Stack():_top(0) {};<br /> void push(T val) {_rep[_top++]=val;} T pop() {return rep[--top];} bool is_empty {return (top==0);} }
( Źródło: stack_N.cpp)
Podkreślam jeszcze raz, że Stack
Szablony parametrów szablonu
Stos jest nie tyle strukturą danych, ile sposobem dostępu do nich. Stos realizuje regułę LIFO czyli Last In First Out. W tym sensie nie jest istotne w jaki sposób dane są na stosie przechowywane. Może to być tablica, jak w powyższych przykładach, ale może to być praktycznie dowolny inny kontener. Np. w Standardowej Bibliotece Szablonów C++ stos jest zaimplementowany jako adapter do któregoś z istniejących już kontenerów. Ponieważ kontenery STL są szablonami, szablon adaptera mógłby wyglądać następująco:
template<typename T,
template<typename X > class Sequence=std::deque >
class Stack {
Sequence<T> _rep;
public:
void push(T e) {_rep.push_back(e);};
T pop() {T top=_rep.top();_rep.pop_back();return top;}
bool is_empty() const {return _rep.empty();}
};Konkretyzując stos możemy wybrać kontener, w którym będą przechowywane jego elementy:
Stack<double,std::vector> sv;Można zamiast szablonu użyć zwykłego parametru typu:
template<typename T,typename C > class stos { C rep; public: ... }
( Źródło: stack_adapter.cpp)
i używać go w następujący sposób:
stos<double,std::vector<double> > sv;W przypadku użycia szablonu jako parametru szablonu zapewniamy konsystencję pomiędzy typem T i kontenerem C, uniemożliwiając pomyłkę podstawienia niepasujących parametrów:
stos<double,std::vector<int> > sv; <i>błąd: niezgodność typow</i>Uczciwość nakazuje jednak w tym miejscu stwierdzić, że właśnie takie rozwiązanie jest zastosowane w STL-u. Ma ono tę zaletę, że możemy adaptować na stos dowolny kontener, niekoniecznie będący szablonem.
Na koniec jeszcze jedna uwaga: szablony kontenerów z STL posiadają po dwa parametry typów, z tym, że drugi posiada wartość domyślną (standard dopuszcza dowolną ilość argumentów w implemetacji kontenerów STL jak długo będą one posiadały wartości domyślne). Autorzy D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty" ostrzegają, że w tej sytuacji kompilator może nie zaakceptować wyrażenia:
stos<double,std::vector> sv;ponieważ ignoruje fakt istnienia wartości domyślnej dla drugiego parametru szablonu std::vector. Mamy wtedy niezgodność pomiędzy przekazanym argumentem szablonu
template<typename T> std::vector<T,typename A = std::allocator<T> >;
oraz deklaracją paremetru Sequence jako:
template<typename X > class Sequence ;która zakłada tylko jeden parametr szablonu. Można wtedy zmienić deklarację szablonu stos i podać domyślny argument dla szablony w liście parametrów:
template<typename T,template<typename X ,typename A = std::allocator<X> > class C > class stos {...}
W praktyce używane przeze mnie kompilatory (g++ wersja >= 3.3) nie wymagały takiej konstrukcji. Przyznaję, że nie udało mi się doczytać czy jest to cecha kompilatora g++, czy nowego standardu C++ (autorzy D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty" opierali się na poprzednim wydaniu standardu).
Konkretyzacja na żądanie
Jak już wspomniałem wcześniej, konkretyzacja szablonów może odbywać się
"na żądanie". W takim przypadku kompilator będzie konkretyzował
tylko funkcje napotkane w kodzie. I tak, jeśli np. nie użyjemy w naszym
kodzie funckji Stack
template<typename T,int N> void Stack<T,N>::sort() { bubble_sort(_rep,N); };
Możemy teraz np. używać
Stack<std::complex<double>> sc; sc.push( std::complex<double>(0,1)); sc.pop();
ale nie
sc.sort();
( Źródło: stack_sort.cpp)
Natomiast konkretyzacja jawna
template Stack<std::complex<double>>;
( Źródło: stack_sort.cpp)
nie powiedzie się, bo kompilator będzie się starał skonkretyzować wszystkie składowe klasy Stack, w tym metodę sort().
Typy stowarzyszone
W klasach poza metodami i polami możemy definiować również typy, które będziemy nazywali stowarzyszonymi z daną klasą. Jest to szczególnie przydatne w przypadku szablonów. Rozważmy następujący przykład:
template<typename T> Stack { public: typedef T value_type; ... }
Możemy teraz używać tej definicji w innych szablonach
template<typename S> void f(S s) { typename S::value_type total; słowo typename jest wymagane, inaczej kompilator założy, że S::value_type odnosi się do statycznej składowej klasy while(!s.is_empty() ) { total+=s.pop(); } return total; }
( Źródło: stack_N.cpp)
Bez takich możliwości musielibyśmy przekazać typ elementów stosu w osobnym argumencie. Mechanizm typów stowarzyszonych jest bardzo czesto używany w uogólnionym kodzie.
| Załącznik | Wielkość |
|---|---|
| Max_oop.cpp | 620 bajtów |
| Max_template.cpp | 1.2 KB |
| Convert.cpp | 767 bajtów |
| Dot_product.cpp | 414 bajtów |
| Deduce_N.cpp | 283 bajty |
| Max_method.cpp | 170 bajtów |
| Stack.cpp | 573 bajty |
| Stack_N.cpp | 842 bajty |
| Stack_adapter.cpp | 501 bajtów |
| Stack_sort.cpp | 806 bajtów |
Programowanie uogólnione
Wprowadzenie
W poprzednim wykładzie wprowadziłem pojęcia szablonów funkcji i klas. Są to bardzo ważne konstrukcje języka C++ dające programistom bezpośrednie, czyli z poziomu języka, wsparcie dla tworzenia uogólnionych funkcji i typów (nazywanych też funkcjami lub typami parametryzowanymi). Uogólnienie polega na tym, że za jednym zamachem definiujemy całe rodziny klas lub funkcji. Po podstawieniu za parametry konkretnych argumentów szablonu dostajemy już egzemplarz "zwykłego" typu (klasy) lub funkcji (nazywane również instancjami szablonu). Argumenty szablonu mogą reprezentować typy i w ten sposób dostajemy narzędzie umożliwiające pisanie ogólnego kodu parametryzowanego typem używanych w nim zmiennych, typem argumentów wywołania funkcji itp.
Szablony okazały się bardzo silnym narzędziem, których zastosowanie daleko przekracza implementację prostych kontenerów i można spokojnie stwierdzić, że ich prawdziwy potencjał jest ciągle odkrywany. Szablony idealnie wspierają styl programowania nazywany programowaniem uogólnionym. Polega on na generalizowaniu algorytmów i struktur danych tak, aby były w dużej mierze niezależne od typów danych, na których działają lub z których się składają. Mam nadzieję, że po lekturze poprzedniego wykładu Państwo już widzą, że to jest właśnie to, do czego szablony zostały wymyślone. Nie oznacza to, że automatycznie każdy program używajacy szablonów jest od razu programem uogólnionym. Tak jak i w przypadku tworzenia zwykłych (bez szablonów) programów, trzeba się sporo natrudzić, aby uzyskać uniwersalny, łatwy do ponownego wykorzystania kod. Ten wykład ma właśnie za zadanie przekazać Państwu podstawowe wiadomości na temat pisania dobrych programów uogólnionych.
W programowaniu uogólnionym ważną rolę gra pojęcie konceptu. Koncept to asbtrakcyjna definicja rodziny typów. To pojęcie pełni podobną rolę jak interfejs w programowaniu uogólnionym, ale przynależność do tej rodziny jest określona proceduralnie: do konceptu należą typy, które spełniają pewne wymagania. Czyli jeśli coś kwacze jak kaczka to jest to kaczka, a nie: to jest kaczka jeśli należy do rodziny "kaczowatych". Koncepty omówię w dalszej części tego wykładu.
Co to jest programowanie uogólnione łatwiej jest pokazać na przykładach niż opisać. Niewątpliwie najważniejszą i najbardziej znaną aplikacją programowania ogólnego jest Standardowa Biblioteka Szablonów (STL - Standard Template Library), będąca oficjalną częścią standardu C++. W tych wykladach będę się bardzo często posługiwał przykładami z STL-a, ale szczegółowe nauczenie posługiwania się tą biblioteką nie jest celem tego wykładu. Powinni jednak Państwo zrobić to sami. Dlatego zachęcam do analizy przykładów zamieszczonych na wykładzie oraz wykonywanie podanych ćwiczeń.
Drugim znakomitycm źródłem przykladów uogólnionego kodu jest repozytorium bibliotek boost. Stamtąd też będę podawał przykłady i znów gorąco zachęcam Państwa do zaglądania tam samemu.
Programowanie uogólnione samo w sobie szczególnie obiektowe nie jest, choć oczywiście wymaga możliwości definiowania własnych typów. Oba style programowania: uogólniony i obiektowy można oczywiście stosować razem. Każdy ma swoje charakterystyczne cechy i aby je podkreślić jeszcze raz przypomnę podstawy programowania obiektowego rozumianego jako programowanie z użyciem interfejsów(klas abstrakcyjnych) i funkcji wirtulanych.
Polimorfizm dynamiczny
Sercem programowania obiektowego, oczywiście poza koncepcją klasy i obiektu, jest polimorfizm dynamiczny, czyli możliwość decydowania o tym jaka funkcja zostanie wywołana pod daną nazwą nie w momencie kompilacji (czyli pisania kodu), ale w samym momecie wywołania. Zilustrujemy to na przykładzie. W tym celu skorzystamy z "matki wszystkich przykładów programowania obiektowego", czyli klasy kształtów graficznych:).
Problem jest następujący: nasz program w pewnym momencie musi manipulować kształtami graficznym: rysować, przesuwać, obracać itp. Jest w miarę oczywiste, że każdy kształt będzie posiadał swoją klasę. Następnym krokiem jest ocena które operacje w naszym kodzie wymagają szczególowej znajomości kształtu, a które tylko ogólnych jego własności. Ewidentnie operacja rysowania obiektu należy do tych pierwszych i musi być zdefiniowana w klasie danego kształtu. Mówimy, że "obiekt wie jak się narysować". Często mówi się o tym również jako o ustaleniu odpowiedzialności, czy o podziale obowiązków. Tak więc ustaliliśmy, że do obowiązków obiektu należy umiejętność narysowania się. Jeśli tak, to właściwie cała część kodu manipulującego kształtami nie musi znać szczegółów ich implementacji. Weźmy na przykład fragment aplikacji odpowiedzialny za odświeżanie ekranu. Zakładamy, że wskaźniki do wyświetlanych kształtów są przechowywane w tablicy shape_table:
for(size_t i=0;i<n;++i) shape_table[i]->draw();
kod źródłowy
Programista piszący ten kod nie musi wiedziec jakiego typu kształt jest przechowywany w danym elemencie tablicy shape_table i jak jest zaimplementowana funkcja draw. Istotne jest by każdy obiekt, którego wkaźnik przechowywany jest w tej tablicy posiadał metodę draw. Innymi słowy programista korzysta tu tylko ze znajomości i dostępności interfejsu obiektów typu kształt, a resztę wykonuje kompilator, który generuje kod zapewniający wywołanie odpowiedniej funkcji. Aby taki interfejs zdefiniować tworzymy abstrakcyjną klasę obiektów typu kształt:
class Shape { protected: long int _x; long int _y; public: Shape(long x,long y):_x(x),_y(y){}; long get_x() const {return _x;} long get_y() const {return _y;} virtual void draw() = 0; virtual ~Shape() {}; };
( Źródło shape.h)
Klasa ta stanowić będzie klasę bazową dla wszystkich klas opisujących kształty. Klasa Shape jest klasą abstrakcyjną, ponieważ zawiera niezaimplementowaną wirtualną czystą fukcję void draw(). Kod definiujący konkretne klasy kształtów może wyglądać następująco:
class Rectangle: public Shape { protected: long _ur_x; long _ur_y; public: Rectangle(long ll_x,long ll_y,long ur_x,long ur_y): Shape(ll_x,ll_y),_ur_x(ur_x-ll_x),_ur_y(ur_y-ll_y) {}; virtual void draw() { std::cerr<<"rectangle : "<<_x<<" "<<_y<<" : "; std::cerr<<_ur_x+_x<<" "<<_ur_y+_y<<std::endl; } long get_ur_x() const {return _ur_x;}; long get_ur_y() const {return _ur_y;}; };
( Źródło rectangle.h)
i
class Circle: public Shape { protected: long _r; public: Circle(long x, long y,long r) :Shape(x,y), _r(r) {} virtual void draw() { std::cerr<<"Circle : "<<_x<<" "<<_y<<" : "<<_r<<std::endl; } long get_r() const {return _r;}; };
( Źródło circle.h)
Teraz możemy zdefiniować już funkcję odświeżającą ekran:
void draw_shapes(Shape *table[],size_t n) { for(size_t i=0;i<n;++i) table[i]->draw(); }
( Źródło draw.cpp)
Funkcja draw_shapes wykorzystuje zachowanie polimorficzne: to która funkcja draw zostanie wywołana zależy od tego jaki konkretny kształt jest wskazywany przez element tablicy. Łatwo się o tym przekonać wykonując np. następujący kod
int main() { Shape *list[4]; list[0]=new Circle(0,0,100); list[1]=new Rectangle(20,20,80,80); list[2]=new Circle(10,10,100); list[3]=new Rectangle(20,0,80,10); draw_shapes(list,4); }
kod źródłowy
W ten sposób zaimplementowaliśmy podstawowy paradygmat programowania obiektowego: rozdzielenie interfejsu od implementacji za pomocą abstrakcyjnej klasy bazowej i wykorzystanie funkcji wirtualnych. Ważną częścią tego procesu jest więc właśnie odpowiedni wybór interfejsów (klas bazowych).
Polimorfizm statyczny
Patrząc na kod funkcji draw_shapes możemy zauważyć, że korzysta on jedynie z własności posiadania przez wskazywane obiekty metody draw(). To sygnatura, czyli typ parametru wywołania tej funkcji określa, że musi to być wskaźnik na typ Shape. Z poprzedniego wykładu pamiętamy, że możemy zrezygnować z wymuszania typu argumentu wywołania funkcji poprzez użycie szablonu funcji:
template<typename T> void draw_template(T table[],size_t n) { for(size_t i=0;i<n;++i) table[i].draw(); }
( Źródło draw_template.h)
Taką funkcję możemy wywołać dla dowolnej tablicy, byle tylko przechowywany typ posiadał metodę draw. Mogą to być obiekty typów Circle i Rectangle (nie Shape, obiekty klasy Shape nie istnieją!), ale też inne zupełnie z nimi nie związane. Ilustruje to poniższy przykład:
class Drawable { public: void draw() {cerr<<"hello world!"<<endl;} }; int main() { Drawable table_d[1]={Drawable()}; Circle table_c[2]={Circle(10,10),Circle(0,50)}; draw_template(table_d,1); draw_template(table_c,2); }
kod źródłowy
Korzystając z szablonów uzyskaliśmy więc również pewien efekt zachowania polimorficznego. W przeciwieństwie do poprzedniego przykładu jest to polimorfizm statyczny: to kompilator zadecyduje na podstawie typu tablicy jaką funkcję draw wywołać. Oczywiście w rozważanym przypadku to podejście jest całkowicie nieadekwatne, mamy bowiem do czynienia z niejednorodną rodziną kształtów, a wybór konkretnych kształtów dokunuje się podczas wykonywania programu. Podając przykład z szablonami chciałem tylko podkreślić różnice pomiędzy tymi dwoma technikami. Przykłady kiedy to szablony okazują się lepszym rozwiązaniem zostały podane w poprzednim wykładzie.
Polimorfizm statyczny vs. dynamiczny
Jak już wspomniałem każdy styl posiada swoje cechy, które w zależności od okoliczności mogą być postrzegane jako wady lub zalety. Poniżej podaję zebrane głowne właściwości każdego podejścia.
- Dziedzieczenie i funkcje wirtualne
- umożliwia pracę ze zbiorami niejednorodnych obiektów i korzysta z polimorfizmu dynamicznego
- wymaga wspólnej hierarchii dziedziczenia
- wymusza korzystanie ze wskaźników lub referencji i funkcji wirtualnych
- zazwyczaj generuje mniejszy kod.
- Szablony
- implementuje polimorfizm statyczny
- bezpiecznie obsługuje jednorodne zbiory obiektów
- nie trzeba korzystać ze wskaźników i referencji ani funkcji wirtualnych
- nie musimy korzystać ze wspólnej hierarchii dziedziczenia.
Koncepty
Przyjrzyjmy się jeszcze raz deklaracji funkcji draw_shapes i draw_template. Kiedy programista widzi deklarację:
void draw_shapes(Shape *table[])
wie, że interfejs wykorzystywany przez funkcję draw jest zdefiniowany przez klasę Shape. Aby go poznać musi przeczytać kod i dokumentację tej klasy. Natomiast kiedy programista widzi deklarację:
template<typename T> void draw_template(T table[],size_t n);
to musi prześledzić kod funkcji draw_templates aby poznać ograniczenia nałożone na argument szablonu T. W tym przypadku nie jest to trudne, ale ogólnie może to być nietrywialne zadanie.
Zamiast jednak definiować ograniczenia i warunki dla każdego szablonu osobno, możemy szukać wspólnych, powtarzających się zestawów warunków. Taki zestaw nazwiemy konceptem i będziemy go traktować jako abstrakcyjną definicję całej rodziny typów, niezależną od konkretnego szablonu. Typ spełniający warunki konceptu nazywamy modelem konceptu lub mówimy, że modeluje ten koncept. Mając wybrany, dobrze przygotowany zestaw konceptów dla danej dziedziny, możemy się nimi posługiwać przy definiowaniu typów i algorytmów uogólnionych.
Koncepty mogą tworzyć hierachie analogiczne do hierarachii dziedziecznia. Mówimy, że koncept A jest bardziej wyspecjalizowany niż B (A is-refinement-of B), jeśli zestaw ograniczeń konceptu B zawiera się w zestwie ograniczeń konceptu A. Będę też używał określenia A jest "uszczegółowieniem" B.
Pojęcie konceptu pełni więc przy programowaniu za pomocą szablonów podobną rolę jak pojęcie interfejsu przy programowaniu za pomocą abstrakcyjnych klas bazowych i polimorfizmu dynamicznego. W przeciwieństwie do interfejsu jest to jednak pojęcie bardziej "ulotne", bo nie narzucamy go za pomocą formalnej definicji klasy abstrakcyjnej. Koncepty definiujemy poprzez mniej lub bardziej ścisłe wypisanie nakładanych przez nie ograniczeń. Ograniczenia te mogą zawierać między innymi:
- Prawidłowe wyrażenia. Zestaw wyrażeń języka C++, które muszą się poprawnie kompilować.
- Typy stowarzyszone. Ewentualne dodatkowe typy występujące w prawidłowych wyrażeniach.
- Semantyka: zanczenie wyrażeń. Jednym ze sposobów określanie semantyki jest podawanie niezmienników, czyli wyrażeń, które dla danego konceptu są zawsze prawdziwe.
- Złożoność algorytmów. Gwarancje co do czasu i innych zasobów potrzebnych do wykonania danego wyrażenia.
Programowanie uogólnione polega więc na wyszukiwaniu konceptów na tyle ogólnych, aby pasowały do dużej liczby typów i na tyle szczegółowych, aby zezwalały na wydajną implementację.
Definiowanie konceptów
Weźmy za przykład szablon funkcji max z poprzedniego wykładu
template<typename T> max(T a,T b) {return (a>b)?a:b;}
i zastanówmy się, jakie koncepty możemy odkryć w tak prostym kodzie.
Zacznijmy od gramatyki. Jakie warunki musi spełniać typ T, aby podstawienie go jako argument szablonu max dawało poprawne wyrażenie? Oczywistym warunkiem jest, że dla tego typu musi być zdefiniowany operator porównania bool operator>(...). Specjalnie nie wyspecyfikowałem sygnatury tego operatora. Nie ma np. znaczenia jak parametry są przekazywane, co więcej operator>(...) może być zdefiniowany jako składowa klasy i posiadać tylko jeden jawny argument. Ważne jest to, że jeśli x i y są obiektami typu T to wyrażenie:
x>y
jest poprawne (skompiluje się).
Łatwiej jest przeoczyć fakt, że ponieważ argumenty wywołania są zwracane i przekazywane przez wartość, to typ T musi posiadać konstruktor kopiujący. Oznacza to, że jeśli x i y są obiektami typu T to wyrażenia:
T(x); T x(y); T x = y;
są poprawne.
Przykład 2.1
Spełnienie obydwu tych warunków zapewni nam poprawność gramatyczną wywołania szablonu z danym typem, tzn. kod się skompiluje.
A co z poprawnością semantyczną? Mogłoby sie wydawać, że jest bez znaczenia jak zdefiniujemy operator>(...). Koncept typu T jest jednak częścią kontraktu dla funkcji max. Kontraktu zawieranego pomiędzy twórcą tego wielce skomplikowanego kodu, a jego użytkownikiem. Kontrakt stanowi, że jeżeli użytkownik dostarczy do funkcji argumenty o typach zgodnych z konceptem i o wartościach spełniających być może inne warunki wstępne, to twórca funkcji gwarantuje, że zwróci ona poprawny wynik.
Zastanówny się więc jak zdefiniować poprawność dla funkcji maksimum. Z definicji maksimum żaden element argument funkcji max nie może być większy od wyniku, czyli wyrażenie
musi być zawsze prawdziwe. Jasne jest, że jeśli dla jakiegoś typu X zdefiniujemy operator porównania tak, aby zwracał zawsze prawdę
bool operator>(const X &a,const X &b) {return 1;}
lub aby był równoważny operatorowi równości:
bool operator>(const X &a,const X &b) {return a==b;}
to wyrażenie 2.1 nie może być prawdziwe dla żadnej wartości a i b. Aby funkcja max mogła spełnić swój warunek końcowy musimy narzucić pewne ograniczenia semantyczne na operator>(). Te warunki to żądanie, aby relacja większości definiowana przez ten operator byłą relacją porządku częściowego, a więc aby spełnione było
To rozumowanie możnaby ciągnąć dalej i zauważyć, że nawet z tym ograniczeniem uzyskamy nieintuicyjne wyniki w przypadku, gdy obiekty a i b będą nieporównywalne, tzn. \(!(a>b)\) i \(!(b>a)\).
Poprawność semantyczną konstruktora kopiującego jest trudniej zdefiniować, ograniczymy się więc tylko do stwierdzenia, że wykonanie operacji 2.1 powoduje powstanie kopii obiektu x (cokolwiek by to nie znaczyło).
Comparable i Assignable
Reasumując, dostajemy zbiór warunków, które musi spełniać typ T, aby móc go podstawić do szablonu funkcji max. Czy to oznacza, że zdefiniowaliśmy już poprawny koncept? Żeby się o tym przekonać spróbujmy go nazwać. Narzuca się nazwa w stylu Comparable, ale wtedy łatwo zauważyć, że istnienie konstruktora kopiującego nie ma z tym nic wspólnego. Próbujemy upchnąc dwa niezależne pojęcia do jednego worka. Co więcej bardzo łatwo jest zrezygnować z konieczności posiadania konstruktora kopiujacego, zmieniając deklarację max na:
template<typename T> const T& max(const T&,const T&);
Teraz argumenty i wartość zwracana przekazywane są przez referencję i nie ma potrzeby kopiowania obiektów.
Logiczne jest więc wydzielenie dwu konceptów: jednego definiującego typy porównywalne, drugiego - typy "kopiowalne". Dalej możemy zauważyć, że istnienie operatora > automatycznie pozwala na zdefiniowanie operatora < poprzez:
bool operator<(const T& a,const T&b) {return b>a;};
Podobnie istnienie konstruktora kopiującego jest blisko związane z istnieniem operatora przypisania.
Tak więc dochodzimy do dwu konceptów: Comparable reprezentującego typy, których obiekty można porównywać za pomocą operatorów < i > oraz Assignable reprezentujacego typy, których obiekty możemy kopiować i przypisywać do siebie. Taką zabawę można kontynuować, pytając np. co z operatorem porównania operator==()?, co z konstruktorem defaultowym? itd. Widać więc, że koncepty to sprawa subietywna, ale to żadna nowość. Wybór używanych abstrakcji jest zawsze sprawą mniej lub bardziej subiektywną i silnie zależną od rozpatrywanego problemu. O tym czy dwa pojęcia włączymy do jednego konceptu czy nie decyduje np. odpowiedź na pytanie czy prawdopodobne jest użycie kiedykolwiek któregoś z tych pojęć osobno?
Tak więc zanim zaczniemy defniować koncepty musimy ustalić w jakim kontekście je rozpatrujemy. Na tym wykladzie kontekstem jest STL i oba wprowadzone koncepty są wzorowane na koncetach z STL-a. Należy jednak nadmienić, że pojęcie konceptu nie pojawia się wprost w definicji stadardu C++. Najlepiej koncepty STL przedstawione są na stronach firmy SGI dokąd Państwa odsyłam.
STL
Standardowa Biblioteka Szablonów (STL) to doskonałe narzędzie programistyczne zawarte w standardzie C++. Stanowi ona również znakomity, niejako sztandarowy, przykład programowania uogólnionego. Na tę bibliotekę można patrzeć więc dwojako: jako rozszerzenie języka C++ o dodatkowe funkcje lub jako na zbiór konceptów stanowiących podstawę do projetowania programów uogólnionych. Ja chciałbym podkreślić tutaj ten drugi aspekt, podkreślając jednak, że dobre poznanie możliwości STL-a może bardzo ułatwić Państwu prace programistyczne.
Biblioteka składa się zasadniczo z dwu części: uogólnionych kontenerów i uogólnionych algorytmów. Trzecią cześcią, niejako sklejającą te dwie, są iteratory.
Kontenery to obiekty służące do przechowywania innych obiektów. Kontenery w STL są jednorodne, tzn. mogą przechowywać tylko zbiory (kolekcje) obiektów tego samego typu. Kluczem do efektywnego programowania uogólnionego jest jednak sprawa ujednolicenia dostępu do zawartości kontenera. Rozważmy dla przykładu dwa typowe kontenery vector i list, implementujące odpowiednio "inteligentną" tablicę oraz listę dwukierunkową. Naturalnym sposobem dostępu do tablicy jest indeksowanie:
std::vector<int> v(10); v[8]=1;
a listy przeglądamy po kolei, przesuwając się o jeden element w przód czy w tył
Uwaga! To nie jest kod STL-owy !!! lista<int> l; l.reset(); ustawia element bieżacy na początek listy for(int i=0;i<8;i++) l.next(); przesuwa element bieżący o jeden element do przodu l.current()=1; zwraca referencję do elementu bieżącego
Widać, że w takim sformułowaniu praktycznie nie jest możliwe napisanie ogólnego kodu np. dodającego wszystkie elementy kontenera czy wyszukującego jakiś element w kontenerze. Ponadto opisany sposób dostępu do listy ogranicza nas do korzystania z jednego bieżącego elementu na raz.
Rozwiązaniem tego problemu zastosowanym w STL jest koncept iteratora, który definiuje abstrakcyjny interfejs dostępu do elementów kontenera. W STL iterator posiada semantykę wskaźnika, w szczególności może być zwykłym wskaźnikiem, choć normalnie jest to wskaźnik inteligentny. Każdy kontener posiada zestaw funkcji zwracających iteratory do swojego początku i na swój koniec. Korzystając z nich można listę przeglądać następująco
std::list<int> l; tu jakoś inicjalizujemy liste for(list<int>::iterator it=l.begin();it!=l.end();it++) { każdy kontener definiuje typ stowarzyszony nazwany iterator cout<<*it<<endl; korzystamy z iteratorów jak ze zwykłych wskaźników } }
Przykładowy ogólny algorytm oparty o iteratory może wyglądać w ten sposób:
template <class InputIterator, class T> T accumulate(InputIterator first, InputIterator last, T init) { T total=init; for(;; first;!= last;++first) total+= *first; return total; }
( Źródło: accumulate.cpp)
Oczywiście nie da się zignorować fundamentalnych różnic pomiędzy listą
a wektorem. Dlatego np. iterator wektora zezwala na konstrukcje
it[i], a iterator listy już nie. Oznacza to, że algorytm, który
działa dla iteratorów wektora (np. sort), nie musi działać dla
iteratora listy. W języku konceptów oznacza to, że
std::vector
Kontenery
Standard C++ definiuje dwa zestawy kontenerów wchodzące w skład STL:
- Sekwencje czyli pojemniki, w których kolejność elementów jest ustalana przez korzystającego z pojemnika (klienta) są to:
- vector
- deque
- list
- Kontenery asocjacyjne, czyli pojemniki, w których klient nie ma kontroli nad kolejnością elementów, są to:
- set
- map
- multiset
- multimap
Ponadto różni dostawcy oferują dodatkowe pojemniki. Na uwagę zasługuje znakomita darmowa implementacja STL firmy Silicon Graphics, która miedy innymi wchodzi w skład pakietu g++ i dostarcza dodatkowo takich kontenerów jak: lista jednokierunkowa slist oraz tablice haszujące hash_set czy hash_map (zob. STL). Hierachię konceptów kontenerów typu sekwencji przedstawia rysunek 2.1, a kontenerów asocjacyjnych rysunek 2.2.
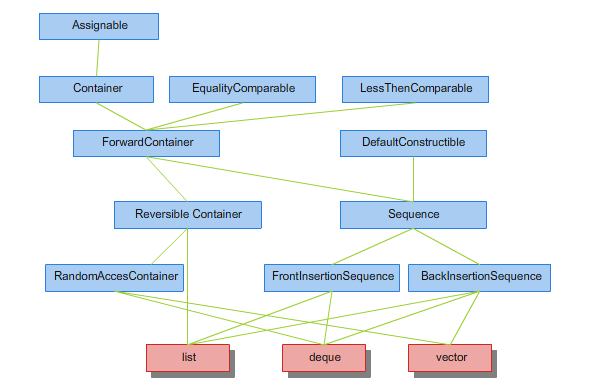 Rysunek 2.1. Hierarchia konceptów dla pojemników typu sekwencyjnego.
Rysunek 2.1. Hierarchia konceptów dla pojemników typu sekwencyjnego.
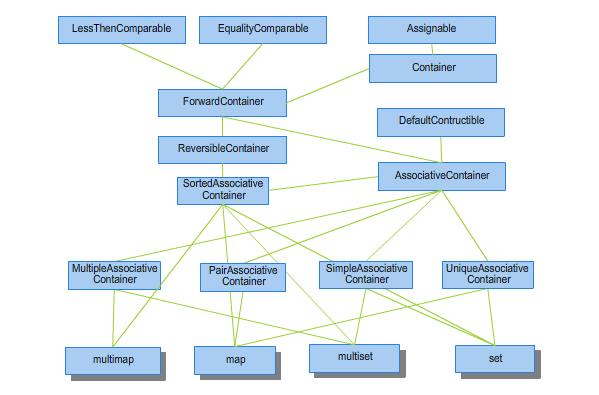 Rysunek 2.2. Hierarchia konceptów dla pojemników typu asocjacyjnego.
Rysunek 2.2. Hierarchia konceptów dla pojemników typu asocjacyjnego.
Nie będę tu omawiał tych wszystkich konceptów. Ich szczegółowe opisy znajdują się na stronie http://www.sgi.com/tech/stl/. Tutaj chciałbym tylko dodać parę luźnych komentarzy.
Po pierwsze, rodzi się pytanie czy taka skomplikowana taksonomia jest potrzebna? W końcu patrząc na rysunki widać, że konceptów jest dużo więcej niż typów kontenerów. Rzeczywiście, do posługiwania się biblioteką w zasadzie wystarczy zaznajomić się z opisami kontenerów i hierarchią iteratorów (zob. rysunek 2.3). Podane klasyfikacje przydają się dopiero kiedy dodajemy własne elementy do biblioteki. Dobierając do implemetacji najbardziej ogólny koncept spełniający nasze wymagania zwiększamy potencjał ponownego użycia naszego kodu z innymi komponentami biblioteki, czy kodem innych developerów.
Kontenery z STL są właścicielami swoich elementów, zniszczenie kontenera powoduje zniszczenie jego elementów. Wszytkie operacje wkładania elementów do kontenera używają przekazywania przez wartość, czyli kopiują wkładany obiekt. Jeżeli chcemy, aby czas życia elementów kontenera był dłuższy od czasu życia kontenera, należy użyć wskaźników.
Kontenery różnią się nie tylko rodzajem iteratorów, jaki implementują, ale również rodzajem operacji, które można wykonać bez unieważnienia istniejących iteratorów. Pokażę to na przykładzie:
std::vector<int>::iterator it; int i; std::vector<int> v(1); std::vector<int> buff(100); staramy się zająć pamięć za v v[0]=0; it=v.begin(); i=(*it); OK, przypisuje i=0 for(int i=0;i<10;++i) v.push_back(i); ponieważ przekraczamy koniec wektora, kontener zaalokuje dodatkową pamięć. Może się to wiązać z koniecznośćią przeniesienia zawartości wektora v w inne miejsce pamięci. To spowoduje, że wskaźnik it przestanie pokazywać na początek wektora v std::cerr<<(*it)<<std::endl ; niezdefiniowane std::cerr<<"iterator nieprawidlowy"<<std::endl; for(;it != v.end(); ++it) potencjalnie nieskończona pętla std::cerr<<*it<<std::endl; ; std::cerr<<"iterator prawidlowy"<<std::endl; for(it=v.begin();it != v.end(); ++it) std::cerr<<*it<<std::endl; ;
( Źródło: invalid.cpp)
Bardzo Państwa na ten problem uczulam. Efekt działania powyższego kodu jest gorzej niż zły: jest niezdefiniowany!, tzn. będzie zależał od implementacji kompilatora, od zadeklarownych wcześniej zmiennych itp. Proszę np. spróbować wykomentować linijkę
std::vector<int> buff(100); staramy się zająć pamięć za v
i porównać wynik działania programu. Może się również zdarzyć, że program zadziała poprawnie (wbrew pozorom jest to najgorsza możliwa sytuacja!).
Ważne są gwarancje złożoności metod kontenera. Ewidentnie każdy rodzaj kontenera może dostarczyć każdego rodzaju operacji, różny będzie jednak czas ich wykonywania. I tak rząd O(1) jest gwarantowany w operacji indeksowania wektora. Natomiast operacja dodania elementu w środku wektora jest rzędu O(N). Z listą jest odwrotnie i dlatego listy w STL nie posiadają operacji indeksowania.
Nie wszystkie własności kontenerów są zdefiniowane w konceptach. Każdy kontener może definiować dodatkowe metody właściwe tylko dla niego.
Iteratory
Iteratory to koncept, który uogólnia pojęcie wskaźnika. Hierarchię konceptów iteratorów przedstawia rysunek 2.3. Zaznaczono na nim również które koncepty kontenerów wymagają danego modelu iteratora.
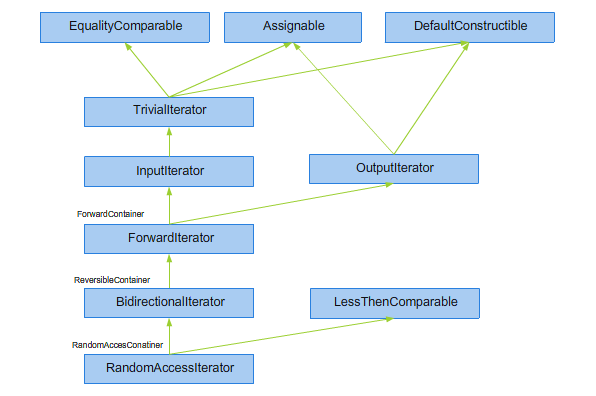 Rysunek 2.3. Hierarchia konceptów dla iteratorów.
Rysunek 2.3. Hierarchia konceptów dla iteratorów.
Najprostsze iteratory pojawiające sie w STL-u to iteratory wejściowe i wyjściowe. Wprawdzie żaden kontener nie posiada iteratorów tego typu, ale iteratory wejściowe, umożliwiające tylko jednoprzebiegowe odczytanie wartości kontenera, są częstym wymaganiem dla argumentów algorytmów nie zmieniających elementów kontenera (non mutable algorithms).
Należy pamiętać, że iterator nie wie na jaki kontener wskazuje, czyli poprzez iterator nie ma dostępu do interfejsu kontenera.
Iteratory pozwalają na określanie zakresu elementów w kontenerze poprzez podanie iteratora wskazującego na początek i na pierwszy element poza końcem zakresu. Zakres oznaczamy poprzez (it1,it2) (zob. rysunek 2.4).
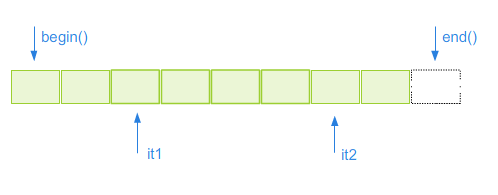 Rysunek 2.4. Zakres.
Rysunek 2.4. Zakres.Z tego powodu dozwolona jest instrukcja pobrania adresu pierwszego elementu poza końcem tablicy.
double x[10]; double *end=&x[10]; //zwykłe wskażniki mogą być użyte jako iteratory std::cout<<accumulate(x,end,0)<<endl; <i>suma elementów tablicy</i>
Każdy kontener posiada motody begin() i end(), zwracające iterator na początek i "poza koniec". Typowa pętla obsługi kontenera wygląda więc następująco:
typedef vector<int>::iterator iterator; vector<it> v(100); for(iterator it=v.begin();it!=v.end();++it) { ... }
( Źródło: accumulate.cpp)
Proszę zwrócić uwagę na wykorzystanie operatora != do sprawdzenia końca zakresu. Tylko iteratory o dostępie swobodnym mogą być porównywane za pomocą operatora operator<(). Reszta jest tylko EqualityComparable.
Algorytmy
Algorytmy działają na zakresach elementów kontenera definiowanych przez dwa iteratory, a nie na kontenerach. Umożliwia to jednolity dostęp do różnych kontenerów. Takie podejście ma też inne konsekwencje, jak już pisałem iterator nie wie z jakiego kontenera pochodzi, w szczególności oznacza to, że algorytmy ogólne nie mogą usuwać elementów z kontenera.
Oczywiście część algorytmów, np. sort, wymaga bardziej wyrafinowanych iteratorów, nie dostarczanych przez każdy kontener. Wiele jednak jednoprzebiegowych algorytmów zadawala się iteratorami wejściowymi.
Poza iteratorami uogólnione algorytmy wykorzystują obiekty funkcyjne czyli funktory. Obiekt funkcyjny to koncept będący uogólnieniem pojęcia fukcji, czyli coś do czego można zastosować składnię wywołania funkcji. W C++ mogą to być funkcje, wskaźniki do funkcji oraz obiekty klas, w których zdefiniowano operator()(...) .
Funktory w STL są podzielone ze względu na liczbę argumentów wywołania. Generator nie przyjmuje żadnego argumentu, UnaryFunction posiada jeden argument, a BinaryFunction - dwa argumenty wywołania. Ważną podklasą są funkcje zwracające wartość typu bool, nazywane predykatami. Rozróżniamy więc UnaryPredicate i BinaryPredicate.
Żeby zilustrować użycie algorytmów i funktorów rozważmy następujący przykład. Najpierw definiujemy funktor, który posłuży nam do generowania sekwencji obiektów:
template<typename T> class SequenceGen { private: T _start; T _step; public: SequenceGen(T start = T(),T step = 1 ): _start(start),_step(step){}; T operator()() {T tmp=_start; _start+=_step; return tmp;} };
( Źródło: bind.cpp)
Za pomocą obiektu klasy SequenceGen możemy wypełnić wektor sekwencją 20 pierwszych nieparzystych liczb całkowitych:
const size_t n = 20 ; vector<int> v(n); generate_n(v.begin(),n,SequenceGen<int>(1,2));
( Źródło: bind.cpp)
Standardowy algorytm
template <class OutputIterator, class Size, class Generator> OutputIterator generate_n(OutputIterator first, Size n, Generator gen);
służy właśnie do wypełniania kontenerów za pomocą n kolejnych wyników wywołania funktora gen. Powyższy kod ilustruje typowy sposób opisu algorytmów w STL. Nazwy parametrów szablonu odpowiadają nazwom konceptów, które muszą modelować.
W tak wypełnionym kontenerze poszukamy pierwszego elementu większego od czterech (powinno to być pięć). Służy do tego algorytm
template<class InputIterator, class Predicate> InputIterator find_if(InputIterator first, InputIterator last, Predicate pred);
Który przeszukuje zakres [first,last) do napotkania pierwszego elementu, dla którego predykat pred jest prawdziwy i zwraca iterator do tego elementu. Jeśli takiego elementu nie ma, to find_if zwraca last. Do zakończenia programu potrzebujemy jeszcze predykatu, który testuje czy dana wartość jest większa od czterech. Zamiast go implementować skorzystamy z adaptera funkcji bind2nd. Ta funkcja przyjmuje funktor dwuargumentowy (AdaptableBinaryFunction) F(T,U) i jakąś wartość x typu U i zwraca funktor jednoparametrowy F(T,x). Korzystając z predefiniowanego predykatu greater możemy napisać:
vector<int>::iterator it= find_if(v.begin(),v.end(), bind2nd(greater<int>(),4)); if(it!=v.end()) cout<<*it<<endl; else cout<<"nie znaleziono zadanego elementu"; }
( Źródło: bind.cpp)
STL wprowadza więc do C++ elementy programowania funkcyjnego.
Debugowanie
Sprawdzanie konceptów
Programowanie uogólnione korzysta istotnie z pojęcia konceptu. Koncept opisuje abstrakcyjne typy danych (czy funkcji), które mogą być użyte jako argumenty danego szablonu. Definiowanie konceptu polega tylko na jego opisie. C++ nie posiada żadnego mechanizmu pozwalającego na bardziej formalną definicję. Co za tym idzie, nie można też automatycznie sprawdzać czy nasz typ modeluje żądany koncept.
Oczywiście kompilator podczas konkretyzacji szablonu sprawdza syntaktyczną zgodność przekazanego typu z wymaganiami szablonu. Nie jest to jednak idealne narzędzie diagnostyczne. Po pierwsze, komunikat o błedzie może być bardzo zawiły i na pewno nie będzie się odnosił do nazwy konceptu. Po drugie, może się okazać, że szablon, który konkretyzujemy nie wykorzystuje wszystkich możliwych wyrażeń konceptu. Zresztą idea konceptu polega na rozdzieleniu definicji abstrakcyjnego typu od definicji szablonu, którego ten typ może być argumentem. Rozwiazaniem jest napisanie własnego zestawu szablonów, których jedynem zadaniem jest sprawdzanie zgodności przekazanych argumentów szablonu z definiowanym przez ten szablon konceptem. Niestety, można w ten sposób sprawdzać tylko zgodność syntaktyczną.
Idea tworzenia takich szablonów jest prosta (zob. http://www.boost.org/libs/concept_check/concept_check.htm): dla każdego konceptu tworzymy szablon zawierający funkcję constraints(), która zawiera wszystkie możliwe poprawne wyrażenia dla danego konceptu. Np. dla konceptu Comparable możemy zdefiniować:
template<typename T> struct ComparableConcept { void constraints() { require_boolean_expr( a > b); require_boolean_expr( a < b); }; T a,b; };
( Źródło: concept_check.cpp)
Szablon require_boolean_expr
template <class TT> void require_boolean_expr(const TT& t) { bool x = t; ignore_unused_variable_warning(x); używa zmiennej x aby kompilator nie generował ostrzeżenia }
( Źródło: concept_check.cpp)
sprawdza czy jego argument, a więc wartość zwracana przez operatory, może być konwertowana na bool.
Zwracam uwagę, że nie możemy w kodzie szablonu Comparable użyć defaultowego konstruktora, bo nie jest on wymagany. Dlatego zmienne a i b nie były zdefiniowane wewnątrz funkcji constraints(), tylko jako pola składowe klasy. Ponieważ nie tworzymy żadnej instancji tej klasy, to nie będą wywoływane konstruktory, a więc kompilator nie będzie generował ich kodu.
Teraz potrzebujemy jeszcze sposobu, aby skompilować, ale nie wywołać,
funkcję ComparableConcept
template <class Concept> inline void function_requires() { void (Concept::*x)() = &Concept::constraints; ignore_unused_variable_warning(x); }
( Źródło: concept_check.cpp)
Możemy teraz używać szablonu Comparable w następujący sposób:
main() { function_requires<ComparableConcept<int> >(); function_requires<ComparableConcept<std::complex> >(); błąd }
( Źródło: concept_check.cpp)
Bardziej skomplikowane koncepty możemy sprawdzać korzystając z klas sprawdzających dla innych konceptów, np:
template <class Container> struct Mutable_ContainerConcept { typedef typename Container::value_type value_type; typedef typename Container::reference reference; typedef typename Container::iterator iterator; typedef typename Container::pointer pointer; void constraints() { sprawdzamy czy spełnia wymagania konceptu Container function_requires< ContainerConcept<Container> >(); function_requires< AssignableConcept<value_type> >(); function_requires< InputIteratorConcept<iterator> >(); i = c.begin(); i = c.end(); c.swap(c2); } iterator i; Container c, c2; };
Biblioteka boost, skąd wzięty został ten przykład, posiada implementację szablonów dla każdego konceptu z STL (http://www.boost.org/libs/concept_check/concept_check.htm). Hierachia, którą można tam odczytać, różni się trochę od tej, którą wcześniej zaprezentowałem i która jest opisana w http://www.sgi.com/tech/stl/. Główna różnica to wprowadzenie rozróżnienia pomiędzy kontenerami, które umożliwiaja modyfikację swoich elementów (MutableContainer) i tych, które na to nie pozwalają (Container).
Archeotypy
Klasy sprawdzające koncepty służą do pomocy w implementacji typów będących modelami danego konceptu. Możemy jednak mieć sytuację odwrotną: implementujemy jakiś algorytm ogólny i chcemy się dowiedzieć jaki koncept jest wymagany dla parametrów szablonu? Chcemy wybrać jak najogólniejszy koncept, który jeszcze pozwala na poprawne działanie algorytmu. Pomóc mogą nam w tym archeotypy. Są to klasy, które dokładnie implementują interfejs danego konceptu. Opierając się na http://www.boost.org/libs/concept_check/concept_check.htm, przedstawię teraz implementację archeotypu dla konceptu Comparable.
Koncept Comparable nie wymaga posiadania konstruktora defaultowego, konstruktora kopiujacego oraz operatora przypisania, dlatego w naszym archeotypie zdefiniujemy je jako prywatne:
class comparable_archetype { private: comparable_archetype() {}; comparable_archetype(const comparable_archetype &) {}; comparable_archetype &operator=(const comparable_archetype &) { return *this;}; public: comparable_archetype(dummy_argument) {}; };
( Źródło: archeotype.cpp)
Aby móc tworzyć obiekty typu comparable_archetype dodaliśmy niestandardowy konstruktor z argumentem sztucznego typu:
class dummy_argument {};
używanego tylko na tę okazję (jego nazwa powinna być unikatowa).
Operator operator<() nie musi zwracać wartości typu bool, a jedynie wartość typu konwertowalnego na bool, dlatego tworzymy taki typ:
struct boolean_archetype { operator const bool() const {return true;} };
i podajemy go jako typ zwracany przez operatory porównania
boolean_archetype operator<(const comparable_archetype &, const comparable_archetype &){ return boolean_archetype(); }; boolean_archetype operator>(const comparable_archetype &, const comparable_archetype &){ return boolean_archetype(); };
( Źródło: archeotype.cpp)
Teraz możemy już przetestować nasz szablon max.
template<typename T> const T &max(const T &a,const T &b) {return (a>b)?a:b;} main() { comparable_archetype ca(dummy_argument()); max(ca,ca); }
( Źródło: archeotype.cpp)
Poprawna kompilacja tego kodu przekonuje nas, że koncept Comparable jest wystarczajacy, przynajmniej syntaktycznie. Proszę zwrócić uwagę, że jeśli użyjemy orginalnego szablonu
template<typename T> T max(T a,T b) {return (a>b)?a:b;}
( Źródło: archeotype.cpp)
to kod się nie skompiluje, bo zabraknie konstruktora kopiujacego.
Większość konceptów jest uszczegółowieniem innych konceptów. Implementacja archeotypów w biblitece boost zezwala na takie konstrukcje i gorąco zachęcam do zapoznania się z nią.
| Załącznik | Wielkość |
|---|---|
| Shape.h | 463 bajty |
| Rectangle.h | 510 bajtów |
| Circle.h | 374 bajty |
| Draw.cpp | 119 bajtów |
| Draw_template.h | 310 bajtów |
| Accumulate.cpp | 891 bajtów |
| Invalid.cpp | 974 bajty |
| Bind.cpp | 518 bajtów |
| Concept_check.cpp | 742 bajty |
| Archeotype.cpp | 990 bajtów |
Szablony II
Wprowadzenie
Mechanizm szablonów jest bardzo użyteczny ale może się okazać, że kod ogólny, który szablon implementuje, nie nadaje się do stosowania w każdym przypadku. W tej sytuacji mamy do dyspozycji dodatkowe własności implementacji szablonów w C++: przeciążanie i specjalizację. W poniższym wykładzie omówię sposób stosowania tych mechanizmów i różnice pomiędzy nimi.
Przeciążanie szablonów funkcji
Przeciążenie szablonu funkcji, podobnie jak przeciążenie zwykłych funkcji, definiuje nam nowy szablon. Możemy za pomocą przeciążenia zdefiniować np. funkcję służącą do znajdywania maksymalnego elementu w tablicy:
template<typename T> T max(T *data,size_t n) { T _max = data[0]; for(size_t i=0;i<n;i++) if(data[i]>_max) _max=data[i]; return _max; }
Oba szablony: powyższy i wcześniej zdefiniowany
template<typename T> T max(T a,T b) {return (a>b)?a:b;};
Przykład 3.1
mogą ze sobą współistnieć i kompilator automatycznie wybierze poprawną definicję na podstawie argumentów wywołania funkcji. Oczywiście w obu przypadkach zadziała mechanizm automatycznej dedukcji argumentu szablonu.
int i,j,k; double x,t[20]; k=max(i,j); //wywołanie max(int,int) x=max(t,k); //wywołanie max<double>(double *,int)
( Źródło: max_overload.cpp)
Możemy jednak chcieć nie tyle zdefiniować nową funkcję, ile zmienić kod już istniejącego szablonu, tak aby dla pewnego podzbioru parametrów działał inaczej. Np. działanie funkcji max dla dwu wskaźników nie koniecznie jest tym, czego byśmy sobie życzyli. Możemy się spodziewać, że w tej sytuacji funkcja powinna zwrócić wskaźnik do większej wartości, a nie wskaźnik o wyższym adresie. Definiujemy więc nowy przeciążony szablon funkcji max:
template<typename T> T* max(T *a, T *b) { return ((*a)>(*b))?a:b; }
( Źródło: max_overload.cpp)
Przykład 3.2
Teraz sytuacja nie jest już jednoznaczna. Kompilator, napotykając wyrażenie
int i,j; max(&i,&j);
może dopasować zarówno oryginalny szablon 3.1 z T = int* lub szablon 3.2 z T = int. I choć wydaje się że, otrzymamy błąd kompilacji, to do głosu dochodzi mechanizm rozstrzygania przeciążenia i kompilator wybierze dopasowanie drugiego szablonu jako “bardziej wyspecjalizowanego”, tzn. do którego pasuje mniejszy zbiór argumentów. Ewidentnie algorytm rozstrzygania przeciążenia szablonów funkcji nie jest prosty, polega on na częściowym porządkowaniu przeciążonych funkcji według stopnia ich specjalizacji. Dokładny opis tego algorytmu można znaleźć w D. Vandervoorde, N. Josuttis "C++ Szablony. Vademecum profesjonalisty", rozdz. 12. Z grubsza rzecz biorąc szablon funkcji F jest bardziej wyspecjalizowany niż szablon G jeśli każdy zestaw argumentów, który da się dopasować do F da sie również dopasować do szablonu G, ale nie na odwrót. W naszym przypadku do szablonu 3.2 da się dopasować argumenty typu (T *,T *), które ewidentnie można dopasować również do szablonu 3.1. Na odwrót już nie: (int,int) pasuje do 3.1, a do szablonu 3.2 nie.
Specjalizacja szablonów funkcji
Przy dotychczasowych definicjach szablonów max
template<typename T> T max(T a, T b); //(1) template<typename T> T* max(T *a, T *b); //(2) template<typename T> T max(T *data,size_t n); //(3)
będziemy dalej mieli kłopoty z funkcją max wywołaną dla argumentów typu char*. Takie argumenty zwyczajowo oznaczają napisy. Zgodnie z tym, co napisałem wcześniej, wywołany zostanie dla nich przeciążony szablon (2) i porówna tylko pierwsze litery napisów, co ewidentnie nie jest tym czego się oczekuje.
Na szczęście można dokonać specjalizacji tego szablonu dla argumentów typu char * i const char *:
template<> char *max<char *>(char *a,char *a) { return (strcmp(a,b)>0)?a:b; } template<> const char* max<const char *>(const char *a,const char *a) { return (strcmp(a,b)>0)?a:b; }
Jak zwykle możemy pominąć argumenty szablonu podane w nawiasach ostrych za nazwą szablonu, jeśli mogą być one wydedukowane na podstawie argumentów wywołania i najczęściej spotkamy się z następującym kodem:
template<> char *max(char *a,char *a) { return (strcmp(a,b)>0)?a:b; } template<> const char* max(const char *a,const char *a) { return (strcmp(a,b)>0)?a:b; }
( Źródło: max_spec.cpp)
Powyższe specjalizacje są pełne, tzn. określają dokładnie wszystkie argumenty wywołania szablonu. Dlatego lista parametrów szablonu w tych szablonach jest pusta. Tylko takie specjalizacje są dozwolone dla szablonów funkcji. Specjalizacja, w przeciwieństwie do przeciążenia, musi dotyczyć już istniejącego szablonu. Dlatego niedozwolona jest specjalizacja:
template<> const char* max<char *>(char *a,const char *a) { return (strcmp(a,b)>0)?a:b;}
( Źródło: max_spec.cpp)
Przykład 3.3
ponieważ argumenty są typu char * i const char *, i jako takie nie pasują do żadnego z istniejących szablonów (1-3). Musimy więc zdefiniować kolejne przeciążenie:
template<typename T> const T* max(T *a,const T*b) { return (*a)>(*b))?a:b; }
i dopiero wtedy kompilacja kodu 3.3 jest możliwa. Sytuację podsumowuje rysunek 3.1.
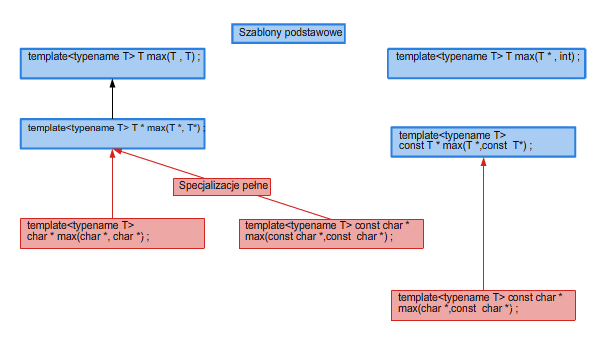 Rysunek 3.1.
Rysunek 3.1.
Jawne podstawienie argumentów szablonu w miejsce parametru może prowadzić, w przypadku istnienia szablonów przeciążonych, do powstanie szeregu przeciążonych funkcji. Wtedy obowiązują "zwykłe" reguły rozstrzygania przeciążenia, np. wyrażenie
max<int>(0,0);
spowoduje "wygenerowanie" trzech funkcji:
int max(int,int); int *max(int *,int*); int max(int *,int);
( Źródło: max_over_explicit.cpp)
Ponieważ zero lepiej pasuje do int-a niż do wskaźnika na int, wybrana zostanie pierwsza z powyższych funkcji.
Funkcje zwykłe a szablony
Obok szablonów mogą istnieć zwykłe funkcje o tej samej nazwie. Algorytm rozstrzygający przeciążenie preferuje dopasowanie zwykłych funkcji nad szablonami, więc jeśli zdefiniujemy sobie funkcję
int max(int i, int j);
to kompilator dokona następujących podstawień:
max(0,1); //zwykla funkcja int max(int,int) max(0,1.0); //zwykla funkcja int max(int,int) z rzutowaniem double na int max(1.0,1.0); //szablon max<double>(double, double)
( Źródło: max_func.cpp)
Z pozoru specjalizacje pełne opisane w poprzedniej części zachowują się jak zwykłe funkcje i moglibyśmy napisać:
char *max(char *a,char *a) { return (strcmp(a,b)>0)?a:b;}
zamiast
template<> char *max<char *>(char *a,char *a) { return (strcmp(a,b)>0)?a:b;}
Jest tak jednak tylko, jeśli możliwa jest dedukcja argumentów szablonu. W przypadku szablonu
template<typename T,typename U> T convert(U u) { return static_cast<T>(u); };
możemy zdefiniować np. specjalizacje:
template<> int convert<int,double>(double u) {...}; template<> double convert<double,double>(double u) {...};
i używać ich podając jawnie pierwszy, niededukowalny argument szablonu:
convert<int>(3.14); convert<double>(2.71);
natomiast zdefiniowanie dwóch funkcji o tej samej nazwie i argumentach wywołania, różniących się tylko zwracanym typem, nie jest możliwe.
Nieudane podstawienie nie jest błędem
Jawne podstawienie wszystkich argumentów szablonu funkcji generuje nam jedną lub więcej funkcji "zwykłych". Może się jednak zdażyć, że niektóre podstawienia generują niepoprawny kod:
template<typename T> typename T::value t(T x) { cerr<<"t1"<<endl; };
Wywołanie
t<int>(0);
( Źródło: sfinae.cpp)
prowadzi do int::value i jest nieprawidłowe. Spowoduje to błąd kompilacji, ale tylko wtedy, jeśli nie będzie innych przeciążonych szablonów funkcji t. Jeśli dodamy przeciążenie
template<typename T> void t(T x ) {cerr<<"t2"<<endl;};
( Źródło: sfinae.cpp)
to wyrażenie t
Specjalizacje szablonów klas
Podobnie jak dla szablonów funkcji również dla szablonów klas istnieje możliwość podania różnych implementacji dla różnych zestawów argumentów szablonu. W przeciwieństwie jednak do szablonów funkcji, szablony klas nie mogą być przeciążane, a jedynie specjalizowane. Oznacza to, że w programie może istnieć tylko jeden szablon podstawowy o danej nazwie. Szablon podstawowy to szablon, w którego definicji nie występują nawiasy ostre po nazwie szablonu. Wszystkie szablony prezentowane do tej pory były podstawowe. Z tej reguły wynika, że trzy zdefiniowane do tej pory szablony stosu
template<typename T> Stack {...}; template<typename T,int N = 100> Stack {...}; //błąd szablon Stack już istnieje template<typename T,template<typename X> C> Stack { C<T> _rep; } //błąd szablon Stack już istnieje
nie mogą istnieć razem! Oczywiście w przypadku zastosowania domyślnych parametrów szablonu pierwsza definicja jest niepotrzebna, ale również bardziej pożyteczny trzeci szablon jest niedozwolony.
To ograniczenie można po części obejść, dokonując specjalizacji częściowej, która jest dozwolona tylko dla szablonów klas i daje możliwość specjalizacji szablonu dla pewnego podzbioru jego argumentów, a nie dla pojedynczego zestawu, jak specjalizacja pełna. Oczywiście specjalizacja pełna też jest możliwa. Rozważmy następujący przykład, definiując szablon podstawowy:
template<typename T,int N = 100> class Stack {};
możemy dokonać następujących specjalizacji:
template<typename T> class Stack<T,666> {}; template<typename T,int N> class Stack<T*,N> {}; template<int N> class Stack<double ,N> {}; template<int N> class Stack<int *,N> {}; template<> class Stack<double,666>{}; template<> class Stack<double *,44> {};
( Źródło: stack_spec.cpp)
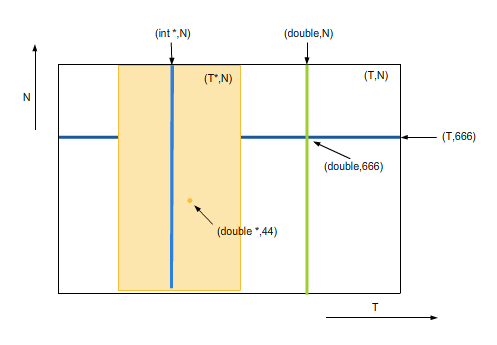 Rysunek 3.2. Symboliczne przedstawienie zbiorów argumentów dla różnych specjalizacji szablonu Stack
Rysunek 3.2. Symboliczne przedstawienie zbiorów argumentów dla różnych specjalizacji szablonu StackKażda z tych specjalizacji definiuje pewien podzbiór parametrów szablonu podstawowego (zob. rysunek 3.2). Jeśli któryś z podzbiorów zawiera się w drugim, to mówimy, że jedna specjalizacja jest bardziej wyspecjalizowana od drugiej. Hierarchia specjalizacji dla powyższego przykładu pokazana jest na rysunek 3.3. Jeżeli jakiś zestaw parametrów należy do dwóch (lub więcej) podzbiorów, które się przecinaja, ale żeden nie zawiera się w drugim, to dla tych parametrów kompilator nie bedzie w stanie wybrać specjalizacji.
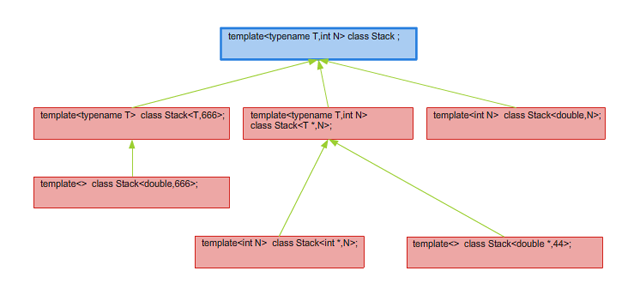 Rysunek 3.3. Uporządkownie specjalizacji szablonu Stack
Rysunek 3.3. Uporządkownie specjalizacji szablonu StackOczywiście ten przykład jest bardzo sztuczny i trudno sobie wyobrazić powód tworzenia takich specjalizacji. Rozważmy bardziej realistyczny przypadek: deklarujemy szablon podstawowy, ale bez podawania jego definicji; będziemy korzystać jedynie z jego specjalizacji:
template<typename T,int N = 100, typename R = T*> class Stack;
Następnie definiujemy dwie specjalizacje. Pierwszą dla stosów opartych o zwykłe tablice:
template<typename T,int N> class Stack<T,N,T*> { T _rep[N]; unsigned int _top; public: Stack():_top(0){}; void push(T e) {_rep[_top++]=e;} T pop() {return _rep[--_top];} };
i drugą opartą o kontenery STL:
template<typename T,int N,template<typename E> class Sequence> class Stack<T,N,Sequence<T> > { Sequence<T> _rep; public: void push(T e) {_rep.push_back(e);}; T pop() {T top = _rep.top();_rep.pop_back();return top;} bool is_empty() const {return _rep.empty();} };
( Źródło: Stack_2.cpp)
Korzystając z tych specjalizacji możemy pisać następujący kod.
main() { Stack<int,100,int *> s_table; Stack<int,100> s_default ; Stack<int,0,std::vector<int> > s_container; }
( Źródło: Stack_2.cpp)
W każdym przypadku kompilator wybierze implementację odpowiednią dla podanych parametrów.
Szablony a dziedziczenie
Szablony klas mogą oczywiście dziedziczyć z innych klas. Deklaracja
template<typename T> Stack: public Container { ... };
oznacza, że każda instancja danego szablonu Stack
class special Stack_int : public Stack<int> {...}
Definiując specjalizację szablonu klasy możemy dziedziczyć z innych specjalizacji tej samej klasy; nie może to jednak prowadzić do rekurencji. Jeśli napiszemy:
template<typename T,int N> Stack {...}; template<typename T> Stack<T*,N>: private Stack<void *,N> {...};
( Źródło: stack_void.cpp)
to kompilator odmówi skompilowania tego kodu z powodu rekurencyjnej definicji specjalizacji szablonu Stack. Wszystko będzie w porządku jeśli dodamy specjalizację dla typu void *:
template<int N> class Stack<void *,N> {...}
( Źródło: stack_void.cpp)
Dlaczego mielibyśmy jednak dziedziczyć implementację klasy void*?
Powodem jest unikanie powielania kodu. Ponieważ każda konkretyzacja
(instancja) szablonu jest osobną klasa, to dla każdej generowany jest
pełny kod potrzebnych funkcji. Jeśli te funkcje są proste, to
nie jest to kłopot. W praktyce implementacja stosu musi zwykle
uwzględniać dynamiczne zarządzanie pamięcią i może być dużo bardziej
skomplikowana, a zatem generowany kod będzie odpowiednio większy.
Ogólnie jest to nie do uniknięcia, ale ponieważ wszystkie wskaźniki
mają ten sam rozmiar i można je rzutować na void * to możemy
wykorzystać implementację Stack
template<typename T,size_t N> Stack<T*,N>: private Stack<void *,N> { public: T* pop() { return static_cast<T*>(Stack<void *>::pop()); }; void push(T *e) { Stack<void *>::push(e); } bool is_empty() {return Stack<void *>::is_empty();} };
( Źródło: stack_void.cpp)
Korzystamy tu z automatycznej konwersji T* na void *. W ten
sposób, np. kod funkcji Stack
Zależne klasy bazowe
Szablon klasy może również dziedziczyć z innego szablonu klasy, którego argumenty bedą zależały od jego parametrów:
template <typename T> class Base<T> {...}; template<typename S> class Derived: public Base<S> {};
Przy tych definicjach klasa Derived
Z zależnymi klasami bazowymi wiąże się jednak pewna zasada, związana z wyszukiwaniem nazw, która może być sporym zaskoczeniem. Rozważmy następujący przykład:
template<typename T> class Base { public: Base():basefield(0){}; int basefield; }; template<typename T> class DD :public Base<T> { public: void f() {std::cerr<<basefield<<std::endl;} };
( Źródło: base.cpp)
Ten kod się nie skompiluje przy pomocy kompilatora C++ zgodnego ze standardem. Np. nie skompiluje go kompilator g++-3.4, a g++-3.3 tak. Powód tego faktu jest następujący: nazwa basefield, występująca w klasie DD jest nazwą niezależną (od parametru szablonu). Klasa bazowa, w której ta nazwa jest zdefiniowana jest klasą bazową zależną (od parametru szablonu). Według standardu kompilator nie wyszukuje nazw niezależnych w zależnych klasach bazowych. Kompilator g++-3.4 jest bliżej stadardu niż g++-3.3 i stąd to całe zamieszanie. Aby kod się skompilował należy uczynić tę nazwę zależną, np. poprzez kwalifikowanie jej nazwą klasy:
template<typename T> class DD :public Base<T> { public: void f() {std::cerr<<DD::basefield<<std::endl;} };
( Źródło: base.cpp)
lub przez
template<typename T> class DD :public Base<T> { public: void f() {std::cerr<<this->basefield<<std::endl;} };
( Źródło: base.cpp)
CRTP
Dziedziczenie szablonów można też wykorzystać do przydatnej "sztuczki", zwanej po angielsku "couriously reccuring template pattern" (autorem tego idiomu jest James O. Coplien). Rozważmy następujący problem: chcemy zaimplementować mechanizm automatycznego liczenia ilości obiektów danej klasy. To standardowe zadanie na zastosowanie konstruktorów, destruktorów i statycznych składowych klasy:
class Countable { protected: static size_t _counter; public: Countable() {++_counter;} Countable(const Countable &) {++_counter;} virtual ~Countable {--_counter} static size_t counter() {return _counter;} }; size_t Countable::_counter = 0;
Oczywiście wpisywanie tego kodu do każdej klasy, której obiekty chcemy zliczać jest nużące i łamie zasadę niepowielania kodu. Postaramy się więc wykorzystać kod klasy Countable, dziedzicząc go w innych klasach:
class MyClass1 : public Countable { ... }; class MyClass2 : public Countable { ... };
Niestety ponieważ obie klasy MyClass1 i MyClass2 dziedziczą z tej samej klasy, dziedziczą również ten sam wspólny licznik. Tak więc zliczaniu podlegać będą obiekty obu klas wspólnie. W rozwiązaniu pomogą nam szablony. Wystarczy uczynić klasę Countable szablonem
template<typename T> class Countable { protected: static size_t _counter; public: Countable() {++_counter;} Countable(const Countable &) {++_counter;} virtual ~Countable() {--_counter} static size_t counter() {return _counter;} }; template<typename T> size_t Countable<T>::_counter = 0;
( Źródło: countable.cpp)
i używać go w następujący sposób:
class MyClass1 : public Countable<MyClass1> { ... }; class MyClass2 : public Countable<MyClass2> { ... };
( Źródło: countable.cpp)
Ponieważ każda konkretyzacja szablonu jest osobną klasą, klasy MyClass1 i MyClass2 dziedziczą z różnych klas bazowych i będą posiadać różne liczniki, ale ciągle wspólne w ramach każdej klasy. Parametryzowanie klasy bazowej typem klasy dziedziczącej gwarantuje jej unikatowość.
| Załącznik | Wielkość |
|---|---|
| max_overload.cpp | 506 bajtów |
| Max_spec.cpp | 953 bajty |
| Max_over_explicit.cpp | 393 bajty |
| Sfinae.cpp | 307 bajtów |
| Stack_spec.cpp | 968 bajtów |
| Stack_2.cpp | 672 bajty |
| Stack_void.cpp | 1010 bajtów |
| Base.cpp | 364 bajty |
| Countable.cpp | 661 bajtów |
Testowanie
Wstęp
Programowanie rozumiane jako pisanie kodu jest tylko częścią procesu tworzenia oprogramowania. Analiza i opis tego procesu jest przedmiotem inżynierii oprogramowania i znacznie wykracza poza ramy tego wykładu. Niemniej chciałbym pokrótce w tym wykładzie poruszyć jedno zagadnienie związane bezpośrednio z programowaniem - testowanie. Testowanie jest nieodłączną częścią programowania i powinno być obowiązkiem każdego programisty. Jak będę się starał Państwa przekonać, testowanie to może być coś więcej niż "tylko" sprawdzenie poprawności kodu.
Testowanie
Testowanie wydaje się oczywistą koniecznością w przypadku każdego programu komputerowego (choć co rok zdarza mi się spotkać studentów przekonanych o swojej nieomylności:)). Mniej oczywiste jest stwierdzenie kto, gdzie, kiedy i co ma testować. To w ogólności bardzo złożony problem, ale tu chciałbym się ograniczyć do tzw. testów jednostkowych. Wyrażenie "test jednostkowy" należy interpretować jako test jednej jednostki. Przez pojedynczą jednostkę będziemy rozumieli: funkcję, metodę lub klasę. Zadaniem takiego testu jest sprawdzenie czy dana jednostka działa poprawnie.
Dlaczego w ogóle pisać takie testy? Czy nie wystarczy przetestowanie całego programu? Testować cały program też oczywiście trzeba. Służą do tego liczne testy odbioru, integracyjne itp., wykonywane poprzez dedykowane zespoły. Ale im większą część kodu testujemy, tym trudniejsze są testy i tym trudniej będzie znaleźć przyczynę wykrytej nieprawidłowości działania programu. Testy jednostkowe wykrywają błędy (a przynajmniej ich część) "u źródła", często w bardzo prostym kodzie, a więc ich poprawianie może być dużo szybsze.
Jak się zastanowić, to testowanie każdej wykonanej jednostki przed użyciem jej w dalszym kodzie powinno być oczywistą koniecznością. No, ale równie oczywiste jest, że należy uprawiać sporty, nie palić papierosów, nie jeździć po pijanemu, itp. Statystyki dobitnie jednak pokazują, że natura człowiecza grzeszną jest i łatwo ulegamy słabościom, w tym wypadku pokusie nietestowania programów, a powodem jest jeden z siedmiu grzechów głównych czyli lenistwo. Testy nie piszą, ani nie wykonuja się same, w rzeczywistości wymagają całkiem sporego nakładu pracy (czasami większego niż pisanie testowanego kodu!). Część programistów traktuje ten wysiłek jako "czas stracony", tzn. nie wykorzystany na pisanie kodu, za który im płacą.
To wszystko jest prawdą, ale w rzeczywistości nie możemy uniknąć tej straty czasu. Jest to tylko kwestia wyboru gdzie i ile tego czasu stracimy: czy na pisanie testów w trakcie kodowania jednostek i poprawianie prostych błędów, czy na szukanie błędów w dużo większych fragmentach programu? Doświadczenie wykazuje, że czas potrzebny na znalezienie i poprawienie błędu jest w tym drugim przypadku dużo większy, w krańcowych przypadkach poprawienie programu może być wręcz niemożliwe. Testy jednostkowe skalują się liniowo z rozmiarem pisanego kodu, a nie ekspotencjalnie jak np. testy integracyjne. Oczywiście testy jednostkowe nie rozwiążą wszystkich problemów, jeśli mamy zły projekt całości to nic nam nie pomogą idealnie działające jednostki, ale przynajmniej będzie nam łatwiej się o tym przekonać.
Jak już napisałem testy służą do sprawdzania poprawności działania danej jednostki: ciągłego sprawdzanie działania tej jednostki. Ponieważ kod się nieustannie zmienia, powinniśmy wykonywać testy cały czas aby sprawdzić czy te zmiany wynikające, np. z poprawienia wykrytych błędów, nie wprowadziły nowych usterek. Aby to było możliwe testy musza być łatwe do wykonywania czyli zautomatyzowane. Nie mogą polegać na tym, że puszczamy program, a następnie przeglądamy wydruk. Musimy "nacisnąć guzik" a w odpowiedzi zapali nam się szereg "światełek": zielone wskażą testy zaliczone, a czerwone testy niezaliczone. Taki automatyczny proces testujący może być zintegrowany z innymi narzędzimi programistycznymi, takimi jak np. make.
Refaktoryzacja
Wysiłek włożony w napisanie takich powtarzalnych testów nie jest zaniedbywalny, ale korzyści są duże. Możliwość przetestowania kodu w dowolnym momencie to więcej niż tylko świadomość, że nasz obecny kod przeszedł testy. Taka możliwość, w połączeniu z narzędziami zarządzającymi kodem źródłowym, pozwala na bezpieczne dokonywanie zmian według schematu: zmieniamy, testujemy, jeśli testy się nie powiodą szukamy błedów, jeśli ich nie znajdujemy to cofamy zmiany. Takie podejście jest szczególnie pomocne, a właściwie niezbędne, podczas programowania przyrostowego i refaktoryzacji.
Programowanie przyrostowe to technika zalecana dla większości projektów, która polega na programowaniu "malymi krokami", czyli na kolejnym dodawaniu nowych funkcji do istniejącego działajacego kodu. Testy umożliwiają sprawdzenie czy dodany kod nie wprowadził błędów do starej części. Oczywiście każdy przyrost wymaga stworzenia nowego zestawu testów.
Refaktoryzacja to zmiana kodu bez zmiany jego funkcjonalności w celu poprawy jego jakości.
Projektowanie sterowane testami
Pisanie testu sprawdza również nasze zrozumienie tego, co dana jednostka ma robić. W tym sensie testy stanowią sformalizowany zapis wymagań. To zaleta, którą trudno przecenić. Jeżeli nie wiemy jak przestestować daną jednostkę, to najprawdopodobniej nie powinniśmy się wcale brać za jej kodowanie. Dlatego niektóre metodologie (np. extreme programming) zalecają projektowanie sterowane testami, czyli zaczęcie pisania programu od pisania testów do niego. Przebieg pracy przy takim podejściu wygląda następująco:
- Piszemy test
- Kompilujemy test
- Test się nie kompiluje
- Piszemy tyle kodu aby test sie skompilował
- Test się kompiluje
- Wykonujemy test
- Test najprawdpodobniej nie wykonuje się poprawnie
- Poprawiamy/dopisujemy kod tak aby test się wykonał
- Test wykonuje się poprawnie
Osobiście wydaje mi się, że zalety tego podejścia są ogromne. Nawet jeśli brakuje czasu i ochoty na pisanie testów, to należy po prostu zastanowić się nad sposobem przetestowania naszego kodu zanim zaczniemy go pisać. To znakomicie zmusza do ścisłego określenia tego, co właściwie nasz program ma robić.
Testy
Po tej całej propagandzie - czas na testowanie w praktyce. Przetestujemy przykłady wprowadzone w poprzednich rozdziałach, zaczynając od funkcji max:
template<typename T> T max(T a,T b) {return (a>b)?a:b;}
Być może część z Państwa oburzy się: jak to? testować tę jedną linijkę? Gdyby chodziło o tę jedną linijkę to rzeczywiście wystarczy na nią popatrzeć (i mieć wiarę w kompilator), ale przypominam, że dodaliśmy do niej dwie przeciążone wersje i dwie specjalizacje. A to oznacza, że ta linijka nie działa poprawnie w każdym przypadku. Napiszemy więc testy, które to wyłapią. Jak już pisałem będzie to jednoczesne zdefiniowanie tego jak funkcja max ma działać. Po chwili zastanowienia ustalamy więc, że nasza funkcja max zwraca:
- większą z dwu przekazanych wartości (większą w sensie porównania operatorem >)
- jeśli argumentami są wskaźniki to max zwraca wskaźnik na większą wartość
- jeśli argumentami są wskaźniki na char to max traktuje je jako napisy i zwraca wskaźnik do napisu większego zgodnie z uporządkowaniem leksykalnym.
Testować funkcję max będziemy poprzez porównanie wartości zwracanej do wartości poprawnej, którą sami wskażemy:
assert(max(1,2)==2); assert(max(2,1)==2);
Należy też sprawdzić przypadek symetryczny
assert(max(1,1)==1); assert(max(2,2)==2);
Testowanie szablonu jest trudne, bo w zasadzie musimy rozważyć przekazanie argumentów dowolnego typu. Co więcej, ten typ wcale nie musi posiadać operatora porównania ==. Aby sprawdzić działanie max na jakimś typie niewbudowanym posłużymy się własną klasą:
class Int { private: int _val; public: Int(int i):_val(i) {}; int val()const {return _val;}; friend bool operator>(const Int &a,const Int &b) { return a._val>b._val; } };
Kod testowy może teraz wyglądać następująco:
Int i(5); Int j(6); assert(max(i,j).val() == 6); assert(max(j,i).val() == 6); assert(max(j,j).val() == 6); assert(max(i,i).val() == 5);
Następnie testujemy wersję wskaźnikową:
assert(max(&i,&j)->val() == 6); assert(max(&j,&i)->val() == 6); assert(max(&j,&j)->val() == 6); assert(max(&i,&i)->val() == 5);
i na koniec wersję dla napisów (const char *):
assert(0==strcmp(max("abcd","acde"),"acde")); assert(0==strcmp(max("acde","abcd"),"acde")); assert(0==strcmp(max("abcd","abcd"),"abcd")); assert(0==strcmp(max("acde","acde"),"acde"));
oraz (char *):
char s1[]="abcde"; char s2[]="ac"; assert(0==strcmp(max(s1,s2),s2)); assert(0==strcmp(max(s2,s1),s2)); assert(0==strcmp(max(s1,s1),s1)); assert(0==strcmp(max(s2,s2),s2));
Napisy zostały tak dobrane, żeby miały pierwszy znak identyczny, ponieważ procedura ogólna dla wskaźników porównuje właśnie pierwsze znaki. To pokazuje jak ważny jest wybór danych testowych. Testy jednostkowe są testami "białej skrzynki", tzn. piszący testy ma wgląd do implementacji testowanego kodu (powinien to być ten sam programista), można więc przygotować dane testowe tak, aby pokrywały możliwie wiele ścieżek wykonywania programu, warunków brzegowych itp.
Oczywiście bezbłędne przejście powyższych testów nie gwarantuje nam jeszcze poprawności funkcji max (tego zresztą nie zagwarantuje nam żaden test), ale bardzo zwiększa prawdopodobieństwo tego, że tak jest.
Pozostaje nam do wytestowanie procedura szukająca maksimum w tablicy. To zadanie zostawiam jako ćwiczenie dla czytelników.
Powyższy przykład może budzić pewne obawy. Kod funkcji max liczy
około 20 linii, a kod testujący 40. No cóż, testowanie kosztuje, tylko
czy możemy sobie pozwolić na zrezygnowanie z niego? Rozważmy powyższy
przykład, te dwadzieścia linii kodu definiującego szablon max jest dużo
bardziej skomplikowane niż te czterdzieści linii kodu testujacego, tak że jeśli
porównamy czas pisania, to nie wypada to już tak źle. Kod szablonu
max zawiera przeciążenia i specjalizację, czyli wykorzystany jest
algorytm rozstrzygania przeciążenia. Osobiście nie ufam swojej
znajomości tego algorytmu na tyle, aby nie sprawdzić kodu. Jeżeli i tak
wykonujemy jakieś testy to warto zainwestować trochę więcej pracy i
przygotować porządny zestaw testujący. Może też się zdarzyć, że
będziemy chcieli dodać kolejne przeciążenia, które mogą wpłynąć w
niezamierzony sposób na przeciążenia już istniejące. Gotowy programik
testujący pozwoli nam to szybko wykryć.
Pozostaje jeszcze sprawa poprawności samego programu testującego, w końcu to też jest kod i może zawierać błędy. Czy więc musimy pisać kod testujący program testujący, i tak dalej w nieskończoność? Na szczęście nie, błędy w kodzie testującym mogą mieć dwa efekty. Pierwszy to wykazanie błędu, który nie jest błędem, w tej sytuacji taki błąd wykrywa się sam. Musimy tylko pamiętać podczas szukania źródeł wykazanych przez program testujacy usterek, że mogą one pochodzić z kodu testującego. Drugi rodzaj błędu to nie wykrycie błędu w programie. Występowanie tego rodzaju błedów testujemy poprzez wprowadzanie do programu zamierzonych błędów i sprawdzając czy nasze testy je wykryją.
CppUnit
Rysunek 4.1 przedstawia częściową hierachię klas w szkielecie CppUnit.
 Rysunek 4.1. Częściowa hierarchia klas w szkielecie CppUnit.
Rysunek 4.1. Częściowa hierarchia klas w szkielecie CppUnit.
Jest to bardzo mała część, uwzględniająca tylko te klasy, które zostaną użyte w naszym przykładzie. Proszę przede wszystkim zwrócić uwagę na hierachię klasy Test. Jest to klasyczny wzorzec Kompozyt (zob. E. Gamma, R. Helm, R. Johnson, J. Vlissides "Wzorce projektowe. Elementy oprogramowania obiektowego wielokrotnego użytku"), umożliwiający dowolne składanie i zagnieżdżanie testów. Jest to możliwe dzieki temu, że klasa TestSuite może zawierać inne testy, w tym też inne TestSuite.
Każda klas z tej hierarchii zawiera funkcję run(TestResult *result), która wywołuje funkcję runTest(), którą musimy przeładować definiując nasz własny test. Klasa TestResult, a raczej jej obiekty, służą do zbierania wyników testów.
Nasz przykład z max możemy zapisać następująco:
#include <cppunit/TestResult.h> #include <cppunit/TestCase.h> class Max_test : public CppUnit::TestCase { public: void runTest() { assert(max(1,2)==1); <i>sztucznie wprowadzony błąd!</i> assert(max(2,1)==2); assert(max(1,1)==1); assert(max(2,2)==2); . . . };
( Źródło: max_test_case.cpp)
Powyższy test możemy wywołać następująco:
main() { CppUnit::TestResult result; Max_test max; max.run( &result ); }
Jak na razie większym kosztem uzyskaliśmy ten sam efekt co programik z poprzedniego podrozdziału :). Czas więc wykorzystać jakieś własności szkieletu.
Zaczniemy od wykorzystania, zamiast standardowego makra assert, makr szkieletu CppUnit:
#include <cppunit/TestResult.h> #include <cppunit/TestCase.h> #include <cppunit/TestAssert.h> class Max_test : public CppUnit::TestCase { public: void runTest() { CPPUNIT_ASSERT_EQUAL(1,max(1,2)); <i>sztucznie wproadzony bład!</i> CPPUNIT_ASSERT_EQUAL(2,max(2,1)); CPPUNIT_ASSERT_EQUAL(1,max(1,1)); CPPUNIT_ASSERT_EQUAL(2,max(2,2)); . . . };
( Źródło: max_test_runner.cpp)
Jednak wykonanie tego samego kodu main co poprzednio nie da żadnych wyników! To dlatego, że makra CPPUNIT_ASSERT_... nie powodują przerwania programu tylko zapisanie wyników do obiektu typu TestResult. Najłatwiej odczytać te wyniki nie uruchamiając testów samemu tylko za pośrednictwem obiektu TextUi::TestRunner.
#include <cppunit/ui/text/TestRunner.h> main() { Max_test *max = new Max_test; CppUnit::TextUi::TestRunner runner; runner.addTest( max ); <i>max musi byc wskaźnikiem utworzynym za pomocą new bo runner przejmuje go na własność i sam zwalnia przydzieloną dla niego pamięć</i> runner.run(); }
( Źródło: max_test_runner.cpp)
Teraz uruchomienie programu spowoduje wydrukowanie na std::cout raportu z wykonania testu. Ciągle jednak jest to niewspółmierne do włożonego wysiłku. Postaramy się więc teraz zacząć strukturyzować nasze testy. Możemy oczywiście stworzyć kilka różnych klas testujących z inną funkcją runTest() każda, ale zamiast tego wykorzystamy klasę TestFixture. Rzut oka na rysunek 4.1 pokazuje, że nie jest to Test, ale przerobimy ją na test za pomocą TestCaller.
Zaczynamy od zdefiniowanie szeregu testów w jednej klasie:
#include <cppunit/TestFixture.h> #include <cppunit/TestAssert.h> class Max_test : public CppUnit::TestFixture { Int i,j; public: Max_test():i(5),j(6) {}; void int_test() { CPPUNIT_ASSERT_EQUAL(1,max(1,2)); <i>sztucznie wprowadzony bład!</i> ... CPPUNIT_ASSERT_EQUAL(1,max(2,2)); <i>sztucznie wprowadzony bład!</i> } void class_test() { CPPUNIT_ASSERT_EQUAL( 6,max(i,j).val() ); ... } void class_ptr_test() { CPPUNIT_ASSERT_EQUAL( 6,max(&i,&j)->val() ); ... } void const_char_test() { CPPUNIT_ASSERT_EQUAL(strcmp(max("abcd","acde"),"acde"),0); ... } void char_test() { char s1[]="abcde"; char s2[]="ac"; CPPUNIT_ASSERT_EQUAL(strcmp(max(s1,s2),s2),0); ... CPPUNIT_ASSERT_EQUAL(strcmp(max(s2,s2),s2),1); <i>sztucznie wprowadzony bład!</i> }
( Źródło: max_test_caller.cpp)
Podzieliliśmy nasz test na kilka mniejszych, z których każdy testuje zachowanie jednej klasy argumentów funkcji max. Zmienne używane wspólnie zadeklarowalismy jako składowe klasy i inicjalizujemy w konstruktorze. Potem pokażemy jak można wywoływać dodatkowy kod inicjalizujący przed wykonaniem każdej metody, ale na razie ten mechanizm nie jest nam potrzebny.
No, ale jak wywołać te testy? Klasa TestFixture nie jest testem i nie posiada funkcji runTest. Aby móc jej użyć musimy skorzystać z szablonu TestCaller. Szablon TestCaller przyjmuje jako swój parametr klasę TextFixture, w naszym przypadku Max_test. W konstruktorze obiektów tej klasy podajemy nazwę testu i adres metody klasy Max_test, która ten test implementuje. Tak skonstruowany obiekt jest już testem i możemy go przekazać do obiektu runner:
main() { CppUnit::TextUi::TestRunner runner; runner.addTest( new CppUnit::TestCaller<Max_test>( "int_test", &Max_test::int_test ) ); ... <i>podobnie dla reszty metod klasy Maxtest</i> runner.run(); }
( Źródło: max_test_caller.cpp)
Teraz wykonanie programu spowoduje wywołanie 5 testów. Co ważne - niepowodzenie ktorejś z asercji w jednym teście przerywa wykonywanie tego testu, ale nie ma wpływu na wykonywanie się innych testów.
Zamiast dodawać testy do "wykonywacza" pojedynczo, możemy je najpierw pogrupować za pomocą obiektów TestSuite:
main() { CppUnit::TextUi::TestRunner runner; CppUnit::TestSuite *obj_suite = new CppUnit::TestSuite; CppUnit::TestSuite *ptr_suite = new CppUnit::TestSuite; obj_suite->addTest( new CppUnit::TestCaller<Max_test>( "int_test", &Max_test::int_test ) ); obj_suite->addTest( new CppUnit::TestCaller<Max_test>( "class_test", &Max_test::class_test ) ); ptr_suite->addTest( new CppUnit::TestCaller<Max_test>( "class_ptr_test", &Max_test::class_ptr_test ) ); ptr_suite->addTest( new CppUnit::TestCaller<Max_test>( "const_char_test", &Max_test::const_char_test ) ); ptr_suite->addTest( new CppUnit::TestCaller<Max_test>( "char_test", &Max_test::char_test ) ); runner.addTest(obj_suite); runner.addTest(ptr_suite); runner.run(); }
Obiekty TestSuite są testami i możemy je dalej grupować:
CppUnit::TestSuite *max_suite = new CppUnit::TestSuite; max_suite->addTest(obj_suite); max_suite->addTest(ptr_suite); runner.addTest(max_suite); runner.run();
Widać, że szkielet CppUnit daje nam sporo możliwości, ale ciągle jest to niewspółmierne do włożonego wysiłku. Powodem tego jest prostota użytego przykładu, który nie wymaga takich narzędzi. Pakiet CppUnit posiada jednak o wiele więcej możliwości, między innymi:
- W klasie TextFixture można przeładować funkcje void setUp() i void tearDown(), które będą wywoływane odpowiednio przed i po wykonaniu każdego testu. Mogą być użyte do konstrukcji środowiska testowego i jego rozmontowania. Nie używałem tej możliwości, bo nie była ona potrzebna w tak prostym przykładzie.
- Bardzo często chcemy wykonać razem wszystkie testy zdefiniowane w jednej klasie. CppUnit dostarcza makr ułatwiających grupowanie wszystkich metod danej klasy w jeden TestSuite.
- Szkielet CppUnit oferuje poza CPPUNIT_ASSERT_EQUAL szereg innych makr ulatwiających pisanie testów.
- Stosunkowo łatwo można zmienić format wyświetlania wyników testów np. dodanie
runner.setOutputter( new CppUnit::XmlOutputter( &runner.result(), std::cout ) );
spowoduje wypisanie wyników testu w formacie XML.
| Załącznik | Wielkość |
|---|---|
| Max_test_case.cpp | 1.54 KB |
| Max_test_runner.cpp | 1.84 KB |
| Max_test_caller.cpp | 1.15 KB |
Klasy cech
Wprowadzenie
Rozważmy próbę implementacji ogólnej funkcji sumowania elementów tablicy (zob. D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty", rozdz. 15). Korzystając z wiadomości o szablonach i konwencjach używanych w STL możemy napisać:
template<typename T> T sum(T *beg,T *end) { T total = T(); for(;beg!<nowiki>=</nowiki>end;++beg) total +<nowiki>=</nowiki> *beg; return total; }
( Źródło: sum1.cpp)
Przykład 5.1
Ten prosty kod ma jednak co najmniej dwa problemy. Pierwszy związany jest z linijką
T total <nowiki>=</nowiki> T();
i wiąże się z ustaleniem zerowej wartości dla danego typu. Powyższa linijka oznacza, że zmienna total jest inicjalizowana konstruktorem domyślnym klasy T. W przypadku typów wbudowanych będzie to inicjalizacja wartością zerową, czyli tak jak tego oczekujemy. W przypadku innych typów możemy mieć tylko nadzieję, że konstruktor defaultowy istnieje i robi to co trzeba :). Popatrzmy na możliwe alternatywy:
T total;
W przypadku typów zdefiniowanych przez użytkownika wywoływany jest defaultowy konstruktor (domyślny jeśli żaden inny nie jest zdefinowany). W przypadku typów wbudowanych wartość jest niekreślona!
T total <nowiki>=</nowiki> 0;jest z kolei niepoprawne dla typów, na które nie ma rzutowania z liczb całkowitych.
Problem można ominąć jeżeli się zauważy, że dla niepustych zakresów tzn. beg!=end nie potrzebujemy wcale wartości zerowej:
template<typename T> T sum(T *beg,T *end) { T total= *beg; ++beg; while(beg != end ) { total += *beg; beg++; } return total; }
Jeśli jednak dopuszczamy podanie zakresu pustego, to funkcja powinna zwrócić zero i problem powraca.
Drugi problem z przykładem 5.1 to typ zmiennej total. Popatrzmy na zastosowanie funkcji sum.
char name[]="@ @ @"; int length=strlen(name); cout<<sum(name,&name[length]]);
Programik powinien wypisać sumę wartości znaków w napisie "name". Łatwo sprawdzić że wypisuje znak o kodzie zero. Problem polega na tym, że typ T niekoniecznie musi pomieścić wynik dodawania elementów typu T. W tym przykładzie dodawanie znaków dało wynik 256 (co za niezwykły zbieg okoliczności), który już nie mieści się w zakresie tego typu.
Prostym rozwiązaniem jest dodanie dodatkowego parametru szablonu:
template<typename R,typename T> R sum(T *beg,T *end) { R total = R(); while(beg != end ) { total += *beg; beg++; } return total; }
( Źródło: sum2.cpp)
i wtedy zastosowanie
cout<<sum<int>(name,&name[length]])<<endl;
da już oczekiwany wynik. Zaletą tego rozwiązania jest jego prostota i duża elastyczność. Wadą - zwiększenie liczby parametrów szablonu, co zawsze zwiększa złożoność kodu i możliwości popełnienia błędu, zwłaszcza, że typ R jest w większości przypadków określony przez typ T i nie wnosi niezależnej informacji.
Klasy cech
Pomocą mogą służyć klasy cech: klasy, których funkcją jest dostarczanie dodatkowych informacji o danym typie. W naszym przypadku możemy zadeklarować szablon:
template<typename T> struct sum_traits;i jego specjalizacje:
template<> struct sum_traits<char> { typedef int sum_type; }; template<> struct sum_traits<int> { typedef long int sum_type; }; template<> struct sum_traits<float> { typedef double sum_type; }; template<> struct sum_traits<double> { typedef double sum_type; };
Szablon sum przerabiamy teraz na
template<typename T> typename sum_traits<T>::sum_type sum(T *beg,T *end) { typedef typename sum_traits<T>::sum_type sum_type; sum_type total = sum_type(); while(beg != end ) { total += *beg; beg++; } return total; }
( Źródło: sum3.cpp)
Wadą tego podejścia jest konieczność definiowania specjalizacji szablonu sum_traits dla każdego typu, którego sumę będziemy chcieli obliczyć. Można tego uniknąć definiując szablon ogólny
template<typename T> struct sum_traits { typedef T sum_type; };
i możemy już wtedy użyć
complex<double> *c1,*c2; sum(c1,c2);
bez dodatkowych definicji. To czy należy implementować uniwersalną definicję klasy cech zależy od tego czy istnieje sensowna wartość domyślna dla danej cechy. W naszym przypadku, definiując powyższy szablon, zyskujemy na wygodzie ale tracimy na bezpieczeństwie, bo łatwiej jest teraz wywołać funkcję sum z nieodpowiednim typem zmiennej total.
Cechy wartości
Możemy spróbować rozwiązać za pomocą klas cech również problem inicjalizacji zmiennej total, definiując w każdej klasie odpwiednią wartość zerową dla danego typu. Pytanie jak to zrobić? Nasuwa się użycie stałych składowych statycznych:
template<> struct sum_traits<char> { typedef int sum_type; static const sum_type zero = 0; };
Sęk w tym, że standard zezwala na incijalizowanie w klasie statycznych stałych jedynie dla typów całkowitoliczbowych. Taka sama konstrucja dla double już nie jest możliwa.
template<> struct sum_traits<float> { typedef double sum_type; static const sum_type zero = 0.0; niedozwolone };
Inicjalizator
const typename sum_traits<float>::sum_type sum_traits<float>::zero = 0.0;
musi być umieszczony w kodzie źródłówym. Po pierwsze nie bardzo wiadomo gdzie go umieścić (nie może być w pliku nagłówkowym, bo łamało by to zasadę jednokrotnej definicji). Po drugie kompilator najprawdopodobniej nie umiałby powiązać nazwy stałej i jej wartości w czasie kompilacji.
Inną możliwością jest użycie funkcji statycznych rozwijanych w miejscu wywołania:
template<> struct sum_traits<char> { typedef int sum_type; static sum_type zero() {return 0;} }; template<> struct sum_traits<float> { typedef double sum_type; static sum_type zero() {return 0.0;} };
Odpowiadający temu podejściu kod funkcji sum bedzie wyglądał następująco:
template<typename T> typename sum_traits<T>::sum_type sum(T *beg,T *end) { typedef typename sum_traits<T>::sum_type sum_type; sum_type total = sum_traits<T>::zero(); while(beg != end ) { total += *beg; beg++; } return total; }
Dobry kompilator powinien bez trudu rozwinąć definicję funkcji i podstawić odpowiednią wartość bezpośrednio w kodzie.
Parametryzacja klasami cech
Opisana powyżej implementacja funkcji sum i związanej z nią klasy sum_traits jest mało elastyczna. Wybierając typ przekazanej tablicy wybieramy typ zmiennej total. Może się jednak zdażyć, że chcemy sumować int we float, a float we float.
Możemy dodać dodatkowy parametr do szablonu, który będzie definiował wybraną klasę cech. Ale to jest powrót do rozwiązania odrzuconego na początku. Rozwiązaniem może być uczynienie tego parametru parametrem domyślnym, tak, aby nie trzeba było podawać go jawnie w typowych przypadkach. Jest to bardzo dobre rozwiązanie w przypadku użycia klas cech w szablonach klas. Problem w tym, że szablony funkcji nie dopuszczają stosowania parametrów domyślnych. Możemy to obejść za pomocą przeciążenia definiując:
template<typename Traits,typename T > typename Traits::sum_type sum(T *beg,T *end) { typedef typename Traits::sum_type sum_type; sum_type total = sum_type(); while(beg != end ) { total += *beg; beg++; } return total; }; template<typename T > typename sum_traits<T>::sum_type sum(T *beg,T *end) { return sum<sum_traits<T>, T>(beg,end); } struct char_sum { typedef char sum_type; };
( Źródło: sum4.cpp)
main() { char name[]="@ @ @"; int length=strlen(name); cout<<(int)sum(name,&name[length]])<<endl; cout<<(int)sum<char_sum>(name,&name[length]])<<endl; cout<<(int)sum<char>(name,&name[length]])<<endl; }
( Źródło: sum4.cpp)
iterator_traits
Na koniec spróbujmy uogólnić funkcję sum, aby działała nie tylko ze wskaźnikami, ale i iteratorami.
template<typename IT> sum(IT *beg,IT *end);
Widać, że tu użycie klas cech jest już niezbędne, musimy bowiem dowiedzieć się na obiekty jakiego typu wskazuje iterator. Nie można do tego celu użyć typów stowarzyszonych IT::value_type, bo jako iterator może zostać podstawiony zwykły wskaźnik. Dlatego w STL istnieje klasa iterator_traits, definiująca podstawowe typy dla każdego rodzaju iteratora. Korzystając z tej klasy można zdefiniować ogólny szalon funkcji sum
template<typename II> typename sum_traits<typename iterator_traits<II>::value_type>::sum_type sum(II beg,II *end) { typedef typename iterator_traits<IT>::value_type value_type; typedef typename sum_traits<value_type>::sum_type sum_type; sum_type total = sum_traits<value_type>::zero(); while(beg != end ) { total += *beg; beg++; } return total; }
Zanim omówię klasę iterator_trais podam rozwiązanie zastosowane w STL. Tam funkcja nazywa się accumulate i jest zaimplementowana następująco:
template <class InputIterator, class T> T accumulate(InputIterator first, InputIterator last, T init) { for (; first != last; ++first) init = init + *first; return init; }
Przykład 5.2
Dodanie dodatkowego parametru wywołania funkcji rozwiązuje za jednym zamachem oba nasze problemy: parametr ten dostarcza zarówno typu, jak i wartości początkowej dla zmiennej sumującej. Są jednak inne algorytmy w STL, które wymagają więcej informacji o iteratorze i muszą je pobrać za pomocą iterator_traits.
Dla iteratorów nie będących wskaźnikami iterator_traits po prostu przepisują ich typy stowarzyszone:
template <class Iterator> struct iterator_traits { typedef typename Iterator::iterator_category iterator_category; typedef typename Iterator::value_type value_type; typedef typename Iterator::difference_type difference_type; typedef typename Iterator::pointer pointer; typedef typename Iterator::reference reference; };
Dla typów wskaźnikowych jest podana odpowiednia specjalizacja.
template <class T> struct iterator_traits<T*> { typedef random_access_iterator_tag iterator_category; typedef T value_type; typedef ptrdiff_t difference_type; typedef T* pointer; typedef T& reference; };
Widać więc, że każdy iterator nie będący wskaźnikiem musi mieć zdefiniowane odpowiednie typy stowarzyszone. Ułatwia to szablon klasy iterator, z którego można dziedziczyć:
namespace std { template<class Category, class T, class Distance = ptrdiff_t, class Pointer = T*, class Reference = T&> struct iterator { typedef T value_type; typedef Distance difference_type; typedef Pointer pointer; typedef Reference reference; typedef Category iterator_category; };
Na uwagę zasługuje typ iterator_category. Ten typ służy do automatycznego wyboru odpowiednich funkcji w oparciu o kategorię iteratora. Kategorie odpowiadają konceptom iteratorów i są reprezentowane przez puste klasy. W STL zdefiniowano pięć kategorii iteratorów:
namespace std { struct input_iterator_tag {}; struct output_iterator_tag {}; struct forward_iterator_tag: public input_iterator_tag {}; struct bidirectional_iterator_tag: public forward_iterator_tag {}; struct random_access_iterator_tag: public bidirectional_iterator_tag {}; }
Aby zilustrować zastosowanie typu iterator_category przedstawię implementację funkcji distance(), która oblicza odległość pomiędzy dwoma iteratorami. Potrzeba użycia iterator_category bierze się stąd, że dla iteratorów o dostępie swobodnym możemy policzyć ją bezpośrednio przez odejmowanie:
template <class _RandomAccessIterator> inline typename iterator_traits<_RandomAccessIterator>::difference_type __distance(_RandomAccessIterator __first, _RandomAccessIterator __last, random_access_iterator_tag) { return __last - __first; }
Dla reszty musimy po kolei zwiekszać jeden iterator aż osiągniemy drugi:
template <class _InputIterator> inline typename iterator_traits<_InputIterator>::difference_type __distance(_InputIterator __first, _InputIterator __last, input_iterator_tag) { typename iterator_traits<_InputIterator>::difference_type __n = 0; while (__first != __last) { ++__first; ++__n; } return __n; }
Do wyboru pomiędzy tymi dwoma implementacjami służy właśnie iterator_category:
template <class _InputIterator> inline typename iterator_traits<_InputIterator>::difference_type distance(_InputIterator __first, _InputIterator __last) { typedef typename iterator_traits<_InputIterator>::iterator_category _Category; return __distance(__first, __last, _Category()); }
numeric_limits
Przykładem klasy cech zawartej w standardzie C++ jest szablon
numeric_limits, który zastępuje używane w C makra, zdefiniowane
w pliku limits.h. Szablon numeric_limits posiada specjalizację dla
każdego typu podstawowego wbudowanego (zob. tab. 5.1]) i zawiera informację na temat różnych cech ich implementacji (zob. tab. 5.2]).
Warto zwrócić uwagę na następującą konstrukcję: szablon
numeric_limits definiuje stałą logiczną is_specialised.
Domyślnie jest ona równa false. Każda specjalizacja szablonu
ustawia ją na true. W ten sposób stała
std::numeric_limits
namespace std { template<class T> class numeric_limits; enum float_round_style; enum float_denorm_style; template<> class numeric_limits<bool>; template<> class numeric_limits<char>; template<> class numeric_limits<signed char>; template<> class numeric_limits<unsigned char>; template<> class numeric_limits<wchar_t>; template<> class numeric_limits<short>; template<> class numeric_limits<int>; template<> class numeric_limits<long>; template<> class numeric_limits<unsigned short>; template<> class numeric_limits<unsigned int>; template<> class numeric_limits<unsigned long>; template<> class numeric_limits<float>; template<> class numeric_limits<double>; template<> class numeric_limits<long double>; }
Tablica 5.1. Specjalizacje szablonu numeric_limits
namespace std { template<class T> class numeric_limits { public: static const bool is_specialized = false; static T min() throw(); static T max() throw(); static const int digits = 0; static const int digits10 = 0; static const bool is_signed = false; static const bool is_integer = false; static const bool is_exact = false; static const int radix = 0; static T epsilon() throw(); static T round_error() throw(); static const int min_exponent = 0; static const int min_exponent10 = 0; static const int max_exponent = 0; static const int max_exponent10 = 0; static const bool has_infinity = false; static const bool has_quiet_NaN = false; static const bool has_signaling_NaN = false; static const float_denorm_style has_denorm = denorm_absent; static const bool has_denorm_loss = false; static T infinity() throw(); static T quiet_NaN() throw(); static T signaling_NaN() throw(); static T denorm_min() throw(); static const bool is_iec559 = false; static const bool is_bounded = false; static const bool is_modulo = false; static const bool traps = false; static const bool tinyness_before = false; static const float_round_style round_style = round_toward_zero; }; }
Tablica 5.2. Szablon numeric_limits
| Załącznik | Wielkość |
|---|---|
| Sum1.cpp | 284 bajty |
| Sum2.cpp | 294 bajty |
| Sum3.cpp | 692 bajty |
| Sum4.cpp | 975 bajtów |
Funkcje typów i inne sztuczki
Wprowadzenie
Funkcja jest podstawowym pojęciem w większości języków programowania, z którym wszyscy jesteśmy dobrze obeznani. Funkcje przyjmują zestaw argumentów i zwracają jakąś wartość. Szablony dają ciekawą możliwość interpretowania ich jako funkcji typów: funkcje których argumentem są typy, a wartością zwracaną typ lub jakaś wartość. Weźmy dla przykładu szablon sum_traits z poprzedniego modułu. Można interpretować go jako dwie funkcje przyjmujące typ poprzez parametr szablonu i zwracające albo wartość
sum_traits<int>::zero();
albo typ
sum_traits<int>::sum_typeTakie funkcje możemy definiować poprzez wypisanie wszystkich specjalizacji pełnych jak w przypadku sum_traits albo przez wykorzystanie specjalizacji częściowych, jak np. dla iterator_traits. Najciekawsza możliwość to jednak pisanie "obliczalnego kodu" takich funkcji, przy czym "obliczenia" dokonują się w czasie kompilacji. Przykłady takich funkcji zostaną podane na tym wykładzie. W realnych zastosowaniach wykorzystuje się kombinację wszystkich powyższych możliwości.
Korzystając z szablonów można również uogólnić pojęcie listy i definiować listy typów. Umożliwiają one między innymi indeksowany dostęp do swoich składowych, przekazywanie zmiennej liczby parametrów typu do szablonów i automatyczną generację hierarchii klas opartych na tych typach. Listy typów omówię w drugiej części tego wykładu.
Funkcje typów
If-Then-Else
Zacznę od przydatnej konstrukcji implementującej możliwość wyboru jednego z dwu typów na podstawie stałej logicznej (typu bool). Dokonujemy tego za pomocą szablonu podstawowego
template<bool flag,typename T1,typename T2> struct If_then_else { typedef T1 Result; };
który będzie podstawiany dla wartości flag=true i jego specjalizacji dla wartości flag=false:
template<typename T1,typename T2> struct If_then_else<false,T1,T2> { typedef T2 Result; };
Teraz możemy go np. wykorzystać do wybrania większego z dwu typów:
template<typename T1,typenameT2> struct Greater_then { typedef typename If_then_else<sizeof(T1)>sizeof(T2),T1,T2>::result result; };
Sprawdzanie czy dany typ jest klasą
Następny przykład to szablon służący do sprawdzania czy dany typ jest klasą. Wykorzystamy w tym celu operator sizeof() i przeciążane szablony funkcji razem z zasadą "nieudane podstawienie nie jest błędem" (zob. wykład 3.5). Potrzebujemy więc wyrażenia, które nie ma sensu dla dla typów nie będacych klasami. Takim wyrażeniem będzie int C::* oznaczające wskaźnik do pola składowego klasy C typu int. Cały szablon wygląda następująco.
template<typename T> class Is_class { //najpierw definiujemy dwa typy różniące sie rozmiarem typedef char one; typedef struct {char c[2];} two; //teraz potrzebne bedą dwa przeładowane szablony template<typename U> static one test(int U::*); template<typename U> static two test(...); //to który szablon został wybrany sprawdzamy poprzez sprawdzenie rozmiaru zwracanego typu enum {yes = (sizeof(test<T>(0))==sizeof(one) )}; };
( Źródło: is_class.cpp)
Operator sizeof(test
Jeśli typ T jest klasą to int T::* jest poprawne (na tym
etapie nie jest istotne czy klasa w ogóle posiada taką składową) i
mechanizm rozstrzygania będzie pracował dalej, sprawdzając czy argument
wywołania jest zgodny z int T::*. W tym przypadku jest to zero,
które może być użyte jako wskaźnik, więc podstawienie się powiedzie.
Oczywiście drugie podstawienie też by się powiodło
ale jest mniej specjalizowane. W wyniku zmienna yes otrzyma
wartość true.
Warto zauważyć, że gdybyśmy zamiast zera podstawili jako argument
funkcji test
Sprawdzanie możliwości rzutowania
Kolejny przykład wykorzystuje tę samą technikę w celu stwierdzenia czy jeden z typów można rzutować na drugi.
template<typename T,typename U> class Is_convertible { typedef char one; typedef struct {char c[2];} two; <i>tym razem korzystamy ze zwykłych przeciążonych funkcji</i> static one test(U); static two test(...); static T makeT(); public: enum {yes = sizeof(test(makeT()) )==sizeof(one), same_type=false }; };
( Źródło: convertible.cpp)
Teraz sprawdzane są dwie przeciążone funkcje. makeT() zwraca obiekt typu T więc jeśli typ T może być rzutowany na U to wybrane zostanie dopasowanie pierwszej funkcji jako bardziej wyspecjalizowanej. Funkcja makeT() została użyta zamiast np. T(), bo konstruktor defaultowy może dla tego typu nie istnieć. Dodatkowa specjalizacja
template<typename T> class Is_convertible<T,T> { public: enum {yes = true, same_type=true }; };
( Źródło: convertible.cpp)
pozwala nam użyć tej klasy do identyfikacji identycznych typów.
Zdejmowanie kwalifikatorów
Każdy typ w C++ może być opatrzony dodatkowymi kwalifikatorami, takimi jak const czy & (referencja). Mając dany typ T dodanie do niego kwalifikatora jest proste. Z pozoru jednak może się to wiązać z możliwością wygenerowania niepoprawnych podwójnych kwalifikatorów np. const const T. Okazuje się jednak, że o ile
const const int i =0;
jest konstrukcją nieprawdłową, to w przypadku argumentów szablonu nadmiarowe kwalifikatory zostaną zignorowane. Wyrażenie:
template<typename T> struct const_const { const T t = T(); }; const_const<const int> a;
jest poprawne i pole t będzie typu const int. To samo tyczy się referencji. Pomimo tych udogodnień może być konieczna operacja usunięcia jednego lub obydwu kwalifikatorów i uzyskanie gołego typu podstawowego. W tym celu możemy zdefiniować szablon (zob. D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty", rozdz. 17)
template<typename T> struct Strip { typedef T arg_t; typedef T striped_t; typedef T base_t; typedef const T const_type; typedef T& ref_type; typedef T& ref_base_type; typedef const T & const_ref_type; };
i jego specjalizację dla typów z kwalifikatorem const
template<typename T> struct Strip< T const> { typedef const T arg_t; typedef T striped_t; typedef typename Strip<T>::base_t base_t; typedef T const const_type; typedef T const & ref_type; typedef T & ref_base_type; typedef T const & const_ref_type; };
i dla referencji
template<typename T> struct Strip<T&> { typedef T& arg_t; typedef T striped_t; typedef typename Strip<T>::base_t base_t; typedef base_t const const_type; typedef T ref_type; typedef base_t & ref_base_type; typedef base_t const & const_ref_type; };
( Źródło: strip.cpp)
Proszę zwrócić uwagę na konstrukcję
typedef typename Strip<T>::base_t base_t;
Ponieważ typ T może oznaczać typ kwalifikowany za pomocą const, wykorzystujemy rekurencyjne odwołanie aby uzyskać typ podstawowy. Jest to przykład techniki metaprogramowania, która bardziej szczegółowo będzie omówiona w wykładzie 8.
Cechy typów
Jednym z rodzajów klas cech (omawianych w poprzednim wykładzie) są cechy typów. Nie są one specjalizowane do jednego konkretnego celu, ale służą do dostarczania ogólnych informacji na temat dowolnych typów. Wymieniamy je w tym wykładzie, ponieważ do ich implementacji często stosowane są różne techniki opisane powyżej. Bardzo dobry szczegółowy opis implementacji cech typów znajduje się w D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty". Gotową implementację typu boost::type_traits można znaleźć w repozytorium boost. Inna - to biblioteka Loki opisana w A. Alexandrescu "Nowoczesne projektowanie w C++".
Cechy promocji
Załóżmy, że postanowiliśmy zaimplementować możliwość dodawania wektorów:
template<typename T> std::vector<T> operator+(const std::vector<T> &a, const std::vector<T> &b) { assert(a.size()==b.size()); std::vector<T> res(a); for(size_t i=0;i<a.size();++i) res[i]+=b[i]; return res; }
( Źródło: promote.cpp)
Teraz polecenia
std::vector<double> x(10); std::vector<double> y(10); x+y;
( Źródło: promote.cpp)
skompilują się, ale
std::vector<int> l(10); x+l;
już nie. Ponieważ dodawanie double do int jest dozwolone, to rozsądne by było aby nasza implemenatacja też na to zezwalała. Przerabiamy więc nasz operator+() (lub dodajemy przeciążenie):
template<typename T,typename U> std::vector<T> operator+(const std::vector<T> &a, const std::vector<U> &b) { assert(a.size()==b.size()); std::vector<T> res(a); for(size_t i=0;i<a.size();++i) res[i]+=b[i]; return res; }
Kłopot z tą definicją to typ zwracany, który zależy teraz od kolejności składników dodawania, a nie od ich typu. Abu rozwiązać ten problem zdefiniujemy sobie klasę cech, która będzie określała typ wyniku na podstawie typu składników. Wybierzemy następującą strategię: jeśli typy mają różny rozmiar to wybieramy typ większy, jeżeli mają ten sam rozmiar to liczymy na specjalizacje:
template<typename T1,typename T2> struct Promote { typedef typename If_then_else<(sizeof(T1) > sizeof(T2)), T1, typename If_then_else< (sizeof(T1)< sizeof(T2)), T2, void>::Result >::Result Result; };
( Źródło: promote.cpp)
Dla identycznych typów wynik jest jasny (choć jak przekonuje nas przykład 5.1 typ sumy nie musi być typem składników), ale niemniej musimy go zdefiniować:
template<typename T> struct Promote<T,T> { typedef T Result; };
( Źródło: promote.cpp)
Resztę musimy definiować ręcznie korzystając ze specjalizacji pełnych. Można to sobie uprościć definiując makro
#define MK_PROMOTE(T1,T2,Tr) \ template<> class Promotion<T1, T2> { \ public: \ typedef Tr Result; \ }; \ \ template<> class Promotion<T2, T1> { \ public: \ typedef Tr Result; \ }; MK_PROMOTE(bool, char, int) MK_PROMOTE(bool, unsigned char, int) MK_PROMOTE(bool, signed char, int)
( Źródło: promote.cpp)
Listy typów
Definicja
Listy typów są ciekawą konstrukcją zaproponowaną przez Alexandrescu. Ich szczegółowy opis i zastosowania można znaleźć w A. Alexandrescu "Nowoczesne projektowanie w C++". Definicja listy typów opiera się na rekurencyjnej implementacji listy znanej miedzy innymi z Lisp-a: lista składa się z pierwszego elementu (głowy) i reszty (ogona), co możemy zapisać jako:
template<typename H,typename T> struct Type_list { typedef H head; typedef T tail; }
( Źródło: typelist.h)
Do tego potrzebna nam jest jeszcze definicja pustego typu:
class Null_type {};
jako znacznika końca listy. I tak:
Type_list<int,Null_type>
oznacza jednoelementową listę (int)
Type_list<double,Type_list<int,Null_type> >
listę dwuelemntową (double,int) i tak dalej.
Length
Ta prosta struktura daje zadziwiająco wiele możliwości. Na początek napiszemy funkcję zwracającą długość listy. W tym celu skorzystamy z rekurencyjnej definicji: długość listy to jeden plus długość ogona, długość listy pustej wynosi zero. Tę definicję implementujemy następująco:
template<typename T> struct Length; template<> struct Length<Null_type> { enum {value = 0}; }; template<typename H,typename T> struct Length<Type_list<H,T> > { enum {value = 1 + Length<T>::value}; };
( Źródło: typelist.h)
Indeksowanie
Tą samą techniką możemy zaimplementować indeksowany dostęp do elementów listy. Znów korzystamy z rekurencji: element o indeksie i to albo głowa (jeśli i==0), albo element o indeksie i-1 w jej ogonie.
template<typename T,size_t I> struct At; template<typename T,typename H> struct At<T,0> { typedef T result; }; template<typename T,typename H> struct At<T,I> { typedef typename At<H,I-1>::result result; };
( Źródło: typelist.h)
Generowanie switch-a
W bibliotece boost jest zaimplementowana klasa any, której obiekty mogą reprezentować dowolną wartość (zob. boost). Żeby taką wartość odczytać musimy użyć odpowiedniej konkretyzacji szablonu funkcji any_cast:
boost::any val; cout<<any_cast<int>(val)<<endl;
Jeśli w szablonie podstawimy nie ten typ co trzeba, to otrzymamy wyjątek. Chcemy teraz napisać funkcję, która drukuje wartości typu any, przy czym wiemy, że przechowywane są w nich wartości tylko kilku wybranych typów (np. int, double, string). Ponieważ any udostępnia informację o typie przechowywanej w niej wartości moglibyśmy taką funkcję print_any() zaimplementować następująco:
print_any(std::ostream &of,boost::any val) { if(val.type()==typeid(int) ) of<<any_cast<int>(val)<<std::endl; else if val.type()==typeid(double) ) of<<any_cast<double>(val)<<std::endl; else if val.type()==typeid(string) ) of<<any_cast<string>(val)<<std::endl; else of<<"unsuported type"<<std::endl; }
Sprobujemy teraz zaimplementować to samo za pomocą list typów, dodatkowo
zażądamy aby móc drukować również wartości typu vector
Jak zwykle musimy sformułować problem rekurencyjnie: sprawdzamy czy typ val jest typem głowy listy; jeśli tak to drukujemy, jeśli nie to próbujemy drukować val używając ogona listy.
template<typename T> void print_val(std:ostream &of,boost::any val) { typedef typename T::Head Head; typedef typename T::Tail Tail; if(val.type()==typeid() ) { of<<any_cast<Head>(val)<<std::endl; } else if (val.type()==typeif(std::vector<Head>)) { of<<any_cast<std::vector<Head> >(val)<<std::endl; } else print_val<Tail>(of,val); }
( Źródło: any_print.h)
Potrzebujemy jeszcze warunku kończącego rekurencję
template<> void print_val<Null_type>(std::ostream &of,boost::any) { of<<"don't know how to print this"<<std::endl; }
i możemy już używać naszego szablonu:
typedef TypeList<double, Type_list<int, Type_list<string, Null_type> > > my_list; print_val<my_list>(val);
( Źródło: typelist.cpp)
| Załącznik | Wielkość |
|---|---|
| Is_class.cpp | 675 bajtów |
| Convertible.cpp | 887 bajtów |
| Strip.cpp | 1.43 KB |
| Promote.cpp | 1.77 KB |
| Typelist.h | 886 bajtów |
| Any_print.h | 780 bajtów |
| Typelist.cpp | 656 bajtów |
Klasy wytycznych
Wprowadzenie
Klasy wytycznych, nazywane również klasami reguł (policy classes) służą do parametryzowania zachowania innych klas. Rozważmy przykład funkcji accumulate. Posiada ona również przeciążoną wersję umożliwiającą postawienie dowolnej operacji zamiast dodawania:
template <class InputIterator, class T, class BinaryFunction> T accumulate(InputIterator first, InputIterator last, T init, BinaryFunction binary_op);
Jedyna zmiana w implementacji klasy w stosunku do przykładu 5.2 to zmiania operacji sumowania na:
init = binary_op(init, *first);
Pomimo, że pojawił się dodatkowy szablon klasy, to nie jest to typowa klasa wytycznych. Zachowanie jest określone nie tyle przez ten parametr, co przez funktor przekazany jako argument wywołania.
Możemy jednak zmienić trochę implementację:
template <class Operation, class InputIterator, class T > T accumulate(InputIterator first, InputIterator last, T init) { for (; first != last; ++first) init = Operation::op(init,*first) return init; }
Takiego szablonu możemy używać następująco:
template<typename T> Sumation { static op(const T &a,const T &b) { return a+b; } }; accumulate<Summation<double> >accumulate(first,last,0.0);
Klasa (szablon) Summation jest właśnie klasą wytycznych. W zasadzie nie ma powodów aby implementować funkcję accumulate za pomocą klas wytycznych, poza być może nadzieją na trochę bardziej efektywny kod.
W następnej części przedstawię bardziej realistyczny, ale i bardziej skomplikowany przykład.
Projektowanie za pomocą klas wytycznych
Problemem w uniwersalnych bibliotekach jest duża ilość możliwych implementacji pojedynczego komponentu. Dzieje się tak kiedy implementując komponent możemy podjąć kilka prawie niezależnych od siebie decyzji. Projektując kontener mamy np. do wyboru różne sposoby alokacji pamięci i różne strategie obsługi błędów. Te zagadanienia są w dużej mierze ortogonalne do siebie. Jeśli więc mamy trzy strategie przydziału pamięci i trzy strategie obsługi błędu, to w sumie dostajemy dziewięć możliwych kombinacji. Decyzja o możliwości pracy w środowisku wielowątkowym zwiększą tę liczę dwukrotnie.
Klasy wytycznych mogą pomóc opanować ten kombinatoryczny wzrost ilości możliwości. Idea polega na tym, aby za każdą decyzję odpwiedzialną zrobić jedną klasę wytyczną, przekazywaną jako parametr szablonu. W przytoczonym przykładzie szablon kontenera mógłby posiadać dwa parametry wytycznych
template<typename T,
typename Allocator_policy,
typename Checking_policy>
Kontener;i potrzebowalibyśmy 6 (3 Allocator_policy i 3 Checking_policy) różnych klas wytycznych. Sześć może się wydawać niewiele mniejsze od dziewięciu, ale takie podejście skaluje się liniowo z liczbą wytycznych: dodanie nowej strategii alokacji pamięci wymaga jednej dodatkowej klasy, a liczba kombinacji zwieksza się do 12. W praktyce wszystkie wytyczne miałyby wartości domyślne.
Stack
br>
Pokażę teraz jak to działa w praktyce na przykładzie znanego już nam szablonu klasy Stack, w którym na początek dokonam drobnych zmian:
template<typename T = int , size_t N = 100> class Stack { private: T rep[N]; size_t _top; public: Stack():_top(0) {} void push(const T &val) {_rep[_top++]=val;} void pop() {--_top;} const T& top() const {return _rep[top-1];} bool is_empty {return !_top;} }
Zmiany polegają na rozdzieniu operacji odczytywania wierzchołka stosu i zdejmowania elementu ze stosu. Umożliwia to między innymi przekazywanie wartości zwracanej ze stosu przez referencje, poza tym jest to bardziej bezpieczne.
Ten kod jest, delikatnie rzecz ujmując, bardzo prościutki. Możemy rozbudowywać go w co najmniej dwu kierunkach. Po pierwsze można użyć dynamicznej alokacji pamięci, po drugie możemy zaimplementować sprawdzanie zakresu aby wykryć próbę włożenia elementu na pełny stos, lub zdjęcia/odczytania elementu ze stosu pustego. W tym przypadku mamy różne możliwości reakcji na te błędy.
Żeby zaimplementować sprawdzanie zakresu dodajemy nowy parametr do szablonu Stack, który będzie określał klasę wytyczną dla tej strategii:
template<typename T = int , size_t N = 100, typename Checking_policy = No_checking_policy > class Stack { private: T _rep[N]; size_t _top; public: Stack():_top(0) {}; void push(const T &val) { Checking_policy::check_push(_top,N); _rep[_top++]=val; } void pop() { Checking_policy::check_pop(_top); --_top; } const T& top() const { Checking_policy::check_top(_top); return _rep[top-1]; } bool is_empty() { return !_top; } };
( Źródło: stack1.h)
Klasa
struct No_checking_policy { static void check_push(size_t,size_t) {}; static void check_pop(size_t) {}; static void check_top(size_t) {}; };
( Źródło: checking_policy.h)
implementuje najprostszą strategię sprawdzania zakresu: brak sprawdzania. Proszę zauważyć, że w tym wypadku najprawdopodobniej żaden kod nie zostanie dodany: kompilator "wyoptymalizuje" puste funckje.
Inne możliwe strategie to np.
class Abort_on_error_policy { public: static void check_push(size_t top,size_t size) { if(top >= size) { std::cerr<<"trying to push elemnt on full stack: aborting"<<std::endl; abort(); } }; i podobnie dla pozostałych funkcji sprawdzających };
( Źródło: checking_policy.h)
Programując w C++ wstyd by było nie użyć wyjątków:
struct Std_exception_on_error_policy { static void check_push(size_t top,size_t size) { if(top >= size) { throw std::range_error("over the top"); } }; i podobnie dla pozostałych funkcji sprawdzających };
( Źródło: checking_policy.h)
Teraz możemy prosto konfigurować szablon Stack podając mu odpowiednie argumenty:
Stack<int,10> s_no_check; Stack<double ,100,Abort_on_error_policy> s_abort; Stack<int *,25,Std_exception_on_error_policy> s_except;
( Źródło: policy1.cpp)
W celu zaimplementowania różnych strategii przydziału pamięci dodajemy dodatkowy parametr szablonu, który sam będzie szablonem:
template<typename T = int , size_t N = 100, typename Checking_policy = No_checking_policy, template<typename U,size_t M> class Allocator_policy = Static_table_allocator > class Stack;
Szablon typu Allocator_policy posiada jeden typ stowarzyszony i szereg funkcji:
template<typename T,size_t N = 0> struct Static_table_allocator { typedef T rep_type[N]; void init(rep_type &,size_t) {}; void expand_if_needed(rep_type &,size_t) {}; void shrink_if_needed(rep_type &size_t) {}; void dealocate(rep_type &){}; static size_t size() {return N;}; };
( Źródło: allocator2.h)
Szablon Stack implementujemy teraz następująco:
template<...> class Stack { typedef typename Allocator_policy<T,N>::rep_type rep_type; rep_type _rep; size_t _top; Allocator_policy<T,N> alloc; public: Stack(size_t n = N):_top(0) { alloc.init(_rep,n); }; void push(const T &val) { alloc.expand_if_needed(_rep,_top); Checking_policy::check_push(_top,alloc.size()); _rep[_top++]=val; } void pop() { Checking_policy::check_pop(_top); --_top; alloc.shrink_if_needed(_rep,_top); } const T& top() const { Checking_policy::check_top(_top); return _rep[top-1]; } bool is_empty() { return !_top; } ~Stack() {alloc.dealocate(_rep);} };
( Źródło: stack2.h)
Szablon
template<typename T,size_t N > struct Expandable_new_allocator { typedef T * rep_type; size_t _size; void init(rep_type &rep,size_t n) {_size=n;rep = new T [_size];}; void expand_if_needed(rep_type & rep,size_t top) { if(top == _size) { _size=2*_size; T *tmp= new T[_size]; std::copy(rep,&rep[top],tmp); delete [] rep; rep = tmp; } }; void shrink_if_needed(rep_type &size_t) { }; void dealocate(rep_type &rep){delete [] rep;}; size_t size() const {return _size;}; };
( Źródło: allocator2.h)
definiuje strategię dynamicznego przydziału pamięci "na żądanie". Możemy teraz dowolnie składać nasze strategie:
int n=10; Stack<int,0,Std_exception_on_error_policy,Expandable_new_allocator > s1(n); Stack<int,10,Abort_on_error_policy,Static_table_allocator > s2(n);
( Źródło: policy2.cpp)
Widać, że takie podejście jest bardzo elastyczne, użytkownik może praktycznie dowolnie konfigurować sobie zachowanie klasy Stack, zwłaszcza, że ma możliwość tworzenia własnych klas wytycznych.
Oczywiście powyższy przykład nie jest do końca dopracowany. Przede wszystkim strategie przydziału pamięci i strategie sprawdzenia zakresu nie są całkowicie niezależne. Np. w funkcji push jeśli powiedzie się wywołanie funkcji expand_if_needed() to nie ma potrzeby wywoływania funkcji check_push(). Po drugie - całkowicie pominęliśmy kwestię diagnostyki funkcji alokujących pamięć. Możliwe rozwiązanie to przekazanie Checkin_policy jako argumentu szablonu do allocator_policy. Można też rozważyć posiadanie dwu różnych klas wytycznych, jednej dla obsługi błędów przekroczenia zakresu, drugiej do obsługi błędów przydziału pamięci.
Dziedziczenie wytycznych
Stosowanie wytycznej Checking_policy sprowadzało się do używania funkcji statycznych. W przypadku wytycznej Allocator_policy musieliśmy utworzyć obiekt tej klasy, ponieważ niektóre implementacje tej wytycznej posiadają stan (w tym przypadku jest to zmienna _size). Alternatywnym sposobem użycia takiej wytycznej jest wykorzystanie dziedziczenia:
template<typename T = int , size_t N = 100, typename Checking_policy = No_checking_policy, template<typename U,size_t M> class Allocator_policy = Static_table_allocator > class Stack: private Checking_policy, private Allocator_policy<T,N> { typedef typename Allocator_policy<T,N>::rep_type rep_type; rep_type _rep; size_t _top; public: Stack(size_t n = N):_top(0) { init(_rep,n); }; void push(const T &val) { expand_if_needed(_rep,_top); Checking_policy::check_push(_top,this->size()); _rep[_top++]=val; } void pop() { Checking_policy::check_pop(_top); --_top; this->shrink_if_needed(_rep,_top); } const T& top() const { Checking_policy::check_top(_top); return _rep[top-1]; } bool is_empty() { return !_top; } ~Stack() {this->dealocate(_rep);} };
( Źródło: stack3.h)
Główna zmiana to konieczność kwalifikowania nazw niektórych funkcji przez this-> tak, aby stały się nazwami zależnymi (zob. wykład 3.7.1). Skorzystałem z dziedziczenia prywatnego aby zaznaczyć, że dziedziczę implementację a nie interfejs (Stack nie jest Allocator_policy). Jednak odziedziczenie również interfejsu klasy Allocator_policy poprzez dziedziczenie publiczne może być użyteczne. Aby się o tym przekonać rozważymy kolejną modyfikację naszego przykładu: przeniesiemy zmienną _rep z klasy Stack do klasy wytycznej np.
template<typename T,size_t N > class Dynamic_table_allocator { protected: typedef T * rep_type; rep_type _rep; size_t _size; void init(size_t n) {_size=n;_rep = new T[_size];}; void expand_if_needed(size_t) {}; void shrink_if_needed(size_t) {}; void dealocate(){delete [] _rep;}; size_t size() const {return _size;}; public: void resize(size_t n) { T *tmp= new T[n]; std::copy(_rep,&_rep[(_size<n)?_size:n],tmp); delete [] _rep; _rep = tmp; _size=n; } };
( Źródło: allocator3_1.h)
Pociąga to za sobą zmiany w klasie Stack:
template<typename T = int , size_t N = 100, typename Checking_policy = No_checking_policy, template<typename U,size_t M> class Allocator_policy = Static_table_allocator > class Stack: private Checking_policy, public Allocator_policy<T,N> { size_t _top; public: Stack(size_t n = N):_top(0) { Stack::init(n); }; void push(const T &val) { Stack::expand_if_needed(_top); Checking_policy::check_push(_top,this->size()); Stack::_rep[_top++]=val; } void pop() { Checking_policy::check_pop(_top); --_top; Stack::shrink_if_needed(_top); } const T& top() const { Checking_policy::check_top(_top); return Stack::_rep[top-1]; } bool is_empty() { return !_top; } Stack() { Stack::dealocate();} };
( Źródło: stack3_1.h)
Zmieniłem również sposób uzależniania nazw niezależnych na kwalifikację ich nazwą klasy Stack. Teraz możemy korzystać z interfejsu klasu Dynamic_table_allocator w klasie Stack.
Stack<int,n,Std_exception_on_error_policy,Dynamic_table_allocator > s(n); s.resize(20);
( Źródło: policy3_1.cpp)
| Załącznik | Wielkość |
|---|---|
| Stack1.h | 812 bajtów |
| Checking_policy.h | 1.17 KB |
| Policy1.cpp | 257 bajtów |
| Allocator2.h | 1.25 KB |
| Stack2.h | 1.16 KB |
| Policy2.cpp | 242 bajty |
| Stack3.h | 1.11 KB |
| Allocator3_1.h | 1.37 KB |
| Stack3_1.h | 1.08 KB |
| Policy3_1.cpp | 315 bajtów |
Metaprogramowanie
Metaprogramowanie
Ogólnie rzecz biorąc metaprogramowanie oznacza pisanie programów, które piszą programy lub pisania programu, który pisze się sam. W naszym kontekście będzie to oznaczało wykonywanie obliczeń za pomocą szablonów, przy czym obliczenia te są wykonywane podczas kompilacji. Podstawą do tych obliczeń jest rekurencyjna konkretyzacja szablonów. Taką metodą można generować w czasie kompilacji całkiem skomplikowane fragmenty kodu, stąd określenie metaprogramowanie. Przykłady takich "metaszablonów" poznaliśmy już na wykładzie o funkcjach typów. W szczególności działanie na listach typów to właśnie przykłady metaprogramowania. W tym wykładzie przyjrzymy się dokładniej temu zagadnieniu i przeanalizujemy kolejne przykłady.
Potęgi
Zaczniemy od bardzo prostego przykładu (zob. D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty", rozdz. 17). Napiszemy szablon który ma za zadanie obliczać potęgi liczby 3. Ponieważ w programowaniu za pomocą szablonów musimy posługiwać się rekurencją to zaczynamy od sformułowania problemu w sposób rekurencyjny. To akurat jest bardzo proste:
Przykład 8.1
Za pomocą szablonów implementujemy to tak ( Źródło: Pow.cpp):
template<int N> struct Pow3 { enum {val=3*Pow3<N-1>::val}; }; template<> struct Pow3<0> { enum {val=1}; };
teraz możemy już użyć w programie np. wyrażenie:
i=Pow3<4>::val;
Podstawową zaletą metaprogramowania i głównym powodem jego używania jest fakt, że to wyrażenie jest obliczane w czasie kompilacji i efekt jest taki sam jak podstawienia:
i=81;Można też zastosować szablon funkcji:
template<int N> int pow3() { return 3*pow3<N-1>(); }; template<> int pow3<0>() {return 1;} cout<<pow3<4>()<<endl;
( Źródło: Powf.cpp)
Nietrudno jest uogólnić powyższy kod tak aby wyliczał potęgi dowolnej liczby:
template<int K,int N> struct Pow { enum {val=K*Pow<K,N-1>::val}; }; template<int K> struct Pow<K,0> { enum {val=1}; };
( Źródło: Pow.cpp)
Tutaj już nie można wykorzystać szablonu funkcji, bo nie zezwala on na
specjalizację częściową.
Ograniczeniem dla takich obliczeń jest implementacja kompilatora,
przede wszystkim założony limit głebokości rekurencyjnego
konkretyzowania szablonów. Dla kompilatora g++ jest on ustawiany za
pomocą opcji i defaultowo wynosi 500, dlatego już konkretyzacja Pow<1,500>::val się nie powiedzie.
Konkretyzacja szablonów wymaga też pamięci i może się zdarzyć, że
kompilator wyczerpie limit pamięci lub czasu.
Kolejne ograniczenie to konieczność rachunków na liczbach całkowitych.
Wiąże się to z faktem, że tylko stałe całkowitoliczbowe mogą być
parametrami szablonów.
Ciąg Fibonacciego
Po opanowaniu powyższych przykładów obliczanie wyrazów ciągu Fibonacciego jest prostym zadaniem. Przytoczymy je jednak tutaj, aby zaprezentować pewną bardzo sympatyczną cechę metaprogramowania za pomocą szablonów. Ciąg Fibonacciego jest definiowany rekurencyjnie:
Przykład 8.2
więc jego implementacja jest natychmiastowa:
template<int N> struct Fibonacci { enum {val = Fibonacci<N-1>::val+Fibonacci<N-2>::val}; }; template<> struct Fibonacci<1> { enum {val = 1}; }; template<> struct Fibonacci<2> { enum {val = 1}; };
( Źródło: fibonacci_template.cpp)
Przykład ten nie wart byłby może i wspomnienia gdyby nie fakt, że rekurencyjna implementacja ciągu Fibonacciego jest bardzo nieefektywna. Jeśli zaimplementujemy ją w zwykłym kodzie
int fibonacci(int n) { if(n==1) return 1; if(n==2) return 1; return fibonacci(n-1)+fibonacci(n-2); }
( Źródło: fibonacci.cpp)
to obliczanie fibonacci(45) zajmie np.na moim komputerze ok. 8 sekund. Tymczasem szablon kompiluje sie poniżej jednej sekundy! Skąd taka różnica? Czyżby kompilator był bardziej wydajny niż generowany przez niego kod? W przypadku zwykłego kodu długi czas wykonania bierze się z ogromnej liczby wywołań funkcji fibonacci. Liczba ta rośnie wykładniczo z n i większość czasu jest marnowana na wielokrotne wywoływanie funkcji z tymi samymi argumentami.
W przypadku użycia metaprogramu szablony konkretyzowane są tylko raz. Więc jeśli już raz policzymy np. Fibonacci<25>::val to kolejne żądanie nie spowoduje już rozwinięcia rekurencyjnego, a tylko podstawienie istniejącej wartości. Jak widzieliśmy zysk jest ogromny. Takie pamiętanie wyników raz wywołanych funkcji nazywane jest też programowaniem dynamicznym. Jedynym znanym mi językiem, który bezpośrednio wspiera taki mechanizm jest Mathematica.
Pierwiastek kwadratowy
Rozważymy teraz trudniejszy przykład szablonu obliczającego pierwiastek kwadratowy (zob. D. Vandervoorde, N. Josuttis: "C++ Szablony, Vademecum profesjonalisty", rozd. 17), choć tak naprawdę ten kod jest bardziej uniwersalny i, jak zobaczymy, łatwo za jego pomocą zaimplementować inne funkcje. Ponieważ jesteśmy ograniczeni do arytmetyki liczb całkowitych, tak naprawdę nie liczymy pierwiastka z n ale jego przybliżenie: największą liczbę całkowitą k, taką że k*k<=n. W tym celu zastosujemy algorytm przeszukiwania binarnego:
int sqrt(int n,int low, int high) { if(low==high) return low; int mid=(low+high+1)/2; if(mid*mid > n ) return sqrt(n,low,mid-1); else return sqrt(n,mid,high); }
co już łatwo przetłumaczyć na szablon:
template<int N,int L=1,int H=N> struct Sqrt{ enum {mid=(L+H+1)/2}; enum {res= (mid*mid> N)? (int)Sqrt<N,L,mid-1>::res : (int)Sqrt<N,mid,H>::res}; }; template<int N,int L> struct Sqrt<N,L,L> { enum {res=L}; };
( Źródło: sqrt.cpp)
Łatwo sprawdzić, że kod ten działa poprawnie. Niestety posiada on istotną wadę. W trakcie konkretyzacji szablonu konkretyzowane są oba szablony występujące w wyrażeniu warunkowym, nawet ten, który nie będzie potem używany. Tak więc wykonywana jest duża liczba konkretyzacji, z których tylko ułamek jest potrzebny (zob. rysunek). Jakie to obciążenie dla kompilatora to łatwo sprawdzić kompilując kod, w którym wywołujemy Sqrt<10000>. Ja nie doczekałem się na koniec kompilacji.
Na szczęście istnieje rozwiązanie - należy użyć szablonu If_then_else (zob. wykład 6.2.1):
template<int N,int L=1,int H=N> struct Sqrt{ enum {mid=(L+H+1)/2}; typedef typename If_then_else< (mid*mid> N), Sqrt<N,L,mid-1>, Sqrt<N,mid,H> >::Result tmp; enum {res= tmp::res}; }; template<int N,int L> struct Sqrt<N,L,L> { enum {res=L}; };
( Źródło: sqrt_ifte.cpp)
Ten kod powoduje już tylko konkretyzację rzeczywiście wymaganych szablonów, a tych jest dużo mniej: rzędu \(O(\log N)\). Tym razem kompilacja wyrażenia Sqrt<10000> powiedzie się bez trudu.
Pow(x)
Jak dotąd używaliśmy metaprogramowania do wyliczania wartości stałych. Teraz postaramy się wygenerować funkcje. Zacznijmy od pytania: po co? Pomijając syndrom Mount Everestu (wchodzę na niego bo jest), to głównym powodem jest nadzieja uzyskania bardziej wydajnego kodu. Weźmy dalej za przykład liczenie potęgi, tym razem dowolnej liczby zmiennoprzecinkowej:
double pow_int(double x,int n) { double res=1.0; for(int i=0;i<n;++i) res*=x; return res; };
( Źródło: powx.cpp)
Patrząc na ten kod widzimy, że w pętli wykonywana jest bardzo prosta instrukcja. Możemy więc się obawiać, że instrukcje związane z obsługą pętli mogą stanowić spory narzut. Co więcej, ich obecność utrudnia kompilatorowi optymalizację kodu oraz może uniemożliwić rozwinięcie funkcji w miejscu wywołania. Najlepiej by było zaimplementować tę funkcję w ten sposób:
pow(x,n)= x*...*x; /*n razy*/
np.:
double pow2(double x) {return x*x;} double pow3(double x) {return x*x*x;} double pow4(double x) {return x*x*x*x;} ...
Wymaga to jednak kodowania ręcznego dla każdej potęgi, której potrzebujemy. Ten sam efekt możemy osiągnąc za pomocą następującego szablonu funkcji:
template<int N> inline double pow(x) {return x*pow<N-1>(x);} template<> inline double pow<0>(x) {return 1.0;}
( Źródło: powx.cpp)
pod warunkiem, że kompilator rozwinie wszystkie wywołania.
Poniżej zamieszczam wyniki pomiarów wykonania 100 milionów wywołań każdej funkcji ( Źródło: powx.cpp). Czas jest podany w sekundach. Zamieściłem wyniki dla różnych ustawień optymalizacji.
| pow_int(x,5) | pow<5>(x) | |
| -O0 | 7.22 | 14.78 |
| -O1 | 0.37 | 0.04 |
| -O2 | 0.42 | 0.05 |
| -O3 | 0.42 | 0.05 |
Widać dramatyczną różnicę po włączeniu optymalizacji. Wiąże się to prawdopodobnie z umożliwieniem rozwijania funkcji inline. Potem wyniki już się nie zmieniają ale widać, że szablon pow wygenerował funkcję 10 razy szybszą od pozostałych. Pokazuje to dobitnie, że optymalizacja ręczna ciągle ma sens.
Sortowanie bąbelkowe
Zakończymy ten wykład bardziej skomplikowanym przykładem pokazującym, że metaprogramowanie można stosować nie tylko do obliczeń numerycznych. Popatrzmy na kod implementujący sortowanie bąbelkowe:
inline void swap (int &a,int &b) {int tmp=a;a=b;b=tmp;}; void bubble_sort_function (int* data, int N) { for(int i = N-1; i>0; --i) for(int j=0;j<i;++j) if(data[j]>data[j+1]) swap(data[j],data[j+1]); }
( Źródło: bubble_template.cpp)
Znów widzimy tu dwie pętle i wszystkie uwagi dotyczące funkcji pow_int tu też się stosują. Postaramy się więc zdefiniować szablon, który dokona rozwinięcia tych obu pętli. Np. dla N=3 chcielibyśmy otrzymać następujący kod:
//i=2 j=0 if(data[0]>data[1]) swap(data[0],data[1]); //i=2 j=1 if(data[1]>data[2]) swap(data[1],data[2]); //i=1 j=0 if(data[0]>data[1]) swap(data[0],data[1]);
Jeśli Państwo śledzili wykład (przynajmniej ten), to już Państwo wiedzą, że pierwszym krokiem musi być przepisanie kodu sortowania na postać rekurencyjną:
void bubble_sort_function (int* data, int N) { for(int j=0;j<N-1;++j) if(data[j]>data[j+1]) swap(data[j],data[j+1]); if(N>2) bubble_sort_function(data,N-1); }
To jeszcze nie to co trzeba, bo musimy zapisać pętle w postaci rekurencyjnej. Jeśli oznaczymy sobie:
void loop(int * data,int N) { for(int j=0;j<N-1;++j) if(data[j]>data[j+1]) swap(data[j],data[j+1]); }
to łatwo zauważyć, że loop można zdefiniować następująco:
loop(int *data,int N) { if(N>0) { if(data[0]>data[1]) swap(data[0],data[1]); loop(++data,N-1); } }
co natychmiast tłumaczy się na szablony:
template<int N> inline void loop(int *data) { if(data[0]>data[1]) std::swap(data[0],data[1]); loop<N-1>(++data); } template<> inline void loop<0>(int *data) {};
Szablon funkcji bubble_sort_template ma więc postać:
template<int N> inline void bubble_sort_template(int * data) { loop<N-1>(data); bubble_sort_template<N-1>(data); } template<> inline void bubble_sort_template<2>(int * data) { loop<1>(data); };
( Źródło: bubble_template.cpp)
Poniżej znów podaję porównanie czasu wykonywania się 100 milionów wywołań funkcji bubble_sort_function i bubble_sort_template dla tablicy zawierającej 12 liczb całkowitych w kolejności malejącej.
| bubblesortfunction(a,12) | bubblesorttemplate<12>(a) | |
| -O0 | 43.3 | 42.2 |
| -O1 | 21.0 | 4.8 |
| -O2 | 20.0 | 3.5 |
| -O3 | 20.0 | 3.6 |
Widać, że wersja na szablonach jest ok. 4-5 razy szybsza. Zachęcam do
własnych eksperymentów.
Zaprojektowany szablon działa tylko dla tablic liczb całkowitych. Jest
to ewidentne ograniczenie, które powinniśmy zlikwidować poprzez dodanie
doatkowego parametru szablonu. Niestety, prowadzi to do konieczności
dokonania specjalizacji częściowej, która nie jest dozwolona dla
szablonów funkcji. Na szczeście nie jest trudno przepisać naszą
implementację używając szablonów klas. Pozostawiam to jako ćwiczenie
dla czytelników :).
Rozmiar kodu
Jak pokazałem, kod generowany przez szablon bubble_sort_template jest
bardziej efektywny. Dzieje się to jednak kosztem jego rozmiaru. Są ku
temu dwa powody. Po pierwsze podwójna pętla wewnątrz procedury
bubble_sort_function wykonuje \((N-1)*(N-2)/2\) iteracji i tyle
linijek powinien mieć w pełni rozwinięty kod w szablonie
bubble_sort_template. Po drugie każda instancja szablonu jest
osobną funkcją, stąd bubble_sort_template<50> i
bubble_sort_template<51> generują osobny kod każda. W celu
sprawdzenia tych przewidywań przedstawiam poniżej rozmiar wynikowego
kodu w bajtach dla programu, który kompilował funkcję
bubble_sort_template
| N | size |
| 10 | 9333 |
| 30 | 17846 |
| 50 | 21847 |
| 70 | 40399 |
| 90 | 33296 |
| 100 | 53606 |
Widać, że choć rozmiar w zasadzie rośnie z \(N\), to ta zależność nie jest nawet monotoniczna. Wynika to pewnie z tego, że dla większych \(N\) kompilator nie dokonuje całkowitego rozwiniecią kodu.
| Załącznik | Wielkość |
|---|---|
| Powf.cpp | 184 bajty |
| Pow.cpp | 412 bajtów |
| Fibonacci_template.cpp | 315 bajtów |
| Fibonacci.cpp | 211 bajtów |
| Sqrt.cpp | 821 bajtów |
| Sqrt_ifte.cpp | 1.04 KB |
| Powx.cpp | 1.21 KB |
| Bubble_template.cpp | 1.86 KB |
Szablony wyrażeń
Wprowadzenie
Rozważmy implementację funkcji całkującej inne funkcje:
double integrate(double (*f)(double ),double min,double max,double ds) { double integral=.0; for(double x=min;x<max;x+=ds) { integral+=f(x); } return integral*ds; }
( Źródło: integrate.cpp)
Pomijając prostotę zaimplementowanego algorytmu numerycznego, możemy jej używać następująco:
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl;
Jest to standardowy sposób implementowania takich zagadnień w C czy w Fortranie. W C++ szablony dają nam większe możliwości. Funkcja integrate przyjmuje jako swój pierwszy argument wskaźnik do jednoargumentowej funkcji zwracającej double, ale to co jest naprawdę istotne to to, że można użyć w stosunku do niego notacji wywołania funkcji: f(x). W C++ możemy wyposażyć w tę możliwość każdą klasę poprzez zdefiniowanie w niej metody operator(). Jeśli zdefiniujemy funkcję integrate jako szablon, to będziemy mieli możliwość przekazywania również takich obiektów nazywanych obiektami funkcyjnymi lub funktorami.
template<typename F> double integrate(F f,double min,double max,double ds) { double integral=.0; for(double x=min;x<max;x+=ds) { integral+=f(x); } return integral*ds; }
( Źródło: integrate_temp.cpp)
Wywołanie
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl;
dalej zadziała, ale można używać również:
class sina { double _a; public: sina(double a): _a(a) {}; double operator()(double x) {return sin(_a*x);} }; std::cout<< ::integrate(sina(0),0,3.1415926,0.01)<<std::endl; std::cout<< ::integrate(sina(1),0,3.1415926,0.01)<<std::endl; std::cout<< ::integrate(sina(2),0,3.1415926,0.01)<<std::endl;
( Źródło: integrate_temp.cpp)
Widać tu już pierwszą zaletę funktorów: jako obiekty mogą one posiadać stan. W przypadku funkcji do takich celów musielibyśmy używać zmiennych globalnych. Ale żeby móc funktora używać musimy go najpierw zdefiniować. Pytanie na które bedę się starał odpowiedzieć na tym wykładzie brzmi: czy możemy definicję funktora uprościć? Np. czy nie moglibyśmy pisać
integrate(sin(2*x),...)
lub
integrate(1.0/(1.0+x),...)
Okazuje się, że można i technika, która to umożliwia, nosi nazwę "szablonów wyrażeń". Z pozoru wydaje się to być tylko ciekawostką, ale w następnej części tego wykładu pokażemy jak za pomocą tej techniki można istotnie przyspieszyć program.
Naszym celem jest napisane kodu, który będzie generował funktory
automatycznie z "normalnych" wyrażeń typu \(\displaystyle 1/(1+x)\) i umożliwi pisanie wyrażeń w rodzaju:
integrate(1/(1+x),0,1,0.01);
\(\displaystyle x\) oznacza tu zmienną, po której całkujemy. Oznacza to, że kompilator musi wyrażenie \(\displaystyle 1/(1+x)\) przekształcić na funktor
class _some_functor_ { public: double operator()(double x) return {1/(1+x);} }
Zmienne
Chińczycy mówią, że podróż stumilową zaczyna się od pierwszego kroku. Zróbmy więc pierwszy krok i spróbujmy doprowadzić do prawidłowej kompilacji i wykonania wyrażenie:
integrate(x,...);
Żeby to działało prawidłowo, x musi być funktorem który zwraca własny argument:
class Variable { public: double operator()(double x) { return x; } };
( Źródło: expr_templates.h)
Możemy więc już wykonać całkę \(\displaystyle \int_0^1x\;\) d \(\displaystyle x\)
Variable x; integrate(x,0,1,0.001);
co nie jest jakimś porywającym wyczynem:). Żeby się posunąć dalej potrzebujemy kolejnych elementów.
Stałe
Ewidentnie potrzebujemy stałych (literałów). Stała to funktor, który zwraca wartość niezależną od swojego argumentu:
class Constant { double _c; public: Constant(double c) :_c(c){}; double operator()(double x) {return _c;} };
( Źródło: expr_templates.h)
Niestety literałów nie możemy używać bezpośrednio w naszym wyrażeniu:
integrate(1.0,0,1,0.001);
nie zadziała. Musimy pisać
integrate(Constant(1.0),0,1,0.001);
Można by wprawdzie przeładować definicje integrate dla argumentów typu double ale chyba nie warto, zważywszy na to, że całkowanie stałej nie jest zbyt kłopotliwe.
Następnym krokiem będzie dodanie wyrażeń arytmetycznych.
Dodawanie
Zaczniemy od dodawania. Potrzebne będą dwa elementy: klasa funktor, która symbolizuje dodawanie oraz odpowiednio zdefiniowany operator dodawania.
Funktor symbolizujący dodawanie musi mieć dwie składowe odpowiadające dwu składnikom tej operacji. Przypominamy, że każdy z tych składników też jest funktorem, a więc posiada jednoargmentowy operator()(double). Operacja dodawania polegać więc bedzie na dodaniu wyników obu funktorów składowych:
template<typename LHS,typename RHS > class AddExpr { LHS _lhs; RHS _rhs; public: AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {}; double operator()(double x) { return _lhs(x)+_rhs(x); } };
( Źródło: expr_templates.h)
Pozostaje nam tylko zdefiniować operator dodawania, który z dwu składników utworzy nam obiekt typu AddExpr. Ponieważ możemy dodawać cokolwiek, to operator dodawania będzie szablonem:
template<typename LHS,typename RHS > Add<LHS,RHS> operator+(const LHS &l, const RHS &r) { return Add<LHS,RHS>(l,r); };
( Źródło: expr_templates.h)
Żeby móc dodawać stałe potrzebujemy jeszcze specjalizacji szablonu dla przypadku, w którym jeden z argumentów jest typu double):
template<typename LHS > Add<LHS,Constant> operator+(const LHS &l, double r) { return Add<LHS,Constant>(l,Constant(r)); }; template<typename RHS > Add<Constant,RHS> operator+(double l, const RHS &r) { return Add<Constant,RHS>(Constant(l),r); };
( Źródło: expr_templates.h)
Widać, że w identyczny sposób możemy zaimplementować pozostałe trzy działania. Odpowiadające im klasy nazwiemy odpowiednio SubsExpr, MultExpr i DivExpr (pominąłem jednoargumentowy operator-()). Ich kod można zaobaczyć w Źródło: expr_templates.h.
Funkcje
Analogicznie implementujemy funkcje np.:
template<typename Arg> class SinExpr{ Arg _arg; public: SinExpr(const Arg& arg) :_arg(arg) {}; double operator()(double x) {return sin(_arg(x));} }; template<typename Arg> SinExpr<Arg> sin(const Arg&a) { return SinExpr<Arg>(a);}
i operatory unarne (jednoargumentowe), takie jak operator negacji:
template<typename LHS> class NegativeExpr { LHS _lhs; public: NegativeExpr(const LHS &l) :_lhs(l) {}; double operator()(double x) { return - _lhs(x); } }; template<typename LHS> NegativeExpr<LHS> operator-(const LHS &l) { return NegativeExpr<LHS>(l); };
( Źródło: expr_templates.h)
Jak to działa?
Mam nadzieję, że zasada działania szablonów wyrażeń jest już jasna, ale prześledźmy jeszcze raz przykład wyrażenia:
\Variable x; 1.0/(1.0+x)
Kompilator dokonuje rozkładu gramatycznego i interpretuje to wyrażenia jako:
operator/(1.0,operator+(1,x))
Wiedząc, że x jest typu Variable, kompilator stara się znaleźć
odpowiednie szablony operatorów. Najpierw dopasuje wewnętrzny
operator+
operator/(double,operator+<Variable>(double 1.0 , Variable x))
a potem wiedząć, że typ zwracany przez ten operator
to AddExpr
operator/<AddExpr<Constant,Variable> >
(double 1.0,
AddExpr<Constant,Variable>
operator+<Variable>(double 1.0 ,
Variable x)
)Po zastąpieniu skonkretyzowanych operatorów ich definicjami powstanie kod, który generuje tymczasowy obiekt:
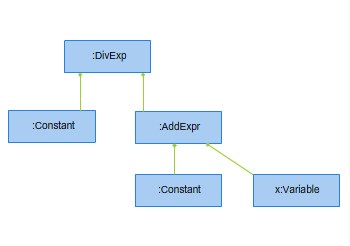 Rysunek 9.1. Funktor wygenerowany z wyrażenia .
Rysunek 9.1. Funktor wygenerowany z wyrażenia .
expr=DivExpression<Constant, AddExpr<Constant,Variable> >(Constant(1.0), AddExpr<Constant,Variable>(Constant(1.0),Variable() );
Przedstawienie tego obiektu zamieszczone jest na rysunku 9.1.
Widać, że obiekt expr reprezentuje drzewo rozkładu wyrażenia \(\displaystyle 1.0/(1.0+x)\). Wywołanie operatora nawiasów spowoduje rekurencyjne wywoływanie operatorów nawiasów wyrażeń składowych i w konsekwencji obliczenie tego wyrażenia.
Proszę zwrócić uwagę, że opisana technika szablonów wyrażeń składa się z dwóch części. Pierwsza to klasy reprezentujące wyrażenia: Constant,Variable,AddExpr, itd., za pomocą których budujemy drzewo rozkładu gramatycznego. Druga - to przeciążone operatory i funkcje, które to drzewo generują.
Zmienne różnych typów
W przedstawionym przykładzie ograniczyliśmy się do wyrażeń typu double. W duchu programowania uogólnionego postaramy się zmienić nasz kod tak, aby można było wybierać typ wyrażenia poprzez parametr szablonu.
Okazuje się to jednak nie tak proste. Łatwo jest dodać dodatkowy parametr do klas reprezentujących wyrażenia:
template<typename T> class Variable { public: T operator()(T x) { return x; } }; template<typename T> class Constant { T _c; public: Constant(T c) :_c(c){}; T operator()(T x) {return _c;} }; template<typename T, typename LHS,typename RHS > class AddExpr { LHS _lhs; RHS _rhs; public: AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {}; T operator()(T x) { return _lhs(x)+_rhs(x); } };
ale niestety operatory arytmetyczne nie będą miały jak automatycznie wydedukować typu T.
template<typename T,typename LHS,typename RHS > Add<T,LHS,RHS> operator+(const LHS &l, const RHS &r) { return Add<T,LHS,RHS>(l,r); };
Typ T nie pojawia się w argumentach wywołania, a więc nie może być wydedukowany. Mamy więć kłopot.
Rozwiązaniem może być dodanie dodatkowej klasy Expr "opakowującej" wyrażenia, która będzie przenosiła informację o typie:
template<typename T,typename R = Variable<T> > class Expr { R _rep; public: Expr() {}; Expr(R rep):_rep(rep) {}; T operator()(T x) {return _rep(x);} R rep() const {return _rep;}; };
( Źródło: expr_templates_T.h)
Odpowiednie operatory dodawania będą teraz wyglądały następująco:
template<typename T,typename LHS,typename RHS > Expr<T,AddExpr<T,LHS,RHS> > operator+(const Expr<T,LHS> &l, const Expr<T,RHS> &r) { return Expr<T,AddExpr<T,LHS,RHS> >(AddExpr<T,LHS,RHS>(l.rep(),r.rep())); }; template<typename T,typename LHS > Expr<T,AddExpr<T,LHS,Constant<T> > > operator+(const Expr<T,LHS> &l, T r) { return Expr<T,AddExpr<T,LHS,Constant<T> > > (AddExpr<T,LHS,Constant<T> >(l.rep(),Constant<T>(r))); };
Ponieważ teraz typ T pojawia się w argumentach wywołania, jest możliwa jego dedukcja. Pełna implementacja wszystkich operatorów znajduje się w Źródło: expr_templates_T.h.
W porównaniu z poprzednią implementacją jedyna zmiana to taka, że zmienne musimy teraz deklarować jako:
Expr<double> x;
lub równoważnie
Expr<double,Variable<double> > x;
Teraz możemy również definiować zmienne innych typów:
Expr<complex<double> > z; Expr<int> i;
Niestety, to ciągle nie jest koniec naszych kłopotów, nie możemy bowiem mieszać wyrażeń różnych typów. Jeśli np. zdefiniujemy:
Expr<double> x;
int i;to wyrażenia
x+1;
x+i;nieskompilują się. Oczywiście możemy pisać:
x+1.0; x+(double)i;
ale jest to niewygodne; zwłaszcza jeśli będziemy chcieli użyć zmiennych zespolonych
Expr<std::complex<double> > c; double x; std::complex<double>(x)+c
wydaje się trochę skomplikowane. Można jednak, używając cech promocji, tak zmodyfikować nasz kod, aby potrafił automatycznie konwertować typy. Jest to przedmiotem jednego z ćwiczeń do tego wykładu.
Więcej zmiennych
Jak na razie generowaliśmy funktory jednoargumentowe. Powyższa technika daje się łatwo zastosować również do funktorów dwuargumentowych. W tym celu musimy mieć możność rozróżnienia pierwszego i drugiego argumentu. Dlatego wprawadzamy dwie klasy, które zastąpią klasę Variable. Klasa
class First { public: double operator()(double x) { return x; } double operator()(double x,double) { return x; } };
reprezentuje pierwszy argument i może występować w funktorach jedno- lub dwuargumentowych, więc ma dwa operatory nawiasów. Klasa
class Second { public: double operator()(double,double y) { return y; } };
reprezentuje drugi argument funktora, więc może występować tylko jako funkcja dwuargumentowa, stąd tylko jeden dwuargumentowy operator nawiasów. Podobnie klasa
class Constant { double _c; public: Constant(double c) :_c(c){}; double operator()(double) {return _c;} double operator()(double,double) {return _c;} };
dorobiła się drugiego operatora nawiasów. Ostatnia zmiana to dodanie dwuargumentowego operatora nawiasów dla klasy
template<typename LHS,typename RHS > class AddExpr { LHS _lhs; RHS _rhs; public: AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {}; double operator()(double x) { return _lhs(x)+_rhs(x); } double operator()(double x,double y) { return _lhs(x,y)+_rhs(x,y); } };
I podobnie dla reszty działań. Operatory pozostają bez zmian.
Biblioteka lambda
Jako przykład zastosowania opisanych (lub podobnych) technik może służyć biblioteka lambda z repozytorium boost. Korzystając z tej biblioteki możemy używać predefiniowanych zmiennych _1, _2 i _3, które oznaczają odpowiednio pierwszy, drugi i trzeci argument. Korzystając z nich możemy przyklad z wykładu 2.6.3 zapisać następująco:
std::generate_n(v.begin(),n,SequenceGen<int>(1,2)); std::vector<int>::iterator it=find_if(v.begin(),v.end(),_1>4); std::cout<<*it<<std::endl;
Szablony wyrażeń wektorowych
Wszystko to piękne, ale po co? Używając wyrażeń szablonowych zyskujemy być może na wygodzie, ale dzieje się to kosztem znacznego skomplikowania kodu, a co za tym idzie - czasu kompilacji. Kod jest również dużo trudniejszy do zdebugowania. Powyższy przykład ma głównie walor edukacyjny. Teraz pokażę jak tę technikę można zastosować do problemu, w którym daje ona istotne korzyści.
Rozważmy w tym celu kolejny typowy przykład wykorzystania C++. Przeładowywanie operatorów pozwala nam prosto rozszerzyć język o operacje wektorowe. Implementacja np. operatora dodawania dla dwóch wektorów mogłaby wyglądać następująco:
template<typename T> vector<T> operator+(const vector<T> &lhs, const vector<T> &rhs) { vector<T> res(lhs) ; for(size_t i=0;i<rhs.size();++i) res[i]+=rhs[i]; return res; }
Potrzebne są jeszcze przeładowane wersje tego operatora, w których jeden z argumentów jest double-em. Zakładając, że zdefiniujemy pozostałe potrzebne operatory, możemy teraz pisać kod tak jakby typy wektorowe i operacje na nich były wbudowane w język (to zresztą było jednym z kryteriów przy projektowaniu C++):
vector<double> v1(100,1); vector<double> v2(100,2); vector<double> res(100); res=1.2*v1+v1*v2+v2*0.5; [cpp] <p>Niestety, powyższy kod traci wiele przy bliższej analizie. Jeśli popatrzymy na definicję operatorów, to zauważymy, że ta linijka w rzeczywistości generuje coś takiego: </p> [cpp] vector<double> tmp1(100); tmp1=0.5*v2; vector<double> tmp2(100); tmp2=v1*v2; vector<double> tmp3(100); tmp3=tmp1+tmp2 vector<double> tmp4(100); tmp4=1.2*v1; vector<double> tmp5(100); tmp5=tmp3+tmp4; res=tmp5
Tworzymy pięć(!) tymczasowych wektorów (przydzielając na nie pamięć!) i sześć razy kopiujemy wektory!! Pisząc ten sam kod ręcznie napisalibyśmy:
for(int i=0;i<100;i++) res[i]=1.2*v1[i]+v1[i]*v2[i]+v2[i]*.5;
Niepotrzebny jest żaden obiekt tymczasowy i tylko jedno kopiowanie. Ponadto można liczyć, że kompilator lepiej zoptymalizuje tak prosty kod np. eliminując jedno mnożenie:
for(int i=0;i<100;i++) res[i]=v1[i]*(1.2+v2[i])+v2[i]*.5;
Te dodatkowe niepotrzebne kopiowania i tymczasowe obiekty stanowią duży narzut, a co za tym idzie mocno ograniczją użyteczność tego typu bibliotek, a to wielka szkoda. Na ratunek przychodzą nam opisane wcześniej szablony wyrażeń. Jak widzieliśmy w poprzednim wykładzie, korzystając z tej techniki najpierw tworzymy reprezentację wyrażenia, a dopiero potem ją wykonujemy. Postaramy się więc napisać kod, który będzie tworzył reprezentację wyrażeń wektorowych, a dopiero potem obliczał je w jednej ostatniej pętli, generowanej przez operator przypisania. Podobnie jak w poprzednim przykładzie kod będzie prostszy jeśli ograniczymy się do wektorów jednego typu (double).
Zaczynamy więc od zdefiniowania nowej klasy Vector. Nie możemy użyć std::vector bezpośrednio, bo potrzebujemy przeładować operator przypisania, ale możemy wykorzystać std::vector do implementacji naszej klasy, np. korzystając z dziedziczenia:
class Vector : public vector<double> { public: Vector():vector<double>(){}; Vector(int n):vector<double>(n){}; Vector(int n,double x):vector<double>(n,x){}; Vector(const Vector& v):vector<double>(static_cast<vector<double> >(v)){}; Vector(const vector<double>& v):vector<double>(v) {}; Vector &operator=(const Vector& rhs) { vector<double>::operator=(static_cast<vector<double> >(rhs)); } template<typename V> Vector &operator=(const V &rhs) { for(size_t i =0 ;i<vector<double>::size();++i) (*this)[i]=rhs[i]; return *this; } };
Dziedziczymy cały interfejs z std::vector ale musimy zdefiniować własne konstruktory. Definiujemy też nowy operator przypisania. Korzystając z szablonów możemy uczynić argumentem operatora przypisania jakiekolwiek wyrażenie, które posiada operator indeksowania. Implementacja klasy Vector nie jest istotna jak długo posiada operator indeksowania i szablon operatora przypisania.
Podobnie jak poprzednio, potrzebne jeszcze będzie wyrażenie reprezentujące skalar, który zachowuje sie jak wektor o wszystkich polach takich samych:
class Const_vector { double _c; public: Const_vector(double c):_c(c) {}; double operator[](int i) const {return _c;} };
Następnie definiujemy wyrażenie reprezentujace sumę dwóch wektorów:
template<typename LHS,typename RHS> class AddVectors { const LHS &_lhs; /* bład ! */ const RHS &_rhs; /* bład ! */ public: AddVectors(const LHS &lhs,const RHS &rhs): _lhs(lhs),_rhs(rhs){}; double operator[](int i) const {return _lhs[i]+_rhs[i];} };
Proszę zwrócić uwagę, że pola _lhs i _rhs są referencjami. Gdyby tak nie było inicjalizacja klasy wymagałaby kopiowania i stracilibyśmy cały zysk. Niestety, to nie jest jeszcze poprawna implementacja. Żeby to zauważyć przyjrzyjmy sie operatorowi dodawania:
template<typename LHS,typename RHS> inline AddVectors<LHS,RHS> operator+(const LHS &lhs,const RHS &rhs) { return AddVectors<LHS,RHS>(lhs,rhs); }
a dokładniej - tej jego wersji, w której jeden z argmentów jest typu double:
template<typename LHS> inline AddVectors<LHS,Const_vector> operator+(const LHS &lhs,double rhs) { return AddVectors<LHS,Const_vector>(lhs,Const_vector(rhs) ); }
i symetryczny.
W takim przypadku operator+(...) tworzy tymczasowy obiekt typu
Const_vector, który przekazuje do konstruktora
AddVectors
template<typename T> struct V_expr_traits { typedef T const & op_type; } ; template<> struct V_expr_traits<Const_vector> { typedef Const_vector op_type; } ;
za pomocą której definiujemy pola składowe AddVectors jako:
typename V_expr_traits<LHS>::op_type _lhs; typename V_expr_traits<RHS>::op_type _rhs;
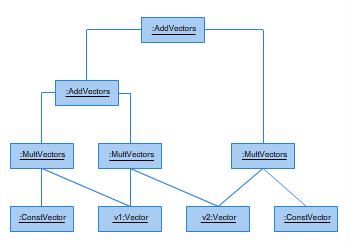 Rysunek 9.2. Obiekt wygenerowany z wyrażenia v1*(1.2+v2)+v2*.5.
Rysunek 9.2. Obiekt wygenerowany z wyrażenia v1*(1.2+v2)+v2*.5.
Pomijając te aspekty, widać więc, że implementacja jest całkowicie analogiczna do przykładu z funktorami, tyle że operator nawiasów został zastąpiony operatorem indeksowania. Zakładając, że zaimplementujemy pozostałe klasy i operatory to kompilator z wyrażenia
v1*(1.2+v2)+v2*.5;
stworzy nam obiekt przestawiony na rysunku 9.2.
Dopiero próba przypisania tego obiektu do wektora res spowoduje wywołanie w pętli operatora indeksowania dla tego obiektu, co pociągnie za sobą efektywnie obliczenie wyrażenia
for(int i=0;i<n;++i) res[i]=v1[i]*(1.2+v2[i])+v2[i]*.5;
zgodnie z naszymi zamiarami.
Efektywność kodu
Aby sprawdzić jak działa to w praktyce, porównałem czas wykonania wyrażenia
v1*(1.2+v2)+v2*.5;
korzystając ze "zwykłej" implementacji operatorów arytmetycznych i z szablonów wyrażeń. Pomiaru dokonywałem poprzez umieszczenie tego wyrażenia w pętli:
Vector v1(100,1); Vector v2(100,2); Vector res(100); for(size_t j = 0;j< 10000000;++j){ res=1.2*v1+v1*v2+v2*0.5; f(res); }
Czas wykonania programu mierzyłem poleceniem systemowym time. Wyniki są następujace (w sekundach):
| zwykłe | szablony | |
| -O0 | 720 | 311 |
| -O1 | 36 | 6.3 |
| -O2 | 30 | 5.5 |
| -O3 | 30 | 5.5 |
Proszę zauważyć, że znów włączanie optymalizacji daje dramatyczny 20 - 50-krotny wzrost szybkości programu. Podkreślam raz jeszcze, że opcja -O0, czyli brak optymalizacji, jest domyślną opcją dla kompilatora g++. Widać też, że używanie szablonów wyrażeń daje pięciokrotny wzrost szybkości programu. Oczywiście ten wynik będzie silnie zależał od konkretnych zastosowań. Jak zwykle gorąco zachęcam do własnych eksperymentów.
| Załącznik | Wielkość |
|---|---|
| Integrate.cpp | 311 bajtów |
| Integrate_temp.cpp | 638 bajtów |
| Expr_templates.h | 3.72 KB |
| Expr_templates_T.h | 4.2 KB |
Inteligentne wskaźniki
Wstęp
Wskaźniki to jeden z bardziej pożytecznych elementów języka C/C++, ale na pewno najbardziej niebezpieczny. Zabawa z gołymi wskaźnikami przypomina żonglerkę odbezpieczonymi granatami. To nie jest już kwestia czy nastąpi wybuch, ale kiedy on nastąpi. Możliwości wywołania wybuchu i jego konsekwencje są wielorakie:
- Możemy usunąć wskaźnik nie zwalniając pamięci na którą on wskazuje. Jeśli żaden inny wskaźnik nie wskazuje na ten obszar to jest on bezpowrotnie stracony dla naszej aplikacji i mamy do czynienia z wyciekiem pamięci.
- Możemy zwolnić ten sam obszar pamięci kilkakrotnie. Powoduje to zwykle krach całej aplikacji.
- Podobnie jeśli spróbujemy zdereferencjonować wskaźniki null.
- No i oczywiście mamy całe spektrum możliwości sięgnięcia za pomocą wskaźnika tam gdzie nie powinniśmy, odczytując lub co gorsza zmieniając nie te zmienne co trzeba.
Jeśli więc nie czujemy się jak Rambo, albo nie przymierzając sam Chuck Norris, to powinniśmy poszukać jakichś zabezpieczeń. W C++ zabezpieczenia są dostarczane poprzez możliwość definicji własnych typów klas. Dzięki klasom możemy nie korzystać z dynamicznej alokacji pamięci bezpośrednio, ale za pośrednictwem klas, które dbają o alokacje w konstruktorach, dealokację w destruktorach, zwiększają i zmmniejszają pamięć na żądanie, itp. Przykładem takiego podejścia są np. kontenery STL, których jedną z zalet jest właśnie zarządzanie własną pamięcią. Jeśli jednak ciągle potrzebujemy wskaźników to możemy rozważyć opakowanie ich w klasy. Jest to możliwe dzięki możliwości jakie w C++ daje przeładowywanie operatorów, w szczególności możemy przeładowywać operatory dereferencjonowania operator*() i operator->(). W ten sposób możemy upodobnić zachowanie definiowanych przez nas typów do zachowania wskaźników. Takie typy nazywamy inteligentnymi wskaźnikami, ponieważ dostarczają nam dodatkowej funkcjonalności ponad zwykłe zachowanie wskaźnika.
Tak jak i u ludzi, rodzaje inteligencji wskaźników bywają różne i inteligentne wskaźniki występują w najróżniejszych wariacjach. Podział tych wariantów można przeprowadzić na wiele sposobów, ja skoncentruję sie na dwóch grupach:
- Zachowanie wskaźników podczas kopiowania, przypisywania i niszczenia. Nazwiemy to prawami własności.
- Zachowanie się operatorów operator*() i operator->(). Nazwiemy to kontrolą dostępu.
Poniżej krótko przedstawię przegląd głównych możliwości w każdej z powyższych grup.
Prawa własności
Głównym powodem używania inteligentnych wskaźników jest uzyskanie kontroli nad operacjami kopiowania, przypisywania i niszczenia wskaźnika. W tym kontekście mówimy często, że wskaźnik jest albo nie jest właścicielem obiektu na który wskazuje. Poniżej przedstawiam cztery typowe schematy wskaźników.
Głupie wskaźniki
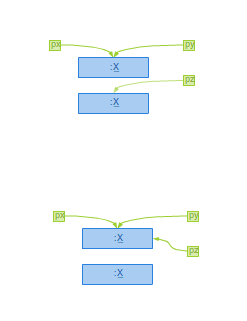 Rysunek 10.1. Zwykłe wskaźniki.
Rysunek 10.1. Zwykłe wskaźniki.
Zwykłe (nieinteligentne) wskaźniki, nie są właścicielami obiektów, na które wskazują. Kopiowanie czy przypisanie prowadzi do współdzielenia referencji (oba wskaźniki wskazują na ten sam obiekt) często niezamierzonej. Zniszczenie wskaźnika nie powoduje zniszczenia (dealokacji pamięci) obiektu, na który on wskazuje. Przedstawia to rysunek 10.1, na którym zilustrowano przebieg wykonania kodu:
void f() { X *px( new X); X py(px); X pz(new X); pz=py; } f();
Zliczanie referencji
Wskaźniki zliczające referencje są niejako właścicielami grupowymi obiektu, na który wskazują.
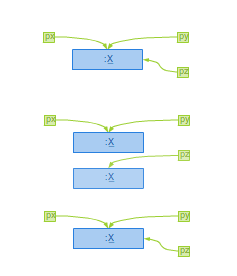 Rysunek 10.2. Wskaźniki zliczające referencje.
Rysunek 10.2. Wskaźniki zliczające referencje.
Kopiowanie i przypisanie powoduje współdzielnie referencji, ale kontrolowane, w tym sensie, że monitorowana jest liczba wskaźników do danego obiektu. Na zasadzie "ostatni gasi światło" zniszczenie wskaźnika powoduje zniszczenie obiektu wtedy gdy był to jedyny (ostatni) wskaźnik na ten obiekt. Liczenie referencji reprezentuje więc prostą wersję "odśmiecacza" (garbage-collector). Zachowanie się tego typu wskaźników prezentuje rysunek 10.2, w oparciu o analogiczny kod.
void f() { ref_ptr<X> px(new X); ref_ptr<X> py(px); ref_ptr<X> pz(new X); pz=py; } f();
Głęboka/fizyczna kopia
Takie wskaźniki są pojedynczymi właścicielami obiektów, na które wskazują i zachowują się jak wartości, a nie wskaźniki. Kopiowanie bądź przypisanie powoduje fizyczne kopiowanie obiektu wskazywanego. Zniszczenie wskaźnika powoduje zniszczenie wskazywanego obiektu. Od zwykłych wartości obiektów różnią się tym, że mają zachowanie polimorficzne i używane są tam gdzie polimorfizm jest nam potrzebny, a więc nie możemy użyć bezpośrednio samych obiektów. Zachowanie kodu
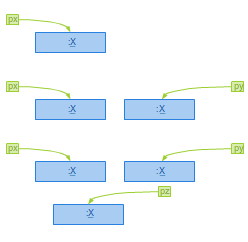 Rysunek 10.3. Wskaźniki wykonujące kopie fizyczne.
Rysunek 10.3. Wskaźniki wykonujące kopie fizyczne.
void f() { clone_ptr<X> px(new X); clone_ptr<X> py(px); cloen_ptr<X> pz(new X); pz=py; }<br /> f();
ilustruje rysunek 10.3.
Zastosowanie wskaźników z głębokim kopiowaniem zilustruję na przykładzie podanego już wcześniej przykładu z kształtami geometrycznymi. W programie wykorzystującym takie kształty na pewno zachodzi konieczność kopiowania kształtów. Załóżmy, że wybraliśmy (myszką) jakiś kształt i wskaźnik do niego jest przechowywany w zmiennej Shape *selected. Załóżmy, że jest to obiekt typu Circle. Teraz chcemy uzyskać kopię tego kształtu. Przypisanie
Shape *copy=selected;
oczywiście nie zadziała, bo uzyskamy dwa wskaźniki na jeden obiekt. A my potrzebujemy drugiego obiektu. Bez koniecznośći polimorfizmu wystarczyłoby użyć konstruktora kopiującego:
Shape *copy=new Shape(*selected);
Niestety, w naszym przypadku ten kod się nawet nie skompiluje, bo klasa Shape jest klasą abstrakcyjną. Nawet gdyby nie była, to i tak zostałby utworzony obiekt typu Shape, a nie Circle. W celu zaimplementowania kopiowania polimorficznego możemy wyposażyć naszą klasę Shape w funkcję
virtual Shape *clone() const = 0
następnie zdefiniować ją w każdej podklasie:
class Circle:public Shape { ... Circle *clone() {return new Circle(*this);}; }
i wtedy możemy skopiować (sklonować) nasz obiekt za pomocą
Shape *copy = selected->clone();
Możemy teraz tę technikę, nazywaną również wzorcem prototypu lub fabryką klonów (zob. E. Gamma, R. Helm, R. Johnson, J. Vlissides "Wzorce projektowe. Elementy oprogramowania obiektowego wielokrotnego użytku"), zastosować w implementacji inteligentnego wskaźnika clone_ptr
clone_ptr<Shape> selected; ... clone_ptr<Shape> copy(selected);
auto_ptr
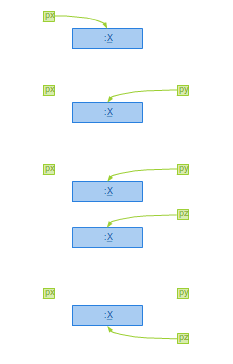 Rysunek 10.4. Wskaźniki auto_ptr.
Rysunek 10.4. Wskaźniki auto_ptr.
Wskaźniki auto_ptr (jedyne inteligentne wskaźniki dostępne w standardzie C++) są pojedynczymi, bardzo zaborczymi, właścicielami obiektu, na który wskazują. Tak zaborczymi, że nie dopuszczają możliwości współdzielenia obiektu ani jego kopiowania. Próba skopiowania albo przypisania prowadzi do przekazania własności: obiekt kopiowany(przypisywany) oddaje/przekazuje prawo własności do posiadanego obiektu drugiemu obiektowi. Oznacza to, że obiekt kopiowany lub przypisywany jest zmieniany w trakcie tych operacji. Ilustruje to rysunek 10.4 na podstawie kodu
void f() { auto_ptr<X> px(new X); auto_ptr<X> py(px); auto_ptr<X> pz(new X); pz=py; } f();
To bardzo nieintuicyjne zachowanie: obiekty auto_ptr nie są modelami konceptu Assignable. Wskaźniki te zostały wprowadzone aby wspomagać bezpieczną alokację zasobów (głównie pamięci) według wzorca "alokacja zasobów jest inicjalizacją" (zob. B. Stroustrup "Język C++"). Rozważmy następujący przykład:
int f() { BigX *p = new BigX; <i>... tu coś się dzieje</i> delete p; return wynik; }
Jest to typowe zastosowanie dynamicznej alokacji pamięci. Problem polega na tym, że jeżeli pomiędzy przydziałem pamięci a jej zwolnieniem coś się stanie, to będziemy mieli wyciek pamięci. To coś to może być np. dodatkowe wyrażenie return lub rzucony wyjątek. W obu przypadkach zniszczone zostaną wszystkie statycznie zaalokowane obiekty, w tym i wskaźnik p. Ale ponieważ jest to zwykły wskaźnik jego zniszczenie nie spowoduje zwolnienia wskazywanej przez niego pamięci. Rozwiązaniem jest właśnie uczynienie go obiektem będącym właścicielem wskazywanej pamięci:
int f() { auto_ptr<BigX> p(new BigX);<br /> <i>... tu coś się dzieje</i><br /> return wynik; }
Teraz przy wyjściu z funkcji zostanie wywołany destruktor p, a on zwolni przydzieloną pamięć.
Wzkaźniki auto_ptr mogą być przekazywane i zwracane z funkcji. Jeśli przekażemy auto_ptr do funkcji przez wartość, to spowodowane tym kopiowanie spowoduje, że własność zostanie przekazana na argument funkcji i pamięć zostanie zwolniona kiedy funkcja zakończy swoje działanie.
template<typename T> void val(T p) { }; auto_ptr<X> px(new X); val(px); <i>px zawiera wskaźnik null. pamięć jest zwolniona</i> cout<<px.get()<<endl; <i>zwraca opakowany wskaźnik na X, powinien być zero</i>
Jeśli przekażemy auto_ptr przez referencje to kopiowania nie będzie, przekazanie własności bedzie zależeć od tego czy wkaźnik zostanie skopiowany lub przypisany wewnątrz funkcji.
template<typename T> void ref_1(T &p) { T x = p; }; template<typename T> void ref_2(T &p) { };<br /> auto_ptr<X> px(new X); ref_2(px); <i>nic sie nie zmieniło</i> cout<<px.get()<<endl; <i>wypisuje jakiś adres</i> ref_1(px) <i>px zawiera wskaźnik null. pamięć jest zwolniona</i> cout<<px.get()<<endl; <i>zwraca opakowany wskaźnik na X, powinien być zero</i>
W przypadku przekazania auto_ptr jako referencji do stałej sprawa jest bardziej skomplikowana. Obecny standard stanowi, że wskaźnik auto_ptr przekazany jako referencja do stałej, nie przekazuje własności, tzn. operacje, które by do tego prowadziły nie skompilują się. Z tych samych powodów nie powinien skompilować się kod używający kontenerów STL zawierających wskaźniki auto_ptr.
template<typename T> void cref_1(const T &p) { T x = p; }; template<typename T> void cref_2(const T &p) { };<br /> auto_ptr<X> px(new X); cref_2(px); <i>OK, nic się nie stanie</i> cout<<px.get()<<endl; <i>wypisuje jakiś adres</i> cref_1(px) <i>nie skompiluje się</i><br /> std::vector<auto_ptr<X>> v(10); <i>nie skompiluje się</i>
( Źródło: auto_ptr.cpp)
Różne implementacje różnie sobie z tym radzą i w praktyce wynik kompilowania powyższych fragmentów kodu może być różny na różnych platformach. Jest to dość techniczne zagadnienie, zainteresowane osoby odsyłam do D. Vandevoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty" i N.M. Josuttis "C++ Biblioteka standardowa, podręcznik programisty".
Kontrola dostępu
Poza kontrolą rodzaju praw własności, inteligentny wskaźnik daje nam możliwość kontroli nad operacjami dostępu do wskazywanego obiektu poprzez operatory operator->() i operator*(). Wpływać na zachowanie tych operatorów możemy dwojako. Po pierwsze w oczywisty sposób możemy wykonać dodatkowy kod zanim zwrócimy z nich odpowiednią wartość:
T &operator*() { <i>zrób coś</i> return *_p; }
Ten dodatkowy kod może np. sprawdzać czy wskaźnik _p nie jest zerowy, może zliczać wywołania, itp.
Po drugie możemy zmienić zwracany typ. Wbudowane operatory * i -> zwracają odpowiednio T& i T*. Oczywiście my możemy zwrócić cokolwiek, ale żeby to miało jakiś sens powinny to być obiekty zachowujące sie jak T& i T*. Takie obiekty które "zachowują się jak" coś, ale nie są tym (kwacze jak kaczka, ale to nie jest kaczka) nazywamy obiektami zastępczymi (proxy).
Proxy
Dlaczego moglibyśmy chcieć używać obiektów zastępczych?
Typowe zastosowanie to implementacja operacji przypisania do obiektów, które tak naprawdę obiektami nie są. Weźmy jako przykład ostream_iterator dostarczany przez STL, który zezwala traktować plik wyjściowy jak kontener z iteratorem typu OutputIterator:
vector<int> V(10,7); copy(V.begin(), V.end(), ostream_iterator<int>(cout, "\n"));
Przypatrzny się temu przykładowi bliżej. Jeśli zdefiniujemy
ostream_iterator<int>(cout, "\n") iout;
to w zasadzie jedyną dozwoloną operacją jest przypisanie i zwiększenie następujące po sobie:
(*iout) = 666; ++iout;
Ewidentnie nie istnieje żaden obiekt, do którego referencje moglibyśmy zwrócić. Możemy jednak zwrócić obiekt zastępczy, który będzie definiował operator przypisania:
class writing_proxy { std::ostream &_out; public: writing_proxy(std::ostream &out):_out(out) {};<br /> void operator=(const T &val) { _out<<val; } };
( Źródło: out.cpp)
Tę klasę zamkniemy wewnątrz klasy ostream_iterator
template<typename T> class ostream_iterator: public std::iterator <std::output_iterator_tag, T > {<br /> class writing_proxy { <i>...</i> };<br /> std::string _sep; std::ostream &_out; writing_proxy _proxy; public: ostream_iterator(std::ostream &out,std::string sep): _out(out),_sep(sep),_proxy(_out){}; void operator++() {_out<<_sep;} void operator++(int) {_out<<_sep;} writing_proxy &operator*() {return _proxy;}; };
( Źródło: out.cpp)
Dziedziczenie z klasy iterator zapewni nam, że nasz ostream_iterator posiada wszystkie typy stowarzyszone wymagane przez iteratory STL. To z kolei pociąga za soba możliwość użycia iterator_traits (zob. wykład 5.5). Bez tego nie moglibyśmy używać ostream_iterator w niektórych algorytmach STL.
Teraz możemy juz używać wyrażeń typu:
ostream_iterator<int> io(std::cout,""); (*io)=44;
( Źródło: out.cpp)
Wywołanie *io zwraca writing_proxy. Następnie wywoływany jest
writing_proxy::operator=(44)}
który wykonuje operację
std::cout<<44;
Widać też, że operacja
i=(*io)
się nie powiedzie (nie skompiluje). W tym przypadku jest to pożądane zachowanie, bo taka operacja nie ma sensu. Jeśli byśmy jednak chcieli umożliwić działanie operacji przypisania w drugą stronę, możemy w obiekcie proxy zdefiniować operator konwersji na typ T.
operator T() {return T();}; <i>uwaga bzdurny przykład!!!</i>
Wtedy wykonanie
i=(*io)
przypisze zero do zmiennej i. W ten sposób obiekty proxy pozwalają nam rozróżniać użycie operatora * do odczytu i do zapisu.
Obiekty zastępcze stanowią zresztą często spotykany wzorzec projektowy (zob. E. Gamma, R. Helm, R. Johnson, J. Vlissides "Wzorce projektowe. Elementy oprogramowania obiektowego wielokrotnego użytku"). Poniżej przedstawię jeszcze jedną "sztuczkę" opisaną w A. Alexandrescu "Nowoczesne Projektowanie w C++", służącą do automatycznego obudowywania funkcji wywoływanych za pośrednictwem inteligentnego wskaźnika wywoływaniami innych funkcji.
Opakowywanie wywołań funkcji
Załóżmy, że mamy obiekt typu:
struct Widget { void pre() {cout<<"pre"<<endl;}; void post() {cout<<"post"<<endl;}; void f1() {cout<<"f1"<<endl;} void f2() {cout<<"f2"<<endl;} }
( Źródło: pre_post.cpp)
Niech
Smart_prt<Widget> pw(new Widget);
bedzię inteligentnym wskaźnikiem do Widget. Chcemy aby każde wywołanie funkcji z Widget np.
pw->f1()
zostało poprzedzone przez wywołanie funkcji pre(), a po nim nastapiło wywołanie funkcji post(). Jedną z możliwości jest oczywiście zmiana kodu funkcji f?, tak aby wywoływały na początku pre() i post() na końcu. Można też dodać zestaw funkcji opakowywujących:
f1_wrapper() {pre();f1();post();}
Jest to jednak niepotrzebne duplikowanie kodu i możliwe do zastosowania tylko jeśli mamy możliwość zmiany kodu klasy Widget.
Można jednak zrobić inaczej. Zdefiniujemy pomocniczą klasę
template<typename T> struct Wrapper { T* _p; Wrapper(T* p):_p(p) {_p->pre();} ~Wrapper() {_p->post();} T* operator->() {return _p;} };
( Źródło: pre_post.cpp)
W klasie inteligentnego wskaźnika przedefiniujemy operator->()
tak, aby zwracał Wrapper
template<typename T> struct Smart_ptr { T *_p; Smart_ptr(T *p):_p(p) {}; ~Smart_ptr(){delete _p;}; Wrapper<T> operator->() {return Wrapper<T>(_p);}; T &operator*() {return *_p}; };
( Źródło: pre_post.cpp)
Jeśli teraz wywołamy
pw->f1();
to bedą się dziać następujace rzeczy:
- zostanie wywołany
pw.operator->();
operator ten zwraca obiekt tmp typu Wrapper
- zostanie wywołany konstruktor
tmp=Wrapper<Widget>(p);
który wywoła
p->pre();
- Jeśli operator->() zwróci obiekt, który posiada operator->() to jest on wywoływany rekurencyjnie, aż zostanie zwrócony typ wskaźnikowy. Tak więc zostanie wywołany tmp.operator->(), który zwroci p.
- Poprzez ten wskaźnik zostanie wywołana funkcja
p->f1();
- Zakończy się wywołanie pw.operator->(), a więc zostanie wywołany destruktor obiektu tymczasowego tmp, który wywoła
p->post();
Widać więc, że w końcu zostanie wykonana sekwencja wywołań:
p->pre(); p->f1(); p->post();
i tak bedzie dla dowolnej wywoływanej metody. Jeśli jednak wywołamy funkcję f1() za pomocą wyrażenia:
(*pw).f1();
to ten mechanizm nie zadziała i nie ma możliwości, aby go w tej sytuacji zaimplementować. Może to być traktowane jako wada, bo nie jesteśmy w stanie zapewnić, że każde wywołanie funkcji zostanie opakowane, ale z drugiej strony mamy do dyspozycji możliwość wyboru pomiędzy opakowanym i nieopakowanym wywołaniem funkcji.
Współdzielenie reprezentacji
Opisując inteligentne wskaźniki nie można nie wspomnieć o technice implementacyjnej, która jest ściśle z nimi zwiazana, a mianowicie o współdzieleniu reprezentacji. Technika ta polega na oddelegowaniu całego (lub prawie całego) zachowania klasy do innego obiektu, nazywanego reprezentacją, a w obiekcie klasy przechowywanie tylko uchwytu do reprezentacji (zob rysunek 10.5).
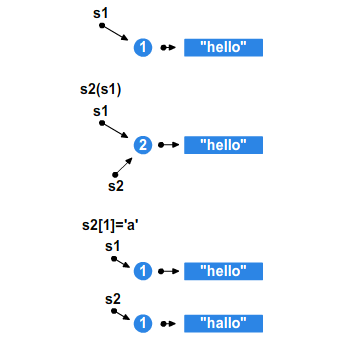 Rysunek 10.5.
Rysunek 10.5.
class Wichajster { public: void do_something() {_rep->do_something();} private: WichajsterRep _rep; }
Techniki tej używamy np. kiedy chcemy oszczędzić czas i miejsce potrzebne na kopiowanie obiektów. Kilka kopii obiektów klasy Wichajster może współdzielić jedną reprezentację korzystając np. ze zliczania referencji. Istotną różnicą w stosunku do inteligentnych wskaźników jest zachowanie w przypadku zmiany jednego z obiektów. W przypadku wskaźników, współdzielenie referencji jest planowaną cechą podejścia: kiedy zmieniamy obiekt poprzez jeden ze wskaźników wszystkie inne wskaźniki wskazują na zmieniony obiekt.
W przypadku współdzielenia reprezentacji chcemy cały czas rozróżniać obiekty, współdzielenie jest tylko technicznym środkiem optymalizacji. Wymaga to zastosowania techniki "copy on write", tzn. w momencie, w którym dokonujemy na obiekcie operacji mogącej go zmienić i jeśli posiada on współdzieloną reprezentację, to tworzymy nową fizyczna kopię tej reprezentacji i dopiero ją zmieniamy. Przedstawione to jest na rysunku 10.5. W przypadku metod łatwo stwierdzić, które zmieniaja obiekt, a które nie, problem jest tylko z metodami, które zwracaja referencje do wnętrza obiektu. Takie metody mogą służyć zarówno do zapisu, jak i do odczytu. Częściowym rozwiązaniem może być użycie obiektów proxy, tak jak to opisano w poprzednim podrozdziale. Szczegółowy opis tej techniki znajduje się w S. Meyers "Język C++ bardziej efektywny".
Iteratory
Iteratory to kolejny rodzaj inteligentnych wskaźników. Jeżli chodzi o prawa własności czy kontrolę dostępu to w większości zachowują się jak zwykłe wskaźniki. Wyjątkiem są specjalne iteratory, takie jak ostream_iterator, czy back_inserter, wspomniane powyżej. Ale zasadniczo inteligencja iteratorów umiejscowiona jest w operacjach arytmetycznych. Chodzi głównie o operator operator++() ponieważ wyposażone są w niego wszystkie iteratory kontenerów z STL. To właśnie jest zresztą podstawowa rola iteratora: przechodzenie do kolejnych elementów, semantyka wskaźnika to już wybór twórcow STL.
Implementacje
Widać, że różnorodność inteligentnych wskaźników może przyprawić o zawrót głowy. A nie rozważyliśmy jeszcze wszystkich kwestii dotyczących ich zachowania. Wyczerpująca dyskusja na ten temat znajduje się w A. Alexandrescu "Nowoczesne projektowanie". Tam też podana jest implemenatcja uniwersalnego szablonu klasy inteligentnego wskaźnika parametryzowanego kilkoma klasami wytycznymi. Alternatywą jest użycie szeregu klas (szablonów) implementujacych jeden typ wskaźnika każda. Zbiór takich klas można znaleźć w bibliotece boost(). Bardzo dobre opisy implementacji inteligentnych wskaźników znajdują się również w D. Vandevoorde, N. Josuttis: "C++ Szablony, Vademecum profesjonalisty" i S. Meyers "Język C++ bardziej efektywny".
Tutaj dla przykładu zaprezentuję implementację wskaźnika zliczającego referencję paramtryzowanego jedną klasą wytyczną. Jest to podejście zbliżone do D. Vandevoorde, N. Josuttis: "C++ Szablony, Vademecum profesjonalisty".
Zliczanie referencji
Implementacje zliczania referencji różnią się przede wszystkim miejscem, w którym umieszczony zostanie licznik. Dwie główne możliwości to wewnątrz lub na zewnątrz obiektu, na który wskazujemy. Pierwsza możliwość jest ewidentnie możliwa tylko wtedy, jeśli mamy dostęp do kodu tej klasy. W każdej z tych dwu grup mamy dalsze możliwości, np.
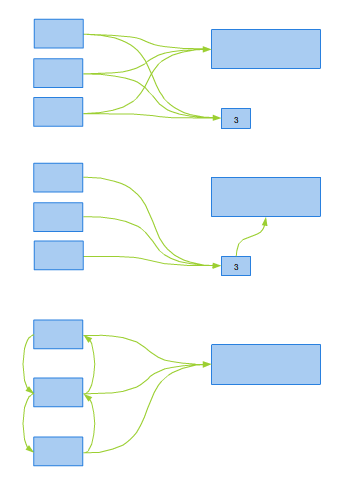 Rysunek 10.6. Wskaźniki ze współdzieleniem referencji.
Rysunek 10.6. Wskaźniki ze współdzieleniem referencji.
- Obiekt wskazywany udostępnia miejsce na licznik, zarządzaniem licznikiem zajmuje się wskaźnik
- Obiekt wskazywany udostępnia nie tylko licznik, ale i interfejs do zarządzania nim.
- Licznik jest osobnym obiektem. Każdy wskaźnik posiada wskaźnik na obiekt wskazywany i wskaźnik na licznik (zob. rysunek 10.6).
- Licznik jest osobnym obiektem który zawiera również wskaźnik do obiektu wskazywanego. Każdy wskaźnik zawiera tylko wskaźnik do licznika (zob. rysunek 10.6).
- Nie ma licznika, wskaźniki do tego samego obiektu połączone są w listę (zob. rysunek 10.6).
Pokażę teraz przykladową implementację szablonu wskaźnika parametryzowanego jedną klasą wytyczną, określającą którąś z powyższych strategii, aczkolwiek przy jednej wytycznej jest to wysiłek, który pewnie sie nie opłaca, jako że kod wspólny jest dość mały. Ale implementacja ta może stanowić podstawę do rozszerzenia o kolejne wytyczne.
Najpierw musimy się zastanowić nad interfejsem lub raczej konceptem klasy wytycznej. W sumie najłatwiej to zrobić implemetując konkretną wytyczną. Zaczniemy od osobnego zewnętrznego licznika (zob. strategia 3). Klasa wytyczna musi zawierać wskaźnik do wspólnego licznika:
template<typename T> struct Extra_counter_impl { ... private: size_t *_c; };
i funkcje zwiekszające i zmniejszające licznik:
public: bool remove_ref() {--(*_c);return *_c==0;}; void add_ref() {++(*_c);}; size_t count() {return *_c;}; };
Funkcja zmniejszająca licznik zwraca prawdę, jeśli usunięta została ostatnia referencja do wskazywanego obiektu. Potrzebna też będzie funkcja niszcząca licznik:
void cleanup() { delete _c; _c=0; }
Potrzebne będą dwa konstruktory: defaultowy, który nic nie robi:
Extra_counter_impl():_c(0) {};
i konstruktor inicjalizujący licznik obiektu powstającego po raz pierwszy:
Extra_counter_impl(T* p):_c(new size_t) {*_c=0;};
który przydziela pamięć dla licznika. Argument T* p służy tylko do rozróżnienia tych konstruktorów.
Korzystając z tej klasy nietrudno jest napisać szablon inteligentnego wskaźnika. Obiekt licznika może być składową tego szablonu lub możemy dziedziczyć z klasy wytycznej (zob. wykład 7). Niestety, okaże się, że bedziemy mieli problem próbując zaimplementować inne strategie, w szczególności strategię w której licznik i wskaźnik na obiekt wskazywany znajdują się w tym samym obiekcie (zob. strategia 4). Dlatego zmienimy trochę naszą implementację wytycznej i założymy, że obiekty tej klasy będą zawierać również wskaźnik na obiekt wskazywany
T *_p;
i dodamy funkcję:
T* pointee() {return _p;}
Musimy jeszcze poprawić funkcję czyszczącą:
void cleanup() { delete _c; delete _p; _p=0; }
( Źródło: ref_ptr.h)
i jeden z konstruktorów:
Extra_counter_impl(T* p):_c(new size_t),_p(p) {*_c=0;};
Szablon wskaźnika korzystający z tak zdefiniowanej klasy wytycznej może wyglądać następująco:
template<typename T,
typename counter_impl = Extra_counter_impl<T> >
class Ref_ptr {
public:
Ref_ptr() {};
Ref_ptr(T *p):_c(p) {
_c.add_ref();
};
~Ref_ptr() {detach();}
Ref_ptr(const Ref_ptr &p):_c(p._c) {
_c.add_ref();
}
Ref_ptr &operator=(const Ref_ptr &rhs) {
if(this!=&rhs) {
detach();
_c=rhs._c;
_c.add_ref();
}
return *this;
}
T* operator->() {return _c.pointee();}
T &operator*() {return *(_c.pointee());}
size_t count() {return _c.count();};
private:
mutable counter_impl _c;
void detach() {
if (_c.remove_ref() ) _c.cleanup();
};
};( Źródło: ref_ptr.h)
auto_ptr
Implementacja wskaźnika auto_ptr oparta jest o dwie funkcje. Jedna zwalnia przechowywany wskaźnik zwracając go na zewnątrz i oddając własność:
T* release() { T *oldPointee = pointee; pointee = 0; return oldPointee; }
( Źródło: auto_ptr.h)
pointee jest przechowywanym (zwykłym) wskaźnikiem.
private:
T *pointee;Druga funkcja zamienia przechowywany wskaźnik na inny, zwalniając wskazywaną przez niego pamięć:
void reset(T *p = 0) { if (pointee!= p) { delete pointee; pointee = p; } }
( Źródło: auto_ptr.h)
Za pomocą tych funkcji można już łatwo zimplementować resztę szablonu, np.:
template<class T> class auto_ptr { public: explicit auto_ptr(T *p = 0): pointee(p) {} template<class U> auto_ptr(auto_ptr <U> & rhs): pointee(rhs.release()) {} ~auto_ptr() { delete pointee; } template<class U> auto_ptr<T>& operator=(auto_ptr<U>& rhs) { if (this != &rhs) reset(rhs.release()); return *this; } T& operator*() const { return *pointee; } T* operator->() const { return pointee; } T* get() const { return pointee; } }
( Źródło: auto_ptr.h)
Konstruktor kopiujący i operator przypisania są szablonami, w ten
sposób można kopiować również wskaźniki auto_ptr opakowujące
typy, które mogą być na siebie rzutowane, np. można przypisać
auto_ptr
Różne impelentacje auto_ptr różnią się szczegółami dotyczącymi obsługi const auto_ptr i przekazywania auto_ptr przez stałą referencję. Powyższa implentacja wzięta z S. Meyers "Język C++ bardziej efektywny", nie posiada pod tym względem żadnych zabezpieczeń. Szczegółowa dyskusja tego zagadnienia i bardziej zaawansowana implementacja znajduje się w N.M. Josuttis: "C++ Biblioteka standardowa, podręcznik programisty". Temat ten jest też poruszony w D. Vandevoorde, N. Josuttis: "C++ Szablony, Vademecum profesjonalisty". Warto też zaglądnąć do implementacji auto_ptr dostarczonej z kompilatorem g++.
| Załącznik | Wielkość |
|---|---|
| Auto_ptr.cpp | 487 bajtów |
| Out.cpp | 731 bajtów |
| Pre_post.cpp | 721 bajtów |
| Ref_ptr.h | 2.95 KB |
| Auto_ptr.h | 800 bajtów |
Funktory
Wstęp
Na poprzednim wykładzie prezentowane były inteligentne wskaźniki, czyli obiekty, które rozszerzają pojęcie zwykłego wskaźnika. Na tym wykładzie będę omawiał obiekty, które stanowią rozszerzenie pojęcia wskaźnika do funkcji. Motywacja wprowadzenia takich obiektów funkcyjnych jest jednak inna. Funkcje obiektami nie są i wskaźniki do nich nie mają kłoptów z prawami własności, współdzieleniem referencji, itp. Same wskaźniki do funkcji są obiektami ale typów wbudowanych (lub raczej typów złożonych). Możemy je kopiować, przepisywać, przekazywać do funkcji, ale nie mamy nad tym kontroli.
Obiekty funkcyjne posiadaja składnię wywołania funkcji, ale są też pełnoprawnymi obiektami, mogą więc posiadać stan, konstruktory, destruktory i inne metody, jak również typy stowarzyszone, no i oczywiście posiadają też swój własny typ. Te dodatkowe informacje pozwalają na implementowanie wielu ciekawych rozwiązań niedostępnych dla zwykłych funkcji i wskaźników do nich.
Funkcje, wskaźniki i referencje do funkcji
Typy funkcyjne
Zanim zajmiemy się bardziej skomplikowanymi obiektami jakimi są funktory, chciałbym najpierw wyjaśnić kilka faktów dotyczących funkcji i wskaźników do nich. Jak już wspomniałem w poprzednim podrozdziale funkcje nie są obiektami. Nie można ich kopiować ani przypisywać do siebie:
void f(double x) {}; void g(double) = f; <i>niedozwolone</i> void h(double); h=f; <i>niedozwolone</i>
Funkcje posiadają jednak typ. Typ funkcji (nazywany typem funkcyjnym) jest określony przez typ jej wartości zwracanej i typy jej argumentów. Typy funkcyjne możemy używać np. w poleceniu typedef. Wyrażenie:
typedef void f_type(double)
definiuje f_type jako typ funkcji o jednym argumencie typu double i nie zwracającej żadnej wartości. Taki typ ma jednak ograniczone zastosowanie, możemy go używać do deklarowania, ale nie definiowania innych funkcji:
f_type g;
Typ funkcyjny może też być użyty jako parametr szablonu:
template<typename F> Function { F _fun; }; Function<void (double)>
Niewiele jednak będziemy mieli pożytku z pola _fun, bo jak już widzieliśmy, nie będziemy w stanie nic do niego przypisać ani go zainicjalizować.
Możemy również używać typów funkcyjnych w deklaracjach argumentów funkcji. Wyrażenie:
double sum(double (double),...)
oznacza że funkcja sum oczekuje jako pierwszego argumentu funkcji zwracającej double o jednym argumencie typu double. Ten zapis jest jednak mylący! W rzeczywistości nie można przekazać funkcji jako argumentu wywołania i dlatego w deklaracjach argumentów typ funkcyjny jest automatycznie zamieniany na typ wskaźnika do funkcji i powyższa deklaracja jest równoważna deklaracji:
double sum(double (*)(double),...)
Wskaźniki do funkcji
Wskaźniki do funkcji są normalnymi obiektami i mogą być kopiowane i przypisywane:
void f(double x) {}; void (*g)(double) = &f; void (*h)(double); h=&f; (*h)(0.0); (*g)(1.0);
C++ posiada wygodną własność, która jednak zwiększa konfuzję pomiędzy funkcjami i wskaźnikami do nich. Otóż operatory * i & są aplikowane automatycznie do funkcji i powyższy kod można zapisać jako:
void f(double x) {}; void (*g)(double) = f; void (*h)(double); h=&f; h(0.0); g(1.0);
Jest to dość wygodne, ale powoduje, że część ludzi słabo rozróżnia funkcje od wskaźników do nich (Państwo oczywiście już do nich nie należą:).
Referencje do funkcji
Żeby już skończyć ten temat i zupełnie zamieszać Państwu w głowach napiszę, że można też definiować referencje do funkcji:
void f(double x) {}; typedef void f_type(double) f_type &g = f; f_type &h = g; const f_type &ch = g; <i>równoważne z wyrażeniem f_type &ch = g;</i> h=g; <i>niedozwolone h jest refencją do stałej</i>
Należy dodać, że typ const f_type & nie jest obsługiwany przez kompilator g++-3.3 ale przez g++-3.4 już tak.
Dedukcja typów funcyjnych
Ponieważ funktory i funkcje często przekazywane są jako argumenty wywołania szablonów, których typ podlega dedukcji, warto wiedzieć jak ten mechanizn rozpoznaje typ przekazywanej funkcji. Rozważmy najpierw następujacą definicję:
template<typename F> test(F f) { F _fun(f); }
Jeśli teraz wywołamy
void (*g)(double) = f; void (&h)(double) = f; test(f); <i>F = void (*)(double)</i> test(g); <i>F = void (*)(double)</i> test(h); <i>F = void (*)(double)</i>
to w każdym przypadku typ F zostanie wydedukowany jako wskaźnik do funkcji void (*)(double).
Jeśli przypomnimy sobie, że argumenty do funkcji można dla oszczędności przekazywać jako referencje do stałych, to możemy napisać:
template<typename F> test(const F &f) { F _fun(f); }
czeka nas jednak niepospodzianka, kod
void (*g)(double) = f; void (&h)(double) = f; test(f); <i>F = void ()(double), nie skompiluje się</i> test(g); <i>F = void (*)(double)</i> test(h); <i>F = void ()(double) nie skompiluje się</i>
zachowuje się już inaczej. W przypadku przekazania funkcji lub referencji do funkcji, wededukowanym typem będzie typ funkcyjny. Ponieważ nie można inicjalizować zmiennych typu funkcyjnego, wyrażenie F _fun(f) się nie skompiluje. Nie będzie kłopotów jeśli przekażemy wskaźnik do funkcji, ale tym razem musimy to zrobić jawnie, nie nastąpi automatyczna konwersja nazwy funkcji na wskaźnik do niej.
Można by przedefiniować funkcję test następująco:
template<typename F> test(const F &f) { F *_fun(f); }
Teraz wywołania
test(f); <i>F = void ()(double)</i> test(h); <i>F = void ()(double)</i>
skompilują się, ale nie skompiluje się linijka
test(g); <i>F = void (*)(double)</i>
bo pole _fun stanie się typu void (**)(double). Kompilator g+-3.3 nawet tego kodu nie skompiluje, bo nie zezwala na referencje do stałych typów funkcyjnych.
Widać więc, że przy przekazywaniu funkcji najlepiej używać wywołania przez wartość, która i tak jest automatycznie konwertowana na przekazywanie wskaźnika do funkcji.
Obiekty funkcyjne
Definiowanie własnych obiektów funkcyjnych jest możliwe dzięki możliwości przeładowania operatora wywołania (będziemy go też nazywać operatorem nawiasów): operator()(...). Np.
struct Sin { double operator()(double x) {return sin(x);} }
Z obiektów typu Sin możemy teraz korzystać jak z funkcji:
Sin c_sin; c_sin(0);
Nie jest to być może porywający przykład, ale głównym powodem używania obiektów funkcyjnych jest to, że mogą posiadać stan. Skorzystamy z tego, aby umożliwić wybór typu argumentu funkcji sin. Zwyczajowo kalkulatory (ktoś wie co to jest?) zezwalają na podawanie argumentów funkcji trygonometrycznych w radianach, stopniach lub gradusach. Możemy to zaimplemetować następująco:
class Sin { public: enum arg {radian,degree,grad}; Sin(arg s = radian):_state(s) {}; void set_radians() { _state=radian;} void set_degrees() {_state=degree;} void set_grads() {_state=grad;} double operator()(double x) {return sin(conv(x));} private: arg _state; double conv(double x) { switch (_state) { case radian: return x; case degree: return x*(M_PI/180.0); case grad : return x*(M_PI/200.0); } } };
( Źródło: sin.cpp)
Nie jest to najwydajniejsza implementacja, bo za każdym wywołaniem funkcji sin wykonywana jest insrukcja switch. Przerobimy ją więc na:
class BetterSin { public: enum arg {radian,degree,grad}; void set_radians() { _conv=&BetterSin::to_radians;} void set_degrees() { _conv=&BetterSin::to_degrees;} void set_grads() { _conv=&BetterSin::to_grads;} double operator()(double x) {return sin( (this->*_conv)(x) );} BetterSin(arg s = radian) { switch (s) { case radian: set_radians();break; case degree: set_degrees();break; case grad : set_grads();break; } } private: double (BetterSin::* _conv)(double); double to_radians(double x) {return x;}; double to_degrees(double x) {return x*(M_PI/180.0);}; double to_grads(double x) {return x*(M_PI/200.0);}; };
( Źródło: sin.cpp)
Wskaźniki do metod (funkcji składowych)
Ten przykład, który powinien działać szybciej, ilustruje ponadto użycie wskaźników do funkcji składowych (metod). Różnice pomiędzy wskaźnikami do funkcji i wskaźnikami do metod są opisane w D. Vandervoorde, N. Josuttis: "C++ Szablony, Vademecum profesjonalisty" oraz S. B. Lippman "Model obiektu w C++", tutaj zwrócę tylko uwagę na różnice w ich używaniu. Jak już pisałem wskaźniki do funkcji można używać na skróty, bez jawnego wywoływania operatorów & i *. W przypadku wskaźników do metod, musimy pobierać adres jawnie i dereferencjonować go przed wywołaniem. Ponadto każda metoda ma dodatkowy niejawny argument, którym jest wskaźnik na obiekt, przez który została ona wywołana, dlatego wywołując metodę poprzez wskaźnik też musimy ten argument podać:
struct X { void f(){std::cout<<"f1"<<"";}; }; main(){ typedef void (X::*f_ptr)(); //f_ptr pf1=X::f; bład kompilacji f_ptr pf1=&X::f; X x; X *px = new X; (x.*pf1)(); (px->*pf1)(); }
( Źródło: m_ptr.cpp)
Adaptery funktorów
Obiekty mogą jednak posiadać więcej informacji niż tylko swój stan, mogą zawierać również informacje o typie. Przede wszystkim funktory same posiadają typ, konsekwencje tego faktu omówię poźniej, teraz zajmę się typami stowarzyszonymi. Nasuwająca się od razu możliwość, to stowarzyszenie z funktorem typu wartości zwracanej oraz typów jego argumentów. Można stowarzyszyć również informację o liczbie argumentów. W przypadku szablonu Sin i BetterSin moglibyśmy dodać
typedef double result_type; typedef double argument_type; enum {n_arguments = 1};
Taki schemat nazewnictwa nie najlepiej się rozszerza na większą ilość argumentów, ale właśnie takie definicje typów są wymagane dla jednoargumentowych obiektów funkcyjnych w STL. W celu ułatwienia tworzenia własnych funktorów spełniających te wymagania, dostarczony jest szablon klasy, z której można dziedziczyć:
template <class Arg1, class Arg2, class Result> struct binary_function { typedef Arg1 first_argument_type; typedef Arg2 second_argument_type; typedef Result result_type; };
czyli moglibyśmy również napisać:
class BetterSin: public unary_function<double,double> {...};
STL nie wymaga definiowania liczby argumentów.
Podobnie zdefiniowany jest szablon dla funkcji dwuargumentowych:
template <class Arg1, class Arg2, class Result> struct binary_function { typedef Arg1 first_argument_type; typedef Arg2 second_argument_type; typedef Result result_type; };
Opis bardziej uniwersalnego schematu obiektów funkcyjnych, uwzględniający funktory z dowolną ilością argumentów znajduje się w D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty". Dodajmy, że do określenia typów argumentów można użyć listy typów przedstawione w wykładzie 6.3, razem z szablonem indeksowania (zob. A. Alexandrescu "Nowoczesne projektowanie w C++").
My jednak pozostaniemy na razie przy schemacie z STL. Trzeba jasno powiedzieć, że obiekty funkcyjne używane przez algorytmy STL nie muszą posiadać wymienionych typów stowarzyszonych, w szczególności mogą to być zwykłe funkcje. Ale jeśli takie typy posiadają, to można używać ich w adapterach funkcji.
Adaptery funkcji to funktory, które w jakiś sposób modyfikują działanie innych funktorów. STL definiuje dość skromny wybór adapterów, ale na szczęście istnieje wiele innych niezależnych źródeł, w szczególności SGI i boost.
Jak działają adaptery wyjaśnię na przykładzie adaptera binder1st z STL. binder1st reprezentuje funktor jednoargumentowy, powstały przez zastąpienie pierwszego argumentu podanego funktora dwuargumentowego podaną wartością. Rozważmy następujący przykład:
class Cov:public std::binary_function<double,double,double> { const double _ax,_ay,_axy; public: Cov(double ax,double ay,double axy):_ax(ax),_ay(ay),_axy(axy) {}; double operator()(double x,double y) {return _ax*x*x+_ay*y*y+_axy*x*y;} }; main() { Cov f(1.0,2.0,2.0); std::cout<<f(1.0,1.0)<<""; std::cout<<f(1.0,2.0)<<""; std::cout<<::bind1st(f,1.0)(1.0)<<""; std::cout<<::bind1st(f,1.0)(2.0)<<""; }
( Źródło: bind.cpp)
Działanie adaptera nietrudno zrozumieć, jeśli się zrozumiało działanie szablonów wyrażeń (zob. wykład 9). Szablon binder1st można zdefiniować następująco:
template<typename F> class binder1st { typedef typename F::first_argument_type bind_type; typedef typename F::second_argument_type first_argument_type; typedef typename F::result_type result_type; const bind_type _val; F _op; public: binder1st(F op,bind_type val):_op(op), _val(val) {}; result_type operator()(first_argument_type x) { return op(_val,x); } };
( Źródło: bind.cpp)
Podobnie jak w przypadku szablonów wyrażeń, będziemy jeszcze potrzebowali funkcji, która wytworzy nam taki obiekt. To zadanie spełni nam funkcja bind1st:
template<typename F> binder1st<F> bind1st(F op,typename F::first_argument_type val) { return binder1st<F>(op,val); }
( Źródło: bind.cpp)
Na podstawie tego przykładu mam nadzieję, że już łatwo Państwu będzie wywnioskować implementację pozostałych adapterów STL: binder2nd, unary_negate i binary_negate.
STL dostarcza ponadto dodatkowe adaptery, które opakowują zwykłe wskaźniki do funkcji i wskaźniki do metod tak, aby można było ich użyć razem z adapterami obiektów.
Składanie funktorów
Żaden z adapterów zaimplementowanych w STL nie umożliwia składania funktorów, czyli tworzenia funktora poprzez połączenie dwu lub wiecej innych funktorów. Oczywiście istnieje wiele możliwych sposobów składania funkcji, w N.M. Josuttis "C++ Biblioteka standardowa, podręcznik programisty" autor wyróżnia pięć takich adapterów realizujących następujące złożenia:
| \(\displaystyle f(g(x))\) | (unary_compose) |
| \(\displaystyle f(g(x,y))\) | |
| \(\displaystyle f(g(x),h(x))\) | (binary_compose) |
| \(\displaystyle f(g(x),h(y))\) |
Dwa z nich (unary_compose i binary_compose) są zdefiniowane w implementacji STL firmy SGI, a więc dostępne razem z kompilatorem g++.
Implementacja ich jest analogiczna do implementacji binder1st, ale dla wprawy podam tu możliwą implementację złożenia \(\displaystyle f(g(x,y))\).
template<typename F,typename G> class compose_f_gxy_t { typedef typename F::result_type result_type; typedef typename G::first_argument_type first_argument_type; typedef typename G::second_argument_type second_argument_type; F _f; G _g; public: compose_f_gxy_t(F f,G g):_f(f),_g(g) {}; result_type operator()(first_argument_type x, second_argument_type y) { return _f(_g(x,y)); } }; template<typename F,typename G> compose_f_gxy_t<F,G> compose_f_gxy(F f,G g) {return compose_f_gxy_t<F,G>(f,g);};
( Źródło: bind.cpp)
Używamy tego funktora następująco:
std::cout<<compose_f_gxy( __gnu_cxx::compose1(std::ptr_fun(exp), std::negate<double>()), f)(1.0,1.0)<<"";
( Źródło: bind.cpp)
Powyższe wyrażenie efektywnie produkuje funktor obliczający \(\displaystyle \exp(-f(x,y))\) gdzie \(\displaystyle f(x,y)= a_x x^2+a_y y^2+a_{xy}x*y\). Wykorzystaliśmy w nim szereg konstrukcji
- Adapter realizujący złożenie dwu funkcji jednoargumentowych unary_compose (zwrócony przez funkcję compose1()) dostarczony wraz z kompilatorem g++.
- Za pomocą tego adaptera złożyliśmy funkcję \(\displaystyle \exp\) ze standardowej biblioteki C z obiektem funkcyjnym std::negate
predefiniowanym w STL. - Aby móc użyć funkcji \(\displaystyle \exp\) w adapterze musiałem ją opakować za pomocą adaptera std::ptr_fun.
- Funkcję \(\displaystyle \exp(-f)\) złożyłem z \(\displaystyle f(x,y)\) za pomocą compose_f_gxy.
Na powyższym przykładzie widać siłę, ale i też pewne niedogodności używania funktorów, przynajmniej w takiej postaci, jak zdefiniowanej w STL. Podany kod jest dość rozwlekły i mało czytelny, co gorsza, tak zdefiniowanego funktora nie możemy łatwo przechować w jakiejś zmiennej, bo jego typ też jest bardzo skomplikowany (zobacz zadania).
Klasy cech dla funktorów
Programowanie uogólnione za pomocą funktorów mogłoby być prostsze gdybyśmy posiadali jakiś uniwersalny sposób dostępu do informacji o nich. Taki uniwersalny szkielet funktora z możliwościami introspekcji jest opisany w D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty", rozdz.22. Tutaj zaprezentuję tylko możliwą implementację klasy cech dostarczającej informacji o funktorach w stylu STL i wskaźnikach na funkcje.
Załóżmy, że mamy jakiś typ F i chcemy się dowiedzieć czy jest on funktorem czy nie. W C++ nie mamy możliwości sprawdzić czy dana klasa posiada operator nawiasów czy nie. Funktory będziemy więc rozpoznawać po posiadanych typach stowarzyszonych. Skorzystamy z zasady rozstrzygania przeciążenia szablonów funkcji: "nieudane podstawienie nie jest błędem". Podobnie jak w przypadku szablonu Is_class (zob. wykład 6.2.2) wykorzystamy dwa typy:
template<typename F> funktor_info { typedef char one; typedef struct {char a[2];} two;
( Źródło: functor_type.h)
i dwa szablony funkcji:
template<typename C> one test_arg(typename C::argument_type *) ; template<typename C> two test_arg(...) ;
( Źródło: functor_type.h)
Za ich pomocą możemy sprawdzić czy dany typ F posiada zdefiniowany stowarzyszony typ argument_type:
enum {has_argument = (sizeof(test_arg<F>(0))==sizeof(one))};
( Źródło: functor_type.h)
Podobnie możemy zdefiniować jeszcze trzy stałe logiczne:
enum {has_result = (sizeof(test_res<F>(0))==sizeof(one))}; enum {has_first_argument = (sizeof(test_arg1<F>(0))==sizeof(one))}; enum {has_second_argument = (sizeof(test_arg2<F>(0))==sizeof(one))};
( Źródło: functor_type.h)
Pary funkcji test_... są zdefiniowane analogicznie do test_arg. Za pomocą tych stałych możemy wyrazić inne własności obiektu F, np:
enum {has_one_argument = has_argument && !has_first_argument && !has_second_argument}; enum {has_two_arguments = has_first_argument && has_second_argument && !has_argument}; enum {has_no_arguments = !has_argument && !has_first_argument && !has_second_argument}; enum {is_generator = has_result && has_no_arguments}; enum {is_unary_function = has_result && has_one_argument}; enum {is_binary_function = has_result && has_two_arguments}; enum {is_functor = is_generator || is_unary_function || is_binary_function}; enum {is_function= false};
( Źródło: functor_type.h)
Funkcje możemy rozpoznawać za pomocą specjalizacji częściowych:
template<typename A1,typename A2 , typename R > struct functor_info<R (*)(A1,A2) >{ enum {has_result = true}; enum {has_argument = false}; enum {has_first_argument = true}; enum {has_second_argument = true}; ... tak samo jak powyżej };
( Źródło: functor_type.h)
Podobnie dla funkcji zero- i jednoargumentowych. Mając już klasę functor_info można zdefiniować klasę
template<typename F,int n_args = functor_info<F>::n_args> struct functor_traits ;
i jej specjalizacje:
template<typename F> struct functor_traits<F,2> { typedef typename F::result_type result_type; typedef typename F::first_argument_type arg1_type; typedef typename F::second_argument_type arg2_type; typedef std::binary_function<arg1_type,arg2_type,result_type> f_type; enum {n_args=2}; }; template<typename F> struct functor_traits<F,1> { typedef typename F::result_type result_type; typedef typename F::argument_type arg1_type; typedef empty_type arg2_type; typedef std::unary_function<arg1_type,result_type> f_type; enum {n_args=1}; }; template<typename F> struct functor_traits<F,0> { typedef typename F::result_type result_type; typedef empty_type arg1_type; typedef empty_type arg2_type; typedef generator<result_type> f_type; enum {n_args=0}; };
( Źródło: functor_type.h)
Podobnie dla wskaźników do funkcji:
template<typename R,typename A1,typename A2> struct functor_traits<R (*)(A1,A2),2> { typedef R result_type; typedef A1 arg1_type; typedef A2 arg2_type; typedef std::binary_function<arg1_type,arg2_type,result_type> f_type; enum {n_args=2}; }; ...
( Źródło: functor_type.h)
Jeśli teraz użyjemy klasy functor_traits w definicji adaptera binder1st:
template<typename F> class binder1st { typedef typename functor_traits<F>::arg1_type bind_type; typedef typename functor_traits<F>::arg2_type first_argument_type; typedef typename functor_traits<F>::res_type result_type; const bind_type _val; F _op; public: binder1st(F op,bind_type val):_op(op), _val(val) {}; result_type operator()(first_argument_type x) { return _op(_val,x); } }; template<typename F> binder1st<F> bind1st(F op,typename functor_traits<F>::arg1_type val) { return binder1st<F>(op,val); };
to bedziemy mogli używać go z wskaźnikami do funkcji bez konieczności opakowywania ich w adapter ptr_fun.
Można stosunkowo łatwo rozszerzyć kod adaptera binder1st tak, aby można go było używać zarówno do funktorów dwu- jak i jednoargumentowych.
Biblioteki funktorów
Kod przedstawiony w poprzednim podrozdziale daje, mam nadzieję, pewne wyobrażenie o tym, jak można implemetować bardziej zaawansowane funktory i operacje na nich. Widać jednak, że nie jest to zbyt proste: kod szybko staje się skomplikowany i trudny do debugowania.
Na szczeście istnieją już gotowe implementacje. Jak już wspomiałem propozycje bardziej rozwiniętego szkieletu funktorów znajdą państwo w D. Vandervoorde, N. Josuttis "C++ Szablony, Vademecum profesjonalisty", rozdz. 22. Ponadto biblioteka boost oferuje szereg narzędzi, w tym biblioteki lambda i bind. O tej pierwszej już wspominałem przy omawianiu szablonów wyrażeń. Biblioteka lambda dostarcza funkcjonalności adapterów bind... i compose... za pomocą wyrażenia jednego wyrażenia bind. Korzystając z niego, można kod podany w poprzednim podrozdziale zapisać następująco:
#include<boost/lambda/lambda.hpp> #include<boost/lambda/bind.hpp> using namespace boost::lambda; double x=1; std::cout<<bind(f,1.0,_1)(x)<<""; std::cout<<bind(f,1.0,_1)(make_const(2.0))<<""; wyrażenie z biblioteki lambda nie przyjmują stałych stąd konieczność użycia zamienej x, lub wyrażenia makeconstant() std::cout<<bind(exp,-bind(f,_1,_2))(x,x)<<"";
( Źródło: bind_lambda.cpp)
| Załącznik | Wielkość |
|---|---|
| Sin.cpp | 1.42 KB |
| M_ptr.cpp | 258 bajtów |
| Bind.cpp | 518 bajtów |
| Functor_type.h | 5.97 KB |
| Bind_lambda.cpp | 808 bajtów |
Używanie funktorów
Wstęp
W poprzednim wykładzie omawiałem pojęcie obiektu funkcyjnego, jako uogólnienia wskaźników do funkcji. I choć funktory można wywoływać bezpośrednio tak jak funkcje, to dużo częściej używa się ich jako parametrów przekazywanych do innych funkcji, w celu dostarczenia tej funkcji informacji koniecznych do wykonania swojego zadania. W tej kategorii zastosowań mieści się większość bibliotek, w tym STL, gdzie funktory służą jako argumenty do uogólnionych algorytmów. Przykłady takich zastosowań były już podawane w poprzednich wykładach, a na tym wykładzie omówię je trochę bardziej szczegółowo.
Inny popularny schemat użycia wskaźników funkcji (a więc i funktorów) to rozdzielenie miejsca i czasu definicji funkcji od miejsca i czasu jej wykonania. Wygląda to zwykle następująco: Klient definiuje funkcje i przekazuje ich wskaźniki do aplikacji, aplikacja wywołuje te funkcje w wybranym przez siebie czasie. Klient nie ma pojęcia kiedy zostaną wywołane przekazane przez niego funkcje, a aplikacja nie wie jakie one mają działanie. Taka technika funkcji zwrotnych (callbacks) jest podstawą implementacji wielu szkieletów graficznych interfejsów użytkownika i w E. Gamma, R. Helm, R. Johnson, J. Vlissides "Wzorce projektowe. Elementy oprogramowania obiektowego wielokrotnego użytku" wymieniona jest jako wzorzec polecenie. Aby używać funktorów definiowanych na poprzednim wykładzie, we wzorcu polecenie trzeba będzie je trochę dostosować. Zostanie to opisane w drugiej części tego wykładu.
Algorytmy uogólnione i programowanie funkcyjne
Algorytmy stanowią, jak już to opisałem w wykładzie 2, jedną z części biblioteki STL, większośc z tych algorytmów posiada wersje przyjmujące funktor jako jeden z argumentów. Nie jest moim celem przedstawianie tutaj wszystkich algorytmów, jest ich zresztą blisko 100, choć gorąco zachęcam Państwa do zapoznania się z nimi. W tym celu polecam książke N.M. Josuttis "C++ Biblioteka Standardowa. Podręcznik programisty" i stronę http://www.sgi.com/tech/stl/. Znakomita jest też pozycja S. Meyers "STL w praktyce. 50 sposobów efektywnego wykorzystania", jak zresztą wszystkie książki tego autora.
W tym wykładzie chciałbym tylko zwrócić uwagę, że biblioteka algorytmów wprowadza do C++ elementy programowania funkcyjnego. Programowanie funkcyjne polega, z grubsza rzecz biorąc, na zastępowaniu pętli poleceniami, które potrafią wywołać daną funkcję na każdym elemencie danej kolekcji. Taki styl programowania jest często spotykany w językach interpretowanych, np. używa go pakiet Mathematica, podobnie pakiet do obliczeń numerycznych w Perlu: Perl Data Language i wiele innych. Biblioteka STL oferuje tylko namiastkę tego stylu, ale właśnie ją chciałbym przedstawić w tej części wykładu.
Podstawą programowania funkcyjnego są funkcje, które wywołują inne funkcje na każdym obiekcie z kolekcji. STL oferuje kilka takich algorytmów, podstawowym z nich jest for_each.
template <class InputIterator, class UnaryFunction> UnaryFunction for_each(InputIterator first,InputIterator last, UnaryFunction op);
Działanie tego algorytmu polega na wywołaniu podanego funktora op na każdym elemencie zakresu [first,last). Funktor może modyfikować wywoływany obiekt i może powodowac inne skutki uboczne. Jego kopia jest zwracana po wykonaniu wszystkich operacji. Wartość zwracana przez funktor op jest ignorowana. Algorytm zwraca kopię funktora op.
Podobnym algorytmem jest transform. W swojej pierwszej wersji
template <class InputIterator, class OutputIterator, class UnaryFunction> OutputIterator transform(InputIterator first, InputIterator last, OutputIterator result, UnaryFunction op);
działa podobnie jak for_each, z tą różnicą, że wyniki wywołania operacji op na wartościach zakresu [firts,last) są zapisywane poprzez iterator result. Ważną cechą tego algorytmu jest to, że może on operować na dwu wejściowych zakresach. Jego druga wersja
template <class InputIterator1, class InputIterator2, class OutputIterator,class BinaryFunction> OutputIterator transform(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, OutputIterator result, BinaryFunction op);
wywołuje operację binarną op na parach wartości wziętych po jednej z każdego zakresu wejściowego. Wynik zapisywany jest poprzez iterator wyjściowy result.
Warto też zwrócić uwagę na algorytmy numeryczne, które pomimo ich nazwy mogą spokojnie zostać użyte do innych ogólnych zastosowań. Są to:
template <class InputIterator, class T, class BinaryFunction> T accumulate(InputIterator first, InputIterator last, T init, BinaryFunction op);
który oblicza uogólnioną sumę podanego zakresu
iloczyn skalarny inner_product:
template <class InputIterator1, class InputIterator2, class T, class BinaryFunction1, class BinaryFunction2> T inner_product(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, T init, BinaryFunction1 op1, BinaryFunction2 op2);
który oblicza uogólniony iloczyn skalarny
oraz sumy i różnice częściowe:
template <class InputIterator, class OutputIterator, class BinaryOperation> OutputIterator partial_sum(InputIterator first, InputIterator last, OutputIterator result, BinaryOperation binary_op); template <class InputIterator, class OutputIterator, class BinaryFunction> OutputIterator adjacent_difference(InputIterator first, InputIterator last, OutputIterator result, BinaryFunction op);
zwracające poprzez iterator result odpowiednio:
i
Zwłaszcza algorytm adjacent_difference jest ciekawy, umożliwia
bowiem zastosowanie dwuargumentowej operacji do kolejnych par
elementów:
int print(int i,int j) { cout<<"("<<i<<":"<<j<<")"; return 0; } main() { list<int> li; list<int> res; generate_n(back_insert_iterator<list<int> >(li),10,SequenceGen<int>(1,2)); adjacent_difference(li.begin(),li.end(),back_insert_iterator<list<int> >(res),print);
( Źródło: sums.cpp)
Ten przykładzik ilustruje niedogodność posługiwania się algorytmami przyjmującymi zakres wyjściowy, takimi jak adjacent_difference czy transform, do prostego działania funkcją, która nie zwraca żadnych wartości. Do tego przeznaczony jest algorytm for_each. Niestety, ten algorytm nie pozwala bezpośrednio operować na parach kolejnych elementów, tak jak adjacent_difference. To by jeszcze można zasymulować używając odpowiedniego funktora, ale for_each nie potrafi operować na parach elementów pochodzących z dwu zakresów, tak jak potrafi to transpose.
Jest kilka możliwości rozwiązania tego problemu. Możemy np. napisać własne algorytmy (zob. zadania). Możemy też dalej korzystać np. z adjacent_difference ale napisać narzędzia pomagające adoptować takie algorytmy do naszych celów. Jak by to mogło wyglądać?
Patrzac na nasz przykład i deklarację adjacent_difference widzimy, że są dwa problemy: po pierwsze wartość zwracana z funkcji op musi być tego samego typu jak typ elementów w zakresie wejściowym, po drugie musimy jakoś "zjeść" te zwracane wartości. Potrzebny więc będzie funktor opakowujący dowolną funkcję i zwracający wartość zadanego typu, oraz iterator pełniący rolę /dev/null, czyli "czarnej dziury" połykającej wszystko co się do niej zapisze. Mając takie obiekty możemy powyższy kod zapisać następująco:
void print(int i,int j) { cout<<"("<<i<<":"<<j<<")"; } main() { list<int> li; generate_n(back_insert_iterator<list<int> >(li),10,SequenceGen<int>(1,2)); adjacent_difference(li.begin(),li.end(),dev_null<char>(),dummy<char>(print));
Obiekt klasy dev_null
Pomysły można mnożyć. Jako ostatni zaprezentuję iterator, który nie wstawia nic do żądanego kontenera, ale wywołuje na przypisywanym do niego obiekcie jakąś zadaną funkcję:
void p(double x) { std::cout<<"printing "<<x<<""; }; double frac(int i) { return i/10.0; } list<int> li; generate_n(back_insert_iterator<list<int> >(li),10,SequenceGen<int>(1,2)); std::transform(li.begin(),li.end(),function_iterator<double>(p),frac);
Taki iterator łatwo zaimplementować przy pomocy klas proxy (zob. zadania).
Wzorzec Polecenie
Wzorzec polecenie najlepiej omówić na przykładzie. Jak już wspomniałem, typowe zastosowanie to graficzny interfejs użytkownika (GUI). Taki interfejs musi reagować na różne zdarzenia: kliknięcie myszą, naciśnięcie przycisku, wybranie polecenia z menu. Ewidentnie twórca biblioteki GUI nie może wiedziec jakie działanie ma pociągnąć dane zdarzenie. Nawet jednak gdybyśmy sami pisali cały kod, to "zaszycie" polecenia na stałe w kodzie danego elementu interfejsu jest bardzo złą praktyką programistyczną. Dlatego używa się w tym celu funkcji zwrotnych. I tak w jakiejś hipotetycznej klasie
class Window {
znajdziemy na pewno funkcję w rodzaju
on_mouse_click(void (*)(int,int))
służącą do przekazania wskaźnika do funkcji, która zostanie wywołana po naciśnięciu myszką na oknie. Podobnie dla innych komponentów:
class Button { void (*_f)() ; /*wskaźnik do funkcji */ void when_pressed(void (*f)()) {_f=f;}; ... }
Ponieważ typ funkcji określony jest poprzez typ jej parametrów i typ wartości zwracanej to możemy w ten sposób ustawić dowolną fukcję o odpowiedniej sygnaturze. Niestety, jeżeli chcemy wykorzystać dobrodziejstwa jakie daje nam zastosowanie obiektów funkcyjnych zamiast funkcji, musimy je dziedziczyć ze wspólnej klasy bazowej, ponieważ jedną z podstawowych cech funktorów jest to, że posiadają swój typ. Żeby więc móc przekazywać różne funktory za pomocą tej samej sygnatury, musimy je rzutować w górę na wspólny typ. To jest cała esencja wzorca polecenie (zob. E. Gamma, R. Helm, R. Johnson, J. Vlissides "Wzorce projektowe. Elementy oprogramowania obiektowego wielokrotnego użytku").
Oznacza to jednak, że nie możemy skorzystać z całej technologii wyprowadzonej na poprzednim wykładzie. Szablony też nam nie pomogą, ponieważ wenątrz elementów GUI musimy jakoś przechować funktor zwrotny. Aby przechowywać różne funktory musielibyśmy parametryzować nasz element typem funktora, co doprowadziłoby do tego, że typ elementu interfejsu zależałby od konkretnego polecenia, które wywołuje! To uniemożliwiłoby w praktyce jakiekolwiek funkcjonowanie szkieletu.
Żeby więc wykorzystać już istniejące funkcje i funktory musimy je opakować w typ, który będzie zależał tylko od typów wartości zwracanej i argumentów, podobnie jak w przypadku zwykłych funkcji. Poniżej przedstawię zarys konstrukcji szablonu, który umożliwia robienie tego automatycznie. Będę się opierał na implementacji zamieszczonej w A. Alexandrescu: "Nowoczesne projektowanie w C++", ale ograniczę się do funktorów zero-, jedno- i dwuargumentowych.
Uniwersalny funktor
Uniwersalny funktor (nazwiemy go Function) ma z założenia odpowiadać typowi funkcyjnemu, czyli zależeć jedynie od typu wartości zwracanej i typów argumentów. Musi więc być zdefiniowany jako szablon, paremetryzowany właśnie tymi typami. Tu napotykamy pierwszy problem: C++ nie dopuszcza zmiennej liczby parametrów szablonu. Najprostszym nasuwającym się rozwiązaniem jest stworzenie trzech różnych szablonów Function0, Function1 i Function2, każdy z odpowiednią liczbą parametrów. Takie rozwiązanie jest jednak niegodne prawdziwego uogólnionego programisty:). Poszukajmy więc typów, które zawierają w sobie inne typy. Możliwości mamy całkiem sporo, moglibyśmy np. wykorzystać klasy ze zdefiniowanymi odpowiednimi typami stowarzyszonymi, można wykorzystać typy funkcyjne lub typy wskaźników do funkcji, no i listy typów wprowadzonych w wykładzie 6.3 właśnie do takich celów. Orginalne rozwiązanie w A. Alexandrescu "Nowoczesne projektowanie w C++" wykorzystuje listy typów (autor tej pozycji jest ich twórcą), ja użyję typów wskaźnikow do funkcji. To, że bedę używał wskaźników, a nie samych typów funkcji, podyktowane jest względami czysto technicznymi: moja klasa cech functor_traits rozpoznaje typy wskaźników do funkcji, a same typy funkcyjne już nie (choć jest to tylko kwestia dodania odpowiednich specjalizacji). Deklaracja szablonu Function wyglądała będzie więc następująco:
template<typename FT> class Function: public functor_traits<FT>::f_type { typedef typename functor_traits<FT>::result_type res_type; typedef typename functor_traits<FT>::arg1_type arg1_type; typedef typename functor_traits<FT>::arg2_type arg2_type; public: ... };
( Źródło: universal.h)
Dziedziczenie z functor_traits
Jako klasa opakowująca Function musi zawierać
opakowywany funktor. Nie może jednak tego robić bezpośrednio, bo nie
znamy typu tego funktora (a raczej nie chcemy go znać). Function
będzie więc zawierał wskaźnik do abstrakcyjnej klasy
AbstractFunctionHolder
std::auto_ptr<AbstractFunctionHolder<FT> > _ptr_fun;Z tej klasy będą dziedziczyć klasy opakowujące konkretne typy funktorów:
template<typename FT,typename F> class FunctionHolder: public AbstractFunctionHolder<FT> { typedef typename functor_traits<FT>::result_type res_type; typedef typename functor_traits<FT>::arg1_type arg1_type; typedef typename functor_traits<FT>::arg2_type arg2_type; ... private: F _fun; };
( Źródło: universal.h)
Konstruktor klasy FunctionHolder będzie inicjalizował pole _fun:
FunctionHolder(F fun):_fun(fun) {};
Korzystać z niego będzie konstruktor klasy Function, który musi być szablonem aby pozwolić na inicjalizowanie Function dowolnym typem funktora:
template<typename F> Function(F fun): _fun(new FunctionHolder<FT,F>(fun)){};
( Źródło: universal.h)
Ten konstruktor zamienia statyczną informację o typie F na informację dynamiczną zawartą we wskaźniku _ptr_fun. Tę informację odzyskujemy za pomocą polimorfizmu. W celu uzyskania polimorficznego zachowania przy kopiowaniu i przypisywaniu obiektów Function skorzystamy z klonowania:
Function(const Function& f):_fun(f._fun->Clone()) {}; Function &operator=(const Function &f) { _fun.reset(f._fun->Clone()); }
( Źródło: universal.h)
Wymaga to dodania do klasy AbstractFunctionHolder wirtualnych funkcji:
virtual AbstractFunctionHolder* Clone()=0; virtual AbstractFunctionHolder() {};
( Źródło: universal.h)
Klasa FunctionHolder implementuje funkcję Clone() następująco:
FunctionHolder*Clone() {return new FunctionHolder(*this);}
( Źródło: universal.h)
Proszę zwrócić uwage na typ argumentu konstruktorów. Zgodnie z tym co napisałem w wykładzie 11.2, użyłem wywołania przez wartość (F fun), inaczej nie możnaby inicjalizować pola F _fun w przypadku gdyby F był typem funkcyjnym. Należy nadmienić, że implementacja opisana w A. Alexandrescu: "Nowoczesne projektowanie w C++" zawiera właśnie taki błąd, który nie występuje w kodzie biblioteki loki dostępnym w Internecie.
Wywoływanie: operator()
W ten sposób mamy już wszystko poza najważniejszym: operatorem operator()(...), który czyni funktor funktorem.
Zacznijmy od operatora nawiasów w klasie Function. Problem polega na tym, że nie ma możliwości zdefiniowania operatora odpowiadającego przekazanemu typowi funkcyjnemu (można by ewentulanie go zadeklarować), bo wymagałoby to definicji dopuszczającej zmienną liczbę argumengtów (tak, tak, wiem w C jest taka możliwość, ale lepiej z niej nie korzystać, zresztą nie ma potrzeby). Możliwe rozwiązanie to specjalizacja szablonu dla funktorów bez argumentów, z jednym lub z dwoma argumentami i w każdej specjalizacji zdefiniowanie operatora operator()(...) z odpowiednią liczbą argumentów. Okazuje się, że nie ma takiej potrzeby, możemy zdefiniować wszystkie wersje operatora wywołania funkcji w tej samej klasie i polegać na mechaniźmie opóźnionej konkretyzacji: dopóki nie wywołamy operatora ze złą ilością argumentów, to nie będzie on konkretyzowany. Dodajemy więc do klasy Function następujące linijki:
res_type operator()() {return (*_ptr_fun)();}; res_type operator()(arg1_type x) {return (*_ptr_fun)(x);}; res_type operator()(arg1_type x,arg2_type y) { return (*_ptr_fun)(x,y); };
( Źródło: universal.h)
Wskaźnik _ptr_fun jest typu AbstractFunctionHolder*, musimy więc zaimplementować w tej klasie operator nawiasów. Klasa AbstractFunctionHolder* nie posiada wystarczającej w tym celu informacji, więc deklarujemy te funkcje jako czyste funkcje wirtualne, które zostaną zdefiniowane dopiero w klasie pochodnej FunctionHolder. Niestety deklaracja trzech różnych wariantów operatora
virtual res_type operator()() = 0; virtual res_type operator()(arg1_type x) = 0; virtual res_type operator()(arg1_type x,arg2_type y)=0;
i odpowiadające im definicje w klasie FunctionHolder
res_type operator()() {return _fun();}; res_type operator()(arg1_type x) {return _fun(x);}; res_type operator()(arg1_type x,arg2_type y) {return _fun(x,y);};
spowodują błędy w kompilacji już przy konstrukcji klasy. Dzieje się
tak dlatego, że funkcje wirtualne mogą niepodlegać konkretyzacji
opóźnionej i w implementacji kompilatora g++ jej nie podlegają. Tzn.
kiedy kompilator dokonuje konkretyzacji klasy
FunctionHolder
template<typename FT> class AbstractFunctionHolder ; template<typename R,typename A1,typename A2> class AbstractFunctionHolder<R (*)(A1,A2)> { public: virtual R operator()(A1 x, A2 y) = 0; virtual AbstractFunctionHolder* Clone()=0; virtual AbstractFunctionHolder() {}; } ;
( Źródło: universal.h)
i tak samo dla funkcji z jednym i bez argumentów.
Szablon FunctionHolder może dalej definiować wszystkie warianty operatora wywołania. Prześledźmy teraz konkretyzację tych szablonów na przykładzie:
double f(double x) {return x;} Function<double(*)(double)> Func1;
Konstrutor klasy Function
AbstractFunctionHandler<double (*)(double)>
która ma zdefiniowany tylko jeden operator
virtual double operator(double x) = 0
Ale to oznacza, że z trzech wariantów operatora wywołania
zdefiniowanych w FunctionHandler
Używając szablonu Function możemy teraz napisać:
#include"universal.h" Cov f(1.0,2.0,2.0); Function<double (*)(double,double)> fc; fc=compose_f_gxy( __gnu_cxx::compose1(std::ptr_fun(exp), std::negate<double>()), f); std::cout<<fc(1.0,1.0)<<""; Function<double (*)(double)> my_exp(exp); std::cout<<my_exp(1.0)<<"";
( Źródło: test_universal.cpp)
boost::functions
Podobną funkcjonalność dostarcza biblioteka functions z repozytorium boost. Zresztą stamtąd wziąłem pomysł parametryzowania funktorów typem funkcyjnym. Kod używający tej biblioteki będzie wyglądał bardzo podobnie:
#include<boost/function.hpp> using namespace boost; Cov f(1.0,2.0,2.0); boost::function<double (double,double)> fc; fc=compose_f_gxy( __gnu_cxx::compose1(std::ptr_fun(exp), std::negate<double>()), f); std::cout<<fc(1.0,1.0)<<"";
( Źródło: boost_function.cpp)
| Załącznik | Wielkość |
|---|---|
| Sums.cpp | 681 bajtów |
| Universal.h | 2.82 KB |
| Test_universal.cpp | 384 bajty |
| Boost_function.cpp | 1.23 KB |
Wyjątki
Wstęp
Jesteśmy istotami omylnymi, więc niezależnie od naszych starań, pisane przez nas programy bedą zawierały usterki, dostarczane do nich dane nie zawsze będą poprawne, a i sprzęt może nie działać tak jak trzeba.
Nie oznacza to, że należy zaniechać dążenia do pisania bezbłędnego kodu, wprost przeciwnie, jakość kodu powinna być jednym z naszych priorytetów, ale należy się też pogodzić z faktem, że błędy będą występować i powinniśmy być na takie sytuacje przygotowani. Jak to mówią "najwyższą formą zaufania jest kontrola".
Na potrzeby tego wykładu zdefiniujemy bardzo luźno błąd jako wystąpienie sytuacji, która wystąpić nie powinna. Nie będziemy też interesować się bardzo tym, jak błedy wykrywać, ale raczej co zrobić, kiedy takowy wykryjemy. W następnym podrozdziale omówię bardzo pobieżnie różne możliwości reakcji na wystąpienie błędu i wprowadzę pojęcie wyjątku. Reszta wykładu będzie poświęcona zagadnieniom związanym z pisaniem kodu używającego wyjątków.
Wykrywanie błędów
Zanim przejdziemy do sytuacji, w której wiemy, że wystąpił bład, musimy poświęcić kilka akapitów na zastanowienie się czy w ogóle należy błedy wykrywać i obsługiwać. Nawet jeśli większość z Państwa krzyknie "oczywiście, że
tak" (choć podejrzewam, że większość tego sama nie robi: kto ostatnio sprawdzał wartość zwróconą przez funkcję printf?), to
i tak pozostaje pytanie, jakie błędy będziemy starali się wykrywać.
Na to pytanie nie ma jednoznacznej odpowiedzi, jak zresztą na większość pytań dotyczących decyzji projektowych. Różne projekty wymagają różnego poziomu niezawodności, a więc i różnych zabezpieczeń.
Na jednym końcu są programy, które po prostu nie mogą "paść", na drugim np. niektóre progamy symulacyjne, które wykonują się w godzinę lub mniej. Nawet jednak w tej ostatniej sytuacji, różne formy obsługi błędów mogą nam bardzo pomóc w debugowaniu. Linijki typu:
if( NULL==(fin=fopen(input_file_name,"r"))) { fprintf(stderr,"cannot open file input_file_name); exit(1); } }
lub
if( NULL==(p=malloc(n_bytes))) { fprintf(stderr,"cannot allocate memory for ..."); exit(1); } }
mogą nam oszczędzić jeśli nie godzin, to wielu minut frustracji. Proszę zwrócić uwagę, że oba przykłady dotyczą zasobów zewnętrznych, nie do końca pod naszą kontrolą i tym bardziej powinny być sprawdzane, zwłaszcza, że będzie nas to kosztować minutę pisania i prawie tyle co nic w trakcie wykonania.
Kontrola zakresu
A co z bardziej kosztownymi testami? Typowym przykładem jest
sprawdzanie zakresu. Czy np. nasz stos Stack powinien
sprawdzać, czy wykonujemy pop lub top na stosie pustym
albo push na stosie pełnym? Czy powinniśmy sprawdzać
poprawność podanego indeksu w wyrażeniach v[i]?
Mam nadzieję, że Państwo nie oczekują jednoznacznej odpowiedzi na te pytania, bo jej po prostu nie ma. Niestety, tego rodzaju testy mogą być bardzo kosztowne. Operacje dostępu do elementów są bardzo proste, koszt testu będzie pewnie dominujący, a te operacje mogą być bardzo często wykonywane. Z drugiej strony błędy przekroczenia zakresu są bardzo "wredne". Rozważmy np. taki prosty kod:
Stack<int,5> s; for(int i=0;i<1000;i++) s.push(i); int i=0; while(1) std::cerr<<++i<<" "<<s.pop()<<"";
( Źródło: overflow.cpp)
Na moim komputerze powyższy program wykonał 20981 operacji pop(),
zanim padł z komunikatem Naruszenie ochrony pamięci. Proszę
zauważyć, że najpierw zapisał 995 liczb w pamięci należącej nie wiadomo
do kogo! Skutki takiego błędu mogą więc wystąpić w zupełnie innym
miejscu programu.
Nie ma dobrego rozwiązania tego dylematu, ale zawsze może pomóc zdrowy rozsądek. Użycie sprawdzenia zakresu w operacji mnożenia macierzy miałoby katastrofalne skutki dla wydajności kodu. Z drugiej strony jest to prosty kod, w którym łatwo zapewnić aby indeksy nie wychodziły poza zakres. Tutaj więc kontrola zakresu jest niewskazana.
Częstym rozwiązaniem jest włączanie kontroli zakresu podczas
debugowania i wyłączanie jej w "produkcyjnej" wersji programu. Moim
zdaniem może to być bardzo pożyteczne, zwłaszcza w językach, które
dopuszczają włączanie i wyłączanie sprawdzania zakresów za pomocą
opcji kompilacji (oczywiście może to dotyczyć tylko typów
wbudowanych). W przypadku stosu, mogą nam się przydać w tym celu
klasy wytyczne, opracowane w wykładzie 7. Może warto
dodać, że kontenery STL, dostarczające operację indeksowania,
dostarczają również metodę dostępu ze sprawdzaniem: at(int).
Obsługa błędów
Załóżmy więc, że w pogramie mamy przynajmniej kilka linijek wykrywających potencjalne błędy. No i stało się. Wiemy już, że w programie wystąpił błąd, co teraz? Mamy wiele możliwości, wymienię tylko kilka z nich:
- Kończymy program z ewentualnym komunikatem o błędzie.
- Kończymy program, ale najpierw sprzątamy po sobie: zwalniamy zasoby, których nie zwolni system operacyjny, zapisujemy dane, itp.
- Staramy się kontynuować program pomimo błędu, próbując go poprawić, obejść lub zrezygnować z części funkcjonalności.
W tym wykładzie nie będzie interesować nas sama konkretna strategia, ale sposób rozdzielenia procesu wykrycia błędu od wyboru strategii. Jest to problem, który dotyczy każdego kodu, ale głównie funkcji bibliotecznych. Ich projektant/programista może wykryć, że w trakcie ich wykonywania wystąpiła nieprawidłowość, ale nie może jednak wiedzieć jak z takim błędem postąpić. To jest decyzja osoby korzystającej z tej funkcji. Musi więc istnieć jakiś mechanizm przekazywania tej informacji z wywoływanej funkcji na zewnątrz do funkcji wywołującej.
Najprostyszym sposobem jest zwrócenie jakiejś wartości sygnalizującej błąd. Jeśli funkcja nie zwraca żadnego wyniku, to jest to proste; jeśli jednak funkcja ma zwracać jakiś wynik, to nie zawsze da się znaleźć taką wartość, która by jednoznacznie mogła definiować błąd. Rozszerzenia tej metody, to zwrócenie informacji o przebiegu funkcji poprzez dodatkowy argument przekazywany przez referencje. Można też ustawiać i odczytywać jakieś zmienne stanu. Największą wadą tego podejścia jest konieczność każdorazowego sprawdzania tych wartości, co wymaga pisania dużej ilości trywialnego kodu. Z tego powodu sprawdzanie poprawności wywołania takich funkcji jest często opuszczane. W C++ dochodzi jeszcze niemożność zwrócenia wartości z konstruktora (choć oczywiście możemy ustawić w nim zmienną stanu informującą o powodzeniu konstrukcji).
Wyjątki
C++ dostarcza nowego mechanizmu, jakim są wyjątki. Polega on na tym, że funkcja która błąd wykryje i nie chce lub nie może go obsłużyć sama, rzuca wyjątek, który może być dowolnym obiektem. Rzucenie wyjątku powoduje natychmiastowe przerwanie wykonywania funkcji. Procedura wywołująca może ten wyjątek złapać. Wyjątek niezłapany prowadzi do zatrzymania programu, a więc wyjątki nie mogą zostać zignorowane. Zilustruję to na przykładzie naszego stosu, do którego dodam instrukcje rzucające wyjątki w przypadku przekroczenia zakresu (dla prostoty nie będę korzystał z klas wytycznych):
template<typename T = int , size_t N = 100> class Stack { private: T _rep[N]; size_t _top; public: Stack():_top(0) {}; void push(T val) { if(_top == N) { throw "pushing on top of the full stack"; } _rep[_top++]=val; } T pop() { if(is_empty()) { throw "poping form an empty stack"; } return _rep[--_top]; } bool is_empty() const {return (_top==0);} };
( Źródło: stack_except.h)
Polecenie throw służy właśnie do rzucania wyjątków. W tym wypadku
rzucane są stałe napisowe, które będą automatycznie konwertowane na typ
const char *.
Wykonanie programu:
main() { Stack<int,5> s; s.push(1); s.pop(); s.pop(); /* tu będzie rzucony wyjątek */ for(int i=0;i<10;i++) s.push(i); /* tu też gdyby udało się tu dojść */ }
( Źródło: overflow.cpp)
spowoduje przerwanie programu w trakcie wykonywania drugiego polecenia
pop. Komunikat, który się przy tym pojawia jest zależny
od implementacji.
Wyjątki można łapać, korzystając z bloku try:
Stack<int,5> s; s.push(1); try { s.pop(); s.pop(); } catch(const char *msg) { std::cerr<<msg<<std::endl; } try { for(int i=0;i<10;i++) s.push(i); } catch(const char *msg) { std::cerr<<msg<<std::endl; }
( Źródło: stack_except.cpp)
W bloku try umieszczamy instrukcje, które mogą potencjalnie rzucić
wyjątek. Za blokiem try umieszczamy jedną lub więcej klauzul catch,
które te wyjątki łapią. Wyjątek rzucony w bloku try powoduje przekazanie
sterowania do pierwszej pasującej klauzuli catch.
Wyjątki złapane
Przyjrzyjmy się teraz dokładniej mechanizmowi rzucania i łapania wyjątków. Rozważmy prosty przykład:
struct X { int val; X(int i=0):val(i) {cerr<<"constructing "<<val<<"";} X() {cerr<<"destructing "<<val<<endl;} }; void f() { X x(1); throw 0; cout<<"f"; }; main(){ X y(2); try { X z(3); f(); cout<<"try"; } catch(double){cout<<"zlapalem double-a";} catch(int){cout<<"zlapalem int-a";} catch(...){cout<<"zlapalem cos ";} cout<<"main"; }
( Źródło: caught.cpp)
Oto wynik wykonania tego programu:
constructing 2 constructing 3 constructing 1 destructing 1 destructing 3 zlapalem int-a main destructing 2
Co możemy zauważyć?
- Wyjątek przerwał wykonywanie funkcji
f()i blokutry, sterowanie zostało przekazana do klauzulicatch(int). - Przedtem wywołane zostały destruktory obiektów
xiz, czyli lokalnych obiektów w zasięgu blokutry. Ten proces nazywamy "zwijaniem stosu". - Po wykonaniu klauzuli
catchsterowanie zostało przekazane do następnego wyrażenia.
Klauzula catch(...) wyłapuje każdy wyjątek. Jeśli np. pominiemy
klauzulę catch(int):
catch(double){cout<<"zlapalem double-a";} //catch(int){cout<<"zlapalem int-a";} catch(...){cout<<"zlapalem cos ";}
to wynikiem wywołania programu będzie:
constructing 2 constructing 3 constructing 1 destructing 1 destructing 3 zlapalem cos main destructing 2
Z tego przykładu widać też, że w przypadku dopasowywania klauzul
catch nie następuje niejawna konwersja argumentów.
Niezłapane wyjątki
A co się stanie, jeśli wyjątku nie złapiemy? Żeby się o tym przekonać
usuniemy kolejną klauzulę catch:
catch(double){cout<<"zlapalem double-a";} //catch(int){cout<<"zlapalem int-a";} //catch(...){cout<<"zlapalem cos ";}
Wynik programu jest teraz zupełnie inny:
constructing 2 constructing 3 constructing 1 terminate called after throwing an instance of 'int' Abort
Niezłapany wyjątek spowodował wywołanie funkcji abort(), która
zakończyła program bez wywołania destruktorów. Ściśle rzecz
biorąc, niezłapany wyjątek wywołuje funkcję terminate(), która z
kolei domyślnie wywołuje funkcję abort(). Co do tego, czy wywoływane
są destruktory lokalnych obiektów (zwijanie stosu), to jest to
zachowanie zależne od implementacji. Jak widać, w implementacji
g++ w przypadku niezłapania wyjątku destruktory obiektów nie są
wywoływane.
Domyślne zachowanie funkcji terminate() można zmienić, ustawiając
własną funkcję, za pomocą:
namespace std { typedef void (*terminate_handler)(void); terminate_handler set_terminate(terminate_handler new_terminate); }
Funkcja ustawiana w tym poleceniu nie może zwrócić sterowania, taka
próba kończy sie wywołaniem funkcji abort(). Oznacza to, że funkcja
new_terminate() musi kończyć się wywołaniem abort() lub
exit().
void my_terminate() {std::cerr<<"terminating "<<std::endl;exit(1);} main() { std::set_terminate(my_terminate); throw 0; }
( Źródło: terminate.cpp)
Wyjątki w destruktorach
Jeśli podczas opisanego powyżej procesu obsługi wyjątku, wywołana
zostanie funkcja, która sama wywoła wyjątek, to program zostanie
natychmiast przerwany wykonaniem funkcji terminate() (nie dotyczy
to już funkcji wywoływanych wewnątrz klauzuli catch). W
szczególności stanie się to, jeśli któryś z destruktorów wywoływanych w
trakcie zwijania stosu rzuci wyjątek:
struct X { ~X() { std::cerr<<std::uncaught_exception()<<""; throw 0;}; } ; main() { try { X x; } catch(int) {}; try { X x; throw 0; } catch(int) {}; }
( Źródło: destruktor.cpp)
W powyższym kodzie destruktor klasy X jest wołany dwa razy. Po raz
pierwszy, podczas wychodzenia z pierwszego bloku try. Jest to
normalne wywołanie spowodowane wyjściem poza zakres.
Destruktor rzuca wyjątek, który zostaje wyłapany przez
klauzulę catch(int) na końcu bloku. Drugi raz destruktor jest
wołany jako część zwijania stosu po wyjątku rzuconym jawnie w drugim bloku
try. Mimo że łapiemy wyjątki int, i tak w tej sytuacji
wywoływana jest funkcja terminate(), a w konsekwencji i
abort(). Jest to jeden z powodów, dla których destruktory
nie powinny rzucać wyjątków. Funkcja uncaught_exception()
umożliwia rozróżnienie tych dwu kontekstów wywołania destruktora.
Zwraca ona prawdę, jeśli jakiś wyjątek jest właśnie obsługiwany.
Inne powody nie rzucania wyjątków z destruktorow wiążą się z dynamiczną alokacją pamięci i zostaną omówione w kolejnym wykładzie.
Hierachie wyjątków
Jako wyjątek może zostać wyrzucony dowolny obiekt. Umożliwia nam to grupowanie wyjątków w hierarchie za pomocą dziedziczenia. Zilustrujemy to za pomocą hierachii wyjątków z biblioteki standardowej, przedstawionej na rysunku 13.1.
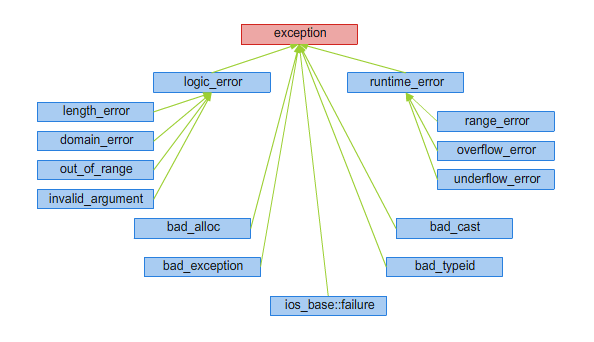 Rysunek 13.1. Hierarchia wyjątków biblioteki standardowej.
Rysunek 13.1. Hierarchia wyjątków biblioteki standardowej.
Można z niej korzystać np. następująco:
main() { try { throw domain_error() ; } catch(invalid_argument &e) { cerr<<e.what()<<""; } catch(logic_error &e) { cerr<<"logic "<<e.what()<<""; } catch(exception &e) { cerr<<"some exception "<<e.what()<<""; } }
( Źródło: hierarchy.cpp)
Kolejność klauzul catch jest ważna, ponieważ klauzule są
sprawdzane po kolei i pierwsza, która pasuje, zostanie wykonana.
Gdybyśmy więc podali kaluzulę catch(Exception &e) jako pierwszą,
przechwyciła by ona wszystkie standardowe wyjątki. Ważne jest też, aby
korzystając z hierarchii dziedziczenia, przechwytywać wyjątki przez
referencję. Inaczej nie zostaną wywołane poprawne funkcje wirtualne.
Zachęcam do eksperymentów z powyższym kodem.
Deklaracje wyjątków
C++ pozwala na deklarowanie listy możliwych wyjątków rzucanych z
funkcji. Służy do tego deklaracja throw(...) umieszczana za
deklaracją listy argumentów funkcji, np.:
void no_throw(int) throw();
deklaruje, że funkcja no_throw nie rzuci żadnego wyjątku, natomiast
void throw_std(int) throw(exception);
deklaruje, że funkcja throw_std będzie rzucać tylko wyjątki ze
standardowej hierarchii. Brak deklaracji oznacza, że funkcja może rzucać
co chce.
Niestety, C++ nie dostarcza nam praktycznie żadnych mechanizmów, które by mogły wymusić konsystencję tych deklaracji. Rozważmy implementację funkcji:
void f(int i) {throw i;} void g() throw(int) {throw 0;}; void no_throw(int i) {f(i;};
Funkcja f proklamuje całemu światu, że może rzucać wyjątek
(poprzez brak deklaracji, że nie może), podobnie funkcja g(), a pomimo to kompilator nie
pozwala na to, aby wywołać ją wewnątrz funkcji, która jawnie deklaruje,
że wyjątku nie rzuci. Proszę to porównać np. z zastosowaniem
kwalifikatora const: funkcja zadeklarowana jako const nie
może wywołać funkcji, które const nie są. W przypadku wyjątków
narzucenie takiej konsystencji spowodowałoby, że potrzeba by
przerabiać ogromne ilości kodu napisanego, zanim mechanizm wyjątków
stał się używany. Sprawia to niestety, że deklaracje wyjątków nie są
zbyt użyteczne, łatwo bowiem niechcący napisać kod, który je złamie. A
konsekwencje tego są poważne. Sprawdzania konsystencji w czasie
kompilacji wprawdzie nie ma, ale jest sprawdzanie w czasie wykonania.
Jeżeli funkcja rzuci wyjątek, który nie znajduje się na jej liście
zadeklarowanych wyjątków, to następuje wywołanie funkcji
unexpected(), która domyślnie wywołuje abort(). Nawet
złapanie tego wyjątku nic nie pomoże.
Kolejnym problemem są szablony funkcji i metody szablonów klas. Ich projektant nie może przewidzieć, z jakimi argumentami zostaną one konkretyzowane, a więc jakie wyjątki mogą zostać rzucone. Dlatego w szablonach lepiej deklaracje wyjątków pomijać. W ogóle, deklaracje wyjątków należy umieszczać tam, gdzie uważamy, że rzucenie każdego innego wyjątku jest przejawem poważnego błędu. Najczęściej jest to sytuacja, kiedy chcemy zadeklarować, że dana funkcja w ogóle nie rzuca wyjątków. Jak już pisałem taką własność powinny posiadać destruktory.
Niespodziewane wyjątki
Podobnie jak w przypadku funkcji terminate(), możemy podstawić
własną funkcję unexpected(). Podobnie jak terminate() funkcja
unexpected() nie zwraca sterowania, może za to sama rzucić
wyjątek. W ten sposób możemy jej użyć do "podmiany"
niespodziewanego wyjątku na inny. Zobaczmy jak to działa:
void f() throw(int) { throw "niespodzianka!"; }; main() { try { f(); } catch(...) {}; }
( Źródło: unexpected.cpp)
Ponieważ f() rzuca const char *, a deklaruje tylko int-a,
powyższy program wywoła funkcję unexpected(), która przerwie program.
Jeżeli podmienimy wyjątek poprzez ustawienie odpowiedniej funkcji:
void unexpected_handler() {throw 0;}; std::set_unexpected(unexpected_handler);
to zamiast const char * zostanie rzucony int i złapany przez
klauzulę catch(...). Tak się stanie ponieważ int jest na
liście wyjątków funkcji f(). Gdyby nie był, to zostałaby wywołana
funkcja terminate(). Jeżeli jednak deklaracja wyjątków funkcji
f() zawierać będzie wyjątek std::bad_exception, to każdy
wyjątek rzucony przez unexpected() i nie znajdujący się na liście
zadeklarowanych wyjątków funkcji f(), jest podmieniany na
std::bad_exception():
void f() throw(int,std::bad_exception) { throw "niespodzianka!"; }; void unexpected_handler() {throw 3.1415926;}; main() { std::set_unexpected(unexpected_handler); try { f(); } catch(std::bad_exception ) {}; }
( Źródło: unexpected.cpp)
Wydajność wyjątków
Autor pozycji "Język C++ bardziej efektywny" S. Meyers sugerował, że użycie mechanizmu wyjątków może spowolnić program, nawet jeśli wyjątki nie będą rzucane. Ponieważ od tego czasu minęło dobrych kilka lat, postanowiłem sam sprawdzić, jak się sprawy mają. W tym celu skorzystałem z następujących programików:
double scin(double x,bool flag) { if(flag) throw 0; return sin(x); } main(){ volatile int f=0; double s=0.0; for(int i=0;i<100000000;++i) { try { s+=scin(rand()/(double)RAND_MAX,f); } catch(int) {}; } }
( Źródło: exceptions.cpp)
oraz
double scin(double x,bool flag) { if(flag) return 0; return sin(x); } main(){ volatile int f=0; double s=0.0; for(int i=0;i<100000000;++i) s+=scin(rand()/(double)RAND_MAX,f); }
( Źródło: no_exceptions.cpp)
Jak widać drugi z nich nie ma nawet śladu wyjątków. W pierwszym podejściu
ustawilem flagę f na zero, co powodowało, że żaden wyjątek nie był rzucany.
Czas wykonania obu programów (w sekundach) podany jest w poniższej tabelce:
| nie rzucane wyjątki | bez wyjątków | rzucane wyjątki | return | |
| -O0 | 15 | 15 | ||
| -O1 | 13 | 4 | ||
| -O2 | 13 | 4 | ||
| -O3 | 4 | 4 | 600 | 4 |
Porównując kolumny 1 i 2, widać, że dla pełnej optymalizacji nie ma
żadnej różnicy. Szczegółowe badanie wykazało, że to włączenie opcji
-finline-functions powoduje skok prędkości pomiędzy dwoma
ostatnimi wierszami w pierwszej kolumnie. Ten sam efekt można uzyskać,
dodając do funkcji scin kwalifikator inline.
Następnie porównałem koszt zwykłego powrotu z funkcji z kosztem rzucenia wyjątku. Wyniki są przedstawione w dwóch ostatnich kolumnach tabelki. Tu widać dramatyczną różnicę: obsługa wyjątku jest ponad 100 razy wolniejsza.
| Załącznik | Wielkość |
|---|---|
| Overflow.cpp | 240 bajtów |
| Stack_except.h | 543 bajty |
| Stack_except.cpp | 330 bajtów |
| Caught.cpp | 469 bajtów |
| Terminate.cpp | 440 bajtów |
| Destruktor.cpp | 242 bajty |
| Hierarchy.cpp | 1.1 KB |
| Unexpected.cpp | 283 bajty |
| Exceptions.cpp | 324 bajty |
| No_exceptions.cpp | 292 bajty |
Zarządzenie pamięcią
Wstęp
Dynamiczna alokacja pamięci to bardzo ważny element języka C. W C do
przydziału i zwolnienia pamięci służą odpowiedno funkcje malloc
(i jego "kuzyni") i free. W C++ są one również dostępne, ale
używane są raczej wyrażenia
new i delete. Ta zmiana ma poważną przyczynę: te wyrażenia
robią więcej niż tylko przydzielanie lub zwalnianie pamięci. Wyrażenie
new tworzy nowy obiekt, a więc nie tylko przydziela pamięc, ale
również inicjalizuje go, używając odpowiedniego konstruktora. Wyrażenie
delete niszczy obiekt, wywołując jego destruktor i dopiero potem
zwalnia zajętą przez niego pamięć. W tym wykładzie pokażę, co tak
naprawdę się dzieje, gdy dynamicznie tworzymy lub niszczymy obiekty.
Wyrażenia new i delete posługują się systemowymi alokatorami
i dealokatorami pamięci. C++ daje nam możliwość
wykorzystania w tym celu własnych implementacji.
Napisanie jednak bardziej wydajnego alokatora
pamięci niż alokator standardowy nie jest łatwe.
Można jednak próbować zwiększyć wydajność przydzielania i zwalniania
pamięci w sytuacjach szczególnych, np. jeśli
używamy dużej ilości małych obiektów o stałym rozmiarze, które muszą
być dynamicznie tworzone i niszczone. Pod koniec wykładu podamy prosty
schemat obsługi pamięci mający zastosowanie w takiej sytuacji.
new
Przyjrzyjmy się najpierw dokładnie procesowi tworzenia pojedynczego, nowego
obiektu za pomocą wyrażenia new:
X *p = new X inicjalizator;lub
X *p = new (lista_argumentow) X inicjalizator;
Druga forma jest nazywana z przyczyn historycznych "placement new"
(pochodzenie tej nazwy wyjaśnię poniżej); inicjalizator
może być dowolnym wyrażeniem inicjalizującym, np.:
X *p1 = new X; X *p2 = new X(); X x,y; X *p3 = new X = x; X *p4 = new X(y); X *p5 = new X(0);
Oczywiście zakładamy istnienie odpowiednich konstruktorów.
Przydział pamięci
Najpierw przydzielana jest "goła" (raw) pamięć. Służy do tego
funkcja przydziału pamięci (alokator) operator new():
void *tmp = operator new(sizeof(X));
lub
void *tmp = operator new(sizeof(X),lista_argumentow);
jeśli użyliśmy formy placement. Nazwa placement pochodzi od operatora
new dostarczanego w bibliotece standardowej, który przyjmuje drugi
argument typu void *:
void* operator new(std::size_t size, void* ptr) throw() {return ptr;};
Operator ten nie przydziela żadnej pamięci tylko zwraca wskaźnik
ptr. Jego wywołanie nie może się nie powieść, dlatego nie rzuca
żadnych wyjątków. Ta forma operatora służy do
umieszczania (placement) obiektu w
zadanym obszarze pamięci:
void *p =malloc(sizeof(X)); X *px=new (p) X;
stąd jego nazwa.
Środowisko C++ dostarcza jeszcze dwu wersji globalnych funkcji
operator new():
void* operator new(std::size_t size) throw(std::bad_alloc); void* operator new(std::size_t size, std::nothrow_t) throw();
ale użytkownik może podać własne definicje, zarówno
globalne, jak i dla pojedynczych klas. Odpowiednia funkcja operator new jest najpierw wyszukiwana w klasie X, a następnie w
przestrzeni globalnej. Jeśli nie znajdzie się definicja odpowiadająca
podanym argumentom, to wystąpi błąd kompilacji. Np. jeśli zażądamy
stworzenia obiektu wyrażeniem:
X *p = new X;to kompilator będzie szukał funkcji:
X::operator new(size_t);
a w drugiej kolejności:
void *tmp =::operator new(sizeof(X));
Wyrażenie
X *p = new (3.15) X;
spowoduje poszukiwanie funkcji:
X::operator new(size_t,double);
lub
::operator new(size_t,double);
Pierwszy argument każdej funkcji operator new musi być typu
size_t i przekazywany jest przez niego rozmiar żądanego obszaru
pamięci.
Każda funkcja operator new zwraca void *. W przypadku
powodzenia zwracany jest wskaźnik do przydzielonego obszaru pamięci:
void *p = operator new(1000);
W przypadku niepowodzenia operator new może rzucić wyjątek
std::bad_alloc lub zwrócić wskaźnik zerowy.
Tworzenie obiektu
Jeśli przydział pamięci powiedzie się, tzn. operator new zwróci
niezerowy wskaźnik, to następuje wywołanie konstruktora klasy X
w celu stworzenia obiektu,
który jest umieszczany w przydzielonej pamięci. Np:
X *p = X(1);
spowoduje wywołanie konstruktora:
X::X(int);
jeśli takowy istnieje. Jeśli konstrukcja się powiedzie (nie rzuci
wyjątku), to proces się kończy. Jeśli jednak wywołany konstruktor
rzuci wyjątek, który zostanie złapany, to wyrażenie delete
postara się zwolnić przydzieloną pamięć w "trybie awaryjnym".
Awaryjne zwolnienie pamięci
W ramach takiej obsługi przerwania, zwalnianie pamięci przydzielonej przez operator new odbywa sie za pomocą odpowiadajacej mu wersji operator delete.
void operator delete(void *p,lista_argumentow) throw();
operator delete odpowiada wersji operatora new z taką sama listą argumentów. Jeśli lista argumentów jest niepusta, to
taki operator nazywamy placement delete.
Przy wywoływaniu placement delete, przekazywana mu jest lista dodatkowych
argumentów, identyczna z listą dodatkowych argumentów operatora placement new,
który pamięć przydzielił.
Biblioteka C++ dostarcza globalnych implementacji operatorów
delete, odpowiadających trzem wspomnianym powyżej operatorom
new, ale można też dodawać własne definicje, zarówno w klasie jak
i w przestrzeni globalnej. Jeśli kompilator nie znajdzie żadnej
odpowiedniej definicji operator delete, to żadna funkcja
zwalniająca nie zostanie wywołana.
Rozważmy następujący przykład:
struct X { X(int); /* rzuca wyjątek typu int*/ void *operator new(size_t) throw(std::bad_alloc); void *operator delete(void *p) throw(); }
Wyrażenie:
try { X *p = new X(1); } catch(int){};
spowoduje wywołanie:
void *tmp=X::operator new(sizeof(X)); X::operator delete(tmp);
Dodanie do klasy X dwu operatorów:
void *operator new(size_t,double) throw(std::bad_alloc); void *operator delete(void *p,double) throw();
spowoduje, że wyrażenie:
try { X *p = new (3.14) X(1); } catch(int){};
wywoła:
void *tmp=X::operator new(sizeof(X),3.14); X::operator delete(tmp,3.14);
Tę logikę zaburza trochę fakt istnienia wyróżnionej wersji funkcji
operator delete. Są to składowe klas posiadające drugi parametr
typu size_t:
void X::operator delete(void *p,size_t size);
Jeśli klasa nie posiada jednoargumentowego operatora delete, to
powyższy operator jest traktowany jak jednoargumentowy (non
placement). Za drugi argument podstawiany jest automatycznie rozmiar
zwalnianego obiektu. Rozważmy, więc teraz taki przykład:
struct X { X(int); /* rzuca wyjątek typu int*/ void *operator new(size_t) throw(std::bad_alloc); void *operator delete(void *p,size_t) throw(); }
Wyrażenie:
try { X *p = new X(1); } catch(int){};
wywoła:
void *tmp=X::operator new(sizeof(X)); X::operator delete(tmp,sizeof(X));
a wyrażenie:
try { X *p = new (3) X(1); } catch(int){};
wywoła:
void *tmp=X::operator new(sizeof(X),3); X::operator delete(tmp,3);
Proszę zwrócić uwagę na różnicę w wartości drugiego argumentu przekazanego
do operator delete.
delete
Stworzony dynamicznie obiekt niszczymy wyrażeniem
delete p;które najpierw wywołuje destruktor klasy X:
p->~X();
Jeśli to wywołanie się nie powiedzie (zostanie rzucony wyjątek) to mamy
kłopot, bo nie zostanie wywołany operator delete w celu
zwolnienia pamięci. Jest to kolejny powód aby nie rzucać wyjątków z
destruktora. Poniższy programik ilustruje ten problem, doprowadzając
do szybkiego wyczerpania pamięci:
class X { char a[100000]; public: ~X() {throw 0;} }; main() { while(1){ X *p = new X; try { delete p; } catch(int) {}; } }
Jeśli jednak nic złego się nie wydarzy, to po wywołaniu destruktora
przydzielona pamięć zostaje zwolniona za pomocą funkcji operator delete(). O zwalnianiu pamięci dużo już napisałem przy omawianiu wyrażenia new. W przypadku wyrażenia delete dzieje się to jednak trochę inaczej. Wyrażenie delete używa do zwolnienia pamięci tylko funkcji operator delete() niebędących typu
placement, tzn. posiadające jeden lub ewentualnie dwa argumenty:
void operator delete(void p) throw(); void operator delete(void p,size_t) throw();
Jest to niezależne od tego jaki operator new został użyty do
przydzielenia pamięci. Czyli jeśli zdefiniujemy, np.:
struct X { X(int); /* rzuca wyjątek typu int*/ void *operator new(size_t) throw(std::bad_alloc); void *operator new(size_t,size_t) throw(std::bad_alloc); void *operator new(size_t,double) throw(std::bad_alloc); void *operator delete(void *p,size_t) throw(); void *operator delete(void *p,double) throw(); }
to wyrażenia:
X p1 = new X; X p2 = new (1) X; X p3 = new (3.14) X; delete p3; delete p2; delete p1;
spowodują wywołanie:
void *tmp1 = X::operator new(sizeof(X)); void *tmp2 = X::operator new(sizeof(X),1); void *tmp3 = X::operator new(sizeof(X),3.14); X::operator delete(tmp3,sizeof(X)); X::operator delete(tmp2,sizeof(X)); X::operator delete(tmp1,sizeof(X));
operator new
Z powyższego opisu widać, że wpływ na proces dynamicznego tworzenia
obiektu możemy mieć tylko poprzez własne definicje przydzielającego
pamięć operatora new. Zanim jednak napiszemy własną wersję
takiego operatora, przyjrzymy się dokładniej właściwościom
standardowego operatora new.
Jak już wiemy funkcja operator new musi posiadać co najmniej jeden
argument typu size_t. Standardowy operator new posiada
tylko ten jeden argument:
void* operator new(std::size_t size) throw(std::bad_alloc);
Jeśli wszystko pójdzie dobrze, to operator new zwraca wskaźnik
do obszaru pamięci o rozmiarze co najmniej size; jeśli przydział
się nie powiedzie, to rzuca wyjątek std::bad_alloc.
Dokładniej rzecz biorąc operator new rzuca wyjątek tylko wtedy
jeśli nie ustawiona jest funkcja obsługi błędów. Do jej ustawiania
służy funkcja:
namespace std { typedef void (new_handler*)(); new_hadler set_new_handler(new_handler f); }
Funkcja set_new_handler ustawia nową funkcję obsługi błędów i
zwraca wskaźnik do poprzedniej funkcji obsługi lub null, jeśli
funkcja nie była ustawiona. Przekazanie wskaźnika null jako
argumentu powoduje, że nie będzie ustawiona żadna funkcja obsługi. To co
się dzieje wewnątrz operator new wygląda mniej wiecej tak:
while(1) { void *p = przydziel pamiec; if(proba powiodla sie) return p; new_handler handler = set_new_handler(0); set_new_handler(handler); if(handler) handler(); else throw std::bad_alloc(); }
Funkcja handler musi więc uzyskać więcej pamięci, rzucić
wyjątek albo przerwać program. Może też ustawić inną funkcję obsługi,
inaczej program będzie się wykonywał w niekończącej się pętli.
nothrow
Trzecia forma operatora new dostarczonego w bibliotece
standardowej to wersja no_throw. Operator new nie musi
rzucać wyjątku w razie niepowodzenia, ale musi wtedy zwrócić wskaźnik
zerowy (null). Aby wywołać tę wersję operatora new korzystamy
z tego, że posiada ona drugi argument typu nothrow_t.
void* operator new(std::size_t size, const std::nothrow_t&) throw();
W tym celu zdefiniowana została globalna stała typu std::nothrow_t:
namespace std { struct nothrow_t {}; extern const nothrow_t nothrow; }
Wersję nothrow używamy więc następująco:
X *p=new (std::nothrow) X; if(!p) {...};
operator delete
Operator delete musi posiadać co najmniej jeden parametr będący
wskaźnikiem na zwalniany obszar pamięci:
void operator delete(void* ptr) throw();
Może to być wskaźnik zerowy, wtedy operator new nic nie robi.
Operator delete nie rzuca wyjątków.
Jak już opisałem to powyżej, dwuargumentowa wersja będąca składową klasy:
void operator delete(void* ptr) throw();
zachowuje się, w większości przypadków jak wersja jednoargumentowa i drugi argument zostaje automatycznie inicjalizowany rozmiarem zwalnianej pamięci.
Tablice
W powyższej dyskusji ograniczyłem się do tworzenia pojedynczych obiektów. C++ zezwala na tworzenie tablic obiektów:
X *px = new X[10];
Powyższe wyrażenie przydziela pamięć na 10 obiektów klasy X i
tworzy je za pomocą konstruktorów standardowych.
W przypadku niepowodzenia konstrukcji niszczy skonstruowane obiekty (jeśli takowe istnieją) i zwalnia pamięć. Alokacja gołej pamięci jest dokonywana poprzez:
void * operator new[] {size_t);
i zwalniana za pomocą:
void * operator new[] {size_t);
Przeładowywanie operatorów new i delete
Po tym przydługim, technicznym wprowadzeniu, możemy wreszcie pokusić
się o napisanie własnego operatora new lub przeładowanie
istniejącego. Do wyboru mamy wersję globalną lub funkcję składową
jakiejś klasy. Globalny alokator pamięci to poważna sprawa: dotyczy
działania całego programu i musi przydzielać pamięć dowolnych
rozmiarów. Trudno będzie pod tym względem pobić działanie standardowej
wersji operator new. Dlatego częściej będziemy chcieli definiować
operatory new we własnych klasach.
Na co musimy zwrócić w takim przypadku uwagę? Mam
nadzieję, że przekonałem Państwa, że do każdego operatora new
należy dopisać odpowiednią wersję operatora delete, inaczej nie
będziemy w stanie zapewnić bezpiecznego zachowania w sytuacji, w
której zostanie rzucony wyjątek z konstruktora.
Musimy też uważać na jawne zwalnianie pamięci. Jeśli w jednej klasie
zdefiniujemy kilka operatorów placement new, to nie będziemy
mogli ich rozróżnić w poleceniu delete!.
Musimy też zadbać aby operator new albo rzucał wyjątek, albo
zwracał wskaźnik pusty w razie niemożności przydziału pamięci. W
innym przypadku wyrażenie new nie rozpozna, że przydział pamięci
się nie powiódł i będzie próbować tworzyć obiekt w nieprzydzielonej
pamięci.
A co z obsługą new_handler? W zasadzie możemy jej nie
implementować i jeśli robimy to tylko na własny użytek, to pewnie nic
złego się nie stanie. Ale jeśli operator new jest częścią
zewnętrznego interfejsu klasy, to prędzej czy później któryś z
użytkowników może się postarać skorzystać z set_new_handler().
W końcu jeżeli nazywamy naszą funkcję operator new, a nie np.
allocate(), to sugerujemy, że będzie ona miała funkcjonalność
operator new. Zwykle robimy to po to, aby skorzystać z
istniejącego już kodu, który używa wyrażeń new. Jeśli chcemy
tworzyć obiekty i przydzielać pamięć, ale nie zależy nam na
interfejsie new, lepiej nazwać nasze alokatory inaczej.
Memory pool
Jak już sygnalizowałem na wstępie, konieczność zdefiniowania własnego
operatora new pojawia się, gdy chcemy uzyskać wydajność lepszą
niż oferowana przez standardowy operator new. Rozważmy więc
sytuację, kiedy używamy wielu małych przedmiotów o takim samym
rozmiarze. Typowy przykład to inteligentne wskaźniki. W jaki więc
sposób moglibyśmy wydajnie przydzielać i zwalniać pamięć dla takich obiektów?
Jednym z prostszych sposobów jest przydzielenie za pomocą stadardowego alokatora pewnej ilości pamięci, a następnie przydzielanie z niej po kawałku pamięci na pojedyncze obiekty.
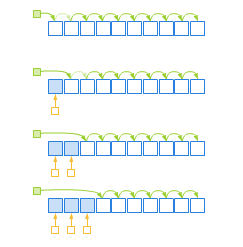
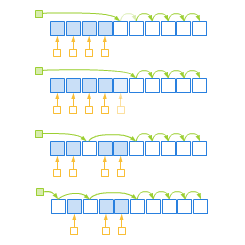 Rysunek 14.1. Działanie zasobnika pamięci.
Rysunek 14.1. Działanie zasobnika pamięci.
Dokładniej wygląda to tak (zob. animacja 14.1): przydzielamy
obszar pamięci mogący pomieścić N kawałków żądanego przez nas
rozmiaru. Na początku wszystkie te kawałki łączymy w listę. Ponieważ na
liście bedą się znajdowały tylko kawałki nieprzydzielonej pamięci,
możemy umieścić wskaźnik do następnego kawałka na liście w samym
kawałku. Nasz alokator nie ma więc żadnego narzutu pamięci poza
wskaźnikiem do pierwszego elementu listy (głowa).
Kiedy potrzebujemy przydzielić pamięć, to usuwamy z listy jej pierwszy element i zwracamy wskaźnik do niego. Kiedy chcemy zwolnić pamięć przyłączamy zwalniany kawałek na początku listy. Obie te operacje są bardzo szybkie. Jeśli mamy wystarczająco dużo pamięci, możemy zrezygnować ze zwalniania jej pojedynczo, tylko zwolnić cały obszar naraz, gdy nie będzie nam już potrzebny.
Kiedy będziemy potrzebowali więcej kawałków niż może ich pomieścić nasz obszar, możemy przydzielić nowy.
Napisanie klasy obsługującej taki schemat pozostawiam jako ćwiczenie.
Tutaj wykorzystam gotową klasę pool dostarczaną w bibliotece boost::pool.
Ewidentnie taki schemat nie nadaje się do implementacji globalnej wersji
operator new, która przydziela pamięć dowolnych rozmiarów.
Idealnie pasuje jednak do klasowego operatora new.
Deklarujemy więc:
#include<boost/pool/pool.hpp> struct X { int _val; char c[1000];/* to tylko zwiększa rozmiar klasy*/ static boost::pool<> pool; public: X(int i=0):_val(i) {}; operator int() {return _val;}; void *operator new(size_t) throw(std::bad_alloc); void operator delete(void *) throw(); };
( Źródło: X_new.h)
Składowa pool jest składową statyczną, ponieważ musi istnieć
niezależnie od obiektów klasy. Podobnie operatory new i
delete automatycznie są traktowane jako metody statyczne.
Ponieważ składowe statyczne klasy są inicjalizowane na zewnątrz,
dodajemy do kodu linijkę:
boost::pool<> X::pool(sizeof(X));
która tworzy obiekt X::pool służący do przydzielania pamięci w kawałkach
po sizeof(X) bajtów.
Następnie definiujemy operator new:
void * X::operator new(size_t size) throw(std::bad_alloc) { while(1) { void *p = pool.malloc(); if(p) return p; std::new_handler handler = std::set_new_handler(0); std::set_new_handler(handler); if(handler) handler(); else throw std::bad_alloc(); } }
( Źródło: X_new.cpp)
Sam przydział pamięci jest najłatwiejszy: korzystamy z gotowej
funkcji malloc() z klasy boost::pool<>. Reszta kodu
implementuje zachowanie się operatora w przypadku braku pamięci, co
funkcja _pool.malloc() sygnalizuje poprzez zwrócenie wskaźnika
zerowego.
Operator delete jest dużo prostszy:
void X::operator delete(void *p) throw() { if(p) pool.free(p); }
Alokatory
Trudno omawiać zarządzanie pamięcią w wykładzie dotyczącym programowania uogólnionego i nie wspomnieć o alokatorach STL. W poprzedniej części wykładu używałem słowa alokator na określenie każdej funkcji przydzielającej pamięć. W STL alokator jest konceptem i oznacza klasy, których obiekty służą do przydzielania pamięci dla standardowych kontenerów. Biblioteka C++ dostarcza standardową implementację szablonu alokatora, której konkretyzacje przekazywane są jako domyślny drugi lub trzeci argument szablonów kontenerów:
namespace std { template<class T, class Allocator=allocator<T> > class vector; template<class T, class Compare = less<T>, class Allocator = allocator<T>> class set; }
Dlatego można używać kontenerów i nie wiedzieć nawet, że alokatory istnieją.
Wymagane elementy szablonu kontenera opiszę na przykładzie możliwej implementacji alokatora standardowego allocator.h:
template <class T> class allocator {...};
Alokator jest szablonem przyjmujacym jako argument typ obiektów, dla których będzie przydzielał pamięć. Ponieważ parametrem szablonu kontenera jest typ, a nie szablon, można by sądzić, że alokator klasą być nie musi, bo możemy tworzyć konkretne alokatory dla konkretnych typów, np.:
vector<int,alokator_int> v;
Alokator musi jednak być szablonem, bo wewnątrz kontenera może zajść
potrzeba przydzielenia pamięci dla obiektu innego typu niż typ
przechowywany T. Dzieje się tak w przypadku kontenerów opartych na
węzłach, takich jak listy czy kontenery asocjacyjne. Taki kontener
musi przydzielić pamięć na węzęł, a nie na element typu T. Żeby
móc to zrobić alokator posiada wewnętrzną strukturę:
template <class U> struct rebind { typedef pool_allocator U other; };
Kontener może z niej korzystać następująco:
typedef typename allocator<T>::rebind<node<T> >::other node_allocator;
Obiekty klasy node_allocator przydzielają pamięć na obiekty klasy
node<T>, a nie T.
Alokator definiuje szereg typów stowarzyszonych:
public: typedef T value_type; typedef value_type* pointer; typedef const value_type* const_pointer; typedef value_type& reference; typedef const value_type& const_reference; typedef size_t size_type; typedef size_t difference_type;
i operator zwracający adres elementu typu T:
pointer address(reference x) const { return &x; } const_pointer address(const_reference x) const { return x; };
Miało to umożliwić używanie niestandardowych typów wskaźnikowych i referencyjnych. W praktyce te typy i funkcje muszą być zdefiniowane dokładnie tak jak powyżej (zob. S. Meyers "STL w praktyce. 50 sposobów efektywnego wykorzystania" oraz N.M. Josuttis "C++ Biblioteka Standardowa. Podręcznik programisty").
Kontener używa obiektów klasy allocator, wobec czego musimy mieć
możność tworzenia i niszczenia ich:
pool_allocator() {} pool_allocator(const pool_allocator&) {} ~pool_allocator() {}
Ważnym ograniczeniem narzuconym przez standard C++ jest wymaganie, aby każde dwa obiekty alokatora tej samej klasy były równoważne. Rownoważność oznacza, że pamięc przydzielona przez jeden obiekt alokatora może być zwolniona przez drugi. W naszym przypadku alokator nie posiada żadnego stanu i jego konstruktory i destruktor nic nie robią, zatem ten warunek jest spełniony. Alokator nie musi posiadać operatora przypisania, więc uniemożliwimy jego użycie:
private: void operator=(const pool_allocator&);
Dochodzimy wreszcie do funkcji, które zarządzają pamięcią. Funkcja:
pointer allocate(size_type n, const_pointer = 0) { return static_cast<pointer>(::operator new(n)); };
przydziela pamięć dla n elementów typu T. Pamięć nie jest
inicjalizowana. Proszę zwrócić uwagę, że w przeciwieństwie do
operator new czy malloc, allocate zwraca wskaźnik
T *, a nie void *. Drugi parametr funkcji allocate może
być użyty przez bardziej wyrafinowane schematy przydziału pamięci.
Tworzeniem obiektu wewnątrz przydzielonej pamięci zajmuje się funkcja
vvoid construct(pointer p, const value_type& x) { new(p) value_type(x); }
korzystająca ze standardowego placement new. Funkcja:
void deallocate(pointer p, size_type n) throw() { ::operator delete(p); }
zwalnia pamięć wskazywaną przez wskaźnik p.
Funkcja deallocate() nie wywołuje destruktora. Robi to funkcja:
void destroy(pointer p) { p-> ~value_type(); }
Na koniec została pomocnicza funkcja:
size_type max_size() const { return static_cast<size_type>(-1) / sizeof(T); }
która zwraca największą wartość możliwą do przekazania do funkcji
allocate. Nie oznacza to jednak, że przydział tej pamięci musi
się powieść.
Koncept alokatora wymaga jeszcze dwu operatorów testujących równoważność obiektów alokatora. Ponieważ kontenery wymagają, aby każde dwa obiekty były równoważne, te operatory zdefiniowane są następująco:
template <class T> inline bool operator==(const allocator<T>&, const allocator<T>&) { return true; } template <class T> inline bool operator!=(const allocator<T>&, const allocator<T>&) { return false; }
Na koniec zabezpieczmy się jeszcze tylko na wypadek możliwości
skonkretyzowania szablonu allocator<void> poprzez odpowiednią
specjalizację:
template<> class allocator<void> { typedef void value_type; typedef void* pointer; typedef const void* const_pointer; template <class U> struct rebind { typedef allocator<U> other; }; };
| Załącznik | Wielkość |
|---|---|
| X_new.cpp | 470 bajtów |
| X_new.h | 326 bajtów |
Wyjątkowo odporny kod
Wstęp
W poprzednim wykładzie opisałem mechanizm obsługi błędów za pomocą
wyjątków. Jest to bardzo silny mechanizm: rzucony wyjątek powoduje
natychmiastowe przekazanie sterowania do najbliższej klauzuli
catch, niejako "tnąc" w poprzek dowolnie głęboko zagnieżdżone
funkcje. To oczywiście jest jedną z jego podstawowych zalet, ale musimy
podchodzić do tej własności bardzo ostrożnie.
W tym wykładzie zwrócę uwagę na kilka niebezpieczeństw wynikających z obsługi wyjątków i na sposoby zapobiegania im.
Wyjątkowe niebezpieczeństwa
W zasadzie korzystanie z wyjątków jest proste: funkcja, która stwierdza wystąpienie błędu, a nie umie go sama obsłużyć, przekazuje odpowiedzialność swoim przełożonym, rzucając wyjątek. Jej przełożeni mogą zrobić to samo (wystarczy, że nie przechwycą wyjątku). Zakładamy jednak, że gdzieś w tej hierarchii wyjątek zostanie złapany przez kogoś, kto wie jak go obsłużyć. W praktyce sprawa może być bardziej skomplikowana. Rzucony wyjątek powoduje natychmiastowe przerwanie nie tylko funkcji, która go rzuciła, ale również wszystkich funkcji, przez które "przelatuje". Jeśli te funkcje nie są na to przygotowane, to wyjątek może narobić dodatkowych szkód. Typowy przykład to niezwolnione zasoby:
void f() { przydziel_zasob(); g(); /*może rzucić wyjątek*/ zwolnij_zasob(); }
Rzucenie wyjątku z g() spowoduje wyciek zasobu (zwykle pamięci). Taki przykład był już rozważany w Wykładzie 10
Podane tam rozwiązanie to technika "przydział zasobu jest
inicjalizacją", czyli oddelegowanie zarządzania zasobem do osobnej
klasy, której konstruktor przydziela zasób, a destruktor zwalnia:
void f() { Zasob x; g(); /*może rzucić wyjątek*/ } /* niejawnie wywoływany destruktor x. Zasob() */
Wtedy podczas zwijania stosu zasób zostanie zwolniony automatycznie. Proszę zauważyć jednak, że jeśli nie przechwycimy wyjątku, to zasób może dalej pozostać niezwolniony. Rozwiązaniem może być kod:
void f() { przydziel_zasob(); try { g(); /*może rzucić wyjątek*/ } cath(...) {zwolnij_zasob();throw;} zwolnij_zasob(); }
Po zwolnieniu zasobu rzucamy (podrzucamy?) ponownie ten sam wyjątek. W
ten sposób funkcja f() staje się "przeźroczysta dla wyjątków"
(exception-neutral).
Konstruktory
Szczególnym przypadkiem mogącym prowadzić do wycieku pamięci są wyjątki rzucane z konstruktora. Rozważmy następujący kod:
struct BigRsource { char c[10000000]; }; struct BadBoy { BadBoy() {throw 0;}; }; struct X { BigResource *p1; BadBoy p2; X: p1(new BigResource) {} X() { delete p1; } }
Na pierwszy rzut oka jest to pierwszorzędny przykład programowania obiektowego: pamięć jest przydzielana w konstruktorze i zwalniana w destruktorze, nie ma więc możliwości wycieku. Prześledźmy jednak, co się stanie, gdy napiszemy:
try { X x; } catch(...) {};
Konstruktor najpierw przydzieli pamięć dla wskaźnika p1. Załóżmy,
że ta alokacja się powiedzie. Następnie zostanie wywołany konstruktor
BadBoy, który rzuci wyjątek. Wyjątek nie zostanie złapany w
konstruktorze X, więc sterowanie zostane przekazane do klauzuli
catch. Nastąpi zwinięcie stosu, ale destruktor obiektu x
nie zostanie wywołany! Dzieje się tak dlatego, że w C++
destruktory nie są wołane dla obiektów, których konstrukcja się nie
powiodła. W taki sposób tracimy 10MB. Możliwe rozwiązania są podobne
jak w poprzednim wypadku: korzystamy z auto_ptr:
struct X { std::auto_ptr<BigResource> p1; BadBoy p2; X: p1(new BigResource) {} X() { delete p1; } };
lub sami łapiemy wyjątek:
struct X { BigResource *p1; BadBoy p2; X: try {p1(new BigResource) {}} catch(...){delete p1;}; ~X() { delete p1; } }
Proszę zwrócić uwagę na blok try, który otacza cały
konstruktor łącznie z listą inicjalizatorów.
The bad, the good and the ugly
Jeżeli wyjątek został rzucony przez metodę jakiegoś obiektu, to dla dalszego działania programu ważne jest, w jakim stanie go pozostawił. Wyróżnimy trzy możliwości:
The bad. Obiekt jest w stanie niekonsystentnym, nie są zachowane niezmienniki jego typu, być może nastąpił wyciek zasobów. Nieokreślone jest zachowanie wywoływanych metod, w szczególności może nie powieść się destrukcja obiektu.
The ugly. Obiekt jest w stanie konsystentnym, ale niezdefiniowanym.
The good. Obiekt pozostaje w stanie, w jakim był przed rzuceniem wyjątku. Jest to semantyka transakcji: commit--rollback.
Ewidentnie najbardziej pożądanym zachowaniem jest stan ostatni. Nie zawsze da się jednak zapewnić takie zachowanie bez ponoszenia dużych kosztów. Wtedy możemy zadowolić się stanem drugim. Stan pierwszy to oczywista katastrofa.
Przykład: stos
Rozważmy stos z dynamiczną obsługą pamięci. Przykład takiego stosu był podany w Wykładzie 7. Żeby nie wprowadzać komplikacji, nie będziemy tu korzystać z klas wytycznych:
template <class T,size_t N = 10> class Stack { size_t nelems; size_t top; T* v; public: bool is_empty() const; void push(const T&); T pop(); Stack(size_t n = N); Stack(); Stack(const Stack&); Stack& operator=(const Stack&); };
W powyższym konstruktorze może nie powieść się tylko operacja
tworzenia tablicy v. Ale wtedy, zgodnie z tym co już omawialiśmy w
poprzednim wykładzie, wyrażenie new samo po sobie posprząta. Nie
musimy się martwić stanem pozostawionego obiektu, bo jeśli konstrukcja
się nie powiedzie, to obiektu po prostu nie ma.
Z konstruktorem kopiującym jest już trochę gorzej:
template <class T,size_t N> Stack<T,N>::Stack(const Stack<T,N>& s): v(new T[nelems = s.nelems]) { if( s.top > 0 ) for(top = 0; top < s.top; top++) v[top] = s.v[top]; /* tu może zostać rzucony wyjatek */ }
Podobnie jak poprzednio, w wypadku niepowodzenia wyrażenie new
posprząta po sobie. Ale wyjątek może zostać rzucony również przez
operator przypisania klasy T. Wtedy będziemy mieli do czynienia z
wyciekiem pamięci, ponieważ nie zostanie wywołany destruktor stosu,
który zwalnia pamięć v. Taki przykład już omawialiśmy na początku
wykładu. Rozwiązaniem jest użycie auto_ptr lub przechwycenie wyjątku:
template <class T,size_t N> Stack<T,N>::Stack(const Stack<T,N>& s): v(new T[nelems = s.nelems]) { try { if( s.top > 0 ) for(top = 0; top < s.top; top++) v[top] = s.v[top]; /* tu może zostać rzucony wyjatek */ } catch(...) { delete [] v; throw ; } }
To rozwiązanie zakłada, że destrukcja v powiedzie się, tzn. że operator
przypisania:
v[top] = s.v[top];
pozostawił lewą stronę w stanie umożliwiającym jej destrukcję.
Sytuacja jest groźniejsza w przypadku operatora przypisania:
template <class T,size_t N> Stack<T,N>& Stack<T,N>::operator=(const Stack<T,N>& s) { delete [ ] v; v = new T[nelems=s.nelems]; if( s.top > 0 ) for(top = 0; top < s.top; top++) v[top] = s.v[top]; return *this; }
Wyjątek rzucony przez wyrażenie new zostawia stos w stanie złym,
z wiszącym luźno wskaźnikiem v. Wyjątek rzucony przez operator
przypisania elementów tablicy v w najlepszym przypadku zostawia
stos w stanie niezdefiniowanym. Implementacja, która w wypadku
wystąpienia wyjątku zostawia stos w takim stanie, w jakim go zastała,
jest podana poniżej:
template <class T,size_t N> Stack<T,N>& Stack<T,N>::operator=(const Stack<T,N>& s) { T *tmp; try { tmp = new T[nelems=s.nelems]; if( s.top > 0 ) for(size_t i = 0; i < s.top; i++) tmp[i] = s.v[i]; } catch(...) {delete [] tmp,throw;} swap(v,tmp); delete [] tmp; top=s.top; return *this; }
Przejdźmy teraz do podstawowych funkcji stosu, zaczynając od funkcji push:
template <class T,size_t N> void Stack<T,N>::push(const T &element) { if( top == nelems ) { T* new_buffer = new T[nelems += N]; for(int i = 0; i < top; i++) new_buffer[i] = v[i]; delete [] v; v = new_buffer; } v[top++] = element; }
Załóżmy na początek, że nie ma potrzeby zwiększania pamięci, wykonywane jest więc tylko polecenie:
v[top++] = element;
Jak już zauważyliśmy, przypisanie może się nie powieść, wtedy stos
zostanie w stanie złym lub niezdefiniowanym, ponieważ top zostanie
zwiększone. Lepiej jest więc napisać:
v[top] = element; ++top;
Zobaczmy, co się dzieje, jeśli zażądamy zwiększenia pamięci.
Niepowodzenie wyrażenia new zostawi nas ze zwiększonym polem
nelems, pomimo że pamięć się nie zwiększyła. Wyjątek z operatora
przypisania zostawi nas z wyciekiem pamięci, ponieważ pamięć
przydzielona do new_buffer nigdy nie zostanie zwolniona.
Uwzględaniając te uwagi, poprawimy funkcję push następująco:
template <class T,size_t N> void Stack<T,N>::push(T element) { if( top == nelems ) { T* new_buffer; size_t new_nelems; try { new_nelems=nelems+N; new_buffer = new T[new_nelems]; for(int i = 0; i < top; i++) new_buffer[i] = v[i]; } catch(...) { delete [] new_buffer;} swap(v,new_buffer); delete [] new_buffer; nelems = new_nelems; } v[top] = element; ++top; }
Na koniec została nam jeszcze funkcja pop:
template <class T,size_t N> T Stack<T,N>::pop() { if( top == 0 ) throw std::domain_error("pop on empty stack"); return v[--top]; /* tu może nastąpić kopiowanie */ }
Jak widać funkcja pop może rzucić jawnie wyjątek
std::domain_error. Z tym wyjątkiem nie ma problemów.
Potencjalny problem stwarza za to wyrażenie:
return v[--top]; /* tu może nastąpić kopiowanie */
Ponieważ zwracamy v[--top] przez wartość, to może nastąpić
kopiowanie elementu typu T. Nie musi, ponieważ kompilator ma prawo
wyoptymalizować powstały obiekt tymczasowy. Jeżeli jednak zostanie
wywołany konstruktor kopiujący, to może rzucić wyjątek. Wtedy stos
pozostanie w zmienionym stanie, bo wartość top zostanie zmniejszona.
Rozważmy też wyrażenie:
x = s.pop();
Jeżeli operacja przypisania się nie powiedzie, to stracimy bezpowrotnie jeden element stosu. Można by powiedzieć, że to już nie jest sprawa stosu, ale lepiej po prostu rozdzielić operacje modyfikujące stan stosu od operacji tylko ten stan odczytujących:
template <class T,size_t N> void Stack<T,N>::pop() { if( top == 0 ) throw std::domain_error("pop on empty stack"); --top; } template<class T,size_t N> T &Stack<T,N>::top() { if( top == 0 ) throw std::domain_error("pop on empty stack"); return v[top-1]; } template<class T,size_t N> const T &Stack<T,N>::top() const { if( top == 0 ) throw std::domain_error("pop on empty stack"); return v[top-1]; }
W przeciwieństwie do pop() operacja top() może zwracać
wartość przez referencje. Funkcja pop() robić tego w ogólności
nie mogła, bo potencjalnie niszczyła obiekt zdejmowany ze stosu.
Kolejny stos
Zaprezentowana w poprzedniej części implementacja stosu wymagała, aby
parametr szablonu T posiadał:
- konstruktor domyślny.
- bezpieczny (względem wyjątków) operator przypisania.
- destruktor nie rzucający wyjątków.
Proszę zauważyć, że konstruktor domyślny właściwie niczemu nie służy.
Jest potrzebny tylko po to, aby stworzyć tablicę obiektów, które potem
będą tak naprawdę nadpisywane za pomocą operatora przypisania. Taka
inicjalizacja i przypisanie jest w C++ dokonywana za pomocą
konstruktora kopiującego. Na zakończenie przedstawię implementację
klasy Stack, która od typu T potrzebuje tylko destruktora i
konstruktora kopiującego. W tym celu będziemy przydzielać "gołą"
pamięć oraz tworzyć i niszczyć w niej obiekty bezpośrednio. Do tego celu
wykorzystamy alokator opisany w poprzednim wykładzie.
Zaczniemy od zdefiniowania pomocniczej klasy do zarządzania pamięcią:
template<typename T,typename Allocator = std::allocator<T> > struct Stack_impl : public Allocator{ size_t _top; size_t _size; T* _buffer; Stack_impl(size_t n): _top(0), _size(n), _buffer(Allocator::allocate(_size)) {}; Stack_impl() { for(size_t i=0;i<_top;++i) destroy(_buffer++); deallocate(_buffer,_size); } void swap(Stack_impl& rhs) throw() { std::swap(_buffer,rhs._buffer); std::swap(_size,rhs._size); std::swap(_top,rhs._top); } };
Jedyne miejsce, gdzie może zostać rzucony wyjątek to funkcja
allocate(), ale wtedy żadna pamięć nie zostanie przydzielona ani
żaden obiekt nie zostanie stworzony. Korzystamy tu też z żądania, aby
alokator był bezstanowy, inaczej funkcja swap musiałaby też
zamieniać składowe alokatorów.
Klasa Stack korzysta z klasy Stack_impl:
template<typename T,size_t N = 10, typename Allocator = std::allocator<T> > class Stack { private: Stack_impl<T,Allocator> _impl;
( Źródło: stack_sutter.h)
Konstruktory:
public: Stack(size_t n = N):_impl(n) {}; Stack(const Stack& rhs):_impl(rhs._impl) { while(_impl._top < rhs._impl._top) { _impl.construct(_impl._buffer+_impl._top, rhs._impl._buffer[_impl._top]); ++_impl._top; } }
( Źródło: stack_sutter.h)
robią się teraz prostsze. Nie ma potrzeby definiowania destruktora.
Destruktor domyślny sam wywoła destruktor pola _impl. Jeżeli w
konstruktorze kopiującym zostanie rzucony wyjątek w funkcji
construct, to wywołany podczas zwijania stosu destruktor Stack_impl
wywoła destruktory stworzonych obiektów i zwolni pamięć.
Operator przypisania korzysta z "triku":
Stack &operator=(const Stack& rhs) { Stack tmp(rhs); _impl.swap(tmp._impl); return *this; }
( Źródło: stack_sutter.h)
Tworzymy kopię prawej strony i zamieniamy z lewą stroną. Obiekt
tmp jest obiektem lokalnym, więc zostanie zniszczony. Jeśli nie
powiedzie się kopiowanie, to stos pozostaje w stanie niezmienionym.
Proszę zauważyć, że jest to bezpieczne nawet w przypadku
samopodstawienia s=s.
Funkcja push stosuje podobną technikę:
void push(const T &elem) { if(_impl._top==_impl._size) { Stack tmp(_impl._size+N); while(tmp._impl._top < _impl._top) { _impl.construct(tmp._impl._buffer+tmp._impl._top, _impl._buffer[tmp._impl._top]); ++tmp._impl._top; } _impl.swap(tmp._impl); } _impl.construct(_impl._buffer+_impl._top,elem); ++_impl._top; }
( Źródło: stack_sutter.h)
Funkcje top() i pop() pozostają praktycznie niezmienione, z
tym, że funkcja pop() niszczy obiekt na wierzchołku stosu:
T &top() { if(_impl._top==0) throw std::domain_error("empty stack"); return _impl._buffer[_impl._top-1]; } void pop() { if(_impl._top==0) throw std::domain_error("empty stack"); --_impl._top; _impl.destroy(_impl._buffer+_impl._top); } bool is_empty() { return _impl._top==0; } };
( Źródło: stack_sutter.h)
| Załącznik | Wielkość |
|---|---|
| Stack_sutter.h | 1.81 KB |