Miara układu wektorów
Macierz Grama. Wyznacznik Grama
Zajmiemy się teraz przypadkiem, gdy sam iloczyn skalarny (oznaczony w tym rozdziale przez \(g\)) jako odwzorowanie dwuliniowe symetryczne jest odwzorowaniem dwuliniowym skojarzonym z formą kwadratową. Tą forma kwadratową jest kwadrat normy
Niech teraz \(v_1,...,v_k\) będzie dowolnym ciągiem wektorów przestrzeni \(V\). Definiujemy macierz
\(\left [ \begin{array} {lcccr} \ g(v_1,v_1) \ .\ .\ .\ g(v_1,v_k)\\ \ g(v_2,v_1) \ .\ .\ .\ g(v_2,v_k)\\ \ ..................................\\ \ g(v_k,v_1) \ . \ .\ .\ g(v_k,v_k) \end{array} \right ].\) (1.1)
Macierz tę nazywamy macierzą Grama ciągu wektorów \(v_1,...,v_k\). Wyznacznik tej macierzy nazywamy wyznacznikiem Grama tego ciągu.





Zauważmy od razu, że wyznacznik Grama nie zależy od kolejności
wektorów \(v_1,...,v_k\). Istotnie, przestawieniu dwu wektorów w
ciągu \(v_1,...,v_k\) odpowiada jednoczesne przestawienie dwu kolumn
i dwu wierszy w macierzy Grama. A zatem możemy mówić o wyznaczniku
Grama układu wektorów. Wyznacznik Grama układu \(v_1,...,v_k\)
oznaczać będziemy przez \({\rm G} (v_1,...,v_k)\).
Jeżeli \(V\) jest skończenie wymiarowa, to macierz odwzorowania dwuliniowego \(g\) przy dowolnej bazie ortonormalnej jest macierzą jednostkową. W szczególności, wyznacznik tej macierzy jest dodatni. Ze wzoru (0.3) z Wykładu XI wynika, że wyznacznik macierzy \(g\) przy jakiejkolwiek bazie jest dodatni.
Twierdzenie 1.1
Wyznacznik Grama dowolnego układu wektorów jest zawsze większy lub równy zeru. Jest równy zeru wtedy i tylko wtedy, gdy układ wektorów jest liniowo zależny.
Dowód
Oznaczmy przez \(U\) przestrzeń rozpiętą na danych wektorach \(v_1,...,v_k\). Przestrzeń ta jest wyposażona w iloczyn skalarny \(g\) (dokładniej mówiąc, zawężenie \(g\) do \(U\times U\)).
Jeśli wektory \(v_1,..., v_k\) są liniowo zależne, to pewien wektor \(v_j\) jest kombinacją liniową wektorów pozostałych. Wtedy \(j\)-ta kolumna macierzy Grama jest kombinacją liniową pozostałych kolumn. Oznacza to, że wyznacznik tej macierzy jest równy zeru.
Załóżmy teraz, że wektory \(v_1,..., v_n\) są liniowo niezależne. Stanowią więc bazę przestrzeni \(U\). Macierz Grama tego układu, jest macierzą \(g\) przy bazie \(v_1,...,v_n\) przestrzeni \(U\). A zatem, na podstawie uwagi, którą zrobiliśmy bezpośrednio przed twierdzeniem, wyznacznik tej macierzy jest dodatni (w
szczególności niezerowy).Przykład 1.2
Niech dane będą dwa wektory \(v\) i \(u\). Mamy macierz Grama
Fakt, że wyznacznik tej macierzy jest nieujemny jest nierównością Schwarza.
Niech \(e_1,...,e_n\) będzie bazą ortonormalną przestrzeni \(V\) i niech \(v_1,...,v_n\) będzie dowolnym układem wektorów przestrzeni \(V\). Tak jak zdefiniowaliśmy macierz przejścia od jednej bazy do drugiej, tak samo możemy zdefiniować macierz przejścia od bazy \(e_1,..., e_n\) do układu \(v_1,...,v_n\). Mianowicie, definiujemy macierz \(P=[v_{ij}]\) wzorami
\(\displaystyle v_j=\sum _{i=1}^n v_{ij} e_i.\) (1.2)
Macierz \(P\) jest macierzą współrzędnych wektorów \(v_1,...,v_n\) w bazie \(e_1,...e_n\). Zupełnie tak samo jak
wzór (0.3) z Wykładu XI otrzymujemy wzór następujący
\(\left [ \begin{array} {lcccr} \ g(v_1,v_1) \ .\ .\ .\ g(v_1,v_k)\\ \ ..................................\\ \ g(v_k,v_1) \ . \ .\ .\ g(v_k,v_k) \end{array} \right ] =P^*P,\) (1.3)
gdzie \(P\) jest macierzą zdefiniowaną formułą (1.2).
Otrzymaliśmy więc
Twierdzenie 1.3
Wyznacznik Grama układu wektorów \(v_1,...,v_n\) jest równy \(({\rm det} P)^2\), gdzie \(P\) jest macierzą utworzoną ze współrzędnych wektorów \(v_1,...,v_n\) w bazie ortonormalnej \(e_1,...,e_n\).
Miara układu wektorów
Niech \(V\) będzie skończenie wymiarową euklidesową przestrzenią wektorową. Niech \(U\) będzie dowolną jej podprzestrzenią. Mamy wtedy \(V=U\oplus U^{\perp}\). Niech \(v\in V\) będzie dowolnym wektorem. Wektor ten rozkłada się jednoznacznie na sumę \(v=u+u'\), gdzie \(u\in U\) i \(u'\in U^{\perp}\). Zdefiniujmy liczbę
\(d(v,U)= \Vert u'\Vert .\) (2.4)
Niech teraz \(V\) będzie dowolną (niekoniecznie skończenie
wymiarową) euklidesową przestrzenią wektorową i \(v_1,...,v_n\)
dowolnym ciągiem wektorów.
Zdefiniujemy liczbę \({\rm vol} (v_1,...,v_n)\) , którą nazywać będziemy miarą układu \(v_1,...,v_n\) (lub \(n\)-wymiarową objętością). Definicja będzie indukcyjna.
Definicja 2.1
Jeżeli \(n=1\), to miarą wektora \(v_1\) jest jego długość \(\Vert v_1\Vert\). Jeżeli określona już jest miara układów \(n\)-elementowych, to miarą układu \(v_1,...,v_n, v\) jest liczba zdefiniowana wzorem


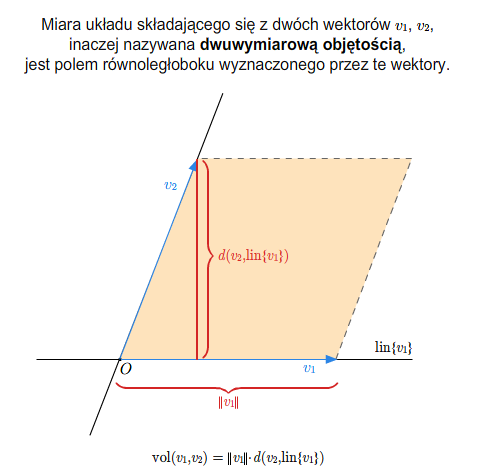
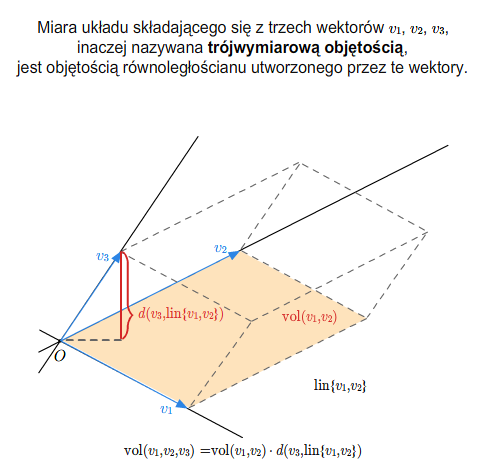
Definicja ta jest zgodna z naszą intuicją i wiadomościami wyniesionymi ze szkoły.
Miara układu dwóch wektorów jest polem równoległoboku wyznaczonego przez te wektory. Miara układu trzech liniowo niezależnych wektorów jest objętością równoległościanu utworzonego przez te wektory.
Z definicji miary układu wektorów łatwo wynika, że \({\rm vol} (v_1,...,v_n) =0\), jeśli wektory \(v_1,...,v_n\) są liniowo zależne.
Udowodnimy teraz twierdzenie
Twierdzenie 2.2
Dla każdego układu wektorów \(v_1,..., v_n\) zachodzi równość
\({\rm vol} (v_1,...,v_n) = \sqrt{{\rm G} (v_1,...,v_n)}.\) (2.5)
Dowód
Dowód jest indukcyjny ze względu na \(n\).
Dla \(n=1\) twierdzenie jest trywialne. Załóżmy, że jest prawdziwe dla pewnego \(n\).
Niech dany będzie układ wektorów \(v_1,...,v_n,v\). Jeśli układ ten jest liniowo zależny, to po obydwu stronach (2.5) mamy zero. Możemy więc założyć, że dany układ wektorów jest liniowo niezależny.
W \((n+1)\)-wymiarowej przestrzeni \(V'={\rm lin} \{v_1,...,v_n, v\}\) weźmy \(n\)-wymiarową podprzestrzeń \(U={\rm lin} \{ v_1,...,v_n\}\). Oznaczmy przez \(d\) liczbę \(d=d(v, U)\). Niech \(v= u+u'\), gdzie \(u\in U\) i \(u'\in U^{\perp}\), zaś \(U^{\perp}\) jest dopełnieniem ortogonalnym do \(U\) w \(V'\). W szczególności \(g(u,u')=0\). Ponieważ \(v_1,...,v_n\) jest bazą \(U\), wektor \(u\) możemy zapisać jako
Zachodzą następujące równości
A zatem mamy równość
\(\displaystyle \sum _{i=1}^n x_ig(v_i ,v) +(-1)(\Vert v\Vert ^2 -d^2)=0.\) (2.6)
Oczywiście \(g(u, v_j)= g(v,v_j)\) dla każdego \(j=1,...n\). Stąd
dla \(j=1,...,n\). Zatem
\(\displaystyle \sum _{i=1}^n x_ig(v_i,v_j)+(-1)g(v,v_j)=0.\) (2.7)
Przyjmijmy \(x_{n+1}=-1\). Łącząc (2.6) i
(2.7) otrzymujemy układ \(n+1\) równości
\(\displaystyle \left \{ \begin{array} {l} \ \sum _{i}^n x_ig(v_i,v_j)+x_{n+1} g(v,v_j)=0,\ \ j=1,...,n\\ \ \sum _{i}^n x_ig(v_i ,v) +x_{n+1}(\Vert v\Vert ^2 -d^2)=0. \end{array} \right .\) (2.8)
Potraktujmy ten układ jako jednorodny układ \(n+1\) równań
liniowych z \(n+1\) niewiadomymi \(x_1,...,x_{n+1}\). Wiemy, że układ ten ma niezerowe rozwiązanie \((x_1,...,x_n, -1)\). A zatem
wyznacznik macierzy współczynników tego układu jest równy \(0\).
Macierz współczynników tego układu jest następująca
\(\left [\begin{array} {lccccr} \ g(v_1,v_1) \ . \ . \ . \ g(v_n, v_1) \ \ \ \ \ \ g(v,v_1)\\ \ ....................................................... \\ \ g(v_1,v_n) \ .\ . \ .\ \ g(v_n,v_n)\ \ \ \ \ g(v,v_n ) \\ \ g(v_1, v) \ \ .\ . \ . \ \ \ g(v_n,v)\ \ \ \ \ g(v,v)-d^2 \end{array} \right ]\) (2.9)
Korzystając teraz z liniowości wyznacznika ze względu na ostatnią
kolumnę otrzymujemy równość wyznaczników następujących macierzy
\(\left [\begin{array} {lccccr} \ g(v_1,v_1)\ .\ .\ .\ g(v_n,v_1)\ g(v,v_1) \\ \ ...............................................\\ \ g(v_1,v_n) \ .\ . \ . \ g(v_n,v_n) \ g( v,v_n) \\ \ g(v_1,v)\ .\ .\ . \ \ g(v_n,v) \ \ \ \ g(v,v) \end{array} \right ],\) (2.10)
\(\left [\begin{array} {lccccl} \ g(v_1,v_1)\ .\ .\ .\ g(v_n,v_1)\ \ \ \ 0 \\ \ ...............................................\\ \ g(v_1,v_n) \ .\ . \ . \ g(v_n,v_n) \ \ \ \ 0\\ \ g(v_1,v)\ .\ .\ . \ \ g(v_n,v) \ \ \ \ \ \ d^2 \end{array} \right ],\) (2.11)
Wyznacznik pierwszej macierzy jest równy \({\rm G} ( v_1,...,v_n,v)\),
zaś wyznacznik drugiej macierzy jest równy \(d^2 {\rm G} (v_1,...,v_n)\). Dowód twierdzenia jest zakończony.
Z powyższego twierdzenia wynika natychmiast następujący
Wniosek 2.3
Miara układu wektorów nie zależy od uporządkowania wektorów tworzących układ.
Ponadto udowodniliśmy następujący wzór
Twierdzenie 2.4
Dla dowolnych wektorów \(v_1,...v_n,v\) zachodzi wzór
\({\rm G} (v_1,...,v_n,v)=d^2 G(v_1,...,v_n),\) (2.12)
gdzie liczba \(d=d(v,U)\) zdefiniowana jest formułą
(2.4) i \(U={\rm lin} \{v_1,...,v_n\}\).
Miara dowolnego ortonormalnego układu wektorów jest równa 1. Wynika to łatwo zarówno z definicji jak i z formuły (2.5). Innymi słowy, objętość kostki rozpiętej na układzie ortonormalnym jest równa 1.
Niech \(f\) będzie endomorfizmem przestrzeni euklidesowej \(V\). Załóżmy, że \(V\) jest skończenie wymiarowa. Ustalmy pewną bazę ortonormalną \(e_1,...,e_n\). Miara układu wektorów \((e_1,...,e_n)\) jest równa 1. Jeśli \(f\) jest endomorfizmem przestrzeni \(V\), to \(f\) przeprowadza daną bazę w układ \(f(e_1),...,f(e_n)\). Kolumny macierzy \(A\) odwzorowania \(f\) przy bazie \(e_1,...,e_n\) są współrzędnymi wektorów \(f(e_1),...,f(e_n)\) w bazie \(e_1,..., e_n\). A zatem, na podstawie Twierdzenia 1.2 i Twierdzenia 2.2, otrzymujemy
Wniosek 2.5
Miara wektorów \(f(e_1),...,f(e_n)\) jest równa mierze bazy \(e_1,..., e_n\) wtedy i tylko wtedy, gdy \({\rm det} f=\pm 1\).
O endomorfizmie \(f\) mówimy, że zachowuje objętość, jeśli jego wyznacznik jest równy \(\pm 1\). Oczywiście izometrie maja tę własność, ale odwzorowań zachowujących objętość jest o wiele więcej. Każdy automorfizm pomnożony przez odpowiedni skalar jest odwzorowaniem zachowującym objętość. Endomorfizm, którego wyznacznik jest równy 1 nazywa się endomorfizmem unimodularnym.
Ogół macierzy kwadratowych o wymiarach \(n\) na \(n\), których wyznacznik równy jest 1 jest podgrupą grupy \(GL(n;{\mathbb R} )\). Grupę tę oznacza się \(SL (n;\mathbb R)\) i nazywa się grupą specjalną. Elementy tej grupy nazywa się macierzami unimodularnymi.