Przestrzenie afiniczne II
Podprzestrzenie afiniczne
Niech \(V_0\) będzie podprzestrzenią przestrzeni \(V\), zaś \(X_0\) - niepustym podzbiorem \(X\). Mówimy, że \(X_0\) jest podprzestrzenią \(X\) o kierunku \(V_0\), jeśli spełnione są dwa następujące warunki:
- PA 1) \(\overrightarrow {xy}\in V_0\) dla każdych \(x,y\in X_0\).
- PA 2) \(x+v\in X_0\) dla każdych \(x\in X_0\) i \(v\in V_0\).
Jest oczywiste, że jeśli spełnione są te warunki, to \((X_0,V_0)\) z operacjami zaczepiania wektora w punkcie i wyznaczania wektora przez parę punktów zawężonymi z przestrzeni \((X,V)\) jest przestrzenią afiniczną.
Przykład 1.1
Podzbiór składający się z jednego (dowolnego) punktu przestrzeni \(X\) jest podprzestrzenią afiniczną o kierunku \(\{0\}\). Cała przestrzeń \(X\) jest podprzestrzenią o kierunku \(V\).

Przykład 1.2
Niech \(x_0\in X\) i \(V_0\) będzie podprzestrzenią wektorową \(V\). Rozważmy zbiór
\(x_0+ V_0=\{ x_0+v\,|\, v\in V_0\}.\) (1.1)
Niech \(x=x_o+ v\), \(y=x_0+ w\), gdzie \(v,w\in V_0\). Z Twierdzenia 1.1 wiemy, że
Podobnie, jeśli \(x_0 +v\), gdzie \(v\in V_0\), to
dla \(w\in V_0\). A zatem zbiór zdefiniowany przez(1.1)
jest podprzestrzenią afiniczną o kierunku \(V_0\).
Przypomnijmy sobie, że zbiór rozwiązań układu równań liniowych jest właśnie postaci (1.1). A zatem mamy twierdzenie.
Twierdzenie 1.3
Jeśli układ równań liniowych ma rozwiązanie, to zbiór wszystkich rozwiązań tego układu jest podprzestrzenią afiniczną przestrzeni \({\mathbb K} ^n\) o kierunku będącym przestrzenią rozwiązań odpowiadającego układu jednorodnego.
W szczególności podprzestrzeń dana jednym równaniem, tzn. równaniem
\(a_0+a_1x_1+...+a_nx_n=0\) (1.2)
jest \((n-1)\) wymiarową podprzestrzenią \({\mathbb K} ^n\) (lub dowolnej \(n\)-wymiarowej przestrzeni afinicznej \(X\) z wprowadzonym okładem współrzędnych), o ile któryś ze skalarów \(a_1,..., a_n\) jest różny od zera. Podprzestrzeń \((n-1)\)-wymiarową nazywa się hiperpłaszczyzną. Równanie (1.2) nazywa się
równaniem ogólnym hiperpłaszczyzny.
Podprzestrzeń jednowymiarową nazywamy prostą afiniczną. Podprzestrzeń dwuwymiarową nazywamy płaszczyzną afiniczną.
Mamy następujący lemat.
Lemat 1.4
Jeśli \((X_0,V_0)\) oraz \((X_0,W_0)\) są podprzestrzeniami afinicznymi to \(V_0=W_0\).
Dowód
Niech \(x\in X_0\) i \(v\in V_0\). Wtedy \(x+v\in X_0\). Ponieważ \((X_0,W_0)\) jest podprzestrzenią afiniczną, więc \(v=\overrightarrow {x (x+v)}\in W_0\).
Dzięki temu lematowi wystarczy mówić " niech \(X_0\) będzie podprzestrzenią afiniczną", bo kierunek podprzestrzeni \(X_0\) jest wyznaczony jednoznacznie.
Zauważmy teraz, że każda podprzestrzeń afiniczna jest taka jak w (Przykładzie 1.2).

Twierdzenie 1.5
Niech \(X_0\) będzie podprzestrzenią afiniczną o kierunku \(V_0\). Dla dowolnego punktu \(x_0 \in X_0\) mamy
Dowód
Z definicji podprzestrzeni afinicznej wynika, że \(x_0+V_0\subset X_0\). Odwrotnie, jeżeli \(x\in X_0\), to \(\overrightarrow {x_0x}\in V_0\), a zatem \(x=x_0+\overrightarrow {x_0 x}\in x_0 +V_0\).
Kierunek dowolnej podprzestrzeni afinicznej \(X_0\) jest równy przestrzeni
\(\{ \overrightarrow {x_o x}\, |\, x\in X_0\},\) (1.3)
gdzie \(x_0\) jest dowolnie wybranym punktem przestrzeni \(X\), lub, co na jedno wychodzi, przestrzeni
\(\{\overrightarrow {xy}\, |\, x,y \in X_0\}.\) (1.4)
Załóżmy, że mamy dwie podprzestrzenie tej samej przestrzeni afinicznej \((X,V)\).
Mówimy, że podprzestrzeń afiniczna \((X_0, V_0)\) jest równoległa do podprzestrzeni \((X_1, V_1)\), jeśli \(V_0\subset V_1\). Podprzestrzenie \((X_0,V_0)\), \((X_1,V_1)\) są równoległe, jeśli \(V_0=V_1\).
Zachodzi następujące (zgodne z intuicją) twierdzenie.
Twierdzenie 1.6
Jeżeli podprzestrzeń \(X_0\) jest równoległa do \(X_1\), to albo \(X_0\subset X_1\), albo \(X_0\cap X_1=\emptyset\).
Dowód
Przypuśćmy, że \(X_0\cap X_1\ne\emptyset\). Niech \(x_0\in X_0\cap X_1\). Jeżeli \(V_0\), \(V_1\) sa kierunkami \(X_0\) i \(X_1\) odpowiednio, to \(X_0=x_0+V_0\) i \(X_1= x_0+V_1\). Wobec tego \(X_0\subset X_1\).
Twierdzenie 1.7
Niech \({X_t}_{\{t\in T\}}\) będzie dowolną rodziną podprzestrzeni przestrzeni \(X\). Jeśli \(\bigcap _{t\in T}X_t\ne \emptyset\), to \(\bigcap _{t\in T}X_t\) jest podprzestrzenią afiniczną \(X\).
Dowód
Niech \(V_t\) będzie kierunkiem \(X_t\) dla każdego \(t\in T\). Jeśli \(\displaystyle x_0\in \bigcap _{t\in T} X_t\), to
a więc
Zbiory wypukłe
Niech dane będą dwa różne punkty \(p\), \(q\) przestrzeni afinicznej \(X\) o kierunku będącym przestrzenią wektorową nad ciałem \({\mathbb R}\). Prosta przechodząca przez te punkty może być opisana jako zbiór wszystkich punktów postaci \(y=p+t\overrightarrow {pq}\), \(t\in {\mathbb R}\). Odcinkiem wyznaczonym przez te punkty nazywamy zbiór
Jeśli \(X\) jest przestrzenią wektorową (lub w przestrzeni
afinicznej ustalony jest punkt bazowy), to \(\overline {pq} = \{ (1-t)p+tq\ |\ t\in [0,1]\}\).
Zbiór \(A\subset X\) nazywamy wypukłym, jeśli dla każdej pary punktów \(p,q\in A\) odcinek \(\overline {pq}\) zawiera się w zbiorze \(A\).
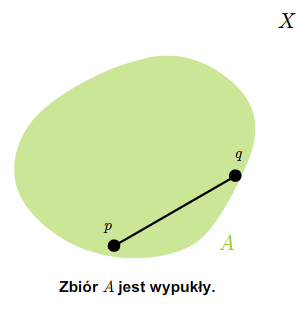
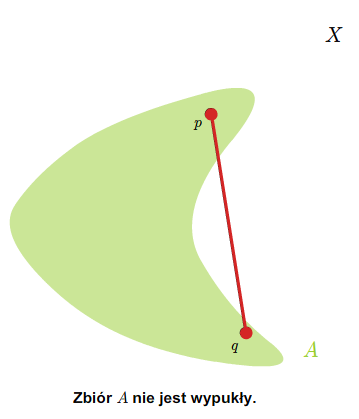
Oczywiste jest następujące twierdzenie
Twierdzenie 2.1
Przecięcie dowolnej rodziny zbiorów wypukłych jest zbiorem wypukłym.
Jeżeli \(A\) jest dowolnym podzbiorem przestrzeni \(X\), to przez \({\rm conv} A\) oznaczamy przecięcie wszystkich zbiorów wypukłych zawierających \(A\). Na mocy Twierdzenia 2.1 jest to zbiór wypukły o tej własności, że każdy zbiór wypukły zawierający \(A\) zawiera \({\rm conv} A\). Zbiór \({\rm conv} A\) nazywa się wypukłą otoczką zbioru \(A\).
Odwzorowania afiniczne
Niech \(V,W\) będą przestrzeniami wektorowymi nad ciałem \({\mathbb K}\) i niech \((X,V)\), \((Y,W)\) będą przestrzeniami afinicznymi. Odwzorowanie
nazywamy odwzorowaniem afinicznym, jeśli istnieje odwzorowanie liniowe
takie, że dla każdych \(x', x''\in X\) zachodzi równość
\(\overrightarrow {f(x')f(x'')}= \varphi (\overrightarrow {x'x''}).\) (3.5)
Warunek ten można zastąpić warunkiem równoważnym:
\(f(x+v) =f(x)+\varphi (v)\) (3.6)
dla każdych \(x\in X\) i \(v\in V\).
Mówimy, że \(\varphi\) jest odwzorowaniem liniowym indukowanym przez odwzorowanie afiniczne \(f\).
Odwzorowanie indukowane jest dla danego odwzorowania afinicznego jedyne. Mamy mianowicie
Lemat 3.1
Jeżeli \(f\) jest odwzorowaniem afinicznym indukującym odwzorowania liniowe \(\varphi _1\) i \(\varphi _2\), to \(\varphi _1=\varphi _2\).
Dowód
Niech \(v\in V\) i \(x\in X\). Zachodzą równości
Dowód następującego twierdzenia jest standardowy
Twierdzenie 3.2
Złóżenie odwzorowań afinicznych jest odwzorowaniem afinicznym. Jeśli odwzorowanie afiniczne jest bijekcją, to odwzorowanie odwrotne jest afiniczne.
Obraz podprzestrzeni afinicznej przez odwzorowanie afiniczne jest podprzestrzenią afiniczną.
Przeciwobraz podprzestrzeni afinicznej przez odwzorowanie afiniczne jest podprzestrzenią afiniczną.
Przykład 3.3
Odwzorowanie identycznościowe przestrzeni afinicznej \(X\) jest odwzorowaniem afinicznym indukującym odwzorowanie identycznościowe.
Przykład 3.4
Odwzorowanie stałe, tzn. \(f:X\ni x\longrightarrow y_0\in Y\), gdzie \(y_0\) jest ustalonym punktem przestrzeni \(Y\), jest odwzorowaniem afinicznym indukującym odwzorowanie zerowe. Przypomnijmy, że jedynym odwzorowaniem liniowym stałym jest odwzorowanie zerowe.
Przykład 3.5
Odwzorowanie liniowe przestrzeni wektorowej jest odwzorowaniem afinicznym indukującym samo siebie.
Przykład 3.6
Niech \(v\) będzie ustalonym wektorem przestrzeni wektorowej \(V\). Zdefiniujmy odwzorowanie
Odwzorowanie to nazywa się translacją (lub przesunięciem równoległym) o wektor \(v\). Odwzorowanie to jest odwzorowaniem afinicznym indukującym identyczność przestrzeni \(V\).
Dla dwóch wektorów \(v,w\in V\) zachodzi równość \(t_{v}\circ t_{w}= t_{v+w}\). W szczególności \(t_v\circ t_w= t_w\circ t_v\).
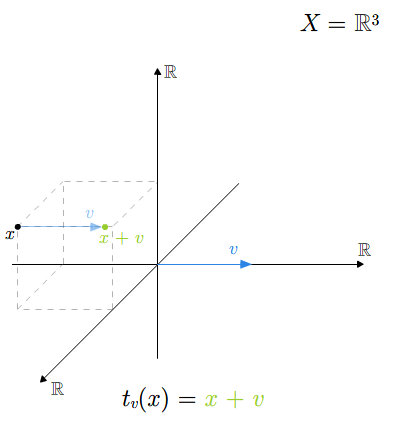
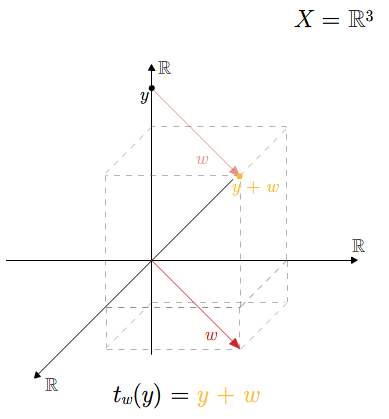
Niech \(f: X\longrightarrow Y\) będzie odwzorowaniem afinicznym
indukującym odwzorowanie liniowe \(\varphi : V\longrightarrow W\).
Załóżmy, że dane są punkty bazowe \({\rm o}\) w \(X\) i \({\rm o} '\) w \(Y\).
Niech \(w\in W\) będzie takim wektorem, że \(f({\rm o} )= {\rm o} '+ w\). Dla każdego \(x\in X\) zachodzi wzór
\(f(x) = {\rm o} ' + \varphi (\overrightarrow { ox } )+w.\) (3.7)
Z formuły (3.7) wynika, że każde odwzorowanie afiniczne \(f: V\longrightarrow W\) przestrzeni wektorowych jest złożeniem odwzorowania liniowego i translacji w przestrzeni \(W\).
Taka sama konkluzja dotyczy sytuacji, gdy przestrzenie afiniczne wyposażymy w strukturę przestrzeni liniowych przez wybranie punktów bazowych.
Odwzorowanie afiniczne, tak jak i odwzorowanie liniowe, ma przedstawienie macierzowe. Niech \(({\rm o} ; e_1,...,e_n)\) będzie układem bazowym w \((X,V)\) zaś \(({\rm o} ' ; e'_1,...,e'_m )\) układem bazowym w \((Y,W)\).
Niech \(A\) będzie macierzą \(\varphi\) przy danych bazach przestrzeni \(V\) i \(W\).
Załóżmy, że punkt \(x\) ma współrzędne \((x_1,...,x_n)\), wektor \(w\) ma współrzędne \((w_1,...,w_m)\), zaś punkt \(y=f(x)\) współrzędne \((y_1,...,y_m)\).
Macierzą odwzorowania afinicznego \(f\) nazywamy macierz
\(\left [\begin{array} {lccccr} \ \ \ \ \ \ \ \ \ \ \ \ w_1\\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ A \ \ \ \ \ \ \ . \\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ \ \ \ \ \ \ \ \, \ w_m\\ \ 0\ \ ...\ \ 0 \ \ \ 1 \end{array} \right ]\) (3.8)
lub w skrócie
\(\left [\begin{array} {lccccr} \ \ A \ \ w \\ \ \ 0\ \ 1 \end{array} \right ]\) (3.9)
Posługując się formułami rachunku macierzowego, otrzymujemy równość
\(\left [\begin{array} {lccccr} \ \ \ \ \ \ \ \ \ \ \ \ w_1\\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ A \ \ \ \ \ \ \ . \\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ \ \ \ \ \ \ \ \, \ w_m\\ \ 0\ \ ...\ \ 0 \ \ \ 1 \end{array} \right ] \left [\begin{array} {l} \ x_1 \\ \ .\\ \ .\\ \ .\\ \ x_n\\ \ 1 \end{array} \right ]= \left [\begin{array} {l}\ y_1 \\ \ .\\ \ .\\ \ .\\ \ y_m\\ \ 1 \end{array} \right ].\) (3.10)
Macierz \(A\) nazywamy częścią liniową macierzy afinicznej
(3.9), zaś wektor \(w\) jej częścią translacyjną. Przy tak ustalonej metodzie zapisu macierzy odwzorowań afinicznych stosują się odpowiednie reguły rachunku macierzowego.
Na przykład, złożeniu odwzorowań afinicznych odpowiada iloczyn ich macierzy
\(\left [ \begin{array} {lr} \ \ \ A\ \ w\\ \ \ \ 0\ \ \ 1 \end{array} \right ] \left [\begin{array} {lr} \ \ \ B\ \ v\\ \ \ \ 0\ \ \ 1 \end{array} \right ]= \left [\begin{array} {lr} \ \ \ AB\ \ A(v)+w\\ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ 1\ \ \ \ \end{array} \right ].\) (3.11)