Wykorzystanie kryptografii

Wykorzystanie kryptografii

Bieżący moduł przedstawia koncepcje związane z wykorzystaniem mechanizmów kryptograficznych w systemach informatycznych.

Potwierdzanie autentyczności danych

Szyfrowanie asymetryczne, jak już wiemy z poprzedniego modułu, można wykorzystać do osiągnięcia własności autentyczności danych. Zastosować można potencjalnie 2 metody przedstawione poniżej.

Metoda 1:

• szyfrujemy całą wiadomość kluczem prywatnym nadawcy
• kosztowne obliczeniowo - koszt rośnie z wielkością wiadomości

Metoda 2:

• tworzymy skrót wiadomości o ustalonym z góry rozmiarze n
• szyfrujemy kluczem prywatnym nadawcy tylko skrót
• koszt mały - n małe
• koszt stały - nie rośnie z wielkością wiadomości i zależy tylko od n

Druga metoda wykorzystuje pojęcie skrótu, który jest wynikiem zastosowania pewnej funkcji matematycznej na treści wiadomości. Funkcja skrótu to jednokierunkowa funkcja \(h[M]\), a więc taka, która daje jednoznaczny wynik \(d=h[M]\) (skrót, ang. message digest, fingerprint) o stałym rozmiarze, przy wieloznacznym argumencie (M). Jej zadaniem w naszym przypadku jest dostarczyć odbiorcy narzędzia do zweryfikowania czy treść wiadomości nie została zmodyfikowana, przez osoby niepowołane.
W istocie, w dziedzinie transmisji danych skróty wiadomości, lub ich odpowiedniki, powszechnie wykorzystywane są w celu potwierdzania integralności wiadomości od lat 70-tych ubiegłego wieku, choć zwykle ukrywają się pod różnymi nazwami:

• suma kontrolna (checksum) - negatywne potwierdzenia, retransmisje
• funkcja kontrolna (data integrity check)
• funkcja kontrolna wiadomości (message integrity check)
• funkcja ściągająca (contraction function)
• kod uwierzytelniający informacji (data authentication code)

Własności jakie musi posiadać odpowiednia dla nas funkcja skrótu to:

• kompresja: oznaczająca, że rozmiar skrótu musi być mniejszy od rozmiaru samej wiadomości \(|d|<|M|\)
• łatwość obliczeń: czas wielomianowy wyznaczenia \(h[M]\) dla dowolnego \(M\)
• odporność na podmianę argumentu: dla danego \(h[M]\) obliczeniowo trudne znalezienie \(M^\prime\) takiego, że \(h[M] = h[M^\prime]\)
• odporności na kolizje: obliczeniowo trudne znalezienie dwóch dowolnych argumentów \(M \neq M^\prime\) takiego, że \(h[M] = h[M^\prime]\)

Zastosowania funkcji skrótu mogą obejmować:

• zapewnienie integralności wiadomości bez klucza kryptograficznego
• zapewnienie integralności oraz autentyczności wiadomości: MAC - message authentication code (z kluczem kryptograficznym)

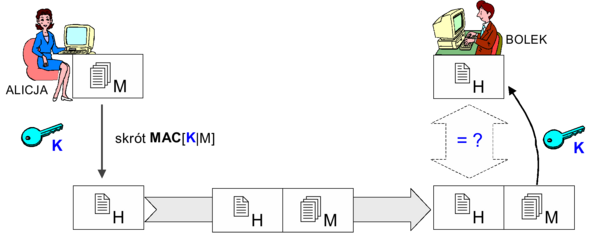
Rysunek '1'. Zastosowanie funkcji skrótu

Podpis cyfrowy

Funkcje skrótu można wykorzystać do zrealizowania ciekawego i niezwykle ważnego narzędzia, jakim jest podpis cyfrowy. Najczęściej wykorzystywana jest w tym celu jest funkcja mieszająca HMAC z kluczem k asymetrycznym (keying hash function) - \(h_k[M]\). Wartość skrótu HMAC jest zaszyfrowana kluczem prywatnym nadawcy, być może dodatkowo z wykorzystaniem ziarna (salt) lub zawołania (challenge).
Proces generowania i weryfikowania podpisu HMAC z kluczem przedstawia rysunek 2. Nadawca (Alicja) po przygotowaniu wiadomości M przygotowuje jej skrót H, który poddaje szyfrowaniu swoim kluczem prywatnym, który z założenia zna i posiada tylko nadawca. Po połączeniu M z zaszyfrowanym skrótem H' całość przekazuje do odbiorcy dowolnym kanałem komunikacyjnym. Tan następuje deszyfracja H' (przy użyciu otwarcie dostępnego klucza publicznego nadawcy) oraz niezależne wyliczenie skrótu H dla otrzymanego M. Porównanie H wyliczonego z odszyfrowanym wskazuje na autentyczność i nienaruszalność wiadomości M lub jej brak. Gdyby M została zmodyfikowana w trakcie transmisji do odbiorcy, wyliczony skrót nie pasowałby do odszyfrowanego z H'. Natomiast, gdyby nadawcą nie była Alicja, posłużenie się jej kluczem publicznym przy odszyfrowaniu H' nie dałoby skrótu identycznego z wyliczony przez odbiorcę H.

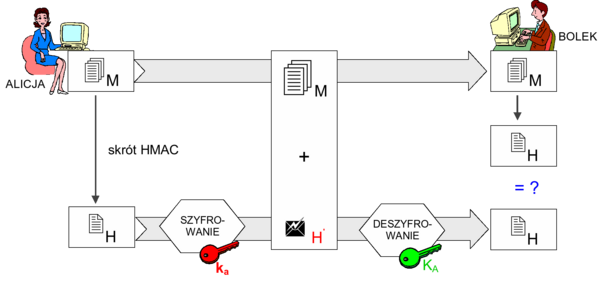
Rysunek '2'. Zastosowanie funkcji skrótu

Osiąganie poufności, autentyczności i nienaruszalności danych

Możliwe jest jednoczesne osiągnięcie własności poufności, autentyczności i nienaruszalności wiadomości. Uzyskuje się to poprzez znane już szyfrowanie (np. asymetryczne) pary M + H' z poprzedniego przykładu, przed przesłaniem do odbiorcy. Przy tym szyfrowaniu musi oczywiście być wykorzystany odpowiedni klucz publiczny odbiorcy. Schemat ten przedstawia rysunek 3.

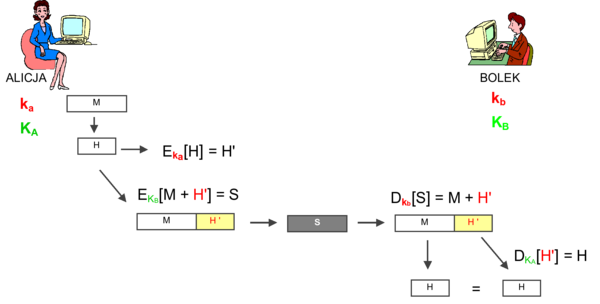
Rysunek '3'. Osiąganie poufności, autentyczności i nienaruszalności

Algorytmy skrótu

Pierwsze z powszechnie stosowanych algorytmów generowania skrótu na potrzeby ochrony autentyczności i nienaruszalności informacji - MD i MD2 (autorstwa Rona Rivesta) powstały w latach '80. Algorytm MD nie został nigdy oficjalnie opublikowany. Był wykorzystywany jako autorskie rozwiązanie w systemie pocztowym RSADSI. Natomiast MD2 został ustandaryzowany w dokumencie RFC 1319. W 1990 Ralph Merkle (Xerox) zaproponował algorytm HMAC o nazwie SNEFRU - kilkukrotnie szybszy od MD2. Na to Rivest odpowiedział algorytmem MD4 (RFC 1320). WWwww W roku 1992 złamano SNEFRU i wykryto pewną słabość MD4 w wersji 2-rund i wkrótce Rivest wzmocnił algorytm otrzymując trochę wolniejszy MD5 (RFC1321).

Algorytm MD5

Algorytm MD5 posiada następujące cechy charakterystyczne:

• wykorzystuje 128b wektor IV
• wykonuje 64 iteracje (4 rundy po 16 kroków)
• daje skrót 128b
• teoretyczna odporność na kolizje 2⁶⁴ jest współcześnie uznawana za zbyt słabą

Algorytm SHA (Secure Hash Algorithm)

Algorytm SHA został opracowany przez NSA (National Security Agency) i przyjęty przez NIST jako standard federalny w 1993r. Wersja oryginalna SHA (SHA-0) jest zbliżona do MD4. Algorytm ten posiada następujące cechy charakterystyczne:

• przekształca wiadomość o długości do 2⁶⁴b w skrót 160b
• wykorzystuje 160b wektor IV
• wykonuje 80 iteracji (4 rundy po 20 kroków)

Stosunkowo szybko wykryto słabości SHA-0 (choć ich natury nigdy nie opublikowano) i opracowano SHA-1 (ratyfikowany przez NIST), który jest często spotykany do dziś. Wykazuje odporność na kolizje 160b skrótu - 2⁸⁰ , która jest współcześnie uznawana również za zbyt słabą.

Algorytmy SHA-256 / SHA-384 / SHA-512

Niedawno zaproponowano zupełnie nowe funkcje skrótu: SHA-256, SHA-384 oraz SHA-512, przystosowane do współpracy z kluczami AES (odpowiednio 128b, 192b i 256b). Dają skróty odpowiednio 256b, 384b i 512b. Nie doczekały się jeszcze szerszej analizy jednak dość powszechnie uznawane są za bezpieczne. Mają większą złożoność obliczeniową od poprzedników wymienionych wyżej. W praktyce okazuje się, iż algorytm SHA-384 ma identyczny koszt obliczeniowy co SHA-512, co czyni SHA-384 w praktyce bezużytecznym. Powszechnie spotykane są zatem jedynie SHA-256 oraz SHA-512.

Algorytm RIPE-MD

Algorytm ten powstał w ramach europejskiego (EU) projektu RACE Integrity Primitives Evaluation - Message Digest. W uproszczeniu mówiąc jest to ulepszony wariant MD4 (zmodyfikowane rotacje i kolejność słów wiadomości) Oferuje skrót 128b. Wykorzystuje rejestr strumieniowy. Podczas generowania skrótu wykonuje równoległe 2 przebiegi (za każdym razem z innym zadanym parametrem) w każdej iteracji. Po każdej iteracji oba wyniki łączone z rejestrem strumieniowym. Prawdopodobnie posiada dużą odporność na ataki.

Algorytm HAVAL

Algorytm HAVAL generuje skrót o zmiennej długości: 128b, 160b, 192b, 224b lub 256b. Można i jego uznać za wariant MD4, względem oryginału zmodyfikowano operacje rotacji. Stosuje wyrafinowane funkcje nieliniowe (o własności lawinowości), w każdej iteracji wykonuje inne permutacje. I posiada prawdopodobnie duża odporność na ataki.

Algorytm ElGamal

Ostatnim z wymienionych algorytmów jest ElGamal. Algorytm ten początkowo opracowano właśnie dla realizacji podpisu cyfrowego HMAC. Podpisem wiadomości M jest para (a, b), taka że:
\(a=g^k \bmod p\)
\(b:: M = (xa + kb) \bmod p-1\)
Weryfikacja podpisu cyfrowego następuje pomyślnie jeśli \((y^a a^b) \bmod p == g^M \bmod p\).

Standardy podpisu cyfrowego

W systemach informatycznych powszechnie spotykane są standardy podpisu cyfrowego opracowane w USA. Należą do nich starszy DSS i nowszy SHS

Standard DSS (Digital Signature Standard)

DSS jest to standard NIST z kategorii FIST (Federal Information processing STandard) w wersjach z 1991 i 1993 roku. Obejmuje użycie skrótu SHA-1 oraz algorytmu DSA (Digital Signature Algorithm).

Standard SHS (Secure Hash Standard)

Standard SHS to nowszy projekt NIST z 2001. Obejmuje użycie rodziny SHA-256 / SHA-384 / SHA-512.

Ataki na funkcje skrótu

Najpowszechniej znanym atakiem na funkcje skrótu jest atak urodzinowy. Poniżej przedstawiona zostanie koncepcja tego ataku.

Atak urodzinowy

Paradoks dnia urodzin po lega na dokonaniu następujących obserwacji:

Obserwacja 1:

• pytanie: ile osób potrzeba na tej sali, aby z prawdopodobieństwem 50% znalazła się wśród nich taka, która obchodzi urodziny tego samego dnia co autor tych slajdów? (funkcja mieszająca odwzorowuje zbiór ludzi na 365 lub 366 dni roku)
• odpowiedź: oczywiście 183.

Obserwacja 2:

• pytanie: a ile potrzeba osób, aby wśród nich znalazły się 2 obchodzące urodziny tego samego dnia?
• odpowiedź: tylko 23.

Uogólnienie tego paradoksu przebiega następująco. Mamy dany rozmiar n danych wejściowych (ludzi - w przykładzie urodzin) oraz rozmiar k zbioru wynikowego (daty urodzin). Dla n mamy możliwych n(n-1)/2 par danych wejściowych i dla każdej pary oba elementy dadzą ten sam wynik z prawdopodobieństwem 1/k. Zatem, potrzeba k/2 par aby z prawdopodobieństwem 50% wśród nich była taka jak szukamy - gdzie oba elementy mają tę samą wartość wyniku (datę urodzin). W efekcie jeśli \(n>\sqrt{k}\) to szanse powodzenia są duże. Dla skrótu 128b potrzeba 2¹²⁸ wiadomości aby znaleźć tę, która dała określony skrót, ale wystarczy 2⁶⁴ wiadomości aby znaleźć 2 o identycznym skrócie (znaleźć tzw. kolizję).
Jako komentarz można podać, iż w połowie 2004 r. zespół kryptoanalityków pod kierunkiem Xuejia Lai wykazał zaskakujące kolizje w MD5 podając 2 ciągi po 128 B różniące się zaledwie 6-cioma bajtami. Natomiast na początku 2005 r. zespół kierowany przez Xiaoyuna Wanga wykazał w rodzinie SHA kolizje łatwiejsze niż należy oczekiwać z teoretycznej odporności. Mianowicie w przypadku SHA-1: kolizje dla 2⁶⁹ operacji (przy teoretycznej 2⁸⁰), dla SHA-1 w uproszczonej wersji (58-rund): kolizje dla 2³³ operacji i dla SHA-0: kolizje dla 2³⁹ operacji.

Zarządzanie kluczami

W procesie pozyskiwania i wykorzystania kluczy kryptograficznych występują pewne istotne problemy. Należą do nich poniższe:

problem przekazania klucza

• jak partnerowi komunikacji przekazać w sposób bezpieczny klucz niezbędny do szyfrowania / deszyfrowania?

problem zmiany klucza

• jak go regularnie zmieniać?

problem doboru systemu szyfrowania

• czy wybrać tajny klucz symetryczny? - występuje w tym przypadku, jak pamiętamy, problem skalowalności: 10 osób = 45 kluczy, 100 osób = 4950 kluczy
• czy raczej wybrać publiczny klucz asymetryczny? - tu występuje problem autentyczności skąd pewność jego prawdziwości

Nie istnieje uniwersalne rozwiązanie wszystkich wymienionych problemów, jednak poniżej przedstawiona metoda zaproponowana przez Whitfielda Diffiego i Martina Hellmana jest częściowym rozwiązaniem problemu przekazania klucza. Jest to metoda ciekawa i powszechnie spotykana, dlatego warta bliższego poznania.

Metoda Diffiego-Hellmana (DH)

Metoda Diffiego-Hellmana pozwala partnerom uzgodnić tajny klucz bez ryzyka ujawnienia go podsłuchującym. Początkowo ustalamy wspólny jednorazowy symetryczny klucz sesji (dla każdej sesji inny). Na potrzeby ustalenia klucza sesji wykorzystamy model asymetryczny.
DH wykorzystuje multiplikatywną grupę modulo p - oznaczaną \(\mathbb{Z}_p^*\).
Przez \(\alpha\\) oznaczmy element pierwotny grupy \(\mathbb{Z}_p^*\). Zatem \(\alpha\\) generujące całą grupę.
Czyli zamiast 1, ..., p-1 możemy grupę traktować jako 1, \(\alpha\, \alpha^2, ... , \alpha^{p-2}\).
Schemat postępowania w metodzie DH przedstawia rysunek 4.
Każdy z użytkowników wybiera sobie w nieistotny sposób wartość klucza prywatnego k. Natomiast klucz publiczny K dobiera jako \(\alpha^k\). Klucz ten jest swobodnie i otwarcie przykazywany drugiej stronie komunikacji.
Klucz sesji dobierany jest przez każdą ze stron w taki sposób, że obie uzyskują identyczną wartość \(\Phi\\), przy czym przechwycenie obu transmitowanych kluczy publicznych nie wystarcza do jego uzyskania.

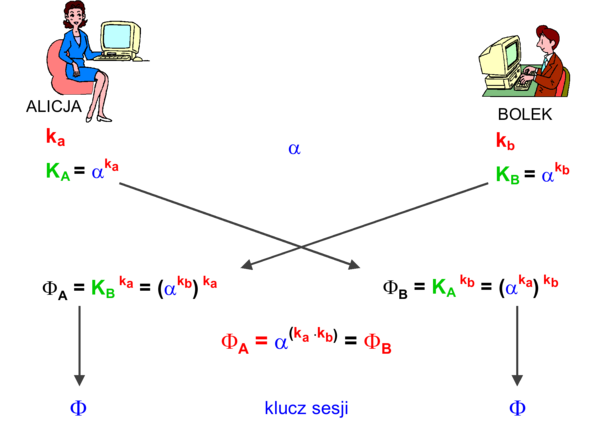
Rysunek '4'. Schemat postępowania w metodzie DH
Metoda D-H nie jest, jak już zaznaczono, idealnym rozwiązaniem. Jest m.in. podatna n atak man-in-the-middle. Przyjmijmy, iż Edziu, znając \(\alpha\\), może skutecznie wkroczyć na etapie negocjacji klucza. Alicja i Bolek będą porozumiewać się poprzez Edzia za pomocą kluczy,
które - jak im się będzie wydawać - wymienili ze sobą.

Dystrybucja kluczy publicznych

Rozważmy możliwe sposoby pozyskiwania kluczy publicznych szyfrowania asymetrycznego. Istnieją następujące warianty:

1. pobranie klucza bezpośrednio od właściciela
2. pobranie klucza z centralnej bazy danych
3. pobranie z własnej prywatnej bazy danych zapamiętanego wcześniej klucza pozyskanego sposobem 1 lub 2

Należy zwrócić uwagę, iż w ogólności istnieje ryzyko podstawienia przez nieuczciwą osobę (atakującego) własnego klucza pod klucz domniemanego użytkownika.
Rozwiązaniem tego problemu, które zyskało dotychczas największą akceptację jest certyfikacja kluczy publicznych.

Certyfikacja

Certyfikację stosuje się w celu uniknięcia podstawienia fałszywego klucza publicznego. Certyfikat jest poświadczeniem autentyczności podpisanym przez osobę (instytucję) godną zaufania, nazywaną urzędem poświadczającym CA (Certification Authority). certyfikat ma najczęściej formę dokumentu elektronicznego. Certyfikat zawiera podstawowe dane identyfikujące właściciela. W ogólnym przypadku, urząd poświadczający CA potwierdza, iż informacja opisująca właściciela klucza jest prawdziwa, a klucz publiczny faktycznie do niego należy. Certyfikat posiada też okres ważności wyznaczający czas przez który certyfikowane dane można uważać za poprawne. Niezależnie od okresu ważności certyfikowane klucze mogą zostać uznane za niepoprawne, np. gdy zaistnieje podejrzenie, iż ktoś nieuprawniony wszedł w posiadanie tajnego klucza prywatnego, odpowiadającego certyfikowanemu kluczowi publicznemu. Urząd poświadczający CA musi przechowywać listę niepoprawnych i nieaktualnych certyfikatów. Oczywiście, unieważnienie klucza jest także rodzajem certyfikatu.
Struktura podstawowa typowego certyfikatu jest przedstawiona na rysunku 5. Oprócz wymienionych tam pól poszczególne certyfikaty mogą zawierać dodatkowe, specyficzne dla konkretnego urzędu CA lub zastosowań, do których certyfikaty są przeznaczone. Przykłady rzeczywistych certyfikatów możemy znaleźć w każdej przeglądarce internetowej.
Jednym z najpopularniejszych współcześnie rodzajów certyfikatów są te zgodne ze standardem ITU-T X.509. Budowa certyfikatu X.509 v.3 obejmuje szereg elementów. Należą do nich:

• struktura podstawowa uzupełniona o zestaw danych identyfikacyjnych podmiotu certyfikatu
• sposób wykorzystania klucza (przeznaczenie, np. do szyfrowania danych, do szyfrowania kluczy, do uzgadniania kluczy, do podpisywania danych, do osiągnięcia niezaprzeczalności)
• informacje o polityce certyfikacji wydawcy certyfikatu (np. ograniczenia długości ścieżki certyfikacji, punkty dystrybucji list certyfikatów unieważnionych).

Ponadto istnieje opcjonalna możliwość tworzenia dodatkowych pól / parametrów identyfikacyjnych, wg potrzeb komunikujących się podmiotów.

Rysunek '5'. Schematyczna struktura typowego certyfikatu
Dystrybucja kluczy przy wykorzystaniu certyfikatów przebiega następująco:

• w celu uzyskania certyfikatu użytkownik zwraca się do urzędu certyfikującego CA dostarczając mu swój klucz publiczny
• do zweryfikowania certyfikatu niezbędny jest tylko i wyłącznie klucz publiczny urzędu certyfikującego
• alternatywnie użytkownik może przesłać swój certyfikat do innych użytkowników z prośbą o poświadczenie jego autentyczności.

W tym ostatnim przypadku mówimy o systemie wzajemnej certyfikacji (sieci wzajemnego zaufania, ang. web of trust). Certyfikat użytkownika, dajmy na to - Alicji, poświadcza (podpisuje) z reguły kilko (kilkunastu) użytkowników. Jeśli po pobraniu przez Bolka, stwierdza on, że wśród podpisów znajdują się jakieś należące do zaufanych mu osób, uznaje on certyfikat za poświadczony.
Zarówno rozwiązania instytucjonalne z urzędami certyfikującymi, jaki i system wzajemnego zaufania mają swoich zwolenników.
W każdym przypadku istnieje dylemat, komu na tyle zaufać, aby mógł być on w pełni wiarygodny i poświadczać (wydawać) certyfikaty? Problem ten dotyczy przede wszystkim pierwszego kontaktu, zwłaszcza w relatywnie anonimowej sieci globalnej Internet, gdzie wzajemne kontakty, „w cztery oczy", nie są raczej najbardziej typowym sposobem komunikacji. Skąd zatem pewność, że certyfikat został pobrany z właściwego urzędu, czy że podpisy poświadczające jego autentyczność rzeczywiście są godne zaufania. ile może istnieć instytucji cieszących takim zaufaniem, iż certyfikaty przez nie podpisane możemy śmiało uznawać za rzetelnie zweryfikowane i autentyczne.
Rozwiązaniem tego problemu jest system, w którym certyfikat musi przebyć pewną kilkuetapową procedurę uwierzytelniającą, a urzędy CA mogą tworzyć wielopoziomową hierarchię. Urzędy danego poziomu hierarchii wystawiają certyfikaty kluczy publicznych urzędom lub użytkownikom znajdującym się na niższym poziomie. Na szczycie znajduje jeden z nielicznych urzędów centralnych, który swym powszechnie uznanym autorytetem ostatecznie poświadcza poprawność całej procedury uwierzytelniającej certyfikat.

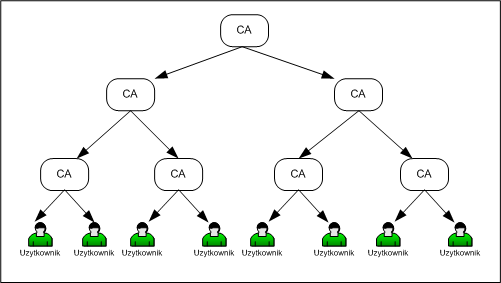
Rysunek '6'. Hierarchia urzędów poświadczających
Taka hierarchia urzędów poświadczających jest podstawą funkcjonowania niezwykle ważnego współcześnie mechanizmu informatycznego - infrastruktury kluczy publicznych - PKI (Public Key Infrastructure). Infrastruktura kluczy publicznych obejmuje sprzęt, oprogramowanie, ludzi, polityki bezpieczeństwa i procedury konieczne do utworzenia, zarządzania, przechowywania, dystrybucji i unieważniania certyfikatów kluczy publicznych w skali najczęściej ogólnonarodowej lub światowej. PKI oferuje często dodatkowe certyfikaty, np. Certyfikaty Znacznika Czasu (dla wiarygodnego potwierdzania czasu). W sieci Internet, PKI wykorzystuje specyfikację X.509 (PKIX, RFC 2459).
PKI jest hierarchicznym systemem urzędów certyfikujących oferujących publicznie swoje usługi. Do usług tych należy między innymi:

• weryfikacja tożsamości użytkowników ubiegających się o certyfikaty
• zarządzanie kluczami kryptograficznymi
  • generowanie par kluczy dla użytkowników
  • bezpieczne przechowywanie kluczy
• zarządzanie certyfikatami
  • wystawienie certyfikatów kluczy publicznych
  • generowanie list certyfikatów unieważnionych CRL (Certificate Revocation List)

Komponenty systemu PKI to:

• urzędy CA
• punkty rejestrujące, poręczające zgodność kluczy z identyfikatorami (lub innymi atrybutami) posiadaczy certyfikatów
• użytkownicy certyfikatów podpisujący cyfrowo dokumenty
• klienci weryfikujący podpisy cyfrowe i ścieżki certyfikacji do zaufanego CA
• repozytoria przechowujące i udostępniające certyfikaty i listy unieważnień.

Repozytoriami certyfikatów i list unieważnień mogą być np.:

• serwery LDAP
• respondery OCSP
• serwery WWW
• serwery FTP
• serwery DNS (DNSsec)
• agenci systemu katalogowego X.500 (DSA - Directory System Agents)
• korporacyjne bazy danych

Mimo wysokiej przydatności systemów PKI, nie wszystkie problemy związane z certyfikacją zostały w pełni rozwiązane. Pozostaje przykładowo problem jednoznacznej identyfikacji podmiotu - jaki jest adekwatny kompromis pomiędzy pełnymi danymi identyfikującymi a prywatnością podmiotu? Rozwiązanie tego problemu na ogół przybliża się wprowadzając różne klasy certyfikacji o różnym poziomie zaufania.
Inny problem to problem pierwszego certyfikatu - jak bezpiecznie certyfikować CA? Możliwym rozwiązaniem jest wzajemna certyfikacja różnych urzędów z PKI. Wielość hierarchicznych ośrodków certyfikacji umożliwia współpracę pomiędzy niezależnymi strukturami, również w zakresie wzajemnej certyfikacji. Innym powszechnie spotykanym rozwiązaniem są certyfikaty wybranych urzędów najwyższego poziomu hierarchii wbudowane na stałe w aplikacje (przeglądarki WWW, np. Netscape Navigator ma ponad 30 predefiniowanych certyfikatów urzędów CA). Wówczas, zakładając, iż integralność wersji binarnej aplikacji dystrybuowanej przez producenta nie została naruszona (co, notabene, można weryfikować również technikami kryptograficznymi), można przyjąć autentyczność kluczy publicznych zawartych w tych wbudowanych certyfikatach i bezpiecznie się nimi posługiwać do potwierdzania autentyczności urzędów niższego szczebla hierarchii.
Mechanizmem pobierania certyfikatów CA powszechnie uznanym za standardowy jest przekazywanie ich jako typ MIME application/x-x509-ca-cert. Z kolei do popularnych protokołów wymiany informacji niezbędnych do właściwego zarządzania infrastrukturą kluczy publicznych zaliczyć można CMP (Certificate Management Protocol) oraz SCVP (Simple Certificate Validation Protocol).
W myśl polskiego ustawodawstwa wyróżnia się dwa rodzaje certyfikatów:

Certyfikaty zwykłe (tzw. powszechne)

• obejmują takie zastosowania jak szyfrowanie danych, poczta, www, urządzenia sieciowe, oprogramowanie

Certyfikaty kwalifikowane:

• wywołują skutki prawne równoważne podpisowi własnoręcznemu
  (Ustawa z dn. 18.09.2001 o podpisie elektronicznym)
• przeznaczone dla osób fizycznych, wydawane na podstawie umowy i po (osobistej) weryfikacji tożsamości w Punkcie Rejestracji CA
• znajdują zastosowanie w każdym przypadku składania oświadczenia woli (również e‑faktury)
• nie służą do szyfrowania dokumentów

W naszym kraju istnieje wiele urzędów certyfikacji. Jedne z najstarszych to np.:

• Unizeto Certum www.certum.pl
• Signet www.signet.pl
• Sigillum www.sigillum.pl

Kryptograficzne zabezpieczenie danych

Współcześnie dostępna jest ogromna ilość aplikacji szyfrowania plików i całych katalogów (fragmentów systemu plików). Można tu wymienić np. moduł jądra Linux loop-AES (od wersji 2.4 jądra nosi nazwę cryptoloop). Oferuje on szyfrowanie całego systemu plików na poziomie jądra za pomocą urządzenia blokowego /dev/loop[1-8]. Przykładowe polecenie montowania zaszyfrowanego systemu plików pokazuje poniższa komenda powłoki systemu operacyjnego:

mount -t ext3 crypto.raw /mnt/crypto -oencryption=aes-256

Innym przykładem środowiska szyfrowania plików jest EncFS. Tworzy ono z wybranego katalogu wirtualny system plików w przestrzeni użytkownika, korzystając ze standardowego modułu jądra FUSE (Filesystem in USErspace). Przykładowe wywołanie operacji tego środowiska jest przedstawione poniżej:

encfs ~/.crypto.vfs ~/tajne_dane

Wykonanie tego polecenia za pierwszym razem powoduje utworzenie pliku .crypto.vfs z zaszyfrowanym systemem plików, na podstawie zawartości katalogu tajne_dane. Przy kolejnych wywołaniach następuje podmontowanie .crypto.vfs z do katalogu tajne_dane. Odmontowanie niepotrzebnego już katalogu tajne_dane przebiega standardowo:

fusermount -u ~/tajne_dane

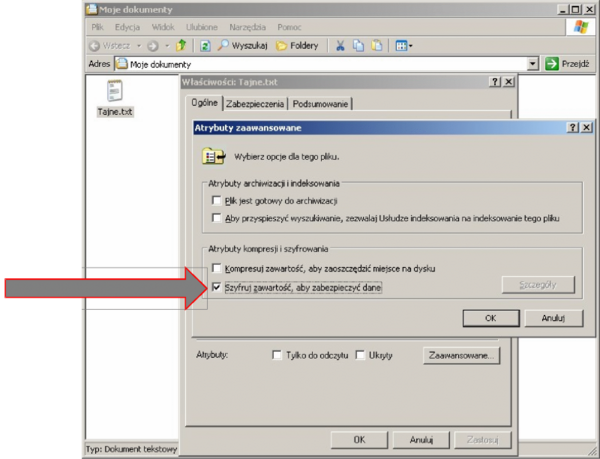
W systemie MS Windows z kolei zawarty jest moduł EFS (Encrypted File System), działający na partycjach NTFS od wersji Windows 2000. EFS działa jako usługa systemowa - przeźroczyście dla aplikacji użytkownika. Usługa ta wykorzystuje algorytm DESX, będący autorską odmianą 3DES firmy Microsoft. Przykład uaktywnienia funkcji szyfrowania pliku poprzez graficzny interfejs użytkownika pokazuje rysunek 7.
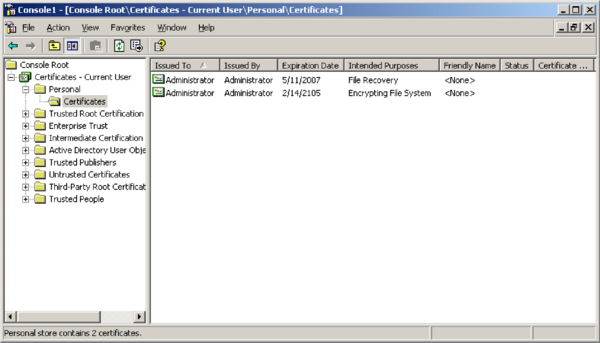
Występują dwa rodzaje kluczy EFS tworzonych automatycznie przy pierwszym uaktywnieniu usługi (rysunek 8):

• klucz właściciela pliku przechowywany w certyfikacie użytkownika (na rysunku należy do użytkownika Administrator)
• klucz uniwersalny usługi systemowej odtwarzania danych z kopii zapasowych - Data Recovery Agent (na rysunku również wystawiony przez i dla użytkownika Administrator, lecz nie jest dostępny ani dla niego, ani dla żadnego innego konta poza usługą Data Recovery Agent).

Rysunek '7'. Uaktywnienie funkcji szyfrowania pliku w MS Windows

Rysunek '8'. Uaktywnienie funkcji szyfrowania pliku w MS Windows
Ponadto istnieje wiele narzędzi kryptograficznego zabezpieczania komunikacji. Do najpopularniejszych rozwiązań należą protokoły komunikacyjne:

• SSH (Secure Shell)
• SSL (Secure Sockets Layer) i TLS (Transport Layer Security)
• PCT (Private Communication Technology)

oraz komponenty aplikacji użytkowych, takie jak:

• dla poczty elektronicznej: PGP, PEM, S/MIME, MIME/PGP, MSP
• dla usługi www: S-HTTP
• dla systemów e-commerce: SET (Secure Electronic Transactions).

Rozwiązania te i ich implementacje będą szerzej przedstawione w następnych modułach.

Zadania

1. Dlaczego nadal wykorzystywane są oba systemy kryptograficzne: symetryczny i asymetryczne? Inaczej mówiąc: dlaczego szyfrowanie asymetryczne, oferujące więcej własności bezpieczeństwa, nie wyparło całkowicie szyfrowania symetrycznego?
2. Rozważmy przypadek szczególny ataku man-in-the-middle na realizację metody D-H: co się stanie jeśli Edziu przechwytując komunikację pomiędzy Alicją i Bolkiem zastąpi \(K_A=\alpha^{ka}\) oraz \(K_B=\alpha^{kb}\) przez wartość 1?