Podstawowe elementy kryptografii

Mechanizmy kryptografii są powszechnie wykorzystywane w dziedzinie bezpieczeństwa systemów komputerowych. Stanowią bardzo uniwersalne narzędzie osiągania poufności, integralności czy autentyczności, są stosowane w procedurach uwierzytelniania, do ochrony danych składowanych i komunikacji sieciowej. Należą niewątpliwie do najważniejszych mechanizmów bezpieczeństwa.
Bieżący moduł przedstawia elementarne pojęcia dziedziny kryptografii i prezentuje podstawowe koncepcje algorytmów szyfracji. Celem dydaktycznym modułu jest wyrobienie intuicji działania popularnych technik kryptograficznych i ich własności. Kolejny moduł przedstawi podstawowe zastosowania mechanizmów kryptograficznych w informatyce.

Podstawowe pojęcia

Kryptografia jest dziedziną kryptologii - nauki operującej bardzo formalnym i relatywnie skomplikowanym aparatem matematycznym. Nie jest celem tego modułu przedstawienie tego aparatu, lecz jedynie przybliżenie istoty operacji szyfrowania i deszyfrowania. Wymaga to jednak minimalnej ilości jasno definiowanych terminów. Niniejszy rozdział przedstawia podstawowe pojęcia, które wykorzystywane będą w dalszej części modułu.
Kryptologia jest to wiedza naukowa obejmująca kryptografię i kryptoanalizę.
Kryptografia jest dziedziną obejmująca zagadnienia związane z utajnieniem danych (w kontekście przesyłania wiadomości i zabezpieczenia dostępu do informacji) przed niepożądanym dostępem. Przez utajnienie należy tu rozumieć taką operację, która powoduje że wiadomość jest trudna do odczytania (rozszyfrowania) przez podmiot nie znający tzw. klucza rozszyfrowującego - dla takiego podmiotu wiadomość będzie wyłącznie niezrozumiałym ciągiem wartości (znaków).
Kryptoanaliza natomiast to dziedzina kryptologii zajmująca się łamaniem szyfrów, czyli odczytywaniem zaszyfrowanych danych bez posiadania kluczy rozszyfrowujących.
Dane, które poddawane będą operacjom ochrony kryptograficznej nazywać tu będziemy po prostu tekstem jawnym lub wiadomością czytelną.
Kryptogramem (szyfrogramem) będziemy nazywali zaszyfrowaną postać wiadomości czytelnej.
Klucz szyfrowania to ciąg danych służących do szyfrowania wiadomości czytelnej w kryptogram za pomocą algorytmu szyfrowania. Klucz ten jest odpowiednio ustalany (uzgadniany) przez nadawcę w fazie szyfrowania.
Klucz rozszyfrowujący jest z kolei ciągiem danych służących do rozszyfrowania kryptogramu do postaci wiadomości czytelnej za pomocą algorytmu deszyfrowania. Naturalnie, klucz ten odpowiada w pewien sposób kluczowi szyfrowania wykorzystanemu w fazie szyfrowania.
W niektórych przypadkach będziemy mieli do czynienia z ciekawą własnością przemienności kluczy. Przemienność kluczy oznacza, że role dwóch kluczy z pary mogą ulec przestawieniu. Mianowicie informację zaszyfrowaną jednym kluczem można rozszyfrować tylko przy pomocy odpowiadającego mu drugiego klucza z pary, i odwrotnie, informację zaszyfrowaną drugim kluczem można rozszyfrować wyłącznie przy pomocy klucza pierwszego.

Proste szyfry

Teraz przejdziemy do zademonstrowania prostych operacji kryptograficznych, które wykorzystywane są również w bardzo skomplikowanych procesach szyfrowania i deszyfrowania. Świadomość ich funkcjonowania jest niezbędna dla zrozumienia istoty aktualnie wykorzystywanych algorytmów szyfrowania.

Szyfrowanie metodą podstawiania

Szyfrowanie metodą podstawiania jest prawdopodobnie najprostszą koncepcją utajniania informacji. Było już stosowane w czasach antycznych. Przykładem a przykład może u posłużyć szyfr wykorzystywany przez Juliusza Cezara do utajniania korespondencji wojskowej, nazywany na jego cześć szyfrem Cezara (notabene jest to jedno z pierwszych nazwisk związanych z kryptografią).
Działanie tej metody szyfrowania polega na wykonaniu na każdym znaku wiadomości czytelnej przekształcenia szyfrującego polegającego na zastąpieniu tego znaku innym o pozycji w alfabecie przesuniętej o zadaną ilość znaków względem znaku szyfrowanego. Przy czym pozostajemy wyłącznie w dziedzinie alfabetu wejściowego (przesunięcie pozycji jest w istocie rotacją - „zapętla się" po osiągnięciu końcowego znaku alfabetu na jego początek). Operację taką nazywa się z tego powodu monogramem.
Operację szyfrującą na znaku x możemy zatem zapisać formalnie jako \(f(x) = x + \Delta\), gdzie dodawanie oznacza zmianę (rotację!) pozycji znaku w alfabecie, a symbol \(\Delta\) oznacza wartość przesunięcia przy podstawianiu. Należy zaobserwować, iż w istocie zatem wartość \(\Delta\) jest kluczem szyfrowania. Jest to również klucz deszyfrowania, gdzie deszyfrowanie polega na „odejmowaniu" pozycji znaku o wartość \(\Delta\). Dla szyfru Cezara wartość \(\Delta\) jest stała i wynosi 3. Natomiast dla kodu nazywanego Captain Midnight \(\Delta\) jest kluczem zmiennym.

szyfr Cezara: \("A" \Rightarrow ( "A" + 3 ) = "D"\)
kod Captain Midnight: \("A" \Rightarrow ( "A" + \Delta); \Delta = 1,...,26\)

Rysunek '1'. Przykłady monogramów
Szyfry monoalfabetyczne mogą być konstruowane i opisywane różnymi wzorami matematycznymi. W powyższym przykładzie funkcję podstawienie zapisywaliśmy \(f(x)\). W kryptologii częściej stosuje się zapis \(E[x|k]\), gdzie \(E[]\) jest operacją szyfrowania (ang. encryption), a k oznacza użyty klucz. W niniejszym module będziemy stosowali najczęściej uproszczony zapis postaci \(E_k[x]\)
Oto przykłady formalnych definicji przekształceń monoalfabetycznych:

\(f(x) = x + k\)
\(E[x|k] = x + k\)
\(E_k[x] = x + k\)
\(f(x) = x \cdot k \bmod n\)
\(E[x|k] = x \cdot k \bmod n\)
\(f(x) = (x \cdot a + b) \bmod n\)
\(E[x|a,b] = (x \cdot a + b) \bmod n\)

Szyfrowanie metodą przestawiania

Inną podstawową operacją kryptograficzną jest przestawianie treści wiadomości czytelnej. Polega ono na przestawieniu kolejności wystąpienia znaków („wymieszaniu") testu jawnego. Kryptogram rozszyfrowujemy wykonując odwrotne przestawianie.
Najprostszym przypadkiem szyfrowania metodą przestawiania jest przestawienie losowe. W jego przypadku kolejne znaki wiadomości czytelnej przyjmują przypadkowe pozycje w kryptogramie. Takie szyfrowanie ma sens dla relatywnie niedużych wiadomości (rysunek 2).

Rysunek '2'. Przykład szyfrowania metodą przestawiania losowego
W rzeczywistych przypadkach, przestawienie nie jest losowe, lecz wynika z określonego wzoru zadanego np. figurą geometryczną. Najprostszą przydatną figurą transpozycji jest prostokąt. Dokładniej mamy do czynienia z macierzą prostokątną, w której pozycje wpisujemy wiadomość czytelną (lub też kolejne bloki całej wiadomości, których długości odpowiadają ilości elementów macierzy - czyli inaczej - jej rozmiarowi). Wiadomość wpisywana jest do macierzy, przyjmijmy, wierszami. Kryptogram tworzy się spisując zawartość tak wypełnionej macierzy, ale kolumnami (rysunek 3).
Rolę klucza szyfrowania pełnią wymiary figury transpozycji. W przykładzie z rysunku byłby to rozmiar macierzy: k = (5,4).
W celu utrudnienia złamania szyfru, operację transpozycji można powiązać w permutacją kolejności kolumn, przed spisaniem zawartości macierzy do krytpogramu. Innymi słowy, można przykładowo spisywać najpierw zawartość kolumny 2-giej, potem 5-tej, później 3-ciej, dopiero dalej 1-szej i na końcu 4-tej. Klucz szyfrowania przyjmuje tu postać: k = (5,4;2-5-3-1-4).
Dalsze wzmocnienie jakości szyfrowania można osiągnąć poprzez dodatkowe skomplikowanie operacji szyfrowania. Można stosować macierze o wierszach zmiennej długości bądź przestawienie przekątnokolumnowe, albo też szyfry siatkowe czy zastosować całkiem inną figurę transpozycji.

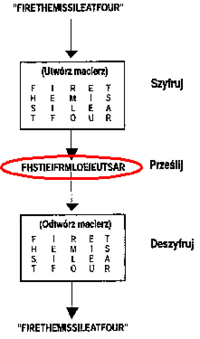
Rysunek '3'. Przykład szyfrowania metodą przestawiania losowego

Zasada Kerckhoffsa

Najprostsze z przedstawionych metod szyfrowania opierają swoją siłę na tajności procedury szyfrowania. Każdy, kto pozna tę procedurę, bez większego trudu i w relatywnie krótkim czasie jest w stanie odtworzyć wiadomość czytelną z dowolnego kryptogramu.
Szyfry najczęściej spotykane współcześnie w systemach informatycznych opierają swą siłę nie na tajności samego algorytmu lecz jedynie na tajności zmiennego parametru tego algorytmu, jakim jest klucz. Jest to zgodne z powszechnie uznaną regułą, nazywaną zasadą Kerckhoffsa:

Algorytm szyfrowania i deszyfrowania jest jawny

Rysunek '4'. Zasada Kerckhoffsa
Zgodnie z tą zasadą, algorytm może być, a nawet z wielu względów powinien być publicznie znany. Przemawia za tym ułatwienie publicznej oceny i dyskusji jakości, jakie potencjalnie oferuje powszechna dostępność każdego nowo-opracowanego algorytmu dla światowej rzeszy kryptoanalityków. Dzięki temu, łatwiej i wcześniej można wykryć ewentualne luki w koncepcji algorytmu bądź w samej jego konstrukcji.

Szyfrowanie z kluczem

Rysunek 5 przedstawia ogólny schemat szyfrowania z użyciem klucza, jaki stosować będziemy w niniejszym module. Użytkownicy uczestniczący w komunikacji, na tym schemacie - Alicja i Bolek, posługują się swoimi kluczami, odpowiednio - K_A oraz K_B, aby przesłać zaszyfrowaną wiadomość od Alicji do Bolka. Alicja poddaje szyfrowaniu wiadomość czytelną M z użyciem klucza szyfrowania K_A operacją \(E_K_A[M]\) uzyskując szyfrogram S
Następnie szyfrogram S jest przesyłany do Bolka, który poddaje go operacji \(D_K_B[S]\) rozszyfrowania z kluczem K_B.

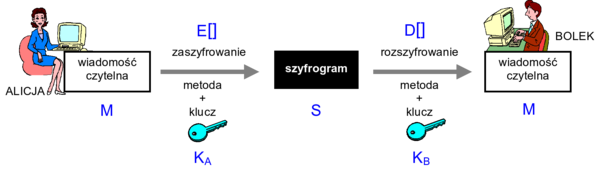
Rysunek '5'. Schemat ogólny szyfrowania z kluczem
Formalny zapis tych operacji przedstawia rysunek 6. Wynika z niego własność szyfrowania z kluczem: \(D_K_B[E_K_A[M]] = M\).

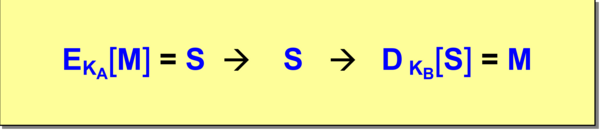
Rysunek '6'. Formalny zapis operacji szyfrowania z kluczem
W przypadku szyfrowania z kluczem spotykane są dwa schematy: szyfrowanie symetryczne i asymetryczne.

Szyfrowanie symetryczne

Szyfrowanie symetryczne jest schematem, który posiada następujące cechy

występuje wspólny dla obu uczestników komunikacji tajny klucz K_A-B (dalej oznaczany po prostu K)
stąd zapis formalny operacji szyfrowania symetrycznego ma postać:
\(E_K[M] = S \rightarrow S \rightarrow D_K[S] = M\)

Rysunek '7'. Ogólny schemat szyfrowania symetrycznego
Własność szyfrowania symetrycznego ma zatem postać: \(D_K[E_K[M]] = M\).
Szyfrowanie symetryczne jest o tyle ciekawe, że wymaga posłużenia się tylko jednym kluczem, dla obu uczestników komunikacji i w obu jej kierunkach (choć można wyobrazić sobie wariant tego schematu z oddzielnym kluczem na każdy kierunek). Uczestników takiej komunikacji może oczywiście być więcej niż dwoje i wówczas cała grupa może posługiwać się wspólnym kluczem. Jednak my będziemy tu zakładali zachowanie poufności komunikacji w pojedynczym kanale komunikacyjnym łączącym tylko dwoje uczestników. W związku z tym, pojedynczy klucz przypisany jest wyłącznie do jednej pary użytkowników i musi on być utajniony wobec innych osób.
Konieczność utrzymania tajności klucza w obrębie jednej pary użytkowników rodzi szereg praktycznych problemów:

tożsamość problemu poufności wiadomości z problemem tajności klucza

wiadomość jest bezpieczna dopóki osoba trzecia nie pozna tajnego klucza K

problem dystrybucji klucza

jak uzgodnić wspólny klucz bez osób trzecich, będąc oddalonym o setki, a nawet tysiące kilometrów?

problem skalowalności

dla 2 komunikujących się w systemie osób wymagane jest przechowywanie przez każdą z nich 1 klucza; dla 3 osób - 3 kluczy (przez każdą osobę); 4 os. = 6 kluczy; 10 os. = 45 kluczy; 100 os. = 4950 kluczy; ...

autentyczność

tajność klucza nie zapewnia autentyczności - nie można wykazać formalnie która z dwóch stron jest rzeczywistym nadawcą wiadomości, skoro obie posługują się tym samym kluczem.

Przykłady algorytmów symetrycznych

Algorytm DES (Data Encryption Standard)

Algorytm DES (Data Encryption Standard) został opracowany w latach '70. przez firmę IBM na zamówienie NSA (National Security Agency) - rządowej agencji USA, będącej odpowiednikiem Agencji Bezpieczeństwa Wewnętrznego. Zespołem odpowiedzialnym za opracowanie DES w IBM kierował Horst Feistel. Zmodyfikowany przez NSA, algorytm DES został przyjęty jako standard krajowy w 1976 przez NBS (National Bureau of Standards, obecnie NIST = National Institute of Standards and Technology) i objęty ochroną patentową oraz ograniczeniami ekportowymi. Należy od razu podkreślić, iż ochrona patentowa tego algorytmu już wygasła. W 1977 DES został opublikowany przez nieporozumienie między NSA a NBS (NSA spodziewało się, że standardem stanie się sam układ sprzętowy, lecz NBS opublikowało na tyle dużo szczegółów, iż możliwe stały się implementacje programowe tego algorytmu).
Algorytm DES pracuje na 64-bitowych blokach tekstu jawnego, co odpowiada 8 znakom 8-bitowego kodu ASCII. Klucz składa się z 64 bitów, przy czym 8 z nich jest bitami parzystości. Zatem w istocie, w trakcie wyboru klucza można określić jedynie 56 bitów.
Aktualnie standard DES nie jest już uważany za dostatecznie silny mechanizm kryptograficzny dla większości zastosowań, jednak wciąż jest bardzo często demonstrowany jako bardzo reprezentatywny przykład algorytmu symetrycznego szyfrowania. Dalej przedstawiony zostanie uproszczony szkic działania algorytmu DES, którego celem jest umożliwienie nabrania pewnej intuicji co do sposobu konstrukcji i pracy współczesnych algorytmów kryptograficznych.
Algorytm działa w kilku wyraźnie zaznaczających się etapach nazywanych tu fazami. Fazy działania, znane dość powszechnie jako sieć Feistela, są następujące

wstępna permutacja wejściowego bloku danych (na podstawie tabeli transpozycji)
podział bloku na lewą i prawą połowę o długości 32 bitów każda
16 jednakowych rund - cykli operacji podstawiania i przestawiania wykorzystujących pewną funkcję f, w czasie których dane zostają połączone z kluczem
połączenie lewej i prawej połowy bloku
permutacja końcowa (odwrotność permutacji wstępnej)

Schematycznie sieć Feistela przedstawia rysunek 8.

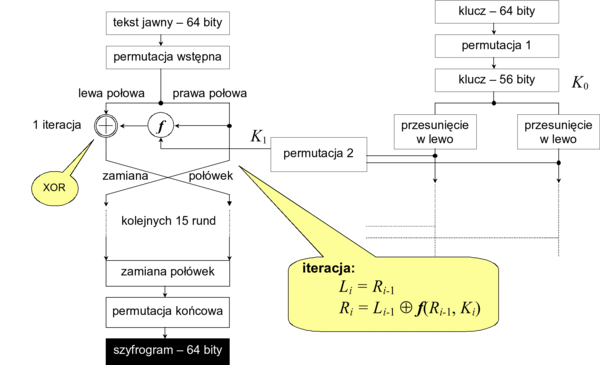
'Rysunek '8'. Sieć 'Feistela
Najbardziej skomplikowaną fazą jest każdy z 16 rund wykorzystujących funkcję f. Rundy te są w istocie iteracjami tych samych operacji. Każda kolejna runda, dokonuje tych samych obliczeń, ale na wynikach obliczeń z poprzedniej rundy i specjalnym podkluczu K_i generowanym z 56b klucza K₀ (64-bitowego klucza powstałego po usunięciu 8 bitów parzystości z wejściowego klucza szyfrowania).
Początek każdej iteracji składa się z następujących kroków:

56 bitów klucza dzielone jest na dwie połowy po 28 bitów
w każdej iteracji bity obu połówek są cyklicznie przesuwane w lewo o jeden lub dwa bity, w zależności od numeru iteracji
ostatecznie wykonywana jest permutacja kompresująca, dzięki której z 56b klucza, otrzymujemy 48b podklucz K_i używany w funkcji f(L_i, K_i)
a połówki klucza podawane jest do następnej iteracji i+1

Kulminacyjnym etapem wykonania kolejnej rundy jest funkcja f. Jej działanie jest następujące:

prawa połowa R_i-₁ rozszerzana jest z 32 bitów do 48 bitów za pomocą permutacji rozszerzonej (e-blok) i sumowana mod 2 z 48 bitami podklucza K_i danego cyklu
otrzymany wynik poddawany jest operacji podstawienia poprzez wykorzystanie bloków podstawień (S-bloki):
- ciąg 48 bitów dzielony jest na 8 bloków po 6 bitów
- każdy ciąg 6 bitów jest redukowany do 4 bitów funkcją podstawienia
- z 48 bitów otrzymujemy 32b ciąg, który poddawany jest permutacji zwykłej
- następnie sumowany mod 2 z lewą połową L_i-1 bloku wejściowego

No koniec iteracji następuje zamiana lewej i prawej połowy bloku miejscami.
Bloki podstawień (S-bloki; z ang. Substitution blocks) są zdefiniowane w standardzie DES i można je znaleźć w literaturze przedmiotowej. Każdy z 8 S-bloków jest inny, jednak w ogólności S-blok należy postrzegać jako tabelę 4 wiersze na 16 kolumn. Element tabeli jest 4b liczbą (podstawiana wartość). Wybór wiersza i kolumny za pomocą 6b wejścia wygląda następująco:

pierwszy i ostatni bit 6b ciągu tworzy 2b liczbę
liczba ta wybiera wiersz
pozostałe środkowe 4 bity wybierają kolumnę

Wskazany element tabeli (4 bity) jest podawany na wyjście jako wynik podstawienia.

Deszyfrowanie w algorytmie DES

Operacje deszyfrowania kryptogramu uzyskanego algorytmem DES są realizowane za pomocą tej samej sieci co operacje szyfrowania bloku tekstu jawnego. Różnica polega jedynie na tym, iż klucze stosowane są w kolejności odwrotnej od K₁₆ do K₁.

Kryptoanaliza algorytmu DES

Istotą trudności kryptoanalizy algorytmu DES metodą przeszukiwania wyczerpującego jest złożoność obliczeniowa procesu dopasowania kolejnych możliwych wartości klucza. W latach 80-tych ubiegłego wieku wymagała ona czasu liczonego w setki/tysiące lat. W efekcie uczyniła ten standard odpornym na atak metodą przeszukiwania wyczerpującego.

Tryby pracy algorytmu DES

Standard przewiduje wykorzystanie algorytmu DES w różnych trybach pracy nazywanych ECB, CBC, CFB i OFB. Dwa pierwsze to tryby blokowe, w których algorytm DES jest wykonywany wprost dokładnie tak jak na przedstawionym wcześniej szkicu, operując na kolejnych 8-znakowych blokach szyfrowanej wiadomości czytelnej.
Tryb ECB (Electronic CodeBook) jest to podstawowy tryb szyfrowania blokowego. Jego własności można przedstawić następująco:

cały tekst jawny jest dzielony na bloki 64b (ostatni blok, jeśli nie jest 8 znakowy, zostaje uzupełniony do 8 znaków nieistotnym wypełnieniem - ang. padding)
każdy 64b blok jest szyfrowany niezależnie
dla danego bloku i danego klucza wynik szyfrowania będzie zawsze ten sam
jeśli blok wystąpi w wiadomości częściej niż raz - za każdym razem otrzyma taki sam blok szyfrogramu ECB
przy pewnym standardowym formacie wiadomości (np. rozpoczynających się od tych samych stałych pól) stanowi ten tryb istotne ułatwienie dla kryptoanalityka.

Tryb CBC (Cipher Block Chaining) jest wolny od tej ostatniej wady. Umożliwia on uzależnienie postaci bloku kryptogramu nie tylko od treści szyfrowanego bloku wiadomości jawnej, lecz również od pewnego dodatkowego parametru - wektora inicjującego. Jego własności można przedstawić następująco:

na pierwszym 64b bloku jest wykonywana operacja XOR z pewnym wektorem początkowym (IV = Initialization Vector) znanym nadawcy i odbiorcy
\(S_1 = E_K [M_1 \oplus \; IV ]\)
wynikowy ciąg jest podawany na wejście algorytmu DES
na każdym kolejnym 64b bloku jest wykonywany XOR z zaszyfrowanym poprzednim blokiem przed podaniem na wejście algorytmu DES
\(S_i = E_K [M_i \oplus S_{i-1}]\)
powtórzone takie same bloki 64b dadzą bloki zaszyfrowane różnej postaci
deszyfrowanie:
\(M_i = D_K [S_i] \oplus S_{i-1}\)

Tryby blokowe nadają się doskonale do szyfrowania gotowych wiadomości, jednak nie są odpowiednia dla szyfrowania strumienia danych asynchronicznych, np. wprowadzanych z klawiatury lub pojawiających się w protokołach komunikacyjnych, w których nie można z góry określić tempa pojawiania się danych do przesłania (i zaszyfrowania) oraz ich ilości, w efekcie dających teksty zmiennej długości. W tym celu wprowadzono tryby szyfrowania strumieniowego szyfrujące każdorazowo po jednym znaku 8-bitowym: CFB (Cipher FeedBack) oraz OFB (Output FeedBack) - tzw. tryby sprzężenia zwrotnego. Opisują je następujące własności:

w CFB na wejście funkcji szyfrującej podawana jest zawartość 64b rejestru przesuwnego - początkowo zawiera on IV, który jest szyfrowany: \(R_1 = E_K[ IV ]\)
na ośmiu najstarszych bitach rejestru jest wykonywany XOR ze znakiem szyfrowanym \(M_i: S_i = R_i \oplus M_i\)
zawartość rejestru jest przesuwana w lewo 8b, a jako 8 najmłodszych jest wpisywany szyfrogram \(S_i\) wprowadzonego znaku (\(R_{i+1}\))
wadą tego podejścia jest fakt iż uszkodzenie 1 bitu (np. w transmisji) propaguje się na 9 kolejnych znaków szyfrogramu
w OFB w miejsce 8 najmłodszych bitów wpisywany jest tylko szyfrogram 8 najstarszych (bez XOR z porcją tekstu szyfrowanego)
w trybie OFB błędy się nie propagują - uszkodzenie 1 bitu wpłynie tylko na rozszyfrowanie 1 znaku (zawierającego ten bit) - kryptoanalityk kontrolujący szyfrowany strumień może kontrolować zmiany w tekście jawnym

Powyższa dyskusja oraz znajomość praktycznych implementacji standardu DES skłania do następujących wniosków:

ECB jest trywialny - nie powinien być stosowany do szyfrowania sesji danych; może być wykorzystany do przesłania kluczy oraz IV
w trybie CBC mogą z kolei występować problemy implementacyjne związane z IV
- celem IV jest upodobnienie bloków szyfrogramu do postaci losowych danych
- typowe IV wartości nijak nie przypominają losowych (często zawierają powtarzające się najstarsze bity lub mają inną łatwą do przewidzenia strukturę)
- nawet jeśli IV byłby prawdziwie losowy, to trzeba go przekazać odbiorcy (skoro jest losowy)
- np. wysyłając w pierwszym bloku szyfrogramu (wydłuża to szyfrogram stanowiąc problem z małymi porcjami szyfrowanych danych)

Algorytm CDMF (Commercial Data Masking Facility)

Stany Zjednoczone, ojczyzna standardu DES, jak zresztą również inne kraje, traktują technologie kryptograficzne na równi z militarnymi i stosują ograniczenia w ich wykorzystaniu. Jednym z nich jest embargo eksportowe na wszelkie algorytmy i systemy kryptograficzne opracowane w USA. Również standard DES był objęty tymi ograniczeniami, a dokładniej jego ustandaryzowana postać posługująca się kluczem 56-bitowym. Natomiast algorytm CDMF, opracowany również przez IBM, został przygotowany specjalnie z myślą o wykorzystaniu również poza Stanami Zjednoczonymi i jest wolny od ograniczeń eksportowych. W istocie jest to wersja uproszczona DES operująca kluczem 40b, a dokładniej jest to algorytm DES uzupełniony o wstępną metodę skracania klucza 56b do 40b.

Odporność algorytmu DES

Algorytm DES był przez wiele lat bezpieczny. Ze względu na złożoność obliczeniową kryptoanalizy, przy dostępnej mocy obliczeniowej, proces odnajdywania klucza metodą przeszukiwania wyczerpującego był wystarczająco nieefektywny, by uczynić ataki nieopłacalnymi. Jednak w 1998 r. algorytm DES z kluczem 56b został złamany w 56 godzin kryptoanalizy metodą przeszukiwania wyczerpującego. Koszt sprzętu (EFF DES Cracker) wówczas szacowano na 250 tys. USD. Rok później zajęło to już 22 godziny. Dziś to kwestia minut.

Algorytm 3DES (Triple DES)

Istnieją jednak propozycje wzmocnienia siły algorytmu DES, np. poprzez praktyczne zwiększanie długości klucza. I tak algorytm 3DES stosuje jednocześnie trzy kolejne iteracje szyfrowania i deszyfrowania tekstu jawnego oryginalnym algorytmem DES. Każda iteracja może używać innego klucza 56b, co w efekcie daje klucz 168b. W praktyce najczęściej spotykany jest tryb DES-EDE (encrypt-decrypt-encrypt) z dwoma kluczami (razem 112b), wg rysunku 9:

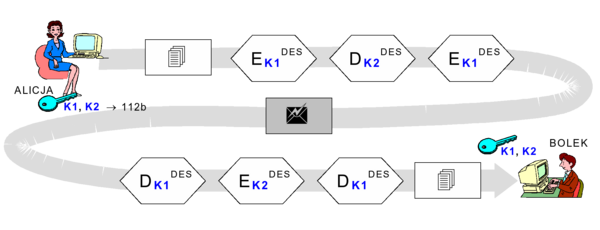
Rysunek '9'. Schemat działania algorytmu 3DES

Algorytm IDEA (International Data Encryption Algorithm)

Algorytm IDEA został opracowany w 1991r. przez Swiss Federal Institute of Technology
(w zespole, którym kierowali James L. Massey i Xuejia Lai). W ogólnej koncepcji jest dość podobny do algorytmu DES, występują jedynie różnice w szczegółach. Przykładowo algorytm IDEA charakteryzują:

64b bloki danych (jak DES)
klucz 128b
64b blok dzielony na 16b podbloki
a 128b klucz na 16b podklucze
8 iteracji (w DES jest 16, ale w IDEA 1 iteracja odpowiada 2 w DES)

Fazy działania algorytmu IDEA przedstawiają się następująco:

w każdym kroku cztery 16b podbloki danych poddawane są operacji dodawania modulo 2, dodawania modulo 2¹⁶ i mnożenia modulo 2¹⁶ z innymi blokami i z sześcioma 16b podkluczami.
pomiędzy każdym krokiem następuje zamiana drugiego i trzeciego podbloku.

Algorytm IDEA stosuje podklucze o następującej charakterystyce:

128-bitowy klucz jest dzielony na osiem 16-bitowych podkluczy
pierwszych 6 podkluczy jest używanych w pierwszej iteracji,
2 pozostałe podklucze - w kolejnej
następnie cały 128b klucz rotuje o 25 pozycji w lewo
tak otrzymany klucz jest ponownie dzielony na osiem 16b podkluczy, z których pierwsze 4 uzupełniają podklucze w drugiej iteracji, a kolejne 4 są przydzielane do trzeciej iteracji
w kluczu jest powtarzana rotacja o 25 pozycji w lewo - klucz jest ponownie dzielony na 8 podkluczy używanych w kolejnych krokach.

Opisane wyżej czynności powtarzane są do momentu przydzielenia kluczy do wszystkich kroków, przy czym w fazie zakończenia zamiast sześciu podkluczy, stosuje się tylko cztery podklucze. Łącznie w algorytmie wykorzystuje się 52 podklucze, które generowane są z wejściowego klucza szyfrującego.

Rysunek '10'. Siatka operacji w pojedynczej iteracji algorytmu IDEA
Deszyfracja przebiega następująco:

podklucze używane do deszyfrowania odpowiadają podkluczom szyfrowania podanym w odwrotnej kolejności,
operacje arytmetyczne przy użyciu czterech podkluczy są wykonywane nie na początku, ale na końcu deszyfrowania.

Algorytm Rijndeal

Algorytm Rijndeal został opracowany w 1999 przez Belgów: Joana Daemena i Vincenta Rijmena. Bloki wejściowe mają po 128, 196 lub 256 bitów. Klucze również mają długość 128b, 196b lub 256b. W zależności od wielkości bloku stosowana jest różna liczba iteracji: 10 (128b), 12 (196b) lub 14 (256b). Każda iteracja to następująca sekwencja wykonywana na poszczególnych bajtach danych i klucza:

podstawienie (S-bloki)
przesuwanie (rzędów i kolumn bloku-macierzy)
XOR.

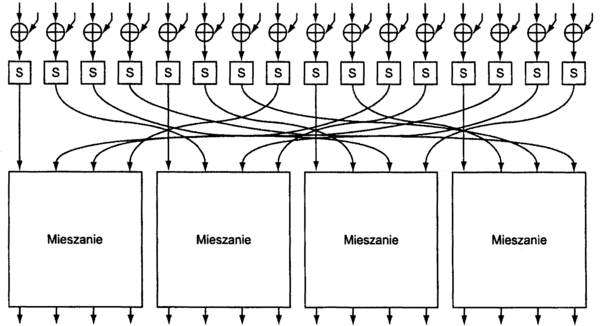
'Rysunek '11'. Uproszczony schemat pojedynczej iteracji algorytmu 'Rijndeal

Standard AES (Advanced Encryption Standard)

Standard AES jest następcą standardu DES obowiązującym w USA od 2001 r. Wykorzystuje algorytm Rijndeal. Algorytm ten wygrał oficjalną rywalizację z innymi zgłoszonymi do konkursu algorytmami, m.in. Serpent, Twofish, RC6, MARS. Stosuje tryb blokowy (blok 128b) i strumieniowy, klucze 128b, 192b, 256b (choć teoretycznie dopuszczalne również inne kombinacje). W standardzie wprowadzono też ciekawy nowy strumieniowy tryb licznikowy (CTR - Counter Mode), w którym dedykowany rejestr jest inkrementowany wraz z kolejnymi operacjami szyfrowania porcji danych. Tryb ten oferuje możliwość zrównoleglenia operacji na różnych porcjach danych.

Inne algorytmy symetryczne

Algorytmy RC2 / RC4 / RC5 / RC6

RC2, RC4, RC5 i RC6 to prawnie zastrzeżone algorytmy opracowane przez Ronalda Rivesta (pracownika MIT i jednocześnie założyciela firmy RSA Data Security), chociaż od 1994 kod źródłowy niektórych z nich jest szeroko dostępny w Internecie. Są to bardzo wydajne algorytmy symetryczne (ok. 10 razy szybsze od DES) o zmiennej długości klucza (do 2048b). RC2, RC5, RC6 to szyfry blokowe, natomiast RC4 jest szyfrem strumieniowym. Co ciekawe, niemal od samego początku swego istnienia posiadały specjalny status eksportowy USA dla kluczy 40b lub 56b (dla instytucji powiązanych z interesami USA). Dziś są powszechnie wykorzystywane w Lotus Notes, Apple OCE (Open Collaboration Enviromnent), Oracle, protokołach SSL i S-HTTP, sieciach bezprzewodowych i komórkowych.

Algorytmy z rodziny CAST

Określenie CAST opisuje schemat zastosowany w rodzinie zbliżonych do DES algorytmów kryptograficznych o zmiennej długości kluczy i bloków. Najpowszechniej znany reprezentant to szyfr CAST-128 opublikowany w 1997 [RFC 2144].

Algorytm SAFER

To algorytm blokowy opracowany przez kolejną ważną postać kryptografii komputerowej - Jamesa L. Masseya. Popularne są: wersja z kluczem 64b (SAFER-K64) obejmująca 6 rund oraz wersja z kluczem 128b (SAFER-K128) - do 12 rund (rekomendowane 10).

Algorytm Blowfish

Algorytm Blowfish, bardzo popularny zwłaszcza w produktach open source, został opracowany w 1994 r. przez Bruce'a Schneiera. Blok danych ma 64 bity, a klucz podstawowy długość do 448b. W algorytmie występuje 16 iteracji wykorzystujących 18 kluczy pomocniczych (wyznaczanych każdorazowo przed szyfrowaniem i deszyfrowaniem) i 4 S-bloki 256-elementowe o wartościach zależnych od: klucza podstawowego, danych oraz liczby \(\pi\). Deszyfrowanie jest operacją identyczną z szyfrowaniem - jedynie odwrotna zostaje kolejność kluczy pomocniczych.

Szyfrowanie asymetryczne

Istotą szyfrowania asymetrycznego jest wyodrębnienie dwóch kluczy o odmiennych rolach: klucz prywatny i klucz publiczny. I tak przyjmiemy dalej iż odbiorca Bolek posiada parę kluczy: prywatny klucz k_b oraz publiczny klucz K_B. Z założenia klucz prywatny jest tajny znany wyłącznie właścicielowi. Publiczny klucz, natomiast, może być powszechnie znany. Aby przekazać zaszyfrowaną postać wiadomości do tego odbiorcy należy zaszyfrować wiadomość czytelną jego kluczem publicznym. Odszyfrowanie jest możliwe tylko przy użyciu klucza prywatnego, odpowiadającego użytemu uprzednio kluczowi publicznemu.
Operacje szyfrowania opisuje zatem ogólny wzór:
\(E_K_B [M] = S\)
a deszyfrację:
\(D_k_b [S] = M\)

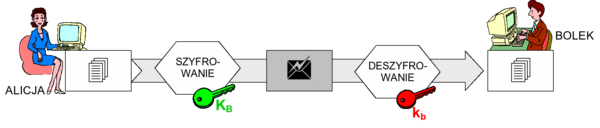
Rysunek '12'. Ogólny schemat szyfrowania asymetrycznego
Istotne jest iż znajomość klucza publicznego K_B nie wystarcza do naruszenia poufności szyfrogramu uzyskanego przy zastosowaniu tego klucza.
Szyfrowanie asymetryczne idealnie nadaje się do zastosowania w następujących celach:

zapewnienie poufności (rys. 13)

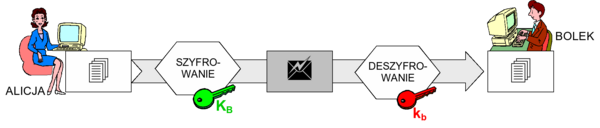
Rysunek '13'. Ogólny schemat zapewnienia poufności w szyfrowaniu asymetrycznym

zapewnienie autentyczności (rys. 14)

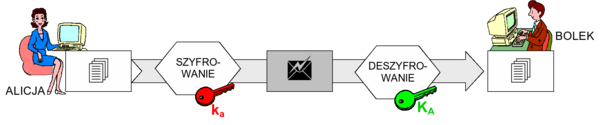
Rysunek '14'. Ogólny schemat zapewnienia autentyczności w szyfrowaniu asymetrycznym

Przykłady algorytmów asymetrycznych

Algorytm RSA (Rivest–Shamir–Adleman)

Algorytm RSA został opublikowany w 1978 roku przez Ronalda Rivesta, Adi Shamira i Leonarda Adlemana. Niedawno wygasła jego ochrona patentowa. Algorytm ten pozwala w zasadzie dowolnie ustalić długość klucza. Wymaga użycia 2 dużych liczb pierwszych (przez duże rozumiemy tu liczby co najmniej stucyfrowe w systemie dziesiętnym). Do szyfrowania i deszyfrowania wykorzystuje operacje potęgowania dyskretnego. W efekcie wymaga dużej liczby działań arytmetycznych (jest zdecydowanie wolniejszy od DES - nawet do 1000 razy).
Dobór kluczy jest najbardziej istotnym elementem pracy algorytmu. Schematycznie przedstawia ją rysunek 15.

Rysunek '15'. Ogólny schemat pracy algorytmu RSA
Schemat ten wymaga następujących wyjaśnień:

liczba względnie pierwsza z (p-1) i (q-1) to inaczej Wykładnik Uniwersalny: dzieli się tylko przez 1, siebie oraz (p-1) i (q-1), czyli Najmniejsza Wspólna Wielokrotność, albo inaczej: Największy Wspólny Dzielnik (e, (p-1)(q-1)) = 1
odwrotność e można łatwo wyznaczyć rozszerzonym algorytmem Euklidesa.

Złamanie tak ustalonego klucza wymagałoby znalezienia efektywnej metody faktoryzacji dużych liczb - póki co takowa nie istnieje.

Algorytm ElGamala (ELG)

Algorytm ten został opublikowany w 1985 roku, ale nie jest chroniony patentem. Brak również w jego przypadku ograniczeń eksportowych USA - wykorzystuje koncepcję (i patent) Diffiego-Helmana lecz ów patent wygasł w 1997 r. Szyfrowanie wymaga każdorazowo losowo wybranej wartość k, dlatego też ten sam tekst jawny każdorazowo daje inny szyfrogram. Niestety wadą tego algorytmu jest fakt, iż szyfrogram jest dwukrotnie dłuższy od tekstu jawnego.
Generowanie kluczy przebiega następująco:

wybieramy losowo liczbę pierwszą p
wykorzystujemy multiplikatywną grupę modulo p - \(\mathbb{Z}_p^*\)
gdzie p jest liczbą pierwszą, a \(\mathbb{Z}_p\) jego ciałem skończonym (\(GF(p) lub \mathbb{Z} /p \mathbb{Z}\))
wybieramy liczbę g, która jest elementem pierwotnym (generatorem) grupy \(\mathbb{Z}_p^*\)
generator - generuje ciąg \(1, g, g^2, g^3, ...\)
z którego tylko skończenie wiele należy do \(\mathbb{Z}_p^*\) (potem zaczną się powtarzać modulo p)
w ogólności mamy q elementów: \(1, g, g^2, ... , g^{q-1} (g^q \bmod p = 1)\)
istnieje przynajmniej jedno g generujące całą grupę! (tzn. \(q = p-1\))
czyli zamiast 1, ..., p-1 możemy grupę traktować jako \(1, g, g^2, ... , g^{p-2}\)

W dalszej kolejności:

wybieramy losowo liczbę \(x<p\)
obliczamy \(y=q^x \bmod p\)
klucz publiczny stanowią y, g i p - zarówno g, jak i p mogą być wspólnie wykorzystywane przez grupę użytkowników (mod p)
kluczem prywatnym jest x

Szyfrowanie przebiega następująco:

wybieramy losowo liczbę k względnie pierwszą z p
obliczamy \(a=g^k \bmod p\)
obliczamy \(b=y^k \cdot M \bmod p\)
szyfrogram to para (a,b)

Deszyfrowanie przebiega następująco:

\(M=b/a^x \bmod p\)
ponieważ \(a^x \equiv g^{kx} \bmod p\)
\(b/a^x \equiv y^k \cdot M/a^x \equiv g^{xk} \cdot M/g^{kx} \equiv M \bmod p\)

Literatura

[1] Janusz Stokłosa, Tomasz Bilski, Tadeusz Pankowski, "Bezpieczeństwo danych w systemach informatycznych", PWN, 2001

Zadania

Na czym polega kodowanie ROT-13 powszechnie wykorzystywane w Internecie?
Na czym polega i do czego służy kodowanie MIME?
Jaki będzie szyfrogram dla przykładu z rysunku 3, w przypadku użycia klucza k = (5,4;2-5-3-1-4)?
Wektor inicjujący IV powinien być każdorazowo unikalny, ale nie musi być tajny. Dlaczego?
Dlaczego wersja 40b algorytmu DES była od początku wolna od ograniczeń eksportowych?