Języki bezkontekstowe i ich gramatyki

W tym wykładzie rozpoczniemy omawianie drugiej w hierarchii Chomsky'ego rodziny języków formalnych, a mianowicie języków bezkontekstowych. Przedstawimy gramatyki bezkontekstowe i ich prostsze, a zarazem równoważne, postacie.

Gramatyki języków bezkontekstowych

Języki typu (2), zwane językami bezkontekstowymi, są rodziną szerszą niż omówione wcześniej języki regularne. Jak stwierdziliśmy w poprzednich wykładach gramatyki regularne generują poprawne napisy poprzez ciąg przepisywań metodą "od lewej do prawej". Natomiast gramatyki bezkontekstowe, zwane w lingwistyce gramatykami bezkontekstowych struktur frazowych, generują poprawne napisy poprzez sekwencję przepisywań, która ma strukturę drzewa. Ze względu na tę właśnie strukturę, gramatyki bezkontekstowe nadają się bardzo dobrze do opisu syntaktyki języków programowania. Z tego też powodu nastąpił szybki rozwój teorii gramatyk i języków bezkontekstowych.

Na wstępie przypomnijmy, że każda produkcja jakiejkolwiek gramatyki bezkontekstowej \(\displaystyle G = (V_N,V_T,v_0,P)\) ma postać \(\displaystyle v \rightarrow x_1\ldots.x_k\) lub \(\displaystyle v \rightarrow 1\), gdzie \(\displaystyle v \in V_N\;,\; x_i \in (V_N \cup V_T)\). Często korzystać będziemy z możliwości przedstawienia graficznego takiej produkcji. Mianowicie każdej produkcji odpowiada etykietowane drzewo z wyróżnionym wierzchołkiem początkowym.

Rysunek 1

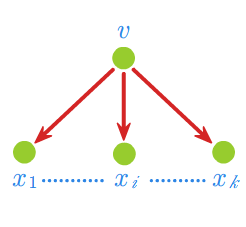
Drzewo odpowiadające pojedynczej produkcji z gramatyki \(\displaystyle G\) nazywane jest drzewem elementarnym. Mając dowolne yprowadzenie w gramatyce \(\displaystyle G\), można przedstawić je graficznie w postaci etykietowanego drzewa. Niech

\(\displaystyle v_0 \rightarrow w_1 \rightarrow \ldots.. \rightarrow w_n = w\)

będzie wyprowadzeniem słowa \(\displaystyle w\) w gramatyce \(\displaystyle G\). Drzewo reprezentujące to wyprowadzenie powstaje z połączenia drzew elementarnych odpowiadających pojedynczym produkcjom występującym w wyprowadzeniu słowa \(\displaystyle w\) w taki sposób, aby spełnić poniższe warunki:

wierzchołek początkowy jest etykietowany przez \(\displaystyle v_0\),
każdy wierzchołek nie będący liściem, czyli wierzchołkiem maksymalnym w drzewie, jest oznaczony przez elementy z \(\displaystyle V_N\),
jeśli \(\displaystyle v \in V_N\) jest symbolem nieterminalnym występującym w słowie \(\displaystyle w_i\) w wyprowadzeniu \(\displaystyle w\), to bezpośrednie następniki wierzchołka etykietowanego przez \(\displaystyle v\) są oznaczone przez symbole \(\displaystyle x_1,\ldots, x_k\) (porządek od lewej do prawej), gdzie \(\displaystyle v \rightarrow x_1\ldots x_k \;\; \in \;\;P\) i ta

właśnie produkcja została wykorzystana w bezpośrednim wyprowadzeniu \(\displaystyle w_i\mapsto w_{i+1}\), to znaczy we fragmencie wyprowadzenia \(\displaystyle v_0 \mapsto^* w_n = w,\)

wierzchołki maksymalne drzewa (ciąg liści "od lewej strony") to słowo \(\displaystyle w\), przy czym, jeśli wszystkie wierzchołki maksymalne są etykietowane przez 1, to \(\displaystyle w = 1\), a w przeciwnym razie wierzchołki oznaczone przez \(\displaystyle 1\) pomijamy.

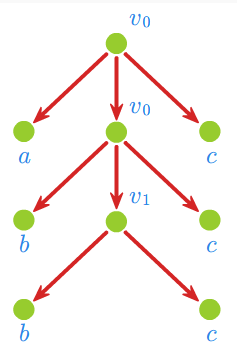
Przykład 1.1

Niech \(\displaystyle G = (V_N,V_T,v_0,P)\), gdzie \(\displaystyle V_N = \{v_0, v_1\}, V_T = \{a,b,c\},\)
\(\displaystyle P = \{v_0 \rightarrow av_0c,\;\; v_0 \rightarrow bv_1c, v_1 \rightarrow bv_1c, v_1\rightarrow bc\}.\)

Wówczas wyprowadzeniu

\(\displaystyle v_0 \mapsto av_0c \mapsto abv_1cc \mapsto abbccc\)

odpowiada drzewo

Rysunek 2

W poniższym przykładzie, jak i w dalszych wykładach symbolem \(\displaystyle \overline A\) oznaczamy kopię alfabetu \(\displaystyle A\), o której zakładać będziemy, że jest to zbiór rozłączny z oryginalnym alfabetem.

Przykład 1.2

Język Dycka.
Określamy bezkontekstową gramatykę \(\displaystyle G = (V_N,V_T,v_0,P)\), w której \(\displaystyle V_N=\{v_0,v_1 \},\displaystyle V_T=A \cup \overline A,\displaystyle \; A=\left\{ a\right\} ,\; \overline{A}=\left\{ \overline{a}\right\} , \displaystyle P=\\)
\(\displaystyle{ v_0 \rightarrow 1,\; v_0 \rightarrow v_1v_0, \; v_1 \rightarrow av_0\overline{a} \}\).
Język generowany przez tę gramatykę, nazywany językiem Dycka, oznaczany jest przez \(\displaystyle D^*_A\). Język Dycka zwany jest też językiem "poprawnych nawiasów" przy interpretacji symboli \(\displaystyle a,\overline{a}\) jako lewego i prawego nawiasu. \(\displaystyle L(G)=\left\{ 1,a\overline{a},aa\overline{a}\overline{a},a\overline{a}a\overline{a},aa\overline{a}\overline{a}a\overline{a},\ldots \right\}.\) Język Dycka można zdefiniować także dla alfabetu \(\displaystyle A=\{a_{1},...,a_{n}\}\) mającego więcej niż dwa symbole. Do zbioru praw gramatyki \(\displaystyle G\) wprowadza się wszystkie możliwe prawa postaci \(\displaystyle v_1 \rightarrow a_iv_0\overline{a_i}\). W tym przypadku dla języka Dycka używa się oznaczenia \(\displaystyle D^*_n\), aby zaznaczyć liczbę elementów alfabetu \(\displaystyle A\).
Język Łukasiewicza.
Język Łukasiewicza jest generowany przez gramatykę bezkontekstową \(\displaystyle G = (V_N,V_T,v_0,P)\), gdzie \(\displaystyle V_N=\{v_0 \}\), \(\displaystyle V_{T}=\left\{ a,b,+,*\right\}\),\(\displaystyle v_{0}=v\) oraz \(\displaystyle P= \{v \rightarrow a, v \rightarrow b, v \rightarrow +vv, v \rightarrow *vv \}\). Język Łukasiewicza jest więc zbiorem \(\displaystyle L(G)=\left\{ a,\: b,+ab,*b+ab,*+ab+ab,\ldots \right\}\)
Używając tego języka, możemy zapisywać wyrażenia algebraiczne bez użycia nawiasów (notacja polska, prefiksowa), interpretując \(\displaystyle +\) jako operator dodawania, \(\displaystyle *\) jako operator mnożenia oraz \(\displaystyle a\) i \(\displaystyle b\) jako argumenty. Używając nawiasów, przy powyżej interpretacji, możemy ten język zapisać następująco:

\(\displaystyle L(G)=\left\{ a,\: b,\: a+b,\: b*(a+b),\: (a+b)*(a+b),\ldots \right\}.\)

Wprost z definicji gramatyk - regularnej i bezkontekstowej - wynika, że rodzina języków regularnych jest podrodziną rodziny języków bezkontekstowych. Z lematu o pompowaniu dla języków regularnych wiemy, że język \(\displaystyle L = \{a^n b^n \; : \; n= 1,2,\ldots \}\) nie jest regularny. Łatwo uzasadnić, że język ten jest bezkontekstowy, bo jest generowany przez gramatykę:

\(\displaystyle G= (\{ v_0 ,v_1 \} , \{a,b\} , v_0 ,\{ v_0 \rightarrow av_1b, v_1 \rightarrow 1, v_1 \rightarrow av_1 b \}).\)

Zatem rodzina języków regularnych jest właściwą podrodziną rodziny języków bezkontekstowych, czyli \(\displaystyle mathcal{L}_{3}\subseteq \! \! \! \! \! _{/\; \, }\mathcal{L}_{2}.\)

Przejdziemy teraz do omówienia pewnych własności gramatyk bezkontekstowych, które prowadzą do ich uproszczenia. Występujące w poniższym twierdzeniu sformułowanie "produkcja wymazująca" oznacza produkcję \(\displaystyle v\rightarrow 1\) .

Twierdzenie 1.1

Niech \(\displaystyle G = (V_N,V_T,v_0,P)\) będzie dowolną gramatyką bezkontekstową.

Istnieje gramatyka bezkontekstowa \(\displaystyle G'\) bez produkcji wymazującej taka, że \(\displaystyle L(G') = L(G) \backslash \{ 1\}.\)
Jeśli \(\displaystyle 1 \in L(G)\), to istnieje równoważna \(\displaystyle G\) gramatyka bezkontekstowa \(\displaystyle G''=(V''_N ,V_T ,v_0'' , P'')\) taka,

że jedyną produkcją wymazującą w \(\displaystyle P''\) jest produkcja \(\displaystyle v_0'' \rightarrow 1\) i symbol \(\displaystyle v_0''\) nie występuje po prawej stronie żadnej produkcji z \(\displaystyle P''\).

Dowód

Dowód podaje konstrukcję odpowiednich gramatyk. Dla dowodu punktu 1 rozważmy ciąg zbiorów

\(\displaystyle \begin{array} {l} U_{1}=\left\{ v\in V_{N}\, :\, v\rightarrow 1\in P\right\} ,\\ U_{i+1}=U_{i}\cup \left\{ v\in V_{N}\, :\, v\rightarrow x\in P,\, x\in U_{i}^{*}\right\} \end{array}\)

określony dla \(\displaystyle i=1,2\ldots\) . Jest to ciąg podzbiorów \(\displaystyle V_{N}\) taki, że \(\displaystyle U_1 \subseteq U_2 \subseteq \ldots \subseteq V_N\). Ponieważ zbiór symboli nieterminalnych \(\displaystyle V_{N}\) jest skończony, więc istnieje indeks \(\displaystyle k\) taki, że \(\displaystyle U_k = U_{k+1}\). Zatem ciąg \(\displaystyle U_i\) jest skończony. Stąd równoważność

\(\displaystyle v \mapsto^*_G 1 \Longleftrightarrow \; v \in U_k. (*)\)

Zatem \(\displaystyle 1 \in L(G)\) wtedy i tylko wtedy, gdy \(\displaystyle v_0 \in U_k.\) Konstruujemy teraz gramatykę \(\displaystyle G' = (V_N,V_T,v_0,P')\), przyjmując \(\displaystyle V_N,V_T\) i \(\displaystyle v_0\) jak w gramatyce \(\displaystyle G\) . Natomiast nowy zbiór praw \(\displaystyle P'\) zawiera zmodyfikowane prawa gramatyki \(\displaystyle G\) . Jeśli prawo \(\displaystyle v\rightarrow x\in P\) , to do zbioru \(\displaystyle P'\) wprowadzamy prawa \(\displaystyle v\rightarrow x'\) , gdzie \(\displaystyle x'\neq 1\) i \(\displaystyle x'\) powstaje z \(\displaystyle x\) przez wymazanie dowolnej liczby (także \(\displaystyle 0\) ) symboli ze zbioru \(\displaystyle U_{k}\) . Pozostaje teraz uzasadnienie równości

\(\displaystyle L(G')=L(G)-\left\{ 1\right\}.\)

Dowód inkluzji \(\displaystyle \; \subseteq\)
Zauważmy, że dla każdego prawa \(\displaystyle v\rightarrow x'\in P'\) istnieje prawo \(\displaystyle v\rightarrow x\in P\) takie, że \(\displaystyle x\) różni się od \(\displaystyle x'\) wyłącznie pewną ilością symboli z \(\displaystyle U_{k}\) . Z równoważności \(\displaystyle (*)\) wynika, że symbole ze zbioru \(\displaystyle U_{k}\) prowadzą w dalszym ciągu generowania do słowa pustego. A więc dla każdego wyprowadzenia niepustego słowa w gramatyce \(\displaystyle G'\) istnieje w gramatyce \(\displaystyle G\) wyprowadzenie tego samego słowa. Wystarczy w wyprowadzeniu w gramatyce \(\displaystyle G'\) w miejsce praw postaci \(\displaystyle v\rightarrow x'\in P'\) wprowadzić prawa \(\displaystyle v\rightarrow x\in P,\) by otrzymać wyprowadzenie tego samego słowa w \(\displaystyle G\) .

Dowód inkluzji \(\displaystyle \; \supseteq\)
Określamy gramatykę pomocniczą \(\displaystyle \overline{G}=(V_{N},V_{T},v_{o},P\cup P')\) . Zbiór praw tej gramatyki rozszerza \(\displaystyle P'\) o wszystkie prawa wymazujące ze zbioru \(\displaystyle P\) . Z definicji wynika, że \(\displaystyle L(G)\subseteq L(\overline{G})\) , więc \(\displaystyle L(G)-\left\{ 1\right\} \subseteq L(\overline{G})-\left\{ 1\right\}\) . Dla dowodu wystarczy więc pokazać, że

\(\displaystyle L(\overline{G})-\left\{ 1\right\} \subseteq L(G').\)

Niech \(\displaystyle w\in L(\overline{G})-\left\{ 1\right\}\) i niech \(\displaystyle v_{0}\mapsto_{\overline{G}}....\mapsto_{\overline{G}}w\) będzie wyprowadzeniem słowa \(\displaystyle w\) w \(\displaystyle \overline{G}\) . Jeśli w tym wyprowadzeniu wszystkie prawa należą do \(\displaystyle P'\) , to oczywiście słowo \(\displaystyle w\in L(G')\) . Jeśli w wyprowadzeniu słowa \(\displaystyle w\) występuje prawo wymazujące, to oznacza, że dla pewnego \(\displaystyle y_{i}\in U_{k},\, \, \, x_{p}\rightarrow v_{1}v_{2}\in P'\) oraz \(\displaystyle x_{p}\rightarrow v_{1}y_{i}v_{2}\in P'\) wyprowadzenie ma postać

\(\displaystyle \begin{array} {ccccc} & x_{p}\rightarrow v_{1}y_{i}v_{2} & & y_{i}\rightarrow 1 & \\ v_{0}\mapsto \cdots x_{1}\ldots x_{p}\ldots x_{n} & \mapsto & x_{1}\ldots v_{1}y_{i}v_{2}\ldots y_{m} & \mapsto & \end{array}\) \(\displaystyle \mapsto x_{1}\ldots v_{1}v_{2}\ldots x_{n}\mapsto \cdots \mapsto w\)

Jednak, jak łatwo zauważyć, słowo \(\displaystyle w\) można także wygenerować, pomijając to prawo wymazujące i wykorzystując wyłącznie prawa z \(\displaystyle P'\)

\(\displaystyle \begin{array} {cccc} & x_{p}\rightarrow v_{1}v_{2} & & \\ v_{0}\mapsto x_{1}\ldots x_{p}\ldots x_{n} & \mapsto & x_{1}\ldots v_{1}v_{2}\ldots x_{n} & \mapsto \cdots \mapsto w, \end{array}\)

co kończy dowód punktu 1.

Przechodząc do dowodu punktu 2, załóżmy, że \(\displaystyle 1\in L(G)\) i niech \(\displaystyle G'\) będzie gramatyką taką jak w punkcie 1. Definiujemy teraz gramatykę

\(\displaystyle G''=(V_{N}\cup \left\{ v_{0}''\right\} ,V_{T},v_{0}'',P'\cup \left\{ v_{0}''\rightarrow 1,\: v_{0}''\rightarrow v_{0}\right\} ),\)

która spełnia żądane w twierdzeniu warunki i \(\displaystyle L(G)=L(G'')\) .

Z udowodnionego powyżej twierdzenia i z definicji gramatyk bezkontekstowych i kontekstowych (definicja 2.1. z wykładu 2) wynika następujące stwierdzenie

Wniosek 1.1

Rodzina języków bezkontekstowych (typu (2)) zawiera się w rodzinie jezyków kontekstowych (typu (1))

\(\displaystyle \mathcal{L}_{2}\subseteq \mathcal{L}_{1}.\)

Przejdziemy teraz do zagadnienia upraszczania gramatyki bezkontekstowej. Wprowadzimy następującą definicję.

Definicja 1.1

Mówimy, że gramatyka bezkontekstowa \(\displaystyle G\) jest właściwa, jeśli zbiór praw nie zawiera produkcji wymazującej oraz produkcji typu \(\displaystyle v_1 \rightarrow v_2\), gdzie \(\displaystyle v_{1},v_{2}\in V_{N}\) .

Lemat 1.1

Dla każdej gramatyki bezkontekstowej \(\displaystyle G\) generującej język bez słowa pustego istnieje równoważna jej gramatyka bezkontekstowa \(\displaystyle H\) właściwa.

Dowód

W dowodzie przedstawimy konstrukcję gramatyki o żądanych własnościach. Na podstawie udowodnionego powyżej twierdzenia możemy przyjąć, że \(\displaystyle G = (V_N,V_T,v_0,P)\) jest bez produkcji wymazującej. Dla usunięcia produkcji w postaci \(\displaystyle v_1 \rightarrow v_2\) określamy ciąg zbiorów \(\displaystyle U_i(x)\) dla \(\displaystyle x \in V_N \cup V_T\), przyjmując \(\displaystyle U_{1}(x)=\left\{ x\right\}\) oraz dla \(\displaystyle i=1,2\ldots \displaystyle U_{i+1}(x)=U_{i}(x)\cup \left\{ y\in V_{N}\cup V_{T}\, :\, \exists u\in U_{i}(x),\, u\rightarrow y\in P\right\} .\)

Ciąg \(\displaystyle U_i(x)\) jest skończony (stabilizuje się), a więc \(\displaystyle U_k(x)=U_{k+1}(x)\) dla pewnego \(\displaystyle k\) i dla każdego \(\displaystyle l>k\) mamy równość \(\displaystyle U_l(x)=U_k(x)\). Dla dowolnego \(\displaystyle v \in V_N\) oraz \(\displaystyle z\in V_{N}\cup V_{T}\) prawdziwa jest równoważność

\(\displaystyle v \mapsto^* z \Longleftrightarrow z \in U_k(v),\)

która w szczególności dla symbolu terminalnego \(\displaystyle a \in V_T\) oznacza, że \(\displaystyle a \in L(G)\) wtedy i tylko wtedy, gdy \(\displaystyle a \in U_k(v_0).\)

Określamy teraz gramatykę \(\displaystyle H= (V_N,V_T,v_0,\displaystyle \overline{P})\) , w której zbiór \(\displaystyle \overline{P}\) zawiera produkcje postaci:

\(\displaystyle v_0 \rightarrow a\) dla każdego \(\displaystyle a \in V_T \cap U_k(v_0),\)
\(\displaystyle v \rightarrow z_1... z_n\) dla \(\displaystyle v \in V_N\), \(\displaystyle n \geqslant 2\) oraz dla

każdego \(\displaystyle z_j \in V_N \cup V_T\), \(\displaystyle j=1,..., n\) takiego, że istnieje prawo \(\displaystyle \overline v \rightarrow x_1... x_n \in P\), \(\displaystyle \overline v \in U_k(v)\) i \(\displaystyle z_j \in U_k(x_j)\).

W gramatyce \(\displaystyle H\) nie występują prawa postaci \(\displaystyle v_1 \longrightarrow v_2\). Gramatyka \(\displaystyle H\) nie zawiera praw wymazujących oraz \(\displaystyle L(G)=L(H)\), co kończy dowód lematu.

Dalsze rozważania prezentują mozliwości upraszczania gramatyk bezkontekstowych poprzez usunięcie pewnych nieistotnych symboli nieterminalnych, a także poprzez zastąpienie danej gramatyki przez równoważną o prostszej strukturze.

Niech \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) będzie gramatyką bezkontekstową, generującą niepusty język. Mówimy, że symbol nieterminalny \(\displaystyle v\in V_{N}\) jest użyteczny, jeśli istnieje słowo \(\displaystyle w\in L(G)\) i wyprowadzenie tego słowa takie, że

\(\displaystyle v_{0}\mapsto^{*}xvy\mapsto^{*}w\)

dla pewnych \(\displaystyle x,y\in (V_{N}\cup V_{T})^{*}\) . W przeciwnym wypadku mówimy, że symbol \(\displaystyle v\) jest bezużyteczny. Symbole nieużyteczne można usunąć z gramatyki bez uszczerbku dla generowanego przez tę gramatykę języka. Przekonuje o tym następujące twierdzenie.

Twierdzenie 1.2

Dla dowolnego niepustego języka bezkontekstowego \(\displaystyle L\) istnieje gramatyka bezkontekstowa bez bezużytecznych symboli nieterminalnych, która generuje ten język.

Konstrukcja takiej gramatyki, a więc i dowód tego twierdzenia wynika bezpośrednio z następujących dwóch lematów.

Lemat 1.2

Dla każdej gramatyki bezkontekstowej \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje równoważna gramatyka bezkontekstowa \(\displaystyle \overline{G}=(\overline{V}_{N},V_{T},v_{0},\overline{P})\) taka, że dla dowolnego \(\displaystyle v\in \overline{V}_{N}\) istnieje \(\displaystyle w\in V_{T}^{*}\) oraz

\(\displaystyle v\mapsto_{\overline{G}}^{*}w.\)

Dowód

Określamy rekurencyjnie ciąg podzbiorów zbioru symboli nieterminalnych \(\displaystyle V_{N}\) :
\(\displaystyle U_{1}=\left\{ v\in V_{N}\: :\: v\rightarrow w\in P,\: w\in V_{T}^{*}\right\}\) oraz dla \(\displaystyle i=1,2,\ldots\)
\(\displaystyle U_{i+1}=U_{i}\cup \left\{ v\in V_{N}\: :\: \: v\rightarrow x\in P,\: x\in (U_{i}\cup V_{T})^{*}\right\}\) . Zbiory te tworzą ciąg wstępujący i stabilizujący się dla pewnego \(\displaystyle p\) . Oznacza to, że \(\displaystyle U_{1}\subseteq U_{2}\subseteq \ldots \subseteq U_{p}=U_{p+1}\) . Przyjmujemy z definicji \(\displaystyle \overline{V}_{N}=U_{p}\) oraz

\(\displaystyle \overline{P}=\left\{ v\rightarrow x\in P,\: v\in \overline{V}_{N},\: x\in (V_{T}\cup \overline{V}_{N})^{*}\right\}\)

Tak określona gramatyka \(\displaystyle \overline{G}=(\overline{V}_{N},V_{T},v_{0},\overline{P})\) ma własności gramatyki postulowanej w tezie lematu. Pozostaje udowodnić równoważność określonej gramatyki \(\displaystyle \overline{G}\) i gramatyki \(\displaystyle G\) . W tym celu wystarczy pokazać dla dowolnego \(\displaystyle v\in V_{N}\) i \(\displaystyle w\in V^{*}_{T}\) , że jeśli \(\displaystyle v\mapsto^{*}_{G}w\) , to \(\displaystyle v\in \overline{V}_{N}\) . Udowodnimy tę implikację indukcyjnie ze względu na długość wyprowadzenia. Dla \(\displaystyle n=1\) istnienie wyprowadzenia \(\displaystyle v\mapsto^{*}_{G}w\) oznacza, że \(\displaystyle v\rightarrow w\in P\) . Stąd zaś wynika, że \(\displaystyle v\in U_{1}\subset \overline{V}_{N}\) . Dla dalszej części rozumowania załóżmy, że implikacja jest prawdziwa dla wyprowadzenia o długości nie większej od \(\displaystyle n\) i niech

\(\displaystyle v\mapsto_{G}z\mapsto_{G}^{*}w\)

będzie wyprowadzeniem o długości \(\displaystyle n+1\) dla słowa \(\displaystyle w\in V_{T}^{*}\) . Niech \(\displaystyle z=y_{1}v_{1}y_{2}v_{2}\ldots v_{k}y_{k+1},\) dla pewnych \(\displaystyle v_{1},...,v_{k}\in V_{N}\) oraz \(\displaystyle y_{1},...,y_{k+1}\in V_{T}^{*}\) . Oznaczmy dla słowa \(\displaystyle z\) symbolem \(\displaystyle N(z)\) słowo otrzymane przez wymazanie wszystkich symboli terminalnych, a symbolem \(\displaystyle T(z)\) słowo otrzymane przez wymazanie wszystkich symboli nieterminalnych. Wtedy \(\displaystyle N(z)=v_{1}\ldots v_{k},\; T(z)=y_{1}\ldots y_{k+1}\) . Wówczas istnieją słowa \(\displaystyle w_{1},\ldots ,w_{k}\in V_{T}^{*}\) takie, że \(\displaystyle w=y_{1}w_{1}y_{2}\ldots y_{k}w_{k}y_{k+1}\) i dla każdego \(\displaystyle i=1,\ldots ,k\) istnieją wyprowadzenia \(\displaystyle v_{i}\mapsto^{*}_{G}w_{i}\) o długości mniejszej lub równej od \(\displaystyle n\) . Korzystając z założenia indukcyjnego, wnioskujemy, że dla każdego \(\displaystyle i=1,\ldots ,k,\: \: v_{i}\in \overline{V}_{N}\) , a to oznacza z definicji \(\displaystyle \overline{V}_{N}\) , że istnieje \(\displaystyle j\) takie, że dla każdego \(\displaystyle i=1,\ldots ,k,\: \: v_{i}\in U_{j}\) . Ostatecznie więc \(\displaystyle v\in \overline{V}_{N}\) .

Lemat 1.3

Dla każdej gramatyki bezkontekstowej \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje równoważna gramatyka bezkontekstowa \(\displaystyle \overline{\overline{G}}=(\overline{\overline{V}}_{N},\overline{\overline{V}}_{T},v_{0},\overline{\overline{P}})\) taka, że dla dowolnego \(\displaystyle x\in \overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T}\) istnieją słowa \(\displaystyle u_{1},u_{2}\in (\overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T})^{*}\) oraz

\(\displaystyle v_{0}\mapsto^{*}_{\overline{\overline{G}}}u_{1}xu_{2}.\)

Dowód

Dla rekurencyjnego określenia ciągu podzbiorów zbioru \(\displaystyle V_{N}\cup V_{T}\) przyjmujemy:

\(\displaystyle U_{1}=\left\{ v_{0}\right\}\) oraz dla \(\displaystyle k=1,2,\ldots \displaystyle U_{k+1}=U_{k}\cup \left\{ x\in alph_{(V_{N}\cup V_{T})}y\: :\: v\rightarrow y\in P,\: v\in U_{k}\right\},\)

gdzie \(\displaystyle alph_{(V_{N}\cup V_{T})}y\) oznacza zbiór symboli terminalnych i nieterminalnych występujących w słowie \(\displaystyle y\) . Zbiory te tworzą stabilizujący się dla pewnego \(\displaystyle p\) ciąg wstępujący \(\displaystyle U_{1}\subseteq U_{2}\subseteq \ldots \subseteq U_{p}=U_{p+1}\) . Przyjmijmy

\(\displaystyle \overline{\overline{V}}_{N}=U_{P}\cap V_{N},\: \: \: \overline{\overline{V}}_{T}=U_{P}\cap V_{T}.\)

Zbiór \(\displaystyle \overline{\overline{P}}\) definiujemy jako zawierający te i tylko te prawa z \(\displaystyle P\) , w których wszystkie symbole tworzące słowa należą do \(\displaystyle \overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T}\) . Łatwo zauważyć, że tak określona gramatyka \(\displaystyle \overline{\overline{G}}= (\overline{\overline{V}}_{N},\overline{\overline{V}}_{T},v_{0},\overline{\overline{P}})\) spełnia tezę lematu.

W świetle uzyskanych rezultatów dowolną gramatykę bezkontekstową generującą niepusty język można przekształcić w oparciu o Lemat 1.2 na równoważną, a następnie raz jeszcze przekształcić uzyskaną gramatykę stosując konstrukcję opisaną w dowodzie Lematu 1.3, uzyskując ostatecznie gramatykę bez bezużytecznych symboli nieterminalnych, czyli spełniającą tezę powyższego twierdzenia.

Warto podkreślić, iż istotna jest kolejność przekształcania gramatyk. Zmiana kolejności może sprawić, iż nie uzyskamy pożądanego efektu. Załóżmy, dla ilustracji, że w gramatyce \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje wyprowadzenie \(\displaystyle v_{0}\mapsto^{*}_{G}u_{1}v_{1}u_{2}v_{2}u_{3}\) dla pewnych \(\displaystyle v_{1},v_{2}\in V_{N}\) oraz \(\displaystyle u_{1},u_{2},u_{3}\in (V_{N}\cup V_{T})^{*}\) i jest to jedyna możliwość wygenerowania z \(\displaystyle v_{0}\) słowa, w którym występuje \(\displaystyle v_{1}\) . Istnieje także słowo \(\displaystyle w\in V_{T}^{*}\) i wyprowadzenie \(\displaystyle v_{1}\mapsto^{*}_{G}w\) . Z symbolu \(\displaystyle v_{2}\) nie da się natomiast w gramatyce \(\displaystyle G\) wyprowadzić żadnego słowa terminalnego. Zastosowanie drugiego z powyższych lematów, uzasadniających twierdzenie, nie usunie symboli \(\displaystyle v_{1}\) i \(\displaystyle v_{2}\) z alfabetu nieterminalnego. Lemat pierwszy usunie tylko \(\displaystyle v_{2}\) . Symbol \(\displaystyle v_{1}\) pozostanie, pomimo iż jest bezużyteczny.

Gramatyki w postaci Chomsky'ego i Greibach

Wprowadzimy teraz określenia dwóch szczególnych postaci gramatyk bezkontekstowych, a mianowicie gramatyki w postaci normalnej Chomsky'ego oraz gramatyki w postaci normalnej Greibach.

Definicja 2.1

Gramatyka bezkontekstowa \(\displaystyle G = (V_N,V_T,v_0,P)\) jest

w postaci normalnej Chomsky'ego, jeśli wszystkie prawa są w formie: \(\displaystyle v \rightarrow v_1v_2 \;\) lub \(\displaystyle \; v \rightarrow a,\) gdzie \(\displaystyle v, v_1, v_2 \in V_N\), \(\displaystyle a \in V_T\).
w postaci normalnej Greibach, jeśli wszystkie prawa są w formie:

\(\displaystyle v\rightarrow ax,\)

gdzie \(\displaystyle a\in V_{T},\: x\in V_{N}^{*}\) .

Łatwo zaobserwować, że gramatyka zarówno w postaci normalnej Chomsky'ego, jak i w postaci Greibach jest gramatyką właściwą oraz że język generowany przez te gramatyki nie zawiera słowa pustego. Ponadto drzewo wywodu dowolnego słowa w gramatyce w postaci normalnej Chomsky'ego jest binarne.

Twierdzenie 2.1

Dla każdej gramatyki bezkontekstowej \(\displaystyle G\), generującej język bez słowa pustego, istnieje równoważna gramatyka \(\displaystyle H\) w postaci normalnej Chomsky' ego.

Dowód

Zakładamy, że gramatyka \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) jest właściwa. Konstruujemy gramatykę \(\displaystyle H_{1}=\left( V_{N}\cup \overline{V}_{T},V_{T},v_{0},P_{1}\right)\) , gdzie \(\displaystyle \overline{V}_{T}=\left\{ v_{a}\, :\, a\in V_{T}\right\}\) jest kopią alfabetu terminalnego. Zbiór produkcji \(\displaystyle P_{1}\) powstaje z \(\displaystyle P\) przez zamianę w każdej produkcji, której prawa strona nie jest pojedynczą literą terminalną, symbolu \(\displaystyle a\) na \(\displaystyle v_a\) oraz dodaniu produkcji \(\displaystyle v_a \rightarrow a\) dla każdego \(\displaystyle a\in V_{T}\) . Prawdziwa jest równość \(\displaystyle L(G)=L(H_1)\) i w gramatyce \(\displaystyle H_1\) nie występują produkcje typu \(\displaystyle v \rightarrow \overline v\).

Aby uzyskać równoważną gramatykę \(\displaystyle H\) w postaci normalnej Chomsky' ego, produkcje typu \(\displaystyle v \rightarrow v_1... v_n\) dla \(\displaystyle n \geqslant 2\) i \(\displaystyle v_i \in V_N\) występujące ewentualnie w \(\displaystyle H_1\) zastępujemy

produkcjami: \(\displaystyle v \rightarrow v_1u_1,\; u_1 \rightarrow v_2 u_2, ... , u_{n-2} \rightarrow v_{n-1} v_n,\)

dodając do zbioru symboli nieterminalnych nowe elementy \(\displaystyle u_{1},\ldots ,u_{n-2}\) . Skonstruowana w ten sposób gramatyka \(\displaystyle H\) jest w normalnej postaci Chomsky'ego oraz \(\displaystyle L(G)=L(H)\) .

Przedstawiamy poniżej algorytm przekształcający gramatykę bezkontekstową właściwą w gramatykę mającą postać normalną Chomsky'ego.

Algorytm PostaćNormalnaChomsky'ego - buduje gramatykę bezkontekstową w postaci normalnej Chomsky'ego

  1  Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa właściwa.
  2  Wyjście: \(\displaystyle G'=(V_N', V_T', v_0', P')\) - gramatyka bezkontekstowa w postaci
     normalnej Chomsky'ego.
  3  \(\displaystyle P' \leftarrow \emtyset\);                           \(\displaystyle \triangleright\) nowy zbiór produkcji budujemy sukcesywnie 
  4  \(\displaystyle V_N' \leftarrow V_N\);                            \(\displaystyle \triangleright\) tak jak i nowe symbole nieterminalne
  5  \(\displaystyle V_T' \leftarrow V_T\);                          \(\displaystyle \triangleright\) symbole terminalne pozostają takie same
  6  \(\displaystyle v_0' \leftarrow v_0\);                                      \(\displaystyle \triangleright\) podobnie jak symbol startowy
  7  for each  \(\displaystyle a \in V_T'\) do
  8    \(\displaystyle V_N'\leftarrow V_N'\cup \{ v_a \}\)                          \(\displaystyle \triangleright\) dodaj nowy symbol nieterminalny
  9  end for
 10  \(\displaystyle k\leftarrow 1\)                                                    \(\displaystyle \triangleright\) licznik produkcji
 11  for \(\displaystyle (v \rightarrow x_1x_2...x_m) \in P\) do
 12    if \(\displaystyle m=1\)  and  \(\displaystyle x_1 \in V_T\) then
 13      \(\displaystyle P' \leftarrow P' \cup \{v \rightarrow x_1\}\);                     \(\displaystyle \triangleright\) takie produkcje są dopuszczone
 14    else
 15      for \(\displaystyle i\leftarrow 1\)  to  \(\displaystyle m\) do
 16        if \(\displaystyle x_i \in V_T'\) then
 17          \(\displaystyle P' \leftarrow P' \cup \{v_{x_i} \rightarrow x_i\}\);
 18          \(\displaystyle x_i \leftarrow v_{x_i}\);                    \(\displaystyle \triangleright\) zmień \(\displaystyle (v \rightarrow x_1x_2...x_m)\) na parę produkcji
 19        end if
 20      end for
 21      \(\displaystyle V_N'\leftarrow V_N' \cup \{ u_1^k, u_2^k,\dots, u_{m-2}^k\}\);                \(\displaystyle \triangleright\) nowe symbole nieterminalne
 22      \(\displaystyle P'\leftarrow P' \cup \{v\rightarrow x_1 u^k_1\}\)           \(\displaystyle \triangleright\) nowe produkcje w miejsce \(\displaystyle (v \rightarrow x_1x_2...x_m)\)
 23      \(\displaystyle P'\leftarrow P' \cup \{u_{m-2}\rightarrow x_{m-1}x_m\}\)
 24      for \(\displaystyle i\leftarrow 1\)  to  \(\displaystyle m-3\) do
 25        \(\displaystyle P' \leftarrow P' \cup \{u_i \rightarrow x_{i+1}u_{i+1}\}\);
 26      end for
 27    end if
 28  end for
 29  return \(\displaystyle G'=(V_N', V_T', v_0', P')\);

Przykład 2.1

Gramatykę \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) , dla której \(\displaystyle V_{N}=\{v_0, u,w \}\), \(\displaystyle V_{T}=\{a,b\}\), a zbiór praw dany jest poniżej

\(\displaystyle \begin{aligned} \nonumber v_0 &\rightarrow bu\ |\ aw \\ \nonumber u &\rightarrow buu\ |\ av_0b\ |\ a \\ \nonumber w &\rightarrow aaww\ |\ b \end{aligned}\)

sprowadzimy do postaci normalnej Chomsky'ego.

Do zbioru \(\displaystyle P'\) od razu włączamy produkcje \(\displaystyle u \rightarrow a\) oraz \(\displaystyle w \rightarrow b\). Poniżej, dla każdej z pozostałych produkcji wypisane są (po dwukropku) produkcje dodawane do \(\displaystyle P'\):

\(\displaystyle \begin{aligned} \nonumber v_0 \rightarrow bu &: v_b \rightarrow b;\ \ v_0 \rightarrow v_bu \\ \nonumber v_0 \rightarrow aw &: v_a \rightarrow a;\ \ v_0 \rightarrow v_aw \\ \nonumber u \rightarrow buu &: u \rightarrow v_bd_1;\ \ d_1 \rightarrow uu \\ \nonumber u \rightarrow av_0b &: u \rightarrow v_ad_2;\ \ d_2 \rightarrow v_0v_b \\ \nonumber w \rightarrow aaww &: w \rightarrow v_ad_3;\ \ d_3 \rightarrow v_ad_4;\ \ d_4 \rightarrow ww \end{aligned}\)

Ostatecznie gramtyka ma postać:

\(\displaystyle \begin{aligned} \nonumber v_0 &\rightarrow v_bu\ |\ v_aw \\ \nonumber u &\rightarrow v_bd_1\ |\ v_ad_2\ |\ a \\ \nonumber w &\rightarrow v_ad_3\ |\ b \\ \nonumber d_1 &\rightarrow uu \\ \nonumber d_2 &\rightarrow v_0v_b \\ \nonumber d_3 &\rightarrow v_ad_4 \\ \nonumber d_4 &\rightarrow ww \\ \nonumber v_a &\rightarrow a \\ \nonumber v_b &\rightarrow b \end{aligned}\)

Uwaga 2.1

Rozumowanie z dowodu twierdzenia o postaci Chomsky'ego można zastosować do gramatyk regularnych prawoliniowych. W wyniku tego uzyskujemy łatwo fakt, że postać normalna Chomsky'ego oznacza tu gramatykę o prawach typu:

{ \(\displaystyle v \rightarrow av'\) lub \(\displaystyle v \rightarrow a\) lub \(\displaystyle v \rightarrow 1\). }

Podobne twierdzenie, w którym mowa o postaci normalnej Greibach podamy poniżej. Przypomnijmy następujące oznaczenie. Dla dowolnego symbolu nieterminalnego \(\displaystyle v\in V_{N}\) w gramatyce \(\displaystyle G\) przez \(\displaystyle P(v)\) oznaczamy podzbiór zbioru produkcji \(\displaystyle P\) zawierający wyłącznie takie produkcje, które po lewej stronie mają symbol \(\displaystyle v\) . Twierdzenie poprzedzimy dwoma lematami. Obserwacja sformułowana w pierwszym lemacie jest oczywista

Lemat 2.1

Niech \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) będzie gramatyką bezkontekstową, a \(\displaystyle v\rightarrow xuy\,\) prawem tej gramatyki dla pewnych \(\displaystyle v,u\in V_{N},\, x,y\in \left( V_{N}\cup V_{T}\right) ^{*}\) . Gramatyka \(\displaystyle \overline{G}=\left( V_{N},V_{T},v_{0},\overline{P}\right)\) , w której

< center>\(\displaystyle \overline{P}=(P - \left\{ v\rightarrow xuy\right\}) \cup \left\{ v\rightarrow xzy\, :\, u\rightarrow z\in P\right\}\)

jest równoważna \(\displaystyle G\) .

Usuniętą produkcję \(\displaystyle v \rightarrow xuy\) nazywać będziemy niekońcową v-produkcją.

Definicja 2.2

Niech \(\displaystyle G=(V_N, V_T, v_0, P)\) będzie gramatyką bezkontekstową.

Produkcję \(\displaystyle v \rightarrow vx,\)

gdzie \(\displaystyle v \in V_N\), \(\displaystyle x \in (V_N \cup V_T)^*\) nazywamy lewostronnie rekursywną.

Kolejny lemat wskazuje możliwość wyeliminowania lewostronnej rekursji z gramatyki generującej język bezkontekstowy.

Lemat 2.2

Niech \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) będzie gramatyką bezkontekstową oraz \(\displaystyle v\in V_{N}\) . Zakładając niepustość zbioru \(\displaystyle P_{1}(v)=\left\{ v\rightarrow vx\in P(v)\, :\, x\in \left( V_{N}\cup V_{T}\right) ^{*}\right\}\) niech

\(\displaystyle P_{2}(v)=P(v) - P_{1}(v)\) . Gramatyka \(\displaystyle \overline{G}=\left( V_{N}\cup \left\{ u\right\} ,V_{T},v_{0},\overline{P}\right)\) , gdzie \(\displaystyle u\notin V_{N}\) ,

\(\displaystyle \overline{P}= (P - P_{1}(v)) \cup \left\{ v\rightarrow xu\, :\, v\rightarrow x\in P_{2}(v)\right\} \displaystyle \cup \left\{ u\rightarrow x\, :\, v\rightarrow vx\in P_{1}(v)\right\} \displaystyle \cup \left\{ u\rightarrow xu\, :\, v\rightarrow vx\in P_{1}(v)\right\}\)

jest równoważna gramatyce \(\displaystyle G\) .

Dowód

Zaobserwujmy, że w gramatyce \(\displaystyle G\) każdy ciąg produkcji ze zbioru \(\displaystyle P_{1}(v)\) musi zakończyć produkcja z \(\displaystyle P_{2}(v)\) . Zatem wyprowadzenie

\(\displaystyle v\mapsto_{G}vx_{1}\mapsto_{G}vx_{2}x_{1}\mapsto_{G}\cdots \cdots \mapsto_{G}vx_{k}\ldots x_{1}\mapsto_{G}xx_{k}\ldots x_{1}\)

można w gramatyce \(\displaystyle \overline{G}\) przeprowadzić następująco:

\(\displaystyle v\mapsto_{\overline{G}}xu\mapsto_{\overline{G}}xx_{k}u\mapsto_{\overline{G}}\cdots \mapsto_{\overline{G}}xx_{k}\cdots x_{2}u\mapsto_{\overline{G}}xx_{k}\ldots x_{1}\)

W podobny sposób można każde wyprowadzenie w \(\displaystyle \overline{G}\) przeprowadzić w \(\displaystyle G\) .

Udowodnimy teraz twierdzenie o postaci normalnej Greibach.

Twierdzenie 2.2

Dla każdej gramatyki bezkontekstowej \(\displaystyle G\), generującej język bez słowa pustego, istnieje równoważna gramatyka bezkontekstowa \(\displaystyle H\) w postaci normalnej Greibach.

Dowód

Załóżmy, że gramatyka \(\displaystyle G\) jest w postaci normalnej Chomsky'ego. W alfabecie nieterminalnym \(\displaystyle V_{N}=\left\{ v_{0},\ldots ,v_{n}\right\}\) wprowadzamy porządek zadany przez indeksy symboli nieterminalnych. Gramatykę \(\displaystyle G\) przekształcimy teraz na równoważną taką, że jeśli \(\displaystyle v_{i}\rightarrow v_{j}x\) jest prawem nowej gramatyki, to \(\displaystyle j>i.\) Efekt taki uzyskamy, przekształcając prawa kolejno, zgodnie z porządkiem wprowadzonym w zbiorze \(\displaystyle V_{N}\) i symbolem nieterminalnym występującym po lewej stronie prawa. Załóżmy, że dla pewnego \(\displaystyle k\), wszystkich \(\displaystyle i=0,\ldots ,k-1\) , gdzie \(\displaystyle 1\leqslant k\leqslant n\) jest:

\(\displaystyle \text{jeśli } \;\; v_{i}\rightarrow v_{j}x \; \; \text{jest prawem}, \; \text{to} \; j>i\)

oraz istnieje \(\displaystyle j<k\) takie, że

\(\displaystyle v_{k}\rightarrow v_{j}x\; \; \; \text{jest prawem}.\)

W oparciu o lemat 2.1 prawo \(\displaystyle v_{k}\rightarrow v_{j}x\) zastępujemy prawami \(\displaystyle v_{k}\rightarrow v_{l}yx\) , gdzie \(\displaystyle v_{j}\rightarrow v_{l}y\in P\) lub \(\displaystyle v_{k}\rightarrow ayx\) , gdzie \(\displaystyle v_{j}\rightarrow ay\in P\) . Stąd, że \(\displaystyle j<k\) , to \(\displaystyle l>j\) . Powtarzamy to postępowanie (co najwyżej \(\displaystyle k-1\) razy), aż uzyskamy nierówność \(\displaystyle l\geqslant k\) lub prawo \(\displaystyle v_{k}\rightarrow ax\) , gdzie \(\displaystyle a\in V_{T}\) . W przypadku, gdy otrzymamy \(\displaystyle l=k\) , czyli lewą rekursję \(\displaystyle v_{k}\rightarrow v_{k}x\) , stosujemy Lemat 2.2, wprowadzając nowy symbol nieterminalny \(\displaystyle v_{n+k+1}\) . Analogicznie postępujemy, gdy w gramatyce \(\displaystyle G\) występuje lewa rekursja \(\displaystyle v_{k}\rightarrow v_{k}x\) dla \(\displaystyle k=0,...,n\).

W wyniku wprowadzonych przekształceń uzyskamy, równoważną wyjściowej, gramatykę ze zbiorem produkcji \(\displaystyle \overline{P}\) , w którym

\(\displaystyle \begin{array} {ll} v_{i}\rightarrow v_{j}x\; \; \textrm{oraz} \displaystyle & \; j>i,\;i=0,...,n-1,\;j=1,...,n\; \\ v_{i}\rightarrow ax,\; \; \textrm{gdzie} \displaystyle & \;i=0,...,n, \; a\in V_{T}\\ v_{i}\rightarrow x,\; \; \textrm{gdzie} \displaystyle & \; i=n+1,...,2n+1, \end{array}\)

gdzie pierwszą literą słowa \(\displaystyle x\), które występuje w trzecim typie produkcji, jest symbol nieterminalny różny od \(\displaystyle v_i\) (nie jest to lewa rekursja). Zauważmy, że każda produkcja z \(\displaystyle \overline{P}(v_{n})\) ma postać \(\displaystyle v_{n}\rightarrow ax\) oraz każda produkcja z \(\displaystyle \overline{P}(v_{n-1})\) ma postać \(\displaystyle v_{n-1}\rightarrow v_{n}x\) lub \(\displaystyle v_{n-1}\rightarrow ax\) . A więc dla \(\displaystyle i=0,...,n\) każda produkcja z \(\displaystyle \overline{P}(v_{i})\) jest postaci \(\displaystyle v_{i}\rightarrow v_{j}x,\: j>i\) lub \(\displaystyle v_{i}\rightarrow ax\) .

Stosujemy teraz Lemat 2.1 do praw ze zbioru \(\displaystyle \overline{P}(v_{n})\) i \(\displaystyle \overline{P}(v_{n-1})\) , tak by prawe strony otrzymanych produkcji zaczynały się symbolem terminalnym. Następnie stosujemy Lemat 2.1 do praw ze zbioru \(\displaystyle \overline{P}(v_{n-2}),\ldots ,\overline{P}(v_{1})\) . Po tych zmianach prawe strony produkcji zaczynają się symbolem terminalnym. Natomiast żadna z produkcji należących do \(\displaystyle \overline{P}(v_{i})\) dla \(\displaystyle i=n+1,\ldots ,2n +1\) nie jest lewą rekursją, co wynika z konstrukcji gramatyki \(\displaystyle \overline{G}\) i z Lematu 2.2. Produkcje te zaczynają się symbolem nieterminalnym i w związku z tym stosujemy kolejny raz Lemat 2.1. W rezultacie uzyskujemy bezkontekstową gramatykę \(\displaystyle H\) w postaci normalnej Greibach równoważną wyjściowej gramatyce \(\displaystyle G\) .

Prezentowany teraz algorytm PrzekształćDlaGreibach przekształca gramatykę bezkontekstową, realizując powyższe dwa lematy, czyli usuwając v-produkcje niekońcowe i eliminując lewostronną rekursję. Zakładamy, bez utraty ogólności, że na wejściu algorytm otrzymuje gramatykę w postaci normalnej Chomsky'ego.

Algorytm PrzekształćDlaGreibach - buduje gramatykę bezkontekstową taką, że każda produkcja jest postaci \(\displaystyle v_k \rightarrow v_jx\), \(\displaystyle k < j\) lub jej prawa strona zaczyna się od symbolu terminalnego

  1  Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa w postaci Chomsky'ego.
  2  Wyjście: \(\displaystyle G'=(V_N', V_T, v_0, P')\) - gramatyka bezkontekstowa
 bez niekońcowych \(\displaystyle v\)-produkcji i bez lewostronnej rekursji.
  3  \(\displaystyle V_N' \leftarrow V_N\);                                                  \(\displaystyle \triangleright\displaystyle V_N'=\{v_0,\dots, v_n\}\)
  4  \(\displaystyle V_T' \leftarrow V_T\);
  5  \(\displaystyle P' \leftarrow P\);
  6  for \(\displaystyle k \leftarrow 1\)  to  \(\displaystyle n\) do
  7    for \(\displaystyle r=1\)  to  \(\displaystyle k\) do
  8      for \(\displaystyle j=0\)  to  \(\displaystyle k-1\) do
  9        for each \(\displaystyle (v_k \rightarrow v_jx_1\dots x_s) \in P'\) do
 10          \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_jx_1\dots x_s\}\);
 11          for each \(\displaystyle (v_j \rightarrow y_1\dots y_l) \in P'\) do
 12            \(\displaystyle P' \leftarrow P' \cup \{v_k \rightarrow y_1\dots y_lx_1\dots x_s\}\);
 13          end for
 14        end for
 15      end for
 16    end for
 17    for \(\displaystyle j=0\)  to  \(\displaystyle k-1\) do
 18      for each \(\displaystyle (v_k \rightarrow v_jx_1\dots x_s) \in P'\) do
 19        \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_jx_1\dots x_s\}\);
 20      end for
 21    end for
 22  end for
 23  for \(\displaystyle k \leftarrow 0\) to  \(\displaystyle n\) do
 24    for each \(\displaystyle (v_k \rightarrow v_kx_1\dots x_s) \in P'\) do
 25      \(\displaystyle V_N'\leftarrow V_N' \cup \{ v_{n+k+1} \}\);
 26      \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_kx_1\dots x_s\}\);
 27      \(\displaystyle P' \leftarrow P' \cup \{v_{n+k+1} \rightarrow x_1\dots x_s\}\);
 28      \(\displaystyle P' \leftarrow P' \cup \{ v_{n+k+1} \rightarrow x_1\dots x_s v_{n+k+1}\}\);
 29    end for
 30    for each \(\displaystyle (v_k \rightarrow y_1 \dots y_s) \in P'\) do 
 31      if \(\displaystyle y_1 \neq v_k\) then
 32        \(\displaystyle P' \leftarrow P' \cup \{v_k \rightarrow y_1 \dots y_s v_{n+k+1}\}\);
 33      end if
 34    end for
 35  end for
 36  return \(\displaystyle G'=(V_N', V_T, v_0, P')\);

Kolejny algorytm PostaćNormalnaGreibach przekształca gramatykę bezkontekstową do postaci normalnej Greibach. Zakładamy, że algorytm ten otrzymuje na wejściu gramatykę bezkontekstową właściwą.

Algorytm PostaćNormalnaGreibach - buduje gramatykę bezkontekstową w postaci normalnej Greibach

  1  Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa właściwa.
  2  Wyjście: \(\displaystyle G'=(V_N', V_T', v_0', P')\) - gramatyka bezkontekstowa w postaci normalnej Greibach.
  3  \(\displaystyle G \leftarrow\)PostaćNormalnaChomsky'ego\(\displaystyle (G)\);                            \(\displaystyle \triangleright\displaystyle V_N=\{v_0,...,v_n\}\)
  4  \(\displaystyle G' \leftarrow\)PrzekształćDlaGreibach\(\displaystyle (G)\);                   \(\displaystyle \triangleright\displaystyle V_N' \subset \{v_0,...,v_{2n+1}\}\),\(\displaystyle V_T'=V_T\)
  5  for \(\displaystyle i\leftarrow n-1\)  downto  \(\displaystyle 0\) do
  6    for \(\displaystyle j\leftarrow 1\)  to  \(\displaystyle n-i\) do
  7      for each \(\displaystyle (v_i \rightarrow v_{i+j}x_1\dots x_s)\in P'\) do
  8        \(\displaystyle P'\leftarrow P' \setminus \{ v_i \rightarrow v_{i+j}x_1\dots x_s \}\)
  9        for each \(\displaystyle (v_{i+j} \rightarrow z_1 \dots z_l)\in P'\) do 
 10          if \(\displaystyle z_1\in V_T\) then
 11            \(\displaystyle P'\leftarrow P'\cup \{v_i \rightarrow z_1 \dots z_l x_1\dots x_s\}\);
 12          end if
 13        end for
 14      end for
 15    end for
 16  end for
 17  for \(\displaystyle i\leftarrow n+1\)  to  2n+1 do
 18    for each  \(\displaystyle (v_i\rightarrow x_1\dots x_s)\in P'\) do
 19      \(\displaystyle P' \leftarrow P' \setminus \{ v_i\rightarrow x_1\dots x_s \}\)
 20      for each  \(\displaystyle (x_1 \rightarrow z_1 \dots z_l)\in P'\) do
 21        \(\displaystyle P'\leftarrow P' \cup \{ v_i \rightarrow z_1 \dots z_l x_2 \dots x_s \}\)
 22      end for
 23    end for
 24  end for
 25  \(\displaystyle v_0'\leftarrow v_0\);
 26  return \(\displaystyle G'=(V_N', V_T', v_0', P')\);

Przykład 2.2

Gramatykę \(\displaystyle G=\left( V_{N},V_{T},v_{1},P\right)\) , dla której \(\displaystyle V_{N}=\{v_1, v_2, v_3 \}\), \(\displaystyle V_{T}=\{a,b\}\), a zbiór praw dany jest poniżej

\(\displaystyle \begin{aligned} \nonumber v_1 &\rightarrow v_2v_3 \\ \nonumber v_2 &\rightarrow v_3v_1\ |\ b \\ \nonumber v_3 &\rightarrow v_1v_2\ |\ a, \end{aligned}\)

sprowadzimy do postaci normalnej Greibach.

Stosujemy procedurę PrzekształćDlaGreibach, wykorzystującą lematy 2.1 oraz 2.2. Prawe strony produkcji rozpoczynających się od \(\displaystyle v_1\) i \(\displaystyle v_2\) rozpoczynają się symbolami terminalnymi lub nieterminalami o wyższych indeksach niż odpowiednio 1 i 2, zatem jedyna produkcja, do której zastosujemy lemat 2.1, to \(\displaystyle v_3 \rightarrow v_1v_2\). Usuwamy ją, a ponieważ prawa jej strona rozpoczyna się nieterminalem \(\displaystyle v_1\), zastępujemy ten nieterminal prawą stroną produkcji \(\displaystyle v_1 \rightarrow v_2v_3\) i nowo otrzymaną produkcję \(\displaystyle v_3 \rightarrow v_2v_3v_2\) dodajemy do \(\displaystyle P\). Ponieważ pierwszy nieterminal po prawej stronie ma niższy indeks niż 3, znowu stosujemy tę samą operację: usuwamy produkcję \(\displaystyle v_3 \rightarrow v_2v_3v_2\) i na jej miejsce wstawiamy produkcje powstałe w wyniku zastąpienia pierwszego \(\displaystyle v_2\) z prawej jej strony łańcuchami \(\displaystyle v_3v_1\) oraz \(\displaystyle b\), czyli prawymi stronami produkcji, po których lewej stronie jest \(\displaystyle v_2\). Otrzymujemy zatem dwie nowe produkcje: \(\displaystyle v_3 \rightarrow v_3v_1v_3v_2\) oraz \(\displaystyle v_3 \rightarrow bv_3v_2\). Teraz każda produkcja jest następującej postaci: albo prawa jej strona zaczyna się terminalem, albo nieterminalem o indeksie większym lub równym indeksowi nieterminala stojącego z lewej strony.

Następny krok to wyeliminowanie lewostronnej rekursji. Stosujemy lemat 2.2 do produkcji \(\displaystyle v_3 \rightarrow v_3v_1v_3v_2\). Usuwamy ją z \(\displaystyle P\) i w jej miejsce wstawiamy produkcje \(\displaystyle v_3 \rightarrow bv_3v_2w_3\), \(\displaystyle v_3 \rightarrow aw_3\), \(\displaystyle w_3 \rightarrow v_1v_3v_2w_3\).

Po zakończeniu działania procedury PrzekształćDlaGreibach otrzymujemy następującą gramatykę:

\(\displaystyle \begin{aligned} \nonumber v_1 &\rightarrow v_2v_3 \\ \nonumber v_2 &\rightarrow v_3v_1\ |\ b \\ \nonumber v_3 &\rightarrow bv_3v_2w_3\ |\ aw_3\ |\ bv_3v_2\ |\ a \\ \nonumber w_3 &\rightarrow v_1v_3v_2\ |\ v_1v_3v_2w_3 \end{aligned}\)

Wszystkie prawe strony produkcji mających po lewej stronie \(\displaystyle v_3\) zaczynają się od terminala. W pętli (linie 5. - 16.) zastępujemy tymi prawymi stronami nieterminale \(\displaystyle v_3\) stojące jako pierwsze nieterminale po prawej stronie produkcji postaci \(\displaystyle v_2 \rightarrow v_3 x\); w naszym przypadku jedyną taką produkcją jest produkcja \(\displaystyle v_2 \rightarrow v_3v_1\); teraz zarówno produkcje postaci \(\displaystyle v_3 \rightarrow x\) jak i \(\displaystyle v_2 \rightarrow x\) rozpoczynają się terminalami. Po tym przekształceniu gramatyka ma postać:

\(\displaystyle \begin{aligned} \nonumber v_1 &\rightarrow v_2v_3 \\ \nonumber v_2 &\rightarrow bv_3v_2w_3v_1\ |\ aw_3v_1\ |\ bv_3v_2v_1\ |\ av_1\ |\ b \\ \nonumber v_3 &\rightarrow bv_3v_2w_3\ |\ aw_3\ |\ bv_3v_2\ |\ a \\ \nonumber w_3 &\rightarrow v_1v_3v_2\ |\ v_1v_3v_2w_3 \end{aligned}\)

Prawymi stronami produkcji postaci \(\displaystyle v_2 \rightarrow x\) zastępujemy teraz nieterminale \(\displaystyle v_2\) stojące jako pierwsze nieterminale po prawej stronie produkcji postaci \(\displaystyle v_1 \rightarrow v_2x\). W naszym przypadku jedyną taką produkcją jest produkcja \(\displaystyle v_1 \rightarrow v_2v_3\). Gramatyka wygląda teraz tak:

\(\displaystyle \begin{aligned} \nonumber v_1 &\rightarrow bv_3v_2w_3v_1v_3\ |\ aw_3v_1v_3\ |\ bv_3v_2v_1v_3\ |\ av_1v_3\ |\ bv_3 \\ \nonumber v_2 &\rightarrow bv_3v_2w_3v_1\ |\ aw_3v_1\ |\ bv_3v_2v_1\ |\ av_1\ |\ b \\ \nonumber v_3 &\rightarrow bv_3v_2w_3\ |\ aw_3\ |\ bv_3v_2\ |\ a \\ \nonumber w_3 &\rightarrow v_1v_3v_2\ |\ v_1v_3v_2w_3 \end{aligned}\)

Ostatecznie, po ukończeniu pętli, każda produkcja mająca po lewej stronie \(\displaystyle v_1\), \(\displaystyle v_2\) lub \(\displaystyle v_3\) zaczyna się terminalem, po którym następuje ciąg nieterminali. Te produkcje są więc w postaci normalnej Greibach.

W ostatnim kroku sprowadzamy do żądanej postaci nieterminale \(\displaystyle w_i\). Obie \(\displaystyle w_3\)-produkcje przekształcamy, zastępując pierwszy nieterminal stojący po ich prawych stronach (czyli \(\displaystyle v_1\)) prawymi stronami produkcji postaci \(\displaystyle v_1 \rightarrow x\). Obie \(\displaystyle w_3\)-produkcje zostaną z \(\displaystyle P\) usunięte, a na ich miejsce dodane zostaną produkcje

\(\displaystyle \nonumber w_3 &\rightarrow bv_3v_2w_3v_1v_3v_3v_2\ |\ aw_3v_1v_3v_3v_2\ |\ bv_3v_2v_1v_3v_3v_2 \\ \begin{array}{lll}\nonumber & & |\ av_1v_3v_3v_2\ |\ bv_3v_3v_2 \end{array}\)

oraz

\(\displaystyle \nonumber w_3 &\rightarrow bv_3v_2w_3v_1v_3v_3v_2w_3\ |\ aw_3v_1v_3v_3v_2w_3\ |\ bv_3v_2v_1v_3v_3v_2w_3 \\ \begin{array}{lll}\nonumber & & |\ av_1v_3v_3v_2w_3\ |\ bv_3v_3v_2w_3 \end{array}\)

Ostatecznie, gramatyka w postaci Greibach ma postać:

\(\displaystyle \nonumber v_1 &\rightarrow bv_3v_2w_3v_1v_3\ |\ aw_3v_1v_3\ |\ bv_3v_2v_1v_3\ |\ av_1v_3\ |\ bv_3 \\ \nonumber v_2 &\rightarrow bv_3v_2w_3v_1\ |\ aw_3v_1\ |\ bv_3v_2v_1\ |\ av_1\ |\ b \\ \nonumber v_3 &\rightarrow bv_3v_2w_3\ |\ aw_3\ |\ bv_3v_2\ |\ a \\ \nonumber w_3 &\rightarrow bv_3v_2w_3v_1v_3v_3v_2\ |\ aw_3v_1v_3v_3v_2\ |\ bv_3v_2v_1v_3v_3v_2 \\ \begin{array}{lll}\nonumber & & |\ av_1v_3v_3v_2\ |\ bv_3v_3v_2 bv_3v_2w_3v_1v_3v_3v_2w_3 \\ \nonumber & & |\ aw_3v_1v_3v_3v_2w_3\ |\ bv_3v_2v_1v_3v_3v_2w_3\ \\ \nonumber & & |\ av_1v_3v_3v_2w_3\ |\ bv_3v_3v_2w_3 \end{array}\)