Języki kontekstowe i automat liniowo ograniczony. Maszyna Turinga

W tym wykładzie omówimy języki i gramatyki kontekstowe oraz ich własności. Wprowadzimy automat liniowo ograniczony i uzasadnimy równość rodziny języków kontekstowych i rodziny języków rozpoznawanych przez automaty liniowo ograniczone. Zdefiniujemy maszynę Turinga i pokażemy równoważność tego modelu z wybranymi innymi modelami obliczeń.

W tym wykładzie omówimy kolejną rodzinę języków hierarchii Chomsky'ego, a mianowicie języki kontekstowe. Przedstawimy kilka własnosci gramatyk kontekstowych, czyli typu (1) oraz wprowadzimy pojęcie automatu liniowo ograniczonego. Wprowadzimy też najogólniejszy model obliczeń, a mianowicie maszynę Turinga.

Języki kontekstowe

Języki kontekstowe to kolejna rodzina języków w hierarchii Chomsky'ego. Rozszerza ona istotnie rodzinę języków bezkontekstowych. Wykorzystanie tej rodziny języków formalnych jest dość ograniczone. Brak jest bowiem praktycznych metod konstrukcji parserów dla tych gramatyk.

Ta część wykładu prezentuje gramatyki równoważne gramatykom kontekstowym, posiadające pewne określone własności. Te własności wykorzystuje się przy uzasadnieniu faktu, że rodzina języków kontekstowych pokrywa się z rodziną języków rozpoznawanych przez automaty liniowo ograniczone. Biorąc pod uwagę to, że zastosowania tej rodziny języków formalnych nie są powszechne oraz to, że dowody dla przedstawionych poniżej twierdzeń są mocno techniczne, postanowiliśmy zrezygnować z rygorystycznej prezentacji tego materiału i pominąć dowody. Zainteresowany Student może je znaleźć w literaturze wskazanej do tego przedmiotu.

Definicja 1.1

Gramatykę $\displaystyle G=(V_{N},V_{T},v_{0},P)$ nazywamy rozszerzającą, jeśli każde prawo jest postaci $\displaystyle x\rightarrow y$ , gdzie $\displaystyle x,y\in (V_{N}\cup V_{T})^{*}$ i spełniona jest nierówność $\displaystyle \mid x\mid \leqslant \mid y\mid$ lub jest to prawo $\displaystyle v_{0}\rightarrow 1$ i wtedy $\displaystyle v_{0}$ nie występuje po prawej stronie w żadnej produkcji z $\displaystyle P$ .

Wprost z definicji wynika, że gramatyka kontekstowa jest gramatyką rozszerzającą. Prawdziwe jest również następujące twierdzenie.

Twierdzenie 1.1

Dla dowolnej gramatyki $\displaystyle G=(V_{N},V_{T},v_{0},P)$ rozszerzającej istnieje równoważna gramatyka kontekstowa.

Wprowadzimy teraz gramatyki z markerem końca.

Definicja 1.2

Gramatyką z markerem końca $\displaystyle \sharp$ nazywamy gramatykę $\displaystyle G_{\sharp }=(V_{N}\cup \{\sharp \},V_{T},v_{0},P)$ taką, że $\displaystyle \sharp \notin V_{N}\cup V_{T}$ oraz prawa są postaci: $\displaystyle u\rightarrow v$ , $\displaystyle \sharp u\rightarrow \sharp v$ lub $\displaystyle u\sharp \rightarrow v\sharp$ , gdzie $\displaystyle u,v\in (V_{N}\cup V_{T})^{*}$ i w słowie $\displaystyle u$ występuje co najmniej jeden symbol nieterminalny z $\displaystyle V_{N}$ . Językiem generowanym przez tę gramatykę nazywamy zbiór

$\displaystyle L(G_{\sharp })=\{w\in V_{T}^{*}:\: \sharp v_{0}\sharp \mapsto^{*}\sharp w\sharp \}.$

Gramatyka z markerem końca $\displaystyle G_{\sharp }$ jest kontekstowa (typu $\displaystyle 1$ ), jeśli jej prawa po wymazaniu markera $\displaystyle \sharp$ spełniają warunki gramatyki rozszerzającej. Oczywiście dla dowolnej gramatyki kontekstowej istnieje równoważna gramatyka kontekstowa z markerem końca. Prawdziwe jest również następujące twierdzenie:

Twierdzenie 1.2

Dla dowolnej gramatyki kontekstowej z markerem końca istnieje równoważna gramatyka kontekstowa.

Dowód

Niech $\displaystyle G_{\sharp }=(V_{N}\cup \{\sharp \},V_{T},v_{0},P)$ będzie dowolną gramatyką kontekstową z markerem końca. Zakładamy, bez ograniczania ogólności rozważań, że w zbiorze $\displaystyle P$ nie występuje prawo $\displaystyle v_{0}\rightarrow 1$ (po wymazaniu markera $\displaystyle \sharp$ ). Dla każdego symbolu $\displaystyle x$ ze zbioru $\displaystyle V=V_{N}\cup V_{T}$ określamy trzy symbole $\displaystyle \, ^{\sharp }x,x^{\sharp },^{\: \sharp }x^{\sharp }$ oraz oznaczamy odpowiednio przez $\displaystyle \, ^{\sharp }V,V^{\sharp },^{\sharp }V^{\sharp }$ zbiory tych symboli. Dla $\displaystyle u=u_{1}...u_{k}$ takiego, że $\displaystyle k\geqslant 1$ i $\displaystyle u_{i}\in V$ dla $\displaystyle i=1,...,k$ wprowadzamy także następujące oznaczenia:

$\displaystyle \, ^{\sharp }u=\, ^{\sharp }u_{1}u_{2}...u_{k}$ , $\displaystyle u^{\sharp }=u_{1}...u_{k-1}u_{k}^{\sharp }$ oraz $\displaystyle \, ^{\sharp }u^{\sharp }=\, ^{\sharp }u_{1}u_{2}...u_{k-1}u_{k}^{\sharp }$ gdy $\displaystyle k>1$ .

Przy takich oznaczeniach definiujemy gramatykę

$\displaystyle G_{1}=(V_{N}\cup \, ^{\sharp }V\cup V^{\sharp }\cup ^{\sharp }V^{\sharp },V_{T},\, ^{\sharp }v_{0}^{\sharp },P_{1}),$

w której zbiór praw $\displaystyle P_{1}$ składa się ze wszystkich praw uzyskanych zgodnie z poniższymi warunkami:

jeśli $\displaystyle u\rightarrow w\in P$ , to $\displaystyle u\rightarrow w,\: ^{\#}u\rightarrow \, ^{\#}w,\: u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},$
jeśli $\displaystyle \, ^{\#}u\rightarrow \, ^{\#}w\in P$ , to $\displaystyle \: u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},$
jeśli $\displaystyle u^{\#}\rightarrow w^{\#}\in P$ , to $\displaystyle u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},$
$\displaystyle \, ^{\#}x\rightarrow x,\: x^{\#}\rightarrow x,\: ^{\#}x^{\#}\rightarrow x\in P_{1}$

dla wszystkich $\displaystyle x\in V$ .

Określona w ten sposób gramatyka $\displaystyle G_{1}$ jest gramatyką rozszerzającą i równoważną wyjściowej. Dla gramatyki $\displaystyle G_{1}$ istnieje, zgodnie z poprzednim twierdzeniem, równoważna gramatyka kontekstowa, co kończy dowód twierdzenia.

Prawdziwe jest także następujące twierdzenie (porównaj z 1.1).

Twierdzenie 1.3

Dla dowolnej gramatyki kontekstowej (rozszerzającej) istnieje równoważna gramatyka kontekstowa (rozszerzająca) o tej własności, że każde prawo, w którym występuje symbol terminalny, jest postaci $\displaystyle v\rightarrow a$ , gdzie $\displaystyle v\in V_{N},\: a\in V_{T}$ .

Mówimy, że gramatyka $\displaystyle G$ jest rzędu $\displaystyle n>0$ , jeśli dla każdego prawa $\displaystyle x\rightarrow y$ tej gramatyki spełniony jest warunek $\displaystyle \mid x\mid \leqslant n$ i $\displaystyle \mid y\mid \leqslant n$ . Kolejne twierdzenie stwierdza możliwość dalszego uproszczenia praw gramatyki rozszerzającej.

Twierdzenie 1.4

Dla każdej gramatyki rozszerzającej istnieje równoważna gramatyka rozszerzająca rzędu $\displaystyle 2$ .

Na koniec wprowadzimy jeszcze jeden rodzaj gramatyk równoważnych gramatykom kontekstowym. Są to mianowicie gramatyki liniowo ograniczone.

Definicja 1.3

Gramatyka $\displaystyle G=(V_{N},V_{T},v_{0},P)$ jest liniowo ograniczona, jeśli każde prawo jest jednej z następujących postaci:

$\displaystyle v_{0}\rightarrow v_{0}v,\: v_{1}v_{2}\rightarrow z_{1}z_{2},\: v\rightarrow x,$

gdzie $\displaystyle x\in V_{N}\cup V_{T},\: v,v_{1},v_{2},z_{1},z_{2}\in V_{N}$ oraz $\displaystyle v_{0}\notin \{x,z_{1},z_{2},v\}$ .

Twierdzenie 1.5

Dla dowolnej gramatyki kontekstowej $\displaystyle G$ istnieje gramatyka liniowo ograniczona $\displaystyle G_{1}$ , która jest równoważna $\displaystyle G$ lub też generuje język $\displaystyle L(G)\setminus \{1\}$ .

Dowód

W świetle poprzednich twierdzeń możemy przyjąć, że gramatyka kontekstowa $\displaystyle G=(V_{N},V_{T},v_{0},P)$ ma prawa wyłącznie w następujących postaciach:

$\displaystyle v_{0}\rightarrow 1,$
$\displaystyle v\rightarrow x$ gdzie $\displaystyle v\in V_{N},\: x\in V_{N}\cup V_{T},$
$\displaystyle v\rightarrow v_{1}v_{2}$ gdzie $\displaystyle v,v_{1},v_{2}\in V_{N},$
$\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}$ gdzie $\displaystyle v_{1},v_{2},v_{3},v_{4}\in V_{N}.$

Określamy gramatykę $\displaystyle G_{1}=(V_{N}\cup \{z_{0},z_{1}\},V_{T},z_{0},P_{1})$ , gdzie $\displaystyle z_{1},z_{2}$ są nowymi symbolami nieterminalnymi, a więc nie należą do $\displaystyle V_{N}$ . Natomiast zbiór praw $\displaystyle P_{1}$ składa się ze wszystkich praw ze zbioru $\displaystyle P$ postaci 2 i 4 oraz $\displaystyle z_{0}\rightarrow z_{0}z_{1},\: z_{0}\rightarrow v_{0},\:$ praw $\displaystyle z_{1}v\rightarrow vz_{1},\: vz_{1}\rightarrow z_{1}v$ dla $\displaystyle v\in V_{N}$ i praw $\displaystyle v_{1}z_{1}\rightarrow v_{3}v_{4}$ dla każdego prawa postaci 4 w gramatyce $\displaystyle G$ . Skonstruowana gramatyka jest liniowo ograniczona i spełnia tezę twierdzenia.

Automat liniowo ograniczony

Określimy teraz systemy, zwane automatami liniowo ograniczonymi, który rozpoznają języki kontekstowe.

Definicja 2.1

Automatem liniowo ograniczonym nazywamy system $\displaystyle \mathcal{A}_{LO}=(\Sigma _{T},S,P,s_{0},S_{F})$ , w którym $\displaystyle \Sigma _{T}$ jest skończonym alfabetem, $\displaystyle S$ skończonym zbiorem stanów, $\displaystyle S\cap \Sigma _{T}=\emptyset$ oraz wyróżniony jest podzbiór $\displaystyle \Sigma _{I}\subset \Sigma _{T}$ . Zbiór $\displaystyle \Sigma _{T}$ zwany jest alfabetem taśmy, a $\displaystyle \Sigma _{I}$ - alfabetem wejściowym. Wyróżnione są także: element $\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}$ zwany markerem końca, stan początkowy $\displaystyle s_{0}\in S$ oraz $\displaystyle S_{F}\subset S$ - zbiór stanów końcowych. Natomiast relacja przejść $\displaystyle P\subset (S\times \Sigma _{T})\times (S\times \Sigma _{T}\times \{-1,0,1\})$ spełnia następujące warunki:

jeśli $\displaystyle (s_{1},\#)P(s_{2},a,k)$ , to $\displaystyle a=\#,$
jeśli $\displaystyle (s_{1},a)P(s_{2},\#,k)$ , to $\displaystyle a=\#.$

Fakt, że $\displaystyle (s_{1},a)P(s_{2},b,k)$ , zapisujemy zazwyczaj jako $\displaystyle (s_{1},a)\rightarrow (s_{2},b,k)$ . Do opisu działania automatu liniowo ograniczonego wygodnie jest wprowadzić pojęcie konfiguracji (podobnie jak dla automatów ze stosem).

Konfiguracją automatu liniowo ograniczonego jest słowo $\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}$ , w którym $\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}$ . Pomiędzy dwoma konfiguracjami $\displaystyle d_{1},d_{2}$ zachodzi relacja bezpośredniego następstwa $\displaystyle d_{1}\mapsto d_{2}$ wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie $\displaystyle s_{1},s_{2}\in S$ , $\displaystyle a,b,c\in \Sigma _{T}$ oraz $\displaystyle v,w\in \Sigma _{T}^{*}:$

$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vs_{2}bw$ oraz $\displaystyle (s_{1},a)P(s_{2},b,0),$
$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vbs_{2}w$ oraz $\displaystyle (s_{1},a)P(s_{2},b,1),$
$\displaystyle d_{1}=vcs_{1}aw$ , $\displaystyle d_{2}=vs_{2}cbw$ oraz $\displaystyle (s_{1},a)P(s_{2},b,-1).$

Przechodnie domknięcie relacji $\displaystyle \mapsto$ oznaczać będziemy symbolem $\displaystyle \mapsto^{*}$ i określać mianem obliczenia wykonanego przez automat liniowo ograniczony.

Język rozpoznawany przez automat liniowo ograniczony $\displaystyle \mathcal{A}_{LO}$ to zbiór słów nad alfabetem $\displaystyle \Sigma _{I}$ , pod działaniem których automat wykonuje obliczenie prowadzące do stanu końcowego, czyli

$\displaystyle L(\mathcal{A}_{LO})=\left\{ w\in \Sigma _{I}^{*}\: :\: s_{0}\#w\#\mapsto^{*}vs,\; v\in \Sigma _{T}^{*},\, s\in S_{F}\right\} .$

Język $\displaystyle L\subset \Sigma _{I}^{*}$ jest rozpoznawany (akceptowany) przez automat liniowo ograniczony, jeśli istnieje automat $\displaystyle \mathcal{A}_{LO}$ taki, że $\displaystyle \mathcal{L}(\mathcal{A}_{LO})=L.$

Rysunek 1

Opiszemy teraz możliwe ruchy automatu liniowo ograniczonego. Automat ten może czytać słowo wejściowe w dwóch kierunkach. Jego głowica może poruszać się w lewo lub w prawo. Automat może wymieniać czytaną literę na inną, ale nie rozszerza miejsca zajętego na taśmie przez czytane słowo. Działa niedeterministycznie. Czytając literę $\displaystyle a$, będąc w stanie $\displaystyle s$, automat ma kilka możliwości działania. Może mianowicie:

zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 1. Głowica czytająca automatu pozostaje w poprzedniej pozycji,
zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 2. Głowica czytająca automatu przesuwa się w prawo,
zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 3. Głowica czytająca automatu przesuwa się w lewo.

Związek pomiędzy rodziną języków kontekstowych a wprowadzoną rodziną automatów liniowo ograniczonych ustalają poniższe twierdzenia.

Twierdzenie 2.1

Dla dowolnego języka kontekstowego $\displaystyle L$ istnieje automat liniowo ograniczony $\displaystyle \mathcal{A}_{LO}$ taki, że $\displaystyle \mathcal{L}(\mathcal{A}_{LO})=L$ .

Dowód

Można założyć, bez ograniczenia ogólności naszych rozważań, że gramatyka $\displaystyle G=(V_{N},V_{T},v_{0},P)$ generująca język $\displaystyle L$ ma prawa wyłącznie następujących postaci:

(G) $\displaystyle v\rightarrow x$ , gdzie $\displaystyle v\in V_{N},x\in V_{N}\cup V_{T},x\neq v_{0},$
(G) $\displaystyle v_{0}\rightarrow v_{0}v_{1}$ , gdzie $\displaystyle v_{1}\in V_{N},v_{1}\neq v_{0},$
(G) $\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}$ , gdzie $\displaystyle v_{1},...,v_{4}\in V_{N},v_{3},v_{4}\neq v_{0},$
(G) $\displaystyle v_{0}\rightarrow 1,$ jeśli $\displaystyle 1\in L$ .

Określamy automat liniowo ograniczony $\displaystyle \mathcal{A}_{LO}=(\Sigma _{T},S,P,s_{0},S_{F})$ , przyjmując $\displaystyle \Sigma _{T}=V_{N}\cup V_{T}\cup \{\#,\flat \}$ , $\displaystyle S=\{s_{0},s_{1},s_{2},s_{3},s_{4}\}\cup \{s_{v_{1}}: \displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\in P\}$ , $\displaystyle \Sigma _{I}=V_{N}\cup V_{T}$ , $\displaystyle S_{F}=\{s_{3}\}$ , $\displaystyle s_{0}$ - stan początkowy. Relacja przejść automatu $\displaystyle \mathcal{A}_{LO}$ zdefiniowana jest poniżej:

(A) $\displaystyle (s_{0},\#)\rightarrow (s_{0},\#,1),$
(A) $\displaystyle (s_{0},\#)\rightarrow (s_{4},\#,1)$ jeśli $\displaystyle 1\in L,$
(A) $\displaystyle (s_{0},x)\rightarrow (s_{0},x,1)$ , $\displaystyle (s_{0},x)\rightarrow (s_{0},x,-1)$ dla każdego $\displaystyle x\in V_{N}\cup V_{T},$
(A) $\displaystyle (s_{0},x)\rightarrow (s_{0},v,0)$ jeśli $\displaystyle v\rightarrow x\in P$ i $\displaystyle x\neq v_{0},$
(A) $\displaystyle (s_{0},v_{3})\rightarrow (s_{v_{1}},v_{1},1),\; (s_{v_{1}},v_{4})\rightarrow (s_{0},v_{2},0)$ jeśli $\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\in P,$
(A) $\displaystyle (s_{0},v_{0})\rightarrow (s_{1},v_{0},-1),$
(A) $\displaystyle (s_{1},\#)\rightarrow (s_{2},\#,1),$
(A) $\displaystyle (s_{1},\flat )\rightarrow (s_{2},\flat ,1),$
(A) $\displaystyle (s_{2},v_{0})\rightarrow (s_{3},\flat ,1),$
(A) $\displaystyle (s_{3},v_{1})\rightarrow (s_{0},v_{0},0)$ , gdy $\displaystyle v_{0}\rightarrow v_{0}v_{1}\in P,$
(A) $\displaystyle (s_{3},\#)\rightarrow s_{3},\#,1),\; (s_{4},\#)\rightarrow (s_{3},\#,1).$

Określony automat $\displaystyle \mathcal{A}_{LO}$ rozpoznaje tylko te słowa, które są generowane przez gramatykę $\displaystyle G$ , symulując wstecz każde wyprowadzenie gramatyki $\displaystyle G$ .

Prawdziwe jest również następujące twierdzenie.

Twierdzenie 2.2

Dla dowolnego języka $\displaystyle L$ rozpoznawanego przez automat liniowo ograniczony $\displaystyle \mathcal{A}_{LO}$ istnieje gramatyka kontekstowa $\displaystyle G$ taka, że $\displaystyle L(G)=L$ .

W dowodzie konstruuje się odpowiednią gramatykę.Zasada tej konstrukcji jest następująca. Z symbolu startowego gramatyka generuje dowolne słowa, ustawiając zawsze na prawym końcu symbol nieterminalny związany z przejściem automatu do stanu końcowego. Następnie korzysta się z możliwości zamiany takiego symbolu nieterminalnego na inne. W ten sposób gramatyka symuluje wstecz działanie automatu, wprowadzając symbole nieterminalne odpowiadające stanom automatu. Dojście do stanu początkowego automatu w tej symulacji jest równoznaczne z usunięciem ostatniego symbolu nieterminalnego i wygenerowaniem słowa dokładnie tego samego, które rozpoznaje automat.

Udowownimy teraz zamkniętość rodziny języków kontekstowych ze względu na iloczyn mnogościowy.

Twierdzenie 2.3

Dla dowolnych języków kontekstowych $\displaystyle L_{1},L_{2}\subset A^{*}$ iloczyn mnogościowy tych języków $\displaystyle L_{1}\cap L_{2}$ jest językiem kontekstowym.

Dowód

(szkic) Załóżmy, że języki $\displaystyle L_{1},L_{2}$ są rozpoznawane przez automaty liniowo ograniczone, $\displaystyle \mathcal{A}^{1}_{LO}$ i $\displaystyle \mathcal{A}_{LO}^{2}$ . Opiszemy konstrukcję automatu liniowo ograniczonego $\displaystyle \mathcal{A}_{LO}$ , który rozpoznawać będzie wyłącznie słowa akceptowane równocześnie przez oba automaty. Działanie tego automatu jest następujące. Każde słowo będzie czytane trzy razy. Przy pierwszym czytaniu automat $\displaystyle \mathcal{A}_{LO}$ dubluje litery, to znaczy w miejsce litery $\displaystyle a$ wprowadza parę $\displaystyle (a,a)$ . Po zakończeniu tej procedury automat wraca do skrajnej lewej pozycji i rozpoczyna symulację automatu $\displaystyle \mathcal{A}^{1}_{LO}$ . Jeśli ta symulacja doprowadzi do zaakceptowania czytanego słowa przez automat $\displaystyle \mathcal{A}^{1}_{LO}$ , to automat $\displaystyle \mathcal{A}_{LO}$ rozpoczyna obliczenie od początku, symulując teraz pracę automatu $\displaystyle \mathcal{A}_{LO}^{2}$ . Jeśli i ta symulacja zakończy się zaakceptowaniem czytanego słowa, to automat przechodzi do ustalonego stanu końcowego, a to oznacza akceptację tego słowa. Działając w opisany sposób, automat $\displaystyle \mathcal{A}_{LO}$ rozpoznaje język $\displaystyle L_{1}\cap L_{2}$ , a to w świetle udowodnionego powyżej twierdzenia oznacza, że przecięcie języków kontekstowych $\displaystyle L_{1}\cap L_{2}$ jest językiem kontekstowym.

Ponieważ dalsze własności domkniętości rodziny języków kontekstowych pokrywają się z własnościami języków typu (0), więc omówimy te własności wspólnie, co będzie mieć miejsce w następnym wykładzie.

Maszyna Turinga

Przejdziemy teraz do prezentacji ogólnego modelu maszyny liczącej, który został wprowadzony w 1936 roku przez Alana M. Turinga. Na cześć swego autora został on nazwany (jednotaśmową) maszyną Turinga. Model ten jest podobny w swojej idei do rozważanych wcześniej automatów liniowo ograniczonych, przy czym jednym z podstawowych założeń (i różnic względem automatów) jest nieskończony dostęp do pamięci. Maszyna Turinga może wydawać się na początku pojęciem bardzo abstrakcyjnym. Jednak, jak później zobaczymy, stanowi ona jedną z podstawowych koncepcji współczesnej informatyki. Pozwala na formalne zdefiniowanie pojęcia algorytmu oraz jego złożoności obliczeniowej. Jako model obliczeń pozwala odpowiedzieć także na bardzo ważne pytanie: czy każdy problem można rozwiązać algorytmicznie?

Jednotaśmowa maszyna Turinga jest podobna w swej idei do automatu liniowo ograniczonego, pominięte jednak zostaje, jak wspomnieliśmy, ograniczenie dostępu do pamięci. Omawiana maszyna jest abstrakcyjnym tworem w skład którego wchodzą:

dwustronnie nieskończona taśma zbudowana z komórek zawierających symbole z pewnego zadanego alfabetu,
głowica, która może czytać i zapisywać symbole w komórkach taśmy oraz poruszać się w prawo lub lewo o jedną komórkę lub pozostawać na tej samej pozycji podczas jednego kroku czasowego,
działający sekwencyjnie mechanizm odpowiedzialny za sterowanie maszyną; mechanizm ten na podstawie symbolu odczytanego z komórki pod głowicą oraz stanu, w którym aktualnie znajduje się maszyna, dokonuje zapisu symbolu w tejże komórce, przechodzi do kolejnego stanu i przesuwa głowicę w prawo, lewo lub też nie zmienia pozycji głowicy.

Podamy teraz formalną definicję maszyny Turinga. Aby zachować analogię do poprzednich wykładów, zdefiniujemy maszynę w języku konfiguracji.

Definicja 3.1

(Jednotaśmowa deterministyczna) maszyna Turinga jest to system $\displaystyle \mathbf{MT}=(\Sigma _{T},S,f,s_{0},S_{F})$ , w którym $\displaystyle \Sigma _{T}$ jest skończonym alfabetem, $\displaystyle S$ skończonym zbiorem stanów, $\displaystyle S\cap \Sigma _{T}=\emptyset$ oraz wyróżniony jest podzbiór $\displaystyle \Sigma _{I}\subset \Sigma _{T}$ . Zbiór $\displaystyle \Sigma _{T}$ zwany jest alfabetem taśmy, a $\displaystyle \Sigma _{I}$ - alfabetem wejściowym. Wyróżnione są także: element $\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}$ zwany markerem końca, stan początkowy $\displaystyle s_{0}\in S$ oraz $\displaystyle S_{F}\subset S$ - zbiór stanów końcowych. Natomiast funkcja przejść jest funkcją częściową $\displaystyle f:\: (S\times \Sigma _{T})\rightarrow (S\times \Sigma _{T}\times \{-1,0,1\}$ .

Konfiguracją maszyny Turinga jest słowo $\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}$ , w którym $\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}$ . Pomiędzy dwiema konfiguracjami $\displaystyle d_{1},d_{2}$ zachodzi relacja bezpośredniego następstwa $\displaystyle d_{1}\mapsto d_{2}$ wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie $\displaystyle s_{1},s_{2}\in S$ , $\displaystyle a,b,c\in \Sigma _{T}$ oraz $\displaystyle v,w\in \Sigma _{T}^{*}$:

$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vs_{2}bw$ oraz $\displaystyle f(s_{1},a)=(s_{2},b,0),$
$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vbs_{2}w$ oraz $\displaystyle f(s_{1},a)=(s_{2},b,1)$ i $\displaystyle w\neq 1,$
$\displaystyle d_{1}=vs_{1}\#$ , $\displaystyle d_{2}=vbs_{2}\#$ oraz $\displaystyle f(s_{1},\#)=(s_{2},b,1),$
$\displaystyle d_{1}=vcs_{1}aw$ , $\displaystyle d_{2}=vs_{2}cbw$ oraz $\displaystyle f(s_{1},a)=(s_{2},b,-1),$
$\displaystyle d_{1}=s_{1}\#w$ , $\displaystyle d_{2}=s_{2}\#bw$ oraz $\displaystyle f(s_{1},\#)=(s_{2},b,-1).$

Przechodnie domknięcie relacji $\displaystyle \mapsto$ oznaczać będziemy symbolem $\displaystyle \mapsto^{*}$ i określać mianem obliczenia wykonanego przez maszynę Turinga. Konfiguracja $\displaystyle d_{1}\in (\Sigma _{T}\cup S)^{*}$ jest końcowa, jeśli stąd, że $\displaystyle d_{1}\mapsto d_{2}$ , wynika $\displaystyle d_{2}=d_{1}.$ Mówimy, że maszyna Turinga zatrzymuje się w $\displaystyle d_{1}$ wtedy i tylko wtedy, gdy $\displaystyle d_{1}$ jest konfiguracją końcową.

Zauważmy, że wprowadzenie markera końca jest zabiegiem czysto formalnym. Pozwala on z jednej strony na oznaczenie słowa wejściowego, a z drugiej strony wskazuje na elementy taśmy, które były zmieniane (czy to przez wprowadzenie słowa wejściowego, czy też poprzez ruch głowicy).

Definicja 3.2

Język rozpoznawany przez maszynę Turinga $\displaystyle MT$ jest to zbiór

$\displaystyle L(\mathbf{MT})=\left\{ w\in \Sigma _{T}^{*}\: :\: \sharp s_{0}w\sharp \mapsto^{*}\sharp w_{1}s_{F}w_{2}\sharp ,\; dla\: pewnych\: w_{1},w_{2}\in \Sigma _{T}^{*},s_{F}\in S_{F}\right\} .$

Język $\displaystyle L\subset \Sigma _{I}^{*}$ jest rozpoznawany (akceptowany) przez maszynę Turinga, jeśli istnieje $\displaystyle MT$ taka, że $\displaystyle L(\mathcal{MT})=L.$ Klasę języków rozpoznawanych przez maszynę Turinga oznaczamy $\displaystyle \mathcal{L}(MT)$ .

We wprowadzonym przez nas ujęciu formalnym, działanie maszyny Turinga należy wyobrażać sobie następująco. W pierwszym etapie na taśmę zostają zapisane symbole słowa wejściowego (z alfabetu $\displaystyle \Sigma_I$), a następnie komórki przyległe zostają oznaczone symbolami $\displaystyle \sharp$. Jednocześnie maszyna jest sprowadzana do stanu $\displaystyle s_0$, a głowica zostaje ustawiona nad pierwszym symbolem słowa wejściowego. W tym momencie rozpoczyna się sekwencyjne przetwarzanie zawartości taśmy przez maszynę. Jeśli maszyna "zatrzyma się", tzn. w dwóch kolejnych chwilach czasowych nie wykona ruchu i jednocześnie nie zmieni stanu i symbolu taśmy, sprawdzany jest jej aktualny stan. Jeśli stan był akceptujący (czyli należał do zbioru $\displaystyle S_F$), to maszyna zaakceptowała słowo, w przeciwnym razie - słowo odrzuciła (gdyż nie może już osiągnąć stanu ze zbioru $\displaystyle S_F$). Należy zwrócić uwagę na to, że dla niektórych konfiguracji początkowych maszyna może nigdy się nie zatrzymać, a mimo to słowo zostanie przez nią zaakceptowane. To samo tyczy się odrzucania słów, jednak w tej sytuacji dowód, że słowo nie zostanie zaakceptowane, może być problematyczny. Zaprezentowane podejście ma na celu uproszczenie i tak już dość technicznych dowodów twierdzeń pojawiających się w tym wykładzie. Związki pomiędzy akceptowaniem a zatrzymywaniem maszyny Turinga zostaną skomentowane później (zob. Wniosek 4.1). W pierwszej kolejności przedstawiamy dwa przykłady:

Przykład 3.1

Skonstruujemy maszynę Turinga $\displaystyle MT_1$, która rozpoznaje język postaci $\displaystyle L=\left\{0^{2^n}\; : \; n\geqslant 0\right\}$. Zamierzone działanie maszyny $\displaystyle MT_1$ można opisać następująco:

Przejdź od lewego markera do prawego, zaznaczając symbolem $\displaystyle \diamondsuit$ co drugie $\displaystyle 0$.
Jeśli było tylko jedno $\displaystyle 0$, to akceptuj.
Jeśli w kroku 1. obszar pomiędzy markerami zawierał nieparzystą ilość $\displaystyle 0$, to odrzuć.
Powróć do lewego markera.
Powtórz działanie od 1.

Zwróćmy uwagę, że o ile jasne jest, w jaki sposób maszyna ma akceptować słowa wejściowe, odrzucanie tych słów nie zostało zdefiniowane. Aby ominąć ten problem, wprowadzimy jeden dodatkowy stan (nie należący do stanów końcowych), po osiągnięciu którego maszyna się zatrzymuje (tzn. nie wykonuje ruchów i przepisuje na taśmie wciąż ten sam symbol).

Określamy kolejno elementy składowe maszyny $\displaystyle MT_1$:

$\displaystyle \Sigma_I=\left\{0\right\}\quad,\quad \Sigma_T=\left\{0,\diamondsuit,\clubsuit,\sharp\right\},$

$\displaystyle S=\left\{s_0,s_1,s_2,s_3,s_4,s_A,s_R\right\}\quad, \quad S_F=\left\{s_A\right\}.$

Pozostaje jeszcze zdefiniować funkcję przejść:

$\displaystyle \begin{array} {c|c|c|c|c|} (s_0,\sharp)\mapsto (s_R,\sharp,0) & (s_1,\diamondsuit)\mapsto(s1,\diamondsuit,1)\\ \hline (s_0,0)\mapsto(s_1,\clubsuit,1) & (s_1,0) \mapsto(s_2,\diamondsuit,1)\\ \hline & (s_1,\sharp)\mapsto(s_A,\sharp,0)\\ \hline (s_2,\diamondsuit)\mapsto(s_2,\diamondsuit,1) & (s_3,0)\mapsto(s_2,\diamondsuit,1)\\ \hline (s_2,\sharp)\mapsto(s_4,\sharp,-1) & (s_3,\diamondsuit)\mapsto(s_3,\diamondsuit,1)\\ \hline (s_2,0)\mapsto(s_3,0,1) & (s_3,\sharp)\mapsto(s_R,\sharp,0)\\ \hline (s_4,0)\mapsto(s_4,0,-1) & \\ \hline (s_4,\diamondsuit)\mapsto(s_4,\diamondsuit,-1) & \\ \hline (s_4,\clubsuit)\mapsto(s_2,\clubsuit,1) & \\ \hline (s_A,\sharp)\mapsto(s_A,\sharp,0) & (s_R,\sharp)\mapsto(s_R,\sharp,0)\\ \hline \end{array}$

W miejsce tabeli wygodniej jest zobrazować funkcję przejść maszyny Turinga na etykietowanym grafie skierowanym. Zostało to zrobione na poniższym rysunku:

Rysunek 2

Łatwo zauważyć, że wprowadzona funkcja przejścia określa maszynę spełniającą postawione przez nas warunki. Symbol $\displaystyle \clubsuit$ został wprowadzony dla odróżnienia wystąpienia pojedynczego zera od sytuacji, gdy liczba zer jest nieparzysta i większa od $\displaystyle 1$.

Aby lepiej zrozumieć działanie maszyny $\displaystyle MT_1$, zasymulujemy jej działanie na dwóch słowach wejściowych, przy czym pierwsze z nich będzie należało do języka $\displaystyle L$, a drugie nie:

\(\displaystyle \begin{array} {c c c c c c c c} &\sharp s_0 0000 \sharp & \mapsto & \sharp \clubsuit s_1 000 \sharp &\mapsto & \sharp \clubsuit \diamondsuit s_2 00 \sharp &\mapsto & \sharp \clubsuit \diamondsuit 0 s_3 0 \sharp\\ \mapsto & \sharp \clubsuit \diamondsuit 0 \diamondsuit s_2 \sharp&\mapsto& \sharp \clubsuit \diamondsuit 0 s_4 \diamondsuit \sharp &\mapsto& \sharp \clubsuit \diamondsuit s_4 0 \diamondsuit \sharp &\mapsto & \sharp \clubsuit s_4 \diamondsuit 0 \diamondsuit \sharp \\ \mapsto & \sharp s_4 \clubsuit \diamondsuit 0 \diamondsuit \sharp &\mapsto & \sharp \clubsuit s_1 \diamondsuit 0 \diamondsuit \sharp &\mapsto & \sharp \clubsuit \diamondsuit s_1 0 \diamondsuit \sharp &\mapsto & \sharp \clubsuit \diamondsuit \diamondsuit s_2 \diamondsuit \sharp\\ \mapsto & \sharp \clubsuit \diamondsuit \diamondsuit \diamondsuit s_2 \sharp & \mapsto & \sharp \clubsuit \diamondsuit \diamondsuit s_4 \diamondsuit \sharp & \mapsto & \sharp \clubsuit \diamondsuit s_4 \diamondsuit \diamondsuit \sharp& \mapsto & \sharp \clubsuit s_4 \diamondsuit \diamondsuit \diamondsuit \sharp\\ \mapsto & \sharp s_4 \clubsuit \diamondsuit \diamondsuit \diamondsuit \sharp& \mapsto & \sharp \clubsuit s_1 \diamondsuit \diamondsuit \diamondsuit \sharp & \mapsto & \sharp \clubsuit \diamondsuit s_1 \diamondsuit \diamondsuit \sharp& \mapsto & \sharp \clubsuit \diamondsuit \diamondsuit s_1 \diamondsuit \sharp\\ \mapsto & \sharp \clubsuit \diamondsuit \diamondsuit \diamondsuit s_1 \sharp &\mapsto & \sharp \clubsuit \diamondsuit \diamondsuit \diamondsuit s_A \sharp& \circlearrowleft \end{array}\)

Wykazaliśmy więc, że $\displaystyle \sharp s_0 0000 \sharp \mapsto^* \sharp \clubsuit \diamondsuit \diamondsuit \diamondsuit s_A \sharp$. Zatem $\displaystyle 0^4 \in L(MT_1)$.

Animacja 1

Dla porównania:

$\displaystyle \begin{array} {c c c c c c c c} &\sharp s_0 000 \sharp & \mapsto & \sharp \clubsuit s_1 00 \sharp &\mapsto & \sharp \clubsuit \diamondsuit s_2 0 \sharp &\mapsto & \sharp \clubsuit \diamondsuit 0 s_3 \sharp\\ \mapsto &\sharp \clubsuit \diamondsuit 0 s_R \sharp & \circlearrowleft \end{array}$

Czyli zgodnie z naszym założeniem $\displaystyle 0^3\not \in L(MT_1)$.

Animacja 2

Przykład 3.2

Przedstawimy maszynę Turinga $\displaystyle MT_2$ akceptującą język

$\displaystyle L=\left\{w \overleftarrow{w} \: : \: w\in \left\{0,1\right\}^*\right\},$

gdzie $\displaystyle \overleftarrow{w}$ oznacza lustrzane odbicie słowa $\displaystyle w$. Elementy języka $\displaystyle L$ nazywamy palindromami. Definiujemy alfabet maszyny:

$\displaystyle \Sigma_I=\left\{0,1\right\}\quad,\quad \Sigma_T=\left\{0,1,\sharp\right\},$

oraz zbiory stanów

$\displaystyle S=\left\{s_0,r_0,r_0',q_0,r_1,r_1',q_1,l,s_A,s_R\right\}\quad, \quad S_F=\left\{s_A\right\}.$

Funkcję przejść maszyny $\displaystyle MT_2$ określa tabela:

$\displaystyle \begin{array} {c|c|c|c|c|} (s_0,\sharp)\mapsto (s_A,\sharp,0) & (s_0,0)\mapsto (r_0,\sharp,1) & (s_0,1)\mapsto (r_1,\sharp,1)\\ \hline (r_0,\sharp)\mapsto (s_R,\sharp,0) & (r_0,0)\mapsto (r_0',0,1) & (r_0,1)\mapsto (r_0',1,1)\\ \hline (r_0',\sharp)\mapsto (q_0,\sharp,-1) & (r_0',0)\mapsto (r_0',0,1) & (r_0',1)\mapsto (r_0',1,1)\\ \hline & (q_0,0)\mapsto (l,\sharp,-1) & (q_0,1)\mapsto (s_R,\sharp,-1)\\ \hline (r_1,\sharp)\mapsto (s_R,\sharp,0) & (r_1,0)\mapsto (r_1',0,1) & (r_1,1)\mapsto (r_1',1,1)\\ \hline (r_1',\sharp)\mapsto (q_1,\sharp,-1) & (r_1',0)\mapsto (r_1',0,1) & (r_1',1)\mapsto (r_1',1,1)\\ \hline & (q_1,0)\mapsto (s_R,\sharp,0) & (q_1,1)\mapsto (l,\sharp,-1)\\ \hline (l,\sharp)\mapsto (s_0,\sharp,1) & (l,0)\mapsto (l,0,-1) & (l,1)\mapsto (l,1,-1)\\ \hline (s_R,\sharp)\mapsto (s_R,\sharp,0) & & \\ \hline (s_A,\sharp)\mapsto (s_A,\sharp,0) & & \\ \hline \end{array}$

co dla przejrzystości zobrazowano na Rysunku 3.

Rysunek 3

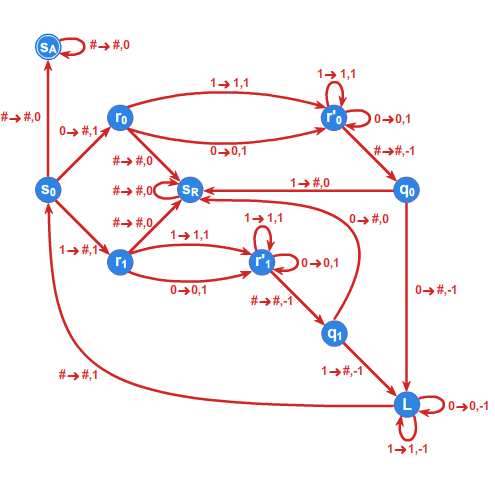
Inne możliwe definicje maszyn Turinga

Istnieje kilka możliwych definicji maszyny Turinga, które jak się okazuje są równoważne pod względem możliwości obliczeniowych (tzn. rozpoznają dokładnie tę samą klasę języków). Naszkicujemy kilka wybranych podejść.

Maszyna wielotaśmowa

W tym modelu zakłada się, że głowica ma do dyspozycji nie tylko jedną, ale wiele taśm, na których może zapisywać i odczytywać symbole. Zakłada się przy tym, że słowo wejściowe znajduje się na pierwszej taśmie. Aby symulować maszynę wielotaśmową na jednej taśmie, należy zamienić alfabet taśmy na alfabet $\displaystyle (\Sigma_T)^k$, gdzie $\displaystyle k$ oznacza ilość taśm. W tym momencie zapis na taśmie $\displaystyle i$-tej jest realizowany przez zmianę odpowiedniej współrzędnej litery z nowego alfabetu (zob. Rys. 4.a). Czyli w opisywanym przypadku funkcja przejść będzie operowała na następujących zbiorach:

$\displaystyle f:\: (S\times \Sigma^k_{T} )\rightarrow (S \times \Sigma^k_{T} \times \{-1,0,1\} ).$

Taśma jednostronnie nieskończona

Model ten zakłada, że taśma jest ograniczona z jednej ze stron. Różnica w porównaniu z rozważaną przez nas maszyną Turinga polega na tym, że nie jest dozwolone przesuwanie lewego markera (tzn. funkcja przejść nie może zawierać przejść typu punkt 5 definicji 3.1. W tej sytuacji, aby symulować maszynę z taśmą obustronnie nieskończoną na maszynie z taśmą ograniczoną z jednej strony, wystarczy zasymulować taśmę obustronnie nieskończoną poprzez rozszerzenie alfabetu (zob. Rys. 4.b).

Rysunek 4

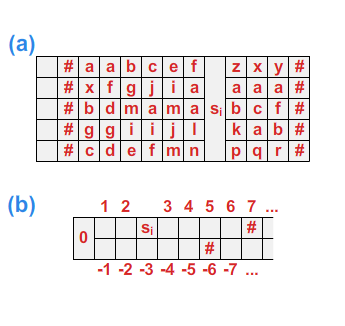
Wielogłowicowa maszyna wielotaśmowa

W tym podejściu zakłada się dodatkowo, że każda z taśm posiada swoją głowicę. Inaczej mówiąc, mamy do czynienia z iloczynem kartezjańskim $\displaystyle k$ niezależnych maszyn jednotaśmowych. Akceptowany język jest w tym momencie $\displaystyle k$-wymiarowy. Oczywiście, słowo postaci $\displaystyle (w,1,\dots,1)\in (\Sigma_T^*)^k$ można w naturalny sposób utożsamiać z $\displaystyle w\in \Sigma_T$. Z drugiej strony maszynę wielogłowicową można symulować na jednotaśmowej w następujący sposób:

Jako zbiór stanów bierzemy $\displaystyle S^k$.
Słowa startowe $\displaystyle w_1,\dots, w_k$ zapisujemy jako konfigurację początkową maszyny jednotaśmowej w postaci: $\displaystyle \sharp (s_0)^k \$ \dot{1} w_1 \$ \dot{2} w_2 \$ \dots \$ \dot{k} w_k \$.$ Symbole $\displaystyle \$$ mają za zadanie wirtualnego rozdzielenia taśm. Symbole $\displaystyle \dot{i}$ wskazują na położenie $\displaystyle i$-tej głowicy na taśmie.
W trakcie symulacji przechodzimy pomiędzy markerami i wykonujemy przejścia dla kolejnych głowic.

Widać już, że formalne podanie funkcji przejść jest w omawianym przypadku bardzo techniczne. Musimy zapewnić możliwość poszerzania obszaru zapisu na poszczególnych taśmach, co jest realizowane poprzez dopisanie nowego symbolu i przepisywanie przyległych symboli, aż do markera włącznie. Następnie należy wrócić do poprzedniego miejsca zapisu i symulować działanie kolejnych głowic. Wymaga to wprowadzenia sporej liczby stanów pomocniczych. Nie będziemy zagłębiać się w te techniczne szczegóły. Mamy nadzieję że sama idea konstrukcji jest w tym momencie zrozumiała.

Najbardziej ogólna definicja maszyny tego typu dopuszcza dodatkowo, aby głowice mogły przeglądać pozostałe taśmy, dzięki czemu zapewnia się komunikację między głowicami. Symulacja takiej maszyny na jednej taśmie jest podobna w swej idei do metody przedstawionej wcześniej.

Maszyna niedeterministyczna

Ten typ maszyn ma ogromne znaczenie dla teorii złożoności. Z tego powodu przyglądniemy mu się dokładniej. Różnica pomiędzy niedeterministyczną maszyną Turinga a maszyną deterministyczną polega na tym, że funkcja przejść może pozwalać na kilka różnych przejść na skutek tego samego symbolu czytanego (gdyż funkcja przejść w tym przypadku będzie multi-funkcją).

Definicja 4.1

(Jednotaśmowa) niedeterministyczna maszyna Turinga jest to system $\displaystyle \mathbf{NMT}=(\Sigma _{T},S,f,s_{0},S_{F})$, w którym $\displaystyle \Sigma _{T}$ jest skończonym alfabetem, $\displaystyle S$ skończonym zbiorem stanów, $\displaystyle S\cap \Sigma _{T}=\emptyset$ oraz wyróżniony jest podzbiór $\displaystyle \Sigma _{I}\subset \Sigma _{T}$ . Podobnie jak poprzednio zbiór $\displaystyle \Sigma _{T}$ zwany jest alfabetem taśmy, a $\displaystyle \Sigma _{I}$ - alfabetem wejściowym. Wyróżnione są także: element $\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}$ zwany markerem końca, stan początkowy $\displaystyle s_{0}\in S$ oraz $\displaystyle S_{F}\subset S$ - zbiór stanów końcowych. Natomiast funkcja przejść jest funkcją częściową $\displaystyle f:\: (S\times \Sigma _{T})\rightarrow \mathcal{P}(S\times \Sigma _{T}\times \{-1,0,1\})$ gdzie $\displaystyle \mathcal{P}(A)$ oznacza zbiór podzbiorów zbioru $\displaystyle A$.

Konfiguracją maszyny Turinga jest słowo $\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}$ , w którym $\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}$ , przy czym pomiędzy dwiema konfiguracjami $\displaystyle d_{1},d_{2}$ zachodzi relacja bezpośredniego następstwa $\displaystyle d_{1}\mapsto d_{2}$ wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie $\displaystyle s_{1},s_{2}\in S$ , $\displaystyle a,b,c\in \Sigma _{T}$ oraz $\displaystyle v,w\in \Sigma _{T}^{*}$:

$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vs_{2}bw$ oraz $\displaystyle f(s_{1},a)\ni(s_{2},b,0),$
$\displaystyle d_{1}=vs_{1}aw$ , $\displaystyle d_{2}=vbs_{2}w$ oraz $\displaystyle f(s_{1},a)\ni(s_{2},b,1)$ i $\displaystyle w\neq 1,$
$\displaystyle d_{1}=vs_{1}\#$ , $\displaystyle d_{2}=vbs_{2}\#$ oraz $\displaystyle f(s_{1},\#)\ni(s_{2},b,1),$
$\displaystyle d_{1}=vcs_{1}aw$ , $\displaystyle d_{2}=vs_{2}cbw$ oraz $\displaystyle f(s_{1},a)\ni(s_{2},b,-1),$
$\displaystyle d_{1}=s_{1}\#w$ , $\displaystyle d_{2}=s_{2}\#bw$ oraz $\displaystyle f(s_{1},\#)\ni(s_{2},b,-1).$

Tak jak poprzednio, przechodnie domknięcie relacji $\displaystyle \mapsto$ oznaczać będziemy symbolem $\displaystyle \mapsto^{*}$ i określać mianem obliczenia wykonanego przez maszynę Turinga. Konfiguracja $\displaystyle d_{1}\in (\Sigma _{T}\cup S)^{*}$ jest końcowa, jeśli stąd, że $\displaystyle d_{1}\mapsto d_{2}$ , wynika $\displaystyle d_{2}=d_{1}.$

Pomimo tego, że postawiona definicja maszyny niedeterministycznej jest bardzo podobna do maszyny deterministycznej, występuje tutaj jedna bardzo istotna różnica. Słowo wejściowe może prowadzić do wielu różnych obliczeń wykonanych, w szczególności jedno z obliczeń może doprowadzać do zatrzymania maszyny, a inne nie.

Przykład maszyny niedeterministycznej podamy później, przy okazji omawiania klas złożoności obliczeniowej.

Definicja 4.2

Język rozpoznawany przez niedeterministyczną maszynę Turinga $\displaystyle NMT$ jest to zbiór

$\displaystyle L(\mathbf{NMT})=\left\{ w\in \Sigma _{T}^{*}\: :\: \sharp s_{0}w\sharp \mapsto^{*}\sharp w_{1}s_{F}w_{2}\sharp ,\; dla\: pewnych\: w_{1},w_{2}\in \Sigma _{T}^{*},s_{F}\in S_{F}\right\} .$

Język $\displaystyle L\subset \Sigma _{I}^{*}$ jest rozpoznawany (akceptowany) przez niedeterministyczną maszynę Turinga, jeśli istnieje $\displaystyle \mathcal{NMT}$ taka, że $\displaystyle L(\mathcal{NMT})=L.$

Podkreślamy fakt, że aby maszyna niedeterministyczna zaakceptowała słowo wejściowe, wystarczy, aby wśród wszystkich możliwych obliczeń znalazło się co najmniej jedno akceptujące.

Wprost z definicji wynika że każda maszyna deterministyczna jest także maszyną niedeterministyczną, co oznacza, że języki rozpoznawane przez maszyny deterministyczne są zawarte w klasie języków rozpoznawanych przez maszyny niedeterministyczne. Przeciwna inkluzja jest gwarantowana przez następujące twierdzenie.

Twierdzenie 4.1

Dla każdej niedeterministycznej maszyny Turinga $\displaystyle \mathcal{NMT}$ istnieje maszyna deterministyczna $\displaystyle \mathcal{MT}$ taka, że

$\displaystyle L(\mathcal{NMT})=L(\mathcal{MT}).$

Dowód

(Szkic). Aby sprawdzić, czy maszyna niedeterministyczna akceptuje dane słowo wejściowe, należy przejrzeć wszystkie możliwe obliczenia wykonywane, tworzące drzewo obliczeń. Poziomy drzewa tworzone są przez kroki czasowe, wierzchołki stanowią obliczenia wykonane w danym kroku czasowym, a gałęzie zadane są przez relację bezpośredniego następstwa. W celu sprawdzenia, czy maszyna akceptuje dane słowo, przeglądamy drzewo obliczeń poziomami (por. algorytm BFS) i akceptujemy, gdy przeglądana konfiguracja była akceptująca. Tą techniką przeglądamy wszystkie możliwe obliczenia wykonane w $\displaystyle 1,2,3,\dots$ krokach.

Do dokonania symulacji najwygodniej jest użyć maszyny $\displaystyle 3$-głowicowej z możliwością czytania na wszystkich taśmach. Wprowadzamy te taśmy kolejno do przechowywania słowa wejściowego, symulacji działania maszyny niedeterministycznej i adresowania wyboru przejść ze zbioru przejść danego przez funkcję przejść. Symulacja przebiega w czterech krokach:

Rozpocznij ze słowem wejściowym $\displaystyle w$ na taśmie $\displaystyle 1$ oraz pustymi taśmami $\displaystyle 2$ i $\displaystyle 3$.
Przekopiuj taśmę $\displaystyle 1$ na taśmę $\displaystyle 2$.
Użyj taśmy $\displaystyle 2$ do symulacji $\displaystyle w$, wykorzystując taśmę $\displaystyle 3$ do wyboru przejść funkcji przejść $\displaystyle f$. Jeśli po wykonaniu skończonego zbioru instrukcji według adresowania z taśmy $\displaystyle 3$ otrzymano konfigurację akceptującą, to akceptuj. W przeciwnym razie, przejdź do następnego punktu.
Zamień ciąg adresowy na następny w kolejności leksykograficznej. Jeśli zapisany ciąg jest ostatnim możliwym ciągiem adresowym o długości $\displaystyle N$, zapisz na taśmie $\displaystyle 3$ pierwszy w kolejności leksykograficznej ciąg adresowy o długości $\displaystyle N+1$ oraz przejdź do $\displaystyle 2$.

Wniosek 4.1

Dla każdej maszyny Turinga $\displaystyle \mathcal{MT}$ istnieje maszyna Turinga $\displaystyle \mathcal{MT}'$ taka, że

$\displaystyle L(\mathcal{MT})=L(\mathcal{MT}')$

oraz dla każdego $\displaystyle w\in L(\mathcal{MT}')$ maszyna $\displaystyle \mathcal{MT}'$ zatrzymuje się na $\displaystyle w$.

Dowód

Wystarczy przerobić maszynę $\displaystyle \mathcal{MT}$ na maszynę niedeterministyczną $\displaystyle \mathcal{NMT}$ posiadającą dodatkowy stan $\displaystyle s_A$ oraz taką, że dla każdego stanu ze zbioru $\displaystyle S_F$ pod wpływem dowolnego symbolu z $\displaystyle \Sigma_T$ maszyna $\displaystyle \mathcal{NMT}$ posiada dodatkowe przejście do $\displaystyle s_A$, w którym już pozostaje i nic nie zmienia. Stąd widać, że $\displaystyle L(\mathcal{MT})=L(\mathcal{NMT})$.

Twierdzenie 4.1 pozwala na otrzymanie maszyny $\displaystyle \mathcal{MT}'$ akceptującej ten sam język co $\displaystyle \mathcal{NMT}$ z dodatkowym założeniem, że gdy $\displaystyle \mathcal{NMT}$ osiąga stan $\displaystyle s_A$, maszyna $\displaystyle \mathcal{MT}'$ się zatrzymuje. Zauważmy, że stan $\displaystyle s_A$ można osiągnąć tylko dla słów akceptowanych prze $\displaystyle \mathcal{NMT}$, a z drugiej strony, każde słowo akceptowane przez $\displaystyle \mathcal{NMT}$ prowadzi do co najmniej jednego obliczenia kończącego się w $\displaystyle s_A$.