Materiały elektroniczne - wykłady
Wstęp: poprawność i złożoność algorytmu
Wykład Algorytmy i struktury danych jest poświęcony przede wszystkim koncepcyjnym i strukturalnym metodom efektywnego rozwiązywania problemów na komputerze. Podstawowym elementem przy rozwiązywaniu zadanego problemu jest dobór algorytmu i struktury danych. Najważniejszymi aspektami algorytmu są jego poprawność i złożoność (czasowa i pamięciowa).
W przypadku złożoności czasowej, z reguły wyróżnimy pewną operację dominującą, a czas będziemy traktować jako liczbę wykonanych operacji dominujących. W ten sposób nasza analiza będzie zależna jedynie od algorytmu, a nie od implementacji i sprzętu. W przypadku sortowania, operacją dominującą jest przeważnie porównanie dwóch elementów, a w przypadku przeglądania drzewa - jedno przejście w drzewie między wierzchołkami. W przypadku algorytmów tekstowych operacją dominującą jest porównanie dwóch symboli. Zazwyczaj określamy pewien parametr \( n \), będący rozmiarem problemu wejściowego i określamy złożoność jako funkcję \( T(n) \), której argumentem jest rozmiar problemu. Z reguły będziemy przyjmować, że każda operacja arytmetyczna na małych liczbach daje się wykonać w jednym kroku. Przez "małe" rozumiemy liczby mające \( O(\log n) \) bitów.
Złożoność algorytmu może być rozumiana w sensie złożoności najgorszego przypadku lub złożoności średniej. Złożoność najgorszego przypadku nazywamy złożonością pesymistyczną - jest to maksymalna złożoność dla danych tego samego rozmiaru \( n \). W praktyce ważniejsza może się okazać złożoność średnia lub oczekiwana. W tym przypadku \( T(n) \) jest średnią (oczekiwaną) wartością złożoności dla wszystkich problemów rozmiaru \( n \). Tego typu złożoność zależy istotnie od tego, jaka się pod tym kryje przestrzeń probabilistyczna danych wejściowych. Z reguły zakładamy, że wszystkie dane wejściowe tego samego rozmiaru mogą się pojawić z tym samym prawdopodobieństwem. Jednakże jest to często mało realistyczne założenie. Przestrzeń probabilistyczna danych wejściowych może być bardzo skomplikowana. Prowadzić to może do bardzo trudnych (i wykraczających poza ten kurs) analiz.
Rozważmy następujący przykład. Przypuśćmy, że chcemy znaleźć pierwszą jedynkę w n-elementowej tablicy zerojedynkowej i nasz algorytm przegląda tablicę od strony lewej sprawdzając kolejne elementy. Niech operacją dominującą będzie sprawdzenie jednego elementu. Jeśli nie ma jedynki, to wykonamy \( n \) sprawdzeń. Jest to maksymalna liczba, zatem złożoność pesymistyczna wynosi \( T(n)=n \). Jeśli każdy ciąg binarny jest dany z tym samym prawdopodobieństwem, to łatwo policzyć, że złożoność średnia jest ograniczona przez stałą.
Do wyrażania złożoności stosujemy opis asymptotycznego wzrostu funkcji: \( f(n)\ =\ O(g(n)) \) oznacza, że \( f(n) \le c\cdot g(n) \) dla pewnej stałej \( c \). Gdy \( g(n)=n \), to mówimy, że \( f(n) \) jest liniowa, oraz dla \( g(n)=n^2 \) mówimy, że złożoność \( f(n) \) jest kwadratowa. Jeśli \( g(n) \) jest wielomianem, to wtedy mówimy o złożoności wielomianowej.
Będziemy używać dodatkowych notacji:
\( f(n)=\Theta(g(n)),\ f(n)=\Omega(n) \). Były one wprowadzone na wykładach z matematyki dyskretnej.
PRZYKŁAD
\( \frac{1}{100}\cdot n^2- 2n = \Theta(n^2 ), n^5+2^n = \Theta(2^n), n!=\Omega(10^n) \),
Konwencje językowe. Jaki jest najlepszy język do opisu algorytmu? Jest to przykład problemu nierozstrzygalnego. Niewątpliwie język ojczysty jest najlepszym językiem potocznym, a ulubiony język programowania jest najlepszym językiem do implementacji algorytmu. Język, którym będziemy opisywać algorytmy, jest gdzieś pomiędzy tymi językami - język potoczny nie wystarcza, a konkretny język programowania może spowodować, że "prosty" algorytm się zrobi nieczytelny. Będziemy używać, o ile się da, nieformalnych konstrukcji programistycznych, a w przypadkach bardzo prostych będziemy się starali pisać algorytm w języku Pascalopodobnym.
Poprawność algorytmu: niezmienniki, własność stopu
Przez poprawność algorytmu rozumiemy to, że daje on takie odpowiedzi, jakich oczekujemy. Oczywiście algorytm musi być poprawny, aby miało sens rozpatrywanie jego złożoności.
Pojęcie niezmiennika
Poprawność algorytmu sprowadza się do spełniania określonych niezmienników na różnych etapach wykonywania tego algorytmu. Rozważmy kilka przykładów pozwalających zrozumieć znaczenie niezmiennika.
Załóżmy, że mamy zbiór \( S \) składający się z \( n \) przedmiotów. Niektóre z przedmiotów są czarne, a niektóre białe. Zakładamy, że liczba czarnych przedmiotów jest nieparzysta.
Algorytm Biało-czarne1
while |S|> 1 do begin pobierz dwa przedmioty z S; if przedmioty są różnego koloru then wstaw z powrotem czarny end; return kolor ostatniego przedmiotu w S;
Załóżmy, że mamy 10000001 czarnych przedmiotów i 1000000001 białych, jaki jest ostatni przedmiot? Rozpatrzmy niezmiennik: parzystość liczby czarnych przedmiotów.
Ponieważ na początku mamy nieparzystą liczbę czarnych przedmiotów, zatem wynikiem jest kolor czarny.
Rozpatrzmy modyfikację tego algorytmu, zakładamy że \( n \) jest niezerowe.
Algorytm Biało-czarne2
while |S|> 1 do begin pobierz dwa przedmioty z S; if co najmniej jeden jest biały then wstaw z powrotem jeden biały; end; return kolor ostatniego przedmiotu w S;
Załóżmy, że mamy 10000001 czarnych przedmiotów i 1000000001 białych, jaki jest ostatni przedmiot? Tym razem rozważmy niezmiennik: znak liczby białych przedmiotów. (Znak liczby jest równy 0, jeśli jest ona równa zeru, 1 - jeśli jest większa od zera.) Zatem ostatnim przedmiotem jest przedmiot biały.
Własność stopu
Jednym z podstawowych elementów poprawności algorytmu jest własność stopu: dla poprawnych danych wejściowych algorytm zatrzymuje się w skończonym czasie.
Na przykładzie czterech krótkich algorytmów pokażemy, że sprawdzanie własności stopu może nie być czynnością trywialną.
Algorytm Suma-Kwadratów-Cyfr
while ((n <>4) and (n <> 1)) do n:= suma kwadratów cyfr liczby n;
Algorytm 6174
// n jest czterocyfrową liczbą naturalną niepodzielną przez 1111 // pierwszymi cyframi n mogą być zera while (n<>6174) do n1:= największa liczba czterocyfrowa, której cyfry są permutacją cyfr liczby n; n2:= najmniejsza liczba czterocyfrowa, której cyfry są permutacją cyfr liczby n; n:= n1 - n2
W przypadku liczb trzycyfrowych rolę liczby 6174 pełni liczba 495. W przypadku liczb pięciocyfrowych nie ma takiej pojedyńczej liczby.
Rozpatrzmy następujący algorytm (zaprojektowany podobno przez
Fibonacciego) na rozkład ułamka na sumę parami różnych ułamków Egipskich,
tzn. ułamków postaci \( \frac{1}{q_i} \).
Rozkład Egipski jest postaci \( \hspace{0.4cm} \frac{p}{q}\ =\ \frac{1}{q_1}+\frac{1}{q_2}+\frac{1}{q_3}+\frac{1}{q_4}+\ldots , \hspace{0.4cm} \) gdzie \( q_1 < q_2 < q_3 < \ldots \) są liczbami naturalnymi:
Każdy ułamek ma rozkład Egipski, oto przykład takiego rozkładu:
\( 31/311\ =\ 1/12 + 1/63 + 1/2799 + 1/8708 \)
Niech \( DolnyEgipt(x) \) oznacza najwięszy ułamek Egipski (tzn. postaci \( \frac{1}{q} \)) nie przekraczający x.
Przykłady:
\( DolnyEgipt(2/3)=1/2,\ DolnyEgipt(4/5)=1/2,\ \)
\( DolnyEgipt(2/5)=1/3,\ DolnyEgipt(2/7)=1/4. \)
Niech \( 1\le p < q \) będą dwiema względnie pierwszymi liczbami naturalnymi. Następujący algorytm oblicza rozkład (niekoniecznie najkrótszy) nieskracalnego ułamka \( \frac{p}{q} \) na ułamki Egipskie.
Algorytm Rozkład-Egipski\( (p,q) \)
(algorytm Fibonacciego) x:=p/q; while (x>0) do y:=DolnyEgipt (x); output y; x:=x-y;
Nasz algorytm dla wejścia (31,311), tzn. \( x=31/311 \), wyprodukuje 10 składników w rozkładzie Egipskim.
Dla wejścia \( \frac{7}{15} \) otrzymamy jako wynik następujący ciąg ułamków Egispskich: \( \hspace{0.5cm} \frac{1}{3},\ \frac{1}{8},\ \frac{1}{120}. \)
Algorytm ma własność stopu ponieważ liczniki kolejnych dodatnich wartości \( x \) (przedstawionych jako nieskracalne ułamki) maleją
(pozostawiamy dowód tego faktu jako ćwiczenie).
Oto przykład ciągu kolejnych wartości \( x \): 4/5 -> 3/10 -> 1/10. Liczniki maleją: \( 4>3>1 \).
W pewnym momencie licznik liczby \( x \) dochodzi do jedynki, wtedy następna wartość \( x \) staje się zerem i algorytm zatrzymuje się.
Zatem algorytm wykonuje co najwyżej \( p \) iteracji dla wejścia \( p/q \).
Innym przykładem związanym z ułamkami jest następujący algorytm.
Mamy zbiór ułamków \(X\;=\; \{1/1,\; 1/2,\; 1/3,\; \ldots 1/100\}\).
dopóki zbiór ma co najmniej 2 elementy wykonaj
pobierz dwa różne elementy \(a,b\) z tego zbioru i włóż \(f(a,b)\).
return(ostatni jedyny element).
Jaki będzie wynik jeśli \(f(a,b)\,=\,ab/(a+b)\),
a jaki jeśli \(f(a,b)\,=\,ab+a+b.\) ?
W pierwszym przypadku niezmiennikiem jest wartość sumy odwrotności elementów zbioru X,
w drugim przypadku jeśli do odwrotności każdego elementu dodamy 1, to wartość iloczynu
otrzymanych liczb jest niezmiennikiem.
Rozpatrzmy jeszcze jeden ciekawy przykład związany z własnością stopu.
Załóżmy, że mamy ciąg cykliczny liczb całkowitych
zadany przez tablicę \(A[0..n-1]\), czyli pozycja \(0\) jest następną po pozycji \(n-1\)..
Nasz obecny algorytm jednocześnie dla każdej pozycji zmieniai jej wartość na wartość
różnicy między wartością na danej pozycji i cyklicznie następnej. Pytamy się dla jakich \( n\) algorytm ten
zatrzymuje się dla każdych danych całkowitoliczbowych w tablicy długości \(n+1\).
Algorytm Ciąg-cykliczny
while ciąg nie składa się z samych zer do pom:= A[0] for i=0 to n-2 A[i]:=|A[i]-A[i+1| A[n-1]:=|A[n-1]-pom|
Pierwsze trzy algorytmy mają własność stopu. W pierwszym łatwo to sprawdzić, gdyż dla \( n>100 \) następna wartość jest istotnie mniejsza.
Pozostawiamy jako ćwiczenie znalezienie najkrótszego koncepcyjnie dowodu własności stopu dwu pierwszych algorytmów (nie chodzi nam tu o brutalny dowód polegający na sprawdzeniu wszystkich przypadków przez komputer). Algorytm Ciąg-cykliczny, pomimo swojej prostoty, ma nietrywialą własność stopu (dla ciągu o długości będącej potęgą dwójki).
Następny algorytm jest bardziej abstrakcyjny. Pochodzi on od Collatza (jak również od polskiego matematyka Ulama).
Algorytm Collatza
while n \neq 1 do if n parzyste then n := n div 2; else n := 3*n+1;
Algorytm Collatza jest bardzo zagadkowy. Nie wiadomo, czy dla każdej dodatniej liczby całkowitej \( n \) ma on własność stopu. Problem ten postawił L. Collatz w roku 1937, wiadomo, że własność stopu zachodzi dla każdego \( 1 \le n \le 10^{16} \).
dla \(n = 27\) cały proces zajmuje aż 111 kroków z maksymalną wartością 9232Rozważmy jeszcze jeden bardzo dziwny algorytm. Niech \(x^R\) oznacza wartość liczby będącej odwróceniem zapisu dziesiętnego liczby x, np \(12^R=21\).
Algorytm Dziwny
while x <> x^R do x := x+x^R;
Algorytm Dziwny jest również zagadkowy. Nie wiadomo, czy dla każdej dodatniej liczby całkowitej \( n \) ma on własność stopu W szczególności najciekawszy jest przypadek liczby 196.
Jeśli zamiast zapisu dziesiętnego weźmiemy binarny to algorytm nie zawsze ma własność stopu, np. dla liczby 22 zapisanej binarnie nigdy sie nie zatrzyma. W tym przypadku co kilka iteracji otrzymamy liczbę (zapisaną binarnie) typu \(10 1^k 01 0^k \) dla coraz większych k.
Opis algorytmu za pomocą niezmienników
Niezmienniki są często podstawową konstrukcji algorytmu na poziomie koncepcyjnym. Opisujemy jedynie co dana część algorytmu ma wykonać w sensie zachowania odpowiedniego niezmiennika. Reszta jest czasami prostą sprawą natury inżynieryjno-technicznej.
Zademonstrujemy to na następujacym przykładzie posegregowania tablicy liczbowej \( A[1..n] \) względem elementu \( x \). Dla zbiorów pozycji \( X,Y \) tablicy \( A \) piszemy \( X < Y \) gdy każda pozycja w X jest mniejsza od każdej pozycji w \( Y \). Piszemy \( A[X] < a \) gdy wartości na pozycjach X są mniejsze od a (podobnie z równością).
Zdefiniujmy następujący niezmiennik
Nazwy M,R,W biorą się od Mniejsze, Równe, Większe.
Naszym problemem jest poprzestawiać elementy tablicy tak aby dla pewnych zbiorów M,R,W dających w sumie cały zbiór pozycji zachodził niezmiennik \( \alpha(M,R,W) \) (algorytmy tego typu maja zastosowanie w implmentacji bardzo praktycznego algorytmu Quicksort).
Algorytm wykonuje swoje zadanie startując od zbiorów pustych i zwiększając zbiory. Chcemy aby algorytm działał w miejscu (dodatkowa pamięć stała) i w każdej iteracji wykonywał stałą liczbę operacji.
Algorytm PosegregujTablicę
M:= ∅; R:= ∅; W:= ∅; while |M|+|R|+|W| <n do zwiększ o jeden sumę |M|+|R|+|W| zachowując niezmiennik alpha(M,R,W,x) w czasie i dodatkowej pamięci O(1)
Algorytm ten jest silnikiem algorytmu QuickSort, który jest praktycznie najszybszym algorytmem sortowania.
Możliwe są różne scenariusze tego algorytmu poprzez dospecyfikowanie niezmiennika. Na przykład możemy zażądąc aby zbiory M,R,W były sąsiednimi przedziałami, tworzącymi razem sufiks (lub prefiks) tablicy, lub aby M było prefiksem a W sufiksem tablicy. Otrzymamy różne algorytmy w pewnym sensie izomorficzne. Naturalnym jest aby zażądać, by każdy ze zbiorów M, R, W był przedziałem, nawet jeśli tego nie zażądamy to tak będzie po zakończeniu algorytmu. Jeśli zbiory są przedziałami to pojedyńcza iteracja polega na manipulacji w okolicy końców przedziałów.
Możemy problem ouogólnić i segregować tablicę względem większej liczby elementów, np. względem elementów \( x < y \). Teraz zamiast dwóch segmentów M, R, W tablicy A mamy pięć zbiorów pozycji, a niezmiennik zamienia się na
\( Z1 < Z2 < Z3 < Z4 < Z5,\ A[Z1] < x,\ A[Z2]=x, \)
\( x < A[Z3] < y,\ A[Z4]=y,\ A[Z5]>y. \)
Poprawność i złożoność 10 prostych algorytmów
Poniżej dokonamy pobieżnej analizy złożoności obliczeniowej dziesięciu prostych algorytmów i wykażemy, że ich złożoności są lepsze od złożoności kwadratowej rozwiązań naiwnych, chociaż nasze algorytmy będą niewiele bardziej skomplikowane od naiwnych.
Poza dwoma z nich (działającymi w czasie czas \( O(n \log n), \)) wszystkie algorytmy działają w czasie liniowym.
Dokładne analizy pozostawiamy jako ćwiczenia.
Algorytm 1. Przywódca ciągu
Przywódcą ciągu jest element, który występuje w ciągu więcej razy niż połowa długości tego ciągu. Naszym problemem jest policzenie przywódcy ciągu danego w tablicy \( A[1..n] \). Dla uproszczenia przyjmijmy, że w tym ciągu jest przywódca. Łatwo zmodyfikować algorytm tak, by sprawdzał istnienie przywódcy.
Algorytm Liczenie-Przywódcy
ile := 0; for i := 1 to n do if (ile = 0) then ile:= ile+1 ; j := i; else if (A[i]=A[j]) then ile:=ile+1; else ile :=ile-1; return A[j];
Przyspieszenie wynika z następującej własności problemu: jeśli mamy dwa różne elementy w tablicy, to możemy je usunąć i przywódca pozostanie taki sam.
Algorytm można zmodyfikować tak, aby w czasie liniowym liczył słabego przywódcę: element, który występuje w tablicy więcej niż \( n/5 \) razy. W tym przypadku potrzebne są cztery liczniki odpowiadające czterem kandydatom na słabego przywódcę. Algorytm liczy element, który jest kandydatem na słabego przywódcę (jeśli istnieje taki przywódca, to na pewno jest nim wyliczony element). Jeśli istnieje słaby przywódca i mamy pięć różnych elementów, to można je usunąć bez zmiany wyniku. Pozostawiamy napisanie odpowiedniego algorytmu jako ćwiczenie.
Problem można rozwiązać inaczej, sortując tablicę, wtedy mamy złożoność \( O(n log n) \). Podamy potem również rozwiązanie metodą "dziel i zwyciężaj".
W animacji kolorem żółtym na końcu jest zaznaczony licznik słabego przywódcy, a jego nazwa jest umieszczona w niebieskim kwadraciku.
Algorytm 2. Szukanie sumy
Mamy dane dwie tablice posortowane rosnąco \( A,B \) i liczbę \( x \), pytamy, czy istnieją \( a \in A,\ b \in B \) takie, że \( x=a+b \).
Algorytm Szukanie Sumy
i := 1; j := n; while (i < = n and j > 0) do if (A[i]+B[j]=x) then return true; else if (A[i]+B[j] < x) then i:=i+1; else j:=j-1; return false;
Przyspieszenie jest możliwe dzięki odpowiedniej kolejności sprawdzania \( i,j \) i pominięciu zbędnych sprawdzeń.
Algorytm 3. Maksymalny segment
Dla tablicy \( A[1..n] \, \) liczymy maksymalną wartość z zera i ze wszystkich liczb \( \sum_{k=i}^j\ A[k] \), gdzie \( 1\le i\le j\le n \).
Algorytm Maksymalny-Segment;wynik := 0; sufiks := 0; for i := 1 to n do sufiks:= max(A[i]+sufiks,0); wynik:= max(wynik,sufiks);
Przyspieszenie w stosunku do algorytmu kwadratowego następuje dzięki wprowadzeniu dodatkowej zmiennej sufiks. Po każdym zakończeniu pętli "for" zachodzi: wynik jest maksymalną sumą przedziału zawierającego się w \( [1..i] \) oraz sufiks jest maksymalną sumą segmentu, który jest sufiksem przedziału \( [1..i] \).
Algorytm 4. Najbliższy mniejszy sąsiad w ciągu
Dla każdego \( i > 1 \) zdefiniujmy najbliższego mniejszego (lewego) sąsiada \( i \) jako
\( Lewy[i] =max \{j < i : A[j] < A[i] \} \).
Dla uproszczenia zakładamy, że \( A[i]> 0 \) dla \( i>0 \) oraz \( A[0]=0 \).
Algorytm Najbliższy-Mniejszy-Sąsiad
for i := 1 to n do j := i-1; while ( A[j] >= A[i]) do j := Lewy[j]; Lewy[i] := j;
Przyspieszenie w stosunku do algorytmu naiwnego następuje dzięki temu, że nie ma potrzeby sprawdzania tablicy dla indeksów istotnie wewnątrz przedziału \( [Lewy[i-1]...(i-1)] \). Niech \( k_i \) będzie liczbą tych \( j \), dla których \( A[j]>=A[i] \) (w wierszu 3). Wystarczy pokazać, że suma wszystkich \( k_i \) jest liniowa ze względu na n. Może się zdarzyć, że niektóre \( k_i \) mają wartość liniową. Zauważmy jednak, że dany indeks \( j \) pojawia się co najwyżej raz w sytuacji, gdy \( A[j] >= A[i] \), potem będzie "przeskoczony".
Opiszemy teraz nieformalnie alternatywny algorytm korzystajacy ze stosu.
Zamiast indeksu lewego sasiada bedziemy teraz liczyc wartosc lewego sasiada, inaczej mowiac
liczymy pierwsza wartosc na lewo mniejsza od danej wartosci.
Niech y oznacza element na wierzcholku stosu.
Czytamy kolejne elementy.
Po wczytaniu kolejnego elementu x usuwamy elementy ze stosu dopoki x<y.
W tym momencie znajdujemy lewego sasiada x, jego wartoscia jest y.
Wrzucamy x na stos.
Zalozmy ze A jest permutacja liczb 1,2,..n. Wtedy mozliwy jest jeszcze inny algorytm liniowy.
Trzymamy elementy tablicy w liscie dwukierunkowej.
Dla k=n,n-1,..2 wykonujemy:
lewym sasiadem k zostaje jego poprzednik na liscie.
Nastepnie element k usuwamy z listy.
Algorytm 5. Najdalszy mniejszy sąsiad w permutacji
W tym algorytmie zakładamy że na wejściu jest permutacja A elementów od 1 do n.
Dla każdego \( i > 1 \) zdefiniujmy najdalszego mniejszego (prawego) sąsiada \( i \) jako
\( Najd\_Prawy[i] =max \{j>i : A[j] < A[i] \} \).
W trakcie algorytmu obliczamy tablicę Pozycja, będącą odwrotościa permutacji.
Załóżmy, że początkowo Najd_Prawy[i]=0, Pozycja[i]=0, dla każdego i.
Algorytm Najdalszy-Prawy-Mniejszy-Sąsiad
min:=1; for i := 1 to n do Pozycja[A[i]]:=i; while min <= n and Pozycja[min] <> 0 do Najd_Prawy[Pozycja[min]]:=i; min := min+1;
Algorytm ten dziła oczywiście w czasie liniowym. Jego wadą jest ograniczenie się do permutacji.
Algorytm 6. Najdłuższy malejący podciąg
Niech \( A[1], A[2],\ldots A[n] \) będzie ciągiem \( n \) dodatnich liczb.
Następujący algorytm oblicza długość najdłuższego malejącego podciągu (w kolejności od lewej do prawej strony).
Algorytm Najdłuższy-Malejący
wynik := 1; for i := 1 to n do x := A[i]; A[i]:=0; k := min { j <= i : x >= A[j]}; A[k] := x; wynik := max(k, wynik);
Poprawność algorytmu nie jest całkowicie oczywista, uzasadnienie można znależć w rozwiązaniu stosownego zadania (patrz Ćwiczenia). Jeśli wejściem jest [5,2,1,3,7] to w momencie gdy algorytm kończy obliczenia, tablica A jest równa [7,3,1,0,0]. Zauważmy, że [7,3,1] wcale nie jest podciągiem (w kierunku od lewej do prawej strony) tablicy wejściowej. Niemniej wynik jest poprawny.
Złożoność alorytmu istotnie zależy od implementacji instrukcji:
\( k := min \{ j : x \ge A[j]\} \).
Ponieważ wszystko się odbywa w tablicy, możemy minimum policzyć łatwo w czasie logarytmicznym stosując szukanie binarne w posortowanej tablicy (segment tablicy \( A[1..i] \) jest posortowany). Zatem całkowity koszt algorytm jest \( O(n \log n) \) przy dosyć prostej implementacji.
Algorytm może, po niewielkim dodatkowym wysiłku procesora, podać najdłuższy malejący podciąg, albo też rozkład na minimalną liczbę podciągów niemalejących. Nie jest jasne, jak policzyć leksykograficznie minimalny i leksykograficznie maksymalny podciąg malejący o długości \( k \), gdzie \( k \) jest wynikiem powyższego algorytmu. Możemy się też zastanowić nad efektywnym algorytmem znajdowania liczby wszystkich takich ciągów długości \( k \).
Algorytm 7. Dwu-Pakowanie
Załóżmy, że mamy dowolnie dużą liczbę pudełek, każde o rozmiarze R, oraz n przedmiotów o rozmiarach \( r[1], r[2],\ldots r[n] \). Zakładamy, że \( R \ge r[1]\ge r[2]\ldots \ge r[n] \).
Mamy włożyć przedmioty do pudełek, co najwyżej dwa do jednego pudełka.
Pozostawiamy jako ćwiczenie analizę następującego algorytmu, który oblicza minimalną liczbę pudełek do zapełnienia.
Algorytm Dwu-Pakowanie
wynik := n; for i := 1 to n do if (i < wynik and r[i]+r[wynik] <= R) wynik := wynik-1;
Algorytm 8. Równoważność cykliczna ciągów
Niech \( u,v \) będą całkowitoliczbowymi ciągami długości \( n \) zadanymi tablicami o zakresie [0..n-1]. Jest to wyjątek, z reguły poprzednio przyjmowaliśmy, że tablica zaczyna się od pozycji jeden.
Mówimy, że u, v sa cyklicznie równoważne gdy \( v\ =\ u[k+1.. n-1]u[0.. k] \) dla pewnego przesunięcia cyklicznego k.
Niech \( x \mod n \) oznacza resztę modulo n, np. dla \( n=9 \) mamy: \( 88 \mod n\ =\ 7 \) .
Naiwny algorytm sprawdzałby równość \( v\ =\ u[k+1.. n-1]u[0.. k] \) dla każego k, za każdym razem wykonując być może liniową liczbę operacji (w sumie kwadratową).
Następujący algorytm jest niewiele bardziej skomplikowany w porówaniu z naiwnym, działa w czasie liniowym i daje w wniku (zatrzymując się) wartość true wtedy i tylko wtedy gdy
ciągi są cyklicznie równoważne.
Algorytm Równoważność-Cykliczna
i:=-1; j:=-1; while true do if (i>n-1) or (j > n-1) then return false; k:=1; while u[(i+ k) mod n]=v[(j+ k) mod n] and k <= n do k:=k+1; if k > n then return true; if u[(i+ k) mod n] > v[(j+ k) mod n] then i:=i+k else j:=j+k;
Problem poprawności jest tutaj znacznie bardziej skomplikowany niż dosyć oczywista złóżoność liniowa. Pozostawiamy to jako ćwiczenie.
Algorytm 9. Liczba inwersji permutacji
Niech \( P[0..n-1] \) będzie permutacją liczb \( 0,\ 1,\ 2\ ..n-1 \) zadaną tablicą o zakresie [0..n-1].
Liczbą inwersji jest liczba par \( i < j \) takich że \( P[i]>P[j] \).
Na przkład mamy 15 inwersji w permutacji
\( P[0..6]\ =\ [5,\ 4,\ 3,\ 6,\ 0,\ 1,\ 2] \)
Pomocniczą tablicą będzie \( Licz[0..n] \), załóżmy że początkowo zawiera ona same zera.
Funkcja logiczna \( odd() \) sprawdza czy liczba jest nieparzysta. Funkcja \( div \) jest dzieleniem całkowitoliczbowym, pomijamy resztę.
Funkcja \( \log( n) \) zwraca całkowitoliczbową część logarytmu przy podstawie 2, np. \( \log( 1025)\ =\ 10 \).
Końcową wartością zmiennej \( wynik \) jest liczba inwersji permutacji P.
Algorytm Liczba-Inwersji (algorytm Ryttera)
wynik:=0 repeat log n times for i:=0 to n-1 do if odd(P[i]) then Licz[P[i]]:=Licz[P[i]]+1 else wynik:=wynik+Licz[P[i]+1] ; for i=0 to n-1 do Licz[i]:=0; P[i]:=P[i] div 2
Algorytm naiwny liczyłby wynik sprawdzając wszystkie pary \( i < j \), a więc w czasie kwadratowym.
Nasz algorytm liczy to w czasie \( O(n \log n) \). Złożoność jest oczywista, poprawność jest mniej oczywista.
Oznaczmy \( \delta(x)=x\ div\ 2,\ \ \delta^0(x)=x,\ \ \delta^{k+1}(x)=\delta(\delta^{k}(x)) \).
Poprawność algorytmu wynika z nastepujacego faktu:
dla każdych liczb naturalnych \( x < y \) istnieje dokladnie jedna liczba naturalna k taka że
\( \delta^k(x)+1=\delta^k(y)\ \ \textrm{oraz}\ \ odd(\delta^k(y)) \).
Funkcję dzielenia można łatwo wyeliminowac i pozostawić jedynie operacje arytmetyczne dodawania i odejmowania.
Przy okazji algorytmów sortowania można skonstruować kilka innych algorytmów dla tego samego probemu.
Możemy terza liczyć inwersję dla każdego ciągu elementów, niekoniecznie będącego permutacją.
Liczba zamian elementów w insertion-sort jest równa liczbie inwersji,
podobnie algorytm merge-sort możemy rozbudować tak aby liczył liczbę inwersji w czasie rzędu n log n.
Algorytmy inserion-sor, merge-sort poznamy w następnych modułach.
Ograniczymy się tutaj jedynie do algorytmu licznia inwersji między dwiema posortowanymi rosnąco tablicami \( A[1..n]\),\([1..n] \).
W poniższym algorytmie zakładamy że tablice A, B są posortowane rosnąco.
Wynikiem jest liczba par \( (i,j) \) taich,że \( A[i]>B[j] \).
Algorytm Inwersje-Między-AB
wynik:=0; i:=1; j:=1; ; while i < = n do if j < =n and A[i] > B[j] then j:=j+1; else wynik:=wynik+j-1; i:=i+1;
Algorytm 10. Generacja permutacji
Niech \( P[1..n] \) będzie permutacją liczb 1,2,..n. Oznaczmy przez \( P_0=[1,2,3\ldots n] \) permutację identycznościową.
Operacja \( rotacja(k,P) \) polega na rotacji cyklicznej pierwszych k elementów tablicy P: \( k \)-ty element wędruje na początek. Na przykład:
Następujący algorytm generuje wszystkie permutacje, każdą dokladnie raz.
Operacja \( wypisz \) wypisuje w kolejnym wierszu tablicę P.
Algorytm Generacja-Permutacji
P:= P_0; j:=n; wypisz(P); while j > 1 do rotacja(j,P); if j <> P[j] wypisz(P); j:=n; else j:=j-1
Algorytm ten ma następujacą ciekawą własność: jesli zdefiniujemy rotację jako operację odwrotna do tej którą mamy (pierwszy element wędruje
za \( k \)-ty element) to algorytm w dalszym ciągu jest poprawny: wypisuje dokładnie raz każdą permutację.
Mozna rozwazyc jeszcze prostsza operacje zmiany jednej permutacji w druga: wymiana elementu na pozycji 1-szej z elementem na pozyci k-tej.
Pokazac ze mozna wygenerowac wszystkie permutacje stosujac za kazdym razem pojedyncza operacje takiej zamiany.
Jednakze ten algorytm ma musi miec zupelnie inna strukture.
Na przyklad dla \( n=4 \) ciag pozycji k moze byc nastepujacy: 2 3 2 3 2 4 3 2 3 2 3 4 2 3 2 3 2 4 3 2 3 2 3 .
Rozważmy podobny algorytm do algorytmu Generacja-Permutacji generowania podzbiorów k-elemntowych (kombinacji)
zbioru n-elementowego, każda konfiguracja jest ciągiem K zerojedynkowym mającym dokładnie k jedynek.
Inaczej mowiąc chcemy wygenerowąc każdy taki ciąg dokładnie raz. K jest jednocześnie traktowane jako ciąg i jako tablica n-elementowa.
Oznaczmy przez SzukajWzorzec(01,K) długośc najkrótszego prefiksu ciągu K kończącego się na 01. Na przykład SzukajWzorzec(01,111100001001) = 9.
Algorytm Generacja-kombinacji
K := 1^k 0^(n-k); j:=n-1; Załóżmy że 0 < k < n while j < n do wypisz(K); rotacja(j+1,K); j:= SzukajWzorzec(01,K)
Koszt zamortyzowany
Jeśli mamy ciąg operacji \( op_1,op_2,\ldots, op_n \), to koszt zamortyzowany jednej z nich jest sumarycznym kosztem wykonania wszystkich operacji podzielonym przez liczbę operacji. Inaczej mówiąc jest to, dla danego ciągu operacji, "średni" koszt jednej z nich. Zauważmy, że nie mówimy tu nic o prawdopodobieństwie - model jest deterministyczny. Na przykład w algorytmie Najbliższy-Mniejszy-Sąsiad rozważmy ciąg operacji
\( op_i \): while \( ( A[j] >= A[i])\ j = Lewy[j] \)
Koszt pojedynczej operacji może być liniowy, również sumaryczny koszt ciągu tych operacji \( op_1,op_2,\ldots, op_n \) jest liniowy. Zatem pesymistyczny koszt jednej operacji jest tutaj liniowy, natomiast zamortyzowany koszt jednej operacji jest ograniczony przez stałą. W tym przypadku wiemy, że każde sprawdzenie \( A[j]>=A[i]) \) z wynikiem negatywnym odbywa się tylko raz dla danej wartości \( j \). Możemy powiedzieć, że księgujemy koszt operacji elementom \( j \) o tej własności. Nieformalna metoda księgowania kosztów polega na rozdzielaniu (księgowaniu) kosztu, a następnie szacowaniu sumarycznej złożoności poprzez sumowanie wszystkich zaksięgowanych kosztów. Operacje pożyczają w pewnym sensie fundusze na pokrycie kosztów z różnych źródeł. Metoda ta będzie wykorzystana do analizy algorytmu dla interesującego problemu Find-Union.
Typowym przykładem liczenia kosztu w sposób zamortyzowany jest analiza generacji reprezentacji binarnych kolejnych liczb naturalnych od 0 do \( 2^n-1 \) przez dodawanie jedynki. W jednym kroku zastępujemy najdłuższy ciąg jedynek od końca zerami, następnie wstawiamy jedną jedynkę. Ponieważ w sumie wstawiliśmy \( 2^n-1 \) jedynek w ciągu \( 2^n- 1 \) operacji, to zamortyzowana liczba operacji zamiany zera na jedynkę wynosi 1.
Zasada magazynu. W ostatnim przykładzie możemy powiedzieć, że analizowaliśmy koszt tzw. metodą magazynu. W każdej operacji koszt jest proporcjonalny do liczby przedmiotów włożonych do magazynu lub do liczby przedmiotów wyjętych z magazynu. Magazyn początkowo jest pusty. Wtedy całkowity koszt jest proporcjonalny do liczby przedmiotów włożonych. W przypadku generowania liczb binarnych do magazynu wkładamy nowe jedynki, a wyjmujemy te jedynki, które zamieniamy na zera.
Potencjał - Fundusz Ubezpieczeń Kosztów Algorytmicznych
Metodę magazynu można uogólnić na tzw. metodę potencjału. Niech \( \Phi_i \) będzie pewną liczbą naturalną (włączając zero) odpowiadającą potencjałowi po wykonaniu \( i \)-tej operacji. Wyglądałoby to mniej tajemniczo, gdybyśmy zamiast \( \Phi(i) \) pisali \( Bilans(i) \).
Niech \( koszt(i) \) będzie rzeczywistym kosztem wykonania i-tej operacji.
Zakładamy, że potencjał jest początkowo zero, nigdy nie jest ujemny oraz że:
Wtedy całkowity koszt jest tego samego rzędu co \( \sum wplata(i) \). W naszych poprzednich przykładach rozmiar magazynu jest w tym sensie potencjałem.
Można powiedzieć obrazowo, że potencjał jest kapitałem Funduszu Ubezpieczeń Kosztów Algorytmicznych. Jeśli wszystkie wpłaty są takie same, to koszt zamortyzowany jednej operacji jest wpłatą (składką), którą ta operacja wpłaca do funduszu.
Operacja najpierw wpłaca swoją składkę, a następnie pobiera z funduszu tyle, żeby proporcjonalnie (być może z dokładnością do stałego współczynnika) zapłacić za swój koszt wykonania.
Dzięki temu, że wiele operacji pobiera z funduszu znacznie mniej niż wpłaca, niektóre operacje mogą jednorazowo pobrać dużą kwotę, którą płacą za koszt wykonania. Istotne jest jedynie, żeby Fundusz nie zbankrutował i kapitał nie zszedł poniżej zera. Możliwa jest również sytuacja, gdy Fundusz startuje z kapitałem początkowym. Wtedy kapitał ten wlicza się do całkowitego kosztu algorytmu, który się dodaje do sumy składek.
Rozważmy przykłady ilustrujące wykorzystanie potencjału. Najistotniejsze jest określenie składek.
Tablica dynamiczna
Przypuśćmy, że mamy dynamiczną tablicę. W każdym momencie wiemy, ile elementów w tablicy jest aktywnych, elementy nieaktywne zaznaczamy. W każdej operacji, jeśli liczba elementów nieaktywnych jest mniejsza od \( \frac{1}{4} \) wielkości tablicy, to tworzymy tablicę dwa razy mniejszą i tam przepisujemy elementy aktywne. Starą tablicę zwalniamy. W przeciwnym wypadku jeśli chcemy dodać element, który spowoduje przepełnienie tablicy, to całą tablicę kopiujemy do tablicy dwa razy większej. Początkowo tablica ma rozmiar 1. Zakładamy, że operacją dominującą jest kopiowanie aktywnego elementu do nowej tablicy. Jeśli mamy \( n \) operacji, to całkowity koszt kopiowania jest liniowy. Wystarczy w każdej operacji dać składkę 4 jednostek do Funduszu (potencjału). Wtedy koszt jednej dużej operacji przepisywania zamortyzuje się zmianą potencjału.
Zastąpienie kolejki dwoma stosami
Jedną kolejkę Q można zastąpić dwoma stosami \( S1,\ S2 \). Jeśli pierwszy element stosu lub kolejki w reprezentacji poziomej jest w ciągu na pierwszej pozycji (tzn. pobieramy \( e_1 \), stawiamy za \( e_n \)), oraz \( Q = (e_1,e_2,..,e_k) \), to dla pewnego \( j \) mamy:
\( S1 = (e_n,e_{n-1},...,e_j),\ S2 = (e_{1},e_{2}, ...,e_{j-1}) \).
Inaczej mówiąc, pierwszy element kolejki jest na wierzchołku drugiego stosu, a ostatni element kolejki jest na wierzchołku pierwszego stosu.
Operacja wstawiania do Q odpowiada wstawieniu elementu do \( S1 \), operacja pobrania z Q odpowiada pobraniu elementu z S2 z tym, że jeśli \( S2 \) jest pusty, to przepisujemy najpierw wszystkie elementy z S1 do S2. Niech operacją dominującą będzie jedna operacja stosowa (wstawienie lub pobranie pojedynczego elementu ze stosu). Wtedy ciąg \( n \) operacji kolejkowych, startujących od pustej kolejki, ma koszt liniowy w tej implementacji. Wystarczy, że każda operacja wkłada do Funduszu składkę 3 jednostek. Dowód tego pozostawiamy jako ćwiczenie.
Zastąpienie kolejki dwustronnej trzema stosami
Rozważmy podobny problem - z tym, że nasza kolejka jest dwustronna, możemy wkładać i pobierać element z każdego z dwóch końców kolejki. Wtedy możemy taką kolejkę zastąpić trzema stosami tak, że teraz również każda operacja kolejkowa będzie mieć zamortyzowany koszt stały. Elementy kolejki trzymamy w dwóch stosach S1, S2 tak, jak poprzednio. Niezmiennikiem jest to, że oba stosy są niepuste, lub mają w sumie co najwyżej jeden element. Zapewniamy zachodzenie niezmiennika wykorzystując trzeci stos. W momencie, gdy jeden ze stosów ma więcej niż jeden element, a drugi jest pusty, korzystając z trzeciego stosu, doprowadzamy do reprezentacji aktualnej kolejki przez stosy S1 i S2 tak, aby miały one tę samą liczbę elementów (z dokładnością do 1). Pozostawiamy jako ćwiczenie dowód (metodą potencjału) tego, że zamortyzowany koszt jest stały.
Ćwiczenia
Wstęp: elementarne techniki algorytmiczne i struktury danych
W tym drugim, wstępnym module opiszemy nieformalnie kilka podstawowych technik algorytmicznych i elementarnych struktur danych. Niektóre z nich były wstępnie omawiane na kursie Metody programowania. Teraz rozważymy je przede wszystkim w aspekcie złożoności obliczeniowej i analizy algorytmów.
Metoda dziel i zwyciężaj
Metoda ta polega na podzieleniu problemu na podproblemy, które rozwiązujemy niezależnie, a następnie "scalamy". Metoda działa dobrze, gdy "scalanie" podproblemów jest łatwe, oraz same podproblemy są "małe" w stosunku do rozmiaru problemu \( n \).
Jako przykład rozważmy jeszcze raz problem wyznaczenia przywódcy tablicy (patrz Wstęp: poprawność i złożoność algorytmów.). Stosując metodę dziel i zwyciężaj, możemy otrzymać następujący algorytm:
Algorytm Rekurencyjny Przywódca
if n=1 then przywódcą jest pojedynczy element tablicy else podziel tablicę na dwie połowy; rekurencyjnie oblicz przywódcę lewej i prawej połowy tablicy; sprawdź w czasie O(n), który z nich jest przywódcą całości
Jeśli algorytm ten wykonuje \( T(n) \) kroków, to:
\( T(n)\ =\ T(\lfloor \frac{n}{2}\rfloor)+T(\lceil \frac{n}{2}\rceil)+O(n),\ T(1)=1 \)
Rozwiązaniem jest \( T(n)=O(n \log n) \) (jak wiadomo z kursu matematyki dyskretnej).
Metoda zachłanna
Metoda ta dobrze działa w sytuacjach, gdy maksymalizujemy lub minimalizujemy pewną wartość. Algorytm w każdej iteracji ma do wyboru pewną liczbę "lokalnych" akcji. W przypadku maksymalizacji wybiera tę, która lokalnie maksymalizuje wartość docelową. W przypadku minimalizacji wybiera akcję o minimalnej wartości. Przedyskutujemy tę metodę na następujących dwóch przykładach.
Wieże na szachownicy
Przypuśćmy, że mamy szachownicę \( n \) na \( n \), na polu \( (i,j) \)-tym leży \( x(i,j) \) monet. Chcemy umieścić \( n \) wież na szachownicy tak, aby żadne dwie się nie atakowały. Zyskiem jest suma monet na wybranych pozycjach. Lokalna akcja to wybranie jednej dopuszczalnej pozycji. Zysk akcji to liczba monet na pozycji. Algorytm zachłanny działa trywialnie: wybieramy pozycję z maksymalnym \( x(i,j) \). Można łatwo zobaczyć, że ten algorytm niekoniecznie da optymalny zysk - da jednak co najmniej połowę optymalnego zysku. Pozostawiamy to jako ćwiczenie. Bardziej formalnie można wyrazić ten problem w terminach skojarzeń w grafach. Najciekawszym przypadkiem jest sytuacja, gdy tablica \( x(i,j) \) jest zerojedynkowa.
Minimalne Sklejanie Par
Przypuśćmy, że mamy ciąg \( n \) nieujemnych liczb \( p_1,p_2,\ldots,p_n \). Lokalna akcja sklejania polega na pobraniu dwóch elementów z ciągu i zastąpieniu ich przez sumę ich wartości. Kosztem akcji jest suma wartości "sklejanych" elementów. Ciąg operacji sklejania kończy się, gdy skleiliśmy wszystko do jednej wartości.
Interesuje nas obliczenie minimalnego sumarycznego kosztu sklejania \( n \) elementów w jeden element. Metoda zachłanna zawsze wybiera akcję o minimalnej wartości.
Algorytm Schemat-Zachłanny
while zbiór możliwych lokalnych akcji jest niepusty do wykonaj akcję o minimalnym koszcie; return suma kosztów wykonanych akcji;
Można to zapisać bardziej formalnie:
Algorytm Optymalne-Sklejanie-Par
wynik:= 0; while mamy co najmniej dwa elementy do zastąp dwa najmniejsze elementy a,b przez a+b wynik:= wynik + a+b;
Pozostawiamy jako ćwiczenie dowód tego, że algorytm ten wyznacza ciąg sklejeń o najmniejszym koszcie. Co będzie, jeśli zamiast obliczać minimalny koszt chcielibyśmy wyznaczyć ciąg, który maksymalizuje sumaryczny koszt? Pozostawiamy to jako ćwiczenie. Algorytm ten jest "szkieletem" efektywnego konstruowania tzw. "drzewa Huffmana".
W naszym przykładzie mogliśmy sklejać elementy, które niekoniecznie są sąsiednie, kolejność elementów w ciągu nie odgrywała roli. Zastanówmy się, co będzie, gdy wprowadzimy do gry kolejność elementów. Załóżmy teraz, że możemy sklejać tylko elementy sąsiednie. Tak zmodyfikowany problem nazwijmy problemem Minimalnego Sklejania Sąsiadów. Możemy w poprzednim algorytmie zastąpić zwrot "dwa najmniejsze elementy" przez "dwa sąsiednie elementy o minimalnej sumie".
Niespodziewanie, nasz algorytm nie zawsze oblicza minimalną wartość, czyli nie jest poprawny. Kontrprzykładem jest ciąg
\( (p1,p2,p3,p4) = (100,99,99,100). \)
Programowanie dynamiczne
Rozwiązaniem danego problemu często jest kombinacja rozwiązań podproblemów, na które można problem rozłożyć. Natomiast nie od razu wiemy, jaka dekompozycja jest optymalna; początkowo mamy niedeterministyczny wybór wielu różnych dekompozycji. W sytuacji, gdy nie wiemy, jaka dekompozycja jest optymalna, nie możemy uruchomić rekursji, ponieważ na każdym etapie mielibyśmy wiele wyborów i w sumie złożoność mogłaby być wykładnicza.
W takich sytuacjach stosujemy metodę zwaną programowaniem dynamicznym. Metoda ta, z grubsza biorąc, wygląda następująco: Jeśli problem możemy rozbić na podproblemy i liczba wszystkich potencjalnych podproblemów jest wielomianowa, to zamiast korzystać z rekursji możemy obliczyć wartości wszystkich podproblemów stosując odpowiednią kolejność: od "mniejszych" podproblemów do "większych". Rozmiary problemów muszą być odpowiednio zdefiniowane, nie powinno być zależności cyklicznej.
Wartości obliczone dla podproblemów zapamiętujemy w tablicy. Mając obliczone wartości podproblemów, na które można rozbić dany problem, wartość problemu obliczamy korzystając z wartości zapamiętanych w tablicy.
Najistotniejsze jest tutaj określenie zbioru potencjalnych podproblemów. Z reguły zbiór ten jest znacznie większy niż zbiór podproblemów będących częściami jednego optymalnego rozwiązania.
Spróbujmy skonstruować wielomianowy algorytm dla problemu minimalnego sklejania sąsiadów korzystając z programowania dynamicznego. Jeśli mamy dany ciąg \( p_1,p_2, \ldots p_n \), to w tym przypadku podproblem można utożsamić z pewnym przedziałem \( [i..j] \). Niech \( wynik[i,j] \) będzie wartością problemu minimalnego sklejania sąsiadów dla ciągu \( (p_i,p_{i+1}, \ldots p_j) \);
oznaczmy ponadto
\( \sigma_{i,j}\ =\ \sum_{k=i}^j\ p_k \)
Algorytm Optymalne-Sklejanie-Sąsiadow
for i:=1 to n do wynik[i,i]:=0; for j:=2 to n do for i:=j-1 downto 1 do wynik[i,j] := min(i <= k < j) (wynik[i,k]+wynik[k+1,j]+sigma[i,j]) return wynik[1,n];
W algorytmie zasadniczą instrukcję
\( wynik[i,j] := \min_{i \le k < j}\ (wynik[i,k]+wynik[k+1,j]+\sigma_{i,j}) \)
można wykonywać w dowolnym przyzwoitym porządku ze względu na (i,j) (na przykład po przekątnych, zaczynając od głównej przekątnej). Przyzwoitość polega na tym, że jest już ostatecznie policzone to, z czego w danym momencie korzystamy.
Algorytm ma złożoność czasową \( O(n^3) \) i jest to "typowa" złożoność algorytmów tego typu. Duża złożoność wynika stąd, że liczymy wartości dla mnóstwa podproblemów, które mogą być zupełnie nieistotne z punktu widzenia optymalnego rozwiązania.
Dygresja
Problem sklejania sąsiadów można rozwiązać inaczej, modyfikując w sposób nietrywialny algorytm Optymalne-Sklejanie-Par. W algorytmie tym instrukcję
zastąp dwa najmniejsze elementy \( a,b \) przez \( a+b \)
zamieńmy na:
zastąp dwa sąsiednie elementy \( a,b \) o minimalnej sumie przez \( a+b \)
przesuń \( a+b \) przed najbliższy na prawo (w ciągu) element \( c \) większy od \( a+b \)
(na koniec ciągu, jeśli takiego \( c \) nie ma)
Otrzymany algorytm (wersja algorytmu Garsia-Wachsa) liczy koszt minimalnego sklejania sąsiadów. Jest to przykład pozornie prostego algorytmu, dla którego odpowiedź na pytanie, "dlaczego to działa" jest niezwykle skomplikowana i wykracza poza zakres tego kursu. Pozostawiamy jako ćwiczenie implementację tego algorytmu w czasie \( O(n \log n) \), przy założeniu, że jest on poprawny. Jeśli liczby \( p_i \) są liczbami naturalnymi z przedziału \( [1..n] \), to istnieje nawet (bardzo trudna) implementacja w czasie liniowym.
Konstruowanie algorytmu metodą transformacji
Algorytm efektywny otrzymujemy często startując od prostszego, ale mało efektywnego algorytmu.
Następnie staramy się za pomocą prostych transformacji przekształcić prosty algorytm w algorytm docelowy. Można to również nazwać stosowaniem metody kolejnych przybliżeń w aspekcie inżynierii algorytmicznej. Czasami można to (w przenośni algorytmicznej) nazwać chirurgią algorytmiczną, ponieważ możemy amputować chore lub zbędne tkanki algorytmu, aby go usprawnić. Czasami, zamiast amputacji, potrzebne jest wzmocnienie algorytmu poprzez doszycie pewnej dodatkowej części (np. funkcji buty siedmiomilowe, funkcji większy-biceps lub czaso-przyspieszacz). Oczywiście w chirurgii zdarzają się pomyłki i można doszyć to, czego nie należałoby doszywać, np. funkcję czaso-wstrzymywacz. Słaba kondycja algorytmu może mieć przyczyny niezwiązane z chirurgią, np. nadwaga algorytmiczna, lub tzw. połknięcie paradygmatu. Istotna jest również prostota algorytmu. Stosując zbyt wiele transformacji i udziwnień, możemy przerobić algorytm, który jest naiwny, ale zrozumiały, w genialny algorytm, który jest zdziwaczały i niezrozumiały. Algorytm, który stracił zdrowy rozsądek, może być świetnym wynikiem teoretycznym, może być nawet przedmiotem podziwu w sensie artystycznym, ale jego praktyczne stosowanie może być niewielkie (nie dotyczy to dydaktyki).
Większość prostych algorytmów z wykładu Wstęp: poprawność i złożoność algorytmów można potraktować jako produkty transformacji algorytmów naiwnych. Pokazanie tego pozostawiamy jako ćwiczenie. Pokażemy teraz dwa proste przykłady transformacji.
Liczba inwersji
Mając dane dwie posortowane rosnąco tablice \( A[1..n], B[1..n] \), należy wyznaczyć liczbę (inwersji) par \( i,j \) takich, że \( A[i]>B[j] \). Liczbę inwersji między tablicami \( A \), \( B \) oblicza następujący naiwny algorytm:
Algorytm Liczba-Inwersji-Naiwnie
wynik := 0; for i := 1 to n do j:= 0; while j < n and A[i] > B[j+1] do j := j+1; wynik := wynik + j;
Algorytm ma złożoność kwadratową. Załóżmy, że początkową wartością \( j \) jest zero. Wtedy przyglądając się dokładniej algorytmowi widzimy, że bez szkody dla poprawności instrukcję \( j := 0; \) można przesunąć przed pętlę for i złożoność stanie się liniowa. Dowód pozostawiamy jako ćwiczenie. W ten sposób mamy prostą transformację kwadratowego algorytmu naiwnego na algorytm liniowy.
Przykład ten był dosyć ubogi i dlatego przedyskutujemy dodatkowo bardziej skomplikowany przykład. Podamy transformację pewnego prostego algorytmu \( B(n) \) w nietrywialny algorytm \( A_n \). Transformacja ta bazuje na własnościach \( B(n) \). Kluczem do efektywnej transformacji jest analiza własności algorytmu \( B(n) \).
Wykrywanie fałszywej monety
Mamy zbiór monet o numerach 1,2,..,N, wszystkie o tej samej wadze, i wiemy że wśród nich jest dokładnie jedna fałszywa moneta o innej wadze. Modelem algorytmu jest ciąg ważeń na wadze szalkowej. Niech waga(A) oznacza sumę wag monet ze zbioru A. W jednym ważeniu możemy wykonać operację Porównaj(A,B), gdzie A,B są rozłącznymi podzbiorami zbioru \( \{ 1,2,\ldots,N\} \). Otrzymujemy jedną z trzech możliwych odpowiedzi:
- L - gdy waga(A)<waga(B)
- P - gdy waga(A)>waga(B)
- R - gdy wagi są równe.
Algorytmem w naszym modelu jest ciąg operacji \( op_1, op_2,..., op_n \) taki, że z otrzymanego ciągu odpowiedzi można jednoznacznie wyznaczyć fałszywą monetę i określić, czy jest ona cięższa czy lżejsza niż inne. Operację Porównaj(A,B) będziemy w skrócie zapisywać jako parę (A,B). Nasz algorytm można zatem zapisać jako ciąg par rozłącznych zbiorów, na przykład:
Algorytm dla n=2, N=3: ({1}, {2}), ({1}, {3})
Algorytm dla n=3, N=12: ({1,2,3,10},{4,5,6,11}), ({1,2,3,11},{7,8,9,10}), ({1,4,7,11},{2,5,8,12})
Naszym głównym zadaniem jest dla danego n znalezienie algorytmu ważeń, który maksymalizuje N.
Pokażemy najpierw, jak rozwiązać zadanie dla \( N=3^{n-1} \). Załóżmy, że liczba monet jest potęgą trójki i monety są ponumerowane \( 0,1,2.. 3^{n}-1 \) . Niech S(k,0), S(k,1) oznaczają zbiory numerów monet, które na k-tym bicie (licząc od końca) w reprezentacji trójkowej mają odpowiednio 0, 1. Gdybyśmy wiedzieli od razu, czy fałszywa moneta jest lżejsza czy cięższa, to mamy następujący prosty algorytm, który działa podobnie jak wyszukiwanie ternarne:
\( (S(1,0), S(1,1)), (S(2,0),S(2,1)), ... (S(n,0),S(n,1)) \)
Ponieważ nie znamy statusu fałszywej monety, dodajemy jedno porównanie i otrzymujemy algorytm B(n), który obsługuje za pomocą n ważeń \( N = 3^{n-1} \) monet (mamy teraz tylko n-1 bitów ternarnych).
\( B(n)= (S(1,0),S(1,2)), (S(1,0),S(1,1)), ... (S(n-1,0),S(n-1,1)) \)
Dzięki dodaniu na początku jednego ważenia, już po pierwszych dwóch ważeniach wiemy, jaki jest status fałszywej monety (lżejsza, cięższa). Poza tym wynikiem pierwszych dwóch ważeń nie może być LP ani PL. Te dwie własności algorytmu B(n) są kluczem do transformacji tego algorytmu w algorytm \( A_n \).
Jeśli mamy w naszym modelu algorytmy
\( A1(n) = (A_1,B_1),(A_2,B_2)...(A_{n},B_{n}) \) oraz \( A2(n) = (C_1,D_1),(C_2,D_2)...(C_{n},D_{n}) \),
to definiujemy algorytm
\( A1 \cup A2 = (A_1 \cup C_1, B_1 \cup D_1), (A_1 \cup C_2, B_2 \cup D_2) ... (A_n \cup C_n, B_n \cup D_n) \)
Załóżmy, że mamy algorytm \( A_{n-1} = (A_1,B_1),(A_2,B_2)...(A_{n-1},B_{n-1}) \) na zbiorze rozmiaru \( N_{n-1} \) i oznaczmy przez \( przeskaluj(A_{n-1}) \) algorytm, który działa na zmodyfikowanych numerach monet: do każdego numeru dodajemy \( 3^{n-1} \). Ponadto dodajemy jedno porównanie:
Docelowy algorytm definiujemy rekurencyjnie:
\( A_n= przeskaluj(A_{n-1}) \cup B(n) \)
Poprawność takiej konstrukcji wynika stąd, że na podstawie wyników dwóch pierwszych ważeń wiemy, czy fałszywa moneta jest mniejsza od \( 3^{n-1} \). Jeśli tak, to traktujemy odpowiedzi jak w B(n), jeśli nie, to jak w A(n-1). Zostawiamy jako ćwiczenie opisanie sposobu takiego przełączania się.
W ten sposób mamy algorytym, który za pomocą n ważeń obsługuje \( N_n \) monet, gdzie
\( N_2=3; N_n=3^{n-1}+N_{n-1} \)
Dla n = 2,3,4,5,6,7 mamy więc: \( N_n = 3, 12, 39, 120, 363, 1092 \).
Dygresja
Teoretycznie interesujące w tym jest to, że są to maksymalne wartości N. Pozostawiamy dowód jako ćwiczenie. Istnieją różne optymalne algorytmy dla tego problemu. Wzór rekurencyjny na liczbę monet można zapisać również w postaci
\( N_2=3; N_n=3*N_{n-1}+3 \).
Na podstawie tego wzoru można otrzymać drugi algorytm, który pozostawiamy jako ćwiczenie. Jest jeszcze następujący zwarty wzór, z którego wynika trzeci algorytm rozwiązujący problem bezpośrednio (bez rekursji)
\( N_n=(3^{n}-3)/2 \).
Na razie byliśmy zainteresowani głównie zmaksymalizowaniem liczby \( N_n \) oraz ogólną strukturą algorytmów ważenia. Pozostawiamy jako ćwiczenie pokazanie, że wszystkie trzy powyższe algorytmy można zaimplementować tak, aby wypisywały one na wyjściu odpowiadającą im ciągi ważeń w czasie liniowym ze względu na rozmiar wyjścia.
Dwa dodatkowe zadania o wadze szalkowej
Waga czwórkowa
Zupełnie innym problemem jest obliczenie minimalnej liczby odważników potrzebnych do zważenia na wadze szalkowej przedmiotu o wadze \( n \).
Zakładamy, że mamy tylko odważniki o wagach będących potęgami czwórki.
W tym przypadku algorytm opiera się na obserwacji, że na lewo w ciągu generuje się co janwyżej przeniesienie jednej jedynki (reprezentującej następną wartść czwórki).
Algorytm korzysta istotnie z reprezentacji czwórkowej liczby \( n \). Niech
oznacza reprezentację czwórkową liczby \( n \)
Cały algorytm nieformalnie wygląda następująco:
Algorytm WagaCzwórkowa
\( x_0 = 0 \), \( y_0 = 1 \)for \( i:=0 \) to \( k-1 \) do \[ \begin{array}{rcl} n_{i+1} = 0 & \Longrightarrow & (x_{i+1}, y_{i+1}):= (x_i, x_i+1) \\ n_{i+1} = 1 & \Longrightarrow & (x_{i+1}, y_{i+1}):= (x_i+1, \min(x_i+2, y_i+2)) \\ n_{i+1} = 2 & \Longrightarrow & (x_{i+1}, y_{i+1}):= (\min(x_i+2, y_i+2), y_i+1) \\ n_{i+1} = 3 & \Longrightarrow & (x_{i+1}, y_{i+1}):= (y_i+1, y_i) \end{array} \] \( wynik\:=\ x_k \)
Pozostawiamy jako ćwiczenie modyfikację (rozszerzeie) algorytmu tak aby obliczał on liczbę możliwych ważeń używających minimalnej liczby odważników.
Permutacje wagowe
Przedstawimy jeszcze jeden problem związany z wagą. Rozważmy wagę szalkową, na której początkowo obie szalki są puste. Mamy do dyspozycji odważniki o numerach \( 1,2,\ldots,n \). Waga i-tego odważnika wynosi \( a_i \) i wagi są parami różne. Dla danej permutacji \( \Pi \) numerów odważników będziemy je wkładać na wagę zgodnie z permutacją. Kładziemy kolejno odważniki w kolejności \( \Pi \) na lewą lub prawa szalkę, raz położony odważnik nie zmienia już nigdy swego położenia na szalce (wybór szalki jest niedeterministyczny). Otrzymujemy ciąg wyników ważenia: +1, gdy lewa szalka przeważa, a -1 w przeciwnym wypadku. Ciąg ten oznaczamy przez Input. Mówimy, że permutacja \( \Pi \) jest zgodna z ciągiem wyników ważeń, danych tablicą Input. Zajmiemy się problemem: dany jest na wejściu ciąg Input wyników ważeń i mamy znaleźć jakąkolwiek permutację \( \Pi \) zgodną z ciągiem Input. Takich permutacji może być wiele. Zauważmy, że liczba permutacji wynosi n!, a liczba ciągów wyników ważeń wynosi \( 2^n \), co jest liczbą znacznie mniejszą.
Następujący algorytm znajduje pewną permutację zgodną Input. Zakładamy, że
Algorytm Permutacja-Wagowa
p:=1; q:=n; for i:=n downto 1 do if (i > 1) and (Input[i-1] <> Input [i]) then Wynik[i]:= q; q:=q-1; else Wynik[i]:= p; p:=p+1
Jeśli \( Input \) = [+1,+1,+1,-1,-1,-1,+1,+1,-1], to \( Wynik \) = [6, 5, 4, 7, 3, 2, 8, 1, 9]. Ciąg \( Input \) jest zrealizowany przez następujący ciąg wyborów wkładania kolejnego odważnika:
gdzie L oznacza połóż na lewą szalkę, P na prawą.
Nie jest jasne, jak policzyć efektywnie liczbę wszystkich permutacji zgodnych z danym ciągiem wyników, albo znaleźć jakąś szczególną permutację, np. leksykograficznie pierwszą lub ostatnią. Co stanie się, jeśli tablica \( Input \) zawiera również zera (wagi szalek są równe)? Wtedy nie każdy ciąg \( Input \) jest realizowalny. Jak to można efektywnie sprawdzać?
Znaczenie struktury danych
Podstawową strukturą danych jest struktura "obsługująca" operacje Delete(x,S), Insert(x,S), dla zadanego zbioru S. Operacja delete pobiera z S i zwraca jako wartość "pewien" element S. Nie interesuje nas na razie, który element zostanie usunięty. Niedeterminizm pozwala nam użyć w takim wypadku jednej z kilku struktur danych, które omawiamy poniżej. W niektórych zastosowaniach istotne jest, który element jest pobierany, i wtedy nazwy operacji Insert i Delete często zmieniamy na nazwy bardziej odpowiadające terminologicznie tym strukturom. Będziemy jednak też używać nazewnictwa Delete, Insert, o ile nie prowadzi to do niejednoznaczności. Elementarne struktury danych, w których określone są operacje Insert, Delete, to:
- lista,
- stos,
- kolejka.
Są one punktem wyjścia do bardziej skomplikowanych struktur, w szczególności różnego typu drzew.
Prosty przypadek kolejki priorytetowej
Wariantem kolejki jest kolejka priorytetowa typu min. Jest to struktura danych, która "obsługuje" ciąg operacji insert, delete, gdzie operacja delete zawsze pobiera minimalny (maksymalny) element. Operację tę nazwiemy w tym przypadku DeleteMin (DeleteMax). Operacja delete jest tutaj w dużym stopniu zdeterminowana.
Załóżmy, że ciąg operacji Insert można podzielić na dwa ciągi następujące po sobie; w każdym z nich w operacji Insert wstawiamy elementy w porządku rosnącym. Wtedy kolejkę priorytetową można łatwo zaimplementować tak, by operacje Insert, Delete można było wykonać w czasie stałym.
Pokażemy na przykładzie algorytmu Optymalne-Sklejanie-Par zastosowanie tego typu kolejki priorytetowej. W algorytmie tym podstawową operacją jest:
zastąp dwa minimalne elementy \( a,b \) przez \( a+b \).
Operacja ta jest równoważna operacjom:
\( a = DeleteMin(S) \); \( b = DeleteMin(S) \); \( Insert(a+b,S) \);
W szczególnym przypadku, rozważonym poniżej, operacje Insert, DeleteMin można zaimplementować w czasie stałym. Załóżmy, że początkowy zbiór \( S \) jest posortowany i jego elementy są umieszczone na stosie \( ST \) w kolejności rosnącej (od szczytu "w dół"). Załóżmy, że mamy dodatkowo zwykłą kolejkę \( Q \) początkowo pustą. Wtedy ciąg operacji
\( a = DeleteMin(S) \); \( b = DeleteMin(S) \); \( Insert(a+b,S) \)
możemy wykonać w czasie stałym: element minimalny jest na wierzchołku \( ST \) lub na początku kolejki \( Q \), element \( a+b \) wstawiamy na koniec \( Q \). Zatem algorytm Optymalne-Sklejanie-Par możemy zaimplementować w czasie liniowym, gdy początkowy zbiór jest od razu posortowany. Widzimy na tym przykładzie, w jaki sposób złożoność algorytm zależy od struktury danych związanych z algorytmem.
W następujących dwóch przykładach możemy sobie pozwolić na niedeterministyczny wariant operacji Delete.
Maksymalna bijekcja
Przypuśćmy, że mamy funkcję \( f : \{1,2,\ldots n\}\rightarrow\{1,2,\ldots n\} \), zadaną tablicą \( f[1..n] \), i chcemy znaleźć rozmiar maksymalnego podzbioru, na którym ta funkcja jest bijekcją.
Dwie funkcje
Jest to zadanie bardzo podobne. Mamy dwie częściowo określone funkcje \( f_1, f_2 \) ze zbioru \( [1..n] \) w siebie. Chcemy znaleźć taką permutację \( \pi = (i_1,i_2,\ldots i_n) \), żeby \( \pi(f_k(i)) > \pi(i), \forall \ 1\le i\le n,\ k=1,2 \), jeśli \( f_k(i) \) określone.
Oba te przykłady możemy wyrazić w terminach teorii grafów. Zbiorem wierzchołków jest tutaj zbiór \( [1..n] \). W pierwszym przykładzie krawędzie są postaci \( (i,f(i)) \), w drugim postaci \( (i,f_k(i) \), gdzie \( k=1,2 \).
W pierwszym przykładzie chcemy znaleźć maksymalny podzbiór grafu, na którym podgraf indukowany jest zbiorem cykli.
W drugim przypadku mamy szczególny przypadek tzw. sortowania topologicznego grafu. Wierzchołek nazywamy roboczym, gdy nie wchodzi do niego żadna krawędź. Niech \( S \) będzie początkowo zbiorem wszystkich wierzchołków roboczych. Algorytmy dla obu powyższych problemów działają w podobny sposób. Pobieramy element \( v \in S \), odpowiednio przetwarzamy i usuwamy z grafu. Wskutek usunięcia \( v \) pewne nowe wierzchołki stają się roboczymi i wstawiamy je do S. Kontynuujemy, dopóki S jest niepusty.
W przypadku problemu maksymalnej bijekcji po prostu usuwamy \( v \), a w przypadku numeracji \( \pi \) \( \pi(v) \) staje się kolejnym numerem. Pomimo interpretacji teorio-grafowej nie musimy implementować żadnej reprezentacji grafu: wszystko się dzieje w wejściowych tablicach i w dodatkowej tablicy licznik[v], w której trzymamy dla każdego \( v \) liczbę krawędzi aktualnie wchodzących do \( v \). Konkretną implementację pozostawiamy jako ćwiczenie. Zbiór S jest tutaj zbiorem wierzchołków roboczych, które są w pewnym sensie akcjami do wykonania. Do S wkładamy akcje, które mamy wykonać; kolejność nie jest istotna. S może być listą, stosem lub kolejką.
Panorama Warszawy
Rozważmy inny przykład algorytmu, którego złożoność istotnie zależy od (bardzo prostej) struktury danych (lista jednokierunkowa, która się zamienia w drzewo skierowane w stronę korzenia).
Przypuśćmy, że mamy na wejściu \( n \) trójek postaci \( [p,q,s] \), gdzie \( p,q \in \{1,2,\ldots,n\} , s\ge 0 \). Każdej trójce odpowiada funkcja \( f_{p,q,s} \) taka, że:
\( f_{p,q,s}(i)\ =\ s \), gdy \( p \le i \le q \), oraz \( f_{p,q,s}(i)\ =\ 0 \) w przeciwnym przypadku.
Naszym zadaniem jest dla każdego \( 1 \le i \le n \) obliczyć wartość \( F(i) \) będącą maksimum z danych funkcji \( f_{p,q,s} \) dla argumentu \( i \). Można podać następującą interpretację. Każda funkcja \( f_{p,q,s} \) opisuje kształt wieżowca w Warszawie patrząc z prawej strony Wisły. Wtedy funkcja \( F \) opisuje panoramę centrum Warszawy.
Załóżmy, że trójki \( (p,q,s) \) są posortowane ze względu na \( s \). Wtedy rozważamy kolejno funkcje \( f_{p,q,s} \) w kolejności rosnącego \( s \) i nadajemy za każdym razem końcowe wartości dla pozycji z przedziału \( [p,q] \), dla których jeszcze wartości nie są obliczone. Taki algorytm miałby złożoność kwadratową.
Początkowo elementy trzymamy w liscie jednokierunkowej, element i-ty wskazuje na (i+1)-szy dla i<n+1. Element n na n+1. Zakładamy więc, że mamy na przykład tablicę NEXT taką, że NEXT[i]=i+1, dla i<n+1, NEXT[n+1]=n+1, oraz początkowo Wynik[i]=0 dla każdego i. Trójki trzymamy w trzech tablicach, i-ta trójka jest dana przez P[i], Q[i], S[i]. Nasze podstawowe założenie:
tablica S jest posortowana malejąco
Jeśli przetwarzamy w kolejnej iteracji przedział \( [p,q] \), to zaczynamy od elementu p i poruszamy się na liście dopóki nie przekroczymy q, w tym momencie jesteśmy w jakimś elemencie r. Wszystkie elementy, które przeglądaliśmy, zmieniają swoje dowiązanie na r. W pewnym sensie możemy powiedzieć, że kompresujemy ścieżkę, którą przeszliśmy. Koszt iteracji to, z grubsza, długość ścieżki (liczba dowiązań, które się zmieniły). Z listy jednokierunkowej robi nam się drzewo jednokierunkowe.
Algorytm Panorama-Warszawy1
for i := 1 to n do j := P[i]; while j <= Q[i] do Wynik[j] := max( Wynik[j],S[i] ); j:=NEXT[j]; Kompresja ścieżki: k := P[i]; while k < j do pom :=NEXT[k]; NEXT[k] := j; k :=pom;
Algorytm ten powstał w ten sposób, że do algorytmu naiwnego doszyliśmy dodatkową część: Czaso-Przyspieszacz.
Dosyć łatwo pokazać, że czas tego algorytmu będzie rzędu co najwyżej \( n^{3/2} \), a więc lepszy niż algorytmu naiwnego. Jeśli "kompresujemy" ścieżkę długości k (w części Czaso-Przyspieszacz), to zmniejszamy sumaryczną odległość elementów do korzenia (elementu n) o wielkość co najmniej taką, jak suma liczb 1,2,3..,k, a więc mniej więcej o \( k^2 \). Początkowa suma jest rzędu \( n^{2} \). Za każdym razem zmniejszamy tę sumę o kwadrat kosztu danej iteracji.
Jeśli mamy n liczb, których kwadraty w sumie dają \( n^2 \), to suma tych liczb jest co najwyżej \( n^{3/2} \). Zapisując bardziej matematycznie:
Podobne algorytmy poznamy w module o problemie find-union, wtedy też będziemy mogli lepiej zanalizować algorytm rozwiązujący problem Panoramy.
Rozważmy jeszcze przypadek (nazwijmy go "specjalnym"), gdy wszystkie przedziały odpowiadające wejściowym funkcjom maja wspólne przecięcie teorio-mnogościowe. Nazwijmy ten przypadek specjalnym. Wtedy mamy bardzo prosty algorytm działający w czasie liniowym.
Algorytm Panorama-Warszawy2
lewy:=Q[1]+1; prawy:=Q[1]; for i := 1 to n do for j := lewy-1 downto P[i] do Wynik[j] := max( Wynik[j],S[i] ); for j := prawy+1 to Q[i] do Wynik[j] := max( Wynik[j],S[i] ); lewy:=min(lewy,P[i]), prawy:=max(prawy,Q[i]);
Dlaczego przypadek specjalny jest interesujący? Otóż wykorzystując algorytm dla tego przypadku, możemy łatwo otrzymać algorytm typu dziel i zwyciężaj działający w czasie \( O(n \log n) \).
Podzielmy przedział [1..n] na dwie połowy. Rozważmy najpierw tylko te wieżowce, których przedziały są całkowicie w lewej części. Stosujemy do nich algorytm rekurencyjny. Podobnie robimy dla prawej połowy. Zostają nam jeszcze wieżowce, których przedziały mają punkty wspólne z obu połówkami, a to jest właśnie przypadek specjalny, który rozwiązaliśmy w prosty sposób.
Pomimo tego wydaje się, że algorytm Panorama-Warszawy1 jest znacznie prostszy, gdyż nie wymaga rekursji ani specjalnych przypadków.
Sortowanie kolejkowe i stosowe
Działanie stosu i kolejki świetnie ilustrują różne warianty problemu sortowania z użyciem stosów i kolejek. Niech \( \pi \) będzie permutacją liczb \( \{1,2,\ldots n\} \). Możemy posortować \( \pi \) stosując niedeterministyczny algorytm:
while na wyjściu nie są wypisane wszystkie elementy do wykonaj dokładnie jedną z trzech instrukcji: (1) wstaw kolejny element pi(i) do jednej z kolejek; i=i+1 (2) lub wypisz pi(i) na wyjściu; i=i+1 (3) lub pobierz i wypisz na wyjściu pierwszy element jednej z kolejek
Zdefiniujmy liczbę kolejkową permutacji \( \pi \) jako minimalną liczbę kolejek potrzebnych do posortowania permutacji \( \pi \). Na przykład dla \( \pi=(1,2,3) \) liczba ta wynosi 0, a dla \( \pi=(3,2,1) \) wynosi 2.
Jak wyznaczyć liczbę kolejkową w czasie liniowym? Porównajmy ten problem z problemem maksymalnego malejącego podciągu. Pozostawiamy to jako ćwiczenie.
Podobnie definiujemy liczbę stosową. W tym wypadku w powyższym nieformalnym algorytmie zastępujemy kolejkę przez stos. Można również zdefiniować liczbę kolejkowo-stosową, pytając o minimalną liczbę stosów i kolejek, które razem posortują daną permutację. Jest to trudne pytanie.
W poprzedniej wersji sortowania każdy element może trafić tylko do jednej kolejki. Rozważmy teraz wersję, w której mamy \( k \) kolejek \( Q_1,Q_2,Q_3, \ldots Q_k \) i element może trafiać do kolejek o coraz mniejszych numerach.
Pojedyncza operacja polega na wstawieniu kolejnego elementu z \( \pi \) do jednej z kolejek, wypisaniu bezpośrednio na wyjście, o ile jest on pierwszym niepobranym elementem w \( \pi \) lub pierwszym elementem pewnej kolejki, albo przełożeniu pierwszego elementu pewnej kolejki \( Q_i \) do kolejki \( Q_j \) dla \( j < i \).
Można pokazać, że do posortowania każdej permutacji wystarczy logarytmiczna liczba kolejek.
Podobny fakt zachodzi, gdy kolejki zastąpimy stosami. Pozostawiamy ten problem (zarówno dla kolejek jak i dla stosów) jako ćwiczenie.
Sortowanie kolejkowe
Załóżmy, że każdy element ciągu \( \pi \) jest początkowo listą jednoelementową. Oznaczmy zbiór tych list przez \( S \). Załóżmy też, że umiemy scalić dwie posortowane listy w czasie proporcjonalnym do sumy ich długości za pomocą operacji merge (patrz następne wykłady).
Algorytm Sortowanie-Kolejkowe-1
while |S| > 1 do lista1 := delete(S); lista2 := delete(S); insert(merge(lista1,lista2),S)
Pozostawiamy jako ćwiczenie pokazanie tego, że jeśli S jest kolejką, to algorytm ten działa w czasie \( O(n \log n) \), a jeśli \( S \) jest stosem, to algorytm działa w czasie kwadratowym. Widać na tym przykładzie przewagę kolejki nad stosem. Załóżmy, że mamy posortować tablicę \( A[0,1,\ldots, n-1] \) i \( n \) jest potęgą dwójki. Wtedy następujący algorytm wykonuje ten sam ciąg scaleń co algorytm Scalanie-Kolejkowe. Dowód tego pozostawiamy jako ćwiczenie.
Algorytm Sortowanie-Kolejkowe-2
Scalanie-Kolejkowe bez kolejki m := 1; while m < n do for i:=0 to n/(2m) do merge(A[i..i+m-1], A[i+m..i+2m-1]); m := 2m;
Ćwiczenia
Sortowanie przez porównania: BubbleSort, SelectionSort, InsertionSort
Ten wykład poświęcimy prostym algorytmom sortowania. Zanalizujemy ich wady i zalety, co przygotuje nas do poszukiwania algorytmów lepszych. Zacznijmy od zdefiniowania problemu.
Definicja problemu
Niech \( (U,\le) \) będzie zbiorem liniowo uporządkowanym z relacją porządkującą \( \le \) i niech \( c_1, c_2, \ldots, c_n \) będzie ciągiem \( n \) elementów z \( U \), dla pewnego całkowitego \( n > 0 \). Należy znaleźć permutację \( c_{i_1}, c_{i_2},\ldots,c_{i_n} \) taką, że \( c_{i_1}\le c_{i_2}\le \ldots \le c_{i_n} \).
Uwaga: dla pary elementów \( x, y \in U \) będziemy pisali \( x < y \) (\( x > y \)), gdy \( x \le y \) (\( y \le x \)) oraz \( x \ne y \).
W tym wykładzie przyjmujemy, że elementy ciągu \( c \) znajdują się w tablicy \( a[1..n] \), tzn. \( a[1] = c_1, a[2] = c_2, \ldots, a[n] = c_n \). Będziemy także chcieli, żeby posortowany ciąg \( c \) znajdował się nadal w tablicy \( a \), tzn. wynikiem sortowania ma być \( a[1] = c_{i_1} \le a[2] = c_{i_2} \le \ldots \le a[n] = c_{i_n} \). Dla wygody dalszych rozważań przyjmijmy, że tablica \( a \) jest indeksowana od \( 0 \), i że \( a[0] \) zawiera element, który nie jest większy od żadnego elementu z \( a[1..n] \), tzn. dla każdego \( i = 1,2, \ldots, n \), \( a[0] \le a[i] \).
Zauważmy, że w tak sformułowanym problemie sortowania nic nie wiemy o naturze elementów z \( U \). Na \( U \) mogą składać się zarówno liczby całkowite lub rzeczywiste, jak i \( U \) może być zbiorem rekordów, które należy posortować według ich kluczy. Jedynym sposobem ustalenie porządku w tablicy \( a \) jest porównywanie jej elementów parami. Operacja porównania będzie operacją dominującą w naszych algorytmach. Ponieważ będziemy chcieli ustalić wynik także w tablicy \( a \), potrzebna nam jest jeszcze operacja zamiany dwóch elementów w tablicy. Operacją tą będzie operacja \( Exchange(i,j) \) polegająca na zamianie elementów w tablicy \( a \) z pozycji \( i \) oraz \( j \), \( 1\le i, j \le n \).
Sortowanie bąbelkowe (BubbleSort)
Sortowanie przez wybór (SelectionSort)
Na sortowanie bąbelkowe można spojrzeć jeszcze inaczej. W każdej fazie przepychamy na pierwsze miejsce w nieuporządkowanej części tablicy element najmniejszy. Symetrycznie moglibyśmy sortować poczynając od elementów nawiększych. W sortowaniu przez wybór nie przepychamy elementu największego (najmniejszego) na jego miejsce w ciągu uporządkowanym, tylko znajdujemy jego pozycję, a następnie znaleziony element - największy w części nieuporządkowanej - zamieniamy z elementem, który znajduje się na docelowej pozycji elementu największego. Niech \( Max(i) \) będzie funkcją, której wartością jest pozycja największego elementu w podtablicy \( a[1..i] \). Oto schemat algorytmu sortowania przez wybór:
Algorytm Schemat algorytmu sortowania przez wybór
schemat SelectionSort for i := n downto 2 do begin j := Max(i); Exchange(i,j) end;
Dlaczego użyliśmy słowa schemat? Zauważmy, że do pełnego zdefinowania algorytmu, a także dla jego analizy, niezbędne jest zdefiniowanie funkcji \( Max \). W klasycznym sortowaniu przez wybór pozycję elementu największego w podtablicy \( a[1..i] \) wyznaczamy przeszukując podtablicę od lewej do prawej, pamiętając w zmiennej pomocniczej pozycję dotychczas największego elementu i modyfikując wartość tej zmiennej każdorazowo po napotkaniu elementu większego od dotychczas największego. Oto pełny zapis algorytmu sortowania przez wybór - algorytmu SelectionSort.
Algorytm Sortowanie przez wybór
SelectionSort for i := n downto 2 do begin j := 1; for k := 2 to i do if a[k] > a[j] then j := k; Exchange(i,j) end;
Nietrudno zauważyć, że algorytm SelectionSort wykonuje taką samą liczbę porównań, co algorytm bąbelkowy. Jednak w tym przypadku maksymalna liczba zamian wynosi tylko \( n-1 \).
Należy podkreślić, że w implementacji schematu sortowania przez wybór mamy swobodę w realizacji funkcji \( Max \). Wykorzystamy to w algorytmie sortowania z użyciem struktury danych zwanej kopcem.
Sortowanie przez wstawianie
Sortowanie przez porównania: MergeSort, HeapSort i QuickSort
Czy można sortować przez porównania w czasie szybszym niż kwadratowy? Odpowiedź jest pozytywna.
Sortowanie przez wstawianie z wyszukiwaniem binarnym
Rozważmy jeszcze raz algorytm sortowania przez wstawianie. W tym algorytmie jedna faza polega głównie na umiejscowieniu wstawianego elementu w uporządkowanym ciągu - w fazie \( i \)-tej element \( a[i] \) wstawiamy do uporządkowanego ciągu \( a[1..i-1] \), dla \( i = 2,3, \ldots, n \). Miejsce, w które należy wstawić element \( a[i] \), można znaleźć za pomocą wyszukiwania binarnego.
Algorytm Sortowanie przez wstawianie z wyszukiwaniem binarnym
InsertionSortWithBinarySearch for i := 2 to n do begin //a[1..i-1] jest już posortowana x := a[i] //odkładamy element z pozycji i //binarne wyszukiwanie największego j <= i takiego, że a[j-1] <= x l := 0; p := i; while (p - l) > 1 do //Niezmiennik: a[l] <= x oraz x < a[p] jeśli tylko p < i begin s := (l+p) div 2; if x < a[s] then p := s; else l := s; end j := l+1; //x zostanie wstawiony na pozycję j; //elementy większe przesuwamy o 1 pozycję w prawo for k := i downto j+1 do a[k] := a[k-1]; a[j] := x end;
W tym algorytmie liczbę wykonywanych porównań można wyznaczyć następująco: w iteracji o numerze \( i \) zewnętrznej pętli for wykonuje się co najwyżej \( \lceil \log i \rceil \) porównań pomiędzy elementami sortowanego ciągu, co w sumie daje
\( \sum_{i = 2} \lceil \log i \rceil = n\lceil \log n \rceil - 2^{\lceil \log n \rceil} + 1 \)
porównań.
Otrzymaliśmy więc algorytm, w którym wykonuje się \( O(n\log n) \) porównań niezbędnych do wyszukiwania miejsc dla wstawianych elementów, ale (niestety) liczba przesunięć elementów w tablicy, koniecznych do zrobienia tych miejsc, jest w pesymistycznym przypadku kwadratowa. Ta obserwacja jest niezwykle pouczająca. Mówi ona, że dobór operacji dominujących dla analizy złożoności algorytmu jest kluczowy dla jakości tej analizy.
Sortowanie przez wstawianie z wyszukiwaniem binarnym jest też warte wspomnienia dlatego, że jego pomysłodawcą był wybitny polski matematyk Hugo Steinhaus. O tej metodzie sortowania Steinhaus wspomina w drugim wydaniu swojej znakomitej książki Kalejdoskop matematyczny z roku 1950.
Sortowanie przez scalanie (MergeSort)
Sortowanie przez scalanie w miejscu
Słabością algorytmu MergeSort jest pomocnicza tablica używana do scalania. Czy można jej się pozbyć? Tak, można to zrobić na dwa sposoby. Pierwszy sposób polega na wykonywaniu scaleń w miejscu, czyli w samej tablicy \( a \). Niestety liczba porównań i przemieszczeń elementów znacząco rośnie, choć jest nadal liniowa. Sam algorytm nie jest intuicyjny i pominiemy go w tych notatkach. Drugi sposób polega na wykonaniu sortowania przez scalanie przy złamaniu zasady, że długości scalanych ciągów różnią się co najwyżej o 1. Z opisanej procedury Merge-1 wynika, że scalanie dwóch ciągów możemy wykonać w taki sposób, żeby długość pomocniczej tablicy była równa długości krótszego ze scalanych ciągów. Rozważmy teraz procedurę \( Merge-2(p,r,s) \), która scala uporządkowane ciągi \( a[p..s] \) z \( a[s+1..r] \). Zakładamy przy tym, że \( s-p+1 \le r-s \) (lewy ciąg jest nie dłuższy niż prawy) oraz \( p-1 \ge s-p+1 \) (początek tablicy jest wystarczająco długi, żeby można go wykorzystać do scalania). Scalanie będzie się odbywało z pomocą podtablicy \( a[1..p-1] \). Będziemy przy tym uważali, żeby nie zgubić zawartości tej podtablicy. Oto nasza procedura \( Merge-2(p,r,s) \).
Algorytm Scalanie-2
procedure Merge-2(p,r,s); begin //zamiana a[p..s] z a[1..s-p+1] for i := p to s do Exchange(i-p+1,i); //właściwe scalanie i := 1; j := s+1; k := p-1; while (i <= s-p+1) and (j <= r)do //Niezmiennik: a[p..k] - scalone podciągi a[1..i-1], a[s+1..j-1] begin k := k+1; if a[i] <= a[j] then begin Exchange(i,k); i := i+1 end else begin Exchange(k,j); j := j+1 end end; //jeśli nie wyczerpaliśmy ciągu a[1..s-p+1], //to przepisujemy go na koniec tablicy a for j := i to s-p+1 do begin k := k+1; Exchange(j,k) end end;
Zauważmy, że po wykonaniu powyższego algorytmu mamy następującą sytuację:
- podtablica \( a[1..p-1] \) zawiera te same elementy, które znajdowały się w niej przed rozpoczęciem scalania (być może przepermutowane),
- podtablica \( a[p..r] \) jest już uporządkowana.
Oznaczmy przez MergeSortBis(p,r) procedurę, która sortuje przez scalanie podtablicę \( a[p..r] \). Załóżmy przy tym, że \( p-1 \ge \frac{r-p+1}{2} \). Procedurę MergeSortBis implementujemy podobnie jak algorytm MergeSort, tylko zamiast procedury Merge-1 wykorzystujemy procedurę \( Merge-2 \). Możemy teraz opisać algorytm "sortowania przez scalanie w miejscu". Idea algorytmu jest następująca. Dzielimy tablicę \( a \) na dwie (prawie) równe części \( a[1..\lceil \frac{n}{2} \rceil] \) oraz \( a[\lceil \frac{n}{2} \rceil + 1..n] \). Sortujemy prawą część tablicy algorytmem \( MergeSortBis \) wykorzystując lewą część jako tablicę pomocniczą. Dalsza część algorytmu ma strukturę rekurencyjną. Załóżmy, że w tablicy \( a \) mamy już posortowany sufiks \( a[p..n] \) dla pewnego \( 1 < p\le \lceil \frac{n}{2} \rceil + 1 \). Jeśli \( p-1 = 1 \), to kończymy sortowanie wstawiając \( a[1] \) do uporządkowanego ciągu \( a[2..n] \), tak jak w sortowaniu przez wstawianie. Jeśli \( p > 2 \), wówczas dzielimy tablicę \( a[1..p-1] \) na podtablicę \( a[1..\lceil \frac{p-1}{2}\rceil] \) i \( a[\lceil \frac{p-1}{2}\rceil + 1..p-1] \), sortujemy przez scalanie podtablicę \( a[\lceil \frac{p-1}{2}\rceil + 1..p-1] \), scalamy uporządkowaną podtablicę \( a[\lceil \frac{p-1}{2}\rceil + 1..p-1] \) z podtablicą \( a[p..n] \) i sortujemy dalej rekurencyjnie przy założeniu, że \( a[\lceil \frac{p-1}{2}\rceil + 1..n] \) jest już posortowane.
Algorytm sortowania przez scalanie w miejscu można teraz zapisać następująco.
Algorytm SortowaniePrzezScalanie w Miejscu
if n > 1 then begin p := n - floor(n/2) + 1; MergeSortBis(p,n); while p > 2 do begin l := p - floor((p-1)/2) +1; MergeSortBis(l,p-1); Merge-2(l,n,p-1); p := l end; Scal a[1] z a[2..n]. end
Zastanówmy się teraz nad złożnością przedstawionego algorytmu. Zanalizujemy najpierw liczbę porównań. Odzielnie analizujemy porównania wykonywane dla sortowania procedurą \( MergeSortBis \), a oddzielnie dla scaleń procedurą \( Merge-2 \). \( MergeSortBis \) jest wywoływana dla ciągów o długościach \( \lfloor \frac{n}{2} \rfloor, \lfloor \frac{n}{4} \rfloor, \ldots \). Jeżeli sortowanie ciągu długości \( k \) wymaga co najwyżej \( k\log k \) porównań, to liczba porównań we wszystkich sortowaniach wynosi co najwyżej
Scalenia kosztują nas co najwyżej tyle porównań, ile wynosi długość scalonego ciągu. Długość taka oczywiście nigdy nie przekracza \( n \). Długości kolejnych, krótszych scalanych podtablic wynoszą odpowiednio \( \lfloor \frac{n}{4} \rfloor, \lfloor \frac{n}{8} \rfloor, \ldots, 1 \). Wszystkich scaleń jest więc nie więcej niż \( \log n \). Liczba porównań we wszystkich scaleniach nie przekracza więc \( n\log n \). Zatem liczba wszystkich porównań wykonywanych w algorytmie sortowania przez scalanie w miejscu nie przekracza nigdy \( 2n\log n \). Niestety przemieszczeń będzie znacznie więcej. Każde porównanie może wymagać zamiany miejscami dwóch elementów (dwa przemieszczenia, trzy instrukcje przypisania). Dlatego liczba przemieszczeń może wynieść prawie \( 4n\log n \). W sumie jednak mamy algorytm działający w miejscu i o złożoności czasowej \( O(n\log n). \)
Na koniec zauważmy jedno drobne "oszustwo". Procedura \( MergeSort \) i wzorowana na niej procedura \( MergeSortBis \) są procedurami rekurencyjnymi. Implementacja rekursji wymaga stosu, w tym przypadku o logarytmicznej wysokości. Żeby mieć w pełni algorytm sortowania w miejscu, powinniśmy pozbyć się stosu. W przypadku zwykłego sortowania przez scalanie, a takie jest zaimplementowane w \( MergeSortBis \), bardzo łatwo z góry ustalić, kiedy i które podtablice są ze sobą scalane. Załóżmy, że sortujemy przez scalanie procedurą \( MergeSort \) tablicę o długości \( 2^k \), dla pewnego \( k > 0 \). Zauważmy, że w takim przypadku scalamy najpierw podtablice jednoelementowe \( a[1] \) z \( a[2] \), \( a[3] \) z \( a[4] \), itd., potem podtablice dwuelementowe \( a[1..2] \) z \( a[3..4] \), \( a[5..6] \) z \( a[7..8] \), itd., a na koniec podtablicę \( a[1..2^{k-1}] \) z \( a[2^{k-1}+1..2^k] \). Łatwo zaimplementować taki ciąg scaleń za pomocą iteracji. Szczegóły tej implementacji i jej uogólnienie na tablice o długościach różnych od potęg dwójki, pozostawiamy jako dobre ćwiczenie algorytmiczno-programistyczne.
Sortowanie kopcowe (HeapSort)
Sortowanie szybkie (QuickSort)
Sortowanie: dolna granica, sortowanie pozycyjne
Czy można sortować szybciej niż w czasie \( O(n\log n) \)? Tak, jeśli wiemy coś więcej o sortowanym ciągu. Na przykład, gdy liczba inwersji w ciągu jest liniowa ze względu na jego długość, algorytm InsertionSort posortuje taki ciąg w czasie liniowym. Zastanówmy się teraz, w jaki sposób można posortować tablicę \( a[1..n] \), jeśli wiemy, że jej elementami są liczby całkowite z przedziału \( 0..m-1 \) dla pewnego \( m\ge 1 \). Jest wiele rozwiązań tego zadania. Jednym z nich jest tzw. sortowanie kubełkowe. Bierzemy \( m \) kubełków \( B[0..m-1] \). Do kubełka \( B[i] \) wrzucamy wszystkie elementy z tablicy \( a \) o wartości równej \( i \). Następnie wypisujemy zawartości kubełków, poczynając od kubełka \( B[0] \). Kubełki reprezentujemy jako listy jednokierunkowe. Oto dokładniejszy zapis algorytmu sortowania kubełkowego.
Algorytm Sortowanie kubełkowe (BucketSort)
for i := 0 to m-1 do zainicjuj B[i] jako listę pustą; for i := n downto 1 do wstaw a[i] na początek listy B[a[i]]; scal listy B w jedną listę, dołączając listę B[i+1] po liście B[i]; wpisz kolejne elementy z posortowanej listy na kolejne pozycje w tablicy a;
Zauważmy, że przeglądanie tablicy \( a \) od końca i wrzucanie jej elementów na początki list \( B \) gwarantuje, że tablica \( a \) zostanie posortowana stabilnie. Oznacza to, że względny porządek pomiędzy elementami o tej samej wartości nie ulega zmianie. Analiza złożoności czasowej tego algorytmu jest bardzo prosta. Kroki 1-2 wykonują się w czasie \( O(m) \), kroki 3-4 w czasie \( O(n) \), krok 5 można wykonać w czasie \( O(m) \), jeśli pamiętamy wskaźniki na końce list, lub w czasie \( O(n+m) \), gdy musimy przejrzeć każdą listę w poszukiwaniu jej końca. Krok 6 zabiera czas \( O(n) \). Otrzymujemy zatem algorytm sortujący, który działa w czasie \( O(n+m) \). Gdy \( m \) jest rzędu co najwyżej \( n \), nasz algorytmy wykonuje tylko liniową liczbę operacji!
Ten sam wynik można osiągnąć za pomocą sortowania przez zliczanie. W tym algorytmie dla każdej wartości \( i = 0, 1, \ldots, m-1 \) zliczamy, ile razy pojawia się ona w tablicy \( a[1..n] \). Taka informacja pozwala już łatwo określić pozycje elementów o wartości \( i \) w posortowanej tablicy. W tym celu wystarczy wiedzieć, ile jest elementów o wartościach mniejszych. Elementy o tej samej wartości \( i \) umieszczamy następnie na pozycjach docelowych, w kolejności ich początkowego występowania w tablicy \( a \). Oto formalny zapis algorytmu:
Algorytm Sortowanie przez zliczanie
//zliczanie wystąpień poszczególnych wartości w tablicy a for i := 0 to m-1 do t[i] := 0; for j := 1 to n do t[a[j]] := t[a[j]] + 1; //obliczenie dla każdego i liczby elementów nie większych od i for i := 1 to m-1 do t[i] := t[i] + t[i-1]; //w tablicy posortowanej elementy o wartości i znajdują się //na pozycjach od t[i-1]+1 do t[i], jeśli tylko przyjmiemy, że t[0] = 0 //w sortowaniu wykorzystujemy pomocniczą tablicę b //sortowane elementy umieszczamy w tablicy b na ich docelowych pozycjach for j := n downto 1 do begin b[t[a[j]]] := a[j]; t[a[j]] := t[a[j]] - 1; // t[a[j]] jest ostatnią wolną pozycją dla //kolejnego (od końca) elementu o wartości a[j] end; a := b; //przepisanie posortowanej tablicy b do a
Podobnie jak w sortowaniu kubełkowym nasz algorytm działa w czasie \( O(n+m) \) i jest algorytmem liniowym dla każdego \( m \), które jest rzędu co najwyżej \( n \).
Ten algorytm, tak jak sortowanie kubełkowe, jest algorytmem stabilnym. Stabilność wykorzystamy do zaadaptowania sortowania przez zliczanie do sortowania leksykograficznego w czasie liniowym słów o tych samych długościach. Załóżmy, że \( \Sigma = \{0 < 1 < ... < m-1\} \) jest uporządkowanym alfabetem \( m \)-elementowym i danych jest \( n \) słów \( w[1], w[2], \ldots, w[n] \) nad alfabetem \( \Sigma \), każde o długości \( k \). Inaczej mówiąc, słowo \( w[i] \) jest tablicą \( w[i][1..k] \) o wartościach z \( \Sigma \). W porządku leksykograficznym \( w[i] \) jest mniejsze od \( w[j] \) wtedy i tylko wtedy, gdy istnieje \( 1\le l \le k \) takie, że \( w[i][s] = w[j][s] \) dla każdego \( s = 1,2,...,l-1 \) oraz \( w[i][l] < w[j][l] \). Algorytm sortowania leksykograficznego jest teraz bardzo prosty. W sortowaniu słowa są przetwarzane od końca. Algorytm jest wykonywany w \( k \) fazach ponumerowanych malejąco \( k, k-1, \ldots,1 \). Przed rozpoczęciem fazy o numerze \( i \) słowa \( w \) są już uporządkowane leksykograficzne względem swoich sufiksów o długościach równych \( k-i \), czyli podsłów składających się ze znaków z pozycji \( i+1,i+2,\ldots,k \). W fazie \( i \)-tej sortujemy słowa \( w \) stabilnie względem znaków z pozycji \( i \). Stabilność gwarantuje, że porządek słów, które posiadają te same elementy na pozycji \( i \)-tej, będzie wyznaczony przez ich wcześniej już uporządkowane sufiksy. Poniżej przedstawiamy formalny opis algorytmu sortowania leksykograficznego. W tym algorytmie w tablicy \( a \) będziemy przechowywali indeksy słów \( w \) uporządkowanych względem swoich sufiksów.
Algorytm Sortowanie leksykograficzne słów o tych samych długościach
for j := 1 to n do a[j] := j; for faza := k downto 1 do //sortowanie stabilnie słów w[a[1]], w[a[2]],..., w[a[n]] //względem elementów z pozycji o numerze faza begin //sortowanie przez zliczanie for i := 0 to m-1 do t[i] := 0 for j := 1 to n do t[w[a[j]][faza]] := t[w[a[j]][faza]] + 1; for i := 1 to m-1 do t[i] := t[i] + t[i-1]; for j := n downto 1 do begin b[t[w[a[j]][faza]]] := a[j]; t[w[a[j]][faza]] := t[w[a[j]][faza]] - 1 end; a := b end
Po zakończeniu wykonywania powyższego algorytmu mamy \( w[a[1]]\le w[a[2]]\le \ldots \le w[a[n]] \). Analiza tego algorytmu jest niezmiernie prosta. Wykonujemy \( k \) faz. Czas działania każdej fazy wynosi \( O(n+m) \). Cały algorytm działa więc w czasie proporcjonalnym do \( kn + km \). Dla \( m \) rzędu co najwyżej \( n \) mamy algorytm o złożoności \( O(kn) \). Zauważmy, że wielkość \( kn \) to rozmiar danych - \( n \) słów, każde o długości \( k \). Dostaliśmy więc algorytm liniowy, sortujący leksykograficznie słowa o tej samej długości nad alfabetem o rozmiarze rzędu co najwyżej \( n \). Zauważmy, że słowa nad alfabetem \( \Sigma = \{0,\ldots, m-1\} \) można interpretować jako liczby całkowite bez znaku zapisane w układzie pozycyjnym przy podstawie \( m \). Dlatego uprawnione jest mówić w tym miejscu o sortowaniu pozycyjnym (ang. RadixSort).
Powstaje naturalne pytanie, czy jesteśmy w stanie sortować w czasie liniowym słowa o różnych długościach. Odpowiedź jest pozytywna. Poniżej przedstawiamy szkic takiego algorytmu. Szczegóły implementacyjne pozostawiamy czytelnikom. Załóżmy, że chcemy posortować leksykograficznie \( n \) słów \( w_1, w_2, \ldots, w_n \) nad alfabetem \( \Sigma = \{0,1,\ldots, m-1\} \). Dla dalszych rozważań przyjmijmy, że \( m \) jest rzędu co najwyżej \( n \). Niech \( l_i\ge 1 \) będzie długością \( i \)-tego słowa. Zauważmy, że rozmiar danych w tym zadaniu wynosi \( \sum_{i=1}^n l_i \). Będziemy chcieli, żeby nasz algorytm sortował słowa \( w \) w czasie liniowym ze względu na tę wielkość. Niech \( l_{max} \) będzie długością najdłuższego słowa. Zauważmy, że bardzo łatwo zaadaptować do rozwiązania tego zadania algorytm sortowania słów o takich samych długościach. Wystarczy każde słowo uzupełnić do długości \( l_{max} \) symbolem, który będzie traktowany jako mniejszy od każdego symbolu z \( \Sigma \). W naszym przypadku tym symbolem może być po prostu -1. Niestety takie podejście daje algorytm, którego czas działania wynosi \( O(nl_{max}) \), co może być znacząco większe od rozmiaru danych. Na przykład dla danych składających się z jednego słowa o długości \( n \) i pozostałych słów o stałych długościach, niezależnych od \( n \), dostajemy algorytm działający w czasie \( O(n^2) \), podczas gdy dane mają rozmiar \( O(n) \). Jak widać, bezpośrednie stosowanie algorytmu dla słów o takich samych długościach nie daje oczekiwanych wyników. Możemy go jednak wykorzystać troszeczkę sprytniej. Zauważmy, że po wykonaniu fazy o numerze \( i \) wszystkie słowa, których długości są krótsze niż \( i \), znajdują się na samym początku uporządkowanego ciągu słów. Żeby je tam umieścić, nie musimy ich sortować ze słowami o długościach co najmniej \( i \). Dlatego zamiast tablicy indeksów słów będziemy słowa sortowane w danej fazie trzymać na liście słów \( a \). Druga obserwacja dotyczy organizacji procesu sortowania. Zauważmy, że w algorytmie sortowania słów o tych samych długościach, na początku każdej fazy zerujemy liczniki wystąpień symboli. Ponieważ dopuszczamy alfabet o rozmiarze rzędu \( n \), to zerowanie liczników w każdej fazie prowadziłoby nadal do algorytmu kwadratowego ze względu na \( n \). Więcej, nie możemy też obliczać sum prefiksowych w tablicy \( t \) (krok 11) tak jak dotychczas, ponieważ to też dawałoby algorytm kwadratowy. Żeby temu zapobiec skorzystamy z pomysłu z sortowania kubełkowego. Użyjemy kubełków \( B \) do rozrzucania słów. Żeby jednak nie inicjować w każdej fazie wszystkich kubełków, będziemy inicjować tylko te, które w danej fazie zostaną wykorzystane. W tym celu wystarczy, żebyśmy mieli w ręku uporządkowaną listę symboli z alfabetu, aktywnych w danej fazie - tzn. tych, które występują w słowach \( w \) na pozycjach o numerach równych numerowi fazy. Podsumujmy zatem, co jest nam potrzebne, żeby nie wykonywać niepotrzebnych operacji podczas wykonywania jednej fazy. Niewątpliwie dla każdej fazy potrzebna jest lista numerów słów o długościach równych numerowi fazy. Takie słowa byłyby dołączane na początku listy słów uporządkowanych wcześniej, w fazach o większych numerach. Niech \( L_i \) będzie listą numerów słów o długościach równych \( i \). Taką listę łatwo stworzyć w czasie \( O(n+l_{max}) \) sortując leksykograficznie pary \( (l_i,i) \) - długość słowa i jego numer. Do tego celu można wykorzystać algorytm sortowania słów o tych samych długościach. Żeby otrzymać listy aktywnych symboli w fazach wystarczy posortować leksykograficznie wszystkie pary \( (pozycja,symbol) \), otrzymane w wyniku przejrzenia wszystkich słów \( w \). Takich par jest \( \sum_{i = 1}^n l_i \), a więc tyle, ile wynosi rozmiar danych. Znowu mamy do czynienia z sortowaniem słów o takich samych długościach. Takie sortowanie składa się z dwóch faz. W fazie o numerze 2 alfabet ma rozmiar \( m \), natomiast w fazie o numerze 1 rozmiar alfabetu wynosi \( l_{max} \). Tak więc sortowanie wykonuje się w czasie \( O(\sum_{i = 1}^n l_i) \). Niech \( S_i \) będzie uporządkowaną listą tych symboli z \( \Sigma \), które występują na pozycji o numerze \( i \) w słowach \( w \). Możemy teraz przystąpić do opisu algorytmu sortowania słów zmiennej długości. Zakładamy, że listy \( L_i \) oraz \( S_i \) są już zbudowane.
Algorytm Sortowanie leksykograficzne słów o różnych długościach
zainicjuj a jako pustą listę; for faza := l(max) downto 1 do begin dla każdego symbolu s z listy S_i uczyń pustą listę B[i]; na początku listy a umieść listę L_i; przeglądaj listę a od początku do końca i każde napotkane słowo wstaw na koniec listy B o numerze równej wartości symbolu z pozycji faza w tym słowie; przeglądaj listy B w kolejności numerów znajdujących się na liście S_i i połącz je w jedną listę a, dopisując każdą kolejną listę na koniec listy złożonej z dotychczas scalonych list; end;
Zauważmy, że każda faza w tym algorytmie jest wykonywana w czasie proporcjonalnym do liczby słów o długościach równych co najmniej numerowi tej fazy, co gwarantuje, że cały algorytm działa w czasie proporcjonalnym do \( \sum_{i = 1}^n l_i \), czyli w czasie liniowym.
Wszystkie rozważane dotychczas algorytmy sortowały porównując ze sobą elementy porządkowanego zbioru. W żadnym z nich pesymistyczna liczba wykonywanych porównań nie była mniejszego rzędu niż \( n\log n \).
Czy za pomocą porównań można sortować istotnie szybciej?
Odpowiedź brzmi NIE.
Dolna granica dla problemu sortowania - drzewa decyzyjne
Załóżmy, że chcemy posortować \( n \) różnych elementów \( x_1, \ldots, x_n \) i jedynym sposobem ustalenia porządku pomiędzy nimi jest porównywanie ich w parach. Wynikiem sortowania jest permutacja \( x_{i_1} < x_{i_2} < \ldots < x_{i_n} \). Możliwych wyników sortowania jest oczywiście tyle, ile wszystkich permutacji zbioru \( n \)-elementowego, czyli \( n! \). Każdy algorytm sortowania przez porównania można zapisać za pomocą drzewa decyzyjnego.
Drzewo decyzyjne jest drzewem binarnym, w którym wszystkie węzły różne od liści mają po dwóch synów. W tych węzłach zapisujemy pary indeksów \( i:j \), \( 1 \le i < j \le n \). Każda taka para \( i:j \) oznacza, że interesuje nas wynik porównania \( x_i \) z \( x_j \). Jeśli wynikiem porównania jest TAK, co oznacza, że \( x_i \) jest mniejsze od \( x_j \), kierujemy się do lewego poddrzewa, zadając jako kolejne to pytanie, które odpowiada parze elementów zapisanych w korzeniu lewego poddrzewa (o ile to nie jest liść). Jeśli wynikiem porównania jest NIE, co w tym przypadku oznacza, że \( x_i \) nie jest mniejsze od \( x_j \), przechodzimy do prawego poddrzewa. Bez straty ogólności możemy założyć, że w naszym drzewie nie wykonujemy redundantnych porównań, tzn. nie pytamy o wynik porównania, jeśli tylko ten wynik można wywnioskować z odpowiedzi na wcześniej zadane pytania. Sortowanie polega na przejściu w drzewie od korzenia do pewnego liścia (węzła bez synów). Jeśli odpowiedzi na zadane pytania pozwalają na wskazanie porządku w zbiorze \( \{x_1,x_2,\ldots,x_n\} \), stosowna permutacja wyznaczająca ten porządek znajduje się właśnie w liściu na końcu ścieżki.
Na rysunku poniżej przedstawiono sortujące drzewo decyzyjne dla 3 elementów.

Niech \( S(n) \) oznacza minimalną liczbę porównań zawsze wystarczającą do posortowania \( n \) elementów. Liczbę \( S(n) \) można z dołu oszacować za pomocą drzewa decyzyjnego.
Pesymistyczna złożoność algorytmu opisanego za pomocą drzewa decyzyjnego, to oczywiście wysokość tego drzewa, czyli długość najdłuższej ścieżki od korzenia do liścia w tym drzewie mierzona liczbą krawędzi. Drzewo decyzyjne sortujące \( n \) elementów jest drzewem binarnym o \( n! \) liściach. Najmniejsza wysokość drzewa binarnego o \( k \) liściach wynosi \( \lceil \log k \rceil \). Wynika stąd, że każdy algorytm sortujący przez porównania wykonuje w pesymistycznym przypadku \( C(n)\ =\ \lceil \log n! \rceil \) porównań. Można pokazać, że \( \lceil \log n! \rceil \ge n\log n -1.45n \).
Zatem zachodzi
Podobne dolne ograniczenie zachodzi, gdy pytamy o średnią liczbę porównań w modelu losowych permutacji, tzn. gdy każdy z \( n! \) wyników sortowania jest możliwy z jednakowym prawdopodobieństwem \( \frac{1}{n!} \). W tym wykładzie pominiemy dowód tego faktu.
Dokładne liczenie pesymistycznej liczby porównań dla problemu sortowania
Problem dokładnego wyznaczenia liczby \( S(n) \) jest jednym z fundamentalnych problemów w kombinatoryczno-algorytmicznej teorii sortowania. Hugo Steinhaus postawił ten problem w Kalejdoskopie matematycznym, nazywając go problemem turniejowym. Stąd bywa też nazywany problemem Steinhausa.
Knuth poświęcił duży fragment swojej klasycznej już książki The Art of Computer Programming (tom 3) problemowi optymalnego sortowania.
Ford Jr i Johnson odkryli algorytm (oznaczany dalej FJA), który wymaga liczby porównań bliskiej, a czasem dokładnie równej teoretycznej dolnej granicy \( C(n) \). Dla \( n\le11 \) niezależnie odkryli tę metodę również Trybuła i Czen. Oznaczmy przez \( F(n) \) liczbę porównań wymaganą przez FJA do posortowania \( n \) elementów.
Początkowe wartości \( C(n) \) i \( F(n) \) przedstawia tabela.
\\n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\ C(n) & 0 & 1 & 3 & 5 & 7 & 10 & 13 & 16 & 19 & 22 & 26 & 29 & 33 & 37 & 41 & 45 & 49 & 53 & 57 & 62 & 66 & 70 \\ F(n) & 0 & 1 & 3 & 5 & 7 & 10 & 13 & 16 & 19 & 22 & 26 & 30 & 34 & 38 & 42 & 46 & 50 & 54 & 58 & 62 & 66 & 71 \\
\end{array} \)
Jak widać, dla \( n\le11 \) i \( n=20,21 \) zachodzi \( F(n)=C(n) \), zatem FJA jest optymalny w tych przypadkach. Dla \( n=12,13,\ldots,19,22 \) mamy \( F(n)=C(n)+1 \). Prowadząc wyczerpujące obliczenia komputerowe, Wells odkrył, że \( S(12)=F(12)=30 \). Knuth postawił problem znalezienia następnej wartości \( S(13) \). Przypuszczał on, że \( S(13)=33 \) i \( S(14)=37 \). Udoskonalając metodę Wellsa i intensywnie wykorzystując obliczenia komputerowe, Marcin Peczarski (w swoich pracach magisterskiej i doktorskiej na Wydziale MIMUW) pokazał, że:
Aktualne wersje użytych programów można znaleźć na stronie Marcina Peczarskiego http://www.mimuw.edu.pl/~marpe.
Okazuje się zatem, że FJA jest optymalny dla \( n\le15 \) i \( n=20,21,22 \). Z drugiej strony najmniejszą liczbą elementów, dla której znamy algorytm lepszy od FJA jest 47. Schulte Mönting znalazł algorytm, który najpierw sortuje 5 elementów i 42 elementy za pomocą FJA, używając odpowiednio 7 i 171 porównań, a następnie scala posortowane ciągi za pomocą 22 dalszych porównań. Algorytm ten potrzebuje więc łącznie 200 porównań, podczas gdy FJA potrzebuje ich 201.
Wiadomo, że FJA nie jest optymalny dla nieskończenie wielu wartości \( n \), a wszystkie znane lepsze algorytmy są kombinacją sortowania i scalania. Za pomocą wyczerpującego przeszukiwania komputerowego Peczarski pokazał również, że 47 jest najmniejszą liczbą elementów, dla której istnieje algorytm typu: sortuj \( m \) i \( n-m \) elementów za pomocą FJA, a następnie scal posortowane ciągi, przy czym łączna liczba porównań jest mniejsza niż potrzebna do bezpośredniego posortowania \( n \) elementów za pomocą FJA.
Opiszemy teraz działanie FJA. Sortowanie \( n \) elementów \( u_1,u_2,\ldots,u_n \) za pomocą FJA można podzielić na 3 fazy.
Faza 1. Wykonujemy porównania dowolnie wybranych \( \lfloor n/2\rfloor \) rozłącznych par elementów. Powiedzmy, że są to porównania:
\( u_1\!:\!u_2,\ u_3\!:\!u_4,\ \ldots, \ u_{2\lfloor n/2\rfloor-1}\!:\!u_{2\lfloor n/2\rfloor}. \)
Gdy \( n \) jest liczbą nieparzystą, to element \( u_n \) nie jest w tej fazie porównywany.
Faza 2. Używając rekurencyjnie FJA, sortujemy \( \lfloor n/2\rfloor \) większych elementów znalezionych w fazie 1. Dostajemy posortowany ciąg elementów, który oznaczamy \( a_1,a_2,\ldots,a_{\lfloor n/2\rfloor} \). Przez \( b_i \) oznaczamy element, który był porównywany w fazie 1 z elementem \( a_i \) i okazał się od niego mniejszy. Gdy \( n \) jest liczbą nieparzystą, to element \( u_n \), który nie był porównywany w fazie 1 oznaczamy przez \( b_{\lceil n/2\rceil} \).
Faza 3. Elementy \( b_1,a_1,a_2,\ldots,a_{\lfloor n/2\rfloor} \) tworza ciąg posortowany, nazwijmy go łańcuchem głównym. Pozostałe elementy \( b_2,b_3,\ldots,b_{\lceil n/2\rceil} \) wstawiamy binarnie do łańcucha głównego w następującej kolejności:
\( b_3,b_2;\ b_5,b_4;\ b_{11},b_{10},\ldots,b_6;\ \ldots; \ b_{t_k},b_{t_k-1},\ldots,b_{t_{k-1}+1};\ \ldots, \)
gdzie \( t_k=(2^{k+1}+(-1)^k)/3 \). Kolejne wstawiane elementy wydłużają łańcuch główny. Przy czym element \( b_i \) dla \( i\le\lfloor n/2\rfloor \) jest wstawiany do tej części łańcucha głównego, gdzie są elementy mniejsze od \( a_i \).
Kolejność wstawianych elementów można zapamiętać za pomocą następującej reguły. Wypisujemy w wierszu kolejne potęgi liczby 2, poczynając od 4. Następnie w drugim wierszu wypisujemy liczby, poczynając od 1, tak by suma dwóch kolejnych liczb była równa liczbie znajdującej się nad lewą z nich w pierwszym wierszu. Wreszcie pod każdą liczbą z drugiego wiersza wypisujemy kolejne dodatnie liczby całkowite mniejsze od niej, ale większe od liczby znajdującej się w drugim wierszu w kolumnie bezpośrednio po lewej stronie.
Indeksy kolejnych wstawianych elementów odczytujemy w ten sposów, że pomijamy pierwszy wiersz i pierwszą kolumnę, a następnie odczytujemy liczby wypisane w kolejnych kolumnach od lewej do prawej, a w każdej kolumnie od góry do dołu.
Liczbę porównań wykonywanych przez FJA opisują ciekawe wzory, które można znależć np. we wspomnaienj wyżej książce Knutha.
Ćwiczenia
Selekcja
Rozważmy następujący problem:
Dany jest zbiór \( A \) składający się z \( n \) liczb oraz liczba \( k \). Należy wyznaczyć \( k \)-ty co do wielkości element zbioru \( A, \) tzn. takie \( a\in A \), że \( |\{ x\in A : x < a \}|=k-1 \).
Dla niektórych wartości \( k \) (np. 1 lub n) problem jest bardzo prosty i wymaga jedynie wyznaczenia minimalnej lub maksymalnej wartości w A, co możemy zrobić w czasie \( O(n) \). Znacznie ciekawszym problemem jest np. znajdowanie mediany, czyli \( \lfloor \frac{n}{2} \rfloor \)-tego co do wielkości elementu. Tu niestety problem jest bardziej skomplikowany.
Możemy zauważyć, że szybkie (np. o złożoności \( O(n) \)) znajdowanie mediany pozwoliłoby tak poprawić algorytm sortowania QuickSort, żeby nawet w pesymistycznym przypadku działał w czasie \( O(n\log n) \).
Najprostszym rozwiązaniem naszego problemu może być uporządkowanie zbioru, np. algorytmem MergeSort, i wskazanie k-tego elementu. Takie postępowanie wymaga czasu \( \Omega(n\log n) \).
Jednak można łatwo zauważyć, że nasz problem jest znacznie prostszy od problemu sortowania. Czy można rozwiązać go szybciej? Okazuje się, że jest to możliwe. W następnej części wykładu przedstawimy dwa algorytmy, które rozwiązują nasz problem znacznie sprytniej.
Algorytm Hoare'a
Algorytm jest oparty na tym samym pomyśle, co algorytm sortowania QuickSort.
Dla danej tablicy A[1..n] oraz liczby k, algorytm wybiera element dzielący m (np. pierwszy element z tablicy), a następnie używa go do podzielenia tablicy na dwie części. Do pierwszej części tablicy - A[1..r] - zostają przeniesione elementy o wartościach mniejszych lub równych m. Do drugiej części (A[r+1..n]) - elementy o wartościach większych lub równych m.
Ponieważ naszym zadaniem jest jedynie wyznaczenie k-tego co do wielkości elementu tablicy, możemy zamiast 2 wywołań rekurencyjnych (jak to było w przypadku algorytmu QuickSort) wykonać tylko jedno wywołanie rekurencyjne.
Jeśli \( k\le r \), to poszukiwana wartość znajduje się w pierwszej części tablicy, wpp. możemy zawęzić poszukiwania do drugiej części tablicy, jednak zamiast wyszukiwać k-tej wartości musimy poszukiwać (k-r)-tej wartości.
Algorytm Hoare'a
function AlgHoara(A[1..n],k); begin if n=1 and k=1 then return A[1]; // Partition m:=A[1]; l:=1; r:=n; while(l<r) do begin while (A[l]<m) do l++; while (m<A[r]) do r--; if (l <=r) then begin tmp:=A[l]; A[l]:=A[r]; A[r]:=tmp; l++; r--; end; end; if (k<=r) then return AlgHoara(A[1..r],k) else return AlgHoara(A[r+1..n],k-r) 18 end;
Analiza algorytmu
Niestety, w pesymistycznym przypadku ten algorytm może zachowywać się bardzo źle. Dla uporządkowanego ciągu i k=n czas działania algorytmu wynosi \( O(n^2) \). Jednak tak jak w przypadku algorytmu QuickSort, w średni koszt działania algorytmu jest znacznie lepszy i wynosi O(n).
Algorytm magicznych piątek
Algorytm Hoare'a w pesymistycznym przypadku może wymagać bardzo długiego czasu działania. Możemy tak zmodyfikować poprzedni algorytm, aby zapewnić liniowy czas działania nawet w najgorszym przypadku.
Kluczem do nowego algorytmu jest lepszy wybór elementu dzielącego (zmienna m z 5-linii algorytmu Hoare'a). Element ten jest obliczany w następujący sposób:
- dzielimy ciąg \( A \) na podciągi 5-elementowe \( P_1,\ldots,P_{\lceil |A|/5 \rceil} \),
- każdy z podciągów sortujemy, otrzymując \( P'_1,\ldots,P'_{\lceil |A|/5 \rceil} \),,
- wybieramy z każdego podciągu 3-ci co do wielkości element otrzymując krótszy ciąg \( M \),
- jako m wybieramy medianę ciągu \( M \) (którą to obliczamy rekrurencyjnie).
Dzięki takiemu znacznie bardziej skomplikowanemu wyborowi możemy zagwarantować bardziej równomierny podział ciągu \( A \) na podciągi elementów mniejszych (\( A_{ < } \)), oraz większych (\( A_{>} \)) od m.
Algorytm
function AlgorytmMagicznychPiatek(A[1..n], k); begin if n<=10 then posortuj tablicę A return A[k] else begin podziel elementy z tablicy A na podciągi 5-elementowe: P(1),...,P(n/5) (jeśli n nie jest wielokrotnością 5, uzupełnij ostatni podciąg wartościami infty) Niech M={ P_i [3] : 1 <= i <= n/5} (zbiór median ciągów P(i)); m:=AlgorytmMagicznychPiatek(M, ceil(|M|/2)); A_< :={ A[i] : A[i] < m}; A_= :={ A[i] : A[i] = m}; A_> :={ A[i] : A[i] > m}; if |A_<| <= k then return AlgorytmMagicznychPiatek(A_<,k) else if |A_< |+|A_=| <= k then return m else return AlgorytmMagicznychPiatek(A_>, k-|A_<|-|A_=|); end end
Analiza złożoności czasowej
Na pierwszy rzut oka algorytm wygląda bardzo podobnie do algorytmu Hoare'a. Nowy algorytm jest jednak znacznie bardziej efektywny: nawet w pesymistycznym przypadku algorytm kończy działanie po \( O(n) \) krokach.
Złożoność algorytmu możemy opisać następującym równaniem rekurencyjnym.
- rozmiar zbioru |M| możemy ograniczyć przez \( \lceil n/5 \rceil \)
- ze względu na dodatkowy czas poświęcony na obliczanie mediany m, możemy podać lepsze ograniczenia na rozmiary zbiorów \( A_{ < },\ A_{>} \):

Ćwiczenia
- Podaj algorytm wyznaczający drugi co do wielkości element zbioru, używający przy tym minimalnej liczby porównań.
- Podaj algorytm sprawdzający, czy dany ciąg zawiera element występujący co najmniej n/k razy (np. n/3 razy). !!todo: trzeba to trochę jaśniej napisać!!
- Czy liczbę 5 w algorytmie "Magicznych piątek" można zastąpić przez inną wartość, np. 3,4,6,7?
- Dane są trzy tablice A[1..n], B[1..n], C[1..n]. Elementy każdej z tych tablic są uporządkowane rosnąco. Podaj efektywny sposób na znajdowanie mediany wśród wszystkich elementów.
Wyszukiwanie
W niniejszym wykładzie opiszemy podstawowe techniki dotyczące wyszukiwania. Zajmiemy się również prostymi strukturami słownikowymi, które oprócz wyszukiwania umożliwiają dodawanie i usuwanie elementów.
Wyszukiwanie liniowe
Jeśli nie dysponujemy żadną dodatkową wiedzą na temat zbioru, który chcemy przeszukiwać, niestety musimy sprawdzić wszystkie jego elementy.
function Szukaj(x, A[1..n]) begin for i:=1 to n do if A[i]=x return i; return brak poszukiwanego elementu; end
Oczywiście w pesymistycznym przypadku (np. gdy zbiór nie zawiera poszukiwanego elementu) koszt czasowy, to \( O(n) \).
Wyszukiwanie binarne
W niektórych przypadkach czas poszukiwania możemy znacząco zmniejszyć. Dzieje się tak na przykład, gdy przeszukiwany zbiór przechowujemy w rosnąco uporządkowanej tablicy. W takim przypadku wystarczy jedynie \( O(\log n) \) operacji, by odnaleźć poszukiwany element lub stwierdzić jego brak.
Algorytm utrzymuje zakres \( [l,\ldots,r] \), w którym może znajdować się element; przy każdym porównaniu zakres zostaje zmniejszony o połowę.
function WyszukiwanieBinarne(x, A[1..n]) { zakładamy, że tablica A jest uporządkowana rosnąco } begin l:=1;r:=n; while (l<=r) do begin { niezmiennik: poszukiwany element może znajdować się w zakresie A[l..r] } m:=(l+r) div 2; if (A[m]<;x) then l:=m+1 else if (A[m]>x) then r:=m-1 else return m; { ponieważ A[m]=x } end; return brak poszukiwanego elementu; end;
Proste słowniki: drzewa poszukiwań binarnych
Podstawowe operacje słownika to wyszukiwanie, wstawianie i usuwanie klucza. Drzewa poszukiwań binarnych (bez dodatkowych specjanych wymagań) mogą być traktowane jako prosty słownik. Sa to zwykłe drzewa binarne, których klucze spełniają następujące własności:
Dla dowolnego węzła x:
- wszystkie klucze w lewym poddrzewie węzła x mają wartości mniejsze niż klucz węzła x,
- wszystkie klucze w prawym poddrzewie węzła x mają wartości większe lub równe niż klucz węzła x.
Dodatkowe wymaganie dotyczące kluczy umożliwia nam efektywne wyszukiwanie elementów w drzewie.
function Szukaj(węzeł, klucz) if (węzeł==nil) return BRAK ELEMENTU if (węzeł.klucz=klucz) then return ELEMENT ISTNIEJE else if (klucz < węzeł.klucz) then return Szukaj(węzeł.lewePoddrzewo, klucz) else if (klucz > węzeł.klucz) then return Szukaj(węzeł.prawPoddrzewo, klucz) end;
Wstawianie do drzewa jest bardzo zbliżone do wyszukiwania: musimy przejść po drzewie (rozpoczynając w korzeniu), aby odnaleźć wolne miejsce, w którym możemy dodać nową wartość.
procedure Dodaj(węzeł, klucz) if (klucz < węzeł.klucz) then if węzeł.lewePoddrzewo=nil then utwórz nowy węzeł z wartością klucz wskaźnik do nowego węzła zapisujemy w węzeł.lewePoddrzewo else Dodaj(węzeł.lewePoddrzewo, klucz) else if (klucz >= węzeł.klucz) then if węzeł.prawePoddrzewo=nil then utwórz nowy węzeł z wartością klucz wskaźnik do nowego węzła zapisujemy w węzeł.prawePoddrzewo else Dodaj(węzeł.prawePoddrzewo, klucz) end;
Możemy również usuwać wartości z drzewa, niestety ta operacja jest bardziej skomplikowana.
procedure Usuń(węzeł, klucz) if (klucz < węzeł.klucz) then Usuń(węzeł.lewePoddrzewo, klucz) else if (klucz > węzeł.klucz) then Usuń(węzeł.prawePoddrzewo, klucz) else begin { klucz = węzeł.klucz if węzeł jest liściem, then { usuń węzeł z drzewa } UsunProstyPrzypadek(węzeł) else if węzeł.lewePoddrzewo <> nil then niech x oznacza skrajnie prawy węzeł w poddrzewie węzeł.lewePoddrzewo wezel.klucz:=x.klucz; UsunProstyPrzypadek(x); else analogiczne postępowanie dla węzeł.prawPoddrzewo (jednak poszukujemy węzła na skrajnie lewej ścieżce) end
Procedura UsunProstyPrzypadek oznacza usuwanie z drzewa węzła, który ma co najwyżej jednego syna.
procedure UsunProstyPrzypadek(węzeł) begin poddrzewo:=nil; ojciec:=węzeł.ojciec; if węzeł.lewePoddrzewo <> nil then poddrzewo:=węzeł.lewePoddrzewo; else poddrzewo:=węzeł.prawePoddrzewo; if ojciec=nil then korzen:=poddrzewo; else if ojciec.lewePoddrzewo=węzeł then { węzeł jest lewym synem } ojciec.lewePoddrzewo:=poddrzewo; else { węzeł jest prawym synem } ojciec.prawePoddrzewo:=poddrzewo;
Wszystkie podane operacje mają pesymistyczny koszt \( O(h) \) gdzie \( h \) oznacza wysokość drzewa. Niestety w najgorszym przypadku drzewo może mieć bardzo dużą wysokość -- nawet \( O(n) \) (np. dla ciągu operacji Dodaj \( (1,2,3,\ldots) \).
Adresowanie bezpośrednie
W przypadku gdy zbiór, który przechowujemy, pochodzi z niewielkiego uniwersum (na przykład elementy zbioru to liczby z zakresu \( 1,\ldots,n \)), możemy wszystkie operacje słownikowe (dodaj, usuń, szukaj) wykonać znacznie szybciej i prościej.
Dla uniwersum \( 1,\ldots,n \) zbiór możemy reprezentować przez tablicę \( n \)-elementową. Początkowo w każdej komórce tablicy wpisujemy wartość false.
- dodanie elementu \( i \) do zbioru wymaga jedynie ustawienia wartości \( i \)-tej komórki na true,
- analogicznie, usunięcie elementu \( i \) do zbioru wymaga ustawienia wartości \( i \)-tej komórki na false,
- sprawdzenie, czy element \( i \) należy do zbioru, wykonujemy przez sprawdzenie stanu \( i \)-tej komórki.
Wszystkie powyższe operacje możemy wykonać używając stałej liczby kroków.
Haszowanie
Czy możemy wykorzystać adresowanie bezpośrednie do dowolnych zbiorów? Okazuje się, że tak. Co prawda w pesymistycznym przypadku koszt jednej operacji może wynosić nawet \( O(n) \), jednak w praktycznych zastosowaniach ta metoda sprawuje się doskonale.
W tym rozdziale będziemy zakładać, że elementy uniwersum \( U \) to dodatnie liczby całkowite. Dodatkowo zakładamy, że dysponujemy tablicą \( A[0,\ldots,m-1] \).
Ponieważ elementami mogą być bardzo duże liczby całkowite, nie możemy zastosować metody adresowania bezpośredniego. Jednak możemy wybrać funkcję haszującą:
Funkcja każdemu elementowi uniwersum przypisuje odpowiednie miejsce w tablicy \( A \). Jeśli \( |U|>m \), to z oczywistych względów znajdą się takie pary różnych elementów \( x,y\in U \), dla których \( f(x)=f(y) \). W takim przypadku mówimy o istnieniu kolizji. Właśnie ze względu na ryzyko wystąpienia kolizji musimy nieznacznie zmodyfikować metodę adresowania bezpośredniego - zamiast przechowywać w tablicy wartość logiczną (prawda/fałsz), musimy zapisywać wartość przechowywanego elementu.
Rozwiązywanie kolizji metodą łańcuchową
Jedną z metod rozwiązywania kolizji jest utrzymywanie w każdej komórce tablicy listy elementów do niej przypisanych. Początkowo tablica \( A \) wypełniona jest wartościami nil.
procedure Inicjalizacja; begin for i:=0 to m-1 do A[i]:=nil; end;
Dodanie elementu \( x \) do tablicy wymaga odczytania jego adresu z funkcji haszującej, a następnie dodania go na początek listy \( A[h(x)] \)
procedure Dodaj(x); begin dodaj element x na początek listy A[h(x)] end;
Sprawdzenie, czy element \( x \) jest w zbiorze, wymaga w pesymistycznym przypadku sprawdzenia całej listy \( A[h(x)] \)
function Szukaj(x); begin l:=A[h(x)]; while (l!=nil) do begin if (l.wartość=x) then return element istnieje l:=l.nast; end; return brak elementu end;
Usuwanie elementu z tablicy jest bardzo podobne do wyszukiwania i również w pesymistycznym przypadku wymaga sprawdzenia całej listy.
procedure Usuń(x); begin l:=A[h(x)];p:=nil; while (l!=nil) do begin if (l.wartość=x) then begin { usuwamy element l z listy A[h(x)] } if p=nil then A[h(x)]:=l.nast; else p.nast:=l.nast; return; end p:=l; l:=l.nast; end; end;
Analiza metody łańcuchowej
Haszowanie to metoda, która bardzo dobrze sprawdza się w praktyce, zastanówmy się przez chwilę, czy dobre własności tej metody można udowodnić.
Niech:
- m oznacza rozmiar tablicy,
- n oznacza liczbę elementów, które przetrzymujemy w tablicy,
- przez \( \alpha \) oznaczamy współczynnik zapełniania tablicy \( \frac{n}{m} \)
Załóżmy, że dysponujemy idealną funkcją haszującą, dla której przypisanie każda wartość \( h(x) \) jest równie prawdopodobna, czyli \( P(\{h(x)=i\})=\frac{1}{m} \).
Przy takim założeniu oczekiwana długość listy elementów \( A[h(x)] \) ma długość \( \frac{n}{m} \) (oczekiwana liczba sukcesów w n próbach Bernoulli'ego).
Stąd oczekiwana złożoność operacji Szukaj, Dodaj, Usuń wynosi:
\( T(n,m)=\frac{n}{m}+O(1) \)
Wybór funkcji haszujących
Od wyboru dobrej funkcji haszującej w dużej mierze zależy efektywność naszej struktury danych. Niestety, nie można podać ścisłej procedury wyboru takiej funkcji.
Dla liczb całkowitych możemy przykładowo wybrać jedną z następujących funkcji (\( m \) oznacza rozmiar tablicy):
- \( f(x)=(x\,\mod\, p)\ \mod\ m \) (gdzie \( p>m \) jest liczbą pierwszą);
- \( f(x)=(qx\,\mod\, p)\ \mod\ m \) (gdzie \( p,q \) są liczbami pierwszymi);
- \( f_{a,b}(x)=((ax+b)\,\mod\, p)\ \mod\ m \) (gdzie \( p \) jest liczbą pierwszą, \( 1\le a < p \), \( 0 \le b < p \)).
Jeśli nie dysponujemy żadną dodatkową wiedzą na temat elementów które będzie zawierać tablica, rozsądnym rozwiązaniem jest wybór funkcji \( f_{a,b} \) dla losowych wartości \( a,b \).
Adresowanie otwarte
Adresowanie otwarte jest metodą pozwalającą uniknąć utrzymywania list elementów w tablicy haszującej. Oczywiście wymaga to opracowania innej metody rozwiązywania konfliktów. Każda komórka tablicy zawiera teraz wartość NIL lub element zbioru.
Niech \( m \) oznacza rozmiar tablicy haszującej. Zdefiniujmy funkcję \( H(x,k) \), wyznaczającą listę pozycji \( H(x,0),\ldots,H(x,m-1) \), na których może znajdować się element \( x \).
Mając daną funkcję \( h(x) \), możemy zdefiniować \( H(x,k) \), jako:
- \( H(x,k)=(h(x)+k)\ \mod\ m \) --- adresowanie liniowe;
- \( H(x,k)=(h(x)+a_1\cdot k+a_2\cdot k^2)\ \mod\ m \) --- adresowanie kwadratowe;
- \( H(x,k)=(h(x)+h_2(x)\cdot k)\ \mod\ m \) --- podwójne haszowanie, przy czym \( h_2(x) \) jest funkcją haszującą, która przyjmuje wartości z zakresu \( 1,\ldots,m-1 \).
Wyszukiwanie elementów możemy wykonać nieznacznie modyfikując poprzednie rozwiązanie -- zamiast przeszukiwać listę elementów, musimy przeszukać ciąg pozycji zdefiniowany przez funkcję \( H(x,k) \).
function Szukaj(x); begin k:=0; while (A[H(x,k)!=nil) do begin if (A[H(x,k)].wartość=x) then return element istnieje k:=k+1; end; return brak elementu end;
Wstawianie elementów możemy wykonać przez analogiczne modyfikacje; usuwanie jest zwykle znacznie trudniejsze.
Filtry Bloom'a
Ciekawym połączeniem adresowania bezpośredniego z haszowaniem są filtry Bloom'a. Polegają one na rozlużnieniu założeń naszej struktury:
- ograniczamy się do operacji Dodaj i Szukaj,
- pozwalamy na nieprawidłowe odpowiedzi dla operacji Szukaj (jednak z małym prawdopodobieństwem).
Nasza struktura to bitowa tablica o rozmiarze m, początkowo tablica jest wypełniona zerami. Zakładamy również, że mamy do dyspozycji k funkcji haszujących \( h_i(x) : U arrow \{ 0,\ldots,m-1\} \).
Dodanie elementu x sprowadza się do ustawienia wszystkich bitów \( A[h_i(x)] \) dla \( i=1,\ldots,k \) na wartość 1.
procedure Dodaj(x); begin for i:=1 to k do A[h_i(x)]:=1; end;
Analogicznie, sprawdzenie, czy element x należy do zbioru, wymaga sprawdzenia bitów \( A[h_i(x)] \) dla \( i=1,\ldots,k \). Jeśli wszystkie mają wartość 1, to uznajemy, że element należy do zbioru. Oczywiście powoduje to pewien odsetek błędnych odpowiedzi. Jeśli jednak dobrze dobierzemy funkcje, a wypełnienie tablicy nie będzie zbyt duże, to taka struktura będzie dobrze sprawować się w praktyce.
function Szukaj(x); begin for i:=1 to k do if A[h_i(x)]=0 then return brak elementu return element istnieje end;
Ćwiczenia
- Podaj metodę przygotowywania zrównoważonego drzewa BST (o wysokość \( O(\log n) \)) dla zadanego zbioru kluczy \( a_1,\ldots,a_n \).
- W jaki sposób efektywnie dodać do drzew BST operację LiczbaElementówzZakresu(x,y) zwracającą liczbę elementów drzewa o wartościach z zakresu \( [x,\ldots,y] \)?
- Ile jest różnych drzew BST zawierających klucze \( 1,\ldots,n \)?
- W jaki sposób można wykorzystać drzewa BST do sortowania ciągu liczb?
Słowniki
Słownik to struktura danych reprezentująca dynamiczny (tzn. mogący zmieniac się w czasie) zbiór elementów (kluczy), na którym można wykonywać następujące operacje:
- Find(S,x): zwraca klucz x ze słownika S, albo NULL jeśli tego klucza nie ma w słowniku;
- Insert(S,x): wstawia klucz x do słownika S;
- Delete(S,x): usuwa klucz x ze słownika S.
W tym module dotyczącym słowników implementowanych za pomocą drzew będziemy zakładali, że uniwersum wszystkich potencjalnych elementów słownika jest liniowo uporządkowane, a podstawowym mechanizmem w zarządzaniu słownikiem będzie porównywanie kluczy.
Drzewa AVL
W drzewach poszukiwań binarnych (BST, od ang. Binary Search Tree) pesymistyczny koszt wymienionych wyżej operacji słownikowych jest proporcjonalny do wysokości drzewa. Kształt drzewa - więc i jego wysokość - zależy od ciągu wykonywanych na nim operacji. Nietrudno podać przykład ciągu operacji konstruującego drzewo o \( n \) węzłach i wysokości \( \Theta(n) \). W drzewach AVL (Adelson-Velskij, Landis [AVL]) do warunku BST umożliwiającego wyszukiwanie w czasie proporcjonalnym do wysokości drzewa, dołożono warunek zrównoważenia, gwarantujący, że wysokość drzewa zawsze pozostaje logarytmiczna względem jego rozmiaru:
W każdym węźle wysokości obu jego poddrzew różnią się co najwyżej o 1.
W każdym węźle przechowywany jest dodatkowy atrybut, "współczynnik zrównoważenia", przyjmujący wartości:
"-" jeśli lewe poddrzewo jest o 1 wyższe niż prawe;
"0" jeśli oba poddrzewa są takiej samej wysokości;
"+" jeśli prawe poddrzewo jest o 1 wyższe niż lewe.
Jako ćwiczenie pozostawiamy dowód faktu, że drzewo AVL o \( n \) węzłach ma wysokość \( O(\log n) \).
Pokażemy teraz, jak wykonywać wszystkie operacje słownikowe na drzewach AVL z kosztem co najwyżej proporcjonalnym do wysokości drzewa (czyli logarytmicznym). Operacja Find jest wykonywana tak samo jak w zwykłych drzewach BST: schodzimy w dół drzewa po ścieżce od korzenia do szukanego węzła (albo do węzła zewnętrznego NULL), o wyborze lewego lub prawego poddrzewa na każdym poziomie rozstrzygając na podstawie porównania szukanego klucza z zawartością aktualnego węzła na ścieżce. Operacje Insert i Delete są bardziej skomplikowane, ponieważ wymagają aktualizowania współczynników zrównoważenia, a niekiedy również przywracania warunku AVL.
Rotacje
Do zmiany kształtu drzewa w celu jego zrównoważenia służy mechanizm rotacji. Po wykonaniu rotacji pojedynczej ROT1\( (p,q) \) węzła \( p \) z jego ojcem \( q \) oba węzły zamieniają się rolami ojciec-syn, przy zachowaniu własności BST:
(symetryczny przypadek, w którym \( p \) jest prawym synem \( q \), stanowi lustrzane odbicie powyższego).
W rotacji podwójnej ROT2(p,q,r) uczestniczą trzy węzły: \( p \), jego ojciec \( q \) i jego dziadek \( r \), przy czym albo \( p \) jest lewym synem, a \( q \) prawym (ten właśnie przypadek jest zilustrowany poniżej), albo odwrotnie. Po rotacji \( p \) staje się korzeniem całego drzewa, przy zachowaniu własności BST:
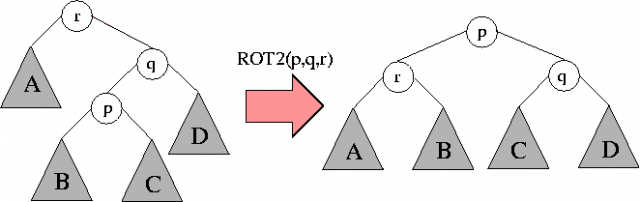
Nietrudno zauważyć, że rotacja podwójna ROT2(p,q,r) jest w rzeczywistości złożeniem dwóch rotacji pojedynczych ROT1(p,q) i ROT1(p,r). Koszt wykonania jednej rotacji jest stały.
Wstawianie i usuwanie węzłów w drzewach AVL
Podczas operacji Insert tak samo jak dla zwykłych drzew BST schodzimy po ścieżce od korzenia w dół do węzła zewnętrznego NULL i w jego miejscu tworzymy nowy liść ze wstawianym kluczem. Następnie wracamy po ścieżce do korzenia, aktualizując współczynniki zrównoważenia. Jeśli stwierdzamy, że wysokość aktualnie rozważanego poddrzewa nie zmieniła się w stosunku do sytuacji przed wykonaniem Insert, to kończymy operację, a jeśli stwierdzamy, że wysokość poddrzewa wzrosła (mogła wzrosnąć co najwyżej o 1!), kontynuujemy marsz w górę drzewa. Jeśli w wyniku wzrostu wysokości jednego z poddrzew aktualnie rozważanego węzła został w nim zaburzony warunek AVL, to przywracamy go za pomocą rotacji. Z dokładnością do symetrii mamy wtedy dwa przypadki (w obydwu zakładamy, że \( p \) jest węzłem, w którym zaburzony został warunek AVL wskutek wzrostu wysokości jego prawego poddrzewa o korzeniu \( q \); w pierwszym przypadku zakładamy, że wzrosła wysokość prawego poddrzewa \( q \), a w drugim - lewego).
Zauważmy, że w obydwu przypadkach po rotacji wysokość całego poddrzewa jest taka sama jak przed całą operacją, zatem wykonanie jednej rotacji (pojedynczej lub podwójnej) kończy operację Insert.
Poniższa animacja ilustruje przykładową historię wstawiania do drzewa AVL.
Operację Delete, tak samo jak w przypadku usuwania ze zwykłego drzewa BST, sprowadzamy do przypadku usuwania węzła mającego co najwyżej jednego syna. Zauważmy, że w drzewie AVL albo sam węzeł, albo jego jedyny syn musi być liściem. Po usunięciu węzła wracamy po ścieżce do korzenia, aktualizując współczynniki zrównoważenia. Jeśli stwierdzamy, że wysokość aktualnie rozważanego poddrzewa nie zmieniła się w stosunku do sytuacji przed wykonaniem Delete, kończymy operację, a jeśli stwierdzamy, że wysokość poddrzewa spadła (mogła spaść co najwyżej o 1!), to kontynuujemy marsz w górę drzewa. Jeśli w wyniku spadku wysokości jednego z poddrzew aktualnie rozważanego węzła został w nim zaburzony warunek AVL, to przywracamy go za pomoca rotacji. Z dokładnością do symetrii mamy wtedy dwa przypadki (w obydwu zakładamy, że \( p \) jest węzłem, w którym zaburzony został warunek AVL wskutek spadku wysokości jego lewego poddrzewa, a \( q \) jest korzeniem prawego poddrzewa \( p \); w pierwszym przypadku zakładamy, że współczynnik zrównoważenia w \( q \) przed operacja Delete był równy "0" lub "+", a w drugim, że "-").
W pierwszym przypadku, jeśli współczynnik zrównoważenia w \( q \) przed operacją Delete był równy "0", po rotacji wysokość całego poddrzewa jest taka sama jak przed całą operacją, wykonanie rotacji kończy więc operację Delete. Jeśli jednak współczynnik był równy "+", wysokość spada o 1. W przypadku 2 wysokość całego poddrzewa również spada o 1 i trzeba kontynuować marsz w stronę korzenia. Operacja Delete może zatem wymagać wykonania logarytmicznej liczby rotacji. Poniższa animacja ilustruje operację usuwania elementu z drzewa AVL.
Samoorganizujące się drzewa BST
Mechanizm równoważenia drzew AVL jest dość skomplikowany w implementacji i wymaga przechowywania w węzłach dodatkowych informacji. Wynalezione przez Sleatora i Tarjana [ST], opisane poniżej drzewa splay to drzewa BST, w których wykorzystuje się rotacje do ich równoważenia, jednak nie trzeba przechowywać żadnych dodatkowych atrybutów w węzłach. Chociaż możliwe jest utworzenie niezrównoważonego drzewa splay i pojedyncza operacja może mieć nawet koszt liniowy względem aktualnego rozmiaru drzewa, to koszt zamortyzowany operacji słownikowych w tej strukturze danych jest logarytmiczny.
Wszystkie operacje w drzewie splay są wykonywane z wykorzystaniem pomocniczej procedury splay\( (S,x) \), która przekształca drzewo \( S \) w taki sposób, że jego korzeniem staje się węzeł z kluczem \( x \) (albo - jeśli klucza \( x \) nie ma w \( S \) - węzeł z kluczem \( y \) takim, że w \( S \) nie ma żadnego klucza między \( \min(x,y) \) a \( \max(x,y) \)). Operacja Find\( (S,x) \) sprowadza się zatem do wywołania splay\( (S,x) \) i sprawdzenia, czy \( x \) jest w korzeniu.
W celu wykonania operacji Insert\( (S,x) \) wywołujemy najpierw splay\( (S,x) \), w wyniku czego w korzeniu znajduje się klucz \( y \); bez straty ogólności możemy przyjąć, że \( y < x \). Odcinamy prawe poddrzewo \( R \) węzła \( y \), jego ojcem (a zarazem nowym korzeniem) zostaje węzeł z kluczem \( x \), którego prawym poddrzewem czynimy \( R \).
Operację Delete\( (S,x) \) zaczynamy od wywołania splay\( (S,x) \), sprowadzając usuwany klucz do korzenia. Niech \( L \) i \( R \) będą, odpowiednio, lewym i prawym poddrzewem uzyskanego drzewa. Odcinamy korzeń i - jeśli \( L \) jest niepuste - wywołujemy splay\( (L,x) \), a następnie przyłączamy \( R \) jako prawe poddrzewo korzenia.
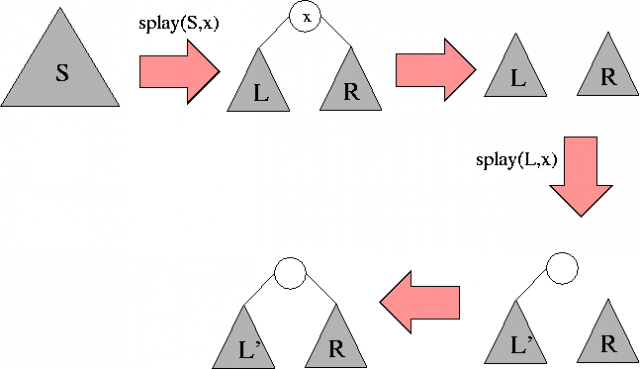
Sama procedura splay\( (S,x) \) jest zdefiniowana następująco: najpierw szukamy węzła \( v \) z kluczem \( x \) w \( S \) tak jak w zwykłym drzewie BST (jeśli klucza \( x \) nie ma w drzewie, to jako \( v \) bierzemy ostatni węzeł na ścieżce przed węzłem zewnętrznym NULL). Następnie, dopóki \( v \) nie stanie się korzeniem, wykonujemy sekwencję rotacji zgodnie z poniższym schematem:
1. Jeżeli \( v \) jest synem korzenia \( w \), to wykonujemy ROT1\( (v, w) \).
2. Jeżeli \( v \) ma ojca \( w \) i dziadka \( u \), przy czym oba węzły \( v \) i \( w \) są lewymi synami, albo oba prawymi, to wykonujemy ROT1\( (w,u) \), a następnie ROT1\( (v,w) \).
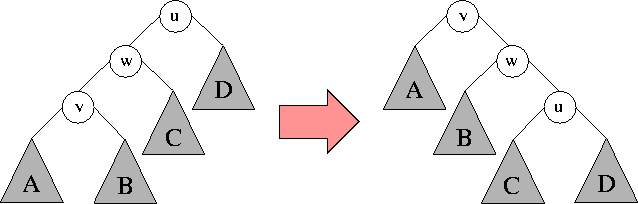
3. Jeżeli \( v \) ma ojca \( w \) i dziadka \( u \), przy czym jeden z węzłów \( v \), \( w \) jest lewym synem, a drugi prawym, to wykonujemy ROT1\( (v,w) \), a następnie ROT1\( (v,u) \) (czyli w sumie rotację podwójną ROT2\( (v,w,u) \)).
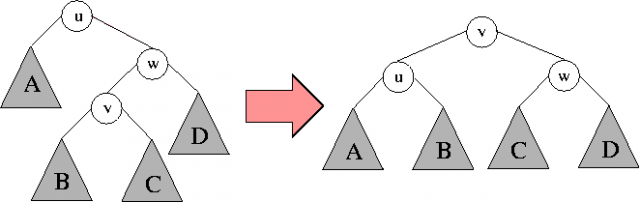
Oto przykład działania procedury splay:
W analizie kosztu zamortyzowanego operacji na drzewach splay posłużymy sie metodą księgowania, z każdym węzłem w drzewie związując pewną liczbę jednostek kredytu. Przez \( T \) oznaczmy drzewo o korzeniu \( x \) i zdefiniujmy \( \mu(x) = \lfloor\lg |T|\rfloor \) (czasem będziemy też używać oznaczenia \( \mu(T) \)). Będziemy zachowywali niezmiennik
"Liczba jednostek kredytu w węźle \( x \) jest zawsze równa \( \mu(x) \)." (***)
Prawdziwy jest
Lemat
Do wykonania operacji splay\( (S,x) \) z zachowaniem niezmiennika (***) potrzeba co najwyżej \( 3(\mu(S)-\mu(x))+1 \) jednostek kredytu.
Żmudny, techniczny dowód lematu pozostawiamy jako ćwiczenie. Z lematu wynika bezpośrednio, że dowolna operacja splay na drzewie rozmiaru \( n \) wymaga zużycia \( O(\lg n) \) jednostek kredytu, a ponieważ do wykonania operacji Insert i Delete z zachowaniem niezmiennika oprócz tych potrzebnych do wywołań splay potrzeba \( O(\lg n) \) dodatkowych jednostek kredytu (na korzeń), wnioskujemy, że koszt zamortyzowany operacji słownikowych na drzewach splay jest logarytmiczny.
B-drzewo - słownik na dysku
Drzewa BST, nawet w takich jak opisane powyżej wersjach zrównoważonych, nie najlepiej nadają się do przechowywania na dysku komputera. Specyfika pamięci dyskowej polega na tym, że czas dostępu do niej jest znacznie (o kilka rzędów wielkości) dłuższy niż do pamięci wewnętrznej (RAM), a odczytu i zapisu danych dokonuje się większymi porcjami (zwanymi blokami lub stronami). Chaotyczne rozmieszczenie węzłów drzewa BST na dysku bez brania pod uwagę struktury tego rodzaju pamięci prowadzi do większej niż to naprawdę konieczne liczby dostępów.
Wynalezione na początku lat sześćdziesiątych XX wieku przez Bayera i MacCreighta [BM] B-drzewa to drzewa poszukiwań wyższych rzędów. W węźle drzewa BST mamy dwa wskaźniki do lewego i prawego syna i jeden klucz, który rozdziela wartości przechowywane w lewym i prawym poddrzewie. W węźle drzewa poszukiwań rzędu \( l \) jest \( l \) wskaźników do synów \( p_1, p_2, \ldots, p_l \) oraz \( l-1 \) kluczy \( k_1 < k_2 < \ldots < k_{l-1} \), które rozdzielają elementy poszczególnych poddrzew: wartości w poddrzewie wskazywanym przez \( p_i \) muszą mieścić się w przedziale otwartym \( (k_{i-1}..k_i) \) dla \( 1\le i\le j \) (przyjmując, że \( k_0 = -\infty \) oraz \( k_l = \infty \)). Rozmiar węzła w B-drzewie dobiera się zwykle tak, aby możliwie dokładnie wypełniał on stronę na dysku - pojedynczy węzeł może zawierać nawet kilka tysięcy kluczy i wskaźników. Zachowanie zrównoważenia umożliwione jest dzięki zmiennemu stopniowi wypełnienia węzłów. Dokładna definicja B-drzewa rzędu \( m \) (\( m\ge 3 \)) jest następująca:
(1) Korzeń jest liściem, albo ma od 2 do \( m \) synów.
(2) Wszystkie liście są na tym samym poziomie.
(3) Każdy węzeł wewnętrzny oprócz korzenia ma od \( \lceil m/2\rceil \) do \( m \) synów. Węzeł mający \( l \) synów zawiera \( l-1 \) kluczy.
(4) Każdy liść zawiera od \( \lceil m/2\rceil-1 \) do \( m-1 \) kluczy.
Warunki (3) i (4) gwarantują wykorzystanie przestrzeni dysku przynajmniej w ok. \( 50\% \), a warunek (2) - niewielką wysokość drzewa (w najgorszym razie ok. \( \log_{m/2} n/(m/2) \), a w najlepszym ok. \( \log_m n/m \) dla drzewa zawierającego \( n \) kluczy). Ponieważ, jak się zaraz przekonamy, koszt operacji słownikowych na B-drzewach jest co najwyżej proporcjonalny do wysokości drzewa, oznacza to na przykład, że dla \( m = 101 \) możemy znaleźć jeden spośród miliona kluczy w drzewie przy pomocy trzech odwołań do węzłów.
Oto przykładowe B-drzewo rzędu 3, zwane też 2-3 drzewem (1-2 klucze i 2-3 synów w węźle):
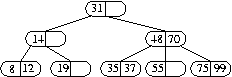
Operacja Find w B-drzewie jest analogiczna jak w drzewach BST. Poszukiwanie klucza \( x \) rozpoczynamy od korzenia. W aktualnym węźle zawierającym klucze \( k_1 < k_2 < \ldots < k_{l-1} \) szukamy klucza \( x \) (sekwencyjnie lub binarnie). Jeśli to poszukiwanie kończy się niepowodzeniem, to albo - jeśli aktualny węzeł jest liściem - klucza \( x \) w ogóle nie ma w drzewie, albo, mając wyznaczony indeks \( i \) o tej własności, że \( k_{i-1} < x < k_i \) (przy założeniu, że \( k_0 = -\infty \) oraz \( k_l = \infty \)), rekurencyjnie poszukujemy klucza \( x \) w poddrzewie o korzeniu wskazywanym przez \( p_i \).
Operacja Insert\( (S,x) \) zaczyna się od odszukania (jak w operacji Find) liścia, w którym powinien znaleźć się wstawiany klucz. Jeśli ten liść nie jest całkowicie wypełniony (czyli zawiera mniej niż \( m-1 \) kluczy), po prostu wstawiamy \( x \) w odpowiednie miejsce w węźle, przesuwając część kluczy (koszt tego zabiegu jest pomijalnie mały w porównaniu z kosztem odczytu i zapisu węzła na dysk). W przeciwnym razie po dołożeniu nowego klucza węzeł jest przepełniony i będziemy musieli przywrócić warunek zrównoważenia.
Najpierw próbujemy wykonać przesunięcie kluczy: ta metoda daje sie zastosować, jeśli któryś z dwóch sąsiednich braci przepełnionego węzła (który nie musi koniecznie być liściem) ma mniej niż \( m-1 \) kluczy. Dla ustalenia uwagi przyjmijmy, że jest to lewy brat i oznaczmy go przez \( p \), sam przepełniony węzeł przez \( q \), a klucz rozdzielający wskaźniki do \( p \) i \( q \) w ich ojcu przez \( k \). Klucz \( k \) przenosimy z ojca do \( p \) jako największy klucz w tym węźle, w jego miejsce w ojcu przenosimy najmniejszy klucz z \( q \), po czym skrajnie lewe poddrzewo \( q \) czynimy skrajnie prawym poddrzewem \( p \). Przesunięcie kluczy w prawo wykonuje się symetrycznie. Po takim zabiegu warunki równowagi zostają odtworzone i cała operacja się kończy.
Jeśli przepełniony węzeł nie ma niepełnego sąsiada, to wykonujemy rozbicie węzła. Listę kluczy dzielimy na trzy grupy: \( \lceil(m-1)/2\rceil \) najmniejszych kluczy, jeden klucz środkowy oraz \( \lfloor(m-1)/2\rfloor = \lceil m/2\rceil-1 \) największych kluczy. Z pierwszej i trzeciej grupy tworzymy nowe węzły, a środkowy klucz wstawiamy do ojca (co może spowodować jego przepełnienie i konieczność kontynuowania procesu przywracania zrównoważenia o jeden poziom wyżej) i odpowiednio przepinamy poddrzewa. Kiedy następuje przepełnienie korzenia, rozbijamy go na dwa węzły i tworzymy nowy korzeń mający dwóch synów (to jest właśnie powód, dla którego korzeń stanowi wyjątek w warunku (3)) - to jest jedyna sytuacja, w której wysokość B-drzewa się zwiększa.
Operację Delete\( (S,x) \) również zaczynamy od odszukania węzła z kluczem do usunięcia. Poddrzewa rozdzielane przez klucz \( x \) oznaczmy przez \( p \) i \( q \). Tak jak przy usuwaniu z BST, w miejsce \( x \) przenosimy - znajdujący się w liściu - największy klucz z \( p \) (albo największy z \( q \)). Lukę po przeniesionym kluczu niwelujemy zsuwając pozostałe. Jeśli jest ich co najmniej \( \lceil m/2\rceil-1 \), cała operacja jest zakończona, natomiast w razie niedoboru w celu przywrócenia równowagi musimy dokonać przesunięcia kluczy albo sklejenia węzłów. Jeśli któryś z dwóch sąsiednich braci węzła z niedoborem ma co najmniej o jeden klucz więcej niż dozwolone minimum, to - podobnie jak przy wstawianiu - przesuwamy skrajny klucz z niego do ojca w miejsce klucza rozdzielającego braci, który z kolei wędruje do węzła z niedoborem. Niemożność wykonania przesunięcia kluczy oznacza, że brat węzła z niedoborem ma dokładnie \( \lceil m/2\rceil-1 \) kluczy. Sklejamy te dwa węzły w jeden, wstawiając jeszcze pomiędzy ich klucze klucz rozdzielający z ojca i odpowiednio przepinając poddrzewa. Powstaje w ten sposób węzeł o \( 2\lceil m/2\rceil-2 \le m-1 \) kluczach, a z ojca ubywa jeden klucz, co może spowodować w nim niedobór i konieczność kontynuowania procesu przywracania zrównoważenia wyżej w drzewie. Jeśli korzeń traci swój jedyny klucz, usuwamy ten węzeł, a jego jedynego syna czynimy nowym korzeniem - to jest jedyna sytuacja, w której wysokość B-drzewa maleje.
Literatura
[AVL] G. M. Adelson-Velskij, E. M. Landis, An algorithm for the organization of information, Soviet Math. Doklady 3, 1962, 1259-1263.
[BM] R. Bayer, E. M. McCreight, Organization and Maintenance of Large Ordered Indexes, Acta Informatica 1, 1972, 173-189.
[CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, 'Wprowadzenie do algorytmów', WNT, Warszawa 2004.
[ST] D.D. Sleator, R.E. Tarjan, Self-Adjusting Binary Search Trees, Journal of the ACM 32:3, 1985, 652-686.
Ćwiczenia
Kolejki priorytetowe
Złączalna kolejka priorytetowa
Kolejka priorytetowa to jedna z podstawowych abstrakcyjnych struktur danych, wykorzystywana między innymi w takich zastosowaniach jak:
- algorytm Dijkstry wyznaczania najkrótszych ścieżek w grafach;
- algorytm Prima znajdowania minimalnego drzewa rozpinającego;
- symulacja sterowana zdarzeniami;
- metoda zamiatania w geometrii obliczeniowej;
- kodowanie Huffmana;
- sortowanie (algorytm Heapsort).
Oferuje ona następujące operacje:
- MakePQ(): tworzy nową, pustą kolejkę;
- Insert(H,x): wstawia element x (o kluczu z pewnego liniowo uporządkowanego uniwersum) do kolejki H;
- FindMin(H): zwraca element o najmniejszym kluczu w kolejce H;
- DelMin(H): zwraca element o najmniejszym kluczu w kolejce H, usuwając go przy tym z H.
Ten zestaw operacji często rozszerza się o:
- DecreaseKey(H,x,y): nadaje kluczowi elementu x w kolejce H nową, mniejszą wartość y;
- Delete(H,x): usuwa element x z kolejki H.
Jeśli struktura danych udostępnia dodatkowo operację łączenia kolejek
- Meld(H1,H2): zwraca nową kolejkę, zawierającą wszystkie elementy z kolejek H1 i H2, niszcząc je przy tym;
to nazywamy ją złączalną kolejką priorytetową.
Najprostszą, choć niezbyt efektywną implementację kolejki priorytetowej stanowi zwykła lista. Znacznie efektywniejszy jest kopiec binarny (wykorzystywany w algorytmie HeapSort), nie pozwala on jednak na szybkie łączenie kolejek. Przedstawione na tym wykładzie struktury danych: kopiec dwumianowy i kopiec Fibonacciego, umożliwiają efektywne wykonywanie wszystkich operacji złączalnej kolejki priorytetowej.
Oto tabela kosztów poszczególnych operacji w wymienionych implementacjach, przy założeniu, że w kolejce(ach) jest aktualnie \( n \) elementów:
| Operacja | Lista | Kopiec Binarny | Kolejka Dwumianowa | Fibonacciego(*) |
|---|---|---|---|---|
| MakePQ | 1 | 1 | 1 | 1 |
| Insert | 1 | \( \lg n \) | \( \lg n \) | 1 |
| FindMin | \( n \) | 1 | \( \lg n \) | 1 |
| DelMin | \( n \) | \( \lg n \) | \( \lg n \) | \( \lg n \) |
| DecreaseKey | 1 | \( \lg n \) | \( \lg n \) | 1 |
| Delete | 1 | \( \lg n \) | \( \lg n \) | \( \lg n \) |
| Meld | 1 | \( n \) | \( \lg n \) | 1 |
(*) - koszt zamortyzowany
Uwaga: wyszukiwanie elementu nie należy do zestawu operacji (złączalnej) kolejki priorytetowej, dlatego w przypadku operacji DecreaseKey i Delete zakładamy, że jako parametr przekazywane jest dowiązanie do elementu, którego ma dotyczyć operacja.
Drzewa i kolejki dwumianowe
Wynaleziona w roku 1978 przez J. Vuillemina [V] kolejka dwumianowa to kolekcja drzew dwumianowych o następującej rekurencyjnej definicji: \( B_0 \) jest drzewem jednowęzłowym, a korzeń drzewa \( B_{k+1} \) (drzewa dwumianowego stopnia \( k \)) ma \( k+1 \) synów stanowiących korzenie drzew \( B_0 \),...,\( B_{k} \) (w tej właśnie kolejności, idąc od prawej do lewej).
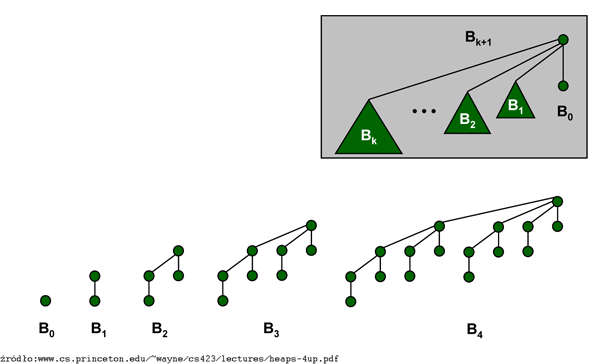
Poniższy lemat dotyczy podstawowych własności drzew dwumianowych:
Lemat
Drzewo dwumianowe \( B_k \)
(a) ma \( 2^k \) węzłów;
(b) ma wysokość \( k \);
(c) ma dokładnie \({k \choose i}\) węzłów na poziomie \( i \), dla \( 0\le i\le k \) (stąd nazwa 'drzewo dwumianowe');
(d) można otrzymać dołączając do drzewa \( B_{k-1} \) drugie drzewo \( B_{k-1} \) jako skrajnie lewego syna korzenia.
Dowód lematu pozostawiamy jako ćwiczenie.
Kolejka dwumianowa to lista drzew dwumianowych uporządkowana ściśle rosnąco względem stopni (idąc od prawej do lewej), przy czym każde drzewo spełnia warunek kopca: klucz w ojcu jest niewiększy niż klucze w synach. Z lematu 1(a) wynika, że w skład kolejki dwumianowej zawierającej \( n \) kluczy drzewo \( B_i \) wchodzi wtedy i tylko wtedy, gdy \( i \)-tym bitem rozwinięcia binarnego liczby \( n \) jest 1; w szczególności łączna liczba drzew to \( O(\lg n) \).
Operacje na kolejce dwumianowej
Ponieważ z warunku kopca wynika, że w każdym drzewie wchodzącym w skład kolejki element najmniejszy znajduje się w korzeniu, operacja FindMin wymaga jednokrotnego przejścia listy drzew. Jej koszt to \( O(\lg n) \) dla \( n \)-elementowej kolejki.
Najważniejszą operacją na kolejce dwumianowej, za pomocą której definiuje się większość pozostałych, jest Meld (łączenie kolejek).Jej działanie przypomina mechanizm dodawania liczb binarnych, przy czym sumowaniu jedynek na pozycji \( i \) w dodawanych liczbach odpowiada łączenie dwóch drzew dwumianowych stopnia \( i \) (zobacz lemat 1(d)): korzeń z mniejszym kluczem (w celu zachowania warunku kopca) zostaje korzeniem wynikowego drzewa \( B_{i+1} \) ('przeniesienia'), a drugi korzeń zostaje jego skrajnie prawym synem. Łączenie dwóch kolejek polega na przejściu obydwu list drzew i złączeniu drzew jednakowych stopni. Jego koszt jest proporcjonalny do sumy długości list.
Operacja Insert (wstawienie węzła) stanowi w zasadzie szczególny przypadek Meld (łączenie z kolejką jednoelementową).Operacja DelMin(H) polega na znalezieniu i usunięciu z listy H drzewa z najmniejszym kluczem, odcięciu jego korzenia (ten klucz jest wynikiem całej operacji) i połączeniu listy jego synów (stanowiącej poprawną kolejkę dwumianową) z H. Łączny koszt to \( O(\lg n) \) dla \( n \)-elementowej kolejki.Operację DecreaseKey wykonuje się podobnie jak poprawianie kopca binarnego przy wstawianiu elementu: zmniejszony klucz wędruje w górę swojego drzewa dwumianowego, zamieniając się miejscami z ojcem dopóty, dopóki nie zostanie odtworzony warunek kopca. W myśl lematu 1(b) maksymalna wysokość drzewa w \( n \)-elementowej kolejce to \( O(\lg n) \), więc koszt takiej operacji jest logarytmiczny.Operacja Delete sprowadza się do przesunięcia klucza, który mamy usunąć, do korzenia (jak w DecreaseKey), a potem usunięcia tego korzenia (jak w DelMin).
Kopce Fibonacciego
Ta struktura danych, wynaleziona przez Fredmana i Tarjana w roku 1984 [FT], stanowi ulepszenie kolejki dwumianowej, które pozwala uzyskać stały (w sensie zamortyzowanym) koszt operacji DecreaseKey, dominującej w algorytmie Dijkstry i jemu pokrewnych. Podstawowy pomysł polega tu na leniwym wykonywaniu operacji, tzn. odkładaniu pracy związanej z zarządzaniem strukturą danych do momentu, kiedy jest to naprawdę niezbędne. Podobnie jak kolejka dwumianowa, kopiec Fibonacciego to lista drzew, z których każde spełnia warunek kopca. Drzewa te nie są już jednak drzewami dwumianowymi (chociaż są im na tyle bliskie, że mają zbliżone własności) i nie są uporządkowane względem stopni korzeni.
Operacja Meld (łączenie kolejek) to po prostu sklejenie dwóch list drzew, bez prób porządkowania względem stopni korzeni czy eliminacji powtórzeń. Jej koszt to oczywiście O(1). Tak jak poprzednio, Insert stanowi szczególny przypadek Meld (łączenie z kolejką jednoelementową). Podczas operacji DelMin przychodzi czas na wykonanie odkładanej wcześniej pracy. Najpierw usuwany jest korzeń zawierający najmniejszy klucz, a jego synowie są dołączani do listy korzeni. Następnie odbywa się konsolidacja listy drzew, mająca na celu doprowadzenie do sytuacji, w której wszystkie korzenie na liście będą miały różne stopnie. Polega ona na przejściu przez listę korzeni i łączeniu drzew jednakowego stopnia - tak samo, jak łączyło się drzewa dwumianowe - a przy okazji uaktualnieniu wskaźnika do korzenia zawierającego najmniejszy klucz. Można ją zrealizować w czasie proporcjonalnym do liczby konsolidowanych drzew, jeśli skorzystamy z pomocniczej tablicy indeksowanej stopniami korzeni: pod indeksem \( i \) przechowujemy w niej wskaźnik do (jedynego) korzenia stopnia \( i \) w przetworzonej części listy, albo NULL, jeśli w tym fragmencie listy korzenia o stopniu \( i \) nie ma.
Oto oszacowanie kosztu zamortyzowanego operacji DelMin: Każdemu drzewu w kopcu Fibonacciego w chwili jego pojawienia się na liście przypisujemy jednostkę kredytu. Niech \( t \) oznacza liczbę drzew w kopcu przed wykonaniem operacji, \( d \) - stopień korzenia zawierającego najmniejszy klucz, zaś \( k \) - liczbę wykonań operacji łączenia drzew. Żeby wykonać Delmin, musimy wykonać pracę proporcjonalną do \( t+d+k \). Ponieważ przy każdym połączeniu drzew uwalniana jest jednostka kredytu, uzyskujemy w ten sposób \( k-1 \) jednostek. Jak pokażemy później (Tw. 2), rozmiar drzewa w kopcu Fibonacciego jest wykładniczy względem stopnia korzenia. Wynika z tego, że po konsolidacji, kiedy wszystkie drzewa w kopcu będą miały różne stopnie, ich liczba \( t+d-k+2 \) będzie \( O(\lg n) \), gdzie \( n \) to rozmiar kopca po operacji. Tak więc do wykonania koniecznej pracy i utrzymania niezmiennika "jedna jednostka kredytu związana z każdym drzewem w kopcu" wystarczy \( O(\lg n) \) dodatkowych jednostek kredytu - i taki właśnie jest koszt zamortyzowany operacji DelMin.
Operacja DecreaseKey\( (H, x, y) \) mogłaby polegać na zmniejszeniu wartości klucza oraz - o ile został naruszony warunek kopca - odcięciu poddrzewa o korzeniu \( x \) i dołączeniu go do listy korzeni. To jednak, zbyt gwałtownie zmniejszając rozmiary poddrzew, powodowałoby, że twierdzenie 2 nie byłoby prawdziwe, a nasza analiza operacji DelMin przestałaby działać. Bedziemy zatem odcinać poddrzewa, ale w sposób kontrolowany: każdy nie będący korzeniem węzeł może stracić co najwyżej jednego syna. Jeśli sytuacja wymaga odcięcia drugiego syna, to taki węzeł sam zostaje odcięty od swojego ojca (co może oczywiście spowodować dalsze rekurencyjne odcięcia). Do utrzymywania informacji o stanie węzła wystarcza znacznik logiczny, który ma wartość TRUE wtedy i tylko wtedy, gdy dany węzeł stracił dokładnie jednego syna od czasu, kiedy sam stał się synem innego węzła (w wyniku łączenia drzew).
Argumentacja, że koszt zamortyzowany operacji DecreaseKey to \( O(1) \), jest następująca: Oprócz kredytu przypisywanego do drzew będziemy dodatkowo przypisywać dwie jednostki kredytu każdemu węzłowi \( v \), który traci jednego syna, kosztem kredytu obciążając operację, która spowodowała odcięcie (dla każdej operacji jest co najwyżej jeden taki węzeł). Kiedy następuje odcięcie drugiego syna \( v \) (a więc także i odcięcie samego węzła \( v \) od ojca), koszt tego zabiegu pokrywa jedna jednostka kredytu, a druga pozostaje przypisana do nowo wstawionego na listę drzewa o korzeniu \( v \) (w celu utrzymania niezmiennika "jedna jednostka kredytu związana z każdym drzewem w kopcu"). Podczas jednej operacji DecreaseKey może nastąpić cała seria odcięć, ale wszystkie (oprócz być może ostatniego) są już wcześniej z góry opłacone. Operacja Delete\( (H, x) \) polega na odcięciu węzła \( x \) od ojca (o ile \( x \) nie jest korzeniem) - jak w DecreaseKey - a następnie usunięciu \( x \), bedącego teraz korzeniem - jak w Delmin. Koszt zamortyzowany tej operacji to \( O(\lg n) \) dla \( n \)-elementowego kopca.
Aby nasza analiza operacji na kopcach Fibonacciego była kompletna, pozostaje jeszcze udowodnić:
Twierdzenie [Twierdzenie 2]
Rozmiar drzewa o korzeniu \( x \) w kopcu Fibonacciego jest wykładniczy względem stopnia \( x \).
Dowód: Niech \( y_1, \ldots, y_k \) będą aktualnymi synami \( x \), w kolejności ich przyłączania do \( x \). Pokażemy, że dla \( i\ge 2 \) węzeł \( y_i \) ma stopień co najmniej \( i-2 \). W chwili przyłączania węzła \( y_i \) węzeł \( x \) miał co najmniej \( i-1 \) synów (węzły \( y_1,\ldots,y_{i-1} \) oraz być może jeszcze jakieś, które zostały później odcięte). Ponieważ przyłączane węzły mają zawsze taki sam stopień, \( y_i \) miał wtedy stopień co najmniej \( i-1 \), a potem mógł stracić co najwyżej jednego syna (bo inaczej sam zostałby odcięty od \( x \)). Oznaczmy przez \( a_k \) najmniejszą możliwa liczbe węzłów w drzewie stopnia \( k \) z kopca Fibonacciego. Z powyższych rozważań wynikają zależności:\( a_0 = 1 \), \( a_k \ge 2+\sum_{i=2}^k a_{i-2} \) (liczba 2 po prawej stronie nierówności bierze sie z uwzględnienia węzłów \( y_1 \) oraz \( x \)). Z łatwej do udowodnienia przez indukcję tożsamości \( F_{k+2} = 2+\sum_{i=2}^k F_i \), gdzie \( F_i \) to \( i \)-ta liczba Fibonacciego (stąd nazwa tej struktury danych!), zdefiniowana rekurencyjnie: \( F_0 = 0, F_1 = 1, F_{i+2} = F_{i+1}+F_i \), wynika, że\( a_k \ge F_{k+2} \). Ogólnie znany (również łatwy do udowodnienia przez indukcję) fakt, że \( F_{k+2}\ge\phi^k \), gdzie \( \phi = (1+\sqrt{5})/2 = 1.618... \), kończy dowód twierdzenia.
Literatura
Literatura
[CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, 'Wprowadzenie do algorytmów', WNT, Warszawa 2004.
[FT] Michael L. Fredman, Robert E. Tarjan, 'Fibonacci heaps and their uses in improved network optimization algorithms', Journal of the ACM 34(3), 1987, 596-615.
[V] Jean Vuillemin, 'A data structure for manipulating priority queues', Communications of the ACM 21(4), 1978, 309-315.
Ćwiczenia
Find-Union
Sumowanie zbiorów rozłącznych
Niekiedy przydatne okazuje się grupowanie elementów w rozłączne zbiory. Struktura danych dla zbiorów rozłącznych pozwala zarządzać taką rodziną dynamicznych (tzn. zmieniających się w czasie) zbiorów rozłącznych. Do każdego zbioru odwołujemy się przez jego reprezentanta (zazwyczaj jest to jakiś element tego zbioru), przy czym wymagamy, żeby dwa zapytania o reprezentanta danego zbioru dawały taki sam wynik, jeśli w międzyczasie sam zbiór się nie zmieniał. Do dyspozycji mamy trzy operacje:
- MakeSet(x): tworzy nowy jednoelementowy zbiór { x }, którego reprezentantem jest oczywiście x (zakładamy, że x nie należy do żadnego innego zbioru w rodzinie);
- Find(x): zwraca reprezentanta zbioru, do którego należy x;
- Union(x,y): łączy dwa zbiory, których reprezentantami są x i y, w nowy zbiór będący ich teoriomnogościową sumą; dwa pierwotne zbiory (zakładamy, że były różne) są przy tym niszczone.
W naszych rozważaniach dotyczących kosztów powyższych operacji w różnych implementacjach struktury danych dla zbiorów rozłącznych będziemy brali pod uwagę dwa parametry: n, czyli łączną liczbę operacji MakeSet (bez straty ogólności można założyć, że wszystkie te operacje są wykonywane na początku), oraz m, czyli łączną liczbę wszystkich operacji MakeSet, Find i Union (w szczególności mamy \( n\le m \)). Nietrudno zauważyć, że liczba operacji Union nie jest większa niż n-1 (bo każda z nich zmniejsza liczbę zbiorów w rodzinie o jeden).
Większość zastosowań struktur danych dla zbiorów rozłącznych sprowadza się do zarządzania pewną dynamicznie rozrastającą się relacją równoważności (jej klasy abstrakcji to nasze zbiory rozłączne). Jako przykłady można wymienić:
- algorytm Kruskala znajdowania minimalnego drzewa rozpinającego;
- rozpoznawanie spójnych składowych w dynamicznie rozrastającym się grafie nieskierowanym;
- generowanie labiryntów;
- rozpoznawanie obszarów na obrazach w postaci cyfrowej.
Implementacja listowa
Oto prosta implementacja struktury danych dla zbiorów rozłącznych: Każdy zbiór jest reprezentowany jako lista swoich elementów. Reprezentantem zbioru jest pierwszy element na liście. Każdy element ma dodatkowo bezpośredni wskaźnik do reprezentanta, dzięki czemu koszt operacji Find to O(1). Operacja MakeSet jest również bardzo prosta i polega na utworzeniu jednoelementowej listy.
Bardziej kłopotliwa jest operacja Union: wprawdzie koszt połączenia dwóch list jest stały, ale trzeba jeszcze we wszystkich elementach listy, która jest dołączana na koniec drugiej, uaktualnić wskaźnik do reprezentanta, co zajmuje czas liniowy względem jej długości. Prosta sztuczka zwana heurystyką łączenia z wyważaniem pozwala zmniejszyć koszt operacji Union (w sensie zamortyzowanym). Polega ona na tym, że podczas operacji Union zawsze dołączamy krótszą listę na koniec dłuższej (wymaga to przechowywania wraz z listą dodatkowego atrybutu "rozmiar"). Jako ćwiczenie pozostawiamy dowód faktu, że teraz koszt wykonania m operacji MakeSet, Find i Union, spośród których n to MakeSet, wynosi \( O(m+n\log n) \).
Implementacja drzewiasta
Alternatywna implementacja to las zbiorów rozłącznych, w którym każde drzewo odpowiada jednemu ze zbiorów z naszej rodziny. Z każdym elementem zbioru jest związany wskaźnik do pewnego innego elementu (jego ojca w drzewie). Wyjątek stanowi reprezentant zbioru (a zarazem korzeń drzewa), którego wskaźnik wskazuje na niego samego. Operacja MakeSet tworzy jednoelementowe drzewo z korzeniem wskazującym na samego siebie. Operacja Union polega na przestawieniu wskaźnika jednego reprezentanta tak, by wskazywał na drugiego. Koszt obydwu tych operacji to oczywiście O(1). <
Operacja Find polega na przejściu po wskaźnikach ścieżki od danego węzła do reprezentanta (czyli korzenia). Jej koszt jest proporcjonalny do głębokości danego węzła w drzewie. Nietrudno podać przykład ciągu operacji, który powoduje powstanie drzewa w kształcie listy, czyli pesymistyczny koszt takiej operacji Find to \( \Theta(n) \) dla rodziny zbiorów zawierającej łącznie n elementów.
Łączenie według wysokości
Podobną do stosowanego dla list "łączenia z wyważaniem" metodą można zapewnić lepsze ograniczenie kosztu operacji Find. W korzeniu każdego drzewa przechowujemy dodatkowy atrybut - jego wysokość - i podczas operacji Union zawsze przyłączamy niższe drzewo do wyższego (remisy rozstrzygając dowolnie). Koszt Union pozostaje stały, a nietrudno pokazać, że teraz wysokość drzewa jest co najwyżej logarytmiczna względem jego rozmiaru, skąd wynika, że pesymistyczny koszt operacji Find to \( O(\lg n) \).
Kompresja ścieżki
Równie prosta, a bardzo skuteczna heurystyka polega na tym, że w ramach operacji Find po wyznaczeniu korzenia v drzewa zawierającego węzeł x przebiegamy ponownie ścieżkę od x do v i przyłączamy wszystkie napotkane węzły bezpośrednio do v. Dzięki temu późniejsze operacje Find dotyczące węzłów na ścieżce od x do v oraz ich potomków będą kosztowały mniej.
Przy stosowaniu kompresji ścieżki utrzymywanie poprawnych wartości atrybutu "wysokość" wykorzystywanego podczas wykonywania Union byłoby zbyt kosztowne. Zamiast tego będziemy przechowywać w węzłach atrybut "ranga", który będziemy wykorzystywać i modyfikować dokładnie tak samo, jak atrybut "wysokość" przy łączeniu według wysokości: podczas operacji Union przyłączamy drzewo o niższej randze do drzewa o wyższej randze, a w przypadku remisu po przyłączeniu zwiększamy rangę korzenia o 1. Tak więc ranga stanowi górne ograniczenie wysokości drzewa, a w myśl zadania 3 jej wartość nie przekracza \( \lfloor\lg n\rfloor \) dla rodziny zbiorów zawierającej łącznie n elementów. Poniższy lemat wylicza kilka dalszych użytecznych własności rang:
Lemat Lemat 1
W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżek
(a) ranga węzła, który nie jest korzeniem, jest mniejsza (ściśle) niż ranga jego ojca;
(b) zawsze kiedy ojciec danego węzła się zmienia, to nowy ojciec ma większą rangę niż stary;
(c) jeśli ranga reprezentanta pewnego zbioru jest równa r, to rozmiar tego zbioru wynosi co najmniej \( 2^r \);
(d) jeśli zbiory zawierają łącznie \( n \) elementów, to jest co najwyżej \( n/2^r \) węzłów rangi r, dla dowolnego \( r\ge 0 \). Dowód lematu pozostawiamy jako ćwiczenie.
Zanim przystąpimy do analizy kosztu opisanych wyżej operacji, zdefiniujemy dwie funkcje: jedną bardzo szybko rosnącą i drugą, rosnącą bardzo wolno. Niech \( F(0) = 1 \),
\( F(k) = 2^{2^{.^{.^{.^2}}\Big\}k}} = 2^{F(k-1)} \) dla k>0.
Oto kilka pierwszych wartości funkcji F:
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| F(k) | 1 | 2 | 4 | 16 | 65536 | \( 2^{65536} \) |
Jak widać, funkcja F rośnie bardzo szybko.
Funkcję logarytm iterowany definiuje się następująco: \( G(n) = \lg^* n = \min\{k:F(k)\ge n\} \). Oto tabelka początkowych wartości funkcji G:
| n | 0..1 | 2 | 3..4 | 5..16 | 17..65536 | \( 65537..2^{65536} \) |
| G(n) | 0 | 1 | 2 | 3 | 4 | 5 |
Funkcja G rośnie niesłychanie wolno i dla wszystkich n mających jakiekolwiek praktyczne znaczenie nie przekracza wartości 5.
Na potrzeby analizy kosztu zamortyzowanego operacji na lesie zbiorów rozłącznych przyporządkujemy każdy węzeł do jednego z ponumerowanych bloków: jeśli mianowicie dany węzeł ma rangę r, to przyporządkowujemy go do bloku o numerze \( \lg^* r \). Ponieważ rangi węzłów mieszczą się w zakresie od 0 do \( \lfloor \lg n\rfloor \), mamy \( \lg^* n \) bloków o numerach od 0 do \( \lg^* \lfloor \lg n\rfloor = \lg^*n -1 \). Możemy juz udowodnić
Twierdzenie 2 (Hopcroft, Ullman [HU])
W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżki koszt m operacji, spośród których n to operacje MakeSet, wynosi \( O(m\lg^* n) \).
Dowód: Ponieważ operacje MakeSet i Union mają koszt stały, wystarczy oszacować łączny koszt m operacji Find. Koszt operacji Find(x) jest proporcjonalny do liczby węzłów na ścieżce od x do korzenia (przed kompresją). Rozbijemy koszt każdej takiej operacji na składniki, które zaksięgujemy do różnych pul. Sumując pule, dostaniemy łączny koszt wszystkich operacji Find.
Dla wierzchołka v leżącego na ścieżce od x do korzenia:
Przypadek 1: Jeśli v lub jego ojciec jest korzeniem, to jednostkę kosztu księgujemy do puli KONIEC_ŚCIEŻKI;
Przypadek 2: Jeśli v i ojciec v są w różnych blokach, to jednostkę kosztu księgujemy do puli ZMIANA_BLOKU;
Przypadek 3: Jeśli v i ojciec v sa w tym samym bloku, to jednostkę kosztu księgujemy do puli TEN_SAM_BLOK.
Przypadek 1 dla każdej operacji Find występuje co najwyżej dwukrotnie, więc łączna zawartość puli KONIEC_ŚCIEŻKI to co najwyżej 2m. Podczas pojedynczej operacji Find przypadek 2 może wystąpić co najwyżej \( \lg^* n-1 \) razy (bo jest nie więcej niż \( \lg^*n \) różnych bloków, a w myśl lematu 1(a) rangi na ścieżce do korzenia tworzą ciąg rosnący). Zatem łączna zawartość puli ZMIANA_BLOKU to \( O(m\lg^* n) \).
Pozostaje nam zatem oszacować zawartość puli TEN_SAM_BLOK. Jeśli v jest w bloku o numerze \( g>0 \), przypadek 3 może dla niego zajść co najwyżej \( F(g)-F(g-1) \) razy (wynika to z lematu 1(b): ranga ojca v za każdym razem rośnie, a kiedy v i ojciec v znajdą się w różnych blokach, to dla v już do końca będzie zachodził przypadek 2 lub 1). Dla v należącego do bloku \( g=0 \) przypadek 3 może zajść co najwyżej raz.
Na mocy lematu 1(d) liczbę węzłów w bloku \( g>0 \) można oszacować z góry przez
\( \displaystyle\sum_{r=F(g-1)+1}^{F(g)} n/2^r\le n/2^{F(g-1)+1}(1+1/2+1/4+\cdots)\le n/2^{F(g-1)}=n/F(g) \)
skąd łączny wkład do puli TEN_SAM_BLOK pochodzący od węzłów z bloku \( g>0 \) szacuje się z góry przez \( (F(g)-F(g-1))\cdot n/F(g)\le n \) (to ostatnie oszacowanie jest prawdziwe również dla \( g=0 \)). Sumując po g, dostajemy górne oszacowanie zawartości puli TEN_SAM_BLOK \( O(n\lg^* n) \).
Uwaga: Wynikające z powyższego twierdzenia oszacowanie kosztu zamortyzowanego operacji Find \( O(\lg^* n) \) można poprawić! Robert Tarjan [T1,T2] podał asymptotycznie optymalne oszacowanie tego kosztu przez tzw. funkcyjną odwrotność funkcji Ackermanna, rosnącą jeszcze wolniej niż funkcja \( \lg^* \). Przystępny opis górnego oszacowania (chociaż znacznie bardziej skomplikowany niż powyższy dowód) można znaleźć w książce [CLRS].
Literatura
Literatura
[CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, Wprowadzenie do algorytmów, Wydawnictwa Naukowo-Techniczne, Warszawa 2004.
[HU] J.E.Hopcroft, J.D.Ullman, Set merging algorithms, SIAM Journal on Computing, 2(4) ,1973, 294-303.
[T1] R.E.Tarjan, Efficiency of a good but not linear set union algorithm, J. Assoc. Comput. Mach. 22, 1975, 215-225.
[T2] R.E.Tarjan, A class of algorithms which require non-linear time to maintain disjoint sets, J. Comput. Syst. Sci. 19, 1979, 110-127.
Ćwiczenia
Algorytmy grafowe - najlżejsze ścieżki
Ten wykład poświęcimy wprowadzeniu do algorytmów grafowych. W tym celu rozwiążemy następujący problem ścieżkowy.
Najlżejsze ścieżki z jednym źródłem
W tym wykładzie pisząc graf będziemy mieli zawsze na uwadze graf spójny i nieskierowany. Tradycyjnie przez \( n \) będziemy oznaczali liczbę wierzchołków w grafie, a przez \( m \) liczbę jego krawędzi. Dla każdego grafu mamy zawsze \( n-1 \le m \le n(n-1)/2 \).
Niech \( G=(V,E) \) będzie grafem, a \( w: E arrow \{1,2,...\} \) funkcją przypisująca krawędziom dodatnie liczby całkowite zwane wagami krawędzi. Krawędzie \( (u,w)\in E \) będziemy oznaczali przez \( u-w \).
Ciąg wierzchołków \( p= < v_0, v_1,\ldots , v_k > \) nazywamy ścieżką w \( G \) wtedy i tylko wtedy, gdy \( v_i - v_{i+1} \) jest krawędzią w \( E \), dla każdego \( i = 0, 1,\ldots,k-1 \). Liczbę \( k \) nazywamy długością ścieżki \( p \).
Wagą ścieżki \( p \) nazywamy sumę wag jej krawędzi i oznaczamy także przez \( w(p) \). Przyjmujemy, że waga ścieżki o długości 0 wynosi 0.
Przez \( N(v) \) będziemy oznaczali zbiór sąsiadów wierzchołka \( v \) w grafie \( G \).
Problem (wag) najlżejszych ścieżek z jednym źródłem definiuje się następująco (uwaga: w literaturze przyjęło się też wagę ścieżki nazywać długością i dlatego często mówi się o problemie najkrótszych ścieżek).
Dane:
\( G=(V,E) \) – spójny, nieskierowany graf
\( w: Earrow \{1,2,\ldots\} \) – funkcja przypisująca krawędziom dodatnie liczby całkowite
\( s \) – wyróżniony wierzchołek w G, zwany źródłem
Wynik:
dla każdego wierzchołka \( v \), waga \( w^*(v) \) najlżejszej ścieżki łączącej \( v \) z \( s \).
Na tym wykładzie zajmiemy się tylko wyznaczaniem wag najlżejszych ścieżek. Znalezienie sposobu wyznaczania takich ścieżek pozostawiamy jako ćwiczenie dla czytelnika. Problem najlżejszych scieżek jest problemem bardzo naturalnym. Jeśli mapę drogową potraktować jako graf, w którym wagi to długości odcinków drogowych na mapie, a źródło jest wyróżnionym miastem na mapie (na przykład stolicą państwa), to rozwiązanie problemu najlżejszych ścieżek da nam długości najkrótszych dróg od miasta-źródła do pozostałych miast na mapie.
Znaczenie problemu najlżejszych ścieżek jest dużo większe niż by to wynikało z jego zastosowań. Poszukując wydajnego algorytmu dla rozwiązania tego problemu, postaramy się przedstawić cały proces projektowania, a następnie implementowania algorytmu ze szczególnym uwzględnieniem doboru odpowiednich struktur danych w celu osiągnięcia lepszej wydajności implementacji.
Nasze rozważania rozpoczniemy od schematu algorytmu poszukiwania najlżejszych ścieżek, a następnie zajmiemy się implementacją poszczególnych elementów tego schematu. Rozwiązanie, które zaproponujemy pochodzi od wybitnego holenderskiego informatyka Edgara Dijkstry.
Zastanówmy się, w jaki sposób obliczać wagi najlżejszych ścieżek. Pomoże nam w tym następujące proste spostrzeżenie:
Niech \( < v=v_0,v_1,\ldots,v_k=s> \) będzie najlżejszą ścieżką z wierzchołka \( v \) do źródła \( s \). Wówczas \( w^*(v) > w^*(v_1)>\ldots > w^*(v_k)=0 \).
Spostrzeżenie to mówi, że gdybyśmy obliczali wagi najlżejszych ścieżek od najlżejszej do najcięższej, to dla każdego wierzchołka \( v \) różnego od źródła, sąsiad \( v \) na najlżejszej ścieżce z \( v \) do \( s \) miałby swoją wagę już obliczoną i tym sąsiadem byłby wierzchołek (może być więcej niż jeden wybór), dla którego waga najlżejszej ścieżki do \( s \), powiększona o wagę krawędzi łączącej go z \( v \), jest najmniejsza.
Możemy teraz przystąpić do schematu algorytmu. Algorytm obliczania najlżejszych ścieżek będzie działał w \( n-1 \) fazach. W trakcie działania algorytmu \( L \) będzie zbiorem tych wierzchołków, dla których wagi najlżejszych scieżek prowadzące do \( s \) zostały już obliczone. Przez \( R \) będziemy oznaczali zbiór pozostałych wierzchołków. Podczas obliczeń z każdym wierzchołkiem \( v \) będziemy mieli związana nieujemną wagę \( w[v] \). Dla każdego wierzchołka \( v \in L \) waga \( w[v] \) będzie wagą najlżejszej scieżki łączacej \( v \) z \( s \), czyli \( w[v] = w^*(v) \). Dla każdego wierzchołka \( v \) z \( R \), \( w[v] \) będzie równe wadze najlżejszej ścieżki z \( v \) do \( s \), na której wszystkie wierzchołki poza \( v \) należą do \( L \). Może się zdarzyć, że taka ścieżka nie istnieje. Wówczas przyjmujemy, że \( w[v] \) jest równe \( \infty \) - umownej wartości większej od wszystkich wag występujących w obliczeniach. Jedna faza algorytmu będzie polegała na przeniesieniu do \( L \) wierzchołka z \( R \) o najmniejszej wadze \( w \), a następnie poprawieniu wag \( w \) dla wierzchołków, które pozostały w \( R \). Zauważmy, że wagi \( w \) mogą się zmienić tylko sąsiadom wierzchołka przeniesionego do \( L \), którzy pozostali w \( R \). Oto schemat algorytmu obliczania najlżejszych ścieżek. Nazwiemy go metodą Dijkstry.
Algorytm Metoda Dijkstry
//Inicjacja L := {s}; R := V- {s}; w[s] := 0; for each v in R do if v-s in E then w[v] := w(v-s) else w[v] := infty ; //właściwe obliczenia for i := 1 to n-1 do begin u := wierzchołek z R o minimalnej wadze w[u]; R := R - {u}; L := L + {u}; for each v in (N(u) cap R) do if w[u] + w(u-v) < w[v] then w[v] := w[u] + w(u-v); end; //dla każdego v in V, w[v] = w*(v)
Dlaczego powyższy opis obliczania wag najlżejszych ścieżek nazwaliśmy metodą Dijkstry, a nie algorytmem Dijkstry? Zauważmy, że żeby powyższą metodę móc zaimplementować na komputerze, a także dokonać analizy jej złożoności obliczeniowej, musimy doprecyzować wiele elementów schematu. Należą do nich
- implementacja grafu;
- implementacje zbiorów \( L \) i \( P \) oraz operacji na nich (inicjacja, usuwanie i dodawanie wierzchołka, znajdowanie wierzchołka o minimalnej wadze, zmiana wagi wierzchołka).
Dopiero ścisłe określenie tych elementów da nam pełną implementację metody, a tym samym algorytm, który będzie mógł być poddany analizie.
Zaczniemy od implementacji, w której wszystkie struktury danych są tablicami. Zanim to jednak zrobimy, zastanówmy się, w jaki sposób wygodnie zadać graf jako daną dla algorytmu. Zawyczaj przyjmuje się, że wierzchołki grafu utożsamiamy z liczbami naturalnymi \( 1,2,\ldots, n \), natomiast krawędzie opisujemy jako pary liczb odpowiadające końcom krawędzi. Gdy dodatkowo, tak jak w problemie najlżejszych ścieżek, z każdą krawędzią związana jest waga, to z każdą parą liczb opisującą końce krawędzi podajemy trzecią liczbę - wagę tej krawędzi. Tak więc graf możemy zadać w następujący sposób:
- wiersz pierwszy: para liczb n, m - odpowiednio liczba wierzchołków i krawędzi grafu
- m wierszy, z których każdy zawiera parę (trójkę) liczb reprezentujących końce jednej krawędzi (i jej wagę).
Zauważmy, że jeśli graf jest spójny, jego rozmiar wynosi \( O(m) \), gdzie \( n-1 < m \le \frac{n(n-1)}{2} \).
Taki sposób reprezentacji grafu nie jest wygodny w obliczeniach, ponieważ nie daje on prawie żadnej informacji o strukturze grafu. Dlatego w algorytmach grafowych przyjmuje się, że graf jest implementowany na jeden z dwóch sposobów.
Macierz sąsiedztwa
W implementacji tablicowej zakłada się, że graf jest reprezentowany przez tak zwaną macierz sąsiedztwa. W najczystszej postaci macierz sąsiedztwa jest macierzą kwadratową indeksowaną wierzchołkami grafu, której elementy przyjmują wartości 0 lub 1. Jedynka (1) na przecięciu \( i \)-tego wiersza i \( j \)-tej kolumny mówi, że w grafie jest krawędź o końcach w \( i \) oraz \( j \), zaś zero (0) oznacza, że takiej krawędzi nie ma. W przypadku, gdy krawędzie mają wagi, macierz sąsiedztwa można zmodyfikować w następujący sposób. Jeśli \( i-j \) jest krawędzią w grafie, to na przecięciu tej \( i \)-tego wiersza i \( j \)-tej kolumny wstawiamy wagę \( w(i-j) \). Gdy takiej krawędzi nie ma w grafie, to w to miejsce wstawiamy \( \infty \). W takim przypadku elementy macierzy traktujemy jako wagi bezpośrednich połączeń pomiędzy wierzchołkami w grafie. Żeby być w zgodzie z tą konwencją przyjmujemy, że na przekątnej macierzy sąsiedztwa zawsze stawiamy zera. Podsumowując, w implementacji tablicowej przyjmujemy, że graf jest reprezentowany przez macierz kwadratową \( A[1..n,1..n] \) taką,że
Głównymi zaletami tej reprezentacji są jej prostota i to, że łatwo sprawdzać w czasie stałym, czy dwa wierzchołki są połączone krawędzią w grafie. Wadą jest to, że niezależnie od rozmiaru grafu, rozmiar tej reprezentacji jest zawsze kwadratowy. Tyle też czasu zajmuje jej inicjacja. Nawet jeśli byśmy przyjęli, że taka reprezentacja jest z góry zadana, to okazuje się, że przy tej reprezentacji grafu algorytmy dla znakomitej większości naturalnych problemów grafowych działają w czasie \( \Omega(n^2) \). Nie jest to źle dla grafów gęstych, w których \( m=\Theta(n^2) \), ale gdy chcemy uzyskiwać szybsze algorytmy dla grafów rzadszych, w szczególności liniowe ze względu na rozmiar grafu, to musimy myśleć o innej ich reprezentacji. Taką reprezentacją jest reprezentacja listowa.
Listy sąsiedztw
W tej implementacji dla każdego wierzchołka w grafie pamiętamy listę jego sąsiadów zwaną listą sąsiedztwa. Innymi słowy, graf jest pamiętany w tablicy list \( L[1..n] \), gdzie \( L[i] \) jest listą sasiedztwa wierzchołka \( i \). W przypadku grafu z wagami, jeśli wierzchołek \( j \) występuje na liście wierzchołka \( i \), to z wystąpieniem wierzchołka \( j \) związana jest waga krawędzi \( i-j \). Kolejność wierzchołków na liście może być dowolna. Zauważmy, że suma długości list sąsiedztw wynosi \( 2m \), a zatem rozmiar struktury danych reprezentującej graf wynosi \( O(n+m) \) i jest on liniowy ze względu na rozmiar danych. Listy \( L \) można łatwo zbudować w czasie liniowym. Jeśli więc chcemy uzyskiwać algorytmy, których złożoności jak najlepiej zależą od rozmiaru grafu, a w szczególności są liniowe ze względu na ten rozmiar, należy reprezentować graf przez listy sąsiedztw.
Możemy teraz powrócić do problemu najlżejszych ścieżek i zająć się implementacją schematu Dijkstry.
Implementacja tablicowa
W tej implementacji wszystkie struktury danych są tablicami. Przyjmujemy, że graf jest zadany przez macierz sąsiedztwa \( A[1..n,1..n] \). Zbiór \( R \) jest rerezentowany za pomocą tablicy (wektora charakterystycznego) \( r[1,\ldots,n] \) o wartościach 0-1:
Tablica \( w[1..n] \) służy do obliczania wag najlżejszych ścieżek. Oznaczmy przez \( MinR \) funkcję, której wartością jest wierzchołek w R o najmniejszej wadze \( w \). Jeśli jest więcej niż jeden taki wierzchołek, to wynikiem funkcji może być dowolny z nich. Oto jedna z możliwych implementacji tej funkcji.
function MinR; begin min := 0; for i := 1 to n do if w[i] < min then min_v := i; return min_v end
Czas działania tej funkcji wynosi \( O(n) \).
Możemy teraz przedstawić pierwszą implementację metody Dijkstry.
Algorytm Metoda Dijkstry - implementacja tablicowa
//Inicjacja for v := 1 to n do begin r[v] := 1; w[v] := A[v,s] end; r[s] := 0; //właściwe obliczenia for i := 1 to n-1 do begin u := MinR; r[u] := 0; for v := 1 to n do if r[v] = 1 then if w[u] + A[u,v] < w[v] then w[v] := w[u] + A[u,v] end; //dla każdego v \in V, w[v] = w*(v)
W powyższej implementacji grupy wierszy 2-8, 12-14 oraz 15-18 odpowiadają dokładnie tym samym grupom wierszy w opisie metody Dijkstry. Analiza złożoności czasowej powyższego algorytmu nie nastręcza żadnych trudności. Inicjacja zajmuje czas \( O(n) \), każdy obrót pętli for z wiersza 10 zajmuje także czas \( O(n) \), a zatem cały algorytm działa w czasie \( \Theta(n^2) \). Dla grafów gęstych, czyli zawierających rzędu \( n^2 \) wierzchołków, jest to algorytm optymalny. Zwróćmy także uwagę na jego wyjątkowo prosty i elegancki zapis. Co jednak, gdy zadany graf nie jest grafem gęstym? Czy wówczas możemy obliczać wagi najlżejszych ścieżek szybciej?
Implementacja listowa
Pierwszym krokiem, jaki podejmiemy, jest przyjęcie reprezentacji grafu przez listy sąsiedztw. Załóżmy, że jest to jedyna zmiana w implementacji. Oto zapis metody Dijsktry przy tej zmianie.
Algorytm Metoda Dijkstry - implementacja listowa
//Inicjacja for v := 1 to n do begin r[v] := 1; w[v]:= \infty end; r[s] := 0; w[s] := 0; for each v \in L[s] do w[v] := w(v-s); //właściwe obliczenia for i := 1 to n-1 do begin u := MinR; r[u] := 0 ; for each v \in L[u] do if r[v] = 1 then if w[u] + w(u-v) < w[v] then w[v] := w[u] + w(u-v); end; //dla każdego v \in V, w[v] = w*(v)
Dokonajmy analizy złożoności obliczeniowej tego algorytmu. Inicjacja, tak jak poprzednio, zajmuje czas \( O(n+m). \) Rozważmy teraz jeden obrót pętli for z wiersza 10. Niestety wiersz 12 nie uległ zmianie i tak jak poprzednio zajmuje czas \( \Theta(n) \). To powoduje, że cały algorytm działa w czasie \( \Theta(n^2) \). Mamy jednak pewien zysk w wierszach 15-17. Zauważmy, że w tych wierszach, dla każdego wierzchołka różnego od źródła przeglądamy dokładnie raz jego listę sąsiedztwa, a obsługa jednego wierzchołka na liście zajmuje stały czas. Tak więc łączny koszt wykonania pętli for z wiersza 15 wynosi \( O(m) \). Przyjrzyjmy się jakiego rodzaju operacje wykonujemy w naszym algorytmie. Nietrudno spostrzec, że kluczowe dla wydajności naszego algorytmu są operacje na zbiorze \( R \). Zbiór \( R \) jest zbiorem zmieniającym się dynamicznie podczas wykonywania algorytmu i składa się z wierzchołków grafu z przypisanymi im wagami. Na zbiorze \( R \) wykonywane są następujące operacje:
- \( MakeR \): zbuduj zbiór \( R \), na który składają się wszystkie wierzchołki poza źródłem i których wagami są wagi krawędzi łączące je ze źródłem lub \( \infty \), gdy takie krawędzie nie istnieją - wiersze 1-7
- \( MinR \): znajdź w \( R \) wierzchołek o minimalnej wadze - wiersz 11
- \( DeleteMinR \): usuń z \( R \) znaleziony wierzchołek o minimalnej wadze - wiersz 12
- \( DecreaseKeyR(v,w') \): zmień wagę wierzchołka \( v \) na mniejszą wagę \( w' \) - wiersz 17
Powyższe operacje są operacjami kolejki priorytetowej. Powstaje pytanie, którą z licznych implementacji kolejki priorytetowej tu wykorzystać. Skupimy się na dwóch implementacjach.
Kopiec zwyczajny
W tej implementacji zbiór reprezentujemy za pomocą kopca zwyczajnego, o którym była mowa przy okazji sortowania kopcowego. Koszty wykonania poszczególnych operacji wynoszą w tym przypadku:
- \( MakeR \) - \( O(n) \)
- \( MinR \) - \( O(1) \)
- \( DeleteMinR \) - \( O(\log n) \)
- \( DecreaseKeyR \) - \( O(\log n) \)
Szczegóły implementacyjne metody Dijkstry z wykorzystaniem kopca zwyczajnego zostawiamy jako zadanie dla Czytelnika. Tak zaimplementowany algorytm obliczania najlżejszych ścieżek działa w czasie \( O(m\log n) \) i jest on asymptotycznie szybszy od algorytmu tablicowego dla każdego \( m \) rzędu mniejszego niż \( \frac{n^2}{\log n} \).
Kopiec Fibonacciego
Zauważmy, że operacją mającą decydujący wpływ na taką właśnie złożoność jest operacja zmniejszenia wagi \( DecreaseKeyR \). Wiemy jednak, że w kopcach Fibonacciego zamortyzowany koszt tej operacji jest stały. To jest wystarczające do naszych celów, tym bardziej, że koszty pozostałych operacji są takie same (koszt \( DeleteMinR \) jest kosztem zamortyzowanym) jak w kopcu zwyczajnym. Zatem jeśli do implementacji zbioru \( R \) wykorzystamy kopiec Fibonacciego, czas działania metody Dijkstry wyniesie \( O(n\log n + m) \). Na praktyczne zachowanie się tego algorytmu duży wpływ ma jednak skomplikowana budowa kopców Fibonacciego.
Ćwiczenia
Algorytmy grafowe - przeszukiwanie grafów
Z poprzedniego wykładu wiemy, że gdy celem jest ułożenie algorytmu o złożoności liniowej ze względu na rozmiar grafu (czyli sumę liczb wierzchołków i krawędzi), graf powinien być reprezentowany przez listy sąsiedztw. Na tym wykładzie przyjmiemy taką właśnie reprezentację grafu wejściowego. Rozwiązanie każdego problemu grafowego, które zależy od poznania struktury połączeń w całym grafie, wymaga przeszukania jego wierzchołków i krawędzi. Takie przeszukanie polega na odwiedzeniu każdego wierzchołka i zbadaniu krawędzi opuszczających już odwiedzone wierzchołki. Jeśli okazuje się, że drugi koniec badanej krawędzi nie był jeszcze odwiedzony, dołącza się go do zbioru wierzchołków odwiedzonych. Przeszukiwania dokonujemy z wykorzystaniem dynamicznego zbioru \( S \), w którym przechowujemy odwiedzane wierzchołki i których sąsiedztwa nie są jeszcze do końca zbadane. Zakładamy, że na zbiorze \( S \) wykonywane są następujące operacje:
\( Insert(S,v) \): wstaw do zbioru \( S \) wierzchołek \( v \);
\( Get(S) \): funkcja, której wynikiem jest (dowolny) wierzchołek z \( S \), wywoływana tylko wtedy, gdy \( S \ne \emptyset \);
\( Delete(S,v) \): usuń z \( S \) wierzchołek \( v \) (zazwyczaj będzie to wierzchołek \( Get(S) \).
Informacje o tym, które wierzchołki zostały już odwiedzone, będziemy przechowywać w tablicy logicznej \( visited[1..n] \). Wartością \( visited[v] \) jest PRAWDA (TRUE) wtedy i tylko wtedy, gdy wierzchołek \( v \) został już odwiedzony. Do przechodzenia list sąsiedztw posłuży nam tablica \( current[1..n] \). Wartością \( current[v] \) jest pierwszy wierzchołek na liście \( L[v] \) - sąsiad \( v \) - który nie był jeszcze oglądany od strony \( v \), co oznacza że krawędź opuszczająca \( v \) w kierunku tego sąsiada nie została jeszcze zbadana.
Inicjacja każdego przeszukiwania wygląda następująco:
for each v \in V do begin current[v] := pierwszy wierzchołek na liście sąsiedztwa L[v]; visited[v] := FALSE; //markujemy, że wierzchołek v nie był jeszcze odwiedzony end;
Załóżmy, że przeszukiwanie grafu rozpoczynamy z wybranego wierzchołka \( s \). Wówczas schemat przeszukiwania z \( s \) można zapisać następująco.
Algorytm Przeszukiwanie grafu - algorytm generyczny
procedure Search(s); begin S := {s}; visited[s] := TRUE; //markujemy s jako odwiedzony while S <> \emptyset do begin u := Get(S); if current[u] <> NIL then //jeśli nie wyczerpaliśmy całej listy sąsiadów wierzchołka u begin //pobierz kolejny wierzchołek z listy sąsiadów i przejdź do następnego // wierzchołka na liście v:= current[u]; current[u] := next(current[u]); if NOT visisted[v] then //jeśli v nie był jeszcze odwiedzony begin visited[v] := TRUE;// markujemy v jako odwiedzony Insert(S,v) //wstaw v do zbioru S end end else //wszystkie krawędzie opuszczające u zostały już zbadane Delete(S,u) end end
Powyższy schemat może być użyty do rozwiązania jednego z najbardziej podstawowych problemów grafowych - problemu spójności. Problem ten formułuje się następująco.
Dane
Graf G=(V,E) (zadany przez listy sąsiedztw)
Wynik
Tablica \( c[1..n] \) o wartościach w zbiorze wierzchołków \( V \) taka, że \( c[u]=c[v] \) wtedy i tylko wtedy, gdy \( u \) i \( v \) należą do tej samej spójnej składowej.
Zauważmy, że problem spójności bardzo łatwo rozwiązać przy użyciu procedury \( Search(s) \). Jeśli przeszukiwanie rozpoczynamy od nieodwiedzonego wierzchołka \( s \), to w wyniku wykonania \( Search \) zostaną odwiedzone wszystkie wierzchołki w grafie \( G \) osiągalne z \( s \). Innymi słowy odwiedzona zostanie cała spójna składowa zawierająca \( s \). Jeśli dla każdego nowo odwiedzanego wierzchołka \( v \) wykonamy przypisanie \( c[v] := s \), po zakończeniu przeszukiwania spójnej składowej zawierającej \( s \), wartość \( c \) każdego wierzchołka w tej składowej będzie właśnie równa \( s \). Jedyne miejsce, w którym musimy zmieniać procedurę \( Search \) jest wiersz 16. Nowy wiersz 16 powinien mieć postać:
16 visited[v]:=TRUE; c[v]:= s;
Tak zmodyfikowaną procedurę \( Search \) nazwiemy \( SearchCC \) z angielskiego Search Connected Components (czyli wyszukaj spójne składowe). Oto algorytm obliczania spójnych składowych z wykorzystaniem procedury \( SearchCC \).
Inicjacja przeszukiwania grafu. for each v \in V do if NOT visited[v] then //odkryta została nowa spójna składowa zawierająca wierzchołek v SearchCC(v);
Dokonamy teraz analizy złożoności algorytmu obliczania spójnych składowych. Zakładamy przy tym, że każda z operacji na pomocniczym zbiorze \( S \) jest wykonywana w czasie stałym. Zauważmy, że każdy wierzchołek jest dokładnie raz wstawiany do zbioru \( S \) - w momencie odkrycia go jako nieodwiedzonego - i dokładnie raz jest usuwany ze zbioru \( S \) - po zbadaniu całego jego sąsiedztwa. Sąsiadów wierzchołka przeglądamy przechodząc po jego liście sąsiedztwa, a dla każdego elementu listy obliczenia z nim związane zajmują stały czas. Jeśli wierzchołek był już odwiedzony, nic nie robimy, natomiast jeśli nie był odwiedzony, markujemy go jako odwiedzonego i wstawiamy do zbioru \( S \). Obliczenia związane z przeglądaniem sąsiedztw wierzchołków zajmują więc czas proporcjonalny do sumy długości list sąsiedztw, która to suma wynosi \( 2m \). Z naszej analizy wynika, że problem spójnych składowych można rozwiązać w czasie \( O(n+m) \), czyli liniowym ze względu na rozmiar grafu.
W dalszym ciągu tego wykładu będziemy rozważali tylko grafy spójne. Niech \( G=(V,E) \) będzie grafem spójnym, a \( s \) wyróżnionym wierzchołkiem w \( G \). Zanalizujmy raz jeszcze wykonanie procedury \( Search(s) \) dla grafu \( G \). Dla każdego wierzchołka \( v \ne s \) niech \( p[v] \) będzie wierzchołkiem z którego wierzchołek \( v \) zostaje odwiedzony, tzn. \( p[v] \) zostaje zamarkowany jako odwiedzony w wierszu 16, gdy zostaje odkryty na liście sąsiedztwa \( v \). Nietrudno zauważyć, że graf \( (V,\{v-p[v]: v \in V-\{s\}\}) \) jest drzewem rozpinającym grafu \( G \). Jeśli każdą krawędź tego drzewa zorientujemy od \( p[v] \) do \( v \), otrzymamy drzewo o korzeniu \( s \), w którym krawędzie są skierowane od korzenia w kierunku liści. Takie drzewo będziemy nazywali drzewem przeszukiwania grafu. Zauważmy, że wskaźniki \( p \) wyznaczają dla każdego wierzchołka \( v \) jedyną ścieżkę w drzewie łączącą \( v \) z korzeniem \( s \).
Dotychczas nic nie mówiliśmy o implementacji zbioru \( S \). Rozważymy dwie naturalne implementacje. W pierwszej z nich zbiór \( S \) jest kolejką typu FIFO. W tej implementacji wynikiem funkcji \( Get(S) \) jest ten wierzchołek ze zbioru \( S \), który przebywa w nim najdłużej. W drugiej implementacji zbiór \( S \) jest stosem, a wynikiem \( Get(S) \) jest wierzchołek przebywający w \( S \) najkrócej, czyli ostatnio wstawiony. Kolejkę i stos łatwo zaimplementować w taki sposób, żeby każda z wymaganych przez nas operacji na zbiorze \( S \) była wykonywana w czasie stałym. W tym celu można użyć struktury listowej.
Przeszukiwanie wszerz
Czym jest drzewo przeszukiwania, gdy do implementacji zbioru \( S \) użyjemy kolejki? Zauważmy, że do zbioru \( S \) wierzchołki są wstawiane w następującej kolejności. Najpierw pojawia się w \( S \) wyróżniony wierzchołek \( s \). Wierzchołek \( s \) zostanie usunięty (z początku) kolejki dopiero po przejrzeniu jego całej listy sąsiedztwa i wrzuceniu każdego napotkanego na niej wierzchołka na koniec kolejki. Następnie dla każdego sąsiada \( s \) przeglądana jest jego lista sąsiedztwa i każdy wierzchołek dotychczas jeszcze nieodwiedzony zostaje zamarkowany jako odwiedzony i umieszczony na końcu kolejki. W ten sposób po sąsiadach wierzchołka \( s \) w kolejce pojawią się wszyscy sąsiedzi sąsiadów \( s \), którzy nie sąsiadują bezpośrednio z \( s \). W dalszej kolejności w zbiorze \( S \) pojawią się sąsiedzi sąsiadów sąsiadów \( s \), sąsiedzi sąsiadów sąsiadów sąsiadów \( s \), itd. Podzielmy zbiór wierzchołków grafu na warstwy \( W_0, W_1, W_2, \ldots \). Warstwa \( W_0 \) składa się tylko z wierzchołka \( s \). Warstwa \( W_1 \) to sąsiedzi \( s \). Warstwa \( W_2 \) to te wierzchołki grafu, które sąsiadują z co najmniej jednym wierzchołkiem z warstwy \( W_1 \) i nie należą do żadnej z warstw poprzednich, czyli \( W_0 \) i \( W_1 \). Do warstwy \( W_3 \) należą wierzchołki sąsiadujące z co najmniej jednym wierzchołkiem z warstwy poprzedniej (\( W_2 \)) i nie należą do warstw o numerach mniejszych od 3, itd. Nietrudno zauważyć, że \( i \)-ta warstwa składa się ze wszystkich tych wierzchołków, których odległość (długość najkrótszej ścieżki) od \( s \) w grafie \( G \) wynosi dokładnie \( i \). Dla każdego wierzchołka \( v \) wskaźniki \( p[v], p[p[v]],\ldots \) wyznaczają najkrótszą ścieżkę łączącą \( v \) z \( s \). Kolejność w jakiej przeszukiwane są wierzchołki grafu w tym przypadku usprawiedliwia nazwę tego sposobu przeszukiwania jako przeszukiwania wszerz (ang. Breadth First Search, w skrócie BFS). Przemieszczamy się po grafie całą jego szerokością, warstwa po warstwie. Z naszych rozważań wynika, że drzewo przeszukiwania wszerz jest drzewem najkrótszych ścieżek łączących wierzchołki grafu z wyróżnionym wierzchołkiem \( s \). Wynika stąd, że najkrótsze ścieżki łączące wszystkie wierzchołki grafu z jednym wyróżnionym wierzchołkiem można wyznaczyć w czasie liniowym, o ile tylko długości (wagi) krawędzi są jednostkowe.
Przeszukiwanie w głąb
Z przeszukiwaniem w głąb (ang. Depth First Search, w skrócie DFS) mamy do czynienia, gdy do implementacji zbioru \( S \) używamy stosu. Określenie "przeszukiwanie w głąb" bierze się stąd, że zawsze próbujemy kontynuować przeszukiwanie z najpóźniej odkrytego wierzchołka, czyli z tego, który znajduje się na szczycie stosu. Okazuje się, że przeszukując graf w głąb możemy zebrać niezmiernie przydatne informacje o strukturze grafu, które mogą być wykorzystane w konstruowaniu efektywnych algorytmów dla bardzo wielu problemów grafowych. Przeszukiwanie w głąb dużo wygodniej opisać rekurencyjnie. Rozważmy poniższą procedurę \( DFS(v) \), w której dodatkowo numerujemy wierzchołki w kolejności odwiedzania. W tym celu użyjemy globalnej zmiennej \( ost{nr} \), której wartością jest ostatnio nadany numer. Zmienną \( ost{nr} \) inicjujemy na 0. Otrzymaną numerację będziemy nazywali numeracją w głąb.
Algorytm Przeszukiwanie w głąb
procedure DFS(v); //v jest nowo odkrytym wierzchołkiem begin //markujemy v jako odwiedzony visited[v] :=TRUE; //wierzchołkowi v nadajemy kolejny numer ostnr := ostnr + 1; nr[v] := ostnr; //przeglądamy listę sąsiedztwa v i dla każdego nowo odkrytego //wierzchołka wywołujemy procedurę DFS for each u \in L[v] do if NOT visited[u] then DFS(u) end;
Jeśli chcemy przeszukać graf poczynając od wierzchołka \( s \), wystarczy wywołać \( DFS(s) \), inicjując wcześniej tablice \( visited \) i \( current \) oraz zmienną \( ost{nr} \). Zauważmy, że krawędź \( v--u \) zaliczamy do drzewa przeszukiwania (w głąb), jeśli po wejściu do wierzchołka \( v \) odkrywamy, że wierzchołek \( u \) na liście sąsiedztwa \( v \) nie został jeszcze odwiedzony. Krawędzie, które nie należą do drzewa przeszukiwania mają jedną bardzo ważną własność.
Krawędź niedrzewowa łączy zawsze potomka z przodkiem w drzewie przeszukiwania w głąb.
Dowód powyższej własności jest niezwykle prosty. Załóżmy nie wprost, że istnieje niedrzewowa krawędź \( v-u \) taka, że wierzchołki \( v \), \( u \) nie są w relacji potomek-przodek. Bez straty ogólności możemy przyjąć, że \( v \) zostaje odwiedzony wcześniej niż \( u \). Załóżmy, że \( u \) zostaje odwiedzony w wyniku wywołania przeszukiwania \( DFS \) podczas przeglądania listy sąsiedztwa \( v \). Wówczas jednak \( u \) znajdzie się w poddrzewie przeszukiwania o korzeniu w \( v \). Ponieważ \( u \) jest na liście \( v \), do takiego wywołania dojść musi – sprzeczność z założeniem, że \( u \), \( v \) nie są w relacji potomek-przodek.
Numeracja w głąb pozwala łatwo sprawdzić, czy dwa różne wierzchołki \( u \), \( v \) są w relacji przodek-potomek w drzewie przeszukiwania w głąb. Załóżmy, że \( nr[u] < nr[v] \).
Wierzchołek \( u \) jest przodkiem wierzchołka \( v \) w drzewie przeszukiwania w głąb wtedy i tylko wtedy, gdy \( nr[u] < nr[v] \le nr[u] + d[u] \), gdzie \( d[u] \) jest liczbą wierzchołków w poddrzewie o korzeniu w \( u \).
Pokażemy teraz, w jaki sposób zastosować przeszukiwanie w głąb do wyznaczenia wszystkich mostów grafie. Przypomnijmy, że mostem w spójnym grafie \( G \) nazywamy każdą krawędź, której usunięcie rozspójnia ten graf. Zauważmy, że bardzo łatwo wyznaczyć wszystkie mosty w czasie \( O(m(n+m)) \). Wystarczy dla każdej krawędzi sprawdzić w czasie liniowym, czy usunięcie tej krawędzi zwiększa liczbę spójnych składowych w grafie. Przeszukiwanie w głąb pozwala rozwiązać ten problem w czasie liniowym. Zanim przedstawimy stosowny algorytm, spróbujmy scharakteryzować mosty z wykorzystaniem drzewa przeszukiwania w głąb i numeracji w głąb.
Spostrzeżenie 1
Jeśli krawędź jest mostem w grafie, jest krawędzią każdego drzewa rozpinającego tego grafu.
Rozważmy drzewo przeszukiwania w głąb i niech \( u-v \) będzie krawędzią w tym drzewie. Załóżmy także, że \( u \) jest ojcem \( v \).
Spostrzeżenie 2
Krawędź \( u-v \) jest mostem wtedy i tylko wtedy, gdy żadna krawędź niedrzewowa nie łączy wierzchołka z poddrzewa o korzeniu w \( v \) z właściwym przodkiem \( v \). Innymi słowy wtedy i tylko wtedy, gdy oba końce każdej krawędzi niedrzewowej leżą w poddrzewie o korzeniu w \( v \), jeśli tylko jeden z tych końców jest w tym poddrzewie.
Spróbujemy warunek ze spostrzeżenia 2 wyrazić trochę inaczej. Dla każdego wierzchołka \( v \) niech \( low[v] \) będzie najmniejszym numerem w głąb wierzchołka, który można osiągnąć z \( v \) ścieżką składającą z krawędzi drzewowych z poddrzewa o korzeniu w \( v \) i zakończoną co najwyżej jedną krawędzią niedrzewową prowadzącą poza to poddrzewo. Funkcję \( low \) można rekurencyjnie zdefiniować w następujący sposób:
\( low[v] = \min(\{nr[v]\}\cup \{nr[u]: u-v \mbox{ jest krawędzią niedrzewową }\} \cup \{low[u]: u \mbox{ jest synem } v \mbox{ w drzewie przeszukiwania w głąb}\}) \)
Spostrzeżenie 3
Niech \( v-u \) będzie krawędzią drzewa przeszukiwania w głąb taką, że \( v \) jest ojcem \( u \) w tym drzewie. Wówczas krawędź \( v-u \) jest mostem wtedy i tylko wtedy, gdy \( low[u] > nr[v] \).
Powyższe spostrzeżenia pozwalają już na zaproponowanie liniowego algorytmu wyznaczania mostów w spójnym grafie \( G \). Algorytm ten zapiszemy za pomocą rekurencyjnej procedury \( DFS-Bridges(v) \).
Algorytm Mosty
procedure DFS-Bridges(v, ojciec_v) begin visited[v] :=TRUE; ostnr := ostnr + 1; nr[v] := ostnr; low[v] := ostnr; for each u in L[v] do begin if u <> ojciec_v then begin if NOT visited[u] then begin DFS-Bridges(u, v); low[v] := min(low[v],low[u]); end else low[v] := min(low[v],nr[u]); end; if low[v] = nr[v] then krawędź v-ojciec_v jest mostem; end; end;
Żeby wyznaczyć wszystkie mosty wystarczy wywołać \( DFS-Bridges(s) \) dla dowolnego wierzchołka \( s \). Złożoność wyznaczania mostów jest asymptotycznie taka sama jak zwykłego przeszukiwania grafu, czyli \( O(n+m) \).
Ćwiczenia
Algorytmy tekstowe I
Algorytmy tekstowe mają decydujące znaczenie przy wyszukiwaniu informacji typu tekstowego, ten typ informacji jest szczególnie popularny w informatyce, np. w edytorach tekstowych i wyszukiwarkach internetowych. Tekst jest ciągiem symboli. Przyjmujemy, że jest on zadany tablicą \( x[1,\ldots,n] \), elementami której są symbole ze skończonego zbioru A (zwanego alfabetem). Liczba \( n=|x| \) jest długością (rozmiarem) tekstu. W większości naszych algorytmów jedyne operacje dopuszczalne na symbolach wejściowych to porównania dwóch symboli.
Algorytmy na tekstach wyróżniają się tym, że wykorzystują specyficzne, kombinatoryczne własności tekstów. Okresem tekstu \( x \) jest każda niezerowa liczba naturalna \( p \) taka, że \( x[i]=x[i+p] \), dla każdego \( i \), dla którego obie strony są zdefiniowane. Przez per(x) oznaczmy minimalny okres x.
Pojęciem dualnym do okresu jest prefikso-sufiks tekstu. Jest to najdłuższy właściwy (nie będący całym tekstem) prefiks tekstu x będący jednocześnie jego sufiksem. Oczywiste jest, że \( |x|-per(x) \) jest długością prefikso-sufiksu x. Jeśli \( per(x)=|x| \) to prefikso-sufiksem x jest słowo puste o długości zerowej.
Oznaczmy przez \( P[k] \) rozmiar prefikso-sufiksu \( x[1..k] \). Zatem \( per(x)=n-P[n] \), gdzie \( n=|x| \).
Przykład
Dla \( x\ =\ abababababb \) mamy:
\( P[1..11]\ =\ [0,\ 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 0]. \)
Wartość \( P[0] \) jest wartością sztuczną (przyjmiemy, że \( P[0]=-1 \)).
Wprowadzimy również tablicę ‘’'silnych prefikso-sufiksów dla wzorca \( x[1..m] \): jeśli \( j < |x| \), to \( P'[j]=k \), gdzie \( k \) jest maksymalnym rozmiarem słowa będącego właściwym prefiksem i sufiksem \( x[1..j] \) i spełniającego dodatkowy warunek \( x[k+1]\ne x[j+1] \) dla \( j < n \).
Jeśli takiego k nie ma, to przyjmujemy \( P'[j]=-1 \).
Przyjmujemy ponadto, że \( P'[m]=P[m] \).
Wartości tablicy P' mogą być znacznie mniejsze niż wartości tablicy P.
Przykład
Dla \( x\ =\ abaab \) mamy:
\( P[0..5]\ =\ [-1,\ 0,\ 0,\ 1,\ 1,\ 2\ ];\ \ P'[0..5]\ =\ [-1,\ 0,\ -1,\ 1,\ 0,\ 2\ ]. \)
Obliczanie tablicy Prefikso-Sufiksów
Przedstawimy jeden z możliwych algorytmów liniowych obliczania tablicy P. Jest to iteracyjna wersja algorytmu rekurencyjnego, który moglibyśmy otrzymać korzystając z faktu:
Jeśli \( x[j]=x[t+1] \) oraz \( t=P[j-1] \), to \( P[j]= t+1 \)
W algorytmie obliczania \( P[j] \) korzystamy z wartości \( P[k] \), dla \( k < j \).
Algorytm Prefikso-Sufiksy
P[0]:=-1; t:=-1; for j:=1 to m do begin while t=> 0 and x[t+1] <> x[j] do t:=P[t]; t:=t+1; P[j]:=t; end;
Złożoność liniowa wynika stąd, że w każdej iteracji zwiększamy wartość t co najwyżej o jeden, a wykonanie każdej operacji \( t:=P[t] \) zmniejsza wartość t co najmniej o jeden. Proste zastosowanie zasady magazynu (lub potencjału) implikuje, że operacji \( t:=P[t] \) wykonujemy co najwyżej n. Dowód poprawności pozostawiamy jako ćwiczenie.
Minimalne słowo pokrywające
Pokażemy pewne proste zastosowanie tablic prefikso-sufiksów. Słowem pokrywającym tekst x jest każdy taki tekst y, którego wystąpienia w x pokrywają cały tekst x. Na przykład słowo y=aba pokrywa tekst x=ababaaba, natomiast nie pokrywa tekstu abaaababa. Zajmiemy się problemem: obliczyć w czasie liniowym długość najkrótszego słowa pokrywającego dany tekst x.
Niech \( S[i] \) będzie rozmiarem minimalnego słowa pokrywającego tekst \( x[1..i] \).
Następujący algorytm oblicza długość minimalnego słowa pokrywającego tekstu x. Algorytm jest efektywny ponieważ liczy dodatkową tablicę Zakres. W \( i \)-tej iteracji algorytmu pamiętany jest znany dotychczas zakres każdego minimalnego słowa pokrywającego.
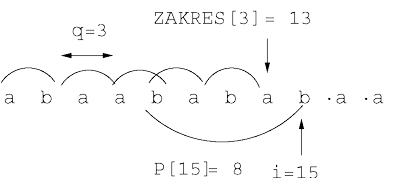
Rysunek 1: \( i \)-ta iteracja algorytmu dla \( i=15 \) oraz słowa \( x\ =\ abaabababaababa\ldots \). Tuż przed rozpoczęciem tej iteracji mamy \( P[i]=8 \), \( S[8]=2,\ Zakres[3]=13 \). Zatem spełniony jest warunek \( i-Zakres[S[P[i]] \le S[P[i]] \). Po zakończeniu \( i \)-tej iteracji mamy \( S[15]=3,Zakres[3]=15 \).
Algorytm Rozmiar-Minimalnego-Pokrycia
for i:=2 to n do begin Zakres [i]=i; S [i]=i; end; for i:=2 to n do if P [i]>0 and i-Zakres[S[P[i]]] <= S[P[i]] then begin S[i] :=S[P[i]]; Zakres[S[P[i]] :=i end; return S[n];
Algorytmy Knutha-Morrisa-Pratta i Morrisa-Pratta
Przedstawimy klasyczne algorytmy Knutha-Morrisa-Pratta (w skrócie KMP) oraz Morrisa-Pratta (w skrócie MP) dla problemu string-matchingu: obliczyć w w tekście \( y \) wszystkie (lub pierwsze) wystąpienia danego tekstu \( x \), zwanego wzorcem.
Algorytmy MP i KMP różnią się jedynie tym że jeden używa tablicy P a drugi P'. Tablica P' jest bardziej skomplikowana, będziemy się zatem głównie koncentrować na algorytmie MP, poza wersją on-line (gdzie waśnie P' ma przewagę).
Oznaczmy \( m=|x|, n=|y| \), gdzie \( m\le n \).
Zaczniemy od obliczania jedynie pierwszego wystąpienia. Algorytm MP przegląda tekst y od lewej do prawej, sprawdzając, czy jest zgodność na pozycji \( j+1 \) we wzorcu x oraz na pozycji \( i+j+1 \) w tekście y. Jeśli jest niezgodność, to przesuwamy potencjalny początek (pozycja i) wystąpienia x w y. Zakładamy, że algorytm zwraca na końcu wartość false, jeśli nie zwróci wcześniej true.
Algorytm Algorytm MP
i:=0; j:=0; while i <= n-m do begin while j < m and x[j+1]=y[i+j+1] do j=j+1; if j=m then return (true); i:=i+j-P[j]; j:=max(0,P[j]) end;
Uwaga: Algorytm działa podobnie gdy zamiast prefikso-sufiksów użyjemy tablicy P' silnych prefisko-sufksów. Algorytm w całości jest wtedy bardziej skomplikowany ze względu na trudniejszy preprocessing (liczenie P' jest trudniejsze od P).
Algorytm MP z tablicą P' zamiast P nazywamy algorytmem Knutha-Morrisa-Pratta i oznaczamy przez KMP.
Operacją dominującą w algorytmach KMP i MP jest operacja porównania symboli: \( x[j+1]=y[i+j+1] \). Algorytmy KMP i MP wykonują co najwyżej 2n-m porównań symboli. Zauważmy, że dla danej pozycji w tekście y jest ona co najwyżej raz porównana z pewną pozycją we wzorcu w porównaniu pozytywnym (gdy symbole są równe). Jednocześnie każde negatywne porównanie powoduje przesunięcie pozycji \( i \) co najmniej o jeden, maksymalna wartość i wynosi n-m, zatem mamy takich porównań co najwyżej n-m, w sumie co najwyżej 2n-m porównań.
Poniższa animacja pokazuje przykładowe działanie algorytmu KMP.
Algorytm dla \( x=ab \), \( y=aa..a \) wykonuje 2n-2porównania, zatem 2n-m jest dolną i jednocześnie górną granicą na liczbę porównań w algorytmie.
Obserwacja. W wersji on-line algorytmu okaże się, że jest zdecydowana różnica między użyciem P' i P; to właśnie jest motywacją dla wprowadzenia silnych prefikso-sufiksów.
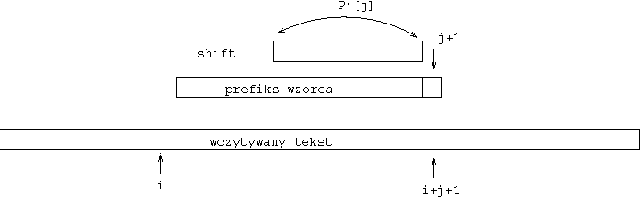
Rysunek 1: Jedna iteracja algorytmu KMP. Przesunięcie \( shift=j-P'[j] \) potencjalnego początku wystąpienia wzorca gdy \( x[j+1]\ne y[i+j+1] \).
Wersja on-line algorytmu KMP
Przedstawimy teraz wersję on-line algorytmu KMP. Wczytujemy kolejne symbole \( y \) i wypisujemy on-line (na bieżąco) odpowiedź:
- 0 - gdy dotychczas wczytany tekst nie zawiera x jako sufiks,
- 1 - jeśli zawiera
Algorytm On-Line-KMP
j:=0; repeat forever read(symbol); while j > -1 and x[j+1] <> symbol do j:=P'[j]; j:=j+1; if j=m then write(1); j := P'[m]; else write(0);
Oznaczmy przez delay(m) maksymalną liczbę kroków algorytmu On-Line-KMP między wczytaniem symbolu i daniem odpowiedzi. Przez delay'(m) oznaczmy podobną wielkość, w sytuacji gdy zamiast tablicy P' użyjemy P.
Przykład
Jeśli \( x=aaaa\dots a \) oraz \( y=a^{m-1}b \), to \( delay(m)=O(1) \), \( delay'(m)=\Theta(m) \).
Z lematu o okresowości wynika, że zachodzi następujący fakt:
\( delay(m)\ =\ \Theta(\log m) \)
Uzasadnienie pozostawiamy jako ćwiczenie.
Wersja ‘’real-time’’ algorytmu Morrisa-Pratta
Pokażemy teraz wersję algorytmu on-line, która działa w czasie rzeczywistym, tzn. czas reakcji między wczytaniem symbolu a daniem odpowiedzi jest O(1), niezależnie od rozmiaru alfabetu. Zamiast KMP użyjemy algorytm MP, którego preprocessing jest prostszy.
Algorytm zachowuje się podobnie jak algorytm On-Line-KMP; podstawowa różnica polega na tym, że algorytm wkłada do kolejki wczytane symbole, które jeszcze nie są przetworzone w sensie algorytmu MP. Rysunek pokazuje relacje tego algorytmu do algorytmu MP. Symbole z wejścia najpierw wędrują do kolejki.

Rysunek 2: Typowa konfiguracja w algorytmie real-time-MP.
Algorytm Real-Time-MP
inicjalizacja: j:=0; Kolejka := emptyset; repeat forever (niezmiennik: |Kolejka| \le (m-j)/2 ) read(symbol); insert(symbol,Kolejka); write(OUTPUT(Kolejka, j));
W celu skrócenia zapisów pojedynczych algorytmów rozbijamy algorytm na dwie części. Zasadnicza część jest zapisana jako osobna funkcja OUTPUT(Kolejka, j). Wynikiem funkcji jest 0 lub 1, w zależności od tego czy ostatnio wczytany symbol kończy wystąpienie wzorca x. Zmienne Kolejka, j są globalne. Oczywiste jest, że opóźnienie (czas reakcji) tego algorytmu jest O(1).
Algorytm OUTPUT(Kolejka, j)
output := 0; (początkowo Kolejka niepusta) repeat 2 times if Kolejka niepusta then if j=-1 then j := 0; delete(Kolejka); else if x[j+1] <> first(Kolejka) then j:=P[j]; else j:=j+1; delete(Kolejka); if j=m (w tym momencie Kolejka=emptyset) output := 1; j := P[m]; return(output);
Oszczędna wersja algorytmu Morrisa-Pratta
Algorytm MP wykonuje co najmniej 2n-m porównań symboli. Załóżmy, że są to operacje dominujące i spróbujmy zmniejszyć stały współczynnik 2 do \( \frac{3}{2} \). Na początku załóżmy, że \( x=ab \). Następujący algorytm znajduje wszystkie wystąpienia wzorca ‘’ab’’ w tekście y.
Algorytm Szukanie-ab
wzorcem jest ab i:=0; while i <= n-m do begin while y[i+2] <> b do i=i+1; if y[i+1]= a then wypisz-wystąpienie;i := i+2 end;
Algorytm MP dla wzorca ‘’ab’’ i tekstu ‘’aaa...aa’’ wykonywał 2n-2 porównań symboli, nowy algorytm jest lepszy. Algorytm Szukanie-ab wykonuje co najwyżej n porównań w tym przypadku. Dla tekstu ‘’abab’’ algorytm wykinuje n+1 porównań.
Pozostawiamy jako ćwiczenie policzenie maksymalnej liczby porównań dla tego algorytmu (wzorzec ‘’ab’’). Widać, że podstawowa idea to sprawdzanie najpierw pierwszego symbolu wzorca różnego od poprzednich.
Uogólnimy algorytm na dowolne wzorce. Niech x zawiera co najmniej dwa różne symbole, \( x=a^kb\alpha \), gdzie \( a\ne b \).Oznaczmy \( x'=b\alpha \) skrócony wzorzec
Przykład
\( x\ =\ aaaabaaaababa \), wtedy \( x'\ =\ baaaababa \), \( \alpha\ =\ aaaababa \).
Podamy nieformalny zarys działania oszczędniejszej wersji algorytmu MP, w której osobno szukamy x' i osobno części \( a^k \).
Niech \( MP' \) będzie taką wersją algorytmu MP, w której szukamy jedynie wzorca \( x' \), ale tablica \( P \) jest obliczona dla wzorca \( x \). Jeśli \( j>0 \) i \( shift\le k \), to wykonujemy przesunięcie potencjalnego początku i wzorca w y o k+1, gdzie \( shift=j-P[j] \).
Inaczej mówiąc, nie szukamy wszystkich wystąpień x', ale jedynie takich, które mają sens z punktu widzenia potencjalnego znalezienia na lewo ciągu \( a^k \).
Tak zmodyfikowany algorytm MP zastosujemy jako część algorytmu Oszczędny-MP. Graficzna ilustracja działania algorytmu Oszczędny-MP jest pokazana na rysunku.
Algorytm Oszczędny-MP
Znajdujemy wystąpienia x' w tekście \( y[k+1..m] \) algorytmem MP';
dla każdego wystąpienia x' sprawdzamy, czy na lewo jest wystąpienie \( a^k \);
nie sprawdzamy tych pozycji w y, których zgodność z pewną pozycją w x jest znana;
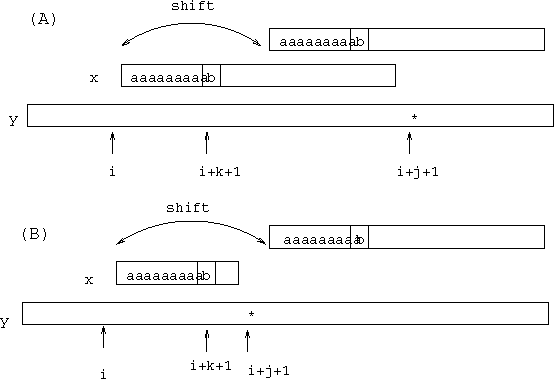
Rysunek 3:Typowa konfiguracja w algorytmie Oszczędny-MP.
Pozostawiamy jako ćwiczenie dokładny zapis algorytmu oraz dokładniejszy dowód tego, że algorytm Oszczędny-MP wykonuje co najwyżej \( \frac{3}{2}n \) porównan.
Ogólna idea jest przedstawiona na rysunku.

Rysunek 4: Ilustracja tego, że liczba operacji dodatkowych jest ograniczona przez \( \frac{1}{2}n \).
Niech zasadniczymi operacjami będą operacje sprawdzania pierwszego b na danej pozycji tekstu y oraz te sprawdzania symboli, które są z wynikiem pozytywnym. Takich operacji jest co najwyżej n. Pozostałe operacje to
(1) sprawdzanie w części \( \alpha \) z wynikiem negatywnym; wtedy przesuwamy wzorzec co najmniej o k,
(2) sprawdzanie części \( a^k \) na lewo od pozytywnego \( b \) (w kwadraciku na rysunku), na pozycjach, gdzie wcześniej było sprawdzanie negatywnego b. Wtedy odległość między pozytywnymi kolejnymi b jest co najmniej 2w, gdzie \( w\le k \) jest liczbą sprawdzanych na lewo symboli a. Zatem ‘’lokalnie’’ przesunięcie jest co najmniej dwukrotnie większe niż liczba dodatkowych operacji.
Suma przesunięć wzorca na tekście \( y \) wynosi co najwyżej n, sumaryczna liczba dodatkowych operacji jest więc co najwyżej \( \frac{1}{2}n \), a liczba wszystkich operacji nie przekracza \( \frac{3}{2}n \).
Obliczanie Tablicy Silnych Prefikso-Sufiksów
Algorytm liczenia silnych prefikso-sufiksów bazuje na następującej relacji między P a P':
\( (t=P[j]\ \textrm{oraz}\ x[t+1]\neq x[j+1])\ \Rightarrow\ P'[j]=t \)
\( (t=P[j],\ t\ge 0,\ \textrm{oraz}\ x[t+1]= x[j+1])\ \Rightarrow\ P'[j]=P'[t] \)
Nie musimy obliczać tablicy P; potrzebna jest jedynie ostatnia wartość \( t=P[j] \), którą obliczamy on-line.
Algorytm Silne-Prefikso-Sufiksy
P'[0]:=-1; t:=-1; for j:= 1 to m do while t => 0 and x[t+1] <> x[j] do t:=P'[t]; t:=t+1; if j=m or x[t+1] <> x[j+1] then P'[j]:=t else P'[j]:=P'[t];
Gdy weźmiemy \( x\ =\ aba^{m-2} \) to
\( P'[0]=-1 \), \( P'[1]=0 \), \( P'[2]=-1 \), oraz dla \( 3\leq j\leq m \) \( P'[j]=1 \).
Jest to jest pesymistyczny przypadek dla algorytmu Silne-Prefikso-Sufiksy, algorytm wykonuje wtedy \( 3m-5 \) porównań symboli.
Ćwiczenia
Algorytmy tekstowe II
Najważniejszymi strukturami danych związanymi z tekstami są te, które dotyczą efektywnej reprezentacji zbioru wszystkich podsłów tekstu. Przed wszystkim interesuje nas to, żeby taka reprezentacja przyspieszała wyszukiwanie słów, a jednocześnie żeby była konstruowalna w czasie liniowym albo prawie liniowym (z dokładnością do logarytmów).
Oznaczmy przez \( Subwords(x) \) wszystkie podsłowa tekstu \( x \), a wszystkie wystąpienia (początkowe pozycje) słowa \( z \) w słowie \( x \) oznaczmy przez \( Occ(z,x) \). (Oznaczenie \( Occ \) jest skrótem od ang. occurrences).
Chcemy znaleźć taką reprezentację zbioru \( Subwords(x) \), by można było łatwo odpowiedzieć na pytanie, czy \( z\in Subwords(x) \), co jest równoważne \( Occ(z,x)\ne \emptyset \), jak również rozwiązywać inne problemy tekstowe. Poza tym chcemy, by rozmiar tej reprezentacji był liniowy, podczas gdy rozmiar \( Subwords(x) \) może być kwadratowy. Spośród wielu dobrych reprezentacji najbardziej znanymi są tablice sufiksowe (oznaczane przez \( SUF \)), drzewa sufiksowe i grafy podsłów (nie rozważane w tym module).
Tablice i drzewa sufiksowe
Niech \( x=a_{1}a_{2}\dots a_{n} \) i niech \( x_{n+1}=\# \) będzie specjalnym znakiem leksykograficznie większym od każdego innego symbolu 9w przyszłości będziemy również używać \( x_{n+1}=\# \) jako najmniejszego symbolu).
Oznaczmy przez \( sufiks_{i}=a_{i}a_{i+1}\dots a_{n} \) sufiks tekstu x zaczynający się na pozycji i-tej.
Niech \( SUF[k] \) będzie pozycją, od której zaczyna się k-ty leksykograficznie sufiks x. Sufiks zaczynający się na pozycji \( (n+1) \)-szej nie jest brany pod uwagę.
Ciąg sufiksów posortowany leksykograficznie wygląda następująco:
\( sufix_{SUF[1]} < sufix_{SUF[2]} < sufix_{SUF[3]} < \ldots sufix_{SUF[n]} \)

Rysunek 1: Tablicą sufiksową tekstu \( x\ =\ babaabababba\# \) jest ciąg \( SUF\ =\ [4,\ 2,\ 5,\ 7,\ 9,\ 12,\ 3,\ 1,\ 6,\ 8,\ 11,\ 10] \)
Oznaczmy przez \( lcp[k] \) długość wspólnego prefiksu \( k \)-tego i następnego sufiksu w kolejności leksykograficznej. Na rysunku wartości najdłuższego wspólnego prefiksu między kolejnymi słowami są przedstawione jako zacienione segmenty. Odpowiadają one tablicy \( lcp\ =\ [1,\ 3,\ 4,\ 2,\ 1,\ 0,\ 2,\ 4,\ 3,\ 2,\ 1] \).
Tablica sufiksowa ma następująca ‘’sympatyczną’’ własność: Niech
\( min_{z}=\min\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \), \( max_{z}=\max\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \).
Wtedy \( Occ(z,x) \) jest przedziałem w tablicy sufiksowej od \( min_{z} \) do \( max_{z} \).
Drzewo sufiksowe jest drzewem, w którym każda ścieżka jest etykietowana kolejnymi symbolami pewnego sufiksu, oraz każdy sufiks \( x \) jest obecny w drzewie. Gdy dwie ścieżki się rozjeżdżają, tworzy się wierzchołek. Mówiąc bardziej formalnie, każdej krawędzi jest przypisane jako etykieta pewne podsłowo \( x \). Krawędzie wychodzące z tego samego węzła różnią się pierwszymi symbolami swoich etykiet (patrz rysunek).
Etykiety są kodowane przedziałami w tekście \( x \): para liczb \( [i,j] \) reprezentuje podsłowo \({a}_i a_{i +1_j}\) (zobacz prawe drzewo na rysunku). Dzięki temu reprezentacja ma rozmiar \( O(n) \). Wagą krawędzi jest długość odpowiadającego jej słowa.
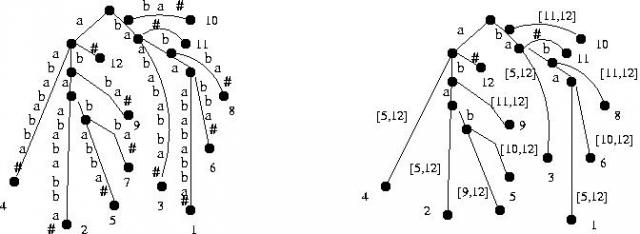
Rysunek 2: Drzewo sufiksowe dla tekstu \( x\ =\ babaabababba \). Na końcu jest dodany znak \( \# \). Końcowe węzły zawierają informację, gdzie zaczyna się sufiks, którym dochodzimy do danego węzła.
Obie reprezentacje pozwalają szybko rozwiązywać problem string-matchingu oraz mają rozmiar liniowy. Niech z będzie wzorcem o długości m, a \( x \) słowem długości n. Z reguły \( m < < n \).
Szukanie podsłów
Pokażemy, jak sprawdzać, czy \( z \) występuje w \( x \).
Używając drzewa sufiksowego (czas \( O(m) \))
Idziemy od korzenia w dół czytając kolejne symbole \( z \), czasami posuwamy się po wewnętrznej etykiecie pewnej krawędzi. Zbiór wystąpień odpowiada zbiorowi liści w poddrzewie węzła, do którego doszliśmy. Jeśli po drodze utknęliśmy i nie dało się dalej schodzić po drzewie, oznacza to, że \( z \notin Subwords(x) \)
Używając tablicy sufiksowej (czas \( O(m \log n) \))
Możemy sprawdzić, czy \( z \) jest prefiksem \( i \)-tego sufiksu w czasie \( O(m) \). Korzystając z tego, wykonujemy rodzaj binarnego szukania. W ten sposób znajdujemy pierwszy sufiks, którego prefiksem jest z. Jeśli jest taki sufiks, to \( z \in Subwords(x) \). W przeciwnym wypadku z nie jest podsłowem x.
Podobnie znajdujemy ostatni sufiks. Zbiór wystąpień odpowiada przedziałowi w tablicy \( SUF \) między obliczonymi pierwszym i ostatnim sufiksem zaczynającym się od z.
Wyznaczanie liczby podsłów
Pokażemy, jak znaleźć liczbę podsłów słowa \( x \) przy pomocy tablicy sufiksowej lub drzewa sufiksowego. Końcowego markera \( \# \) nie traktujemy jako części słowa \( x \). Liczba podsłów jest równa \( |Subwords(x)| \). Jeśli wszystkie symbole słowa są różne to \( |Subwords(x)|={n \choose{2}} \).
Używając drzewa sufiksowego, czas \( O(n) \)
Sumujemy wagi krawędzi drzewa.
Używając tablicy sufiksowej, czas \( O( n) \)
Niech \( SUMA(lcp) \) będzie sumą elementów tablicy \( lcp \). Liczbę podsłów obliczamy jako
\( {n+1\choose{2}}-SUMA(lcp) \)
Pozostawiamy jako ćwiczenie uzasadnienie tego, że liczba podsłów jest poprawnie obliczona (korzystając z drzewa sufisowego lub z tablicy sufiksowej).
Przykład
Dla przykładowego tekstu \( x\ = \) mamy \( |Subwords(x)|=55 \). Proponujemy to wyliczyć z tablicy sufiksowej i drzewa sufiksowego dla\( x \), danego na rysunku. Suma elementów tablicy \( lcp \) wynosi 23. Liczba podsłów to: \( 78-23\ =\ 55 \) Podobnie jak tablicę sufiksową możemy zdefiniować tablicę \( ROT \) odpowiadającą posortowanemu ciągowi wszystkich cyklicznych przesunięć słowa \( x \) (rotacji \( x \)).
Pozostawiamy jako ćwiczenie znalezienie liniowego algorytmu obliczania tablicy \( ROT \), przy założeniu, że mamy liniowy algorytm obliczania tablicy sufiksowej.
Dygresja. Ciekawą klasę słów, dla których tablice \( SUF,\ ROT \) są szczególnie interesujące, stanowią słowa Fibonacciego \( F_n \). W tym szczególnym przypadku załóżmy, że pozycje numerujemy od zera. Dla każdego \( n \) tablica \( ROT \) jest postępem arytmetycznym (modulo długość słowa). Natomiast tablica \( SUF \) jest postępem arytmetycznym, gdy \( n \) jest parzyste.
Słowa Fibonacciego definiujemy następująco:\( F_0=a,\ F_1=ab,\ F_{n+1}\ =\ F_n\cdot F_{n-1} \) Na przykład: \( F_3\ =\ abaab,\ F_4\ =\ abaababa,\ F_5\ =\ abaababaabaab. \) Oznaczmy przez \( SUF_n \) tablicę \( SUF \) dla słowa Fibonacciego \( F_n \); wtedy:
\( SUF_4\ =\ [7\;2\;5\;0\;3\;6\;1\;4], \) \(SUF_5\ =\ [10\;7\;2\;11\;8\;5\;0\;3\;12\;9\;6\;1\;4].\)
Pozostawiamy jako ćwiczenie znalezienie wzoru na \( |Subwords(F_n)| \).
Drzewa sufiksowe =>tablice sufiksowe
W celu znalezienia początkowych pozycji sufiksów w porządku leksykograficznym przechodzimy drzewo sufiksowe metodą DFS, zakładając, że dla każdego węzła lista jego synów jest w kolejności leksykograficznej etykiet krawędzi prowadzących do synów. Wystarczy sprawdzać pierwsze symbole tych etykiet.
Załóżmy, że w liściach mamy początki sufiksów, które do nich prowadzą.
Kolejność odwiedzania liści w naszym przejściu metodą DFS automatycznie generuje elementy tablicy sufiksowej.
Tablice sufiksowe =>drzewa sufiksowe
Pokażemy konstruktywnie następujący istotny fakt:
jeśli znamy tablicę sufiksową i tablicę \( lcp \), to drzewo sufiksowe dla danego tekstu możemy łatwo skonstruować w czasie liniowym.
Przypuśćmy, że \( SUF\ =\ [i_1,i_2,\ldots,i_n] \), a więc:
\( sufiks_{i_1} < sufiks_{i_2} < sufiks_{i_3} < \ldots sufiks_{i_n}. \)
Algorytm Drzewo-Sufiksowe
T := drzewo reprezentujące sufiks(i_1) (jedna krawędź); for k:=2 to n do wstaw nową ścieżkę o sumarycznej etykiecie sufiks(i_k) do T;
Rysunek 3: Wstawianie kolejnego sufiksu \( sufiks_{i_k} \) do drzewa sufiksowego, przed włożeniem wszystkie krawędzie ścieżki roboczej od \( u \) do korzenia są skierowane w lewo.
Opiszemy w jaki sposób wstawiamy kolejny sufiks \( \beta \) do drzewa. Operacja ta jest zilustrowana na rysunku. Załóżmy, że w każdym węźle drzewa trzymamy długość tekstu, który ten węzeł reprezentuje (jako pełna etykieta od korzenia do węzła).
Niech \( \alpha \) będzie poprzednio wstawionym sufiksem, a \( u \) ostatnio utworzonym liściem.
Wtedy wstawienie \( \beta \) polega na znalezieniu maksymalnego wspólnego prefiksu \( \gamma_1 \) tekstów \( \alpha \), \( \beta \). Niech \( \beta=\gamma_1\cdot \gamma_2 \). Znajdujemy węzeł \( v \) odpowiadający ścieżce od korzenia etykietowanej \( \gamma_1 \).
Kluczowym pomyslem algorytmicznym jest tutaj to, że węzła \( v \) szukamy nie od korzenia, ale od ostatnio utworzonego liścia \( u \). Jeśli takiego węzła \( v \) nie ma (jest wewnątrz krawędzi) to go tworzymy. Następnie tworzymy nowy liść \( w \) odpowiadający sufiksowi \( \beta \), oraz krawędź \( (v,w) \) etykietowaną \( \gamma_2 \).
Z tablicy \( lcp \) odczytujemy długość \( \gamma_1 \).
W celu obliczenia \( v \) posuwamy się ścieżką od \( u \) w górę drzewa, aż znajdziemy węzeł oddalony od korzenia o \( |\gamma| \).
Przechodząc drzewo posuwamy się po węzłach drzewa, przeskakując (w czasie stalym) potencjalnie długie teksty na krawędziach.
Koszt operacji wstawienia jest proporcjonalny do sumy: jeden plus zmniejszenie głębokości nowego liścia w stosunku do starego. Suma tych zmniejszeń jest liniowa. \( \gamma_1 \) jest najdłuższym wspólnym prefiksem słów \( sufiks_{i_{k-1}} \) i \( sufiks_{i_k} \). Kluczowe znaczenie w operacji ma znajomość wartości \( |\gamma_1|= lcp[k-1] \). Wiemy kiedy się zatrzymać idąc do góry od węzła \( u \) w kierunku korzenia.
Lokalnie wykonana praca w jednej iteracji jest zamortyzowana zmniejszeniem się głębokości aktualnego liścia w stosunku do poprzedniego. W sumie praca jest liniowa.
Historia algorytmu jest pokazana dla przykładowego tekstu na rysunkach.

Rysunek 4: Pierwsze 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).
Rysunek 5: Ostatnie 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).
Obliczanie tablicy
Niech \( rank(i) \) będzie pozycją \( sufiks_i \) w porządku leksykograficznym. W naszym przykładowym słowie mamy:
\( rank\ =\ [8,\ 2,\ 7,\ 1,\ 3,\ 9,\ 4,\ 10,\ 5,\ 12,\ 1,\ 6] \)
Niech \( lcp'[k]\ =\ lcp[rank[k]-1] \).
Załóżmy, dla uproszczenia, że \( lcp[0]=0 \) oraz że tekst kończy się specjalnym symbolem Obliczamy tablice \( lcp',\ lcp \) następująco:
Algorytm Oblicz-lcp
for k:=1 to n do oblicz lcp'[k] korzystając z faktu, że lcp'[k] => lcp'[k-1]-1; // koszt iteracji O(lcp'[k]-lcp'[k-1]+const) for k:=1 to n do lcp[rank[k]-1] := lcp'[k] \)
Można to zapisać w języku C++ następująco
Algorytm Oblicz-lcp1
for (int i=1; i < =n; i++) R[SUF[i]] = i; l = 0; for (int i=1; i < =n; i++) if (R[i] >; 1) { while (x[l+i] == x[l+SUF[R[i]-1]]); lcp[R[i]-1] = l;} l = max(0, l-1);}
Pozostawiamy jako ćwiczenie dowód tego, że
\( lcp'[k]\ge lcp'[k-1]-1 \).
Jeśli \( lcp'[k-1]-1=t \), to \( lcp'[k] \) obliczamy sprawdzając symbol po symbolu (od lewej do prawej) zgodność prefiksów odpowiednich słów startując od pozycji \( t \). W ten sposób sumaryczny koszt jest liniowy. W każdej iteracji cofamy się o jeden, a potem idziemy do przodu (sprawdzając kolejne symbole). Jest to analiza typu jeden krok do tyłu i kilka do przodu. Liczba iteracji jest liniowa, więc liczba kroków do tyłu też. Ponieważ odległość do celu jest liniowa, to suma kroków też jest liniowa.
Słownik podsłów bazowych i konstrukcja tablicy sufiksowej w czasie O(n log n)
Opiszemy uproszczoną wersję algorytmu Karpa-Millera-Rosenberga (w skrócie algorytmu KMR) rozwiązywania problemów tekstowych metodą słownika podsłów bazowych. Ustalmy pewnie tekst \( x \) długości \( n \).
Zakładamy w tej sekcji, że dodatkowym symbolem jest \( x_{n+1}=\# \), leksykograficznie najmniejszy symbol. Przez segment \( k \)-bazowy rozumiemy segment tekstu \( x[i..i+2^k-1] \) długości \( 2^k \) lub kończący się na \( x_{n+1} \).
Teoretycznie możemy założyć, że po symbolu \( \# \) mamy bardzo dużo takich symboli na prawo i każdy segment startujący w\( x[1..n] \) ma dokładnie długość \( 2^k \).
Słownik podsłów bazowych (w skrócie DBF(x), od ang. dictionary of basic factors) składa się z \( \log n \) tablic
\( NAZWA_0 \), \( NAZWA_1 \), \( NAZWA_2 \),\( \ldots NAZWA_{\log n} \).
Zakładamy, że \( NAZWA_k[i] \) jest pozycją słowa \( x[i..i+2^k-1] \) na posortowanej liście (bez powtórzeń) wszystkich podsłów długości \( 2^k \) słowa \( x \). Jeśli długość wystaje poza koniec \( x \) to przyjmujemy że są tam (wirtualnie) same symbole \( \# \). Poniżej przedstawiamy przykład słownika podsłów bazowych \( DBF(abaabbaa) \).

Algorytm liczenia tablic Nazwa jest bardzo prosty. Załóżmy od razu, że symbole są ponumerowane leksykograficznie. Wtedy \( NAZWA_0 \) jest zasadniczo równa tekstowi \( x \).
Rysunek6: Słowo rozmiaru \( 2^{k+1} \) otrzymuje najpierw nazwę-kompozycję: kombinacją nazw (będących liczbami naturalnymi z przedziału \( [1..n] \)) dwóch podsłów długości \( 2^k \) .
Opis jednej iteracji \( (transformacja: NAZWA_k\ =>\ NAZWA_{k+1} \))
Dla każdego \( i \) tworzymy nazwę-kompozycję slowa \( x[i..i+2^{k+1}-1] \) jako \( NAZWA_k[i], NAZWA_k[i+2^k] \) Każda taka kompozycja jest parą liczb naturalnych. Sortujemy te pary za pomocą algorytmu radix-sort i w ten sposób otrzymujemy tablicę, która koduje (w porządku leksykograficznym) każdą parę liczbą naturalną (pozycją w porządku leksykograficznym). Wartością \( NAZWA_{k+1}[i] \) jest kod pary \( (NAZWA_k[i],NAZWA_k[i+2^k]) \).
Zauważmy, że tablica sufiksowa odpowiada tablicy \( NAZWA_{\lceil \log n \rceil} \). Możemy to podsumować następująco:
1. słownik DBF(x) możemy skonstruować w czasie \( O(n \log n) \)i pamięci \( O(n \log n) \) (jest to również rozmiar słownika).
2. Tablicę sufiksową możemy otrzymać,stosując algorytm KMR, w czasie \( O(n \log n) \) i pamięci \( O(n) \). (Potrzebujemy pamiętać jedynie ostatnie dwie tablice w każdej iteracji.)
Konstrukcja tablicy SUF w czasie O(n): algorytm KS
Opiszemy teraz błyskotliwy algorytm Karkkainena-Sandersa ( w skrócie KS) będący zoptymalizowaną wersją algorytmu KMR liczenia tablicy sufiksowej. Zauważmy, że algorytm KMR oblicza znacznie więcej niż tablica sufiksowa, ponieważ konstruuje słownik podsłów bazowych wielkości \( n \log n \) (mający liczne inne zastosowania, ale jako całość być może niepotrzebny przy liczeniu tablicy sufiksowej)
Główną częścią algorytmu KS jest obliczanie częściowej tablicy sufiksowej w sposób rekurencyjny. Rozbijmy zbiór pozycji [1..n] tekstu \( x \) na dwa zbiory N, M :
Zbiór N składa się z co trzeciej pozycji, a M jest zbiorem pozostałych pozycji.
N = {3,6,9,12,15,....}, M = {1,2,4,5,7,8,10,11,...}
Przez \( SUF[M] \), oznaczmy tablicę sufiksową dla pozycji ze zbioru \( M \), podobnie zdefiniujmy \( SUF[N] \).
\( SUF[M] \) daje posortowany ciąg sufiksów zaczynających się na pozycjach ze zbioru \( M \).
Dla początkowego przykładowego tekstu \( x\ =\ babaabababba\# \) mamy
\( M\ =\ \{1,2,4,5,7,8,10,11\}\ \ \ \ \ N\ =\ \{3,6,9,12\} \)
\( SUF[M]\ =\ [4,\ 2,\ 5,\ 7, \ 1, \ 8,\ 11,\ 10]\ \ \ \ SUF[N]\ =\ [ 9,\ 12,\ 3,\ 6,] \)
Sprowadzenie obliczania \( SUF[M] \) do obliczania tablicy sufiksowej rozmiaru \( \frac{2}{3}n \)
Posortujmy leksykograficznie wszystkie podsłowa długości 3 w słowie \( x \) korzystając z radix-sort. Każdemu takiemu słowu przyporządkujmy nazwę będącą jego pozycją w posortowanym leksykograficznie ciągu, oznaczmy \( kod(z) \) otrzymaną nazwę podsłowa długości 3. Zakładamy, że \( x \) kończy się dodatkowo dwoma symbolami \( \# \), ale rozważamy tylko podsłowa zaczynające się w \( x \). Dla uproszczenia załóżmy, że 3 jest dzielnikiem n.
Tworzymy nowe słowo \( compress(x) \) w następujący sposób:
\( y2\ =\ kod(a_2a_3a_4)\cdot kod(a_5a_6a_7) \ldots kod(a_{n-1}a_{n}a_{n+1}) \)
\( compress(x) \ =\ y1 \& \ y2\ \) ; gdzie \( \& \) jest nowym maksymalnym symbolem
Przykład. Weźmy początkowy przykład \( x\ = \ babaababbba\# \), gdzie \( \# \)jest większe niże a,b. Mamy
\( aab \prec aba\prec bab \prec ba\# \prec bba \), Zatem kody tych trójek są kolejno \( 1,\ 2,\ 3,\ 4, \ 5 \).
Oznaczmy\( kod(z)= < z> \). Wtedy
\( y1\ =\ < bab> < aab> < aba> < bba>\ =\ 3\ 1\ 2\ 5 ; \)
\( y2\ =\ < aba> < aba> < bab> < ba\#>\ =\ 2\ 2\ 3\ 4 \)
\( compress(x)\ =\ =\ 3\ 1\ 2\ 5 \ \& \ 2\ 2\ 3\ 4\ \),
Jeśli mamy tablicę sufiksową dla słowa \( compress(x) \), można łatwo obliczyć \( SUF[M] \) w czasie liniowym. Pozostawiamy to jako ćwiczenie.
Algorytm \( {\Large KS} \) (Karkkainen-Sanders)
x':= compress(x); obliczamy tablicę sufiksową dla x' rekurencyjnie; obliczamy SUF[M] w czasie liniowym, znając tablicę sufiksową dla x'; obliczamy SUF[N] w czasie liniowym (bez rekursji), znając SUF[M]; scalamy posortowane ciągi SUF[M], SUF[N] w tablicę sufiksową dla całego słowa x
Krok 1 algorytmu sprowadza się do radix-sortu, podobnie jak w algorytmie KMR. Kroki 3,4 są proste i ich implementację pozostawiamy czytelnikowi jako ćwiczenie.
Najważniejszy jest krok scalania. Mamy dwie posortowane listy sufiksów i trzeba je scalić w jedną posortowaną listę. Zasadniczym problemem jest implementacja operacji porównania leksykograficznego dwóch (długich) sufiksów w czasie stałym. Jeśli oba sufiksy są typu \( M \) lub oba są typu \( N \), to porównanie jest w czasie stałym, bo mamy posortowane listy takich sufiksów.
Pokażemy na przykładzie kluczową operację porównania sufiksu typu M z sufiksem typu N w czasie stałym.
Przykład
Nierówność \( sufiks_2 < sufiks_{12} \) jest równoważna temu, że zachodzi co najmniej jeden z warunków:
1. \( (a_2 < a_{12}) \)
2. \( \ (a_2=a_{12}, a_3 < a_{13}) \)
3. \( (a_2=a_{12}, a_3=a_{13}, sufiks_4 < sufiks_{14}) \)
Jednakże \( 4,14\in M \), zatem \( sufiks_4 \) i \( sufiks_{14} \), są typu M i można je porównać w czasie stałym.
Niech \( T(n) \) będzie czasem działania algorytmu KS. Zachodzi
\( T(n) \ =\ T(\lceil \frac{2}{3}\cdot n \rceil) + O(n) \)
Rozwiązaniem jest \( T(n)=O(n) \). Mamy więc liniowy algorytm liczenia tablicy sufiksowej. Daje to również liniowy algorytm konstrukcji drzewa sufiksowego.
Istnieje kilka interesujących algorytmów, które konstruują drzewo sufiksowe w czasie liniowym, bez korzystania z tablicy sufiksowej (algorytmy Weinera, McCreighta, Ukkonena). W algorytmach tych współczynnik przy złożoności liniowej wynosi \( \log |A| \), gdzie A jest alfabetem.
Ćwiczenia
NP-zupełność
Ten wykład ma charakter wyłącznie informacyjny i nieformalny. Jest poświęcony klasie bardzo użytecznych problemów, dla których nieznane są algorytmy wielomianowe i nie wiadomo, czy takie algorytmy w ogóle istnieją. Rozpoczniemy od podania algorytmu rozwiązującego następujące zadanie:
Dane: Formuła boolowska \( \phi \) w postaci koniunkcji zmiennych lub ich negacji.
Pytanie: Czy formuła \( \phi \) jest spełnialna, tzn. czy istnieje takie wartościowanie zmiennych, dla którego formuła \( \phi \) przyjmuje wartość 1 (Prawda)?
Przykład: Formuła \( x_1\wedge \neg x_2 \wedge x_3 \wedge x_1 \) przyjmuje wartość 1 tylko dla wartościowania \( x_1 = 1, x_2 = 0, x_3 = 1 \).
Łatwo zauważyć, że formuła \( \phi \) (w postaci z powyższego zadania) jest spełnialna wtedy i tylko wtedy, gdy nie występują w niej jednocześnie zmienna i jej negacja. Ta obserwacja pozwala sformułować bardzo prosty algorytm rozwiązujący nasze zadanie:
Dla każdej zmiennej x z phi sprawdź, czy w phi występują jednocześnie x i neg x. Jeśli taka zmienna nie istnieje, to phi jest spełnialna, w przeciwnym razie phi nie jest spełnialna.
Sprawny programista bardzo szybo zaprogramuje powyższy algorytm. Musimy tylko sprecyzować, co oznacza sformułowanie dana jest formuła boolowska. Innymi słowy musimy podać rozsądny sposób kodowania formuł. Jednym z możliwych może być następujący sposób kodowania: przyjmujemy, że zmienne występujące w formule są ponumerowane kolejno 1,2,\( \ldots \), formułę kodujemy jako ciąg liczb poddzielanych średnikami. Pierwszą liczbą w ciągu jest liczba \( n \) równa liczbie literałów, czyli wystąpień w formule zmiennych lub ich negacji. W formule z przykładu mamy cztery literały. Po liczbie literałów występuje \( n \) liczb ze zbioru \( \{-n,-(n-1),\ldots,-1,1,2,\ldots, n\} \). Jeśli \( i \)-tym literałem jest zmienna \( x_k \), to za \( i \)-tą spośród tych liczb bierzemy \( k \), jeśli zaś \( i \)-tym literałem jest \( \neg x_k \), to \( i \)-tą liczbą będzie \( -k \).
Kodem przykładowej formuły jest \( 4;1;-2;3;1 \)
W każdym rozsądnym kodowaniu przyjmuje się ponadto, że do kodowania liczb stosujemy dowolny zapis o podstawie co najmniej 2 (najczęściej właśnie o podstawie 2). Zauważmy, że przy takim kodowaniu długość kodu formuły wynosi co najwyżej \( cn\log n \) dla pewnej stałej \( c \). Długość kodu danych będziemy nazywali rozmiarem zadania. W przedstawionym powyżej algorytmie literały są porównywane między sobą. Nawet przy bardzo naiwnej implementacji tego algorytmu liczba takich porównań wyniesie co najwyżej \( n^2 \). Jeśli uwzględnimy, że porównywanie kodów dwóch literałów wymaga \( \log n \) porównań bitów, to liczbę wszystkich operacji da się ograniczyć przez \( n^2\log n \), a idąc dalej możemy powiedzieć, że liczbę operacji wykonywanych przez algorytm da się ograniczyć przez \( r^k \), gdzie \( r \) jest rozmiarem danych, a \( k \) stałą całkowitą większą od 0. (W naszym przypadku za \( k \) można wziąć 3.) W takim przypadku mówimy, że algorytm rozwiązuje zadanie w czasie wielomianowym.
Klasą P nazywamy zbiór tych zadań algorytmicznych, dla których istnieją algorytmy rozwiązujące je w czasie wielomianowym.
Utrudnijmy teraz nasze wyjściowe zadanie.
Powiemy, że formuła boolowska jest w postaci koniunkcyjno-normalnej (z ang. w postaci CNF), jeśli jest koniunkcją formuł (klauzul), z których każda jest alternatywą zmiennych lub ich negacji, być może zdegenerowaną do jednego literału. Formuła jest w postaci \( k \)-CNF, jeśli w każdej klauzuli występuje co najwyżej \( k \) literałów.
Ćwiczenie 1
Pokaż, że każdą formułę boolowską można przekształcić do równoważnej (ze względu na spełnialność) formuły w postaci 3-CNF o długości tylko wielomianowo większej od długości formuły wyjściowej.
Oto przykład formuły w postaci 2-CNF: \( (x_1\vee \neg x_2)\wedge(\neg x_1 \vee x_3)\wedge (\neg x_2 \vee \neg x_3) \).
Pokazaliśmy, że zadanie spełnialności formuł w postaci 1-CNF można rozwiązać w czasie wielomianowym. To stwierdzenie pozostaje w mocy także dla formuł w postaci 2-CNF.
Ćwiczenie 2
Zaprojektuj algorytm, który rozwiązuje to zadanie w czasie liniowym, tj. w czasie proporcjonalnym do długości formuły.
Sytuacja zmienia się diametralnie, gdy weźmiemy \( k \geq 3 \). Nie są znane algorytmy, które rozwiązywałyby to zadanie w czasie wielomianowym, nawet dla wielomianów bardzo dużego stopnia, np. 1000. Najlepsze znane algorytmy wymagają czasu co najmniej \( c^r \), gdzie \( c \) jest stałą większą od 1, a \( r \) jest długością kodu formuły. O takich algorytmach mówimy, że działają w czasie wykładniczym. Z praktycznego punktu widzenia oznacza to, że nawet na współczesnych komputerach takie algorytmy mają szanse dać wynik w rozsądnym czasie tylko dla danych o bardzo małych rozmiarach. Można zaryzykować stwierdzenie, że jeżeli dla zadania algorytmicznego znamy tylko rozwiązania działające w czasie wykładniczym, to zadanie to jest praktycznie algorytmicznie nierozwiązywalne.
Jaką interesującą własność ma jeszcze zadanie spełnialności formuł boolowskich? Gdyby ktoś chciał przekonać nas, że dana formuła jest spełnialna wystarczy, żeby podał odpowiednie wartościowanie zmiennych. Zauważmy, że rozmiar takiego wartościowania nie jest większy od długości formuły. Mając takie wartościowanie, w czasie wielomianowym można obliczyć odpowiadającą mu wartość logiczną formuły. Jeśli tą wartością jest 1 (Prawda), to formuła jest spełnialna. Wartościowanie, dla którego formuła jest spełnialna, nazywamy świadectwem spełnialności. Algorytm, który sprawdza spełnialność formuły dla danego wartościowania, nazywamy algorytmem weryfikacji. Innymi słowy, algorytmu weryfikacji można użyć do wykazania w czasie wielomianowym, że dana formuła jest spełnialna, jeżeli tylko istnieje i dane jest odpowiednie świadectwo.
Klasą NP nazywamy zbiór tych zadań algorytmicznych, które można weryfikować w czasie wielomianowym. Skróty P i NP pochodzą z angielskiego, odpowiednio, polynomial time i nondeterministic polynomial time. Niedeterminizm dotyczy pochodzenia świadectwa, ponieważ nie żąda się podania metody jego konstrukcji.
Łatwo zauważyć, że każde zadanie z P należy do NP, ponieważ zadanie takie można zawsze rozwiązać w czasie wielomianowym i do weryfikacji nie potrzebujemy żadnego świadectwa. Zatem \( P \subseteq NP \), a problem P=NP, to problem
Czy \( P \ne NP \)?
Do klasy NP należą tysiące ważnych, praktycznych zadań algorytmicznych, o których nie wiadomo, czy należą do P. Przyjrzyjmy się jeszcze jednemu takiemu zadaniu.
Dane: Nieskierowany graf \( G=(V,E) \) oraz liczba naturalna \( k \).
Pytanie: Czy w \( G \) istnieje klika rozmiaru \( k \), tzn. czy w \( G \) istnieje podgraf \( k \)-wierzchołkowy, w którym każda para różnych wierzchołków jest połączona krawędzią?
Problem kliki z pewnością należy do NP. Dla danego \( k \)-elementowego podzbioru wierzchołków (świadectwa) można łatwo w czasie wielomianowym, zależnym tylko od rozmiaru grafu, sprawdzić, czy wierzchołki te tworzą klikę. Pokażemy teraz, że gdybyśmy w czasie wielomianowym potrafili rozwiązać zadania spełnialności, to także w czasie wielomianowym można by rozwiązać zadanie kliki. W tym celu zadanie kliki sprowadzimy do zadania formuł boolowskich.
Dla każdego wierzchołka \( v\in V \) wprowadzamy \( k \) zmiennych boolowskich \( x_1^v \), \( x_2^v \),\( \ldots \), \( x_k^v \). Zmienna \( x_i^v \) intuicyjnie mówi, że wierzchołek \( v \) jest \( i \)-tym wierzchołkiem w poszukiwanej klice. Skonstruujemy formułę \( \phi \), która jest koniunkcją trzech formuł \( \phi_1, \phi_2 \) i \( \phi_3 \). Oto intuicyjne znaczenie i formalne definicje tych formuł:
- \( \phi_1 = \) dla każdego \( i \), \( 1\leq i \leq k \), istnieje co najmniej jeden wierzchołek \( u \in V \), który jest \( i \)-tym wierzchołkiem w klice.
- \( \phi_1 = \bigwedge_{i = 1}^k(\bigvee_{v\in V} x_i^v). \)
- \( \phi_2 = \) dla każdego \( i \), \( 1\leq i \leq k \), żadne dwa wierzchołki nie są jednocześnie \( i \)-tymi wierzchołkami w klice.
- \( \phi_2 = \bigwedge_{i=1}^k\bigwedge_{u,v\in V, u\ne v} (\neg x_i^u \vee \neg x_i^v). \)
- Dla każdej pary \( u, v \), jeśli \( u \)-\( v \) nie jest krawędzią w grafie, to \( u \) i \( v \) nie są jednocześnie w klice.
- \( \phi_3 = \bigwedge_{u\mbox{--}v\not \in E} \bigwedge_{1\leq i,j \leq k} (\neg x_i^u \vee \neg x_j^v). \)
Pozostawiamy czytelnikowi wykazanie, że formuła \( \phi \) jest spełnialna wtedy i tylko wtedy, gdy w grafie \( G \) istnieje klika rozmiaru \( k \). Łatwo zauważyć, że rozmiar powstałej formuły jest wielomianowo zależny od rozmiaru grafu, a samą formułę można skonstruować w czasie wielomianowym. W tym przypadku mówimy, że zadanie kliki jest redukowalne w czasie wielomianowym do zadania spełnialności. W 1971 roku R. Cook udowodnił, że każde zadanie z NP można w czasie wielomianowym zredukować do zadania spełnialności pewnej formuły boolowskiej. Zadanie, które należy do klasy NP i do którego można zredukować w czasie wielomianowym każde inne zadanie z NP nazywamy zadaniem NP-zupełnym. W tym sensie zadanie spełnialności jest NP-zupełne. Pozostawiamy czytelnikom pokazanie, że zadanie kliki jest też NP-zupełne. W tym celu wystarczy pokazać wielomianową redukcję zadania spełnialności do zadania kliki. Rozwiązanie dowolnego zadania NP-zupełnego w czasie wielomianowym pozwalałoby rozwiązywać w czasie wielomianowym każde zadanie z NP.
Pojęcie klasy P wprowadzili niezależnie Cobham i Edmonds w połowie lat sześćdziesiątych. Edmonds wprowadził też pojęcie klasy NP i jako pierwszy sformułował pytanie, czy P \( \ne \) NP. Metoda redukcji pochodzi od Karpa, który przy jej pomocy pokazał, że wiele ważnych zadań kombinatorycznych jest NP-zupełnych.