Przypomnijmy sobie schemat algorytmu sortowania przez wybór. Podstawowa operacja w tym algorytmie polega na wybraniu największego elementu w zbiorze sortowanych elementów, usunięciu go z tego zbioru i umieszczeniu na ostatniej pozycji w posortowanym ciągu. Następnie postępujemy tak samo z mniejszym zbiorem, znajdując i umieszczając na pozycji docelowej element drugi co do wielkości (licząc od największych). Postępując tak wielokrotnie dostaniemy uporządkowany ciąg elementów ze zbioru, który należało uporządkować. Łatwo zauważyć, że dla wydajnej implementacji powyższego algorytmu musimy umieć szybko znajdować element największy w danym zbiorze elementów oraz usuwać taki element ze zbioru. Dodatkowo musimy pamiętać, że elementy sortowanego zbioru znajdują się w tablicy \( a[1..n] \), a naszym celem jest uporządkowanie tej tablicy. Oto raz jeszcze algorytm sortowania przez wybór.
Algorytm Schemat algorytmu sortowania przez wybór
SelectionSort 1
for i := n downto 2 do
begin
j := Max(i);
Exchange(i,j)
end;
Żeby można było wydajnie zaimplementować ten algorytm, musimy w każdej iteracji mieć tak zorganizowane elementy w podtablicy \( a[1..i] \), żeby łatwo było wyznaczać pozycję elementu największego, a następnie, po zamianie go z \( a[i] \), przywracać szybko właściwą organizację tablicy \( a[1..i-1] \). W tym celu definiujemy warunek \( kopiec(p,r) \), gdzie \( (p,r) \) jest parą indeksów takich, że \( 1\le p \le r \le n \):
\( kopiec(p,r): \) dla każdego \( i = p, p+1,\ldots, r \), jeśli \( 2i \le r \), to \( a[i] \ge a[2i] \), oraz jeśli \( 2i+1\le r \), to \( a[i]\ge a[2i+1] \).
Załóżmy,że zachodzi warunek \( kopiec(1,n) \). Nietrudno zauważyć, że element \( a[1] \) jest największy w całej tablicy \( a \).
Gdy zamienimy \( a[1] \) z \( a[n] \), na pewno zachodzi wtedy warunek \( kopiec(2,n-1) \), ale niestety może nie zachodzić (i zazwyczaj nie zachodzi) \( kopiec(1,n-1) \). Gdybyśmy umieli szybko przywrócić warunek \( kopiec(1,n-1) \), wówczas \( a[1] \) byłoby największe w \( a[1..n-1] \). Zamieniwszy \( a[1] \) z \( a[n-1] \) zredukowalibyśmy znowu rozmiar naszego zadania. Postępując tak jeszcze \( n-3 \) razy, posortowalibyśmy cały ciąg. W jaki sposób zatem poprawić kopiec, gdy został on zepsuty w jednym miejscu?
Rozważmy trochę ogólniejsze zagadnienie. Załóżmy, że zachodzi warunek \( kopiec(p+1,r) \) dla pewnego \( p \), \( 1\le p < r \le n \). W jaki sposób zmodyfikować podtablicę \( a[p..r] \), żeby zachodziło \( kopiec(p,r) \). Sytuacja jest dosyć prosta. Jeśli \( 2p > r \), nic nie musimy robić. Jeśli \( 2p = r \), wystarczy sprawdzić, czy \( a[p] \ge a[r] \). W przypadku odpowiedzi pozytywnej nic nie robimy. Dla \( a[p] < a[r] \) wystarczy zamienić \( a[p] \) z \( a[r] \). A co, gdy \( 2p < r \)? W tym przypadku wybieramy większy z elementów \( a[2p], a[2p+1] \). Niech \( a[t] \) będzie tym elementem. Jeśli \( a[p] \ge a[t] \), warunek \( kopiec(p,r) \) jest spełniony. W przeciwnym razie zamieniamy miejscami \( a[p] \) z \( a[t] \). Jeżeli \( t+1 \le r \), to zachodzi \( kopiec(t+1,r) \). Jeśli żądamy teraz, żeby zachodziło \( kopiec(p,r) \), musimy postąpić w taki sposób, aby spełniony był warunek \( kopiec(t,r) \). A to jest to samo zadanie jak to, które właśnie rozważamy, tylko o mniejszym rozmiarze. Zatem postępujemy analogicznie. Oto formalny zapis tego algorytmu.
Algorytm Poprawianie kopca
PoprawKopiec(p,r);
//zachodzi kopiec (p+1,r) ; po wykonaniu PoprawKopiec(p,r)
//ma zachodzić kopiec(p,r)
begin
s := p; v := a[s];
while 2s <= r do
begin
t := 2s;
if t < r then if a[t+1] > a[t] then t := t+1;
if v => a[t] then
begin
a[s] := v;
s := r+1 //sztuczne zakończenie pętli
end
else
begin
a[s] := a[t];
s := t
end
end;
if s <= r then a[s] := v
end
Ćwiczenie 5
Wykaż, że maksymalna liczba porównań pomiędzy elementami tablicy \( a \) w algorytmie PoprawKopiec(p,r) wynosi \( 2\lfloor \log \frac{r}{p} \rfloor \).
Załóżmy, że zachodzi \( kopiec(1,n) \). Wówczas sortowanie jest bardzo proste.
for i := n downto 2 do
begin
Exchange(1,i) ; //zamiana a[1] z a[i]
PoprawKopiec(1,i-1)
end
Wykonanie \( PoprawKopiec(1,i-1) \) kosztuje pesymistycznie \( 2\lfloor \log (i-1) \rfloor \) porównań. Zatem jeśli zachodzi \( kopiec(1,n) \), sortowanie wymaga co najwyżej \( 2n\log n \) porównań.
Ćwiczenie 6
Ile najwięcej wykonamy przemieszczeń elementów?
Pozostaje pokazać, w jaki sposób przeorganizować wejściową tablicę \( a \), żeby zaszło \( kopiec(1,n) \). Sytuacja staje się jasna, gdy zauważymy, że niezależnie od zawartości tablicy \( a \) zachodzi \( kopiec(\lfloor \frac{n}{2} \rfloor+1,n) \).
Zatem warunek \( kopiec(1,n) \) dostajemy zapewniając kolejno zachodzenie warunków \( kopiec(\lfloor \frac{n}{2} \rfloor,n), kopiec(\lfloor \frac{n}{2} \rfloor-1,n), \ldots, kopiec(1,n) \). Formalnie możemy to zapisać następująco:
for i := n div 2 downto 1 do
PoprawKopiec(i,n);
Nasze dotychczasowe rozważania pozwalają stwierdzić, że liczba porównań potrzebnych do budowy kopca nie jest większa niż \( n\log n \). Dokładniejsza analiza pokazuje, że tych porównań jest co najwyżej \( 4n \) (co najwyżej \( 2n \) przemieszczeń).
Wiemy już w jaki sposób zbudować kopiec i jak go wykorzystać do sortowania. Łącząc obie fazy - fazę budowy kopca i fazę właściwego sortowania - dostajemy algorytm znany pod angielską nazwą HeapSort (Sortowanie kopcowe).
Algorytm Sortowanie kopcowe (HeapSort)
begin
//budowa kopca
for i := n div 2 downto 1 do
PoprawKopiec(i,n);
//właściwe sortowanie
for i := n downto 2 do
begin
Exchange(1,i);
PoprawKopiec(1,i-1)
end
end;
Algorytm HeapSort sortuje w miejscu i wykonuje nie więcej niż \( 2n\log n + O(n) \) porównań i nie więcej niż \( n\log n + O(n) \) przemieszczeń elementów.
Kopiec (Heap)
Pozostaje nam wytłumaczyć, dlaczego w opisie przedstawionego algorytmu pojawia się słowo kopiec. Spójrzmy raz jaszcze na tablicę \( a[1..n] \), dla której zachodzi warunek \( kopiec(1,n) \). Podany warunek narzuca pewną strukturę na zawartość tablicy \( a \). Żeby dostrzec tę strukturę rozważmy zupełne drzewo binarne o \( n \) węzłach. W zupełnym drzewie binarnym wszystkie poziomy są wypełnione węzłami, z wyjątkiem poziomu ostatniego, który jest wypełniany od strony lewej do prawej tak, żeby w całym drzewie było łącznie \( n \) węzłów. Wysokość zupełnego drzewa binarnego wynosi \( \lfloor \log n \rfloor \). Jeśli teraz ponumerujemy węzły drzewa kolejno \( 1, 2,\ldots, n \), poczynając od korzenia, a następnie poziomami i na każdym poziomie z lewa na prawo, to lewym synem węzła o numerze \( i \) w drzewie jest węzeł o numerze \( 2i \), o ile tylko \( 2i \le n \), a prawym synem węzła o numerze \( i \) jest węzeł \( 2i+1 \), o ile \( 2i+1 \le n \).
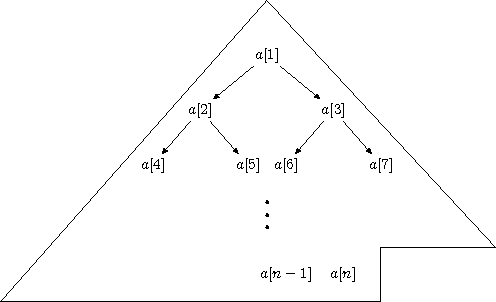
Jak widać, do implementacji zupełnego drzewa binarnego nie potrzebujemy struktury dowiązaniowej. Takie drzewo można ukryć w tablicy. Wówczas \( i \)-ta pozycja w tablicy odpowiada węzłowi o numerze \( i \), natomiast element \( a[i] \) jest wartością (kluczem) umieszczanym w \( i \)-tym węźle drzewa. Warunek \( kopiec(1,n) \) można teraz zapisać następująco:
Dla każdego węzła klucz umieszczony w tym węźle jest nie mniejszy od kluczy znajdujących się w jego synach.
Przyjęło się nazywać kopcem każde drzewo binarne (niekoniecznie zupełne), w którego węzłach klucze są rozmieszczane zgodnie z powyższym warunkiem.
Kopiec zupełny można wykorzystać do implementacji dynamicznego, skończonego multizbioru \( S \) składającego się z elementów z uniwersum z liniowym porządkiem, na którym wykonujemy następujące operacje:
\( Make(S):: S := \emptyset \);
\( Insert(S,e):: \) wstaw nowy element \( e \) do \( S \);
\( Max(S):: \) jeśli \( S \) nie jest pusty, to podaj element maksymalny w \( S \);
\( DeleteMax(S):: \) usuń z \( S \) element \( Max(S) \).
Załóżmy, że znamy górne ograniczenie \( maxN \) na liczbę elementów \( S \). Wówczas do implementacji \( S \) można wykorzystać tablicę \( S[1..maxN] \) ze strukturę kopca zupełnego. Niech \( n \) będzie aktualną liczbą elementów w zbiorze \( S \). Najłatwiejsze do zaimplementowania są operacje utworzenia pustego kopca i sięgnięcia po element maksymalny. Obie można wykonać w czasie stałym.
Algorytm Utwórz pusty kopiec
Algorytm Element maksymalny
Max::
begin
if n > 0 then
return(a[1])
end;
Nietrudno też zapisać operację usuwania elementu maksymalnego. Robiliśmy to już w algorytmie sortowania kopcowego.
Algorytm Usuń element maksymalny
DeleteMax::
begin
if n > 0 then
begin
a[1] := a[n];
n := n - 1;
PoprawKopiec(1,n)
end;
Już wiemy, że operacja \( DeleteMax \) wykonuje się w czasie \( O(\log n) \).
Przed zapisaniem operacji wstawienia nowego elementu rozważmy operację \( IncreaseKey(S,e,f) \), która polega na zamianie wskazanego elementu \( e \) w zbiorze \( S \) na element większy \( f \). Zastanówmy się, co stanie się z kopcem, gdy element w danym węźle zamienimy na element większy. Zauważmy, że może to zaburzyć warunek kopca, ale tylko wtedy, gdy element w ojcu badanego węzła będzie mniejszy od nowo wstawionego elementu. Jeśli teraz zamienimy miejscami te dwa elementy, problem z zachowaniem warunku kopca przesuniemy o jeden poziom w górę drzewa. Postępując dalej w ten sam sposób przywrócimy w końcu warunek kopca, ponieważ w ostateczności znajdziemy się w korzeniu drzewa. Oto procedura \( IncreaseKey \).
Algorytm Zamiana wskazanego elementu na większy
IncreaseKey(i,f)::
//zmiana elementu e=S[i] na większy f
begin
while (i>1) AND (a[i div 2] < f) do
begin
a[i] := a[i div 2 ];
i := i div 2
end;
a[i] := f
end;
Złożoność algorytmu zamiany klucza na mniejszy wynosi \( O(\log i) \) (wykonujemy co najwyżej \( \lfloor \log i \rfloor \) porównań). Mając taką procedurę łatwo już zaproponować algorytm wstawiania nowego elementu do zbioru, który działa w czasie \( O(\log n) \).
Algorytm Wstaw nowy element
Insert(e)::
begin
n := n + 1;
IncreaseKey(n,e)
end;
Dynamiczny zbiór \( S \) z operacjami \( Make \), \( Insert \), \( Max \), \( DeleteMax \) to abstrakcyjna struktura danych zwana kolejką priorytetową typu max. Jednym ze sposobów implementacji kolejki priorytetowej jest kopiec zupełny. Jeśli zamienimy operacje \( Max \) i \( DeleteMax \) na \( Min \) i \( DeleteMin \) (odpowiednio znajdowanie i usuwanie elementu minimalnego), dostaniemy kolejkę priorytetową typu min. Niezwykle łatwo zaadaptować implementację kolejki typu max do implementacji kolejki typu min. Wystarczy w opisach procedur zamienić nierówności przy porównaniach kluczy na nierówności przeciwne. W ten sam sposób łatwo otrzymać odpowiednik operacji \( IncreaseKey \), czyli operację zmniejszenia klucza \( DecreaseKey \). O kolejkach priorytetowych i ich zastosowaniach będzie jeszcze mowa w dalszych wykładach.