Wyszukiwanie
W niniejszym wykładzie opiszemy podstawowe techniki dotyczące wyszukiwania. Zajmiemy się również prostymi strukturami słownikowymi, które oprócz wyszukiwania umożliwiają dodawanie i usuwanie elementów.
Wyszukiwanie liniowe
Jeśli nie dysponujemy żadną dodatkową wiedzą na temat zbioru, który chcemy przeszukiwać, niestety musimy sprawdzić wszystkie jego elementy.
function Szukaj(x, A[1..n]) begin for i:=1 to n do if A[i]=x return i; return brak poszukiwanego elementu; end
Oczywiście w pesymistycznym przypadku (np. gdy zbiór nie zawiera poszukiwanego elementu) koszt czasowy, to \( O(n) \).
Wyszukiwanie binarne
W niektórych przypadkach czas poszukiwania możemy znacząco zmniejszyć. Dzieje się tak na przykład, gdy przeszukiwany zbiór przechowujemy w rosnąco uporządkowanej tablicy. W takim przypadku wystarczy jedynie \( O(\log n) \) operacji, by odnaleźć poszukiwany element lub stwierdzić jego brak.
Algorytm utrzymuje zakres \( [l,\ldots,r] \), w którym może znajdować się element; przy każdym porównaniu zakres zostaje zmniejszony o połowę.
function WyszukiwanieBinarne(x, A[1..n]) { zakładamy, że tablica A jest uporządkowana rosnąco } begin l:=1;r:=n; while (l<=r) do begin { niezmiennik: poszukiwany element może znajdować się w zakresie A[l..r] } m:=(l+r) div 2; if (A[m]<;x) then l:=m+1 else if (A[m]>x) then r:=m-1 else return m; { ponieważ A[m]=x } end; return brak poszukiwanego elementu; end;
Proste słowniki: drzewa poszukiwań binarnych
Podstawowe operacje słownika to wyszukiwanie, wstawianie i usuwanie klucza. Drzewa poszukiwań binarnych (bez dodatkowych specjanych wymagań) mogą być traktowane jako prosty słownik. Sa to zwykłe drzewa binarne, których klucze spełniają następujące własności:
Dla dowolnego węzła x:
- wszystkie klucze w lewym poddrzewie węzła x mają wartości mniejsze niż klucz węzła x,
- wszystkie klucze w prawym poddrzewie węzła x mają wartości większe lub równe niż klucz węzła x.
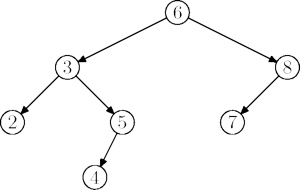
Dodatkowe wymaganie dotyczące kluczy umożliwia nam efektywne wyszukiwanie elementów w drzewie.
function Szukaj(węzeł, klucz) if (węzeł==nil) return BRAK ELEMENTU if (węzeł.klucz=klucz) then return ELEMENT ISTNIEJE else if (klucz < węzeł.klucz) then return Szukaj(węzeł.lewePoddrzewo, klucz) else if (klucz > węzeł.klucz) then return Szukaj(węzeł.prawPoddrzewo, klucz) end;
Wstawianie do drzewa jest bardzo zbliżone do wyszukiwania: musimy przejść po drzewie (rozpoczynając w korzeniu), aby odnaleźć wolne miejsce, w którym możemy dodać nową wartość.
procedure Dodaj(węzeł, klucz) if (klucz < węzeł.klucz) then if węzeł.lewePoddrzewo=nil then utwórz nowy węzeł z wartością klucz wskaźnik do nowego węzła zapisujemy w węzeł.lewePoddrzewo else Dodaj(węzeł.lewePoddrzewo, klucz) else if (klucz >= węzeł.klucz) then if węzeł.prawePoddrzewo=nil then utwórz nowy węzeł z wartością klucz wskaźnik do nowego węzła zapisujemy w węzeł.prawePoddrzewo else Dodaj(węzeł.prawePoddrzewo, klucz) end;
Możemy również usuwać wartości z drzewa, niestety ta operacja jest bardziej skomplikowana.
procedure Usuń(węzeł, klucz) if (klucz < węzeł.klucz) then Usuń(węzeł.lewePoddrzewo, klucz) else if (klucz > węzeł.klucz) then Usuń(węzeł.prawePoddrzewo, klucz) else begin { klucz = węzeł.klucz if węzeł jest liściem, then { usuń węzeł z drzewa } UsunProstyPrzypadek(węzeł) else if węzeł.lewePoddrzewo <> nil then niech x oznacza skrajnie prawy węzeł w poddrzewie węzeł.lewePoddrzewo wezel.klucz:=x.klucz; UsunProstyPrzypadek(x); else analogiczne postępowanie dla węzeł.prawPoddrzewo (jednak poszukujemy węzła na skrajnie lewej ścieżce) end
Procedura UsunProstyPrzypadek oznacza usuwanie z drzewa węzła, który ma co najwyżej jednego syna.
procedure UsunProstyPrzypadek(węzeł) begin poddrzewo:=nil; ojciec:=węzeł.ojciec; if węzeł.lewePoddrzewo <> nil then poddrzewo:=węzeł.lewePoddrzewo; else poddrzewo:=węzeł.prawePoddrzewo; if ojciec=nil then korzen:=poddrzewo; else if ojciec.lewePoddrzewo=węzeł then { węzeł jest lewym synem } ojciec.lewePoddrzewo:=poddrzewo; else { węzeł jest prawym synem } ojciec.prawePoddrzewo:=poddrzewo;
Wszystkie podane operacje mają pesymistyczny koszt \( O(h) \) gdzie \( h \) oznacza wysokość drzewa. Niestety w najgorszym przypadku drzewo może mieć bardzo dużą wysokość -- nawet \( O(n) \) (np. dla ciągu operacji Dodaj \( (1,2,3,\ldots) \).
Adresowanie bezpośrednie
W przypadku gdy zbiór, który przechowujemy, pochodzi z niewielkiego uniwersum (na przykład elementy zbioru to liczby z zakresu \( 1,\ldots,n \)), możemy wszystkie operacje słownikowe (dodaj, usuń, szukaj) wykonać znacznie szybciej i prościej.
Dla uniwersum \( 1,\ldots,n \) zbiór możemy reprezentować przez tablicę \( n \)-elementową. Początkowo w każdej komórce tablicy wpisujemy wartość false.
- dodanie elementu \( i \) do zbioru wymaga jedynie ustawienia wartości \( i \)-tej komórki na true,
- analogicznie, usunięcie elementu \( i \) do zbioru wymaga ustawienia wartości \( i \)-tej komórki na false,
- sprawdzenie, czy element \( i \) należy do zbioru, wykonujemy przez sprawdzenie stanu \( i \)-tej komórki.
Wszystkie powyższe operacje możemy wykonać używając stałej liczby kroków.
Haszowanie
Czy możemy wykorzystać adresowanie bezpośrednie do dowolnych zbiorów? Okazuje się, że tak. Co prawda w pesymistycznym przypadku koszt jednej operacji może wynosić nawet \( O(n) \), jednak w praktycznych zastosowaniach ta metoda sprawuje się doskonale.
W tym rozdziale będziemy zakładać, że elementy uniwersum \( U \) to dodatnie liczby całkowite. Dodatkowo zakładamy, że dysponujemy tablicą \( A[0,\ldots,m-1] \).
Ponieważ elementami mogą być bardzo duże liczby całkowite, nie możemy zastosować metody adresowania bezpośredniego. Jednak możemy wybrać funkcję haszującą:
Funkcja każdemu elementowi uniwersum przypisuje odpowiednie miejsce w tablicy \( A \). Jeśli \( |U|>m \), to z oczywistych względów znajdą się takie pary różnych elementów \( x,y\in U \), dla których \( f(x)=f(y) \). W takim przypadku mówimy o istnieniu kolizji. Właśnie ze względu na ryzyko wystąpienia kolizji musimy nieznacznie zmodyfikować metodę adresowania bezpośredniego - zamiast przechowywać w tablicy wartość logiczną (prawda/fałsz), musimy zapisywać wartość przechowywanego elementu.
Rozwiązywanie kolizji metodą łańcuchową
Jedną z metod rozwiązywania kolizji jest utrzymywanie w każdej komórce tablicy listy elementów do niej przypisanych. Początkowo tablica \( A \) wypełniona jest wartościami nil.
procedure Inicjalizacja; begin for i:=0 to m-1 do A[i]:=nil; end;
Dodanie elementu \( x \) do tablicy wymaga odczytania jego adresu z funkcji haszującej, a następnie dodania go na początek listy \( A[h(x)] \)
procedure Dodaj(x); begin dodaj element x na początek listy A[h(x)] end;
Sprawdzenie, czy element \( x \) jest w zbiorze, wymaga w pesymistycznym przypadku sprawdzenia całej listy \( A[h(x)] \)
function Szukaj(x); begin l:=A[h(x)]; while (l!=nil) do begin if (l.wartość=x) then return element istnieje l:=l.nast; end; return brak elementu end;
Usuwanie elementu z tablicy jest bardzo podobne do wyszukiwania i również w pesymistycznym przypadku wymaga sprawdzenia całej listy.
procedure Usuń(x); begin l:=A[h(x)];p:=nil; while (l!=nil) do begin if (l.wartość=x) then begin { usuwamy element l z listy A[h(x)] } if p=nil then A[h(x)]:=l.nast; else p.nast:=l.nast; return; end p:=l; l:=l.nast; end; end;
Analiza metody łańcuchowej
Haszowanie to metoda, która bardzo dobrze sprawdza się w praktyce, zastanówmy się przez chwilę, czy dobre własności tej metody można udowodnić.
Niech:
- m oznacza rozmiar tablicy,
- n oznacza liczbę elementów, które przetrzymujemy w tablicy,
- przez \( \alpha \) oznaczamy współczynnik zapełniania tablicy \( \frac{n}{m} \)
Załóżmy, że dysponujemy idealną funkcją haszującą, dla której przypisanie każda wartość \( h(x) \) jest równie prawdopodobna, czyli \( P(\{h(x)=i\})=\frac{1}{m} \).
Przy takim założeniu oczekiwana długość listy elementów \( A[h(x)] \) ma długość \( \frac{n}{m} \) (oczekiwana liczba sukcesów w n próbach Bernoulli'ego).
Stąd oczekiwana złożoność operacji Szukaj, Dodaj, Usuń wynosi:
\( T(n,m)=\frac{n}{m}+O(1) \)
Wybór funkcji haszujących
Od wyboru dobrej funkcji haszującej w dużej mierze zależy efektywność naszej struktury danych. Niestety, nie można podać ścisłej procedury wyboru takiej funkcji.
Dla liczb całkowitych możemy przykładowo wybrać jedną z następujących funkcji (\( m \) oznacza rozmiar tablicy):
- \( f(x)=(x\,\mod\, p)\ \mod\ m \) (gdzie \( p>m \) jest liczbą pierwszą);
- \( f(x)=(qx\,\mod\, p)\ \mod\ m \) (gdzie \( p,q \) są liczbami pierwszymi);
- \( f_{a,b}(x)=((ax+b)\,\mod\, p)\ \mod\ m \) (gdzie \( p \) jest liczbą pierwszą, \( 1\le a < p \), \( 0 \le b < p \)).
Jeśli nie dysponujemy żadną dodatkową wiedzą na temat elementów które będzie zawierać tablica, rozsądnym rozwiązaniem jest wybór funkcji \( f_{a,b} \) dla losowych wartości \( a,b \).
Adresowanie otwarte
Adresowanie otwarte jest metodą pozwalającą uniknąć utrzymywania list elementów w tablicy haszującej. Oczywiście wymaga to opracowania innej metody rozwiązywania konfliktów. Każda komórka tablicy zawiera teraz wartość NIL lub element zbioru.
Niech \( m \) oznacza rozmiar tablicy haszującej. Zdefiniujmy funkcję \( H(x,k) \), wyznaczającą listę pozycji \( H(x,0),\ldots,H(x,m-1) \), na których może znajdować się element \( x \).
Mając daną funkcję \( h(x) \), możemy zdefiniować \( H(x,k) \), jako:
- \( H(x,k)=(h(x)+k)\ \mod\ m \) --- adresowanie liniowe;
- \( H(x,k)=(h(x)+a_1\cdot k+a_2\cdot k^2)\ \mod\ m \) --- adresowanie kwadratowe;
- \( H(x,k)=(h(x)+h_2(x)\cdot k)\ \mod\ m \) --- podwójne haszowanie, przy czym \( h_2(x) \) jest funkcją haszującą, która przyjmuje wartości z zakresu \( 1,\ldots,m-1 \).
Wyszukiwanie elementów możemy wykonać nieznacznie modyfikując poprzednie rozwiązanie -- zamiast przeszukiwać listę elementów, musimy przeszukać ciąg pozycji zdefiniowany przez funkcję \( H(x,k) \).
function Szukaj(x); begin k:=0; while (A[H(x,k)!=nil) do begin if (A[H(x,k)].wartość=x) then return element istnieje k:=k+1; end; return brak elementu end;
Wstawianie elementów możemy wykonać przez analogiczne modyfikacje; usuwanie jest zwykle znacznie trudniejsze.
Filtry Bloom'a
Ciekawym połączeniem adresowania bezpośredniego z haszowaniem są filtry Bloom'a. Polegają one na rozlużnieniu założeń naszej struktury:
- ograniczamy się do operacji Dodaj i Szukaj,
- pozwalamy na nieprawidłowe odpowiedzi dla operacji Szukaj (jednak z małym prawdopodobieństwem).
Nasza struktura to bitowa tablica o rozmiarze m, początkowo tablica jest wypełniona zerami. Zakładamy również, że mamy do dyspozycji k funkcji haszujących \( h_i(x) : U arrow \{ 0,\ldots,m-1\} \).
Dodanie elementu x sprowadza się do ustawienia wszystkich bitów \( A[h_i(x)] \) dla \( i=1,\ldots,k \) na wartość 1.
procedure Dodaj(x); begin for i:=1 to k do A[h_i(x)]:=1; end;
Analogicznie, sprawdzenie, czy element x należy do zbioru, wymaga sprawdzenia bitów \( A[h_i(x)] \) dla \( i=1,\ldots,k \). Jeśli wszystkie mają wartość 1, to uznajemy, że element należy do zbioru. Oczywiście powoduje to pewien odsetek błędnych odpowiedzi. Jeśli jednak dobrze dobierzemy funkcje, a wypełnienie tablicy nie będzie zbyt duże, to taka struktura będzie dobrze sprawować się w praktyce.
function Szukaj(x); begin for i:=1 to k do if A[h_i(x)]=0 then return brak elementu return element istnieje end;
Ćwiczenia
- Podaj metodę przygotowywania zrównoważonego drzewa BST (o wysokość \( O(\log n) \)) dla zadanego zbioru kluczy \( a_1,\ldots,a_n \).
- W jaki sposób efektywnie dodać do drzew BST operację LiczbaElementówzZakresu(x,y) zwracającą liczbę elementów drzewa o wartościach z zakresu \( [x,\ldots,y] \)?
- Ile jest różnych drzew BST zawierających klucze \( 1,\ldots,n \)?
- W jaki sposób można wykorzystać drzewa BST do sortowania ciągu liczb?