Proste słowniki: drzewa poszukiwań binarnych

Podstawowe operacje słownika to wyszukiwanie, wstawianie i usuwanie klucza. Drzewa poszukiwań binarnych (bez dodatkowych specjanych wymagań) mogą być traktowane jako prosty słownik. Sa to zwykłe drzewa binarne, których klucze spełniają następujące własności:

Dla dowolnego węzła x:

wszystkie klucze w lewym poddrzewie węzła x mają wartości mniejsze niż klucz węzła x,
wszystkie klucze w prawym poddrzewie węzła x mają wartości większe lub równe niż klucz węzła x.

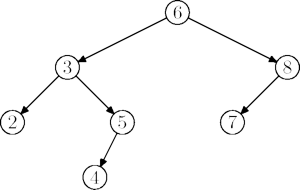
Dodatkowe wymaganie dotyczące kluczy umożliwia nam efektywne wyszukiwanie elementów w drzewie.

function Szukaj(węzeł, klucz) 
    if (węzeł==nil) 
        return BRAK ELEMENTU 
    if (węzeł.klucz=klucz) then 
        return ELEMENT ISTNIEJE 
    else if (klucz < węzeł.klucz) then 
        return Szukaj(węzeł.lewePoddrzewo, klucz) 
    else if (klucz > węzeł.klucz) then 
        return Szukaj(węzeł.prawPoddrzewo, klucz) 
end;

Wstawianie do drzewa jest bardzo zbliżone do wyszukiwania: musimy przejść po drzewie (rozpoczynając w korzeniu), aby odnaleźć wolne miejsce, w którym możemy dodać nową wartość.

procedure Dodaj(węzeł, klucz) 
  if (klucz < węzeł.klucz) then 
    if węzeł.lewePoddrzewo=nil then 
      utwórz nowy węzeł z wartością klucz 
      wskaźnik do nowego węzła zapisujemy w węzeł.lewePoddrzewo 
    else 
      Dodaj(węzeł.lewePoddrzewo, klucz) 
  else if (klucz >= węzeł.klucz) then 
    if węzeł.prawePoddrzewo=nil then 
      utwórz nowy węzeł z wartością klucz 
      wskaźnik do nowego węzła zapisujemy w węzeł.prawePoddrzewo 
    else 
      Dodaj(węzeł.prawePoddrzewo, klucz) 
end;

Możemy również usuwać wartości z drzewa, niestety ta operacja jest bardziej skomplikowana.

  procedure Usuń(węzeł, klucz) 
    if (klucz < węzeł.klucz) then 
      Usuń(węzeł.lewePoddrzewo, klucz) 
    else if (klucz > węzeł.klucz) then 
      Usuń(węzeł.prawePoddrzewo, klucz) 
else begin { klucz = węzeł.klucz 
      if węzeł jest liściem, then 
        { usuń węzeł z drzewa } 
        UsunProstyPrzypadek(węzeł) 
      else
        if węzeł.lewePoddrzewo <> nil then 
          niech x oznacza skrajnie prawy węzeł w poddrzewie węzeł.lewePoddrzewo 
          wezel.klucz:=x.klucz; 
          UsunProstyPrzypadek(x); 
        else 
          analogiczne postępowanie dla węzeł.prawPoddrzewo 
          (jednak poszukujemy węzła na skrajnie lewej ścieżce) 
end

Procedura UsunProstyPrzypadek oznacza usuwanie z drzewa węzła, który ma co najwyżej jednego syna.

procedure UsunProstyPrzypadek(węzeł) 
begin 
    poddrzewo:=nil; 
    ojciec:=węzeł.ojciec; 
    if węzeł.lewePoddrzewo <> nil then 
      poddrzewo:=węzeł.lewePoddrzewo; 
    else 
      poddrzewo:=węzeł.prawePoddrzewo;  
    if ojciec=nil then 
      korzen:=poddrzewo; 
    else if ojciec.lewePoddrzewo=węzeł then { węzeł jest lewym synem } 
      ojciec.lewePoddrzewo:=poddrzewo; 
    else { węzeł jest prawym synem } 
      ojciec.prawePoddrzewo:=poddrzewo;

Wszystkie podane operacje mają pesymistyczny koszt \( O(h) \) gdzie \( h \) oznacza wysokość drzewa. Niestety w najgorszym przypadku drzewo może mieć bardzo dużą wysokość -- nawet \( O(n) \) (np. dla ciągu operacji Dodaj \( (1,2,3,\ldots) \).