Samoorganizujące się drzewa BST

Mechanizm równoważenia drzew AVL jest dość skomplikowany w implementacji i wymaga przechowywania w węzłach dodatkowych informacji. Wynalezione przez Sleatora i Tarjana [ST], opisane poniżej drzewa splay to drzewa BST, w których wykorzystuje się rotacje do ich równoważenia, jednak nie trzeba przechowywać żadnych dodatkowych atrybutów w węzłach. Chociaż możliwe jest utworzenie niezrównoważonego drzewa splay i pojedyncza operacja może mieć nawet koszt liniowy względem aktualnego rozmiaru drzewa, to koszt zamortyzowany operacji słownikowych w tej strukturze danych jest logarytmiczny.

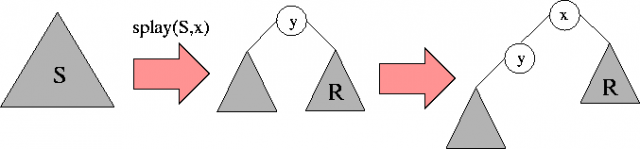
Wszystkie operacje w drzewie splay są wykonywane z wykorzystaniem pomocniczej procedury splay\( (S,x) \), która przekształca drzewo \( S \) w taki sposób, że jego korzeniem staje się węzeł z kluczem \( x \) (albo - jeśli klucza \( x \) nie ma w \( S \) - węzeł z kluczem \( y \) takim, że w \( S \) nie ma żadnego klucza między \( \min(x,y) \) a \( \max(x,y) \)). Operacja Find\( (S,x) \) sprowadza się zatem do wywołania splay\( (S,x) \) i sprawdzenia, czy \( x \) jest w korzeniu.

W celu wykonania operacji Insert\( (S,x) \) wywołujemy najpierw splay\( (S,x) \), w wyniku czego w korzeniu znajduje się klucz \( y \); bez straty ogólności możemy przyjąć, że \( y < x \). Odcinamy prawe poddrzewo \( R \) węzła \( y \), jego ojcem (a zarazem nowym korzeniem) zostaje węzeł z kluczem \( x \), którego prawym poddrzewem czynimy \( R \).

Operację Delete\( (S,x) \) zaczynamy od wywołania splay\( (S,x) \), sprowadzając usuwany klucz do korzenia. Niech \( L \) i \( R \) będą, odpowiednio, lewym i prawym poddrzewem uzyskanego drzewa. Odcinamy korzeń i - jeśli \( L \) jest niepuste - wywołujemy splay\( (L,x) \), a następnie przyłączamy \( R \) jako prawe poddrzewo korzenia.

Sama procedura splay\( (S,x) \) jest zdefiniowana następująco: najpierw szukamy węzła \( v \) z kluczem \( x \) w \( S \) tak jak w zwykłym drzewie BST (jeśli klucza \( x \) nie ma w drzewie, to jako \( v \) bierzemy ostatni węzeł na ścieżce przed węzłem zewnętrznym NULL). Następnie, dopóki \( v \) nie stanie się korzeniem, wykonujemy sekwencję rotacji zgodnie z poniższym schematem:

1. Jeżeli \( v \) jest synem korzenia \( w \), to wykonujemy ROT1\( (v, w) \).
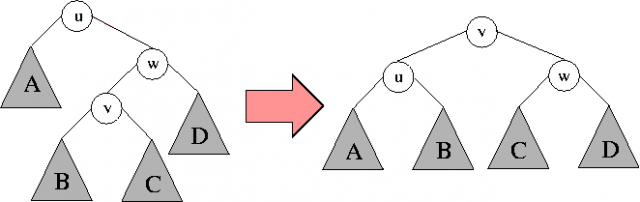
2. Jeżeli \( v \) ma ojca \( w \) i dziadka \( u \), przy czym oba węzły \( v \) i \( w \) są lewymi synami, albo oba prawymi, to wykonujemy ROT1\( (w,u) \), a następnie ROT1\( (v,w) \).

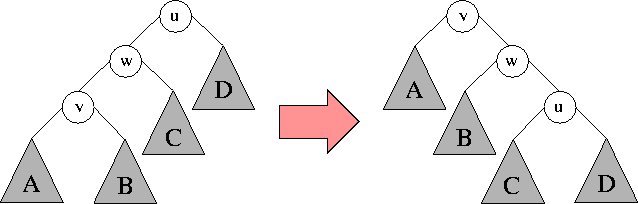
3. Jeżeli \( v \) ma ojca \( w \) i dziadka \( u \), przy czym jeden z węzłów \( v \), \( w \) jest lewym synem, a drugi prawym, to wykonujemy ROT1\( (v,w) \), a następnie ROT1\( (v,u) \) (czyli w sumie rotację podwójną ROT2\( (v,w,u) \)).

Oto przykład działania procedury splay:

W analizie kosztu zamortyzowanego operacji na drzewach splay posłużymy sie metodą księgowania, z każdym węzłem w drzewie związując pewną liczbę jednostek kredytu. Przez \( T \) oznaczmy drzewo o korzeniu \( x \) i zdefiniujmy \( \mu(x) = \lfloor\lg |T|\rfloor \) (czasem będziemy też używać oznaczenia \( \mu(T) \)). Będziemy zachowywali niezmiennik

"Liczba jednostek kredytu w węźle \( x \) jest zawsze równa \( \mu(x) \)." (***)

Prawdziwy jest

Lemat

Do wykonania operacji splay\( (S,x) \) z zachowaniem niezmiennika (***) potrzeba co najwyżej \( 3(\mu(S)-\mu(x))+1 \) jednostek kredytu.

Żmudny, techniczny dowód lematu pozostawiamy jako ćwiczenie. Z lematu wynika bezpośrednio, że dowolna operacja splay na drzewie rozmiaru \( n \) wymaga zużycia \( O(\lg n) \) jednostek kredytu, a ponieważ do wykonania operacji Insert i Delete z zachowaniem niezmiennika oprócz tych potrzebnych do wywołań splay potrzeba \( O(\lg n) \) dodatkowych jednostek kredytu (na korzeń), wnioskujemy, że koszt zamortyzowany operacji słownikowych na drzewach splay jest logarytmiczny.