Kolejki priorytetowe
Złączalna kolejka priorytetowa
Kolejka priorytetowa to jedna z podstawowych abstrakcyjnych struktur danych, wykorzystywana między innymi w takich zastosowaniach jak:
- algorytm Dijkstry wyznaczania najkrótszych ścieżek w grafach;
- algorytm Prima znajdowania minimalnego drzewa rozpinającego;
- symulacja sterowana zdarzeniami;
- metoda zamiatania w geometrii obliczeniowej;
- kodowanie Huffmana;
- sortowanie (algorytm Heapsort).
Oferuje ona następujące operacje:
- MakePQ(): tworzy nową, pustą kolejkę;
- Insert(H,x): wstawia element x (o kluczu z pewnego liniowo uporządkowanego uniwersum) do kolejki H;
- FindMin(H): zwraca element o najmniejszym kluczu w kolejce H;
- DelMin(H): zwraca element o najmniejszym kluczu w kolejce H, usuwając go przy tym z H.
Ten zestaw operacji często rozszerza się o:
- DecreaseKey(H,x,y): nadaje kluczowi elementu x w kolejce H nową, mniejszą wartość y;
- Delete(H,x): usuwa element x z kolejki H.
Jeśli struktura danych udostępnia dodatkowo operację łączenia kolejek
- Meld(H1,H2): zwraca nową kolejkę, zawierającą wszystkie elementy z kolejek H1 i H2, niszcząc je przy tym;
to nazywamy ją złączalną kolejką priorytetową.
Najprostszą, choć niezbyt efektywną implementację kolejki priorytetowej stanowi zwykła lista. Znacznie efektywniejszy jest kopiec binarny (wykorzystywany w algorytmie HeapSort), nie pozwala on jednak na szybkie łączenie kolejek. Przedstawione na tym wykładzie struktury danych: kopiec dwumianowy i kopiec Fibonacciego, umożliwiają efektywne wykonywanie wszystkich operacji złączalnej kolejki priorytetowej.
Oto tabela kosztów poszczególnych operacji w wymienionych implementacjach, przy założeniu, że w kolejce(ach) jest aktualnie \( n \) elementów:
| Operacja | Lista | Kopiec Binarny | Kolejka Dwumianowa | Fibonacciego(*) |
|---|---|---|---|---|
| MakePQ | 1 | 1 | 1 | 1 |
| Insert | 1 | \( \lg n \) | \( \lg n \) | 1 |
| FindMin | \( n \) | 1 | \( \lg n \) | 1 |
| DelMin | \( n \) | \( \lg n \) | \( \lg n \) | \( \lg n \) |
| DecreaseKey | 1 | \( \lg n \) | \( \lg n \) | 1 |
| Delete | 1 | \( \lg n \) | \( \lg n \) | \( \lg n \) |
| Meld | 1 | \( n \) | \( \lg n \) | 1 |
(*) - koszt zamortyzowany
Uwaga: wyszukiwanie elementu nie należy do zestawu operacji (złączalnej) kolejki priorytetowej, dlatego w przypadku operacji DecreaseKey i Delete zakładamy, że jako parametr przekazywane jest dowiązanie do elementu, którego ma dotyczyć operacja.
Drzewa i kolejki dwumianowe
Wynaleziona w roku 1978 przez J. Vuillemina [V] kolejka dwumianowa to kolekcja drzew dwumianowych o następującej rekurencyjnej definicji: \( B_0 \) jest drzewem jednowęzłowym, a korzeń drzewa \( B_{k+1} \) (drzewa dwumianowego stopnia \( k \)) ma \( k+1 \) synów stanowiących korzenie drzew \( B_0 \),...,\( B_{k} \) (w tej właśnie kolejności, idąc od prawej do lewej).
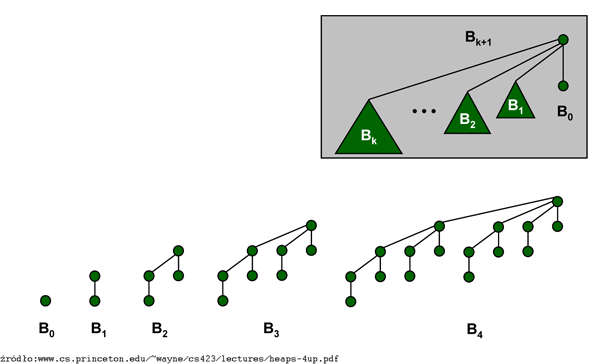
Poniższy lemat dotyczy podstawowych własności drzew dwumianowych:
Lemat
Drzewo dwumianowe \( B_k \)
(a) ma \( 2^k \) węzłów;
(b) ma wysokość \( k \);
(c) ma dokładnie \({k \choose i}\) węzłów na poziomie \( i \), dla \( 0\le i\le k \) (stąd nazwa 'drzewo dwumianowe');
(d) można otrzymać dołączając do drzewa \( B_{k-1} \) drugie drzewo \( B_{k-1} \) jako skrajnie lewego syna korzenia.
Dowód lematu pozostawiamy jako ćwiczenie.
Kolejka dwumianowa to lista drzew dwumianowych uporządkowana ściśle rosnąco względem stopni (idąc od prawej do lewej), przy czym każde drzewo spełnia warunek kopca: klucz w ojcu jest niewiększy niż klucze w synach. Z lematu 1(a) wynika, że w skład kolejki dwumianowej zawierającej \( n \) kluczy drzewo \( B_i \) wchodzi wtedy i tylko wtedy, gdy \( i \)-tym bitem rozwinięcia binarnego liczby \( n \) jest 1; w szczególności łączna liczba drzew to \( O(\lg n) \).
Operacje na kolejce dwumianowej
Ponieważ z warunku kopca wynika, że w każdym drzewie wchodzącym w skład kolejki element najmniejszy znajduje się w korzeniu, operacja FindMin wymaga jednokrotnego przejścia listy drzew. Jej koszt to \( O(\lg n) \) dla \( n \)-elementowej kolejki.
Najważniejszą operacją na kolejce dwumianowej, za pomocą której definiuje się większość pozostałych, jest Meld (łączenie kolejek).Jej działanie przypomina mechanizm dodawania liczb binarnych, przy czym sumowaniu jedynek na pozycji \( i \) w dodawanych liczbach odpowiada łączenie dwóch drzew dwumianowych stopnia \( i \) (zobacz lemat 1(d)): korzeń z mniejszym kluczem (w celu zachowania warunku kopca) zostaje korzeniem wynikowego drzewa \( B_{i+1} \) ('przeniesienia'), a drugi korzeń zostaje jego skrajnie prawym synem. Łączenie dwóch kolejek polega na przejściu obydwu list drzew i złączeniu drzew jednakowych stopni. Jego koszt jest proporcjonalny do sumy długości list.
Operacja Insert (wstawienie węzła) stanowi w zasadzie szczególny przypadek Meld (łączenie z kolejką jednoelementową).Operacja DelMin(H) polega na znalezieniu i usunięciu z listy H drzewa z najmniejszym kluczem, odcięciu jego korzenia (ten klucz jest wynikiem całej operacji) i połączeniu listy jego synów (stanowiącej poprawną kolejkę dwumianową) z H. Łączny koszt to \( O(\lg n) \) dla \( n \)-elementowej kolejki.Operację DecreaseKey wykonuje się podobnie jak poprawianie kopca binarnego przy wstawianiu elementu: zmniejszony klucz wędruje w górę swojego drzewa dwumianowego, zamieniając się miejscami z ojcem dopóty, dopóki nie zostanie odtworzony warunek kopca. W myśl lematu 1(b) maksymalna wysokość drzewa w \( n \)-elementowej kolejce to \( O(\lg n) \), więc koszt takiej operacji jest logarytmiczny.Operacja Delete sprowadza się do przesunięcia klucza, który mamy usunąć, do korzenia (jak w DecreaseKey), a potem usunięcia tego korzenia (jak w DelMin).
Kopce Fibonacciego
Ta struktura danych, wynaleziona przez Fredmana i Tarjana w roku 1984 [FT], stanowi ulepszenie kolejki dwumianowej, które pozwala uzyskać stały (w sensie zamortyzowanym) koszt operacji DecreaseKey, dominującej w algorytmie Dijkstry i jemu pokrewnych. Podstawowy pomysł polega tu na leniwym wykonywaniu operacji, tzn. odkładaniu pracy związanej z zarządzaniem strukturą danych do momentu, kiedy jest to naprawdę niezbędne. Podobnie jak kolejka dwumianowa, kopiec Fibonacciego to lista drzew, z których każde spełnia warunek kopca. Drzewa te nie są już jednak drzewami dwumianowymi (chociaż są im na tyle bliskie, że mają zbliżone własności) i nie są uporządkowane względem stopni korzeni.
Operacja Meld (łączenie kolejek) to po prostu sklejenie dwóch list drzew, bez prób porządkowania względem stopni korzeni czy eliminacji powtórzeń. Jej koszt to oczywiście O(1). Tak jak poprzednio, Insert stanowi szczególny przypadek Meld (łączenie z kolejką jednoelementową). Podczas operacji DelMin przychodzi czas na wykonanie odkładanej wcześniej pracy. Najpierw usuwany jest korzeń zawierający najmniejszy klucz, a jego synowie są dołączani do listy korzeni. Następnie odbywa się konsolidacja listy drzew, mająca na celu doprowadzenie do sytuacji, w której wszystkie korzenie na liście będą miały różne stopnie. Polega ona na przejściu przez listę korzeni i łączeniu drzew jednakowego stopnia - tak samo, jak łączyło się drzewa dwumianowe - a przy okazji uaktualnieniu wskaźnika do korzenia zawierającego najmniejszy klucz. Można ją zrealizować w czasie proporcjonalnym do liczby konsolidowanych drzew, jeśli skorzystamy z pomocniczej tablicy indeksowanej stopniami korzeni: pod indeksem \( i \) przechowujemy w niej wskaźnik do (jedynego) korzenia stopnia \( i \) w przetworzonej części listy, albo NULL, jeśli w tym fragmencie listy korzenia o stopniu \( i \) nie ma.
Oto oszacowanie kosztu zamortyzowanego operacji DelMin: Każdemu drzewu w kopcu Fibonacciego w chwili jego pojawienia się na liście przypisujemy jednostkę kredytu. Niech \( t \) oznacza liczbę drzew w kopcu przed wykonaniem operacji, \( d \) - stopień korzenia zawierającego najmniejszy klucz, zaś \( k \) - liczbę wykonań operacji łączenia drzew. Żeby wykonać Delmin, musimy wykonać pracę proporcjonalną do \( t+d+k \). Ponieważ przy każdym połączeniu drzew uwalniana jest jednostka kredytu, uzyskujemy w ten sposób \( k-1 \) jednostek. Jak pokażemy później (Tw. 2), rozmiar drzewa w kopcu Fibonacciego jest wykładniczy względem stopnia korzenia. Wynika z tego, że po konsolidacji, kiedy wszystkie drzewa w kopcu będą miały różne stopnie, ich liczba \( t+d-k+2 \) będzie \( O(\lg n) \), gdzie \( n \) to rozmiar kopca po operacji. Tak więc do wykonania koniecznej pracy i utrzymania niezmiennika "jedna jednostka kredytu związana z każdym drzewem w kopcu" wystarczy \( O(\lg n) \) dodatkowych jednostek kredytu - i taki właśnie jest koszt zamortyzowany operacji DelMin.
Operacja DecreaseKey\( (H, x, y) \) mogłaby polegać na zmniejszeniu wartości klucza oraz - o ile został naruszony warunek kopca - odcięciu poddrzewa o korzeniu \( x \) i dołączeniu go do listy korzeni. To jednak, zbyt gwałtownie zmniejszając rozmiary poddrzew, powodowałoby, że twierdzenie 2 nie byłoby prawdziwe, a nasza analiza operacji DelMin przestałaby działać. Bedziemy zatem odcinać poddrzewa, ale w sposób kontrolowany: każdy nie będący korzeniem węzeł może stracić co najwyżej jednego syna. Jeśli sytuacja wymaga odcięcia drugiego syna, to taki węzeł sam zostaje odcięty od swojego ojca (co może oczywiście spowodować dalsze rekurencyjne odcięcia). Do utrzymywania informacji o stanie węzła wystarcza znacznik logiczny, który ma wartość TRUE wtedy i tylko wtedy, gdy dany węzeł stracił dokładnie jednego syna od czasu, kiedy sam stał się synem innego węzła (w wyniku łączenia drzew).
Argumentacja, że koszt zamortyzowany operacji DecreaseKey to \( O(1) \), jest następująca: Oprócz kredytu przypisywanego do drzew będziemy dodatkowo przypisywać dwie jednostki kredytu każdemu węzłowi \( v \), który traci jednego syna, kosztem kredytu obciążając operację, która spowodowała odcięcie (dla każdej operacji jest co najwyżej jeden taki węzeł). Kiedy następuje odcięcie drugiego syna \( v \) (a więc także i odcięcie samego węzła \( v \) od ojca), koszt tego zabiegu pokrywa jedna jednostka kredytu, a druga pozostaje przypisana do nowo wstawionego na listę drzewa o korzeniu \( v \) (w celu utrzymania niezmiennika "jedna jednostka kredytu związana z każdym drzewem w kopcu"). Podczas jednej operacji DecreaseKey może nastąpić cała seria odcięć, ale wszystkie (oprócz być może ostatniego) są już wcześniej z góry opłacone. Operacja Delete\( (H, x) \) polega na odcięciu węzła \( x \) od ojca (o ile \( x \) nie jest korzeniem) - jak w DecreaseKey - a następnie usunięciu \( x \), bedącego teraz korzeniem - jak w Delmin. Koszt zamortyzowany tej operacji to \( O(\lg n) \) dla \( n \)-elementowego kopca.
Aby nasza analiza operacji na kopcach Fibonacciego była kompletna, pozostaje jeszcze udowodnić:
Twierdzenie [Twierdzenie 2]
Rozmiar drzewa o korzeniu \( x \) w kopcu Fibonacciego jest wykładniczy względem stopnia \( x \).
Dowód: Niech \( y_1, \ldots, y_k \) będą aktualnymi synami \( x \), w kolejności ich przyłączania do \( x \). Pokażemy, że dla \( i\ge 2 \) węzeł \( y_i \) ma stopień co najmniej \( i-2 \). W chwili przyłączania węzła \( y_i \) węzeł \( x \) miał co najmniej \( i-1 \) synów (węzły \( y_1,\ldots,y_{i-1} \) oraz być może jeszcze jakieś, które zostały później odcięte). Ponieważ przyłączane węzły mają zawsze taki sam stopień, \( y_i \) miał wtedy stopień co najmniej \( i-1 \), a potem mógł stracić co najwyżej jednego syna (bo inaczej sam zostałby odcięty od \( x \)). Oznaczmy przez \( a_k \) najmniejszą możliwa liczbe węzłów w drzewie stopnia \( k \) z kopca Fibonacciego. Z powyższych rozważań wynikają zależności:\( a_0 = 1 \), \( a_k \ge 2+\sum_{i=2}^k a_{i-2} \) (liczba 2 po prawej stronie nierówności bierze sie z uwzględnienia węzłów \( y_1 \) oraz \( x \)). Z łatwej do udowodnienia przez indukcję tożsamości \( F_{k+2} = 2+\sum_{i=2}^k F_i \), gdzie \( F_i \) to \( i \)-ta liczba Fibonacciego (stąd nazwa tej struktury danych!), zdefiniowana rekurencyjnie: \( F_0 = 0, F_1 = 1, F_{i+2} = F_{i+1}+F_i \), wynika, że\( a_k \ge F_{k+2} \). Ogólnie znany (również łatwy do udowodnienia przez indukcję) fakt, że \( F_{k+2}\ge\phi^k \), gdzie \( \phi = (1+\sqrt{5})/2 = 1.618... \), kończy dowód twierdzenia.
Literatura
Literatura
[CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, 'Wprowadzenie do algorytmów', WNT, Warszawa 2004.
[FT] Michael L. Fredman, Robert E. Tarjan, 'Fibonacci heaps and their uses in improved network optimization algorithms', Journal of the ACM 34(3), 1987, 596-615.
[V] Jean Vuillemin, 'A data structure for manipulating priority queues', Communications of the ACM 21(4), 1978, 309-315.