Drzewa i kolejki dwumianowe

Wynaleziona w roku 1978 przez J. Vuillemina [V] kolejka dwumianowa to kolekcja drzew dwumianowych o następującej rekurencyjnej definicji: \( B_0 \) jest drzewem jednowęzłowym, a korzeń drzewa \( B_{k+1} \) (drzewa dwumianowego stopnia \( k \)) ma \( k+1 \) synów stanowiących korzenie drzew \( B_0 \),...,\( B_{k} \) (w tej właśnie kolejności, idąc od prawej do lewej).

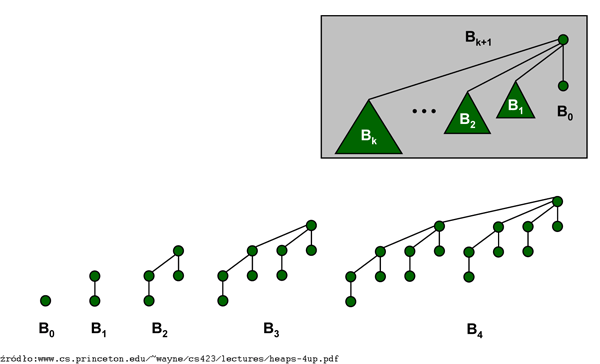
Poniższy lemat dotyczy podstawowych własności drzew dwumianowych:

Lemat

Drzewo dwumianowe \( B_k \)

(a) ma \( 2^k \) węzłów;

(b) ma wysokość \( k \);

(c) ma dokładnie \({k \choose i}\) węzłów na poziomie \( i \), dla \( 0\le i\le k \) (stąd nazwa 'drzewo dwumianowe');

(d) można otrzymać dołączając do drzewa \( B_{k-1} \) drugie drzewo \( B_{k-1} \) jako skrajnie lewego syna korzenia.

Dowód lematu pozostawiamy jako ćwiczenie.

Kolejka dwumianowa to lista drzew dwumianowych uporządkowana ściśle rosnąco względem stopni (idąc od prawej do lewej), przy czym każde drzewo spełnia warunek kopca: klucz w ojcu jest niewiększy niż klucze w synach. Z lematu 1(a) wynika, że w skład kolejki dwumianowej zawierającej \( n \) kluczy drzewo \( B_i \) wchodzi wtedy i tylko wtedy, gdy \( i \)-tym bitem rozwinięcia binarnego liczby \( n \) jest 1; w szczególności łączna liczba drzew to \( O(\lg n) \).