Find-Union
Sumowanie zbiorów rozłącznych
Niekiedy przydatne okazuje się grupowanie elementów w rozłączne zbiory. Struktura danych dla zbiorów rozłącznych pozwala zarządzać taką rodziną dynamicznych (tzn. zmieniających się w czasie) zbiorów rozłącznych. Do każdego zbioru odwołujemy się przez jego reprezentanta (zazwyczaj jest to jakiś element tego zbioru), przy czym wymagamy, żeby dwa zapytania o reprezentanta danego zbioru dawały taki sam wynik, jeśli w międzyczasie sam zbiór się nie zmieniał. Do dyspozycji mamy trzy operacje:
- MakeSet(x): tworzy nowy jednoelementowy zbiór { x }, którego reprezentantem jest oczywiście x (zakładamy, że x nie należy do żadnego innego zbioru w rodzinie);
- Find(x): zwraca reprezentanta zbioru, do którego należy x;
- Union(x,y): łączy dwa zbiory, których reprezentantami są x i y, w nowy zbiór będący ich teoriomnogościową sumą; dwa pierwotne zbiory (zakładamy, że były różne) są przy tym niszczone.
W naszych rozważaniach dotyczących kosztów powyższych operacji w różnych implementacjach struktury danych dla zbiorów rozłącznych będziemy brali pod uwagę dwa parametry: n, czyli łączną liczbę operacji MakeSet (bez straty ogólności można założyć, że wszystkie te operacje są wykonywane na początku), oraz m, czyli łączną liczbę wszystkich operacji MakeSet, Find i Union (w szczególności mamy \( n\le m \)). Nietrudno zauważyć, że liczba operacji Union nie jest większa niż n-1 (bo każda z nich zmniejsza liczbę zbiorów w rodzinie o jeden).
Większość zastosowań struktur danych dla zbiorów rozłącznych sprowadza się do zarządzania pewną dynamicznie rozrastającą się relacją równoważności (jej klasy abstrakcji to nasze zbiory rozłączne). Jako przykłady można wymienić:
- algorytm Kruskala znajdowania minimalnego drzewa rozpinającego;
- rozpoznawanie spójnych składowych w dynamicznie rozrastającym się grafie nieskierowanym;
- generowanie labiryntów;
- rozpoznawanie obszarów na obrazach w postaci cyfrowej.
Implementacja listowa
Oto prosta implementacja struktury danych dla zbiorów rozłącznych: Każdy zbiór jest reprezentowany jako lista swoich elementów. Reprezentantem zbioru jest pierwszy element na liście. Każdy element ma dodatkowo bezpośredni wskaźnik do reprezentanta, dzięki czemu koszt operacji Find to O(1). Operacja MakeSet jest również bardzo prosta i polega na utworzeniu jednoelementowej listy.
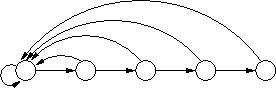
Bardziej kłopotliwa jest operacja Union: wprawdzie koszt połączenia dwóch list jest stały, ale trzeba jeszcze we wszystkich elementach listy, która jest dołączana na koniec drugiej, uaktualnić wskaźnik do reprezentanta, co zajmuje czas liniowy względem jej długości. Prosta sztuczka zwana heurystyką łączenia z wyważaniem pozwala zmniejszyć koszt operacji Union (w sensie zamortyzowanym). Polega ona na tym, że podczas operacji Union zawsze dołączamy krótszą listę na koniec dłuższej (wymaga to przechowywania wraz z listą dodatkowego atrybutu "rozmiar"). Jako ćwiczenie pozostawiamy dowód faktu, że teraz koszt wykonania m operacji MakeSet, Find i Union, spośród których n to MakeSet, wynosi \( O(m+n\log n) \).
Implementacja drzewiasta
Alternatywna implementacja to las zbiorów rozłącznych, w którym każde drzewo odpowiada jednemu ze zbiorów z naszej rodziny. Z każdym elementem zbioru jest związany wskaźnik do pewnego innego elementu (jego ojca w drzewie). Wyjątek stanowi reprezentant zbioru (a zarazem korzeń drzewa), którego wskaźnik wskazuje na niego samego. Operacja MakeSet tworzy jednoelementowe drzewo z korzeniem wskazującym na samego siebie. Operacja Union polega na przestawieniu wskaźnika jednego reprezentanta tak, by wskazywał na drugiego. Koszt obydwu tych operacji to oczywiście O(1). <
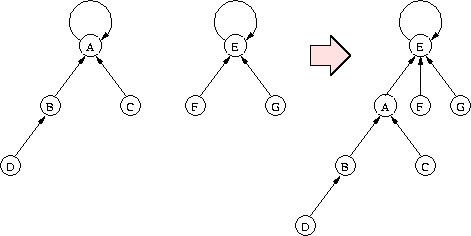
Operacja Find polega na przejściu po wskaźnikach ścieżki od danego węzła do reprezentanta (czyli korzenia). Jej koszt jest proporcjonalny do głębokości danego węzła w drzewie. Nietrudno podać przykład ciągu operacji, który powoduje powstanie drzewa w kształcie listy, czyli pesymistyczny koszt takiej operacji Find to \( \Theta(n) \) dla rodziny zbiorów zawierającej łącznie n elementów.
Łączenie według wysokości
Podobną do stosowanego dla list "łączenia z wyważaniem" metodą można zapewnić lepsze ograniczenie kosztu operacji Find. W korzeniu każdego drzewa przechowujemy dodatkowy atrybut - jego wysokość - i podczas operacji Union zawsze przyłączamy niższe drzewo do wyższego (remisy rozstrzygając dowolnie). Koszt Union pozostaje stały, a nietrudno pokazać, że teraz wysokość drzewa jest co najwyżej logarytmiczna względem jego rozmiaru, skąd wynika, że pesymistyczny koszt operacji Find to \( O(\lg n) \).
Kompresja ścieżki
Równie prosta, a bardzo skuteczna heurystyka polega na tym, że w ramach operacji Find po wyznaczeniu korzenia v drzewa zawierającego węzeł x przebiegamy ponownie ścieżkę od x do v i przyłączamy wszystkie napotkane węzły bezpośrednio do v. Dzięki temu późniejsze operacje Find dotyczące węzłów na ścieżce od x do v oraz ich potomków będą kosztowały mniej.
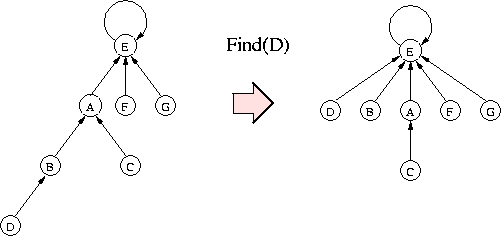
Przy stosowaniu kompresji ścieżki utrzymywanie poprawnych wartości atrybutu "wysokość" wykorzystywanego podczas wykonywania Union byłoby zbyt kosztowne. Zamiast tego będziemy przechowywać w węzłach atrybut "ranga", który będziemy wykorzystywać i modyfikować dokładnie tak samo, jak atrybut "wysokość" przy łączeniu według wysokości: podczas operacji Union przyłączamy drzewo o niższej randze do drzewa o wyższej randze, a w przypadku remisu po przyłączeniu zwiększamy rangę korzenia o 1. Tak więc ranga stanowi górne ograniczenie wysokości drzewa, a w myśl zadania 3 jej wartość nie przekracza \( \lfloor\lg n\rfloor \) dla rodziny zbiorów zawierającej łącznie n elementów. Poniższy lemat wylicza kilka dalszych użytecznych własności rang:
Lemat Lemat 1
W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżek
(a) ranga węzła, który nie jest korzeniem, jest mniejsza (ściśle) niż ranga jego ojca;
(b) zawsze kiedy ojciec danego węzła się zmienia, to nowy ojciec ma większą rangę niż stary;
(c) jeśli ranga reprezentanta pewnego zbioru jest równa r, to rozmiar tego zbioru wynosi co najmniej \( 2^r \);
(d) jeśli zbiory zawierają łącznie \( n \) elementów, to jest co najwyżej \( n/2^r \) węzłów rangi r, dla dowolnego \( r\ge 0 \). Dowód lematu pozostawiamy jako ćwiczenie.
Zanim przystąpimy do analizy kosztu opisanych wyżej operacji, zdefiniujemy dwie funkcje: jedną bardzo szybko rosnącą i drugą, rosnącą bardzo wolno. Niech \( F(0) = 1 \),
\( F(k) = 2^{2^{.^{.^{.^2}}\Big\}k}} = 2^{F(k-1)} \) dla k>0.
Oto kilka pierwszych wartości funkcji F:
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| F(k) | 1 | 2 | 4 | 16 | 65536 | \( 2^{65536} \) |
Jak widać, funkcja F rośnie bardzo szybko.
Funkcję logarytm iterowany definiuje się następująco: \( G(n) = \lg^* n = \min\{k:F(k)\ge n\} \). Oto tabelka początkowych wartości funkcji G:
| n | 0..1 | 2 | 3..4 | 5..16 | 17..65536 | \( 65537..2^{65536} \) |
| G(n) | 0 | 1 | 2 | 3 | 4 | 5 |
Funkcja G rośnie niesłychanie wolno i dla wszystkich n mających jakiekolwiek praktyczne znaczenie nie przekracza wartości 5.
Na potrzeby analizy kosztu zamortyzowanego operacji na lesie zbiorów rozłącznych przyporządkujemy każdy węzeł do jednego z ponumerowanych bloków: jeśli mianowicie dany węzeł ma rangę r, to przyporządkowujemy go do bloku o numerze \( \lg^* r \). Ponieważ rangi węzłów mieszczą się w zakresie od 0 do \( \lfloor \lg n\rfloor \), mamy \( \lg^* n \) bloków o numerach od 0 do \( \lg^* \lfloor \lg n\rfloor = \lg^*n -1 \). Możemy juz udowodnić
Twierdzenie 2 (Hopcroft, Ullman [HU])
W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżki koszt m operacji, spośród których n to operacje MakeSet, wynosi \( O(m\lg^* n) \).
Dowód: Ponieważ operacje MakeSet i Union mają koszt stały, wystarczy oszacować łączny koszt m operacji Find. Koszt operacji Find(x) jest proporcjonalny do liczby węzłów na ścieżce od x do korzenia (przed kompresją). Rozbijemy koszt każdej takiej operacji na składniki, które zaksięgujemy do różnych pul. Sumując pule, dostaniemy łączny koszt wszystkich operacji Find.
Dla wierzchołka v leżącego na ścieżce od x do korzenia:
Przypadek 1: Jeśli v lub jego ojciec jest korzeniem, to jednostkę kosztu księgujemy do puli KONIEC_ŚCIEŻKI;
Przypadek 2: Jeśli v i ojciec v są w różnych blokach, to jednostkę kosztu księgujemy do puli ZMIANA_BLOKU;
Przypadek 3: Jeśli v i ojciec v sa w tym samym bloku, to jednostkę kosztu księgujemy do puli TEN_SAM_BLOK.
Przypadek 1 dla każdej operacji Find występuje co najwyżej dwukrotnie, więc łączna zawartość puli KONIEC_ŚCIEŻKI to co najwyżej 2m. Podczas pojedynczej operacji Find przypadek 2 może wystąpić co najwyżej \( \lg^* n-1 \) razy (bo jest nie więcej niż \( \lg^*n \) różnych bloków, a w myśl lematu 1(a) rangi na ścieżce do korzenia tworzą ciąg rosnący). Zatem łączna zawartość puli ZMIANA_BLOKU to \( O(m\lg^* n) \).
Pozostaje nam zatem oszacować zawartość puli TEN_SAM_BLOK. Jeśli v jest w bloku o numerze \( g>0 \), przypadek 3 może dla niego zajść co najwyżej \( F(g)-F(g-1) \) razy (wynika to z lematu 1(b): ranga ojca v za każdym razem rośnie, a kiedy v i ojciec v znajdą się w różnych blokach, to dla v już do końca będzie zachodził przypadek 2 lub 1). Dla v należącego do bloku \( g=0 \) przypadek 3 może zajść co najwyżej raz.
Na mocy lematu 1(d) liczbę węzłów w bloku \( g>0 \) można oszacować z góry przez
\( \displaystyle\sum_{r=F(g-1)+1}^{F(g)} n/2^r\le n/2^{F(g-1)+1}(1+1/2+1/4+\cdots)\le n/2^{F(g-1)}=n/F(g) \)
skąd łączny wkład do puli TEN_SAM_BLOK pochodzący od węzłów z bloku \( g>0 \) szacuje się z góry przez \( (F(g)-F(g-1))\cdot n/F(g)\le n \) (to ostatnie oszacowanie jest prawdziwe również dla \( g=0 \)). Sumując po g, dostajemy górne oszacowanie zawartości puli TEN_SAM_BLOK \( O(n\lg^* n) \).
Uwaga: Wynikające z powyższego twierdzenia oszacowanie kosztu zamortyzowanego operacji Find \( O(\lg^* n) \) można poprawić! Robert Tarjan [T1,T2] podał asymptotycznie optymalne oszacowanie tego kosztu przez tzw. funkcyjną odwrotność funkcji Ackermanna, rosnącą jeszcze wolniej niż funkcja \( \lg^* \). Przystępny opis górnego oszacowania (chociaż znacznie bardziej skomplikowany niż powyższy dowód) można znaleźć w książce [CLRS].
Literatura
Literatura
[CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, Wprowadzenie do algorytmów, Wydawnictwa Naukowo-Techniczne, Warszawa 2004.
[HU] J.E.Hopcroft, J.D.Ullman, Set merging algorithms, SIAM Journal on Computing, 2(4) ,1973, 294-303.
[T1] R.E.Tarjan, Efficiency of a good but not linear set union algorithm, J. Assoc. Comput. Mach. 22, 1975, 215-225.
[T2] R.E.Tarjan, A class of algorithms which require non-linear time to maintain disjoint sets, J. Comput. Syst. Sci. 19, 1979, 110-127.