Implementacja drzewiasta

Alternatywna implementacja to las zbiorów rozłącznych, w którym każde drzewo odpowiada jednemu ze zbiorów z naszej rodziny. Z każdym elementem zbioru jest związany wskaźnik do pewnego innego elementu (jego ojca w drzewie). Wyjątek stanowi reprezentant zbioru (a zarazem korzeń drzewa), którego wskaźnik wskazuje na niego samego. Operacja MakeSet tworzy jednoelementowe drzewo z korzeniem wskazującym na samego siebie. Operacja Union polega na przestawieniu wskaźnika jednego reprezentanta tak, by wskazywał na drugiego. Koszt obydwu tych operacji to oczywiście O(1). <

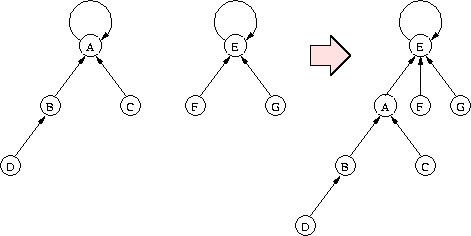
Operacja Find polega na przejściu po wskaźnikach ścieżki od danego węzła do reprezentanta (czyli korzenia). Jej koszt jest proporcjonalny do głębokości danego węzła w drzewie. Nietrudno podać przykład ciągu operacji, który powoduje powstanie drzewa w kształcie listy, czyli pesymistyczny koszt takiej operacji Find to \( \Theta(n) \) dla rodziny zbiorów zawierającej łącznie n elementów.

Łączenie według wysokości

Podobną do stosowanego dla list "łączenia z wyważaniem" metodą można zapewnić lepsze ograniczenie kosztu operacji Find. W korzeniu każdego drzewa przechowujemy dodatkowy atrybut - jego wysokość - i podczas operacji Union zawsze przyłączamy niższe drzewo do wyższego (remisy rozstrzygając dowolnie). Koszt Union pozostaje stały, a nietrudno pokazać, że teraz wysokość drzewa jest co najwyżej logarytmiczna względem jego rozmiaru, skąd wynika, że pesymistyczny koszt operacji Find to \( O(\lg n) \).

Kompresja ścieżki

Równie prosta, a bardzo skuteczna heurystyka polega na tym, że w ramach operacji Find po wyznaczeniu korzenia v drzewa zawierającego węzeł x przebiegamy ponownie ścieżkę od x do v i przyłączamy wszystkie napotkane węzły bezpośrednio do v. Dzięki temu późniejsze operacje Find dotyczące węzłów na ścieżce od x do v oraz ich potomków będą kosztowały mniej.

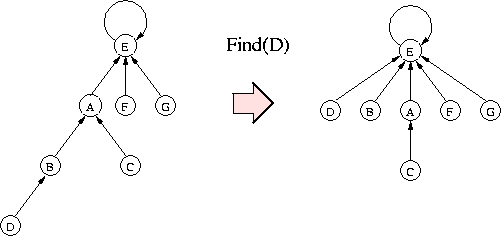
Przy stosowaniu kompresji ścieżki utrzymywanie poprawnych wartości atrybutu "wysokość" wykorzystywanego podczas wykonywania Union byłoby zbyt kosztowne. Zamiast tego będziemy przechowywać w węzłach atrybut "ranga", który będziemy wykorzystywać i modyfikować dokładnie tak samo, jak atrybut "wysokość" przy łączeniu według wysokości: podczas operacji Union przyłączamy drzewo o niższej randze do drzewa o wyższej randze, a w przypadku remisu po przyłączeniu zwiększamy rangę korzenia o 1. Tak więc ranga stanowi górne ograniczenie wysokości drzewa, a w myśl zadania 3 jej wartość nie przekracza \( \lfloor\lg n\rfloor \) dla rodziny zbiorów zawierającej łącznie n elementów. Poniższy lemat wylicza kilka dalszych użytecznych własności rang:

Lemat Lemat 1

W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżek

(a) ranga węzła, który nie jest korzeniem, jest mniejsza (ściśle) niż ranga jego ojca;

(b) zawsze kiedy ojciec danego węzła się zmienia, to nowy ojciec ma większą rangę niż stary;

(c) jeśli ranga reprezentanta pewnego zbioru jest równa r, to rozmiar tego zbioru wynosi co najmniej \( 2^r \);

(d) jeśli zbiory zawierają łącznie \( n \) elementów, to jest co najwyżej \( n/2^r \) węzłów rangi r, dla dowolnego \( r\ge 0 \). Dowód lematu pozostawiamy jako ćwiczenie.

Zanim przystąpimy do analizy kosztu opisanych wyżej operacji, zdefiniujemy dwie funkcje: jedną bardzo szybko rosnącą i drugą, rosnącą bardzo wolno. Niech \( F(0) = 1 \),

\( F(k) = 2^{2^{.^{.^{.^2}}\Big\}k}} = 2^{F(k-1)} \) dla k>0.

Oto kilka pierwszych wartości funkcji F:

k	0	1	2	3	4	5
F(k)	1	2	4	16	65536	\( 2^{65536} \)

Jak widać, funkcja F rośnie bardzo szybko.

Funkcję logarytm iterowany definiuje się następująco: \( G(n) = \lg^* n = \min\{k:F(k)\ge n\} \). Oto tabelka początkowych wartości funkcji G:

n	0..1	2	3..4	5..16	17..65536	\( 65537..2^{65536} \)
G(n)	0	1	2	3	4	5

Funkcja G rośnie niesłychanie wolno i dla wszystkich n mających jakiekolwiek praktyczne znaczenie nie przekracza wartości 5.

Na potrzeby analizy kosztu zamortyzowanego operacji na lesie zbiorów rozłącznych przyporządkujemy każdy węzeł do jednego z ponumerowanych bloków: jeśli mianowicie dany węzeł ma rangę r, to przyporządkowujemy go do bloku o numerze \( \lg^* r \). Ponieważ rangi węzłów mieszczą się w zakresie od 0 do \( \lfloor \lg n\rfloor \), mamy \( \lg^* n \) bloków o numerach od 0 do \( \lg^* \lfloor \lg n\rfloor = \lg^*n -1 \). Możemy juz udowodnić

Twierdzenie 2 (Hopcroft, Ullman [HU])

W lesie zbiorów rozłącznych z łączeniem według rangi i kompresją ścieżki koszt m operacji, spośród których n to operacje MakeSet, wynosi \( O(m\lg^* n) \).

Dowód: Ponieważ operacje MakeSet i Union mają koszt stały, wystarczy oszacować łączny koszt m operacji Find. Koszt operacji Find(x) jest proporcjonalny do liczby węzłów na ścieżce od x do korzenia (przed kompresją). Rozbijemy koszt każdej takiej operacji na składniki, które zaksięgujemy do różnych pul. Sumując pule, dostaniemy łączny koszt wszystkich operacji Find.

Dla wierzchołka v leżącego na ścieżce od x do korzenia:

Przypadek 1: Jeśli v lub jego ojciec jest korzeniem, to jednostkę kosztu księgujemy do puli KONIEC_ŚCIEŻKI;

Przypadek 2: Jeśli v i ojciec v są w różnych blokach, to jednostkę kosztu księgujemy do puli ZMIANA_BLOKU;

Przypadek 3: Jeśli v i ojciec v sa w tym samym bloku, to jednostkę kosztu księgujemy do puli TEN_SAM_BLOK.

Przypadek 1 dla każdej operacji Find występuje co najwyżej dwukrotnie, więc łączna zawartość puli KONIEC_ŚCIEŻKI to co najwyżej 2m. Podczas pojedynczej operacji Find przypadek 2 może wystąpić co najwyżej \( \lg^* n-1 \) razy (bo jest nie więcej niż \( \lg^*n \) różnych bloków, a w myśl lematu 1(a) rangi na ścieżce do korzenia tworzą ciąg rosnący). Zatem łączna zawartość puli ZMIANA_BLOKU to \( O(m\lg^* n) \).

Pozostaje nam zatem oszacować zawartość puli TEN_SAM_BLOK. Jeśli v jest w bloku o numerze \( g>0 \), przypadek 3 może dla niego zajść co najwyżej \( F(g)-F(g-1) \) razy (wynika to z lematu 1(b): ranga ojca v za każdym razem rośnie, a kiedy v i ojciec v znajdą się w różnych blokach, to dla v już do końca będzie zachodził przypadek 2 lub 1). Dla v należącego do bloku \( g=0 \) przypadek 3 może zajść co najwyżej raz.

Na mocy lematu 1(d) liczbę węzłów w bloku \( g>0 \) można oszacować z góry przez

\( \displaystyle\sum_{r=F(g-1)+1}^{F(g)} n/2^r\le n/2^{F(g-1)+1}(1+1/2+1/4+\cdots)\le n/2^{F(g-1)}=n/F(g) \)

skąd łączny wkład do puli TEN_SAM_BLOK pochodzący od węzłów z bloku \( g>0 \) szacuje się z góry przez \( (F(g)-F(g-1))\cdot n/F(g)\le n \) (to ostatnie oszacowanie jest prawdziwe również dla \( g=0 \)). Sumując po g, dostajemy górne oszacowanie zawartości puli TEN_SAM_BLOK \( O(n\lg^* n) \).

Uwaga: Wynikające z powyższego twierdzenia oszacowanie kosztu zamortyzowanego operacji Find \( O(\lg^* n) \) można poprawić! Robert Tarjan [T1,T2] podał asymptotycznie optymalne oszacowanie tego kosztu przez tzw. funkcyjną odwrotność funkcji Ackermanna, rosnącą jeszcze wolniej niż funkcja \( \lg^* \). Przystępny opis górnego oszacowania (chociaż znacznie bardziej skomplikowany niż powyższy dowód) można znaleźć w książce [CLRS].