Algorytmy tekstowe I

Algorytmy tekstowe mają decydujące znaczenie przy wyszukiwaniu informacji typu tekstowego, ten typ informacji jest szczególnie popularny w informatyce, np. w edytorach tekstowych i wyszukiwarkach internetowych. Tekst jest ciągiem symboli. Przyjmujemy, że jest on zadany tablicą \( x[1,\ldots,n] \), elementami której są symbole ze skończonego zbioru A (zwanego alfabetem). Liczba \( n=|x| \) jest długością (rozmiarem) tekstu. W większości naszych algorytmów jedyne operacje dopuszczalne na symbolach wejściowych to porównania dwóch symboli.

Algorytmy na tekstach wyróżniają się tym, że wykorzystują specyficzne, kombinatoryczne własności tekstów. Okresem tekstu \( x \) jest każda niezerowa liczba naturalna \( p \) taka, że \( x[i]=x[i+p] \), dla każdego \( i \), dla którego obie strony są zdefiniowane. Przez per(x) oznaczmy minimalny okres x.

Pojęciem dualnym do okresu jest prefikso-sufiks tekstu. Jest to najdłuższy właściwy (nie będący całym tekstem) prefiks tekstu x będący jednocześnie jego sufiksem. Oczywiste jest, że \( |x|-per(x) \) jest długością prefikso-sufiksu x. Jeśli \( per(x)=|x| \) to prefikso-sufiksem x jest słowo puste o długości zerowej.

Oznaczmy przez \( P[k] \) rozmiar prefikso-sufiksu \( x[1..k] \). Zatem \( per(x)=n-P[n] \), gdzie \( n=|x| \).

Przykład
Dla \( x\ =\ abababababb \) mamy:
\( P[1..11]\ =\ [0,\ 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 0]. \)
Wartość \( P[0] \) jest wartością sztuczną (przyjmiemy, że \( P[0]=-1 \)).

Wprowadzimy również tablicę ‘’'silnych prefikso-sufiksów dla wzorca \( x[1..m] \): jeśli \( j < |x| \), to \( P'[j]=k \), gdzie \( k \) jest maksymalnym rozmiarem słowa będącego właściwym prefiksem i sufiksem \( x[1..j] \) i spełniającego dodatkowy warunek \( x[k+1]\ne x[j+1] \) dla \( j < n \).
Jeśli takiego k nie ma, to przyjmujemy \( P'[j]=-1 \).
Przyjmujemy ponadto, że \( P'[m]=P[m] \).
Wartości tablicy P' mogą być znacznie mniejsze niż wartości tablicy P.

Przykład
Dla \( x\ =\ abaab \) mamy:
\( P[0..5]\ =\ [-1,\ 0,\ 0,\ 1,\ 1,\ 2\ ];\ \ P'[0..5]\ =\ [-1,\ 0,\ -1,\ 1,\ 0,\ 2\ ]. \)

Obliczanie tablicy Prefikso-Sufiksów

Przedstawimy jeden z możliwych algorytmów liniowych obliczania tablicy P. Jest to iteracyjna wersja algorytmu rekurencyjnego, który moglibyśmy otrzymać korzystając z faktu:

Jeśli \( x[j]=x[t+1] \) oraz \( t=P[j-1] \), to \( P[j]= t+1 \)

W algorytmie obliczania \( P[j] \) korzystamy z wartości \( P[k] \), dla \( k < j \).

Algorytm Prefikso-Sufiksy

P[0]:=-1; t:=-1; 
for j:=1 to m do 
  begin 
    while t=> 0 and x[t+1] <> x[j] do t:=P[t]; 
    t:=t+1; P[j]:=t; 
end;

Złożoność liniowa wynika stąd, że w każdej iteracji zwiększamy wartość t co najwyżej o jeden, a wykonanie każdej operacji \( t:=P[t] \) zmniejsza wartość t co najmniej o jeden. Proste zastosowanie zasady magazynu (lub potencjału) implikuje, że operacji \( t:=P[t] \) wykonujemy co najwyżej n. Dowód poprawności pozostawiamy jako ćwiczenie.

Minimalne słowo pokrywające

Pokażemy pewne proste zastosowanie tablic prefikso-sufiksów. Słowem pokrywającym tekst x jest każdy taki tekst y, którego wystąpienia w x pokrywają cały tekst x. Na przykład słowo y=aba pokrywa tekst x=ababaaba, natomiast nie pokrywa tekstu abaaababa. Zajmiemy się problemem: obliczyć w czasie liniowym długość najkrótszego słowa pokrywającego dany tekst x.

Niech \( S[i] \) będzie rozmiarem minimalnego słowa pokrywającego tekst \( x[1..i] \).

Następujący algorytm oblicza długość minimalnego słowa pokrywającego tekstu x. Algorytm jest efektywny ponieważ liczy dodatkową tablicę Zakres. W \( i \)-tej iteracji algorytmu pamiętany jest znany dotychczas zakres każdego minimalnego słowa pokrywającego.

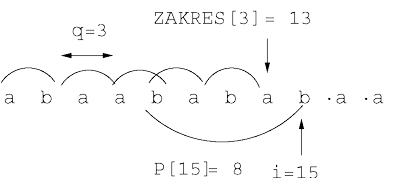
Rysunek 1: \( i \)-ta iteracja algorytmu dla \( i=15 \) oraz słowa \( x\ =\ abaabababaababa\ldots \). Tuż przed rozpoczęciem tej iteracji mamy \( P[i]=8 \), \( S[8]=2,\ Zakres[3]=13 \). Zatem spełniony jest warunek \( i-Zakres[S[P[i]] \le S[P[i]] \). Po zakończeniu \( i \)-tej iteracji mamy \( S[15]=3,Zakres[3]=15 \).

Algorytm Rozmiar-Minimalnego-Pokrycia

for i:=2 to n do begin
    Zakres [i]=i; S [i]=i;
end;
for i:=2 to n  do
    if P [i]>0 and i-Zakres[S[P[i]]] <= S[P[i]] then begin
      S[i] :=S[P[i]]; Zakres[S[P[i]] :=i
    end;
return S[n];

Algorytmy Knutha-Morrisa-Pratta i Morrisa-Pratta

Przedstawimy klasyczne algorytmy Knutha-Morrisa-Pratta (w skrócie KMP) oraz Morrisa-Pratta (w skrócie MP) dla problemu string-matchingu: obliczyć w w tekście \( y \) wszystkie (lub pierwsze) wystąpienia danego tekstu \( x \), zwanego wzorcem.

Algorytmy MP i KMP różnią się jedynie tym że jeden używa tablicy P a drugi P'. Tablica P' jest bardziej skomplikowana, będziemy się zatem głównie koncentrować na algorytmie MP, poza wersją on-line (gdzie waśnie P' ma przewagę).

Oznaczmy \( m=|x|, n=|y| \), gdzie \( m\le n \).

Zaczniemy od obliczania jedynie pierwszego wystąpienia. Algorytm MP przegląda tekst y od lewej do prawej, sprawdzając, czy jest zgodność na pozycji \( j+1 \) we wzorcu x oraz na pozycji \( i+j+1 \) w tekście y. Jeśli jest niezgodność, to przesuwamy potencjalny początek (pozycja i) wystąpienia x w y. Zakładamy, że algorytm zwraca na końcu wartość false, jeśli nie zwróci wcześniej true.

Algorytm Algorytm MP

i:=0;  j:=0; 
while i <= n-m do begin 
  while j < m and x[j+1]=y[i+j+1] do j=j+1; 
  if j=m then return (true); 
  i:=i+j-P[j];  j:=max(0,P[j]) 
end;

Uwaga: Algorytm działa podobnie gdy zamiast prefikso-sufiksów użyjemy tablicy P' silnych prefisko-sufksów. Algorytm w całości jest wtedy bardziej skomplikowany ze względu na trudniejszy preprocessing (liczenie P' jest trudniejsze od P).

Algorytm MP z tablicą P' zamiast P nazywamy algorytmem Knutha-Morrisa-Pratta i oznaczamy przez KMP.

Operacją dominującą w algorytmach KMP i MP jest operacja porównania symboli: \( x[j+1]=y[i+j+1] \). Algorytmy KMP i MP wykonują co najwyżej 2n-m porównań symboli. Zauważmy, że dla danej pozycji w tekście y jest ona co najwyżej raz porównana z pewną pozycją we wzorcu w porównaniu pozytywnym (gdy symbole są równe). Jednocześnie każde negatywne porównanie powoduje przesunięcie pozycji \( i \) co najmniej o jeden, maksymalna wartość i wynosi n-m, zatem mamy takich porównań co najwyżej n-m, w sumie co najwyżej 2n-m porównań.
Poniższa animacja pokazuje przykładowe działanie algorytmu KMP.

Algorytm dla \( x=ab \), \( y=aa..a \) wykonuje 2n-2porównania, zatem 2n-m jest dolną i jednocześnie górną granicą na liczbę porównań w algorytmie.
Obserwacja. W wersji on-line algorytmu okaże się, że jest zdecydowana różnica między użyciem P' i P; to właśnie jest motywacją dla wprowadzenia silnych prefikso-sufiksów.

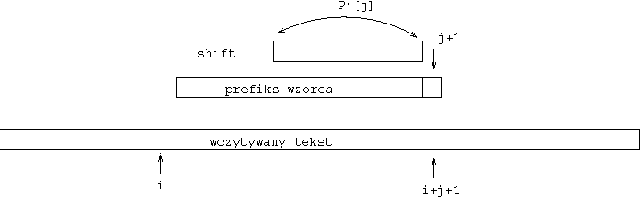
Rysunek 1: Jedna iteracja algorytmu KMP. Przesunięcie \( shift=j-P'[j] \) potencjalnego początku wystąpienia wzorca gdy \( x[j+1]\ne y[i+j+1] \).

Wersja on-line algorytmu KMP

Przedstawimy teraz wersję on-line algorytmu KMP. Wczytujemy kolejne symbole \( y \) i wypisujemy on-line (na bieżąco) odpowiedź:

0 - gdy dotychczas wczytany tekst nie zawiera x jako sufiks,
1 - jeśli zawiera

Algorytm On-Line-KMP

j:=0;  
repeat forever 
    read(symbol); 
    while j > -1 and x[j+1] <> symbol do j:=P'[j]; 
    j:=j+1; 
    if j=m then 
      write(1);  j := P'[m]; 
    else write(0);

Oznaczmy przez delay(m) maksymalną liczbę kroków algorytmu On-Line-KMP między wczytaniem symbolu i daniem odpowiedzi. Przez delay'(m) oznaczmy podobną wielkość, w sytuacji gdy zamiast tablicy P' użyjemy P.

Przykład

Jeśli \( x=aaaa\dots a \) oraz \( y=a^{m-1}b \), to \( delay(m)=O(1) \), \( delay'(m)=\Theta(m) \).

Z lematu o okresowości wynika, że zachodzi następujący fakt:

\( delay(m)\ =\ \Theta(\log m) \)

Uzasadnienie pozostawiamy jako ćwiczenie.

Wersja ‘’real-time’’ algorytmu Morrisa-Pratta

Pokażemy teraz wersję algorytmu on-line, która działa w czasie rzeczywistym, tzn. czas reakcji między wczytaniem symbolu a daniem odpowiedzi jest O(1), niezależnie od rozmiaru alfabetu. Zamiast KMP użyjemy algorytm MP, którego preprocessing jest prostszy.

Algorytm zachowuje się podobnie jak algorytm On-Line-KMP; podstawowa różnica polega na tym, że algorytm wkłada do kolejki wczytane symbole, które jeszcze nie są przetworzone w sensie algorytmu MP. Rysunek pokazuje relacje tego algorytmu do algorytmu MP. Symbole z wejścia najpierw wędrują do kolejki.

Rysunek 2: Typowa konfiguracja w algorytmie real-time-MP.

Algorytm Real-Time-MP

  inicjalizacja:  j:=0; Kolejka := emptyset; 
  repeat forever (niezmiennik: |Kolejka| \le (m-j)/2 ) 
    read(symbol); 
    insert(symbol,Kolejka); 
    write(OUTPUT(Kolejka, j));

W celu skrócenia zapisów pojedynczych algorytmów rozbijamy algorytm na dwie części. Zasadnicza część jest zapisana jako osobna funkcja OUTPUT(Kolejka, j). Wynikiem funkcji jest 0 lub 1, w zależności od tego czy ostatnio wczytany symbol kończy wystąpienie wzorca x. Zmienne Kolejka, j są globalne. Oczywiste jest, że opóźnienie (czas reakcji) tego algorytmu jest O(1).
Algorytm OUTPUT(Kolejka, j)

  output  :=  0; (początkowo Kolejka niepusta)
  repeat 2 times
    if  Kolejka niepusta then
      if  j=-1  then 
        j  :=  0; delete(Kolejka); 
      else if  x[j+1] <> first(Kolejka) then  j:=P[j]; 
      else 
        j:=j+1; delete(Kolejka); 
      if  j=m  (w tym momencie  Kolejka=emptyset) 
       output := 1; j := P[m];  
 return(output);

Oszczędna wersja algorytmu Morrisa-Pratta

Algorytm MP wykonuje co najmniej 2n-m porównań symboli. Załóżmy, że są to operacje dominujące i spróbujmy zmniejszyć stały współczynnik 2 do \( \frac{3}{2} \). Na początku załóżmy, że \( x=ab \). Następujący algorytm znajduje wszystkie wystąpienia wzorca ‘’ab’’ w tekście y.

Algorytm Szukanie-ab

wzorcem jest ab
i:=0; 
while i <= n-m do begin 
while y[i+2] <> b do i=i+1; 
if y[i+1]= a then 
wypisz-wystąpienie;i := i+2 
end;

Algorytm MP dla wzorca ‘’ab’’ i tekstu ‘’aaa...aa’’ wykonywał 2n-2 porównań symboli, nowy algorytm jest lepszy. Algorytm Szukanie-ab wykonuje co najwyżej n porównań w tym przypadku. Dla tekstu ‘’abab’’ algorytm wykinuje n+1 porównań.

Pozostawiamy jako ćwiczenie policzenie maksymalnej liczby porównań dla tego algorytmu (wzorzec ‘’ab’’). Widać, że podstawowa idea to sprawdzanie najpierw pierwszego symbolu wzorca różnego od poprzednich.

Uogólnimy algorytm na dowolne wzorce. Niech x zawiera co najmniej dwa różne symbole, \( x=a^kb\alpha \), gdzie \( a\ne b \).Oznaczmy \( x'=b\alpha \) skrócony wzorzec

Przykład

\( x\ =\ aaaabaaaababa \), wtedy \( x'\ =\ baaaababa \), \( \alpha\ =\ aaaababa \).

Podamy nieformalny zarys działania oszczędniejszej wersji algorytmu MP, w której osobno szukamy x' i osobno części \( a^k \).

Niech \( MP' \) będzie taką wersją algorytmu MP, w której szukamy jedynie wzorca \( x' \), ale tablica \( P \) jest obliczona dla wzorca \( x \). Jeśli \( j>0 \) i \( shift\le k \), to wykonujemy przesunięcie potencjalnego początku i wzorca w y o k+1, gdzie \( shift=j-P[j] \).

Inaczej mówiąc, nie szukamy wszystkich wystąpień x', ale jedynie takich, które mają sens z punktu widzenia potencjalnego znalezienia na lewo ciągu \( a^k \).

Tak zmodyfikowany algorytm MP zastosujemy jako część algorytmu Oszczędny-MP. Graficzna ilustracja działania algorytmu Oszczędny-MP jest pokazana na rysunku.

Algorytm Oszczędny-MP
Znajdujemy wystąpienia x' w tekście \( y[k+1..m] \) algorytmem MP';

dla każdego wystąpienia x' sprawdzamy, czy na lewo jest wystąpienie \( a^k \);
nie sprawdzamy tych pozycji w y, których zgodność z pewną pozycją w x jest znana;

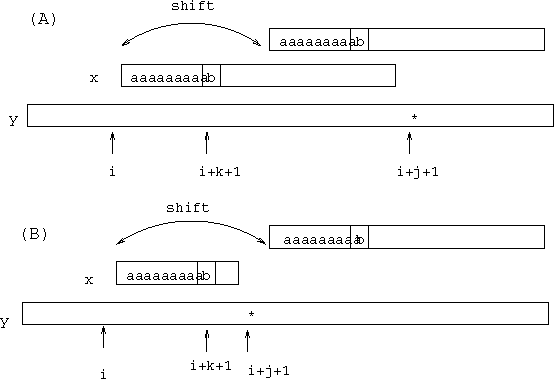
Rysunek 3:Typowa konfiguracja w algorytmie Oszczędny-MP.

Pozostawiamy jako ćwiczenie dokładny zapis algorytmu oraz dokładniejszy dowód tego, że algorytm Oszczędny-MP wykonuje co najwyżej \( \frac{3}{2}n \) porównan.
Ogólna idea jest przedstawiona na rysunku.

Rysunek 4: Ilustracja tego, że liczba operacji dodatkowych jest ograniczona przez \( \frac{1}{2}n \).

Niech zasadniczymi operacjami będą operacje sprawdzania pierwszego b na danej pozycji tekstu y oraz te sprawdzania symboli, które są z wynikiem pozytywnym. Takich operacji jest co najwyżej n. Pozostałe operacje to

(1) sprawdzanie w części \( \alpha \) z wynikiem negatywnym; wtedy przesuwamy wzorzec co najmniej o k,

(2) sprawdzanie części \( a^k \) na lewo od pozytywnego \( b \) (w kwadraciku na rysunku), na pozycjach, gdzie wcześniej było sprawdzanie negatywnego b. Wtedy odległość między pozytywnymi kolejnymi b jest co najmniej 2w, gdzie \( w\le k \) jest liczbą sprawdzanych na lewo symboli a. Zatem ‘’lokalnie’’ przesunięcie jest co najmniej dwukrotnie większe niż liczba dodatkowych operacji.

Suma przesunięć wzorca na tekście \( y \) wynosi co najwyżej n, sumaryczna liczba dodatkowych operacji jest więc co najwyżej \( \frac{1}{2}n \), a liczba wszystkich operacji nie przekracza \( \frac{3}{2}n \).

Obliczanie Tablicy Silnych Prefikso-Sufiksów

Algorytm liczenia silnych prefikso-sufiksów bazuje na następującej relacji między P a P':

\( (t=P[j]\ \textrm{oraz}\ x[t+1]\neq x[j+1])\ \Rightarrow\ P'[j]=t \)

\( (t=P[j],\ t\ge 0,\ \textrm{oraz}\ x[t+1]= x[j+1])\ \Rightarrow\ P'[j]=P'[t] \)

Nie musimy obliczać tablicy P; potrzebna jest jedynie ostatnia wartość \( t=P[j] \), którą obliczamy on-line.

Algorytm Silne-Prefikso-Sufiksy

P'[0]:=-1; t:=-1; 
for j:= 1 to m do 
  while t => 0 and x[t+1] <> x[j] do 
    t:=P'[t]; 
  t:=t+1; 
  if j=m or x[t+1] <> x[j+1] 
    then P'[j]:=t else P'[j]:=P'[t];

Gdy weźmiemy \( x\ =\ aba^{m-2} \) to
\( P'[0]=-1 \), \( P'[1]=0 \), \( P'[2]=-1 \), oraz dla \( 3\leq j\leq m \) \( P'[j]=1 \).
Jest to jest pesymistyczny przypadek dla algorytmu Silne-Prefikso-Sufiksy, algorytm wykonuje wtedy \( 3m-5 \) porównań symboli.

Ćwiczenia

Zadanie 1

Uzasadnij poprawność algorytmu obliczającego długość najkrótszego słowa pokrywającego dany tekst.

Rozwiązanie

Niech \( S[i] \) będzie rozmiarem minimalnego pokrywającego słowa dla prefiksu \( x[1..i] \). Poprawność wynika z następującego faktu: \ \( S[i]=i \ \textrm{lub}\ S[i]=S[P[i]]. \)

Zadanie 2

Udowodnij, że w wersji on-line algorytmu KMP mamy \( delay = O(\log m) \)

Rozwiązanie

Wystarczy wykazać, że
\( P'[i]=j,\ P'[j]=k>0\ \Rightarrow \ i\ge k+j \)
Fakt ten wynika z lematu o okresowości i z definicji tablicy P'.

Zadanie 3

Udowodnij, że w wersji on-line algorytmu KMP mamy \( delay = \Omega(\log m) \)

Rozwiązanie

Słowa Fibonacciego definiujemy następująco:
\( F_0=a,\ F_1=ab,\ F_{n+1}\ =\ F_n\cdot F_{n-1} \)
Na przykład: \( F_3=abaab,\ F_4=abaababa,\ F_5=abaababaabaab. \)
Niech \( F'_n \) oznacza słowo Fibonacciego z obciętymi ostatnimi dwoma symbolami. Jeśli jako wzorzec weźmiemy słowo Fibonacciego \( F_n \), a jako tekst słowo \( F'_ncc \) to przy wczytywaniu \( |F_n-1| \)-ego symbolu algorytm ma opóżnienie logarytmiczne, iterujemy \( \Omega(\log n) \) razy operację: \( j:=P'[j] \).

Zadanie 4

Mamy zbiór słów, każde długości dwa, obliczyć długość minimalnego tekstu który zawiera wszystkie słowa.

Rozwiązanie

Weźmy graf, którego węzłami są litery, a słowa wejściowe odpowiadają krawędziom. Wystarczy znalezć minimalną liczbę krawędzi, które trzeba dołożyć do grafu, by miał on ścieżkę Eulera.

Dygresja Zadanie to było na Olimpiadzie Informatycznej pod nazwą pierwotek abstrakcyjny. Ciekawe jest to, że problem robi się NP-zupełny, gdy wszytkie słowa wejściowe mają długość 3.

Zadanie 5

Udowodnij następującą ciekawą własność kombinatoryczną okresowości w tekstach. Niech \( nwd(p,q) \) oznacza najmniejszy wspólny dzielnik p,q.

Lemat [Lemat o okresowości]
Jeśli x ma okresy p, q oraz \( p+q \le |x| \), to \( nwd(p,q) \) jest również okresem x.

Rozwiązanie

Lemat ten wynika z poprawności algorytmu Euklidesa z odejmowaniem, który oblicza nwd(p,q). Zauważmy, że jeśli \( p>q \) są okresami, to p-q też jest okresem.

Zadanie 6

Lemat o okresowości można wzmocnić, osłabiając założenia. Udowodnij następujący lemat.

Lemat [Silny lemat o okresowości]

Jeśli x ma okresy p, q oraz \( p+q \le |x|+nwd(p,q) \), to \( nwd(p,q) \) jest również okresem x.

Rozwiązanie

Indukcja ze względu na p+q.

Zadanie 7

Udowdnij poprawność algorytmu KMP realtime

Rozwiązanie

Problem jaki musimy rozwiązać to właściwość algorytmu, którą nazwiemy opóżnieniem. Polega ona na tym, że w danym kroku algorytm może wciąż jeszcze rozważać właściwy prefiks aktualnego słowa i nie dotrzeć w ogóle do rozważenia bieżącej litery. Pokażemy jednak, że w momencie, kiedy nastąpi wystąpienie wzorca, kolejka zostanie opróżniona, co wystarczy do dowodu poprawności algorytmu.
Dowód przeprowadzimy nie wprost - załóżmy, że w tym kroku kolejka się nie opróżni i że jest to pierwsze wystąpienie wzorca, którego algorytm nie zdąża wyśledzić. Zacznijmy rozważanie działania algorytmu od ostatniego miejsca wcześniejszego od bieżącego, w którym kolejka się opróżnia. W tym momencie zachodzi \( j < m \) (nawet jeżeli w owym kroku było wystąpienie wzorca w tekście, to ten warunek i tak będzie po tym kroku spełniony) oraz \( |Kolejka|=0 \). Pokażemy, że odtąd aż do miejsca wystąpienia wzorca zachodzić będzie niezmiennik
\( |Kolejka| < m-j. \)
Faktycznie, zastanówmy się co się może wydarzyć w dowolnym, kolejnym kroku algorytmu, a co może zmienić wartość zmiennej \( j \):
Może być dwukrotnie wywołana instrukcja \( j:=P[j] \). Wówczas \( |Kolejka| \) wzrasta o \( 1 \), \( m-j \) wzrasta co najmniej o \( 2 \), czyli niezmiennik dalej zachodzi.
Moze być raz wywołana instrukcja \( j:=P[j] \), a raz \( j:=j+1 \) (w jakiejkolwiek kolejności). Wówczas \( |Kolejka| \) się nie zmienia, \( m-j \) pozostaje bez zmian lub wzrasta, co nie zaburza niezmiennika.
Mogą nastąpić dwie instrukcje powiększające \( j \) o \( 1 \). Wówczas \( |Kolejka| \) maleje o \( 2 \), \( m-j \) także maleje o \( 2 \), zatem niezmiennik pozostaje zachowany.

Kolejka \textit{nie} może się opróżnić, gdyż zakładamy, że to nie nastąpi przed aktualnie rozważanym wystąpieniem wzorca. Instrukcja \( j:=P[m] \) również nie może wystąpić, ponieważ oznaczałoby to wcześniejsze od rozważanego niezauważone przez algorytm wystąpienie wzorca w tekście.

Zatem niezmiennik jest zachowany od ostatniego momentu opróżnienia kolejki do momentu niezauważonego wystąpienia wzorca. W chwili przetworzenia literki, która powoduje wystąpienie zachodzi \( j=m \), czyli na mocy pokazanego niezmiennika \( |Kolejka| < m-m=0 \), \( |Kolejka| < 0 \). To z kolei daje żądaną sprzeczność.

(Rozwiązanie opracował Jakub Radoszewski)

Zadanie 8

Przprowadź dokładny dowód tego, że algorytm Oszczędny KMP wykonuje co najwyżej 3/2 n porównań (schemat dowodu był już opisany w odpowiednim module)

Rozwiązanie

By wykazać, że algorytm Oszczędny-MP wykonuje co najwyżej \( \frac{3}{2}n \) porównań, pogrupujemy te porównania w dwie szufladki: \( A \) i \( B \) . Pokażemy, że w szufladce \( A \) będzie co najwyżej \( n \) porównań, a w szufladce \( B \) co najwyżej \( \frac{n}{2} \) porównań. Do szufladki \( A \) wrzucamy:

Wszystkie udane porównania dokonane w trakcie szukania wzorca \( x' \) .

Wszystkie nieudane porównania pierwszej litery wzorca \( x' \) (czyli litery \( b \) ), dokonane w trakcie szukania wzorca \( x' \) .

Wszystkie porównania początkowych liter \( a \) , za wyjątkiem porównań na tych pozycjach, gdzie wcześniej szukaliśmy litery \( b \) (pierwszej litery wzorca \( x' \)) i nie znaleźliśmy jej.

Do szufladki \( B \) wrzucamy wszystkie pozostałe porównania, czyli:

Wszystkie nieudane porównania dokonane w trakcie szukania wzorca \( x' \) , za wyjątkiem nieudanych porównań pierwszej litery; są to nieudane porównania dokonywane w momencie, gdy znaleźliśmy już jakiś niepusty prefiks \( x' \) .

Porównania początkowych liter \( a \) na tych pozycjach, gdzie wcześniej szukaliśmy litery \( b \) i nie znaleźliśmy jej.

Zauważmy, że w algorytmie MP pozycje tekstu, na których nigdy nie było żadnego udanego porównania to dokładnie te pozycje, na których nie udało się znaleźć pierwszej litery wzorca (lub pozycja jest pod sam koniec tekstu i nie ma już szans na znalezienie wzorca, algorytm już się zakończył). Dodatkowo, zarówno algorytm MP jak i algorytm Oszczędny-MP ma taką właściwość, że jeśli na pewnej pozycji tekstu było udane porównanie, to ta pozycja tekstu już nigdy nie będzie porównywana (o niej ,,wiemy już wszystko). W związku z tym każde porównanie z szufladki \( A \) wykonuje się na innej literze tekstu, czyli tych porównań jest co najwyżej \( n \) .
Spójrzmy teraz, jak zmienia się wskaźnik, na jakiej pozycji szukamy teraz wzorca \( x \) . Zauważmy, że prefikso-sufiks słowa \( x[1\ldots s] \) dla \( s > k \) jest długości co najwyżej \( s - k - 1 \) (litery \( a \) tego prefikso-sufiksu muszą się zaczynać za literą \( b \) na pozycji \( k+1 \) ). W związku z tym w momencie nieudanego porównania, które wystąpiło gdy znaleziony już został niepusty prefiks słowa \( x' \) , wskaźnik ,,gdzie teraz szukamy przesuwa się o conajmniej \( k+1 \) . Tak też jest, gdy znajdziemy całe słowo \( x' \) ( przesuwamy się do prefikso-sufiksu słowa \( x \)) . Dodatkowo, każde nieudane porównanie litery \( b \) z pozycji \( k+1 \) w słowie \( x \) przesuwa wskaźnik o jeden.
W związku z tym:
Porównania z szufladki \( B \) , podpunkt \( 1 \) przesuwają wskaźnik o conajmniej \( k+1 \geq 2 \) .

Po co najwyżej \( k \) porównaniach z szufladki \( B \) , podpunkt \( 2 \) wskaźnik przesunie się o conajmniej \( k+1 \) . Dodatkowo, każde takie porównanie oznacza, że wcześniej na tym miejscu było nieudane porównanie litery \( b \) . Wliczając przesunięcia pochodzące od tych porównań otrzymujemy, że wskaźnik przesunął się o conajmniej \( k+1+L \geq 2L \) , gdzie \( L \) to liczba takich porównań liter \( a \) w jednej próbie znalezienia wzorca \( x \) .

Czyli każde porównanie z szufladki \( B \) przesuwa aktualny wskaźnik (gdzie teraz szukamy) o conajmniej \( 2 \) , czyli tych porównań jest nie więcej niż \( \frac{n}{2} \) .
(Rozwiązanie opracował Marcin Pilipczuk)

Zadanie 9

Słowa cykliczne (de Bruijna): Słowo binarne w długości dokładnie \( 2^n \) nazwiemy cyklicznym (słowem de Bruijna, który to wymyślił) rzędu n gdy każde słowo binarne długości n jest podsłowem słowa ww.
Następujący algorytm generuje takie słowo, co więcej jest ono leksykograficznie pierwsze spośród wszystkich możliwych
Niech Cutfirst(x) oznacza obciecie x o pierwszy symbol, a Append(x,b) dopisanie litery b do słowa x na końcu.

Algorytm Słowa-Cykliczne
1 x := 1111..1 (n jedynek);
2 Z := \( \emptyset \) ; wynik := słowo puste;
3 while istnieje \( b \in \{0,1\} \) takie, że \( Append(Cutfirst(x),b)\notin Z \) do
4 wybierz minimalne takie b ;
5 Append(Cutfirst(x),b);
6 insert(x,Z) ;
7 Append(wynik,b);

Na przykład dla n=3 wynik = 00010111, a dla n=2 wynik = 0011

Udowodnij poprawność algorytmu.

Rozwiązanie

Zadanie ma to związek z pewną metodą konstrukcji cyklu Eulera, chociaż zadanie pozornie wydaje się nie mieć nic wspólnego z grafami. Mamy tu do czynienia z grafem ktorego węzłami są wszystkie słowa binarne długości n-1.
Istnieje krawędż u \rightarrow v o etykieci a, gdy Append(Cutfirst(u),a)=v.
Ciąg operacji w algorytmie Słowa-Cykliczne odpowiada zachłannej ścieżce Eulera która startuje z węzła \( 1^{n-1} \). patrz zadania w module Algorytmy grafowe.