Tablice i drzewa sufiksowe

Niech \( x=a_{1}a_{2}\dots a_{n} \) i niech \( x_{n+1}=\# \) będzie specjalnym znakiem leksykograficznie większym od każdego innego symbolu 9w przyszłości będziemy również używać \( x_{n+1}=\# \) jako najmniejszego symbolu).

Oznaczmy przez \( sufiks_{i}=a_{i}a_{i+1}\dots a_{n} \) sufiks tekstu x zaczynający się na pozycji i-tej.

Niech \( SUF[k] \) będzie pozycją, od której zaczyna się k-ty leksykograficznie sufiks x. Sufiks zaczynający się na pozycji \( (n+1) \)-szej nie jest brany pod uwagę.

Ciąg sufiksów posortowany leksykograficznie wygląda następująco:

\( sufix_{SUF[1]} < sufix_{SUF[2]} < sufix_{SUF[3]} < \ldots sufix_{SUF[n]} \)

Rysunek 1: Tablicą sufiksową tekstu \( x\ =\ babaabababba\# \) jest ciąg \( SUF\ =\ [4,\ 2,\ 5,\ 7,\ 9,\ 12,\ 3,\ 1,\ 6,\ 8,\ 11,\ 10] \)

Oznaczmy przez \( lcp[k] \) długość wspólnego prefiksu \( k \)-tego i następnego sufiksu w kolejności leksykograficznej. Na rysunku wartości najdłuższego wspólnego prefiksu między kolejnymi słowami są przedstawione jako zacienione segmenty. Odpowiadają one tablicy \( lcp\ =\ [1,\ 3,\ 4,\ 2,\ 1,\ 0,\ 2,\ 4,\ 3,\ 2,\ 1] \).
Tablica sufiksowa ma następująca ‘’sympatyczną’’ własność: Niech

\( min_{z}=\min\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \), \( max_{z}=\max\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \).

Wtedy \( Occ(z,x) \) jest przedziałem w tablicy sufiksowej od \( min_{z} \) do \( max_{z} \).

Drzewo sufiksowe jest drzewem, w którym każda ścieżka jest etykietowana kolejnymi symbolami pewnego sufiksu, oraz każdy sufiks \( x \) jest obecny w drzewie. Gdy dwie ścieżki się rozjeżdżają, tworzy się wierzchołek. Mówiąc bardziej formalnie, każdej krawędzi jest przypisane jako etykieta pewne podsłowo \( x \). Krawędzie wychodzące z tego samego węzła różnią się pierwszymi symbolami swoich etykiet (patrz rysunek).

Etykiety są kodowane przedziałami w tekście \( x \): para liczb \( [i,j] \) reprezentuje podsłowo \({a}_i a_{i +1_j}\) (zobacz prawe drzewo na rysunku). Dzięki temu reprezentacja ma rozmiar \( O(n) \). Wagą krawędzi jest długość odpowiadającego jej słowa.

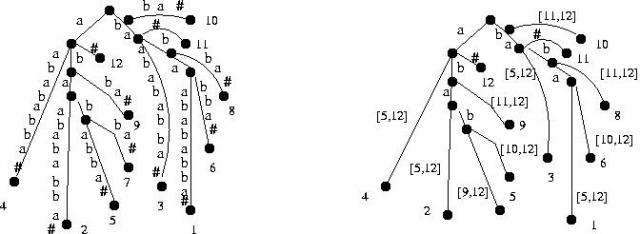
Rysunek 2: Drzewo sufiksowe dla tekstu \( x\ =\ babaabababba \). Na końcu jest dodany znak \( \# \). Końcowe węzły zawierają informację, gdzie zaczyna się sufiks, którym dochodzimy do danego węzła.

Obie reprezentacje pozwalają szybko rozwiązywać problem string-matchingu oraz mają rozmiar liniowy. Niech z będzie wzorcem o długości m, a \( x \) słowem długości n. Z reguły \( m < < n \).

Szukanie podsłów

Pokażemy, jak sprawdzać, czy \( z \) występuje w \( x \).

Używając drzewa sufiksowego (czas \( O(m) \))

Idziemy od korzenia w dół czytając kolejne symbole \( z \), czasami posuwamy się po wewnętrznej etykiecie pewnej krawędzi. Zbiór wystąpień odpowiada zbiorowi liści w poddrzewie węzła, do którego doszliśmy. Jeśli po drodze utknęliśmy i nie dało się dalej schodzić po drzewie, oznacza to, że \( z \notin Subwords(x) \)

Używając tablicy sufiksowej (czas \( O(m \log n) \))

Możemy sprawdzić, czy \( z \) jest prefiksem \( i \)-tego sufiksu w czasie \( O(m) \). Korzystając z tego, wykonujemy rodzaj binarnego szukania. W ten sposób znajdujemy pierwszy sufiks, którego prefiksem jest z. Jeśli jest taki sufiks, to \( z \in Subwords(x) \). W przeciwnym wypadku z nie jest podsłowem x.

Podobnie znajdujemy ostatni sufiks. Zbiór wystąpień odpowiada przedziałowi w tablicy \( SUF \) między obliczonymi pierwszym i ostatnim sufiksem zaczynającym się od z.

Wyznaczanie liczby podsłów

Pokażemy, jak znaleźć liczbę podsłów słowa \( x \) przy pomocy tablicy sufiksowej lub drzewa sufiksowego. Końcowego markera \( \# \) nie traktujemy jako części słowa \( x \). Liczba podsłów jest równa \( |Subwords(x)| \). Jeśli wszystkie symbole słowa są różne to \( |Subwords(x)|={n \choose{2}} \).

Używając drzewa sufiksowego, czas \( O(n) \)

Sumujemy wagi krawędzi drzewa.

Używając tablicy sufiksowej, czas \( O( n) \)

Niech \( SUMA(lcp) \) będzie sumą elementów tablicy \( lcp \). Liczbę podsłów obliczamy jako

\( {n+1\choose{2}}-SUMA(lcp) \)

Pozostawiamy jako ćwiczenie uzasadnienie tego, że liczba podsłów jest poprawnie obliczona (korzystając z drzewa sufisowego lub z tablicy sufiksowej).

Przykład

Dla przykładowego tekstu \( x\ = \) mamy \( |Subwords(x)|=55 \). Proponujemy to wyliczyć z tablicy sufiksowej i drzewa sufiksowego dla\( x \), danego na rysunku. Suma elementów tablicy \( lcp \) wynosi 23. Liczba podsłów to: \( 78-23\ =\ 55 \) Podobnie jak tablicę sufiksową możemy zdefiniować tablicę \( ROT \) odpowiadającą posortowanemu ciągowi wszystkich cyklicznych przesunięć słowa \( x \) (rotacji \( x \)).

Pozostawiamy jako ćwiczenie znalezienie liniowego algorytmu obliczania tablicy \( ROT \), przy założeniu, że mamy liniowy algorytm obliczania tablicy sufiksowej.

Dygresja. Ciekawą klasę słów, dla których tablice \( SUF,\ ROT \) są szczególnie interesujące, stanowią słowa Fibonacciego \( F_n \). W tym szczególnym przypadku załóżmy, że pozycje numerujemy od zera. Dla każdego \( n \) tablica \( ROT \) jest postępem arytmetycznym (modulo długość słowa). Natomiast tablica \( SUF \) jest postępem arytmetycznym, gdy \( n \) jest parzyste.

Słowa Fibonacciego definiujemy następująco:\( F_0=a,\ F_1=ab,\ F_{n+1}\ =\ F_n\cdot F_{n-1} \) Na przykład: \( F_3\ =\ abaab,\ F_4\ =\ abaababa,\ F_5\ =\ abaababaabaab. \) Oznaczmy przez \( SUF_n \) tablicę \( SUF \) dla słowa Fibonacciego \( F_n \); wtedy:

\( SUF_4\ =\ [7\;2\;5\;0\;3\;6\;1\;4], \) \(SUF_5\ =\ [10\;7\;2\;11\;8\;5\;0\;3\;12\;9\;6\;1\;4].\)

Pozostawiamy jako ćwiczenie znalezienie wzoru na \( |Subwords(F_n)| \).

Drzewa sufiksowe =>tablice sufiksowe

W celu znalezienia początkowych pozycji sufiksów w porządku leksykograficznym przechodzimy drzewo sufiksowe metodą DFS, zakładając, że dla każdego węzła lista jego synów jest w kolejności leksykograficznej etykiet krawędzi prowadzących do synów. Wystarczy sprawdzać pierwsze symbole tych etykiet.

Załóżmy, że w liściach mamy początki sufiksów, które do nich prowadzą.

Kolejność odwiedzania liści w naszym przejściu metodą DFS automatycznie generuje elementy tablicy sufiksowej.

Tablice sufiksowe =>drzewa sufiksowe

Pokażemy konstruktywnie następujący istotny fakt:

jeśli znamy tablicę sufiksową i tablicę \( lcp \), to drzewo sufiksowe dla danego tekstu możemy łatwo skonstruować w czasie liniowym.

Przypuśćmy, że \( SUF\ =\ [i_1,i_2,\ldots,i_n] \), a więc:

\( sufiks_{i_1} < sufiks_{i_2} < sufiks_{i_3} < \ldots sufiks_{i_n}. \)

Algorytm Drzewo-Sufiksowe

  T := drzewo reprezentujące sufiks(i_1) (jedna krawędź); 
  for k:=2 to n do 
    wstaw nową ścieżkę o sumarycznej etykiecie sufiks(i_k) do T;

Rysunek 3: Wstawianie kolejnego sufiksu \( sufiks_{i_k} \) do drzewa sufiksowego, przed włożeniem wszystkie krawędzie ścieżki roboczej od \( u \) do korzenia są skierowane w lewo.

Opiszemy w jaki sposób wstawiamy kolejny sufiks \( \beta \) do drzewa. Operacja ta jest zilustrowana na rysunku. Załóżmy, że w każdym węźle drzewa trzymamy długość tekstu, który ten węzeł reprezentuje (jako pełna etykieta od korzenia do węzła).

Niech \( \alpha \) będzie poprzednio wstawionym sufiksem, a \( u \) ostatnio utworzonym liściem.

Wtedy wstawienie \( \beta \) polega na znalezieniu maksymalnego wspólnego prefiksu \( \gamma_1 \) tekstów \( \alpha \), \( \beta \). Niech \( \beta=\gamma_1\cdot \gamma_2 \). Znajdujemy węzeł \( v \) odpowiadający ścieżce od korzenia etykietowanej \( \gamma_1 \).

Kluczowym pomyslem algorytmicznym jest tutaj to, że węzła \( v \) szukamy nie od korzenia, ale od ostatnio utworzonego liścia \( u \). Jeśli takiego węzła \( v \) nie ma (jest wewnątrz krawędzi) to go tworzymy. Następnie tworzymy nowy liść \( w \) odpowiadający sufiksowi \( \beta \), oraz krawędź \( (v,w) \) etykietowaną \( \gamma_2 \).

Z tablicy \( lcp \) odczytujemy długość \( \gamma_1 \).

W celu obliczenia \( v \) posuwamy się ścieżką od \( u \) w górę drzewa, aż znajdziemy węzeł oddalony od korzenia o \( |\gamma| \).

Przechodząc drzewo posuwamy się po węzłach drzewa, przeskakując (w czasie stalym) potencjalnie długie teksty na krawędziach.

Koszt operacji wstawienia jest proporcjonalny do sumy: jeden plus zmniejszenie głębokości nowego liścia w stosunku do starego. Suma tych zmniejszeń jest liniowa. \( \gamma_1 \) jest najdłuższym wspólnym prefiksem słów \( sufiks_{i_{k-1}} \) i \( sufiks_{i_k} \). Kluczowe znaczenie w operacji ma znajomość wartości \( |\gamma_1|= lcp[k-1] \). Wiemy kiedy się zatrzymać idąc do góry od węzła \( u \) w kierunku korzenia.

Lokalnie wykonana praca w jednej iteracji jest zamortyzowana zmniejszeniem się głębokości aktualnego liścia w stosunku do poprzedniego. W sumie praca jest liniowa.

Historia algorytmu jest pokazana dla przykładowego tekstu na rysunkach.

Rysunek 4: Pierwsze 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).

Rysunek 5: Ostatnie 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).

Obliczanie tablicy

Niech \( rank(i) \) będzie pozycją \( sufiks_i \) w porządku leksykograficznym. W naszym przykładowym słowie mamy:

\( rank\ =\ [8,\ 2,\ 7,\ 1,\ 3,\ 9,\ 4,\ 10,\ 5,\ 12,\ 1,\ 6] \)

Niech \( lcp'[k]\ =\ lcp[rank[k]-1] \).

Załóżmy, dla uproszczenia, że \( lcp[0]=0 \) oraz że tekst kończy się specjalnym symbolem Obliczamy tablice \( lcp',\ lcp \) następująco:

Algorytm Oblicz-lcp

for k:=1 to n do 
  oblicz lcp'[k] korzystając z faktu, że lcp'[k] => lcp'[k-1]-1; 
  // koszt iteracji O(lcp'[k]-lcp'[k-1]+const)  
for k:=1 to n do 
  lcp[rank[k]-1] := lcp'[k] \)

Można to zapisać w języku C++ następująco

Algorytm Oblicz-lcp1

for (int i=1; i < =n; i++) R[SUF[i]] = i; 
l = 0;  
for (int i=1; i < =n; i++) 
if (R[i] >; 1) { 
while (x[l+i] == x[l+SUF[R[i]-1]]); 
lcp[R[i]-1] = l;} 
l = max(0, l-1);}

Pozostawiamy jako ćwiczenie dowód tego, że

\( lcp'[k]\ge lcp'[k-1]-1 \).

Jeśli \( lcp'[k-1]-1=t \), to \( lcp'[k] \) obliczamy sprawdzając symbol po symbolu (od lewej do prawej) zgodność prefiksów odpowiednich słów startując od pozycji \( t \). W ten sposób sumaryczny koszt jest liniowy. W każdej iteracji cofamy się o jeden, a potem idziemy do przodu (sprawdzając kolejne symbole). Jest to analiza typu jeden krok do tyłu i kilka do przodu. Liczba iteracji jest liniowa, więc liczba kroków do tyłu też. Ponieważ odległość do celu jest liniowa, to suma kroków też jest liniowa.

Słownik podsłów bazowych i konstrukcja tablicy sufiksowej w czasie O(n log n)

Opiszemy uproszczoną wersję algorytmu Karpa-Millera-Rosenberga (w skrócie algorytmu KMR) rozwiązywania problemów tekstowych metodą słownika podsłów bazowych. Ustalmy pewnie tekst \( x \) długości \( n \).

Zakładamy w tej sekcji, że dodatkowym symbolem jest \( x_{n+1}=\# \), leksykograficznie najmniejszy symbol. Przez segment \( k \)-bazowy rozumiemy segment tekstu \( x[i..i+2^k-1] \) długości \( 2^k \) lub kończący się na \( x_{n+1} \).

Teoretycznie możemy założyć, że po symbolu \( \# \) mamy bardzo dużo takich symboli na prawo i każdy segment startujący w\( x[1..n] \) ma dokładnie długość \( 2^k \).

Słownik podsłów bazowych (w skrócie DBF(x), od ang. dictionary of basic factors) składa się z \( \log n \) tablic

\( NAZWA_0 \), \( NAZWA_1 \), \( NAZWA_2 \),\( \ldots NAZWA_{\log n} \).

Zakładamy, że \( NAZWA_k[i] \) jest pozycją słowa \( x[i..i+2^k-1] \) na posortowanej liście (bez powtórzeń) wszystkich podsłów długości \( 2^k \) słowa \( x \). Jeśli długość wystaje poza koniec \( x \) to przyjmujemy że są tam (wirtualnie) same symbole \( \# \). Poniżej przedstawiamy przykład słownika podsłów bazowych \( DBF(abaabbaa) \).

Algorytm liczenia tablic Nazwa jest bardzo prosty. Załóżmy od razu, że symbole są ponumerowane leksykograficznie. Wtedy \( NAZWA_0 \) jest zasadniczo równa tekstowi \( x \).

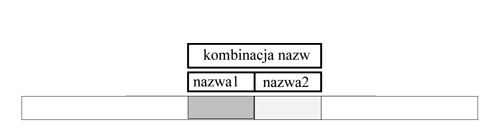
Rysunek6: Słowo rozmiaru \( 2^{k+1} \) otrzymuje najpierw nazwę-kompozycję: kombinacją nazw (będących liczbami naturalnymi z przedziału \( [1..n] \)) dwóch podsłów długości \( 2^k \) .

Opis jednej iteracji \( (transformacja: NAZWA_k\ =>\ NAZWA_{k+1} \))

Dla każdego \( i \) tworzymy nazwę-kompozycję slowa \( x[i..i+2^{k+1}-1] \) jako \( NAZWA_k[i], NAZWA_k[i+2^k] \) Każda taka kompozycja jest parą liczb naturalnych. Sortujemy te pary za pomocą algorytmu radix-sort i w ten sposób otrzymujemy tablicę, która koduje (w porządku leksykograficznym) każdą parę liczbą naturalną (pozycją w porządku leksykograficznym). Wartością \( NAZWA_{k+1}[i] \) jest kod pary \( (NAZWA_k[i],NAZWA_k[i+2^k]) \).

Zauważmy, że tablica sufiksowa odpowiada tablicy \( NAZWA_{\lceil \log n \rceil} \). Możemy to podsumować następująco:
1. słownik DBF(x) możemy skonstruować w czasie \( O(n \log n) \)i pamięci \( O(n \log n) \) (jest to również rozmiar słownika).
2. Tablicę sufiksową możemy otrzymać,stosując algorytm KMR, w czasie \( O(n \log n) \) i pamięci \( O(n) \). (Potrzebujemy pamiętać jedynie ostatnie dwie tablice w każdej iteracji.)

Konstrukcja tablicy SUF w czasie O(n): algorytm KS

Opiszemy teraz błyskotliwy algorytm Karkkainena-Sandersa ( w skrócie KS) będący zoptymalizowaną wersją algorytmu KMR liczenia tablicy sufiksowej. Zauważmy, że algorytm KMR oblicza znacznie więcej niż tablica sufiksowa, ponieważ konstruuje słownik podsłów bazowych wielkości \( n \log n \) (mający liczne inne zastosowania, ale jako całość być może niepotrzebny przy liczeniu tablicy sufiksowej)

Główną częścią algorytmu KS jest obliczanie częściowej tablicy sufiksowej w sposób rekurencyjny. Rozbijmy zbiór pozycji [1..n] tekstu \( x \) na dwa zbiory N, M  :

Zbiór N składa się z co trzeciej pozycji, a M jest zbiorem pozostałych pozycji.

N = {3,6,9,12,15,....}, M = {1,2,4,5,7,8,10,11,...}

Przez \( SUF[M] \), oznaczmy tablicę sufiksową dla pozycji ze zbioru \( M \), podobnie zdefiniujmy \( SUF[N] \).

\( SUF[M] \) daje posortowany ciąg sufiksów zaczynających się na pozycjach ze zbioru \( M \).

Dla początkowego przykładowego tekstu \( x\ =\ babaabababba\# \) mamy

\( M\ =\ \{1,2,4,5,7,8,10,11\}\ \ \ \ \ N\ =\ \{3,6,9,12\} \)

\( SUF[M]\ =\ [4,\ 2,\ 5,\ 7, \ 1, \ 8,\ 11,\ 10]\ \ \ \ SUF[N]\ =\ [ 9,\ 12,\ 3,\ 6,] \)

Sprowadzenie obliczania \( SUF[M] \) do obliczania tablicy sufiksowej rozmiaru \( \frac{2}{3}n \)

Posortujmy leksykograficznie wszystkie podsłowa długości 3 w słowie \( x \) korzystając z radix-sort. Każdemu takiemu słowu przyporządkujmy nazwę będącą jego pozycją w posortowanym leksykograficznie ciągu, oznaczmy \( kod(z) \) otrzymaną nazwę podsłowa długości 3. Zakładamy, że \( x \) kończy się dodatkowo dwoma symbolami \( \# \), ale rozważamy tylko podsłowa zaczynające się w \( x \). Dla uproszczenia załóżmy, że 3 jest dzielnikiem n.

Tworzymy nowe słowo \( compress(x) \) w następujący sposób:

Przykład. Weźmy początkowy przykład \( x\ = \ babaababbba\# \), gdzie \( \# \)jest większe niże a,b. Mamy

\( aab \prec aba\prec bab \prec ba\# \prec bba \), Zatem kody tych trójek są kolejno \( 1,\ 2,\ 3,\ 4, \ 5 \).

Oznaczmy\( kod(z)= < z> \). Wtedy

\( y1\ =\ < bab> < aab> < aba> < bba>\ =\ 3\ 1\ 2\ 5  ; \)

\( y2\ =\ < aba> < aba> < bab> < ba\#>\ =\ 2\ 2\ 3\ 4 \)

\( compress(x)\ =\ =\ 3\ 1\ 2\ 5 \ \& \ 2\ 2\ 3\ 4\ \),

Jeśli mamy tablicę sufiksową dla słowa \( compress(x) \), można łatwo obliczyć \( SUF[M] \) w czasie liniowym. Pozostawiamy to jako ćwiczenie.

Algorytm \( {\Large KS} \) (Karkkainen-Sanders)

x':= compress(x);
obliczamy tablicę sufiksową dla x' rekurencyjnie;
obliczamy SUF[M] w czasie liniowym, znając tablicę sufiksową dla x'; 
obliczamy SUF[N] w czasie liniowym (bez rekursji), znając SUF[M]; 
scalamy posortowane ciągi  SUF[M], SUF[N] w tablicę sufiksową dla całego słowa x 

Krok 1 algorytmu sprowadza się do radix-sortu, podobnie jak w algorytmie KMR. Kroki 3,4 są proste i ich implementację pozostawiamy czytelnikowi jako ćwiczenie.
Najważniejszy jest krok scalania. Mamy dwie posortowane listy sufiksów i trzeba je scalić w jedną posortowaną listę. Zasadniczym problemem jest implementacja operacji porównania leksykograficznego dwóch (długich) sufiksów w czasie stałym. Jeśli oba sufiksy są typu \( M \) lub oba są typu \( N \), to porównanie jest w czasie stałym, bo mamy posortowane listy takich sufiksów.

Pokażemy na przykładzie kluczową operację porównania sufiksu typu M z sufiksem typu N w czasie stałym.

Przykład

Nierówność \( sufiks_2 < sufiks_{12} \) jest równoważna temu, że zachodzi co najmniej jeden z warunków:

1. \( (a_2 < a_{12}) \)
2. \( \ (a_2=a_{12}, a_3 < a_{13}) \)
3. \( (a_2=a_{12}, a_3=a_{13}, sufiks_4 < sufiks_{14}) \)

Jednakże \( 4,14\in M \), zatem \( sufiks_4 \) i \( sufiks_{14} \), są typu M i można je porównać w czasie stałym.

Niech \( T(n) \) będzie czasem działania algorytmu KS. Zachodzi

\( T(n) \ =\ T(\lceil \frac{2}{3}\cdot n \rceil) + O(n) \)

Rozwiązaniem jest \( T(n)=O(n) \). Mamy więc liniowy algorytm liczenia tablicy sufiksowej. Daje to również liniowy algorytm konstrukcji drzewa sufiksowego.

Istnieje kilka interesujących algorytmów, które konstruują drzewo sufiksowe w czasie liniowym, bez korzystania z tablicy sufiksowej (algorytmy Weinera, McCreighta, Ukkonena). W algorytmach tych współczynnik przy złożoności liniowej wynosi \( \log |A| \), gdzie A jest alfabetem.

Ćwiczenia