Tablice sufiksowe =>drzewa sufiksowe

Pokażemy konstruktywnie następujący istotny fakt:

jeśli znamy tablicę sufiksową i tablicę \( lcp \), to drzewo sufiksowe dla danego tekstu możemy łatwo skonstruować w czasie liniowym.

Przypuśćmy, że \( SUF\ =\ [i_1,i_2,\ldots,i_n] \), a więc:

\( sufiks_{i_1} < sufiks_{i_2} < sufiks_{i_3} < \ldots sufiks_{i_n}. \)

Algorytm Drzewo-Sufiksowe

  T := drzewo reprezentujące sufiks(i_1) (jedna krawędź); 
  for k:=2 to n do 
    wstaw nową ścieżkę o sumarycznej etykiecie sufiks(i_k) do T;

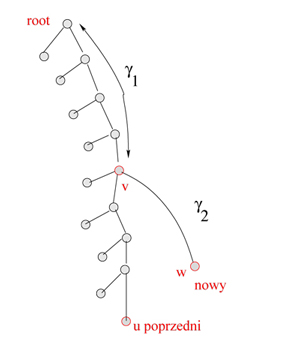
Rysunek 3: Wstawianie kolejnego sufiksu \( sufiks_{i_k} \) do drzewa sufiksowego, przed włożeniem wszystkie krawędzie ścieżki roboczej od \( u \) do korzenia są skierowane w lewo.

Opiszemy w jaki sposób wstawiamy kolejny sufiks \( \beta \) do drzewa. Operacja ta jest zilustrowana na rysunku. Załóżmy, że w każdym węźle drzewa trzymamy długość tekstu, który ten węzeł reprezentuje (jako pełna etykieta od korzenia do węzła).

Niech \( \alpha \) będzie poprzednio wstawionym sufiksem, a \( u \) ostatnio utworzonym liściem.

Wtedy wstawienie \( \beta \) polega na znalezieniu maksymalnego wspólnego prefiksu \( \gamma_1 \) tekstów \( \alpha \), \( \beta \). Niech \( \beta=\gamma_1\cdot \gamma_2 \). Znajdujemy węzeł \( v \) odpowiadający ścieżce od korzenia etykietowanej \( \gamma_1 \).

Kluczowym pomyslem algorytmicznym jest tutaj to, że węzła \( v \) szukamy nie od korzenia, ale od ostatnio utworzonego liścia \( u \). Jeśli takiego węzła \( v \) nie ma (jest wewnątrz krawędzi) to go tworzymy. Następnie tworzymy nowy liść \( w \) odpowiadający sufiksowi \( \beta \), oraz krawędź \( (v,w) \) etykietowaną \( \gamma_2 \).

Z tablicy \( lcp \) odczytujemy długość \( \gamma_1 \).

W celu obliczenia \( v \) posuwamy się ścieżką od \( u \) w górę drzewa, aż znajdziemy węzeł oddalony od korzenia o \( |\gamma| \).

Przechodząc drzewo posuwamy się po węzłach drzewa, przeskakując (w czasie stalym) potencjalnie długie teksty na krawędziach.

Koszt operacji wstawienia jest proporcjonalny do sumy: jeden plus zmniejszenie głębokości nowego liścia w stosunku do starego. Suma tych zmniejszeń jest liniowa. \( \gamma_1 \) jest najdłuższym wspólnym prefiksem słów \( sufiks_{i_{k-1}} \) i \( sufiks_{i_k} \). Kluczowe znaczenie w operacji ma znajomość wartości \( |\gamma_1|= lcp[k-1] \). Wiemy kiedy się zatrzymać idąc do góry od węzła \( u \) w kierunku korzenia.

Lokalnie wykonana praca w jednej iteracji jest zamortyzowana zmniejszeniem się głębokości aktualnego liścia w stosunku do poprzedniego. W sumie praca jest liniowa.

Historia algorytmu jest pokazana dla przykładowego tekstu na rysunkach.

Rysunek 4: Pierwsze 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).

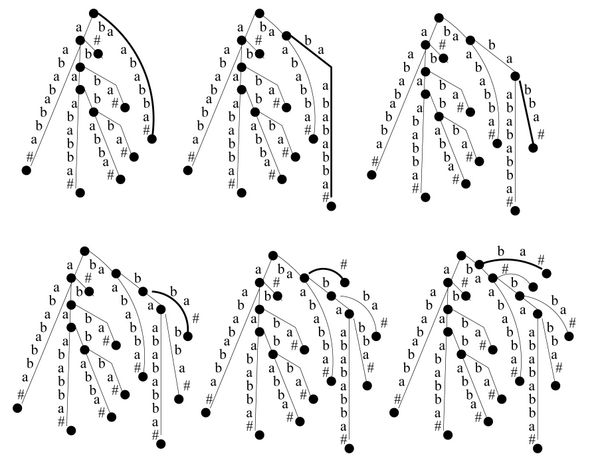
Rysunek 5: Ostatnie 6 iteracji algorytmu Drzewo-Sufiksowe dla tekstu \( babaabababba\# \).