Wstęp do programowania/Wstęp do algorytmów

Wprowadzenie do algorytmów

W pierwszym kroku rozwiązania Al Chuwarizmi polecał podzielić wszystkie współczynniki trójmianu kwadratowego przez współczynnik przy \( x^{2} \), aby uwolnić się od jednego z nich; w końcu pierwiastki przez takie podzielenie nie zmieniają się, a metoda staje się prostsza. Al Chuwarizmi rozważał zatem równania postaci \( x^{2}+bx+c \) dla różnych klas b i c: dodatnich, ujemnych i równych zero. Miał zatem do czynienia z 9 różnymi przypadkami i dla każdego z nich podał metodę wyznaczania pierwiastka takiego równania. Przyjrzyjmy się jednemu z nich: dane są zaczerpnięte bezpośrednio z omawianej księgi. Rozwiązujemy równanie

\( x^{2}+10x = 39 \)

Jest to zatem równanie z klasy równań, w których współczynnik przy x jest dodatni, a wyraz wolny ujemny (dla wygody przenieśliśmy go na prawą stronę, więc po tamtej stronie jawi się nam jako c dodatnie). Oto co proponował Al Chuwarizmi.

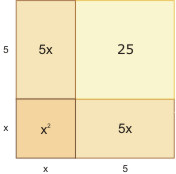
Rysujemy kwadrat o boku x. Po jednej jego stronie doklejamy prostokąt o bokach x oraz \( 10/2 = 5 \), po drugiej pod kątem prostym identyczny prostokąt. Uzupełniamy powstały kąt prosty wyznaczony przez 2 odcinki długości 5 do kwadratu i otrzymujemy duży kwadrat, którego pole wynosi
\( x^{2} + 5x + 5x + 25= 39 + 25 = 64 \)

Bok tego dużego kwadratu ma więc długość 8, a że powstał on przez sklejenie odcinka o długości x oraz odcinka o długości 5, więc \( x = 3 \). Drugi pierwiastek w tym przypadku nas nie interesuje: jest ujemny, a więc go "nie ma" – liczby ujemne nie istniały wówczas w świadomości współczesnych.

Zauważmy, że konstrukcję tę, a zatem i stosowne obliczenia, można powtórzyć dla każdej pary (b,c) w której b > 0, zaś c < 0. Wyrażając jednym wzorem efekt obliczeń uzyskalibyśmy wyrażenie
\( x=\sqrt{c+(\frac{b}{2})^2}-\frac{b}{2} \)
Obliczenie wartości x mogłoby się odbywać według następującego schematu:

1. podziel \( b \) przez \( 2 \) i zapamiętaj wynik na zmiennej pomocniczej \( b' \)
2. podnieś \( b' \) do kwadratu
3. dodaj do otrzymanej liczby wartość \( c \)
4. wyciągnij z otrzymanej sumy pierwiastek kwadratowy
5. odejmij od tego, co uzyskałeś uprzednio zapamiętaną wartość \( b' \)
6. otrzymana liczba jest szukanym (nieujemnym) pierwiastkiem równania \( x^{2}+bx=c \).

Zróbmy parę obserwacji.
Po pierwsze powyższa procedura jest wykonywalna dla każdych danych b,c>0. Zauważmy, że jedyna operacja, która mogłaby sprawić kłopoty z wykonaniem, to odejmowanie w punkcie 5 naszej procedury. Jednak można łatwo sprawdzić, że daje ono zawsze wynik dodatni:
w końcu dla \( c >0 \) mamy \( \sqrt{c+(\frac{b}{2})^2} > \sqrt{(\frac{b}{2})^2}=\frac{b}{2} \).
Po drugie, zastosowaliśmy tu pewne niewielkie, ale ważne uproszczenie algorytmu: użyliśmy w jego opisie pomocniczej zmiennej \( b' \), dzięki której nie musieliśmy dwukrotnie dzielić wartości \( b \) przez \( 2 \). Po trzecie, zapisując wzór na równanie kwadratowe skorzystaliśmy z tradycji notacyjnej, w myśl której w wyrażeniach arytmetycznych zawsze wiadomo, w jakiej kolejności wykonuje się działania. W szczególności w wyrażeniu podpierwiastkowym najpierw dzieliliśmy b przez 2, potem podnosiliśmy wynik do kwadratu, a na końcu dodawaliśmy do niego c. To, co w podanym przez Al Chuwarizmiego przepisie wymagało uściślenia kolejności, można wyrazić wzorem w zwartej formie, umówiwszy się zawczasu co do interpretacji podanej notacji. Niezwykle ważne jest, aby używana notacja była jednoznaczna i abyśmy nie popełniali błędu przy interpretacji wyrażeń, w szczególności żebyśmy byli zgodni co do kolejności wykonywanych działań. Wrócimy do tego zagadnienia w wykładzie o gramatykach.

• Jak będzie działała podana metoda, dla c<realnowiki><realnowiki> = </realnowiki></realnowiki>0?
• Zaprojektuj geometryczną metodę w stylu Al Chuwarizmiego dla równania \( x^{2}= 5x + 6 \). Czy metoda ta da poprawne wyniki dla wszystkich równań postaci \( x^{2} = bx + c \) przy dodatnich b, c?

Co to są zatem algorytmy? Ogólnie określamy tym mianem wszelkie przepisy postępowania, które doprowadzają do uzyskania pożądanego efektu – rozwiązania zadania. W potocznej mowie mówimy czasem o algorytmach postępowania niewiele mających wspólnego z komputerami, jednak dla informatyków algorytmy wiążą się nierozerwalnie z programowaniem.

Prawdziwe problemy pojawiają się, gdy chcemy algorytm zakodować w taki sposób, żeby był dobrze wykonany przez maszynę. Nie możemy sobie pozwolić na odwoływanie się do doświadczenia, machanie rękami, domysły. Komputer niczego się nie domyśla, ba, nie rozumie języka naturalnego i potrzebna będzie nam precyzyjna notacja do komunikacji z nim. Istotą programowania jest bowiem wyrażanie algorytmów w sposób ścisły, podlegający rygorom skończonej liczby reguł, których znaczenie w jednoznaczny sposób jesteśmy określić.

Al Chuwarizmi nie był oczywiście pierwszym człowiekiem, który stosował podejście algorytmiczne do rozwiązywania problemów. W rzeczywistości każdy z nas stosuje algorytmy w rozmaitych sytuacjach życiowych. Człowiek pierwotny miał algorytm polowania na mamuty, czy rozpalania ognia. Dzisiaj często wykonujemy pewne algorytmy, nie zdając sobie sprawy. Warto przytoczyć parę przykładów algorytmów z życia codziennego:

Przepisy kucharskie Typowy przepis zawiera deklaracje obiektów (składników pichcenia) ich początkowe wartości (miary) oraz opis działań doprowadzający do przyrządzenia potrawy.

Zapis nutowy muzyki. Za pomocą szczególnego systemu notacyjnego określa się wysokości i względne czasy trwania nut i pauz między nimi. Można również i tu określić dane: są to zazwyczaj określenia instrumentów, które w partyturze występują, oraz dane początkowe, takie jak metrum czy dynamika poszczególnych części. Zauważmy, że poza standardowymi znakami na pięciolinii, kompozytorzy często stosują dodatkowe określenia takie jak crescendo, poco allegretto, piano, con fuoco itp, pozwalające wykonawcy lepiej wyczuć ich intencje. Szczególnie atrakcyjnie wyglądają niektóre nuty kompozytorów współczesnych, którzy odchodzą czasem od tradycyjnego zapisu nutowego i starają się niekiedy wymyślić i opisać własny system notacyjny, wyrażający ich intencje.

Instrukcje montażu Często do zestawów mebli, czy klocków lego, dołączona jest kartka z instrukcją montażu zapisaną za pomocą sekwencji rycin obrazujących kolejne fazy powstawania składanego obiektu. Użytkownik, porównując zmiany na poszczególnych obrazkach, ma się domyślić, jakie czynności, w jakiej kolejności i za pomocą jakich części ma wykonywać. Zauważmy, że i tu występuje charakterystyczny dla algorytmów opis danych: najczęściej zestaw części składowych jest wyrysowany obok historyjki obrazkowej z zaznaczeniem liczby poszczególnych elementów.
Opisy dojazdu Wyjaśniając jak dotrzeć do danego miejsca (mappy.com), wiele serwisów udostępnia opis drogi z zaznaczeniem kluczowych punktów i decyzji.

Opis układów choreograficznych, scenopisy przedstawień Tutaj też stosuje się specyficzną symbolikę i skróty notacyjne.

Takich przykładów można przytaczać tysiące. Właściwie niemal wszystko, co robimy, podlega jakiemuś algorytmowi działania – przy czym warto podkreślić, że ludzie nie muszą mieć algorytmów objaśnianych dokładnie: wiele mogą wywnioskować z kontekstu, doświadczenia, po prostu domyślając się, o co może chodzić. Kucharce nie trzeba wyjaśniać, co to znaczy "zeszklić cebulkę na ciemnozłoty kolor", a monterowi - co znaczy "zaizolować przewody".

Z komputerami jest jednak inaczej. Są to wyjątkowo głupie urządzenia i jeśli dokładnie nie wytłumaczymy, co mają zrobić, stają się bezradne. Między bajki należy włożyć rozmaite sytuacje znane z literatury fantastyczno-naukowej, w których komputery są równorzędnymi partnerami intelektualnymi dla ludzi. Sztuczna inteligencja, nawet jeśli istnieje, bazuje na ściśle określonych algorytmach działania i nie ma tam miejsca na intuicję, domyślenie się czegokolwiek czy nagłe olśnienie, które są doskonale znane istotom myślącym. Ludzie często nie zdają sobie sprawy, jak wiele w algorytmach, którymi się posługują, zależy od nieuświadamianego kontekstu, jak dużo muszą dopowiadać do rzekomo precyzyjnych procedur działania. Komputery bezlitośnie wyłapują luki w specyfikacji procedur i nie ma mowy, żeby domyśliły się, że wykonują jakąś bezsensowną akcję, typu wydrukowanie żądania zapłacenia 0 zł. Jeśli wyraźnie nie zapiszemy w algorytmie, że takich żądań nie należy generować, to komputer ślepo wykona nasze polecenie, choćby było ono w oczywisty sposób bezsensowne. W dalszych wykładach zobaczymy przykłady, w których algorytmy z pozoru wyglądające na poprawne i kompletne, będą miały luki powodujące błędne działanie.

Znajdź w Internecie przykłady bezsensownego zachowania się komputerów. Spróbuj domyślić się, jakiego rodzaju błąd programisty był przyczyną kompromitacji.

Spróbujmy przymierzyć się do problemu znanego jeszcze ze starożytności. Przy dodawaniu sprowadza się mianowniki do najmniejszej wspólnej wielokrotności. Wyznaczenie jej najczęściej polega na tym, że oblicza się największy wspólny dzielnik, dzieli się jedną z liczb przez niego i wynik mnoży przez drugą. Jak jednak znaleźć największy wspólny dzielnik?

Dla danych liczb całkowitych x, y, z zastrzeżeniem, że \( y \neq 0 \) określamy dwie operacje: wynik i resztę z dzielenia x przez y następująco: &nbsp;&nbsp;\( x \div y = c \), &nbsp;&nbsp;\( x\bmod y = r \), gdzie liczby c i r spełniają następujące zależności: &nbsp;&nbsp;\( x = cy + r \) oraz &nbsp;&nbsp;\( 0 \le r  <  |y| \)

<p>PROBLEM </p> 
<p>[NWD(a,b)]: </p>
<p>Dane są dwie liczby całkowite nieujemne \( a \), \( b \) takie, że \( a + b &gt; 0 \). Wyznacz największą liczbę naturalną \( d \) taką, że \( a\bmod d \) &lt;realnowiki&gt;&lt;realnowiki&gt;= &lt;/realnowiki&gt;&lt;/realnowiki&gt;0 i \( b \bmod d= 0 \). Liczbę tę nazywamy największym wspólnym dzielnikiem \( a \) i \( b \) oraz oznaczamy przez \( (a, b) \). </p>

<b>Read</b>(a,b);             //Wczytujemy a i b, zakładając że użytkownik wie, że a&gt;=b, a+b&gt;0 
<b>while</b> b &gt; 0 <b>do</b> 
<b>begin</b> 
<b>if</b> a&lt; b <b>then</b> zamień(a,b);  //po wykonaniu tej instrukcji zawsze a&gt;=b 
a:=a-b                //tutaj być może raz wykonamy niepotrzebnie odejmowanie zera 
<b>end</b>; 
<b>Write</b>(a)                //wypisujemy wynik, którym jest wartość a 

<b>Read</b>(a,b);        //Wczytujemy a i b, zakładając że użytkownik wie, że a&gt;=b, a+b&gt;0 
<b>while</b> b &gt; 0 do 
<b>begin</b> 
 a:=a mod b;
 zamień (a,b) //reszta jest zawsze mniejsza od dzielnika, więc w ciemno możemy zamienić a z b 
<b>end</b>; 
<b>Write</b>(a)          //Wypisujemy wynik 

\( F_{0}=0 \) 
\( F_{1}=1 \) 
\( F_n = F_{n-1}+F_{n-2} \) dla \( n \ge 2 \)

<b>Read</b>(a,b);       //Wczytujemy a i b, zakładając że użytkownik wie, że a&gt;=b, a+b&gt;0
wynik:=1; 
<b>while</b> b &gt; 0 <b>do</b> 
<b>begin</b> 
<b>if</b> a&lt; b <b>then</b> zamień(a,b); //po wykonaniu tej instrukcji zawsze a&gt;=b 
<b>if</b> parzyste(a) <b>and</b> parzyste(b) <b>then</b> 
<b>begin</b> 
wynik:=wynik*2 
a:=a div 2;
b:=b div 2 
<b>end</b> 
<b>else</b> // w przeciwnym razie 
<b>if</b> parzyste(a) <b>and</b> <b>not</b> parzyste(b) <b>then</b> a:=a div 2 <b>else</b> 
<b>if</b> <b>not</b> parzyste(a) <b>and</b> parzyste(b) <b>then</b> b:=b div 2 <b>else</b>
 a:=a-b 
<b>end</b>;
 wynik:=wynik*a;
 Write(a)

A, B, W - prostokąty dane i wynikowy (odpowiednio)
x1,x2,y1,y2 - współrzędne lewego-górnego, i prawego-dolnego wierzchołka (odpowiednio)
P.x1 - notacja kropkowa do odwoływania się do współrzędnych

W.x1 = max(A.x1, B,x1) 
W.y1 = min(A.y1, B.y1) 
W.x2 = min(A.x2, B.x2) 
W.y2 = max(A.y2, B.y2)

p ε A ∩ B   wtedy i tylko wtedy    p.x ε rzutX(A) ∩ rzutX(B) i p.y ε rzutY(A) ∩ rzutY(B) 
	p ε W    wtedy i tylko wtedy               p.x ε rzutX(W) i p.y ε rzutY(W)

p.x ε rzutX(A) ∩ rzutX(B)  wtedy i tylko wtedy p.x ε rzutX(W) i 
p.y ε rzutY(A) ∩ rzutY(B)  wtedy i tylko wtedy p.y ε rzutY(W)

A.x1 ≤ p.x ≤ A.x2.

B.x1 ≤ p.x ≤ B.x2.

max(A.x1,B.x1) ≤ p.x ≤ min(A.x2,B.x2)

A, B, W - prostokąty dane i wynikowy (odpowiednio) 
x1,x2,y1,y2 - współrzędne lewego górnego, i prawego dolnego wierzchołka (odpowiednio) 
P.x1 - notacja kropkowa do odwoływania się do współrzędnych

W.x1 = min(A.x1, B,x1) W.y1 = max(A.y1, B.y1) W.x2 = max(A.x2, B.x2) W.y2 = min(A.y2, B.y2)

M(p,q,r) > 0   wtw  0 < φ < π M(p,q,r) = 0   wtw  (φ = 0 lub  φ = π) M(p,q,r) < 0   wtw  π < φ < 2π

M(p,q,r)*M(p,q,s) < 0

min(q.x,p.x) ≤ r.x ≤ max(q.x,p.x)   lub   min(q.x,p.x) ≤ s.x ≤ max(q.x,p.x)

min(p.x,q.x) ≤ max(r.x,s.x)  i  min(r.x,s.x) ≤ max(p.x,q.x)

<b>jeśli</b> max(p.x,q.x) &ge; min(r.x,s.x) i max(r.x,s.x) &ge; min(p.x,q.x) i 
	i max(p.y,q.y) &ge; min(r.y,s.y) i max(r.y,s.y) &ge; min(p.y,q.y) <b>to</b> PRZECINAJĄ SIĘ 
<b>wpp</b> ROZŁĄCZNE

Mp=M(r,s,p) 
Mq=M(r,s,q) 
Mr=M(p,q,r) 
Ms=M(p,q,s)

<b>jeśli</b> Mp*Mq &gt; 0 <b>lub</b> Mr*Ms &gt; 0 <b>to</b> ROZŁĄCZNE 
<b>wpp</b> 
<b>jeśli</b> Mp*Mq &lt; 0 <b>lub</b> Mr*Ms &lt; 0 <b>to</b> PRZECINAJĄ SIĘ 
<b>wpp</b> 
Sprawdź_czy_wpółliniowe_się_przecinają(pq, rs)

wynik=ROZŁĄCZNE <b>dla</b> i &isin; [1..4] <b>dla</b> j &isin; [1..4] <b>jeśli</b> PrzecinająSię(r_ir_(i+1 mod 4), q_jq_(j+1 mod 4) <b>to</b> wynik=PRZECINAJĄ SIĘ

M12=M(r_1,r_2,q_1)	N12=M(q_1,q_2,r_1) 
M43=M(r_4,r_3,q_1)	N43=M(q_4,q_3,r_1) 
M14=M(r_1,r_4,q_1)	N14=M(q_1,q_4,r_1) 
M23=M(r_2,r_3,q_1)	N23=M(q_2,q_3,r_1)  
 
<b>jeśli</b> (M12*M43 &lt; 0 i M14*M23 &lt;0) lub (N12*N43 &lt; 0 i N14*N23 &lt;0) <b>to</b> wynik=PRZECINAJĄ SIĘ

Wprowadzenie do programowania

Nieformalny wstęp do programowania

Instrukcji przypisania

Przykład

a:=a-b;

Instrukcji warunkowej

Przykład

if a < b then c:=a else c:=b;

Instrukcji pętli

Przykład

<b>while</b> b &gt; 0 <b>do</b> b:=b div 2;

Instrukcje oddzielamy średnikami i wykonujemy po kolei.
Kolejno omówimy te konstrukcje.

Instrukcja przypisania

Instrukcja przypisania jest postaci v:=E, gdzie przez v oznaczamy zmienną, czyli obiekt, który może przyjmować wartości typu określonego przy wcześniejszej deklaracji, a przez E wyrażenie pochodzące z dziedziny algorytmicznej, której nośnikiem jest typ zmiennej. Wyrażenie jest termem, w skład którego wchodzą stałe, zmienne i operacje dostępne w tej dziedzinie.
Wykonanie instrukcji przypisania odbywa się na dwa takty. Najpierw wyliczana jest wartość wyrażenia E występującego po prawej stronie instrukcji przypisania (w wyrażeniu może wystąpić w szczególności zmienna v z lewej strony przypisania i wtedy bierze się jej starą wartość), a potem obliczoną wartość przypisuje się zmiennej v.

Przykład ilustrujący ilustruje kolejność czynności przy wykonaniu instrukcji przypisania. Zakładamy w nim, że w pamięci komputera są zarezerwowane komórki na wartości wszystkich zmiennych programu. W animacji odwołujemy się do wartości tych komórek. Znaki zapytania oznaczają, że zmienna nie ma jeszcze nadanej wartości. Zakładamy, że ten mały fragment programu jest częścią większej całości i pomijamy szczegóły dotyczące kontekstu.

animacja flash

Instrukcja warunkowa

Instrukcja warunkowa jest postaci if B then I1 else I2 gdzie warunek B jest wyrażeniem logicznym, dającym wartości true lub false (prawda lub fałsz), a I1 oraz I2 są instrukcjami. Instrukcja warunkowa pozwala nam wybrać jeden z dwóch wariantów dalszego wykonania programu w zależności od tego, czy warunek b jest spełniony, czy nie.
Wykonanie instrukcji warunkowej odbywa się również na dwa takty: najpierw obliczana jest wartość warunku B i jeśli jest ona równa true, to wykonujemy I1, a jeżeli nie, wykonujemy I2. Gdy nie chcemy, aby cokolwiek wykonywało się w tym drugim przypadku, wówczas nie piszemy „else I2” i wtedy w przypadku, gdy wartość warunku jest false, nic się nie dzieje. Przykład takiej instrukcji mieliśmy w algorytmie Euklides1 i Euklides3: gdy zmienna a miała wartość większą od b, nie trzeba było niczego zamieniać.
Przykład ilustrujący kolejność czynności przy wykonaniu instrukcji warunkowej.

animacja flash

Instrukcja pętli

Instrukcja pętli jest postaci while B do I gdzie B jest warunkiem logicznym, a I instrukcją, którą pętla ma powtarzać, aż do spełnienia warunku B. Wykonanie pętli zaczyna się od obliczenia wartości warunku. Jeśli wartość ta wynosi false, to pętla nie robi niczego i kończy swoje działanie, ale jeśli wynosi true, to pętla wykonuje instrukcję I, a następnie wraca do sprawdzenia warunku B. Wykonuje tę sekwencję tak długo, aż warunek B przestanie być spełniony. Może się zdarzyć, że warunek B nigdy nie przestanie być spełniony i pozostanie prawdziwy na zawsze. Program wtedy nie zatrzyma się nigdy i mówimy o takiej sytuacji, jako o zapętleniu programu.

Jeśli chcemy zaznaczyć, że zależy nam na wykonaniu ciągu instrukcji, to ciąg ten ujmujemy w nawiasy begin ... end.

Na razie będziemy używali jedynie zmiennych o wartościach całkowitoliczbowych, a w dziedzinie algorytmicznej będą się znajdowały operacje \( +,-,-,*,\div,\) \(mod\) (gdzie dwa minusy nie są pomyłką, tylko zgodnie z tradycją oznaczają dwie różne operacje: jednoargumentową tworzenia liczby przeciwnej i dwuargumentową odejmowania; niestety są one tradycyjnie oznaczane tym samym znakiem) oraz relacje \( < , < =,>,>=,= \) oraz \( < > \), przy czym znaki relacji kolejno oznaczają mniejszość, mniejszość lub równość, większość, większość lub równość, równość i różność. Umawiamy się ponadto, że zachowane są tradycyjne priorytety działań (czyli mnożenie i dzielenie wiąże mocniej niż dodawanie i odejmowanie, minus jednoargumentowy wiąże silniej od mnożenia i dzielenia, a działania są wykonywane od lewej do prawej). W wyrażeniach logicznych używamy standardowych spójników logicznych not, and, or z umową, że not wiąże najsilniej, and słabiej, a or najsłabiej. Wolno nam tworzyć wyrażenia logiczne przez porównanie wartości całkowitoliczbowych za pomocą jednego z powyższych sześciu operatorów relacji. Dopuszczamy także użycie nawiasów, które służą do wymuszania właściwej kolejności obliczeń zarówno w wyrażeniach arytmetycznych, jak i logicznych. Oto kilka przykładów poprawnych wyrażeń logicznych:

i>=0 
(i&gt;=0) <b>and</b> (j&gt;=i) 
<b>not</b> ((k&lt;n) <b>or</b> (j&lt;n))

Przykład ilustrujący kolejność czynności przy wykonaniu instrukcji pętli.

animacja flash

Zmienne indeksowane (tablice)

Często działamy na ciągach zmiennych tego samego typu. Przykładowo taka sytuacja występuje gdy chcemy posortować jakieś dane, albo sprawdzić, czy w zestawie danych znajduje się zadana wartość. Wygodnie wtedy jest używać zmiennych indeksowanych, które realizują pojęcie skończonego ciągu. Zmienna taka ma wtedy jeden wspólny identyfikator, a kolejne elementy oznacza się kolejnymi indeksami, które zazwyczaj są liczbami naturalnymi, choć nie jest to konieczne i w niektórych językach programowania dopuszcza się indeksowanie również innymi typami dyskretnymi (np. znakami).

Zmienne indeksowane nazywają się tablicami. Jeśli A jest tablicą, to A[i] jest jej i-tym elementem. Umawiamy się, że indeksem tablicy może być dowolne poprawne wyrażenie, ale pod warunkiem, że jego wartość mieści się w zakresie określoności tablicy. Zatem odwołanie do elementu spoza zakresu indeksów traktowane jest jako poważny błąd. Często powoduje przerwanie programu bez ostrzeżenia.

W przykładowych zadaniach poniżej proponujemy przećwiczenie podstawowych algorytmów na tablicach. Zakładamy zazwyczaj, że tablica jest zadeklarowana w zakresie \( 1..n \). Dla ułatwienia zrozumienia zapisu pewnych algorytmów stosujemy skrót notacyjny

<b>for</b> k:=1 <b>to</b> n <b>do</b> I

na oznaczenie następującego równoważnego kodu

k:=1; <b>while</b> k&lt;=n <b>do</b> <b>begin</b> I; k:=k+1 <b>end</b>

Konwencja ta powoduje, że dla każdej wartości indeksu, poczynając od \( 1 \), a kończąc na \( n \), wykonamy instrukcję I. Zakresy pętli for mogą być dowolnymi wyrażeniami dającymi wartości całkowite.

<b>program</b> FlagaPolska1(N:integer; A:array[1..N] of integer);
 //Tablica A jest wypełniona zerami i jedynkami 
<b>const</b> bialy = 0;
 czerwony = 1;
<b>var</b> b,c&nbsp;: integer;
 <b>begin</b>
c:=1; b:=n; 
<b>while</b> c &lt; b <b>do</b>
<b>if</b> Kol(c)=czerwony <b>then</b> c:=c+1
<b>else</b> <b>begin</b> 
Z(c,b);
 b:=b-1;
 <b>end</b>;
<b>end</b>.

<b>program</b> FlagaPolska2(N:integer; A:array[1..N] of integer);
//Tablica A jest wypełniona zerami i jedynkami
<b>const</b> bialy = 0;
 czerwony = 1;
<b>var</b> b,c&nbsp;: integer;
 <b>begin</b>
c:=1; b:=n;
 <b>while</b> c &lt; b <b>do</b>
 <b>if</b> Kol(c)=czerwony <b>then</b> c:=c+1 
<b>else</b> <b>begin</b>
 <b>while</b> Kol(b)=biały <b>and</b> (c&lt;b) <b>do</b> b:=b-1;	//pętla po białych od końca tablicy 
<b>if</b> c&lt;b <b>then</b> <b>begin</b>
Z(c,b);
b:=b-1;
 <b>end</b>;
 <b>end</b>;
 <b>end</b>.
 

<b>program</b> FlagaPolska3(N:integer; A:array[1..N] of integer);
//Tablica A jest wypełniona zerami i jedynkami 
<b>const</b> bialy = 0;
 czerwony = 1;
<b>var</b> b,c,kb,kc&nbsp;: integer;
<b>begin</b>
 c:=1; kc:=Kol(c);
 b:=n; kb:=Kol(b);
<b>while</b> c &lt; b <b>do</b>
 <b>if</b> kc=czerwony <b>then</b> <b>begin</b> 
c:=c+1; 
kc:=Kol(c);
<b>end</b> 
<b>else</b> 
<b>if</b> kb=biały <b>then</b> <b>begin</b> 
b:=b-1; 
kb:=Kol(b);
 <b>end</b> 
<b>else</b> <b>begin</b>
 Z(c,b);
 c:=c+1;
 b:=b-1;
 <b>if</b> c &lt; b <b>then</b> <b>begin</b> 
kc:=Kol(c); 
kb:=Kol(b);
 <b>end;</b>;
 <b>end;</b>
 <b>end</b>.

<b>program</b> FlagaPolska4(N:integer; A:array[1..N] of integer);
//Tablica A jest wypełniona zerami i jedynkami
<b>const</b> bialy = 0;
czerwony = 1;
<b>var</b> b,c&nbsp;: integer;
<b>begin</b> 
c:=1; b:=1; 
<b>while</b> c &lt;= N <b>do</b>
<b>if</b> Kol(b)=biały <b>then</b> b:=b+1 
<b>else</b> <b>begin</b>
Z(c,b);
 b:=b+1;
 c:=c+1;
<b>end</b>;
<b>end</b>.

<b>program</b> FlagaTrójkolorowa(N:integer; A:array[1..N] of integer); 
<b>var</b> m,r,w,pom&nbsp;: integer; 
<b>begin</b>
 m:=1; r:=1; w:=N; 
<b>while</b> r &lt;= w <b>do</b> <b>if</b> A[r]=0 <b>then</b> r:=r+1			//przedłużamy segment liczb dodatnich 
<b>else</b> 
<b>if</b> A[r]&lt;0 <b>then</b> <b>begin</b>
 pom:=A[r]; A[r]:=A[m]; A[m]:=pom;	//zamieniamy wartości w A[r] i A[m], po zamianie A[r]=0 i A[m] &lt; 0 
m:=m+1;					//więc zwiększamy oba indeksy r i m r:=r+1; <b>end</b> 
<b>else</b> <b>begin</b>
 pom:=A[r]; A[r]:=A[w]; A[w]:=pom;	//zamieniamy wartości w A[r] i A[w] w:=w-1;					//po zamianie A[w]&gt;0,  ale o A[r] nic nie wiemy <b>end</b>;
 <b>end</b>.

<b>program</b> FlagaTrójkolorowa(N:integer; A:array[1..N] of integer);
<b>var</b> m,r,w,pom&nbsp;: integer;
 <b>begin</b>
m:=1; r:=1; w:=1; 
<b>while</b> w &lt;= N <b>do</b>
 <b>if</b> A[w]&gt;0 <b>then</b> w:=w+1			//przedłużamy segment liczb dodatnich 
<b>else</b>
 <b>if</b> A[w]=0 <b>then</b> <b>begin</b>
 pom:=A[r]; A[r]:=A[w]; A[w]:=pom;	//zamieniamy wartości w A[r] i A[w], po zamianie A[r]=0, A[w] &gt;0 
w:=w+1;					//więc zwiększamy oba indeksy r i w r:=r+1; <b>end</b> 
<b>else</b> <b>begin</b>				//zamieniamy cyklicznie A[m], A[r] i A[w] jeśli m&lt;&gt;r; wpp zamieniamy A[m] i A[w] 
pom:=A[m]; 
A[m]:=A[w]; 
<b>if</b> (m&lt;&gt;r) <b>then</b> <b>begin</b>
A[w]:=A[r]; 
A[r]:=pom; 
<b>end</b>
 <b>else</b> A[w]:=pom; 
m:=m+1; 
r:=r+1; 
w:=w+1;
 <b>end</b>;
 <b>end</b>.

<b>program</b> NajdłuższePlateau1(N:integer; A:array[1..N] of integer); 
<b>var</b> l,p,w,maks: integer;
 koniec:boolean;
<b>begin</b> 
 l:=1; w:=A[l]; maks:=1; 
<b>while</b> l &lt; N <b>do</b> <b>begin</b> 
 p:=l+1; koniec:=false;
<b>while</b> (p &lt;= N) <b>and</b> (<b>not</b> koniec) <b>do</b>		//dopóki jesteśmy w tablicy i poruszamy się wewnątrz segmentu stałego 
<b>if</b> A[p]=w <b>then</b> p:=p+1 
<b>else</b> koniec:=true;
maks:=max(maks, p-l);			//poprawiamy maks 
l:=p; 
<b>if</b> l &lt;= N <b>then</b> w:=A[l];			//ustawiamy nowy początek segmentu 
<b>end</b>;
 <b>end</b>.

<b>program</b> NajdłuższePlateau2(N:integer; A:array[1..N] of integer); 
<b>var</b> w,p,dl,maks: integer;
 koniec:boolean; 
<b>begin</b> 
w:=A[1]; dl:=1; maks:=1; 
<b>for</b> p:=2 <b>to</b> N <b>do</b> <b>begin</b>
<b>if</b> A[p]=w <b>then</b> dl:=dl+1 
<b>else</b> <b>begin</b> 
maks:=max(maks, dl);
 w:=A[p];
 dl:=1;
<b>end</b>;
<b>end</b>;
maks:=max(maks, dl);
<b>end</b>.

<b>program</b> NajdłuższePlateau3(N:integer; A:array[1..N] of integer); 
<b>var</b> i,maks: integer;
<b>begin</b> maks:=1; <b>for</b> i:=2 <b>to</b> N <b>do</b> <b>if</b> A[i]=A[i-maks] <b>then</b> 
maks:=maks+1; 
<b>end</b>.
</pacsal>
 
<p><i>Koszt czasowy</i>: liniowy względem N </p>
<p><i>Koszt pamięciowy</i>: stały </p>
[/collapse]
 
 
<h2> Zadanie 4 (Segment o maksymalnej sumie) </h2> 
 
<p>Napisz program znajdujący w zadanej tablicy A typu array[1..N] of integer, N > 0, maksymalną sumę segmentu (spójnego fragmentu tablicy). Przyjmujemy, że segment pusty ma sumę 0. </p>
 
[collapse collapsed="collapsed" title="Wskazówka 1"]
<p>Najprostsze rozwiązanie to dla wszystkich możliwych segmentów policzyć ich sumę. </p>
[/collapse]
 
 
[collapse collapsed="collapsed" title="Rozwiązanie 1"]
<pascal>
<b>program</b> SegmentOMaksymalnejSumie1(N:integer; A:array[1..N] of integer);
<b>var</b> l,p,j,suma,maks: integer;
<b>begin</b>
maks:=0;
<b>for</b> l:=1 <b>to</b> N <b>do</b> <b>begin</b>		//wybieramy początek segmentu <b>for</b> p:=l <b>to</b> N <b>do</b> <b>begin</b>		//wybieramy koniec suma:=0; <b>for j:=l </b>to<b> p </b>do<b> suma:=suma+A[j];	//liczymy sumę</b> maks:=max(maks,suma);
<b>end</b>;
<b>end</b>;
<b>end</b>.

<b>program</b> SegmentOMaksymalnejSumie2(N:integer; A:array[1..N] of integer);
<b>var</b> l,p,suma, maks: integer;
<b>begin</b>
 maks:=0;
<b>for</b> l:=1 <b>to</b> N <b>do</b> <b>begin</b>
suma:=0; 
<b>for</b> p:=l <b>to</b> N <b>do</b> <b>begin</b>
suma:=suma+A[p];
maks:=max(maks,suma);
<b>end</b>;
<b>end</b>;
<b>end</b>.

<b>program</b>  SegmentOMaksymalnejSumie3(N:integer; A:array[1..N] of integer);
<b>var</b> mini_pref,biez_pref,maks,i: integer;
<b>begin</b>
maks:=0;
mini_pref:=0;
biez_pref:=0;
<b>for</b> i:=1 <b>to</b> N <b>do</b> <b>begin</b>
biez_pref:=biez_pref+A[i];
mini_pref:=min(mini_pref,biez_pref);
maks:=max(maks, biez_pref-mini_pref);
<b>end</b>;
<b>end</b>.

<b>program</b>  SegmentOMaksymalnejSumie4(N:integer; A:array[1..N] of integer); 
<b>var</b> l,p,i,maks,suma: integer;
<b>begin</b>
l:=1;
p:=1;
suma:=0;
maks:=0;
while p &lt;= N <b>do</b> 
<b>if</b> suma+A[p] &lt;= 0 <b>then</b> <b>begin</b>
l:=p+1;
suma:=0;
p:=l;
<b>end</b>
<b>else</b> <b>begin</b>
suma:=suma+A[p];
maks:=max(maks,suma);
p:=p+1; 
<b>end</b>;
<b>end</b>.

<b>program</b>  SegmentOMaksymalnejSumie5(N:integer; A:array[1..N] of integer); 
<b>var</b> i,biez,maks: integer;
<b>begin</b>
maks:=0;
biez:=0;
<b>for</b> i:=1 <b>to</b> N <b>do</b> <b>begin</b>
biez:=max(0,biez+A[i]);
maks:=max(maks, biez);
<b>end</b>;
<b>end</b>.

<b>program</b> CzęśćWspólna(N:integer; A,B:array[1..N] of integer);
//Tablice A i B są posortowane rosnąco 
<b>var</b> ia,ib: integer; 
<b>begin</b> 
ia:=1; ib:=1; 
<b>while</b> (ia &lt;= N) <b>and</b> (ib &lt;= N) <b>do</b>
<b>if</b> A[ia] &lt; B[ib] <b>then</b> ia:=ia+1
<b>else</b> 
<b>if</b> A[ia] &gt; B[ib] <b>then</b> ib:=ib+1 
<b>else</b> <b>begin</b>
write(A[ia], ' ');
ia:=ia+1;
ib:=ib+1;
<b>end</b>;
<b>end</b>.

<b>program</b> Suma(N:integer; A,B:array[1..N] of integer);
//Tablice A i B są posortowane rosnąco 
<b>var</b> ia,ib: integer;
<b>begin</b>
ia:=1; ib:=1;
<b>while</b> (ia &lt;= N) <b>and</b> (ib &lt;= N) <b>do</b>	//dopóki są elementy w obu tablicach 
<b>if</b> A[ia] &lt; B[ib] <b>then</b> <b>begin</b>
write(A[ia], ' ');
ia:=ia+1; 
<b>end</b>
<b>else</b> 
<b>if</b> A[ia] &gt; B[ib] <b>then</b> <b>begin</b> 
write(B[ib], ' ');
ib:=ib+1;
<b>end</b>
<b>else</b> <b>begin</b>
write(A[ia], ' ');
ia:=ia+1;
ib:=ib+1;
<b>end</b>;
<b>for</b> ia:=ia <b>to</b> N <b>do</b> write(A[ia], ' ');	//obsługa końcówki A <b>for</b> ib:=ib <b>to</b> N <b>do</b> write(B[ib], ' ');	//obsługa końcówki B <b>end</b>. 

<b>program</b> Suma(N:integer; A,B:array[1..N] of integer);
//Tablice A i B są posortowane rosnąco 
<b>var</b> ia,ib: integer;
<b>function</b> mniejsze(ia,ib: integer):boolean;		//funkcja porównująca wartości w ia i ib 
<b>begin</b>
mniejsze:=false;
<b>if</b> (ib &gt; N) <b>and</b> (ia &lt;= N) <b>then</b>  mniejsze:=true 
<b>else</b> <b>if</b> (ib &lt;= N) <b>and</b> (ia &lt;= N) <b>then</b>
<b>if</b> A[ia] &lt; B[ib] <b>then</b> mniejsze:=true 
<b>end</b>;
<b>begin</b>						//główny program 
ia:=1; 
ib:=1; 
<b>while</b> (ia &lt;= N) <b>or</b> (ib &lt;= N) <b>do</b>
<b>if</b> mniejsze(ia,ib) <b>then</b> <b>begin</b>
write(A[ia], ' ');
ia:=ia+1;
<b>end</b>
<b>else</b>
<b>if</b> mniejsze(ib,ia) <b>then</b> <b>begin</b>
write(B[ib], ' ');
ib:=ib+1;
<b>end</b>
<b>else</b> <b>begin</b>
write(A[ia], ' ');
ia:=ia+1;
ib:=ib+1;
<b>end</b>;
<b>end</b>.

<b>program</b> Podciąg(N,M:integer; A:array[1..N] of integer; B:array[1..M] of integer);
<b>var</b> ia,ib: integer;
 istnieje: boolean;
<b>begin</b>
<b>if</b> N &gt; M <b>then</b> istnieje:=false	//bo funkcja f miała być rosnąca
<b>else</b> <b>begin</b>
ia:=1;ib:=1;
<b>while</b> (ia &lt;= N) <b>and</b> (ib &lt;= M) <b>do</b>
<b>if</b> A[ia] &lt;&gt; B[ib] <b>then</b> ib:=ib+1 
<b>else</b> <b>begin</b>
ia:=ia+1;
ib:=ib+1;
<b>end</b>;
istnieje:=(ia&gt;N);
<b>if</b> istnieje <b>then</b> write('Tablica A jest podciągiem tablicy B');
<b>end</b>;
<b>end</b>.

<b>program</b> Odwracanie1(N:integer; A:array[0..N-1] of integer);
<b>var</b> l,pom: integer;
<b>begin</b>
l:=0;
<b>while</b> l &lt; (N div 2) <b>do</b> <b>begin</b>
pom:=A[l];
A[l]:=A[N-1-l];
A[N-1-l]:=pom;
l:=l+1; 
<b>end</b>;
<b>end</b>.

<b>program</b> Odwracanie2(N:integer; A:array[0..N-1] of integer);
<b>var</b> l,p,pom: integer; 
<b>begin</b> 
l:=0; p:=N-1; 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
pom:=A[l];
A[l]:=A[p];
A[p]:=pom;
l:=l+1;
p:=p-1; 
<b>end</b>;
<b>end</b>.

<b>procedure</b> OdwracanieTablicy(var A: array[0..N-1] of integer; l,p:integer);
<b>var</b> pom: integer;
<b>begin</b> 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
pom:=A[l];
A[l]:=A[p];
A[p]:=pom;
l:=l+1;
p:=p-1;
<b>end</b>;
<b>end</b>.
</pascsl> 
[/collapse]
 
 
<h2> Zadanie 9 (Przesunięcie cykliczne) </h2> 
 
<p>Dana tablica A typu array[0..N-1] of integer, N > 1, i liczba naturalna k > 1. Napisz program realizujący przesunięcie cykliczne w prawo o k pól, czyli przesuwający zawartość pola A[i] na A[(i+k) mod N] dla każdego i &lt; N. </p>
 
 
[collapse collapsed="collapsed" title="Wskazówka 1"]
<p>Najprościej rozwiązać to zadanie używając dodatkowej pamięci rozmiaru N. </p>
 
 
[collapse collapsed="collapsed" title="Rozwiązanie 1"]
<pascal>
<b>program</b> Przesuń1(N,k:integer; A:array[0..N-1] of integer);
<b>var</b> i: integer;
P: array[0..N-1] of integer;
<b>begin</b> 
<b>for</b> i:=0 <b>to</b> N-1 <b>do</b> P[(i+k) <b>mod</b> N]:=A[i];
<b>for</b> i:=0 <b>to</b> N-1 <b>do</b> A[i]:=P[i]; 
<b>end</b>.

<b>program</b> Przesuń2(N,k:integer; A:array[0..N-1] of integer);
// k &gt; 1 
<b>var</b> dl_cyklu,ile_cykli: integer;
<b>begin</b> 
ile_cykli:=nwd(N,k);
dl_cyklu:=N/nwd(N,k);
<b>for</b> i:=0 <b>to</b> ile_cykli-1 <b>do</b> <b>begin</b> 
akt:=A[i];			       //na akt zapamiętujemy wartość do przesunięcia
nast:=(i+k) <b>mod</b> N;                 //obliczamy dla niej nowe miejsce nast 
<b>for</b> j:=1 <b>to</b> dl_cyklu <b>do</b> <b>begin</b> 
pom:=A[nast];		       //wstawiamy akt na A[nast] 
A[nast]:=akt; 
akt:=pom;	                       //to co tam było, będzie nowym akt nast:=(nast+k)
<b>mod</b> N;            //obliczamy nowe nast 
<b>end</b>; 
<b>end</b>; 
<b>end</b>.

<b>program</b> Przesun3(N,k:integer; A:array[0..N-1] of integer); // k &gt; 1 <b>begin</b> OdwracanieTablicy(A,0,N-k-1); OdwracanieTablicy(A,N-k,N-1); OdwracanieTablicy(A,0,N-1); <b>end</b>. 

  a(0)     a(1)    ...        ...    a(N-k-1) a(N-k)    ...        a(N-1) 
a(N-k-1) a(N-k-2)  ...        ...     a(0)    a(N-k)    ...        a(N-1)
a(N-k-1) a(N-k-2)  ...        ...     a(0)    a(N-1)    ...        a(N-k)
 a(N-k)  a(N-k+1)  ... a(N-1) a(0)    ...     ...       a(N-k-2)  a(N-k-1)

1 2 3 
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

<b>program</b> NastępnaPermutacja(N:integer; A:array[1..N] of integer); 
//Permutacja zapisana w A nie jest ostatnia leksykograficznie 
<b>var</b> i,k,pom: integer; 
<b>begin</b>
i:=N-1;
<b>while</b> A[i] &gt; A[i+1] <b>do</b> i:=i-1; 
k:=N;
<b>while</b> A[k] &lt; A[i] <b>do</b> k:=k-1;
pom:=A[i];
A[i]:=A[k];
A[k]:=pom;
OdwracanieTablicy(A,i+1,N);
<b>end</b>;
<b>end</b>.

<b>program</b> SegmentODanejSumie1(N,W:integer; A:array[1..N] of integer);
//Tablica A zawiera tylko liczby dodatnie 
<b>var</b> l,p,suma: integer;
znalezione: boolean;
<b>begin</b>
<b>if</b> W &lt; 0 <b>then</b> znalezione:=false
<b>else</b> <b>begin</b>
 l:=1;
znalezione:=false;
<b>while</b> (l &lt;= N) and (not znalezione) <b>do</b> <b>begin</b>
p:=l;
suma:=0;
<b>while</b> (p &lt;=  N) and (suma &lt; W) <b>do</b> <b>begin</b>
suma:=suma+A[p]; p:=p+1;
<b>end</b>; 
znalezione:=(suma=W);
l:=l+1; 
<b>end</b>;  //while
<b>end</b>;  //else 
<b>if</b> znalezione <b>then</b> write('W tablicy A istnieje segment o sumie W');
<b>end</b>.

<b>program</b> SegmentODanejSumie2(N,W:integer; A:array[1..N] of integer);
//Tablica A zawiera tylko liczby dodatnie 
<b>var</b> l,p,suma: integer;
znalezione: boolean;
<b>begin</b> 
<b>if</b> W &lt; 0 <b>then</b> znalezione:=false
<b>else</b> <b>begin</b> 
l:=1; p:=1;
suma:=0;
<b>while</b> (suma &lt;&gt; W) <b>and</b> (p &lt;= N) <b>do</b> 
<b>if</b> suma &lt; W <b>then</b> <b>begin</b>		//jeśli suma jest za mała, to przesuwamy prawy koniec segmentu
suma:=suma+A[p];
p:=p+1;
<b>end</b>
<b>else</b> <b>begin</b>			//jeśli za duża, to przesuwamy lewy koniec segmentu 
suma:= suma-A[l];
l:=l+1; 
<b>end</b>;
<b>while</b> (suma &gt; W) <b>do</b> <b>begin</b>           //jeśli suma nadal za duża, to próbujemy ją zmniejszyć 
suma:= suma-A[l];
l:=l+1;
<b>end</b>;
znalezione:=(suma=W);
<b>end</b>;  //else 
<b>if</b> znalezione <b>then</b> write('W tablicy A istnieje segment o sumie W');
<b>end</b>.

<b>program</b> Głosowanie1(N:integer; A:array[1..N] of integer);
{Program wypisuje wartość tego elementu, który występuje ponad połowę razy, o ile taki istnieje, lub komunikat, że takiego elementu nie ma}
<b>var</b> i,j,ile,indeks_lidera: integer;
<b>begin</b> i:=1; indeks_lidera:=0; {Zero oznacza, że lidera jeszcze nie znaleźliśmy} <b>while</b> (i &lt; (N+1) div 2) <b>and</b> (indeks_lidera=0) <b>do</b> <b>begin</b>
ile:=0; 
<b>for j:=i </b>to<b> N </b>do<b> if A[i]=A[j] </b>then<b> ile:=ile+1;</b>
{Tutaj zaczynamy od i, bo nie ma sensu zaczynać wcześniej. I tak, jeśli istnieje lider, to będzie wykryty przy pierwszym jego wystąpieniu} 
<b>if</b> (ile &gt;= N div 2 + 1) <b>then</b> indeks_lidera:=i 
<b>else</b> i:=i+1 
<b>end</b>;
<b>if</b> indeks_lidera &lt;&gt; 0 <b>then</b> write('Liderem jest: ', A[indeks_lidera])
<b>else</b> write('Nie ma lidera')
<b>end</b>.

<b>program</b> Głosowanie2(N:integer; A:array[1..N] of integer);
<b>var</b> ile,i,kand,lider: integer;
<b>begin</b> 
kand:=A[1];		//szukamy kandydata na lidera 
ile&nbsp;:= 1;
<b>for</b> i:=2 <b>to</b> N <b>do</b> <b>begin</b>
<b>if</b> A[i]=kand <b>then</b> ile:=ile+1 
<b>else</b> 
<b>if</b> ile &gt; 0 <b>then</b> ile:=ile-1 
<b>else</b> <b>begin</b> 
kand:=A[i];
ile:=1;
<b>end</b>;
<b>end</b>;
ile:=0;		//sprawdzamy, czy kandydat jest liderem 
<b>for</b> i:=1 <b>to</b> N <b>do</b>
<b>if</b> A[i]=kand <b>then</b> ile:=ile+1;
<b>if</b> (ile &gt;= (N div 2 + 1)) <b>then</b> <b>begin</b>
lider:=kand;
write('Liderem jest: ', kand);
<b>end</b>
<b>else</b>
lider:=0;
<b>end</b>.

<b>const</b> N=100; 
b=10;
<b>type</b> liczba = array[0..N-1] of integer;
dwa_liczba = array[0..2*N-1] of integer;

<b>procedure</b> Suma(A,B:liczba, var C:liczba, var przepełnienie:boolean);
//Sumujemy liczby zapisane w A i B do C; zmienna przepełnienie staje się true, gdy wynik nie mieści się w C. 
<b>var</b> p: integer;
<b>begin</b>
p:=0;
<b>for</b> i:=0 <b>to</b> N-1 <b>do</b> <b>begin</b>
C[i]:=A[i]+B[i]+p;
<b>if</b> C[i] &gt;= b <b>then</b> <b>begin</b>
C[i]:=C[i]-b;
p:=1;
<b>end</b>
<b>else</b> p:=0; 
<b>end</b>;
 przepełnienie:=(p=1);
<b>end</b>;

<b>procedure</b> Różnica(A,B:liczba, var C:liczba, var ujemny:boolean); 
//Odejmujemy od liczby zapisanej w A liczbę z B. Wynik zapisujemy w C, zmienna ujemny informuje o znaku wyniku. 
<b>var</b> p: integer;
<b>begin</b> 
p:=0; 
<b>for</b> i:=0 <b>to</b> N-1 <b>do</b> <b>begin</b>
C[i]:=(A[i]-p)-B[i];
<b>if</b> C[i] &lt; 0 <b>then</b> <b>begin</b>
C[i]:=C[i]+b; 
p:=1; 
<b>end</b>
<b>else</b> p:=0; 
<b>end</b>;
ujemny:=(p=1); 
<b>end</b>;

<b>procedure</b> Iloczyn(A,B:liczba, var C:dwa_liczba); 
//Iloczyn liczb zapisanych w A i B zapisujemy w C.
<b>var</b> p,i,j: integer; 
<b>begin</b>
p:=0; 
<b>for</b> i:=0 <b>to</b> 2*N-1 <b>do</b> C[i]:=0;
<b>for</b> i:=0 <b>to</b> N-1 <b>do</b> <b>begin</b>
<b>for</b> j:=0 <b>to</b> N-1 <b>do</b> <b>begin</b>
w:=A[i]*B[j]+p+C[i+j];
C[i+j]:=w <b>mod</b> b;
p:=w <b>div</b> b;
<b>end</b>;
C[i+N]:=p; 
p:=0; 
<b>end</b>; 
<b>end</b>;

Gramatyki – definiowanie składni i semantyki wyrażeń

Palindromem nazwiemy każde słowo, które czytane wprost jest identyczne, jak czytane wspak, 
czyli takie słowo \( a_1,\ldots,a_n \), że dla każdego \( k\in\{1,...,n\} \) zachodzi 
\( a_k=a_{n-k+1} \).
Parzysty palindrom to palindrom o parzystej długości.

\begin{Rysunek}[rys1-abba] \end{Rysunek} </p>

\begin{Rysunek}[rys3-babab-jedno] \end{Rysunek}

\begin{Rysunek}[rys3-120] \end{Rysunek}

\begin{Rysunek}[semantyka-124] \end{Rysunek}

1. Gramatyka wyrażeń powinna być jednoznaczna. 
2. Wartości wyrażeń powinny być zgodne z tradycją matematyczną, w szczególności należy zachować priorytety operatorów oraz wykluczyć napisy typu \( 2 - - 3 \). 
3. Nawiasy powinny wymusić dowolną kolejność, na której nam zależy. 
4. Operacje niełączne, takie jak odejmowanie i dzielenie powinny być lewostronnie łączne, czyli ich wykonywanie musi być od lewej do prawej (w szczególności np. \( 5-3-1 \) powinno dać wynik \( 1 \), a nie \( 3 \)).

<tt> \( G_Z \)=\( \langle \{ \)&lt;wyrażenie Z&gt;,&lt;składnik&gt;,&lt;czynnik&gt;,&lt;stała&gt;,&lt;zmienna&gt;\( \} \)  \( \{\ \)_,a,b,...,z,0,1,...,9,-,+,\( \div\ \),\( \bmod\ \),(,)\( \} \), P,&lt;wyrażenie Z&gt;\( \rangle \)</tt>

<tt>&lt;wyrażenie Z&gt;&nbsp;::= &lt;składnik&gt; | -&lt;składnik&gt; | &lt;wyrażenie Z&gt; + &lt;składnik&gt; | &lt;wyrażenie Z&gt; -&lt;składnik&gt; &lt;składnik&gt;&nbsp;::= &lt;czynnik&gt; | &lt;składnik&gt; * &lt;czynnik&gt; | &lt;składnik&gt;<b>div</b>&lt;czynnik&gt; | &lt;składnik&gt;<b>mod</b>&lt;czynnik&gt; &lt;czynnik&gt;&nbsp;::= &lt;stała&gt; | &lt;zmienna&gt; | (&lt;wyrażenie Z&gt;) &lt;stała&gt;::= &lt;liczba całkowita bez znaku&gt; &lt;zmienna&gt;&nbsp;::= &lt;identyfikator&gt;</tt>

\begin{rysunek}[Drzewo wywodu dla wyrażenia \( a+b*4 \)] \end{rysunek}

Reprezentacja liczb

Wcale nie jest oczywiste, jak należy reprezentować liczby w komputerze. Powszechnie wiadomo, że bardzo wygodny technologicznie jest układ dwójkowy, zwany też binarnym. Łatwiej jest bowiem reprezentować i rozróżniać dwie wartości, niż jakąkolwiek większą ich liczbę: wystarczy przecież rozróżnić "brak sygnału" od "jest sygnał", żeby reprezentować dwie cyfry binarne. Jakakolwiek próba zwiększenia liczby cyfr, które trzeba by było rozróżniać, wymusiłaby analizę ilościową sygnału, a nie tylko jakościową.

     1011
     0110 
     -- --- 
(1)  0001

     1100 (-4)
     0110 (6) 
     -- --- 
(2)  0010

     0100   (4)
     0110   (6) 
     -- --- 
 (0) 1010 (-6) 
<code> 
 
<p>Bit przeniesienia jest równy 0, ale wynik jest absurdalny. Czegóż innego jednak można się było spodziewać? Przecież liczby 10 nie umiemy w naszym czterobitowym systemie wyrazić. W rzeczywistości dodanie jedynki do największej liczby dodatniej w kodzie uzupełnieniowym (czyli do \( 0111\ldots 1 \) daje nam najmniejszą liczbę ujemną, czyli \( 1000\ldots 0 \), zatem cały reprezentowany przedział się w ten sposób zacykla. Te same uwagi dotyczą rzecz jasna innych działań. Rozpoznać sytuację przepełniania można automatycznie i wiele systemów to robi, ale są środowiska programistyczne, które przechodzą nad tym problemem do porządku dziennego i wykonują błędnie działania bez kontroli przepełnienia. </p>

Algorytm przedstawiania ułamka \( u \) w binarnym systemie pozycyjnym. 
Założenie: \( 0\le u  < 1 \). 
Napisz \( 0 \).. Kolejne cyfry rozwinięcia binarnego będziemy generować w następujący sposób: 
Dopóki otrzymujesz nienapotkane wcześniej wartości \( u \) wykonuj 
1. Pomnóż \( u \) przez 2 
2. Jeżeli otrzymana wartość jest mniejsza od 1, to dopisz cyfrę \( 0 \) 
3. Jeżeli otrzymana wartość jest równa co najmniej 1, dopisz cyfrę  \( 1 \) i odejmij od wyniku 1. Z chwilą, gdy powtórzy się wartość \( u \), zakończ procedurę; wypisany ciąg jest okresowy, a jego okresem jest ciąg bitów między powtórzeniami.

Każdą niezerową liczbę rzeczywistą reprezentujemy za pomocą przybliżenia wymiernego w postaci 
pary \( (m,c) \), gdzie \( m\in[-1,-\frac{1}{2})\cup[\frac{1}{2},1) \) jest mantysą, 
zaś \( c \), nazywane cechą, określa o ile pozycji w prawo (dla \( c \) ujemnych) bądź w lewo (dla \( c \) dodatnich) należy przesunąć mantysę,  aby uzyskać żądaną wartość. Interpretacja takiej reprezentacji wyraża się wzorem 
\( x=m2^c \)

NIE TYLKO ZERO NIE ZMIENIA WARTOŚCI DRUGIEGO ARGUMENTU PRZY DODAWANIU!

DODAWANIE ZMIENNOPOZYCYJNE NIE JEST ŁĄCZNE!

Projektując szybkie algorytmy nie tylko przyspieszamy rozwiązywanie problemów, ale przy okazji ograniczamy
możliwości nawarstwiania się błędów. Szybkie algorytmy nie mają czasu zrobić zbyt 
dużych błędów!

Składnia i semantyka instrukcji

Składnia i semantyka instrukcji

Semantyka instrukcji, to funkcja \( I:{\cal V}\times {\cal P} arrow {\cal V} \)

Rzeczywistość pokaże, że będziemy to nasze życzenie musieli lekko zmodyfikować, ale z grubsza nam na razie wystarczy. Cały problem polega teraz na tym, żeby precyzyjnie tę funkcję zdefiniować. Będziemy musieli zatem podać składnię instrukcji \( P \), a potem dla każdej instrukcji i każdego wartościowania \( V \) określić, do jakiego wartościowania \( V' \) wykonanie tej instrukcji prowadzi. Wprowadźmy następującą notację

\( I_V(P)=V' \) oznacza, że w stanie \( V \) wykonanie instrukcji \( P \) prowadzi do stanu \( V' \).

Zatem samo \( I_V \) będzie oznaczało funkcję ze zbioru \( {\cal P} \) w zbiór \( {\cal V} \). Funkcja ta związana z wartościowaniem \( V \) będzie mówiła, do czego doprowadzi nas wykonanie w tym stanie instrukcji \( P \). Podamy teraz składnię instrukcji naszych programów.

<instrukcja>. ::=<instrukcja pusta>|<instrukcja przypisania>|<instrukcja złożona>| <instrukcja warunkowa>|<instrukcja pętli>|<instrukcja pisania>|<instrukcja czytania>| <wywołanie procedury>

Po kolei będziemy teraz objaśniali składnię i semantykę poszczególnych typów instrukcji.

Instrukcja pusta

Składnia: <instrukcja pusta> ::= \( \varepsilon \). Semantyka: \( I_V(\varepsilon)=V \). Na dobry początek coś bardzo łatwego. Zażyczyliśmy sobie instrukcji pustej, która nie ma widzialnej postaci – jest pustym ciągiem znaków i nic nie robi: wykonana dla każdego wartościowania \( V \), pozostawia je niezmienionym. Jest to może mało ambitne zadanie, ale nie jest zabronione i w pewnych sytuacjach może być wygodne. Odłóżmy na później dyskusję dlaczego.

Instrukcja przypisania

Składnia: <instrukcja przypisania> ::= <zmienna>:=<wyrażenie>. Zauważmy, że wszystkie instrukcje przypisania są postaci x:=E, gdzie x jest symbolem zmiennej, a E wyrażeniem, które umiemy już i zapisywać i interpretować. Semantyka: \( I_V({\tt x:=E})=V' \), gdzie. \( V'(z) = \begin{cases}V(z) & \textrm{\ jeśli } z \neq x \\ I_V(E) & \textrm{\ jeśli } z = x\end{cases} \) Czyli instrukcja przypisania x:=E nie zmienia wartości żadnej zmiennej poza \( x \), której to wyróżnionej zmiennej przypisuje wartość wyrażenia \( E \) przy wartościowaniu \( V \). Widzimy więc, że w wyrażeniu w szczególności może wystąpić ta sama zmienna \( x \), która znajduje się z lewej strony przypisania i jedyne, czego wymagamy, to żeby wartość tego wyrażenia była obliczona dla starego wartościowania.

Instrukcja złożona

Składnia: <instrukcja złożona> ::= begin <ciąg instrukcji> end
<ciąg instrukcji>::=\( \varepsilon \)|<instrukcja>;<ciag instrukcji>
Semantyka:
Zauważmy, że wszystkie instrukcje złożone są postaci begin \( \ P_1;\ldots;P_n\ \)end, gdzie \( P_1,\ldots P_n \) są instrukcjami.
\( I_V ({\tt begin }\ P_1; \ldots;P_n\ {\tt end}) = \begin{cases}V & \textrm{\ jeśli } n = 0 \\ I_V(P_1) & \textrm{\ jeśli } n = 1 \\ I_{I_V(P_1)} ({\tt begin}\ P_2; \ldots;P_n\ {\tt end}) & \textrm{\ jeśli } n > 1\end{cases} \)
Zatem jeśli między nawiasami begin a end nie ma żadnej instrukcji, to semantyka jest taka, jak instrukcji pustej; jeśli jest dokładnie jedna instrukcja, to semantyka jest dokładnie taka, jak tej jedynej instrukcji, a jeśli wewnątrz nawiasów występuje więcej niż jedna instrukcja, to po kolei wykonujemy je przechodząc od stanu \( V=V_0 \) kolejno przez stany \( V_1,\ldots,V_n \), tak że dla każdego \( 1\le i\le n \) zachodzi \( I_{V_{i-1}}(P_i)=V_i \). Wykonanie instrukcji złożonej polega więc na przejściu przez ciąg stanów pośrednich powstających przez wykonanie kolejnych instrukcji składowych. Z przyjętych założeń wynika, że jeśli którakolwiek z instrukcji składowych spowoduje błąd, to wartością całej instrukcji złożonej jest również błąd.

Instrukcja warunkowa

Do zdefiniowania instrukcji warunkowej będzie nam potrzebne rozróżnienie jej dwóch postaci: będziemy je nazywali instrukcją warunkową bez else'a oraz instrukcją warunkową z else.

Składnia:
<instrukcja warunkowa>::=<instrukcja warunkowa bez else>|<instrukcja warunkowa z else>
<instrukcja warunkowa bez else>::= if <wyrażenie logiczne> then <instrukcja>
<instrukcja warunkowa z else>::= if <wyrażenie logiczne> then <instrukcja, ale jeśli warunkowa to tylko z else> else <instrukcja>.

Rzecz jasna symbol <instrukcja, ale jeśli warunkowa to tylko z else> przechodzi na wszystkie instrukcje poza jedną: instrukcją warunkową bez else'a. Może zdziwić nieco ten łamaniec: na pierwszy rzut oka wydaje się niepotrzebną komplikacją wyłączenie w instrukcji z „else” jednego rodzaju instrukcji jako tej, która następuje po „then”. W rzeczywistości był to jeden z poważniejszych błędów koncepcyjnych w historii tworzenia języków programowania: tak właśnie myśleli twórcy znanego i bardzo popularnego w latach 60. języka programowania Algol 60 i przez parę lat programiści programowali za pomocą niejednoznacznych instrukcji. Problem ten stanie się widoczny po zdefiniowaniu semantyki.

Semantyka:
Zauważmy, że wszystkie instrukcje warunkowe są jednej z dwóch postaci: if \( \ B\ \) then \( \ P\ \) lub if \( \ B\ \) then \( \ P_1\ \) else \( \ P_2\ \), gdzie \( B \) jest wyrażeniem logicznym, \( P_1 \) jest dowolną instrukcją poza instrukcja warunkową bez else'a, a \( P_2 \) dowolną instrukcją. Dla pierwszego rodzaju instrukcji określamy semantykę następująco:

\( I_V({\tt if }\ B\ {\tt then }\ P) = \begin{cases}I_V(P) & \textrm{\ jeśli } I_V(B) = true \\ V & \textrm{\ jeśli } I_V(B) = false \end{cases} \)

Dla drugiego rodzaju instrukcji określamy semantykę następująco:

\( I_V({\tt if }\ B\ {\tt then }\ P_1\ {\tt else }\ P_2) = \begin{cases}I_V(P_1) & \textrm{\ jeśli } I_V(B) = true \\ I_V(P_2) & \textrm{\ jeśli } I_V(B) = false\end{cases} \)

Sprawdźmy teraz, że wyłączenie instrukcji warunkowej bez else'a było konieczne w drugim rodzaju instrukcji warunkowej. Rozważmy następującą instrukcję:
Przykład programu:

<b>if</b> x&gt;0 <b>then</b> 
<b>if</b> y&gt;0 <b>then</b> 
x:=1 
<b>else</b> 
x:=0

Gdybyśmy dopuścili instrukcję warunkową bez else'a jako możliwą dla tego, co pojawia się po „then”, wówczas możliwy byłby dwojaki rozbiór gramatyczny tej instrukcji:

• albo „else” odnosiłby się do „if y>0” i wtedy cała instrukcja warunkowa byłaby pierwszego rodzaju – bez else, a po then pojawiłaby się instrukcja warunkowa drugiego rodzaju.
• albo „else” odnosiłby się do „if x>0” i wtedy instrukcja ta byłaby drugiego rodzaju, z tym że po „then” pojawiłaby się instrukcja warunkowa pierwszego rodzaju, bez else'a

W pierwszym przypadku na przykład dla danych początkowych \( x=-1, y=-2 \) wartością zmiennej \( x \) po wykonaniu tej instrukcji byłoby \( -1 \) - nic by się nie zmieniło, gdyż warunek \( x>0 \) byłby niespełniony i w ogóle nie przeszlibyśmy do wykonania tego, co jest po „then”. W drugim przypadku wykonałaby się instrukcja po „else”, czyli x:=0, co spowodowałoby przypisanie zmiennej x wartości \( 0 \). Zatem, w zależności od widzimisię kompilatora, nasz program mógłby dawać dwie różne wartości. Tak określona semantyka nie byłaby więc funkcją.
W naszej gramatyce niejednoznaczności już nie ma. Jedynym możliwym odczytem rozważanej wyżej instrukcji jest pierwszy. Zapamiętajmy

Jeżeli mamy kaskadę if'ów, to „else” zamyka zawsze ostatnio otwarty „if”.

Proszę sprawdzić, że nie ma możliwości innego odczytu kaskady ifów, niż przez zamykanie else'ami najbardziej aktualnych warunków.

Instrukcja pętli

Często spotykamy się z sytuacją, w której pewien ciąg czynności będziemy chcieli wykonywać, aż zostanie spełniony pewien warunek. W takiej sytuacji stosujemy instrukcję pętli, która musi określić, co ma spowodować zakończenie pętli oraz co w każdym obrocie pętli powinno się wykonać. W zasadzie wystarczyłaby jedna postać instrukcji pętli, ale że jest to bardzo często stosowana instrukcja, dozwolimy aby stosować wygodne składniowo warianty.

Składnia:

<instrukcja pętli>::=<instrukcja while> | <instrukcja repeat> | <instrukcja for>
<instrukcja while> ::= while <wyrażenie logiczne> do <instrukcja>
<instrukcja repeat> ::= repeat <ciąg instrukcji> until <wyrażenie logiczne>
<instrukcja for> ::= for <zmienna> := <wyrażenie> to <wyrażenie> do <instrukcja> |
for <zmienna> := <wyrażenie> downto <wyrażenie> do <instrukcja>

Pętla while

Skupimy się na instrukcji while, a następnie pozostałe instrukcje zdefiniujemy korzystając z semantyki pętli while. Semantyka instrukcji while wymaga wprowadzenia dodatkowej kategorii semantycznej. Pętle while są postaci while \( B \) do \( P \). Intencją naszą jest wykonywanie instrukcji \( P \) tak długo, jak długo będzie spełniony warunek \( B \). Co jednak, gdy warunek \( B \) zawsze będzie spełniony? Zgodnie z naszym życzeniem program powinien działać bez końca. I tak właśnie chcielibyśmy, żeby było. Zatem mamy tu do czynienia z nową sytuacją: program ani nie kończy się błędem, ani czymkolwiek innym, co można by nazwać stanem końcowym. Po prostu {zapętla się}. Dla takiej sytuacji wprowadzamy kolejne rozszerzenie dziedziny semantycznej: już nie tylko wektor wartościowań lub błąd może być wynikiem wykonania programu, ale również uznajemy za poprawną wartość semantyczną zapętlenie, które będziemy oznaczali przez loop.
Zatem dodajemy jeszcze jedną wartość do możliwych wyników programu. Poza stanem programu (czyli wektorem wartościowań zmiennych) oraz błędem, mamy też {\em zapętlenie}. Powstaje pytanie, jak określić, czy – zgodnie z warunkiem definiującym semantykę pętli – program zapętli się, czy nie. W końcu chcielibyśmy wiedzieć, którą z wartości końcowych nasz program przyjmie: czy się zapętli, czy dojdzie do stanu końcowego. I tu niespodzianka! Nasza ciekawość nie może zostać zaspokojona, przynajmniej w automatyczny sposób. Nie ma bowiem procedury rozstrzygającej, czy dany program się zatrzyma dla konkretnych danych. Własność tę odkrył w latach 30-tych XX wieku Alan Turing. Turing udowodnił, że nie ma metody sprawdzenia, czy program zatrzyma się, czy nie.

Wkrótce dowiemy się, jak można w wielu przypadkach taki problem rozstrzygnąć. Nauczymy się dowodzenia tego, że program się zatrzyma, ale nie będzie to ogólna metoda, tylko ograniczona do na szczęście dość szerokiej klasy programów.

Semantyka:
Zauważmy, że instrukcja pętli ma postać: while \( \ B\ \) do \( \ P\ \), gdzie \( B \) jest wyrażeniem logicznym, a \( P \) jest dowolną instrukcją. Dla pętli while określamy semantykę następująco:

\( I_V({\tt while }\ B\ {\tt do }\ P) = \begin{cases}V & \textrm{\ jeśli } I_V(B) = false \\ I_{I_V(P)}(\tt while)\ B\ {\tt do }\ P) & \textrm{\ jeśli } I_V(B) = true \end{cases} \)
Widzimy więc, że gdy przy wartościowaniu \( V \) warunek \( B \) ma wartość false, wówczas nic się nie dzieje: pozostajemy przy wartościowaniu \( V \) i idziemy dalej, tak jak gdybyśmy wykonali instrukcję pustą. Jeśli natomiast warunek \( B \) ma wartość true, wówczas wykonujemy instrukcję P i wracamy do punktu wyjścia. Żeby ta definicja była formalnie poprawna, potrzebne jest jeszcze jedno ustalenie. Widać bowiem, że mamy do czynienia z dwiema mozliwościami. Albo po skończonej liczbie obrotów pętli warunek B stanie się fałszywy i wtedy przerywamy wykonanie pętli wychodząc z niego z otrzymanym wartościowaniem, albo warunek B nie stanie się fałszywy nigdy i wtedy właśnie mamy do czynienia z sytuacją zapętlenia się programu. Ustalmy więc, że gdy program się zapętla, to jego semantyką jest pętla - trzecia z możliwości (oprócz wartościowania i błędu). Zapętlenie się programu jest zaraźliwe: wystarczy, żeby choć jedna instrukcja pętli nie zakończyła działania, a wartością całego programu będzie pętla.
Podamy teraz parę przykładów pętli while.

l:=0; 
<b>while</b> b &lt;&gt; 0 <b>do</b>
<b>begin</b>
 b:=b div 2;
 l:=l+1 
<b> end</b>

Ten fragment programu działa różnie w zalezności od tego, czy b jest liczbą ujemną, czy nieujemną. Dla liczb dodatnich oblicza logarytm z b zaokrąglony w dół. Dla zera pozostawia wartość 0. dla liczb ujemnych otrzymujemy zapętlenie, gdyż -1 div 2 = -1 .

Zauważmy, że pętla może ani razu się nie wykonać, jeśli warunek dozoru będzie miał wartość false od razu na początku działania pętli. Często zdarzają się nam sytuacje, kiedy chcielibyśmy, aby pętla wykonała się co najmniej raz i żeby o tym, czy dalej ma się wykonywać, czy nie, decydować pod jej koniec. Taka sytuacja występuje na przykład wtedy, gdy żądamy od użytkownika podania jakiejś danej, na przykład hasła. Powinniśmy tak długo żądać od niego wprowadzenia danej, aż spełni ona pewien warunek (na przykład poprawności hasła lub przekroczenia limitu prób). Ponieważ taka sytuacja jest bardzo typowa, więc wprowadzimy konstrukcję, która umożliwia zrobienie tego prościej niż za pomocą pętli while.

Pętla repeat

Pętla repeat wygląda następująco:

<b>repeat</b> 
P1; 
P2; 
... 
Pn 
<b>until</b> B

Jej semantyka jest równoważna następującemu fragmentowi

<b>begin</b>
 P1;
 P2;
...
 Pn 
<b>while</b> not B <b>do</b>
<b>begin</b> 
P1; 
P2; 
...
 Pn 
<b>end</b>
 {<b>while</b> not b} 
<b>end</b>

Widzimy więc, że zgodnie z tym, co napisaliśmy wcześniej, najpierw jednokrotnie wykonuje się ciąg instrukcji \( P1; \ldots;Pn \), a potem dopóki warunek \( B \) nie będzie spełniony, powtarzamy ten sam ciąg instrukcji. Warto zwrócić uwagę na to, że używając pętli while negujemy warunek z pętli repeat. Pętla while bowiem działa dopóki podany warunek dozoru jest spełniony, a pętla repeat kończy działanie w pierwszej chwili, w której warunek dozoru jest spełniony przy jego sprawdzaniu.

Pętla for

Kolejny rodzaj pętli, bardzo często stosowany, wiąże się najczęściej z przetwarzaniem kolejnych liczb całkowitych, na przykład przy przetwarzaniu tablic, kiedy nimi indeksujemy elementy. Użycie tego rodzaju pętli umożliwia kompilatorowi optymalizację kodu i przyspieszenie jego działania, ale wiąże się z pewnymi niebezpieczeństwami, o których zaraz opowiemy.

Najpierw przyjrzyjmy się postaci pętli. Może być ona dwojakiego rodzaju: for i:=E1 to E2 do P lub for i:=E1 downto E2 do P. W pierwszym przypadku semantyką tej pętli jest semantyka równoważnej jej postaci

i:=E1; 
<b>while</b> i&lt;=E2 <b>do</b>
<b>begin</b>
 P;
 i:=i+1
<b>end</b>

Zaczynamy zatem od przypisania zmiennej sterującej i wartości E1, a następnie wykonujemy instrukcję P oraz zwiększamy i o 1 tak długo, aż przekroczymy wartość E2. W drugim przypadku robimy to samo, tylko w drugą stronę, zmniejszając wartości zmiennej i o 1. Zatem semantyką instrukcji for i:=E1 downto E2 do P jest semantyka następującego kodu

i:=E1;
<b>while</b> i&gt;=E2 <b>do</b>
 <b>begin</b>
 P;
 i:=i-1 
<b>end</b>

W rzeczywistości kompilatory często odbiegają nieco od tej semantyki i wprowadzają usprawnienia, które mogą dawać wyniki różniące się od siebie. Rzecz w tym, że gdy uruchamiamy pętlę for, to kompilator stara się z góry przewidzieć, ile obrotów pętla wykona. Oblicza więc wartości wyrażeń \( E1,E2 \) na początku działania pętli i z góry ustawia stosowny rejestr, który będzie odliczał liczbę wykonanych obrotów pętli, aż ta spadnie do zera. Podobnie będzie postępował z tablicami indeksowanymi zmienną sterującą. Normalnie, gdy odwołujemy się do i-tego elementu tablicy A, to kompilator ustala adres stosownej komórki w następujący sposób. Pobiera adres \( a \) początku tablicy z tabeli symboli, którą sam tworzy na etapie deklaracji, wylicza wartość wyrażenia indeksującego – w tym przypadku \( i \) - oraz dodaje do \( a \) wartość \( i-1 \) przemnożoną przez wielkość w bajtach pojedynczego elementu tablicy.

W przypadku pętli for, gdybyśmy chcieli odwoływać się w każdym kroku do i-tego elementu, to wystarczy wiedzieć, że w poprzednim obrocie pętli byliśmy w poprzednim elemencie, więc uzyskanie aktualnego adresu jest znacznie prostsze – wystarczy wziąć poprzedni adres i dodać do niego liczbę bajtów przypadającą na 1 element tablicy. Jeśli mamy nawet bardziej skomplikowane wyrażenie indeksujące pętli, np. zamiast \( i \) powiedzmy \( 3*i+2 \), to nadal różnica między poprzednim, a bieżącym adresem będzie stała i tę wartość można raz ustalić na początku pętli, a następnie kolejne adresy wyznaczać dodając ją do poprzednich. Stosowne wartości – ostatnio używanego adresu oraz skoku – zazwyczaj przechowywane są w rejestrach procesora i w związku z tym dostęp do nich jest znacznie szybszy.

Aby to wszystko się udało, nie powinno się zmieniać ani wartości zmiennej sterującej pętlą, ani ograniczenia wartości, czyli \( E2 \). Zrobienie jednej z tych dwóch rzeczy powoduje nieobliczalne skutki, więc pętle w stylu for i:=1 to n do begin i:=i+1; n:=n-1 end są przejawem niezrozumienia o co chodzi w pętli for. Na szczęście praktyka pokazuje, że tego typu konstrukcje nie mają żadnego zastosowania, więc po prostu pamiętajmy:

W pętlach for nie wolno zmieniać wartości zmiennej sterującej ani wartości końcowego
ograniczenia pętli.

Ciekawe jest pytanie, jaka jest wartość zmiennej sterującej po wykonaniu pętli for. Przyjmijmy, że jest ona nieokreślona. W każdym razie nie powinno się niczego o niej zakładać. W niektórych bowiem kompilatorach zmienna ta pod koniec pętli przyjmuje wartość równą wartości \( E2, \), a w niektórych o jeden większą, jak to by wynikało z semantyki określonej za pomocą pętli while. W naszym narzędziu do uruchamiania programów zmienna sterująca różni się o 1 od wartości \( E2 \), ale nie należy z tego w żadnym wypadku korzystać.

Instrukcja czytania

Gdyby nasz program nie komunikował się w czasie działania ze światem zewnętrznym, musiałby wszystkie dane mieć wpisane przed uruchomieniem w kodzie. W rzeczywistości komputery wymieniają informację ze światem zewnętrznym i często w trakcie ich działania trzeba podawać pewne dane. Bardzo często jesteśmy w sytuacji, w której komputer żąda od nas podania imienia, nazwiska, wieku, dokonania jakichś wyborów. Co to znaczy, że wprowadzimy takie dane? Program musi je jakoś zapamiętać, czyli nadać pewnym zmiennym wartości przez nas podane. Do tego służy właśnie instrukcja czytania.

Mamy tu jednak zupełnie nową sytuację. Jak uwzględnić w semantyce programu to, co użytkownik poda jako dane wejściowe? Jest to o tyle trudne, że liczba możliwych reakcji użytkownika jest potencjalnie nieograniczona. W związku z tym musimy zmienić znowu nieco naszą dziedzinę semantyczną. Ciąg kolejno podawanych danych będziemy reprezentowali w liście zwanej wejściową. Zakładamy, że wszystko co użytkownik przygotuje, niezależnie od tego, czy zrobi to w momencie, gdy dane są potrzebne, czy zawczasu, zostaje dopisywane na końcu tej listy. Program natomiast pobiera wartości z początku listy – te, które były tam umieszczone jako pierwsze. Technikę, w której dane są podawane nieco wcześniej niż trzeba i wykorzystywane we właściwym momencie nazywamy buforowaniem, a część pamięci wykorzystywaną do przechowywania takich danych buforem.

Składnia:
<instrukcja czytania> ::= Read(<ciąg zmiennych>).
<ciąg zmiennych> ::= <zmienna> | <zmienna>,<ciag zmiennych>

Semantyka:
Zauważmy, że wszystkie instrukcje wejścia są postaci Read(x1,...,xm), gdzie x1,...,xm są zmiennymi.
Aby określić semantykę instrukcji czytania, przyjmijmy, że zawartość listy wejściowej jest równa \( L_{in}=(v_1,\ldots,v_n); n\ge m \). W tej sytuacji jako stan komputera przyjmujemy parę \( (V,L_{in}) \).

Mamy wtedy \( I_{(V,L_{in})}({\tt Read(x1,...,xm))}= (V',L'_{in}) \), gdzie
\( V'(z) = \begin{cases}V(z) & \textrm{\ jeśli } z \notin \{x1,\ldots,xm\} \\ v_k & \textrm{\ jeśli } z = x_k\end{cases} \)
oraz
\( L'_{in}=v_{m+1},\ldots,v_n. \)
W wyniku wykonania instrukcji czytania Read(x1,...,xm) lista wejściowa \( L_{in}=\{v_1,\ldots,v_m\} \) zostanie skrócona o \( m \) początkowych wartości, a wartości \( v_1,\ldots,v_m \) zostają przypisane zmiennym \( x1,\ldots, xm \). Dodajmy jeszcze, że jeśli lista wejściowa jest krótsza niż \( m \), to program zawiesza działanie i czeka aż zostanie uzupełniona o brakujące wartości.

Instrukcja pisania

W przypadku instrukcji czytania musieliśmy wziąć pod uwagę listę wejściową, aby określić semantykę. Podobnie teraz będziemy się musieli odnieść do listy wyjściowej, służącej jako medium komunikacyjne ze światem zewnętrznym. Standardową realizacją takiej listy są monitory ekranowe, ale równie dobrze mogą to być pliki oraz inne urządzenia wyjścia takie jak drukarka czy ploter. Zakładamy zatem istnienie listy wyjściowej, która na początku działania programu jest pusta i w miarę jego działania zapełnia się napisami wygenerowanymi przez program.
Składnia:
<instrukcja pisania> ::= Write(<ciąg wyrażeń>).
<ciąg wyrażeń> ::= <wyrażenie> | <wyrażenie>,<ciag wyrażeń>
Semantyka:
Zauważmy, że wszystkie instrukcje pisania są postaci Write(e1,...,em), gdzie e1,...,em są wyrażeniami.
Aby określić semantykę instrukcji pisania przyjmijmy, że zawartość listy wyjściowej jest równa \( L_{out}=(v_1,\ldots,v_n) \). W tej sytuacji jako stan komputera przyjmujemy trójkę \( (V,L_{in},L_{out}) \). Instrukcja pisania nie zmieni ani wartościowania zmiennych \( V \), ani listy wejściowej \( L_{in} \). Zmieni natomiast listę wyjściową, dopisując na jej końcu wartości wyrażeń.
Formalnie:

\( I_{(V,L_{in},L_{out})}({\tt Write(e1,...,em))}= (V',L'_{in},L'_{out}) \),
gdzie
\( V'=V \)
\( L'_{in}=L_{in} \)
\( L'_{out}=v_1, \ldots, v_n, I_V (e1) , \ldots , I_V(em) \)
W wyniku wykonania instrukcji pisania Write(e1,...,em) lista wyjściowa \( L_{out}=\{v_1,\ldots,v_n\} \) zostanie wydłużona o \( m \) wartości wyrażeń wyliczonych przy wartościowaniu \( V \). Ani wartościowanie \( V \), ani lista wejściowa \( L_{in} \) nie ulegają zmianie przy wykonywaniu instrukcji pisania.

Instrukcja procedury

Wykonywaniu procedur poświęcony będzie osobny wykład. Przyjmijmy na razie, że gdy wywołujemy procedurę, wyliczamy wartości parametrów dla aktualnego wartościowania, a następnie wykonujemy kod procedury, używając wyliczonych wartości jako początkowych w naszych obliczeniach.

<b>function</b> ZnajdźPierwsze(N,x:integer; A:array[1..N] of integer):integer; 
//Tablica A posortowana niemalejąco; szukamy pierwszego wystąpienia x w A 
<b>var</b> l,p,s&nbsp;: integer;
<b>begin</b> 
l:=1; 
p:=N; 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
s:=(l+p)div 2; 
<b>if</b> x &gt; A[s] <b>then</b> l:=s+1
<b>else</b> p:=s; 
<b>end</b>; 
<b>if</b> A[l] = x <b>then</b> ZnajdźPierwsze:=l 
<b>else</b> ZnajdźPierwsze:=0; 
<b>end</b>;

<b>function</b> ZnajdźOstatnie(N,x:integer; A:array[1..N] of integer):integer; 
//Tablica A posortowana niemalejąco; szukamy ostatniego wystąpienia x w A 
<b>var</b> l,p,s&nbsp;: integer; <b>begin</b> 
l:=1; 
p:=N; 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
s:=(l+p+1)div 2;
<b>if</b> x &lt; A[s] <b>then</b> p:=s-1 
<b>else</b> l:=s; 
<b>end</b>; 
<b>if</b> A[l] = x <b>then</b> ZnajdźOstatnie:=l 
<b>else</b> ZnajdźOstatnie:=0; 
<b>end</b>;

<b>function</b> LiczbaWystąpień(N,x:integer; A:array[1..N] of integer):integer; 
//Tablica A posortowana niemalejąco; wyznaczamy liczbę wystąpień x w A 
<b>var</b> p,l: integer; 
<b>begin</b> 
l:= ZnajdźPierwsze(N,x,A); 
p:= ZnajdźOstatnie(N,x,A); 
<b>if</b> l&lt;&gt;0 <b>then</b> LiczbaWystąpień:=p-l+1 
<b>else</b> LiczbaWystąpień:=0 
<b>end</b>;

<b>function</b> LiczbaWystąpień1(N,x:integer; A:array[1..N] of integer):integer; 
//Tablica A posortowana niemalejąco; wyznaczamy liczbę wystąpień x w A 
<b>var</b> p,l,p1,l1: integer; 
<b>begin</b>
 l1:=1; p1:=n;
 <b>while</b> l1&lt;&gt;p1 <b>do</b>
 <b>begin</b>
 s:=(l1+p1) <b>div</b> 2;
 <b>if</b> A[s]&lt;x <b>then</b> l:=s+1
 <b>else</b> p:=s
 <b>end</b>;
 l:=l1;
 l1:=1; p1:=n;
 <b>while</b> l1&lt;&gt;p1 <b>do</b>
 <b>begin</b>
 s:=(l1+p1+1) <b>div</b> 2;
 <b>if</b> A[s]&gt;x <b>then</b> p:=s-1
 <b>else</b> l:=s 
<b>end</b>;
 p:=l1; 
LiczbaWystąpień1:=p-l+1 
<b>end</b>;

<b>function</b> Równy(N:integer; A:array[1..N] of integer):integer; 
//Tablica A posortowana rosnąco; szukamy i, takiego że A[i]=i 
<b>var</b> p,l,s: integer;
<b>begin</b>
 l:=1;
 p:=N;
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
s:=(l+p)div 2; 
<b>if</b> A[s] &lt; s <b>then</b> l:=s+1 
<b>else</b> p:=s; 
<b>end</b>; 
<b>if</b> (A[l]=l) <b>then</b> Równy:=l 
<b>else</b> Równy:=0; 
<b>end</b>;

<b>function</b> MaksBitoniczny(N:integer; A:array[1..N] of integer):integer; 
//Tablica A zawiera ciąg bitoniczny; szukamy maksimum w tym ciągu 
<b>var</b> p,l,s: integer; 
<b>begin</b> 
<b>if</b> N=1 <b>then</b> MaksBitoniczny:=1 
<b>else</b>
 <b>if</b> A[N-1] &lt; A[N] <b>then</b> MaksBitoniczny:=N 
<b>else</b> <b>begin</b>
 l:=1;
 p:=N-1; 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
 s:=(l+p)div 2;
 <b>if</b> A[s] &lt; A[s+1] <b>then</b> l:=s+1 
<b>else</b> p:=s; 
<b>end</b>;
 MaksBitoniczny:=l; 
<b>end</b>; 
<b>end</b>;

<b>function</b> SufitZPierwiastka1(x:integer):integer; 
//Dla x &gt; 0 wyznaczamy sufit z pierwiastka z x 
<b>var</b> i: integer; 
<b>begin</b> 
i:=1; 
<b>while</b> x &gt; i*i <b>do</b> i&nbsp;:= i+1;
 SufitZPierwiastka1&nbsp;:= i;
<b>end</b>;

<b>function</b> SufitZPierwiastka2(x:integer):integer; 
//Dla x &gt; 0 wyznaczamy sufit z pierwiastka z x 
<b>var</b> l,p,s&nbsp;: integer; 
<b>begin</b>
 l:=1; 
p:=x; 
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
s:=(l+p)div 2;
 <b>if</b> x &gt; s*s <b>then</b> l:=s+1 
<b>else</b> p:=s; 
<b>end</b>; 
SufitZPierwiastka2:=l; 
<b>end</b>;

<b>function</b> PodłogaZPierwiastka(x:integer):integer; 
//Dla x &gt; 0 wyznaczamy podłogę z pierwiastka z x 
<b>var</b> l,p,s&nbsp;: integer;
<b>begin</b>
 l:=1;
 p:=x;
 <b>while</b> l &lt; p <b>do</b> <b>begin</b>
 s:=(l+p+1)div 2;
 <b>if</b> x &lt; s*s <b>then</b> p:=s-1 
<b>else</b> l:=s; 
<b>end</b>;
PodłogaZPierwiastka:=l; 
<b>end</b>;

<b>function</b> BinPower(x,n:integer):integer; 
// Dla x,n &gt; 0 wyznaczamy x do potęgi n 
<b>var</b> z,y,i: integer; 
<b>begin</b> 
z:=1; 
y:=x; 
i:=n; 
<b>while</b> i &gt; 0 <b>do</b> <b>begin</b>
<b>if</b> (i mod 2 = 1) <b>then</b> z:=z*y;
 y:=y*y;
 i:=i div 2;
<b>end</b>;
BinPower:=z;
<b>end</b>;

<b>function</b> ZnajdźPierwszyWiększy(C:array[1..N] of integer; l,p,x:integer):integer; 
//Tablica C jest posortowana niemalejąco na odcinku od l do p, zakładamy, że C[p] &gt; x; 
//szukamy indeksu pierwszego elementu z lewej większego od x 
<b>var</b> s: integer;
<b>begin</b>
<b>while</b> l &lt; p <b>do</b> <b>begin</b>
s:=(l+p+1)div 2; 
<b>if</b> x &lt; C[s] <b>then</b> p:=s-1
<b>else</b> l:=s; 
<b>end</b>;
<b>if</b> C[l] &lt;= x <b>then</b> ZnajdźPierwszyWiększy:=l+1
<b>else</b> ZnajdźPierwszyWiększy:=l; 
<b>end</b>;

<b>function</b> MaxNiemalejący(N:integer; A:array[1..N] of integer):integer; 
<b>var</b> ia,ib,z: integer;
 B: array[1..N] of integer; 
<b>begin</b> 
ib:=1;
 B[ib]:=A[1];
 <b>for</b> ia:=2 <b>to</b> N <b>do</b>
 <b>if</b> A[ia] &gt;= B[ib] <b>then</b> <b>begin</b> 
ib:=ib+1;
 B[ib]:=A[ia]; 
<b>end</b> 
<b>else</b> <b>begin</b> 
z:=ZnajdźPierwszyWiększy(B,1,ib,A[ia]); B[z]:=A[ia]; 
<b>end</b>;
 MaxNiemalejący:=ib;
 <b>end</b>;

Dowodzenie poprawności programów

Wprowadzenie

jest := false;
<b>for</b> k:=1 <b>to</b> n <b>do</b> if A[k]=x <b>then</b> jest:=true

jest := false; 
k:=1;
 jest=false, k=1 
<b>while</b> (not jest) and ( k&lt;=n) do  \( {\mbox{\neg jest \Leftrightarrow (\forall 1\le j  <  k: A[j] \neq x \land 1\le k\le n+1)}} \) 
<b>begin</b>
 <b>if</b> A[k]=x <b>then</b> jest:=true;
 k:=k+1
<b>end</b>

 {\( {\mbox{ n\ge 1}} \)}
 k:=1; 
{\( {\mbox{ k=1, n\ge 1}} \)} 
<b>while</b> (k&lt;n) and (A[k]&lt;&gt; x) <b>do</b> {\( {\mbox{(\forall 1\le j  <  k: A[j] \neq x) \land (1\le k\le n)}}\)}
k:=k+1;
{\( {\mbox{ (A[k]=x) \Leftrightarrow ((\exists 1\le j \le n: A[j] = x) \land (1\le k\le n))}} \)} 
jest&nbsp;:= A[k]=x
{\( {\mbox{ (jest) \Leftrightarrow ((\exists 1\le j \le n: A[j] = x) \land (k\le n))}} \)}

\( ((p \land q) \Rightarrow r) \Leftrightarrow ((p\Rightarrow r) \lor (q\Rightarrow r)) \) 
\( ((p \lor q) \Rightarrow r) \Leftrightarrow ((p\Rightarrow r) \land (q\Rightarrow r)) \)

Ilekroć odwołujemy się do tablicy, powinniśmy móc udowodnić, 
że indeks tablicy mieści się w dziedzinie określoności.

 
\( \{ {\mbox{ n\ge 1}}\} \)
 k:=1;
 A[n+1]:=x;
 \( \{{\mbox{ n\ge 1, k=1, A[n+1]=x}}\} \) 
<b>while</b> A[k]&lt;&gt; x <b>do</b>  \( {\mbox{\{(\forall 1\le j  <  k: A[j] \neq x) \land (1\le k\le n+1) \land (A[n+1]=x)}}\} \) 
k:=k+1; 
\( \{{\mbox{ (k\le n) \Leftrightarrow (\exists 1\le j \le n: A[j]=x)}}\} \)
 jest&nbsp;:= k&lt;=n 
\( \{{\mbox{ (jest) \Leftrightarrow (\exists 1\le j \le n: A[j] = x) }}\} \)

\( p \Rightarrow (q \Rightarrow r) \) jest równoważne \( (p \land q) \Rightarrow r \)

\( {\mbox{ n\ge 1}} \) 
<b>if</b> A[n]=x <b>then</b> jest&nbsp;:= true 
<b>else</b>
 <b>begin</b> 
v:=A[n]  // zapamiętujemy ostatnią wartość tablicy 
k:=1; 
A[n]:=x; // i teraz możemy ją zamazać bez obawy o jej utracenie 
<b>while</b> A[k]&lt;&gt; x <b>do</b> // stosujemy znany algorytm ze strażnikiem k:=k+1; 
jest&nbsp;:= k&lt;n;  // ten warunek nieco się zmienił 
A[n]&nbsp;:= v   // a tutaj odtwarzamy zamazaną wartość 
\( {\mbox{ (jest) \Leftrightarrow (\exists 1\le j \le n: A[j] = x)}} \)

program ChlopiRosyjscy(x0,y0:Integer);
var x,y,z:Integer;
 begin
 x:=x0; y:=y0; z:=0;
 while x<>0 do
 begin
if odd(x) then z:=z+y;
x:= x div 2;
y:=y+y
end;
Write(z)
end.

program ChlopiRosyjscy(x0,y0:Integer); 
var x,y,z:Integer;
begin 
x:=x0; y:=y0; z:=0; {x=x0, y=y0, z=0} 
while x<>0 do {z+xy=x0y0} begin 
if odd(x) then z:=z+y;
 {(odd(x) \( \land \) z-y+xy=x0y0) \( \lor (\neg \)odd(x)\( \land \) z+xy=x0y0)
 x:= x div 2; 
{z+2xy=x0y0}
 y:=y+y 
{z+xy=x0y0}
 end; 
{z=x0y0}
 Write(z)
end.

l:=1; p:=n;
<b>while</b> (l &lt; p) <b>do</b>
 <b>begin</b>
 s:=(l+p) <b>div</b> 2;
 <b>if</b> x &gt; A[s] <b>then</b> l&nbsp;:= s+1
 <b>else</b>
 p&nbsp;:=s 
<b>end</b>;
jest&nbsp;:= x = A[l] 
</pascale>
 
<p>Zróbmy parę spostrzeżeń. Po pierwsze, nie sprawdzamy nigdzie, czy przypadkiem A[s] nie równa się x, tylko doprowadzamy za każdym razem do momentu, w którym badany przedział jest jednoelementowy. Moglibyśmy sprawdzić czy A[s]=x wprowadzając dodatkowe sprawdzenie, ale czy to się opłaca, przedyskutujemy później. Po drugie, wybraliśmy akurat ostrą nierówność prowadzącą do przesunięcia indeksu l na prawo od s i wydaje się na pierwszy rzut oka, że równie dobrze byłoby sprawdzić nieostrą nierówność, zastępując instrukcję warunkową następującą: </p> 
 
<pascal>
<b>if</b> x&gt;=A[s] <b>then</b> l:=s
 <b>else</b> p:=s-1

l:=1; p:=n;
 <b>while</b> l &lt; p <b>do</b> {Sort(A) \( \land (1\le l\le p\le n) \land \exists (1\le k \le n: A[k]=x \Leftrightarrow \exists (l\le k \le p: A[k]=x)} \) 
<b>begin</b> 
s:=(l+p) <b>div</b> 2;
 if x &gt; A[s] <b>then</b> l:=s+1 
<b>else</b> p:=s
 <b>end</b>;
 jest&nbsp;:= x=A[l]

<b>program</b> FlagaTrójkolorowa(N:integer; A:array[1..N] of integer);
<b>var</b> m,r,w,pom&nbsp;: integer;
<b>begin</b>
 m:=1; r:=1; w:=N;
<b>while</b> r &lt;= w <b>do</b>
 <b>if</b> A[r]=0 <b>then</b> r:=r+1			//przedłużamy segment liczb dodatnich 
<b>else</b> 
<b>if</b> A[r]&lt;0 <b>then</b> <b>begin</b>
pom:=A[r]; A[r]:=A[m]; A[m]:=pom;	//zamieniamy wartości w A[r] i A[m], po zamianie A[r]=0 i A[m] &lt; 0 
m:=m+1;					//więc zwiększamy oba indeksy r i m 
r:=r+1; 
<b>end</b>
<b>else</b> <b>begin</b> pom:=A[r]; A[r]:=A[w]; A[w]:=pom;	//zamieniamy wartości w A[r] i A[w] w:=w-1;					//po zamianie A[w]&gt;0,  ale o A[r] nic nie wiemy <b>end</b>; <b>end</b>. 

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧
∀ j  (m ≤ j < r) ⇒  A[j] = 0 ∧ 
∀ k  (w < k ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ m ≤ r ∧  r-1 ≤ w ≤ N ∧ N > 0

 
// N > 0 
1:m:=1; r:=1; w:=N; 
// N(m,r,w) 
2:<b>while</b> r &lt;= w <b>do</b> 
// N(m,r,w) &and; r &le; w 
3:  <b>if</b> A[r]=0 <b>then</b> 
// N(m,r,w) &and; r &le; w &and; A[r] = 0 
// N(m,r+1,w) 4:    
r:=r+1 // N(m,r,w) 
5:   <b>else</b> 
6:    <b>if</b> A[r]&lt;0 <b>then</b> <b>begin</b>
// N(m,r,w) &and; r &le; w &and; A[r] &lt; 0 
7:      pom:=A[r];  A[r]:=A[m]; A[m]:=pom; 
// N(m+1,r+1,w) 
8:      m:=m+1; r:=r+1; 
// N(m,r,w) 
<b>end</b> 
9:    <b>else</b> <b>begin</b> 
// N(m,r,w) &and; r &le; w &and; A[r] &gt; 0 
10:     pom:=A[r]; A[r]:=A[w]; A[w]:=pom; 
// N(m,r,w-1) 
11:     w:=w-1; 
// N(m,r,w) 
12:   <b>end</b>; 
// N(m,r,w) &and; r-1=w  

∀ i  (1 ≤ i < 1) ⇒  A[i] < 0 ∧ 
∀ j  (m ≤ j < 1) ⇒  A[j] = 0 ∧ 
∀ k  (N < j ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ 1 ≤ 1 ∧  0 ≤ N ≤ N ∧ N > 0

(N(m,r,w) ∧ r ≤ w ∧ A[r] = 0)  ⇒ N(m,r+1,w)

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧ 
∀ k  (w < j ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ m ∧ w ≤ N ∧ N > 0

∀ j  (m ≤ j < r+1) ⇒  A[j] = 0

r+1-1 ∧ w

m ≤ r+1

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧ pom < 0  ∧ 
∀ j  (m ≤ j < r) ⇒  A[j] = 0 ∧ A[r] = 0  ∧ 
∀ k  (w < j ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ m+1 ≤ r+1 ∧ r ≤ w ≤ N ∧ N > 0

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧ pom < 0  ∧ 
∀ j  (m ≤ j < r) ⇒  A[j] = 0 ∧ A[m] = 0  ∧ 
∀ k  (w < j ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ m+1 ≤ r+1 ∧ r ≤ w ≤ N ∧ N > 0

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧ A[r] < 0  ∧ 
∀ j  (m ≤ j < r) ⇒  A[j] = 0 ∧ A[m] = 0  ∧ 
∀ k  (w < j ≤ N) ⇒  A[k] > 0 ∧ 
1 ≤ m+1 ≤ r+1 ∧ r ≤ w ≤ N ∧ N > 0

∀ i  (1 ≤ i < m) ⇒  A[i] < 0 ∧ 
∀ j  (m ≤ j < r) ⇒  A[j] = 0 ∧ 
∀ k  (w < k ≤ N) ⇒  A[k] > 0 ∧ A[r] > 0 ∧ 
1 ≤ m ≤ r ∧ r-1 ≤ w-1 ≤ N ∧ N > 0

<b>program</b> SegmentODanejSumie2(N,W:integer; A:array[1..N] of integer);
 //Tablica A zawiera tylko liczby dodatnie 
<b>var</b> l,p,suma: integer;
znalezione: boolean;
 <b>begin</b> 
l:=1; p:=1; suma:=0; 
<b>while</b> (suma &lt;&gt; W) <b>and</b> (p &lt;= N) <b>do</b>
 <b>if</b> suma &lt; W <b>then</b> <b>begin</b>		//jeśli suma jest za mała, to przesuwamy prawy koniec segmentu
suma:=suma+A[p]; 
p:=p+1; 
<b>end</b> 
<b>else</b> <b>begin</b>			//jeśli za duża, to przesuwamy lewy koniec segmentu 
suma:= suma-A[l]; l:=l+1; 
<b>end</b>; 
<b>while</b> (suma &gt; W) <b>do</b> <b>begin</b> 
suma:= suma-A[l]; 
l:=l+1; 
<b>end</b>;
znalezione:=(suma=W); 
<b>end</b>.

∀ k  ∀ m (k < l ∧ l ≤ m ≤ N+1) ⇒  A[k]+...+A[m-1] <> W ∧ 
∀ m (l ≤ m < p) ⇒  A[l]+...+A[m-1] < W ∧ 
1 ≤ l ≤ p ≤ N+1 ∧ N,W > 0 ∧ suma=A[l]+....A[p-1] ∧ 
A jest tablicą o wartościach dodatnich

 // N,W > 0, A jest tablicą o wartościach dodatnich 
1: l:=1; p:=1; suma:=0; 
// N(l,p,suma) 
2: <b>while</b> (suma &lt;&gt; W) <b>and</b> (p &lt;= N) <b>do</b> 
// N(l,p,suma) &and; (suma &lt;&gt; W) &and; (p &le; N) 
3:   <b>if</b> suma &lt; W <b>then</b> <b>begin</b> 
// N(l,p,suma) &and; (suma &lt; W) &and; (p &le; N) 
4:     suma:=suma+A[p]; p:=p+1; 
// N(l,p,suma) <b>end</b> 
5:   <b>else</b> <b>begin</b> 
// N(l,p,suma) &and; (suma &gt; W) &and; (p &le; N)
6:     suma:= suma-A[l]; l:=l+1; 
// N(l,p,suma) 
7:   <b>end</b>;
 // N(l,p,suma) &and; (suma=W &or; p = N+1) 
8:   <b>while</b> (suma &gt; W) <b>do</b> <b>begin</b> 
// N(l,p,suma) &and; p = N+1 &and; suma &gt; W 
9:     suma:= suma-A[l]; 
l:=l+1; 
10:  <b>end</b>; 
// N(l,p,suma) &and; (suma=W &or; (p=N+1 &and; suma &lt; W)) 
11: znalezione:=(suma=W); 
//znalezione &hArr; (&exist; l &exist; p 1 &le; l &le; p &le; N+1 &and; A[l]+...A[p-1] = W) 

∀ k  ∀ m (k < 1 ∧ 1 ≤ m ≤ N+1) ⇒  A[k]+...+A[m-1] <> W ∧ 
∀ m (l ≤ m < 1) ⇒  A[l]+...+A[m-1] < W ∧ 
1 ≤ 1 ≤ 1 ≤ N+1 ∧ N,W > 0 ∧ 0=0 ∧ 
A jest tablicą o wartościach dodatnich

∀ k  ∀ m (k < l ∧ l ≤ m ≤ N+1) ⇒  A[k]+...+A[m-1] <> W ∧ 
∀ m (l ≤ m < p+1) ⇒  A[l]+...+A[m-1] < W ∧ 
1 ≤ l ≤ p+1 ≤ N+1 ∧ N,W > 0 ∧ 
suma+A[p]=A[l]+....A[p] ∧ 
A jest tablicą o wartościach dodatnich

∀ k  ∀ m (k < l+1 ∧ l+1 ≤ m ≤ N+1) ⇒  A[k]+...+A[m-1] <> W ∧ 
∀ m (l+1 ≤ m < p) ⇒  A[l+1]+...+A[m-1] < W ∧ 
1 ≤ l+1 ≤ p ≤ N+1 ∧ N,W > 0 ∧ 
suma-A[l]=A[l+1]+....A[p-1] ∧ 
A jest tablicą o wartościach dodatnich

<b>program</b> Głosowanie2(N,W:integer; A:array[1..N] of integer);
<b>var</b> ile,i,kand,lider: integer;
<b>begin</b>
kand:=A[1];		//szukamy kandydata na lidera 
ile&nbsp;:= 1;
 i:=2;
<b>while</b> i &lt;= N <b>do</b> <b>begin</b>
<b>if</b> A[i]=kand <b>then</b> <b>begin</b>
 ile:=ile+1; i:=i+1;
 <b>end</b>
 <b>else</b>
 <b>if</b> ile &gt; 0 <b>then</b> <b>begin</b>
 ile:=ile-1; i:=i+1; 
<b>end</b>
 <b>else</b> <b>begin</b>
 kand:=A[i];
 ile:=1;
 i:=i+1;
 <b>end</b>;
 <b>end</b>;
 ile:=0;		//sprawdzamy, czy kandydat jest liderem 
<b>for</b> i:=1 <b>to</b> n <b>do</b>
<b>if</b> A[i]=kand <b>then</b> ile:=ile+1; 
<b>if</b> (ile &gt;= (N div 2 + 1) <b>then</b> <b>begin</b>
 lider:=kand; 
write('Liderem jest: ', kand);
 <b>end</b> 
<b>else</b>
 lider:=0; 
<b>end</b>.

istnieje permutacja P:1..(i-1)-&gt;1..(i-1), taka że P(A[1..i-1])=kand<sup>ile</sup>@ogon i 
ogon (rozpatrywany jako osobna tablica) nie ma lidera
 N &gt; 0 &and; 1 &le; i &le; N+1 &and; ile &ge; 0

 
// N > 0 
1: kand:=A[1]; 
ile := 1; 
i:=2; 
// N(i,ile,kand) 
2: <b>while</b> i &lt;= N <b>do</b> <b>begin</b> 
// N(i,ile,kand) &and; i &le; N 
3:   <b>if</b> A[i]=kand <b>then</b> <b>begin</b> 
// N(i,ile,kand) &and; i &le; N &and; A[i]=kand 
4:     ile:=ile+1; 
i:=i+1; 
// N(i,ile,kand) 
<b>end</b> 
<b>else</b> 
5:    <b>if</b> ile &gt; 0 <b>then</b> <b>begin</b> 
// N(i,ile,kand) &and; i &le; N &and; A[i] &lt;&gt; kand &and; ile &gt; 0 
6:      ile:=ile-1;
i:=i+1; 
// N(i,ile,kand) 
<b>end</b> 
<b>else</b> <b>begin</b>
 // N(i,ile,kand) &and; i &le; N &and; A[i] &lt;&gt; kand &and; ile &le; 0 
7:      kand:=A[i];
 ile:=1;
 i:=i+1; 
// N(i,ile,kand) 
<b>end</b>; 
8: <b>end</b>; 
//Jeśli w tablicy istnieje lider to jest nim kand 

<b>function</b> BinPower(x,n:integer):integer; 
// Dla x,n &gt; 0 wyznaczamy x do potęgi n 
<b>var</b> z,y,i: integer; 
<b>begin</b>
 z:=1; 
y:=x; 
i:=n; 
<b>while</b> i &gt; 0 <b>do</b> <b>begin</b>
 <b>if</b> (i mod 2 = 1) <b>then</b> z:=z*y;
 y:=y*y;
 i:=i div 2;
 <b>end</b>;
 BinPower:=z;
 <b>end</b>;

x<sup>n</sup>=z*y<sup>i</sup> &and; i&ge; 0

 
// x,n > 0 
1: z:=1; y:=x; i:=n; 
// N(z,y,i) 
2: <b>while</b> i &gt; 0 <b>do</b> <b>begin</b> 
// N(z,y,i) &and; i &gt; 0 
3:   <b>if</b> (i mod 2 = 1) <b>then</b> z:=z*y; 
// N(z,y*y,i div 2) 
4:   y:=y*y; i:=i div 2; 
// N(z,y,i) 
5: <b>end</b>; 
// z= x<sup>n</sup> 

N(z,y,i) ∧ i>0 ∧ i mod 2 = 1 ⇒ N(z*y, y*y, i div 2) 
N(z,y,i) ∧ i>0 ∧ i mod 2 = 0 ⇒ N(z, y*y, i div 2)

Pliki

Wprowadzenie

Jak wiadomo, architektura powszechnie stosowanych komputerów charakteryzuje się tym, że pamięć operacyjna jest ulotna, a jej rozmiar jest niewystarczający do przechowywania dużej liczby danych. W związku z powyższym komputery wyposażane są w pamięci masowe (zewnętrzne) pozwalające na trwały zapis danych o dużych rozmiarach. W rozważaniach teoretycznych często przyjmuje się, że rozmiar pamięć masowej jest nieograniczony.

Konstrukcja nośników danych wykorzystywanych do realizacji pamięci masowych sprawia, że dane zapisywane są i odczytywane w postaci wielobajtowych bloków. Blok danych zgodny z fizyczną charakterystyką danego użadzenia zwany jest rekordem fizycznym. Typowy rozmiary rekordu fizycznego mieści się w zakresie od 512 bajtów do kilku kilobajtów.

Fizyczne właściwości urządzenia na jakim składowane są dane nie powinny rozpraszać uwagi programisty. Działanie programu nie może być zależne od rodzaju nośnika. W związku z tym na poziomie systemu operacyjnego wprowadzono pojęcie pliku. Plik jest logiczną jednostką przechowywania danych. Aby cokolwiek przechować w pamięci masowej, trzeba utworzyć co najmniej jeden plik. Warto w tym miejscu wspomnieć, że nie ma jednej uniwersalnej metody realizacji pojęcia pliku w systemie operacyjnym. Pliki realizowane są w strukturach zwanych systemami plików, które różnie wyglądają w różnych systemach operacyjnych. Często też w obrębie danego systemu operacyjnego mamy do wyboru wiele systemów plików o różnych właściwościach.

Model mentalny pliku

W pewnym uproszczeniu każdy plik możemy wyobrazić sobie jako ciąg kolejnych elementów. Za ostatnim znajduje się znacznik końca pliku. Element który zostanie przewożony przy kolejnym odczycie lub zapisie wskazywany jest przez wskaźnik pliku stojący na początku tego elementu. Proszę jednak pamiętać, że jest to bardzo uproszczony model mentalny pliku, bo choćby wskaźnik końca może być realizowane na różne sposoby. Czasami jest to wyróżniona wartość (inna niż dowolna przechowywana w pliku informacja) zapisana na końcu pliku, a w innych rozwiązaniach informacja o końcu pliku zapisana jest w strukturze systemu zbiorów zwanej FAT (file allocation table).

Typy plików

Ze względu na organizacje danych wewnątrz pliku (na poziomie logicznym), będziemy rozróżniać trzy typy plików: pliki binarne, pliki tekstowe i pliki ogólne.

Pliki binarne

Plik binarny to po prostu ciąg bajtów. Inaczej można powiedzieć, że jest to plik, w którym rekord logiczny ma rozmiar jednego bajta. Dane zawarte w pliku binarnym zawsze traktowane są jak ciąg bajtów, bez względu na rodzaj zapisanej w pliku informacji. Co więcej każdy plik możemy potraktować jak plik binarny i w pewnym sensie „ręcznie” (nie zdając się na system operacyjny) interpretować jego zawartość bajt po bajcie.

Pliki ogólne

Plik ogólny podzielony jest na mniejsze/równe porcje zwane rekordami logicznymi. Generalnie plik ogólny możemy wyobrazić sobie jako zbiór rekordów logicznych ułożonych jeden za drugim podobnie jak komórki w tablicy. W języku Pascal mamy nawet pewne podobieństwa w składni deklaracji typu tablicy i pliku ogólnego. W obydwu przypadkach nazwa typu składowego występuje po słowie kluczowym of. (array[1..n] of integer; file of integer;)

Elementami składowymi pliku nie mogą być inne pliki ani wskaźniki (patrz następny wykład).

Rozmiar rekordu logicznego nie musi być równy rozmiarowi rekordu fizycznego. W związku z tym do manipulowania danymi w pliku potrzebny jest wydzielony obszar pamięci operacyjnej zwany buforem, w którym rekordy fizyczne „przerabiane” są na rekordy logiczne. Bufor stosowany jest również w pozostałych typach plików z uwagi na efektywność zapisu. Jest ona większa, gdy zapis lub odczyt obywa się odpowiednio dużymi porcjami będącymi całkowitą wielokrotnością rekordu fizycznego. Zatem jeśli chcemy pobrać z pliku tylko małą ilość informacji, choćby jeden bajt, do bufora zostanie ściągnięta większa ich porcja: zazwyczaj od kilkuset do kilkunastu tysięcy bajtów i próba odczytu kolejnego bajtu nie będzie już wymagała drogiej komunikacji z urządzeniem zewnętrznym. Zakładamy bowiem, że typowe przetwarzanie plików polega na pobieraniu informacji kolejno bajt po bajcie i wtedy dodatkowe czynności związane z transmisją danych są tak kosztowne, że warto na zapas ściągnąć większą porcję danych, co średnio na pewno się opłaci, nawet jeśli w jakimś konkretnym przypadku tych dodatkowych danych nie wykorzystamy. Podobnie przy zapisywaniu danych program czeka, aż bufor się wypełni i dopiero gdy uzna, że już jest ich wystarczająco dużo, żeby zainicjować fizyczny transfer, uruchomi odpowiednie procedury. Jedną z ról zamknięcia pliku jest wyczyszczenie bufora wyjściowego, czyli spowodowanie wymuszonego transferu danych, które czekały w buforze na transmisję. Często w drukarkach wierszowych użytkownicy skarżą się, że ostatni wiersz się im nie wydrukował i że przy wyłączaniu drukarki nagle się coś jeszcze drukuje. Jest to nic innego jak wydrukowanie wiersza zalegającego w buforze drukarki.

Prędkość działania urządzeń zewnętrznych jest o kilka rzędów wielkości mniejsza niż pamięci operacyjnej. Jest bowiem często związana z fizycznym ruchem pewnego urządzenia (głowicy), a tu nie mamy aż takich możliwości przyspieszania jak w przypadku pamięci rdzeniowych. Mechanika rządzi się swoimi prawami.

Pliki tekstowe

Pliki tekstowe zasługują na szczególną uwagę, gdyż sposób kodowania informacji w tych plikach jest najbardziej rozpowszechnionym standardem, a także dlatego, że w wielu językach programowania stanowią one osobny wyróżniony typ danych z dodatkowym zestawem poleceń. Najprościej mówiąc, plik tekstowy to ciąg znaków z podziałem na wiersze. Można powiedzieć, że podstawową jednostką danych w pliku tekstowym jest jeden znak, co w plikach zakodowanych w ASCII przekłada się na 1 bajt. Ale nie zawsze jeden znak to 1 bajt. W standardzie unicode jeden znak ma dwa bajty, a dodatkowo w standardzie tym występują sekwencje kilku bajtów oznaczające jeden znak. Również koniec wiersza kodowany jest na różne sposoby. W systemie Mac OS X jest to znak powrotu karetki, w systemie UNIX znak przejścia do nowego wiersza, a w systemie MS Windows koniec wiersza oznaczony jest dwoma znakami przejściem do nowego wiersza i powrotem karetki.

Rodzaje dostępu do pliku

Budowa pamięci masowej może też powodować ograniczenia w sposobie dostępu do poszczególnych części pliku. Ze względu na te ograniczenia pliki możemy podzielić na pilik sekwencyjne i pliki o dostępie bezpośrednim.

Pliki o dostępie sekwencyjnym

Pliki o dostępie sekwencyjnym charakteryzują się ograniczoną swobodą poruszania się po rekordach. Aby przeczytać k-ty rekord trzeba przeczytać poprzedzające go k-1 rekordów. Dodatkowo możemy przeskoczyć na początek albo na koniec pliku, ale nigdy w dowolne miejsce wewnątrz pliku.

Pliki o dostępie bezpośrednim

Pliki o dostępie bezpośrednim charakteryzują się tym, że rekordy logiczne są ponumerowane i można odczytywać je w dowolnym porządku dzięki operacji pozwalającej na przeskoczenie do rekordu o podanym numerze. W tego rodzaju plikach wszystkie rekordy logiczne muszą mieć taki sam rozmiar. Pliki o dostępie bezpośrednim realizuje się na takich urządzeniach, w których łatwo można się fizycznie dostać do dowolnego miejsca, niezależnie od jego położenia. Przykładami takich urządzeń są twarde dyski, pamięci flash.

Przetwarzanie plików

Generalnie każde przetwarzanie pliku odbywa się według schematu:

1. Otwarcie pliku 
2. Operacje na danych w pliku 
3. Zamknięcie pliku.

Otwarcie pliku

W momencie otwarcia pliku system tworzy deskryptor pliku (jeżeli wcześniej plik nie został otworzony), w którym przechowywane są między innymi takie informacje jak: określenie urządzenia pamięci masowej, na którym znajduje się plik, nazwa pliku, położenie bufora do przesyłania danych z pliku i do pliku oraz inne informacje. W programie odwołujemy się do pliku przez zmienną, w której umieszczony jest wskaźnik (uchwyt) do deskryptora pliku. W Pascalu operacja otwarcia pliku rozbita jest na dwie instrukcje. Pierwsza Assign(f, nazwa_pliku) wiąże zmienną f z plikiem o podanej nazwie. Tworzony jest deskryptor i umieszczany wskaźnik do niego w zmiennej f. Następnie drugą instrukcją plik otwierany jest od odczytu reset(f), zapisu rewrite(f) lub dopisywania danych append(f); Reset ustawia wskaźnik pliku na początku i przygotowuje plik do odczytu. Rewrite kasuje zawartości pliku (wskaźnik jest na początku) i przygotowuje plik do zapisu. Append nie kasuje zawartości pliku, ustawia wskaźnik na końcu pliku i przygotowuje plik do dopisania kolejnych elementów.

Operacje na danych w pliku (odczyt lub zapis)

W Pascalu jest to odpowiednio instrukcja read(f, zmienna), która powoduje odczyt danych z bieżącego rekordu logicznego (w pliku ogólnym) do zmiennej i przesuniecie wskaźnika pliku na początek kolejnego rekordu logicznego. W przypadku pliku tekstowego zachowanie instrukcji read jest zależne od typu zmiennej. Dla zmiennej typu char odczytywany jest jeden znak, a wskaźnik pliku przesuwa się do następnego zanku. Jeżeli zmienna jest typu liczbowego wtedy następuje odczytanie ciagu znaków odpowiadającego składniowo jednej liczbie danego typu. Jeżeli zmienna jest typu string, to odczytywany jest ciąg znaków, aż do końca bieżącego wiersza, a wskaźnik pliku zatrzymuje się przed znakiem końca wiersza. Aby przetworzyć znak końca wiersza, należy wykonać polecenie readln(f). Po jego wykonaniu wskaźnik pliku ustawia się na początku kolejnego wiersza. Aby zapisać informacje w pliku należy użyć polecenia write(f, zmienna). Polecenie to spowoduje zapisanie zawartości zmiennej do pliku i ustawi wskaźnik pliku na końcu zapisanego rekordu (w pliku ogólnym). W przypadku pliku tekstowego liczba zapisanych znaków zależna jest od typu zmiennej. I tak odpowiednie dla typu char zapisze się jeden znak, a wskaźnik pliku ustawi się za zapisanym znakiem. Dla typu liczbowego zapisze się ciąg znaków opowiadający danej liczbie. Dla typu string zapisane zostaną wszystkie znaki znajdujące się w zmiennej, a wskaźnik pliku ustawi się za ostatnim z zapisanych znaków. Aby zapisać znacznik końca linii, należy użyć polecenia writeln(f).

Zamknięcie pliku

W Pascalu zamknięcie pliku realizowane jest poleceniem Close(f). Uwaga, należy pamiętać o zamknięciu pliku nie tylko ze względu na zwolnienie pamięci zajmowanej przez deskryptor i bufor danych. Zamknięcie pliku ważne jest też ze względu na opóźniony zapis. Opóźniony zapis ma na celu zwiększenie efektywności zapisu danych w pamięci masowej. Polega on na tym, że dane z bufora nie są zapisywane dopóki nie zgromadzi się na tyle duża porcja, by zapis był efektywny (np. porcja równa rozmiarowi rekordu fizycznego). Wiąże się z tym niebezpieczeństwo utraty danych, jeżeli plik nie zostanie poprawnie zamknięty. Wtedy mogą zostać utracone dane, które gromadziły się w buforze i nie zostały jeszcze zapisane. Zamknięcie piku gwarantuje zapisanie danych zalegających w buforze. Czasami twórcy systemu operacyjnego stosują zabezpieczenie, które polega na tym, że w momencie gdy program kończy swoje działanie, automatycznie zapisywane są dane z buforów dla wszystkich niezamkniętych plików używanych przez dany program. Podobne rozwiązanie stosowano kiedyś w drukarkach igłowych, co przejawiało się dosyć zaskakującym zachowaniem drukarki, która czasami w momencie wyłączania, ku zaskoczeniu użytkownika, dodrukowywała brakującą część wiersza.

Dostęp bezpośredni

Warto jeszcze wspomnieć, że w plikach ogólnych i binarnych o dostępie bezpośrednim możliwe jest bezpośrednie przejście do dowolnego rekordu logicznego. Operacje tę realizuje polecenie seek(f, N). Powoduje przejście do rekordu o numerze N, przy czym pierwszy rekord w pliku ma numer 0. Wykonanie instrukcji seek(f, 0) jest równoważne instrukcji Reset(f). Operacja seek nie może być stosowana w plikach tekstowych.

Pliki szczególne input i output

W większości języków programowania definiuje się szczególne pliki: standardowe wejście i wyjście, które w momencie uruchomienia programu są otwarte i gotowe do pracy. Standardowe wejście nazywa się input, a standardowe wyjście output; pierwsze z nich otwarte jest do czytania, drugie do pisania. Plik input jest związany z klawiaturą, a plik output z monitorem ekranowym. Jeśli chcemy przeczytać coś ze standardowego pliku wejściowego, albo wypisać coś do standardowego pliku wyjściowego, to nie musimy ani otwierać ich, ani nawet nazywać w instrukcjach czytania i pisania. Zakładamy, że jeśli w instrukcjach Read/Write nie pojawi się wśród argumentów jako pierwsza zmienna plikowa, to mamy do czynienia z czytaniem/pisaniem w plikach standardowych, tak jak to się dzieje w VIPie.

Przykład przetwarzania plików ogólnego lub binarnego

Przykład

<b>var</b> 
f:file <b>of</b> integer; zmienna:integer;
 <b>begin</b>
 Assign(f, nazwa_pliku); Reset(f);
 <b>while</b> <b>not</b> Eof(f) <b>do</b>
 <b>begin</b>
 Read(f, zmienna);
 Przetwórz(zmienna)
 <b>end</b>;
 Close(f);
 <b>end</b>.

Przykład przetwarzania plików tekstowych

Przykład

<b>var</b> 
f:text; 
ch:char; 
<b>begin</b>
Assign(f, nazwa_pliku);
Reset(f);
 <b>while</b> <b>not</b> Eof(f) <b>do</b>
 <b>begin</b>
 <b>while</b> <b>not</b> Eoln(f) <b>do</b>
 <b>begin</b>
 Read(f, ch) 
Przetwórz(ch) 
<b>end</b>; 
<b>if</b> <b>not</b> Eof(f) <b>then</b> Readln(f);
 <b>end</b>;
 Close(f); 
<b>end</b>.

Powyższy fragment programu należy uznać za wzorcową metodę przetwarzania plików tekstowych znak po znaku. Warto zwrócić uwagę na fakt, który często przyjmujemy za oczywisty. Powyższy program jest poprawny tylko przy założeniu, że Eof(f) \( \Rightarrow \) Eoln(f). Gdyby ta implikacja nie zachodziła, wówczas powyższy program wchodziłby w nieskończona pętlę po dojściu do końca pliku. Jeśli nie mamy pewności, że w realizacji języka programowania, z której korzystamy, ta implikacja nie zachodzi, trzeba tę pętlę zapisać inaczej. W większości realizacji języków programowania to założenie jest prawdziwe.

Przykład użycia wirtualnego czytania

Przy przetwarzaniu plików często mamy problem z tym, że aby poznać wartość elementu, trzeba go wpierw przeczytać. Przy czym należy pamiętać o tym, że element przeczytany z pliku niekoniecznie od razu wykorzystamy i będzie nam psuł czytelnośc algorytmu, gdyż będziemy go przechowywali poza plikiem do dalszego przetworzenia. Przykładowym programem, w którym wspomniany problem może wystąpić, jest następujące zadanie.

Przykład:

Usuń z posortowanego niemalejąco pliku f wszystkie wartości występujące w posortowanym
 niemalejąco pliku g i wynik zapisz w pliku h.

Bez utraty ogólności istoty rozwiązania możemy założyć, że wszystkie 3 pliki są typu file of Integer i zawierają liczby całkowite. Zauważmy, że całkiem prawdopodobnym wynikiem jest plik pusty, gdy się okaże, że wszystkie wartości z f występują w g. Zadanie to chciałoby się rozwiązać za pomocą liniowego algorytmu takiego jak na tablicach. Gdyby dane były zapisane w tablicach F,G,H:array[1..n] of integer, wówczas moglibyśmy zastosować następujący kod:

i:=1; j:=1; k:=1; 
<b>while</b> (i&lt;=n) <b>and</b> (j&lt;=n) <b>do</b> {W H[1..k-1] są elementy F[1..i-1] których nie ma w G[1..j-1] 
<b>if</b> F[i]&lt;G[j] <b>then begin</b> {Nie ma w tablicy G elementu F[i]} 
H[k]:=F[i]; 
i:=i+1; 
k:=k+1; 
<b>end</b> 
<b>else if</b> F[i]&gt;G[j] <b>then</b> {G[j] już nie dotyczy żadnego z elementów F[i..n]}
 j:=j+1 
<b>else</b> {F[i]=G[j]) 
i:=i+1; {zostawiamy j, żeby wytłuc z F[i..n] wszystkie elementy o wartości G[j]} 
<b>if</b> i&lt;=n <b>then</b> {skończyła się tablica G, a w F są jeszcze elementy do skopiowania} 
<b>for</b> i:=i <b>to</b> n <b>do</b>
 <b>begin</b>
 H[k]:=F[i]; 
k:=k+1 
<b>end</b>

Spróbujmy teraz wykonać podobny algorytm z plikami. Musimy zacząć od sprawdzenia, czy oba są niepuste.

Przykład

<b>var</b> 
f,g,h:file of Integer;
 fx,gx:Integer; 
<b>begin</b>
 Assign(f, nazwa_pliku1); Assign(g, nazwa_pliku2);
 Reset(f); Reset(g); Rewrite(h); 
<b>if</b> eof(g) <b>then</b> {Niczego nie wyrzucamy z f; kopiujemy wszystko do h}
 <b>while</b> <b>not</b>(eof(f) <b>do</b>
 <b>begin</b>
 Read(f,fx);
 Write(h,fx)
<b>end</b>
<b>else</b> <b>if not</b> eof(f) <b>then</b> 
<b>begin</b> 
Read(f,fx); 
Read(g,gx); 
{teraz jesteśmy gotowi wystartować z porównywaniem decydującym o tym, który plik awansujemy}
<b>while</b> (<b>not</b> Eof(f)) <b>and</b> (<b>not</b> eof(g)) <b>do</b>
<b>if</b> fx &lt; gx <b>then begin</b>
Write(h,fx); {nie ma w g elementu fx} 
Read(f,fx) 
<b>end</b>
<b>else if</b> fx &gt; gx <b>then</b> Read(g,gx) {stary element fg już był bezużyteczny} 
<b>else</b> {fx=gx}    Read(f,fx} {stary fx nie powinien być przepisany do h}

Jak na razie idzie nieźle. Wyjdziemy z pętli albo wtedy gdy z pliku f przeczytamy ostatni element, albo z g. Zauważmy, że dalsze przetwarzanie, gdyby którykolwiek z plików sie skończył, mogłoby doprowadzic do błędu czytania poza końcem pliku.

Teraz stoimy w obliczu sytuacji, kiedy jeden z plików się skończył (a może oba? - czy jest to możliwe?), trzymamy w ręce ostatni element z tego pliku i musimy jakoś zakończyć algorytm. Nie wolno nam już czytać z pliku, którego ostatni element został przeczytany. Spróbujmy kontynuwać

<b>if</b> eof(f) <b>then</b> {trzeba sprawdzić, czy w pliku g nie ma wartości fx} 
<b>begin</b> 
<b>while</b> (gx &lt; fx) <b>and</b> (not eof(g) <b>do</b> Read(g,gx);
<b>if</b> gx&lt;&gt;fx <b>then</b> Write(h,fx)
<b>end</b> 
<b>else</b> {w pliku g już nie ma niczego, więc tylko wartość gx trzeba wykluczyć z f}
<b>begin</b> 
<b>while</b> (fx &lt;&gt; gx) <b>and</b> (<b>not</b> eof(f)) <b>do</b> 
<b>begin</b> 
Write(h,fx); 
Read(f,fx) 
<b>end</b>;
<b>while</b> (fx = gx) <b>and</b> (<b>not</b> eof(f)) <b>do</b>
 Read(f,fx); {elementów równych gx nie wypisujemy} 
<b>while</b> <b>not</b> eof(f) <b>do</b> {kopiujemy resztę pliku f - elementy większe od gx} 
<b>begin</b>
 Write(h,fx);
 Read(f,fx) 
<b>end</b>;
<b>if</b> fx&lt;&gt;gx <b>then</b> Write(h,fx)  {i nie zapominamy o ostatnim elemencie} 
<b>end</b>
 Close(f);
 Close(g);
 Close(h);
<b>end</b>;

Uff! Okazało się, że najżmudniejsza część programu pojawiła się wtedy, gdy wydawało się, że jesteśmy już blisko końca. Być może da się usprawnić jakoś ten kod w miarę normalnie, my jednak zajmiemy się nieco trikową metodą, ale za to niezwykle skracającą cały kod. Do tego załóżmy, że

• istnieje największa liczba całkowita; nazwijmy ją MAXINT
• w zadanych ciągach jej nie ma.

Napiszemy następującą procedurę

<b>procedure</b> Czytaj(var p:plik; var x:Integer);
{procedura przypisuje zmiennej x wartość MAXINT, jeśli jesteśmy na końcu pliku lub czyta
z pliku p kolejną wartość i podaje ją jako wartość zmiennej x} 
<b>begin</b>
 <b>if</b> eof(p) <b>then</b> x:=MAXINT 
<b>else</b> Read(p,x) 
<b>end;</b>

Teraz wszystko jest bardzo proste. Dzięki procedurze Czytaj uzyskaliśmy pewność, że nie wystąpi błąd przy próbie czytania, nawet jeśli będziemy stali na końcu pliku. Zastosowaliśmy wirtualne czytanie, które nie zawsze daje wartość znajdującą się w pliku. Oto kod po deklaracjach i inicjalizacjach plików.

Czytaj(f,fx); Czytaj(g,gx);
 <b>while</b> (fx &lt; MAXINT) <b>or</b> (g &lt; MAXINT) <b>do</b>
 <b>if</b> fx &lt; gx <b>then begin</b>
 Write(h,fx); {nie ma w g elementu fx} 
Czytaj(f,fx)
 <b>end</b> 
<b>else if</b> fx &gt; gx <b>then</b> Czytaj(g,gx) {stary element fg już był bezużyteczny}
 <b>else</b> {fx=gx}    Czytaj(f,fx} {stary fx nie powinien być przepisany do h}

I już! Nic więcej nie trzeba robić poza zamknięciem plików! Warto zapamiętać ten sposób uproszczenia kodu.

<b>function</b> LiczLinie(f:Text):integer; 
// f otwarty plik tekstowy 
<b>var</b> c:character; 
l:integer; 
<b>begin</b> 
l:=0; 
<b>while</b> <b>not</b> eof(f) <b>do</b> <b>begin</b> 
<b>while</b> <b>not</b> eoln(f) <b>do</b>
 read(f,c);
 readln(f);
 l:=l+1;
 <b>end</b>;
 LiczLinie:=l;
 <b>end</b>; // LiczLinie 
 
<b>function</b> RownoLinijne(s1,s2:string):boolean;
<b>var</b> f1,f2:Text;
<b>begin</b> // RownoLinijne
assign(f1,s1);
 assign(f2,s2);
 reset(f1);
 reset(f2);
 RownoLinijne:=LiczLinie(f1)=LiczLinie(f2);
 close(f1);
 close(f2);
 <b>end</b>; // RownoLinijne

<b>function</b> RownoLinijne(s1,s2:string):boolean;
 <b>var</b> f1,f2:Text;
 c:character;
 <b>begin</b>
 assign(f1,s1);
 assign(f2,s2);
 reset(f1);
 reset(f2);
 <b>while</b> <b>not</b> (eof(f1) <b>or</b> eof(f2)) <b>do</b> <b>begin</b>
 <b>while</b> <b>not</b> eoln(f1) <b>do</b>
 read(f1,c);
 readln(f1);
 <b>while</b> <b>not</b> eoln(f2) <b>do</b>
 read(f2,c);
 readln(f2);
 <b>end</b>;
RownoLinijne:=eof(f1) <b>and</b> eof(f2);
close(f1);
close(f2);
<b>end</b>; // RownoLinijne

<b>procedure</b> Kopiuj(<b>var</b> f,g:Text);
 <b>type</b> pozycja=(odstep,slowo);
 <b>var</b> stan:pozycja;
 c:character;
 <b>begin</b>
 reset(f);
 rewrite(g);
 <b>while</b> <b>not</b> eof(f) <b>do</b> <b>begin</b>
 stan:=odstep;
 <b>while</b> <b>not</b> eoln(f) <b>do</b> <b>begin</b>
 read(f,c);
 <b>case</b> stan <b>of</b>
 odstep:
 <b>if</b> c&lt;&gt;' ' <b>then</b> <b>begin</b>
 write(g,c);
 stan:=slowo;
 <b>end</b>
slowo: 
<b>if</b> c&lt;&gt;' ' <b>then</b> 
write(g,c) 
<b>else</b> <b>begin</b>
stan:=odstep;
writeln(g);
<b>end</b>
<b>end</b>
<b>end</b>
 <b>if</b> stan=slowo <b>then</b> writeln(g);
 readln(f);
 <b>end</b>;
 close(f);
 close(g);
<b>end</b>; // Kopiuj 

<b>procedure</b> Kopiuj(<b>var</b> f,g:Text);
 <b>type</b> pozycja=(odstep,slowo);
 <b>var</b> stan:pozycja;
 c:character;
 <b>begin</b>
 reset(f);
 rewrite(g);
 stan:=odstep;
 <b>while</b> <b>not</b> eof(f) <b>do</b> <b>begin</b>
 <b>if</b> eoln(f) <b>then</b> <b>begin</b>
 readln(f);
 <b>if</b> stan=slowo <b>then</b> <b>begin</b>
 writeln(g);
 stan:=odstep;
 <b>end</b>;
 <b>end</b>
 <b>else</b> <b>begin</b> // <b>not</b> eoln(f)
 read(f,c);
 <b>if</b> c=' ' <b>then</b> <b>begin</b> 
<b>if</b> stan=slowo <b>then</b> <b>begin</b>
 writeln(g);
 stan:=odstep
 <b>end</b> 
<b>end</b> 
<b>else</b> <b>begin</b> // c&lt;&gt;' ' 
write(g,c); 
<b>if</b> stan=odstep <b>then</b>
 stan:=slowo 
<b>end</b> 
<b>end</b> 
<b>end</b>; 
close(f); 
close(g); 
<b>end</b>; // Kopiuj 

<b>procedure</b> Komentarze(wej,wyj:string);
 <b>type</b> stany=(nic,kom1,naw_otw,kom2,kom2_gw,napis);
 <b>var</b> f,g:Text; 
stan:stany;
 c:character;
 <b>begin</b>
 assign(f,wej);
 assign(g,wyj);
 reset(f); 
rewrite(g);
 stan:=nic;
 <b>while</b> <b>not</b> eof(f) <b>do</b> <b>begin</b>
 <b>if</b> <b>not</b> eoln(f) <b>then</b>
 read(f,c);
 <b>case</b> stan <b>of</b>
 nic: 
<b>case</b> c <b>of</b>
 '(': stan:=naw_otw;
 '&#39;&#39;': <b>begin</b> stan:=napis; write(g,c) <b>end</b>;
 <b>else</b> write(g,c);
 <b>end</b>
 naw_otw:
 <b>case</b> c <b>of</b>
 '*': stan:=kom2;
 '&#39;&#39;': <b>begin</b> stan:=napis; write(g,'(&#39;&#39;'); <b>end</b>;
 '{': <b>begin</b> stan:=kom1; write(g,'({'); <b>end</b>
 <b>else</b> <b>begin</b> stan:=nic; write(g,'(',c); <b>end</b>
 <b>end</b> 
kom2:
 <b>case</b> c <b>of</b>
 '*': stan:=kom2_gw;
 <b>end</b>
 kom2_gw:
 <b>case</b> c <b>of</b>
 ')': stan:=nic;
 '*': stan:=kom2_gw;
 <b>else</b> stan:=kom2
 <b>end</b>
 kom1:
 <b>case</b> c <b>of</b> 
'}': stan:=nic 
<b>end</b> 
napis:
 <b>case</b> c <b>of</b>
 '&#39;&#39;': <b>begin</b> stan:=nic; write(g,c); <b>end</b> 
<b>else</b> write(g,c);
<b>end</b>
 <b>end</b>
 <b>end</b>
 <b>else</b> <b>begin</b> // eoln(f) readln(f);
 <b>case</b> stan <b>of</b>
 nic: writeln(g);
 naw_otw: <b>begin</b> stan:=nic; writeln(g,'('); <b>end</b>;
 kom2: // nic 
kom2_gw: stan:=kom2;
 kom1: // nic 
napis: writeln(g) 
<b>end</b> 
<b>end</b> 
<b>end</b> 
close(f); 
close(g); 
<b>end</b>

Pamięć dynamiczna

Pamięć dynamiczna

var px:^Integer;

będzie traktowana jako deklaracja zmiennej wskaźnikowej do obiektu typu całkowitego.

Alokacja i zwalnianie pamięci dynamicznej

Przydział (alokacja) i zwalnianie (dealokacja) pamięci dynamicznej odbywa się za pomocą dwóch procedur: New(z) oraz Dispose(z). Obie te procedury mają jeden argument: zmienną. Wykonanie procedury New(z) powoduje następujące czynności

1. Określenie wielkości elementu alokowanego typu (wielkość ta musi być znana na etapie kompilacji programu)
2. Znalezienie adresu w pamięci, począwszy od którego jest dostępnych tyle kolejnych komórek, ile potrzeba na zaalokowanie żądanego elementu
3. Zarezerwowanie alokowanego obszaru
4. Przypisanie znalezionego adresu zmiennej z

Jeśli nie ma spójnego fragmentu pamięci, w którym można by zaalokować żądany element, to procedura New(z) powoduje błąd.
Procedura Dispose(z) powoduje tylko jedną rzecz

1. Odblokowanie zarezerwowanego obszaru pamięci i zwrócenie go do puli niewykorzystanych obszarów.

Przyjmijmy, że po wykonaniu Dispose(z) wartość zmiennej z jest nieokreślona. W rzeczywistości często kompilatory po zwolnieniu zaalokowanego obszaru pozostawiają starą wartość adresu na zmiennej, której dealokacja dotyczyła. Bardzo niebezpieczne jest używanie tej wartości do czegokolwiek i nie należy nigdy tego robić.
Zatem zmienne dynamiczne operują w rzeczywistości na adresach. W konsekwencji pamięć rezerwowana na zmienną dynamiczną jest taka sama (zazwyczaj 4 bajty) i niezależna od tego, na co ta zmienna wskazuje.

Operacje na zmiennych dynamicznych

Zmienne dynamiczne mają ograniczone możliwości wykonywania na nich działań. Możliwe jest porównanie ich wartości, ale tylko pod kątem równości, czyli z operatorów relacyjnych mamy jedynie dwa, a mianowicie = oraz <>. Nie wolno zatem porównywać zmiennych dynamicznych za pomocą operatorów <,<=,>,>=.

Zmiennym dynamicznym można przypisywać wartości, ale jest to ograniczone do innych zmiennych dynamicznych; nie można budować za ich pomocą żadnych wyrażeń. Odwołanie się do wartości elementu wskazywanego przez zmienną dynamiczną odbywa się za pomocą operatora ^. Zatem

z^, to element wskazywany przez zmienną z

Należy bardzo uważać, żeby odróżniać przypisanie z:=x od przypisania z^:=x^. W pierwszym przypadku nastąpi przypisanie zmiennej z wartości adresu wskazywanego przez zmienną x. W drugim przypadku nastąpi skopiowanie wartości elementu wskazywanego przez zmienną x elementowi wskazywanemu przez zmienną z. Przyjmijmy w poniższych przykładach, że zmienne x oraz z są zadeklarowane jako var x,z:^Integer. Wykonanie następującej sekwencji instrukcji

New(x);
z:=x;
z^:=5;
Write(x^)

spowoduje wypisanie wartości 5, gdyż obie zmienne wskazują na ten sam obszar pamięci.
Jeśli natomiast wykonalibyśmy następującą sekwencję

New(x);
New(z);
z^:=5;
x^:=z^;
z^:=3;
Write(x^);

to wypisałaby się wartość 5, gdyż każda z naszych zmiennych wskazuje na inny obszar pamięci i działa na nim autonomicznie. Zastanówmy się, co stałoby się, gdybyśmy tę sekwencję zakończyli przypisaniem z:=x.

Niebezpieczeństwa stosowania zmiennych dynamicznych

Zmienne dynamiczne stwarzają niebezpieczeństwo nieudolnego wykorzystania tego mocnego mechanizmu programistycznego. Wykonanie ostatniego przypisania w powyższym przykładzie spowodowałoby uratę zaalokowanego obszaru pamięci dla zmiennej z. Po prostu zmienna z po przypisaniu z:=x wskazywałaby na ten sam obszar pamięci, co zmienna x i jakiekolwiek odwołanie do x byłoby teraz równoważne odwołaniu do z (włącznie z Dispose). Pamięć przydzielona wcześniej zmiennej z pozostałaby od tej pory niedostępna. Co gorsza, nie udałoby się już nam jej zwolnić, bowiem wykonanie instrukcji Dispose(z) spowodowałoby zwolnienie pamięci przydzielonej zmiennej x! Obszaru przydzielonego zmiennej z nie wskazywałaby już żadna zmienna i nie można byłoby go zwolnić.
Tego typu działanie powoduje powstanie groźnego w skutkach zaśmiecenia pamięci. System operacyjny bowiem będzie rezerwował zajęty obszar do końca działania programu, nie zauważając, że nikt z tego obszaru nie jest już w stanie skorzystać.
Równie groźne są efekty wzajemnego działania na tym samym obszarze. Wyobraźmy sobie następującą sekwencję instrukcji.

New(x);
x^:=5;
z:=x;
...
Dispose(z);
...
New(z);
z^:=3;
Write(x^);

Efekt działania tego kodu jest nieokreślony. Może się zdarzyć, że zostanie wypisana piątka, może trójka (jeśli przez przypadek zmienna z dostałaby ten sam obszar, który wcześniej zwolniła), a może jeszcze coś innego, jeśli po wykonaniu Dispose(z) jakaś inna zmienna dostałaby zwolniony obszar i coś tam w nim zapisała.
Tego typu błędy są trudne do wykrycia, bo w testach w ogóle mogą nie zostać zauważone. Niedeterministyczny charakter alokacji daje tu ogromną gamę możliwych wyników i nie sposób przewidzieć, jak w konkretnym przebiegu programu będą wyglądały wyniki.

<b>const</b> M = 100;
 D = 100;
<b>type</b> Tab = array[0..D-1] of ^array[0..M-1]; 
Str = record
 T:Tab;
 poczD,konD, poczM, konM:integer; 
end;

<b>function</b> Wstaw(var S:Str; liczba: integer):boolean; 
//wstawiamy liczbę do struktury S (S.T[S.poczD]^[S.poczM] to pierwsza liczba w ciągu, 
//S.T[S.konD]^[S.konM] to pierwsze wolne miejsce w S 
//Wstaw staje się false wtedy i tylko wtedy, gdy struktura S jest pełna 
<b>begin</b> 
<b>if</b> (S.konD=S.poczD <b>and</b> S.konM+1=S.poczM) <b>or</b> ((S.konD+1) mod D = S.poczD <b>and</b> S.konM=M-1 <b>and</b> S.poczM=0) <b>then</b> 
Wstaw:=false 
<b>else</b> <b>begin</b>
 Wstaw:=true; 
<b>if</b> S.konM = 0 <b>and</b> S.poczD &lt;&gt;S.konD <b>then</b> New(S.T[S.konD]); 
S.T[S.konD]^[S.konM]:=liczba; 
S.komM:=(S.komM+1) mod M; 
<b>if</b> S.konM=0 <b>then</b> S.konD:=(S.konD+1) mod D; 
<b>end</b>; 
<b>end</b>;

<b>function</b> Pobierz(var S:Str; var liczba: integer):boolean;
//pobieramy liczbę ze struktury S (S.T[S.poczD]^[S.poczM] to pierwsza liczba w ciągu, 
//S.T[S.konD]^[S.konM] to pierwsze wolne miejsce w S 
//Pobierz staje się false wtedy i tylko wtedy, gdy struktura S jest pusta
<b>begin</b> 
<b>if</b> (S.konD=S.poczD <b>and</b> S.konM=S.poczM) <b>then</b>
Pobierz:=false 
<b>else</b> <b>begin</b> 
Pobierz:=true; 
liczba:=S.T[S.poczD]^[S.poczM];
S.poczM:=(S.poczM+1) mod M; 
<b>if</b> S.poczM=0 <b>then</b> <b>begin</b> 
<b>if</b> S.konD &lt;&gt; S.pocz <b>then</b> Dispose(S.T[poczD]);
 S.poczD:=(S.poczD+1) mod D; 
<b>end</b>; 
<b>end</b>; 
<b>end</b>;

<b>const</b> N = 100; 
<b>type</b> rodzaj = (napis, liczba)
 Dane = record 
case co:rodzaj of 
napis: (s:string) 
liczba: (l:liczba) 
end; 
Eltab = record 
klucz:integer;
 case co:rodzaj of 
napis: (wsk:^string) 
liczba: (l:liczba) 
end; 
<b>var</b> T: array[0..N] of Eltab

<b>procedure</b> Wstaw(klucz: integer; var d: Dane); 
//wstawiamy dane z d do tablicy T na pierwsze wolne miejsce, zaczynając od indeksu klucz mod (N+1) 
//zakładamy, że są wolne miejsca w tablicy T 
<b>var</b> k:integer; 
<b>begin</b> 
k:=klucz mod (N+1);
 <b>while</b> T[k].klucz &lt;&gt; -1 <b>do</b> k:=(k+1) mod (N+1);
 T[k].klucz:=klucz; 
T[k].co:=d.co; 
<b>case</b> d.co <b>of</b>
 napis: New(T[k].wsk); T[k].wsk^:=d.s;
 liczba: T[k].l:=d.l 
<b>end</b>; 
<b>end</b>;

<b>function</b> Daj(klucz: integer; var d: Dane):boolean; 
//pobieramy liczbę lub napis z tablicy T skojarzonych z kluczem klucz 
//zakładamy, że są wolne miejsca w tablicy T 
<b>var</b> i:integer; 
<b>begin</b> 
k:=klucz mod (N+1); 
<b>while</b> T[k].klucz &lt;&gt; klucz <b>and</b> T[k].klucz &lt;&gt; -1 <b>do</b> k:=(k+1) mod (N+1); 
<b>if</b> T[k].klucz = -1 <b>then</b> 
Daj:=false 
<b>else</b> <b>begin</b>
 Daj:=true;
 d.co:=T[k].co;
 <b>case</b> d.co <b>of</b>
 napis: d.s:=T[k].wsk^;
 liczba: d.l:=T[k].l; 
<b>end</b>; 
<b>end</b>; 
<b>end</b>;

<b>const</b> N = 100;
 <b>type</b> rodzaj = (pełny, pusty);
 Eltab = record
 case rodzaj of
 pełny: (d:T)
 pusty: (nast:integer)
 end;
 Str = record 
T:array[1..N] of Eltab;
 pierwszy:integer; 
end;

<b>procedure</b> InitT(var S:Str);
 //wszystkie pola ustawiamy na puste, nast wskazują na następne pole lub zero; pierwszy staje się równy 1 
<b>var</b> i:integer;
 <b>begin</b> 
<b>for</b> i:=1 <b>to</b> N <b>do</b> S.T[i].nast:=(i+1) mod (N+1);
 S.pierwszy:=1;
 <b>end</b>;

<b>function</b> NewT(var S:Str; var nowy:integer):boolean; 
//nowy to indeks któregoś z dotychczas pustych pól w S.T; jeśli takich nie ma, to New będzie miało wartość false 
<b>begin</b>
 <b>if</b> S.pierwszy = 0 <b>then</b> 
New:=false 
<b>else</b> <b>begin</b>
New:=true;
 nowy:=S.pierwszy;
 S.pierwszy:=S.T[S.pierwszy].nast;
 <b>end</b>;
 <b>end</b>;
 

<b>procedure</b> DisposeT(var S:Str; d:integer);
//zwalniamy indeks d w tablicy S.T 
<b>begin</b>
 S.T[d].nast:=S.pierwszy;
 S.pierwszy:=d; 
<b>end</b>;

<b>procedure</b> Sort(var A:array[1..N] of ^string); 
//sortujemy leksykograficznie tablicę wskażników do słów 
<b>var</b> i,j,min: integer;
 pom: ^string;
 <b>begin</b>
 <b>for</b> i:=1 <b>to</b> N <b>do</b> <b>begin</b> 
min:=i; 
<b>for</b> j:=i+1 <b>to</b> N <b>do</b> 
<b>if</b> compare(A[j]^,A[i]^) <b>then</b> min:=j;
 pom:=A[i];
 A[i]:=A[min];
 A[min]:=pom;
 <b>end</b>;
 <b>end</b>;

Procedury i funkcje

Procedury i funkcje

PRZYKŁAD

<b>for</b> i:=1  <b>to</b> n <b>do</b> Write('*')

Jeśli chcielibyśmy ująć tę instrukcję w procedurę, to możemy zrobić to w następujący sposób. W części deklaracyjnej programu, a więc tak, gdzie definiuje się stałe, typy i zmienne umieszczamy deklarację procedury.

PRZYKŁAD

procedure Gwiazdki;
<b>begin</b>
<b>for</b> i:=1  <b>to</b> n <b>do</b> Write('*')
<b>end</b>;

Od tej chwili użycie gdziekolwiek identyfikatora Gwiazdki będzie oznaczało wykonanie zaszytego pod tą nazwą kodu powodującego wypisanie n gwiazdek. W momencie deklaracji procedury musi być jasne, o jakie zmienne chodzi. W naszym przypadku mamy do czynienia ze zmiennymi i oraz n. Muszą one być zadeklarowane zanim przystąpimy do pisania kodu procedury lub ich deklaracje powinny wystąpić w jej wnętrzu. Zmienna i jest tutaj zdecydowanie zmienną pomocniczą - jej zadaniem jest jedynie sterowanie liczbą obrotów pętli. Ze względu jednak na to, że w momencie wykonywania procedury jej wartość ulegnie zmianie (zgodnie z naszą semantyką po wykonaniu pętli będzie nieokreślona), nie chcielibyśmy, aby taka ingerencja pozostawała nieodnotowana. Programista widząc taki fragment kodu:

PRZYKŁAD

i:=5;
Gwiazdki;
Write(i)

mógłby się spodziewać wypisania wartości 5, a tego nie powinniśmy się spodziewać. Mamy tu do czynienia z tzw. efektem ubocznym , czyli zmianą wartości zmiennej nieuwidocznioną bezpośrednio w kodzie. Występowanie efektów ubocznych jest uważane za wadę i przykład złego stylu programistycznego. Utrudnia zrozumienie tekstu i jego analizę poprawnościową.
Aby temu zapobiec, wszelkie pomocnicze zmienne będziemy deklarowali wewnątrz procedury.

PRZYKŁAD

procedure Gwiazdki;
<b>var</b> i: Integer; {deklaracja lokalnej zmiennej i}
<b>begin</b>
<b>for</b> i:=1  <b>to</b> n <b>do</b> Write('*')
<b>end</b>;

Zmienna i jest teraz zadeklarowana lokalnie i nawet jeśliby występowała inna zmienna i na zewnątrz procedury, to ta deklaracja przesłoni tamtą, wskutek czego użycie procedury Gwiazdki nie będzie ingerować w wartość tej zewnętrznej zmiennej. Za chwilę o mechanizmie przesłaniania opowiemy dokładniej, gdyż jest to sprawa ważniejsza i bardziej skomplikowana, niż mogłoby się to na pozór wydawać.
Wywołanie naszej nowej procedury wygląda tak samo. Na przykład, gdyby nam zależało na wypisaniu najpierw w pierwszym wierszu 5 gwiazdek, a potem w kolejnym wierszu 6 gwiazdek, to moglibyśmy to zrobić następująco:

n:=5;
Gwiazdki;
Writeln;
n:=6;
Gwiazdki

Parametry procedur

Zauważmy, że poradziliśmy sobie na razie tylko z jedną z dwóch zmiennych - zmienna n nadal musi być zadeklarowana jakoś inaczej. Dlaczego nie zdecydowaliśmy się na umieszczenie jej również pośród zmiennych lokalnych? Po prostu dlatego, że wartość zmiennej n jest istotna dla wyniku działania procedury (wartość zmiennej i była zupełnie nieistotna; i tak inicjalizowała się ona na początku działania pętli). W tego typu przypadkach, kiedy chcemy wykorzystać wartość pewnej zmiennej, przyjęło się podawać ją, jako parametr procedury . Przy deklaracji procedury, w nagłówku - zaraz po nazwie procedury - podamy listę parametrów wraz z określeniem ich typu. Będzie to równoważne z deklaracją zmiennych występujących jako parametry, których zasięg będzie ograniczony jedynie do treści procedury. Ograniczenie zasięgu takich zmiennych jest niezwykle ważną cechą programowania z użyciem procedur.
Deklaracja naszej procedury będzie wyglądać teraz następująco:

PRZYKŁAD

procedure Gwiazdki(n: Integer);
<b>var</b> i: Integer; {deklaracja lokalnej zmiennej i}
<b>begin</b>
<b>for</b> i:=1  <b>to</b> n <b>do</b> Write('*')
<b>end</b>;

Tym razem wywołanie procedury będzie się nieco różniło. W miejsce parametru można wstawić przy wywołaniu dowolną wartość, również będącą wynikiem wyrażenia. Wyglądać to może przykładowo w taki sposób:
n:=5;

Gwiazdki(n);
Writeln;
Gwiazdki(n+1)

Przy wywołaniu wylicza się wartość wszystkich parametrów zanim zaczniemy wykonywać jakiekolwiek instrukcje procedury. Efektem tego wywołania będzie zatem wypisanie najpierw 5 gwiazdek, a potem 6. Zauważmy, że zmienna n użyta jako parametr procedury ma inne znaczenie, niż ta, która jest zadeklarowana na zewnątrz i której jest nadana wartość 5. Sposób przekazywania wartości do wnętrza procedury przez parametry jest uznawany za wzorcowy. Czyni on kod czytelniejszym i pozwala na wyraźne zaznaczenie, które wartości są dla procedury ważne.
Wprowadźmy jeszcze nomenklaturę dotyczacą parametrów. Ponieważ parametry występują w dwóch różnych odsłonach: przy deklaracji procedury i przy jej wywołaniu, więc nazwijmy inaczej parametry występujące w tych kontekstach. Parametry przy deklaracji nazywa się formalnymi, a przy wywołaniu aktualnymi.
Czasami zadaniem procedury ma być obliczenie jakiejś złożonej wartości i wtedy też zamiast korzystać z efektów ubocznych lepiej jest wprowadzić do nagłówka informację o tym, które zmienne będą miały nadawane nowe wartości. Twórcy wielu języków programowania uznali tę potrzebę za tak istotną, że wprowadzili specjalne mechanizmy rozróżniające tryby wywoływania parametrów. Do tej pory poznaliśmy wywołanie przez wartość: przekazujemy procedurze pewną wartość, a ona na jej podstawie wykonuje stosowne działania.
Drugim trybem w Pascalu jest tzw. wywołanie parametru przez zmienną. Omówimy te dwie metody nieco dokładniej.

Parametry wołane przez wartość

W przypadku wywołania parametru przez wartość w nagłówku procedury podajemy identyfikator zmiennej i jej typ, a w momencie wywołania przekazujemy procedurze wyrażenie, którego wartość przypisujemy osobnej zmiennej powołanej na użytek tego konkretnego wywołania procedury. Zatem jesli nawet nazwa parametru formalnego i aktualnego są identyczne, to w rzeczywistości przy wykonywaniu kodu procedury działamy na kopii wartości - dokładnie w momencie wywołania procedury rezerwowana jest dodatkowa pamięć rozmiaru odpowiadającego typowi parametru i do tej pamięci kopiowana jest wartość wyrażenia odpowiadającego temu parametrowi, wyliczona w momencie wywołania procedury. Późniejsze zmiany wartości tego parametru aktualnego sa możliwe, ale po zakończeniu wywołania procedury oryginalne wartości pozostają niezmienione.

Parametry wołane przez zmienną

Parametry wołane przez stałą

Funkcje

Zdarza się, że w efekcie wywołania procedury chcemy wyznaczyć jakąś wartość. W takiej sytuacji korzystamy najczęściej z jednego z dwóch mechanizmów: życia funkcji lub specjalnego typu parametrów, którym będziemy nadawali wartość w trakcie wykonania procedury.
Zacznijmy od sposobu pierwszego. Jeżeli wartością procedury jest liczba, wartość logiczna, znak, napis lub wskaźnik, możemy użyć funkcji , czyli procedury z wartością. Deklaracja wygląda podobnie, jak w przypadku procedur, z tym że w nagłówku dodajemy na końcu po dwukropku typ wyniku funkcji. Tak więc funkcja, która podwaja wartość całkowitej liczby mogłaby wyglądać tak:

PRZYKŁAD

function Dubluj(n: Integer):Integer;
<b>begin</b>
Dubluj&nbsp;:= 2*n
<b>end</b>;

Widzimy więc, że w pewnym momencie w tekście funkcji następuje przypisanie wartości jej identyfikatorowi. Późniejsze wywołanie zadeklarowanej funkcji polega na użyciu identyfikatora z odpowiednią liczbą argumentów po prawej stronie wyrażenia. Na przykład wywołanie

n2:=Dubluj(n)

spowoduje nadanie zmiennej n2 podwojonej wartości zmiennej n.
Uważa się, że szczególnie w przypadku funkcji efekty uboczne, choć podobnie jak w przypadku procedur możliwe do wywołania, stanowią poważny problem. Nie chcielibyśmy przecież, aby wykonanie instrukcji y:=sin(x) spowodowało np. zmiane zmiennej x czy n . Byłoby to sprzeczne z przyzwyczajeniami matematycznymi. Gorąco odradzam tego typu styl programowania.

Składnia procedur i funkcji

Składnia procedur i funkcji jest podobna do składni całego programu. Najpierw mamy nagłówek, w którym określamy nazwę procedury oraz jej parametry, a następnie deklaracje i instrukcje. Deklaracje dotyczą zmiennych lokalnych dla procedury, niewidocznych z zewnątrz i zajmujących pamięć tylko w czasie wykonywania procedury. Część deklaracyjna jest identyczna jak w wypadku programu: mogą w niej być zdefiniowane stałe, typy, zmienne, procedury i funkcje. W przypadku procedur lub funkcji występujących w deklaracjach innej procedury lub funkcji mówimy o zagnieżdżeniu . Ponieważ zagnieżdżenia mogą być wielostopniowe (podprocedura podprocedury procedury...), więc ważne jest, aby określić reguły zasłaniania widoczności identyfikatorów. Zajmiemy się tym w następnym rozdziale.
Zobaczmy, jak mechanizm procedur można wykorzystać w prostym przykładzie rysowania ramki złożonej z symboli jednego rodzaju. Załóżmy, że chcemy wydrukować ramkę o bokach wypełnionych znakami ch, o i wierszach, oraz j kolumnach, oddaloną od lewego brzegu ekranu o m pozycji.

PRZYKŁAD

<b>procedure</b> ramka(i,j,m:Integer; ch:char);
{procedura narysuje ramkę ze znaków ch o i wierszach, j kolumnach oddaloną od lewego brzegu
ekranu o m pozycji. Zakładamy, że kursor jest na początku wiersza}
<b>procedure</b> powiel (n:integer; ch:znak);
{to jest wewnętrzna procedura procedury ramka}
{Drukujemy znak ch n razy}
<b>var</b> k:Integer;
<b>begin</b>
<b>for</b> k:=1 <b>to</b> n <b>do</b> Write(ch)
<b>end</b>;
<b>procedure</b> margines(m:Integer);
{to jest wewnętrzna procedura procedury ramka}
{Drukujemy m spacji}
<b>begin</b>
powiel(m,' ')
<b>end</b>;
<b>procedure</b> BokPoziomy (j,m:integer; ch:char);
{to jest wewnętrzna procedura procedury ramka}
{Drukujemy oddalony o m spacji od lewego brzegu ekranu ciąg j znaków ch}
<b>begin</b>
margines(m);
powiel(j,ch);
Writeln {Po wydrukowaniu przechodzimy do nowego wiersza}
<b>end</b>;
<b>procedure</b> BokiPionowe (i,j,m:integer; ch:char);
{to jest wewnętrzna procedura procedury ramka}
{Drukujemy dwa boki pionowe wysokości i-2 oddalone od siebie o j-2 spacje
Lewy bok jest oddalony od lewego brzegu ekranu o m spacji}
<b>var</b> k:Integer;
<b>begin</b>
<b>for</b> k:=1 <b>to</b> i-2 <b>do</b>
<b>begin</b>
margines(m);
Write(ch);
powiel(j-2,' ');
Write(ch);
<b>end</b>;
Writeln
<b>end</b>;
<b>begin</b>{ramka}
{ponieważ często kod procedury jest dość daleko od nagłówka, więc do dobrych obyczajów
należy komentowanie, czego dotyczy nadchodzący fragment kodu}
BokPoziomy (j,m,ch);
BokiPionowe(i,j,m,ch);
BokPoziomy (j,m,ch)
<b>end</b>

Jeśli teraz np. w tekście programu użyjemy wywołania

ramka(7,6,0,'*'),

to narysuje się ramka siedem na sześć, złożona z gwiazdek i przylegająca do lewego brzegu ekranu.

Parę słów komentarza. Zauważmy, że procedura ramka zawiera 4 podprocedury, przy czym one nawzajem sie wywołują. Podprocedury margines i powiel nie są w dodatku w ogóle wykorzystywane bezpośrednio przez ramkę. Procedura margines wygląda dziwnie: mogłoby się wydawać, że jest niepotrzebna, gdyż jej wywołanie sprowadza się do prostego wywołania procedury powiel. Jednak do dobrego stylu programowania należy wyodrębnianie i nazywanie inaczej tych fragmentu kodu, które służą innym celom. Procedura powiel jest niewątpliwie ogólniejsza od procedury margines. Ma też inne parametry - w przypadku marginesu zakładamy, że wypisujemy spacje, a nie dowolne znaki. W takim przypadku asekurujemy się np. przed sytuacją, kiedy zmieni się nam koncepcja marginesu i - powiedzmy - każdy wiersz będzie poprzedzony dwoma wykrzyknikami. Gdybyśmy w kodzie zamiast margines(m) pisali powiel(m,' '), to musielibyśmy odszukać wszystkie wywołania procedury powiel, które dotyczyły marginesu i wstawić przed nimi stosowne instrukcje. A tak wystarczy, że w jednym miejscu - wewnątrz procedury margines - zmienimy fragment kodu na .

<b>procedure</b> margines(m:Integer);
<b>begin</b>
Write('!!');
powiel(m,' ')
<b>end</b>;

i o nic więcej nie musimy się martwić.
Ważne jest, aby procedury były skomentowane. Do standardów należy opisanie, co procedura robi oraz wyjaśnienie roli wszystkich parametrów. Jeśli czynimy jakieś nieoczywiste założenie, to musi ono być umieszczone w komentarzu (np. założenie o pozycji kursora)
Konieczne jest, aby parametry przy wywołaniu były podane w tej samej kolejności, co przy deklaracji i aby typy ich były zgodne. W przypadku niezgodności typów wystąpi błąd kompilacji.

Realizacja procedur i funkcji

Rekursja

Rekursja

 
<b>function</b> silnia(n:Integer):Integer;
<b>begin</b> 
<b>if</b> n=0 <b>then</b> silnia&nbsp;:= 1
<b>else</b> silnia&nbsp;:= n*silnia(n-1)
<b>end</b>;

Wywołanie tej funkcji od pewnego naturalnego argumentu \( n\ge 0 \) spowoduje, że identyfikatorowi silnia zostanie nadana wartość \( n! \). Stanie się to w następujący sposób. Najpierw sprawdzimy, czy \( n \) równa się zero. Jeżeli tak, to wynik wyniesie 1. Jeżeli nie, to wywołana zostanie funkcja silnia od parametru \( n-1 \), a jej wynik przemnożony zostanie przez \( n \) dając ostateczną wartość funkcji. Wykonanie instrukcji mnożenia przez \( n \) zostanie więc zawieszone na czas obliczenia wartości \( {silnia}(n-1) \). Zawartość sumatora i wszystkich rejestrów używanych przez komputer do obliczeń zostaną więc automatycznie zapamiętane przez system wykonujący program tak, że \({silnia}(n-1) \) wykona się w czystym środowisku. Po obliczeniu silni z \( n-1 \), zawartość stanu komputera zostanie odtworzona i mnożenie przez \( n \) będzie mogło zostać zakończone.

Rzecz jasna \( {silnia}(n-1) \) zostanie obliczona w analogiczny sposób. Rolę wartości \( n \) przejmie \( n-1 \), zatem wywoła się w miarę potrzeby \( {silnia}(n-2) \) itd. Widać więc, że do wywołania funkcji silnia od jakiegoś dużego parametru wymaga się zawieszenia wykonywania mnożeń na wielu poziomach wywołań rekurencyjnych (po jednym dla każdego \( 1 \le k \le n \)).
Zauważmy, że podobnie jak w przypadku źle skonstruowanych pętli, możemy nabawić się kłopotów wywołując funkcję silnia od argumentu ujemnego. System zacznie wtedy wywoływać kaskadę silni wołanych dla parametrów ujemnych coraz bardziej oddalonych od zera. Gdyby pamięć komputera była nieskończona, spowodowałoby to nieskończone zapętlenie się programu. Każde wywołanie funkcji wymaga jednak zapamiętania aktualnego stanu komputera. Zużywa to dostępną pamięć blokując potrzebny jej fragment do końca wywołania funkcji; w naszym przypadku ten koniec nigdy nie nastąpi. Program zostanie zatem zerwany przez system wykonujący z powodu braku pamięci. Nie jest to jednak jedyna groźba, którą napotykamy stosując rekurencję. Znacznie poważniejszym problemem może okazać się nieprawidłowa organizacja rekurencji powodująca brzemienne w skutkach zużycie czasu wykonywanego programu.
Spróbujmy zastosować technikę rekurencyjną do napisania funkcji obliczającej n-tą liczbę Fibonacciego \( F_n \).

<b>function</b> Fibo(n:integer):Integer;
{funkcja liczy n-ta liczbe Fibonacciego dla n&gt;=0}
<b>begin</b>
<b>if</b> n &lt;= 1 <b>then</b> Fibo&nbsp;:= n
<b>else</b> Fibo&nbsp;:= Fibo(n-2) + Fibo(n-1)
<b>end</b>; {Fibo}

Na pierwszy rzut oka widać, że funkcja powinna dobrze zadziałać. Została napisana zgodnie z podaną wyżej definicją liczb Fibonacciego. Spróbujmy zatem prześledzić, jak będzie się wykonywać dla \( n=4 \). Aby obliczyć wartość \( F_4 \), będziemy musieli wywołać Fibo dla \( n=2 \) i dla \( n=3 \), a następnie dodać te wartości. Zauważmy jednak, że obliczywszy \( { Fibo}(2) \) weźmiemy się za liczenie \( { Fibo}(3) \) od nowa. Do policzenia \( {Fibo}(3) \) będziemy jednak potrzebowali wartości \( {Fibo}(1) \) oraz \( {Fibo}(2) \). Ponieważ komputer nie otrzymał od nas żadnych wskazówek dotyczących wykorzystania raz już obliczonych wartości, więc zacznie od nowa obliczać \( {Fibo}(2) \).
Ta drobna niegospodarność będzie nas dużo kosztować. Liczba wywołań funkcji Fibo będzie bowiem proporcjonalna do wartości wykładniczej ze względu na \( n \). Oznacza to, jak już wiemy, że nawet dla niewielkich stosunkowo danych, rzędu 100, żaden komputer na świecie nie poradzi sobie z zakończeniem obliczeń, niezależnie od tego jak jest szybki i jak wiele czasu mu damy.
Cały problem będzie rozwiązany bezboleśnie, jeżeli tylko nie dopuścimy do więcej niż jednokrotnego wywołania funkcji dla tych samych danych. Wystarczy zatem stworzyć bank danych o obliczonych już wartościach \( F_n \). W tym celu zadeklarujemy sobie tablicę \( F \), w której będziemy przechowywali obliczone już wartości \( F_n \). Aby zaznaczyć, że dana wartość nie została jeszcze obliczona, wypełnimy tablicę minus jedynkami. Funkcję Fibo będziemy zatem liczyli rekurencyjnie jedynie w miarę potrzeby, czyli wtedy, gdy dla danego argumentu liczymy ją po raz pierwszy. Zmodyfikujmy zatem naszą funkcję.

<b>var</b> F:array[0..m] <b>of</b> Integer; 
 
<p><b>function</b> Fibo1(n:integer): Integer;
{
funkcja liczy n-ta liczbe  Fibonacciego  dla  n&gt;=0,  korzystając
przy tym z globalnej tablicy F, przy czym
F[i] = F_i, jezeli F_i jest juz obliczone
F[i] = -1,  jezeli nie jest jeszcze obliczone 
Założenie: n&gt;=0
}
<b>begin</b>
<b>if</b>  F[n]&lt;0  <b>then</b> {Wartosc F[n] nie jest jeszcze obliczona, więc
zaczniemy  od  wypełnienia  tablicy  właściwą
wartością}
<b>if</b> n &lt;= 1 <b>then</b> F[n]:=n
<b>else</b> F[n]&nbsp;:= Fibo1(n-2) + Fibo1(n-1);
{i teraz dopiero nadamy odpowiednią wartośc identyfikatorowi Fibo.
W tablicy F[n] znajduje się zawsze własciwa wartość}
Fibo1&nbsp;:= F[n]
<b>end</b>;{Fibo1}

Wykonanie tego programu dla paru danych szybko przekona nas o skuteczności tego ulepszenia. Tym razem powinniśmy także uważać na stosunkowo nieduży zakres typu integer, i jeżeli chcemy obliczać większe liczby Fibonacciego, musimy użyć innego typu (np. longint).
Rzecz jasna istnieją znacznie prostsze metody pozwalające nam na obliczenie n-tej liczby Fibonacciego. Podobnie jak w przypadku silni, można to zrobić jedną prostą pętlą z czterema przypisaniami. Są jednak problemy, dla których znalezienie nierekurencyjnego rozwiązania ani nie jest proste, ani warte zachodu ze względu na elegancję i efektywność rekurencji w tych przypadkach.
Wielu znane jest zapewne zadanie o wieżach z Hanoi. Legenda głosi, że w pewnej świątyni buddyjskiej w Hanoi znajdują się trzy wbite w ziemię pręty. Na jednym z nich początkowo umieszczono 64 koła o malejących średnicach. Należy te koła przenieść z pierwszego pręta na drugi przy pomocy trzeciego, respektując następujące zasady:

1. jednorazowo można przenieść jeden krążek
2. krążek można nałożyć na dowolny z prętów pod

warunkiem, że kładzie się go na pusty pręt lub na krążek o większej średnicy. Ponoć mnisi przekładają od jakiegoś czasu te krążki, a gdy skończą, nastąpi koniec świata.
Jak można wyobrazić sobie najprostszy algorytm przekładający w możliwie szybki sposób krążki? Przenieść jeden krążek to żadna sztuka. Jak jednak poradzić sobie z ich większą liczbą? Załóżmy indukcyjnie, że umiemy tego dokonać dla \( n-1 \) krążków. Rekurencyjnie nasz algorytm formułuje się bardzo prosto. Aby przełożyć wieżę złożoną z n krążków z jednego pręta na drugi przy pomocy trzeciego, należy \( n-1 \) krążków przełożyć na pręt trzeci, następnie przełożyć krążek \( n \) na pręt drugi, a następnie \( (n-1) \)-elementową wieżę przełożyć z pręta trzeciego na drugi przy pomocy pierwszego.
Zauważmy przy okazji, że liczba przenosin \( n \) krążków, \( T_n \), wymaga dwukrotnego przeniesienia wieży złożonej z \( n-1 \) krążków oraz jednokrotnego przeniesienia jednego krążka. Mamy więc wzór:

\( T_1 = 1; \ T_n=2T_{n-1}+1 \)

zatem

\( T_n=2(2^{n-1}-1)+1=2^n-1 \). Liczba przenosin jest więc wykładnicza ze względu na \( n \). Możemy spać spokojnie. Nawet jeżeli mnisi będą bardzo wydajni, to prędzej nastąpi koniec Układu Słonecznego, aniżeli przełożenie tych 64 krążków (zakładając, że mnisi zaczęli w czasach historycznych).

Procedura, która dokona wygenerowania kolejnych ruchów przenoszących n-elementową wieżę może więc wyglądać następująco. Zakładamy, że zamiast dźwigania krążków komputer będzie wypisywał kolejne ruchy w postaci przenieś krążek z pręta \( i \) na pręt \( j \).

<b>procedure</b> Hanoi (n, skad, dokad:integer);
{ procedura przenosi n krążkow z wieży skąd na wieżę dokąd }
<b>procedure</b> przenies (co, skad, dokad:integer);
{ Tu rzecz jasna można wpisać dowolnie inteligentną procedurę}
<b>begin</b>
writeln ('PRZENIES ', CO, ' Z ', skad, ' NA ', dokad)
<b>end</b>;
<b>begin</b>
<b>if</b> n&lt;=1 then
przenies (1, skad, dokad)
<b>else</b>
<b>begin</b>
{zauważmy, że jeżeli jeden pręt ma numer i, a drugi j, to trzeci
z nich ma numer 6-i-j}
hanoi   (n-1, skad, 6-skad-dokad);
przenies (n,   skad,  dokad );
hanoi   (n-1, 6-skad-dokad, dokad)
<b>end</b>
<b>end</b>;

Nasza procedura będzie teraz działała w czasie wykładniczym ze względu na \( n \). Dzieje się tak w zasadzie zawsze, gdy bez żadnych finezji dokonujemy we wnętrzu procedury więcej niż jednokrotnego wywołania rekurencyjnego tej procedury. Tym razem jednak nie będzie to stanowiło wady rozwiązania - taka jest natura problemu: odpowiedź w postaci ciągu ruchów do wykonania ma długość wykładniczą ze względu na \( n \), więc trudno tu cokolwiek poprawić. Rzecz jasna procedurę należy wywoływać dla danych znacznie mniejszych niż 64.

<b>function</b> Labirynt(M,N:integer; <b>var</b> A:<b>array</b>[1..M,1..N] <b>of</b> integer; i1,j1,i2,j2:integer):boolean; 
// M,N &gt;= 1 
// A zawiera 0 (ściana) i 1 (droga) 
 
<b>function</b> szukaj(i,j:integer):boolean; 
// 1 &lt;= i &lt;= M 
// 1 &lt;= j &lt;= N 
<b>var</b> jest:boolean; 
<b>begin</b>
 <b>if</b> (i=i2) <b>and</b> (j=j2) <b>then</b> 
jest:=true 
<b>else</b> <b>begin</b> 
jest:=false; 
<b>if</b> A[i,j]&gt;0 <b>then</b> <b>begin</b> 
A[i,j]:=-1; <b>if</b> i&gt;1 <b>then</b> jest:=szukaj(i-1,j); 
<b>if</b> <b>not</b> jest <b>and</b> (i&lt;M) <b>then</b> jest:=szukaj(i+1,j); 
<b>if</b> <b>not</b> jest <b>and</b> (j&gt;1) <b>then</b> jest:=szukaj(i,j-1); 
<b>if</b> <b>not</b> jest <b>and</b> (j&lt;N) <b>then</b> jest:=szukaj(i,j+1); 
<b>end</b> 
<b>end</b>; 
szukaj:=jest 
<b>end</b>; // szukaj  
 
<b>var</b> i,j:integer; 
<b>begin</b> // Labirynt
 <b>if</b> <b>not</b>((1&lt;=i1) <b>and</b> (i1&lt;=M) <b>and</b> (1&lt;=j1) <b>and</b> 
(j1&lt;=N) <b>and</b> (1&lt;=i2) <b>and</b> (i2&lt;=M) <b>and</b> (1&lt;=j2) <b>and</b> (j2&lt;=N)) <b>then</b>
Labirynt:=false 
<b>else</b>
 <b>begin</b> 
Labirynt:=szukaj(i1,j1); 
<b>for</b> i:=1 <b>to</b> M <b>do</b> 
<b>for</b> j:=1 <b>to</b> N <b>do</b>
<b>if</b> A[i,j]=-1 <b>then</b> A[i,j]:=1 
<b>end</b> 
<b>end</b>; // Labirynt 

<b>function</b> Zjazd1(M,N:integer; <b>var</b> A:<b>array</b>[1..M,1..N] <b>of</b> integer; i1,j1,i2,j2:integer):boolean; 
// M,N &gt;= 1 
// A zawiera liczby &gt; 0 
 
<b>function</b> szukaj(h,i,j:integer):boolean; 
// 0 &lt; h 
// 1 &lt;= i &lt;= M 
// 1 &lt;= j &lt;= N 
<b>var</b> jest:boolean; 
hpom:integer; 
<b>begin</b> 
jest:=false; 
<b>if</b> (A[i,j]&gt;0) <b>and</b> (h&gt;A[i,j])<b>then</b> <b>begin</b> // h&gt;=A[i,j] w wariancie II 
<b>if</b> (i=i2) <b>and</b> (j=j2) <b>then</b> 
jest:=true 
<b>else</b> <b>begin</b> 
hpom:=A[i,j]; 
A[i,j]:=-A[i,j]; 
<b>if</b> i&gt;1 <b>then</b> jest:=szukaj(hpom,i-1,j); 
<b>if</b> <b>not</b> jest <b>and</b> (i&lt;M) <b>then</b> jest:=szukaj(hpom,i+1,j); 
<b>if</b> <b>not</b> jest <b>and</b> (j&gt;1) <b>then</b> jest:=szukaj(hpom,i,j-1); 
<b>if</b> <b>not</b> jest <b>and</b> (j&lt;N) <b>then</b> jest:=szukaj(hpom,i,j+1); 
<b>end</b> 
<b>end</b>; 
szukaj:=jest 
<b>end</b>; // szukaj 
 
<b>var</b> i,j:integer; 
<b>begin</b> // Zjazd1 
<b>if</b> <b>not</b>((1&lt;=i1) <b>and</b> (i1&lt;=M) <b>and</b> (1&lt;=j1) <b>and</b> (j1&lt;=N) <b>and</b> 
1&lt;=i2) <b>and</b> (i2&lt;=M) <b>and</b> (1&lt;=j2) <b>and</b> (j2&lt;=N)) <b>then</b> 
Zajzd:=false 
<b>else</b> 
<b>begin</b>
Zjazd:=szukaj(A[i1,j1]+1,i1,j1); // wystarczy szukaj(A[i1,j1],i1,j1) w wariancie II 
<b>for</b> i:=1 <b>to</b> M <b>do</b> 
<b>for</b> j:=1 <b>to</b> N <b>do</b> 
<b>if</b> A[i,j]&lt;0 <b>then</b> A[i,j]:=-A[i,j] 
<b>end</b> 
<b>end</b>; // Zjazd1 

<b>function</b> Zjazd2(M,N:integer; <b>var</b> A:<b>array</b>[1..M,1..N] <b>of</b> integer; i1,j1,i2,j2:integer):boolean; 
// M,N &gt;= 1 
// A zawiera liczby &gt; 0 
 
<b>function</b> wdol(h,i,j:integer):boolean;
// sprawdza czy pole (i,j) nie jest zaznaczone i 
// czy przejscie z pola o wysokosci h na pole (i,j) jest rzeczywiscie w dół 
// 1 &lt;= i &lt;= M 
// 1 &lt;= j &lt;= N 
<b>begin</b> 
wdol:=(A[i,j]&gt;0) <b>and</b> (h&gt;A[i,j]) // h&gt;=A[i,j] w wariancie II 
<b>end</b>; //wdol 
 
 
<b>function</b> szukaj(i,j:integer):boolean; 
// 1 &lt;= i &lt;= M 
// 1 &lt;= j &lt;= N 
<b>var</b> jest:boolean; 
hpom:integer; 
<b>begin</b> 
<b>if</b> (i=i2) <b>and</b> (j=j2) <b>then</b> 
jest:=true 
<b>else</b> <b>begin</b> 
jest:=false; 
hpom:=A[i,j];
A[i,j]:=-hpom; 
<b>if</b> i&gt;1 <b>then</b> <b>if</b> wdol(hpom,i-1,j) <b>then</b> jest:=szukaj(i-1,j); 
<b>if</b> <b>not</b> jest <b>and</b> (i&lt;M) <b>then</b> <b>if</b> wdol(hpom,i+1,j) <b>then</b> jest:=szukaj(i+1,j);
 <b>if</b> <b>not</b> jest <b>and</b> (j&gt;1) <b>then</b> <b>if</b> wdol(hpom,i,j-1) <b>then</b> jest:=szukaj(i,j-1);
 <b>if</b> <b>not</b> jest <b>and</b> (j&lt;N) <b>then</b> <b>if</b> wdol(hpom,i,j+1) <b>then</b> jest:=szukaj(i,j+1);
 <b>end</b>; 
szukaj:=jest 
<b>end</b>; // szukaj  
 
<b>var</b> i,j:integer; 
<b>begin</b> // Zjazd2 
<b>if</b> <b>not</b>((1&lt;=i1) <b>and</b> (i1&lt;=M) <b>and</b> (1&lt;=j1) <b>and</b> (j1&lt;=N) <b>and</b> 
(1&lt;=i2) <b>and</b> (i2&lt;=M) <b>and</b> (1&lt;=j2) <b>and</b> (j2&lt;=N)) <b>then</b> 
Zajzd:=false 
<b>else</b> 
<b>begin</b>
Zjazd:=szukaj(i1,j1); 
<b>for</b> i:=1 <b>to</b> M <b>do</b> 
<b>for</b> j:=1 <b>to</b> N <b>do</b> 
<b>if</b> A[i,j]&lt;0 <b>then</b> A[i,j]:=-A[i,j] 
<b>end</b> 
<b>end</b>; // Zjazd2 

<b>type</b> Paleczki = 1..3; 
 
<b>procedure</b> Hanoi(Ile: integer; Skad, Dokad: Paleczki; Dozw: TDozwRuchow); 
 
<b>procedure</b> Rob(Skad, Dokad, Pom: Paleczki; Ile: Integer); 
// Pom jest zawsze rowne 6-Skad-Dokad, ale z parametrem jest czytelniej 
<b>begin</b> 
<b>if</b> Ile &gt; 0 <b>then</b>
<b>if</b> Dozw[Skad, Dokad] <b>then</b> <b>begin</b>
Rob(Skad, Pom, Dokad, Ile-1);
Przenies(Skad,Dokad);
Rob(Pom, Dokad, Skad, Ile-1);
<b>end</b>
<b>else</b> <b>begin</b> 
Rob(Skad, Dokad, Pom, Ile-1);
Przenies(Skad, Pom);
Rob(Dokad, Skad, Pom, Ile-1);
Przenies(Pom, Dokad);
Rob(Skad, Dokad, Pom, Ile-1);
<b>end</b> 
<b>end</b>; //Rob 
 
<b>function</b> CzyDaSie(Skad, Dokad, Pom: Paleczki):boolean 
<b>begin</b> 
<b>if</b> <b>not</b> Dozw[Skad, Dokad] <b>and</b> <b>not</b> (Dozw[Skad, Pom] <b>and</b> Dozw[Pom, Dokad]) <b>then</b> <b>begin</b>
 writeln('Nie da sie przełożyć krążka z ',Skad,' na ',Pom);
CzyDaSie:=false 
<b>end</b> 
<b>else</b> 
CzyDaSie:=true 
<b>end</b> // CzyDaSie 
 
<b>var</b> ok:boolean;
i,j:integer;
<b>begin</b> // Hanoi 
ok:=true; 
<b>for</b> i:=1 <b>to</b> 2 <b>do</b> <b>for</b> j:=i+1 <b>to</b> 3 <b>do</b>
ok:=ok <b>and</b> CzyDaSie(i,j,6-i-j) <b>and</b> CzyDaSie(j,i,6-i-j); 
<b>if</b> ok <b>then</b> Rob(Skad,Dokad,6-Skad-Dokad,Ile); 
<b>end</b>; // Hanoi 

<b>procedure</b> Hetmany(N:integer); 
// N &gt;= 1 
<b>var</b> 
wiersze:<b>array</b>[1..N] <b>of</b> integer;
kolumny:<b>array</b>[1..N] <b>of</b> boolean;
przekgd:<b>array</b>[-(N-1)..N-1] <b>of</b> boolean; // przekątne \ o stałej różnicy 
przekdg:<b>array</b>[2..2*N] <b>of</b> boolean;      // przekątne / o stałej sumie  
 
<b>procedure</b> ustaw(k,i:integer); 
// 1 &lt;= k,i &lt;= N 
<b>begin</b> 
wiersze[k]:=i; 
kolumny[i]:=true; 
przekgd[k-i]:=true; 
przekdg[k+i]:=true; 
<b>end</b>; // ustaw  
 
<b>procedure</b> odstaw(k,i:integer); 
// 1 &lt;= k,i &lt;= N 
<b>begin</b> 
wiersze[k]:=0; 
kolumny[i]:=false; 
przekgd[k-i]:=false; 
przekdg[k+i]:=false; 
<b>end</b>; // odstaw  
 
<b>function</b> wolne(k,i:integer):boolean; 
// 1 &lt;= k,i &lt;= N 
<b>begin</b> 
wolne:=<b>not</b> kolumny[i] &amp; <b>not</b> przekgd[k-i] &amp; <b>not</b> przekdg[k+i]; 
<b>end</b>; // wolne 
 
<b>var</b> jest:boolean; 
 
<b>procedure</b> wypisz; 
<b>var</b> i:integer; 
<b>begin</b> 
jest:=true;
write('Ustawienie: ');
<b>for</b> i:=1 <b>to</b> N <b>do</b> write(i,':',wiersze[i],' '); 
writeln; 
<b>end</b>; // wypisz 
 
<b>procedure</b> rozstaw(k:integer); 
<b>var</b> i:integer; 
<b>begin</b> 
<b>if</b> k=N+1 <b>then</b> 
wypisz 
<b>else</b> 
<b>for</b> i:=1 <b>to</b> N <b>do</b> 
<b>if</b> wolne(k,i) <b>then</b> <b>begin</b> 
ustaw(k,i); rozstaw(k+1); odstaw(k,i); 
<b>end</b> 
<b>end</b>; // rozstaw 
<b>var</b> i:integer; 
 
<b>begin</b> // Hetmany 
<b>for</b> i:=1 <b>to</b> N <b>do</b> wiersze[i]:=0;
 <b>for</b> i:=1 <b>to</b> N <b>do</b> kolumny[i]:=false;
 <b>for</b> i:=-(N-1) <b>to</b> N-1 <b>do</b> przekgd[i]:=false;
 <b>for</b> i:=2 <b>to</b> 2*N <b>do</b> przekdg[i]:=false;
 jest:=false;
 rozstaw(1);
 <b>if</b> <b>not</b> jest <b>then</b> writeln('Nie znaleziono żadnego ustawienia')
<b>end</b> // Hetmany