Ćwiczenia

Ćwiczenia 1: Wstęp

W poniższych zadaniach zdefiniuj opisane funkcje matematyczne.
Możesz, a nawet powinieneś, zdefiniować przydatne funkcje pomocnicze.
Opisz też sposób reprezentacji danych (np.\ punkt możemy reprezentować jako parę współrzędnych).

Wyznacz przecięcie dwóch prostokątów o bokach równoległych do osi współrzędnych i całkowitych współrzędnych wierzchołków.
Rozwiązania
Zdefiniuj funkcję określającą, czy dwa odcinki o końcach o współrzędnych całkowitych przecinają się.
(Dostępna jest tylko dziedzina algorytmiczna liczb całkowitych i wartości logicznych.)
Napisz funkcję określającą, czy dwa równoległoboki mają niepuste przecięcie.
Czy punkt leży wewnątrz wielokąta (niekoniecznie wypukłego, ale bez samoprzecięć).
Wielokąt jest dany w postaci ciągu kolejnych wierzchołków na obwodzie (w kolejności przeciwnej do ruchu wskazówek).

Ćwiczenia 2: Procedury operujące na liczbach

Rozwiązania poniższych zadań to proste procedury operujące na liczbach całkowitych.
Dla każdej procedury rekurencyjnej podaj jej specyfikację, tj. warunek wstępny i końcowy,
oraz uzasadnij jej poprawność.
Poprawność procedur rekurencyjnych można pokazać przez indukcję.

Stopień parzystości liczby całkowitej $x$, to największa taka liczba naturalna $i$, że $x$ dzieli się przez $2^i$.
Liczby nieparzyste mają stopień parzystości 0, liczby 2 i -6 mają stopień parzystości 1,
a liczby 4 i 12 mają stopień parzystości 2.
Przyjmujemy, że 0 ma stopień parzystości -1.

Napisz procedurę parzystość wyznaczającą stopień parzystości danej liczby całkowitej.

Rozwiązania
Napisz procedurę, która przekształca daną liczbę naturalną w taką, w której cyfry występują w odwrotnej kolejności,
np. 1234 jest przekształcane na 4321.

Rozwiązania
Sumy kolejnych liczb nieparzystych dają kwadraty kolejnych liczb naturalnych, zgodnie ze wzorem:
$\sum_{i=1}^k (2 i - 1) = k^2$.
Wykorzystaj ten fakt do napisania procedury sqrt obliczającej sqrt x $ = \lfloor\sqrt{x}\rfloor$
i nie korzystającej z mnożenia, ani dzielenia.

Rozwiązania
Liczbę naturalną nazwiemy rzadką, jeżeli w jej zapisie binarnym żadne dwie jedynki nie stoją obok siebie.
Napisz procedurę rzadkie : int → int, która dla danej liczby naturalnej $n$ zwróci najmniejszą rzadką liczbę naturalną większą od $n$. Na przykład, dla $n = 42 = 101010_2$ mamy $\mathtt{rzadkie}\ 42 = 1000000_2 = 64$.

Rozwiązania
Liczbę naturalną nazwiemy rzadką, jeżeli w jej zapisie binarnym żadne dwie jedynki nie stoją obok siebie.
Napisz procedurę rzadkie : int → int, która dla danej liczby naturalnej $n$ wyznaczy liczbę dodatnich liczb rzadkich, które nie przekraczają $n$.
Na przykład, dla $n = 42 = 101010_2$ mamy rzadkie 42 = 20.

Rozwiązania
Napisz procedurę, która sprawdza, czy dana liczba jest pierwsza.

Rozwiązania
Zaimplementuj kodowanie par liczb naturalnych jako liczby naturalne.
To znaczy, napisz procedurę dwuargumentową, która koduje dwie liczby dane jako argumenty w jednej liczbie naturalnej.
Dodatkowo napisz dwie procedury, które wydobywają z zakodowanej pary odpowiednio pierwszą i drugą liczbę.

Rozwiązania
Napisz procedurę, która dla danej liczby $n$ sprawdzi czy pierścień reszt modulo $n$ zawiera nietrywialne pierwiastki
z 1 (tj. takie liczby $k$, $k \neq 1$, $k \neq n-1$, że $k^2 \equiv 1\ \mod\ n$).
Nota bene, jeśli takie pierwiastki istnieją, to liczba $n$ nie jest pierwsza.
Odwrotna implikacja jednak nie zachodzi --- np. dla $n=4$ nie ma nietrywialnych pierwiastków z 1.

Rozwiązania

Ćwiczenia 3: Rekurencja ogonowa

Rozwiązania poniższych zadań to proste procedury operujące na liczbach całkowitych.
Ich rozwiązanie wymaga zastosowania rekurencji ogonowej.
Dla każdej procedury rekurencyjnej podaj jej specyfikację, tj. warunek wstępny i końcowy,
oraz uzasadnij jej poprawność.
Poprawność procedur rekurencyjnych można pokazać przez indukcję.
Nie zapomnij o uzasadnieniu własności stopu.

Potęgowanie liczb całkowitych (z akumulatorem).

Rozwiązania
[Bentley]
Dana jest funkcja $f: \{1, 2, \dots, n\} \to {\cal Z}$.
Należy znaleźć takie $1 \le a \le b \le n$, że suma $\sum_{i=a}^b f(i)$ jest największa.
Napisz taką procedurę p, że $\mathtt{p}\ f\ n = b - a + 1$ (dla $a$ i $b$ jak wyżej).

Rozwiązania
Napisz procedurę $\mathtt{zera\_silni} : \mathtt{int} \to \mathtt{int}$, która dla danej dodatniej liczby całkowitej $n$ obliczy ile zer znajduje się na końcu zapisu dziesiętnego liczby $n!$.

Rozwiązania
Dana jest funkcja nierosnąca $f: \mathtt{int} \to \mathtt{int}$, taka, że $f(x+1) \ge f(x) - 1$.
Napisz procedurę, która znajduje punkt stały tej funkcji, tzn. taką liczbę $x$, że $f(x) = x$
(lub jeśli punkt stały nie istnieje, to taką liczbę $x$, że $f(x-1) \ge x$ oraz $f(x) \le x$).

Rozwiązania
Dana jest różnowartościowa funkcja $f: \mathtt{int} \to \mathtt{int}$.
Napisz procedurę maksima, która dla danych liczb $l$ i $p$ ($l \le p$) obliczy ile lokalnych maksimów ma funkcja $f$ w przedziale $[l, p]$.
Przypomnij sobie rozwiązania zadań z poprzednich ćwiczeń.
Jeśli rozwiązałeś je nie stosując rekurencji ogonowej, to czy potrafisz je rozwiązać (lepiej) stosując ją?

Ćwiczenia 4 i 5: Listy

Ćwiczenie programistyczne na listy:

Lista $n$ pierwszych liczb naturalnych.
Zdublować elementy listy.
Napisz procedurę last, której wynikiem jest ostatni element listy.
Napisz procedury head i tail, które dla zadanej listy $l$ i liczby całkowitej $n$
zwracają pierwsze/ostatnie $n$ elementów listy $l$.
Jeśli lista $l$ ma mniej elementów niż $n$, to wynikiem powinna być cała lista $l$.
(Nazwy pochodzą od programów head i tail w Uniksie.)
Co jest wynikiem tail (head l n) 1?
Napisz procedurę, która listę par postaci $[(n_1, x_1); (n_2, x_2); \dots; (n_k, x_k)]$ przekształca w listę postaci
$[\underbrace{x_1; \dots; x_1}_{n_1 \mathrm{\ razy}}; \underbrace{x_2; \dots; x_2}_{n_2 \mathrm{\ razy}}; \dots; \underbrace{x_k; \dots; x_k}_{n_k \mathrm{\ razy}}]$.
Napisz procedurę shuffle: α list → α list → α list, która dla danych dwóch list postaci $[x_1; x_2; \dots; x_n]$ oraz $[y_1; y_2; \dots; y_m]$ wyznaczy listę postaci $[x_1; y_1; x_2; y_2; \dots]$. Jeżeli jedna z list jest dłuższa, to jej końcowe elementy trafiają na koniec listy wyikowej.
Na przykład: shuffle [3; 2; 8; 1; 9; 3; 6] [5; 7; 0] = [3; 5; 2; 7; 8; 0; 1; 9; 3; 6].

Rozwiązania
Załóżmy, że dana jest lista $[x_1; x_2; \dots; x_n]$.
Sufiksem tej listy nazwiemy każdą listę, którą można uzyskać przez usunięcie pewnej liczby (od 0 do $n$) jej początkowych elementów.
Tak więc, sufiksami danej listy będzie n.p. ona sama, pusta lista, a także $[x_3; x_4; \dots; x_n]$.

Napisz procedurę tails : α list → α list list,
która dla danej listy tworzy listę wszystkich jej sufiksów, uporządkowaną wg ich długości (wybrać, czy rosnąco, czy malejąco).

Rozwiązania
Napisz funkcję wysun : int list -> int list, która dla danej listy posortowanej niemalejąco wybierze wszystkie jej elementy występujące
więcej niż raz i umieści w liście wynikowej przed elementami występującymi tylko raz. Kolejność oraz liczba poszczególnych elementów występujących wiele razy ma pozostać taka sama jak w liście wejściowej. Podobnie dla elementów występujących raz.
Na przykład: wysun [1;2;2;3;4;5;5;6;6;6;7] = [2;2;5;5;6;6;6;1;3;4;7]

Rozwiązania
Ciąg liczb naturalnych $x_0, x_1, \dots$ nazwiemy ciągiem Bonifacego wyznaczonym przez skończony niepusty ciąg zerojedynkowy $[b_0; \dots; b_{k−1}]$, jeśli $x_0 = 0$, $x_1 = 1$, $x_2 = 1$, a dla $i \ge 3$ zachodzi $x_i = x_{i−1} + x_{i−2}$ jeśli $b_i \mod k = 0$ oraz $x_i = x_{i−1} + x_{i−3}$ dla $b_i \mod k = 1$ (albo inaczej $x_i = x_{i−1} + x_{i−2−b_{i \mod k}}$).
Na przykład ciąg $[1; 1; 0; 1]$ wyznacza ciąg Bonifacego: 0, 1, 1, 1, 2, 3, 5, 7, 10, 15, 25, 35, 50, ...
Napisz funkcję bonifacy : int -> int list -> int, która dla liczby naturalnej n (n ≥ 0) oraz co najmniej trzyelementowej zerojedynkowej listy $[b_0; \dots; b_{k−1}]$ obliczy n-tą liczbę wyznaczonego przez tę listę ciągu Bonifacego.

Rozwiązania
Dane są dwie listy liczb całkowitych uporządkowane niemalejąco.
Oblicz ile różnych liczb występuje na tych listach.
Napisz procedurę zsumuj, która dla danej niemalejącej listy dodatnich liczb całkowitych
$(a_1 \dots a_n)$ obliczy listę $(b_1 \dots b_n)$, gdzie $b_i = \sum_{k=a_i}^n a_k$.
(Pamiętaj o tym, że jeśli $m>n$, $\sum_{k=m}^n a_k = 0$.)
Napisz program wybierający $\max$ i $\min$ z listy i dokonujący (w miarę) jak najmniejszej liczby porównań.
Napisz program wybierający element dominujący z listy większościowej; uzasadnij jego poprawność.
Napisz procedurę podziel : int list → int list list, która dla danej listy postaci
$[a_1; a_2; \dots; a_n]$, zawierającej permutację zbioru $\{1, 2, \dots, n\}$ znajdzie jej podział na jak najliczniejszą listę list postaci:
\[
[[a_1; a_2; \dots; a_{k_1}];
[a_{{k_1}+1}; a_{{k_1}+2}; \dots; a_{k_2}]; \dots;
[a_{{k_{m-1}}+1}; a_{{k_{m-1}}+2}; \dots; a_{k_m}]]
\]
taką że:
\begin{eqnarray*}
\{a_1, a_2, \dots, a_{k_1}\} &=&
\{1, 2, \dots, k_1\} \quad\mbox{(równość zbiorów)},\\
\{a_{{k_1}+1}, a_{{k_1}+2}, \dots, a_{k_2}\} &=&
\{k_1+1, k_1+2, \dots, k_2\},\\
&\vdots& \\
\{a_{{k_{m-1}}+1}, a_{{k_{m-1}}+2}, \dots, a_{k_m}\} &=&
\{k_{m-1}+1, k_{m-1}+2, \dots, k_m\}.
\end{eqnarray*}
Przyjmujemy, że wynikiem dla listy pustej jest lista pusta.

Przykład: $\mathtt{podziel}\, [2; 3; 1; 6; 5; 4; 7; 9; 10; 11; 8] = [[2; 3; 1]; [6; 5; 4]; [7]; [9; 10; 11; 8]]$.
Napisz procedurę mieszaj, która wywołana dla danej listy, obliczy listę powstałą przez
następujące przestawienie elementów: na pozycjach nieparzystych mają kolejno znajdować się $\lceil \frac{n}{2} \rceil$
początkowe elementy danej listy, a na pozycjach parzystych mają znajdować się pozostałe elementy danej listy, w odwrotnej kolejności.
Na przykład: $\mathtt{mieszaj}\ [1;2;3;4;5] = [1;5;2;4;3]$.
Napisz procedurę trojki : int list → (int} * int * int) list,
która dla zadanej listy dodatnich liczb całkowitych, uporządkowanej rosnąco, stworzy listę takich trójek $(a, b, c)$ liczb z danej listy, że:
- $a < b < c$,
- liczby $a$, $b$ i $c$ spełniają nierówność trójkąta, czyli $c < a + b$.
Dana jest lista liczb całkowitych $l = [x_1; \dots ; x_n]$ uporządkowana niemalejąco.
Napisz procedurę: $\mathtt{malo} : \mathtt{int~list} \to \mathtt{int}$, która dla danej listy $l$ oblicza:
\[ \min \left\{|x_i + x_j| : 1 \le i < j \le n \right\} \]
Na przykład, malo [-42, -12, -8, -1, -1, 5, 15, 60] = 2.

Możesz założyć, że dana lista $l$ zawiera przynajmniej dwa elementy.
Dana jest niepusta, rosnąca lista liczb całkowitych $l = [x_1; \dots ; x_n]$.
Napisz procedurę: $\mathtt{fit} : \mathtt{int} \to \mathtt{int~list} \to \mathtt{int}$, która dla danej liczby $c$ i listy $l$ obliczy:
\[\min \left\{|c + x_i + x_j| : 1 \le i, j \le n \right\}\]
Na przykład, fit 42 [-28, -25, -15, -1, 4, 8, 15, 60] = 1, ponieważ $|42 - 28 - 15| = 1$.
Prostokątną tabelę wypełnioną liczbami całkowitymi reprezentujemy jako listę list liczb całkowitych -- każdy wiersz
to lista liczb, a tabela to lista wierszy.
Oczywiście wszystkie listy reprezentujące wiersze są równej długości.

Rozpatrujemy tabele, których wiersze są uporządkowane ściśle rosnąco, a kolumny ściśle malejąco.
Napisz procedurę znajdz : int list list → int → (int * int) list, która znajduje wszystkie pozycje, na
jakich w takiej tabeli znajduje się podana liczba.
Rozważmy następującą metodę kompresji ciągów liczb całkowitych:
Jeżeli w oryginalnym ciągu ta sama liczba powtarza się kilka razy z rzędu, to jej kolejne wystąpienia reprezentujemy za pomocą jednej tylko liczby.
Konkretnie, $i$ powtórzeń liczby $k$ reprezentujemy w ciągu skompresowanym jako $2^{i-1} \cdot (2 \cdot k - 1)$.

Napisz procedurę dekompresuj : int list → int list dekompresującą zadaną listę.
Możesz założyć, że lista skompresowana nie zawiera zer.

Podaj specyfikację (warunek początkowy i końcowy) wszystkich definiowanych procedur i uzasadnij zwięźle ich pełną poprawność.
W przypadku rekurencyjnych procedur iteracyjnych warunek początkowy musi zawierać niezmiennik iteracji.
```
 
      dekompresuj [1; 3; 3; 9; 42; 3];;
      - : int list = [1; 2; 2; 5; 11; 11; 2]
 
```
Rozwiązania
Palindrom, to taka lista $p$, że $p = \mathtt{rev}\ p$.
Napisz procedurę palindrom : α list → int,
która dla danej listy obliczy długość jej najdłuższego spójnego fragmentu, który jest palindromem.
Napisz procedurę podziel : int → α list → α list list,
która dla $k > 0$ i listy $[x_1; \dots; x_n]$ podzieli ją na listę list postaci:
\[ [
[x_1; x_{k+1}; x_{2k+1}; \dots];
[x_2; x_{k+2}; x_{2k+2}; \dots]; \dots;
[x_k; x_{2k}; x_{3k}; \dots]
]\]

Przykład: $\mathtt{podziel}\ 3\ [1;2;3;4;5;6;7] = [[1; 4; 7]; [2; 5]; [3; 6]] $.
[XIII OI]
Mały Jaś dostał od rodziców na urodziny nową zabawkę, w której skład wchodzą rurka i krążki.
Rurka ma nietypowy kształt -- mianowicie jest to połączenie pewnej liczby walców (o takiej samej grubości)
z wyciętymi w środku (współosiowo) okrągłymi otworami różnej średnicy.
Rurka jest zamknięta od dołu, a otwarta od góry.
Krążki w zabawce Jasia są walcami o różnych średnicach i takiej samej grubości co walce tworzące rurkę.

Jaś wymyślił sobie następującą zabawę.
Mając do dyspozycji pewien zestaw krążków zastanawia się, na jakiej głębokości zatrzymałby się ostatni z nich,
gdyby wrzucać je kolejno do rurki centralnie (czyli dokładnie w jej środek).
Każdy kolejny krążek po wrzuceniu spada dopóki się nie zaklinuje (czyli nie oprze się o walec, w którym wycięty jest
otwór o mniejszej średnicy niż średnica krążka), albo nie natrafi na przeszkodę w postaci innego krążka lub dna rurki.

Napisz procedurę krążki : int list → int list → int, która na podstawie listy średnic
otworów w kolejnych walcach tworzących rurkę, oraz listy średnic kolejno wrzucanych krążków obliczy głębokość, na której zatrzyma się
ostatni wrzucony krążek (lub 0 jeśli nie wszystkie krążki zmieszczą się w rurce).

Rozwiązania
System $-2$-kowy jest podobny do systemu binarnego, ale podstawą tego systemu jest liczba $-2$.
Są dwie możliwe cyfry: 0 i 1.
Ciąg cyfr postaci $c_k c_{k-1} \dots c_1 c_0$ reprezentuje liczbę $\sum_{i=0}^k c_i(-2)^i$.
Na przykład, liczbę 42 reprezentujemy jako $1111110_{-2}$.
Kolejne cyfry, od mniej do bardziej znaczących, tworzą listę.
Przyjmujemy, że lista pusta reprezentuje 0.
1. [V OI, zadanie Bankomaty]
  Napisz procedurę $\mathtt{neg2\_of\_int} : \mathtt{int} \to \mathtt{int~list}$, która przekształca daną liczbę całkowitą
  w jej reprezentację w systemie $-2$-kowym.
2. Napisz procedurę $\mathtt{int\_of\_neg2} : \mathtt{int} \to \mathtt{int~list}$, która przekształca reprezentację
  w systemie $-2$-kowym w liczbę całkowitą.
3. Napisz procedurę $\mathtt{inc} : \mathtt{int~list} \to \mathtt{int~list}$, która dla
  danej listy będącej reprezentacją liczby $x$, wyznaczy reprezentację liczby $x+1$.
4. Napisz procedurę $\mathtt{inv} : \mathtt{int~list} \to \mathtt{int~list}$, która dla
  danej listy będącej reprezentacją liczby $x$, wyznaczy reprezentację liczby $-x$.
5. Napisz procedurę $\mathtt{dodawanie} : \mathtt{int~list} \to \mathtt{int~list} \to \mathtt{int~list}$, która dla
  danych dwóch reprezentacji liczb całkowitych w systemie $-2$-ym obliczy reprezentację ich sumy.
  Na przykład: dodawanie [1;0;1;0;0;1;1] [1;0;1] = [0;1;1;1;1;1;1].
Wielomian postaci $a_0 \cdot x^0 + a_1 \cdot x^1 + \cdots + a_n \cdot x^n$ reprezentujemy w postaci listy $[a_0; a_1; \dots; a_n]$.
Napisz procedurę mnóż : float list → float list → float list mnożącą wielomiany.

Uwaga: Pusta lista reprezentuje zerowy wielomian.

Ćwiczenia 6: Struktury danych

Ćwiczenie programistyczne na drzewa i inne struktury danych:

Zdefiniuj typ reprezentujący drzewa o wierzchołkach dowolnego (skończonego) stopnia.
Zdefiniuj garść procedur operujących na takich drzewach (np. głębokość, liczbę elementów, lista elementów w porządku prefiksowym/postfiksowym).
Dana jest deklaracja typu drzew binarnych:
```
 
     type α tree = 
       Node of α tree * α  * α tree | 
       Null;;
 
```
Drzewo nazywamy ultralewicowym jeśli głębokości kolejnych liści (Null), od lewej do prawej, tworzą ciąg nierosnący.
Napisz procedurę ultraleft : α tree → bool, która sprawdza czy dane drzewo jest ultralewicowe.
[II OI, zadanie Obchodzenie drzewa skokami]
Jak obejść wszystkie wierzchołki drzewa (ogólnego) tak, aby odległość między kolejnymi
wierzchołkami nie przekraczała 3.
Dana jest deklaracja typu drzew binarnych:
```
 
      type α tree = 
        Node of α tree * α * α tree | 
        Nil;;
 
```
Napisz procedurę liscie : α tree → α list, która tworzy listę wartości znajdujących się w liściach (Node) drzewa.
Napisz procedurę, która dla dowolnego drzewa binarnego poprawia je tak, że spełnia ono słabszą wersję warunku BST:
dla dowolnego węzła, lewy syn nie jest większy, a prawy nie jest mniejszy, niż węzeł.
Napisz funkcję potnij, która dla danego predykatu $p$ typu $\alpha \to \mathtt{bool}$, oraz drzewa $t$ typu $\mathtt{\alpha\ tree}$, zwróci następujący wynik.
Wybierzmy wszystkie węzły drzewa $t$ zawierające wartości, które spełniają predykat $p$ i usuńmy z drzewa krawędzie łączące te węzły z ich rodzicami (w przypadku korzenia, nie usuwamy żadnej krawędzi).
W rezultacie drzewo $t$ może się rozpaść na pewną liczbę mniejszych drzew.
potnij p t powinno zwrócić listę tych drzew (w dowolnej kolejności).
Napisz procedurę rozcięcie, która znajduje taką krawędź w danym drzewie binarnym, że po jej usunięciu drzewo
rozpada się na dwa drzewa o minimalnej różnicy liczb węzłów.
(Wynikiem procedury powinien być dolny koniec szukanej krawędzi.)

Rozwiązania
[PCh]
Dana jest deklaracja typu drzew binarnych:
type tree = Node of tree * int * tree | Null;;
Napisz procedurę $\mathtt{symetryczne} : \mathtt{tree} \to \mathtt{bool}$, która sprawdza, czy drzewo jest symetryczne (ze względu na odbicie lewo-prawo).
Dana jest deklaracja typu reprezentującego wyrażenia logiczne:
```
 
      type expr = 
        And of expr * expr |
        Or of expr * expr |
        Not of expr | 
        Value of bool;;
 
```
Warianty And, Or i Not reprezentują odpowiednie operacje logiczne,
natomiast wariant Value reprezentuje wartość logiczną true lub false.

Napisz funkcję wartościowania : expr → int,
która dla danego wyrażenia policzy na ile różnych sposobów można przypisać wszystkim
wariantom Value wartości logiczne, tak aby wartość całego wyrażenia wyliczała się do true.

Przykład: wartościowania Or(Value true, Value false) = 3,
gdyż wyrażenie wyliczy się do true, w trzech przypadkach:
Or(Value true, Value true), Or(Value true, Value false), Or(Value false, Value true).
Dana jest deklaracja typu drzew binarnych:
```
 
      type 'a tree = 
        Node of 'a * 'a tree * 'a tree | 
	Null;;
 
```
Skosokość drzewa jest zdefiniowana w następujący sposób:
- skosokość Null wynosi 0,
- skosokość $\mathtt{Node}(x, t_1, t_2)$ jest równa $\max(2 \cdot s_1, 2 \cdot s_2 + 1)$, gdzie $s_1$ i $s_2$ to skosokości, odpowiednio, $t_1$ i $t_2$.
Dla danego drzewa wolno nam w dowolnych jego węzłach zamieniać miejscami lewe i prawe poddrzewa.
Napisz procedurę $\mathtt{skosokosc}: \alpha\ \mathtt{tree} \to \alpha\ \mathtt{tree}$, która przekształca dane drzewo tak, aby zminimalizować jego skosokość.
Na przykład, dla:
```
 
      t = Node(5,
            Node(4, Null, Node(2, Null, Null)), 
            Node(6, 
              Node(1, Null, Null), 
              Node(3, Null, Null)
            )
          )
 
      skosokosc t = Node(5,
                      Node(6, 
                        Node(1, Null, Null), 
                        Node(3, Null, Null)
                      ),
                      Node(4, Node(2, Null, Null), Null) 
                    )
 
```
Skosokość tak uzyskanego drzewa wynosi 6.
[CLR, ćw. 16-4]
Firma planuje zorganizować przyjęcie. Hierarchia stanowisk w firmie ma strukturę drzewa (ogólnego):
```
 
      type tree = Node of (int * tree list);;
 
```
Każdy pracownik charakteryzuje się pewną "towarzyskością" wyrażoną liczbą dodatnią.
Napisz program, który dobierze gości tak, aby:
- na przyjęciu nie był obecny bezpośredni przełożony żadnego z gości,
- suma współczynników towarzyskości gości była maksymalna.
Jak zapewnić, aby szef firmy był na przyjęciu?
Dane jest definicja typu:
```
 
      type tree = 
        Node of tree * tree | 
	Null
 
```
.
Odległością między dwoma wierzchołkami (Node) w drzewie nazywamy minimalną
liczbę krawędzi jakie trzeba przejść z jednego wierzchołka do drugiego.
Średnicą drzewa nazwiemy maksymalną odległość między dwoma węzłami (Node) w drzewie.
Przyjmujemy, że średnica pustego drzewa (Null) jest równa 0.

Napisz procedurę średnica : tree → int, która oblicza średnicę danego drzewa.

Rozwiązania
Dana jest deklaracja typu:
```
        type 'a drzewo = Node of 'a * 'a drzewo * 'a drzewo | Null
 
```
Napisz procedurę polowa:'a drzewo -> 'a drzewo, która znajduje w zadanym drzewie taki węzeł (Node), który jest przodkiem jak najmniejszej liczby liści, ale przynajmniej połowy wszystkich liści drzewa.
Dana jest deklaracja typu drzew:
```
      type tree = 
        Node of int * tree * tree |
        Leaf;;
 
```
Napisz procedurę $\mathtt{odchudzanie}: \mathtt{tree} \to \mathtt{tree}$, która mając dane drzewo binarne, zwraca drzewo powstałe przez usunięcie z niego takich poddrzew
(zastępując Node(...) przez Leaf) aby suma elementów w powstałym drzewie była jak największa.
Dana jest deklaracja typu:
```
 
      type  drzewo =
        Node of α * α drzewo * α drzewo |
        Null 
 
```
Napisz procedurę środek : α drzewo → α drzewo, która znajduje w zadanym drzewie taki
węzeł (Node), dla którego maksymalna spośród jego odległości od liści jest jak najmniejsza.
Wynikiem tej procedury powinno być poddrzewo zakorzenione w wyznaczonym węźle.

Co się zmieni, jeżeli będziemy chcieli znaleźć wierzchołek, dla którego
minimalna spośród jego odległości do liścii jest jak największa?
Dana jest deklaracja typu drzew binarnych, w których węzłach znajdują się liczby całkowite:
```
 
      type tree = 
        Node of int * tree * tree |
        Null 
 
```
Przekrojem drzewa nazwiemy dowolny taki zbiór jego wierzchołków (Node), że na każdej ścieżce
od korzenia do liścia (Null) znajduje się dokładnie jeden wierzchołek należący do przekroju.

Napisz procedurę cut : tree → int, która dla danego drzewa wyznaczy najmniejszą możliwą sumę liczb
znajdujących się w wierzchołkach tworzących przekrój danego drzewa.
Rozważmy drzewo binarne, w którego wierzchołkach pamiętane są różne dodatnie liczby całkowite.
Dane są dwie listy: wyniki obejścia drzewa w porządku infiksowym i prefiksowym.
Napisz procedurę, która odtwarza drzewo na podstawie takich dwóch list.
Napisz procedurę, która przekształca dane drzewo binarne w wyważone drzewo binarne, zachowując kolejność elementów w porządku infiksowym.
Dana jest definicja typu drzew dowolnego stopnia:
```
          type α tree = Node of α * α tree list;;
 
```
Napisz procedurę $\mathtt{liscie} : \alpha\ \mathtt{tree} \to \mathtt{int~list}$, która dla danego drzewa liczy ile w tym drzewie jest liści na poszczególnych głębokościach i zwraca listę liczb postaci $[g_0; g_1; \dots; g_h]$, gdzie $g_i$ to liczba liści znajdujących się na głębokości $i$, a $h$ to wysokość drzewa.
Dana jest deklaracja typu drzew:
```
        type α tree = Node of α  * α tree list;;
 
```
Ścieżkę w drzewie nazwiemy rosnącą, jeżeli wartości w węzłach na tej ścieżce, w kierunku od korzenia w dół, są rosnące.
Napisz procedurę rosnaca: int tree → int list, która znajdzie w danym drzewie najdłuższą ścieżkę rosnącą i zwróci wartości znajdujące się na niej (w kolejności od korzenia w dół). (Uwaga: szukana ścieżka nie musi zaczynać się w korzeniu i nie musi kończyć się w liściu.)

Rozwiązania
Dana jest deklaracja typu drzew:
```
        type α tree = Node of α  * α tree list;;
 
```
Napisz procedurę nieparzyste: α tree → int, która dla danego drzewa policzy ile jest w nim poddrzew zawierających nieparzystą liczbę wierzchołków.
Dana jest deklaracja typu drzew binarnych:
```
 
      type tree = Node of tree * int * tree | Null;;
 
```
Napisz procedurę czapeczka : tree → tree → int, która obliczy na ilu poziomach, idąc od góry,
dane drzewa są identyczne, tzn. na tych poziomach drzewa mają ten sam kształt, a w odpowiadających sobie wierzchołkach są takie same liczby.

Ćwiczenia 7: Moduły

[D.L.Parnas, On the Criteria To Be Used in Decomposing Systems into Modules, CACM 12 (15), 1972]
Rozważmy następujący problem. Należy napisać program, który:

wczyta plik tekstowy,
dany plik składa się z wierszy, a każdy wiersz ze słów oddzielonych białymi znakami,
rozważamy rotacje cykliczne wierszy, powstałe przez przestawienie pewnej liczby słów z początku wiersza na koniec,
program ma wypisać wszystkie możliwe rotacje cykliczne wierszy z wejścia, bez powtórzeń,
w porządku leksykograficznym, oddzielając słowa w wierszach pojedynczymi odstępami.

Podaj jak byś podzielił program na moduły.
Wymyśl zestaw realistycznych modyfikacji, jakie należy wprowadzić (a jeszcze lepiej poproś o to kolegę) i sprawdź, jak sprawuje się wymyślony przez Ciebie podział na moduły.

Zdefiniuj sygnatury/struktury odpowiadające podanym poniżej pojęciom.
Staraj się wykorzystać zdefiniowane wcześniej pojęcia.

Sygnatura półgrupy (typ elementów i operacja łączna).
Sygnatura monoidu (półgrupa z elementem neutralnym).
Struktura monoidu:
- liczby całkowite z dodawaniem,
- funkcje (na liczbach całkowitych) z operacją składania,
- listy (liczb całkowitych) z operacją sklejania,
- macierzy $2 \times 2$ z operacją mnożenia.
Sygnatura grupy (monoid z elementami odwrotnymi).
Sygnatura pierścienia (dodawanie, mnożenie, jedynka, zero, elementy przeciwne).
Struktura pierścienia liczb całkowitych.
Sygnatura ciała (pierścień z elementami odwrotnymi).
Struktura ciała liczb rzeczywistych.
Sygnatura porządku częściowego z operacjami sup i inf.
Struktura implementująca porządek częściowy par liczb całkowitych z operacjami sup i inf.
Przyjmujemy, że $(x_1, y_1) \le (x_2, y_2)$ gdy $x_1 \le x_2$ oraz $y_1 \le y_2$.
Zdefiniuj moduł implementujący przechadzkę -- "kursor" do przechadzania się po drzewach i oglądania go:
```
 
      sig 
        type α tree = 
          Node of α tree * α  *  α tree |
          Null
        type α walk
        make     : α tree  → α walk
        goleft   : α walk → α walk
        goright  : α walk → α walk
        goup     : α walk → α walk
        lookup   : α walk → α tree
        exception OutsideTree
      end
 
```
Wywołanie make d powinno konstruować przechadzkę, w której znajdujemy się w korzeniu drzewa d.
Wywołanie goleft p powinno konstruować przechadzkę powstałą przez przejście do lewego poddrzewa.
Analogicznie powinny działać procedury goright i goup.
Procedura lookup powinna zwrócić poddrzewo zaczepione w wierzchołku drzewa, w którym aktualnie jesteśmy.

Podczas przechadzki po drzewie możemy przebywać jedynie w wierzchołkach Node _.
Jeśli nastąpi próba wejścia do Null'a lub wyjścia ,,ponad'' korzeń, należy podnieść wyjątek OutsideTree.

Ćwiczenia 8: Procedury wyższych rzędów

Ćwiczenia na procedury wyższych rzędów, ale bez standardowych procedur wyższych rzędów przetwarzających listy:

Potęgowanie funkcji.
Zasymuluj działanie na prostych przykładach:
```
 
      iterate 2 (function x -> x * (x+1)) 2
      iterate 3 (function x -> x * (x+1)) 1
 
```
rozrysowując ramki.
W przypadku szybszego potęgowania funkcji co tak na prawdę jest obliczane szybciej: funkcja wynikowa, czy jej wartość?

Rozwiązania
Wygładzenie funkcji z odstępem $dx$ polega na uśrednieniu $f(x - dx)$, $f(x)$ i $f(x + dx)$.
Napisz procedurę wygładzającą daną funkcję z zadanym odstępem.
Zwróć uwagę na kolejność argumentów.
Niech $f : {\cal R} \to {\cal R}$ będzie funkcją:
- wzajemnie jednoznaczną, czyli 1-1 i ,,na'',
- ciągłą,
- rosnącą i to tak, że $\forall_{d>0} f(x+d) - f(x) \ge d$,
- oraz taką, że $f(0)=0$.
Zaimplementuj procedurę odwrotnosc, której wynikiem dla parametru $f$ będzie przybliżenie $f^{-1}$ z dokładnością
zadaną przez stałą epsilon (czyli jeśli $g = (\mathtt{odwrotnosc}\ f)$, to $\forall x\ |g(x) - f^{-1}(x)| \le \mathtt{epsilon}$).
Zaimplementuj aproksymację funkcji za pomocą szeregu Taylora.
Twoja procedura powinna mieć następujące parametry: liczbę sumowanych wyrazów szeregu punkt, w którym
badana jest przybliżana funkcja, oraz daną funkcję.
Wynikiem powinno być przybliżenie funkcji.
Zastosuj przybliżenie pochodnej oraz sumy częściowe szeregów, przedstawione na wykładzie.

Ćwiczenia 9 i 10: Procedury wyższych rzędów i listy

Ćwiczenia na listy z elementami procedur wyższych rzędów:

Napisz procedurę exists, która dla danego predykatu i listy sprawdzi, czy na liście jest element spełniający predykat.
Wykorzystaj wyjątki tak, aby nie przeglądać listy, gdy to już nie jest potrzebne.
Napisz procedurę negującą predykat non: (α → bool) → (α → bool).
Za pomocą tej procedury oraz procedury exists zdefiniuj procedurę forall,
która sprawdza, czy dany predykat jest spełniony przez wszystkie elementy danej listy.
Czy zastosowanie wyjątków w implementacji procedury exists nadal powoduje, że przeglądane są tylko niezbędne elementy listy?
Zapisz procedurę append za pomocą fold_right/fold_left.
Napisz procedurę obliczającą funkcję będącą złożeniem listy funkcji.
Zapisz za pomocą map i flatten procedurę heads,
której wynikiem dla danej listy list, jest lista pierwszych elementów niepustych list składowych.
Puste listy składowe nie powinny wpływać na wynik.

Rozwiązania
Dana jest lista list elementów. Napisz procedurę $\mathtt{ostatki}: \alpha\ \mathtt{list~list} \to \alpha\ \mathtt{list}$, która zwraca listę ostatnich elementów list składowych.
Kolejność elementów w wyniku powinna być taka jak kolejność list składowych, z których pochodzą.
Puste listy składowe nie wpływają na wynik.
Napisz procedurę sumy : int list → int list, która dla danej listy $[x_1;\dots; x_n]$
oblicza listę postaci: $[x_1; x_1 + x_2; x_1+x_2+x_3; \dots; x_1+x_2+\cdots+x_n]$.

Przykład: sumy [1; 5; 2; 7; 12; 10; 5] = [1; 6; 8; 15; 27; 37; 42].

Rozwiązania
Napisz procedurę codrugi : α list → α list, która z danej listy wybiera co drugi element (zaczynając od drugiego).
Na przykład codrugi [1; 2; 3; 4; 5] = [2; 4].
Jaś pracuje wykonując zlecenia, które dostaje od swojego szefa. Wykonuje je w kolejności ich otrzymania. Wykonanie każdego zlecenia zajmuje mu określony czas. Masz daną tablicę par: moment otrzymania zlecenia, czas potrzebny na jego wykonanie, posortowaną ściśle rosnąco po momentach otrzymania zleceń.
Napisz procedurę $\mathtt{zlecenia}: (\mathtt{int} * \mathtt{int})\ \mathtt{list} \to \mathtt{int~list}$, która dla każdego zlecenia wyznaczy ile czasu upłynie od momentu otrzymania zlecenia do momentu jego wykonania.
Na przykład: zlecenia [(-1, 1); (2, 2); (3, 3); (4, 2); (10, 2)] = [1; 2; 4; 5; 2]}.

Rozwiązania
Dany jest ciąg liczb całkowitych (niekoniecznie dodatnich). Element takiego ciągu nazwiemy widocznym, jeśli suma poprzedzających go elementów jest taka sama, jak suma elementów występujących po nim.
Napisz procedurę $\mathtt{widoczne}:\mathtt{int~list} \to \mathtt{int~list}$, która z danej listy liczb całkowitych wybierze te, które są widoczne.

Rozwiązania
Listę nazwiemy ciekawą jeśli żadne dwa kolejne jej elementy nie są sobie równe.
Napisz procedurę podzial : α list → α list list, która daną listę podzieli na
minimalną liczbę spójnych fragmentów (zachowując ich kolejność), z których każdy jest ciekawy.
Na przykład, podzial [3;2;2;5;7;5;4;4;3;1] = [[3;2];[2;5;7;5;4];[4;3;1]].

Rozwiązania
Napisz procedurę $\mathtt{wybory}: \mathtt{int~list} \to \mathtt{int}$, która mając daną posortowaną niemalejąco listę liczb całkowitych, znajdzie liczbę która pojawia się na niej najwięcej razy (w przypadku takiej samej liczby wystąpień, wybierz największą taką liczbę).

Rozwiązania
Dana jest lista liczb całkowitych. Element tej listy nazwiemy prextremum jeśli jest ostro większy lub ostro mniejszy od wszystkich elementów poprzedzających go na danej liście.
Napisz procedurę $\mathtt{prextrema}: \mathtt{int~list} \to \mathtt{int~list}$, która dla danej listy zwraca listę wszystkich jej prextremów.
Elementy na liście wynikowej powinny być w takiej samej kolejności, w jakiej występowały na danej liście.
Na przykład:
prextrema [-2; 1; 0; 1; 3; 2; -1; 5; 4; -3; 2; 1; 7] = [-2; 1; 3; 5; -3; 7]

Rozwiązania
Napisz procedurę $\mathtt{wzrost}: \mathtt{int~list} \to \mathtt{int~list}$, która dla danej listy liczb całkowitych
znajduje w niej najdłuższy spójny fragment ściśle rosnący i zwraca go.
Na przykład:
```
 
      wzrost [3; 4; 0; -1; 2; 3; 7; 6; 7; 8] = [-1; 2; 3; 7]
      wzrost [] = []
 
```
Rozwiązania
Dany jest ciąg $n$ kulek ułożonych w rządku. Każda kulka jest czerwona lub zielona. Maciek chciałby ułożyć kulki naprzemiennie: zielona, czerwona, zielona itd. Niestety liczby kulek zielonych i czerwonych nie muszą być równe. Maćkowi wystarczy jeśli ciąg kulek będzie (od lewej) zaczynał się naprzemiennie od zielonej kulki. Natomiast pewien fragment ciągu kulek od prawej strony może być jednokolorowy. (W szczególności, jeśli w danym ciągu są kulki tylko jednego koloru, to wynikowy ciąg też musi być jednokolorowy.)
Maciek w jednym ruchu może zamienić miejscami dowolnie dwie wybrane kulki w ciągu.
Dana jest deklaracja typu: type kolor = Czerwona | Zielona.
Napisz procedurę $\mathtt{kulki}: \mathtt{kolor~list} \to \mathtt{int}$, która mając daną liste opisującą ciąg kulek (od lewej do prawej) wyznaczy minimalną liczbę ruchów, w jakich Maciek może ułożyć ciąg kulek tak jak to opisano.
Na przykład: kulki [Czerwona, Zielona, Zielona, Zielona, Zielona, Czerwona, Czerwona, Zielona] = 2.
Dana jest lista $[x_1; x_2; \dots; x_n]$ reprezentująca kolejne chwile w czasie -- tzn. $x_i\) reprezentuje chwilę $i$.
Dane są też dwa predykaty $p$ i $q$.
Powiemy, że w chwili $i$ zachodzi ,,$p$ dopóki $q$'', jeżeli istnieje takie $0 \le k \le n-i$, że
zachodzi $p\ x_i, p\ x_{i+1}, \dots, p\ x_{i+k-1}$, oraz $q\ x_{i+k}$.
Inaczej mówiąc, począwszy od chwili $i$ musi zachodzić $p$, dopóki nie zajdzie $q$.
W szczególności, jeżeli zachodzi $q\ x_i$, to $p$ nie musi w ogóle zachodzić.

Napisz taką procedurę dopoki : α list → (α → bool) → (α → bool) → int list, że wynikiem
$\mathtt{dopoki}\ [x_1; x_2; \dots; x_n]\ p\ q$ jest lista tych chwil w czasie, w których zachodzi $p$ dopóki $q$.

Na przykład, dla następujących $p$ i $q$:

$i$ 1 2 3 4 5 6 7 8 9 10 11 12

$p\ x_i$ false true true true false false true true true false false false

$q\ x_i$ false false true false true false false true false false true false

poprawnym wynikiem jest: $[2; 3; 4; 5; 7; 8; 11]$.
Dla danej listy liczb całkowitych $l = [x_1; x_2; \dots; x_n]$, minimum (maksimum) nazwiemy
taki fragment listy $x_i = x_{i+1} = \dots = x_j$, że:
- $1 \le i \le j \le n$,
- jeśli $i > 1$, to $x_{i-1} > x_i$ ($x_{i-1} < x_i$),
- jeśli $j < n$, to $x_j < x_{j+1}$ ($x_j > x_{j+1}$).
Ekstremum oznacza minimum lub maksimum.
Napisz procedurę ekstrema :int list → int, która dla danej listy policzy ile jest na niej ekstremów.

Rozwiązania
System -2-kowy jest podobny do systemu binarnego, ale podstawą tego systemu jest liczba -2. Są dwie możliwe cyfry: 0 i 1.
Ciąg cyfr postaci $c_k c_{k-1} \dots c_1 c_0$ reprezentuje liczbę $\sum_{i=0}^k c_i(-2)^i$.
Na przykład, liczbę 42 reprezentujemy jako $1111110_{-2}$.

Napisz procedurę inc : int list → int list, która dla danej listy będącej reprezentacją liczby $x$,
wyznaczy reprezentację liczby $x+1$.
Przyjmujemy, że lista pusta reprezentuje 0.
Maksymalne plateau w liście (bez rekurencji).
Napisz procedurę plateau : α list → int, która oblicza długość najdłuższego stałego (spójnego) fragmentu danej listy.
Zdefiniuj, za pomocą @ i filter uproszczoną wersję algorytmu quick-sort.
W algorytmie tym elementy sortowanej listy dzielimy na nie większe i większe od pierwszego elementu listy,
po czym obie listy wynikłe z podziału rekurencyjnie sortujemy.

Rozwiązania
Ciąg różnicowy ciągu $[x_1; x_2; \dots; x_n]$, to ciąg postaci $[x_2-x_1; x_3-x_2; \dots; x_n-x_{n-1}]$.
Oblicz ciąg różnicowy zadanej listy liczb całkowitych.
Oblicz listę złożoną z pierwszych elementów kolejnych ciągów różnicowych danej listy,
tzn.: głowy danej listy, gowy jej ciągu różnicowego, głowy ciągu różnicowego jej ciągu różnicowego itd.
Dana jest lista liczb zmiennopozycyjnych $[x_1; x_2; \dots; x_n]$.
Jej uśrednienie, to lista postaci: $[\frac{x_1 +. x_2}{2.0}; \dots; \frac{x_{n-1} +. x_n}{2.0}]$.
Uśrednieniem listy jednoelementowej oraz pustej jest lista pusta.

Napisz procedurę usrednienie : float list → float list, która dla danej listy obliczy jej uśrednienie.
Napisz funkcję od_końca_do_końca : int list → int, która dla danej niepustej
listy $[a_1;...;a_n]$ obliczy $\min_{i=1,2,\dots,n} |a_i - a_{n+1-i}|$.
Załóżmy, że dana jest lista $[x_1; x_2; \dots; x_n]$.
Sufiksem tej listy nazwiemy każdą listę, którą można uzyskać przez usunięcie pewnej liczby (od 0 do $n$) jej początkowych elementów.
Tak więc sufiksami danej listy będzie n.p. ona sama, pusta lista, a także $[x_3; x_4; \dots; x_n]$.

Napisz (za pomocą fold_left/fold_right) procedurę tails : α list → α list list,
która dla danej listy tworzy listę wszystkich jej sufiksów, uporządkowaną wg malejących ich długości.
Rozważmy listę liczb całkowitych $[x_1; x_2; \dots; x_n]$.
Dołkiem na tej liście nazwiemy taki indeks $1 < i < n$, że $x_i < \max(x_1, \dots, x_{i-1})$ oraz $x_i < \max(x_{i+1}, \dots, x_n)$.
Głębokość takiego dołka to $\min(\max(x_1, \dots, x_{i-1}) - x_i, \max(x_{i+1}, \dots, x_n) - x_i)$.
Napisz procedurę $\mathtt{dolek}: \mathtt{int~list} \to \mathtt{int}$, która dla danej listy liczb całkowitych wyznaczy maksymalną głębokość dołka na tej liście.
Jeśli na danej liście nie ma żadnego dołka, to poprawnym wynikiem jest 0.
Lista trójek $[(l_1,s_1,r_1); \dots; (l_k,s_k,r_k)]$ : (α list * int * int) list} reprezentuję listę
elementów typu α w następujący sposób.
Trójka $(l,s,r)$, gdzie $l = [x_1; x_2; \dots; x_s]$ jest $s$-elementową listą elementów typu α,
reprezentuje ciąg $r$-elementowy, poprzez cykliczne powtarzanie elementów ciągu $l$:
\[\underbrace{x_1, x_2, \dots, x_s, x_1, x_2, \dots, x_s, x_1, \dots}_{r \mbox{ elementów}}\]
Z kolei lista trójek reprezentuje listę powstała w wyniku konkatenacji list odpowiadających poszczególnym trójkom.

Napisz procedurę dekompresja : (α list * int * int) list → int → α, która
dla danej listy trójek i indeksu $i$ wyznacza $i$-ty element listy wynikowej.
Rozważmy następującą metodę kompresji ciągów liczb całkowitych:
Jeżeli w oryginalnym ciągu ta sama liczba powtarza się kilka razy z rzędu, to jej kolejne wystąpienia reprezentujemy za pomocą jednej tylko liczby.
Konkretnie, $i$ powtórzeń liczby $k$ reprezentujemy w ciągu skompresowanym jako $2^{i-1} \cdot (2 \cdot k - 1)$.

Napisz procedurę kompresuj : int list → int list kompresującą zadaną listę.
Lista wynikowa powinna być oczywiście jak najkrótsza.
```
 
      kompresuj [1; 2; 2; 5; 11; 11; 2];;
      - : int list = [1; 6; 9; 42; 3]
 
```
Listę nazwiemy dobrą, jeśli zawiera elementy o naprzemiennych znakach (dodatnie i ujemne).
Listę nazwiemy prawie dobrą, jeśli jest dobra lub zawiera co najwyżej jedno zero, a po obu jego stronach jest dobra.
Szukamy najdłuższego spójnego fragmentu danej listy liczb całkowitych, który jest prawie dobry.
Napisz procedurę $\mathtt{prawie}: \mathtt{int~list} \to \mathtt{int}$, która zwraca długość takiego fragmentu.
Na przykład: prawie [3; 2; -2; 0; 42; 22; -12; 15; -4] = 4.
Są dwa takie fragmenty: [2; -2; 0; 42] i [22; -12; 15; -4].
Przy windzie (na parterze) ustawiła się kolejka ludzi, którzy chcą wjechać windą (wszyscy do góry). Jednorazowo windą mogą jechać osoby o łącznym ciężarze nie większym niż $w$.
Do windy zawsze wsiada maksymalnie dużo osób z początku kolejki, których łączny ciężar nie przekracza $w$.
Napisz procedurę winda: int → int list → int, która mając dane $w$ oraz listę ciężarów kolejnych osób czekających na windę policzy minimalną liczbę kursów windy potrzebnych do obsłużenia czekających.
Możesz założyć, że ciężary osób czekających na windę są liczbami dodatnimi, nie większymi od $w$.
Rozwiązując to zadanie, nie możesz tworzyć żadnych własnych procedur rekurencyjnych.
Zamiast tego należy wykorzystać standardowe procedury wyższych rzędów przetwarzające listy.

Rozwiązania
Napisz procedurę buduj_permutacje : α list list → α → α,
która przyjmuje permutację w postaci rozkładu na cykle i zwraca ją w postaci procedury.

Lista składowa postaci $[a_1; \dots; a_n]$, gdzie $a_i \neq a_j$ dla $1 \leq i < j \leq n$,
reprezentuje cykl, czyli permutację przeprowadzającą $a_i$ na $a_{(i \bmod n) + 1}$ dla $1 \leq i \leq n$.
Możesz założyć, że listy składowe są niepuste.

Lista list $[c_1; \dots; c_k]$, gdzie listy $c_i$ dla $1 \leq i \leq k$ reprezentują cykle, reprezentuje permutację złożoną z tych cykli.
Możesz założyć, że wszystkie cykle są rozłączne.

Przyjmujemy, że dla wartości $x$ nie występujących na żadnej z list $c_i$ mamy: buduj_permutacje $[c_0; \dots; c_k]\ x = x$.
W szczególności, przyjmujemy, że pusta lista reprezentuje permutację identycznościową.
```
 
      let p = buduj_permutacje [[2; 1]; [8; 3; 4]; [5; 7; 6; 10]; [11]];;
      map p [1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12];;
      -: int list = [2; 1; 4; 8; 7; 10; 6; 3; 9; 5; 11; 12]
 
```
Napisz procedurę podzial : int list → int list list, która dla danej listy liczb całkowitych
$l=[x_1; x_2; \dots; x_n]$ podzieli ją na listę list $[l_1; \dots; l_k]$, przy czym:
- $l = l_1 @ \dots @ l_k$,
- dla każdej listy $l_i$ wszystkie elementy na takiej liście są tego samego znaku,
- $k$ jest najmniejsze możliwe.
Przykład:
```
 
      podzial [1;3;0;-2;-2;-4;9] = [[1; 3]; [0]; [-2;-2;-4]; [9]]
 
```
Rozwiązania
Lista jest monotoniczna jeśli jest niemalejąca lub nierosnąca.
Napisz procedurę $\mathtt{monotons}: \mathtt{int~list} \to \mathtt{int}$, która dla danej listy wyznaczy minimalną liczbę spójnych fragmentów, na które trzeba ją podzielić, tak żeby każdy fragment był monotoniczny. (Dla pustej listy poprawnym wynikiem jest zero.)
Na przykład, monotons [2; 3; 3; 5; 0; -1; -7; 1; 3; 5; 5; 2; 4; 6] = 4.
Daną listę można podzielić tak: [2; 3; 3], [5; 0; -1; -7], [1; 3; 5; 5], [2; 4; 6].
Napisz procedurę $\mathtt{prefiksy}: \mathtt{int~list} \to \mathtt{int~list~list}$, która dla danej listy liczb całkowitych
zwróci listę wszystkich jej prefiksów zakończonych zerem, w kolejności rosnącej ich długości.
Na przykład:
```
 
      prefiksy [0;1;2;3;0;5;6;0;1] = [[0]; [0;1;2;3;0]; [0;1;2;3;0;5;6;0]]
 
```
Rozwiązania
Prostokątną macierz reprezentujemy jako listę wierszy, a każdy wiersz jest listą elementów. Należy zaimplementować operację transpozycji macierzy:
\[
\mathtt{transpose}: \alpha\ \mathtt{list~list} \to \alpha\ \mathtt{list~list}
\]
Dla przypomnienia, $k$-ty wiersz macierzy jest $k$-tą kolumną macierzy transponowanej i odwrotnie.
Możesz założyć, że:
- dana lista jest niepusta,
- listy składowe są niepuste i są wszystkie tej samej długości.
Na przykład: transpose [[1; 2]; [5; 3]; [0; 1]] = [[1; 5; 0]; [2; 3; 1]]

Rozwiązania
Dany jest typ reprezentujący symbole tworzące wyrażenia arytmetyczne:
```
        type symbol = 
          | Liczba of int
          | Plus | Minus | Razy | Podziel
          | Nawias_Otw | Nawias_Zam
 
```
Masz daną listę symboli tworzących poprawne wyrażenie arytmetyczne. Napisz procedurę $\mathtt{kalkulator}: \mathtt{symbol~list} \to \mathtt{int}$, która obliczy wartość wyrażenia.
Przyjmij, że, o ile nawiasy nie wymuszają innej kolejności, operacje arytmetyczne wykonujemy od lewej do prawej.
Przykład:
```
        kalkulator [Nawias_Otw; Liczba 5; Plus; Liczba 4; Razy; 
                    Liczba 2; Plus; Liczba 3; Nawias_Zam; Razy; Liczba 2] = 42
 
```

\(i\)	1	2	3	4	5	6	7	8	9	10	11	12
\(p\ x_i\)	`false`	`true`	`true`	`true`	`false`	`false`	`true`	`true`	`true`	`false`	`false`	`false`
\(q\ x_i\)	`false`	`false`	`true`	`false`	`true`	`false`	`false`	`true`	`false`	`false`	`true`	`false`

Ćwiczenia 11: Procedury wyższych rzędów i drzewa

Ćwiczenia na drzewa z elementami procedur wyższych rzędów:

Dane są: definicja typu tree i procedura fold_tree:
```
 
      type 'a tree =  Node of 'a * 'a tree list;;
 
      let rec fold_tree f (Node (x, l)) = 
        f x (map (fold_tree f) l);;
 
```
Użyj procedury fold_tree do zaimplementowania:
1. policzenia liczby węzłów w drzewie,
2. sprawdzić czy drzewo jest zrównoważone, tzn. wszystkie jego liście są na tej samej głębokości,
3. sprawdzić czy drzewo regularne, tzn. wszystkie jego wierzchołki, z wyjątkiem liści, są tego samego stopnia,
4. procedury preorder/postorder : 'a tree -> 'a list, która przekształca dane drzewo w listę jego elementów w porządku pre-order/post-order (zwróć uwagę na efektywność).
Dane są: definicja typu bin_tree i procedura fold_bin_tree:
```
 
        type 'a bin_tree = Node of 'a bin_tree * 'a * 'a bin_tree | Null;;
        let rec fold_bin_tree f a t = 
          match t with
            Null -> a |
            Node (l, x, r) -> f x (fold_bin_tree f a l) (fold_bin_tree f a r);;
 
```
Użyj procedury fold_bin_tree do zaimplementowania:
1. policzenia liczby węzłów w drzewie,
2. policzenia wysokości drzewa,
3. policzenia średnicy drzewa,
4. sprawdzenia czy drzewo jest drzewem BST (dla drzewa liczb zmiennopozycyjnych, tzn. typu float tree),
5. sprawdzenia, czy drzewo ma kształ drzewa AVL (tzn., czy dla każdego węzła drzewa wysokości jego obu poddrzew różnią się o co najwyżej 1),
6. zaimplementowania procedury map_bin_tree -- odpowiednika procedury map_tree dla drzew binarnych,
7. skonstruowania listy elementów znajdujących się w wierzchołkach drzewa, w kolejności infiksowej,
8. procedury $\mathtt{path}: \alpha\ \mathtt{tree} \to \alpha\ \mathtt{list}$, która znajduje najdłuższą ścieżkę (jedną z) od korzenia do liścia i zwraca listę wartości znajdujących się w węzłach tworzących tę ścieżkę, w kolejności od korzenia do liścia.
9. zaimplementowania procedury $\mathtt{levels} : \alpha\ \mathtt{tree} \to \alpha\ \mathtt{list~list}$,
  która dla danego drzewa zwraca listę list węzłów drzewa znajdujących się na kolejnych poziomach głębokości.
  Listy składowe powinny być podane w kolejności od korzenia w głąb drzewa.
  Wartości z węzłów znajdujących się na tej samej głębokości powinny być uporządkowane od lewej do prawej.
Zadeklaruj typ danych reprezentujący abstrakcyjną składnię wyrażeń arytmetycznych.
Napisz procedurę obliczającą wartość wyrażenia.

Rozszerz składnię wyrażeń o zmienne.
Procedura obliczająca wartość wyrażenia będzie wymagać dodatkowego parametru --- wartościowania
zmiennych, czyli funkcji, która nazwie zmiennej przyporządkowuje jej wartość.

Ćwiczenia 12: Złożoność czasowa i pamięciowa

Piramida to ostrosłup, którego podstawa jest kwadratem, a boczne ściany to tójkąty równoboczne.
Zlecono Ci pomalowanie bocznych ścian piramidy.
Malując piramidę, możesz wziąć ze sobą wiaderko farby, które starcza na pomalowanie 1m² powierzchni, co trwa 1 minutę.
Zarówno wejście na wysokość $h$ metrów, jak i zejście na dół, trwają po $\frac{h}{2}$ minut.
Podstawa piramidy ma długość $n$ metrów.
Podaj, jakiego rzędu jest czas potrzebny do pomalowania całej piramidy.
Jaka jest asymptotycznie energia potencjalna (wypełnionej) piramidy?
Jedziesz w ciemności samochodem. W odległości $n$ metrów przed samochodem idzie pieszy.
Jak ilość światła, która dociera do oczu kierowcy zależy od $n$?
- Jeżeli pieszy nie ma odblasków, nie jest ciałem doskonale czarnym i równomiernie rozprasza padające na niego światło.
- Jeżeli pieszy ma (idealny) odblask, który padające na niego światło odbija dokładnie tam skąd ono pada
  (a kierowca ma reflektory w oczach).
Zastanówmy się, jaka energia jest potrzebna do napompowania koła rowerowego.
Dla ustalonej objętości dętki, jakiego rzędu jest ta energia w zależności od ciśnienia?
Ciśnienie powietrza jest takie, jak ciężar słupa powietrza naciskającego z góry.
Chcemy się wznieść na taką wysokość, na której ciśnienie powietrza nie przekracza p.
Jakiego rzędu jest to wysokość?
Sformułuj warunek określający, czy element wstawiany do drzewa ma być wstawiony do lewego, czy prawego
poddrzewa, tak aby kolejne elementy były wstawiane na kolejnych poziomach od lewej do prawej.
Dana jest implementacja funkcji sprawdz o treści:
```
 
      let sprawdz (a:int) =
        let n = ???
        in if a < n then -1 else if a = n then 0 else 1;;
 
```
W tej implementacji pod ??? została ukryta pewna liczba całkowita.
Napisz funkcje znajdz, która odwołując się do funkcji sprawdz, znajdzie tę liczbę całkowitą.
Podaj złożoność czasową i pamięciową rozwiązania.

Uwaga: Zakładamy, że typ int reprezentuje dowolne liczby całkowite.
W szczególności nie można zakładać, że typ int jest skończony i tym samym używać stałych takich jak max_int.
[CEOI 2003, uproszczone zadanie Hanoi]
Wiadomo (z EMD), że żeby przełożyć $n$ krążków w łamigłówce ,,wieże Hanoi'' trzeba wykonać $2^n-1$ ruchów.
Napisz procedurę hanoi: int list → int → int, która dla zadanej konfiguracji krążków oraz słupka, na
którym początkowo znajdują się wszystkie krążki wyznaczy minimalną liczbę ruchów potrzebnych do uzyskania danej konfiguracji.

Słupki są reprezentowane jako liczby całkowite od 1 do 3.
Konfiguracja to lista numerów słupków, na których mają się znaleźć krążki, w kolejności od największych krążków do najmniejszych.
[VIII OI, zadanie Łańcuch]
(Przynieść i pokazać chiński łańcuch.)
W jednym ruchu można zawsze zdjąć lub założyć pierwsze ogniwo łańcucha.
Ponadto, jeżeli zdjęte są ogniwa o numerach $1, 2, \dots, k-2$, a ogniwo nr $k-1$
jest założone, to w jednym ruchu można zdjąć lub założyć ogniwo nr $k$.
Początkowo wszystkie ogniwa łańcucha są założone.
Napisz procedurę, której wynikiem jest lista ruchów prowadzących do zdjęcia $n$ ogniw łańcucha.
Oblicz złożoność czasową i pamięciową rozwiązania.

Ćwiczenia 13: Zastosowanie sortowania

W poniższych zadaniach istotne jest posortowanie odpowiednich list:

Tomek ma zabawkę, z której wystają drewniane słupki różnej wysokości.
Jednym uderzeniem młotka może wbić lub wysunąć wybrany słupek o 1.

Napisz procedurę słupki : int list → int, która dla danej listy początkowych wysokości słupków
obliczy minimalną liczbę uderzeń młotka potrzebnych do wyrównania wysokości słupków.
Napisz funkcję elementy : α list → int list → α list, która dla list $[x_1; x_2; \ldots, x_n]$ i
$[y_1; y_2; \ldots; y_m]$ zwraca listę $[x_{y_1}; x_{y_2}; \ldots; x_{y_m}]$.
Możesz założyć, że liczby całkowite $y_i$ w drugiej liście są z przedziału $[1, n]$, gdzie $n$ oznacza długość pierwszej listy.
[II OI]
Napisz procedurę trójkąt : int list → bool, która dla danej listy $[x_1; x_2; \dots; x_n]$ dodatnich liczb
całkowitych sprawdzi, czy taka lista zawiera trójkę elementów $x_i, x_j, x_k$ (dla $i \neq j$, $j \neq k$, $i \neq k$)
spełniających nierówność trójkąta, tzn.:
\[2 \cdot \max(x_i, x_j, x_k) \le x_i + x_j + x_k\]

Podaj złożoność czasową i pamięciową swojego rozwiązania.
(Uwaga: Jeżeli liczby całkowite mają ograniczony zakres, to można to zadanie rozwiązać w stałym czasie.)
Napisz procedurę przedział : int list → int → int, która dla danej listy $[x_1;\dots; x_n]$, oraz dla liczby całkowitej
$r \ge 0$ obliczy taką liczbę całkowitą $c$, że $\left| \left\{i : |x_i - c| \le r \right\}\right|$ jest maksymalne.

Przykład: przedział [2; -2; 5; -1; 11; 8; 4; 5; 8; 7] 2 = 6.

Rozwiązania
Dana jest lista liczb rzeczywistych $[x_1; x_2; \dots; x_n]$.
Napisz procedurę przekładaniec, której wynikiem jest taka permutacja $[x_{p_1}; x_{p_2}; \dots; x_{p_n}]$ danej listy,
dla której suma
\[\sum_{i=1}^{n-1} |x_{p_{i+1}} - x_{p_i}|\]
jest największa.

Rozwiązania
[*]
Dana jest lista liczb całkowitych $[x_1; \dots; x_n]$.
Napisz procedurę pierwsze : int list → int list, która zwróci taką jej spójną podlistę, że:
- każde dwa elementy podlisty są względnie pierwsze,
- zawiera ona maksymalną możliwą liczbę elementów.

Ćwiczenia 14: Koszt zamortyzowany

Rozwiązując poniższe zadania zwróć uwagę na efektywność algorytmów.
W większości zadań należy użyć techniki kosztu zamortyzowanego.

Napisz funkcję, która przekształci zadane drzewo w stóg, zachowując jego kształt (w rozwiązaniu można wykorzystać
zmodyfikowaną procedurę rotate z wykładu).
Jaka jest złożoność tej procedury? W jaki sposób zależy ona od kształtu drzewa?
Rozszerzyć implementację kolejek FIFO o wkładanie i wyjmowanie elementów z obydwu stron (w koszcie zamortyzowanym stałym).
Mamy $n$ kubeczków z wodą, ponumerowanych od 1 do $n$ ($n > 0$).
W kubeczku nr $i$ znajduje się $x_i$ wody, przy czym $0 < x_1 \le x_2 \le \dots \le x_n$.
Powtarzamy $k$ razy (dla $k < n$) nastepującą czynność:
wybieramy dwa (niepuste) kubeczki zawierające jak najmniej wody i wodę z jednego kubeczka dolewamy do drugiego.

Napisz procedurę $\mathtt{zlewki}:\mathtt{float~list} \to \mathtt{int} \to \mathtt{float}$,
która dla danej listy zawierającej liczby $[|x_1; \dots; x_n|]$ oraz liczby $k$ określa
określa ile jest wody w najmniej wypełnionym niepustym kubeczku po wykonaniu $k$ operacji przelewania.
Dana jest definicja typu reprezentującego pory roku: type pora = Wiosna | Lato | Jesień | Zima.
Napisz procedurę $\mathtt{pory} : \mathtt{pora~array} \to \mathtt{int}$, która dla danego ciągu pór roku wyznaczy długość najkrótszego jej spójnego fragmentu, który zawiera podciąg złożony ze wszystkich czterech pór roku i to we właściwej kolejności.
Jeżeli taki fragment nie istnieje, poprawnym wynikiem jest -1.
Na przykład: pory [|Lato; Wiosna; Zima; Jesień; Lato; Zima; Wiosna; Jesień; Lato|] = 6.
Fragment złożony z 6 ostatnich elementów danej tablicy zawiera podciąg: Jesień, Zima, Wiosna, Lato.
Zosia codziennie idąc do szkoły mija sadzawkę w parku i lubi ją obserwować. Zbliża się zima. W tej chwili na sadzawce nie ma lodu, ale wkrótce może się to zmienić. Jeżeli danego dnia temperatura jest ujemna i wynosi $-X^\circ$C, to górne $X$ mm wody na sadzawce zamarza. Jeżeli danego dnia temperatura jest dodatnia i wynosi $+X^\circ$C, to górne $X$ mm lodu topi się, o ile na sadzawce jest tyle lodu. Jeśli temperatura wynosi $0^\circ$C, to sadzawka się nie zmienia. Możesz założyć, że sadzawka nigdy nie zamarza do dna.

Przykład: Poniżej podane są temperatury i czym będzie pokryta sadzawka (od góry) w kolejne dni:
- $+2^\circ$C: nic,
- $-12^\circ$C: 12 mm lodu,
- $+8^\circ$C: 8 mm wody, 4 mm lodu,
- $-4^\circ$C: 4 mm lodu, 4 mm wody, 4 mm lodu,
- $+2^\circ$C: 2 mm wody, 2 mm lodu, 4 mm wody, 4 mm lodu,
- $+4^\circ$C: 10 mm wody, 2 mm lodu – roztopiła się górna warstwa lodu i 2 mm dolnej warstwy,
- $-4^\circ$C: 4 mm lodu, 6 mm wody, 2 mm lodu,
- $+1^\circ$C: 1 mm wody, 3 mm lodu, 6 mm wody, 2 mm lodu,
- $-3^\circ$C: 6 mm lodu, 4 mm wody, 2 mm lodu – zamarza górna warstwa lodu i 2 mm kolejnej warstwy wody.
Napisz procedurę $\mathtt{sadzawka}: \mathtt{int~list} \to \mathtt{int~list}$, która dla danej listy temperatur zwróci listę reprezentującą kolejne warstwy pokrywające sadzawkę po tym okresie – liczby ujemne reprezentują lód, dodatnie wodę, a ich wartość bezwzględna grubość warstwy.
Dla powyższego przykładu, poprawnym wynikiem jest $[-6, 4, -2]$.
Zadanie o katastrofach lotniczych:
Dana jest lista liczb całkowitych$[x_1; \dots; x_n]$.
Dla każdego $i$ trzeba policzyć największe takie $k_i$, że $x_i = \max (x_{i-k_i+1}, \dots x_i)$.
Przyjmujemy, że $x_0 = \infty$.
Zaimplementuj $k$-max-kolejkę, czyli kolejkę, do której można wkładać elementy i dowiadywać się jakie jest maksimum
z $k$ ostatnio włożonych elementów.
Dokładniej, powinny być dostępne następujące operacje na $k$-max-kolejkach:
- init : int → α max_queue -- tworzy nową pustą kolejkę z określonym parametrem $k$,
- put : α max_queue → α → α max_queue -- wkłada element do kolejki,
- get_max : α max_queue → α -- zwraca maksimum z $k$ ostatnich elementów włożonych do kolejki.
Wszystkie operacje na kolejce powinny działać w stałym czasie zamortyzowanym.
Dana jest lista $[x_1; \dots; x_n]$ i stała $0 \le k < n$.
Oblicz listę $[y_1; \dots; y_n]$, gdzie $y_i = \max(x_{\max(i-k,1)}, \dots, x_i)$.
Mamy daną listę liczb całkowitych $l = [a_1, \dots, a_n]$.
Liczbę $a_i$ nazywamy $k$-maksimum, jeżeli jest ona większa od $a_{\max(i-k,1)}, \dots, a_{i-1}, a_{i+1}, a_{\min(i+k,n)}$.
Napisz funkcję kmax : int → int list → int list, dla której wynikiem kmax $k$ $l$ jest podlista
listy $l$ złożona z samych $k$-maksimów.
Dana jest lista $[x_1; \dots; x_n]$.
Dla $1 \le i < j \le n$ powiemy, że elementy $x_i$ i $x_j$ widzą się nawzajem, jeżeli $\min(x_i, x_j) \ge \max(x_{i+1}, \dots, x_{j-1})$.
Napisz procedurę widoczne, która obliczy ile elementów ciągu jest widocznych z kolejnych jego elementów.
Np. widoczne [1; 8; 5; 6; 4] = [1; 3; 2; 3; 1].
Dana jest tablica $n$ dodatnich liczb całkowitych.
Tablica ta opisuje figurę złożoną z $n$ stykających się bokami prostokątów-słupków, których dolne boki leżą na jednej prostej (tzw.~Manhattan skyline).
Kolejne liczby w tej tablicy reprezentują wysokości kolejnych słupków jednostkowej szerokości(od lewej do prawej).

Napisz procedurę \texttt{prostokat: int list → int}, która dla danej tablicy wyznaczy maksymalną powierzchnię prostokąta (o bokach równoległych do boków figury), który można wpisać w figurę opisaną przez tablicę.
[PCh]
Dana jest lista liczb całkowitych $[x_1;\dots;x_n]$.
Napisz procedurę różnica : int list → (int * int), która dla danej listy wyznaczy taką parę liczb $(i,j)$, że:
- $0 < i < j \le n$,
- $x_i \le x_j$, oraz
- $j-i$ jest jak największe.
Jeżeli takie $i$ i $j$ nie istnieją, to poprawnym wynikiem jest (0,0).
[SICP, Ćw 2.29]
Mobil, to ruchoma konstrukcja o budowie rekurencyjnej.
Mobil ma ruchome ramiona, jak w wadze szalkowej, określonej długości.
Na końcu każdego z ramion zawieszony jest ciężarek o określonej masie, lub mniejszy mobil.
- Zaimplementuj strukturę danych reprezentującą mobile.
- Napisz procedurę obliczającą wagę mobila.
- Napisz procedurę sprawdzającą, czy mobil jest wyważony.
- [*] [BOI 1999 --- uproszczone]
  Napisz procedurę, która zrównoważy dany mobil tak, aby jego odważniki miały dodatnie wagi całkowite, a jego całkowita masa była minimalna.
[*][XII OI, zadanie Sumy Fibonacciego]
System Zeckendorfa, to taki system, w którym liczba jest reprezentowana jako ciąg zer i jedynek, a kolejne cyfry mają
takie znaczenie, jak kolejne liczby Fibonacciego ($1, 2, 3, 5, \dots$).
Ponadto, w reprezentacji liczby nie mogą pojawiać się dwie jedynki obok siebie.

Liczby reprezentujemy jako listy zer i jedynek.
Zaimplementuj dodawanie w systemie Zeckendorfa.

Ćwiczenia 15: Funktory

Zaprojektuj i zaimplementuj podane funktory:

Monoid składania funkcji -- funktor, który dla określonego typu t konstruuje
monoid z funkcją identycznościową i operacją składania funkcji (na t).
Zdefiniuj funktor, który dla danego monoidu definiuje operację potęgowania.
Zdefiniuj funktor, który na podstawie dwóch porządków liniowych tworzy porządek leksykograficzny na parach odpowiedniego typu.
Zdefiniuj funktor, który dla danego pierścienia elementów tworzy pierścień macierzy 2x2.
[SICP]
Przypomnijmy sobie pakiet liczb wymiernych z poprzedniego wykładu.
Można go zapisać w postaci funktora, sparametryzowanego (wybranym typem) liczb całkowitych.
Podaj sygnaturę liczb całkowitych zawierającą wszystkie operacje potrzebne do zaimplementowania
pakietu liczb wymiernych ze skracaniem ułamków.
Naszkicuj konstrukcję funktora implementującego taki pakiet liczb wymiernych.
[SICP]
Wyobraźmy sobie pakiet implementujący wielomiany, wraz z rozmaitymi operacjami na wielomianach:
suma, różnica, iloczyn, iloraz, reszta z dzielenia, porównanie, pochodna, itp.
Pakiet taki może być sparametryzowany typem liczb (ciałem), nad którym rozpatrujemy wielomiany.
Podaj odpowiednie sygnatury i naszkicuj sposób implementacji pakietu wielomianów jako funktora.
Czy implementacja jest na tyle ogólna, aby pakiet działał nie tylko dla liczb zmiennopozycyjnych,
ale również dla zespolonych i wymiernych?
[SICP]
Korzystając z wyników poprzednich ćwiczeń podaj, jak można skonstruować pakiet funkcji wymiernych?
[SICP]
Korzystając z wyników poprzednich ćwiczeń podaj, jak można skonstruować pakiet wielomianów dwóch zmiennych?
[SICP]
Porównaj funktory z mechanizmem dziedziczenia w programowaniu obiektowym.
W jaki sposób można zasymulować hierarchię klas za pomocą funktorów?
Co z rzutowaniem typów?
Co z metodami wirtualnymi?

Uwaga: Zadania oznaczone [SICP] są mocno inspirowane zadaniami i materiałem z tejże książki, choć nie ma w niej mowy o funktorach.

Ćwiczenia 16: Programowanie imperatywne

Ćwiczenia na konstrukcje imperatywne:

Napisz moduł Counter o następującej sygnaturze:
```
 
      module type COUNTER = sig
        type counter
        val make : unit -> counter
        val inc : counter -> int
        val reset : unit -> unit
      end;;
 
```
Procedura make tworzy nowy licznik o początkowej wartości 0.
Procedura inc zwiększa licznik o 1 i zwraca jego nową wartość.
Procedura reset ustawia wartość wszystkich liczników na 0.

Podaj złożoność czasową i pamięciową ciągu $m$ operacji, spośród których $n$ to operacje make.
Dana jest tablica liczb całkowitych zawierająca permutację liczb całkowitych od 0 do $n$ (dla $n \ge 0$).
Napisz procedurę $\mathtt{cykl} :\mathtt{int~array} \to \mathtt{int}$, która wyznacza długość najdłuższego cyklu danej permutacji.
Twoja procedura nie może zmieniać danej tablicy.
Na przykład:
```
 
      cykl [|2; 1; 0; 5; 6; 4; 3; 8; 7|] = 4
 
```
Rozwiązania
Dana jest tablica rozmiaru $n+1$ zawierająca liczby od 1 do $n$.
Napisz procedurę, która zwraca (dowolną) wartość powtarzającą się w tablicy.

Twoja procedura powinna działać w stałej pamięci dodatkowej.
Natomiast może modyfikować daną tablicę.
Dana jest tablica znaków, która wypełniona jest nawiasami.
Napisz procedurę $\mathtt{nawiasy}: \mathtt{char~array} \to \mathtt{int}$, która zwróci maksymalną długość spójnego fragmentu tablicy, który jest poprawnym wyrażeniem nawiasowym.

Rozwiązania
Dana jest deklaracja drzew binarnych, w których węzłach znajdują się dodatkowo referencje do węzłów drzewa:
```
 
      type α tree =
        Node of α * α tree * α tree * α tree ref |
        Null;;
 
```
1. Drzewo binarne z fastrygą, to drzewo, w którym każdy węzeł posiada dodatkową referencję na następny węzeł w porządku infiksowym. (Ostatni węzeł powinien zawierać referencję na Null.)
  Napisz procedurę fastryguj : α tree → unit, która sfastryguje dane drzewo.
2. Napisz procedurę w_lewo : α tree → unit, która w każdym węźle drzewa ustawia referencję tak, aby wskazywały na węzeł (Node) znajdujący się na tej samej głębokości w drzewie i najbliżej w lewo od danego węzła. W przypadku skrajnie lewych węzłów, referencja powinna wskazywać na Null.
3. Napisz procedurę potomek : α tree → unit, która w każdym węźle ustawi referencję na najgłębiej położony węzeł (Node) będący jego potomkiem.
4. Powiemy, że drzewo jest porządkowe (BST), jeśli w każdym jego wierzchołku postaci Node(x, left, right, _) wartości w poddrzewie left są mniejsze lub równe x, a wartości w poddrzewie right są większe równe x.
  Napisz procedurę fastryga: α tree → unit, która mając dane drzewo porządkowe tak ustawi w nim referencje, że węzły zawierające takie same wartości będą połączone w listy cykliczne.
  W szczególności, jeśli jakaś wartość występuje tylko raz, to referencja w jej węźle powinna być pętelką.
Dana jest tablica par dodatnich liczb rzeczywistych.
Liczby te, to długości boków pewnych prostokątów o takich samych polach.
Tablica ta jest posortowana rosnąco po pierwszych elementach par, oraz malejąco po drugich elementach par.
Napisz procedurę diagonal: (float * float) array → float, która wyznaczy najkrótszą z przekątnych prostokątów.
Rozważmy zrównoważone drzewo BST, np. drzewo AVL, złożone z $n$ węzłów. (Zrównoważone, czyli o wysokości rzędu $O(\log n)$.) W węzłach drzewa znajdują się różne liczby całkowite.
Samo drzewo nie jest dane, natomiast mamy daną tablicę z liczbami znajdującymi się w węzłach, w kolejności zgodnej z obejściem prefiksowym drzewa. (Obejście prefiksowe, to obejście zgodnie z rekurencyjną zasadą: najpierw korzeń, potem lewe poddrzewo a potem prawe poddrzewo.) Szukamy pewnej wartości w obejściu drzewa.
Napisz procedurę $\mathtt{mediana}: \mathtt{int~array} \to \mathtt{int}$, która mając daną tablicę z obejściem drzewa zwróci medianę z wartości znajdujących się w drzewie. (Jeśli w drzewie jest parzysta liczba wartości, to obie ,,środkowe'' są poprawną medianą.)
[M. Startek]
Rozważmy zrównoważone drzewo BST, np. drzewo AVL, złożone z $n$ węzłów. W węzłach drzewa znajdują się różne liczby całkowite.
Samo drzewo nie jest dane, natomiast mamy daną tablicę z liczbami znajdującymi się w węzłach, w kolejności zgodnej z obejściem prefiksowym drzewa. Szukamy pewnej wartości w obejściu drzewa.
Napisz procedurę $\mathtt{znajdz}: \mathtt{int~array} \to \mathtt{int} \to \mathtt{int}$, która mając daną tablicę z obejściem drzewa i szukaną wartość, zwróci jej pozycję w danej tablicy. Jeśli szukana wartość nie występuje w obejściu drzewa, wynikiem powinno być $-1$.
Rozważmy stóg złożony z $n$ węzłów, zawierających różne liczby całkowite. Stóg jest uporządkowany tak, że wartość w dowolnym węźle jest ostro większa od wartości w jego poddrzewach. Uwaga, stóg nie musi być drzewem pełnym, ani nawet zrównoważonym.
```
      type 'a heap = 
         Node of 'a heap * 'a * 'a heap | 
         Null
 
```
Sam stóg nie jest dany, natomiast mamy daną tablicę z liczbami znajdującymi się w węzłach, w kolejności zgodnej z obejściem infiksowym stogu.
(Obejście infiksowe, to obejście zgodnie z rekurencyjną zasadą: najpierw lewe poddrzewo, potem korzeń a potem prawe poddrzewo.)
Napisz procedurę $\mathtt{rekonstrukcja}: \mathtt{int~array} \to \mathtt{int~heap}$, która mając daną tablicę z obejściem stogu odtworzy go.
[Bentley]
Dana jest $n$-elementowa tablica znaków. Napisz procedurę rotacja\,:\,char array -> int -> unit, która rotuje daną tablicę o zadaną liczbę miejsc cyklicznie w prawo, tzn.:
\[
\mathtt{rotacja} [|x_1; x_2; \dots; x_n|]\ k
\]
zmienia zawartość tablicy na:
\[
[|x_{n-k+1}; \dots; x_n; x_1; \dots ; x_{n-k}|]
\]
Na przykład, wywołanie:
rotacja [|'a'; 'l'; 'a'; 'm'; 'a'; 'k'; 'o'; 't'; 'a'|] 4}
zmienia zawartość tablicy na
[|'k'; 'o'; 't'; 'a'; 'a'; 'l'; 'a'; 'm'; 'a'|].
Słowa Fibonacciego to ciąg napisów zdefiniowany następująco:
\[ F_0 = [||], ~~~~ F_1 = [|'b'|], ~~~~ F_2 = [|'a'|], ~~~~ F_{n} = F_{n-1} @ F_{n-2} \]
Kilka kolejnych słów Fibonacciego to:
$F_3 = [|'a'; {}'b'|]$
$F_4 = [|'a'; {}'b'; {}'a'|]$,
$F_5 = [|'a'; {}'b'; {}'a'; {}'a'; {}'b'|]$,
$F_6 = [|'a'; {}'b'; {}'a'; {}'a'; {}'b'; {}'a'; {}'b'; {}'a'|]$.
Napisz procedurę $\mathtt{slowa}: \mathtt{char~array} \to \mathtt{int}$, która dla danego ciągu znaków wyznaczy największy indeks słowa Fibonacciego, które jest jego podciągiem (niekoniecznie spójnym).
Na przykład: slowa [|'a'; 'b'; 'b'; 'a' ;'b'; 'a'; 'c'; 'a'; 'b'; 'a'; 'b'; 'a'; 'b'|] = 6.
Dana jest tablica liczb całkowitych, której pewna rotacja jest posortowana ściśle rosnąco.
Napisz procedurę minmax : int array -> int * int, która znajduje minimum i maksimum w takiej tablicy.
Dana jest niepusta tablica liczb całkowitych $a = [|x_1; \dots; x_n|]$ zawierająca ciąg ściśle monotoniczny, to jest rosnący lub malejący.
Napisz procedurę $\mathtt{blisko\_zera}: \mathtt{int~array} \to \mathtt{int}$, która zwraca $\min(|x_1|, \dots, |x_n|)$.
Tomek chciałby popłynąć z kolegami jachtem w rejs trwający $k$ dni. Potrzebuje zebrać grupę kolegów, którzy chcą i mogą z nim popłynąć. Od każdego ze swoich kolegów dowiedział się od kiedy do kiedy (włącznie) dysponuje wolnym czasem. Teraz zastanawia się, kiedy wyruszyć w rejs, tak żeby mogli żeglować jak największą grupą. W trakcie rejsu koledzy Tomka mogą się zmieniać (o ile obie osoby mają tego samego dnia wolne).
Napisz procedurę $\mathtt{rejs}: \mathtt{int} \to (\mathtt{int} * \mathtt{int})\ \mathtt{list} \to \mathtt{int}$, która mając daną liczbę $k$ oraz informacje o dostępności kolegów Tomka zwróci maksymalną wielkość załogi (nie licząc Tomka).
Jeżeli rejsu nie da się zorganizować, to poprawnym wynikiem jest 0.
Na przykład: $\mathtt{rejs}\ 20\ [(12, 36); (48, 100); (28, 70); (55, 80); (0, 65); (25, 30)] = 3$.
Tomek chciałby popłynąć z kolegami jachtem w rejs. Potrzebuje zebrać grupę $k$ kolegów, którzy chcą i mogą z nim popłynąć. Od każdego ze swoich kolegów dowiedział się od kiedy do kiedy (włącznie) dysponuje wolnym czasem. Teraz zastanawia się, kiedy wyruszyć w rejs, tak żeby mógł on trwać jak najdłużej. W trakcie rejsu załoga nie może się zmieniać.

Napisz procedurę $\mathtt{rejs}: \mathtt{int} \to (\mathtt{int} * \mathtt{int})\ \mathtt{list} \to \mathtt{int}$, która mając daną liczbę $k$ oraz informacje o dostępności kolegów Tomka zwróci maksymalną długość rejsu. Jeżeli rejsu nie da się zorganizować, to poprawnym wynikiem jest 0.
Na przykład: $\mathtt{rejs}\ 2\ [(12, 36); (48, 100); (28, 70); (50, 80); (0, 69); (25, 30)] = 42$.
Dana jest tablica liczb całkowitych $a=[|x_1; x_2; \dots; x_n|]$.
Tablica ta ma taką własność, że jej ciąg różnicowy ( $(x_{i+1} - x_i)_{i=1, 2, \dots, n-1}$) jest ściśle rosnący.
- [PCh] Napisz procedurę $\mathtt{rozne} : \mathtt{int~array} \to \mathtt{bool}$, która dla danej tablicy sprawdza, czy jej elementy są parami różne.
- Napisz procedurę $\mathtt{minimum} : \mathtt{int~array} \to \mathtt{int}$, która dla danej tablicy wyznacz minimum z jej elementów.
Rozwiązując to zadanie nie wolno Ci tworzyć żadnych własnych procedur rekurencyjnych.
Wolno natomiast korzystać z pętli i innych konstrukcji imperatywnych.

Podaj złożoność czasową i pamięciową swojego rozwiązania.
Dana jest tablica liczb całkowitych $a = [|x_1; x_2; \dots; x_n|]$.
Napisz procedurę $\mathtt{segment} : \mathtt{int~array} \to \mathtt{int}$,
która wyznaczy długość ($j-i+1$) najdłuższego takiego spójnego fragmentu tablicy $a$,
$[|x_i; x_{i+1}; \dots; x_j|]$, dla którego $\min(x_i, x_{i+1}, \dots, x_j) \ge j-i+1$.
Dana jest tablica liczb całkowitych $a = [|x_1; x_2; \dots; x_n|]$.
Napisz procedurę $\mathtt{daleko} : \mathtt{int~array} \to (\mathtt{int} * \mathtt{int})$,
która wyznaczy taką parę indeksów $(i, j)$, że:
- $i < j$,
- $a.(i) < a.(j)$,
- $j - i$ jest maksymalne.
Rozwiązując to zadanie nie wolno Ci tworzyć żadnych własnych procedur rekurencyjnych.
Zamiast tego powinieneś użyć konstrukcji imperatywnych.
[PCh]
Dane są dwie listy (bez zapętleń), które łączą się i od pewnego miejsca są tą samą listą.
Znajdź ten wspólny fragment.
Napisz procedurę sprawdzającą, czy dana lista zawiera cykl.
Czy potrafisz wyznaczyć jego długość?

Ćwiczenia 17: Imperatywne wskaźnikowe struktury danych

Zaimplementuj kolejki FIFO+LIFO jako imperatywne listy dwukierunkowe.
Dana jest definicja typu elementów tworzących listy wskaźnikowe:
```
      type 'a option = None | Some of 'a
      type 'a elem = {v: 'a; mutable next: 'a lista}
      and  'a lista = 'a elem option
 
```
1. Napisz procedurę $\mathtt{petla}: \mathtt{lista} \to \mathtt{unit}$, która mając daną listę jednokierunkową, tworzy z niej listę cykliczną, ale z odwróconym kierunkiem wskaźników.
  Możesz założyć, że dana lista jest poprawną listą jednokierunkową, to znaczy ma koniec i nie zapętla się.
  
  Rozwiązania
2. Napisz procedurę $\mathtt{przeplot}: \mathtt{lista} \to \mathtt{lista} \to \mathtt{unit}$, która splata obie listy w jedną listę postaci: pierwszy rekord pierwszej listy, pierwszy rekord drugiej listy, drugi rekord pierwszej listy, drugi rekord drugiej listy, itd. Jeśli jedna z list jest dłuższa, to jej końcówka stanowi końcówkę listy wynikowej.
  
  Rozwiązania
Napisz procedurę tworzącą cykliczną listę modyfikowalną.
Dane są deklaracje typów:
```
      type elem = { x: int; mutable prev: elem list };;
      type lista = elem list;;
 
```
Napisz procedurę $\mathtt{ustaw} : \mathtt{lista} \to \mathtt{unit}$, która dla danej listy $[x_1; x_2; \dots; x_n]$ typu lista, tak ustawia pola prev, aby (dla $i=1,2,\dots, n$) prowadziło ono z elementu $x_i$ do listy zaczynającej się w elemencie $x_{n-i+1}$.
[XII OI, Skarbonki]
Mamy $n$ skarbonek otwieranych kluczykami.
Do każdej skarbonki jest inny kluczyk.
Kluczyki do skarbonek są powrzucane do skarbonek.
Żeby dostać się do zawartości skarbonki, skarbonkę można otworzyć kluczykiem (jeśli się go ma) lub ją rozbić.

Skarbonki są ponumerowane od 0 do $n-1$.
Na podstawie tablicy $a$ (rozmiaru $n$), takiej, że $a.(i) = $ numer skarbonki, w której znajduje się kluczyk do skarbonki
numer $i$, oblicz minimalną liczbę skarbonek, które należy rozbić, tak aby dostać się do zawartości wszystkich skarbonek.
[X OI, Małpki]
Na drzewie wisi $n$ małpek ponumerowanych od 1 do $n$.
Małpka z nr 1 trzyma się gałęzi ogonkiem.
Pozostałe małpki albo są trzymane przez inne małpki, albo trzymają się innych małpek, albo jedno i drugie równocześnie.
Każda małpka ma dwie przednie łapki, każdą może trzymać co najwyżej jedną inną małpkę (za ogon).
Rozpoczynając od chwili 0, co sekundę jedna z małpek puszcza jedną łapkę.
W ten sposób niektóre małpki spadają na ziemię, gdzie dalej mogą puszczać łapki (czas spadania małpek jest pomijalnie mały).

Zaprojektuj algorytm, który na podstawie opisu tego która małpka trzyma którą, oraz na podstawie opisu łapek puszczanych w
kolejnych chwilach, dla każdej małpki wyznaczy moment, kiedy spadnie ona na ziemię.
Na szachownicy jest ustawionych $n$ wież, które należy pokolorować.
Jeśli dwie wieże się atakują (są w tej samej kolumnie lub wierszu), to muszą być tego samego koloru.
Napisz procedurę kolory: int * int list → int,
która na podstawie listy współrzędnych wież wyznaczy maksymalną liczbę kolorów, których można użyć kolorując wieże.
Podaj złożoność czasową i pamięciową swojego rozwiązania.
Dana jest prostokątna mapa złóż gazu wraz z odwiertami pobierającymi gaz. Mapa jest dana w postaci dwuwymiarowej prostokątnej tablicy liczb całkowitych. Miejsca odwiertów są zaznaczone liczbami ujemnymi. Wartość bezwzględna elementu tablicy oznacza ilość znajdującego się w danym miejscu gazu.

Pola niezerowe stykające się bokami tworzą jedno złoże. Odwierty znajdujące się w danym złożu pozwalają pobrać tyle gazu ile pól obejmuje złoże, po czym ilość gazu we wszystkich polach złoża maleje o 1. Może to spowodować zmniejszenie lub podzielenie się złoża. Dalej odwierty pozwalają pobierać gaz z tak zmienionych złóż.

Napisz procedurę $\mathtt{gaz}: \mathtt{int~array~array} \to \mathtt{int}$, która obliczy łączną ilość gazu, jaką wydobędą odwierty.
Dana jest plansza podzielona na sześciokątne pola, o wymiarach $n \times n$ (patrz rysunek).
$i$-te pole w $j$-tym rzędzie sąsiaduje z polami:
- $i-1$ i $i$ w rzędzie $j-1$,
- $i-1$ i $i+1$ w rzędzie $j$,
- $i$ i $i+1$ w rzędzie $j+1$.
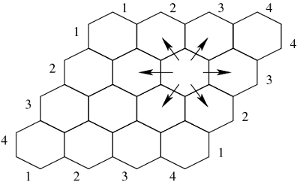Plansza do gry Hex

Dwaj gracze, biały i czarny, grają w grę hex.
Zajmują oni na przemian wolne pola na planszy. Zaczyna gracz biały.
Gracz biały stara się połączyć swoimi polami lewy i prawy brzeg planszy, a gracz czarny górny i dolny brzeg planszy.
Wygrywa gracz, który jako pierwszy połączy odpowiednie brzegi planszy, w ten sposób, że z jednego brzegu na drugi
będzie można przejść przez sąsiadujące pola zajęte przez danego gracza.

Napisz procedurę hex : int → (int * int) list → (bool * int), która na podstawie wielkości planszy $n$,
oraz listy współrzędnych (rząd, pozycja w rzędzie) kolejno zajmowanych przez graczy pól określi, czy wygrał gracz biały
(true), czy czarny (false) i w którym ruchu.
[XIV OI, Biura]
W firmie pracuje $n$ pracowników ponumerowanych od $1$ do $n$.
Każdy pracownik otrzymał służbowy telefon, w którym ma zapisane numery telefonów niektórych swoich współpracowników
(a wszyscy ci współpracownicy mają w swoich telefonach zapisany jego numer).
W związku z dynamicznym rozwojem firmy zarząd postanowił przenieść siedzibę firmy do nowych biurowców.
Postanowiono, że każda para pracowników, którzy będą pracować w różnych budynkach, powinna znać (nawzajem) swoje
numery telefonów, tzn. powinni oni mieć już zapisane nawzajem swoje numery w służbowych telefonach komórkowych.
Równocześnie, zarząd postanowił zająć jak największą liczbę biurowców.

Napisz procedurę biura : int → int * int list → int, która na podstawie liczby pracowników $n$ oraz listy par pracowników
posiadających nawzajem swoje numery telefonów $l=[(a_1,b_1);\dots; (a_m,b_m)]$, wywołana jako $\mathtt{biura}\ n\ l$, obliczy liczbę biurowców.

Rozwiązując to zadanie przyjmij, że $m=O(n)$.
[ONTAK 2007]
Wyobraźmy sobie ciąg zer i jedynek $(x_1, x_2, \dots, x_n)$.
Mamy dany ciąg trójek postaci $(i, j, s)$, gdzie $i$ i $j$ są indeksami w ciągu $(x_i)$, $1 \le i \le j \le n$,
natomiast $s = (\sum_{k=i}^j x_k) \mod 2$.
Niestety dany ciąg trójek jest sfałszowany -- nie istnieje ciąg $(x_i)$, który by go spełniał.
Twoim zadaniem jest znalezienie takiego $k$, że dla pierwszych $k$ danych trójek istniejej jeszcze spełniający je ciąg, a dla $k+1$ już nie.
Napisz procedurę przedzialy: int → (int * int * int) list → int, która dla danego $n$ oraz ciągu trójek oblicza takie $k$.

Ćwiczenia 18: Logika Hoare'a

Udowodnij następującą trójkę:
\[\{ x = x_0,\ y = y_0 \} \mathtt{ y := !x - !y; x := !x - !y; y := !x + !y } \{ x = y_0,\ y = x_0 \}\]
Udowodnij poprawność programu iteracyjnego obliczającego silnię.

[PCh]
Określ dla każdego $n$, co jest wynikiem funkcji coto i udowodnij to.

 
      x := 0;
      y := 1;
      while !y <= n do 
        x := !x - !y;
        y := !y - !x
      done;

Dana jest n-elementowa tablica a, w której znajdują się permutacja zbioru $\{0, 1, \dots n-1\}$.
Na tablicy wolno wykonywać tylko następujące operacje:
- length a -- badać wielkość tabicy n,
- $a.(i)$ -- odczytywać elementy tablicy, oraz
- $\mathtt{zamien}(i,j)$ -- zamieniać elementy wartościami.
Napisz procedurę zamiany : int array → unit, która posortuje daną tablicę
(tj. przekształci ją w permutację identycznościową) wykonując minimalną możliwą liczbę zamian.
Podaj niezmienniki pętli oraz odpowiednie funkcje miary.
Nie muszą one mieć postaci formuł, ale muszą być ściśle określone.
Udowodnij pełną poprawność programu.
Podaj niezmiennik pętli i wykaż poprawność następującego programu:
$ \{ x = x_0 \ge 0 \} $
```
i := 0;
d := 1;
s := 1;
while !s <= !x do
    d := !d + 2;
    s := !s + !d;
    i := !i + 1 
done;
```
$\{ !i = \lfloor{\sqrt{!x_0}}\rfloor \}$

Ćwiczenia 19: Przeszukiwanie grafów

Dany jest graf nieskierowany, którego wierzchołki są ponumerowane od 0 do $n-1$.
Napisz procedurę $\mathtt{path}: \mathtt{graph} \to \mathtt{int}$, która wyznacza długość (liczoną liczbą krawędzi) najdłuższej ścieżki w tym grafie, na której numery wierzchołków tworzą ciąg rosnący.
[II OI, zadanie Klub Prawoskrętnych Kierowców, PCh]
Mamy dany układ ulic, leżących na prostokątnej siatce $m \times n$.
Ulice są jedno- lub dwukierunkowe.
Przyjmujemy, że cztery strony świata są reprezentowane za pomocą liczb całkowitych od 0 do 3:
```
 
      let north = 0 and east = 1 and south = 2 and west = 3;;
 
```
Układ ulic jest dany w formie trójwymiarowej tablicy wartości logicznych ulice: $\mathtt{ulice}.(i).(j).(k)$
określa, czy z punktu o współrzednych $(i,j)$ można przejechać w kierunku k jedną jednostkę odległości.
Można założyć, że tablica ta uniemożliwia wyjechanie poza obszar $\{0,\dots,m-1\} \times \{0,\dots,n-1\}$.

Członkowie Klubu Prawoskrętnych Kierowców na skrzyżowaniach jeżdżą prosto lub skręcają w prawo.
Sprawdź, czy z punktu $(0,0)$ prawoskrętny kierowca może dojechać do punktu $(m-1, n-1)$.
Jaka jest minimalna liczba monet potrzebna do wydania $n$zł reszty, przyjmując, że monety mogą być przekazywane w obie strony.
(Na przykład, żeby otrzymać 9 zł mogę dać 1 zł i otrzymać 10 zł, razem 2).
W obrocie są dostępne monety o zadanych (w postaci tablicy) nominałach.
Dana jest prostokątna mapa wysokości górzystego terenu, w postaci prostokątnej tablicy dodatnich liczb całkowitych, o wymiarach$N \times M$.
Chcemy przejść z pola o współrzędnych$(0,0)$ na pole o współrzędnych$(N-1, M-1)$, ale nie chcemy wspinać się zbyt wysoko.
(Możemy się przesuwać w kierunkach N, W, S, E.)
Napisz procedurę$\mathtt{wysokosc} : \mathtt{int~array~array} \to \mathtt{int}$, która dla danej mapy terenu określi
minimalną największą wysokość, na którą musimy wejść w trakcie podróży.
W parku jest prostokątna sadzawka pokryta lodem. Jaś bawi się na lodzie. Niestety przyszła odwilż i lód zaczął pękać.

Masz daną prostokątną tablicę zawierającą dodatnie liczby całkowite. Jest to mapa sadzawki, a liczby reprezentują moment, w którym lód w danym miejscu pęka.
Napisz procedurę $\mathtt{sadzawka}: \mathtt{int~array~array} \to (\mathtt{int} * \mathtt{int}) \to \mathtt{int}$, która mając daną taką tablicę oraz współrzędne miejsca, w którym bawi się Jaś, wyznaczy moment, w którym Jaś straci możliwość wyjścia na brzeg (bo albo zostanie odcięty od brzegu spękanym lodem, albo wpadnie do wody).

Możesz założyć, że:
- Jaś może poruszać się po polach sąsiadujących ze sobą bokami,
- Jaś porusza się nieporównanie szybciej, niż postępuje pękanie lodu,
- liczby w danej tablicy są z zakresu od 1 do liczba elementów w tablicy.
Dana jest prostokątna mapa $n \times m$ przedstawiająca archipelag na oceanie, reprezentowana jako bool array array.
Elementy tablicy równe true reprezentują ląd, a false wodę.
Na zewnątrz mapy znajduje się ocean.

Wyspy na oceanie są wyspami rzędu 1.
Na wyspach rzędu 1 mogą znajdować się jeziora rzędu 1, na nich mogą znajdować się wyspy rzędu 2 itd.
Ogólnie:
- ocean ma rząd 0,
- wyspa na jeziorze (lub oceanie) rzędu $k$, ma rząd $k+1$,
- jezioro na wyspie rzędu $k$ ma rząd $k$.
Pola wody przylegające do siebie bokami lub rogami należą do tego samego jeziora (lub oceanu).
Pola lądu przylegające do siebie bokami należą do tej samej wyspy.
Napisz procedurę $\mathtt{wyspa}: \mathtt{bool\ array\ array} \to \mathtt{int}$, która dla danej mapy zwróci maksymalny rząd wyspy na mapie.
Jeżeli na oceanie nie ma żadnej wyspy, to procedura powinna zwrócić 0.

Przykład: 69.793N, 108.241W.
[J.Paw.]
Dany jest nieskierowany graf $g$ oraz trzy wierchołki w tym grafie: $u$, $v$ i $w$.
Napisz procedurę $\mathtt{polaczenie}: \mathtt{graph} \to \mathtt{int} \to \mathtt{int} \to \mathtt{int} \to \mathtt{int}$, która mając dane $g$, $u$, $v$ i $w$ wyznaczy minimalną liczbę krawędzi w grafie, jakie są konieczne, żeby wierzchołki $u$, $v$ i $w$ pozostały połączone.
Jeżeli nie jest to możliwe, poprawnym wynikiem jest $-1$.
[XIV OI, zadanie Biura]
Firma ma n pracowników.
Każdy pracownik ma telefon komórkowy, a w nim telefony pewnej grupy innych pracowników.
Przy tym, jeżeli pracownik A ma telefon pracownika B, to pracownik B ma numer pracownika A.
Firma chce podzielić pracowników na grupy, w taki sposób żeby:
- każdych dwóch pracowników albo było w tej samej grupie, albo miało nawzajem swoje numery telefonów,
- liczba grup była maksymalna.
Wyznacz podział pracowników na grupy.
[II OI, zadannie Palindromy]
Podziel dane słowo (listę znaków) na minimalną liczbę palindromów parzystej długości.
Dany jest acykliczny graf skierowany (DAG).
Jego wierzchołki są ponumerowane od 0 do n, a krawędzie są dane w postaci tablicy sąsiedztwa
(kwadratowej tablicy e wartości logicznych; w grafie mamy krawędź $u\!\!\to\!\!v$ wtw., gdy $\mathtt{e}.(u).(v)$).
Powiemy, że wierzchołek u dominuje wierzchołek v, jeżeli dla każdego wierzchołka w,
z którego można dojść do v, z u można dojść do w.

Napisz procedurę zdominowani : bool array array -> int, która na podstawie tablicy opisującej graf
obliczy liczbę wierzchołków, dla których istnieją wierzchołki je dominujące.
[XIV OI, zadanie Powódź]
Dana jest mapa topograficzna miasta położonego w kotlinie, w postaci prostokątnej tablicy typu (int * bool) array array.
Liczby określają wysokość kwadratów jednostkowych, a wartości logiczne określają, czy dany kwadrat należy do terenu miasta.
Przyjmujemy, że teren poza mapą jest położony wyżej niż jakikolwiek kwadrat na mapie.

Miasto zostało całkowicie zalane.
Żeby je osuszyć należy w kotlinie rozmieścić pewną liczbę pomp.
Każda z pomp wypompowuję wodę aż do osuszenia kwadratu jednostkowego, na którym się znajduje.
Osuszenie dowolnego kwadratu pociąga za sobą obniżenie poziomu wody lub osuszenie kwadratów jednostkowych, z
których woda jest w stanie spłynąć do kwadratu, na którym znajduje się pompa.
Woda może przepływać między kwadratami, które stykają się bokami.

Wyznacz minimalną liczbę pomp koniecznych do osuszenia miasta.
Teren nie należący do miasta nie musi być osuszony.
Miasto nie musi tworzyć spójnego obszaru.

Ćwiczenia 20: Przeszukiwanie z nawrotami (ang. back-tracking)

Napisz procedurę, która dla danej liczby $n$ znajdzie jak można obejść szachownicę $n \times n$ skoczkiem.
Skoczek zaczyna obejście w rogu szachownicy, ale może skończyć gdziekolwiek.
Wynikiem powinna być lista par liczb -- kolejnych pozycji skoczka.
Jeżeli rozwiązanie nie istnieje, procedura powinna zgłaszać wyjątek Failure.

Rozwiązania
Napisz procedurę pierwsze, która dla danej liczby całkowitej $n$ ($n>1$) wyznacza
rozbicie $n$ na sumę minimalnej liczby składników będących liczbami pierwszymi.
(Możesz założyć prawdziwość hipotezy Goldbacha.)
Dany jest (multi-)zbiór kostek domina.
Należy wyznaczyć maksymalny łańcuch, jaki można ułożyć z danych kostek, oczywiście zgodnie z zasadami domina.
Rozwiązanie powinno mieć postać procedury domino : (α * α) list → (α * α) list.
Klocki można obracać.
[XIV OI] Atrakcje turystyczne (uproszczone).
Mamy $n$ miejscowości, ponumerowanych od 1 do $n$.
Odległości między miejscowościami są dane w postaci (symetrycznej) tablicy liczb całkowitych, o wymiarach $n \times n$.

Chcemy zwiedzić wszystkie te miejscowości, jednak nie w dowolnej kolejności.
Mamy daną listę ograniczeń postaci $[(i_1, j_1); \dots; (i_k,j_k)]$.
Ograniczenie $(i,j)$ oznacza, że miasto $i$ musi być zwiedzone przed miastem $j$.
Możesz założyć, że ograniczenia da się spełnić.

Na początku wyruszamy z miasta 1, a kończymy podróż w mieście $n$.
Wyznacz minimalną drogę jaką trzeba przejechać, żeby zwiedzić wszystkie miasta.

Ćwiczenia 21 i 22: Spamiętywanie i programowanie dynamiczne

Jaka jest minimalna liczba monet lub banknotów potrzebna do wydania $n$zł reszty, przyjmując, że w obrocie są dostępne monety o zadanych (w postaci tablicy) nominałach?
Na ile sposobów można wydać $n$ zł reszty przyjmując, że w obrocie są dostępne monety o zadanych (w postaci listy) nominałach.
Dana jest kwota $k$ oraz zestaw nominałów banknotów $b = [b_1; b_2; \dots; b_n]$.
Mamy dowolną liczbę banknotów każdego z nominałów.
Napisz procedurę $\mathtt{banknoty}: \mathtt{int} \to \mathtt{int~list} \to \mathtt{int}$, która dla danych $k$ i $b$ obliczy minimalną liczbę różnych nominałów banknotów jakich należy użyć do wydania kwoty $k$.
Jeżeli nie da się wydać kwoty $k$ używając podanych nominałów, to procedura powinna zwrócić -1.
Na przykład, $\mathtt{banknoty}\ 49\ [10, 15, 11, 12, 20] = 3$.
Liczbę 49 można uzyskać na dwa sposoby: $49 = 12 + 12 + 10 + 15 = 11 + 11 + 15 + 12$.
[XII OI, zadanie Banknoty]
W bankomacie znajdują się banknoty o nominałach $b_1, b_2,\dots, b_n$, przy czym banknotów o nominale $b_i$ jest w bankomacie $c_i$.
Jak wypłacić zadaną kwotę używając jak najmniejszej liczby banknotów?
Dana jest tablica zawierająca dostępne nominały monet i banknotów. Tablica ta zawiera dodatnie liczby całkowite i jest uporządkowana rosnąco.
Napisz procedurę $\mathtt{unikat} : \mathtt{int~array} \to \mathtt{int} \to \mathtt{int}$, która dla danej tablicy nominałów i nieujemnej kwoty $k$ zwróci największą taką kwotę, która: nie przekracza $k$ i może być wydana w dokładnie jeden sposób.
Dwa sposoby wydania danej kwoty są różne, jeżeli mają różne multi-zbiory użytych nominałów.
Atomy bajtonium mają po $k$ elektronów ($k > 0$). Elektrony w atomach bajtonium mogą znajdować się na $n$ różnych powłokach, ponumerowanych od 0 do $n-1$, przy czym na każdej powłoce może znajdować się co najwyżej jeden elektron. Masz daną tablicę $t$, posortowaną niemalejąco, zawierającą liczby całkowite z zakresu od 0 do $n^2$. Tablica ta opisuje energię elektronów znajdujących się na poszczególnych powłokach, to znaczy, elektron znajdujący się na powłoce $i$ ma energię $t.(i)$.

Napisz procedurę $\mathtt{energia}: \mathtt{int} \to \mathtt{int~array} \to \mathtt{int} \to \mathtt{int~array}$, która na podstawie liczby $k$, tablicy $t$ oraz energii $e$ wyznaczy orbity, na których powinny znajdować się elektrony w atomie bajtonium tak, żeby ich łączna energia wynosiła $e$. Wynikiem powinna być tablica $k$ numerów powłok z elektronami, uporządkowana rosnąco. Jeżeli uzyskanie danej energii nie jest możliwe, wynikiem powinna być pusta tablica ($[||]$).

Przykład: wynikiem energia 4 [|2; 8; 12; 12; 20|] 42 powinno być [|0; 1; 2; 4|] lub [|0; 1; 3; 4|], natomiast energia 4 [|2; 8; 12; 12; 20|] 60 = [||].
Antyczny bardzo długi kijek został połamany na kawałki. Należy go skleić.
Wszystkie kawałki zostały już ułożone w odpowiedniej kolejności, ale nie wiadomo ile potrzeba kleju.
Długości kolejnych kawałków są dane w postaci listy $l=[x_1;x_2;\dots;x_n]$.
Do slejenia kawałków długości $a$ i $b$ potrzeba $\max(a,b)$ ml kleju.
Po ich sklejeniu otrzymujemy jeden kawałek długości $a+b$.

Napisz procedurę klej : int list → int, która na podstawie długości
kawałków obliczy minimalną ilość kleju (w ml) potrzebną do sklejenia wszystkich kawałków.
Dana jest tablica dodatnich liczb całkowitych $t = [|x_1; x_2; \dots; x_n|]$. Spójny fragment tej tablicy $[|x_i; \dots; x_j|]$ nazwiemy segmentem Fibonacciego rzędu $k$, jeżeli:
- $i = j$ oraz $x_i = x_j = k$, lub
- istnieje takie $l$, $i \le l < j$, że $[|x_i; \dots; x_l|]$ oraz $[|x_{l+1}; \dots; x_j|]$ są segmentami Fibonacciego rzędu $k-1$ i $k-2$ (w dowolnej kolejności).
Napisz procedurę $\mathtt{segment}: \mathtt{int~array} \to \mathtt{int}$, która dla danej tablicy $t$ wyznaczy największy rząd występującego w niej segmentu Fibonacciego.
Jeżeli nie występuje w niej żaden taki segment, to poprawnym wynikiem jest zero.

Przykład: segment [| 1; 3; 2; 3; 4; 5; 3; 6|] = 7. Segment Fibonacciego rzędu 7, to $[|3; 2; 3; 4; 5|]$ ($Fib_7 = 13$).
[XII OI, zadanie Autobus]
Ulice miasta tworzą szachownicę -- prowadzą z północy na południe, lub ze wschodu na zachód, a każda ulica prowadzi na przestrzał przez
całe miasto -- każda ulica biegnąca z północy na południe krzyżuje się z każdą ulicą biegnącą ze wschodu na zachód i vice versa.
Ulice prowadzące z północy na południe są ponumerowane od 1 do $n$, w kolejności z zachodu na wschód.
Ulice prowadzące ze wschód na zachód są ponumerowane od 1 do $m$, w kolejności z południa na północ.
Każde skrzyżowanie $i$-tej ulicy biegnącej z północy na południe i $j$-tej ulicy biegnącej ze wschodu na zachód
oznaczamy parą liczb $(i, j)$ (dla $1 \le i \le n$, $1 \le j \le m$).

Po ulicach miasta kursuje autobus. Zaczyna on trasę przy skrzyżowaniu $(1, 1)$, a kończy przy skrzyżowaniu $(n, m)$.
Ponadto autobus może jechać ulicami tylko w kierunku wschodnim i/lub północnym.

Przy niektórych skrzyżowaniach znajdują się pasażerowie oczekujący na autobus.
Rozmieszczenie pasażerów jest dane w postaci prostokątnej tablicy a $n \times m$ liczb całkowitych --
$a.(i-1).(j-1)$ oznacza liczbę pasażerów czekających przy skrzyżowaniu $(i,j)$.

Napisz procedurę autobus, która na podstawie tablicy a obliczy maksymalną liczbę pasażerów, których może zabrać autobus.
Zakładamy, że w autobusie zmieści się dowolna liczba pasażerów.
[VII OI, zadanie Jajka, zmodyfikowane]
Dostaliśmy $k$ identycznych wytrzymałych strusich jaj. Okazuje się, że są one wytrzymałe na upadki z dużych wysokości. Mieszkamy w $n$-piętrowym wieżowcu.
Chcemy sprawdzić, jakie jest maksymalne piętro $p$ ($0\le p \le n$), z którego jak zrzucimy strusie jajo, to się ono nie zbije.

Napisz funkcję $\mathtt{liczba\_prob} : \mathtt{int} \to \mathtt{int} \to \mathtt{int}$ taką, że $\mathtt{liczba\_prob}\ n\ k$ zwróci najmniejszą (pesymistycznie) liczbę prób zrzucania jaj potrzebną do wyznaczenia $p$ mając do dyspozycji $k$ jaj.
Inaczej mówiąc, szukamy takiej strategii wyznaczenia $p$, która w najgorszym przypadku będzie wymagać jak najmniejszej liczby zrzucań jajek.

Uwagi:
- Jajo zbije się tylko wtedy, gdy zrzucamy je z piętra wyższego niż $p$.
- Jeżeli jajo się zbije, to je tracimy. Jeśli nie, to można je użyć do kolejnej próby.
- Budynek ma $n+1$ kondygnacji, wliczając parter.
- Jeżeli jajo zrzucone z parteru też się zbija, to poprawnym wynikiem jest $-1$.
Na przykład: $\mathtt{liczba\_prob}\ n\ 1 = n + 1$, $~~\mathtt{liczba\_prob}\ 4\ 2 = 3$.
Mamy dany (w postaci listy) ciąg dodatnich liczb całkowitych $[x_1; x_2; \dots; x_n]$.
Na ciągu tym można wykonywać operacje ,,sklejania'', tzn. dwa kolejne elementy ciągu można zastąpić jednym, równym ich sumie.
Napisz procedurę: sklejanie : int list → int obliczającą minimalną liczbę operacji ,,sklejania'', które należy wykonać, aby ciąg był rosnący.
Na przykład, sklejanie [3; 5; 4; 2; 7] = 1.

Równoważne zadanie pojawiło się na konkursie USACO Open Gold w 2009\,r. i zostało opisane w
Delcie.
Na rozgałęzieniach drzewa siedzą wróble.
Każde rozgałęzienie drzewa waży 1 kilogram, a nieujemna waga siedzących na tym rozgałęzieniu wróbli podana jest w drzewie:
```
 
      type drzewo = Leaf | Node of int * drzewo * drzewo
 
```
Waga drzewa to suma wag rozgałęzień i siedzących na nich wróbli.
Drzewo nazwiemy zrównoważonym, jeśli w każdym rozgałęzieniu waga dwóch poddrzew będzie taka sama.
Rzucając celnie kamieniem w rozgałęzienie drzewa możemy przegonić wszystkie wróble z poddrzewa zaczepionego w tym rozgałęzieniu.
Napisz funkcję rownowaga : drzewo → bool, która dla danego drzewa określa, czy da się tak rzucać kamieniami w drzewo,
aby stało się ono zrównoważone. Podaj złożoność czasową i pamięciową swojego rozwiązania.

Dla przykładu, aby zrównoważyć następujące drzewo:
```
 
      Node (3, Node (5, Node (1, Leaf, Leaf), Node (7, Leaf, Leaf)), Node (2, Leaf, Leaf))
 
```
wystarczy raz rzucić kamieniem (w jego lewe poddrzewo).
Każda latarnia jest opisana przez trójkę postaci $(x, y, p)$ oznaczającą, że latarnia może oświetlić (domknięty) odcinek alejki od $x$ do $y$ i pobiera wtedy $p$W energii elektrycznej ($x < y, p> 0$).
Dana jest lista trójek opisujących latarnie, oraz para liczb $(a, b)$, $a < b$, opisująca odcinek alejki, który chcemy oświetlić.
Napisz procedurę $\mathtt{moc}: (\mathtt{int} * \mathtt{int} * \mathtt{int})\ \mathtt{list} \to (\mathtt{int} * \mathtt{int}) \to \mathtt{int}$, która obliczy minimalną moc potrzebną do oświetlenia danego odcinka alejki. Jeżeli jego oświetlenie nie jest możliwe, to poprawnym wynikiem jest $-1$.
Przykład:
```
        moc [(2, 5, 10), (10, 12, 4), (-1, 2, 8), (6, 9, 10), (9, 15, 20),
             (4, 7, 8), (0, 12, 100), (8, 10, 4), (-2, 2, 6)] (1, 11) = 42
 
```
[XVI OI, zadanie Konduktor]
Pociąg na trasie zatrzymuje się na $n$ stacjach, ponumerowanych od 0 do $n-1$.
Dana jest tablica $a$, taka że $a.(i).(j)$ (dla $0 \le i < j < n$) jest równe liczbie pasażerów, którzy
wsiadają na stacji $i$ i wysiadają na stacji $j$.
Możesz wybrać $k$ momentów (między kolejnymi stacjami), kiedy konduktor sprawdza bilety.
Oblicz, jaka jest maksymalna liczba pasażerów, którym zostaną sprawdzone bilety.
Dana jest dwuwymiarowa tablica $a$ wypełniona nieujemnymi liczbami całkowitymi.
Reprezentuje ona mapę prostokątnego lasu, a wartości tablicy odpowiadają liczbie drzew rosnących w różnych miejscach.
Napisz procedurę prostokąt : int array → int → int, która dla zadanej tablicy $a$ oraz liczby $k$
znajdzie w obrębie tablicy (lasu) taki prostokąt, który:
- zawiera przynajmniej $k$ drzew, tzn.\ suma elementów tablicy w prostokącie jest $\ge k$,
- obwód prostokąta jest minimalny.
Wynikiem procedury powinien być obwód tego prostokąta.
Podaj złożoność czasową i pamięciową swojego rozwiązania.

Prostokąt o dolnym lewym rogu $(x_1,y_1)$ i górnym prawym $(x_2,y_2)$ zawiera wszystkie elementy tablicy $a.(i).(j)$ dla
$x_1 \le i \le x_2$, $y_1 \le j \le y_2$, oraz ma obwód $2 \cdot (x_2 - x_1 + 1) + 2 \cdot (y_2 - y_1 + 1)$.
Dana jest prostokątna mapa złóż gazu. Mapa jest dana w postaci dwuwymiarowej prostokątnej tablicy nieujemnych liczb całkowitych, oznaczających ilość znajdującego się w danym miejscu gazu.
Chcemy zakupić prawa do wydobywania gazu z terenu, który ma kształt prostokąta i zawiera łącznie przynajmniej $k$ jednostek gazu.
Napisz procedurę $\mathtt{gaz}: \mathtt{int~array~array} \to \mathtt{int} \to \mathtt{int}$, która obliczy minimalną powierzchnię takiego terenu.
Zosia bardzo lubi czekoladę z orzechami, a im więcej orzechów tym lepiej. Mama pozwoliła Zosi zjeść jeden prostokątny kawałek czekolady składający się z dokładnie $k$ kosteczek. Zosia wpatruje się w tabliczkę czekolady i zastanawia się jaki kawałek wybrać, tak żeby było w nim jak najwięcej orzechów. Kawałek ten może być wybrany z dowolnego miejsca w czekoladzie, nawet ze środka tabliczki. Pomóż Zosi.
Napisz procedurę $\mathtt{orzechy} : \mathtt{int} \to \mathtt{int~array~array} \to \mathtt{int}$, która mając dane: liczbę $k$ ($k > 0$) oraz prostokątną tablicę nieujemnych liczb całkowitych, określającą ile orzechów znajduje się w poszczególnych kosteczkach tabliczki czekolady, wyznaczy maksymalną liczbę orzechów w kawałku czekolady, który może zjeść Zosia.
Możesz założyć, że tabliczka czekolady jest na tyle duża, że zawiera przynajmniej jeden prostokątny kawałek czekolady złożony z dokładnie $k$ kosteczek.
Na przykład, dla $k = 6$ oraz tablicy:
\[
\begin{array}{|c|c|c|c|c|c|}
\hline
0 & 0 & 4 & 1 & 2 & 0 \\\hline
3 & 3 & 8 & 11 & 3 & 2 \\\hline
1 & 3 & 9 & 8 & 1 & 2 \\\hline
2 & 1 & 1 & 2 & 0 & 12 \\\hline
\end{array}
\]
poprawnym wynikiem jest 42.
Mamy most linowy długości$N$ metrów ($N \ge 1$).
Dla każdego metrowego odcinka mostu znamy jego wytrzymałość, to jest maksymalny ciężar jaki może znaleźć się łącznie na moście nie powodując rozerwania lin na tym odcinku.
Możemy rozmieścić$K$ podpór, dzieląc efektywnie most na$K+1$ przylegających do siebie połączonych mostów.
Podpory mają znikomą szerokość i rozmieszczamy je na styku metrowych odcinków mostu.

Przed wjazdem na most zostaną ustawione dwa ograniczenia: maksymalny dopuszczalny ciężar pojazdu$C$ jaki może wjechać na most, oraz minimalna odległość$D$ jaką należy zachować między pojazdami.
Jeśli dwie kolejne podpory znajdują się w odległości$X$, to odcinki łączącego je mostu muszą mieć wytrzymałość przynajmniej $\lceil \frac{X}{D}\rceil \cdot C$.

Ograniczenie$C$ będzie równe minimalnej wytrzymałości całego mostu.
Twoim zadaniem jest wyznaczenie minimalnej możliwej wartości ograniczenia$D$, jakie można uzyskać odpowiednio rozmieszczając podpory.
Napisz procedurę$\mathtt{most}: \mathtt{int~array} \to \mathtt{int} \to \mathtt{int}$, która mając dane wytrzymałości odcinków mostu oraz liczbę podpór$K$ wyznaczy minimalną możliwą wartość ograniczenia$D$.
[XV OI, zadanie Kupno gruntu]
Dana jest kwadratowa tablica $n \times n$ nieujemnych liczb całkowitych $a$, oraz dodatnia liczba całkowita $k$.
Napisz procedurę prostokat : int array array → int → (int * int) * (int * int), która dla tablicy $a$ i
liczby $k$ znajdzie taki prostokątny obszar w obrębie tej tablicy, że suma liczb z tego obszaru jest między $k$, a $2k$.
Ściśle mówiąc, jeśli $\mathtt{prostokat}\ a\ k = ((x_1,y_1), (x_2, y_2))$, to $k \le \sum_{i=x_1}^{x_2} \sum_{j=y_1}^{y_2} a.(i).(j) \le 2k$.
Możesz założyć, że taki obszar istnieje.
[BOI'2003, przeformułowane]
Tomcio chce zrobić model drzewa (acyklicznego nieskierowanego grafu spójnego) z nitki i szklanych koralików i to taki,
w którym koraliki tego samego koloru nie sąsiadują ze sobą.
Nitkę już ma, ale koraliki musi kupić za swoje kieszonkowe.
Ceny koralików różnych kolorów są różne, dla każdego dodatniego całkowitego $n$ w sprzedaży są koraliki
jednego koloru w cenie $n$\,gr za koralik.
Tomcio zastanawia się z jakich koralików zrobić model drzewa, tak aby wydać jak najmniej.

Opis drzewa ma postać struktury listowej, w której każdy węzeł to lista jego synów.
Napisz procedurę koraliki, która na podstawie opisu drzewa obliczy minimalny koszt koralików
potrzebnych do wykonania jego modelu.

Uwaga: Dwa kolory wystarczą do wykonania modelu, ale nie dają minimalnego kosztu.
Możesz założyć, że optymalna liczba kolorów nie przekracza $\log_2 n$, gdzie $n$ to liczba koralików.
[IX OI, zadanie ,,Waga'']
Dany jest zestaw odważników.
Czy można na szalkach wagi położyć część odważników tak, żeby waga nadal była zrównoważona?
Jeśli tak, to jaki najcięższy odważnik można przy tym użyć?
[IX OI, zadanie ,,Nawiasy'']
Dane jest wyrażenie postaci $x_1 \pm x_2 \pm \dots \pm x_n$.
Na ile różnych sposobów można uzyskać wyrażenie równoważne danemu wstawiając nawiasy do wyrażenia $x_1 - x_2 - \dots - x_n$?
Uwaga: wstawiamy $n-1$ par nawiasów w pełni określając kolejność wykonywania odejmowań.
[XI OI, zadanie ,,Sznurki'']
Interesują nas modele drzew (spójnych grafów acyklicznych) wykonane ze sznurka.
Każde drzewo składa się z wierzchołków i pewnej liczby krawędzi łączących różne wierzchołki.
Ten sam wierzchołek może być połączony z wieloma innymi wierzchołkami.
Wierzchołki grafów mają być modelowane przez węzły zawiązane na kawałkach sznurka, a krawędzie przez odcinki sznurka pomiędzy węzłami.
Każdy węzeł może być wynikiem zasuplenia kawałka sznurka lub związania w tym samym miejscu wielu kawałków.
Każda krawędź ma długość 1. Długość sznurka użytego do zrobienia węzłów jest pomijalna.

Chcemy zoptymalizować liczbę i długość kawałków sznurka użytych do wykonania modelu drzewa:
- w pierwszym rzędzie należy zminimalizować liczbę potrzebnych kawałków sznurka,
- zakładając, że liczba kawałków sznurka jest minimalna, należy zminimalizować długość najdłuższego kawałka sznurka.

Ćwiczenia 23 i 24: Programowanie zachłanne

Poniższe zadania rozwiązuje się (mniej lub bardziej) zachłannie.
Dla każdego z nich, oprócz programu, należy uzasadnić poprawność rozwiązania zachłannego.

[CLR, p. 17.1]
Problem wyboru zajęć (historyjka o kinomanie i jak największej liczbie filmów do obejrzenia).
Dany jest zbiór odcinków na prostej.
Jaka jest minimalna liczba gwoździ, za pomocą których można je przybić do prostej?
Każdy odcinek musi być przybity przynajmniej jednym gwoździem.
[CLR, ćw 17.2-4]
Problem tankowania na stacjach benzynowych.
Napisz procedurę $\mathtt{silnie}: \mathtt{int} \to \mathtt{int~list}$, która dla danej dodatniej liczby całkowitej $n$
znajduje najkrótszy taki ciąg dodatnich liczb całkowitych $[x_1; x_2; \dots; x_k]$, że $x_1! + x_2! + \cdots + x_k! = n$.
Na przykład, dla $\mathtt{silnie}\ 42$ poprawnym wynikiem jest n.p. $[3; 4; 3; 3]$.
[PCh]
Dany jest ciąg nawiasów, otwierających i zamykających.
Napisz procedurę nawiasy, która obliczy minimalną liczbę nawiasów które należy obrócić, tak aby uzyskać poprawne wyrażenie nawiasowe.
Jeżeli nie jest to możliwe, to poprawny wynik wynosi -1.
```
 
      type nawias = Otwierający | Zamykający
      val nawiasy : nawias list → int
 
```
W trakcie wakacji n informatyków pojechało razem na obóz informatyczny.
Zamieszkali oni w domkach kempingowych stojących wzdłuż prostej drogi.
Firma telekomunikacyjna chce im zapewnić dostęp do Internetu rozstawiając wzdłuż drogi nadajniki sieci bezprzewodowej.
Jeden nadajnik może obsługiwać co najwyżej k domków znajdujących się od niego w odległości co najwyżej r.
Napisz procedurę wakacje : int → int → int list → int, która na podstawie liczb k i r, oraz
listy współrzędnych domków obliczy minimalną liczbę potrzebnych nadajników.
Ciąg $[x_1; x_2; \dots]$ nazwiemy naprzemiennym, jeżeli:
- $x_1 < x_2 > x_3 < x_4 > \dots$, lub
- $x_1 > x_2 < x_3 > x_4 < \dots$.
Ciąg jednoelementowy i pusty są również naprzemienne.
Napisz procedurę $\mathtt{naprzemienny} : \mathtt{int~array} \to \mathtt{int}$, która mając dany ciąg liczb całkowitych
w postaci tablicy obliczy długość najdłuższego jego naprzemiennego podciągu.
Na przykład, \texttt{naprzemienny [|4;8;6;5;3;4;5;3;7;9;5;7|] = 8}.
Rozważamy ciągi liczb całkowitych $(x_1, x_2, \dots, x_k)$ konstruowane zgodnie z następującymi regułami:
- $x_1 = 1$,
- $x_{i+1} = x_i + f_i$ dla pewnej liczby Fibonacciego $f_i$.
Napisz procedurę $\mathtt{ciag} : \mathtt{int} \to \mathtt{int~list}$,
która dla danej dodatniej liczby całkowitej $n$ wyznaczy najkrótszy taki
ciąg $(x_1, x_2, \dots, x_k)$, że $x_k = n$.
[XII OI, zadanie Lot na marsa]
Bajtazar postanowił polecieć na Marsa, aby zwiedzić istniejące tam stacje badawcze.
Wszystkie stacje na Marsie leżą na okręgu.
Bajtazar ląduje w jednej z nich, a następnie porusza się za pomocą specjalnego pojazdu, który jest napędzany odpowiednim paliwem.
Litr paliwa starcza na metr jazdy.
Zapasy paliwa są jednak niewielkie, różne jego ilości znajdują się w różnych stacjach.
Bajtazar może tankować paliwo na stacji, na której w danym momencie się znajduje, nie więcej jednak, niż dostępna tam jego ilość
(pojemność baku jest nieograniczona).
Musi mu to wystarczyć na dojazd do następnej stacji.
Bajtazar musi zdecydować, gdzie powinien wylądować, tak żeby mógł zwiedzić wszystkie stacje.
Na koniec Bajtazar musi wrócić do stacji, w której wylądował.
W czasie podróży Bajtazar musi poruszać się po okręgu, stale w wybranym jednym z dwóch kierunków.
Firma X podjęła się szeregu zobowiązań, z których wykonaniem zalega.
Wykonanie każdego z nich zajmuje określoną liczbę dni.
Za każdy dzień opóźnienia wykonania każdego z zobowiązań firma płaci określone kary.
Napisz procedurę harmonogram która obliczy optymalną kolejność wykonywania zaległych zobowiązań.
Procedura ta otrzymuje listę trójek postaci: (nazwa czynności, liczba dni, kara za dzień zwłoki).
Jej wynikiem powinna być lista nazw czynności w kolejności, w jakiej należy je wykonywać.
[II OI, zadanie Palindromy]
Podziel dane słowo (listę znaków) na maksymalną liczbę palindromów parzystej długości.
[V OI, zadanie Suma ciągu jedynkowego (uproszczone)]
Dana jest liczba $n \ge 0$ oraz $0 \le s \le \frac{n(n+1)}{2}$.
Podaj podzbiór zbioru $\{1, \dots, n\}$, którego suma elementów jest równa s.
Czy jest to zbiór o minimalnej liczbie elementów?
Napisz procedurę podzial : int → int list, która dla danej nieujemnej liczby całkowitej
przedstawi ją jako sumę jak największej liczby (dodatnich) różnych liczb Fibonacciego.
Na przykład, podzial 42 = [1; 2; 5; 13; 21].
[IV OI, zadanie Lotniska]
W n miastach (ponumerowanych od 1 do n) znajdują się lotniska.
Każde lotnisko ma określoną przepustowość, tj. liczbę połączeń z innymi miastami.
Połączenia takie są zwrotne, czyli połączenie z A do B jest jednocześnie połączeniem z B do A.
Podaj połączenia realizujące dokładnie podane przepustowości, lub stwierdź, że się nie da.
Dane mają postać listy uporządkowanej niemalejąco wg przepustowości miast.
- wersja łatwiejsza: między dwoma miastami może być wiele połączeń,
- wersja trudniejsza: między dwoma miastami może być co najwyżej jedno połączenie.
Dana jest lista par liczb postaci $(x, y)$, $x < y$, opisujących (domknięte) odcinki alejki jakie mogą oświetlić poszczególne latarnie, oraz para liczb $(a, b)$, $a < b$, opisująca odcinek alejki, który chcemy oświetlić.
Napisz procedurę $\mathtt{ile}: (\mathtt{int} * \mathtt{int})\ \mathtt{list} \to (\mathtt{int} * \mathtt{int}) \to \mathtt{int}$, która obliczy minimalną liczbę latarni, jakie są konieczne do oświetlenia danego odcinka alejki.
Przykład:
```
        ile [(1, 4); (7, 9); (-2, 3); (4, 9); (9, 12); (0, 5); (3, 7)] (-1, 11) = 4
 
```
[X OI, zadanie Czekolada]
Dana jest tabliczka czekolady, którą należy połamać na cząstki.
Każde przełamanie kawałka czekolady jest obarczone pewnym kosztem.
Koszt ten nie zależy od wielkości kawałka czekolady, ale od prostej, wzdłuż której łamiemy.
Dla wszystkich prostych, na których leżą krawędzie cząstek czekolady mamy stałe określające koszty łamania.
[III OI, zadanie Wieże]
Na szachownicy $n \times n$ należy ustawić n wież tak, żeby żadne dwie się nie szachowały, a
ponadto każda z tych wież ma wyznaczony prostokąt, w którym ma stać.
Znajdź takie ustawienie, lub stwierdź, że się nie da.
[XI OI, zadanie Most]
Dana jest grupa osób, które chcą przejść nocą przez most.
Mają oni jedną latarkę, która pozwala przejść jednej lub dwóm osobom.
Każda osoba potrzebuje określonego czasu na przejście przez most.
(Możesz założyć, że dane są posortowane.)
Jeśli dwie osoby idą razem, to potrzebują tyle czasu, co wolniejsza z nich.
Jaki jest minimalny czas potrzebny do przejścia wszystkich?
[XII OI, zadanie Samochodziki; OSC, optymalna strategia wymiany stron]
Jasio jest trzylatkiem i bardzo lubi bawić się samochodzikami.
Jasio ma n różnych samochodzików.
Wszystkie samochodziki leżą na wysokiej półce, do której Jasio nie dosięga.
W pokoju jest mało miejsca, więc na podłodze może znajdować się jednocześnie co najwyżej k samochodzików.

Jasio bawi się jednym z samochodzików leżących na podłodze.
Oprócz Jasia w pokoju cały czas przebywa mama.
Gdy Jasio chce się bawić jakimś innym samochodzikiem i jeśli ten samochodzik jest na podłodze, to sięga po niego.
Jeśli jednak samochodzik znajduje się na półce, to musi mu go podać mama.
Mama podając Jasiowi jeden samochodzik, może przy okazji zabrać z podłogi dowolnie wybrany przez siebie
inny samochodzik i odłożyć go na półkę (tak, aby na podłodze nie brakło miejsca).

Mama bardzo dobrze zna swoje dziecko i wie dokładnie, którymi samochodzikami Jasio będzie chciał się bawić.
Dysponując tą wiedzą mama chce zminimalizować liczbę przypadków, gdy musi podawać Jasiowi samochodzik z półki.
W tym celu musi bardzo rozważnie odkładać samochodziki na półkę.

Napisz procedurę samochodziki, która dla danej liczby k oraz listy samochodzików, którymi zechce się
bawić Jasio, obliczy minimalną liczbę razy, kiedy mama będzie musiała Jasiowi podać samochodzik.
[XV OI, zadanie Plakatowanie]
Rozważamy następującą łamigłówkę.
Dana jest tablica nieujemnych liczb całkowitych $a = [|a_1; \dots; a_n|]$.
Jeśli $a_i=a_{i+1} = \dots = a_{j-1} = a_j$ (dla $1 \le i \le j \le n$), to w jednym ruchu można zmniejszyć
wszystkie liczby $a_i, a_{i+1}, \dots, a_j$ o dowolną dodatnią liczbę, nie większą niż $a_i$
(tak żeby po zmniejszeniu nadal były nieujemne).
Napisz procedurę: ruchy : int array → (int * int * int) list, która dla danej tablicy a wyznaczy
najkrótszą sekwencję ruchów potrzebnych do wyzerowania wszystkich liczb $a_1,\dots,a_n$.
Trójka liczb $(i, j, k)$ reprezentuje zmniejszenie liczb $a_i,\dots, a_j$ o k.

Ćwiczenia 25 i 26: Programowanie dynamiczne, zachłanne i back-tracking -- powtórzenie

Rozwiązanie każdego z poniższych zadań wymaga użycia jednej z trzech technik:
back-trackingu, programowania dynamicznego lub zachłannego.
Pytanie której?

[PCh, Zadanie o misjonarzach i kanibalach]
Przez rzekę chcą przeprawić się kanibale i misjonarze.
Kanibali i misjonarzy jest po trzech.
Mają jedną łódkę, którą może płynąć do dwóch osób.
Łódką umieją wiosłować kanibale i tylko jeden misjonarz.
Jeżeli w dowolnej chwili, na dowolnym brzegu rzeki będzie więcej kanibali, niż misjonarzy, to zjedzą oni misjonarzy.
W jaki sposób wszyscy mogą bezpiecznie przeprawić się na drugi brzeg.
[PCh, Zadanie o trzech małżeństwach]
Przez rzekę chcą przeprawić się trzy małżeństwa.
Mają jedną łódkę, którą może płynąć do dwóch osób.
Każda z kobiet może pozostać na brzegu w obecności mężczyzn tylko, jeżeli jest wśród nich jej mąż.
W jaki sposób wszyscy mogą bezpiecznie przeprawić się na drugi brzeg?
[CLR]
Minimalny koszt mnożenia n macierzy, o wymiarach $x_1 \times x_2, x_2 \times x_3, \dots, x_n \times x_{n+1}$.
[CLR 17.2-5]
Dany jest zbiór punktów na osi.
Podaj minimalną liczbę odcinków jednostkowych, jakimi można pokryć punkty z tego zbioru.
Rozważmy taką oto łamigłówkę:
Dana jest lista liczb całkowitych $l = [x_1; x_2; \dots; x_n]$.
W jednym ruchu możemy wybrać dowolne dwa równe elementy listy, usunąć je i wstawić na koniec listy ich sumę.
Takie ruchy możemy powtarzać.
Jaka jest minimalna długość listy jaką można uzyskać?

Napisz procedurę $\mathtt{lamiglowka} : \mathtt{int~list} \to \mathtt{int}$, która dla danej listy $l$ wyznaczy minimalną długość listy jaką można uzyskać.

Na przykład, $\mathtt{lamiglowka}\ [4; 3; 4; 5; 12; 2; 3; 1; 6; 1] = 4$.
Rozważmy taką oto łamigłówkę:
Dana jest lista dodatnich liczb całkowitych $l = [x_1; x_2; \dots; x_n]$. W jednym ruchu możemy wybrać dowolne dwa różne elementy listy, usunąć je i wstawić na koniec listy wartość bezwzględną ich różnicy. Takie ruchy możemy powtarzać. Kończymy, gdy wszystkie elementy listy są sobie równe. Jaka jest minimalna wartość, jaką można na koniec uzyskać na liście?
Napisz procedurę $\mathtt{lamiglowka} : \mathtt{int~list} \to \mathtt{int}$, która dla danej listy $l$ wyznaczy minimalną wartość jaką można uzyskać.
W korytarzu harcują myszy. Korytarz ma długość $n$ metrów.
Dana jest tablica $n$ nieujemnych liczb całkowitych $a$ opisująca gdzie jest ile myszy,
dokładnie na odcinku od $i$ do $i+1$ metrów od wejścia do korytarza jest $a.(i)$ myszy.

Dysponujesz $k$ kotami ($k \le n$).
Twoim zadaniem jest takie rozmieszczenie kotów w korytarzu, żeby złapały jak najwięcej myszy.
Każdy kot może pilnować ustalonego przez Ciebie spójnego fragmentu korytarza (na przykład, może mieć założoną smycz odpowiedniej długości, przymocowaną do podłogi pośrodku pilnowanego fragmentu korytarza).
Fragmenty korytarza pilnowane przez różne koty nie mogą zachodzić na siebie (żeby koty się nie pobiły a smycze nie poplątały), choć mogą się stykać.
Niektóre fragmenty korytarza mogą pozostać niepilnowane przez żadnego kota.

Kot, który pilnuje fragmentu korytarza od $i$ do $j$ metrów od wejścia (dla $i < j$), na którym znajduje się $s = a.(i) + a.(i+1) + \cdots + a.(j-1)$ myszy, złapie: $\max(s - (j-i-1)^2, 0)$ myszy.

Na przykład, dla $k=2$ oraz $a = [|1; 5; 1; 4; 3; 2; 7; 0|]$ poprawnym wynikiem jest 14, jeden kot może pilnować fragmentu korytarza od 1 do 4 metrów od wejścia (łapiąc 6 z 10 myszy), a drugi może pilnować fragmentu korytarza od 4 do 7 metrów od wejścia (łapiąc 8 z 12 myszy).

Napisz procedurę $\mathtt{myszy}: \mathtt{int} \to \mathtt{int~array} \to \mathtt{int}$, która dla danej liczby $k \ge 0$ oraz tablicy $a$, wyznaczy maksymalną liczbę myszy, jakie złapią koty.

Rozwiązanie tego zadania zostało omówione w Delcie
Rozpatrujemy przedstawienia liczby naturalnej $n$ jako sumy różnych składników nieparzystych, tzn. rozważamy takie ciągi $(x_1, \dots, x_k)$, że:
- $1 \le x_i$ i $x_i$ jest nieparzyste (dla $i=1,\dots, k$),
- $x_1 > x_2 > \dots > x_k$,
- $x_1 + \cdots + x_k = n$.
1. Napisz procedurę, która dla danej liczby $n$ obliczy, na ile różnych sposobów można ją przedstawić jako sumę różnych nieparzystych składników.
  Na przykład, dla $n=2$ poprawnym wynikiem jest 0, a dla $n=12$ poprawnym wynikiem jest 3.
2. Napisz procedurę, która dla danej liczby $n$ wyznaczy (pewne) przedstawienie tej liczby jako sumy maksymalnej liczby nieparzystych składników.
  Na przykład, dla $n=42$ poprawnym wynikiem może być [15; 11; 7; 5; 3; 1].
Rozważamy ciągi liczb całkowitych $(x_1, x_2, \dots, x_k)$ konstruowane zgodnie z następującymi regułami:
- $x_1 = 1$,
- $x_{i+1} = x_i + 1$, lub
- $x_{i+1} = x_i \cdot f_i$ dla pewnej liczby Fibonacciego $f_i$.
Napisz procedurę $\mathtt{ciag} : \mathtt{int} \to \mathtt{int~list}$, która dla danej dodatniej liczby całkowitej $n$ wyznaczy najkrótszy taki ciąg $(x_1, x_2, \dots, x_k)$, że $x_k = n$.

Na przykład \texttt{ciag 42} powinno zwrócić $[1; 2; 42]$ lub $[1; 21; 42]$.
Tworzymy ciąg liczb całkowitych $(x_k)$ w następujący sposób:
- $x_0 = 1$,
- dla każdego $k > 0$ wybieramy pewne $0 \le i, j < k$ i przyjmujemy $x_k = x_i + x_j$.
Napisz procedurę ciąg : int → int list, która dla danego $n \ge 1$ znajdzie najkrótszy taki ciąg $x_0, x_1, ..., x_k$, który spełnia powyższe warunki, oraz $x_k = n$.
Wynikiem procedury powinna być lista $[x_0; ...; x_k]$.
Rozważamy ciągi liczb całkowitych $(x_1, x_2, \dots, x_k)$ konstruowane zgodnie z następującymi regułami:
- $x_1 = 1$,
- $x_{i+1} = x_i + 1$, lub
- $x_{i+1} = x_i \cdot p_i$ dla pewnej liczby pierwszej $p_i$.
Napisz procedurę $\mathtt{ciag} : \mathtt{int} \to \mathtt{int~list}$, która dla danej dodatniej liczby całkowitej $n$ wyznaczy najkrótszy taki ciąg $(x_1, x_2, \dots, x_k)$, że $x_k = n$.

Możesz założyć, że dane są procedury:
- $\mathtt{prime}:\mathtt{int}\to\mathtt{bool}$ sprawdzająca czy dana liczba jest pierwsza, oraz
- $\mathtt{primes}:\mathtt{int}\to \mathtt{int~list}$, która dla danej dodatniej liczby całkowitej $n$ zwraca listę liczb pierwszych nie przekraczających $n$ (uporządkowaną rosnąco).
Dla danych dodatnich liczb całkowitych $l$ i $m$ szukamy przedstawienia ułamka $\frac{l}{m}$, jako możliwie najkrótszej sumy odwrotności dodatnich liczb całkowitych: \[\frac{l}{m} = \frac{1}{s_1} + \frac{1}{s_2} + \cdots + \frac{1}{s_k}\]
Napisz procedurę rozklad : int * int → int list, która dla danych liczb $l$ i $m$ wyznaczy szukany ciąg mianowników $[s_1;\dots;s_k]$.
Dana jest dodatnia liczba całkowita $x$.
Interesują nas różne rozkłady $x$ na sumę różnych (dodatnich) liczb Fibonacciego.
Dwa rozkłady, które różnią się jedynie kolejnością składników uznajemy za takie same.
Tylko rozkłady, które mają inne zbiory składników uznajemy za różne.

Napisz procedurę $\mathtt{rozklady} : \mathtt{int} \to \mathtt{int}$, która dla danej liczby $x$
policzy na ile różnych sposobów można przedstawić $x$ jako sumę różnych (dodatnich) liczb Fibonacciego.

Na przykład $\mathtt{rozklady}\ 42 = 6$.
Dana jest lista dodatnich liczb całkowitych $[x_1; x_2; \dots; x_n]$ oraz dodatnia liczba całkowita $k$.
Napisz procedurę podzial : int list → int → int list list, która podzieli daną listę na $k$ spójnych fragmentów
$[[x_1; \dots; x_{n_1}]; [x_{n_1+1}; \dots; x_{n_2}]; \dots; [x_{n_{k-1}+1}; \dots;x_n]]$ w taki sposób, że
$\max \{x_1+ \cdots+ x_{n_1}, x_{n_1+1}+\cdots+ x_{n_2}, \dots, x_{n_{k-1}+1}+ \cdots+ x_n\}$ jest jak najmniejsze.
Jeżeli $k > n$, to w liście wynikowej mogą występować puste listy.

Na przykład podzial [1; 4; 2; 2; 4; 1; 2; 4] 3 = [[1; 4; 2]; [2; 4]; [1; 2; 4]].
Na przystanku autobusowym pojawiają się pasażerowie czekający na autobus. O określonych godzinach podjeżdżają puste autobusy, do których mogą wsiadać pasażerowie. Należy obliczyć minimalną wielkość autobusów, pozwalającą na przewiezienie wszystkich pasażerów (wszystkie autobusy są tej samej wielkości).
Tablica $p$ zawierająca $n$ nieujemnych liczb całkowitych opisuje pojawianie się pasażerów, w chwili $i$ na przystanek przychodzi $p.(i)$ pasażerów.
Tablica $a$ opisuje momenty przyjazdu autobusów na przystanek -- jest ona uporządkowana niemalejąco i zawiera liczby całkowite z zakresu od 0 do $n$.
Napisz procedurę $\mathtt{autobusy}: \mathtt{int~array} \to \mathtt{int~array} \to \mathtt{int}$, taką że $\mathtt{autobusy}\ p\ a$ oblicza minimalną konieczną wielkość autobusów.
Jeżeli nie da się obsłużyć wszystkich pasażerów, to poprawnym wynikiem jest -1.
Na przykład, autobusy [|1; 0; 2; 1; 2; 0; 1; 2; 6; 0; 6; 0|] [|2; 6; 8; 11|] = 7}.
[XVI OI, zadanie Słonie]
Dane jest tablica $p$ długości $n$ zawierająca permutację liczb ze zbioru $\{0,\dots,n-1\}$.
Chcemy posortować tablicę $p$ rosnąco, ale jedyną operacją modyfikującą, którą możemy wykonywać na niej jest zamiana zawartościami dwóch komórek o podanych indeksach.
Zamiana komórek zawierających liczby $x$ i $y$ kosztuje $x+y+1$.
Napisz procedurę koszt : int array → int, która oblicza minimalny koszt posortowania tablicy $p$.
[II OI]
Dany jest zestaw $n$ czynności.
Wykonanie każdej z tych czynności trwa tym dłużej, im później się ją zacznie, konkretnie jeżeli zaczniemy wykonywać czynność $i$ w chwili $t$, to jej wykonanie będzie trwać $a_i t + b_i$.
Jaki jest minimalny czas wykonania wszystkich tych czynności, jeżeli zaczynamy je wykonywać w chwili 0?
Rozważamy drzewa postaci:
```
 
      type expr = 
        NWD of expr * expr | 
        NWW of expr * expr | 
        Number of int
 
```
Drzewa takie reprezentują wyrażenia.
NWD oznacza największy wspólny dzielnik, a NWW najmniejszą wspólną wielokrotność dwóch podwyrażeń.
Argumentami Number są liczby nieujemne.
$\mathtt{Number}\ x$, dla $x>0$ oznacza liczbę $x$.
$\mathtt{Number}\ 0$ oznacza miejsce, w które należy wstawić dodatnią liczbę.

Napisz procedurę $\mathtt{wstaw}: \mathtt{expr} * \mathtt{int} \to \mathtt{int}$, która dla danego drzewa $t$ i dodatniej liczby całkowitej $n$ znajdzie taką najmniejszą dodatnią liczbę całkowitą $x$, że gdy wstawimy $\mathtt{Number}\ x$ w miejsce wszystkich wystąpień $\mathtt{Number}\ 0$ w $t$, to wartością wyrażenia będzie $n$.
Jeżeli taka liczba $x$ nie istnieje, to poprawnym wynikiem jest 0.

Na przykład, dla $t = \mathtt{NWW(NWW(Number 2, Number 0), NWD(Number 0, Number 49))}$ i $n = 42$, $\mathtt{wstaw}\ t\ n = 21$.

Rozwiązania
Przez park biegnie długa prosta alejka. Przy tej alejce, w określonych miejscach, znajduje się $n$ ławeczek. Wzdłuż alejki chcemy zamontować $k$ latarni. Dla każdej ławeczki interesuje nas odległość do najbliżej położonej latarni. Latarnie chcemy rozmieścić tak, żeby maksymalna odległość od ławeczki do najbliżej niej położonej latarni była jak najmniejsza, przy czym latarnie mogą być umieszczone tylko w miejscach o współrzędnych całkowitych.
Masz daną posortowaną tablicę $n$ liczb całkowitych określających położenie ławeczek oraz liczbę $k$. Napisz procedurę $\mathtt{latarnie}: \mathtt{int~array} \to \mathtt{int} \to \mathtt{int~array}$, która na ich podstawie wyznaczy gdzie należy postawić latarnie i zwróci posortowaną tablicę z ich pozycjami.
Na przykład, dla tablicy $[|-4; -3; -1; 2; 2; 3; 8; 10; 11|]$ oraz $k=3$ jednym z możliwych wyników jest $[|-2; 2; 10|]$.
Dane jest drzewo typu:
```
 
      type choinka = 
        Koniuszek | 
        Galaz of choinka | 
        Rozgalezienie of choinka * choinka;;
 
```
opisujące kształt choinki.
1. [PCh]
  W węzłach choinki (Rozgalezienie, Galaz i Koniuszek) możemy umieszczać świeczki.
  Powiemy, że choinka jest oświetlona, jeżeli dla każdej krawędzi (łączącej węzły) choinki przynajmniej w jednym jej końcu znajduje się świeczka.
  Napisz procedurę, która dla danej choinki obliczy minimalną liczbę świeczek potrzebnych do oświetlenia choinki.
2. [PCh]
  Na każdej krawędzi (łączącej węzły) choinki wieszamy jedną bombkę.
  Mamy do dyspozycji trzy rodzaje bombek: czerwone po 2zł, niebieskie po 5zł i srebrne po 7zł.
  Choinkę należy przystroić w taki sposób, żeby na krawędziach o końcach w tym samym węźle wisiały bombki o różnych kolorach, a łączny koszt przystrojenia całej choinki był jak najmniejszy.
3. W węzłach choinki (Rozgalezienie, Galaz i Koniuszek) wieszamy bombki.
  Dostępne są trzy rodzaje bombek:
  - czerwone, wykonane z miedzi, każda taka bombka waży 1kg,
  - srebrne, wykonane z białego złota niskiej próby, każda taka bombka waży 2kg,
  - złote, wykonane ze szczerego złota, każda taka bombka waży 3kg.
  Bombki należy zawiesić tak, aby choinka nie chwiała się, tzn. dla każdego rozgałęzienia łączny ciężar bombek
  zawieszonych po lewej i po prawej stronie musi być taki sam.
  Pytanie czy jest to możliwe, a jeżeli tak, to na ile sposobów?
  
  Napisz procedurę, która dla danej choinki obliczy na ile sposobów można powiesić na niej bombki.

Ćwiczenia 27: Wyszukiwanie wzorców w tekście

Dana jest lista elementów.
Wyznacz wszystkie nietrywialne rotacje cykliczne danej listy, które dają w wyniku ją samą.
Dane są dwa napisy (w postaci tablic znaków) x i y.
Napisz procedurę szukaj : char array → char array → int, która znajduje najdłuższy
spójny fragment w napisie x, który jest prefiksem (fragmentem początkowym) napisu y.
Wynikiem procedury powinna być jego długość.
Okresem ciągu $[x_1; x_2; \dots; x_n]$ nazwiemy najmniejszą dodatnią liczbę całkowitą k,
taką że $x_i = x_{i+k}$, dla $i=1, 2, \dots, n-k$.
Napisz procedurę okresy: int list → int list, której wynikiem dla danej listy $[x_1; x_2; \dots; x_n]$
jest taka lista $[y_1; y_2; \dots; y_n]$, że $y_i$ jest okresem $[x_i; x_{i+1}; \dots; x_n]$.
Niech $(x_1, x_2, \dots, x_n)$ będzie danym niepustym ciągiem liczb.
Okresem całkowitym tego ciągu nazwiemy najmniejszą taką liczbę k, że:
- $1 \le k \le n$,
- k jest dzielnikiem n,
- $x_i = x_{i+k}$ dla wszystkich $i = 1, \dots n-k$.
Zauważmy, że każdy ciąg ma okres całkowity, co najwyżej jest to $k=n$.
Na przykład, okresem całkowitym ciągu $[1;3;2;1;1;3;2;1;1;3;2;1]$ jest 4, a okresem całkowitym ciągu $[1;3;2;1;1]$ jest 5.
Napisz procedurę okres : int array → int, która dla danego ciągu wyznaczy jego okres całkowity.
Dana jest tablica $a$ zawierająca ciąg $n$ elementów.
Napisz procedurę $\mathtt{presuf}: \alpha\ \mathtt{array} \to \mathtt{int}$,
która dla danej tablicy $a$ znajduje długość najdłuższego jej prefikso-sufiksu,
który ma przynajmniej trzy rozłączne wystąpienia w $a$.
Dana jest tablica $a$ zawierająca ciąg $n$ elementów.
Napisz procedurę $\mathtt{double}: \alpha\ \mathtt{array} \to \mathtt{int}$,
która dla danej tablicy $a$ znajduje długość $i$ najdłuższego jej prefiksu, który powtórzony dwukrotnie nadal jest jej prefiksem,
tzn.\ $a.(0) = a.(i)$, $a.(1) = a.(i+1)$, ..., $a.(i-1) = a.(2i-1)$.
[XII OI, zadanie Szablon]
Chcemy wykonać długi napis.
W tym celu najpierw przygotowujemy odpowiedni szablon z wyciętymi literkami.
Następnie taki szablon można przyłożyć we właściwym miejscu do ściany i malujemy po nim farbą.
Malujemy zawsze po całym szablonie, ale dopuszczamy, aby litery były malowane wielokrotnie.
Literki na szablonie znajdują się koło siebie (nie ma tam przerw).
Zadanie polega na wyznaczeniu minimalnej długości szablonu, za pomocą którego można wykonać cały napis.
[XIII OI, zadanie Okresy słów]
Napis Q jest okresem A, jeśli Q jest prefiksem właściwym A oraz A
jest prefiksem (niekoniecznie właściwym) napisu QQ.
Przykładowo, napisy abab i ababab są okresami napisu abababa.
Maksymalnym okresem napisu A nazywamy najdłuższy z jego okresów, lub napis pusty, jeśli A nie posiada okresu.
Dla przykładu, maksymalnym okresem napisu ababab jest abab.
Maksymalnym okresem abc jest napis pusty.

Napisz procedurę, która dla danego (w postaci listy) napisu obliczy listę długości maksymalnych
okresów kolejnych jego prefiksów.
Dana jest tablica $a$ zawierająca $n$ znaków.
Rotacją cykliczną takiej tablicy o $i$ (dla $0 \le i < n$) nazwiemy tablicę powstałą z przeniesienia elementów
$a.(0), \dots, a.(i-1)$ z początku tablicy na jej koniec, przy równoczesnym przesunięciu elementów $a.(i),\dots, a.(n-1)$ o $i$ pozycji w lewo.

Napisz procedurę $\mathtt{minrot}: \mathtt{char~array} \to \mathtt{int}$,
która dla danej tablicy znaków $a$ zwróci taką liczbę $i$, że rotacja tablicy $a$ o $i$ pozycji jest najmniejsza w porządku leksykograficznym,
spośród wszystkich jej rotacji cyklicznych.
Dane są dwa napisy (w postaci tablic znaków) $x$ i $y$.
Napisz procedurę $\mathtt{szukaj}:\mathtt{char~array}\to\mathtt{char~array}\to\mathtt{int}*\mathtt{int}$,
która znajduje najdłuższy spójny fragment występujący w obu napisach.
Wynikiem procedury powinna być para: pozycje jego początków w obu napisach.
Dany jest tekst w postaci tablicy znaków $[|c_1;\dots;c_n|]$.
Napisz procedurę podsłowo : char array → (int * int),
która znajduje takie pozycje w tekście $(i,j)$, że:
- $0 < i \le j \le n$,
- liczba wystąpień $k$ napisu $[|c_i;\dots;c_j|]$ w danym tekście, pomnożona przez jego długość
  (czyli $k \cdot (j-i+1)$) jest maksymalna.
Dla pustej tablicy poprawnym wynikiem jest (0,0).