Trening przed egzaminem

Tym razem proponujemy trening na zadaniach z ubiegłorocznych egzaminów praktycznych. Wcześniej jednak - przypomnienie zasad zaliczania dotyczących egzaminu poprawkowego praktycznego.

Aby przystąpić do egzaminu poprawkowego laboratoryjnego, należy zaliczyć laboratorium, w I lub w II terminie. Podczas egzaminu każdy student pracuje na swoim koncie i może korzystać z dostępnych zasobów elektronicznych (dowolne manuale, zrobione przez siebie zadania) oraz z przyniesionych ze sobą notatek i książek. Kontaktowanie się z innymi osobami będzie karane dwóją z egzaminu. Do rozwiązania będą co najmniej dwa zadania w czasie 3 godzin. Żeby zaliczyć egzamin, wystarczy rozwiązać w pełni jedno zadanie (zaliczane automatycznie przez SIO); za każde następne rozwiązane zadanie uzyskuje się pół oceny więcej od tej wynikającej z wyników egzaminu pisemnego. Osoby, które nie zaliczą części praktycznej, nie będą dopuszczone do części pisemnej egzaminu.

Archiwum

Poniżej treści zadań z poprzednich egzaminów praktycznych. Rozwiązania wzorcowe tych zadań można znaleźć w załącznikach.

Zadanie NAS (Naszyjniki), r. akad. 2015/2016, I termin, zadanie prostsze

Dostępna pamięć: 64MB.

Bajtockie naszyjniki składają się z wielu elementów o różnych kolorach. Ceną danego naszyjnika jest długość jego najdłuższego spójnego fragmentu o tym samym kolorze elementów -- (np. naszyjnik 1 2 1 1 3 1 ma cenę 2).

Bajtazar otrzymał $ \displaystyle n $ niezbyt cennych naszyjników (z których każdy składa się z $ \displaystyle \ell $ elementów) i chciałby z nich otrzymać dokładnie jeden naszyjnik o maksymalnej cenie. Otrzymany naszyjnik również powinien składać sie z $ \displaystyle \ell $ elementów.

Niestety reguły produkcji naszyjników są dosyć restrykcyjne. Jeśli jakiś element naszyjnika był choć raz wykorzystany na $ \displaystyle i $-tej pozycji, to nigdy już nie może wystąpić na innej pozycji.

Czyli zgodnie z regułami w otrzymanym naszyjniku na $ \displaystyle i $-tej pozycji ( $ \displaystyle 1\le i \le \ell $ ) można wykorzystać dokładnie jeden z $ \displaystyle i $-tych elementów wejściowych naszyjników.

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowitą $ \displaystyle n $ i $ \displaystyle \ell $ ( $ \displaystyle 1 \le n \le 100\,000 $, $ \displaystyle 1 \le \ell \le 200\,000 $ ), oznaczającą liczbę naszyjników oraz ich długość. Można założyć, że $ \displaystyle n\cdot \ell \le 2\cdot 10^6 $. Kolejne $ \displaystyle n $ wierszy zawiera opisy naszyjników: $ \displaystyle j $-ty z nich zawiera $ \displaystyle \ell $ liczb całkowitych $ \displaystyle s_i $ ( $ \displaystyle 0 \le s_i \le 1\,000\,000\,000 $ ) oznaczające kolory kolejnych elementów $ \displaystyle j $-tego naszyjnika.

Wyjście
Twój program powinien wypisać na wyjście jedną liczbę całkowitą, oznaczającą maksymalną cenę naszyjnika, który możemy otrzymać.

Przykład
Dla danych wejściowych:
3 4
1 2 1 2
1 1 3 3
3 1 3 2
poprawnym wynikiem jest:
3

Wyjaśnienie do przykładu:
Dla przykładowych naszyjników możemy otrzymać naszyjnik 1 1 1 2 o cenie 3 (pierwszy element pochodzi z naszyjnika numer 1, drugi z naszyjnika numer 2, trzeci element z naszyjnika numer 1 i 4 element z naszyjnika numer 3).

Zadanie TRA (Trasa), r. akad. 2015/2016, I termin, zadanie trudniejsze

Dostępna pamięć: 64MB.

W zadaniu rozważamy silnie spójne grafy skierowane, w których wagi krawędzi zmieniają się w czasie. Dla zadanych wierzchołków $ \displaystyle a $ i $ \displaystyle b $ należy obliczyć najtańszą trasę rozpoczynającą się w wierzchołku $ \displaystyle a $ przechodzącą przez wierzchołek $ \displaystyle b $ i wracającą do $ \displaystyle a $.

Każda krawędź grafu $ \displaystyle e=(u,v) $ ma pewną ustaloną wagę początkową $ \displaystyle c_e $, która następnie ulega zmianie w kolejnych jednostkach czasu o $ \displaystyle p_e $ (jeśli $ \displaystyle p_e>0 $ waga wzrasta, jeśli $ \displaystyle p_e<0 $ waga maleje).

W zadaniu rozważamy graf w jednostkach czasu $ \displaystyle t\in \{1,\ldots,d\} $, można też założyć, że dla zadanych danych wejściowych wartości $ \displaystyle w_e $ i $ \displaystyle p_e $ są tak dobrane, że waga zawsze będzie dodatnia.

Napisz program, który:

wczyta opis grafu $ \displaystyle G $, numery wierzchołków $ \displaystyle a $ i $ \displaystyle b $ oraz maksymalną wartość czasu $ \displaystyle d $,
wyznaczy minimalny koszt trasy z $ \displaystyle a $ do $ \displaystyle b $ i z powrotem, przy założeniu, że możemy wybrać dowolny czas $ \displaystyle t\in \{1,\ldots,d\} $,
wypisze obliczony koszt.

Wejście
W pierwszym wierszu wejścia znajduje się pięć liczb całkowitych $ \displaystyle n, m, a, b, d $, $ \displaystyle 2\le n \le 100\,000 $, $ \displaystyle 1\le m \le 100\,000 $, $ \displaystyle 2\le d \le 10\,000 $, gdzie $ \displaystyle n $ jest liczbą wierzchołków grafu, $ \displaystyle m $ liczbą krawędzi, $ \displaystyle a $ numerem wierzchołka startowego, $ \displaystyle b $ numerem wierzchołka końcowego ( $ \displaystyle a\not=b $ ), $ \displaystyle d $ maksymalnym rozważanym czasem. Wierzchołki są numerowane 1 do $ \displaystyle n $. W następnych $ \displaystyle m $ wierszach znajdują się opisy kolejnych krawędzi. Każdy wiersz zawiera sześć liczb całkowitych: $ \displaystyle n_1, n_2, c_1, p_1, c_2, p_2 $. Liczby $ \displaystyle n_1 $ i $ \displaystyle n_2 $ to numery wierzchołków, które łączy krawędź. Liczby $ \displaystyle c_1 $ i $ \displaystyle c_2 $ oznaczają początkowe wagi krawędzi $ \displaystyle n_1 $ do $ \displaystyle n_2 $ oraz z $ \displaystyle n_2 $ do $ \displaystyle n_1 $. W każdej kolejnej jednostce czasu waga pierwszej krawędzi zmienia się o $ \displaystyle p_1 $, a waga drugiej krawędzi o $ \displaystyle p_2 $. Wiadomo, że dla $$ \displaystyle t=\{1,\ldots,d\} $ każda waga będzie dodatnia i nigdy nie przekroczy $ \displaystyle 10\,000 $.

Wyjście
W pierwszym i jedynym wierszu powinna się znajdować dokładnie jedna liczba całkowita --- minimalny koszt trasy z $ \displaystyle a $ do $ \displaystyle b $ i z powrotem.

Przykład
Dla danych wejściowych:
4 4 1 4 3
1 2 5 -1 10 -1
3 2 12 2 7 2
3 4 8 -1 20 -3
1 4 27 -2 3 0
poprawnym wynikiem jest:
23

Patrz rysunek: http://smurf.mimuw.edu.pl/sites/default/files/trazad.jpg

Jednym z optymalnych rozwiązań dla testu przykładowego jest trasa $ \displaystyle 1 \to 2 \to 3 \to 4 \to 1 $ dla $ \displaystyle t=2 $, kiedy to koszt trasy wynosi 23.

Zadanie EST (Estetyczne ciągi), r. akad. 2015/2016, II termin, zadanie prostsze

Dostępna pamięć: 128MB.

W Bajtocji ciąg liczbowy $ \displaystyle a_1,\ldots,a_k $ jest uważany za estetyczny, jeśli każde dwa kolejne elementy ciągu różnią się co najwyżej o 1:

$ \displaystyle |a_{i+1} - a_i| \le 1\ \mbox{dla}\ 1 \le i < k $

Na przykład ciąg $ \displaystyle 1,1,2,1,0,0 $ jest estetyczny, natomiast $ \displaystyle 1,3,4,3 $ nie jest estetyczny.

Bajtazar otrzymał ciąg składający się z $ \displaystyle n $ liczb: $ \displaystyle s_1,\ldots,s_n $, chciałby z niego otrzymać jak najdłuższy ciąg estetyczny. Może wybrać dowolne elementy wejściowego ciągu i dowolnie zmieniać ich kolejność.

Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ \displaystyle n $ ( $ \displaystyle 1 \le n \le 100\,000 $ ), oznaczającą długość wejściowego ciągu. Kolejne $ \displaystyle n $ wierszy zawiera opis ciągu: $ \displaystyle i $-ty z nich zawiera jedną liczbę całkowitą $ \displaystyle s_i $ ( $ \displaystyle 0 \le s_i \le 1\,000\,000\,000 $ ) oznaczające kolejne elementy wejściowego ciągu.

Wyjście
Twój program powinien wypisać na wyjście jedną liczbę całkowitą, oznaczającą maksymalną długość estetycznego ciągu, który można otrzymać z $ \displaystyle s_1,\ldots,s_n $.

Przykład
Dla danych wejściowych:
7
1
6
2
5
7
6
10
poprawnym wynikiem jest:
4

Wyjaśnienie do przykładu: Dla przykładowego ciągu możemy otrzymać estetyczny ciąg długości 4: 6 5 6 7.

Zadanie POT (Potworzyca), r. akad. 2015/2016, II termin, zadanie trudniejsze

Dostępna pamięć: 512MB.

Potworzyca porusza się po platformach umieszczonych nad przepaścią. Przepaść jest podzielona na $ \displaystyle X \times Y $ kwadratów, nad kwadratem o współrzędnych $ \displaystyle (i,j) $ ( $ \displaystyle 1 \leq i \leq X, 1 \leq j \leq Y $ ) znajduje się jedna platforma, na wysokości $ \displaystyle h_{i,j} $ cm. Jeśli Potworzyca znajduje się na platformie nad kwadratem $ \displaystyle (i,j) $, to może ona w ciągu 1 sekundy się przemieścić na platformę nad polem $ \displaystyle (i',j') $, o ile $ \displaystyle |i-i'| \leq 2 $, $ \displaystyle |j-j'| \leq 2 $, i $ \displaystyle |h_{i,j} - h_{i',j'}| \leq H $, gdzie $ \displaystyle H $ to skoczność Potworzycy. Może ona również w ciągu jednej sekundy przesunąć platformę, na której się znajduje, o 1 cm w górę lub dół. Potworzyca znajduje się na platformie nad $ \displaystyle (1,1) $. Ile czasu potrzebuje, by dostać się do Męża Potwora na platformę nad polem $ \displaystyle (X,Y) $?

Wejście
Pierwszy wiersz wejścia zawiera trzy liczby całkowite $ \displaystyle X $, $ \displaystyle Y $, i $ \displaystyle H $ ( $ \displaystyle 1 \le X,Y \le 500 $, $ \displaystyle 0 \le H \le 1\,000\,000 $ ), oznaczającą wymiary przepaści oraz skoczność Potworzycy. Kolejne $ \displaystyle X $ wierszy zawiera opisy platform: $ \displaystyle i $-ty z nich zawiera $ \displaystyle Y $ liczb całkowitych $ \displaystyle h_{i,1}, \ldots, h_{i,Y} $ oznaczających kolejne wysokości platform, gdzie $ \displaystyle 0 \leq h_{i,j} \leq 1\,000\,000 $.

Wyjście
Twój program powinien wypisać na wyjście jedną liczbę całkowitą, oznaczającą ilość czasu potrzebnego Potworzycy na dotarcie na platformę nad pole $ \displaystyle (X,Y) $ (w sekundach).

Przykład
Dla danych wejściowych:
7 9 25
100 360 110 370 120 380 130 390 140
340 350 900 900 900 280 270 260 150
330 999 900 900 120 900 900 900 400
320 440 180 430 290 420 160 410 250
450 999 999 999 170 999 999 999 240
190 310 999 300 999 999 999 999 230
999 460 200 470 210 480 220 490 520
poprawnym wynikiem jest:
39

Zadanie PAR (Parking), r. akad. 2014/2015, I termin, zadanie prostsze

Dostępna pamięć: 128MB.

Bajtazar pracuje przy obsłudze parkingu w głównej siedzibie firmy ByteSoft. Projektant parkingu, profesor Bajtoni, na co dzień zajmuje się algorytmami grafowymi.

Opis parkingu.
Parking składa się z miejsc parkingowych, ponumerowanych od 1 do $ \displaystyle n $. Między niektórymi parami miejsc występują dwukierunkowe połączenia. Między każdą parą miejsc jest co najwyżej jedno takie połączenie. Na każdym miejscu parkingowym może znajdować się co najwyżej jeden samochód. Główną wadą projektową parkingu jest to, że jeśli dane miejsce parkingowe jest zajęte, żaden samochód nie może przez nie przejechać. Szczęśliwie, jeśli na parkingu nie ma żadnych samochodów, to jest możliwe przejechanie z dowolnego miejsca parkingowego na dowolne inne miejsce parkingowe (innymi słowy mówiąc, graf miejsc parkingowych jest spójny).

Przy miejscu parkingowym numer 1 znajduje się wyjazd z parkingu. Na niektórych miejscach parkingowych są zaparkowane samochody. Pomóż Bajtazarowi stwierdzić, dla każdego samochodu, czy może on wyjechać z parkingu tym wyjazdem. Możesz założyć, że miejsce parkingowe numer 1 jest wolne.

Drugi wiersz wejścia zawiera ciąg bitów $ \displaystyle b_1,\ldots,b_n $, pooddzielanych pojedynczymi odstępami. Bit $ \displaystyle b_i $ oznacza, czy na miejscu parkingowym numer $ \displaystyle i $ znajduje się jakiś samochód (bit 1), czy też nie (bit 0). Możesz założyć, że $ \displaystyle b_1=0 $ oraz że co najmniej jeden bit w ciągu jest równy 1.

Każdy z kolejnych $ \displaystyle m $ wierszy zawiera dwie liczby całkowite $ \displaystyle u_j $ oraz $ \displaystyle v_j $ ( $ \displaystyle 1 \le u_j,v_j \le n $, $ \displaystyle u_j \ne v_j $ ), oznaczające połączenie biegnące między miejscami parkingowymi $ \displaystyle u_j $ i $ \displaystyle v_j $.

Wyjście
Twój program powinien wypisać na wyjście numery wszystkich miejsc parkingowych, na których są zaparkowane samochody, z których każdy (niezależnie) mógłby opuścić parking wyjazdem znajdującym się przy miejscu parkingowym numer 1. Liczby należy wypisać w osobnych wierszach, w kolejności rosnącej.

Przykład
Dla danych wejściowych:
6 7
0 0 1 1 1 0
1 2
2 3
2 4
1 4
4 5
5 6
6 4
poprawnym wynikiem jest:
3
4

Patrz rysunek: http://smurf.mimuw.edu.pl/sites/default/files/parrys-crop.jpg

Zadanie PAD (Parking 2), r. akad. 2014/2015, I termin, zadanie trudniejsze

Dostępna pamięć: 128MB.

Bajtazar pracuje przy obsłudze parkingu w głównej siedzibie firmy ByteSoft. Jest to ten sam parking, który występuje w treści zadania prostszego -- szczegóły można znaleźć w sekcji Opis parkingu.

Przy niektórych miejscach parkingowych znajdują się wyjazdy z parkingu. Samochód może wyjechać danym wyjazdem, tylko jeśli na drodze od jego miejsca parkingowego do wyjazdu nie jest zaparkowany żaden inny samochód (a zatem także i miejsce parkingowe, przy którym znajduje się wyjazd, musi być puste).

Każdego dnia po południu do Bajtazara zgłaszają się kolejni pracownicy firmy, pytając, czy mogą swoimi samochodami wyjechać z parkingu przez wybrane przez siebie wyjazdy. Jeśli Bajtazar odpowiada pracownikowi twierdząco, pracownik wyjeżdża z parkingu -- tak więc nie ma go już na parkingu, gdy zadawane są kolejne zapytania pracowników. Pomóż Bajtazarowi w udzielaniu odpowiedzi na pytania pracowników.

Drugi wiersz wejścia zawiera ciąg bitów $ \displaystyle b_1,\ldots,b_n $, pooddzielanych pojedynczymi odstępami. Bit $ \displaystyle b_i $ oznacza, czy na miejscu parkingowym numer $ \displaystyle i $ znajduje się jakiś samochód (bit 1), czy też nie (bit 0). Możesz założyć, że co najmniej jeden bit w ciągu jest równy 1. W przeciwieństwie do zadania prostszego, nie występuje tu dodatkowe założenie, że $ \displaystyle b_1=0 $.

Każdy z kolejnych $ \displaystyle m $ wierszy zawiera dwie liczby całkowite $ \displaystyle u_j $ oraz $ \displaystyle v_j $ ( $ \displaystyle 1 \le u_j,v_j \le n $, $ \displaystyle u_j \ne v_j $), oznaczające połączenie biegnące między miejscami parkingowymi $ \displaystyle u_j $ i $ \displaystyle v_j $.

Kolejny wiersz wejścia zawiera jedną liczbę całkowitą $ \displaystyle q $ ( $ \displaystyle 1 \le q \le 500\,000 $ ), oznaczającą liczbę zapytań. Każdy z kolejnych $ \displaystyle q $ wierszy zawiera dwie liczby całkowite $ \displaystyle m_k $, $ \displaystyle w_k $ ( $ \displaystyle 1 \le m_k,w_k \le n $, $ \displaystyle m_k \ne w_k $ ) oznaczające zapytanie pracownika parkującego na miejscu $ \displaystyle m_k $, który pyta o możliwość opuszczenia parkingu z użyciem wyjazdu znajdującego się przy miejscu parkingowym numer $ \displaystyle w_k $. Możesz założyć, że przy takim zapytaniu rzeczywiście zachodzi $ \displaystyle b_{m_k}=1 $.

Wyjście
Twój program powinien wypisać na wyjście $ \displaystyle q $ wierszy z odpowiedziami Bajtazara, z których każda to TAK lub NIE.

Przykład
Dla danych wejściowych:
6 7
0 0 1 1 1 0
1 2
2 3
2 4
1 4
4 5
5 6
6 4
6
3 6
5 1
3 1
4 5
4 6
5 1
poprawnym wynikiem jest:
NIE
NIE
TAK
NIE
TAK
TAK

Zadanie WZN (Wzniesienia), r. akad. 2014/2015, II termin, zadanie prostsze

Dostępna pamięć: 128MB.

W tym zadaniu mamy dany graf nieskierowany z całkowitymi dodatnimi wagami na krawędziach. Wzniesieniem w grafie nazywamy ścieżkę prostą złożoną z dwóch krawędzi, z których druga ma większą wagę niż pierwsza. Napisz program, który zliczy wzniesienia w podanym grafie.

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 2 \le n \le 500\,000 $, $ \displaystyle 1 \le m \le 500\,000 $ ) oznaczające liczbę wierzchołków i liczbę krawędzi w grafie. Każdy z kolejnych $ \displaystyle m $ wierszy zawiera trzy liczby całkowite $ \displaystyle u_i $, $ \displaystyle v_i $, $ \displaystyle w_i $ ( $ \displaystyle 1 \le u_i,v_i \le n $, $ \displaystyle 1 \le w_i \le 1\,000\,000 $ ), opisujące nieskierowaną krawędź: jej końce i jej wagę. Możesz założyć, że graf nie zawiera pętli ani krawędzi wielokrotnych.

Wyjście
Twój program powinien wypisać na wyjście jeden wiersz zawierający jedną liczbę całkowitą: liczbę wzniesień w grafie.

Przykład
Dla danych wejściowych:
5 6
1 2 1
2 3 2
3 4 3
4 1 4
1 5 2
5 2 1
poprawnym wynikiem jest:
8

natomiast dla danych wejściowych:
7 6
1 2 1
1 3 1
1 4 2
1 5 2
1 6 3
1 7 3
poprawnym wynikiem jest:
12

Zadanie AUT (Autostrada), r. akad. 2014/2015, II termin, zadanie trudniejsze

Dostępna pamięć: 128MB.

Bajtazar zarządza jednokierunkową dwupasmową autostradą z Bajtyża do Bajtawy. Każdy z dwóch pasów ruchu złożony jest z $ \displaystyle n $ kwadratowych płyt, jak na rysunku http://smurf.mimuw.edu.pl/sites/default/files/autrys1-crop.jpg

Niestety, autostrada często jest blokowana przez demonstracje bitników. Każda grupa protestujących bitników zajmuje jeden odcinek dzielący dwie płyty autostrady, co powoduje, że samochód nie może przejechać przez ten odcinek. Bajtazar przez cały dzień dostaje informacje o pojawieniu się lub zniknięciu grupy protestujących i musi na bieżąco odpowiadać na zapytania, czy autostrada jest przejezdna, czy nie. Pomóż mu!

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 2 \le n \le 500\,000$, $ \displaystyle 1 \le m \le 500\,000 $ ) oznaczające długość autostrady i liczbę zdarzeń. Na początku między każdymi dwiema sąsiednimi płytami da się przejechać.

Każdy z kolejnych $ \displaystyle m $ wierszy zawiera parę liczb $ \displaystyle i $ oraz $ \displaystyle t $ ( $ \displaystyle 0 \le i \le n-1 $, $ \displaystyle 0 \le t \le 2 $ ) określającą zmianę przejezdności między dwiema płytami autostrady. Wartość $ \displaystyle t=0 $ oznacza, że zmiana dotyczy odcinka między punktami $ \displaystyle (i,1) $ i $ \displaystyle (i+1,1) $, $ \displaystyle t=1 $ oznacza, że zmiana dotyczy odcinka między $ \displaystyle (i,0) $ a $ \displaystyle (i,1) $, a $ \displaystyle t=2 $ oznacza, że zmiana dotyczy odcinka między $ \displaystyle (i,1) $ a $ \displaystyle (i,2) $. (Układ współrzędnych według rysunku powyżej.) Każda para liczb oznacza zmianę stanu odcinka przez nią reprezentowanego: jeśli przed zmianą przez odcinek dało się przejechać, to po zmianie się nie da, a jeśli nie dało się przejechać, to po zmianie się da.

Wyjście
Twój program powinien wypisać na wyjście $ \displaystyle m $ wierszy z odpowiedziami Bajtazara, z których każda to TAK lub NIE -- odpowiedź oznacza, czy po kolejnej zmianie przejezdności da się przejechać całą autostradą.

Przykład
Dla danych wejściowych:
10 6
2 0
4 0
2 1
5 2
3 0
4 0
poprawnym wynikiem jest:
TAK
TAK
TAK
TAK
NIE
TAK

Poniższy rysunek przedstawia sytuację na autostradzie po wszystkich zmianach: http://smurf.mimuw.edu.pl/sites/default/files/autrys2-crop.jpg

Zadanie SKI (Skierowanie), r. akad. 2013/2014, I termin, zadanie prostsze

Dostępna pamięć: 256MB.

Dany jest pewien graf nieskierowany. Czy można skierować krawędzie tego grafu tak, by w wynikowym grafie skierowanym nie istniała ścieżka (skierowana) złożona z więcej niż jednej krawędzi?

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 2 \le n \le 500\,000 $, $ \displaystyle 1 \le m \le 500\,000 $ ), oznaczające liczbę wierzchołków i liczbę krawędzi w grafie. Każdy z kolejnych $ \displaystyle m $ wierszy zawiera dwie liczby całkowite $ \displaystyle a_i $, $ \displaystyle b_i $ ( $ \displaystyle 1\le a_i,b_i \le n $, $ \displaystyle a_i \ne b_i $ ), oznaczające krawędź grafu. W grafie nie ma pętli ani krawędzi wielokrotnych.

Wyjście
Twój program powinien wypisać jeden wiersz zawierający jedno słowo TAK lub NIE, w zależności od tego, czy istnieje żądane skierowanie krawędzi grafu.

Przykład
Dla danych wejściowych:
5 6
1 2
2 3
3 4
4 1
1 5
5 3
poprawnym wynikiem jest:
TAK

natomiast dla danych wejściowych:
5 4
1 2
2 3
3 1
4 5
poprawnym wynikiem jest:
NIE

Zadanie PRE (Prelegenci), r. akad. 2013/2014, I termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Uniwersytet Bajtocki organizuje dwudniowy cykl wykładów pt. Bit i bajt. Komitet programowy cyklu chciałby na każdy z dni zaprosić wybitnego specjalistę w dziedzinie informatyki teoretycznej, aby wygłosił tego dnia wykład plenarny. Członkowie komitetu stworzyli listę $n$ wybitnych naukowców, spośród których chcieliby wybrać dwóch prelegentów. Decyzja, których dwóch prelegentów zaprosić, ma swój aspekt finansowy.

Każdy z prelegentów wyznaczył pewną kwotę, którą mu trzeba zapłacić, aby zgodził się wygłosić jeden z wykładów plenarnych. Ponadto niektórzy prelegenci nie lubią się wzajemnie. Jeśli chcieć zaprosić na wykłady dwóch nielubiących się prelegentów, trzeba każdemu z nich zapłacić pewną dodatkową kwotę jako rekompensatę za pracę w trudnych warunkach. Komitet programowy poprosił Cię, abyś pomógł mu wybrać dwóch prelegentów, których zaproszenie jest najbardziej ekonomiczne (czyli, mówiąc wprost, będzie kosztować najmniej pieniędzy).

Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 500\,000 $ ), oznaczającą liczbę prelegentów. W drugim wierszu znajduje się $ \displaystyle n $ liczb całkowitych $ \displaystyle a_1,\ldots,a_n $ ( $ \displaystyle 1 \le a_i \le 100\,000\,000 $ ); liczba $ \displaystyle a_i $ reprezentuje koszt zaproszenia $ \displaystyle i $-tego prelegenta. W trzecim wierszu znajduje się jedna liczba całkowita $ \displaystyle m $ ( $ \displaystyle 1 \le m \le 500\,000 $ ), oznaczająca liczbę par prelegentów, którzy się nie lubią. W kolejnych $ \displaystyle m $ wierszach znajdują się opisy tych par. Każdy taki opis składa się z trzech liczb całkowitych $ \displaystyle u_i $, $ \displaystyle v_i $, $ \displaystyle b_i $ ( $ \displaystyle 1 \le u_i,v_i \le n $, $ \displaystyle u_i \ne v_i $, $ \displaystyle 1 \le b_i \le 100\,000\,000 $ ), które oznaczają, że prelegenci $ \displaystyle u_i $ i $ \displaystyle v_i $ nie lubią się i jeśli obu ich zaprosić na wykłady, trzeba każdemu z nich zapłacić $ \displaystyle b_i $. Pary $ \displaystyle \{u_i, v_i\} $ nie mogą się powtarzać.

Wyjście
Twój program powinien wypisać jeden wiersz zawierający jedną liczbę całkowitą, oznaczającą minimalny koszt zorganizowania wykładów z udziałem dwóch różnych prelegentów.

Przykład
Dla danych wejściowych:
4
3 2 4 8
4
1 2 5
1 3 1
3 2 2
1 4 1
poprawnym wynikiem jest:
9

Wyjaśnienie do przykładu: Komitet programowy powinien zaprosić pierwszego i trzeciego prelegenta, którzy nie lubią się "tylko trochę'".

Zadanie ZET (Żetony I), r. akad. 2013/2014, II termin, zadanie prostsze

Dostępna pamięć: 256MB.

Uwaga: Zadanie prostsze (Żetony I, ZET) różni się od trudniejszego (Żetony II, ZED) jedynie ograniczeniem na $ \displaystyle m_i $.

Jaś ma pewną liczbę jednakowych żetonów, które poustawiał w stosy. Teraz bawi się tak, że w każdym ruchu wybiera stos zawierający największą liczbę żetonów i dzieli go na dwa stosy mniej więcej w połowie. Dokładniej, jeśli stos przed podziałem miał $ \displaystyle m $ żetonów, to stosy powstałe w wyniku podziału mają rozmiary $ \displaystyle \lfloor m/2 \rfloor $ oraz $ \displaystyle \lceil m/2 \rceil $. Jeśli przed wykonaniem operacji jest więcej niż jeden stos o takiej samej, maksymalnej liczbie żetonów, Jaś wybiera dowolny z nich. Jaś kończy wykonywać ruchy w chwili, gdy każdy stos składa się już tylko z jednego żetonu.

Siostra Jasia, Małgosia, co jakiś czas przychodzi do Jasia i pyta go, ile ma różnych wysokości stosów monet. Jaś jest tak zajęty swoją zabawą, że nie ma czasu odpowiadać ciągle na pytania siostry. Poprosił Cię o napisanie programu, który będzie to robił za niego.

Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 1 \le n \le 1000 $ ), oznaczająca początkową liczbę stosów. W drugim wierszu znajduje się $ \displaystyle n $ liczb całkowitych $ \displaystyle m_i $ ( $ \displaystyle 1 \le m_i \le 10^6 $ ), oznaczających początkowe wysokości stosów. W trzecim wierszu znajduje się jedna liczba całkowita $ \displaystyle z $ ( $ \displaystyle 1 \le z \le 500\,000 $ ), oznaczająca liczbę pytań Małgosi. W czwartym wierszu znajduje się $ \displaystyle z $ liczb całkowitych $ \displaystyle k_i $ ( $ \displaystyle 1 \le k_i \le 10^9 $ ). Liczba $ \displaystyle k_1 $ oznacza, że pierwsze pytanie Małgosi nastąpiło po wykonaniu $ \displaystyle k_1 $ ruchów Jasia. Liczba $ \displaystyle k_2 $ oznacza, że drugie pytanie nastąpiło po wykonaniu kolejnych $ \displaystyle k_2 $ ruchów Jasia itd. Możesz założyć, że $ \displaystyle k_1+\ldots+k_z $ nie przekracza liczby ruchów wykonanych przez Jasia w całej grze.

Wyjście
Twój program powinien wypisać $ \displaystyle z $ wierszy. W $ \displaystyle i $-tym wierszu powinna znaleźć się jedna liczba całkowita oznaczająca liczbę różnych stosów żetonów, jakie ma Jaś w chwili, w której Małgosia zadała $ \displaystyle i $-te pytanie.

Przykład
Dla danych wejściowych:
3
9 8 2
3
1 2 3
poprawnym wynikiem jest:
4
3
2

Oto jak wyglądają wysokości stosów po kolejnych ruchach Jasia:

9, 8, 2
8, 5, 4, 2 (pierwsze pytanie Małgosi)
5, 4, 4, 4, 2
4, 4, 4, 3, 2, 2 (drugie pytanie Małgosi)
4, 4, 3, 2, 2, 2, 2
4, 3, 2, 2, 2, 2, 2, 2
3, 2, 2, 2, 2, 2, 2, 2, 2 (trzecie pytanie Małgosi).

Zadanie ZED (Żetony II), r. akad. 2013/2014, II termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Uwaga: Zadanie prostsze (Żetony I, ZET) różni się od trudniejszego (Żetony II, ZED) jedynie ograniczeniem na $ \displaystyle m_i $.

Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 1 \le n \le 1000 $ ), oznaczająca początkową liczbę stosów. W drugim wierszu znajduje się $ \displaystyle n $ liczb całkowitych $ \displaystyle m_i $ ( $ \displaystyle 1 \le m_i \le 10^9 $ ), oznaczających początkowe wysokości stosów. W trzecim wierszu znajduje się jedna liczba całkowita $ \displaystyle z $ ( $ \displaystyle 1 \le z \le 500\,000 $ ), oznaczająca liczbę pytań Małgosi. W czwartym wierszu znajduje się $ \displaystyle z $ liczb całkowitych $ \displaystyle k_i $ ( $ \displaystyle 1 \le k_i \le 10^9 $ ). Liczba $ \displaystyle k_1 $ oznacza, że pierwsze pytanie Małgosi nastąpiło po wykonaniu $ \displaystyle k_1 $ ruchów Jasia. Liczba $ \displaystyle k_2 $ oznacza, że drugie pytanie nastąpiło po wykonaniu kolejnych $ \displaystyle k_2 $ ruchów Jasia itd. Możesz założyć, że $ \displaystyle k_1+\ldots+k_z $ nie przekracza liczby ruchów wykonanych przez Jasia w całej grze.

Przykład
Dla danych wejściowych:
3
9 8 2
3
1 2 3
poprawnym wynikiem jest:
4
3
2

Oto jak wyglądają wysokości stosów po kolejnych ruchach Jasia:

9, 8, 2
8, 5, 4, 2 (pierwsze pytanie Małgosi)
5, 4, 4, 4, 2
4, 4, 4, 3, 2, 2 (drugie pytanie Małgosi)
4, 4, 3, 2, 2, 2, 2
4, 3, 2, 2, 2, 2, 2, 2
3, 2, 2, 2, 2, 2, 2, 2, 2 (trzecie pytanie Małgosi).

Zadanie GRA (Kolorowe grafy), r. akad. 2012/2013, I termin, zadanie prostsze

Dostępna pamięć: 256MB.

W czerwono-zielonym grafie jeden wierzchołek jest wyróżniony, a każda krawędź jest albo czerwona, albo zielona. Poza tym jest to zwykły graf nieskierowany.

Niech $ \displaystyle G $ będzie grafem czerwono-zielonym. Ścieżką w $ \displaystyle G $ nazywamy dowolny ciąg wierzchołków $ \displaystyle v_1,v_2,\ldots,v_k $, taki że każda para wierzchołków $ \displaystyle v_i, v_{i+1} $ (dla $ \displaystyle 1 \le i < k $ ) jest połączona krawędzią, a krawędzie te są na przemian czerwone i zielone (kolor pierwszej krawędzi ścieżki nie ma znaczenia). Naszym zadaniem jest znaleźć długość najkrótszej ścieżki z wierzchołka wyróżnionego do każdego innego wierzchołka grafu lub stwierdzić, że takiej ścieżki nie ma.

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ \displaystyle n $ i $ \displaystyle m $ ( $ \displaystyle 2 \le n \le 500\,000 $, $ \displaystyle 1 \le m \le 500\,000 $ ), oznaczające liczbę wierzchołków i liczbę krawędzi grafu. Zakładamy, że wierzchołek wyróżniony ma numer 1. Każdy z kolejnych $ \displaystyle m $ wierszy zawiera trzy liczby całkowite $ \displaystyle a_i $, $ \displaystyle b_i $ i $ \displaystyle k_i $ ( $ \displaystyle 1 \le a_i,b_i \le n $, $ \displaystyle a_i \ne b_i $, $ \displaystyle k_i \in \{0,1\} $ ), oznaczające końce krawędzi oraz jej kolor (0 - czerwona, 1 - zielona). Każda para wierzchołków jest połączona co najwyżej jedną krawędzią.

Wyjście
Twój program powinien wypisać $ \displaystyle n-1 $ wierszy. $ \displaystyle i $-ty z tych wierszy powinien zawierać jedną liczbę całkowitą: -1, jeśli
nie istnieje ścieżka z wierzchołka 1 do wierzchołka $ \displaystyle i+1 $, lub długość najkrótszej takiej ścieżki w przeciwnym przypadku.

Przykład
Dla danych wejściowych:
6 5
1 2 1
2 3 0
1 4 0
4 5 0
5 3 0
poprawnym wynikiem jest:
1
2
1
-1
-1
natomiast dla danych:
4 4
1 2 0
2 3 0
1 4 0
4 2 1
poprawnym wynikiem jest:
1
3
1

Zadanie MRO (Mrówki), r. akad. 2012/2013, I termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Na prostej stoi $ \displaystyle n $ mrówek. Każda mrówka znajduje się w jakimś punkcie całkowitym o współrzędnej z przedziału $ \displaystyle [1,n] $. Mrówki są bardzo małe, więc w jednym punkcie prostej może stać wiele mrówek.

Treser wydaje mrówkom polecenia następującej postaci: wszystkim mrówkom stojącym w punktach z przedziału $ \displaystyle [l,r] $ nakazuje przemieścić się do punktu $ \displaystyle d $ ( $ \displaystyle d \in [l,r] $ ). Treser chciałby wiedzieć, dla każdego polecenia, ile mrówek wskutek niego musiało zmienić swoje położenie.

Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ \displaystyle n $ i $ \displaystyle q $ ( $ \displaystyle 1 \le n,q \le 500\,000 $ ), oznaczające liczbę mrówek i liczbę wydanych poleceń. Drugi wiersz zawiera niemalejący ciąg $ \displaystyle n $ liczb całkowitych z zakresu od $ \displaystyle 1 $ do $ \displaystyle n $ - są to początkowe pozycje mrówek. Dalej następuje $ \displaystyle q $ wierszy z opisami poleceń. Każdy z tych wierszy zawiera trzy liczby całkowite $ \displaystyle l $, $ \displaystyle r $ i $ \displaystyle d $ ( $ \displaystyle 1 \le l \le d \le r \le n $ ).

Wyjście
Twój program powinien wypisać $ \displaystyle q $ wierszy z odpowiedziami na poszczególne zapytania. Każdy z tych wierszy powinien zawierać jedną liczbę całkowitą: liczbę mrówek, które zmieniły swoje położenie podczas wykonywania danego polecenia.

Przykład
Dla danych wejściowych:
5 3
1 2 2 4 5
3 5 3
1 1 1
1 2 2
poprawnym wynikiem jest:
2
0
1
natomiast dla danych:
6 2
1 2 3 4 5 6
1 4 2
3 6 5
poprawnym wynikiem jest:
3
1

Zadanie ZOL (Żołnierze), r. akad. 2012/2013, II termin, zadanie prostsze

Dostępna pamięć: 256MB.

W szeregu stoi $ \displaystyle n $ żołnierzy, ponumerowanych kolejno od 1 do $ \displaystyle n $ (od lewej do prawej). Generał będzie wydawał żołnierzom polecenie o nazwie obiad. Jeśli generał wyda to polecenie żołnierzowi o numerze $ \displaystyle i $, żołnierz ten będzie musiał najpierw wypowiedzieć na głos numer żołnierza, który stoi z jego lewej strony, potem wypowiedzieć numer żołnierza, który stoi z jego prawej strony, a następnie
udać się czym prędzej na obiad. Kiedy żołnierz znika z szeregu, pozostali żołnierze nieco się przesuwają, tak żeby w szeregu nie pozostała żadna dziura.

Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ \displaystyle n $ ( $ \displaystyle 1 \le n \le 500\,000 $ ), oznaczającą liczbę żołnierzy. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera po jednej liczbie całkowitej z zakresu od 1 do $ \displaystyle n $. Liczba zapisana w $ \displaystyle i $-tym wierszu oznacza numer żołnierza, któremu w $ \displaystyle i $-tym poleceniu generał rozkazał iść na obiad. Liczby w wierszach $ \displaystyle 2,3,\ldots,n+1 $ nie powtarzają się.

Wyjście
Twój program powinien wypisać $ \displaystyle n $ wierszy. $ \displaystyle i $-ty z tych wierszy powinien zawierać dwie liczby całkowite: numery lewego
i prawego sąsiada żołnierza, który w $ \displaystyle i $-tym poleceniu udaje się na obiad. Jeśli ów żołnierz w rozważanym momencie nie ma lewego lub prawego sąsiada, jako numer odpowiedniego sąsiada należy wypisać -1.

Przykład

Dla danych wejściowych:
5
4
2
1
5
3
poprawnym wynikiem jest:
3 5
1 3
-1 3
3 -1
-1 -1

Zadanie SKO (Skojarzenie), r. akad. 2012/2013, II termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Dane jest drzewo, czyli graf spójny o $ \displaystyle n $ wierzchołkach i $ \displaystyle n-1 $ krawędziach. Każda krawędź ma przypisaną wagę - pewną dodatnią liczbę całkowitą. Chcemy w tym drzewie znaleźć skojarzenie (czyli zbiór krawędzi, z których żadne dwie nie zawierają wspólnego wierzchołka) o maksymalnej sumie wag krawędzi.

Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 300\,000 $ ), oznaczającą liczbę wierzchołków drzewa. Wierzchołki są ponumerowane liczbami od 1 do $ \displaystyle n $. Każdy z kolejnych $ \displaystyle n-1 $ wierszy zawiera trzy liczby całkowite $ \displaystyle a_i $, $ \displaystyle b_i $, $ \displaystyle w_i $ ( $ \displaystyle 1 \le a_i, b_i \le n $, $ \displaystyle a_i \ne b_i $, $ \displaystyle 1 \le w_i \le 1000 $ ) oznaczające krawędź o wadze $ \displaystyle w_i $ łączącą wierzchołki $ \displaystyle a_i $ i $ \displaystyle b_i $. Podany na wejściu graf będzie drzewem, czyli nie będzie zawierał cykli.

Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą: wagę szukanego najcięższego skojarzenia w drzewie.

Przykład

Dla danych wejściowych:
7
1 3 2
3 2 1
2 4 5
2 5 7
3 6 10
6 7 1
poprawnym wynikiem jest:
17

Zadanie SZY (Szyna), r. akad. 2011/2012, I termin, zadanie prostsze

Dostępna pamięć: 256MB.

Profesor Makary zbudował układ elektroniczny złożony z $ \displaystyle n $ procesorów. Każdy z procesorów w danej chwili wykonuje pewien typ operacji; typy te oznaczamy dla uproszczenia liczbami całkowitymi (dodatnimi). Procesory mogą komunikować się wzdłuż jednej szyny danych.

Profesor chciałby oprogramować swój układ. W każdej jednostce czasu każdy procesor próbuje wysłać dane wzdłuż szyny do pewnego innego procesora, który w danej chwili wykonuje taki sam typ operacji. W danej jednostce czasu każdy procesor może albo wysyłać dane do jednego innego procesora, albo odbierać dane od jednego innego procesora.

Oprogramowanie profesora musi zabezpieczyć układ przed sytuacją, w której więcej niż jedna para procesorów próbowałaby przesyłać dane wzdłuż tego samego fragmentu szyny. Poza tym, oprogramowanie powinno dbać o to, aby w każdej jednostce czasu komunikowała się możliwie największa liczba par procesorów. Czy pomógłbyś profesorowi w napisaniu takiego oprogramowania?

Wejście

W pierwszym wierszu wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 500\,000 $ ), oznaczająca liczbę procesorów. W drugim wierszu znajduje się $ \displaystyle n $ liczb całkowitych $ \displaystyle p_i $ ( $ \displaystyle 1 \le p_i \le 10^9 $ ), pooddzielanych pojedynczymi odstępami i oznaczających typy operacji wykonywanych przez procesory w pewnej jednostce czasu. Procesory są podane w takiej kolejności, w jakiej są rozmieszczone wzdłuż szyny danych.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą nieujemną, oznaczającą maksymalną liczbę par procesorów, które mogą komunikować się w rozważanej jednostce czasu, z uwzględnieniem opisanych wyżej zasad komunikacji.

Przykład

Dla danych wejściowych:
11
6 4 1 4 1 4 4 6 3 7 3
poprawnym wynikiem jest:
3

Zadanie OSU (Osuszanie), r. akad. 2011/2012, I termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Bajtocja jest położona na stosunkowo bagnistym terenie. Krainę tę można przedstawić jako prostokąt złożony z $ \displaystyle n \cdot m $ pól, z których niektóre są przejezdne, a inne - zajęte przez bagna. Ostatnimi czasy kupcy mieszkający w miastach A i B postanowili wytyczyć szlak handlowy łączący te miasta, czyli sekwencję pól jednostkowych prowadzącą z miasta A do miasta B, w której każde dwa kolejne pola powinny sąsiadować bokiem.

Nie jest jasne, czy da się wytyczyć taką trasę bez osuszania bagien. Twoim zadaniem jest wyznaczyć minimalną liczbę pól z bagnami, jakie trzeba osuszyć, tak aby dało się poprowadzić co najmniej jeden szlak handlowy łączący miasta A oraz B.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 2 \le n, m \le 1\,000 $ ), oddzielone pojedynczym odstępem. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera $ \displaystyle m $ znaków, przy czym:

znak `.' oznacza wolne pole (przejezdne)
znak '#' oznacza bagno
znak `A' oznacza lokalizację miasta A
znak `B' oznacza lokalizację miasta B.

Możesz założyć, że w wejściu znajduje się dokładnie jedna litera `A' i dokładnie jedna litera `B'.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą nieujemną, oznaczającą liczbę pól, które trzeba osuszyć, tak aby istniała ścieżka łącząca miasta A i B.

Przykład

Dla danych wejściowych:
5 6
..#.A.
#####.
.#.#.#
.#.B#.
.#.#..
poprawnym wynikiem jest:
2

Zadanie TAB (Tablica), r. akad. 2011/2012, II termin, zadanie prostsze

Dostępna pamięć: 256MB.

Mamy daną tablicę rozmiaru $ \displaystyle n \times n $ wypełnioną liczbami całkowitymi. Chcielibyśmy stwierdzić, czy w jakimś wierszu tej tablicy są powtarzające się elementy, podobnie czy w jakiejś kolumnie są co najmniej dwa takie same elementy. Trzeba jednak dodać, że elementy tablicy mogą zmieniać się w czasie...

Wejście

W pierwszym wierszu wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 1\,000 $ ), oznaczająca rozmiar tablicy. W $ \displaystyle i $-tym z kolejnych $ \displaystyle n $ wierszy znajduje się $ \displaystyle n $ liczb całkowitych pooddzielanych pojedynczymi odstępami ( $ \displaystyle t_{i1},\ldots,t_{in} $ ), oznaczających poszczególne elementy $ \displaystyle i $-tego wiersza tablicy. W następnym wierszu znajduje się jedna liczba całkowita $ \displaystyle m $ ( $ \displaystyle 1 \le m \le 500\,000 $ ), oznaczająca liczbę zmian elementów tablicy. Każdy z kolejnych $ \displaystyle m $ wierszy zawiera trzy liczby całkowite $ \displaystyle a_i $, $ \displaystyle b_i $ oraz $ \displaystyle k_i $ ( $ \displaystyle 1 \le a_i,b_i \le n $ ), pooddzielane pojedynczymi odstępami i oznaczające przypisania wartości elementów tablicy: element znajdujący się na przecięciu wiersza $ \displaystyle a_i $ i kolumny $ \displaystyle b_i $ zmienia swoją wartość na $ \displaystyle k_i $ ( $ \displaystyle t_{a_ib_i}:=k_i $ ). Wszystkie elementy, jakie kiedykolwiek znajdą się w tablicy, są liczbami całkowitymi z przedziału od $ \displaystyle 0 $ do $ \displaystyle 1\,000\,000 $.

Wyjście

Twój program powinien wypisać na standardowe wyjście $ \displaystyle m+1 $ wierszy. W $ \displaystyle i $-tym wierszu (dla $ \displaystyle 1 \le i \le m $ ) powinny znaleźć się dwa słowa oddzielone pojedynczym odstępem. Jeśli przed wykonaniem $ \displaystyle i $-tej operacji jakiś wiersz tablicy zawiera co najmniej dwie takie same liczby, pierwszym z tych słów powinno być TAK, w przeciwnym razie NIE. Podobnie, jako drugie słowo należy wypisać TAK, jeśli przed wykonaniem $ \displaystyle i $-tej operacji jakaś kolumna tablicy zawiera powtarzające się elementy, a w przeciwnym razie NIE. W wierszu o numerze $ \displaystyle m+1 $ należy wypisać słowa opisujące sytuację w tablicy po wykonaniu ostatniej operacji.

Przykład

Dla danych wejściowych:
3
1 2 3
4 5 6
7 8 9
3
1 2 3
2 2 3
1 2 8
poprawnym wynikiem jest:
NIE NIE
TAK NIE
TAK TAK
NIE TAK
natomiast dla danych:
3
1 2 3
1 2 9
5 6 7
14
2 1 3
2 2 3
2 3 3
2 2 7
2 3 7
2 3 8
3 2 7
2 3 7
1 3 7
3 3 6
2 2 6
2 3 6
2 2 10
3 3 10
poprawnym wynikiem jest:
NIE TAK
NIE TAK
TAK NIE
TAK TAK
TAK TAK
TAK TAK
NIE NIE
TAK TAK
TAK TAK
TAK TAK
TAK TAK
NIE TAK
TAK TAK
NIE TAK
NIE NIE

Zadanie KON (Koncentracja), r. akad. 2011/2012, II termin, zadanie trudnejsze

Dostępna pamięć: 256MB.

Powiemy, że zbiór punktów $ \displaystyle Z $ na płaszczyźnie jest $ \displaystyle d $-skoncentrowany, jeśli każde dwa punkty tego zbioru są oddalone od siebie o nie więcej niż $ \displaystyle d $. W szczególności, każdy jednoelementowy zbiór punktów jest $ \displaystyle d $-skoncentrowany dla dowolnego $ \displaystyle d \ge 0 $.

Mamy dany zbiór punktów $ \displaystyle A $ oraz parametr $ \displaystyle d $. Chcemy stwierdzić, czy punkty ze zbioru $ \displaystyle A $ można podzielić na dwa niepuste zbiory $ \displaystyle d $-skoncentrowane.

Wejście

W pierwszym wierszu wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle d $ ( $ \displaystyle 2 \le n \le 2\,000 $, $ \displaystyle 0 \le d \le 2\,000\,000 $ ) oddzielone pojedynczym odstępem i oznaczające liczbę punktów w zbiorze $ \displaystyle A $ oraz parametr koncentracji. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera dwie liczby całkowite $ \displaystyle x_i $, $ \displaystyle y_i $ ( $ \displaystyle 0 \le x_y,y_i \le 1\,000\,000 $ ), oddzielone pojedynczym odstępem, oznaczające współrzędne $ \displaystyle i $-tego punktu w zbiorze $ \displaystyle A $. Punkty podane na wejściu nie będą się powtarzać.

Wyjście

W pierwszym wierszu wyjścia Twój program powinien wypisać jedno słowo TAK lub NIE, oznaczające, czy zbiór $ \displaystyle A $ można podzielić na dwa rozłączne i niepuste zbiory $ \displaystyle d $-skoncentrowane $ \displaystyle A_1 $ i $ \displaystyle A_2 $.

Jeśli odpowiedzią jest TAK, dwa kolejne wiersze powinny zawierać opis przykładowych zbiorów $ \displaystyle A_1 $ i $ \displaystyle A_2 $, po jednym opisie w wierszu. Opis zbioru $ \displaystyle A_i $ powinien zaczynać się od jednej liczby całkowitej dodatniej $ \displaystyle n_i $, oznaczającej liczbę punktów zawartych w tym zbiorze, a następnie $ \displaystyle n_i $ liczb całkowitych pooddzielanych pojedynczymi odstępami, oznaczających numery punktów przydzielonych do zbioru $ \displaystyle A_i $. Punkty numerujemy od 1 do $ \displaystyle n $ w kolejności występowania w wejściu.

Każda liczba całkowita z zakresu od $ \displaystyle 1 $ do $ \displaystyle n $ powinna pojawić się na liście elementów dokładnie jednego ze zbiorów $ \displaystyle A_1 $, $ \displaystyle A_2 $. Elementy zbiorów $ \displaystyle A_1 $ i $ \displaystyle A_2 $ można wypisać w dowolnej kolejności. Jeśli istnieje więcej niż jedno rozwiązanie, Twój program może wypisać dowolne jedno z nich.

Przykład

Dla danych wejściowych:
7 3
5 3
1 1
4 2
1 3
5 2
2 3
5 1
jednym z poprawnych wyników jest:
TAK
3 6 4 2
4 1 3 5 7

Wyjaśnienie do przykładu: Podział opisany na wyjściu to $ \displaystyle A_1=\{(2,3),(1,3),(1,1)\} $, $ \displaystyle A_2=\{(5,3),(4,2),(5,2),(5,1)\} $.

Zadanie ODC (Odcinki), r. akad. 2010/2011, I termin, zadanie prostsze

Dostępna pamięć: 256MB.

Na płaszczyźnie narysowano $ \displaystyle n $ pionowych odcinków. Można by spytać, ile par odcinków się przecina, tzn. przecięcie ilu nieuporządkowanych par odcinków jest niepuste. No to spytajmy.

Nasze odcinki mają dodatkowo tę sympatyczną własność, że żadne dwa nie mają żadnego wspólnego końca.

Wejście

W pierwszym wierszu standardowego wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 300\,000 $ ), oznaczająca liczbę odcinków. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera trzy liczby całkowite $ \displaystyle x $, $ \displaystyle y_1 $ i $ \displaystyle y_2 $ ( $ \displaystyle 0 \le x, y_1, y_2 \le 10^9 $, $ \displaystyle y_1 < y_2 $ ), pooddzielane pojedynczymi odstępami i oznaczające domknięty odcinek łączący punkty $ \displaystyle (x,y_1) $ i $ \displaystyle (x,y_2) $.

Wyjście

Na standardowe wyjście należy wypisać jeden wiersz zawierający jedną liczbę całkowitą: liczbę par przecinających się odcinków.

Przykład

Dla danych wejściowych:
5
3 1 5
4 2 6
3 2 7
3 3 4
4 7 8
poprawnym wynikiem jest:
3

Wyjaśnienie do przykładu: Przecinają się każde dwa odcinki o odciętej 3 i żadne inne.

Zadanie JAD (Jazda w kółko 2), r. akad. 2010/2011, I termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

W pewnym mieście jest $ \displaystyle n $ skrzyżowań połączonych pewną liczbą jednokierunkowych dróg (przy czym początkowe i końcowe skrzyżowanie każdej drogi są różne). Żadne drogi nie przecinają się poza skrzyżowaniami (w razie potrzeby drogi mogą prowadzić tunelami bądź estakadami). Należy stwierdzić, czy da się w tym mieście wyruszyć z jakiegoś skrzyżowania i przejechawszy pewną niezerową liczbą dróg zgodnie z ich orientacją, wrócić do tego samego skrzyżowania.

Należy zaznaczyć, że opis dróg sporządzono w postaci skondensowanej, opisanej dokładnie w następnym akapicie.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 1\le n\le 300\,000 $, $ \displaystyle 0\le m\le 300\,000 $ ), oddzielone pojedynczym odstępem. Kolejne $ \displaystyle m $ wierszy zawiera opisy grup dróg, po jednym w wierszu. Każdy opis składa się z trzech liczb całkowitych $ \displaystyle a_i $, $ \displaystyle b_i $ oraz $ \displaystyle c_i $ ( $ \displaystyle 1\le a_i \le n $ , $ \displaystyle 1 \le b_i \le c_i \le n $ ), oznaczających, że ze skrzyżowania numer $ \displaystyle a_i $ do każdego ze skrzyżowań $ \displaystyle b_i,\ldots,c_i $ prowadzi jednokierunkowa droga.

Możesz założyć, że nie istnieją dwie drogi mające zarówno to samo skrzyżowanie początkowe jak i końcowe.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedno słowo TAK, jeżeli w mieście istnieje opisana powyżej trasa, lub NIE w przeciwnym przypadku.

Przykład

Dla danych wejściowych:
4 5
1 2 3
1 4 4
2 3 4
3 4 4
4 1 1
poprawnym wynikiem jest:
TAK

Przykładem szukanej trasy jest $ \displaystyle 1\rightarrow 2\rightarrow 3\rightarrow 4 \rightarrow 1 $.

natomiast dla danych:
4 4
1 2 3
1 4 4
2 3 4
3 4 4
poprawnym wynikiem jest:
NIE

Zadanie ROD (Różnica 2), r. akad. 2010/2011, II termin, zadanie prostsze

Dostępna pamięć: 64MB.

Będziemy wykonywać operacje na zbiorze liczb całkowitych $ \displaystyle A $. Na początku $ \displaystyle A = \emptyset $. Każda operacja polega na dodaniu do zbioru elementu, którego w tym zbiorze aktualnie nie ma, bądź usunięciu elementu, który znajduje się aktualnie w zbiorze. Po każdej operacji chcielibyśmy wiedzieć, czy w zbiorze są jakieś dwie liczby różniące się dokładnie o $ \displaystyle d $.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle d $ ( $ \displaystyle 1 \le n \le 300\,000 $, $ \displaystyle 1 \le d \le 10^9 $ ), oddzielone pojedynczym odstępem. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera dwie liczby całkowite $ \displaystyle c_i,a_i $ ( $ \displaystyle 0 \le a_i \le 10^9 $, $ \displaystyle c_i \in \{-1,1\} $ ) oddzielone pojedynczym odstępem i opisujące pojedynczą operację na zbiorze. Jeżeli $ \displaystyle c_i=1 $, to jest to operacja dodania elementu $ \displaystyle a_i $, a w przeciwnym przypadku usuwamy ten element ze zbioru.

Wyjście

Twój program powinien wypisać na standardowe wyjście dokładnie $ \displaystyle n $ wierszy, z których $ \displaystyle i $-ty (dla $ \displaystyle i=1,2,\ldots,n $ ) powinien zawierać jedno słowo TAK lub NIE, w zależności od tego, czy po wykonaniu pierwszych $ \displaystyle i $ operacji zbiór $ \displaystyle A $ zawiera parę liczb różniących się dokładnie o $ \displaystyle d $ czy nie.

Przykład

Dla danych wejściowych:
7 4
1 2
1 10
1 6
-1 2
-1 6
1 9
1 14
poprawnym wynikiem jest:
NIE
NIE
TAK
TAK
NIE
NIE
TAK

Zadanie WZO (Wzorzec), r. akad. 2010/2011, II termin, zadanie trudniejsze

Dostępna pamięć: 64MB.

Mamy dany graf skierowany $ \displaystyle G $, którego krawędzie są etykietowane niepustymi słowami złożonymi z małych liter alfabetu angielskiego. Dla danego słowa $ \displaystyle s $ chcemy sprawdzić, czy istnieje w grafie taki spacer (ścieżka z możliwymi powtórzeniami), że po złączeniu słów z kolejno przechodzonych krawędzi otrzymamy słowo $ \displaystyle s $. Podkreślmy, że przy złączaniu słów leżących na krawędziach bierzemy zawsze całe słowa.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 1 \le n \le 100 $, $ \displaystyle 0 \le m \le 1\,000 $ ), oddzielone pojedynczym odstępem, oznaczające odpowiednio liczbę wierzchołków i krawędzi grafu $ \displaystyle G $. Każdy z kolejnych $ \displaystyle m $ wierszy zawiera opis pojedynczej krawędzi. Opis taki składa się z dwóch liczby całkowitych $ \displaystyle a_i,b_i $ ( $ \displaystyle 1 \le a_i, b_i \le n $ , $ \displaystyle a_i \neq b_i $ ) oraz niepustego słowa $ \displaystyle s_i $ złożonego z małych liter alfabetu angielskiego ( $ \displaystyle 1 \le |s_i| \le 1\,000 $ ). Elementy występujące w opisie krawędzi są oddzielone pojedycznymi odstępami. Opisywana krawędź prowadzi od wierzchołka $ \displaystyle a_i $ do wierzchołka $ \displaystyle b_i $ i jest etykietowana słowem $ \displaystyle s_i $. Pomiędzy parą wierzchołków może być dowolnie wiele krawędzi.

Ostatni wiersz standardowego wejścia zawiera słowo $ \displaystyle s $, składające się z małych liter alfabetu angielskiego ( $ \displaystyle 1 \le |s| \le 100\,000 $ ).

Wyjście

Twój program powinien wypisać na standardowe wyjście dokładnie jeden wiersz, zawierający jedno słowo TAK lub NIE, w zależności od tego, czy w danym grafie istnieje poszukiwany spacer.

Przykład

Dla danych wejściowych:
3 4
1 2 abc
2 1 a
1 2 aaa
2 3 xyz
abcaaaaxyz
poprawnym wynikiem jest:
TAK

natomiast dla danych:
2 3
1 2 aa
2 1 aa
1 2 aa
aaaaa
poprawnym wynikiem jest:
NIE

Zadanie ROZ (Różnica), r. akad. 2009/2010, I termin, zadanie prostsze

Dostępna pamięć: 64MB.

Dany jest ciąg liczb całkowitych $ \displaystyle a_1,a_2,\ldots,a_n $. Napisz program, który sprawdzi, czy w tym ciągu znajdują się dwie liczby różniące się dokładnie o $ \displaystyle d $.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle d $ ( $ 1 \le n \le 300\,000 $, $ \displaystyle -10^9 \le d \le 10^9 $ ), oddzielone pojedynczym odstępem. Drugi wiersz zawiera $ \displaystyle n $ liczb całkowitych $ \displaystyle a_1,a_2,\ldots,a_n $ ( $ \displaystyle -10^9 \le a_i \le 10^9 $ ), pooddzielanych pojedynczymi odstępami.

Wyjście

Jeśli w ciągu $ \displaystyle a $ nie ma żadnej pary elementów różniących się o $ \displaystyle d $, Twój program powinien wypisać na standardowe wyjście jedno słowo NIE. W przeciwnym przypadku Twój program powinien wypisać dwie liczby całkowite $ \displaystyle u,v $ oddzielone pojedynczym odstępem, reprezentujące dwa wyrazy ciągu $ \displaystyle a $ różniące się o $ \displaystyle d $ ( $ \displaystyle u=a_i $, $ \displaystyle v=a_j $, $ \displaystyle i \ne j $, $ \displaystyle u-v=d $ ). Jeżeli istnieje więcej niż jedna poprawna odpowiedź, Twój program może wypisać dowolną z nich.

Przykład

Dla danych wejściowych:
5 3
5 3 4 -2 2
poprawnym wynikiem jest:
5 2

natomiast dla danych:
5 -3
5 3 4 -2 2
poprawnym wynikiem jest:
2 5

natomiast dla danych:
4 1
2 2 2 2
poprawnym wynikiem jest:
NIE

Zadanie DEG (Degeneraty), r. akad. 2009/2010, I termin, zadanie trudniejsze

Dostępna pamięć: 64MB.

Graf $ \displaystyle H = (V_1, E_1) $ jest podgrafem grafu $ \displaystyle G = (V, E) $, jeśli $ \displaystyle V_1 \subseteq V $, $ \displaystyle E_1 \subseteq E $ i $ \displaystyle E_1 \subseteq V_1 \times V_1 $. Mówimy, że graf $ \displaystyle G $ jest $ \displaystyle d $-degeneratem (dla pewnej liczby całkowitej dodatniej $ \displaystyle d $ ), jeśli w każdym podgrafie grafu $ \displaystyle G $ istnieje wierzchołek o stopniu co najwyżej $ \displaystyle d $. Dla danego grafu $ \displaystyle G $ wyznacz najmniejszą liczbę całkowitą dodatnią $ \displaystyle d $ taką, że $ \displaystyle G $ jest $ \displaystyle d $-degeneratem.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 1\le n, m\le 500\,000 $ ), oddzielone pojedynczym odstępem, oznaczające liczby wierzchołków i krawędzi grafu $ \displaystyle G $. Wierzchołki są ponumerowane liczbami naturalnymi $ \displaystyle 1, 2, \ldots, n $. Kolejne $ \displaystyle m $ wierszy opisuje krawędzie: każdy z nich zawiera dwie liczby naturalne $ \displaystyle 1 \leq a_i, b_i \leq n $, $ \displaystyle a_i \neq b_i $ oznaczające krawędź między wierzchołkiami $ \displaystyle a_i $ i $ \displaystyle b_i $. Żadna para $ \displaystyle \{a_i, b_i\} $ nie pojawia się na wejściu więcej niż raz.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą - najmniejszą liczbę całkowitą dodatnią $ \displaystyle d $ taką, że $ \displaystyle G $ jest $ \displaystyle d $-degeneratem.

Przykład

Dla danych wejściowych:
12 16
1 2
2 3
3 1
3 4
4 5
5 8
5 9
5 10
6 8
6 9
6 10
7 8
7 9
7 10
10 11
11 12
poprawnym wynikiem jest:
3

Wyjaśnienie do przykładu: Wierzchołki $ \displaystyle \{5, 6, 7, 8, 9, 10\} $ oraz wszystkie krawędzie między nimi tworzą podgraf, w którym każdy wierzchołek ma stopień co najmniej 3, patrz także poniższy rysunek.

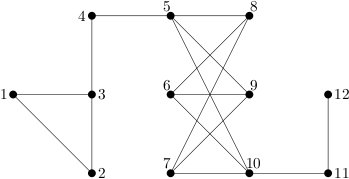Ilustracja przykładu w zadaniu DEG

Zadanie PRZ (Przedziały), r. akad. 2009/2010, II termin, zadanie prostsze

Dostępna pamięć: 64MB.

Dane jest $ \displaystyle n $ przedziałów domkniętych $ \displaystyle [a_i,b_i] $. Jaka jest minimalna wartość bezwzględna różnicy dwóch
liczb należących do dwóch różnych przedziałów? Formalnie, chcemy obliczyć

$ \displaystyle \min\{ |x-y|\ :\ x \in [a_i,b_i],\ y \in [a_j, b_j],\ 1 \le i < j \le n\} $.

Wejście

W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita $ \displaystyle n $ ( $ \displaystyle 2 \le n \le 500\,000 $ ) - liczba przedziałów. Każdy z kolejnych $ \displaystyle n $ wierszy zawiera dwie liczby całkowite $ \displaystyle a_i $ oraz $ \displaystyle b_i $ ( $ \displaystyle 0 \le a_i \le b_i \le 10^9 $ ), oddzielone pojedynczym odstępem i reprezentujące końce $ \displaystyle i $-tego przedziału domkniętego $ \displaystyle [a_i,b_i] $. Można założyć, że wszystkie pary $ \displaystyle (a_i,b_i) $ są różne.

Wyjście

Twój program powinien wypisać na standardowe wyjście jeden wiersz zawierający liczbę całkowitą zdefiniowaną w treści zadania.

Przykład

Dla danych wejściowych:
2
1 2
3 4
poprawnym wynikiem jest:
1

Zadanie CYK (Cykl), r. akad. 2009/2010, II termin, zadanie trudniejsze

Dostępna pamięć: 64MB.

Mamy dany graf nieskierowany $ \displaystyle G=(V,E) $ oraz zbiór dodatkowych krawędzi $ \displaystyle E_1 $, których możemy użyć bądź nie ( $ \displaystyle E \cap E_1 = \emptyset $ ). Ile maksymalnie krawędzi ze zbioru $ \displaystyle E_1 $ możemy dołożyć do grafu, tak aby graf zawierał dokładnie jeden cykl prosty?

Przypomnijmy, że cykl prosty to taki cykl, w którym wierzchołki nie powtarzają się.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się trzy liczby całkowite $ \displaystyle n $, $ \displaystyle m $ oraz $ \displaystyle k $ ( $ \displaystyle 2 \le n \le 500\,000 $, $ \displaystyle 0 \le m,k \le 1\,000\,000 $ ), pooddzielane pojedynczymi odstępami i oznaczające odpowiednio liczbę wierzchołków ( $ \displaystyle |V| $ ) i liczbę krawędzi grafu ( $ \displaystyle |E| $ ) oraz liczbę dodatkowych krawędzi, których możemy użyć ( $ \displaystyle |E_1| $ ). Każdy z kolejnych $ \displaystyle m $ wierszy zawiera dwie liczby całkowite $ \displaystyle a_i $ oraz $ \displaystyle b_i $ ( $ \displaystyle 1 \le a_i < b_i \le n $ ), oddzielone pojedynczym odstępem i oznaczające numery wierzchołków będących końcami $ \displaystyle i $-tej krawędzi ze zbioru $ \displaystyle E $. Dalej następuje $ \displaystyle k $ wierszy, z których każdy zawiera dwie liczby całkowite $ \displaystyle c_i $ oraz $ \displaystyle d_i $ ( $ \displaystyle 1 \le c_i < d_i \le n $ ), oddzielone pojedynczym odstępem i oznaczające numery wierzchołków będących końcami $ \displaystyle i $-tej krawędzi dodatkowej ze zbioru $ \displaystyle E_1 $. Można założyć, że wszystkie pary $ \displaystyle (a_i,b_i) $ oraz $ \displaystyle (c_i,d_i) $ są różne.

Wyjście

Twój program powinien wypisać na standardowe wyjście jeden wiersz zawierający jedną liczbę całkowitą: maksymalną liczbę krawędzi ze zbioru $ \displaystyle E_1 $, po których dodaniu do początkowego grafu $ \displaystyle (V,E) $ graf zawiera dokładnie jeden cykl prosty, lub $ \displaystyle -1 $, jeżeli nie da się tak dobrać krawędzi ze zbioru $ \displaystyle E_1 $, żeby wynikowy graf zawierał dokładnie jeden cykl prosty.

Przykład

Dla danych wejściowych:
9 6 3
1 2
2 3
2 4
5 6
5 7
8 9
1 5
4 6
3 7
poprawnym wynikiem jest:
2

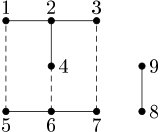Ilustracja pierwszego przykładu w zadaniu CYK

natomiast dla danych:
8 8 2
1 2
2 3
3 4
1 4
5 6
6 7
7 8
5 8
1 3
2 4
poprawnym wynikiem jest:
-1

Ilustracja drugiego przykładu w zadaniu CYK

Wyjaśnienie do przykładu: Kółka na powyższych rysunkach przedstawiają wierzchołki, odcinki - krawędzie grafu, a odcinki przerywane - dodatkowe krawędzie. W pierwszym przykładzie po dodaniu dowolnych dwóch krawędzi graf zawiera dokładnie jeden cykl prosty, natomiast w drugim stworzenie grafu z dokładnie jednym cyklem prostym nie jest możliwe.

Zadanie JED (Jedynki), r. akad. 2008/2009, I termin, zadanie prostsze

Dostępna pamięć: 64MB.

Mamy dany ciąg $ \displaystyle n $ liczb naturalnych $ \displaystyle a=a_1, a_2, \ldots, a_n $. Twoim zadaniem jest wyznaczenie liczby jedynek w zapisie binarnym każdej z sum $ \displaystyle \sum_{i=1}^{k}2^{a_i} $ dla $ \displaystyle k=1,2,\ldots,n $.

Wejście

W pierwszym wierszu znajduje się liczba całkowita $ \displaystyle n $ ( $ \displaystyle 1 \leq n \leq 500\,000 $ ) - liczba elementów ciągu. W drugim wierszu znajduje się $ \displaystyle n $ liczb całkowitych $ \displaystyle a_i $ ( $ \displaystyle 0 \le a_i \le 500\,000 $ ) pooddzielanych pojedynczymi odstępami.

Wyjście

Twój program powinien wypisać $ \displaystyle n $ liczb całkowitych - $ \displaystyle k $-ty wiersz powinien zawierać liczbę jedynek w rozwinięciu binarnym odpowiedniej sumy $ \displaystyle k $ potęg dwójki.

Przykład

Dla danych wejściowych:
4
0 1 2 1
poprawnym wynikiem jest:
1
2
3
2

Wyjaśnienie do przykładu: szukane sumy to kolejno: 1, 3, 7, 9.

Zadanie POD (Podciągi), r. akad. 2008/2009, I termin, zadanie trudniejsze

Dostępna pamięć: 64MB.

Mamy dane ciąg liczb naturalnych $ \displaystyle a=a_1,a_2,\ldots,a_n $ oraz liczbę naturalną $ \displaystyle k $. Ile spójnych (tj. jednokawałkowych) podciągów ciągu $ \displaystyle a $ składa się z co najwyżej $ \displaystyle k $ różnych elementów?

Podciągi uznajemy za różne, jeżeli ich umiejscowienia w ramach ciągu $ \displaystyle a $ są różne. Dodatkowo, rozważamy jedynie podciągi dodatniej długości.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle k $ ( $ \displaystyle 1\le n, k\le 500\,000 $ ), oddzielone pojedynczym odstępem. Drugi wiersz wejścia zawiera $ \displaystyle n $ liczb całkowitych $ \displaystyle a_i $ ( $ \displaystyle 0\le a_i\le 1\,000\,000\,000 $ ), pooddzielanych pojedynczymi odstępami.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą - liczbę spójnych podciągów ciągu $ \displaystyle a $, złożonych z co najwyżej $ \displaystyle k $ różnych elementów.

Przykład

Dla danych wejściowych:
5 2
4 2 3 2 3
poprawnym wynikiem jest:
12

Wyjaśnienie do przykładu: Szukane podciągi to:

pięć ciągów jednoelementowych, z których dwa, tzn. (2) i (3), liczone są dwukrotnie;
cztery ciągi dwuelementowe: (4, 2), (2, 3), (3, 2) i (2, 3);
dwa ciągi trzyelementowe: (2, 3, 2) i (3, 2, 3);
jeden ciąg czteroelementowy (2, 3, 2, 3).

Zauważ, że ciąg (2, 2, 3) jest podciągiem wyjściowego ciągu i zawiera dokładnie dwa różne elementy, jednakże nie jest on spójny.

Zadanie JAZ (Jazda w kółko), r. akad. 2008/2009, II termin, zadanie prostsze

Dostępna pamięć: 256MB.

W pewnym mieście jest $ \displaystyle n $ skrzyżowań i $ \displaystyle m $ dróg, z których każda jest dwukierunkowa oraz zaczyna się i kończy przy jakimś skrzyżowaniu (przy czym początkowe i końcowe skrzyżowanie każdej drogi są różne). Żadne drogi nie przecinają się poza skrzyżowaniami (w razie potrzeby drogi mogą prowadzić tunelami bądź estakadami). Należy stwierdzić, czy da się w tym mieście wyruszyć z jakiegoś skrzyżowania i przejechawszy pewną niezerową liczbą dróg (żadną drogą nie można przy tym przejechać dwukrotnie), wrócić do tego samego skrzyżowania.

Wejście

W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite $ \displaystyle n $ oraz $ \displaystyle m $ ( $ \displaystyle 1\le n\le 200\,000 $, $ \displaystyle 0\le m\le 500\,000 $ ), oddzielone pojedynczym odstępem. Kolejne $ \displaystyle m $ wierszy zawiera opisy dróg, po jednym w wierszu. Każdy opis składa się z dwóch liczb całkowitych $ \displaystyle a_i $ oraz $ \displaystyle b_i $ ( $ \displaystyle 1\le a_i < b_i\le n $ ), oznaczających numery skrzyżowań połączonych drogą. Każde dwa skrzyżowania są połączone co najwyżej jedną drogą.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedno słowo TAK, jeżeli w mieście istnieje opisana powyżej trasa, lub NIE w przeciwnym przypadku.

Przykład

Dla danych wejściowych:
6 7
1 2
1 3
1 4
2 3
2 4
3 4
5 6
poprawnym wynikiem jest:
TAK

Wyjaśnienie. Przykładem szukanej trasy jest $ \displaystyle 1\rightarrow 2\rightarrow 3\rightarrow 1 $.

Natomiast dla danych:
4 3
1 2
2 3
3 4
poprawnym wynikiem jest:
NIE

Zadanie KRO (Krotności), r. akad. 2008/2009, II termin, zadanie trudniejsze

Dostępna pamięć: 256MB.

Dane jest $ \displaystyle n $ przedziałów $ \displaystyle [a_i,b_i] $ z krotnościami. Krotność $ \displaystyle i $-tego przedziału wynosi $ \displaystyle k_i $. Dla liczby całkowitej $ \displaystyle x $ przez $ \displaystyle \mathrm{kro}(x) $ oznaczmy sumę krotności przedziałów, do których należy $ \displaystyle x $. Twoim zadaniem jest wyznaczenie liczby par nieuporządkowanych $ \displaystyle \{x,y\} $, takich że $ \displaystyle \mathrm{kro}(x) > 0 $, $ \displaystyle \mathrm{kro}(y) > 0 $ oraz $ \displaystyle \mathrm{kro}(x) \ne \mathrm{kro}(y) $.

Wejście

W pierwszym wierszu standardowego wejścia znajduje się jedna liczba całkowita $ \displaystyle n $ ( $ \displaystyle 1 \leq n \leq 500\,000 $ ) - liczba przedziałów. W kolejnych $ \displaystyle n $ wierszach znajdują się opisy przedziałów. Opis przedziału składa się z trzech liczb całkowitych $ \displaystyle a_i,b_i,k_i $ ( $ \displaystyle 1\le a_i \le b_i \le 10^9, 1 \le k_i \le 1\,000 $ ) pooddzielanych pojedynczymi odstępami, będących odpowiednio końcami przedziału oraz jego krotnością.

Wyjście

Twój program powinien wypisać na standardowe wyjście dokładnie jedną liczbę całkowitą - liczbę szukanych par liczb.

Przykład

Dla danych wejściowych:
3
1 3 2
3 4 3
3 5 1
poprawnym wynikiem jest:
9

Wyjaśnienie do przykładu: Szukane pary to: $ \displaystyle \{1,3\},\ \{1,4\},\ \{1,5\},\ \{2,3\},\ \{2,4\},\ \{2,5\},\ \{3,4\},\ \{3,5\},\ \{4,5\} $.

Załącznik	Wielkość
jed.cpp	695 bajtów
pod.cpp	766 bajtów
jaz.cpp	901 bajtów
kro.cpp	1.17 KB
roz.cpp	628 bajtów
deg.cpp	926 bajtów
prz.cpp	602 bajty
cyk.cpp	1.25 KB
odc.cpp	696 bajtów
jad.cpp	1.42 KB
rod.cpp	569 bajtów
wzo.cpp	1.48 KB
szy.cpp	395 bajtów
osu.cpp	1.43 KB
tab1.cpp	1.05 KB
tab2.cpp	1.03 KB
kon.cpp	1.53 KB
gra.cpp	1.31 KB
mro.cpp	806 bajtów
zol.cpp	876 bajtów
zol2.cpp	633 bajty
sko.cpp	1006 bajtów
zet.cpp	1.2 KB
zed.cpp	696 bajtów
ski.cpp	851 bajtów
pre.cpp	1.33 KB
wzn.cpp	759 bajtów
aut.cpp	1.41 KB
autrys1-crop.jpg	14.37 KB
autrys2-crop.jpg	16.94 KB
par.cpp	782 bajty
parrys-crop.jpg	10.33 KB
pad.cpp	1.72 KB
est.cpp	1.38 KB
pot.cpp	1.23 KB
nas.cpp	1.7 KB
tra.cpp	1.29 KB
trazad.jpg	43.56 KB