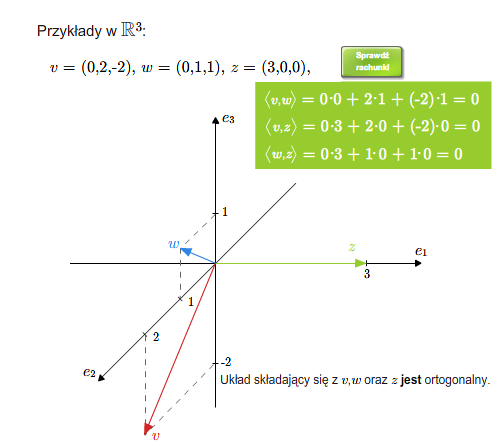
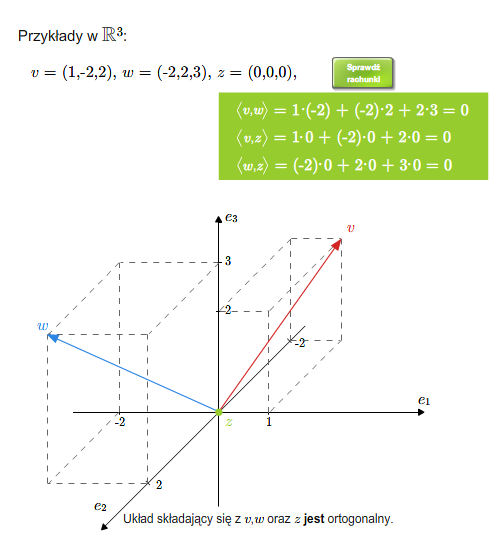
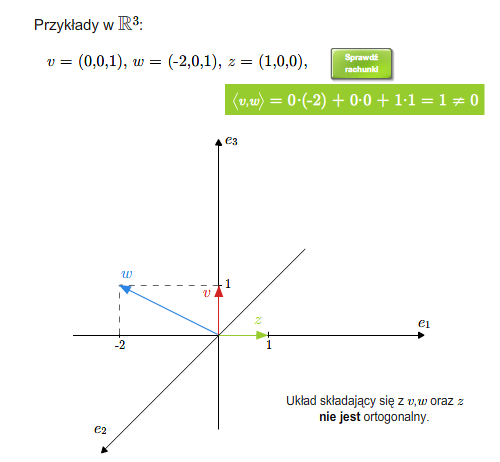
Algebra liniowa z geometrią analityczną
Opis
Zapoznanie z podstawowymi pojęciami algebry liniowej dla przestrzeni skończenie wymiarowych. Wprowadzenie do geometrii analitycznej \(R^n\)
Sylabus
Autorzy
- Barbara Opozda — Uniwersytet Jagielloński, Wydział Matematyki i Informatyki, Instytut Matematyki
- Małgorzata Downarowicz — Uniwersytet Jagielloński, Wydział Matematyki i Informatyki, Instytut Matematyki
- Dominik Kwietniak — Uniwersytet Jagielloński, Wydział Matematyki i Informatyki, Instytut Matematyki
Wymagania wstępne
- Podstawy logiki i teorii mnogości
- Wiadomości ze szkoły
Zawartość
- Ciała i przestrzenie wektorowe:
- grupa, ciało (przemienne), charakterystyka ciała
- przykłady ciał, ciało liczb zespolonych
- definicja przestrzeni wektorowej
- podprzestrzenie, operacje na podprzestrzeniach
- kombinacja liniowa, podzbiór generujący, układ liniowo niezależny, baza, przestrzeń skończenie wymiarowa, wymiar przestrzeni
- Odwzorowania liniowe:
- definicja odwzorowania liniowego
- jądro i obraz odwzorowania liniowego, rząd odwzorowania liniowego
- monomorfizm, epimorfizm, izomorfizm
- przestrzeń dualna, baza dualna, odwzorowanie dualne
- Macierze:
- podstawowe pojęcia
- działania na macierzach
- macierz odwzorowania liniowego
- mnożenie macierzy a składanie odwzorowań liniowych
- macierz dualna a odwzorowanie dualne
- rząd macierzy
- macierz przejścia, macierz odwzorowania liniowego po zmianie bazy
- ślad macierzy i endomorfizmu
- Układy równań liniowych:
- twierdzenie Kroneckera-Capellego
- zbiór rozwiązań układu równań liniowych
- badanie układu równań
- Wyznacznik:
- wyznacznik macierzy i endomorfizmu, metody obliczania wyznacznika, własności wyznacznika
- minory i rząd macierzy
- wzory Cramera
- wzory na wyrazy macierzy odwrotnej
- Endomorfizmy:
- wartość własna i wektor własny
- wielomian charakterystyczny
- bazy i macierze Jordana
- Formy kwadratowe:
- macierz i rząd odwzorowania dwuliniowego
- twierdzenie Lagrange'a i Sylvestera, sygnatura formy kwadratowej
- Euklidesowe przestrzenie wektorowe:
- iloczyn skalarny
- norma wyznaczona przez iloczyn skalarny
- nierówność Schwarza
- baza ortonormalna, ortonormalizacja Grama-Schmidta
- macierz i wyznacznik Grama, miara układu wektorów
- izometrie liniowe, macierz ortogonalna
- Geometria analityczna:
- przestrzeń afiniczna, euklidesowa przestrzeń afiniczna, euklidesowa przestrzeń afiniczna \(R^n\)
- układ bazowy, ukośnokątny (prostokątny) układ współrzędnych
- podprzestrzeń afiniczna, operacje na podprzestrzeniach afinicznych
- równoległość podprzestrzeni afinicznych
- podprzestrzeń rozwiązań układu równań liniowych
- opisy analityczne podprzestrzeni afinicznych
- odległość punktów i niektórych figur
- zbiory wypukłe
- odwzorowania afiniczne, izometrie, postać macierzowa
Literatura
- A. Białynicki-Birula, Algebra liniowa z geometrią, Państwowe Wydawnictwo Naukowe, Biblioteka Matematyczna t.48, Warszawa 1979.
- J. Gancarzewicz, Algebra liniowa z elementami geometrii, Wydawnicwo Naukowe UJ, Kraków, 2001.
- J. Komorowski, Od liczb zespolonych do tensorów, spinorów, algebr Liego i kwadryk, Państwowe Wydawnictwo Naukowe, Warszawa 1978.
- K. Nomizu, Fundamentals of Linear Algebra, McGraw-Hill, Inc., New York 1966.
- K. Sieklucki, Geometria i topologia, część I - Geometria, Państwowe Wydawnictwo Naukowe, Biblioteka Matematyczna t.53, Warszawa 1979, Warszawa 2006.
Grupy i ciała
Grupy
Przez strukturę algebraiczną rozumie się zbiór składający się ze skończonej liczby zbiorów i ze skończonej liczby odwzorowań iloczynów kartezjańskich tych zbiorów w te zbiory. Odwzorowania te nazywa się działaniami.
Zaczniemy od rozważenia najprostszych struktur.
Niech \(G\) będzie zbiorem niepustym. Działaniem wewnętrznym w zbiorze \(G\) nazywamy odwzorowanie \(d:G\times G\longrightarrow G\). Działanie \(d\) jest łączne, jeśli dla każdych \(a,b,c\in G\) zachodzi równość
Mówimy, że działanie \(d\) jest przemienne, jeśli dla każdych
elementów \(a,b\in G\) zachodzi równość
Element \(e\in G\) nazywa się elementem neutralnym ze względu
na działanie \(d\), jeśli dla każdego elementu \(a\in G\) mamy
Łatwo widać, że jeśli istnieje element neutralny, to element taki
jest jedyny w \(G\). Istotnie, niech \(e\) i \(e'\) będą elementami neutralnymi ze względu na \(d\). Zachodzą następujące równości
Działania oznacza się najczęściej znakiem plus, tzn. \(+\), lub
znakiem kropki, która zwykle jest w zapisie pomijana. Oczywiście są też inne sposoby oznaczania działań, np. kółkiem, gwiazdką, etc. Działanie oznaczane znakiem \(+\) nazywa się dodawaniem, działanie oznaczane kropką nazywa się mnożeniem. Jeśli działanie oznaczone jest plusem, to łączność oznacza, że dla każdych \(a,b,c\in G\) mamy \(a+(b+c)= (a+b) +c\). A zatem zapis \(a+b+c\) ma sens. Podobnie dla działania zapisywanego multyplikatywnie, czyli kropką, łączność oznacza, że \(a(bc)=(ab)c\) dla każdych \(a,b,c\in G\), a zapis \(abc\) ma sens. Oczywiście, łączność dodawania oznacza, że zapis \(a_1+...+a_n\) ma sens dla dowolnego \(n\in \mathbb N\), zaś w przypadku mnożenia, zapis \(a_1\cdot ...\cdot a_n\) ma sens dla dowolnego \(n\in \mathbb N\).
Jeśli działanie zapisywane jest w sposób addytywny, tzn. za pomocą znaku \(+\), to element neutralny (o ile istnieje) nazywany jest zerem i oznaczany przez \(0\). W przypadku zapisu multyplikatywnego, element neutralny nazywany jest często jedynką i oznaczany cyfrą \(1\).
Załóżmy, że działanie \(d\) w zbiorze \(G\) ma element neutralny \(e\). Załóżmy najpierw, że działanie to jest zapisywane addytywnie. Mówimy, że element \(a\in G\) ma element przeciwny, jeśli istnieje element \(a'\in G\) taki, że \(a+a'=a'+a=e\). Jeśli działanie zapisywane jest multyplikatywnie, to mówimy, że element \(a\in G\) ma element odwrotny w \(G\), jeśli istnieje element \(a'\in G\), taki że \(aa'=a'a=e\).
Zauważmy, że jeśli działanie jest łączne, ma element neutralny i element \(a\in G\) ma element odwrotny (przeciwny), to element taki jest jedyny. Mianowicie, jeśli \(a'\) i \(a''\) są elementami odwrotnymi do \(a\), to (stosując zapis multyplikatywny) mamy następujące równości
Jeżeli działanie zapisywane jest w sposób addytywny i element \(a\)
ma dokładnie jeden element przeciwny, to element ten oznaczamy przez \(-a\). Ponadto, jeśli \(b\in G\), to przyjmujemy oznaczenie
Jeśli działanie zapisywane jest w sposób multyplikatywny i element \(a\) ma dokładnie jeden element odwrotny, to oznaczamy go przez
\(a^{-1}\). Przyjmujemy także oznaczenie
Definicja 1.1 [Grupa]
Mówimy, że zbiór niepusty \(G\) z działaniem wewnętrznym jest grupą, jeśli działanie to jest łączne, ma element neutralny i każdy element \(G\) ma element odwrotny (przeciwny).
Grupę nazywamy przemienną, lub abelową, jeśli jej działanie jest przemienne.
Załóżmy, że \(G'\) jest niepustym podzbiorem grupy \(G\). Mówimy, że \(G'\) jest podgrupą grupy \(G\), jeśli działanie grupy \(G\) zawężone do \(G'\times G'\) ma wartości w \(G'\) oraz dla każdego elementu \(a\in G'\) jego element odwrotny \(a^{-1}\) również należy do \(G'\).
Łatwo można sprawdzić, że podgrupa z zawężonym działaniem jest grupą.
Ciała
Rozważymy teraz zbiory wyposażone w dwa działania - dodawanie i mnożenie. Przyjmiemy następującą definicję.
Definicja 2.1 [Ciało]
Ciałem (dokładniej mówiąc - ciałem przemiennym) nazywamy zbiór \(\mathbb K\) wyposażony w dwa działania wewnętrzne - dodawanie i mnożenie, które spełniają następujące warunki:
C1) \(\mathbb K\) z dodawaniem jest grupą przemienną,
C2) mnożenie w \(\mathbb K\) jest przemienne i zbiór \(\mathbb K\setminus \{0\}\) z mnożeniem jest grupą,
C3) \(a(b+c)=ab+ac\) dla każdych elementów \(a,\, b,\, c\in \mathbb K\) (prawo rozdzielności mnożenia względem dodawania).
Udowodnimy najbardziej podstawowe własności ciał.
Twierdzenie 2.2 [Własności Ciała]
W ciele zachodzą następujące warunki:
- \(1\ne 0\),
- \(0\cdot a= a\cdot 0=0,\)
- \((-1)\cdot a =-a,\)
- jeżeli \(ab=0\), to \(a=0\) lub \(b=0\),
- jeżeli \(a\ne 0\) i \(b\ne 0\), to \((ab)^{-1}=b^{-1}a^{-1}\)
dla każdych \(a,\, b \in \mathbb K\).
Dowód
Wiemy, że zbiór \(\mathbb K \setminus \{0\}\) jest grupą ze względu na mnożenie, a więc \(1\in \mathbb K\setminus \{0\}\). Stąd mamy pierwszą własność.
Dla udowodnienia drugiej własności zauważmy, że
Dodając do obydwu stron \(-(0\cdot a)\) dostajemy żądaną równość. Korzystając z przemienności mnożenia w całym \(\mathbb K\) dostajemy równość \(a\cdot 0=0\) dla każdego \(a\in \mathbb K\). Stąd i założonej łączności mnożenia w \(\mathbb K\setminus\{0\}\) wynika już łączność mnożenia w całym zbiorze \(\mathbb K\).
Korzystając z drugiej własności dostajemy teraz
Ponieważ dodawanie w \(\mathbb K\) jest przemienne, dostajemy równość \((-1)a +a=0\). Oznacza to, że \((-1)a\) jest elementem przeciwnym do \(a\), co dowodzi trzeciej własności.
Dla dowodu czwartej własności przypuśćmy, że \(a\ne 0\). Wtedy, wykorzystując już udowodnioną własność (2) dostajemy
Własność ta wynika też z aksjomatu C2), bo w aksjomacie tym implicite założono, że \(\mathbb K\setminus \{0\}\) jest zamknięty ze względu na mnożenie.
Własność ostatnia wynika z następujących równości
Konsekwencją trzeciej własności i wcześniejszej umowy (1.1)
jest równość następująca:
dla każdych \(a,\, b,\, c\in \mathbb K\).
Wprowadzimy teraz pojęcie charakterystyki ciała.
Definicja 2.3 [Charakterystyka ciała]
Niech \(\mathbb K\) będzie ciałem. Jeżeli istnieje liczba naturalna \(n\) taka, że
gdzie jedynka w powyższej sumie występuje \(n\) razy, to najmniejszą taką liczbę \(n\) nazywamy charakterystyką ciała. Jeśli taka liczba naturalna nie istnieje, mówimy, że charakterystyka ciała równa jest \(0\).
Ponieważ \(1\ne 0\), więc charakterystyka ciała, jeśli nie jest równa \(0\), musi być większa lub równa \(2\). Ciałem o charakterystyce 2 jest tzw. ciało zero-jedynkowe, które można wprowadzić tak. W zbiorze \(\{0,\, 1\}\) wprowadzamy działania
Łatwo widać, że spełnione są wszystkie warunki definiujące ciało i ciało to ma charakterystykę równą 2.
Ciałami są zbiór liczb wymiernych i zbiór liczb rzeczywistych ze zwykłymi działaniami. Są to oczywiście ciała o charakterystyce \(0\). Ciała te oznaczamy symbolami \(\mathbb Q\) i \(\mathbb R\) odpowiednio.
Ciało liczb zespolonych
Niech \(\mathbb C\) będzie zbiorem \(\mathbb R\times \mathbb R\) wyposażonym w dwa następujące działania:

 Dodawanie liczb zespolonych
Dodawanie liczb zespolonych
Sprawdzenie, że tak zdefiniowana struktura jest ciałem jest kwestią bezpośredniego rachunku. Elementem neutralnym ze względu na dodawanie (zerem w \(\mathbb C\)) jest element \((0,0)\), zaś elementem neutralnym ze względu na mnożenie jest element \((1,0)\). Elementem przeciwnym do elementu \((a,b)\) jest element \((-a,-b)\).


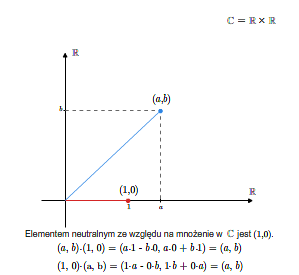
Elementem odwrotnym do niezerowego elementu \((a,b)\) jest element
Ciało liczb zespolonych ma charakterystykę 0.
Element \((0,1)\) oznaczamy przez \(\mathbf i\). Liczbę rzeczywistą \(a\) utożsamiamy z liczbą zespoloną \((a,0)\). Dokładniej mówiąc, odwzorowanie
jest injekcją, czyli zbiór liczb rzeczywistych można uważać za podzbiór
zbioru liczb zespolonych. Co więcej, według powyższych formuł definiujących dodawanie i mnożenie w ciele liczb zespolonych, zwykłe dodawanie i mnożenie liczb rzeczywistych jest zawężeniem dodawania i mnożenia (odpowiednio) z ciała liczb zespolonych. Mówimy, że ciało \(\mathbb R\) jest podciałem ciała \(\mathbb C\).
Liczba zespolona \(\mathbf i =(0,1)\) ma tę własność, że \(\mathbf i ^2=-1\). W związku z tym, liczbę tę zapisywano jako \(\sqrt {-1}\). Oznaczenie to używane było już w XVI wieku, jako formalny symbol, do obliczania pierwiastków wielomianów. Współczesna teoria i symbolika liczb zespolonych pochodzi z XIX wieku.

Liczbę \(\mathbf i\) nazywamy jednostką urojoną i zgodnie z przyjętymi wyżej definicjami i ustaleniami, każdą liczbę zespoloną \((a,b)\) możemy zapisać jako \(a+b\mathbf i\). Liczbę rzeczywistą \(a\) nazywamy częścią rzeczywistą (z łac. realis) liczby zespolonej \(z=a+b\mathbf i\) i oznaczamy ją \(\Re\, z\), zaś liczbę rzeczywistą \(b\) nazywamy częścią urojoną ( z łac. imaginalis) liczby zespolonej \(z\) i oznaczamy ją przez \(\Im\, z\).
Liczby zespolone, jako elementy zbioru \(\mathbb R ^2\), możemy identyfikować z punktami na płaszczyźnie wyposażonej w prostokątny układ współrzędnych. Dokładniej mówiąc, liczbę zespoloną \(z=(a,b)\) przedstawiamy na płaszczyźnie jako punkt o współrzędnych \((a,b)\) lub jako wektor o początku w początku układu współrzędnych (w punkcie o współrzędnych \((0,0)\)) i końcu w punkcie o współrzędnych \((a,b)\). Przyjmując tę geometryczną interpretację liczby zespolonej, zbiór wszystkich liczb zespolonych nazywamy płaszczyzną liczb zespolonych. Dodawaniu liczb zespolonych odpowiada dodawanie wektorów zaczepionych w początku układu współrzędnych.
Dla liczby zespolonej wprowadzamy pojęcie modułu i argumentu. Modułem liczby zespolonej \(z=a+b\mathbf i\) nazywamy liczbę rzeczywistą \(|z|\) określoną wzorem
Biorąc pod uwagę geometryczną interpretację liczb zespolonych, widzimy, że moduł liczby \(z= a+b\mathbf i\) jest odległością punktu \((a,b)\) od początku układu współrzędnych lub długością wektora reprezentującego tę liczbę zespoloną. Moduł liczby zespolonej jest równy zeru wtedy i tylko wtedy, gdy liczba ta jest równa zeru.
Argumentem różnej od zera liczby zespolonej \(z=a+b\mathbf i\) nazywamy każdą liczbę rzeczywistą \(\varphi\) spełniającą układ równań
Umawiamy się, że dla liczby zespolonej \(z=0\) argumentem jest każda liczba rzeczywista. Argumentem głównym liczby zespolonej \(z\ne 0\) nazywamy ten argument, który leży w przedziale \([0,2\pi)\). Argument główny liczby zespolonej (niezerowej) oznaczmy przez \(\arg z\).
Argument główny jest kątem nachylenia wektora \(z\) do dodatniej półosi odciętych. Liczbę zespoloną \(z=a+b\mathbf i\) różną od \(0\) możemy teraz zapisać jako
Każdą liczbę zespoloną możemy zapisać jako
dla pewnego argumentu \(\varphi\). Zapis ten nazywamy trygonometryczną postacią liczby zespolonej.

Można przeliczyć, stosując znane ze szkoły wzory trgonometryczne, że jeśli \(z_1=|z_1|( \cos\varphi _1 +\mathbf i \sin\varphi _1)\) i \(z_2 = |z_2|(\cos\varphi _2 +\mathbf i \sin\varphi _2)\), to

Jeśli przyjmiemy, że \(z^n = z\cdot ...\cdot z\), gdzie \(z\) powtarza się \(n\) razy, to posługując się ostatnim wzorem na mnożenie liczb zespolonych w postaci trygonometrycznej, dostajemy natychmiast tzw. wzory de Moivre'a na \(n\)-tą potęgę liczby zespolonej

Potęgowanie liczb zespolonych
Dla liczby zespolonej \(z=a+b\mathbf i\) definiujemy tak zwaną liczbę sprzężoną \(\overline z\) do liczby \(z\). Mianowicie, definiujemy
Jeśli \(z=|z|(\cos\varphi +\mathbf i \sin \varphi )\), to
Wobec tego liczba sprzężona \(\overline z\) jest obrazem przez odbicie symetryczne względem osi odciętych liczby \(z\), gdzie \(z\)
traktujemy jako punkt płaszczyzny lub wektor.

Na koniec tego wykładu przytoczymy, bez dowodu, bardzo ważną cechę ciała liczb zespolonych, której to cechy nie ma ciało liczb rzeczywistych. Najpierw wprowadźmy następującą definicję
Definicja 3.1 [Algebraiczna domkniętość]
Mówimy, że ciało \(\mathbb K\) jest algebraicznie domknięte, jeśli każdy wielomian jednej zmiennej o współczynnikach z ciała \(\mathbb K\) ma w ciele \(\mathbb K\) miejsce zerowe.
Jak wiadomo, ciało liczb rzeczywistych nie ma takiej własności, bo np. wielomian \(x^2 +1\) nie ma miejsc zerowych w \(\mathbb R\).
W przypadku liczb zespolonych zachodzi następujące twierdzenie, nazywane zasadniczym twierdzeniem algebry
Twierdzenie 3.2
Ciało liczb zespolonych jest algebraicznie domknięte.
Z twierdzenia tego wynika, że każdy wielomian o współczynnikach z ciała \(\mathbb C\) jest rozkładalny na czynniki stopnia 1 o współczynnikach z ciała \(\mathbb K\).
Przestrzenie wektorowe
Definicja przestrzeni wektorowej
Na początku tego wykładu wprowadzimy pojęcie przestrzeni wektorowej - najważniejszej struktury, którą zajmuje się algebra liniowa.
Definicja 1.1 [Przestrzeń wektorowa]
Niech \(V\) będzie zbiorem niepustym wyposażonym w działanie wewnętrzne - dodawanie. Dane jest także ciało \(\mathbb K\) oraz działanie zewnętrzne, tak zwane mnożenie zewnętrzne z lewej strony, będące odwzorowaniem zbioru \(\mathbb K \times V\) w zbiór \(V\). Wartość tego odwzorowania na parze \((\lambda ,v)\in \mathbb K\times V\) oznaczamy przez \(\lambda\cdot v\). Występującą tu kropkę najczęściej pomijamy.
Mówimy, że struktura składająca się ze zbioru \(V\), ciała \(\mathbb K\) oraz dwóch powyższych działań jest przestrzenią wektorową, jeśli spełnionych jest pięć poniższych warunków, zwanych aksjomatami przestrzeni wektorowej:
V1) Zbiór \(V\) z dodawaniem jest grupą przemienną,
V2) Dla każdych \(\lambda\, \mu \in \mathbb K\) i dla każdego \(v\in V\) zachodzi równość \(\lambda(\mu v)=(\lambda\mu )v\).
V3) Dla każdych \(\lambda\, \mu \in \mathbb K\) i dla każdego \(v\in V\) zachodzi równość \((\lambda +\mu )v=\lambda v +\mu v\).
V4) Dla każdego \(\lambda \in \mathbb K\) i każdych \(v,w\in V\) zachodzi równość \(\lambda (v+w)= \alpha v +\alpha w\).
V5) Dla każdego \(v\in V\) zachodzi równość \(1\cdot v= v\).
W pierwszym aksjomacie najczęściej żąda się, tak jak to zrobiliśmy, aby grupa była przemienna, choć przemienność tej grupy jest konsekwencją pozostałych warunków. Proponujemy, aby czytelnik sam sprawdził ten fakt. Aksjomaty V2)- V5) są w definicji niezbędne. Proponujemy, aby czytelnik sprawdził to, znajdując przykład struktury, dla której spełnione są wszystkie warunki oprócz V2), następnie przykład struktury, dla której spełnione są wszystkie warunki oprócz warunku V3), etc. Własność V3) nazywa się łącznością mieszaną, własność V4) - rozdzielnością mnożenia zewnętrznego względem dodawania w ciele i wreszczcie własność V4) - rozdzielnością mnożenia zewnętrznego względem dodawania wewnętrznego.
Jeśli spełnione są wszystkie powyższe aksjomaty, to mówimy także, że \(V\) jest przestrzenią wektorową nad ciałem \(\mathbb K\). Elementy przestrzeni \(V\) nazywamy wektorami, zaś elementy ciała \(\mathbb K\) nazywamy skalarami.
Zauważmy najpierw pewne elementarne własności przestrzeni wektorowych.
Twierdzenie 1.2
Niech \(V\) będzie przestrzenią wektorową nad ciałem \(\mathbb K\). Wtedy dla każdego \(v\in V\) i każdego \(\lambda \in \mathbb K\) zachodzą równości:
Uwaga 1.3
W pierwszej z powyższych równości \(0\) z lewej strony jest zerem w ciele, zaś \(0\) z prawej strony jest zerem w przestrzeni wektorowej. W drugiej równości oba \(0\) są zerami w przestrzeni wektorowej.
Dowód
Dowód trzech pierwszych z powyższych własności jest analogiczny do odpowiednich części dowodu Twierdzenia 2.2. z Wykładu 1. Dla dowodu czwartej własności załóżmy, że \(\lambda \ne 0\) i \(\lambda v=0\). Pomnóżmy obie strony przez \(\lambda ^{-1}\). Otrzymujemy stąd równość \(v=0\).
Podamy teraz kilka przykładów przestrzeni wektorowych.
Przykład 1.4
Dowolny zbiór jednoelementowy jest przestrzenią wektorową nad dowolnym ciałem. Jedyny element takiego zbioru jest zerem w tej przestrzeni. Taką przestrzeń nazywamy przestrzenią zerową.
Przykład 1.5
Każde ciało jest przestrzenią wektorową nad samym sobą.
Ogólniej, jeśli \(\mathbb K\) jest ciałem, to iloczyn kartezjański \(\mathbb K ^n\), \(n\in \mathbb N\), ma naturalną strukturę przestrzeni wektorowej nad ciałem \(\mathbb K\). Dodawanie w \(\mathbb K ^n\) definiujemy następująco
zaś mnożenie zewnętrzne dane jest formułą
Bezpośrednim i łatwym rachunkiem można sprawdzić, że tak zdefiniowana struktura na \(\mathbb K ^n\) jest przestrzenią wektorową nad ciałem \(\mathbb K\).
W kolejnym przykładzie zdefiniujemy strukturę przestrzeni wektorowej na iloczynie kartezjańskim dowolnych przestrzeni wektorowych.
Przykład 1.6
Niech \(V\), \(W\) będą przestrzeniami wektorowymi nad ciałem \(\mathbb K\). Wtedy iloczyn kartezjański \(V\times W\) ma naturalną strukturę przestrzeni wektorowej nad ciałem \(\mathbb K\). Istotnie, jeśli zdefiniujemy dodawanie formułą
dla \(v_1, v_2\in V\) i \(w_1, w_2\in W\), a mnożenie zewnętrzne formułą
dla \(\lambda \in\mathbb K\) i \(v\in V\), \(w\in W\), to otrzymujemy strukturę przestrzeni wektorowej (nad ciałem \(\mathbb K\)) na \(V\times W\).
Przykład 1.7
Załóżmy, że dana jest przestrzeń wektorowa \(V\) nad ciałem \(\mathbb K\) i \(X\) jest dowolnym zbiorem niepustym. Weźmy zbiór wszystkich odwzorowań \(f:X\longrightarrow V\). Oznaczmy ten zbiór przez \(V^X\). W zbiorze \(V ^X\) wprowadzamy dodawanie
dla każdych \(f,g\in V^X\) i dla każdego \(x\in X\). Mnożenie
zewnętrzne definiujemy formułą
dla \(\lambda \in\mathbb K\), \(f\in V\) i \(x\in X\).
Tak określone działania definiują , co łatwo sprawdzić, strukturę przestrzeni wektorowej na \(V^X\) nad \(\mathbb K\).
Jako szczególny przypadek możemy wziąć zbiór wszystkich ciągów nieskończonych o wartościach w dowolnej przestrzeni wektorowej \(V\). Zbiorem \(X\) jest tutaj zbiór liczb naturalnych \(\mathbb N\).
Jeśli za \(X\) weźmiemy zbiór \(\{1,...,n\}\), a \(V\) jest dowolną przestrzenią wektorową, to otrzymamy przestrzeń ciągów o długości \(n\) i wyrazach w \(V\).
Jeśli za \(X\) przyjmiemy pewien przedział w zbiorze liczb rzeczywistych, to zbiór wszystkich funkcji określonych na tym przedziale i o wartościach w zbiorze liczb rzeczywistych jest przestrzenią wektorową.
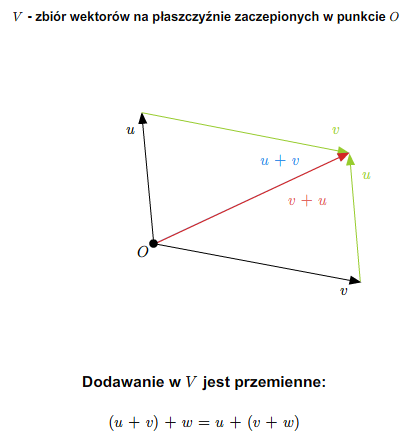
Przykład 1.8
W szkole wprowadza się pojęcie wektora swobodnego na płaszczyźnie. Zbiór wszystkich takich wektorów ze znanymi ze szkoły dodawaniem (przez zastosowanie reguły równoległoboku) i mnożeniem wektorów przez liczby rzeczywiste stanowi przykład przestrzeni wektorowej nad ciałem \(\mathbb R\). Podobnie ma się rzecz ze zbiorem wektorów swobodnych w trójwymiarowej przestrzeni fizycznej.
Można też rozumować tak (pomijając pojęcie wektora swobodnego). Rozważmy płaszczyznę (lub trójwymiarową przestrzeń) z ustalonym punktem (np. początkiem pewnego układu współrzędnych). Bierzemy zbiór wszystkich wektorów zaczepionych w tym punkcie. Wprowadzamy dodawanie wektorów i mnożenie przez liczbę rzeczywistą tak, jak się to robi w szkole. Tak otrzymana struktura jest przestrzenią wektorową nad \(\mathbb R\).
Jeśli płaszczyzna (lub trójwymiarowa przestrzeń fizyczna) jest wyposażona w układ współrzędnych, to tak otrzymaną przestrzeń wektorów można utożsamiać z \(\mathbb R ^2\) (w przypadku płaszczyzny) lub z \(\mathbb R ^3\) (w przypadku trójwymiarowej przestrzeni fizycznej).

















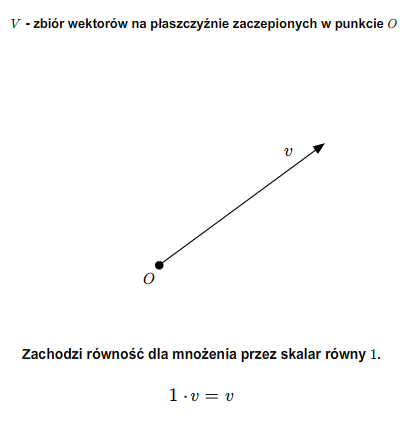
Przestrzeń wektorową \(V\) nad ciałem liczb zespolonych nazywamy przestrzenią wektorową zespoloną. Przestrzeń wektorową nad ciałem liczb rzeczywistych nazywamy przestrzenią wektorową rzeczywistą. Każda przestrzeń wektorowa zespolona jest automatycznie przestrzenią wektorową rzeczywistą (z mnożeniem zewnętrznym będącym zawężeniem do \(\mathbb R\times V\) mnożenia zewnętrznego przez liczby zespolone).
Podprzestrzenie wektorowe
Definicja 2.1
Niech \(V\) będzie przestrzenią wektorową nad ciałem \(\mathbb K\). Załóżmy, że \(W\) jest niepustym podzbiorem zbioru \(V\). Podzbiór \(W\) nazywamy podprzestrzenią wektorową przestrzeni \(V\), jeśli dla każdych \(v,w\in W\) i \(\lambda\in\mathbb K\) mamy
Innymi słowy, podprzestrzeń wektorowa \(W\) przestrzeni \(V\) jest niepustym podzbiorem przestrzeni \(V\) zamkniętym ze względu na działania w \(V\). Jest jasne, że jeśli \(W\) jest podprzestrzenią \(V\), to dla każdych \(\lambda _1,...,\lambda _k \in \mathbb K\) i dla każdych wektorów \(v_1,..., v_k \in W\) wektor równy \(\lambda _1v_1+...+\lambda _kv_k\) należy do podprzestrzeni \(W\).
Jeżeli \(W\) jest podprzestrzenią wektorową przestrzeni \(V\) i \(v\in W\), to \(-v=(-1) v\) również należy do \(W\). A zatem \(0=v+(-1)v \in W\), czyli do każdej podprzestrzeni wektorowej \(W\) musi należeć zero przestrzeni \(V\).
Ponieważ własności działań przestrzeni wektorowej \(V\) zawarte w aksjomatach dziedziczą się łatwo na podzbiór zamknięty ze względu na te działania, więc podprzestrzeń wektorowa jest przestrzenią wektorową (nad tym samym ciałem co przestrzeń \(V\)).
Podamy kilka najważniejszych przykładów podprzestrzeni wektorowych. Oczywiście cała przestrzeń \(V\), a także podzbiór \(\{0\}\subset V\) są podprzestrzeniami wektorowymi \(V\). Są to tak zwane podprzestrzenie trywialne.
Kolejny przykład będzie odgrywać ważną rolę w naszym wykładzie
Przykład 2.2
Jeśli \(a_1,...a_n\) są ustalonymi elementami ciała \(\mathbb K\), to zbiór opisany równaniem liniowym \(a_1x_1+...+a_nx_n=0\), tzn. zbiór
\(\begin{cases} & a_{11}x_1+...+a_{1n}x_n=0,\\ & .\\ & .\\ & .\\ & a_{m1}x_1+...+a_{mn}x_n=0, \end{cases}\) (2.2)
gdzie \(a_{ij}\) dla \(i=1,...,m\), \(j=1,...,n\), są dowolnymi ustalonymi skalarami. Jest to układ \(m\) równań z \(n\) niewiadomymi \(x_1,...x_n\). Zbiór wszystkich rozwiązań tego układu, czyli zbiór wszystkich ciągów \((x_1,....,x_n)\in \mathbb K ^n\) spełniających (2.2), jest podprzestrzenią wektorową przestrzeni \(\mathbb K ^n\).}
Wróćmy teraz do Przykładu 1.7.
Przykład 2.3
Inny przykład wywodzący się z Przykładu 1.7 jest taki. Weźmy przestrzeń \(V=\mathbb R ^{\mathbb N}\) wszystkich nieskończonych ciągów o wyrazach rzeczywistych. Weźmy podzbiór składający się ze wszystkich ciągów zbieżnych do liczb rzeczywistych. Podzbiór ten jest podprzestrzenią \(V\).
Jeżeli \(W\) i \(U\) są podprzestrzeniami wektorowymi przestrzeni \(V\), to ich iloczyn mnogościowy jest też podprzestrzenią wektorową przestrzeni \(V\). Istotnie, \(0\) należy do \(U\) i \(V\), a zatem \(U\cap W\) jest niepusty. Dalej, jeśli \(v, w\in U\cap W\), to obydwa te wektory należą do \(U\), a więc ich suma należy do \(U\), a także należą do \(W\), a więc ich suma należy do \(W\). Czyli \(v+w\in U\cap W\). Podobnie, jeśli \(\lambda \in\mathbb K\) i \(v\in U\cap W\), to \(\lambda v\) należy zarówno do \(U\) jak i do \(W\). Wobec tego \(\lambda v\in U\cap W\).
Równie łatwo można stwierdzić, że jeśli mamy dowolną niepustą rodzinę podprzestrzeni \({W_t}_{\{t\in T\}}\) przestrzeni \(V\), to ich iloczyn mnogościowy \(\bigcap _{t\in T} W_t\) jest podprzestrzenią wektorową.
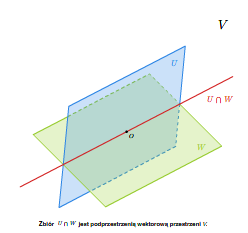
Dodawanie mnogościowe podprzestrzeni wektorowych nie jest dobrą operacją, tzn. suma mnogościowa podprzestrzeni wektorowych na ogól nie jest podprzestrzenią wektorową. Zachodzi następujące twierdzenie, którego dowód proponujemy czytelnikowi
Twierdzenie 2.4
Suma mnogościowa dwóch podprzestrzeni wektorowych \(U\), \(W\) przestrzeni \(V\) jest podprzestrzenią wektorową przestrzeni \(V\) wtedy i tylko wtedy, gdy \(U\subset W\) lub \(W\subset U\).
Zamiast sumy mnogościowej podprzestrzeni rozważa się sumę algebraiczną podprzestrzeni.
Mianowicie, niech \(U\), \(W\) będą podprzestrzeniami wektorowymi przestrzeni \(V\). Definiujemy zbiór
Łatwo sprawdzić, że zbiór ten spełnia warunki podprzestrzeni wektorowej. Sumę tę można uogólnić na skończoną liczbę składników. Jeśli \(W_1,...,W_k\) są podprzestrzeniami wektorowymi przestrzeni \(V\), to
Zbiór ten jest podprzestrzenią wektorową przestrzeni \(V\).
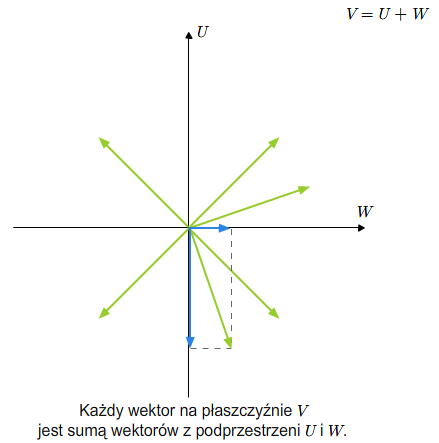
Bardzo ważnym pojęciem dotyczącym sumy algebraicznej podprzestrzeni jest pojęcie sumy prostej podprzestrzeni.
Definicja 2.5 [Suma prosta]
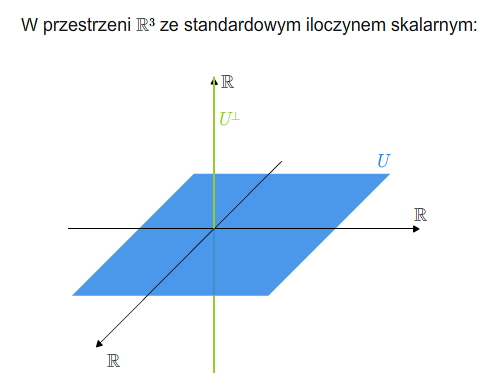
Mówimy, że \(V\) jest sumą prostą swoich podprzestrzeni \(U\) i \(W\), jeśli \(V=U +W\) oraz \(U\cap W=\{0\}\). Piszemy \(V=U\oplus W\).
Jednym z podstawowych powodów, dla których sumy proste są ważne, jest następujące twierdzenie
Twierdzenie 2.6
Jeżeli \(V=U\oplus W\), to każdy wektor \(v\in V\) można jednoznacznie przedstawić jako sumę wektorów przestrzeni \(U\) i \(W\).

Suma prosta podprzestrzeni wektorowych
Dowód
Do pokazania jest jednoznaczność. Niech \(v=u+w\), gdzie \(u\in U\) i \(w\in W\) oraz \(v=u'+w'\), gdzie \(u'\in U\) i \(w'\in W\). Wtedy \(u'-u=w-w'\). Po lewej stronie równości mamy wektor z przestrzeni \(U\), po prawej - z przestrzeni \(W\). A zatem oba należą do \(U \cap W\), czyli muszą być równe zeru.
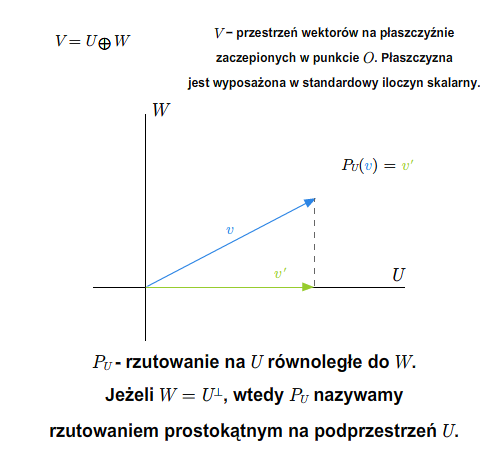
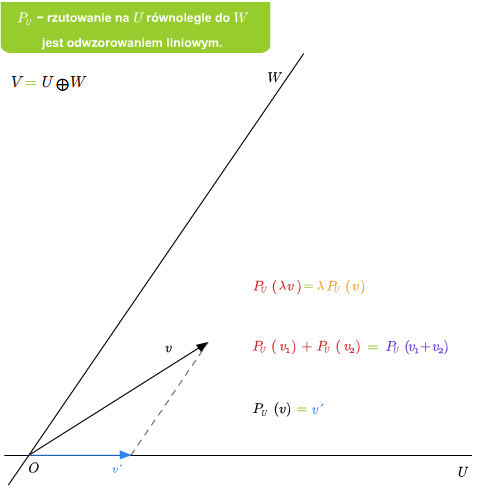
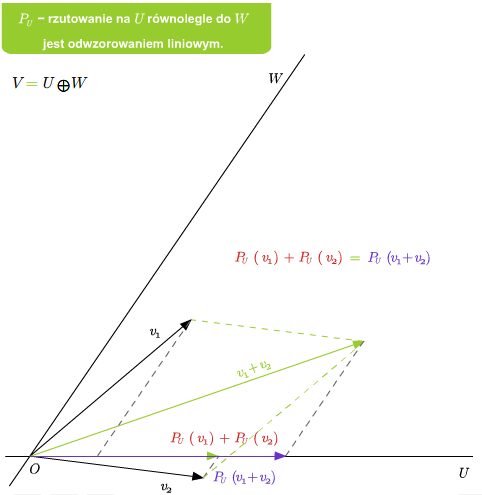
Mając sumę prostą \(V=U\oplus W\) możemy zdefiniować rzutowania. Mianowicie, niech \(v\in V\). Wtedy \(v\) rozkłada się jednoznacznie na sumę \(v=u+w\), gdzie \(u\in U\) i \(v\in V\). Odwzorowanie \(P_U: V\longrightarrow V\), które wektorowi \(v\) przyporządkowuje \(u\) z powyższego rozkładu, nazywamy rzutowaniem na podprzestrzeń \(U\) w kierunku podprzestrzeni \(W\) (lub rzutowaniem na \(U\) równoległym do \(W\)). Podobnie definiuje się rzutowanie \(P_W\) na \(W\) w kierunku \(U\).
Jeżeli \(V=U\oplus W\), to \(W\) nazywamy dopełnieniem algebraicznym do \(U\). Oczywiście \(U\) jest wtedy dopełnieniem algebraicznym do \(W\).
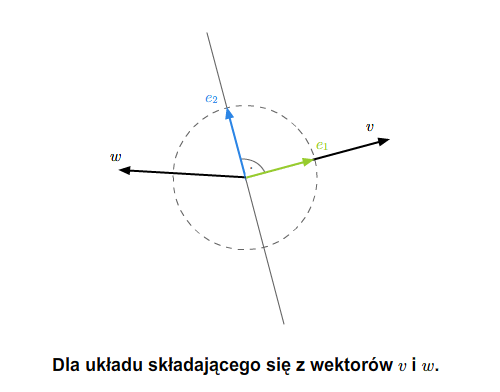
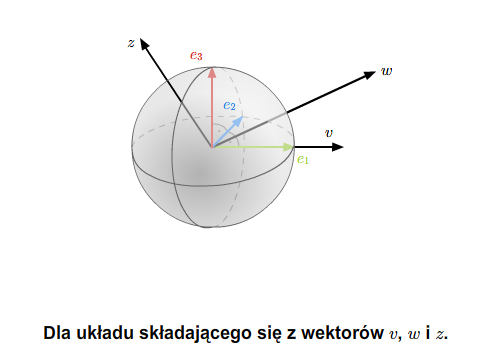
Układy liniowo niezależne, generatory, bazy
Kombinacje liniowe, układy i zbiory liniowo niezależne, układy i zbiory generujące.
Niech \(V\) będzie przestrzenią wektorową nad ciałem \(\mathbb K\).
Kombinacją liniową wektorów \(v_1,..., v_n\in V\) nazywamy wyrażenie
gdzie \(\lambda _1,...,\lambda _n\) są skalarami z ciała \(\mathbb K\). Wartością kombinacji liniowej (1.1) nazywamy wektor równy \(\lambda _1v_1+...+\lambda _nv_n\). Skalary \(\lambda _1,...,\lambda _n\) nazywamy współczynnikami kombinacji liniowej (1.1). Kombinację liniową nazywamy trywialną, jeśli wszystkie jej współczynniki są zerami. Kombinację liniową nazywamy zerową, jeśli jej wartość jest wektorem zerowym. Każda kombinacja liniowa trywialna jest zerowa. Oczywiście nie każda kombinacja zerowa jest trywialna. Na przykład, kombinacja liniowa \(1\cdot v+(-1)\cdot v\) jest zerowa i nietrywialna.
W praktyce mówimy, że wektor \(v\) jest kombinacją liniową pewnych wektorów mając na myśli to, że jest wartością tej kombinacji.
Wprowadzimy teraz fundamentalne dla naszego wykładu pojęcie liniowej niezależności.
Definicja 1.1 [Liniowa niezależność]
Mówimy, że ciąg wektorów \(v_1,..., v_n\) przestrzeni wektorowej \(V\) jest liniowo niezależny, jeśli spełniona jest następująca implikacja:
Jeżeli \(\lambda _1v_1+...\lambda _nv_n =0\) dla pewnych skalarów \(\lambda _1,...,\lambda _n\), to wszystkie te skalary muszą być zerami.
Innymi słowy, ciąg \(v_1,...,v_n\) jest liniowo niezależny, jeżeli każda jego kombinacja liniowa, która jest zerowa, jest trywialna. Kolejność wektorów w ciągu \(v_1,..., v_n\) jest w tej definicji nieistotna. Zamiast mówić o ciągach liniowo niezależnych, mówimy o układach liniowo niezależnych. Słowo układ zawiera najczęściej w sobie informację, że kolejność jego elementów jest nieistotna. Mówimy też o zbiorach liniowo niezależnych. Jasne jest, co to znaczy, że skończony zbiór jest liniowo niezależny. Różnica między zbiorem skończonym a układem jest taka, że w układzie mogą się pojawić wektory jednakowe.
Zbiór pusty uznajemy za liniowo niezależny.
Mówimy, że dowolny zbiór (niekoniecznie skończony) jest liniowo niezależny, jeśli każdy jego podzbiór skończony jest liniowo niezależny. Definicja taka nie prowadzi do żadnej sprzeczności z definicją liniowej niezależności w przypadku zbiorów skończonych, ponieważ zachodzi następujący lemat
Lemat 1.2 [Podukład]
Niech \(v_1,...v_n\) będzie układem liniowo niezależnym. Wtedy każdy jego podukład jest też liniowo niezależny.
Dowód
Można założyć, że dany podukład składa się z wektorów \(v_1,..., v_k\), gdzie \(k<n\). Niech \(\lambda _1v_1+...+\lambda _kv_k=0\). Wtedy
Korzystając teraz z liniowej niezależności wektorów \(v_1,...,v_n\) dostajemy, że wszystkie współczynniki \(\lambda _1,...,\lambda _k\) są zerami.
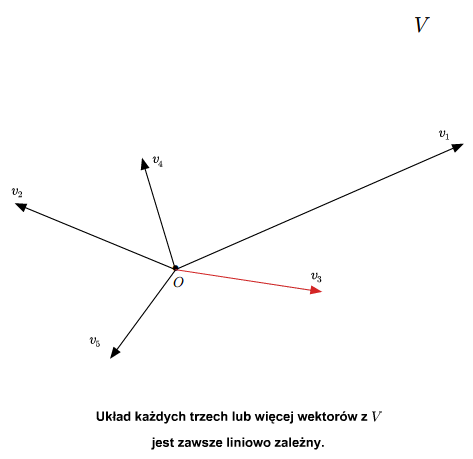
Mówimy, że wektory \(v_1,...,v_n\) są liniowo zależne, jeśli nie są liniowo niezależne. A zatem, wektory \(v_1,...,v_n\) są liniowo zależne, jeśli istnieją skalary \(\lambda_1,...,\lambda _n\in \mathbb K\), nie wszystkie równe zeru takie, że \(\lambda _1v_1+...+\lambda _nv_n =0\). Wtedy pewien wektor wśród \(v_1,..., v_n\) mianowicie każdy, przy którym współczynnik w kombinacji \(\lambda _1v_1+...+\lambda _nv_n=0\) jest niezerowy) da się przedstawić jako kombinacja liniowa pozostałych wektorów. Przypuśćmy, że \(\lambda _1\ne 0\). Wtedy
Podkreślmy, że liniowa zależność wektorów \(v_1,...,v_n\) nie oznacza, że każdy wektor wśród \(v_1,...v_n\) jest kombinacją liniową pozostałych wektorów.

 Al-3-2
Al-3-2
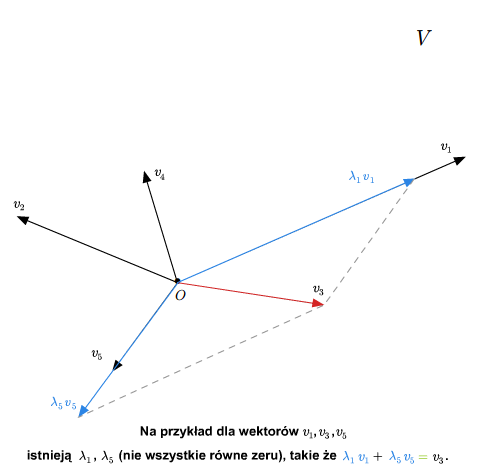 AL-3-3
AL-3-3
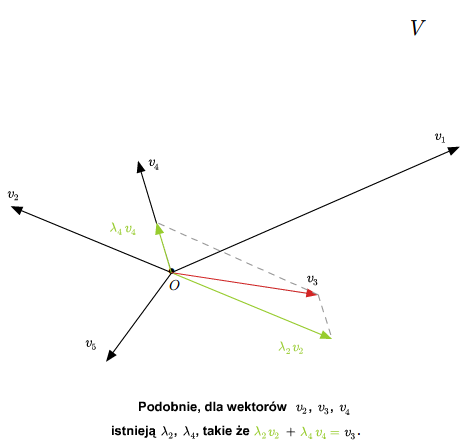 AL-3-4
AL-3-4
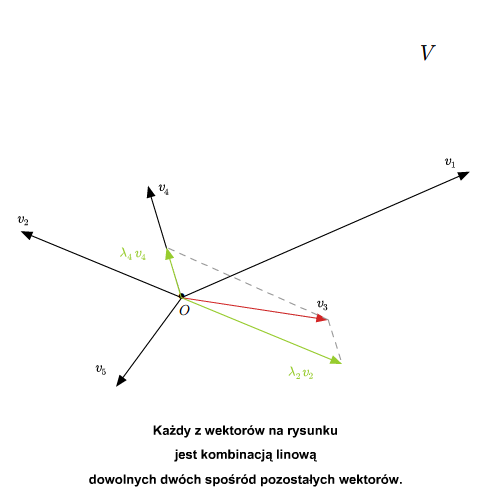 AL-3-5
AL-3-5
Każdy układ zawierający \(0\) lub dwa jednakowe wektory jest liniowo zależny. Ponadto, układ dwóch wektorów \(u,v\in V\) jest liniowo zależny wtedy i tylko wtedy, gdy wektory te są proporcjonalne, tzn. \(v=\lambda u\) lub \(u=\gamma v\) dla pewnych \(\lambda, \gamma \in \mathbb K\). Sprawdzenie tych faktów pozostawiamy jako ćwiczenie.
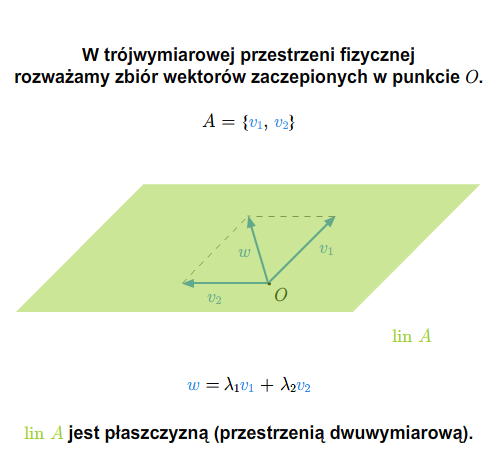
Niech teraz \(A\) będzie dowolnym podzbiorem przestrzeni \(V\). Bierzemy rodzinę wszystkich podprzestrzeni wektorowych zawierających podzbiór \(A\). Rodzina ta jest niepusta, bo cała przestrzeń \(V\) należy do tej rodziny. A zatem przecięcie wszystkich zbiorów tej rodziny jest podprzestrzenią wektorową zawierającą \(A\) (najmniejszą w sensie inkluzji). Oznaczmy tę podprzestrzeń symbolem \( lin A\). Jeżeli \(A\) jest zbiorem pustym, wtedy \( lin A=\{0\}\). Jeżeli \(W= lin A\), to mówimy, że \(A\) generuje (rozpina) podprzestrzeń \(W\). Oczywiście można też mówić o układzie \(A\) i podprzestrzeni generowanej przez ten układ. Jest oczywiste, że jeśli \(A\subset B\), to \( lin A\subset lin B\). Jeśli \(W\) jest podprzestrzenią wektorową, to \( lin\, W =W\), a zatem dla dowolnego podzbioru \(A\) mamy równość \( lin ( lin A)= lin A\).
Twierdzenie 1.3 [Span]
Niech \(A\) będzie niepustym podzbiorem przestrzeni wektorowej \(V\). Wtedy


Dowód
Łatwo można sprawdzić, że zbiór znajdujący się po prawej stronie równości(1.2) jest podprzestrzenią wektorową zawierającą \(A\). A zatem \( A\) zawiera się w tym zbiorze. Odwrotnie, jest oczywiste, że każdy element tego zbioru (wartość kombinacji liniowej pewnych wektorów zbioru \(A\)) jest elementem podprzestrzeni wektorowej \( lin A\).
W dalszym ciągu będziemy wykorzystywali następujące lematy.
Lemat 1.4
Niech \(v_1,..., v_n\) będą wektorami liniowo niezależnymi i \(w\notin lin \{v_1,...,v_n\}\). Wtedy wektory \(v_1,...,v_n, w\) są liniowo niezależne.
Dowód
Niech
Gdyby \(\lambda\ne 0\), to wektor \(w\) byłby kombinacją liniową wektorów \(v_1,...,v_n\), a zatem należałby do \( lin \{v_1,...,v_n \}\), co byłoby sprzeczne z założeniem. A więc \(\lambda =0\) i w konsekwencji mamy zerową kombinację liniową wektorów liniowo niezależnych \(v _1,...,v_n\). A zatem wszystkie \(\lambda _1\), ..., \(\lambda _n\) są zerami.
Lemat 1.5
Niech wektor \(w\) będzie kombinacją liniową wektorów \(v_1,...v_n\), t.j. \(w=\lambda _1v_1 +...+\lambda _n v_n\), dla pewnych skalarów \(\lambda _1,...,\lambda _n\). Jeżeli \(\lambda _1\ne 0\), to
Dowód
Ponieważ \(w\) jest kombinacją liniową wektorów \(v_1,...v_n\), więc \( lin \{w,v_2,...,v_n\}\subset lin \{ v_1,...,v_n\}\).
Z drugiej strony, ponieważ \(\lambda _1\ne 0\), więc
Zatem każda kombinacja liniowa wektorów \(v_1,...v_n\) jest też kombinacją liniową wektorów \(w,v_2,...,v_n\).
Twierdzenie 1.6
Niech \(w_1,...,w_m\), \(v_1,...v_n\) będą wektorami przestrzeni \(V\). Jeżeli \(w_1,...,w_m\) są liniowo niezależne oraz \(w_1,..., w_m \in lin \{v_1,...,v_n\}\), to \(m\le n\).
Dowód
Dla dowodu niewprost przypuśćmy, że \(m>n\). Wektor \(w_1\) jest kombinacja liniową wektorów \(v_1,...,v_n\). Po ewentualnym spermutowaniu wektorów \(v_1,...,v_n\), możemy przyjąć, że w tej kombinacji współczynnik przy \(v_1\) jest różny od \(0\). Z powyższego lematu mamy, że
Ponieważ \(w_2\) należy do tej przestrzeni, więc jest kombinacją liniową wektorów \(w_1,v_2,...,v_n\). W kombinacji tej przynajmniej jeden ze współczynników przy wektorach \(v_2,...,v_n\) musi być różny od zera. W przeciwnym bowiem przypadku, \(w_1,w_2\) byłyby liniowo zależne. Po ewentualnym spermutowaniu wektorów \(v_2,...,v_n\) możemy założyć, że współczynnik przy \(v_2\) jest różny od zera. A zatem, korzystając z Lematu 1.5,
dostajemy, że
Postępujemy podobnie dalej, tzn. zastępujemy kolejne wektory \(v_3,...\) wektorami \(w_3,...\). Ponieważ założyliśmy, że \(m>n\), więc dochodzimy do sytuacji, gdy \( lin \{w_1,...w_n\}= lin\{v_1,...v_n\}\). Oznacza to sprzeczność, gdyż wektor \(w_{n+1}\) musiałby być kombinacją liniową wektorów \(w_1,...,w_n\).
Baza i wymiar przestrzeni
Wprowadzimy teraz kolejne fundamentalne dla naszego wykładu pojęcie.
Definicja 2.1 [Baza]
Mówimy, że podzbiór (lub układ, lub ciąg) \(A\) przestrzeni wektorowej \(V\) jest bazą tej przestrzeni, jeśli jest liniowo niezależny i generuje \(V\).
Bazą przestrzeni zerowej jest zbiór pusty.
Twierdzenie 2.2 [Baza]
Załóżmy, że wektory \(v_1,...,v_n\) generują przestrzeń wektorową \(V\). Z wektorów \(v_1,..., v_n\) można wybrać bazę przestrzeni \(V\).
Dowód
Weźmy wszystkie podukłady układu \(v_1,...,v_n\) i wśród tych, które są liniowo niezależne, wybierzmy maksymalny, czyli o maksymalnej długości. (Taki podukład nie musi być jedyny.) Możemy założyć, że \(v_1,...,v_m\) jest takim podukładem. Twierdzimy, że jest to baza \(V\). Gdyby bowiem nie była to baza, to któryś z pozostałych wektorów \(v_{m+1},..., v_n\), powiedzmy \(v_{m+1}\), nie byłby kombinacją liniową wektorów \(v_1,...,v_m\). A zatem wektory \(v_1,...,v_{m+1}\) byłyby liniowo niezależne, na podstawie Lematu 1.4. Oznacza to, że podukład \(v_1,...,v_m\) nie byłby maksymalnym podukładem liniowo niezależnym.
Definicja 2.3 [Skończona wymiarowość]
Mówimy, że przestrzeń wektorowa jest skończenie wymiarowa, jeśli ma skończony układ generujący.}
Z powyższych twierdzeń wynika następujący wniosek
Twierdzenie 2.4
Przestrzeń skończenie wymiarowa \(V\) ma bazę.
Wykażemy ponadto
Twierdzenie 2.5
W przestrzeni skończenie wymiarowej wszystkie bazy są równoliczne, czyli mają tyle samo elementów.
Dowód
Niech \(B_1=\{e_1,..., e_n\}\) będzie skończoną bazą przestrzeni \(V\), a zatem, skończonym zbiorem generującym \(V\). Załóżmy, że \(B_2\) jest inną bazą tej przestrzeni. Wtedy każdy skończony podzbiór \(B_2\) jest liniowo niezależny. Z Twierdzenia 1.6 wynika, że każdy taki podzbiór ma co najwyżej \(n\) elementów. Oznacza to, że zbiór \(B_2\) jest skończony i ma co najwyżej \(n\) elementów. Zamieńmy teraz rolami bazy \(B_1\) i \(B_2\). Potraktujmy \(B_2\) jako zbiór generujący \(V\), zaś \(B_1\) jako zbiór liniowo niezależny. I znowu z Twierdzenia 1.6 wynika, że zbiór \(B_1\) ma co najwyżej tyle elementów co zbiór \(B_2\).
Na podstawie powyższego twierdzenia możemy podać następującą definicję wymiaru przestrzeni skończenie wymiarowej.
Definicja 2.6 [Wymiar]
Wymiarem przestrzeni skończenie wymiarowej nazywamy liczbę wektorów pewnej (lub, co na jedno wychodzi, każdej) bazy tej przestrzeni. Wymiar przestrzeni \(V\) oznaczamy symbolem \(\dim V\).
Kolejne twierdzenie jest natychmiastową konsekwencją powyższych rozważań.
Wniosek 2.7
Przestrzeń wektorowa jest skończenie wymiarowa wtedy i tylko wtedy, gdy ma bazę skończoną. Jeżeli \(e_1,...,e_n\) jest bazą przestrzeni \(V\), to każdy wektor \(v\) przestrzeni \(V\) da się w sposób jednoznaczny przedstawić jako kombinacja liniowa wektorów \(e_1,...,e_n\).
Dowód
Sprawdźmy jednoznaczność w ostatniej tezie. Jeśli \(e_1,...,e_n\) jest ustaloną bazą i \(v=\lambda _1e_1+...\lambda_ne_n\) oraz \(v=\lambda' _1e_1+...\lambda'_ne_n\), to \((\lambda_1 -\lambda' _1)e_1+...+(\lambda_n-\lambda'_n)e_n=0\). Z liniowej niezależności wektorów bazy dostajemy, że \(\lambda _i=\lambda'_i\) dla każdego \(i=1,...n\).
Jeżeli mamy bazę \(e_1,...,e_n\) przestrzeni wektorowej \(V\) i wektor \(v=\lambda _1e_1+...+\lambda _ne_n\), to skalary \(\lambda _1,...,\lambda _n\) nazywamy współrzędnymi wektora \(v\) w bazie \(e_1,..., e_n\).
Najważniejszym i najłatwiejszym przykładem bazy jest tak zwana baza kanoniczna przestrzeni \(\mathbb K ^n\). Mianowicie, baza ta jest ciągiem
Bardzo często kolejność wektorów bazy jest istotna. Aby to podkreślić,
mówimy, że baza jest uporządkowana. Baza kanoniczna jest uporządkowana w naturalny sposób.
Twierdzenie 2.8
Niech \(v_1,...,v_m\) będzie układem liniowo niezależnym w skończenie wymiarowej przestrzeni wektorowej \(V\). Układ ten można uzupełnić do bazy, a zatem istnieje baza przestrzeni \(V\) zawierająca dany układ liniowo niezależny.
Dowód
Niech \(W_1 = lin \{ v_1,..., v_m\}\). Jeżeli \(W_1\ne V\), to istnieje wektor \(v_{n+1}\) w \(V\), który nie należy do \(W_1\). Wtedy, na podstawie Lematu 1.4, zbiór \(v_1,...,v_n, v_{m+1}\) jest liniowo niezależny. Jeśli zbiór ten nie jest bazą \(V\), postępujemy tak jak poprzednio. To znaczy, bierzemy wektor \(v_{m+2}\notin lin \{v_1,...,v_n,v_{n+1}\}\) i dołączamy go do poprzednich wektorów. Postępując tak skończoną ilość razy otrzymujemy bazę przestrzeni \(V\).
Z twierdzenia tego wynika natychmiast
Wniosek 2.9
Każda podprzestrzeń \(W\) przestrzeni skończenie wymiarowej \(V\) jest skończenie wymiarowa i jej wymiar jest nie większy od wymiaru przestrzeni \(V\). Bazę \(e_1,...,e_n\) przestrzeni \(V\) można wybrać w ten sposób, że pierwsze jej wektory \(e_1,..., e_m\) stanowią bazę podprzestrzeni \(W\).
Dowód
Zauważmy jeszcze, że jeśli \(V\) jest przestrzenią skończenie wymiarową a \(U\) jest jej podprzestrzenią taką, że \(\dim U=\dim V\), to \(V=U\). Istotnie, wybierzmy pewną, powiedzmy \(n\)-elementową, bazę przestrzeni \(U\). Rozrzerzmy ją do bazy przestrzeni wektorowej \(V\). Ale ta rozrzerzona baza też musi mieć \(n\) elementów, a zatem wybrana baza przestrzeni \(U\) jest też bazą przestrzeni \(V\). To oczywiście implikuje, że \(U=V\).
Jeżeli mamy zbiór (lub układ wektorów) \(A\) przestrzeni wektorowej \(V\) i podprzestrzeń \( lin A\) jest skończenie wymiarowa, to rzędem \(A\) nazywamy liczbę \(\dim lin A\). Rząd \(A\) oznaczać będziemy symbolem \( rk A\).
Twierdzenie 2.10
Niech \(U\), \(W\) będą podprzestrzeniami przestrzeni skończenie wymiarowej przestrzeni wektorowej \(V\). Zachodzi wtedy wzór
Dowód
Wiemy już, że przestrzenie \(U\), \(W\), \(U\cap W\) są skończenie wymiarowe.
Niech \(e_1,...,e_m\) będzie bazą \(U\cap W\). Na podstawie Twierdzenia 2.8 wiemy, że układ ten można rozszerzyć do bazy przestrzeni \(U\) oraz do bazy przestrzeni \(W\).
Oznaczmy te bazy przez \(e_1,...,e_m, e_{m+1} ...e_{n_1}\) oraz \(e_1,..., e_m,e'_{m+1},..., e'_{n_2}\) odpowiednio. Twierdzimy, że zbiór
\(e_1,...,e_m, e_{m+1},..., e_{n_1},e'_{m+1},..., e'_{n_2}\) (2.3)
jest bazą przestrzeni \(U+W\).
Sprawdźmy najpierw generowanie. Niech \(v\in U + W\). Wtedy \(v=u+w\), gdzie \(u\in U\) i \(w\in W\). Istnieją skalary \(\alpha _1,..., \alpha _{n_1}\) oraz \(\beta _1,..., \beta _{n_2}\) takie, że
Wobec tego
Sprawdzimy teraz liniową niezależność układu (2.3). Niech
\(0=\lambda _1 e_1+...+ \lambda _m e_m + \lambda _{m+1}e_{m+1}+ ...+\lambda _{n_1} e_{n_1} + \lambda ' _{m+1}e'_{m+1}+...+\lambda ' _{n_2} e'_{n_2}.\) (2.4)
Oznaczmy przez \(w\) wektor \(\lambda ' _{m+1}e'_{m+1}+...+\lambda '_{n_2} e'_{n_2}\), zaś przez \(u\) wektor \(\lambda _1 e_1+...+\lambda _m e_m + \lambda _{m+1}e_{m+1}+ ...+\lambda _{n_1}e_{n_1}\). Wtedy \(u=-w\). Wektor \(u\) należy do \(U\), a wektor \(w\) do \(W\). A zatem obydwa te wektory należą do podprzestrzeni \(U\cap W\). Oznacza to, że \(w =\gamma _1e_1+... +\gamma _m e_m\) i w konsekwencji mamy
Z liniowej niezależności układu \(e_1,...,e_m,e'_{m+1},..., e'_{n_2}\) dostajemy, że skalary \(\lambda '_{m+1},..., \lambda '_{n_2}\) są równe zeru. Wracając teraz do równości (2.4) i korzystając z liniowej niezależności układu \(e_1,..., e_{n_1}\) otrzymujemy, że \(\lambda _1,...,\lambda _{n _1}\) są również równe zeru.
Dowód został zakończony.
Wróćmy teraz do pojęcia sumy prostej zdefiniowanego w poprzednim wykładzie.
Na podstawie Twierdzenia 2.10 mamy
Wniosek 2.11
Jeśli \(V\) jest skończenie wymiarowa i \(V=U\oplus W\), to \(\dim V=\dim U +\dim W\).
Mamy ponadto
Twierdzenie 2.12
Niech \(V\) będzie skończenie wymiarową przestrzenią wektorową a \(U\) jej podprzestrzenią. Istnieje wtedy dopełnienie algebraiczne do \(U\).
Dowód
Niech \(e_1,...e_m\) będzie bazą \(U\). Rozszerzmy ten układ do do bazy przestrzeni \(V\). Oznaczmy tę rozszerzoną bazę przez \(e_1,...,e_m, e_{m+1},..., e_n.\) Oznaczmy przez \(W\) przestrzeń rozpiętą na wektorach \(e_{m+1},..., e_n\). Wtedy \(V=U\oplus W\).
Zauważmy, że dopełnienie algebraiczne nie jest wyznaczone jednoznacznie.
Zakończymy ten wykład uwagami o przestrzeniach nieskończenie wymiarowych.
Przestrzeń \(V\) nazywa się przestrzenią nieskończenie wymiarową, jeśli nie jest skończenie wymiarowa. Mamy następujący lemat
Lemat 2.13
Jeśli przestrzeń \(V\) zawiera nieskończony zbiór wektorów liniowo niezależnych, to \(V\) jest nieskończenie wymiarowa.
Dowód
Gdyby przestrzeń \(V\) była skończenie wymiarowa, to na podstawie Twierdzenia 1.6, każdy zbiór liniowo niezależny tej przestrzeni byłby skończony.
Dowodzi się, co wykracza poza ramy tego wykładu, że w każdej przestrzeni wektorowej (również nieskończenie wymiarowej) istnieje baza i wszystkie bazy danej przestrzeni są równoliczne (czyli bijektywne).
Odwzorowania liniowe
Definicja odwzorowania liniowego
Definicja 1.1 [Odwzorowanie liniowe]
Niech \(V\), \(W\) będą przestrzeniami wektorowymi nad ciałem \(\mathbb K\) i niech \(f: V\longrightarrow W\) będzie odwzorowaniem. Mówimy, że \(f\) jest liniowe, jeśli spełnione są następujące warunki
L 1) dla każdych wektorów \(u,v\in Vf(u+v)=f(u)+f(v)\),
L 2) dla każdych \(\lambda \in \mathbb K\) i \(v\in Vf(\lambda v)=\lambda f(v)\).
Własność pierwszą nazywamy addytywnością odwzorowania \(f\), drugą - jednorodnością \(f\).
Zespół warunków L 1) i L 2) można zastąpić jednym z następujących warunków L 3) lub L4).
L 3) Dla każdych \(\lambda ,\mu \in \mathbb K\) i dla każdych \(u,v\in V\) zachodzi równość \(f(\lambda u+\mu v)=\lambda f(u) +\mu f(v)\).
L 4) Dla każdych skalarów \(\lambda _1,...,\lambda _k\in \mathbb K\), wektorów \(v_1,...,v_k\in V\) i każdego \(k\in \mathbb N\), zachodzi równość
Dowód równoważności warunków L 3) i L 4) polega na zastosowaniu indukcji.
Zauważmy od razu, że \(f(0)=f(0\cdot v)= 0\cdot f(v)\), gdzie \(v\) jest dowolnym wektorem przestrzeni \(V\). A zatem, dla odwzorowania liniowego zawsze mamy \(f(0)=0\).
Przykład 1.2
Odwzorowanie stale równe zeru jest liniowe. Odwzorowanie identycznościowe dowolnej przestrzeni wektorowej na siebie jest liniowe. Odwzorowanie to oznaczać będziemy przez \(I\).
Przykład 1.3
Weźmy przestrzeń \(V\) wszystkich funkcji ciągłych na przedziale \((a,b)\subset \mathbb R\) o wartościach w \(\mathbb R\). Odwzorowanie
jest odwzorowaniem liniowym.
Podobny przykład otrzymuje się dla całki oznaczonej.
Rozważmy jeszcze przestrzeń \(U\) funkcji różniczkowalnych na przedziale \((a,b)\subset \mathbb R\) i odwzorowanie przyporządkowujące funkcji z \(U\) jej pochodną. Odwzorowanie to jest liniowe.
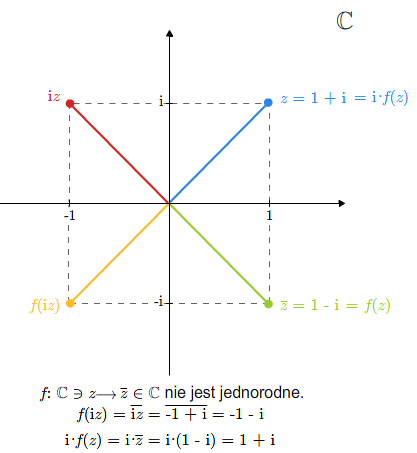
Przykład 1.4
Rozważmy odwzorowanie \(f:\mathbb C\ni z \longrightarrow \overline z\in \mathbb C\). Jeśli potraktujemy odwzorowanie \(f\) jako odwzorowanie przestrzeni wektorowych nad ciałem \(\mathbb C\), to odwzorowanie to nie jest liniowe, bo nie jest jednorodne.
Jeśli jednak potraktujemy \(\mathbb C\) jako przestrzeń wektorową nad ciałem \(\mathbb R\), to odwzorowanie \(f\) jest liniowe. Mówimy, że \(f\) jest \(\mathbb R\)-liniowe, ale nie jest \(\mathbb C\)-liniowe.
Własności odwzorowań liniowych. Obraz i jądro.
Omówimy teraz podstawowe własności odwzorowań liniowych.
Twierdzenie 2.1
Złożenie odwzorowań liniowych jest odwzorowaniem liniowym. Jeśli odwzorowanie liniowe jest bijekcją, to odwzorowanie odwrotne jest też liniowe.
Dowód
Tezy pierwszej dowodzi się bezpośrednim rachunkiem, co zostawiamy czytelnikowi. Dla sprawdzenia drugiej tezy ustalmy, że \(f:V\longrightarrow W\) jest liniową bijekcją. Niech \(w,w'\in W\). Wtedy istnieją jedne jedyne wektory \(v,v'\in V\) takie, że \(w=f(v)\) i \(w'=f(v')\). Zatem \(v=f^{-1}(w)\) i \(v' =f^{-1}(w')\). Niech \(\lambda, \mu\) będą dowolnymi skalarami. Zachodzą równości
Istotne cechy odwzorowań liniowych, często wykorzystywane w dalszej części wykładu, opisują następujące lematy
Lemat 2.2
Niech \(A\) będzie zbiorem generującym przestrzeń \(V\) i odwzorowania \(f, h: V\longrightarrow W\) będą liniowe. Jeśli \(f_{|A }=h_{|A}\), to \(f=h\).
Dowód
Niech \(v\in V\) będzie dowolnym wektorem. Istnieją wektory \(v_1,...,v_n\) ze zbioru \(A\) oraz skalary \(\lambda _1,...,\lambda _n\) takie, że \(v=\lambda _1v_1+...+\lambda _nv_n\). Ponieważ obydwa odwzorowania \(f\) i \(h\) są liniowe, więc \(f(v)=\lambda _1f(v_1)+...+\lambda _nf(v_n)= \lambda _1h(v_1)+...+\lambda _nh(v_n)=h(v)\).
Lemat 2.3
Niech \(B\) będzie bazą przestrzeni \(V\) i \(\tilde f: B\longrightarrow W\) będzie dowolnym odwzorowaniem.
Istnieje dokładnie jedno odwzorowanie liniowe \(f: V\longrightarrow W\) takie, że \(\tilde f =f_{| B}\)
Dowód
Dla dowolnego \(v\) istnieją wektory \(e_1,..., e_n\) należące do bazy i skalary \(\lambda _1,..., \lambda _n\) takie, że \(v=\lambda _1e_1+...+\lambda _ne_n\). Wybór wektorów z bazy i skalarów jest jednoznaczny. A zatem \(f\) zadane formułą
\(f(v)= \lambda _1\tilde f(e_1)+...+\lambda _n\tilde f(e_n)\) (2.1)
jest dobrze określone. Łatwo sprawdzić, że jest liniowe. Jest też oczywiste, że \(f\) musi być zadane formułą (2.1). Stąd jedyność \(f\) (lub z poprzedniego lematu).
Ostatni lemat mówi, że odwzorowanie liniowe może być zadane na bazie. Lemat dotyczy także przestrzeni nieskończenie wymiarowych.
Twierdzenie 2.4
Niech \(f: V\longrightarrow W\) będzie odwzorowaniem liniowym. Jeżeli \(U\) jest podprzestrzenią \(V\), to obraz podprzestrzeni \(U\) przez odwzorowanie f, czyli \(f(U)\), jest podprzestrzenią \(W\). Jeżeli \(U\) jest podprzestrzenią \(W\), to przeciwobraz podprzestrzeni \(U\) przez odwzorowanie \(f\), czyli \(f^{-1}(U)\), jest podprzestrzenią \(V\).
Dowód
Jeżeli \(w, z\in f(U)\), to \(w=f(v)\) i \(z=f(u)\) dla pewnych \(u, v\in U\). Zatem \(v+u\in U\) i \(w+z=f(v)+f(u)=f(v+u)\in f(U)\). Ponieważ \(\lambda u\in U\), więc \(\lambda z= \lambda f(u)=f(\lambda u)\in f(U)\) dla dowolnego skalara \(\lambda\).
Niech \(u,v\in f^{-1}(W)\). Wtedy \(f(u),f(v)\in W\) i, w konsekwencji, \(f(u)+f(v)\in W\). Zatem \(f(u+v)=f(u)+f(v)\in W\). Podobnie \(f(\lambda u)=\lambda f(u)\in W\) dla dowolnego \(\lambda\).
Dla odwzorowania liniowego definiuje się dwie ważne podprzestrzenie - obraz i jądro odwzorowania liniowego.
Definicja 2.5 [Jądro odwzorowania]
Niech \(f:V\longrightarrow W\) będzie odwzorowaniem liniowym. Jądrem odwzorowania \(f\) nazywamy podprzestrzeń \(f^{-1}(\{0\})\). Jądro oznaczamy symbolem \(\ker f\). Obrazem \(f\) nazywamy podprzestrzeń \(f(V)\) przestrzeni \(W\). Przestrzeń tę oznaczamy \( im f\). Wymiar przestrzeni \( im f\) nazywamy rzędem odwzorowania \(f\) i oznaczamy \( rk f\).
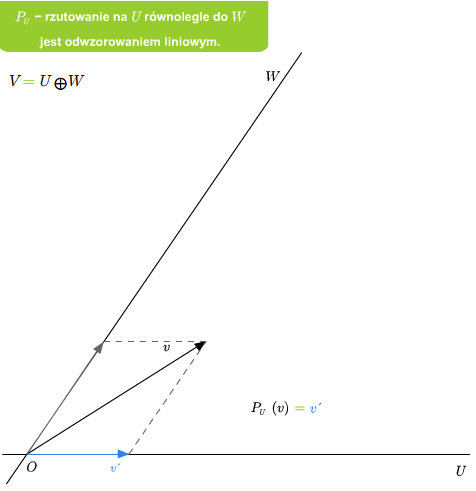
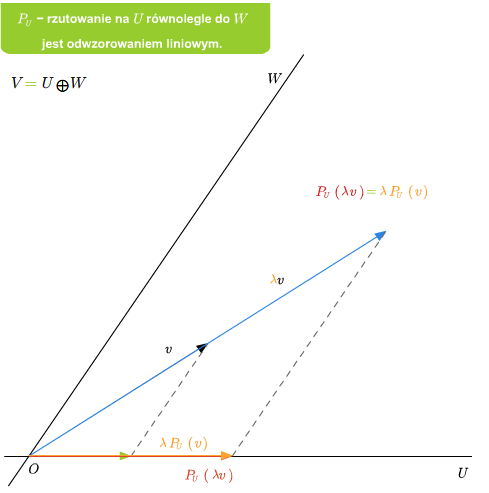
Przykład 2.6
Jeśli dana jest suma prosta \(V=U\oplus W\), to rzutowanie \(P_U\) na U równolegle do \(W\) jest liniowe. Ponadto \(\ker P_U=W\) oraz \( im P_U=U\).
Kolejny lemat wykorzystamy w dalszej części wykładu.
Lemat 2.7
Jeśli zbiór \(A\) generuje przestrzeń \(V\) i \(f:V\longrightarrow W\) jest odwzorowaniem liniowym, to \(f(A)\) generuje przestrzeń \( im f\).
Dowód
Oczywiście \(f(A)\subset im f\), a więc \( lin f(A)\subset im f\). Niech \(w\in im f\) i niech \(v\in V\) będzie takim wektorem, że \(f(v)=w\). Istnieją skalary \(\lambda _1,...,\lambda _n\in \) oraz wektory \(v_1,...,v_n\in A\) takie, że \(v=\lambda _1v_1+...+\lambda _nv_n\). Zatem \(w= f(v)= \lambda _1 f(v_1)+...+\lambda _n f(v_n)\in lin f(A)\).
Monomorfizmy. epimorfizmy, izomorfizmy
Definicja 3.1 [Monomorfizm]
Niech \(f\) będzie odwzorowaniem liniowym Odwzorowanie \(f\) nazywa się monomorfizmem, jeśli jest różnowartościowe. Odwzorowanie \(f\) nazywa się epimorfizmem, jeśli jest surjekcją. Odwzorowanie, które jest jednocześnie monomorfizmem i epimorfizmem (czyli liniowa bijekcja) nazywa się izomorfizmem.
Podamy teraz łatwe, ale bardzo ważne, twierdzenie charakteryzujące monomorfizmy.
Twierdzenie 3.2
Niech \(f:V\longrightarrow W\) będzie odwzorowaniem liniowym. Odwzorowanie to jest monomorfizmem wtedy i tylko wtedy, gdy \(\ker f=\{0\}\).
Dowód
Oczywiście \(0\in\ker f\). Niech \(f\) będzie monomorfizmem. Jeśli \(v\ne 0\), to \(f(v)\ne f(0)=0\). Oznacza to, że jedynym elementem zbioru \(\ker f\) jest wektor zerowy. Odwrotnie, jeśli \(\ker f\) składa się tylko z elementu zerowego i \(f(v)=f(u)\), to \(f(v-u)=f(v)-f(u)=0\), a więc \(u-v\in\ker f\). Ponieważ \(\ker f=\{0\}\), więc \(u=v\). Zatem \(f\) jest różnowartościowe.
Kolejne twierdzenie zawiera pewną charakteryzację monomorfizmów, epimorfizmów i izomorfizmów.
Twierdzenie 3.3
Niech \(f: V\longrightarrow W\) będzie odwzorowaniem liniowym.
- Jeżeli \(f\) jest monomorfizmem, to \(f\) przekształca każdy zbiór liniowo niezależny na zbiór liniowo niezależny.
- Jeżeli \(f\) przekształca injektywnie pewną bazę przestrzeni \(V\) na zbiór liniowo niezależny, to \(f\) jest monomorfizmem.
- Jeżeli \(f\) jest epimorfizmem, to \(f\) przekształca każdy zbiór generujący \(V\) na zbiór generujący przestrzeń \(W\).
- Jeżeli \(f\) przekształca pewien zbiór generujący \(V\) na zbiór generujący \(W\), to \(f\) jest epimorfizmem.
- Jeżeli \(f\) jest izomorfizmem, to przekształca każdą bazę przestrzeni \(V\) na bazę przestrzeni \(W\).
- Jeżeli \(f\) przekształca injektywnie pewną bazę przestrzeni \(V\) na bazę przestrzeni \(W\), to \(f\) jest izomorfizmem.
Dowód
Rozważmy implikację 1.
Niech \(B\) będzie zbiorem liniowo niezależnym w \(V\). Niech \(w_1,...,w_n\) będą różnymi między sobą wektorami z \(f(B)\) takimi, że \(\lambda _1 w_1+...+\lambda _nw_n =0\). Istnieją \(v_1,...,v_n\in B\) (różne między sobą, bo \(f\) jest injekcją) takie, że \(w_1=f(v_1),...,w_n=f(v_n)\). Mamy równości: \(f(\lambda _1 v_1+...+\lambda _nv_n) =\lambda _1 f(v_1)+...+\lambda _nf(v_n)=0\). Ponieważ \(f\) jest monomorfizmem, więc \(\lambda _1 v_1+...+\lambda _nv_n =0\). Wobec tego, ponieważ \(v_1,...,v_n\) są liniowo niezależne, wszystkie \(\lambda _i\), dla \(i=1,...,n\), są równe zeru.
Dla dowodu drugiej implikacji, załóżmy, że \(B\) jest bazą przestrzeni \(V\), przekształconą injektywnie na zbiór liniowo niezależny. Niech \(f(v)=0\). Istnieją skalary \(\lambda _1,...,\lambda _n\in \mathbb K\) oraz wektory \(v_1,...,v_n\in B\) takie, że \(v=\lambda _1v_1+...+\lambda _nv_n\). Mamy więc równość: \(0=\lambda _1f(v_1)+...+\lambda _n(v_n)\). Ponieważ \(f\) jest injekcją na bazie, więc wektory \(f(v_1),...,f(v_n)\) są różne między sobą. A zatem \(f(v_1),...,f(v_n)\) jest skończonym podzbiorem \(f(B)\). Jest liniowo niezależny, a więc wszystkie skalary \(\lambda _1\),...,\(\lambda _n\) są równe \(0\) i, w konsekwencji, \(v=0\).
Dowód pozostałych implikacji zostawiamy czytelnikowi.
Założenie w implikacji 2. w przypadku przestrzeni skończenie wymiarowych można sformułować tak:
Dla pewnej bazy \(e_1,...,e_n\) przestrzeni \(V\) układ \(f(e_1),...,f(e_n)\) jest liniowo niezależny.
Podobnie formułuje się założenie w implikacji 6.
Z powyższego twierdzenia, a także z dobrze już znanych faktów, że w skończenie wymiarowej przestrzeni każdy układ liniowo niezależny można uzupełnić do bazy i z każdego układu generatorów można wybrać bazę, dostajemy natychmiast
Wniosek 3.4
Niech \(V,W\) będą przestrzeniami skończenie wymiarowymi tego samego wymiaru. Niech \(f:V\longrightarrow W\) będzie odwzorowaniem liniowym. Następujące warunki są równoważne
- f jest monomorfizmem.
- f jest epimorfizmem.
- f jest izomorfizmem.
Z twierdzenia (3.3) wynika także
Wniosek 3.5
Jeżeli \(f:V\longrightarrow W\) jest izomorfizmem liniowym i przestrzeń \(V\) jest skończenie wymiarowa, to \(W\) jest też skończenie wymiarowa oraz \(\dim V=\dim W\).
Rząd odwzorowania liniowego
Kolejne twierdzenie opisuje ważny związek między wymiarami jądra i obrazu danego odwzorowania liniowego.
Twierdzenie 4.1
Niech \(f:V\longrightarrow W\) będzie odwzorowaniem liniowym. Jeżeli \(V\) jest skończenie wymiarowa, to
Dowód
Jeżeli \(\ker f=V\) lub \(\ker f=\{0\}\), twierdzenie jest trywialne. Załóżmy, że \(\ker f\ne V\) i \(\ker f\ne\{0\}\). Niech \(e_1,..., e_k\) będzie bazą \(\ker f\). Rozszerzmy tę bazę do bazy całej przestrzeni \(V\). Niech \(e_1,...,e_k,e_{k+1},..., e_{n}\) będzie bazą rozszerzoną. Twierdzimy, że wektory \(f(e_{k+1}),..., f(e_{n})\) stanowią bazę przestrzeni \( im f\).
Sprawdźmy najpierw, że wektory te generują przestrzeń \( im f\). Jeśli \(w\in im f\), to istnieje \(v\in V\) taki, że \(f(v)=w\). Wektor \(v\) da się przedstawić jako kombinacja liniowa wektorów bazy \(e_1,..., e_n\), tzn. \(v=\lambda _1e_1 +...+\lambda _ne_n\). Zatem
Aby sprawdzić liniową niezależność tych wektorów, załóżmy, że
dla pewnych skalarów \(\lambda _{k+1},...\lambda _n\). Wtedy \(f(\lambda _{k+1}e_{k+1}+...+ \lambda _{n}e_{n})=0\), czyli \(\lambda _{k+1}e_{k+1}+...+ \lambda _{n}e_{n} \in \ker f\). Wobec tego istnieją skalary \(\lambda _1,...,\lambda _k\) takie, że
Ponieważ układ wektorów \(e_1,...,e_k, e_{k+1},..., e_n\) jest liniowo niezależny, wszystkie skalary w powyższej równości, w szczególności skalary \(\lambda _{k+1},..., \lambda _n\), są równe \(0\).
Z Twierdzenia 2.7 otrzymujemy natychmiast
Wniosek 4.2
Niech \(V\) i \(W\) będą skończenie wymiarowe. Dla odwzorowania liniowego \(f:V\longrightarrow W\) jego rząd spełnia nierówność
Przestrzeń dualna
Przypomnijmy sobie Przykład 7. z Wykładu 2. Wiemy z niego, że ogół odwzorowań prowadzących z niepustego zbioru \(V\) do przestrzeni wektorowej \(W\) jest przestrzenią wektorową z działaniami wprowadzonymi w Przykładzie 7. Przypomnijmy, że
dla \(f,h\in W^V\), \(v\in V\) i \(\lambda \in\mathbb K\). Niech \(V,W\) będą, jak w całym tym wykładzie, przestrzeniami wektorowymi nad jednym ciałem \(\mathbb K\) i \(f, h:V\longrightarrow W\) - odwzorowaniami liniowymi. Łatwo widać, że suma tych odwzorowań, a także iloczyn odwzorowania liniowego przez skalar są odwzorowaniami liniowymi. Zatem ogół odwzorowań liniowych z przestrzeni \(V\) do \(W\) stanowi podprzestrzeń wektorową przestrzeni \(W^V\).
Rozważmy sytuację szczególną. Za \(W\) weźmy ciało \(\mathbb K\). Przestrzeń odwzorowań liniowych prowadzących z \(V\) do \(\mathbb K\) oznaczmy przez \(V^*\). Przestrzeń tę nazywamy przestrzenią dualną do \(V\). A zatem
Załóżmy teraz, że przestrzeń \(V\) jest skończenie wymiarowa i ma wymiar \(n\). Niech \(e_1,..., e_n\) będzie bazą tej przestrzeni. Zdefiniujemy ciąg \(e^*_1,..., e^*_n\) elementów przestrzeni \(V^*\) następująco. Pamiętając o tym, że odwzorowanie liniowe możemy zadać na bazie, określamy
\(e^*_i(e_j)=\delta _{ij},\) (5.2)
gdzie \(\delta _{ij}\) jest tzw. deltą Kroneckera. Symbol ten zdefiniowany jest następująco: \(\delta _{ij}=0\) dla \(i\ne j\) oraz \(\delta _{ij}=1\) dla \(i=j\).
Udowodnimy teraz
Twierdzenie 5.1
Ciąg \(e^*_1,..., e^*_n\) jest bazą przestrzeni \(V^*\).
Dowód
Układ \(e^*_1,..., e^*_n\) jest liniowo niezależny. Istotnie, niech
\(\lambda _1e^*_1+...+\lambda _ne ^*_n=0.\) (5.3)
Zero występujące z prawej strony tej równości oznacza odwzorowanie tożsamościowo równe zeru. Oznaczmy przez \(\alpha\) odwzorowanie określone przez lewą stroną równości (5.3). Dla każdego \(v\in V\) mamy \(\alpha (v)=0\). W szczególności dla każdego wektora \(e_i\) bazy \(e_1,...,e_n\) mamy \(\alpha (e_i)=0\). Wstawiając do obu stron równości (5.3) kolejne wektory bazy \(e_1,..., e_n\) stwierdzamy, że \(\lambda _1\),..., \(\lambda _n\) są równe zeru.
Aby stwierdzić że \(e^*_1,..., e^*_n\) stanowię zbiór generatorów przestrzeni \(V^*\) wystarczy sprawdzić, że dla każdego \(\alpha \in V^*\) mamy
\(\alpha =\alpha (e_1)e^*_1+...+\alpha (e_n)e^*_n.\) (5.4)
Dla sprawdzenia tej równości, wystarczy porównać wartości
odwzorowań liniowych znajdujących się po obydwu jej stronach na
kolejnych wektorach bazy \(e_1,...,e_n\).
Formuła (5.4) jest sama w sobie ważna i bardzo pożyteczna.
Zauważmy jeszcze, że jeśli \(f:V\longrightarrow W\) jest liniowe, to
definiując odwzorowanie
otrzymujemy odwzorowanie liniowe. Sprawdzenie zostawiamy czytelnikowi. Odwzorowanie to nazywamy odwzorowaniem dualnym (lub transponowanym) do \(f\).
Korzystając bezpośrednio z definicji odwzorowania dualnego, łatwo sprawdzić następujący fakt
Twierdzenie 5.2
Niech \(f: V \longrightarrow W, h: W \longrightarrow Z\) będą odwzorowaniami liniowymi. Zachodzi równość odwzorowań
Macierze
Definicja macierzy, podstawowe pojęcia
Niech ustalone będzie ciało \(\mathbb K\) i dwie liczby naturalne \(m\), \(n\).
Macierzą o wyrazach z ciała \(\mathbb K\) i wymiarach \(m\) na \(n\) nazywamy każdą funkcję
Macierz taką zapisujemy w postaci tabelki
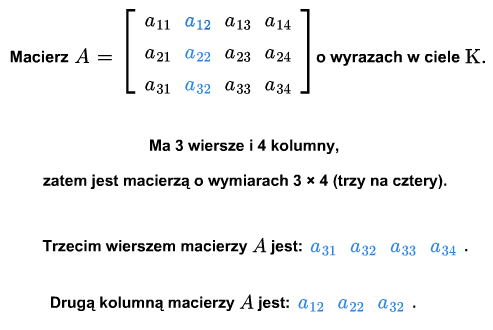
\(A= \left [\begin{array} {crclc} \ a_{11} &\cdot&\cdot &\cdot & a_{1n}\\ \ \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot \ \ \ & \cdot \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot\ \ \ & \cdot \\ \ \cdot &\ \ \ \cdot&\cdot &\cdot \ \ \ & \cdot \\ \ \\ \ a_{m1}&\cdot&\cdot &\cdot & a_{mn} \end{array} \right ]\) (1.1)
Macierz zapisujemy również na wiele innych sposobów, w zależności od tego jaką jej cechę chcemy wziąć pod uwagę lub podkreślić. I tak, możemy zapisać macierz jako \(A_{m\times n}\) (określono wymiary macierzy), \([a_{ij}]\) (oznaczono wyrazy macierzy), \(A=A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array}}\), (nazwano wyrazy, określono wymiary) lub po prostu \(A\) (dokładniejsze informacje są niepotrzebne lub wynikają z kontekstu).
Ciąg \(a_{i1},..., a_{in}\), \(i=1,...,m\) nazywamy \(i\)-tym wierszem macierzy (1.1). Ciąg \(a_{1j},...,a{mj}\), \(j=1,...,n\), nazywamy \(j\)-tą kolumną macierzy (1.1).
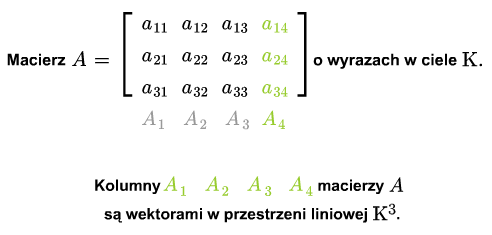
Niech \(A_1,...,A_n\) będą kolumnami macierzy \(A\). Jest to ciąg wektorów z \(\mathbb K ^m\). Rząd układu kolumn \(A_1,...,A_m\) nazywamy rzędem macierzy i oznaczamy \( rk A\).

Mamy następujący lemat przydatny w rachunku macierzy
Lemat 1.1
Niech dany będzie układ wektorów \(w_1,...,w_k\), \(k>1\), przestrzeni wektorowej \(V\). Wtedy \( rk \{w_1,...,w_k\}= rk \{ u_1, w_2,...,w_k\}\), gdzie \(u_1 =w_1 +\lambda _2w_2+...+\lambda_kw_k\) i \(\lambda _2,...,\lambda _k\) są dowolnymi skalarami.
Dowód
Pokażemy, że \( lin \{w_1,...,w_k\}= lin \{u_1,w_2,...,w_k \}\). Oczywiście prawa strona zawiera się w lewej. Ponieważ \(w_1=u_1-\lambda _2w_2-...-\lambda _k w_k\), więc lewa strona zawiera się w prawej.
Mówimy krótko, że rząd układu wektorów nie zmieni się, jeśli do któregoś z jego wektorów dodamy kombinacją liniową wektorów pozostałych.
A zatem rząd układu kolumn nie zmieni się, jeśli do którejś kolumny dodamy kombinację liniową pozostałych kolumn.
Oczywiście, jeśli spermutujemy kolumny, to, choć macierz najczęściej istotnie się zmieni, jej rząd się nie zmieni.
Jeśli którąkolwiek z kolumn macierzy \(A\) pomnożymy przez niezerowy skalar, to rząd macierzy nie zmieni się.
Wszystkie wymienione wyżej operacje na macierzy, tj. dodanie do danej kolumny kombinacji liniowej pozostałych kolumn, pomnożenie kolumny przez niezerowy skalar, permutowanie kolumn, nazywamy operacjami dopuszczalnymi (ze względu na rząd macierzy).
Macierz \(A_{m\times n}\) nazywamy kwadratową, jeśli \(m=n\).
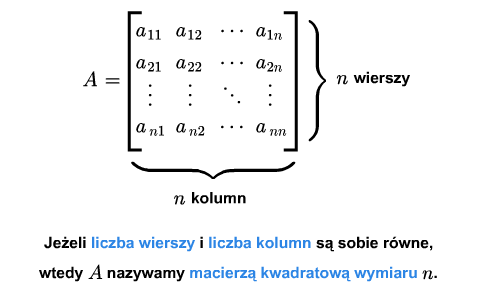
W przeciwnym wypadku mówimy, że macierz jest prostokątna (dla podkreślenia, że nie jest kwadratowa). Dla macierzy kwadratowej podaje się jeden wymiar.
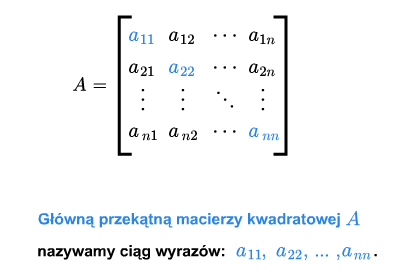
Dla macierzy kwadratowej \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le n\\ 1\le j\le n \end{array} }\) definiujemy główną przekątną jako ciąg \(a_{11},..., a_{nn}\).
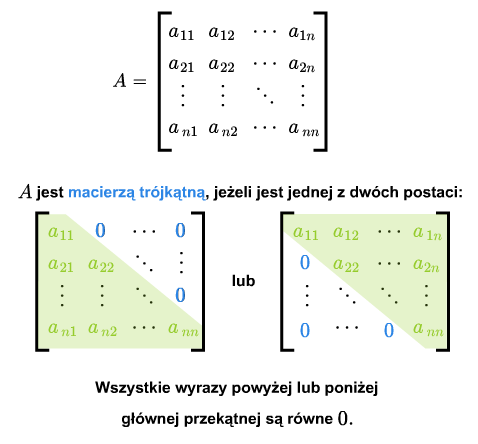
W macierzy kwadratowej można wyróżnić wyrazy leżące ponad przekątną i wyrazy leżące poniżej przekątnej. Macierz kwadratowa nazywa się macierzą trójkątną, jeśli wszystkie jej wyrazy leżące ponad główną przekątną lub wszystkie wyrazy leżące poniżej głównej przekątnej są zerami.
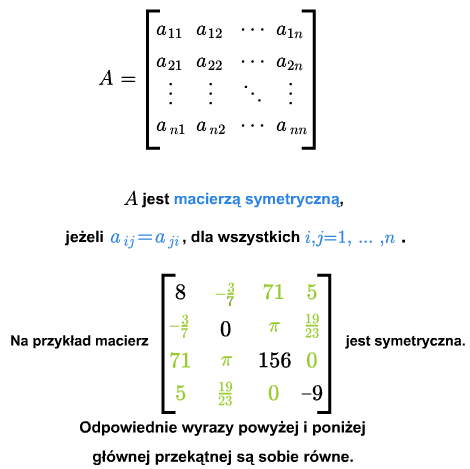
Macierz kwadratową \(A={[a_{ij}]}_{1\le i,j\le n}\) nazywa się symetryczną, jeśli \(a_{ij} =a_{ji}\) dla każdych \(i,j=1,...,n\).
Macierz \(A\) nazywa się antysymetryczną (lub skośnie symetryczną), jeśli \(a_{ij}=-a_{ji}\) dla każdych \(i,j=1,...,n\). W macierzy skośnie symetrycznej wszystkie wyrazy leżące na głównej przekątnej są równe zeru.
Macierz kwadratowa nazywa się diagonalną, jeśli wszystkie jej wyrazy poza główną przekątną są zerami.
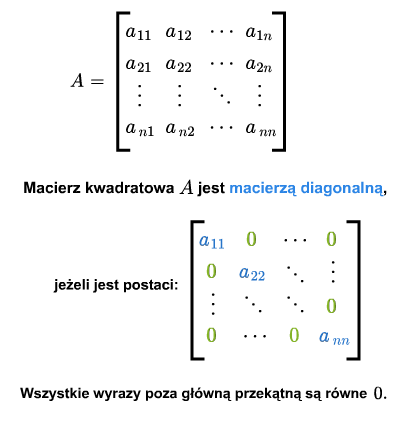
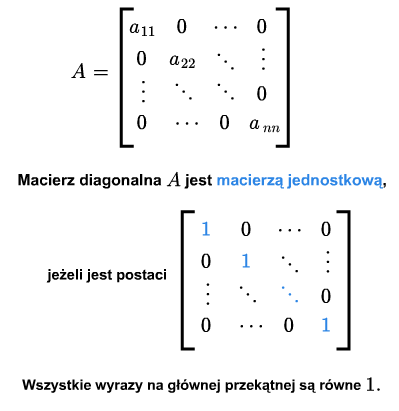
Macierz kwadratowa nazywa się jednostkową, jeśli jest diagonalna a na jej głównej przekątnej są same jedynki. Macierz tę oznaczać będziemy przez \(I\) lub \(I_{n\times n}\).
Oznaczyliśmy już(w Wykładzie 3.) przez \(I\) odwzorowanie identycznościowe danej przestrzeni wektorowej. Okaże się wnet, że nie ma tu wielkiej kolizji oznaczeń.
Operacje na macierzach
Zbiór wszystkich macierzy o wymiarach \(m\) na \(n\) i wyrazach z \(\mathbb K\) oznaczmy przez \(M(m,n;\mathbb K)\). Zbiór ten jest podprzestrzenią przestrzeni \(\mathbb K ^X\), gdzie \(X=\{1,..., m\}\times \{1,...,n\}\) (porównaj Przykład 7. Wykładu 2.)
W szczególności, działania w \(M(m,n;\mathbb K)\) są określone następująco. Niech
Sumą macierzy \(A\) i \(B\) jest macierz następująca
Jeśli \(\lambda\in\mathbb K\), to macierz \(\lambda A\) jest
zdefiniowana tak

Z Przykładu 7. Wykładu 2. wiemy, że dodawanie w \(M(m,n;\mathbb K)\) jest łączne, przemienne, ma element neutralny (który jest macierzą składająca się z samych zer) i każda macierz ma macierz przeciwną. Macierzą przeciwną do macierzy (1.1) jest macierz
Ustalimy teraz jaki jest wymiar przestrzeni \(M(m,n;\mathbb K)\). Rozważmy odwzorowanie
Z grubsza mówiąc, odwzorowanie to polega na przepisaniu kolejnych wierszy jeden po drugim w jednym ciągu. Oczywiście odwzorowanie to jest bijekcją.
Ponadto, łatwo widać, że odwzorowanie to jest liniowe. Zatem odwzorowanie to jest izomorfizmem. Mamy więc
Wniosek 2.1
Zachodzi równość \(\dim M(m,n;\mathbb K)=mn\).
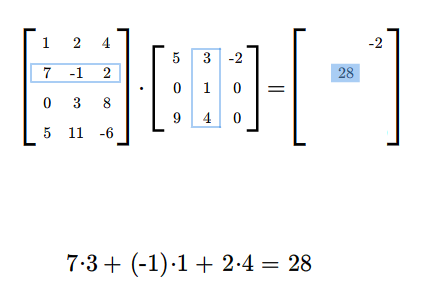
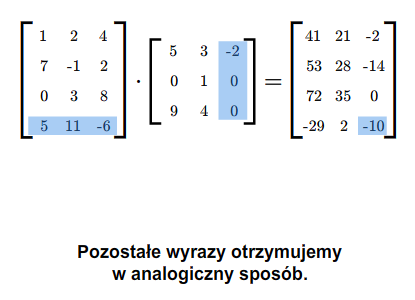
Załóżmy teraz, że mamy dwie macierze: \(A=A_{m\times k}\) i \(B=B_{k\times n}\). Możemy zdefiniować iloczyn tych macierzy \(A B\) według następującego przepisu. Jeżeli \(\displaystyle A= [a_{il}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le l\le k \end{array} }\) i \(\displaystyle B=[b_{lj}]_ {\tiny\begin{array} {l} 1\le l\le k\\ 1\le j\le n \end{array} }\), to \(AB\) jest macierzą \(C=[c_{ij}]\) o wymiarach \(m\) na \(n\), której wyrazy określone są formułą
dla wszystkich wskaźników \(i,j\), gdzie \(i=1,...,m\) oraz \(j=1,..., n\).
Podkreślmy mocno, że możemy wykonać mnożenie \(AB\) tylko takich macierzy \(A\), \(B\), dla których liczba kolumn macierzy \(A\) jest równa liczbie wierszy macierzy \(B\). W rezultacie mnożenia otrzymujemy macierz, która ma tyle wierszy co macierz \(A\) i tyle kolumn co macierz \(B\).
Mnożąc macierze najpierw sprawdzamy, czy możemy je pomnożyć, następnie ustalamy wymiary iloczynu macierzy. Potem wyliczamy wyrazy iloczynu (w dowolnej kolejności), być może tylko te, które chcemy znać.
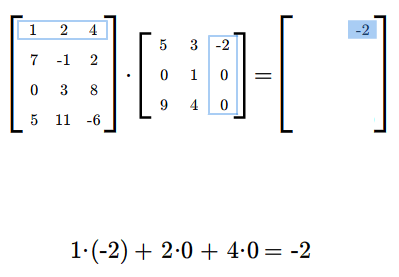
Mnożenie macierzy jest łączne, tzn. jeśli \(A,B,C\) są takie, że można wykonać mnożenia \(AB\) i \(C(AB)\), to można też wykonać mnożenia \(CA\) i \((CA)B\) oraz \(C(AB)=(CA)B\). Można tę własność bezpośrednio przerachować. W następnym wykładzie pokażemy, że łączność ta jest konsekwencją łączności składania odwzorowań.
Zachodzi też następująca własność rozdzielności mnożenia macierzy względem dodawania macierzy. Jeśli \(A, B\in M(k,n;\mathbb K)\) i \(C\in M(m,k;\mathbb K)\), to \(C(A+B)=CA+CB\). Podobnie można sformułować prawo rozdzielności \((A+B)C\). Objaśnimy tę własność w następnym wykładzie. Można też te własności bezpośrednio sprawdzić.
Nietrudno sprawdzić, że jeśli \(A=A_{m\times n}\) oraz \(I=I_ n\times n}\), to \(AI=A\). Podobnie, jeśli \(A=A_{m\times n}\) oraz \(I=I_{m\times m}\), to \(IA=A\).
Przez \(n\)-tą potęgę \(A^n\) macierzy kwadratowej \(A\) rozumiemy iloczyn \(n\) egzemplarzy macierzy \(A\).
Przykład 2.2
Dowolna potęga macierzy diagonalnej jest macierzą diagonalną. Jeśli
to
Przykład 2.3
Niech
Indukcyjnie można udowodnić, że
gdzie
Przykład 2.4
Jeśli
to stosując indukcję można stwierdzić, że
gdzie \(\{a_m\}\) jest ciągiem Fibonacciego, czyli ciągiem zdefiniowanym wzorem rekurencyjnym
Przykład 2.5
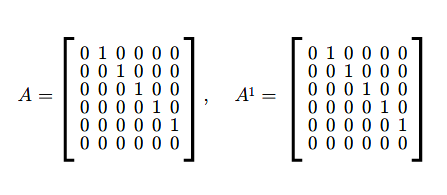
Niech \(A\in M(n,n;\mathbb K)\)
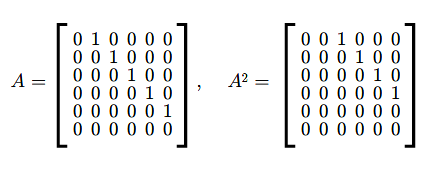
\(A=\left [\begin{array} {lcccccr} \ 0 &1& & & & 0\\ \ 0& 0& 1& & & 0\\ \ .&. & .& .& .& .\\ \ 0 & & & 0 & 1 & 0\\ \ 0 & & & & 0 & 1\\ \ 0 & & & & &0 \end{array} \right ]\) (2.2)
Łatwo sprawdzić, że \(A^{n}=0\).
Jeżeli dany jest wielomian \(W(t)=a_0 +a_1t+....+a_r t^r\) jednej zmiennej \(t\) o współczynnikach z ciała \(\mathbb K\) i \(A\) jest macierzą kwadratową, to przez \(W(A)\) rozumiemy macierz
gdzie \(I\) jest macierzą jednostkową takiego samego wymiaru co macierz \(A\). Każdy wielomian \(W(t)\), dla którego \(W(A)=0\), nazywa się anihilatorem macierzy \(A\).
Ogólna grupa liniowa
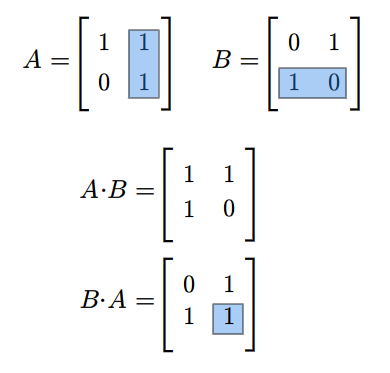
Rozważmy teraz przestrzeń macierzy kwadratowych \(M(n,n;\mathbb K)\). Każde dwie macierze \(A,B\in M(n,n;\mathbb K)\) można pomnożyć w obydwu kolejnościach, tzn. można znaleźć zarówno iloczyn \(AB\) jak i \(BA\). Na ogół macierze \(AB\) i \(BA\) są różne. Na przykład weźmy następujące macierze (istniejące dla każdego ciała \(\mathbb K\))
Mamy
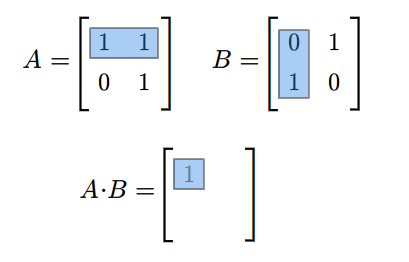
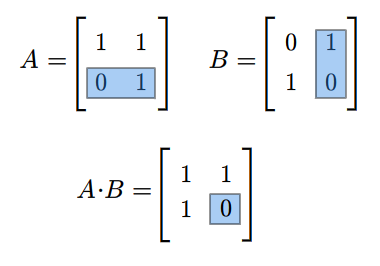
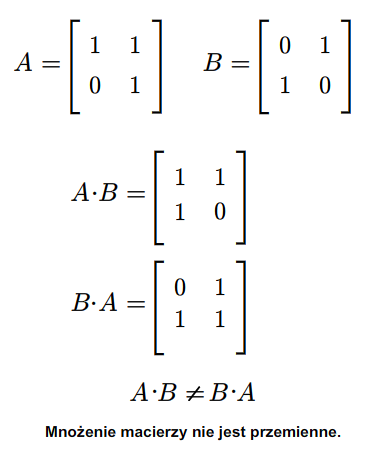
Macierz kwadratową \(A\in M(n,n:\mathbb K)\) nazywamy odwracalną, jeśli istnieje macierz \(B\in M(n,n;\mathbb K)\) taka, że
\(AB=BA=I.\) (3.3)
Macierz \(B\) spełniająca (3.3) jest jedyna.
Przypuśćmy, że \(AB'=B'A=I\). Pomnóżmy równość \(AB=I\) obustronnie z lewej strony przez \(B'\). Mamy następujące równości \(B'(AB)=B'\). Korzystając z łączności mnożenia macierzy otrzymujemy
\(B'=(B'A)B=IB=B\). A zatem \(B=B'\). Mogliśmy również skorzystać z pierwszego wykładu, z fragmentu poprzedzającego definicję grupy.
Macierz \(B\) spełniającą warunek (3.3) nazywamy macierzą odwrotną do \(A\). Oznaczamy tę macierz przez \(A^{-1}\).
Zbiór macierzy \(A\in M(n,n;\mathbb K)\) odwracalnych stanowi grupę. Grupa ta, poza przypadkiem \(n=1\), jest nieprzemienna. Grupę tę oznaczamy \(GL(n;\mathbb K)\) i nazywamy ogólną grupą liniową nad ciałem \(\mathbb K\).
Niech będzie daną macierzą. Macierzą dualną (lub transponowaną) do macierzy \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} }\) nazywamy macierz \(A^*= [a_{ji}]_ {\tiny\begin{array} {l} 1\le j\le n\\ 1\le i\le m \end{array} }\). A zatem macierz \(A^*\) powstaje z macierzy \(A\) przez zamianę wierszy na kolumny.
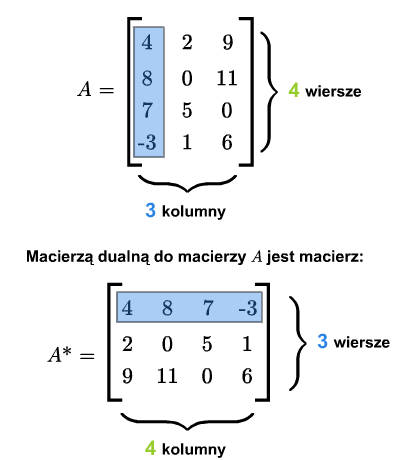
Macierz dualna do macierzy \(A^*\) jest macierzą \(A\), czyli \((A^*)^*=A\). Macierz kwadratowa \(A\) jest symetryczna wtedy i tylko wtedy, gdy \(A^*=A\). Macierz kwadratowa \(A\) jest skośnie symetryczna wtedy i tylko wtedy, gdy \(A^*=-A\).
Macierze a odwzorowania liniowe
W niniejszym wykładzie wszystkie rozważane przestrzenie są skończenie wymiarowe a bazy są uporządkowane.
Macierz odwzorowania liniowego
Niech dane będą przestrzenie wektorowe \(V\) i \(W\) nad ciałem \(\mathbb K\) oraz odwzorowanie liniowe \(f:V\longrightarrow W\).
Niech \(e_1,...,e_n\) będzie bazą przestrzeni wektorowej \(V\), zaś \(e'_1,...,e'_m\) bazą przestrzeni \(W\). Dla odwzorowania liniowego \(f\) mamy
\(\begin{array} {rcl} &&f(e_1) =a_{11}e'_1+... +a_{m1}e'_m,\\ &&\ \ \ .\\ &&\ \ \ .\\ &&\ \ \ .\\ &&f(e_n)= a_{1n}e'_1+...+a_{mn}e'_m. \end{array}\) (1.1)
dla pewnych skalarów \(a_{ij}\), \(i=1,...,m\), \(j=1,...,n\). Inaczej zapisując
dla każdego \(j=1,...,n\).


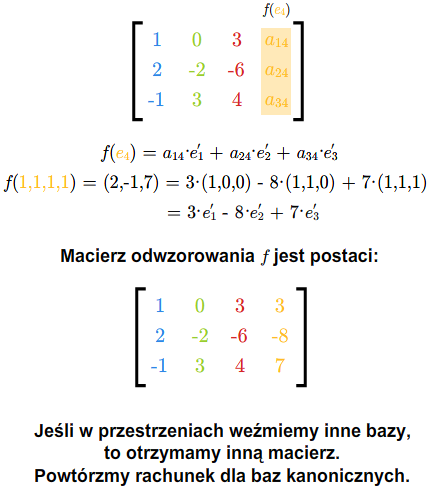




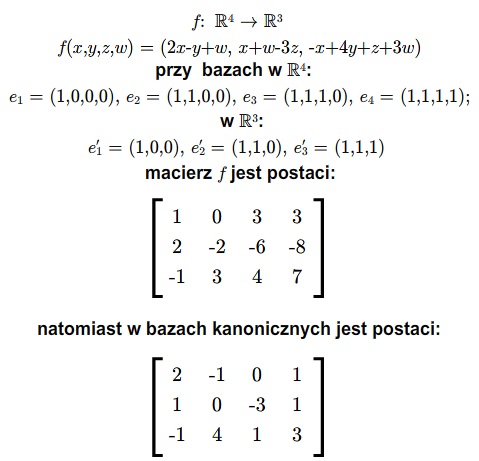
Otrzymaliśmy więc macierz \(A=[a_{ij}]_ {\tiny\begin{array} {l} 1\le i\le m\\ 1\le j\le n \end{array} }\), która całkowicie opisuje odwzorowanie liniowe \(f\). Istotnie, jeśli znamy wartości odwzorowania liniowego na bazie, to znamy to odwzorowanie. Macierz tę nazywamy macierzą odwzorowania \(f\) przy bazach \(e_1,...,e_n\) i \(e'_1,...,e'_m\).
Jeśli mamy daną macierz \(A\), ustalone bazy w przestrzeniach \(V\), \(W\), to macierz ta jest macierzą odwzorowania liniowego \(f:V\longrightarrow W\). Odwzorowanie to jest dane formułą (1.1).
Wygodnie jest myśleć o macierzach jako o odwzorowaniach liniowych. Jeśli żadne szczególne przestrzenie nie są wyróżnione, to macierz \(A=A_{m\times n}\) możemy traktować jako odwzorowanie liniowe \(f:\mathbb K ^n\longrightarrow \mathbb K^m\) dane przepisem (1.1), gdzie \(e_1,...,e_n\) jest bazą kanoniczną przestrzeni \(\mathbb K ^n\), zaś \(e'_1,...,e'_m\) jest bazą kanoniczną przestrzeni \(\mathbb K ^m\).
Jeśli \(A\) jest macierzą odwzorowania \(f:V\longrightarrow W\) i przez \(A_1,..., A_n\) oznaczymy kolumny macierzy \(A\), to każda kolumna \(A_j\) jest ciągiem współrzędnych wektora \(f(e_j)\) w bazie \(e'_1,..., e'_m\). Oznacza to, że układ kolumn macierzy \(A\) można uważać za wektory (wyrażone we współrzędnych w bazie \(e_1,...,e_n\)) \(f(e_1),...,f(e_n)\). Rząd odwzorowania \(f\) jest więc rzędem układu wektorów \(A_1,..., A_n\) macierzy \(A\).
Mamy więc
Twierdzenie 1.1
Jeśli \(A\) jest macierzą odwzorowania \(f:V\longrightarrow W\) przy pewnych bazach przestrzeni \(V\) i \(W\), to \( rk A= rk f\).
Niech \(f,h :V\longrightarrow W\) będą dwoma odwzorowaniami liniowymi. Wiemy, że suma tych odwzorowań jest odwzorowaniem liniowym. Przy danych bazach \(e_1,...,e_n\), \(e'_1,...,e'_m\) przestrzeni \(V\) i \(W\) odpowiednio, macierz odwzorowania \(f+h\) jest sumą macierzy \(A_f+A_h\), gdzie \(A_f\) jest macierzą odwzorowania \(f\) a \(A_h\) macierzą odwzorowania \(h\). A zatem dodawanie macierzy odpowiada dodawaniu odwzorowań liniowych. Podobnie mnożeniu macierzy przez skalar odpowiada mnożenie odwzorowania liniowego przez skalar.
Załóżmy teraz, że mamy trzy przestrzenie wektorowe \(V\), \(W\), \(U\). Załóżmy ponadto, że \(e_1,...,e_n\) jest bazą \(V\), \(e'_1,...,e'_k\) jest bazą \(W\) i \(e''_1,...,e''_m\) jest bazą \(U\). Niech \(f:V\longrightarrow W\) i \(h:W\longrightarrow U\) będą odwzorowaniami liniowymi. Oznaczmy przez
macierze odwzorowania \(f\), \(h\) i \(h\circ f\) odpowiednio, przy danych bazach. Zachodzą następujące równości
Z drugiej strony
Zatem
Oznacza to, że
Krótko mówiąc, mnożenie macierzy odpowiada składaniu odwzorowań liniowych. Ponieważ składanie odwzorowań jest łączne, więc mnożenie macierzy jest łączne. Wspomnieliśmy już tę własność w poprzednim wykładzie. Teraz uzasadniliśmy jej prawdziwość.
Zauważmy także, że jeśli \(h_1, h_2: W\longrightarrow U\), to \((h_1+h_2)\circ f= h_1\circ f +h_2\circ f\). Jeśli \(f_1, f_2:V\longrightarrow W\), to \(h\circ (f_1+f_2)=h\circ f_1 +h\circ f_2\). W języku macierzy oznacza to, że \((B_1 +B_2)A=B_1A+B_2A\) oraz \(B(A_1+A_2)=BA_1+BA_2\) (jeśli występujące tu dodawania i mnożenia macierzy można wykonać). Te własności rachunku macierzy również wymieniliśmy w poprzednim wykładzie.
Macierz dualna i odwzorowanie dualne
Niech \(e^*_1,..., e^*_n\) będzie bazą dualną do bazy \(e_1,...,e_n\) przestrzeni \(V\) i \(e'^*_1,...,e'^*_m\) bazą dualną do bazy \(e'_1,...,e'_m\) przestrzeni \(W\). Rozważmy odwzorowanie dualne \(f^*:W^* \longrightarrow V^*\). Chcemy znaleźć macierz \(f^*\) przy wyróżnionych właśnie bazach dualnych. Oznaczmy poszukiwaną macierz przez \(B=[b_{ji}]_ {\tiny\begin{array} {l} 1\le j\le n\\ 1\le i\le m \end{array} }\), czyli
Po obydwu stronach powyższej równości mamy wektory z \(V^*\), czyli odwzorowania liniowe określone na \(V\) i o wartościach w \(\mathbb K\). Obliczymy wartość tych odwzorowań na wektorach bazy \(e_1,..., e_n\). Otrzymujemy
Z drugiej strony
A zatem \(a_{is}=b_{si}\), co oznacza, że macierz \(B\) jest macierzą dualna do macierzy \(A\).
Macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego, jeśli w przestrzeniach dualnych wybierzemy bazy dualne.
Stąd, że dla odwzorowań liniowych zachodzi formuła \((f \circ h)^* = h^* \circ f^*\), otrzymujemy analogiczną formułą dla macierzy.
Twierdzenie 2.1
Jeśli iloczyn \(AB\) jest wykonalny, to wykonalny jest iloczyn \(B^* A^*\) oraz
Udowodnimy teraz następujące twierdzenie
Twierdzenie 2.2
Rząd odwzorowania dualnego do \(f\) jest równy rzędowi odwzorowania \(f\).
Dowód
Wiemy, że
\( rk f^*=\dim W^*-\dim ker f^*=\dim W-\dim\ker f^*.\) (2.2)
Przyjrzyjmy się więc przestrzeni \(\ker f^*\). Mamy
Weźmy bazę \(w_1,...,w_k\) przestrzeni \( im f\). Jeśli \( im f= W\), to \( rk f=\dim W\) i \(\ker f^*= \{0\}\). Twierdzenie w tym przypadku jest prawdziwe..
Jeśli \( im f\ne W\), to układ \(w_1,...,w_k\) rozszerzmy do bazy
przestrzeni \(W\). Przestrzeń \(U\) rozpięta na wektorach \(w_{k+1},...,w_m\) jest dopełnienieniem algebraicznym do \( im f\) w \(W\), czyli \(W=U\oplus im f\). Zauważmy,
że odwzorowanie
jest izomorfizmem. Oczywiście odwzorowanie \(\phi\) jest liniowe. Jeśli \(\phi(\beta)=0\), to \(\beta_{|U}\) i \(\beta _{| im f}\) są odwzorowaniami zerowymi. A zatem, \(\beta\) jest odwzorowaniem zerowym na całym \(W\). Odwzorowanie \(\phi\) jest więc monomorfizmem.
Jest też epimorfizmem. Jeśli bowiem \(\gamma :U\longrightarrow \mathbb K\) jest liniowe, to odwzorowanie liniowe \(\beta: W\longrightarrow \mathbb K\) zdefiniowane na bazie przestrzeni \(W\) następująco: \(\beta (w_i)=0\) dla \(i=1,...,k\),\(\beta (w_i)=\gamma (w _i)\) dla \(i=k+1,..., m\), jest takie, że \(\phi (\beta)=\gamma\).
Ponieważ \(\phi\) jest izomorfizmem, więc \(\dim\ker f^* = \dim U ^* =\dim U =m-k =\dim W- rk f\). Porównując tę równość z równością z pierwszego zdania tego dowodu otrzymujemy żądaną tezę.
Z powyższego twierdzenia i stąd, że macierz odwzorowania dualnego jest macierzą dualną do macierzy odwzorowania danego wynika następujący wniosek
Wniosek 2.3
Dla dowolnej macierzy \(A\) zachodzi równość \( rk A= rk A^*\).
Przypomnijmy sobie teraz operacje dopuszczalne na macierzy (ze względu na rząd macierzy). Korzystając z równości \({rk} A={rk} A^*\) dostajemy natychmiast kilka kolejnych operacji dopuszczalnych, tzn. nie zmieniających rzędu macierzy. Mianowicie, dodając do danego wiersza macierzy \(A\) kombinację liniową pozostałych wierszy tej macierzy, nie zmieniamy jej rzędu. Mnożąc dowolny wiersz przez niezerowy skalar nie zmieniamy rzędu macierzy. I wreszczcie, permutując wiersze macierzy nie zmieniamy jej rzędu.
Tak jak w dowodzie twierdzenia o istnieniu bazy z Wykładu 2. możemy stwierdzić, że rząd skończonego układu wektorów jest równy maksymalnej liczbie wektorów liniowo niezależnych, które można wybrać z danego układu wektorów.
A zatem mamy następujące twierdzenie
Twierdzenie 2.4 [Rząd macierzy]
Niech \(A\in M(m,n;\mathbb K)\).
- Rząd macierzy A jest równy maksymalnej liczbie kolumn liniowo niezależnych, które można wybrać z macierzy \(A\).
- Rząd macierzy A jest równy maksymalnej liczbie wierszy liniowo niezależnych, które można wybrać z macierzy \(A\).
Macierz odwrotna, ogólna grupa liniowa
Załóżmy teraz, że \(V=W\) i \(f:V\longrightarrow V\) jest endomorfizmem. Wybieramy jedną bazę, tzn. bazę \(e_1,...,e_n\) przestrzeni \(V\), i definiujemy macierz kwadratową \(A=[a_{ij}]_ {\small 1\le i,j\le n}\) formułą
\(\begin{array} {rcl} &&f(e_1) =a_{11}e_1+... +a_{n1}e_n,\\ &&\ \ \ .\\ &&\ \ \ .\\ &&\ \ \ .\\ &&f(e_n)= a_{1n}e_1+...+a_{nn}e_n. \end{array}\) (3.3)
Ponieważ mnożenie macierzy odpowiada składaniu odwzorowań, więc odwracalność macierzy \(A\) jest równoważna izomorficzności odwzorowania \(f\). Ponadto macierz odwrotna \(A^{-1}\) do macierzy \(A\) jest macierzą odwzorowania odwrotnego \(f^{-1}\).
Ogólną grupę liniową \(GL(n;\mathbb K)\) możemy traktować jako grupę wszystkich izomorfizmów liniowych \(f:\mathbb K^n\longrightarrow\mathbb K^n\), z działaniem będącym składaniem odwzorowań. Pamiętamy, że grupa ta dla \(n>1\) jest nieprzemienna. Zauważyliśmy już, że macierz kwadratowa \(A\) jest odwracalna wtedy i tylko wtedy, gdy jest macierzą izomorfizmu. Odwzorowanie liniowe \(f:\mathbb K ^n\longrightarrow \mathbb K^n\) jest izomorfizmem wtedy i tylko wtedy, gdy \( rk f=n\). Oznacza to, że prawdziwe jest następujące twierdzenie
Twierdzenie 3.1
Macierz kwadratowa \(A=A_{n\times n}\) jest odwracalna wtedy i tylko wtedy, gdy \( rk A=n\).
Macierz przejścia
Niech \(e_1,...,e_n\) będzie bazą przestrzeni \(V\) i niech \(e'_1,..., e'_n\) będzie inną bazą tej samej przestrzeni. Istnieją jednoznacznie określone skalary \(p_{ij}\), \(1\le i,j\le n\), takie, że
\(\displaystyle e'_j=\sum _{i=1}^n p_{ij}e_i,\) (4.4)
dla \(j=1,...n\). Macierz \(P=[p_{ij}]_{1\le i, j\le }\) nazywa się macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\). Macierz przejścia jest macierzą izomorfizmu przestrzeni \(V\), który przekształca bazę \(e_1,...,e_n\) na bazę \(e'_1,...,e'_n\) i macierz ta jest utworzona przy bazie \(e_1,...,e_n\). W szczególności, macierz przejścia jest macierzą odwracalną.
Zamieńmy rolami dane bazy. Istnieją jednoznacznie wyznaczone skalary \(q_{ij}\), \(1\le i,j\le n\), takie, że
Macierz \([q_{ij}]\) oznaczmy przez \(Q\).
Otrzymujemy więc następujące równości
dla każdego \(i=1,...,n\). Oznacza to, że \(\displaystyle \sum _{j=1}^n p_{lj}q_{ji}=\delta _{li}\) i, w konsekwencji, macierze \(P\) i \(Q\) są wzajemnie odwrotne.
Niech teraz \(f:V\longrightarrow V\) będzie odwzorowaniem liniowym. Niech \(A\) będzie macierzą tego odwzorowania przy bazie \(e_1,...,e_n\) i \(B\) będzie macierzą tego samego odwzorowania \(f\) przy bazie \(e'_1,...,e'_n\). Chcemy ustalić związek między macierzami \(A\) i \(B\).
Mamy następujące równości
Z drugiej strony
Otrzymaliśmy równość \(AP=PB\). A zatem udowodniliśmy następujące twierdzenie
Twierdzenie 4.1
Jeżeli \(A\) jest macierzą endomorfizmu \(f\) przy bazie \(e_1,..., e_n\) i \(B\) jest macierzą tego samego endomorfizmu przy bazie \(e'_1,..., e'_n\), to
gdzie \(P\) jest macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\).
Wyznacznik
Odwzorowania wieloliniowe
Niech \(V\) będzie \(n\)-wymiarową przestrzenią wektorową nad ciałem \(\mathbb K\) o charakterystyce różnej od 2. Niech dane będzie odwzorowanie \(\phi :V^k\longrightarrow \mathbb K\). Mówimy, że odwzorowanie \(\phi\) jest k-liniowe, jeśli dla każdego \(i= 1,...,k\) oraz dla dowolnie ustalonych wektorów \(v_1,...,v_{i-1},v_{i+1},..., v_k\) odwzorowanie
\(V\ni v\longrightarrow \phi (v_1,...,v_{i-1},v,v_{i+1},..., v_k)\in \mathbb K\)
jest liniowe. Na przykład, odwzorowanie \(\mathbb R ^k\ni (a_1,...,a_k)\longrightarrow a_1...a_k\in \mathbb R\) jest \(k\)-liniowe.
Zbiór wszystkich odwzorowań \(k\)-liniowych \(\phi :V^k\longrightarrow \mathbb K\) oznaczmy przez \({\cal L} ^k(V)\). W naturalny sposób (tak jak w Przykładzie 7. Wykładu I) zbiór ten
jest wyposażony w strukturę przestrzeni wektorowej.
Mówimy, że odwzorowanie \(\phi\) jest antysymetryczne, jeśli dla
każdej permutacji \(\rho\) ciągu \(1,...,k\) zachodzi wzór
\(\phi (v_{\rho (1)}, ..., v_{\rho (k)}) = sgn \,\rho\ \phi (v_1,...,v_k),\)
gdzie \( sgn\ \rho\) oznacza znak permutacji \(\rho\). Podobnie definiuje się odwzorowanie symetryczne. Mianowicie, \(\phi\) jest symetryczne, jeśli dla każdej permutacji \(\rho\) zachodzi równość.
\(\phi (v_{\rho (1)}, ..., v_{\rho (k)}) = \phi (v_1,...,v_k).\)
Wyżej wspomniane mnożenie liczb rzeczywistych jest k-liniowe symetryczne.
W niniejszym wykładzie odwzorowania antysymetryczne będą odgrywać główną rolę. Zacznijmy od następującego lematu.
Lemat 1.1
Dla odwzorowania \(k\)-liniowego \(\phi\) następujace warunki są równoważne.
- \(\phi\) jest antysymetryczne,
- \(\phi (v_1,...,v_k)=0\) dla dowolnych wektorów \(v_1,...,v_k\in V\) takich, że dwa spośród \(v_1,...,v_k\) są jednakowe.
- Jeśli \(v_1,...,v_k\) są liniowo zależne, to \(\phi (v_1,..., v_k)=0\).
Dowód
Załóżmy 1. Niech wektory \(v_iv_j\) będą jednakowe w ciągu wektorów \(v_1,...,v_k\). Niech \(\rho\) oznacza permutację, która
zamienia \(i\) na \(j\). Znak tej permutacji jest równy \(-1\). Po zastosowaniu tej permutacji ciąg wektorów \(v_1,...,v_k\) nie ulega zmianie. Wobec tego \(\phi (v_{\rho (1)},...,v_{\rho (k)})=\phi (v_1,...,v_k)\). Z drugiej strony
\(\phi (v_{\rho (1)},...,v_{\rho (k)})=- \phi (v_ 1,...,v_k).\)
Dodajmy do obu stron tej równości \(\phi (v_{\rho (1)},...,v_{\rho (k)})=\phi (v_1,...,v_k)\). Dostajemy równość
\((1+1) \phi (v_1,...,v_k)=0.\)
Wynika stąd, że \(\phi (v_1,...,v_k)=0\), bo ciało \(\mathbb K\) ma charakterystykę różną od 2.
Odwrotnie, jeśli \(\phi\) spełnia warunek 2), to dla każdych wektorów \(v_1,..., v_k\) i dla każdych \(i< j\), \(i,j=1,...,k\) mamy
\(0=\phi (v_1,...,v_{i-1},v_i +v_j, v_{i+1},..., v_{j-1}, v_{i}+v_{j}, v_{j+1},...,v_k).\)
Stąd, że \(\phi\) spełnia warunek 2. oraz z \(k\)-liniowości odwzorowania \(\phi\) dostajemy
\(\phi (v_1,...,v_{i-1}, v_j,v_{i+1},...,v_{j-1},v_i, v_{j+1},..., v_k)=-\phi (v_1,..., v_k).\)
Ponieważ każda permutacja jest złóżeniem pewnej liczby \(s\) transpozycji i znak permutacji jest równy \((-1)^s\), więc \(\phi\) jest antysymetryczne.
Załóżmy, że spełniony jest warunek 2. Jeśli ciąg \(v_1,..., v_k\)
jest liniowo zależny, to pewien wektor z tego ciągu jest kombinacją liniową pozostałych wektorów. Korzystając z \(k\)-liniowości \(\phi\) i z warunku 2. dostajemy natychmiast, że \(\phi (v_1,...,v_n )=0\). Na koniec, załóżmy 3). Jeśli, któreś wektory w ciągu \(v_1,..., v_n\) są równe, to ciąg \(v_1,..., v_n\) jest liniowo zależny , a zatem \(\phi (v_1,...,v_n)=0\). Dowód lematu jest zakończony.
Jest oczywiste, że suma odwzorowań \(k\)-liniowych antysymetrycznych
jest odwzorowaniem \(k\)-liniowym antysymetrycznym i odwzorowanie
\(k\)-liniowe antysymetryczne pomnożone przez skalar jest też antysymetryczne. A zatem ogół odwzorowań antysymetrycznych stanowi podprzestrzeń przestrzeni \({\cal L} ^k(V)\). Oznaczmy tę podprzestrzeń przez \({\cal L} ^k_a (V)\). Elementy przestrzeni
\({\cal L}^k_a(V)\) nazywamy też \(k\)-formami na przestrzeni \(V\). Choć teoria \(k\)-form jest ważna i interesująca, na potrzeby naszego wykładu zajmiemy się tylko szczególnymi przypadkami, tzn. szczególnymi przypadkami \(k\). Po pierwsze, znamy już przestrzeń 1-form. Przestrzenią tą jest przestrzeń dualna \(V^*\), 1-formami odwzorowania liniowe określone na \(V\) i o wartościach w ciele \(\mathbb K\).
Zajmiemy się teraz \(n\)-formami, gdzie \(n=\dim V\).
Niech \(e_1,...,e_n\) będzie bazą przestrzeni wektorowej \(V\) i \(\omega \in {\cal L}\). Niech \(v_1,..., v_n\in V\). Każdy z tych wektorów przedstawimy jako kombinację liniową wektorów bazy. A zatem \(\displaystyle v_j=\sum _{i=1}^n a_{ij}e_i\) dla każdego \(j=1,...,n\). Korzystając z Lematu 1.1 otrzymujemy następujące równości
\(\begin{aligned}\omega (v_1,...,v_n)&=\omega (\sum _{{i_1}=1}^n{a_{i_11}} {e_{i_1}},...,\sum _{{i_n}=1}^n{a_{i_nn}}e_{i_n}) \\ &= \sum _{{i_1},...,{i_n}=1}^n {a_{{i_11}}}\cdot\cdot\cdot {a_{{i_nn}}}\omega ({e_{i_1}},...,{e_{i_n}})\\ &= \sum _{\small{\begin{array} {l} \ \ \ \ {i_1},...,{i_n}\\ \ { i_a}\ne {i_b} \ {\rm dla}\ a\ne b \end{array} }} {a_{i_1 1}}\cdot\cdot\cdot{a_{i_n n}}\omega ({e_{i_1}},...,{e_{i_n}}) \end{aligned}\)
Ponieważ ciąg różnowartościowy \(i_1,...,i_n\) jest permutacją ciągu
\(1,...,n\), więc dostajemy
\(\begin{aligned}\omega (v_1,...,v_n)&=\sum _{\rho\in{\cal S}_n} {a_{\rho (1)1}}\cdot\cdot\cdot{a_{\rho (n)n}} \omega (e_{\rho (1)},..., e_{\rho (n)})\\ &=\sum _{\rho\in{\cal S}_n} sgn\, \rho \,{a_{\rho (1)1}}\cdot\cdot\cdot{a_{\rho (n)n}} \omega (e_1,..., e_n)\\ &= \omega (e_1,...,e_n) \left (\sum _{\rho\in{\cal S}_n} sgn\, \rho \, {a_{\rho (1)1}}\cdot\cdot\cdot{a_{\rho (n)n}}\right ), \end{aligned}\)
gdzie \({\cal S} _n\) oznacza zbiór wszystkich permutacji ciągu \(1,...,n\). Ostatecznie, dla każdego \(\omega \in{\cal L}\), zachodzi wzór
\(\displaystyle \omega (v_1,...,v_n)=\omega (e_1,...,e_n) \left (\sum _{\rho\in{\cal S}_n} sgn\, \rho \ {a_{\rho (1)1}}\cdot\cdot\cdot{a_{\rho (n)n}}\right )\) (1.1)
Skalar
\(\displaystyle \sum _{\rho\in{\cal S}_n} sgn\, \rho \ {a_{\rho (1)1}}\cdot\cdot\cdot{a_{\rho (n)n}}\)
nie zależy od \(\omega\). A zatem przestrzeń \(\mathcal L_{a}^{n}\) jest 1-wymiarowa i każda \(n\)-forma jest wyznaczona jednoznacznie przez zdefiniowanie \(\omega (e_1,..., e_n)\) dla dowolnie wybranej bazy \(e_1,..., e_n\).
Wyznacznik macierzy. Podstawowe własnosci
W przypadku, gdy \(V=\mathbb K ^n\) mamy bazę kanoniczną \(e_1,...,e_n\) tej przestrzeni. Każda \(n\)-forma na \(\mathbb K^n\) może być zadana na bazie kanonicznej.
Rozważmy teraz przestrzeń \(M(n,n;\mathbb K)\). Przypomnijmy, że jest to przestrzeń wszystkich macierzy kwadratowych o wymiarach \(n\) na
\(n\) i o wyrazach w ciele \(\mathbb K\). Niech \(A\in M(n,n;\mathbb K)\). Niech \(A_1,..., A_n\) oznaczają kolumny macierzy. Kolumny są wektorami przestrzeni \(\mathbb K ^n\). Macierz możemy traktować jako ciąg kolumn \(A_1,...,A_n\). Na podstawie wyżej przeprowadzonych rozważań, możemy stwierdzić prawdziwość następującego twierdzenia
Twierdzenie 2.1
Istnieje dokładnie jedno odwzorowanie \(n\)-liniowe antysymetryczne
\(\omega _o:M(n,n;\mathbb K)\ni A\longrightarrow \omega_o (A_1,...,A_n)\in \mathbb K\)
takie, że \(\omega _o(e_1,...,e_n)=1\), gdzie \(e_1,...,e_n\) jest bazą kanoniczną przestrzeni \(\mathbb K ^n\).
Odwzorowanie \(\omega _o\) nazywa się wyznacznikiem i oznacza symbolem \(\det\).
Symbol \(\det A\) oznacza wartość odwzorowania \(\det\) na ciągu kolumn \(A_1,...,A_n\) macierzy \(A\).
Podkreślamy, że wyznacznik macierzy definiuje się tylko dla macierzy
kwadratowych. Na podstawie formuły (1.1) otrzymujemy natychmiast następujący wzór na wyznacznik macierzy \(A=[a_{ij}]\in M(n,n;\mathbb K)\)
\(\displaystyle \det A= \sum _{\rho\in{\cal S}_n} sgn\, \rho \ {a_{\rho (1)1}}...{a_{\rho (n)n}}\) (2.2)

Przykład 2.2
Niech dana będzie baza \(v_1,...,v_n\) przestrzeni wektorowej \(V\). Niech \(P\) będzie macierzą przejścia od bazy \(v_1,..., v_n\) do bazy \(-v_1,v_2..,v_n\). Widać od razu, że \(\det A=1\).
Dowiedziemy teraz kilku podstawowych własności wyznacznika.
Twierdzenie 2.3
Dla dowolnych macierzy \(A,B\in M(n,n;\mathbb K)\) zachodzi wzór
\(\det AB=\det A\, \det B.\) (2.3)
Dowód
Niech \(A=[a_{ij}]\) i \(B=[b_{ij}]\). Wiemy, że wyrazy \(c_{ij}\) macierzy \(C=AB\) wyrażają się wzorem
\(\displaystyle c_{ij}=\sum _{l=1}^n a_{il}b_{lj}.\) (2.4)
Niech \(A_1,...,A_n\) oznaczają kolumny macierzy \(A\) zaś \(C_1,...,C_n\) - kolumny macierzy \(C\). Na podstawie formuły (2.4 ) mamy wzór
\(\displaystyle C_j=\sum _{l=1}^n b_{lj}A_l.\) (2.5)
Otrzymujemy następujące równości
\(\begin{aligned}\det AB&=\det (C_1,...,C_n)\\ &=\det \left (\sum _{l_1=1}^nb_{l_11}{A_{l_1}},...,\sum _{l_n=1}^nb_{l_nn}{A_{l_n}}\right )\\ &= \sum _{{l_1},...,{l_n}=1}^n {b_{l_11}}...{b_{l_nn}}\, \det ({A_{l_1}},...,{A_{l_n}})\\ &=\sum _{\small{\begin{array} {l} \ \ \ \ \ \ \ l_1,...,l_n\\ \ {l_a}\ne {l_b}\ {\rm dla}\ a\ne b\end{array} }} {b_{l_11}}...{b_{l_nn}}\, \det ({A_{l_1}},...,{A_{l_n}})\\ &= \sum _{\rho \in {\cal S}_n}{b_{\rho (1)1}}...{b_{\rho (n)n}}\, \det ({A_{\rho (1)}},...,{A_{\rho (n)}})\\ &= \sum _{\small{\rho \in {\cal S}_n}} sgn\, \rho \ {b_{\rho (1)1}}...{b_{\rho (n)n}}\, \det\, A\\ &=\det A\, \det B \end{aligned}\)
Korzystając z definicji wyznacznika, łatwo widać, że wyznacznik macierzy jednostkowej \(I\) jest równy \(1\). A zatem, jeśli \(A\) jest macierzą odwracalną, to
\(1=\det I=\det (AA^{-1})=(\det A)(\det A^{-1}).\)
Oznacza to, że macierz odwracalna ma wyznacznik różny on zera, a wyznacznik macierzy odwrotnej jest odwrotnością wyznacznika macierzy danej. Mamy więc wzór
\(\det (A^{-1})=(\det A)^{-1}\) (2.6)
dla macierzy odwracalnej \(A\). Macierz, której wyznacznik jest różny od zera nazywa się macierzą nieosobliwą.
Załóżmy teraz, że macierz \(A\) ma niezerowy wyznacznik. Wtedy kolumny macierzy \(A\), jako wektory przestrzeni \(\mathbb K ^n\) są liniowo niezależne (na podstawie (Lematu 1.1). Oznacza to, że, jeśli \(A\) potraktujemy jako odwzorowanie liniowe z \(\mathbb K ^n\) do \(\mathbb K ^n\), to \(A\) jest izomorfizmem. A zatem macierz \(A\) jest odwracalna. Mamy więc
Twierdzenie 2.4
Macierz \(A\) jest odwracalna wtedy i tylko wtedy, gdy jest nieosobliwa.
Twierdzenie 2.5
Jeżeli \(A\in M(n,n;\mathbb K)\), to \(\det A^*=\det A\).
Dowód
Oznaczmy przez \(B=[b_{ij}]\) macierz dualną do \(A=[a_{ij}]\). A zatem \(b_{ij}=a_{ji}\). Mamy
\(\displaystyle \det B=\sum _{\rho \in{\cal S}_n} sgn\rho\ b_{\rho (1)1}\cdot\cdot\cdot b_{\rho (n)n}.\)
Dla każdej permutacji \(\rho \in{\cal S}\) weźmy \(\rho ^{-1}\). Jeśli \(\rho (i)=j\), to \(\rho ^{-1} (j)=i\). Zatem iloczyn \(b_{\rho (1)1}\cdot\cdot\cdot b_{\rho (n)n}\) jest równy iloczynowi \(b_{1\rho ^{-1}(1)}\cdot\cdot\cdot b_{n\rho ^{-1}(n)}\) (po ewentualnym spermutowaniu czynników). Ponieważ odwzorowanie \({\cal S}_n\ni \rho \longrightarrow \rho ^{-1}\in {\cal S }_n\) jest bijekcją i dla każdej permutacji \(\rho\) zachodzi równość \( sgn \ \rho = sgn\ {\rho }^{-1}\), zatem
\(\begin{aligned}\det B&=\sum _{\rho \in{\cal S}_n} sgn\, \rho \, b_{1\rho (1)}\cdot\cdot\cdot n_{n\rho (n)}\\ &= \sum _{\rho \in{\cal S}_n} sgn \, \rho \, a_{\rho (1)1}\cdot\cdot\cdot a_{\rho (n)n}=\det A. \end{aligned}\)
Z powyższego twierdzenia dostajemy następujący wzór na wyznacznik macierzy \(A=[a_{ij}]\)
\(\displaystyle \det A= \sum _{\rho \in{\cal S}_n} sgn\, \rho \,\ a_{1\rho (1)}\cdot\cdot\cdot a_{n\rho (n)}.\) (2.7)
Wyznacznik jest \(n\)-liniową antysymetryczną funkcją wierszy.
Zauważmy teraz, że jeśli w macierzy \(A\) do pewnej kolumny (lub
pewnego wiersza) dodamy kombinację liniową pozostałych kolumn (lub pozostałych wierszy), to wyznacznik macierzy się nie zmieni. Wynika to z wieloliniowości wyznacznika i z warunku 2. Lematu 1.1. Jeśli zamienimy miejscami dwie kolumny (lub dwa wiersze), to wyznacznik zmieni swój znak. Jeśli pewną kolumnę macierzy \(A\) pomnożymy przez skalar \(\lambda\), to dla otrzymanej w ten sposób macierzy \(A'\) mamy wzór \(\det A'=\lambda \det A\). W szczególności, wymienione właśnie operacje na macierzach są takie, że, po ich zastosowaniu do danej macierzy, wyznacznik macierzy się nie zmieni lub łatwo kontrolujemy ewentualne zmiany wyznacznika tej macierzy. Mówimy, że są to operacje elementarne (lub dopuszczalne ze względu na wyznacznik). Oczywiście sensowne jest mnożenie wierszy lub kolumn przez skalary różne od \(0\).
Udowodnimy teraz pewną pożyteczną rachunkową własność wyznacznika.
Twierdzenie 2.6
Niech \(A\in (k,k;\mathbb K)\), \(B\in M(k,n-k;\mathbb K)\), \(C\in M(n-k,n-k;\mathbb K)\) zaś \(O\) oznacza zerową macierz z \(M(n-k,k;\mathbb K)\). Zachodzi wzór
\(\det\left [\begin{array} {lr} \ A \ B\\ \ O\ C \end{array} \right ]=\det A\ \det C\) (2.8)
Dowód
Dla ustalonych macierzy \(A\) i \(B\) rozważmy następujące odwzorowanie
\(\phi :M( n-k,n-k;)\ni C\longrightarrow \phi (C)= \det\left [\begin{array} {lr} \ A \ B\\ \ O\ C. \end{array} \right ]\)
Odwzorowanie \(\phi\), jako odwzorowanie \(n-k\) rzędów macierzy \(C\) jest \((n-k)\)-liniowe i antysymetryczne. A zatem, na podstawie rozważań z początku tego wykładu, wiemy, że
\(\phi (C)= \phi (I) \ \det C,\)
gdzie \(I\) jest macierzą jednostkową. Pokażemy, że \(\phi (I)=\det A\). Ustalmy macierz \(B\) i rozważmy odwzorowanie
\(\psi :M(k,k;\mathbb K)\ni A\longrightarrow \psi (A)=\det \left [\begin{array} {lr} \ A \ B\\ \ O\ I. \end{array} \right ]\)
Traktując to odwzorowanie jako odwzorowanie \(k\) kolumn macierzy \(A\), widzimy, że odwzorowanie to jest \(k\)-liniowe antysymetryczne. A zatem, tak jak wyżej, dostajemy
\(\psi (A)=\psi (I) \ \det A .\)
Wystarczy teraz udowodnić, że
\(\det \left [\begin{array} {lr} \ I \ B\\ \ O\ I \end{array} \right ]=1,\)
gdzie \(I\) w odpowiednim miejscu oznacza macierz jednostkową odpowiedniego wymiaru. Ostatni wzór zostawiamy jako ćwiczenie.
W szczególności, zachodzi wzór
\(\det \left [ \begin{array} {lcccr} \ 1\ a_{12}\ .\ .\ .\ a_{1n}\\ \ 0\ \ \ \ \ \\ \ . \ \ \ \ \ \ \\ \ .\ \ \ \ \ \ \ B \ \\ \ . \ \ \ \ \ \ \\ \ 0\ \ \ \ \ \ \ \ \end{array} \right ]= \det B,\) (2.9)
gdzie \(B\in M(n-1,n-1;\mathbb K)\).
Udowodnimy teraz twierdzenie o tzw. rozwinięciu Laplace'a względem \(j\)-tej kolumny.
Twierdzenie 2.7
Niech \(A=[a_{ij}]\in M(n,n;\mathbb K)\). Dla każdego ustalonego
wskaźnika \(j\) (\(j=1,...,n\)) zachodzi wzór
\(\det A = a_{1j}\Delta _{1j}+...+a_{nj}\Delta _{nj},\) (2.10)
gdzie \(\Delta _{ij}\) oznacza wyznacznik macierzy otrzymanej z
macierzy \(A\) powstałej z macierzy \(A\) przez wykreślenie \(i\)-tego wiersza i \(j\)-tej kolumny, pomnożony przez \((-1) ^{i+j}\).
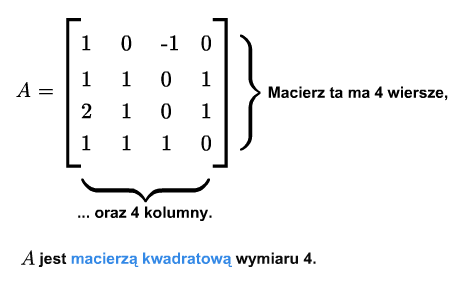





Dowód
Niech \(A_1,...,A_n\) będą kolumnami macierzy \(A\). Macierz
\(A\) traktujemy jako ciąg kolumn, tzn. \(A= [A_1,...,A_n]\). Jeśli \(e_1,...,e_n\) jest bazą kanoniczną przestrzeni \(n\), to
\(\displaystyle A_j =\sum _{i=1}^n a_{ij} e_i.\)
Zatem, pamiętając o tym, że wyznacznik jest \(n\)-liniową antysymetryczną funkcją kolumn, dostajemy
\(\displaystyle \det A= \sum _{i=1}^n a_{ij}\det [ A_1,...,A_{j-1}, e_i, A_{j+1},...,A_n].\)
Wystarczy zauważyć, że
\(\displaystyle \det [A_1,..., A_{j-1}, e_i,A_{j+1},..., A_n] = \Delta _{ij}.\)
W tym celu przesuńmy \(j\)-tą kolumnę macierzy \([A_1,..., A_{j-1}, e_i,A_{j+1},..., A_n]\) w lewo na pierwsze miejsce. Wykonujemy
\(j-1\) transpozycji. W tak otrzymanej macierzy przesuńmy \(i\)-ty wiersz na pierwsze miejsce. W tym celu dokonujemy \(i-1\) transpozycji. Po tych operacjach dostajemy macierz postaci
\(\left [ \begin{array} {lcccr} \ 1\ a_{i2}\ .\ .\ .\ a_{in}\\ \ 0\ \ \ \ \ \\ \ . \ \ \ \ \ \ \\ \ .\ \ \ \ \ \ \ A_{ij} \ \\ \ . \ \ \ \ \ \ \\ \ 0\ \ \ \ \ \ \ \ \end{array} \right ],\)
gdzie \(A_{ij}\) jest macierzą otrzymaną z macierzy \(A\) przez wykreślenie \(i\)-tego wiersza i \(j\)-tej kolumny.
Korzystając ze wzoru (2.9) otrzymujemy
\(\det [A_1,..., A_{j-1}, e_i,A_{j+1},..., A_n] =(-1)^{j-1}(-1) ^{i-1}\det A_{ij}= \Delta _{ij}.\)
Na podstawie Twierdzenia 2.5 otrzymujemy wzory na rozwinięcie
Laplace'a względem \(i\)-tego wiersza.
Twierdzenie 2.8
Niech \(A=[a_{ij}]\in M(n,n;\mathbb K)\). Dla każdego ustalonego wskaźnika \(i\) (\(i=1,...,n\)) zachodzi wzór
\(\det A = a_{i1}\Delta _{i1}+...+a_{in}\Delta _{in},\) (2.11)
Zastosowania wyznacznika. Układy równań liniowych
Minory i rząd macierzy. Macierz odwrotna
Ponieważ w wykładzie tym intensywnie będziemy korzystać z poprzedniego wykładu, musimy dokonać tych samych wstępnych ustaleń, a mianowicie, zakładamy, że wszystkie rozważane przestrzenie są skończenie wymiarowe nad ciałem \(\mathbb K\) o charakterystyce różnej od \(2\).
Niech dana będzie macierz \(A=[a_{ij}]\in M(m,n;\mathbb K )\). Wiemy, że rząd tej macierzy jest równy rzędowi układu kolumn \(A_1,..., A_n\in \mathbb K ^m\) tej macierzy. Jest też równy rzędowi układu wierszy tej macierzy, bo rząd macierzy \(A\) jest równy rzędowi macierzy dualnej. Wiemy też, że rząd układu wektorów jest równy maksymalnej liczbie wektorów liniowo niezależnych, które można wybrać z tego układu wektorów.
Wprowadzimy teraz pojęcie minora macierzy. Niech \(k\) będzie pewną liczbą naturalną nie większą od \(m\) i \(n\). Ustalmy ciągi wskaźników \(1\le i_1<...<i_k\le m\), \(1\le j_1<...<j_k\le n\). Oznaczmy przez
macierz powstałą przez wybór wyrazów stojących na przecięciu wierszy o numerach \(i_1,...,i_k\) i kolumn o numerach \(j_1,..., j_k\). Otrzymujemy macierz kwadratową o wymiarach \(k\) na \(k\). Wyznacznik tak otrzymanej macierzy nazywamy minorem rzędu \(k\) macierzy \(A\).

Następujący lemat będzie przydatny w dalszych rozumowaniach.
Lemat 1.1
Kolumny \(A_{j_1},..., A_{j_k}\) są liniowo niezależne wtedy i tylko wtedy, gdy istnieją takie wskaźniki \(1\le i_1<...<i_k\le m\), że \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\).
Dowód
Załóżmy najpierw, że kolumny \(A_{j_1},...,A_{j_k}\) są liniowo niezależne. Wtedy macierz \(A_{j_1,...,j_k}=[A_{j_1},...,A_{j_k}]\) składająca się tylko z tych kolumn ma rząd równy \(k\). Ponieważ rząd macierzy danej jest równy rzędowi macierzy dualnej, więc wsród wierszy macierzy \(A_{j_1,...,j _k}\) istnieje \(k\) liniowo niezależnych wektorów. Niech będą to wiersze o numerach \(1\le i_1<...<i_k\le m\). Oznacza to, że w macierzy \(A^{i_1,...,i_k}_{j_1,...,j_k}\) wiersze o numerach \(i_1,...,i_k\) są liniowo niezależne, czyli rząd tej macierzy jest równy \(k\). A zatem \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\).
Załóżmy teraz, że \(\det A^{i_1,...,i_k}_{j_1,...,j_k}\ne 0\). Wtedy wiersze tej macierzy są liniowo niezależne. A zatem rząd macierzy \([A_1,...,A_k]\) jest równy \(k\) (bo nie może być większy). Oznacza to, że \(k\) kolumn tej macierzy stanowi układ liniowo niezależny.Z powyższego lematu wynika natychmiast następujące twierdzenie.
Twierdzenie 1.2
Dla dowolnej macierzy \(A\) jej rząd jest równy \(k\) wtedy i tylko wtedy, gdy istnieje niezerowy minor rządu \(k\) tej macierzy i każdy minor rzędu większego od \(k\) jest zerowy.
Przed udowodnieniem kolejnego twierdzenia przypomnijmy, że dla macierzy \(A=[a_{ij}]\) wprowadziliśmy wielkości \(\Delta _{ij}=(-1)^{i+j} \det A_{ij}\), gdzie \(A_{ij}\) jest macierzą otrzymaną z macierzy \(A\) przez wykreślenie \(i\)-tego wiersza i \(j\)-tej kolumny.
Twierdzenie 1.3
Niech \(A\in M(n,n;\mathbb K)\) będzie macierzą odwracalną i niech \(B=[b_{ij}]\) oznacza jej macierz odwrotną. Wtedy
Dowód
Wystarczy sprawdzić, że \(AB=I\). Niech \(C= AB\) i \(C=[c_{ij}]\). Korzystając z rozwinięcia Laplace'a otrzymujemy
gdzie \(D\) jest macierzą powstałą z macierzy \(A\) przez zastąpienie \(j\)-tego wiersza \(i\)-tym wierszem. Jeśli \(i=j\), to macierz \(A\) jest równa macierzy \(D\). Jeśli \(i\ne j\), to w macierzy \(D\) są dwa takie same wiersze. A zatem \(c_{ij}=\delta _{ij}\) i w konsekwencji \(C=I\).




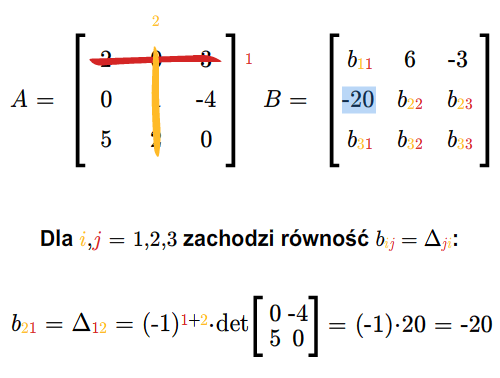



Układy równań liniowych
Układem równań liniowych nazywamy układ równań
\(\left\{ \begin{array} {lr} \ a_{11}x_1+...+a_{1n}x_n =b_1\\ .........................................\\ \ a_{m1}x_1+...+a_{mn}x_n=b_m, \end{array} \right .\) (2.1)
gdzie \(x_1,..., x_n\) są niewiadomymi, zaś \(a_{ij}\), \(b_i\), gdzie \(i=1,...,m\); \(j=1,....n\) są skalarami z pewnego ciała \(\mathbb K\). Rozwiązaniem tego układu nazywamy każdy ciąg \((x_1,...,x_n)\in \mathbb K ^n\), który spełnia (2.1). Skalary \(a_{ij}\) nazywają się współczynnikami układu równań. Skalary \(b_1,...,b_m\) nazywają się wyrazami wolnymi układu (2.1). Jeżeli wszystkie wyrazy wolne są równe zeru, układ równań (2.1) nazywa się jednorodnym. Układ taki rozważaliśmy już w Wykładzie II. W przeciwnym wypadku mówimy, że układ jest niejednorodny. Współczynniki układu (2.1) stanowią macierz \(A=[a_{ij}]\) o \(m\) wierszach i \(n\) kolumnach. Wyrazy wolne
układamy w jednokolumnową macierz
Podobnie, niewiadome ułożymy w jednokolumnową macierz
Układ równań (2.1) można teraz zapisać w postaci macierzowej
\(Ax=b.\) (2.2)
Jeżeli w układzie równań (2.1) zastąpimy wyrazy wolne zerami, to otrzymujemy tzw. układ jednorodny skojarzony z (2.1)
\(\left\{ \begin{array} {lr} \ a_{11}x_1+...+a_{1n}x_n =0\\ .........................................\\ \ a_{m1}x_1+...+a_{mn}x_n=0 \end{array} \right .\) (2.3)
Traktując macierz \(A\) jako odwzorowanie
\(A:\mathbb K ^n\ni x\longrightarrow Ax\in \mathbb K^m,\) (2.4)
widzimy, że jądrem tego odwzorowania jest zbiór rozwiązań układu jednorodnego
(2.3). A zatem zbiór rozwiązań układu jednorodnego jest podprzestrzenią wektorową \(\mathbb K^n\). Na podstawie twierdzenia opisującego relację wymiaru jądra i wymiaru obrazu danego odwzorowania liniowego wiemy, że wymiar tej przestrzeni jest równy \(n - rk A\). Oznaczmy tę przestrzeń przez \(V_o\). Niech teraz \(x_o=({x_o}_1,...,{x_o}_n)\) będzie pewnym rozwiązaniem układu (2.1). Niech \((v_1,...,v_n)\) będzie dowolnym rozwiązaniem układu skojarzonego (2.3). Wtedy
jest również rozwiązaniem układu (2.1).
Jeśli teraz mamy dwa rozwiązania \(({x_o}_1,..., {x_o}_n)\), \(({x}_1,..., {x}_n)\) układu (2.1), to ciąg \((x_1-{x_o}_1,... ,x_n-{x_o}_n)\) jest rozwiązaniem układu (2.3). Udowodniliśmy następujące twierdzenie
Twierdzenie 2.1
Jeżeli układ równań (2.1) ma rozwiązanie oraz
jest pewnym rozwiązaniem (2.1), to zbiór wszystkich rozwiązań układu (2.1) jest równy zbiorowi
gdzie \(V_o\) jest zbiorem wszystkich rozwiązań układu jednorodnego
(2.3). Przestrzeń \(V_o\) jest \((n-k)\)-wymiarowa, gdzie
\(k= rk A\).
W twierdzeniu powyższym zakłada się, że istnieje rozwiązanie układu równań (2.1). O ile układ jednorodny zawsze posiada rozwiązanie, bo, na przykład, ciąg \((0,...,0)\) jest rozwiązaniem takiego układu, o tyle układ niejednorodny niekoniecznie ma rozwiązanie. Proste kryterium rozwiązywalności układu niejednorodnego daje następujące twierdzenie Kroneckera-Capellego.
Twierdzenie 2.2
Układ równań (2.1) ma rozwiązanie wtedy i tylko wtedy, gdy
gdzie \([A,b]\) jest macierzą utworzoną z macierzy \(A\) przez dopisanie do niej kolumny wyrazów wolnych.
Dowód
\(x_1A_1+...+x_nA_n=b.\) (2.5)
Macierz \([A,b]\), o której mówi się w powyższym twierdzeniu, nazywa się macierzą rozszerzoną układu (2.1).
Twierdzenie Kroneckera-Capellego dotyczy każdego układu równań, tzn. liczba równań i liczba niewiadomych mogą być dowolne. Kolejne twierdzenie, twierdzenie Cramera, dotyczy tylko tych układów, w których liczba równań jest równa liczbie niewiadomych.






Twierdzenie 2.3
\(\left\{\begin{array} {l} \ a_{11}x_1+...+a_{1n}x_n=b_1 \\ \ .......................................\\ \ a_{n1}x_1+...+a_{nn}x_n=b_n \end{array} \right .\) (2.6)
taki, że \(\det A\ne 0\). Wtedy układ (2.6) ma dokładnie jedno rozwiązanie i rozwiązanie to jest dane wzorami
\(x_i= {{\det A_{(i)}\over \det A}},\) (2.7)
dla \(i=1,...,n\), gdzie \(A_{(i)}\) jest macierzą otrzymaną z macierzy \(A\) przez zastąpienie \(i\)-tej kolumny kolumną wyrazów wolnych.
Dowód
Rozważmy postać macierzową układu (2.6). Mamy więc równanie macierzowe \(Ax=b.\). Obłóżmy obustronnie to równanie przez \(A^{-1}\). Ponieważ \(\det A\ne 0\), macierz odwrotna \(A^{-1}\) istnieje. Mamy więc
Wykorzystamy teraz wzory na wyrazy macierzy odwrotnej. Oznaczmy wyrazy tej macierzy przez \(c_{ij}\). A zatem \(c_{ij}= (-1)^{i+j}{{\det A_{ji}}\over{\det A} }\).
Mamy następujące równości
Ostatnia równość wynika z rozwinięcia Laplace'a wyznacznika. W ten sposób udowodniliśmy istnienie rozwiązania, jego jedyność i wzory(2.7), które nazywają się wzorami Cramera.






Ustalmy jeszcze, jakie operacje można wykonać na układzie równań, aby otrzymać układ równoważny, tzn. taki, który ma dokładnie taki sam zbiór rozwiązań. Na pewno można równania permutować. Poza tym do danego równania można dodać kombinację liniową pozostałych równań. Każde równanie można pomnożyć przez niezerowy skalar. Wymienione operacje służą do rozwiązywania układów równań liniowych tzw. metodą Gaussa, która będzie omówiona na ćwiczeniach.
Endomorfizmy. Twierdzenie Jordana
Wyznacznik, ślad, wartość własna, wielomian charakterystyczny endomorfizmu i macierzy
W wykładzie tym zakładamy, że wszystkie przestrzenie są skończenie wymiarowe nad ciałem \(\mathbb K\) o charakterystyce równej \(0\).
Mówimy, że macierze kwadratowe \(A, B\in M(n,n;\mathbb K)\) są podobne, jeśli istnieje taka macierz nieosobliwa \(P\), dla której \(B=P^{-1}AP\). Macierze podobne mają ten sam wyznacznik, bo

Zdefiniujemy teraz ślad macierzy. Tak jak wyznacznik, ślad macierzy definiuje się tylko dla macierzy kwadratowych. Dla macierzy \(A=[a_{ij}]\in M(n,n;\mathbb K)\) definiujemy jej ślad \(tr A\) jako sumę jej wyrazów leżących na głównej przekątnej, to znaczy
Odwzorowanie
jest liniowe.
Pamiętamy, że mnożenie macierzy jest na ogół nieprzemienne. Mamy natomiast następujące twierdzenie
Twierdzenie 1.1
Dla dowolnych macierzy \(A,B\in M(n,n;\mathbb K )\) zachodzi równość
Dowód
Niech \(A=[a_{ij}]\), \(B=[b_{ij}]\). Oznaczmy przez \(C=[c_{ij}]\) macierz \(AB\) i przez \(D=[d_{ij}]\) macierz \(BA\). Mamy następujące równości
Z twierdzenia tego wynika, że macierze podobne mają taki sam ślad. Istotnie, \( tr (P^{-1}AP)= tr (P^{-1}(AP))= tr ((AP)P^{-1})= tr (A(PP^{-1}))= tr A\).
Niech \(f:V\longrightarrow V\) będzie endomorfizmem. Niech \(e_1,..., e_n\); \(e'_1,...,e'_n\) będą bazami przestrzeni \(V\). Jeśli \(A\) jest macierzą \(f\) przy bazie \(e_1,..., e_n\) zaś \(B\) jest macierzą \(f\) przy bazie \(e'_1,..., e'_n\), to \(B=P^{-1}AP\), gdzie \(P\) jest macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\). A zatem \(\det B=\det A\). Oznacza to, że niżej wprowadzona definicja ma sens, tzn. nie zależy od wyboru bazy \(e_1,...,e_n\).
Definicja 1.2
Wyznacznikiem endomorfizmu \(f:V\longrightarrow V\) nazywamy wyznacznik dowolnej macierzy tego endomorfizmu.
Podobnie definiuje się ślad endomorfizmu. Mianowicie, mając endomorfizm \(f\) bierzemy dowolną jego macierz \(A\) (tzn. macierz przy dowolnej bazie) i definiujemy \( tr f\) jako \( tr A\). Definicja nie zależy od wyboru bazy, bo macierze podobne mają ten sam ślad.
Wprowadzimy teraz kolejne definicje.
Definicja 1.3
Mówimy, że skalar \(\lambda\) jest wartością własną endomorfizmu \(f:V\longrightarrow V\), jeśli istnieje niezerowy wektor \(v\in V\) taki, że \(f(v)=\lambda v\). Każdy taki wektor \(v\) nazywamy wektorem własnym odpowiadającym wartości własnej \(\lambda\).
Definiuje się też wartości własne i wektory własne macierzy
Definicja 1.4
Mówimy, że skalar \(\lambda\) jest wartością własną macierzy \(A\in M(n,n;\mathbb K )\), jeśli istnieje niezerowy wektor \(v\in \mathbb K^n\) taki, że \(Av=\lambda v\). Każdy taki wektor \(v\) nazywamy wektorem własnym odpowiadającym wartości własnej \(\lambda\).
W powyższej równości \(Av=\lambda v\) wektor \(v\) jest traktowany jako \(1\)-kolumnowa macierz.
Istotną cechę wektorów i wartości własnych opisuje następujące twierdzenie
Twierdzenie 1.5
Jeżeli \(\lambda _1,...,\lambda _k\) są różnymi między sobą wartościami własnymi endomorfizmu \(f\) i \(v_1,...,v_k\) są wektorami własnymi odpowiadającymi tym wartościom własnym, to wektory \(v_1,...,v_k\) są liniowo niezależne.
Dowód
Dowód jest indukcyjny ze względu na \(k\). Dla \(k=1\) twierdzenie jest oczywiste. Załóżmy, że jest prawdziwe dla liczb mniejszych od pewnego \(k\).
Przypuśćmy, że wektory \(v_1,...,v_k\) spełniają założenia twierdzenia i wektory te są liniowo zależne. Możemy założyć, że \(v_k\) jest kombinacją liniową wektorów \(v_1,...,v_{k-1}\). Niech
Nie wszystkie \(\mu _1,...,\mu _{k-1}\) są równe zeru. Możemy przyjąć, że \(\mu _1\ne 0\). Obłóżmy powyższą równość przez \(f\). Wtedy
Z drugiej strony
Zatem
Ponieważ \(v_1,...,v_l\) są liniowo niezależne i \(\mu _1\ne 0\), więc \(\lambda _k=\lambda _1\). Jest to sprzeczne z założeniem, że \(\lambda _1,..., \lambda _k\) są różne miedzy sobą.
Mamy następujące twierdzenie charakteryzujące wartości własne.
Twierdzenie 1.6
Skalar \(\lambda\) jest wartością własną endomorfizmu \(f\) wtedy i tylko wtedy, gdy
gdzie \( I\) jest odwzorowaniem identycznościowym przestrzeni \(V\).
Dowód
Jeżeli \(\lambda\) jest wartością własną \(f\) i \(v\) jest wektorem własnym odpowiadającym wartości własnej \(\lambda\), to \((f-\lambda I)(v)=0\), czyli odwzorowanie \(f-\lambda I\) nie jest monomorfizmem. A zatem \(\det (f-\lambda I)=0\). Odwrotnie, jeśli \(\det (f-\lambda I)=0\), to \(f-\lambda I\) nie jest monomorfizmem, a zatem istnieje niezerowy wektor \(v\) taki, że \((f-\lambda I)(v)=0\). Oznacza to, że \(\lambda\) jest wartością własną \(f\) a \(v\) jest wektorem własnym odpowiadającym tej wartości własnej.
Wybierzmy bazę przestrzeni \(V\). Niech \(A\) będzie macierzą \(f\) przy tej bazie. Wtedy, dla każdego \(t\in \mathbb K\) mamy \(\det (f-t I) = \det (A-t I)\).
Jest jasne, jeśli skorzystamy na przykład ze wzoru na wyznacznik macierzy \(A=[a_{ij}]\) z Wykładu VII, tzn. ze wzoru
\(\displaystyle \det A= \sum _{\rho \in \S _n} sgn\ \rho \ a_{\rho (1)1}\cdot\cdot\cdot a_{\rho (n)n},\) (1.1)
że \(\det (f-t I)=\det (A-t I )\), traktowany jako funkcja argumentu \(t\) jest wielomianem stopnia \(n\). Wielomian ten nazywamy wielomianem charakterystycznym endomorfizmu \(f\). Oznaczmy go przez \(W_f\). W wielomianie tym współczynnik przy
\(t^n\) jest równy \((-1)^n\), wyraz wolny jest równy \(\det A =\det f\), zaś współczynnik przy \(t^{n-1}\) jest równy \((1)^{n-1} tr A= tr f\). Istotnie, wstawiając za \(t\) wartość \(0\) dostajemy wyraz wolny wielomianu \(W_f\), czyli wyraz wolny jest równy \(\det f\). Wielomian \(W_f\) możemy zapisać jako
gdzie \(W(t)\) jest wielomianem stopnia mniejszego lub równego
\(n-1\). Widać stąd, że współczynnik przy \(t^n\) jest równy
\((-1)^n\). Zauważmy jednak, że wielomian \(W(t)\) jest stopnia silnie mniejszego od \(n-1\). Istotnie, ciągle mając na uwadze wzór (1.1), widzimy, że składniki zawierające \(t^{n-1}\) mogą powstać tylko przy pomnożeniu \(n-1\) wyrazów macierzy \(A-t I\) leżących na głównej przekątnej. Ale permutacja \(n\)-elementowego zbioru, która jest identycznością na \(n-1\) elementach jest identycznością na całym zbiorze. Oznacza to, że składniki wielomianu \(W_f(t)\) zawierające \(t^{n-1}\) powstają tylko z iloczynu \((a_{11}-t)\cdot\cdot\cdot (a_{nn}-t)\). Teraz łatwo widać, że współczynnik przy \(t^{n-1}\) jest równy \((-1)^{n-1} tr A\).
Podprzestrzenie niezmiennicze. Baza i macierz Jordana.
Niech \(U\) będzie podprzestrzenią przestrzeni \(V\). Mówimy, że podprzestrzeń ta jest \(f\)-niezmiennicza (dokładniej mówiąc, niezmiennicza ze względu na \(f\)), jeśli \(f(U)\subset U\). Jeśli \(U\) jest podprzestrzenią \(f\)-niezmienniczą, to po zawężeniu \(f\) do \(U\) dostajemy endomorfizm przestrzeni \(U\). Oznaczmy go przez \(\tilde f\). Endomorfizm ten ma swój wielomian charakterystyczny \(W_{\tilde f}\). Zachodzi następujący lemat.
Lemat 2.1
Jeżeli \(U\) jest podprzestrzenią \(f\)-niezmienniczą, to wielomian charakterystyczny \(W_{\tilde f}\) dzieli wielomian charakterystyczny \(W_f\).
Dowód
Niech \(e_1,...,e_k\) będzie bazą przestrzeni \(U\). Rozszerzamy ją do bazy \(e_1,...,e_k, e_{k+1},...,e_n\) przestrzeni \(V\). Macierz \(A\) endomorfizmu \(f\) w tej bazie ma postać blokową
gdzie \(B\) jest macierzą \(\tilde f\) w bazie \(e_1,...,e_k\). Mamy wtedy (na podstawie Twierdzenia 2.6 z Wykładu VII)
Macierzą Jordana nazywa się macierz postaci
\(\left [\begin{array} {lccccr} \ A_1 & 0 & 0 &...& 0\\ \ 0 &A_2&0 &...&0\\ \ & & & & \\ \ . & .& . & . & 0\\ \ . & . & . & .& 0\\ \ . & .& . & .& 0\\ \ & & & & \\ \ 0& 0& 0& 0& A_l, \end{array} \right ],\) (2.2)
gdzie \(A_1\), ..., \(A_l\) są macierzami kwadratowymi postaci
\(\left [\begin{array} {lcccccr} \ \lambda _i &1& & & & 0\\ \ 0& \lambda _i& 1& & & 0\\ \ .&. & .& .& .& .\\ \ 0 & & & \lambda _i & 1 & 0\\ \ 0 & & & &\lambda _i & 1\\ \ 0 & & & & &\lambda _i \end{array} \right ]\) (2.3)
dla \(i=1,...l\). Macierze \(A_1,..., A_l\) nazywamy klatkami Jordana. Jeżeli macierz \(A_i\) jest jedna klatką Jordana (2.3) o wymiarach \(n_i\) na \(n_i\), to \((A_i-\lambda _i I )^{n_i}=0\). Oczywiście \(\lambda _i\) jest wartością własną macierzy \(A_i\).
Zwróćmy uwagę na to, że klatki mogą też być wymiaru \(1\times 1\).
Każda klatka odpowiada pewnej wartości własnej macierzy \(A\). Dla danej wartości własnej odpowiadające jej klatki mogą mieć różne wymiary. Klatek w danym wymiarze też może być dowolna ilość.
Przypuśćmy, że dla danego endomorfizmu \(f\) istnieje taka baza \(e_1,...,e_n\), przy której macierz tego endomorfizmu jest macierzą Jordana. Poukładajmy klatki tej macierzy tak, aby na początku (tzn. począwszy od lewego górnego rogu macierzy) były klatki odpowiadające wartości własnej \(0\) - najpierw wymiaru 1\(\times\)1, potem wymiaru 2\(\times\)2, potem 3\(\times\)3, etc. Po klatkach odpowiadających wartości własnej \(0\), umieszczamy klatki odpowiadające pozostałym wartościom własnym. Dla każdej wartości własnej układamy klatki od najmniejszych do największych. Takie ukladanie klatek odpowiada permutowaniu bazy \(e_1,..., e_n\). Macierz po takim układaniu jest ciągle macierzą Jordana endomorfizmu \(f\), a spermutowana baza jest bazą Jordana dla \(f\). Bazę tę oznaczmy przez \(\mathcal B\).
Obserwując macierz \(\mathcal B\) łatwo odczytać pewne cechy odwzorowania \(f\).
Dla ustalonej klatki mamy pewien ciąg wektorów bazy Jordana odpowiadający tej klatce. Ciąg taki zaczyna się od wektora własnego. Każdy wektor własny z bazy \(\mathcal B\) odpowiadający jakiejś wartości własnej rozpoczyna pewien ciąg wektorów (może być 1-wyrazowy) odpowiadający jednej klatce macierzy Jordana.
Z bazy Jordana \(\mathcal B\) można wybrać bazę podprzestrzeni \(\ker f\). Wektory tej bazy to wektory odpowiadające wszystkim klatkom 1\(\times\)1 dla wartości własnej \(0\) oraz pierwsze wektory (oczywiście ciągle z bazy \(\mathcal B\)) odpowiadające wszystkim kolejnym klatkom Jordana dla wartości własnej \(0\).
Z bazy \(\mathcal B\) można wybrać bazę podprzestrzeni \( im f\). W szczególności wszystkie wektory bazy \(\mathcal B\), które odpowiadają klatkom dla niezerowych wartości własnych stanowią część takiej bazy.
Ostatnie wektory ciągów odpowiadających poszczególnym klatkom Jordana i wartości własnej \(0\) rozpinają podprzestrzeń dopełniajacą do \( im f\). Bierzemy tu pod uwagę wszystkie klatki Jordana odpowiadające wartości własnej \(0\).


Udowodnimy teraz twierdzenie Jordana.
Twierdzenie 2.2 [Jordana]
Niech \(f: V\longrightarrow V\) będzie endomorfizmem, dla którego wielomian charakterystyczny rozkłada się na iloczyn czynników stopnia 1. Istnieje baza Jordana dla \(f\).
Dowód
Dowód jest indukcyjny ze względu na wymiar \(n\) przestrzeni \(V\). Jeśli \(n=1\), to twierdzenie jest trywialne. Załóżmy, że twierdzenie jest prawdziwe dla przestrzeni wymiaru mniejszego od \(n\).
Załóżmy najpierw, że \(f\) nie jest monomorfizmem, czyli \(\dim im f<n\). Podprzestrzeń \( im f\) jest \(f\)-niezmiennicza. Niech \(\tilde f: im f \longrightarrow im f\) będzie zawężeniem \(f\) do \( im f\). Wielomian charakterystyczny dla \(\tilde f\) dzieli wielomian charakterystyczny dla \(f\). Zatem rozkłada się na iloczyn czynników stopnia 1. Możemy zastosować założenie indukcyjne dla edomorfizmu \(\tilde f\) przestrzeni \(f\). Niech \(\dim im f =m\) i \(w_1,..., w_m\) będzie bazą Jordana dla \(\tilde f\). Jeżeli \( im f\oplus \ker f=V\), to do bazy \(w_1,...,w_m\)dopisujemy dowolną bazę podprzestrzeni \(\ker f\) i mamy bazę Jordana dla \(f\).
Załóżmy teraz, że \( im f\cap \ker f\ne \{0\}\). Oczywiście \(\ker\tilde f=\ker f\cap im f\). Z bazy Jordana \(w_1,...,w_m\) wybieramy bazę przestrzeni \(\ker\tilde f\). Niech będzie to ciąg \(w_{i_1},...,w_{i_k}\). Wszystkie te wektory są wektorami własnymi \(\tilde f\) odpowiadającymi wartości własnej \(0\). Każdy z nich rozpoczyna pewien ciąg wektorów odpowiadający jednej klatce Jordana endomorfizmu \(\tilde f\). Oznaczmy przez \(\tilde w_{1},...,\tilde w_{k}\) ostatnie wektory tych ciągów. Ponieważ wektory te należą do \( im f\), więc istnieją wektory \(v_1,...,v_k\in V\) takie, że
Bierzemy uzupełnienie \(u_1,..., u_{n-m-k}\) ciągu \(w_{i_1},...,w_{i_k}\) do bazy przestrzeni \(\ker f\).
Twierdzimy, że ciąg
\(w_1,...,w_m, v_1,...,v_k, u_1,...,u_{n-m-k}\) (2.4)
jest bazą przestrzeni \(V\). Wektorów tych jest \(n\), a zatem wystarczy sprawdzić ich liniową niezależność.
Niech
\(\begin{array} {rcl} \alpha _1w_1+...+\alpha _mw_m+&& \beta _1v_1+...+\beta _kv_k\\&&+\gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0. \end{array}\) (2.5)
Obłóżmy tę równość przez \(f\). Dostajemy równość
\(\alpha _1\tilde f(w_1)+...+\alpha _m\tilde f(w_m)=-\beta _1\tilde w _1-...-\beta _k\tilde w_k.\) (2.6)
Korzystając z uwagi poprzedzającej dowodzone twierdzenie wiemy, że
obie strony równości (2.6) muszą być zerami. A zatem \(\beta _1,...,\beta _k\) są równe zeru. Wracamy teraz do równości (2.5).
Mamy
\(\alpha _1w_1+...+\alpha _mw_m+ \gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0.\) (2.7)
Zatem
Pamiętając o tym, jak zostały wybrane wektory \(u_1,...,u_{n-m-k}\),
otrzymujemy, że \(\gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0\). Wynika stąd, że \(\gamma_1=...=\gamma _{n-m-k}=0\). Wracając teraz do
równości (2.7) otrzymujemy, że \(\alpha _1=...=\alpha _m =0\).
Na koniec zauważmy, że baza 2.4 jest bazą Jordana dla \(f\). Widać to natychmiast, jeśli ułożymy ją następująco. Na początku
a potem pozostałe wektory ciągu \(w_1,..., w_n\) w takiej kolejności
jak były.
Jeśli \(0\) nie jest wartością własną endomorfizmu \(f\) (\(f\) jest monomorfizmem), to weźmy pewną wartość własną \(\lambda\). Ponieważ wielomian charakterystyczny rozkłada się na czynniki stopnia 1, wartość własna istnieje. Zamiast \(f\) rozważmy endomorfizm \(F=f-\lambda I\). Na podstawie powyższego dowodu wiemy, że istnieje baza Jordana dla \(F\). Baza Jordana dla \(F\) jest też bazą Jordana dla \(f=F+\lambda I\).
Wniosek 2.3
Dla każdego endomorfizmu przestrzeni zespolonej istnieje baza i macierz Jordana.
Euklidesowe przestrzenie wektorowe
Iloczyn skalarny
Zaczniemy od definicji iloczynu skalarnego
Definicja 1.1 Iloczyn Skalarny
Niech \(V\) będzie przestrzenią wektorową nad ciałem \({\mathbb R}\). Odwzorowanie
nazywa się iloczynem skalarnym, jeśli spełnia trzy następujące warunki:
- S1) jest dwuliniowe,
- S2) jest symetryczne,
- S3) jest dodatnio określone, tzn. dla każdego \(v\in V\) zachodzi
nierówność \(g(v,v)\ge 0\) i \(g(v,v)=0\) wtedy i tylko wtedy, gdy \(v=0\).
Wartość iloczynu skalarnego na wektorach \(v,w\) oznaczamy także przez \(<v,w>\) lub \(v\cdot w\). Jak zwykle kropkę często pomijamy w zapisie. Nazwa iloczyn skalarny pochodzi stąd, że wynikiem takiego mnożenia jest skalar. Zwróćmy także uwagę na to, że wybór ciała liczb rzeczywistych jest tutaj nieprzypadkowy. W innych ciałach nie mamy skalarów większych od zera.
Zbierzemy teraz kilka najważniejszych przykładów iloczynów skalarnych.
Przykład 1.2
W przestrzeni \({\mathbb R} ^n\) mamy tzw. standardowy (lub kanoniczny) iloczyn skalarny. Mianowicie, dla wektorów \(v=(v_1,.... v_n),\ \ w=(w_1,...,w_n)\in {\mathbb R} ^n\) definiujemy
Ogólniej, niech \(\lambda _1,...,\lambda _n\) będą dowolnymi liczbami dodatnimi. Definiujemy iloczyn skalarny
Przykład 1.3
Rozważmy przestrzeń funkcji ciągłych określonych na przedziale \([a,b]\). Definiujemy iloczyn skalarny
Przykład 1.4
Niech \(e_1,...,e_n\) będzie bazą przestrzeni wektorowej \(V\) nad ciałem \({\mathbb R}\). Definiujemy iloczyn skalarny formułą
gdzie \((v_1,...,v_n)\), \((w_1,...,w_n)\) są współrzędnymi wektorów \(v\) i \(w\) w danej bazie.
Istotne w tym przykładzie jest to, że każda skończenie wymiarowa przestrzeń wektorowa nad ciałem \({\mathbb R}\) może być łatwo wyposażona w iloczyn skalarny.
Definicja 1.5 [Norma]
Normą na przestrzeni wektorowej \(V\) nad ciałem \({\mathbb R}\) nazywamy funkcję
Formy kwadratowe
Niech \(V\) będzie przestrzenią wektorową nad ciałem o charakterystyce różnej od 2. Odwzorowanie
nazywamy formą kwadratową, jeśli istnieje odwzorowanie
dwuliniowe
takie, że
dla każdego \(v\in V\). Mówimy, że odwzorowanie dwuliniowe \(\Phi\) indukuje formę kwadratową \(f\).
Udowodnimy najpierw następujący lemat
Lemat 0.1
Dla formy kwadratowej \(f:V\longrightarrow {\mathbb K}\) istnieje dokładnie jedno odwzorowanie dwuliniowe symetryczne \(\phi : V^2\longrightarrow {\mathbb K}\) indukujące \(f\).
Dowód
Niech \(\Phi\) będzie pewnym odwzorowaniem dwuliniowym indukującym \(f\). Zdefiniujmy odwzorowanie \(\phi\) następująco
Odwzorowanie to jest dwuliniowe, symetryczne i indukuje \(f\).
Zauważmy, że tutaj właśnie wykorzystaliśmy założenie, że
charakterystyka ciała \({\mathbb K}\) jest różna od \(2\).
Jedyność symetrycznego \(\phi\) indukującego \(f\) wykazujemy jak następuje.
Niech \(\phi '\), \(\phi ''\) będą odwzorowaniami dwuliniowymi symetrycznymi indukującymi \(f\). Wtedy \(\phi =\phi '-\phi ''\) jest odwzorowaniem dwuliniowym symetrycznym takim, że \(\phi (v,v)=0\) dla każdego \(v\in V\). Wykorzystując dwuliniowość i symetrię \(\phi\) otrzymujemy następujące równości
dla dowolnych wektorów \(u,v\in V\). A zatem \(\phi ' (u,v)=\phi ''(u,v)\) dla dowolnych \(u,v\in V\).
Jedyne dwuliniowe odwzorowanie symetryczne indukujące \(f\) nazywa się odwzorowaniem dwuliniowym skojarzonym z formą kwadratową \(f\).
Dla odwzorowania dwuliniowego \(\Phi\) rozważamy odwzorowanie
\(\tilde \Phi:V\ni v\longrightarrow \{ V\ni u\longrightarrow \Phi (u,v)\in {\mathbb K}\}\in V^*.\) (0.1)
Odwzorowanie to jest oczywiście liniowe.
Od tego momentu zakładamy, że wszystkie rozważane w tym wykładzie przestrzenie są skończenie wymiarowe.

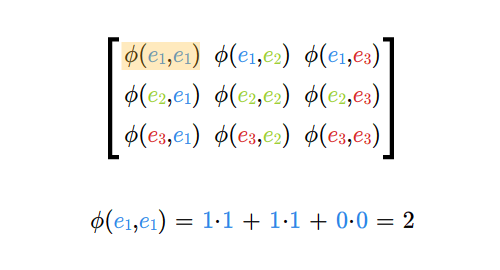







Niech \(e_1,...e_n\) będzie bazą przestrzeni \(V\) zaś \(e^*_1,...,e^*_n\) będzie jej bazą dualną. Znajdźmy macierz odwzorowania \(\tilde \Phi\) przy tak wybranych baz. Skorzystajmy ze wzoru (5.4) z Wykładu IV.
Otrzymujemy następujące równości
Oznacza to, że poszukiwana macierz \(\tilde \Phi\) jest równa
macierzy \([\Phi (e_i, e_j)]\). Macierz tę nazywamy macierzą
odwzorowania dwuliniowego w bazie \(e_1,...,e_n\).
Jeżeli \(\phi\) jest odwzorowaniem dwuliniowym skojarzonym z formą
kwadratową \(f\), to macierz tę nazywa się macierzą formy
kwadratowej \(f\) przy bazie \(e_1,...,e_n\). Macierz formy kwadratowej jest symetryczna. Rząd tej macierzy jest rzędem odwzorowania liniowego \(\tilde\phi\) i nazywa się rzędem formy kwadratowej \(f\).
Mając bazę \(e_1,...,e_n\) przestrzeni \(V\) i macierz formy kwadratowej \(f\) możemy znaleźć wartość \(f\) na dowolnym wektorze \(v\in V\). Mianowicie, jeśli \(\phi\) jest odwzorowaniem dwuliniowym skojarzonym z \(f\), \(a_{ij}=\phi(e_i,e_j)\) oraz \(v=v_1e_1+...+e_ne_n\), to
\(\displaystyle f(v)=\sum _{i,j=1}^n v_iv_ja_{ij}.\) (0.2)
Zobaczmy jeszcze, jak zmienia się macierz odwzorowania
dwuliniowego, jeśli zmienimy bazę. Niech więc dane będą dwie bazy
przestrzeni wektorowej \(V\): \(e_1,...,e_n\), \(e'_1,...e'_n\). Niech \(P\) będzie macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\), tzn.
dla \(j=1,...,n\) (porównaj rozdział 4. Wykładu VI). Jeśli \(\Phi :V\times V\longrightarrow {\mathbb K}\) jest odwzorowaniem dwuliniowym, to
zachodzą następujące równości
A zatem przy zmianie bazy macierz odwzorowania dwuliniowego zmienia się według wzoru
\(A'= P^* A P,\) (0.3)
gdzie \(A\) jest macierzą \(\Phi\) przy bazie \(e_1,...,e_n\), zaś \(A'\) jest macierzą \(\Phi\) przy bazie \(e'_1,...,e'_n\).
Co prawda udowodniliśmy już, że rząd macierzy \(\Phi\) nie zależy od wyboru bazy, ale warto zauważyć, że wynika to również z powyższego wzoru, bo \(P\) jest macierzą nieosobliwą.
Formy kwadratowe w przestrzeni nad ciałem \({\mathbb R}\)
Celem tego rozdziału jest pokazanie, że w przestrzeni wektorowej nad ciałem \({\mathbb R}\), każda forma kwadratowa ma macierz szczególnie prostej postaci.
Rozważymy najpierw formy kwadratowe w przestrzeniach euklidesowych. Udowodnimy teraz twierdzenie Lagrange'a
Twierdzenie 1.1
Niech \(f\) będzie formą kwadratową na skończenie wymiarowej przestrzeni euklidesowej \(V\). Istnieje baza ortonormalna \(e_1,...,e_n\) przestrzeni \(V\), przy której macierz \(A\) formy kwadratowej \(f\) jest diagonalna i \(a_{11}\ge...\ge a_{nn}\), gdzie \(a_{11},...,a_{nn}\) są wyrazami głównej przekątnej macierzy \(A\).
Dowód
Dowód twierdzenia jest indukcyjny ze względu na wymiar przestrzeni \(V\).
Dla \(n=1\) twierdzenie jest trywialne. Załóżmy, że jest prawdziwe dla \((n-1)\).
Niech \(f\) będzie formą kwadratową na \(n\)-wymiarowej przestrzeni euklidesowej \(V\). W przestrzeni \(V\) mamy naturalną topologię. Albo wprowadzimy ją przez normę (którą mamy, bo iloczyn skalarny definiuje normę), albo bierzemy dowolny izomorfizm liniowy \(h: V\longrightarrow {\mathbb R} ^n\) i mówimy, że podzbiór \(C\) przestrzeni \(V\) jest otwarty wtedy i tylko wtedy, gdy \(h(C)\) jest otwarty w \({\mathbb R} ^n\). Ponieważ każde odwzorowanie liniowe przestrzeni \({\mathbb R} ^n\) jest ciągłe, więc tak zdefiniowana topologia nie zależy od wyboru izomorfizmu \(h\). Tak czy inaczej, sfera jednostkowa
jest zbiorem zwartym a forma kwadratowa jest odwzorowaniem ciągłym na \(V\) (porównaj wzór (0.2)).
A zatem istnieje wektor \(e_1\in S ^{n-1}\), w którym funkcja \(f\) osiąga swoje maksimum. Niech \(W\) będzie dopełnieniem ortogonalnym do podprzestrzeni \({\rm lin} \{e_1\}\). Podprzestrzeń \(W\) jest \((n-1)\)-wymiarowa.
Na podstawie założenia indukcyjnego wiemy, że dla \(\tilde f=f_{|W}\) istnieje baza ortonormalna \(e_2,...,e_n\) przestrzeni \(W\), przy której macierz \(\tilde f\) jest diagonalna i wyrazy na głównej przekątnej tworzą ciąg niemalejący. Twierdzimy, że \(e_1,...,e_n\) jest bazą \(V\) spełniającą żądane warunki.
Po pierwsze \(e_1,...e_n\) jest oczywiście bazą ortonormalną \(V\) i \(\phi (e_1,e_1)=f(e_1) \ge f(e_i)= \phi (e_i,e_i)\) dla każdego \(i=2,...n\), bo wszystkie \(e_2,...,e_n\) należą do \(S ^{n-1}\). Wystarczy teraz pokazać, że \(\phi (e_1,e_i)=0\) dla każdego \(i=2,...n\). W tym celu, dla ustalonego wskaźnika \(i=2,...,n\), rozważmy funkcję
Wektor \((\cos \tau )\, e_1 +(\sin\tau )\, e_i\) należy do \(S ^{n-1}\) dla każdego \(\tau\). Ponieważ \(f\) osiąga w \(e_1\) maksimum, więc funkcja \(F\) osiąga maksimum w \(\tau =0\). Zatem \(F'(0)=0\).
Mamy następujące równości
Łatwo stad wyliczyć, że
Wobec tego \(\phi (e_1, e_i)=0\), co kończy dowód twierdzenia.
Udowodnimy teraz twierdzenie o bezwładności form kwadratowych, zwane także twierdzeniem Sylvestera.
Twierdzenie 1.2 [Sylvestera]
Niech \(V\) będzie \(n\)-wymiarową przestrzenią wektorową nad ciałem \({\mathbb R}\). Dla każdej formy kwadratowej \(f\) na \(V\) istnieje baza \(e_1,...,e_n\), przy której macierz \(f\) jest postaci blokowej
gdzie \({\rm I} _k\) jest macierzą jednostkową o wymiarach \(k\) na \(k\).
Liczby \(p\) i \(q\) nie zależą od wyboru bazy \(e_1,...,e_n\).
Dowód
Na przestrzeni wektorowej \(V\) wprowadzamy dowolny iloczyn skalarny (porównaj Przykład 1.4 z Wykładu X) Z twierdzenia Lagrange'a wiemy, że istnieje baza ortonormalna, przy której macierz formy \(f\) jest taka, jak to opisano w poprzednim twierdzeniu. Uporządkujmy tę bazę tak, aby na głównej przekątnej najpierw (tzn. począwszy od lewego górnego rogu) pojawiły się wyrazy dodatnie, potem ujemne i na końcu wyrazy zerowe. Wystarczy teraz pomnożyć wektory bazy odpowiadające niezerowym wyrazom macierzy pomnożyć przez przez odpowiedni skalar. Jeśli \(\phi (e_i,e_i) = a_{ii}\ne 0\), to \(e_i\) zastępujemy wektorem \({1\over {\sqrt {|a_{ii}|}}}e_i.\)
Udowodnimy teraz druga część twierdzenia. Widać, że \(p+q\) jest rzędem formy kwadratowej \(f\), a zatem nie zależy od wyboru bazy. Załóżmy, że dla dwóch baz \(e_1,...,e_n\) i \(e'_1,...e'_n\) spełniających tezę twierdzenia mamy pary liczb \(p, q\) oraz \(p',q'\) odpowiednio. Wiemy, że \(p+q=p'+q'\). Wystarczy więc pokazać, że \(p=p'\).
Dla dowodu nie wprost przypuśćmy, że \(p'>p\). Niech \(U\) będzie podprzestrzenią wektorową generowaną przez wektory \(e_{p+1},...,e_n\), zaś \(W\) - podprzestrzenią generowaną przez wektory \(e'_1,...,e'_{p'}\). Mamy następujący ciąg równości i nierówności
Wobec tego \(\dim (U\cap W)\ge p'-p>0\). Istnieje więc wektor \(0\ne v\in (U\cap W)\). Niech \(v=v_1e_1+...+v_ne_n\) i
\(v=v'_1e'_1+...+v'_ne'_n\). Ponieważ \(v\in U\), więc
Ponieważ \(v\in W\), więc
Porównując te nierowności widzimy, że \(f(v)=0\). Ponieważ \(v\in U\), więc \(v=v_{p+1}e_{p+1}+...+v_{p+q}e_{p+q}\). Korzystając z tego, że \(0=f(v)=-(v_{p+1})^2-...-(v_{p+q})^2\), otrzymujemy, że \(v=0\), co jest sprzeczne z naszym założeniem. Dowód twierdzenia jest zakończony.
Z twierdzenia Sylvestera wynika, że przy pewnej bazie \(e_1,...,e_n\) forma kwadratowa dana jest w postaci kanonicznej, tj. wyraża się wzorem
\(f(v)=(v_1)^2+...+(v_p)^2-(v_{p+1})^2-...-(v_{p+q})^2,\) (1.4)
dla \(\displaystyle v=\sum _{i=1}^nv_ie_i\).
Definicja 1.3 [Sygnatura]
Parę liczb \((p,q)\) nazywamy sygnaturą formy kwadratowej.
Mówimy, że forma kwadratowa \(f\) jest półokreślona dodatnio, jeśli w powyższym przedstawieniu (1.4) są same plusy. Jeśli są same plusy i \(p=n=\dim V\), to mówimy, że forma kwadratowa jest dodatnio określona. Podobnie definiuje się formy półokreślone ujemnie i określone ujemnie. Forma kwadratowa nazywa się formą określoną, jeśli jest określona dodatnio lub ujemnie.
Niech \(f:V\longrightarrow V\) będzie endomorfizmem. Mówimy, że odwzorowanie \(f\) jest symetryczne, jeśli
dla każdych wektorów \(v,w\in V\).
Niech \(\phi\) będzie odwzorowaniem dwuliniowym (symetrycznym) zdefiniowanym formułą
Odwzorowanie to jest odwzorowaniem skojarzonym pewnej formy kwadratowej. Ze wzoru (1.4) z Wykładu XI i z twierdzenia Lagrange'a wynika, że istnieje baza ortonormalna, przy której macierz odwzorowania \(f\) jest diagonalna. Jest to bardzo szczególny przypadek endomorfizmu mającego bardzo prostą macierz
Jordana.
Miara układu wektorów
Macierz Grama. Wyznacznik Grama
Zajmiemy się teraz przypadkiem, gdy sam iloczyn skalarny (oznaczony w tym rozdziale przez \(g\)) jako odwzorowanie dwuliniowe symetryczne jest odwzorowaniem dwuliniowym skojarzonym z formą kwadratową. Tą forma kwadratową jest kwadrat normy
Niech teraz \(v_1,...,v_k\) będzie dowolnym ciągiem wektorów przestrzeni \(V\). Definiujemy macierz
\(\left [ \begin{array} {lcccr} \ g(v_1,v_1) \ .\ .\ .\ g(v_1,v_k)\\ \ g(v_2,v_1) \ .\ .\ .\ g(v_2,v_k)\\ \ ..................................\\ \ g(v_k,v_1) \ . \ .\ .\ g(v_k,v_k) \end{array} \right ].\) (1.1)
Macierz tę nazywamy macierzą Grama ciągu wektorów \(v_1,...,v_k\). Wyznacznik tej macierzy nazywamy wyznacznikiem Grama tego ciągu.





Zauważmy od razu, że wyznacznik Grama nie zależy od kolejności
wektorów \(v_1,...,v_k\). Istotnie, przestawieniu dwu wektorów w
ciągu \(v_1,...,v_k\) odpowiada jednoczesne przestawienie dwu kolumn
i dwu wierszy w macierzy Grama. A zatem możemy mówić o wyznaczniku
Grama układu wektorów. Wyznacznik Grama układu \(v_1,...,v_k\)
oznaczać będziemy przez \({\rm G} (v_1,...,v_k)\).
Jeżeli \(V\) jest skończenie wymiarowa, to macierz odwzorowania dwuliniowego \(g\) przy dowolnej bazie ortonormalnej jest macierzą jednostkową. W szczególności, wyznacznik tej macierzy jest dodatni. Ze wzoru (0.3) z Wykładu XI wynika, że wyznacznik macierzy \(g\) przy jakiejkolwiek bazie jest dodatni.
Twierdzenie 1.1
Wyznacznik Grama dowolnego układu wektorów jest zawsze większy lub równy zeru. Jest równy zeru wtedy i tylko wtedy, gdy układ wektorów jest liniowo zależny.
Dowód
Oznaczmy przez \(U\) przestrzeń rozpiętą na danych wektorach \(v_1,...,v_k\). Przestrzeń ta jest wyposażona w iloczyn skalarny \(g\) (dokładniej mówiąc, zawężenie \(g\) do \(U\times U\)).
Jeśli wektory \(v_1,..., v_k\) są liniowo zależne, to pewien wektor \(v_j\) jest kombinacją liniową wektorów pozostałych. Wtedy \(j\)-ta kolumna macierzy Grama jest kombinacją liniową pozostałych kolumn. Oznacza to, że wyznacznik tej macierzy jest równy zeru.
Załóżmy teraz, że wektory \(v_1,..., v_n\) są liniowo niezależne. Stanowią więc bazę przestrzeni \(U\). Macierz Grama tego układu, jest macierzą \(g\) przy bazie \(v_1,...,v_n\) przestrzeni \(U\). A zatem, na podstawie uwagi, którą zrobiliśmy bezpośrednio przed twierdzeniem, wyznacznik tej macierzy jest dodatni (w
szczególności niezerowy).Przykład 1.2
Niech dane będą dwa wektory \(v\) i \(u\). Mamy macierz Grama
Fakt, że wyznacznik tej macierzy jest nieujemny jest nierównością Schwarza.
Niech \(e_1,...,e_n\) będzie bazą ortonormalną przestrzeni \(V\) i niech \(v_1,...,v_n\) będzie dowolnym układem wektorów przestrzeni \(V\). Tak jak zdefiniowaliśmy macierz przejścia od jednej bazy do drugiej, tak samo możemy zdefiniować macierz przejścia od bazy \(e_1,..., e_n\) do układu \(v_1,...,v_n\). Mianowicie, definiujemy macierz \(P=[v_{ij}]\) wzorami
\(\displaystyle v_j=\sum _{i=1}^n v_{ij} e_i.\) (1.2)
Macierz \(P\) jest macierzą współrzędnych wektorów \(v_1,...,v_n\) w bazie \(e_1,...e_n\). Zupełnie tak samo jak
wzór (0.3) z Wykładu XI otrzymujemy wzór następujący
\(\left [ \begin{array} {lcccr} \ g(v_1,v_1) \ .\ .\ .\ g(v_1,v_k)\\ \ ..................................\\ \ g(v_k,v_1) \ . \ .\ .\ g(v_k,v_k) \end{array} \right ] =P^*P,\) (1.3)
gdzie \(P\) jest macierzą zdefiniowaną formułą (1.2).
Otrzymaliśmy więc
Twierdzenie 1.3
Wyznacznik Grama układu wektorów \(v_1,...,v_n\) jest równy \(({\rm det} P)^2\), gdzie \(P\) jest macierzą utworzoną ze współrzędnych wektorów \(v_1,...,v_n\) w bazie ortonormalnej \(e_1,...,e_n\).
Miara układu wektorów
Niech \(V\) będzie skończenie wymiarową euklidesową przestrzenią wektorową. Niech \(U\) będzie dowolną jej podprzestrzenią. Mamy wtedy \(V=U\oplus U^{\perp}\). Niech \(v\in V\) będzie dowolnym wektorem. Wektor ten rozkłada się jednoznacznie na sumę \(v=u+u'\), gdzie \(u\in U\) i \(u'\in U^{\perp}\). Zdefiniujmy liczbę
\(d(v,U)= \Vert u'\Vert .\) (2.4)
Niech teraz \(V\) będzie dowolną (niekoniecznie skończenie
wymiarową) euklidesową przestrzenią wektorową i \(v_1,...,v_n\)
dowolnym ciągiem wektorów.
Zdefiniujemy liczbę \({\rm vol} (v_1,...,v_n)\) , którą nazywać będziemy miarą układu \(v_1,...,v_n\) (lub \(n\)-wymiarową objętością). Definicja będzie indukcyjna.
Definicja 2.1
Jeżeli \(n=1\), to miarą wektora \(v_1\) jest jego długość \(\Vert v_1\Vert\). Jeżeli określona już jest miara układów \(n\)-elementowych, to miarą układu \(v_1,...,v_n, v\) jest liczba zdefiniowana wzorem




Definicja ta jest zgodna z naszą intuicją i wiadomościami wyniesionymi ze szkoły.
Miara układu dwóch wektorów jest polem równoległoboku wyznaczonego przez te wektory. Miara układu trzech liniowo niezależnych wektorów jest objętością równoległościanu utworzonego przez te wektory.
Z definicji miary układu wektorów łatwo wynika, że \({\rm vol} (v_1,...,v_n) =0\), jeśli wektory \(v_1,...,v_n\) są liniowo zależne.
Udowodnimy teraz twierdzenie
Twierdzenie 2.2
Dla każdego układu wektorów \(v_1,..., v_n\) zachodzi równość
\({\rm vol} (v_1,...,v_n) = \sqrt{{\rm G} (v_1,...,v_n)}.\) (2.5)
Dowód
Dowód jest indukcyjny ze względu na \(n\).
Dla \(n=1\) twierdzenie jest trywialne. Załóżmy, że jest prawdziwe dla pewnego \(n\).
Niech dany będzie układ wektorów \(v_1,...,v_n,v\). Jeśli układ ten jest liniowo zależny, to po obydwu stronach (2.5) mamy zero. Możemy więc założyć, że dany układ wektorów jest liniowo niezależny.
W \((n+1)\)-wymiarowej przestrzeni \(V'={\rm lin} \{v_1,...,v_n, v\}\) weźmy \(n\)-wymiarową podprzestrzeń \(U={\rm lin} \{ v_1,...,v_n\}\). Oznaczmy przez \(d\) liczbę \(d=d(v, U)\). Niech \(v= u+u'\), gdzie \(u\in U\) i \(u'\in U^{\perp}\), zaś \(U^{\perp}\) jest dopełnieniem ortogonalnym do \(U\) w \(V'\). W szczególności \(g(u,u')=0\). Ponieważ \(v_1,...,v_n\) jest bazą \(U\), wektor \(u\) możemy zapisać jako
Zachodzą następujące równości
A zatem mamy równość
\(\displaystyle \sum _{i=1}^n x_ig(v_i ,v) +(-1)(\Vert v\Vert ^2 -d^2)=0.\) (2.6)
Oczywiście \(g(u, v_j)= g(v,v_j)\) dla każdego \(j=1,...n\). Stąd
dla \(j=1,...,n\). Zatem
\(\displaystyle \sum _{i=1}^n x_ig(v_i,v_j)+(-1)g(v,v_j)=0.\) (2.7)
Przyjmijmy \(x_{n+1}=-1\). Łącząc (2.6) i
(2.7) otrzymujemy układ \(n+1\) równości
\(\displaystyle \left \{ \begin{array} {l} \ \sum _{i}^n x_ig(v_i,v_j)+x_{n+1} g(v,v_j)=0,\ \ j=1,...,n\\ \ \sum _{i}^n x_ig(v_i ,v) +x_{n+1}(\Vert v\Vert ^2 -d^2)=0. \end{array} \right .\) (2.8)
Potraktujmy ten układ jako jednorodny układ \(n+1\) równań
liniowych z \(n+1\) niewiadomymi \(x_1,...,x_{n+1}\). Wiemy, że układ ten ma niezerowe rozwiązanie \((x_1,...,x_n, -1)\). A zatem
wyznacznik macierzy współczynników tego układu jest równy \(0\).
Macierz współczynników tego układu jest następująca
\(\left [\begin{array} {lccccr} \ g(v_1,v_1) \ . \ . \ . \ g(v_n, v_1) \ \ \ \ \ \ g(v,v_1)\\ \ ....................................................... \\ \ g(v_1,v_n) \ .\ . \ .\ \ g(v_n,v_n)\ \ \ \ \ g(v,v_n ) \\ \ g(v_1, v) \ \ .\ . \ . \ \ \ g(v_n,v)\ \ \ \ \ g(v,v)-d^2 \end{array} \right ]\) (2.9)
Korzystając teraz z liniowości wyznacznika ze względu na ostatnią
kolumnę otrzymujemy równość wyznaczników następujących macierzy
\(\left [\begin{array} {lccccr} \ g(v_1,v_1)\ .\ .\ .\ g(v_n,v_1)\ g(v,v_1) \\ \ ...............................................\\ \ g(v_1,v_n) \ .\ . \ . \ g(v_n,v_n) \ g( v,v_n) \\ \ g(v_1,v)\ .\ .\ . \ \ g(v_n,v) \ \ \ \ g(v,v) \end{array} \right ],\) (2.10)
\(\left [\begin{array} {lccccl} \ g(v_1,v_1)\ .\ .\ .\ g(v_n,v_1)\ \ \ \ 0 \\ \ ...............................................\\ \ g(v_1,v_n) \ .\ . \ . \ g(v_n,v_n) \ \ \ \ 0\\ \ g(v_1,v)\ .\ .\ . \ \ g(v_n,v) \ \ \ \ \ \ d^2 \end{array} \right ],\) (2.11)
Wyznacznik pierwszej macierzy jest równy \({\rm G} ( v_1,...,v_n,v)\),
zaś wyznacznik drugiej macierzy jest równy \(d^2 {\rm G} (v_1,...,v_n)\). Dowód twierdzenia jest zakończony.
Z powyższego twierdzenia wynika natychmiast następujący
Wniosek 2.3
Miara układu wektorów nie zależy od uporządkowania wektorów tworzących układ.
Ponadto udowodniliśmy następujący wzór
Twierdzenie 2.4
Dla dowolnych wektorów \(v_1,...v_n,v\) zachodzi wzór
\({\rm G} (v_1,...,v_n,v)=d^2 G(v_1,...,v_n),\) (2.12)
gdzie liczba \(d=d(v,U)\) zdefiniowana jest formułą
(2.4) i \(U={\rm lin} \{v_1,...,v_n\}\).
Miara dowolnego ortonormalnego układu wektorów jest równa 1. Wynika to łatwo zarówno z definicji jak i z formuły (2.5). Innymi słowy, objętość kostki rozpiętej na układzie ortonormalnym jest równa 1.
Niech \(f\) będzie endomorfizmem przestrzeni euklidesowej \(V\). Załóżmy, że \(V\) jest skończenie wymiarowa. Ustalmy pewną bazę ortonormalną \(e_1,...,e_n\). Miara układu wektorów \((e_1,...,e_n)\) jest równa 1. Jeśli \(f\) jest endomorfizmem przestrzeni \(V\), to \(f\) przeprowadza daną bazę w układ \(f(e_1),...,f(e_n)\). Kolumny macierzy \(A\) odwzorowania \(f\) przy bazie \(e_1,...,e_n\) są współrzędnymi wektorów \(f(e_1),...,f(e_n)\) w bazie \(e_1,..., e_n\). A zatem, na podstawie Twierdzenia 1.2 i Twierdzenia 2.2, otrzymujemy
Wniosek 2.5
Miara wektorów \(f(e_1),...,f(e_n)\) jest równa mierze bazy \(e_1,..., e_n\) wtedy i tylko wtedy, gdy \({\rm det} f=\pm 1\).
O endomorfizmie \(f\) mówimy, że zachowuje objętość, jeśli jego wyznacznik jest równy \(\pm 1\). Oczywiście izometrie maja tę własność, ale odwzorowań zachowujących objętość jest o wiele więcej. Każdy automorfizm pomnożony przez odpowiedni skalar jest odwzorowaniem zachowującym objętość. Endomorfizm, którego wyznacznik jest równy 1 nazywa się endomorfizmem unimodularnym.
Ogół macierzy kwadratowych o wymiarach \(n\) na \(n\), których wyznacznik równy jest 1 jest podgrupą grupy \(GL(n;{\mathbb R} )\). Grupę tę oznacza się \(SL (n;\mathbb R)\) i nazywa się grupą specjalną. Elementy tej grupy nazywa się macierzami unimodularnymi.
Przestrzenie afiniczne I
Definicja przestrzeni afinicznej. Własności
Niech \(X\) będzie zbiorem niepustym a \(V\) przestrzenią wektorową nad ciałem \({\mathbb K}\). Załóżmy, że dane są dwie operacje (odwzorowania)
\(X\times X\ni (x,y)\longrightarrow \overrightarrow {xy}\in V,\) (1.1)
\(X\times V\ni (x, v )\longrightarrow x+v \in X.\) (1.2)
Znak "plus" jest tutaj symbolem użytym w nowym znaczeniu. Mamy
ciągle "plus" oznaczający dodawanie w przestrzeni wektorowej i
"plus" oznaczający dodawanie w ciele. Z kontekstu zawsze wynika,
co oznacza "plus" pojawiający się w danej formule.
Mówimy, że \(X\) jest przestrzenią afiniczną o kierunku \(V\), jeśli spełnione są dwa następujące warunki
A1) Dla każdych \(x\in X\), \(v\in V\) zachodzi równoważność: \(x+v=y\) wtedy i tylko wtedy, gdy \(\overrightarrow {xy}=v\).
A2) Dla każdych \(x,y, z \in X\overrightarrow{xy}+\overrightarrow{yz}=\overrightarrow{xz}\).
Elementy przestrzeni afinicznej \(X\) nazywamy punktami. Odwzorowanie (1.1) nazywa się wyznaczaniem wektora przez parę punktów. Odwzorowanie (1.2) nazywa się zaczepianiem wektora w punkcie.
Przestrzeń afiniczną zapisujemy także jako parę \((X,V)\). Używamy także określenia przestrzeń afiniczna \(X\) nad \(V\). Wymiarem przestrzeni afinicznej nazywamy wymiar przestrzeni wektorowej \(V\) i oznaczamy \(\dim X\).
Zbierzmy na początek kilka podstawowych własności przestrzeni afinicznych.
Twierdzenie 1.1
Dla każdych punktów \(x,y\in X\) i każdych wektorów \(v,w\in V\) zachodzą następujące warunki:
- \(\overrightarrow {xx} = 0\),
- \(x+0 = x\), gdzie \(0\) jest wektorem zerowym w \(V\).
- \(\overrightarrow {xy} = 0\) wtedy i tylko wtedy, gdy \(x=y\),
- \(-\overrightarrow {xy} = \overrightarrow {yx}\),
- \(x = y\) wtedy i tylko wtedy, gdy \(\overrightarrow {zx}= \overrightarrow {zy}\) dla każdego \(z\in X\),
- \(x=y\) wtedy i tylko wtedy, gdy istnieje \(z\in X\) takie, że \(\overrightarrow {zx}= \overrightarrow {zy}\),
- \(\overrightarrow {x(y+v)} = \overrightarrow {xy}+v\),
- \(x + (v + w) = (x + v) + w\).
- \(\overrightarrow {(x+v)(y+w)} = \overrightarrow{xy} + (w-v)\)
Dowód
- 1) Korzystając z A2) otrzymujemy równość
Dodając do obu stron \(-\overrightarrow {xx}\) otrzymujemy żądaną równość.
- 2) Korzystając z A1) i udowodnionej już własności 1) dostajemy
równość \(x+ 0=x\), bo \(\overrightarrow{xx}=0\).
- 3) Z aksjomatu A1) i udowodnionej już własności 2) wiemy, że \(\overrightarrow {xy}=0\) wtedy i tylko wtedy, gdy \(y=x+0=x\).
- 4) Z aksjomatu A2) i własności 1) otrzymujemy równości
- 5) i 6) Następująca implikacja jest oczywista.
Jeśli \(x=y\), to dla każdego punktu \(z\in X\) zachodzi równość \(\overrightarrow {zx} =\overrightarrow {zy}\).
Udowodnimy implikację:
Jeśli istnieje punkt \(z\in X\) taki, że \(\overrightarrow {zx}=\overrightarrow {zy}\), to \(x=y\).
Korzystając z własności 4) i aksjomatu A2) dostajemy implikacje
Z własności 3) mamy równość \(x=y\).
- 7) Korzystając z aksjomatu A2) otrzymujemy równość
Stosując teraz A1) dostajemy
- 8) Na podstawie 6) wiemy, że \(x+(v+w) =(x+v)+w\) wtedy i tylko wtedy, gdy
Lewa strona ostatniej równości jest równa (na podstawie własności 6) i 1))
Dla prawej strony zachodzą równości (również na podstawie 6) i 1))
- 9) Wykorzystując udowodnione już własności otrzymujemy
Z własności 8) wynika, że możemy stosować zapis \(x+v+w\).
Przykład 1.2
Każda przestrzeń wektorowa \(V\) jest przestrzenią afiniczną nad samą sobą. Operacje zaczepiania wektora w punkcie i wyznaczania wektora przez parę punktów dane są następująco. Dla \(v,w \in V\)
W ostatnim wzorze z lewej strony mamy zaczepianie wektora \(w\) w punkcie \(v\), z prawej strony dodawanie wektorów w \(V\).
Przykład 1.3
Dowolny zbiór jednoelementowy jest przestrzenią afiniczną nad przestrzenią wektorową \(\{0\}\).
Przykład 1.4
Najlepiej znanym przykładem przestrzeni afinicznej jest przykład znany ze szkoły. Mianowicie, płaszczyzna lub trójwymiarowa przestrzeń fizyczna ze znanymi ze szkoły operacjami zaczepiania wektora swobodnego w punkcie i wyznaczania wektora swobodnego przez parę punktów są oczywiście przestrzeniami afinicznymi. Płaszczyzna i trójwymiarowa przestrzeń fizyczna są zbiorami punktów. Proponujemy, aby czytelnik prześledził na tym przykładzie wszystkie własności z Twierdzenia 1.1. Własności te w większości wydają się całkiem oczywiste, ale pamiętajmy, że definicja przestrzeni afinicznej (tak samo zresztą jak definicje przestrzeni wektorowej, ciała czy grupy) jest definicją aksjomatyczną i wszystkie własności tej struktury, choćby wydawały się najbardziej oczywiste, muszą być wywiedzione z aksjomatów.





Punkt bazowy, układ bazowy
Ustalmy pewien punkt \({\rm o}\) w przestrzeni afinicznej \((X,V)\). Punkt ten nazwiemy punktem bazowym. Rozważmy odwzorowanie
\(\Phi _{{\rm o}}: X \ni x \longrightarrow \overrightarrow {{\rm o} x}\in V.\) (2.3)
Odwzorowanie to jest bijekcją. Istotnie, odwzorowanie odwrotne dane jest formułą
Ponieważ \(\Phi _{{\rm o}}\) jest bijekcją, więc możemy przenieść
strukturę przestrzeni wektorowej z \(V\) na \(X\). Robimy to tak, aby odwzorowanie \(\Phi\) było izomorfizmem liniowym, tzn. definiujemy działania w \(X\) następująco:
Dla \(x,y\in X\) punkt \(x+y\) jest równy takiemu punktowi \(z\in X\), że \(\overrightarrow {{\rm o} x} +\overrightarrow {{\rm o} y} = \overrightarrow {{\rm o} z}\).
Dla \(x\in X\) i \(\lambda \in {\mathbb K}\) punkt \(\lambda x\) zdefiniowany jest jako punkt \(z\in X\) taki, że \(\overrightarrow {{\rm o} z}= \lambda \overrightarrow {{\rm o} x}.\)
Innymi słowy,
Łatwy eksperyment pokazuje, że struktura przestrzeni wektorowej na \(X\) wprowadzona przez zadanie punktu bazowego, w istotny sposób
zależy od tego punktu.
Niech teraz dany będzie punkt bazowy \(o\) i baza przestrzeni wektorowej \(V\). Załóżmy, że przestrzeń \(V\) jest skończenie wymiarowa i \(e_1,...,e_n\) jest daną bazą tej przestrzeni.
Układ \(({\rm o} ;e_1,...,e_n)\) nazywamy układem bazowym przestrzeni afinicznej \(X\). Układ bazowy nazywa się też układem współrzędnych. Punkt \({\rm o}\) jest początkiem tego układu zaś \(e_1,...e_n\) są wektorami wyznaczającymi osie współrzędnych. Taki układ współrzędnych nazywa się ukośnokątnym układem współrzędnych (dla podkreślenia, że nie musi to być układ prostokątny). Na razie zresztą nie mamy pojęcia prostopadłości w przestrzeni afinicznej.
Mając dany układ bazowy \(({\rm o} ;e_1,...,e_n)\) każdemu punktowi \(x\in X\) możemy przyporządkować ciąg współrzędnych \((x_1,...,x_n)\) wektora \(\overrightarrow {ox}\) w bazie \(e_1,..., e_n\), tzn. \(\overrightarrow {{\rm o} x} =x_1e_1+...+x_ne_n\). Ciąg ten nazywamy współrzędnymi punktu \(x\) w danym układzie bazowym (układzie współrzędnych).


Afiniczna niezależność punktów
Niech \((X,V)\) będzie przestrzenią afiniczną i \(A= {\{x_t\}}_{t\in T}\) zbiorem punktów przestrzeni \(X\). Oznaczmy jeden z elementów zbioru wskaźników \(T\) przez \(0\). Mówimy, że zbiór \(A\) jest afinicznie niezależny, jeśli zbiór wektorów
jest liniowo niezależny. Definicja ta zależy a priori od wyboru
punktu \(x_0\). Za chwilę wykażemy, że zależność ta jest tylko
pozorna.
Zbiór punktów nazywa się afinicznie zależnym, jeśli nie jest afinicznie niezależny. Podobne definicje afinicznej zależności i niezależności obowiązują dla układu punktów. Dwa punkty są afinicznie zależne wtedy i tylko wtedy, gdy są równe. Pojedynczy punkt uważamy za afinicznie niezależny.
Udowodnimy teraz twierdzenie
Twierdzenie 3.1
Niech \({\rm o}\) będzie punktem bazowym przestrzeni afinicznej \(X\). Punkty \(x_0,x_1,...x_n\) są afinicznie zależne wtedy i tylko wtedy, gdy istnieją skalary \(r_0,...,r_n\) nie wszystkie równe zeru takie, że \(r_0+...+ r_n=0\) oraz
\(r_0\overrightarrow {{\rm o} x_0} +...+r_n\overrightarrow {{\rm o} x_n} =0,\) (3.4)
Dowód
Załóżmy najpierw, że \(\{ x_0,...x_n\}\) są afinicznie zależne, czyli \(\overrightarrow {x_0x_1},...,\overrightarrow {x_0x_n}\) są liniowo zależne. Istnieją więc skalary \(r_1,...,r_n\) nie wszystkie równe zeru, takie, że
Zdefiniujmy \(r_0=-r_1-...-r_n\). Zachodzą równości
Odwrotnie załóżmy, że istnieją skalary \(r_0,...,r_n\) nie wszystkie
równe zeru, których suma jest równa zeru i takie, że \(\sum _{i=0}^n r_0\overrightarrow {{\rm o} x_i}=0.\)
Zachodzą następujące równości
Ponieważ nie wszystkie skalary \(r_0,...r_n\) są równe zeru a ich
suma jest równa zeru, więc wśród skalarów \(r_1,...,r_n\) istnieje
skalar niezerowy. A zatem \(\overrightarrow {x_0x_1},...,\overrightarrow {x_0x_n}\) są liniowo zależne, co kończy dowód twierdzenia.
Warunek w powyższym twierdzeniu zależy a priori od wyboru punktu bazowego, ale nie zależy od wyboru \(x_0\). W definicji punkt bazowy w ogóle się nie pojawia. Ponieważ warunek definicyjny i warunek z twierdzenia są sobie równoważne afiniczna zależność nie zależy ani od wyboru punktu \(x_0\), ani od wyboru punktu bazowego.
W \(n\)-wymiarowej przestrzeni afinicznej może istnieć co najwyżej \(n+1\) punktów afinicznie niezależnych. Na fizycznej płaszczyźnie każde trzy niewspółliniowe punkty są afinicznie niezależne i każda większa liczba punktów stanowi zbiór afinicznie zależny.
Ustalmy pewien układ bazowy \(({\rm o} ;e_1,...,e_n)\) w przestrzeni afinicznej \((X,V)\). Jeśli dane są punkty \(x\), \(y\) i ich współrzędne \((x_1,...,x_n)\), \((y_1,...,y_n)\) w danym układzie bazowym, to wektor \(\overrightarrow {xy}\) ma współrzędne \((y_1-x_1,...,y_n-x_n)\) w bazie \(e_1,...,e_n\).
Niech dane będą punkty \(x_0,...,x_m\in X\) i niech
będą współrzędnymi punktu \(x_i\), dla \(i=0,...,m\), w danym układzie bazowym.
Mamy następujące równości
Wektory \(\overrightarrow {x_0x_1},...,\overrightarrow {x_0x_m}\), \(m\le n\), są liniowo niezależne wtedy i tylko wtedy, gdy
Udowodniliśmy
Twierdzenie 3.2
Punkty \(x_0,..., x_m\), \(m\le n=\dim X\), są afinicznie niezależne wtedy i tylko wtedy, gdy
Podobnie uzasadnia się następujące twierdzenie.
Twierdzenie 3.3
Punkty \(x_0,..., x_n\), \(n=\dim X\), są afinicznie niezależne wtedy i tylko wtedy, gdy
Przestrzenie afiniczne II
Podprzestrzenie afiniczne
Niech \(V_0\) będzie podprzestrzenią przestrzeni \(V\), zaś \(X_0\) - niepustym podzbiorem \(X\). Mówimy, że \(X_0\) jest podprzestrzenią \(X\) o kierunku \(V_0\), jeśli spełnione są dwa następujące warunki:
- PA 1) \(\overrightarrow {xy}\in V_0\) dla każdych \(x,y\in X_0\).
- PA 2) \(x+v\in X_0\) dla każdych \(x\in X_0\) i \(v\in V_0\).
Jest oczywiste, że jeśli spełnione są te warunki, to \((X_0,V_0)\) z operacjami zaczepiania wektora w punkcie i wyznaczania wektora przez parę punktów zawężonymi z przestrzeni \((X,V)\) jest przestrzenią afiniczną.
Przykład 1.1
Podzbiór składający się z jednego (dowolnego) punktu przestrzeni \(X\) jest podprzestrzenią afiniczną o kierunku \(\{0\}\). Cała przestrzeń \(X\) jest podprzestrzenią o kierunku \(V\).

Przykład 1.2
Niech \(x_0\in X\) i \(V_0\) będzie podprzestrzenią wektorową \(V\). Rozważmy zbiór
\(x_0+ V_0=\{ x_0+v\,|\, v\in V_0\}.\) (1.1)
Niech \(x=x_o+ v\), \(y=x_0+ w\), gdzie \(v,w\in V_0\). Z Twierdzenia 1.1 wiemy, że
Podobnie, jeśli \(x_0 +v\), gdzie \(v\in V_0\), to
dla \(w\in V_0\). A zatem zbiór zdefiniowany przez(1.1)
jest podprzestrzenią afiniczną o kierunku \(V_0\).
Przypomnijmy sobie, że zbiór rozwiązań układu równań liniowych jest właśnie postaci (1.1). A zatem mamy twierdzenie.
Twierdzenie 1.3
Jeśli układ równań liniowych ma rozwiązanie, to zbiór wszystkich rozwiązań tego układu jest podprzestrzenią afiniczną przestrzeni \({\mathbb K} ^n\) o kierunku będącym przestrzenią rozwiązań odpowiadającego układu jednorodnego.
W szczególności podprzestrzeń dana jednym równaniem, tzn. równaniem
\(a_0+a_1x_1+...+a_nx_n=0\) (1.2)
jest \((n-1)\) wymiarową podprzestrzenią \({\mathbb K} ^n\) (lub dowolnej \(n\)-wymiarowej przestrzeni afinicznej \(X\) z wprowadzonym okładem współrzędnych), o ile któryś ze skalarów \(a_1,..., a_n\) jest różny od zera. Podprzestrzeń \((n-1)\)-wymiarową nazywa się hiperpłaszczyzną. Równanie (1.2) nazywa się
równaniem ogólnym hiperpłaszczyzny.
Podprzestrzeń jednowymiarową nazywamy prostą afiniczną. Podprzestrzeń dwuwymiarową nazywamy płaszczyzną afiniczną.
Mamy następujący lemat.
Lemat 1.4
Jeśli \((X_0,V_0)\) oraz \((X_0,W_0)\) są podprzestrzeniami afinicznymi to \(V_0=W_0\).
Dowód
Niech \(x\in X_0\) i \(v\in V_0\). Wtedy \(x+v\in X_0\). Ponieważ \((X_0,W_0)\) jest podprzestrzenią afiniczną, więc \(v=\overrightarrow {x (x+v)}\in W_0\).
Dzięki temu lematowi wystarczy mówić " niech \(X_0\) będzie podprzestrzenią afiniczną", bo kierunek podprzestrzeni \(X_0\) jest wyznaczony jednoznacznie.
Zauważmy teraz, że każda podprzestrzeń afiniczna jest taka jak w (Przykładzie 1.2).

Twierdzenie 1.5
Niech \(X_0\) będzie podprzestrzenią afiniczną o kierunku \(V_0\). Dla dowolnego punktu \(x_0 \in X_0\) mamy
Dowód
Z definicji podprzestrzeni afinicznej wynika, że \(x_0+V_0\subset X_0\). Odwrotnie, jeżeli \(x\in X_0\), to \(\overrightarrow {x_0x}\in V_0\), a zatem \(x=x_0+\overrightarrow {x_0 x}\in x_0 +V_0\).
Kierunek dowolnej podprzestrzeni afinicznej \(X_0\) jest równy przestrzeni
\(\{ \overrightarrow {x_o x}\, |\, x\in X_0\},\) (1.3)
gdzie \(x_0\) jest dowolnie wybranym punktem przestrzeni \(X\), lub, co na jedno wychodzi, przestrzeni
\(\{\overrightarrow {xy}\, |\, x,y \in X_0\}.\) (1.4)
Załóżmy, że mamy dwie podprzestrzenie tej samej przestrzeni afinicznej \((X,V)\).
Mówimy, że podprzestrzeń afiniczna \((X_0, V_0)\) jest równoległa do podprzestrzeni \((X_1, V_1)\), jeśli \(V_0\subset V_1\). Podprzestrzenie \((X_0,V_0)\), \((X_1,V_1)\) są równoległe, jeśli \(V_0=V_1\).
Zachodzi następujące (zgodne z intuicją) twierdzenie.
Twierdzenie 1.6
Jeżeli podprzestrzeń \(X_0\) jest równoległa do \(X_1\), to albo \(X_0\subset X_1\), albo \(X_0\cap X_1=\emptyset\).
Dowód
Przypuśćmy, że \(X_0\cap X_1\ne\emptyset\). Niech \(x_0\in X_0\cap X_1\). Jeżeli \(V_0\), \(V_1\) sa kierunkami \(X_0\) i \(X_1\) odpowiednio, to \(X_0=x_0+V_0\) i \(X_1= x_0+V_1\). Wobec tego \(X_0\subset X_1\).
Twierdzenie 1.7
Niech \({X_t}_{\{t\in T\}}\) będzie dowolną rodziną podprzestrzeni przestrzeni \(X\). Jeśli \(\bigcap _{t\in T}X_t\ne \emptyset\), to \(\bigcap _{t\in T}X_t\) jest podprzestrzenią afiniczną \(X\).
Dowód
Niech \(V_t\) będzie kierunkiem \(X_t\) dla każdego \(t\in T\). Jeśli \(\displaystyle x_0\in \bigcap _{t\in T} X_t\), to
a więc
Zbiory wypukłe
Niech dane będą dwa różne punkty \(p\), \(q\) przestrzeni afinicznej \(X\) o kierunku będącym przestrzenią wektorową nad ciałem \({\mathbb R}\). Prosta przechodząca przez te punkty może być opisana jako zbiór wszystkich punktów postaci \(y=p+t\overrightarrow {pq}\), \(t\in {\mathbb R}\). Odcinkiem wyznaczonym przez te punkty nazywamy zbiór
Jeśli \(X\) jest przestrzenią wektorową (lub w przestrzeni
afinicznej ustalony jest punkt bazowy), to \(\overline {pq} = \{ (1-t)p+tq\ |\ t\in [0,1]\}\).
Zbiór \(A\subset X\) nazywamy wypukłym, jeśli dla każdej pary punktów \(p,q\in A\) odcinek \(\overline {pq}\) zawiera się w zbiorze \(A\).
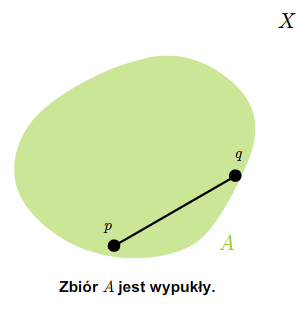
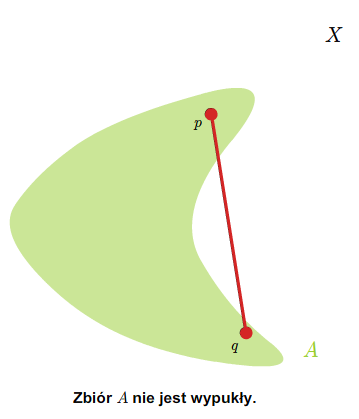
Oczywiste jest następujące twierdzenie
Twierdzenie 2.1
Przecięcie dowolnej rodziny zbiorów wypukłych jest zbiorem wypukłym.
Jeżeli \(A\) jest dowolnym podzbiorem przestrzeni \(X\), to przez \({\rm conv} A\) oznaczamy przecięcie wszystkich zbiorów wypukłych zawierających \(A\). Na mocy Twierdzenia 2.1 jest to zbiór wypukły o tej własności, że każdy zbiór wypukły zawierający \(A\) zawiera \({\rm conv} A\). Zbiór \({\rm conv} A\) nazywa się wypukłą otoczką zbioru \(A\).
Odwzorowania afiniczne
Niech \(V,W\) będą przestrzeniami wektorowymi nad ciałem \({\mathbb K}\) i niech \((X,V)\), \((Y,W)\) będą przestrzeniami afinicznymi. Odwzorowanie
nazywamy odwzorowaniem afinicznym, jeśli istnieje odwzorowanie liniowe
takie, że dla każdych \(x', x''\in X\) zachodzi równość
\(\overrightarrow {f(x')f(x'')}= \varphi (\overrightarrow {x'x''}).\) (3.5)
Warunek ten można zastąpić warunkiem równoważnym:
\(f(x+v) =f(x)+\varphi (v)\) (3.6)
dla każdych \(x\in X\) i \(v\in V\).
Mówimy, że \(\varphi\) jest odwzorowaniem liniowym indukowanym przez odwzorowanie afiniczne \(f\).
Odwzorowanie indukowane jest dla danego odwzorowania afinicznego jedyne. Mamy mianowicie
Lemat 3.1
Jeżeli \(f\) jest odwzorowaniem afinicznym indukującym odwzorowania liniowe \(\varphi _1\) i \(\varphi _2\), to \(\varphi _1=\varphi _2\).
Dowód
Niech \(v\in V\) i \(x\in X\). Zachodzą równości
Dowód następującego twierdzenia jest standardowy
Twierdzenie 3.2
Złóżenie odwzorowań afinicznych jest odwzorowaniem afinicznym. Jeśli odwzorowanie afiniczne jest bijekcją, to odwzorowanie odwrotne jest afiniczne.
Obraz podprzestrzeni afinicznej przez odwzorowanie afiniczne jest podprzestrzenią afiniczną.
Przeciwobraz podprzestrzeni afinicznej przez odwzorowanie afiniczne jest podprzestrzenią afiniczną.
Przykład 3.3
Odwzorowanie identycznościowe przestrzeni afinicznej \(X\) jest odwzorowaniem afinicznym indukującym odwzorowanie identycznościowe.
Przykład 3.4
Odwzorowanie stałe, tzn. \(f:X\ni x\longrightarrow y_0\in Y\), gdzie \(y_0\) jest ustalonym punktem przestrzeni \(Y\), jest odwzorowaniem afinicznym indukującym odwzorowanie zerowe. Przypomnijmy, że jedynym odwzorowaniem liniowym stałym jest odwzorowanie zerowe.
Przykład 3.5
Odwzorowanie liniowe przestrzeni wektorowej jest odwzorowaniem afinicznym indukującym samo siebie.
Przykład 3.6
Niech \(v\) będzie ustalonym wektorem przestrzeni wektorowej \(V\). Zdefiniujmy odwzorowanie
Odwzorowanie to nazywa się translacją (lub przesunięciem równoległym) o wektor \(v\). Odwzorowanie to jest odwzorowaniem afinicznym indukującym identyczność przestrzeni \(V\).
Dla dwóch wektorów \(v,w\in V\) zachodzi równość \(t_{v}\circ t_{w}= t_{v+w}\). W szczególności \(t_v\circ t_w= t_w\circ t_v\).
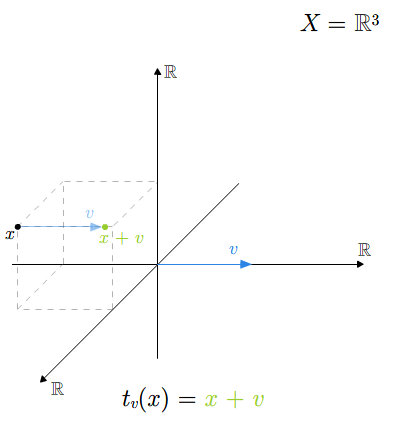
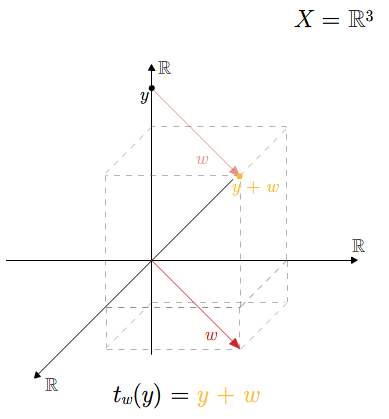
Niech \(f: X\longrightarrow Y\) będzie odwzorowaniem afinicznym
indukującym odwzorowanie liniowe \(\varphi : V\longrightarrow W\).
Załóżmy, że dane są punkty bazowe \({\rm o}\) w \(X\) i \({\rm o} '\) w \(Y\).
Niech \(w\in W\) będzie takim wektorem, że \(f({\rm o} )= {\rm o} '+ w\). Dla każdego \(x\in X\) zachodzi wzór
\(f(x) = {\rm o} ' + \varphi (\overrightarrow { ox } )+w.\) (3.7)
Z formuły (3.7) wynika, że każde odwzorowanie afiniczne \(f: V\longrightarrow W\) przestrzeni wektorowych jest złożeniem odwzorowania liniowego i translacji w przestrzeni \(W\).
Taka sama konkluzja dotyczy sytuacji, gdy przestrzenie afiniczne wyposażymy w strukturę przestrzeni liniowych przez wybranie punktów bazowych.
Odwzorowanie afiniczne, tak jak i odwzorowanie liniowe, ma przedstawienie macierzowe. Niech \(({\rm o} ; e_1,...,e_n)\) będzie układem bazowym w \((X,V)\) zaś \(({\rm o} ' ; e'_1,...,e'_m )\) układem bazowym w \((Y,W)\).
Niech \(A\) będzie macierzą \(\varphi\) przy danych bazach przestrzeni \(V\) i \(W\).
Załóżmy, że punkt \(x\) ma współrzędne \((x_1,...,x_n)\), wektor \(w\) ma współrzędne \((w_1,...,w_m)\), zaś punkt \(y=f(x)\) współrzędne \((y_1,...,y_m)\).
Macierzą odwzorowania afinicznego \(f\) nazywamy macierz
\(\left [\begin{array} {lccccr} \ \ \ \ \ \ \ \ \ \ \ \ w_1\\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ A \ \ \ \ \ \ \ . \\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ \ \ \ \ \ \ \ \, \ w_m\\ \ 0\ \ ...\ \ 0 \ \ \ 1 \end{array} \right ]\) (3.8)
lub w skrócie
\(\left [\begin{array} {lccccr} \ \ A \ \ w \\ \ \ 0\ \ 1 \end{array} \right ]\) (3.9)
Posługując się formułami rachunku macierzowego, otrzymujemy równość
\(\left [\begin{array} {lccccr} \ \ \ \ \ \ \ \ \ \ \ \ w_1\\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ A \ \ \ \ \ \ \ . \\ \ \ \ \ \ \ \ \ \ \ \ \ \ .\\ \ \ \ \ \ \ \ \ \ \ \ \, \ w_m\\ \ 0\ \ ...\ \ 0 \ \ \ 1 \end{array} \right ] \left [\begin{array} {l} \ x_1 \\ \ .\\ \ .\\ \ .\\ \ x_n\\ \ 1 \end{array} \right ]= \left [\begin{array} {l}\ y_1 \\ \ .\\ \ .\\ \ .\\ \ y_m\\ \ 1 \end{array} \right ].\) (3.10)
Macierz \(A\) nazywamy częścią liniową macierzy afinicznej
(3.9), zaś wektor \(w\) jej częścią translacyjną. Przy tak ustalonej metodzie zapisu macierzy odwzorowań afinicznych stosują się odpowiednie reguły rachunku macierzowego.
Na przykład, złożeniu odwzorowań afinicznych odpowiada iloczyn ich macierzy
\(\left [ \begin{array} {lr} \ \ \ A\ \ w\\ \ \ \ 0\ \ \ 1 \end{array} \right ] \left [\begin{array} {lr} \ \ \ B\ \ v\\ \ \ \ 0\ \ \ 1 \end{array} \right ]= \left [\begin{array} {lr} \ \ \ AB\ \ A(v)+w\\ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ 1\ \ \ \ \end{array} \right ].\) (3.11)
Euklidesowe przestrzenie afiniczne
Własności euklidesowych przestrzeni afinicznych
Jeżeli \(X\) jest przestrzenią afiniczną o kierunku \(V\) i \(V\) jest euklidesową przestrzenią wektorową, to przestrzeń \(X\) nazywamy euklidesową przestrzenią afiniczną.
Mając wybrany punkt bazowy mamy też bijekcję \(\Phi _{{\rm o}} : X\longrightarrow V\) zdefiniowana w 2. paragrafie Wykładu XIII. Za pomocą tej bijekcji można przenieść nie tylko strukturę przestrzeni wektorowej z \(V\) na \(X\), ale także iloczyn skalarny. Tak jak w przypadku struktury liniowej, przeniesiony iloczyn skalarny w istotny sposób zależy od wyboru punktu bazowego.
W euklidesowej przestrzeni afinicznej właściwym pojęciem geometrycznym jest odległość punktów, którą definiujemy przy pomocy normy wektora. Mianowicie, dla dowolnych punktów \(x,y\in X\) odległość \(d(x,y)\) definiujemy wzorem
Łatwo sprawdzić, że jest to dobrze zdefiniowana funkcja odległości.
Mówimy, że wektor \(v\in V\) jest prostopadły do podprzestrzeni afinicznej \(X_0\), jeśli \(v\) jest prostopadły do każdego wektora kierunku tej podprzestrzeni.
Twierdzenie 15.1
Niech \(X_0\) będzie podprzestrzenią afiniczna przestrzeni \(X\). Dla każdego punktu \(x\in X\) istnieje dokładnie jeden punkt \(x'\in X_0\) taki, że \(\overrightarrow { xx'}\) jest prostopadły do \(X_0\). Dla każdego punktu \(y\in X_0\) zachodzi nierówność
przy czym równość zachodzi wtedy i tylko wtedy, gdy \(y=x'\).
Dowód
Niech \(V_0\) będzie kierunkiem \(X_0\). Niech \(x_0\in X_0\) i \(x\in X\). Niech \(V_0^{\perp}\) będzie dopełnieniem ortogonalnym do \(V_0\). Rozłóżmy wektor \(\overrightarrow {x_0x}\) na sumę wektorów \(v+w\), gdzie \(v\in V_0\) i \(w\in V_0^{\perp}\). Zdefiniujmy
Punkt ten należy do \(X_0\). Ponadto
A zatem \(\overrightarrow {xx'}\) jest prostopadły do \(X_0\).
Załóżmy, że \(x''\in X_0\) jest również takim punktem, że \(\overrightarrow {xx''}\in V_0^{\perp}\). Zachodzą równości
Z drugiej strony \(\overrightarrow {x'x''}\in V_0\), bo oba punkty \(x',x''\) należą do \(X_0\). A zatem \(x'=x''\).
Niech \(y\in X_0\). Wtedy \(\overrightarrow {xy} =\overrightarrow {xx'}+ \overrightarrow {x'y}\). Składniki sumy po prawej stronie tej równości są prostopadłe, a zatem, z twierdzenia Pitagorasa, mamy
A zatem \(d^2(x,y)\ge d^2(x,x')\) i równość zachodzi wtedy i tylko wtedy, gdy \(y=x'\).
Odwzorowanie \(X \ni x\longrightarrow x'\in X_0\) nazywamy rzutowaniem prostokątnym na podprzestrzeń \(X_0\). Oznaczmy to odwzorowanie przez \(\Pi _{X_0}\). Punkt \(x'=\Pi _{X_0}(x)\) można otrzymać jako przecięcie \(X_0\) i podprzestrzeni \(x+V_0^{\perp}\).
Liczbę \(d(x,x')\) nazywamy odległością punktu \(x\) od podprzestrzeni \(X_0\). Oznaczać ją będziemy przez \(d(x,X_0)\).
Twierdzenie 15.2
Rzutowanie prostokątne w euklidesowej przestrzeni afinicznej \(X\) jest odwzorowaniem afinicznym indukującym rzutowanie prostokątne w przestrzeni \(V\).
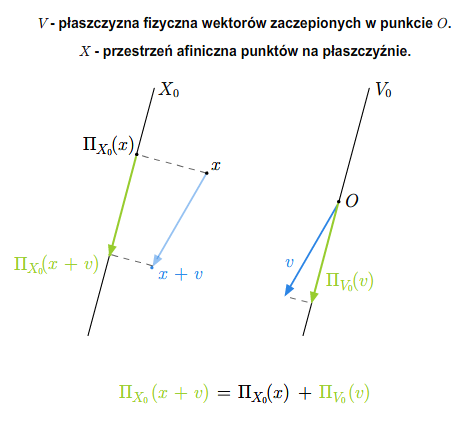
Dowód
Niech \(\Pi _{V_0}\) oznacza rzutowanie prostokątne na podprzestrzeń wektorową \(V_0\). Z dowodu poprzedniego twierdzenia wiemy, że \(x' =x_0 + v\), gdzie \(\overrightarrow {x_0x}=v+w\) i \(v\in V_0\), \(w\in V_0^{\perp}\). Niech \(z\in V\) i \(z =z'+z''\), gdzie \(z'\in V_0\) i \(z''\in V_{0}^{\perp}\).
Zachodzą następujące równości
Zatem
Zdefiniujemy teraz odbicie symetryczne względem podprzestrzeni \(X_0\). Definiujemy to odwzorowanie formułą
Odwzorowanie \(S_{X_0}\) nazywa się też symetrią względem podprzestrzeni \(X_0\).
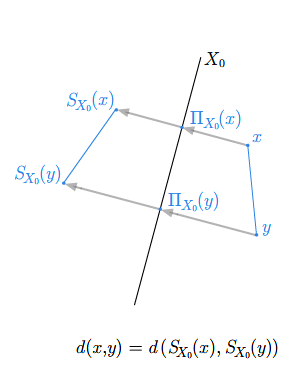
Twierdzenie 15.3
Odbicie symetryczne względem podprzestrzeni jest odwzorowaniem afinicznym.
Dowód
Twierdzimy, że symetria \(S_{X_0}\) indukuje odwzorowanie liniowe \(\varphi\) zdefiniowane wzorem
Niech \(z\in V\) będzie dowolnym wektorem i niech \(z=z'+z''\), gdzie \(z'\in V_0\), \(z''\in V_0^{\perp}\). Oznaczmy przez \(x'\) punkt \(\Pi _{X_0}(x)\). Zachodzą następujące równości
Izometrią euklidesowej przestrzeni afinicznej \(X\) nazywamy odwzorowanie zachowujące odległość, tzn. odwzorowanie \(f:X\longrightarrow X\) takie, że dla każdych \(x,y\in X\) zachodzi równość
Jest oczywiste, że odwzorowanie afiniczne indukujące izometrię liniową jest izometrią. Istotnie, wystarczy zauważyć, że jeśli \(f\) indukuje izometrię \(\varphi\), to
Zachodzi też twierdzenie odwrotne.
Twierdzenie 15.4
Izometria jest odwzorowaniem afinicznym indukującym izometrię liniową.
Dowód
Niech \(o\in X\) będzie ustalonym punktem przestrzeni \(X\). Niech dane będą dwa dowolne wektory \(v,w\in V\). Oznaczmy przez \(x,y\) punkty \(o+v\) i \(o+w\) odpowiednio. Definiujemy odwzorowanie \(\varphi :V\longrightarrow V\) formułą
Zachodzą równości
Porównując te równości i korzystając z tego, że \(f\) zachowuje
odległość punktów otrzymujemy równość
dla dowolnych wektorów \(v,w\in V\). Z Twierdzenia 1.10 z Wykładu X
wiemy, że \(\varphi\) jest odwzorowaniem liniowym. Pozostaje więc
zauważyć, że
dla dowolnych \(x\) i \(z\). W tym celu zauważamy, że zachodzą
równości
Twierdzenie 15.5
Odbicie symetryczne jest izometrią.
Dowód
Korzystamy z dowodu Twierdzenia 15.3. Mamy równość \(2z'-z= z'-z''\) i kolejne równości (pamiętamy, że \(z'\cdot z''=0\))
A zatem \(\varphi\) jest odwzorowaniem liniowym zachowującym normę. Jest więc izometrią liniową.
Na koniec tego paragrafu podamy bez dowodu
Twierdzenie 15.6
Każda izometria \(n\)-wymiarowej afinicznej przestrzeni euklidesowej \(X\) jest złożeniem co najwyżej \(n+1\) odbić symetrycznych względem hiperpłaszczyzn.
Analityczny opis podprzestrzeni afinicznej podprzestrzeni euklidesowej
Rozważmy \(n\)-wymiarową afiniczną podprzestrzeń euklidesową. Bez utraty ogólności możemy założyć, że jest to przestrzeń afiniczna \({\mathbb R}^n\) o kierunku \({\mathbb R} ^n\) wyposażonym w standardowy iloczyn skalarny. W przypadku wymiarów \(2\) i \(3\) można też myśleć o tych przestrzeniach jako o znanych ze szkoły płaszczyźnie i trójwymiarowej przestrzeni fizycznej z ustalonym prostokątnym układem współrzędnych.
Przypomnijmy, że hiperpłaszczyzna afiniczna jest opisana jednym równaniem liniowym
\(a_0+ a_1x_1+...+ a_nx_n =0,\) (2.2)
gdzie któryś ze skalarów \(a_1,...,a_n\) jest różny od \(0\), czyli \(a_1^2+...+a_n^2\ne 0\). Jeśli wszystkie te skalary są równe zeru, to równanie opisuje całą przestrzeń \({\mathbb R} ^n\) lub zbiór pusty. W dalszych rozważaniach zakładamy, że zadane równania nie będą opisywały tego typu trywialnych sytuacji. Równanie (2.2) nazywa się równaniem
ogólnym hiperpłaszczyzny. W przypadkach \(n=2\), \(n=3\) rozpoznajemy znane ze szkoły równania ogólne prostej na płaszczyźnie i
płaszczyzny w trójwymiarowej przestrzeni.
Kierunek hiperpłaszczyzny danej równaniem (2.2) jest dany równaniem jednorodnym
\(a_1x_1+...+a_nx_n=0.\) (2.3)
A zatem, jeśli oznaczymy
to hiperpłaszczyzna wektorowa (2.3) jest równa
Wektor \(a\) jest prostopadły do hiperpłaszczyzny. Ponieważ \(a\) jest niezerowy, rozpina prostą prostopadłą do danej hiperpłaszczyzny wektorowej. Wektor \(a\) jest prostopadły do przestrzeni afinicznej (2.2).
Ogólniej, mówimy, że dwie podprzestrzenie afiniczne są prostopadłe, jeżeli ich kierunki są prostopadłe, czyli każde dwa wektory wzięte z tych podprzestrzeni (różnych) są prostopadłe.
Jeśli układ równań liniowych
\(\left \{\begin{array} {l} \ a_{10}+a_{11}x_1+...+ a_{1n}x_n=0\\ \ ..............................................\\ \ a_{m0}+ a_{m1}x_1+...+a_{mn}x_n=0 \end{array} \right .\) (2.4)
ma rozwiązanie, to opisuje \((n-k)\)-wymiarową podprzestrzeń afiniczną \(L\) przestrzeni \({\mathbb R} ^n\), gdzie \(k={\rm rk} A\) i \(A=[a_{ij}]\in M(m,n;{\mathbb R})\) jest macierzą układu
(2.4). Każde z równań opisuje hiperpłaszyznę (zgodnie z umową zakładamy, że zadane równania ogólne nie opisują sytuacji trywialnych) i koniunkcja \(m\) równań opisuje zbiór będący przecięciem tych hiperpłaszczyzn. Układ (2.4) nazywamy równaniem krawędziowym podprzestrzeni \(L\).
Każdy z wektorów
\(a_1=(a_{11},...,a_{1n}), \ \ .\ \ .\ \ .\ \ , a_m=(a_{m1},...,a_{mn})\) (2.5)
jest prostopadły do przestrzeni \(L\). Wektory te generują dopełnienie ortogonalne do kierunku podprzestrzeni \(L\) opisanego układem równań
\(\left \{\begin{array} {l} \ a_{11}x_1+...+ a_{1n}x_n=0\\ \ ..............................................\\ \ a_{m1}x_1+...+a_{mn}x_n=0 \end{array} \right .\) (2.6)
Oczywiście, jeśli \(m>k\) oznacza to, że w układzie (2.2) są równania niepotrzebne a wektory \(a_1,..., a_m\) są liniowo zależne. Na ogół, podprzestrzeń zadana jest najmniejszą możliwą liczbą równań, czyli \(m=k\). W szczególności, prosta w trójwymiarowej przestrzeni jest zadana dwoma równaniami. Prosta taka jest krawędzią przecięcia dwóch
płaszczyzn.
Każda hiperpłaszczyzna jest zbiorem rozwiązań pewnego równania liniowego, a każda \(n-m\)-wymiarowa podprzestrzeń \(L\) jest zbiorem rozwiązań pewnego układu \(m\) równań. Istotnie, niech \(V\) oznacza kierunek przestrzeni \(L\). Weźmy dopełnienie ortogonalne \(V^{\perp}\) do podprzestrzeni \(V\). Niech \(a_1,...,a_m\) będzie bazą \(V^{\perp}\). Kierunek \(V\) dany jest układem równań (2.6), gdzie \(a_{ij}\) dane są przez (2.5). Przypuśćmy, że dany jest jakiś punkt podprzestrzeni \(L\), np. punkt o współrzędnych \((b_1,...,b_n)\). Wstawiamy te współrzędne do układu (2.4) w miejsce \(x_1,..., x_n\) i otrzymujemy wyrazy wolne \(a_{10},...,a_{m0}\).
Równanie ogólne dla danej hiperpłaszczyzny nie jest jedyne. Można je pomnożyć przez niezerowy skalar i otrzymać inne równanie (proporcjonalne do poprzedniego) opisujące tę samą hiperpłaszczyznę. Jest to jedyna dowolność jaka tu występuje. Istotnie, dla danej hiperpłaszczyzny \(L\) dopełnienie ortogonalne do jej kierunku jest \(1\)-wymiarowe, a zatem generowane przez wektory proporcjonalne. W przypadku równania krawędziowego dowolność jest znacznie większa. Na przykład, łatwo widać, że prosta w trójwymiarowej przestrzeni może być krawędzią przecięcia rozmaitych układów płaszczyzn. Równanie ogólne hiperpłaszczyzny, w którym wektor \(a=(a_1,...,a_n)\) jest jednostkowy nazywa się równaniem normalnym hiperpłaszczyzny.
Niech \(L\) będzie \(k\)-wymiarową podprzestrzenią o kierunku \(V\). Niech teraz \(v_1,...,v_k\) będzie bazą podprzestrzeni wektorowej \(V\). Niech dany będzie pewien punkt \(x_0=(x_{01},...,x_{0n})\) podprzestrzeni afinicznej \(X\). Wiemy, że \(X=x_0+V\) a \(V\) jest zbiorem wszystkich kombinacji liniowych wektorów \(v_1,...,v_k\). A zatem podprzestrzeń \(L\) jest zbiorem punktów o współrzędnych \((x_1,...,x_n)\) wyrażonych wzorami
\(\left \{\begin{array} {l} \ x_1=x_{01}+t_1v_{11}+...+t_kv_{k1}\\ \ ..........................................\\ \ x_n=x_{0n} +t_1v_{1n}+...+t_kv_{kn}, \end{array} \right .\) (2.7)
gdzie \((v_{i1},...,v_{in})\) są współrzędnymi wektora \(v_i\) dla \(i=1,...,k\) i \(t_1,..., t_k\) są parametrami przebiegającymi zbiór \({\mathbb R}\). Równanie to może też być zapisane bez użycia współrzędnych, tzn. w postaci
\(x=x_0 +t_1v_1+...t_kv_k.\) (2.8)
Układ (2.7) lub równanie (2.8)
nazywa się równaniem parametrycznym podprzestrzeni \(L\). W szczególności, mamy równanie parametryczne prostej (jest jeden parametr) i
równanie parametryczne płaszczyzny (są dwa parametry). Zamiana równania parametrycznego na ogólne lub krawędziowe (dla danej podprzestrzeni) jak również operacja odwrotna będą przerobione na ćwiczeniach.
Dysponujemy już metodą na znajdowanie rzutu prostokątnego punktu na podprzestrzeń afiniczną.
Załóżmy, że mamy \((n-m)\) - wymiarową podprzestrzeń \(L\) daną równaniem krawędziowym (lub ogólnym) (2.4) (lub (2.2)). Mamy więc wektory prostopadłe \(a_1,...,a_m\) rozpinające przestrzeń \(V^{\perp}\).
Dany jest też punkt, powiedzmy \(p=(p_1,...,p_n)\), który chcemy zrzutować prostokątnie na podprzestrzeń. Możemy więc napisać równanie parametryczne podprzestrzeni \(L^{\perp}(p):=p+V^{\perp}\). Wstawiamy kolejne \(x_1\),...,\(x_n\) z tego równania (wyrażone przez parametry \(t_1,...,t_m\) i pewne stałe) do równania krawędziowego. Otrzymujemy układ \(m\) równań ze względu na niewiadome \(t_1,...,t_m\). Rozwiązujemy ten układ (istnieje jedno jedyne rozwiązanie, bo istnieje dokładnie jeden rzut prostokątny punktu na podprzestrzeń) i otrzymujemy parametry, które odpowiadają punktowi przecięcia podprzestrzeni \(L\) z podprzestrzenią \(L^{\perp}(p)\). Z równania parametrycznego obliczamy współrzędne punktu odpowiadającego takim parametrom.
Na przykład, niech dana będzie hiperpłaszczyzna \(L\) opisana równaniem ogólnym
i punkt \(p=(p_1,...p_n)\). Oznaczmy przez \(p'=(p'_1,...,p'_n)\) rzut prostokątny punktu \(p\) na \(L\) i przez \(a\) wektor \((a_1,...,a_n)\). Równanie parametryczne prostej
prostopadłej do \(L\) i przechodzącej przez punkt \(p\) jest
następujące
Po wstawieniu \(x_1,...,x_n\) do równania ogólnego dostajemy
A zatem punkt przecięcia \(L\) i \(L^{\perp}(p)\)odpowiada parametrowi
\(t_0= -{{a_0+a_1p_1+...+a_np_n}\over{\Vert a\Vert ^2}}.\) (2.9)
Punkt \(p'\) ma współrzędne
Jeśli podprzestrzeń \(L\) dana jest równaniem parametrycznym
(2.8), to rzut prostokątny znajdujemy następująco. Wektory \(v_1,...,v_k\) traktujemy jako wektory rozpinające dopełnienie ortogonalne do \(V^{\perp}\). A zatem mamy równanie krawędziowe przestrzeni \(L^{\perp}(p)\). Wstawiając \(x_1,...,x_n\) z danego równania parametrycznego do równania krawędziowego podprzestrzeni \(L^{\perp}(p)\) otrzymujemy układ równań ze względu na niewiadome \(t_1,...,t_k\). Rozwiązujemy ten układ i rozwiązanie wstawiamy do równania parametrycznego.
Załóżmy na przykład, że dana jest prosta \(L\)
i punkt \(p=(p_1,...,p_n)\). Hiperpłaszczyzna \(L^{\perp}(p)\)
prostopadła do \(L\) i przechodząca przez punkt \(p\) ma równanie ogólne
gdzie \(a_0=-v_1p_1-...-v_np_n\) i \(v=(v_1,...,v_n)\). Po wstawieniu za \(x_1,...,x_n\) wyrażeń z parametrem i rozwiązaniu równania ze względu na niewiadomą \(t\) otrzymujemy wzór na wartość parametru \(t_0\) odpowiadającego punktowi przecięcia, czyli punktowi \(p'\). Ostatecznie, rzut prostokątny \(p'\) punktu \(p\) jest dany wzorem
\(p' =x_0 + {{(v\cdot (p-x_o))}\over {\Vert v\Vert ^2}}v.\) (2.10)
Odległość punktu od podprzestrzeni
Odległością dwóch zbiorów \(B\), \(C\) zawartych w afinicznej przestrzeni euklidesowej nazywamy liczbę
W przypadku rozważanej przez nas przestrzeni \({\mathbb R} ^n\)
gdzie \(x=(x_1,...,x_n),\ y=(y_1,...,y_n)\).
Z Twierdzenia 15.1 wynika, że odległość punktu \(p\) od podprzestrzeni afinicznej \(L\) jest równa \(d(p,p')\), gdzie \(p'\) jest rzutem prostokątnym punktu \(p\) na \(L\). Z rozważań prowadzonych w ostatnim rozdziale wiemy, że odległość punktu \(p\) od hiperpłaszczyzny \(L\) dana jest wzorem
\(\Vert (\overrightarrow {p,p'}) \Vert= {{| a_0+a_1p_1+...+a_np_n| }\over{\Vert a\Vert }}.\) (3.11)
Aby obliczyć odległość punktu od dowolnej podprzestrzeni (danej równaniem krawędziowym lub parametrycznym) możemy postępować podobnie, tzn. znaleźć rzut prostokątny danego punktu na podprzestrzeń i znaleźć odległość punktu danego od jego rzutu prostokątnego.
Załóżmy, że podprzestrzeń \(L\) dana jest równaniem parametrycznym
\(x=x_0+t_1v_1+...+t_kv_k.\) (3.12)
i \(v_1,...,v_k\) są liniowo niezależne.
Do obliczania odległości punktu od tak zadanej podprzestrzeni można skorzystać z wyznacznika Grama. Mianowicie, korzystając z Twierdzenia 2.4 z Wykładu XII, otrzymujemy
A zatem
\(d(p,p') = \sqrt{{{\rm G} (v_1,...,v_k, p-x_0)}\over {{\rm G} (v_1,...,v_k)}}\) (3.13)
Miara układu punktów
Niech dane będą a punkty \(x_0,...,x_k\). Liczbę
\({1\over {k !}} {\rm vol} (\overrightarrow {x_0x_1},...,\overrightarrow {x_0x_k})\) (4.14)
nazywamy miarą \(k\)-wymiarową lub objętością \(k\)-wymiarową układu punktów \(x_0,...,x_k\) i oznaczamy symbolem
\({\rm vol} (x_0,...,x_k).\) (4.15)
Miara punktów jest równa zeru wtedy i tylko wtedy, gdy punkty te są afinicznie zależne.
W przypadku \(k=1\) miara jest odległością punktów, w przypadku \(k=2\) miara jest polem trójkąta o zadanych wierzchołkach, zaś w przypadku \(k=3\) - objętością czworościanu o zadanych wierzchołkach. A zatem wprowadzone pojęcie objętości jest zgodne ze szkolną wiedzą. Korzystając z Twierdzenia 2.1 Wykładu XII mamy wzór
\({\rm vol} \{x_0,...,x_k\} ={1\over {k!}}\sqrt{{\rm G} (\overrightarrow {x_0x_1},...,\overrightarrow {x_0x_k})}.\) (4.16)
Objętości innych figur otrzymujemy rozkładając je na sumy figur takich jak odcinki, trójkąty, czworościany etc.
Wzajemne położenie podprzestrzeni
Hiperpłaszczyzna \(L\) rozcina całą przestrzeń na dwie półprzestrzenie. Ustalmy, jak opisać sytuację, gdy dwa punkty \(x,y\) nie leżące w \(L\), znajdują się w jednej z tych półprzestrzeni (po jednej stronie \(L\)) lub w dwu różnych półprzestrzeniach. Załóżmy najpierw, że hiperpłaszczyzna dana jest równaniem ogólnym \(a_0+a_1x_1+...+a_nx_n=0\). W szczególności mamy wektor \(a=(a_1,...,a_n)\) prostopadły do hiperpłaszczyzny. Możemy też łatwo znaleźć jakiś punkt \(x_o\in L\). Np., jeśli \(a_i\ne 0\), to \(x_0=(0,...,{{-a_0}\over {a_i}},..., 0)\) jest takim punktem. Punkty \(x\), \(y\in {\mathbb R}^n\) leżą po jednej stronie \(L\), wtedy i tylko wtedy, gdy
Jeśli hiperpłaszczyzna dana jest równaniem parametrycznym \(x_0+ t_1v_1+....+t_{n-1}v_{n-1}\), to punkty \(x,y\) leżą po tej samej
stronie hiperpłaszczyzny \(L\), wtedy i tylko wtedy wyznaczniki
\({\rm det} [v_1,...,v_{n-1},\overrightarrow {x_0, x}]\), \({\rm det} [v_1,...,v_{n-1},\overrightarrow {x_0, y}]\) mają ten sam znak, gdzie
\(v_1,...,v_{n-1}\) wypisane we współrzędnych stanowią kolumny w powyższych macierzach.
Wiemy już, co oznacza, że podprzestrzenie są prostopadłe lub równoległe.
Podprzestrzenie afiniczne nazywamy wichrowatymi (lub skośnymi), jeśli nie są równoległe i nie mają wspólnego punku. Dobrze znany jest przykład prostych skośnych w \({\mathbb R} ^3\).