Języki automaty i obliczenia
Forma zajęćWykład (30 godzin) + ćwiczenia (30 godzin)
Opis
Teoria jezyków formalnych, automatów i gramatyk w zakresie hierarchii Chomsky'ego.
Sylabus
Autorzy
- Maria Foryś — Uniwersytet Jagielloński
- Wit Foryś — Uniwersytet Jagielloński
- Adam Roman — Uniwersytet Jagielloński
Wymagania wstępne
- Logika i teoria mnogości
- Algebra liniowa z geometrią analityczną
- Matematyka dyskretna
- Algorytmy i struktury danych
Zawartość
- Alfabet, słowo, język - elementy teorii półgrup; półgrupy i monoidy wolne
- Gramatyki – model obliczeń; hierarchia Chomsky'ego
- Języki regularne; automat skończenie stanowy; automat minimalny i algorytmy; automaty deterministyczne i niedeterministyczne; algorytm determinizacji; własności języków regularnych; lemat o pompowaniu i języki nieregularne; wyrażenia regularne i algorytmy; twierdzenie Kleenego; problemy rozstrzygalności
- Języki bezkontekstowe; własności języków bezkontekstowych, gramatyka - postać Chomsky'ego i Greibach oraz algorytmy upraszczania; automat ze stosem; równoważność gramatyki bezkontekstowej i automatu ze stosem - algorytmy; lemat o pompowaniu i języki, które nie są bezkontekstowe; jednoznaczność, problem przynależności i algorytm CYK; problemy rozstrzygalności
- Języki kontekstowe i typu (0); własności; automat liniowo ograniczony; maszyna Turinga i jej wersje
- Podstawowe klasy złożoności w języku maszyn Turinga
- Języki maszyn Turinga i języki typu (0); teza Churcha; problemy rozstrzygalności
Literatura
- M. Foryś, W. Foryś, Teoria automatów i języków formalnych, AOW EXIT, Warszawa 2005.
- J. Gruska, Foundations of computing, Thompson, 1997.
- J.E. Hopcroft, J.D. Ulman, Introduction to automata theory, languages and computing, Addison-Wesley, 1979.
- A. Salomaa, Computation and automata, Cambridge Univ.Press, 1985.
- M. Sipser, Introduction to the theory of computation, PWS Publishing Company, Boston 1997.
Słowa, katenacja - elementy teorii półgrup, półgrupy i monoidy wolne
Definicje, oznaczenia i podstawowe własności
Przyjmijmy, że \(\mathbb{N}=\left\{ 1,2,\ldots \right\}\) oznacza zbiór liczb naturalnych, a \(\mathbb{N}_{0}\) zbiór liczb naturalnych wraz z 0. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie.
Definicja 1.1
Zbiór \(S\), w którym określone jest działanie łączne, to znaczy spełniające warunek
nazywamy półgrupą.
Przykład 1.1
Zbiór liczb naturalnych z dodawaniem \((\mathbb{N},+)\) tworzy półgrupę.
Definicja 1.2
Półgrupę \(M\), w której istnieje element neutralny działania, to znaczy element \(1_{M}\in M\) spełniający warunek
nazywamy monoidem.
Przykład 1.2
- (1) Zbiór liczb naturalnych z mnożeniem \((\mathbb{N},\cdot ,1)\) jest monoidem.
- (2) Zbiór liczb naturalnych z zerem \((\mathbb{N}_{0},+,0)\) jest monoidem ze względu na dodawanie.
- (3) Monoidem jest \((A^A,\circ,id_A)\) - zbiór odwzorowań dowolnego zbioru \({A}\) w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym.
Dwa pierwsze monoidy są przemienne, czyli działanie jest przemienne, a trzeci jest nieprzemienny.
Każdy monoid jest półgrupą.
Dla uproszczenia notacji będziemy opuszczać kropkę "\(\cdot\)" oznaczającą działanie oraz używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to \((\mathbf{S},\cdot )\) będzie oznaczać półgrupę, a \((\mathbf{M},\cdot ,\, 1_{\mathbf{M}})\) monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn \(x_1...x_n,\) a także \(x^n=x...x\) (n razy) jest określony jednoznacznie bez potrzeby wprowadzania nawiasów. Dla dowolnych liczb naturalnych \(m,n\in \mathbb{N}\) zachodzą wzory
Dla dowolnego \(x \in M\) przyjmujemy z definicji
Strukturę monoidu \(M\) przenosimy na zbiór potęgowy \(\mathcal{P}(M)\) wszystkich podzbiorów monoidu \(M\), określając dla dowolnych \(A,B \in\mathcal{P}(M)\) działanie
\((\mathcal{P}(M),\cdot, \{1_{M}\})\) jest monoidem.
Podobnie przenosimy strukturę półgrupy z \(S\) na \(\mathcal{P}(S)\).
Dla dowolnego podzbioru monoidu
(półgrupy) i dla dowolnej liczby \(n \in \mathbb{N}\) zapis \(A^n\) oznacza n-krotny iloczyn
zbioru \({A}\) przez siebie rozumiany w powyższym sensie.
W szczególności \(A^{1}=A.\)
W przypadku monoidu przyjmujemy z definicji
Definicja 1.3
Homomorfizmem półgrup \((S,\cdot)\;,\;\;(S',*)\) nazywamy odwzorowanie
\(h~:S~\longmapsto~S'\) takie, że
Homomorfizmem monoidów \((M,\cdot,1_{M}),\;(M',*,1_{M'})\) nazywamy odwzorowanie \(h:M \longmapsto M'\)
takie, że
Przykład 1.3
Odwzorowanie \(h:{\mathbb{Z}}_{mod\, 3}\longrightarrow {\mathbb{Z}}_{mod\,6}\) takie, że
jest homomorfizmem półgrupy \((\mathbb{Z}_{mod\,3},\cdot )\) w półgrupę \((\mathbb{Z}_{mod\,6},\cdot )\), ale nie jest homomorfizmem monoidu \((\mathbb{Z}_{mod\,3},\cdot,1 )\) w monoid \((\mathbb{Z}_{mod\,6},\cdot,1 )\), bo wartością 1 z monoidu \((\mathbb{Z}_{mod\,3},\cdot, 1 )\) nie jest jedynka monoidu \((\mathbb{Z}_{mod\,6},\cdot,1 )\).
Definicja 1.4.
Niech \((S,\cdot),\;\;(M,\cdot,1_{M})\) będą odpowiednio dowolną półgrupą, monoidem.
- \((T,\cdot)\) nazywamy podpółgrupą \({S}\) wtedy i tylko wtedy, gdy \(T\subset S\) i \(T^2 \subset T.\)
- \((N,\cdot,1_{M})\) nazywamy podmonoidem \(M\) wtedy i tylko wtedy, gdy \(N\) jest podpółgrupą \(M\) i \(1_{M} \in N.\)
Przykład 1.4.
\((\mathbb{Z}_{mod\,6},\cdot )\) jest monoidem. Podzbiór \(\{2,4\}\), jako zamknięty na działanie \(\cdot _{mod\, 6}\), tworzy podpółgrupę \(\mathbb{Z}_{mod\, 6}\). \((\{2,4\},\cdot _{mod\, 6})\) jest monoidem z \(4\) jako elementem neutralnym, ale nie podmonoidem \(\mathbb{Z}_{mod\, 6}\).
Niech \(X\) będzie dowolnym podzbiorem monoidu \(M\). Zbiór
jest podmonoidem monoidu \(M\).
Jest to najmniejszy, w sensie inkluzji podmonoid monoidu \(M\) zawierający zbiór \(X\).
Gdy spełniona jest równość \(X^*={M}\), to mówimy, że \(X\) jest zbiorem generatorów monoidu \(M\).
Zachodzą następujące własności:
- 1. Zbiór generatorów nie jest wyznaczony jednoznacznie.
- 2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór \({M}\).
Podobnie dla dowolnego podzbioru \(X\) półgrupy \({S}\) zbiór
jest podpółgrupą \({S}\) i to najmniejszą w sensie inkluzji zawierającą zbiór \(X\).
Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup.
Przykład 1.5.
W monoidzie \((\mathbb{N}_{0},+,0)\) podmonoid generowany przez zbiór generatorów \(X=\{2\}\) składa się z liczb parzystych i nieujemnych.
Definicja 1.5
Niech \(S\) będzie półgrupą. Relację równoważności \(\rho \subset {S}^2\) nazywamy:
- (1) prawą kongruencją w półgrupie \({S}\), jeśli \(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow xz\;\rho\; yz,\)
- (2) lewą kongruencją w półgrupie \({S}\), jeśli \(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy,\)
- (3) kongruencją, jeśli jest prawą i lewą kongruencją, tzn. \(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy \;\; i \;\; xz\;\rho\; yz.\)
Zastępując w powyższej definicji półgrupę \(S\) na monoid \(M\) otrzymamy dualnie pojęcia prawej kongruencji,
lewej kongruencji i kongruencji zdefiniowane w monoidzie.
Mając kongruencję \(\rho\) określoną w półgrupie \({S}\) (monoidzie
\(M)\) możemy utworzyć półgrupę ilorazową \({S}/\rho\) (monoid ilorazowy \({M}/\rho\)), której elementami
są klasy równoważności (abstrakcji) relacji \(\rho\).
Dla dowolnego homomorfizmu półgrup \(h:{S}\longmapsto {S}'\) określamy relację
Relacja \(Ker_h\) jest kongruencją w półgrupie \({S}.\)
Dla homomorfizmu monoidów \(h:{M}\longmapsto {M}'\) relacja \(Ker_h\) jest kongruencją w monoidzie \(M\).
Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać.
Twierdzenie 1.1
Niech \(h:{S}\longmapsto {S}'\) będzie dowolnym epimorfizmem półgrupy \({S}\) na półgrupę \({S}'.\) Półgrupa \({S}'\) jest izomorficzna z półgrupą ilorazową \({S}/_{Ker_h}\).
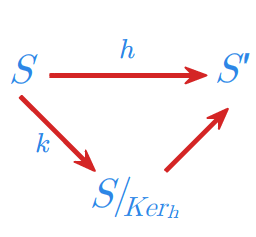
Twierdzenie 1.2
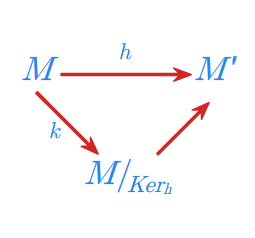
Niech \(h:{M}\longmapsto {M}'\) będzie dowolnym epimorfizmem monoidu \({M}\) na monoid \({M}'.\) Monoid \({M}'\) jest izomorficzny z monoidem ilorazowym \({M}/_{Ker_h}\).
Półgrupy wolne i monoidy wolne
Niech \({A}\) oznacza dowolny zbiór.
Definicja 2.1
Wolnym monoidem \(A^*\) o bazie \({A}\) nazywamy zbiór wszystkich skończonych ciągów:
Ciąg pusty \({(n=0)}\) oznaczamy symbolem "1" i z definicji jest on elementem neutralnym określonego powyżej działania, nazywanego katenacją lub konkatenacją.
Przyjmujemy następującą konwencję zapisu:Ta inkluzja uzasadnia użycie wprowadzonego wcześniej oznaczenia \(A^*\).
\(A^*\) jest najmniejszym podmonoidem
monoidu \(A^*\) zawierającym \(A.\)
Definicja 2.2
Wolną półgrupą \(A^+\) nad alfabetem \(A\) nazywamy zbiór wszystkich skończonych ciągów:
wraz z działaniem katenacji.
Używa się także określeń - wolny monoid o bazie \(A\) i wolna półgrupa o bazie \(A\).
- Elementy alfabetu \({A}\) nazywamy literami.
- Elementy wolnego monoidu (półgrupy) nazywamy słowami i oznaczać bedziemy w wykładzie najczęściej literami \(u,v,w\).
- Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy językiem.
Długością słowa \(w \in A^*\) nazywamy liczbę \(|w|\) będącą długością ciągu określającego to słowo. Słowo puste 1, czyli odpowiadające ciągowi pustemu ma długość równą 0.
Przykład 2.1
- (1) Wolna półgrupa \(\{0,1\}^+\) składa się z ciągów binarnych.
- (2) Wolny monoid \(\{0,1\}^*\) składa się z ciągów binarnych i ciągu pustego.
Definicja 2.3
Niech \(A\) i \(B\) będą alfabetami. Podstawieniem nazywamy homomorfizm
Twierdzenie 2.1.
Niech \({A}\) oznacza dowolny zbiór, a \(({M},\cdot,1_{M})\) dowolny monoid.
- (1) Każde odwzorowanie
- daje się jednoznacznie rozszerzyć do homomorfizmu
\(h:A^*\longmapsto {M}.\)
- (2) Homomorfizm \({h}\) jest epimorfizmem wtedy i tylko wtedy, gdy \(f(A)\) jest zbiorem generatorów \({M}.\)
Dowód
- (1) Przyjmujemy
- Tak określone \(h\) jest jedynym rozszerzeniem przekształcenia \(f\).
- (2) \(f(A)^*=M \Leftrightarrow \forall s \in {M}\;\; s=f(a_1)...f(a_n)=h(a_1...a_n)\) dla pewnego \(a_1...a_n \in A^*\Leftrightarrow h\) jest suriekcją.
Przyjmując w powyższym twierdzeniu jako \(A\) dowolny zbiór generatorów monoidu \({M}\) oraz jako funkcję \(f\) włożenie \(id_{A}:A\longrightarrow \mathbf{M}\) równe identyczności na \({A}\) dochodzimy do następującego wniosku.
Wniosek 2.1.
Każdy monoid \({M}\) jest homomorficznym obrazem wolnego monoidu \(A^*\) utworzonego nad dowolnym zbiorem generatorów \({M}.\)
Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.
Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup).
Twierdzenie 2.2.
Monoid \({M}\) jest wolny wtedy i tylko wtedy, gdy każdy element \(m \in {S}={M}\setminus \{1\}\) ma jednoznaczny rozkład na elementy zbioru \(A={S}\setminus {S}^2.\)
Dowod
Załóżmy, że monoid \({M}\) jest wolny, to znaczy \({M}=B^*\) dla pewnego zbioru (bazy) \(B.\)
- Udowodnimy, że \(A{}\) jest zbiorem generatorów monoidu \(M\). W tym celu wykażemy, że zachodzi inkluzja \({S}\subset ({S}\setminus {S}^2)^+.\)Dowód przeprowadzimy nie wprost. Załóżmy więc, że
- Udowodnimy, że \(A{}\) jest zbiorem generatorów monoidu \(M\). W tym celu wykażemy, że zachodzi inkluzja
- i niech \({m}\) oznacza element z tego zbioru o najmniejszej długości w \(B^*.\)
Wnioskujemy stąd kolejno:
\(m\in {S}^2\)
\(m=s_1s_2\) dla pewnych \(s_1,s_2\in {S}\),
- przy czym długość \(s_1,s_2\) jest silnie mniejsza niż długość \(m.\) Zatem
- a to oznacza, że
- Otrzymana sprzeczność kończy dowód faktu, że \(A={S}\setminus {S}^2\) jest zbiorem generatorów monoidu \({M}.\)
- Pokażemy teraz, że \(A \subset B.\)
Niech \(m=b_1...b_k \in {S}\setminus {S}^2\) dla pewnych \(b_i \in B\), \(i=1,...,k.\)
Jeśli \(k>1\), to \(m\in {S}^2\), co jest sprzeczne z wyborem \(m.\) Zatem \({k=1}\), co implikuje \(A\subset B.\)
- Pokażemy teraz, że \(A \subset B.\)
Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy \(B\), a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru \(A={S}\setminus {S}^2.\)
Niech teraz \({M}\) oznacza monoid z jednoznacznością rozkładu na elementy zbioru \(A~=~S~\setminus~S^2\). Rozszerzamy identyczność \(id_A:A\longmapsto {M}\) do homomorfizmu \(h:A^*\longmapsto {M}.\) Z założenia wynika, że każdy element \(m \in {S}\) można przedstawić jako iloczyn
Zatem
Homomorfizm \(h\) jest izomorfizmem, więc monoid \({M}\) jako izomorficzny z \(A^*\) jest wolny.
Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup.
Twierdzenie 2.3.
Półgrupa \({S}\) jest wolna wtedy i tylko wtedy, gdy każdy element \(x \in {S}\) ma jednoznaczny rozkład na elementy zbioru \({S}\setminus {S}^2.\)
Wniosek 2.2.
Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów.
Przyklad 2.2.
- (1) Półgrupa \((\mathbb{N},+ )\) jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - \(\mathbb{N}\setminus (\mathbb{N}+\mathbb{N})=\left\{ 1\right\}\).
- (2) Dla \(\mathbb{N}_2=\{n \in \mathbb{N}:n\geq 2\}\) półgrupa \((\mathbb{N}_2,+ )\) nie jest to półgrupą wolną.
Nie ma jednoznaczności rozkładu na elementy z \(\mathbb{N}_2\setminus (\mathbb{N}_2+\mathbb{N}_2)=\{2,3\}\).
Na przykład \(6=2+2+2=3+3\).
Gramatyka jako model obliczen. Hierarchia Chomsky'ego
W tym wykładzie wprowadzimy ogólne pojęcie systemu przepisującego, zdefiniujemy gramatykę, czyli szczególny typ systemu przepisującego oraz określimy cztery typy gramatyk wprowadzone przez Noama Chomsky'ego.
Teoria języków formalnych i automatów tworzy i bada pewne modele obliczeń, można popularnie powiedzieć modele komputera, zwane automatami lub gramatykami. Jednym z głównych i ogólnych problemów wokół którego skupione są badania tej teorii jest problem możliwości i ograniczeń obliczeniowych. Początki tych rozważań sięgają lat trzydziestych ubiegłego stulecia i wiążą się z pracami K.Goedla i późniejszymi A.Turinga i A.Churcha. Równolegle do teorii automatów problematyka ta jest intensywnie badana w ramach teorii obliczalności i teorii złożoności.
W tym wykładzie wprowadzimy pierwszy z tych modeli, mianowicie gramatykę. Określimy także sposób wyprowadzenia (generowania) słowa zgodnie z regułami gramatycznymi i zdefiniujemy język opisywany przez gramatykę. Przedstawimy również podstawowe typy gramatyk wprowadzone do lingwistyki teoretycznej i później do teorii języków formalnych przez Noama Chomsky'ego, twórcę pojęcia gramatyki transformacyjno-generatywnej, co miało miejsce w roku 1957.
Przez gramatykę rozumie się systematyczny opis wybranego języka naturalnego, opis, który obejmuje jego składnię (syntaktykę), znaczenie (semantykę) i fonologię, czyli dźwiękowy system języka. Reguły składni określają regularności rządzące kombinacjami słów, semantyka bada znaczenie słów i zdań, a fonologia wyróżnia dźwięki i ich dopuszczalne zestawienia w opisywanym języku.
Teoria języków formalnych bada wyłącznie syntaktyczne własności języków. Język rozumiany jest abstrakcyjnie, jako zbiór skończonych napisów. Zatem opierając się na wiadomościach z poprzedniego wykładu możemy powiedzieć, że język (formalny) \(L\) to dowolny podzbiór wolnego monoidu \(A^{*}\). Baza tego wolnego monoidu, czyli zbiór \({A}\) to alfabet, a sam wolny monoid możemy interpretować, jako zbiór wszystkich możliwych napisów utworzonych w tym alfabecie. Na ogół język \(L\) jest właściwym podzbiorem \(A^{*}\), czyli składa się z pewnych tylko ("poprawnych") napisów. Wyróżniając język \(L\) zazwyczaj wprowadzamy pewne kryteria, które muszą spełniać napisy z tego języka. Dlatego o elementach języka \(L\) mówimy, że spełniają te kryteria lub że są syntaktycznie poprawne.
Jak już powiedzieliśmy teoria języków formalnych tworzy pewne modele obliczeń lub inaczej systemy opisu języków zwane gramatykami i automatami. Od tych systemów żąda się, aby spełniały warunki efektywności analitycznej i efektywności syntetycznej. Pierwszy z warunków oznacza, że system opisu prowadzi do algorytmu, który w skończonej liczbie kroków rozstrzyga, czy dowolne słowo należy, czy też nie należy do tego języka. Spełnienie warunku drugiego daje w rezultacie algorytm, który umożliwia wygenerowanie wszystkich słów danego języka.
Gramatyka to system, którego działanie opiera się na procesie sekwencyjnego przepisywania, czyli modyfikowania pewnych napisów (słów). Przepisywanie to realizowane jest poprzez reguły przyjęte w danym systemie jako dopuszczalne. Idea ta związana jest z nazwiskami takich logików jak Axel Thue czy Emil Post. W roku 1957 Noam Chomsky, lingwista amerykański, stworzył pewien matematyczny formalizm opisu języków naturalnych zwany gramatykami generacyjnymi.
Gramatyki te opisują wybrane, najbardziej istotne cechy syntaktyczne języków, w szczególności ich strukturalne regularności.
Idee Chomsky'ego bardzo szybko przeniknęły do innych dziedzin nauki. Stworzona teoria znalazła istotne zastosowanie w badaniach nad językami programowania. Z powodzeniem gramatyki Chomsky'ego służą również do budowania modeli procesów biologicznych, czy też procesów badanych przez nauki o społeczeństwie. Teoria gramatyk rozwinęła się w wielu kierunkach, służąc jako formalny opis sekwencyjnych zmian różnorakich obiektów, takich jak, termy, grafy, obrazy, czy fraktale.
System przepisujący
Definicja 1.1
System przepisujący jest to para \(RS=(A,P)\), gdzie
\({A}\) jest dowolnym skończonym zbiorem (alfabetem),
\(P \subseteq A^* \times A^*\) - skończoną relacją (zbiorem praw).
Fakt, że para \((u,v) \in P\) zapisujemy, \(u~\rightarrow~v \in P\) i nazywamy prawem przepisywania lub produkcją w systemie \(RS\).
Definicja 1.2
Niech \(RS=(A,P)\) będzie dowolnym systemem przepisującym, a \(\;\;x,y~\in~A^*\) dowolnymi słowami.
System \(RS\) przepisuje słowo \(x\) na słowo \(y\) (generuje \(y\) z \(x\)) bezpośrednio, co oznacza się symbolem
jeśli istnieją słowa \(x_1 , x_2 \in A^*\) oraz prawo \(u~\rightarrow~v \in P\) takie, że
\(x = x_1 ux_2,\;\; y = x_1 vx_2.\)
System \(RS\) przepisuje słowo \(x\) na słowo \(y\) (generuje \(y\) z \(x\)), co oznacza się symbolemBezpośrednie wyprowadzenie \("\mapsto "\) jest relacją na
wolnym monoidzie \(A^*\), a wyprowadzenie \("\mapsto^*"\) zwrotnym i przechodnim domknięciem tej relacji.
Rysunek 1
Niech \(RS=(\{a,b,c\},\{(ba,ab),(ca,ac),(cb,bc)\} )\) będzie systemem przepisującym. W systemie \(RS\) słowo \(aabbcc\) można wyprowadzić ze słowa \(cabbac\) (rysunek 1).
Rozważa się systemy przepisujące generujące lub rozpoznające język.
Definicja 1.3
Niech \(RS=(A,P)\) będzie dowolnym systemem przepisującym, a \(I\) dowolnym, ustalonym podzbiorem \(A^{*}\).
- językiem generowanym przez \(RS\) nazywamy zbiór
- językiem rozpoznawanym przez \(RS\) nazywamy zbiór:
Przykład 1.2
Jeśli w przykładzie 1.1 (patrz przykład 1.1.) przyjmiemy \(I=\{cab \},\) to
Gramatyka, której definicję teraz wprowadzimy, jest szczególnym systemem Thuego. Można powiedzieć, że jest to system Thuego tak określony, aby poprzez wskazanie jedynie poprawnych sposobów generowania napisów definiować język. Gramatyka to jedno z najważniejszych pojęć teorii języków formalnych. Używany poniżej, dla \(u \in A^*\) i \(B \subset A\), symbol \(\# _{B} u\) oznacza liczbę wystąpień liter z alfabetu \(B\) w słowie \({u}\).
Definicja 1.4
Gramatyka jest to system \(G = (V_N,V_T,P,v_0)\), w którym
\(V_N \neq \emptyset\) - skończony zbiór symboli nieterminalnych (alfabet nieterminalny),
\(V_T \neq \emptyset\) - skończony zbiór symboli terminalnych (alfabet terminalny),
\(P \subseteq (V_N \cup V_T)^+ \times (V_N \cup V_T)^*\) - skończona relacja, zbiór produkcji (praw),
\(v_0 \in V_N\) - symbol początkowy (startowy).
Ponadto zakładamy, że \(V_N \cap V_T = \emptyset\;\;\;\) i dla każdego \(\;\;(u,v) \in P\;\;\; \# _{V_N} u \geq 1\).
A zatem w gramatyce alfabety terminalny i nieterminalny są rozłącznymi zbiorami, a słowo \(u\) występujące po lewej stronie produkcji zawiera co najmniej jeden symbol nieterminalny. Fakt, że para \((u,v) \in P,\) zapisujemy:/p>
Wykorzystujemy też zdefiniowane dla systemów przepisujących pojęcia generowania bezpośredniego \("\mapsto "\) i generowania \("\mapsto^* "\).
Definicja 1.5
Językiem generowanym przez gramatykę \(G = (V_N,V_T,P,v_0)\) nazywamy zbiór:
Łatwo zauważyć, że pomiędzy językiem a generującą go gramatyką nie ma odpowiedniości wzajemnie jednoznacznej. Dany język może być generowany przez wiele gramatyk, czasem o bardzo różnej strukturze i własnościach. Stąd potrzeba wprowadzenia pojęcia równoważności językowej dla gramatyk.
Definicja 1.6
Gramatyki \(G_1\) i \(G_2\) są równoważne (językowo) wtedy i tylko wtedy, gdy \(L(G_1) = L(G_2)\).
Przykład 1.3
- (1) Gramatyka \(G_1 = (V_N,V_T,P,v_0)\), w której \(V_N = \{v_0\}, \;\; V_T = \{a\}, \;\; P = \{ v_0 \rightarrow v_0a, \; v_0 \rightarrow a \},\) generuje język
- (2) Gramatyka \(G_2 = (V_N,V_T,P,v_0)\), w której \(V_N = \{v_0\}, \;\; V_T = \{a\}, \;\; P = \{ v_0 \rightarrow v_0v_0, \; v_0 \rightarrow a \},\) generuje język \(L(G_2) = \{ a^n : n = 1,2,... \}\).
- (3) Gramatyka \(G_{3}=\left( V_{N},V_{T},P,v_{0}\right)\), w której \(V_{N}=\left\{ v_{0},v_{1},w,w_{1},w_{2},z,z_{1},z_{2},z_{3}\right\} , \; \; V_{T}=\left\{ a,b,c\right\}\),
- generuje język
- (4) Gramatyka \(G_4 = (V_N,V_T,P,v_0)\), w której \(V_N = \{v_0, v_1, v_2 \}, \;\; V_T = \{a,b,c\}\),
- generuje język
\(L(G_4) = \{ a^n b^n c^n : n = 1,2,... \}.\)
Gramatyki \(G_1\) i \(G_2\) są równoważne. Równoważne również są gramatyki \(G_3\) i \(G_4\).
Klasyfikacja Chomsky'ego
Wprowadzimy teraz cztery typy gramatyk określonych, jak powiedziano już wcześniej, przez Noama Chomsky'ego.
Definicja 2.1
Gramatyka \(G = (V_N,V_T,P,v_0)\) jest typu \(\textbf{(i)}\) dla \(i=0,1,2,3\) wtedy i tylko wtedy, gdy spełnia następujące warunki:
- typ(0): każda gramatyka, czyli system spełniajacy definicję 1.4 (patrz definicja 1.4.)
- typ(1): kontekstowa, czyli gramatyka, w której każde prawo ze zbioru \(P\) ma postać
\(u_1 vu_2 \rightarrow u_1 xu_2,\) - gdzie \(u_1 , u_2 \in (V_N \cup V_T)^*, \; \; v \in V_N , \;\; x \in (V_N \cup V_T)^+\) lub
\(v_0 \rightarrow 1,\) przy czym, jeśli \(v_0 \rightarrow 1 \in P\), to \({v_0}\) nie występuje po prawej stronie w żadnym prawie z \(P\),
- typ (2): bezkontekstowa, czyli gramatyka, w której każde prawo ze zbioru \(P\) ma postać
\(v \rightarrow x,\) gdzie \(v \in V_N, \;\; x \in (V_N \cup V_T)^*\),
- typ (3): regularna, czyli gramatyka, w której każde prawo ze zbioru \(P\) ma postać
\(v \rightarrow v'x\;\;\; lub \;\;\;v \rightarrow x,\) gdzie \(v,v' \in V_N, \;\; x \in V_T^*\).
Przykład 2.1
Gramatyki z przykładu 1.3 (patrz przykład 1.3.) są odpowiednio
- (1) \(G_1\) - typu (3)
- (2) \(G_2\) - typu (2)
- (3) \(G_3\) - typu (1)
- (4) \(G_4\) - typu (0)
Natomiast język \(L(G_1)=L(G_2)\) jest typu (3),
język \(L(G_3)=L(G_4)\) jest typu (1).
W oparciu o wprowadzone typy gramatyk określamy odpowiadające im rodziny (klasy) języków, oznaczając przez
- \(\bf \mathcal{L}_{0}\): - rodzinę wszystkich języków typu 0,
- \(\bf \mathcal{L}_{1}\): - rodzinę wszystkich języków typu 1, czyli języków kontekstowych,
- \(\bf \mathcal{L}_{2}\): - rodzinę wszystkich języków typu 2, czyli języków bezkontekstowych,
- \(\bf \mathcal{L}_{3}\): - rodzinę wszystkich języków typu 3, czyli języków regularnych.
Pomiędzy wprowadzonymi rodzinami języków zachodzą następujące zależności:
Inkluzje pierwsza i trzecia wynikają bezpośrednio z definicji odpowiednich klas języków, a więc z definicji gramatyk regularnej i bezkontekstowej oraz kontekstowej i typu (0). Natomiast fakt, że \(\bf \mathcal{L}_{2}\subset \bf \mathcal{L}_{1},\) udowodnimy później. Podobnie z dalszych rozważań wynika, że powyższe inkluzje są właściwe.
Gramatyki spełniają warunek efektywności syntetycznej. Systemami, które realizują warunek fektywności analitycznej, są automaty. Automaty działają w ten sposób, iż pod wpływem zewnętrznego sygnału zmieniają swój stan. W efekcie tej zmiany rozpoznają bądź nie ciągi takich sygnałów reprezentowane przez słowa. Zatem działanie automatu polega na testowaniu kolejno słów z \(A^{*}\) i określaniu, które z nich są rozpoznawane (spełniają określone kryteria), a które nie są rozpoznawane. Ogół słów rozpoznanych przez automat tworzy język rozpoznawany przez ten automat. Dla każdej z określonych powyżej rodzin języków, w sensie Chomsky'ego określa się odpowiadającą jej rodzinę automatów.
Język \(L\) jest typu (i) dla \(i=0,1,2,3\) wtedy i tylko wtedy, gdy jest rozpoznawany przez jakiś automat z odpowiedniej rodziny. Definicje automatów i ich własności wprowadzane będą sukcesywnie przy prezentowaniu poszczególnych rodzin języków.
Automat skończenie stanowy
W rozdziale tym zdefiniujemy automat - drugi, obok gramatyki, model obliczeń. Określimy język rozpoznawany przez automat i podamy warunki równoważne na to, by język był rozpoznawany.
Automaty
Wprowadzimy teraz pojęcie automatu. Jak już wspomnieliśmy w wykładzie drugim automat to drugi, obok gramatyki, model obliczeń będący przedmiotem badań teorii języków i automatów. Model realizujący warunek efektywności analitycznej, czyli taki na podstawie którego możliwe jest sformułowanie algorytmu rozstrzygającego w skończonej liczbie kroków, czy dowolne słowo należy, czy też nie należy do języka rozpoznawanego przez ten automat. Lub inaczej możemy powiedzieć, że taki automat daje algorytm efektywnie rozstrzygający, czy dowolne obliczenie sformułowane nad alfabetem automatu jest poprawne.
Wprowadzony w tym wykładzie automat, zwany automatem skończenie stanowym, jest jednym z najprostszych modeli obliczeń. Jest to model z bardzo istotnie ograniczoną pamięcią. Działanie takiego automatu sprowadza się do zmiany stanu pod wpływem określonego zewnętrznego sygnału czy impulsu.
Pomimo tych ograniczeń urządzenia techniczne oparte o modele takich automatów spotkać możemy dość często. Jako przykład służyć mogą automatyczne drzwi, automaty sprzedające napoje, winda, czy też urządzenia sterujące taśmą produkcyjną.
Przykład 1.1.
Drzwi automatycznie otwierane są sterowane automatem, którego działanie opisać można, przyjmując następujące oznaczenia. Fakt, że osoba chce wejść do pomieszczenia zamykanego przez takie drzwi, identyfikowany przez odpowiedni czujnik, opiszemy symbolem \(\displaystyle WE\). Zamiar wyjścia symbolem \(\displaystyle WY\). Symbol \(\displaystyle WEWY\) będzie związany z równoczesnym zamiarem wejścia jakiejś osoby i wyjścia innej. Wreszcie symbol \(\displaystyle BRAK\) oznaczał będzie brak osób, które chcą wejść lub wyjść. Zatem zbiór \(\displaystyle \{ WE, WY,WEWY,BRAK \}\), to alfabet nad którym określimy automat o \(\displaystyle 2\) stanach: \(\displaystyle OTWARTE, ZAMKNIĘTE\) poniższym grafem.
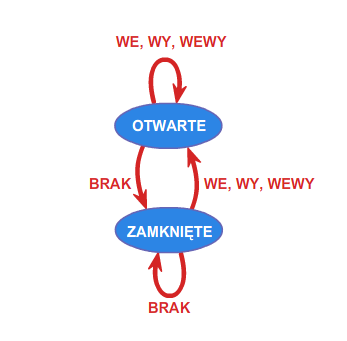
Automaty reagują więc na określone sygnały zewnętrzne reprezentowane przez litery alfabetu \(\displaystyle A\), zmieniając swój stan. Jeśli ustalimy stan początkowy automatu oraz dopuszczalne stany końcowe, to automat będzie testował dowolne słowo z \(\displaystyle A^{*}\) , startując ze stanu początkowego. Jeśli rezultatem finalnym działania automatu (obliczenia) będzie stan końcowy, to słowo będzie rozpoznawane przez automat, a obliczenie określone takim słowem poprawne. Automaty można graficznie reprezentować jako etykietowane grafy skierowane. W takim grafie każdy wierzchołek odpowiada stanowi automatu, a każda strzałka pomiędzy wierzchołkami \(\displaystyle u\) i \(\displaystyle v\), etykietowana symbolem \(\displaystyle a\), oznacza rzejście automatu ze stanu \(\displaystyle u\) do stanu \(\displaystyle v\) pod wpływem litery \(\displaystyle a\). Podamy teraz definicję automatu. Niech \(\displaystyle A\) oznacza dowolny alfabet. Od tego momentu wykładu zakładamy, że alfabet jest zbiorem skończonym.
Definicja 1.1
Automatem nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A} \displaystyle =(S,f)\), w którym
\(\displaystyle S\) - jest dowolnym skończonym zbiorem zwanym zbiorem stanów,
\(\displaystyle f: S \times A \rightarrow S\) - jest funkcją przejść.
Automat będąc w stanie \(\displaystyle s_{i}\) po przeczytaniu litery \(\displaystyle a\) zmienia stan na \(\displaystyle s_{j}\) zgodnie z funkcją przejścia \(\displaystyle f(s_{i},a)=s_{j}\) .
Funkcję przejść rozszerzamy na cały wolny monoid \(\displaystyle A^{*}\) do postaci
przyjmując:
dla każdego \(\displaystyle s \in S\;\;\;f(s,1) = s\) oraz
dla każdego \(\displaystyle s \in S,\;\;a \in A\) i dla dowolnego \(\displaystyle w \in A^*\)
Działanie automatu pokazane jest na poniższej animacji 2.
Zdefiniowany powyżej automat \(\displaystyle \mathcal{A}\) nazywamy skończonym lub
skończenie stanowym ze względu na założenie skończoności zbioru stanów \(\displaystyle S\).
Przykład 1.2.
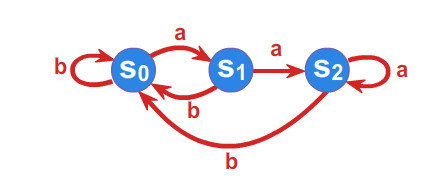
Niech \(\displaystyle A=\left\{ a,b\right\}\) będzie alfabetem, a \(\displaystyle \mathcal{A}=(S,f)\) automatem takim, że
\(\displaystyle S=\left\{ s_{0},s_{1},s_{2}\right\}\) , a funkcja przejść zadana jest przy pomocy tabelki
Automat możemy również jednoznacznie określić przy pomocy grafu.
Podamy teraz bardzo interesujący przykład zastosowania automatów skończonych. Przedstawimy mianowicie wykorzystanie tak zwanych automatów synchronizujących w przemyśle. Automat synchronizujący nad alfabetem \(\displaystyle A\) to automat \(\displaystyle (S,f)\) o następującej własności: istnieje stan \(\displaystyle t \in S\) oraz słowo \(\displaystyle w \in A^*\) takie, że dla każdego stanu \(\displaystyle s\) tego automatu \(\displaystyle f(s, w)=t\). Istnieje więc pewne uniwersalne słowo \(\displaystyle w\), pod wpływem którego wszystkie stany przechodzą w jeden, ustalony stan automatu \(\displaystyle t \in S\). Mówimy, że następuje wtedy synchronizacja wszystkich stanów automatu.
Poniżej prezentujemy przykład zaczerpnięty z pracy Ananicheva i Volkova (D. S. Ananichev, M. V. Volkov, Synchronizing Monotonic Automata, Lecture Notes in Computer Science, 2710(2003), 111-121.), ukazujący ideę użycia automatów synchronizujących w tej dziedzinie.


Przykład 1.3.
Załóżmy, że pewna fabryka produkuje detale w kształcie kwadratu z "wypustką" na jednym boku (patrz rys. 3). Po wyprodukowaniu detale należy umieścić w opakowaniach w ten sposób, by wszystkie były w tej samej orientacji - mianowicie "wypustką" w lewo.
Załóżmy ponadto dla uproszczenia, że detale mogą przyjmować jedną z czterech orientacji (rys. 4): "wypustką" w górę, w dół, w lewo lub w prawo.
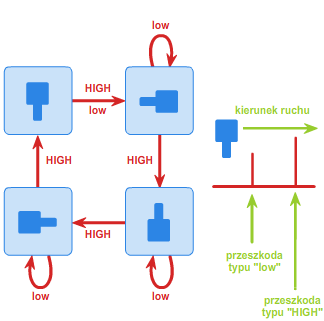
Należy zatem skonstruować takie urządzenie (orienter), które będzie ustawiało wszystkie detale w żądanej orientacji. Oczywiście istnieje wiele metod rozwiązania tego problemu, ale z praktycznego punktu widzenia potrzebne jest rozwiązanie najprostsze i najtańsze. Jednym z takich sposobów jest umieszczanie detali na pasie transmisyjnym z zamontowaną wzdłuż niego pewną ilością przeszkód dwojakiego rodzaju: niskich (low) oraz wysokich (HIGH). Wysoka przeszkoda ma tę własność, że każdy detal, który ją napotka, zostanie obrócony o 90 stopni w prawo (zakładamy, że elementy jadą od lewej do prawej strony). Przeszkoda niska obróci o 90 stopni w prawo tylko te detale, które są ułożone "wypustką" w dół. Na rys. 5 przedstawione zostały przejścia pomiędzy orientacjami detali w zależności od napotkania odpowiedniej przeszkody.
Można zauważyć, że automat z rysunku 5 jest automatem synchronizującym. Słowem, które go synchronizuje, jest następująca sekwencja przeszkód:
low-HIGH-HIGH-HIGH-low-HIGH-HIGH-HIGH-low.
Niezależnie od tego, w jakiej orientacji początkowej znajduje się detal, po przejściu przez powyższą sekwencję przeszkód zawsze będzie ułożony "wypustką" w lewo. Sytuację przedstawia poniższa animacja 3:
Rozszerzymy teraz wprowadzone pojęcie automatu w ten sposób, by uzyskać możliwość efektywnego rozstrzygania, czy dowolne słowo utworzone nad alfabetem \(\displaystyle A\) reprezentuje poprawne obliczenie, czyli spełnia kryteria określone przez rozszerzony automat.
Definicja 1.2.
Język \(\displaystyle \; L~\subset A^* \;\) jest rozpoznawany (akceptowany) wtedy i tylko wtedy, gdy istnieje automat skończony \(\displaystyle \mathcal{A} \displaystyle = (S,f) , \;\) stan \(\displaystyle \; s_0 \in S \;\) oraz zbiór \(\displaystyle \; T \subset S \;\) takie, że
Stan \(\displaystyle s_0 \;\) nazywamy stanem początkowym, a \(\displaystyle \; T \;\) zbiorem stanów końcowych automatu \(\displaystyle \mathcal{A}\) .
Rozszerzony w powyższy sposób automat, poprzez dodanie stanu początkowgo i zbioru stanów końcowych, w dalszym ciągu nazywamy automatem i oznaczamy jako piątkę \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) lub czwórkę \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\), jeśli wiadomo, nad jakim alfabetem rozważamy działanie automatu.
Fakt, że język \(\displaystyle \; L \;\) jest rozpoznawany przez automat \(\displaystyle \mathcal{A},\) zapisujemy jako
Rodzinę wszystkich języków rozpoznawalnych nad alfabetem \(\displaystyle A\) oznaczamy przez \(\displaystyle \mathcal{REC}(\mathcal{A}^{*})\) .
Podobnie jak w przypadku gramatyk nie ma jednoznacznej odpowiedniości pomiędzy językami rozpoznawalnymi a automatami. Wprowadza się więc relację, która identyfikuje automaty rozpoznające ten sam język.
Definicja 1.3.
Automaty \(\displaystyle \mathcal{A}_{1}\) i \(\displaystyle \mathcal{A}_{2}\) są równoważne, jeśli rozpoznają ten sam język, czyli
W dalszych rozważaniach języków rozpoznawanych ograniczymy się do automatów \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\), które spełniają warunek \(\displaystyle f(s_0,A^*) = S.\) Nie zawęża to naszych rozważań. Jeśli bowiem język \(\displaystyle \; L \;\) jest rozpoznawany przez pewien automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\), to jest również rozpoznawany przez automat
który spełnia powyższy warunek. Zauważmy, że przyjmując to założenie, upraszczamy strukturę automatu. Z punktu widzenia grafu automatu można powiedzieć, że nie występują w nim wierzchołki (stany) nieosiagalne z \(\displaystyle s_0\). Poniżej przedstawiamy algorytm usuwający z automatu stany nieosiągalne ze stanu początkowego.
Algorytm UsuńStanyNieosiągalne - usuwa z automatu \(\displaystyle \mathcal{A}\) stany nieosiągalne
Wyjście: A'=(S', A, f', s_0, T') - automat równoważny automatowi A bez stanów nieosiągalnych.
for each p in S do
zaznaczone[p] <- 0;
end for
zaznaczone[s_0] <- 1;
OZNACZ (s_0);
S' <- {s in S: zaznaczone[s]=1};
T' <- T cap S';
flag <-false # jeśli nie dodamy stanu to na końcu pętli nadal flag=false
f' <- f;
for each p in S do
for each a in A do
if f'(p,a)=NULL then
f'(p,a)<- s_f; # f'(p,a) była nieokreślona
flag <-true;
end if
end for
end for
if flag=true then
S'<- S' cup {s_f};
end if
return A'=(S', A, f', s_0, T');
Algorytm Procedure Oznacz
procedure OZNACZ (x in S)
for each p in S
flag <-false
for each a in A do
if f(x,a)=p then
flag <-true
end if
end for
if flag=true and zaznaczone [p]=0 then
zaznaczone [p] <- 1;
OZNACZ (p);
end if
end for
end procedure
Powyższy algorytm, dla ustalonego alfabetu \(\displaystyle A\), posiada złożoność \(\displaystyle O(|A| \cdot |S|)\), czyli liniową względem liczby stanów.
Przedstawiając automat przy pomocy grafu przyjmujemy następującą konwencję. Jeśli w automacie występuje stan początkowy, oznaczać go będziemy zieloną strzałką wchodzącą do tego stanu. Jeśli w automacie występują stany końcowe, oznaczać je będziemy niebieską obwódką.
Przykład 1.4.
Jeśli w przykładzie 1.2 (patrz przykład 1.2.) przyjmiemy stan \(\displaystyle s_{0}\) jako stan początkowy, \(\displaystyle T=\left\{ s_{2}\right\}\) jako zbiór stanów końcowych, to automat \(\displaystyle \mathcal{A} = (S,A,f,s_0,T)\) rozpoznaje język
złożony ze słów, kończących się na \(\displaystyle a^2\) .
Słowo \(\displaystyle aba\) nie jest akceptowane.
Słowo \(\displaystyle abaa\) jest akceptowane.
Każdy automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) wyznacza w wolnym monoidzie \(\displaystyle A^*\) prawą kongruencję, nazywaną prawą kongruencją automatową, określoną w następujący sposób:
\(\displaystyle \forall u,v \in A^*\)
Dla automatu skończonego (o skończonym zbiorze stanów), a takie rozważamy, relacja \(\displaystyle \sim _{A}\) ma skończony indeks, czyli skończoną liczbę klas równoważności.
Przykład 1.5.
Automat z przykładu 1.2 (patrz przykład 1.2.) ze stanem \(\displaystyle s_{0}\) jako początkowym wyznacza relację równoważności o trzech klasach:
\(\displaystyle [1]=A^*\left\{ b \right\}\cup \left\{ 1\right\}\),
\(\displaystyle [a]=A^*\left\{ ba\right\} \cup \left\{ a\right\}\),
\(\displaystyle [a^2]=A^*\left\{ a^2 \right\}.\)
Na odwrót, każda prawa kongruencja \(\displaystyle \rho \subset (A^*)^2\) wyznacza automat, zwany ilorazowym, w następujący sposób:
\(\displaystyle \mathcal{A} \displaystyle _\rho\) jest automatem ze stanem początkowym \(\displaystyle [1]_\rho\). \(\displaystyle \mathcal{A}_{\rho }\) jest automatem skończonym wtedy i tylko wtedy, gdy relacja \(\displaystyle \rho\) ma skończony indeks.
Z definicji prawej kongruencji wynika, że funkcja przejść \(\displaystyle f^*\) jest określona poprawnie.
Definicja 1.4.
Niech \(\displaystyle \mathcal{A} \displaystyle =(S,f)\) i \(\displaystyle \, \mathcal{B} \displaystyle =(T,g)\) będą dowolnymi automatami. Odwzorowanie \(\displaystyle \varphi:S\longrightarrow T\) nazywamy homomorfizmem automatów wtedy i tylko
wtedy, jeśli
Homomorfizm automatów oznaczamy \(\displaystyle \varphi :\mathcal{A}\longrightarrow \mathcal{B}\) .
Twierdzenie 1.1.
Prawdziwe są następujące fakty:
(1) Dla dowolnej prawej kongruencji \(\displaystyle \; \rho \; \subset \; (A^*)^2\)
(2) Dowolny automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) jest izomorficzny z automatem \(\displaystyle \mathcal{A}_{\sim _{\mathcal{A}}}\) ,
(3) Dla dowolnych automatów \(\displaystyle \mathcal{A}_1 \displaystyle = (S_1,A,f_1,s^1_0,T_1)\) i \(\displaystyle \mathcal{A}_2 \displaystyle = (S_2,A,f_2,s^2_0,T_2)\) prawdziwa jest równoważność
\(\displaystyle \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2}\: \: \Longleftrightarrow \:\) istnieje epimorfizm \(\displaystyle \varphi :\mathcal{A}_1\longrightarrow \mathcal{A}_2\) taki, że \(\displaystyle \varphi(s^1_0) = s^2_0\).
Dowód
(1) Identyczność relacji wynika wprost z definicji automatu ilorazowego \(\displaystyle \mathcal{A} \displaystyle _\rho\) oraz prawej kongruencji \(\displaystyle \sim _{A_{\rho }}\) .
(2) Rozważmy automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) i odwzorowanie
gdzie \(\displaystyle \forall s\in S\)
Istnienie słowa \(\displaystyle w\) wynika z faktu, że \(\displaystyle s_0\) jest stanem początkowym, natomiast z definicji relacji \(\displaystyle \sim _{\mathcal{A}}\) wynika, że odwzorowanie \(\displaystyle \psi\) jest poprawnie określone.
Odwzorowanie \(\displaystyle \psi\) ma być homomorfizmem, czyli dla każdego stanu \(\displaystyle s\in S\) i dowolnego słowa \(\displaystyle w\in A^{*}\) spełniać warunek
Warunek ten wynika z następujących równości
gdzie \(\displaystyle f(s_0,u)=s\).
Z prostych obserwacji wynika, że \(\displaystyle \psi\) jest suriekcją i iniekcją.
(3) Dowód implikacji "\(\displaystyle \Rightarrow\)"
Załóżmy, że \(\displaystyle \: \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2 }\) . Niech
będzie odwzorowaniem takim, że
\(\displaystyle \forall s\in S_1\) \(\displaystyle \varphi (s) = f_2(s^2_0,w),\;\;\text{gdzie}\;\; w\in A^{*}\;\; i \;\; f_1(s^1_0,w) = s.\)
Stąd, że \(\displaystyle s^1_0\) jest stanem początkowym automatu \(\displaystyle \mathcal{A}_1,\)
wynika, że istnieje słowo \(\displaystyle \; w \in A^* \;\) potrzebne do określenia epimorfizmu \(\displaystyle \varphi\).
Z założenia \(\displaystyle \: \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2}\)
wynika, że \(\displaystyle \varphi \;\) jest poprawnie zdefiniowaną funkcją.
Uzasadnienie faktu, że \(\displaystyle \varphi\) jest homomorfizmem, jest analogiczne jak w punkcie (2) dla \(\displaystyle \psi\).
\(\displaystyle \varphi\) jest suriekcją, gdyż \(\displaystyle \; s^2_0 \;\) jest stanem początkowym automatu \(\displaystyle \mathcal{A}_2\) .
\(\displaystyle \; \varphi (s^1_0) = s^2_0, \;\) ponieważ \(\displaystyle \; f_1(s^1_0,1) = s^1_0\).
Dowód implikacji "\(\displaystyle \Leftarrow\)"
Niech \(\displaystyle \varphi :\mathcal{A}_1\longrightarrow \mathcal{A}_2\) będzie epimorfizmem
takim, że \(\displaystyle \; \varphi (s^1_0) = s^2_0 \;\).
Wówczas prawdziwy jest następujący ciąg wnioskowań.
To oznacza, że \(\displaystyle \sim _{\mathcal{A}_1}\subseteq \sim _{\mathcal{A}_2}\) .
Symbolem \(\displaystyle S^S\) oznaczamy rodzinę wszystkich funkcji określonych na zbiorze \(\displaystyle S\) i przyjmujących wartości w \(\displaystyle S\). Łatwo zauważyć, iż rodzina ta wraz ze składaniem odwzorowań jest monoidem \(\displaystyle (S^S,\circ)\) .
Definicja 1.5.
Niech \(\displaystyle \mathcal{A} \displaystyle = (S,f)\) będzie dowolnym automatem. Reprezentacją automatu \(\displaystyle \mathcal{A}\) nazywamy funkcję \(\displaystyle \tau _{\mathcal{A}}:A^{*}\longrightarrow S^{S}\) , określoną dla dowolnych \(\displaystyle w \in A^*\) i \(\displaystyle \; s \in S \;\) równością
Reprezentacja automatu jest homomorfizmem monoidu \(\displaystyle A^*\) w monoid \(\displaystyle S^S\), bowiem dla dowolnych \(\displaystyle v,w \in A^*\) spełnione są warunki
Definicja 1.6.
Niech \(\displaystyle \mathcal{A} \displaystyle = (S,f)\) będzie dowolnym automatem. Monoidem przejść automatu \(\displaystyle \mathcal{A}\) nazywamy monoid
Następujące wnioski są konsekwencjami rozważań przeprowadzonych powyżej.
Wniosek 1.1.
(1) Monoid przejść automatu \(\displaystyle \mathcal{A}\) jest podmonoidem monoidu \(\displaystyle S^S\) i zbiór \(\displaystyle \left\{ \tau _{\mathcal{A}}(a):a\in A\right\}\) jest zbiorem generatorów tego monoidu.
Wynika to z faktu, że \(\displaystyle \tau _{\mathcal{A}}\) jest epimorfizmem i z twierdzenia 2.1 z wykładu 1. (patrz twierdzenie 2.1. wykład 1)
(2) Monoid przejść automatu skończonego jest skończony.
(3) Monoid przejść automatu \(\displaystyle \mathcal{A}\) jest izomorficzny z monoidem ilorazowym \(\displaystyle A^{*}/_{Ker_{\tau _{\mathcal{A}}}}\) .
Jest to wniosek z twierdzenia o rozkładzie epimorfizmu, które w tym przypadku ilustruje poniższy diagram.
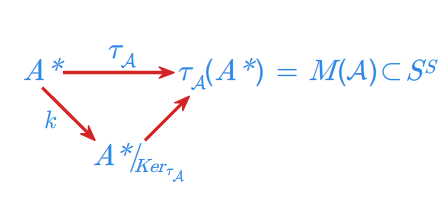
Przykład 1.6.
Określimy monoid przejść dla automatu z przykładu 1.2 (patrz przykład 1.2.). Wypisujemy kolejne funkcje \(\displaystyle \tau _{\mathcal{A}}(w)\) dla \(\displaystyle w\in \{a,b\}^{*}\) . Zauważmy, że ze względu na występujące w tabelce powtórzenia, będące wynikiem równości, np. \(\displaystyle \tau _{\mathcal{A}}(b^2)=\tau _{\mathcal{A}}(b),\) nie ma potrzeby określać funkcji \(\displaystyle \tau _{\mathcal{A}}(b^{n})\) dla \(\displaystyle n\geq 3\) . Podobna obserwacja ma miejsce w innych przypadkach, co sprawia, że tabelka zawiera skończoną liczbę różnych funkcji.
Poniżej zamieszczamy algorytm obliczający monoid przejść dla automatu skończenie stanowego.
Algorytm WyznaczMonoidPrzejść - wyznacza monoid przejść dla automatu
Wejście: A=(S, A, f, s_0, T) - automat
Wyjście: M - monoid przejść dla \mathcal{A}
L <- emptyset; #L jest listą
M <- emptyset;
for each a in A cup {1} do
insert (L, {tau_A(a)}); # gdzie tau_A(a)(s)=f(s, a) dla każdego s in S
end for
while L not = emptyset; do
tau_A(w) <- first(L);
M <- M cup tau_A(w);
for each a in A do
for each s in S do
tau'_A(wa)(s)<- f(tau_A(w)(s),a);
end for
if tau'_A(wa) not in L cup M
insert (L, tau'_A(wa));
end if
end for
end while
return M;
Procedura insert\(\displaystyle (L, x)\) wkłada na koniec listy \(\displaystyle L\) element \(\displaystyle x\). Funkcja first\(\displaystyle (L)\) wyjmuje pierwszy element znajdujący się na liście \(\displaystyle L\) i zwraca go. Algorytm działa w następujący sposób: najpierw na listę \(\displaystyle L\) wkładane są elementy monoidu przejść \(\displaystyle \tau_{\mathcal{A}}(a)\) dla każdej litery \(\displaystyle a \in A \cup 1\). Te funkcje można obliczyć bezpośrednio z tabelki reprezentującej funkcję przejścia automatu \(\displaystyle \mathcal{A}\). Następnie z listy po kolei ściągane są poszczególne funkcje \(\displaystyle \tau_{\mathcal{A}}(w)\). Każda z nich dodawana jest do zbioru \(\displaystyle M\), a następnie algorytm sprawdza dla każdej litery \(\displaystyle a \in A\), czy funkcja \(\displaystyle \tau_{\mathcal{A}}(wa)\)
istnieje już na liście \(\displaystyle L\) lub w zbiorze \(\displaystyle M\). Jeśli nie, to funkcja ta dodawana jest do listy. Procedura powyższa trwa do czasu, gdy lista \(\displaystyle L\) zostanie pusta. Wtedy wszystkie elementy monoidu przejść
znajdą się w zbiorze \(\displaystyle M\).
Przeanalizujmy działanie algorytmu dla automatu z przykładu 1.2 (patrz przykład 1.2.).
Na początku na listę \(\displaystyle L\) włożone zostaną funkcje \(\displaystyle \tau_{\mathcal{A}}(1)\), \(\displaystyle \tau_{\mathcal{A}}(a)\) oraz \(\displaystyle \tau_{\mathcal{A}}(b)\). Z listy zdejmujemy funkcję \(\displaystyle \tau_{\mathcal{A}}(1)\) i dodajemy ją do zbioru \(\displaystyle M\). Ponieważ \(\displaystyle \forall a \in A\displaystyle \tau_{\mathcal{A}}(1a)=\tau_{\mathcal{A}}(a)\), a funkcje \(\displaystyle \tau_{\mathcal{A}}(a)\) oraz \(\displaystyle \tau_{\mathcal{A}}(b)\) znajdują się już na liście, zatem nie dodajemy ich do \(\displaystyle L\). Bierzemy kolejny element listy, \(\displaystyle \tau_{\mathcal{A}}(a)\), dodajemy go do \(\displaystyle M\) i obliczamy funkcje \(\displaystyle \tau_{\mathcal{A}}(aa)\) oraz \(\displaystyle \tau_{\mathcal{A}}(ab)\). Ponieważ \(\displaystyle \tau_{\mathcal{A}}(aa)\) nie jest tożsama z żadną funkcją ze zbioru \(\displaystyle L \cup M\), dodajemy ją do listy. Funkcja \(\displaystyle \tau_{\mathcal{A}}(ab)\) również nie jest równa żadnej z funkcji należących do zbioru \(\displaystyle L \cup M\), zatem wstawiamy ją na koniec listy. Na liście \(\displaystyle L\) mamy zatem teraz następujące elementy: \(\displaystyle \tau_{\mathcal{A}}(b)\), \(\displaystyle \tau_{\mathcal{A}}(a^2)\) oraz \(\displaystyle \tau_{\mathcal{A}}(ab)\). Zdejmujemy z listy funkcję \(\displaystyle \tau_{\mathcal{A}}(b)\), dodajemy ją do \(\displaystyle M\) i obliczamy \(\displaystyle \tau_{\mathcal{A}}(ba)\) oraz \(\displaystyle \tau_{\mathcal{A}}(bb)\). Pierwsza z tych funkcji jest nowa, tzn. nie jest tożsama z żadną funkcją ze zbioru \(\displaystyle L \cup M\) więc dodajemy ją na koniec listy. Druga z nich równa jest funkcji \(\displaystyle \tau_{\mathcal{A}}(b)\), więc nie dodajemy jej do listy. W tym momencie zbiór \(\displaystyle M\) zawiera następujące elementy: \(\displaystyle \tau_{\mathcal{A}}(1)\), \(\displaystyle \tau_{\mathcal{A}}(a)\), \(\displaystyle \tau_{\mathcal{A}}(b)\), natomiast lista zawiera elementy \(\displaystyle \tau_{\mathcal{A}}(a^2)\), \(\displaystyle \tau_{\mathcal{A}}(ab)\), \(\displaystyle \tau_{\mathcal{A}}(ba)\). Zdejmujemy z \(\displaystyle L\) funkcję \(\displaystyle \tau_{\mathcal{A}}(a^2)\), dodajemy ja do \(\displaystyle M\) i ponieważ \(\displaystyle \tau_{\mathcal{A}}(a^2a)=\tau_{\mathcal{A}}(a^2)\) i \(\displaystyle \tau_{\mathcal{A}}(a^2b)=\tau_{\mathcal{A}}(b)\), nic nie dodajemy do \(\displaystyle L\). Zdejmujemy teraz z listy funkcję \(\displaystyle \tau_{\mathcal{A}}(ab)\), dodajemy ją do \(\displaystyle M\) i ponieważ \(\displaystyle \tau_{\mathcal{A}}(aba)\) nie należy do \(\displaystyle L \cup M\) dodajemy ją do listy. \(\displaystyle \tau_{\mathcal{A}}(abb)=\tau_{\mathcal{A}}(b)\), więc tej funkcji nie dodajemy do \(\displaystyle L\). Z \(\displaystyle L\) ściągamy \(\displaystyle \tau_{\mathcal{A}}(ba)\), dodajemy ją do \(\displaystyle M\) i widzimy, że \(\displaystyle \tau_{\mathcal{A}}(baa)=\tau_{\mathcal{A}}(a^2)\) oraz \(\displaystyle \tau_{\mathcal{A}}(bab)=\tau_{\mathcal{A}}(b)\), więc nic nie dodajemy do \(\displaystyle L\). Na liście pozostała funkcja \(\displaystyle \tau_{\mathcal{A}}(aba)\). Ściągamy ją z listy i dodajemy do \(\displaystyle M\). Widzimy, że \(\displaystyle \tau_{\mathcal{A}}(abaa)=\tau_{\mathcal{A}}(a^2)\) i \(\displaystyle \tau_{\mathcal{A}}(abab)=\tau_{\mathcal{A}}(b)\), zatem nic nie dodajemy do listy \(\displaystyle L\). Lista jest w tym momencie pusta i działanie algorytmu zakończyło się. Ostatecznie mamy
co zgadza się z wynikiem otrzymanym w przykładzie.
Twierdzenie poniższe zbiera dotychczas uzyskane charakteryzacje języków rozpoznawanych.
Twierdzenie 1.2.
Niech \(\displaystyle \; L \subset A^* \;\) będzie dowolnym językiem. Równoważne są następujące warunki:
- (1) Język \(\displaystyle \; L \;\) jest rozpoznawalny,
- (2) Język \(\displaystyle \; L \;\) jest sumą wybranych klas równoważności pewnej prawej kongruencji \(\displaystyle \rho\) na \(\displaystyle \; A^* \;\) o skończonym indeksie: \(\displaystyle L = \bigcup_{w\in L}[w]_\rho.\)
- (3) Język \(\displaystyle \; L \;\) jest sumą wybranych klas równoważności pewnej kongruencji \(\displaystyle \rho\) na \(\displaystyle \; A^* \;\) o skończonym indeksie: \(\displaystyle L = \bigcup_{w\in L}[w]_\rho.\)
- (4) Istnieje skończony monoid \(\displaystyle \; M \;\) i istnieje epimorfizm \(\displaystyle \varphi : A^* \longrightarrow M\) taki, że \(\displaystyle L = \varphi^{-1}(\varphi (L)).\)
Dowód
Dowód równoważności czterech powyższych warunków przeprowadzimy zgodnie z następującym schematem:
\(\displaystyle 4 \Longrightarrow 3\)
Dany jest homomorfizm
gdzie \(\displaystyle M\) jest skończonym monoidem.
Określamy relację \(\displaystyle \; \rho \;\) na \(\displaystyle A^*\), przyjmując dla dowolnych \(\displaystyle u, v \in A^*\)
Tak określona relacja jest kongruencją. Natomiast jej skończony indeks wynika z faktu, że monoid \(\displaystyle \; M \;\) jest skończony. Pokażemy teraz, że:
Inkluzja \(\displaystyle \; \subseteq \;\) jest oczywista.
Inkluzja w przeciwną stronę (\(\displaystyle L \supseteq \bigcup_{w\in L}[w]_\rho,\)) oznacza, że każda klasa równoważności relacji
\(\displaystyle \; \rho \;\) albo cała zawiera się w języku \(\displaystyle L\), albo cała zawiera się w uzupełnieniu języka \(\displaystyle L\).
Załóżmy, że \(\displaystyle \; u \in [w]_\rho\) dla pewnego \(\displaystyle w \in L. \;\)
Oznacza to, że
Implikuje to ostatecznie, że \(\displaystyle u \in L\).
\(\displaystyle 3 \Longrightarrow 2\)
Każda kongruencja jest prawą kongruencją.
\(\displaystyle 2 \Longrightarrow 1\)
Niech \(\displaystyle \; \rho \;\) będzie prawą kongruencją o skończonym indeksie na \(\displaystyle \; A^* \;\) taką, że
Automat \(\displaystyle \mathcal{A}_{\rho } \displaystyle = (A^*/\rho,f^*,[1]_\rho,T),\) dla którego
akceptuje język \(\displaystyle L\).
\(\displaystyle 1 \Longrightarrow 4\)
Niech język \(\displaystyle \; L=L(\mathcal{A}) \;\), gdzie \(\displaystyle \mathcal{A} \displaystyle = (S,f,s_0,T)\).
Określamy odwzorowanie
przyjmując dla każdego \(\displaystyle v\in A^{*}\)
Jest to odwzorowanie kanoniczne monoidu \(\displaystyle \; A^* \;\) na monoid ilorazowy, a więc jest to epimorfizm.
\(\displaystyle A^{*}/_{Ker\tau _{\mathcal{A}}}\) jest monoidem skończonym, ponieważ \(\displaystyle \; S \;\) jest zbiorem skończonym.
Dla dowodu równości \(\displaystyle L = \varphi^{-1}(\varphi (L))\) wystarczy udowodnić
inkluzję \(\displaystyle L \supset \varphi^{-1}(\varphi (L))\). (Inkluzja \(\displaystyle \; L \subseteq \varphi^{-1}(\varphi (L))\;\)
wynika z definicji przeciwobrazu.)
Niech \(\displaystyle \; u \in \varphi^{-1}(\varphi (L)) .\;\) Oznacz to, że
W szczególności
czyli \(\displaystyle u \in L. \)
Wyrażenia regularne. Automat minimalny
W tym wykładzie określimy rodzinę języków regularnych wolnego monoidu \(A^{*}\) oraz pewien formalny opis tych języków zwany wyrażeniami regularnymi.
Dla języka rozpoznawalnego \(L\) wprowadzimy pojęcie automatu minimalnego rozpoznającego \(L\) i prawej kongruencji syntaktycznej, która odgrywa istotną rolę w problemach związanych z automatem minimalnym.
Wyrażenia regularne
Definicja 1.1
Niech \(A\) będzie skończonym alfabetem. Rodzina \(\mathcal{REG}(A^{*})\) języków regularnych nad alfabetem \(A\) to najmniejsza, w sensie inkluzji, rodzina \(\mathcal{R}\) języków zawartych w \(A^*\) taka, że:
- (1) \(\emptyset \in\mathcal{R}\), \(\forall a \in A \;\;\; \{ a \} \in\mathcal{R}\)
- (2) jeśli \(X, Y \in\mathcal{R}\), to \(X \cup Y, \;\; X \cdot Y \;\; \in\mathcal{R}\)
- (3) jeśli \(X \in\mathcal{R}\), to \(X^* = \bigcup_{n=0} ^\infty X^n \in\mathcal{R}\)
Wprost z definicji wynika, że \(\left\{ 1\right\} =\emptyset ^{*}\in \mathcal{R}\) oraz że dla dowolnego języka regularnego zachodzi równość \(X\in \mathcal{R}\) jest
Wprowadzona w ten sposób definicja rodziny języków regularnych wymaga uzasadnienia faktu, iż definiowany obiekt, definiowana rodzina, istnieje. Zauważmy więc, że warunki 1-3 definicji 1.1 (patrz definicja 1.1.) spełnia na przykład rodzina \(\mathcal{P}(A^{*})\) wszystkich podzbiorów \(A^*\), a zatem klasa takich rodzin nie jest pusta. Ponadto łatwo możemy stwierdzić, że jeśli rodziny \(\mathcal{R}_{1},\: \mathcal{R}_{2}\) spełniają warunki 1-3 powyższej definicji, to rodzina \(\mathcal{R}_{1}\cap \mathcal{R}_{2}\) również spełnia te warunki. Stąd możemy wyprowadzić wniosek, że najmniejsza rodzina spełniającą te warunki, to przecięcie
po wszystkich rodzinach \(\mathcal{R}\) spełniających warunki 1-3 definicji 1.1. (patrz definicja 1.1.)
Zauważmy, że w świetle powyższej definicji fakt, że \(X \in\mathcal{REG}(A^{*})\) oznacza, że \(X\) można uzyskać z liter alfabetu i zbioru pustego \(\emptyset\) poprzez zastosowanie wobec tych "elementarnych klocków" skończonej liczby działań: sumy, katenacji i gwiazdkowania. Na odwrót, każdy zbiór otrzymany w ten sposób jest elementem rodziny \(\mathcal{REG}(A^{*})\). Ta obserwacja prowadzi do pojęcia wyrażeń regularnych, formalnego zapisu języków regularnych.
Definicja 1.2
Niech \(A\) będzie alfabetem, a zbiór \(\{+ , \star , \emptyset , (,)\}\) alfabetem rozłącznym z \(A\). Słowo \({\bf \alpha} \in {\bf (}A \cup \{ + , \star , \emptyset , (,)\}{\bf )}^*\) jest wyrażeniem regularnym nad alfabetem \({A}\) wtedy i tylko wtedy, jeśli:
- (1) \({\bf \alpha} = \emptyset\)
- (2) \({\bf \alpha} = a \in A \;\; ({\bf \alpha}\) jest literą)
- (3) \({\bf \alpha}\) jest w postaci \(({\bf \beta} + {\bf \gamma}), ({\bf \beta} {\bf \gamma} ), {\bf \gamma} ^*\), gdzie \({\bf \beta}, {\bf \gamma}\)są wyrażeniami regularnymi nad alfabetem \(A\).
Przyjmujemy oznaczenia:
Rodzinę wyrażeń regularnych nad alfabetem \(A\) oznaczamy symbolem \(\mathcal{WR}\). Łatwo zauważyć związek pomiędzy wyrażeniami regularnymi oraz wprowadzoną wcześniej rodziną \(\mathcal{REG}(A^{*})\), regularnych języków wolnego monoidu \(A^{*}\). Związek ten ustala poniższa definicja.
Definicja 1.3
Wartościowaniem wyrażenia regularnego nazywamy odwzorowanie
określone następująco:
- (1) \(\mid \emptyset \mid = \emptyset\)
- (2) \(\mid a \mid = \{ a \}\)
- (3) \(\mid ({\bf \alpha} + {\bf \beta})\mid = \mid {\bf \alpha} \mid \cup \mid {\bf \beta} \mid\)
\(\mid ({\bf \alpha} {\bf \beta}) \mid = \mid {\bf \alpha} \mid \cdot \mid {\bf \beta} \mid\)
\(\mid {\bf \alpha}^* \mid = \mid {\bf \alpha} \mid ^*\)
Odwzorowanie określające wartość wyrażenia regularnego nie jest, jak można zauważyć, iniekcją. Oznacza to, że różne wyrażenia regularne mogą mieć tę samą wartość, czyli określać ten sam język regularny. Prostym przykładem tego faktu są wyrażenia regularne \(a^*\) oraz \((a^*)^*\). Zwróćmy uwagę na wartość wyrażenia regularnego oznaczonego symbolem \(1\).
Jest mianowicieWprowadza się następującą relację równoważności w rodzinie wyrażeń regularnych.
Definicja 1.4
Wyrażenia regularne \({\bf \alpha} , {\bf \beta}\) nazywamy równoważnymi i oznaczamy \({\bf \alpha} = {\bf \beta}\), jeśli \(\mid {\bf \alpha} \mid = \mid {\bf \beta} \mid\).
Problem równoważności wyrażeń regularnych jest rozstrzygalny i jest PSPACE-zupełny. Wrócimy do tego problemu w kolejnych wykładach.
Oto przykłady równoważnych wyrażeń regularnych
gdzie \(\alpha ,\alpha _{1},\alpha _{2},\alpha _{3}\in \mathcal{WR}\).
Wprost z definicji wyrażenia regularnego wynika następujaca równoważność:
Fakt 1.1
\(L\in \mathcal{REG}(A^{*}) \Longleftrightarrow L = \mid {\bf \alpha} \mid\) dla pewnego \({\bf \alpha} \in\mathcal{WR}\).
Wyrażenia regularne dają bardzo wygodne narzędzie zapisu języków należących do rodziny \(\mathcal{REG}(A^{*})\).
Np. język nad alfabetem \(\{ a,b\}\) złożony ze wszystkich słów zaczynających się lub kończących na literę \(a\) zapisujemy jako \(a(a+b)^* +(a+b)^*a\).
Z kolei wyrażenie regularne \(a^+ b^+\) oznacza język \(L=\{a^nb^m : n,m\geq 1\}\).
Dla dalszego uproszczenia zapisu przyjmiemy w naszym wykładzie następującą umowę. Jeśli język \(L\) jest wartością wyrażenia regularnego \(\alpha\), czyli \(L= \mid \alpha \mid\), to będziemy zapisywać ten fakt jako \(L= \alpha\). Będziemy zatem mówić w dalszym ciągu wykładu o języku \(\alpha\). Z tych samych powodów, dla dowolnego alfabetu \(A=\{a_1,.....,a_n\}\) będziemy używać zapisu \(A\) w miejsce \(a_1 +.....+a_n\).
Zauważmy na koniec rozważań o wyrażeniach regularnych, że dość prosty w zapisie język \(L=\{a^nb^n : n\geq 1\}\) nie należy do rodziny \(\mathcal{REG}(A^{*})\) i nie można go zapisać przy pomocy wyrażeń regularnych.
Kończąc ten fragment wykładu poświęcony wyrażeniom regularnym warto wspomnieć o problemie "star height", czyli głębokości zagnieżdżenia gwiazdki w wyrażeniu regularnym. Mając wyrażenia regularne \(\alpha ,\alpha _{1},\alpha _{2}\in \mathcal{WR}\) głębokość zagnieżdżenia gwiazdki definiuje się jako liczbę \(sh(\alpha )\) równą \(0\), gdy \(\alpha\) jest literą z alfabetu lub zbiorem pustym, równą \(max\{i,j\},\) gdy \(\alpha =\alpha _{1}\cup \alpha _{2}\) lub \(\alpha =\alpha _{1}\cdot \alpha _{2}\) i \(sh(\alpha _{1})=i\), \(sh(\alpha _{2})=j\) oraz równą \(i+1\) dla \(\alpha =(\alpha _{1})^{*}\). Głębokość zagnieżdżenia gwiazdki dla języka regularnego \(L\) określa się jako najmniejszą liczbę \(sh(L)=sh(\alpha )\), gdzie \(\alpha\) jest wyrażeniem regularnym reprezentującym język \(L\). Głębokość zagnieżdżenia gwiazdki jest więc jakby miarą złożoności pętli występujących w automacie rozpoznającym język \(L\). Ustalono, że dla alfabetu złożonego z jednej litery głębokość zagnieżdżenia gwiazdki jest równa co najwyżej 1 oraz że dla alfabetu o co najmniej dwóch literach dla dowolnej liczby \(k\in \Bbb N\) można wskazać język regularny \(L\) taki, że \(sh(L)=k\). Problemem otwartym pozostaje określenie algorytmu określającego głębokość zagnieżdżenia gwiazdki dla dowolnego języka w klasie języków regularnych.
Prawa kongruencja syntaktyczna i kongruencja syntaktyczna
Opis języka regularnego za pomocą wyrażeń regularnych jest bardzo wygodny, ale nie jedyny. W kolejnych wykładach będziemy wprowadzać inne reprezentacje języków regularnych, takie jak automaty czy gramatyki. Pojęcia, które wprowadzimy teraz, są również narzędziami dla opisu i badań własności języków regularnych. W szczególności służą do konstrukcji możliwie najprostszego automatu rozpoznającego dany język regularny, zwanego automatem minimalnym.
Definicja 2.1.
Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. W monoidzie \(\; A^* \;\) wprowadzamy następujące dwie relacje:
- (1) prawą kongruencję syntaktyczną \(\; P_L^r , \;\) przyjmując
dla dowolnych słów \(u, v \in A^*\)
\(u \; P_L^r \; v \;\;\) wtedy i tylko wtedy, gdy spełniony jest warunek\(\forall w \in A^* \;\; uw \in L \; \Leftrightarrow \; vw \in L,\)
- (2) kongruencję syntaktyczną \(\; P_L , \;\) przyjmując
dla dowolnych \(u, v \in A^*\)
\(u \; P_L \; v \;\;\) wtedy i tylko wtedy, gdy spełniony jest warunek\(\forall w_1, w_2 \in A^* \;\; w_1uw_2 \in L \; \Leftrightarrow \; w_1vw_2 \in L.\)
Łatwo stwierdzić, że nazwy wprowadzonych relacji pokrywają się z ich własnościami, to znaczy relacja \(P_L^r\) jest rzeczywiście prawą kongruencją, a \(P_L\) kongruencją.
Przykład 2.1.
Niech \(A=\{ a,b\}\) będzie alfabetem.
- (1)Dla języka \(L=a^+b^+\) relacja
- (a) \(P_L^r\) ma \(4\) klasy równoważności: \(\;\;L, \;\;A^*baA^*+b^+,\;\; a^+, \;\;1\),
- (b) \(P_L\) ma \(5\) klas równoważności: \(L, \;\;A^*baA^*,\;\;b^+,\;\; a^+, 1\).
- (2) Dla języka \(L=\{a^nb^n : n\geq 1\}\) obie relacje mają nieskończony indeks
- (a) dla \(P_L^r\) klasami równoważności są zbiory
\(L_i =\{a^nb^{n-i} : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}_0\), \(A^* \setminus\bigcup_{i=0}^\infty L_i\).
- (a) dla \(P_L^r\) klasami równoważności są zbiory
- (b) dla \(P_L\) klasami równoważności są zbiory
\(L_i =\{a^nb^{n-i} : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}_0\),
\(L'_i =\{a^{n-i}b^n : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}\),
\(A^* \setminus[\bigcup_{i=1}^\infty (L_i\cup L'_i )\cup L_0 ]\).
- (b) dla \(P_L\) klasami równoważności są zbiory
Udowodnimy następujące własności relacji \(\; P_L^r \;\) oraz \(\; P_L \;\).
Twierdzenie 2.1.
Prawa kongruencja syntaktyczna \(\; P_L^r \;\) jest największą w sensie inkluzji spośród wszystkich
prawych kongruencji \(\rho\) takich, żeKongruencja syntaktyczna \(\; P_L \;\) jest największą w sensie inkluzji spośród wszystkich
kongruencji \(\rho\) takich, żeDowód
Dowód przeprowadzimy dla prawej kongruencji syntaktycznej. Uzasadnienie tezy dla kongruencji \(\; P_L \;\) przebiega podobnie. Niech \(\;\rho \;\) będzie dowolną prawą kongruencją spełniającą założenia i niech \(u\rho v\). Zatem dla każdego \(w\in A^{*}\) jest
W konsekwencji \(\rho \subseteq P_L^r.\) W
szczególności więc dla dowolnego \(u \in A^*\) ma miejsce inkluzja \([u]_\rho \; \subseteq \; [u]_{P_L^r}.\) Zatem \(L\subset \bigcup _{w\in L}[w]_{P^{r}_{L}}\).
Aby udowodnić inkluzję w stronę przeciwną ustalmy dowolne \(\; u \in L \;\) i niech \(v \in [u]_{P_L^r}.\)
Przyjmując \(\; w =1 \;\) w definicji (patrz definicja 2.1.) relacji \(\; {P_L^r} \;\) otrzymamy równoważność
\(\; u \in L \; \Leftrightarrow \; v \in L \;.\) A więc \(\; v \in L \;.\)
Wniosek 2.1.
Jeśli język \(L\) jest regularny, to relacja \(\; P_L^r \;\) jest największą w sensie inkluzji spośród wszystkich prawych kongruencji takich, że język \(L\) jest sumą jej pewnych klas równoważności, a relacja \(\; P_L \;\) jest największą w sensie inkluzji spośród wszystkich kongruencji spełniających analogiczny warunek. Obie relacje mają skończony indeks, czyli dzielą wolny monoid \(A^*\) na skończoną liczbę klas równoważności.
Pojęcie, które wprowadzimy teraz - monoid syntaktyczny języka - wiąże teorię języków formalnych, a w szczególności teorię języków rozpoznawalnych, z teorią półgrup. Związek ten stanowi podstawę dla bardziej zaawansowanych problemów teorii języków i automatów wykraczających poza ramy tego wykładu.
Definicja 2.2.
Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. Monoidem syntaktycznym języka \(\; L \;\) nazywamy strukturę ilorazową
Dualnie, tworząc iloraz \(S(L) = A^+/P_L\), wprowadza się pojęcie półgrupy syntaktycznej języka \(\; L \;\). Oba wprowadzone tu pojęcia zilustrowane będą w trakcie dalszych rozważań.
Automat minimalny
Określenie języka rozpoznawalnego postuluje istnienie automatu o skończonej liczbie stanów, działającego w odpowiedni sposób. Należałoby zatem wskazać algorytm budowy takiego automatu dla języka rozpoznawalnego. Oczywiście interesuje nas algorytm prowadzący do automatu o możliwie najprostszej postaci. Najprostsza postać, w tym kontekście, oznacza najmniejszą liczbę stanów.
Definicja 3.1.
Automat \(\mathcal{A} = (S,A,f,s_0,T)\) rozpoznający język \(L\) nazywamy automatem minimalnym, jeśli posiada najmniejszą liczbę stanów spośród wszystkich automatów rozpoznających język \(L.\)
Kwestią istnienia takiego automatu minimalnego zajmujemy się teraz. W kolejnym wykładzie przedstawimy algorytmy konstrukcji automatu minimalnego.
W poniższym twierdzeniu występuje automat ilorazowy \({A}_{P^{r}_{L}}\) określony przez prawą kongruencję \(P_L^r\).
Twierdzenie 3.1.
Dla dowolnego automatu \({A} = (S,A,f,s_0,T) \;\) rozpoznającego język \(\; L \subset A^* \;\) istnieje jedyny epimorfizm \(\varphi :\mathcal{A}\longrightarrow \mathcal{A}_{P^{r}_{L}}\) taki, że \(\varphi (s_{0})=[1]_{P^{r}_{L}}.\)
Dowód
Prawa kongruencja automatowa \(\sim _{\mathcal{A}}\) ma skończony indeks i \(L=\bigcup _{u\in L}[u]_{\sim _{\mathcal{A}}}\). Zatem z twierdzenia (patrz Twierdzenie 2.1.) wynika, że
Istnienie epimorfizmu \(\; \varphi \;\) wynika z twierdzenia 1.1, wykład 3. Epimorfizm ten określony jest dla dowolnego stanu \(s\in S\) równością \(\varphi(s) = f^*([1]_{P_L^r},w) = [w]_{P_L^r},\) gdzie \(w\) jest słowem takim, że \(f(s_0,w)=s\).
Jest to jedyny epimorfizm spełniający warunki tezy dowodzonego twierdzenia. Dla każdego epimorfizmu \(\; \psi \;\) takiego, że \(\psi :\mathcal{A}\longrightarrow \mathcal{A}_{P^{r}_{L}}\) i \(\psi (s_{0})=[1]_{P^{r}_{L}}\) mamy\(\;\forall s \in S\)
gdzie \(f(s_0,w) = s .\) Tak więc \(\; \psi = \varphi .\)
Zatem udowodnione twierdzenie zapewnia nas o istnieniu automatu minimalnego, co formułujemy w następującym wniosku.
Wniosek 3.1.
Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. Automat
gdzie \(\; T = \{ [w]_{P_L^r} \; : \; w \in L \}, \;\) jest automatem minimalnym rozpoznającym język \(\; L \;\). Oznaczać go będziemy symbolem \(\mathcal{A}_{L}\).
Następne twierdzenie charakteryzuje monoid przejść automatu minimalnego i podaje kolejny warunek równoważny na to, żeby język \(L\) był rozpoznawany przez automat.
Twierdzenie 3.2.
Niech \(L\subset A^{*}\) będzie dowolnym językiem.
- 1. Dla dowolnego języka \(L\in \mathcal{REC}(A^{*})\) monoid przejść automatu minimalnego \(\mathcal{A}_{L}\) jest izomorficzny z monoidem syntaktycznym \(M(L)\) języka \(L\), czyli
- 2. (tw. J.Myhill'a) Język \(\; L \subset A^* \;\) jest rozpoznawalny wtedy i tylko wtedy, gdy \(\; M(L) \;\) jest monoidem skończonym.
Dowód
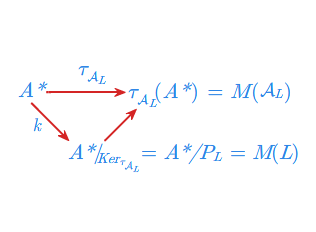
Dla dowodu punktu 1 wykażemy, że
gdzie zgodnie z definicją dla dowolnych \(w,u\in A^{*}\)
Korzystamy teraz z twierdzenia o rozkładzie epimorfizmu, które w tym przypadku ma postać:
czyli \(M(\mathcal{A}_{L})\sim M(L)\).
Dla dowodu punktu 2 załóżmy, że język \(\; L \;\) jest rozpoznawalny.
Zatem
Z twierdzenia (patrz twierdzenie 2.1.) wnioskujemy, że \(\rho \subseteq P_L .\) Oznacza to, że indeks relacji \(\; P_L \;\) jest niewiększy od indeksu \(\; \rho, \;\) a co za tym idzie, \(\; M(L) = A^*/P_L \;\) jest monoidem skończonym.
Dla dowodu implikacji w stronę przeciwną rozważmy epimorfizm kanonicznyrówność
Z twierdzenia 3.1 (patrz twierdzenie 3.1.) wynika, że określenie klas abstrakcji prawej kongruencji syntaktycznej \(P^r_L\) prowadzi do określenia minimalnego automatu rozpoznającego język \(L\). Prezentowane poniżej twierdzenia wskazują sposób konstrukcji prawej kongruencji syntaktycznej dla języka \(L\).
Twierdzenie 3.3.
Niech \(\; L \subset A^* \;\) będzie dowolnym językiem,
a \(\; \Theta_L \subset A^* \times A^* \;\) relacją
równoważności o dwóch klasach równoważności \(L\) i \(A^* \setminus L\).
Przez \(\; \rho_i \;\) dla \(\; i \in {\Bbb N}\) oznaczmy zstępujący ciąg relacji określony następująco:
\(\rho_1 = \Theta_L ,\;\;\) a dla \(\; i = 2,...\) przyjmijmy
\(\rho_i = \{ (u,w) \in \; A^* \times A^* \; : \; (ua,wa) \in \; \rho_{i-1} \;\;\; \forall a \in A \cup \{1\}\}.\)
Wtedy \(\;\; \bigcap \rho_i = P_L^r \;\;\).
Dowód
Na początku uzasadnimy, że \(\; \bigcap \rho_i \;\) jest prawą kongruencją na \(\; A^*\). Załóżmy więc, że słowa \(\; x , y \in A^* \;\) są w relacji \(x \; \bigcap \rho_i \;y \;\). Wybierzmy dowolne słowo \(z\in A^{*}\) i niech \(k\) oznacza długość tego słowa. Z założenia wynika, iż \(x\, \rho _{i+k}\, y\), co w świetle definicji ciągu relacji \(\rho _{i}\) implikuje, że \(xz\: \rho _{i}\: yz.\) Ponieważ \(i\) jest dowolne wnioskujemy ostatecznie, że \(xz \; \bigcap \rho_i \; yz \;,\) co kończy dowód faktu, że \(\; \bigcap \rho_i \;\) jest prawą kongruencją.
Dowiedziemy teraz równościDla uzasadnienia inkluzji \(\bigcap \rho_i \;\subseteq\; P_L^r\) zauważmy, że jeśli \(x \; \bigcap \rho_i \; y ,\) to dla dowolnego \(z\in A^{*}\) mamy \(xz \; \bigcap \rho_i \; yz\), a w szczególności \(xz \; \rho_1 \; yz.\) Z definicji relacji \(\rho _{1}\) dla dowolnego \(z\in A^{*}\) prawdziwa jest równoważność
A więc \(x \;\; P_L^r \;\; y\). Inkluzję w stronę przeciwną pokażemy, dowodząc indukcyjnie ze względu na \(i=1,2,...,\) że dla dowolnych \(\;x , y \in A^* \;\) prawdziwa jest następująca implikacja
Załóżmy zatem, że \(x \;\; P_L^r \;\; y.\) Z definicji \(\; P_L^r \;\) wynika, że dla dowolnego \(z \in A^*\) prawdziwa jest równoważność
Przyjmując \(\; z=1 \;\) otrzymujemy żądaną własność dla \(\rho _{1}.\) Załóżmy teraz, że prawdziwa jest implikacja
dla \(i = 1,...,n-1\) oraz dla dowolnych \(x , y \in A^*.\) Stąd, że \(P_L^r\) jest prawą kongruencją, wnioskujemy, że dla dowolnego \(\; a \in A \cup \{1\} \;\) spełniona jest relacja \(xa \;\; P_L^r \;\; ya.\) Korzystając z założenia indukcyjnego, mamy \(xa \;\; \rho_{n-1} \;\; ya\) dla dowolnego \(\; a \in A \cup \{1\} \;\). A to oznacza z definicji \(\; \rho_i \;\), że \(x \;\; \rho_n \;\;y\) i kończy dowód.
Kolejne twierdzenie charakteryzuje relację \(P^r_L\) dla języka rozpoznawalnego i orzeka, iż w przypadku języka rozpoznawalnego ciąg relacji \(\rho_i\), aproksymujacych \(P^r_L\), jest skończony. Równoważność dwóch pierwszych warunków poniższego twierdzenia nazywana bywa często w literaturze twierdzeniem A.Nerode.
Twierdzenie 3.4.
Następujące warunki są równoważne:
- (1) Język \(L\) jest rozpoznawalny.
- (2) Relacja \(P^r_L\) ma skończony indeks.
- (3) Ciąg relacji \(\rho_i\) stabilizuje się, co oznacza, że istnieje \(i\in {\Bbb N}\) takie, że
\(\rho_i = \rho_{i+1}=....\) Dla najmniejszego takiego \(i\) prawdziwa jest równość \(\rho_i = P^r_L.\)
Dowód
Dowód poprowadzimy według następujacego schematu:
\(1 \Longrightarrow 2\)
\(P^r_L\) jest największą w sensie inkluzji relacją spełniająca warunki punktu 2 z twierdzenia 1.3 z wykładu 3 (patrz twierdzenie 1.2 wykład 3). Z tego samego twierdzenia wynika skończoność indeksu.
\(1 \Longleftarrow 2\)
Relacja \(P^r_L\) jest prawą kongruencją, ma skończony indeks oraz
Z twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2 wykład 3) wynika więc, że język \(L\) jest rozpoznawalny.
\(2 \Longrightarrow 3\) Dowód poprowadzimy nie wprost. Załóżmy więc, że dla każdego \(i\in {\Bbb N}\) jest \(\rho_i \neq \rho_{i+1}.\) Oznacza to, że dla każdego \(i\in {\Bbb N}\) indeksy relacji \(\rho _{i}\) tworzą ciąg silnie rosnący, to znaczy spełniają zależność \(ind\rho_i < ind\rho_{i+1}.\) Ponieważ \(ind\rho_1 = 2,\) to dla każdego \(i\in {\Bbb N}\) prawdziwa jest nierówność \(ind\rho_i > i.\) A to prowadzi do wniosku, że dla dowolnego \(i\in {\Bbb N}\)
Zatem indeks relacji \(P^r_L\) jest nieskończony, co jest sprzeczne z założeniem.
\(2 \Longleftarrow 3\)
Udowodnimy indukcyjnie ze względu na \(j\), że każda z relacji \(\rho_j\) dla \(j=1,...,i\) ma skończony indeks. Oczywiście \(ind\rho_1 = 2.\) Załóżmy teraz, że relacja \(\rho_j\) ma skończony indeks. Z definicji relacji \(\rho_{j+1}\) wynika, że jej klasy równoważności powstają przez podział klas równoważności \([w]_{\rho_j}\) na skończoną liczbę klas relacji \(\rho_{j+1}\) (skończona jest liczba możliwych do spełnienia warunków prowadzących do podziału). Oznacza to, że indeks relacji \(\rho_{j+1}\) jest również skończony, a więc relacja \(P^r_L\) ma również skończony indeks.
Wykorzystamy powyżej udowodnione własności do konstrukcji automatu minimalnego rozpoznającego język \(L\). Warto zauważyć, iż punktem wyjścia dla tej konstrukcji jest język \(L\) zadany, na przykład, poprzez wyrażenie regularne.
Przykład 3.1.
Niech do języka \(L\) należą wszystkie słowa nad alfabetem \(A=\{a,b\}^*\) zaczynające się lub kończące literą \(a\). Skonstruujemy minimalny automat akceptujący język \(L\).
- \(\rho _{1}:\) \(L=aA^* +A^* a,\;\; A^{*}\setminus L =bA^*b +b+1\)
- \(\rho _{2}:\) \(aA^*a+a,\;\; bA^*a, \;\; bA^*b +b+1,\)
- \(\rho _{3}:\) \(aA^*a+a,\;\; bA^*a, \;\; bA^*b +b, \;\;1,\)
Ponieważ \(\rho _{3}=\rho _{4}\), to \(P^r_L=\rho _{3}\) i automat minimalny ma \(4\) stany.
Przyjmujemy \(s_0 =[1]\), \(s_1=bA^*a\), \(s_2=aA^*a+a\), \(s_3=bA^*b +b\)
oraz \(T=\{s_1,s_2\}\), a automat minimalny \(\mathcal{A}_{L}=\left( A^{*}/_{\rho _{3}},f^{*},s_{0},T\right)\)
Przykład 3.2.
Dla języka \(L=\left\{ w \in \{ a,b\}^* :\#_a w =2k, \#_b w =2l+1 ,\; k,l\geq 0 \right\}\) określimy ciąg relacji \({\rho}_i\), a
następnie relację \(P^{r}_{L}\). Umożliwi nam to, w świetle
powyższych rozważań, zbudowanie automatu minimalnego rozpoznającego
ten język. Poniżej wypisane są klasy równoważności relacji \(\rho _{1}\) oraz \(\rho _{2}\), \(\rho _{3}=\rho _{2}\), co
kończy proces obliczania relacji \(\rho _{i}\) i daje równość \(\rho _{2}=P^{r}_{L}\).
- \(\rho _{1}:\) \(L, A^{*}\setminus L\)
- \(\rho _{2}:\) \(L, L_1, L_2, L_3\), gdzie
\(L_1=\left\{ w \in \{ a,b\}^* :\#_a w =2k, \#_b w= 2l, \; k,l\geq 0 \right\},\)
\(L_2\left\{ w \in \{ a,b\}^* :\#_a w =2k+1, \#_b w= 2l+1, \; k,l\geq 0 \right\},\)
\(L_3=\left\{ w \in \{ a,b\}^* :\#_a w =2k+1, \#_b w= 2l, \; k,l\geq 0 \right\},\)
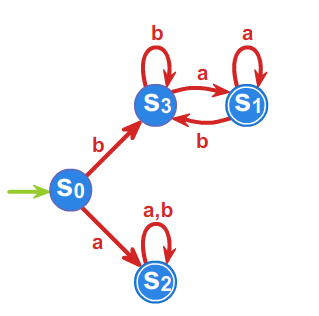
Przyjmując \(s_0 =L_1=[1]\), \(s_1=L_3\), \(s_2=L_2\), \(s_3=L\) oraz \(T=\{s_3\}\)
automat minimalny \(\mathcal{A}_{L}=\left( A^{*}/_{\rho _{2}},f^{*},s_{0},T\right)\) przedstawiony jest przy pomocy grafu: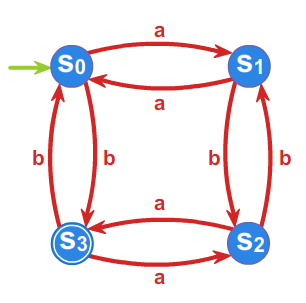
Powyższe twierdzenia podają również sposób konstrukcji monoidu syntaktycznego języka \(L\).
Algorytmy konstrukcji automatu minimalnego
W tym wykładzie podamy algorytmy konstrukcji automatu minimalnego i twierdzenia dowodzące ich poprawności.
Algorytmy konstrukcji automatu minimalnego
Dla języka rozpoznawanego \(L\) konstrukcję automatu minimalnego można rozpocząć, startując z opisu języka danego na przykład przez wyrażenie regularne lub też jakiegoś automatu rozpoznającego ten język. W niniejszym wykładzie przedstawimy algorytmy konstrukcji automatu minimalnego obejmujące oba wspomniane punkty startu. Jako pierwszy, nawiązując do rezulatów przedstawionych w poprzednim wykładzie, prezentujemy algorytm, dla którego punktem wyjścia jest język \(L\). Prezentację poprzedzimy wprowadzeniem pewnej operacji na słowach zwanej pochodną J.Brzozowskiego.
Definicja 1.1.
Niech \(\; L \subset A^* \;\) będzie dowolnym językiem, a \(\; u \in A^* \;\) dowolnym słowem. Pochodną Brzozowskiego (residuum) z języka \(L\) względem słowa \(u\) nazywamy język
Podczas obliczeń pochodnych Brzozowskiego (residuów języka \(L\)) można wykorzystać poniższe równości.
Niech \(L_1, L_2\subset A^* \;\) będą dowolnymi językami, \(a \in A\) dowolną literą, a \(u,v \in A^*\) dowolnymi słowami. Prawdziwe są następujące równości:
Przykład 1.1.
Obliczmy wszystkie pochodne dla języka \(L=a^+b^+\). Okazuje się, że są tylko cztery różne pochodne liczone względem \(a\), \(b\), \(ab\) i słowa pustego \(1\). Mianowicie:
\(a^{-1}L=a^*b^+\),
\(b^{-1}L= \emptyset\),
\(ab^{-1} L=b^*\),
\(1^{-1}L=L\).
Dla wszystkich innych słów otrzymujemy uzyskane powyżej języki, co wynika z własności pochodnych (patrz wyżej wypisane równości) i z następujacych obliczeń:
\(\forall n \in \mathbb{N} \quad (a^n)^{-1}L=a^*b^+\),
\(\forall n \in \mathbb{N} \quad (b^n)^{-1}L= \emptyset\),
\(\forall n \in \mathbb{N} \quad (ab^n)^{-1} L=b^*\).
Zauważmy również, nawiązując raz jeszcze do rezulatów przedstawionych w poprzednim wykładzie, że prawdziwa jest następująca równoważność wiążąca wprowadzone pojęcie pochodnej Brzozowskiego z prawą kongruencją syntaktyczną:
Rozpisując z definicji lewą stronę tej równoważności, otrzymujemy, iż dla dowolnego słowa \(z \in A^*\) słowo \(uz \in L\) wtedy i tylko wtedy, gdy \(vz \in L\). A to równoważnie oznacza (znów z definicji), że \(u^{-1}L=v^{-1}L.\)
Z uzasadnionej równoważności oraz twierdzenia 3.4 o prawej kongruencji syntaktycznej z poprzedniego wykładu wnioskujemy równoważność rozpoznawalności języka \(L\) i skończonej ilości różnych pochodnych Brzozowskiego tego języka.
Pierwszy z przedstawianych algorytmów będzie konstruował automat minimalny, wyznaczając prawą kongruencję automatową poprzez zastosowanie metody pochodnych Brzozowskiego. Metoda ta umożliwia przeprowadzanie odpowiednich obliczeń bezpośrednio na wyrażeniach regularnych. Ogólny opis algorytmu jest następujący. Stany konstruowanego automatu minimalnego etykietowane są zbiorami odpowiadającymi pewnym językom. Mając dany język \(L\), ustanawiamy stan początkowy automatu jako \(L\), wpisujemy go na listę \(\mathcal{L}\) i obliczamy \(a^{-1}L\) dla każdej litery \(a \in A\). Jeśli wśród obliczonych wartości znajduje się język niewystępujący na liście, dodajemy go do listy. Obliczenia pochodnych Brzozowskiego wykonujemy, dopóki będziemy uzyskiwać nowe języki (nowe stany). Funkcja przejść konstruowanego automatu minimalnego zdefiniowana jest następująco:
Obliczone języki określają stany automatu minimalnego.
Automatem minimalnym dla automatu \(\mathcal{A}=(S, A, f, s_0, T)\) będzie zatem automat
gdzie:
- \(S_L=\{u^{-1}L:\ u \in A^*\}\),
- \(s_0^L = L\),
- \(T_L = \{u^{-1}L:\ u \in L\}\),
- \(f_L(u^{-1}L,a) = a^{-1}(u^{-1}L)=(ua)^{-1}L\).
Jeśli zdefiniujmy odwzorowanie \(\nu: S \rightarrow S_L\), kładąc:
\(\nu(s)=u^{-1}L, \mbox{ gdzie } s=f(s_0,u),\)
to można dowieść, że \(\nu\) jest dobrze określone, jest epimorfizmem oraz \(\nu(s_0) = s_0^L\) - porównaj twierdzenie 3.1 z wykładu 4. Prawdą jest też, iż \(s \in T\) wtedy i tylko wtedy, gdy \(\nu(s) \in T_L\) oraz że następujący diagram komutuje:
tutaj diagram
Formalny zapis algorytmu przedstawiony jest poniżej.
Algorytm Minimalizuj1 - algorytm minimalizacji wykorzystujący pochodne Brzozowskiego
1 Wejście: \(L\) - język
2 Wyjście: automat minimalny \(\mathcal{A}'=(S_L, A, f_L, s_L, T_L)\) taki, że \(L\mathcal{A}'=L\)
3 \(S_L \leftarrow \{L\}\);
4 włóż\((\mathcal{L},L)\);
5 while \(\mathcal {L}\ne \emptyset\) do
6 \(M \leftarrow\) zdejmij(\(\mathcal {L}\));
7 for each \(a \in A\) do
8 \(N \leftarrow a^{-1}M\);
9 if \(N \cap S_L = \emptyset\) then
10 \(S_L \leftarrow S_L \cup \{N\}\);
11 włóż\((\mathcal{L},N)\);
12 end if
13 end for
14 end while
15 for each \(M \in S_L\) do
16 for each \(a \in A\) do
17 \(f_L(M,a) \leftarrow a^{-1}M\);
18 end for
19 end for
20 \(s_L \leftarrow L\);
21 \(T_L \leftarrow \{u^{-1}L:\ u \in L\}\);
22 return \(\mathcal{A}'\);
Funkcja zdejmij\((\mathcal{L})\), występująca w linii 6., zdejmuje z kolejki \(\mathcal{L}\) pierwszy element i zwraca go jako swoją wartość. Procedura włóż\((\mathcal{L},L)\), występująca w liniach 4. oraz 11., wstawia na koniec kolejki \(\mathcal{L}\) element \(L\).
Przykład 1.2.
Dla języka \(L=a^+b^+\) z przykładu 1.1 (patrz przykład 1.1.) w wyniku działania powyższego algorytmu otrzymamy czterostanowy automat
\(\mathcal{A}_L=(S_L,A, f, L, T),\) gdzie \(S_L= \{L, a^*b^+ ,\emptyset, b^*\}\), a funkcja przejść zadana jest grafem:
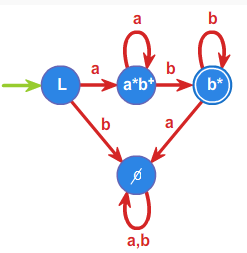
Prezentowane poniżej twierdzenie uzasadnia kolejny algorytm konstrukcji automatu minimalnego. Tym razem punktem wyjścia jest dowolny automat rozpoznający język \(L\).
Analogicznie do konstrukcji relacji \(\rho _{i}\), przedstawionej w wykładzie 4, możemy określić ciąg odpowiednich relacji na zbiorze stanów dowolnego automatu rozpoznającego język \(L\). Relacje te służą do efektywnego określenia automatu minimalnego, równoważnego zadanemu.
Twierdzenie 1.1.
Niech \(\mathcal{A}= (S,A,f,s_0,T)\) będzie dowolnym automatem i niech \(L = L(\mathcal{A})\). Przez \(\approx _\mathcal{A} \subset S \times S\) oznaczmy relację równoważności zawierającą dwie klasy równoważności \(T\) i \(S\setminus T\). Przez \(\overline \rho_i\) dla \(i\in \Bbb N\)
oznaczmy zstępujący ciąg relacji określony następująco:
\(\overline \rho _1 = \approx _\mathcal{A}\), a dla \(i = 2,...\) przyjmijmy
\(\overline \rho _i = \{ (s,t) \in \; S \times S \; : \;\; \forall a \in A \cup \{1\} \; \; f(s,a) \overline{\rho}_{i-1} f(t,a) \;\}. \;\).
Wtedy \(\bigcap \overline \rho_i\) jest największą prawą kongruencją automatową zawartą w relacji \(\overline \rho_1 = \approx _ \mathcal{A}\) i automat minimalny ma postać
Dowód tego twierdzenia przebiega analogicznie do dowodu twierdzenia 3.3 z wykładu 4 (patrz twierdzenie 3.3. wykład 4).
Algorytm działajacy w oparciu o powyższe twierdzenie na podstawie zadanego automatu \(A = (S, A, f, s_0, T)\), konstruuje efektywnie automat minimalny dla \(\mathcal{A}\), obliczając ciąg relacji \(\rho _1\). Proces konstrukcji przebiega w sposób iteracyjny. Zaczynamy od zdefiniowania relacji \(\approx_\mathcal{A}\), która posiada tylko dwie klasy abstrakcji: do pierwszej z nich należą wszystkie stany końcowe, a do drugiej - wszystkie pozostałe stany. Tak więc
Definiujemy pierwszą z relacji \(\overline \rho\), czyli relację \(\overline \rho_1\) jako równą \(\approx_ \mathcal {A}\), a następnie, dla każdej obliczonej już relacji \(\overline \rho_i-1\), obliczamy relację \(\overline \rho_i\) w następujący sposób:
Nowo obliczona relacja \(\overline \rho_i\) albo podzieli jedną lub kilka klas abstrakcji relacji \(\overline \rho_{i-1}\), albo będzie identyczna z relacją \(\overline \rho_{i-1}\). Jeśli zajdzie ta druga sytuacja, to znaczy, że dla każdego \(j>i\) w oczywisty sposób spełniona jest równość \(\overline \rho_j=\overline \rho_i\), czyli ciąg relacji ustabilizuje się. W tym momencie algorytm kończy swoje działanie i klasy abstrakcji relacji \(\overline \rho_i\) będą reprezentować stany automatu minimalnego.
Algorytm Minimalizuj2 - algorytm minimalizacji automatu wykorzystujący stabilizujący się ciąg relacji
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat taki, że \(\displaystyle L=L(\mathcal{A})\).
2 Wyjście: automat minimalny \(\displaystyle \mathcal{A}'=(S',A',f', s_0', T')\) dla \(\displaystyle \mathcal{A}\).
3 \(\displaystyle \overline{\rho}_1\displaystyle \leftarrow\displaystyle \approx_{\mathcal{A}}\);
4 \(\displaystyle i \leftarrow 1\);
5 repeat
6 \(\displaystyle \slash \slash\) oblicz \(\displaystyle \overline{\rho}_i\): \(\displaystyle s_1 \overline{\rho}_i s_2 \Leftrightarrow (s_1 \overline{\rho}_{i-1} s_2) \wedge (\forall a \in A\ f(s_1, a) \overline{\rho}_{i-1} f(s_2,a))\);
7 \(\displaystyle i \leftarrow i+1\);
8 empty\(\displaystyle (\overline{\rho}_i)\)
9 for each \(\displaystyle (s_1,s_2)\in S\times S\) do
10 flag\(\displaystyle \leftarrow\)true;
11 for each \(\displaystyle a\in A\)
12 if not \(\displaystyle f(s_1, a) \overline{\rho}_{i-1} f(s_2,a)\) then
13 flag\(\displaystyle \leftarrow\)false;
14 end if
15 end for
16 if flag=true and \(\displaystyle s_1 \overline{\rho}_{i-1} s_2\) then
17 \(\displaystyle \overline{\rho}_{i} \leftarrow \overline{\rho}_{i} \cup \{(s_1,s_2)\}\);
18 end if
19 end for
20 until \(\displaystyle \overline{\rho}_i = \overline{\rho}_{i-1}\)
21 \(\displaystyle S' \leftarrow S \slash \overline{\rho}_i\);
22 for each \(\displaystyle [s]_{\overline{\rho}_i} \in S \slash \overline{\rho}_i\) do
23 for each \(\displaystyle a \in A\) do
24 \(\displaystyle f'([s]_{\overline{\rho}_i},a) \leftarrow [f(s,a)]_{\overline{\rho}_i}\);
25 end for
26 end for
27 \(\displaystyle s_0' \leftarrow [s_0]_{\overline{\rho}_i}\);
28 \(\displaystyle T' \leftarrow \{[t]_{\overline{\rho}_i}:\ t \in T\}\);
29 return \(\displaystyle \mathcal{A}'=(S', A, f', s_0', T')\);
Przykład 1.3.
Zminimalizujemy automat \(\displaystyle \mathcal{A}=(S,A,f,s_0,T)\), dla którego
\(\displaystyle S=\left\{ s_{0},s_{1},s_{2},s_{3},s_{4},s_5 \right\}, A=\{a,b\}, T=\left\{s_1, s_{2},s_{4}\right\}\) ,
a funkcja przejść określona jest przy pomocy grafu.
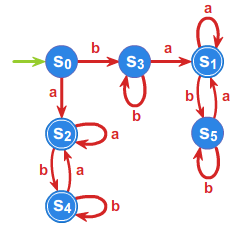
Rysunek 2
Konstruujemy ciąg relacji \(\displaystyle \overline{\rho}_i\).
Na początku \(\displaystyle \overline{\rho}_1\) dzieli \(\displaystyle S\) na dwie klasy abstrakcji; pierwsza zawiera stany końcowe, a druga -- wszystkie pozostałe, czyli uzyskujemy dwa zbiory \(\displaystyle \{s_1,s_2,s_4\}\) oraz \(\displaystyle \{s_0, s_3, s_5\}\).
Obliczmy \(\displaystyle \overline{\rho}_2\) (pierwszy przebieg pętli w liniach 5.-20. algorytmu). Aby dwa elementy (stany) \(\displaystyle s\) i \(\displaystyle t\) były ze sobą w relacji \(\displaystyle \overline{\rho}_2\) muszą być ze sobą w relacji \(\displaystyle \overline{\rho}_1\) oraz musi zachodzić
\(\displaystyle \forall a \in A \;\; f(s, a) \overline{\rho}_1 f(t,a).\)
Czyli kolejna, nowa relacja może ewentualnie podzielić już istniejące zbiory zdefiniowane przez poprzednią relację. Nie może
więc zajść taka sytuacja, że w jednej klasie abstrakcji relacji \(\displaystyle \overline{\rho}_{i+1}\) znajdą się elementy z różnych klas
abstrakcji relacji \(\displaystyle \overline{\rho}_i\).
Rozważmy najpierw zbiór \(\displaystyle \{s_1, s_2, s_4\}\). Oczywiście każde dwa stany z tego zbioru są ze sobą w relacji \(\displaystyle \overline{\rho}_1\). Zauważmy, że \(\displaystyle f(s_2, a)=f(s_4,a)=s_2\), \(\displaystyle f(s_2,b)=f(s_4,b)=s_4\), więc
\(\displaystyle s_2 \overline{\rho}_2 s_4\) (bo \(\displaystyle s_2 \overline{\rho}_1 s_2\) oraz \(\displaystyle s_4 \overline{\rho}_1 s_4\)). Ponieważ \(\displaystyle f(s_1,b)=s_5\) i \(\displaystyle f(s_2,b)=s_4\), a wiemy, że \(\displaystyle s_5\) nie jest w relacji \(\displaystyle \overline{\rho}_1\) z \(\displaystyle s_4\), zatem stany \(\displaystyle s_1\) i \(\displaystyle s_2\) nie mogą być ze sobą w relacji \(\displaystyle \overline{\rho}_2\), a to oznacza, że także stany \(\displaystyle s_1\) i \(\displaystyle s_4\) nie mogą być ze sobą w relacji \(\displaystyle \overline{\rho}_2\).
W analogiczny sposób można sprawdzić, że relacja \(\displaystyle \overline{\rho}_2\) nie podzieli zbioru \(\displaystyle \{s_0, s_3, s_5\}\). Ostatecznie, po pierwszym wykonaniu pętli algorytmu minimalizacji obliczyliśmy relację \(\displaystyle \overline{\rho}_2\), która dzieli \(\displaystyle S\) na następujące podzbiory:
W kolejnym kroku obliczamy \(\displaystyle \overline{\rho}_3\). Zbiór \(\displaystyle \{s_1\}\) oczywiście nie może być już podzielony na mniejsze podzbiory. Łatwo zauważyć, że \(\displaystyle \overline{\rho}_3\) nie podzieli także zbioru \(\displaystyle \{s_2, s_4\}\).
Rozważmy teraz zbiór \(\displaystyle \{s_0, s_3, s_5\}\). Mamy \(\displaystyle f(s_3, a)=f(s_5, a)\) oraz \(\displaystyle f(s_3, b)=s_3\), \(\displaystyle f(s_5, b)=s_5\) i wiadomo, że \(\displaystyle s_3 \overline{\rho}_2 s_5\), zatem \(\displaystyle s_3\) i \(\displaystyle s_5\) będą ze sobą w relacji \(\displaystyle \overline{\rho}_3\).
Ponieważ \(\displaystyle f(s_0, a)=s_2\) i \(\displaystyle f(s_3, a)=s_1\), ale \(\displaystyle s_2\) i \(\displaystyle s_1\) nie są
ze sobą w relacji \(\displaystyle \overline{\rho}_2\), zatem nie mogą być także ze sobą w relacji \(\displaystyle \overline{\rho}_3\). Relacja \(\displaystyle \overline{\rho}_3\) dzieli więc zbiór \(\displaystyle \{s_0, s_3, s_5\}\) na zbiory \(\displaystyle \{s_0\}\) oraz
\(\displaystyle \{s_3, s_5\}\).
Podział zbioru \(\displaystyle S\) przez relację \(\displaystyle \overline{\rho}_3\) wygląda więc
następująco:
Relacja \(\displaystyle \overline{\rho}_4\) nie podzieli już ani zbioru \(\displaystyle \{s_2, s_4\}\), ani zbioru \(\displaystyle \{s_3, s_5\}\), więc uzyskujemy równość \(\displaystyle \overline{\rho_4}=\overline{\rho}_3\) i ponieważ ciąg relacji się ustabilizował, algorytm kończy działanie.
Podsumowując, mamy:
- \(\displaystyle \overline{\rho} _{1}\)
- \(\displaystyle \{s_1, s_{2},s_{4}\}, \{s_{0},s_{3},s_5\},\)
- \(\displaystyle \overline{\rho} _{2}\)
- \(\displaystyle \{s_{1}\},\{s_2,s_{4}\}, \{s_{0},s_{3},s_5\},\)
- \(\displaystyle \overline{\rho} _{3}\)
- \(\displaystyle \{s_{1}\},\{s_2,s_{4}\}, \{s_{0}\},\{s_{3},s_5\}.\displaystyle \overline{\rho} _{3}=\overline{\rho} _{4}\) i równoważny minimalny automat \(\displaystyle \mathcal{A}_L=(S,f^*,s_0,T)\) ma \(\displaystyle 4\) stany.
\(\displaystyle q_0=\{s_{0}\}, q_1=\{s_{1}\}, q_2 = \{s_2,s_{4}\}, q_3 =\{s_{3},s_5\}\), \(\displaystyle T=\{q_1 ,q_2\}\).
Jak łatwo zauważyć jest to automat z przykładu 3.1 zamieszczonego w wykładzie 4 (patrz przykład 3.1. wykład 4).}}
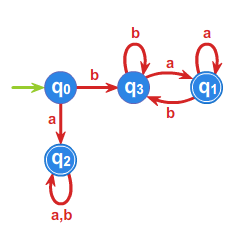
Jednym z najczęściej stosowanych algorytmów automatu minimalnego jest algorytm, który buduje "tabelkę" na podstawie której określa się automat minimalny. Poprawność tego algorytmu również uzasadnia twierdzenie 1.1 (patrz twierdzenie 1.1.).
W algorytmie tym wyznaczać będziemy tzw. stany rozróżnialne. Algorytm działa w czasie \(\displaystyle O(|A|n^2)\), gdzie \(\displaystyle |A|\) jest mocą alfabetu, a \(\displaystyle n\) -- liczbą stanów automatu wejściowego, czyli podlegajacego minimalizacji. Złożoność pamięciowa jest również \(\displaystyle O(|A|n^2)\). Prezentowany algorytm nosi nazwę algorytmu Hopcrofta-Ullmana. Znana w literaturze jest pewna zmodyfikowana wersja tego algorytmu. Jest to algorytm Aho-Sethiego-Ullmana, który ma tę samą złożoność czasową, ale lepszą złożoność pamięciową - \(\displaystyle O(|A|n)\). Natomiast w ramach ćwiczeń prezentujemy jeszcze jeden
algorytm, znany jako algorytm minimalizacji Hopcrofta. Czas działania tego algorytmu wynosi \(\displaystyle O(n \log n)\).
Niech \(\displaystyle \equiv\) będzie relacją zdefiniowaną przez funkcję przejść automatu w następujący sposób:
Definicja 1.2.
Stany \(\displaystyle p\) i \(\displaystyle q\) są równoważne, jeśli \(\displaystyle p \equiv q\).
Jeśli stany nie są równoważne, to będziemy mówić, że są rozróżnialne.
Zadaniem algorytmu jest wyznaczenie stanów równoważnych, celem ich utożsamienia ze sobą. Algorytm musi zdecydować, dla każdej pary
stanów \(\displaystyle (p,q)\), czy są one rozróżnialne. Jeśli pod koniec działania algorytmu okaże się, że nie stwierdziliśmy rozróżnialności tych
stanów, to znaczy, że są one równoważne; następuje ich utożsamienie, czyli "połączenie" ich w jeden stan. Gdy takiego połączenia dokonamy
dla wszystkich par stanów, wobec których nie stwierdziliśmy ich rozróżnialności, powstanie automat o minimalnej liczbie stanów.
W praktyce algorytm nie wyznacza stanów równoważnych, ale stany rozróżnialne, gdyż jest to po prostu łatwiejsze. Po wyznaczeniu
wszystkich par stanów rozróżnialnych pozostałe pary stanowić będą stany równoważne.
W algorytmie wykorzystywać będziemy tablicę list \(\displaystyle \mathcal{L}[p,q]\), po jednej liście dla każdej pary stanów. Funkcja initialize \(\displaystyle(\mathcal{L}[p,q])\) inicjalizuje listę pustą, funkcja zdejmij \(\displaystyle(\mathcal{L}[p,q])\) zdejmuje jeden z elementów, natomiast funkcja włóż \(\displaystyle (\mathcal{L}[p,q],x)\) wkłada element \(\displaystyle x\) na listę
\(\displaystyle \mathcal{L}[p,q]\). Funkcja empty \(\displaystyle (\mathcal{L}[p,q])\) zwraca wartość true gdy lista jest pusta, oraz false w przeciwnym wypadku. Zwróćmy uwagę, że elementami każdej z list \(\displaystyle \mathcal{L}[p,q]\) są pary stanów \(\displaystyle (s,t)\in S\times S\).
Algorytm Minimalizuj3 - algorytm minimalizacji wykorzystujący relację \(\displaystyle \equiv\)
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat
2 Wyjście: \(\displaystyle \mathcal{A}'=(S', A, f', s_0', T')\) - automat minimalny taki, że \(\displaystyle L(\mathcal{A}')=L(\mathcal{A})\).
3 for each \(\displaystyle p \in T\) do
4 for each \(\displaystyle q \in S \backslash T\) do
5 zaznaczone\(\displaystyle [p,q] \leftarrow 1\);
6 initialize(\(\displaystyle \mathcal{L}[p,q]\))
7 end for
8 end for
9 for each \(\displaystyle (p,q) \in (T \times T) \cup ((S \backslash T) \times (S \backslash T))\) do
10 zaznaczone\(\displaystyle [p,q] \leftarrow 0\);
11 end for
12 for each \(\displaystyle (p,q) \in (T \times T) \cup ((S \backslash T) \times (S \backslash T))\) do
13 flag\(\displaystyle \leftarrow\)false
14 for each \(\displaystyle a \in A\) do
15 if zaznaczone\(\displaystyle [f(p,a),f(q,a)]=1\) then
16 flag\(\displaystyle \leftarrow\)true;
17 end if
18 end for
19 if flag=true then
20 OZNACZ\(\displaystyle (p,q)\); \(\displaystyle \triangleright\) para \(\displaystyle (f(p,a),f(q,a))\) była oznaczona dla pewnego \(\displaystyle a\);
21 else
22 for each \(\displaystyle a \in A\) do
23 if \(\displaystyle f(p,a)\neq f(q,a)\) then
24 włóż\(\displaystyle (\mathcal{L}[p,q],(f(p,a),f(q,a)))\);
25 end if
26 end for
27 end if
28 end for
29 \(\displaystyle S' \leftarrow S \slash_\equiv\); \(\displaystyle \triangleright\) relacja \(\displaystyle \equiv\) jest dopełnieniem tabeli zaznaczone
30 for each \(\displaystyle [s]_{ \equiv} \in S \slash_\equiv\) do
31 for each \(\displaystyle a \in A\) do
32 \(\displaystyle f'([s]_{\equiv},a) \leftarrow [f(s,a)]_{\equiv}\);
33 end for
34 end for
35 \(\displaystyle s_0' \leftarrow [s_0]_{\equiv}\);
36 \(\displaystyle T' \leftarrow \{[t]_{\equiv}:\ t \in T\}\);
37 return \(\displaystyle \mathcal{A}'=(S', A, f', s_0', T')\);
Występujaca w algorytmie procedura Oznacz opisana jest poniżej.
Algorytm
1 procedure OZNACZ\(\displaystyle (p,q \in S)\)
2 if zaznaczone\(\displaystyle [p,q]=1\)
3 return
4 end if
5 zaznaczone\(\displaystyle [p,q]\leftarrow 1\)
6 while not empty\(\displaystyle (\mathcal{L}[p,q])\) do
7 OZNACZ(zdejmij\(\displaystyle (\mathcal{L}[p,q]))\)
8 end while
9 end procedure
Działanie algorytmu łatwo przedstawić na tabelce, która złożona jest z kwadratów - pól, odpowiadających parom stanów automatu. Fakt znalezienia przez algorytm pary stanów rozróżnialnych zaznaczamy symbolem "x" w polu tabelki odpowiadającym tej parze, co wykorzystamy w przykładzie.
Przykład 1.4.
Zminimalizujemy automat przedstawiony na rysunku 4, używając algorytmu Minimalizuj3.
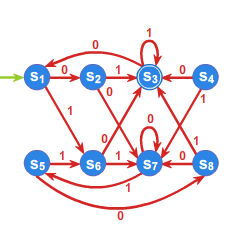
Proces działania algorytmu i konstrukcji tabelki przedstawiony jest na poniższej animacji 1.
Wypełniona tabelka po zakończeniu działania algorytmu przedstawiona jest na rysunku 5.
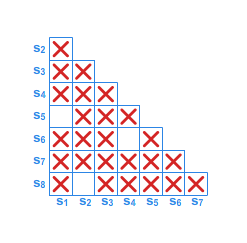
Z tabelki odczytujemy, że stanami równoważnymi są stany \(\displaystyle s_1, s_5\), stany \(\displaystyle s_2, s_8\) oraz stany \(\displaystyle s_4, s_6\). Automat minimalny przedstawiony jest na rysunku 6.
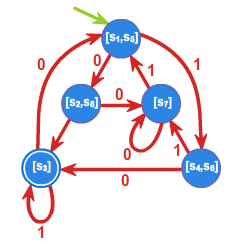
Automat niedeterministyczny. Lemat o pompowaniu
W tym wykładzie zdefiniujemy automat niedeterministyczny, udowodnimy jego równoważność z automatem deterministycznym oraz podamy algorytm konstrukcji równoważnego automatu deterministycznego. Wprowadzimy także automaty niedeterministyczne z pustymi przejściami. W ostatniej części wykładu sformułujemy lemat o pompowaniu dla języków rozpoznawanych przez automaty skończenie stanowe.
Automat niedeterministyczny
Wprowadzony wcześniej automat jest modelem obliczeń, czy też mówiąc ogólniej, modelem procesu o bardzo prostym opisie. Stan procesu zmienia się w sposób jednoznaczny pod wpływem sygnału zewnętrznego reprezentowanego przez literę alfabetu. Opisem tych zmian jest więc funkcja. Pewnym uogólnieniem powyższej sytuacji może być dopuszczenie relacji, która opisuje zmiany stanu. W efekcie opis zmiany stanów staje się niedeterministyczny w tym sensie, że z danego stanu automat przechodzi w pewien zbiór stanów. Jak udowodnimy pó{z}niej, z punktu widzenia rozpoznawania lub poprawnych obliczeń, takie uogólnienie nie rozszerza klasy języków rozpoznawanych przez automaty.
Definicja 1.1.
Automatem niedeterministycznym nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,f),\) w którym \(\displaystyle S\) jest dowolnym zbiorem, zwanym zbiorem stanów, a \(\displaystyle f: S \times A \rightarrow \displaystyle \mathcal{P}(S)\) funkcją przejść.
Funkcję przejść rozszerzamy do funkcji \(\displaystyle f: S \times A^* \rightarrow\displaystyle \mathcal{P}(S)\) określonej na całym wolnym monoidzie \(\displaystyle A^*\) w następujący sposób:
dla każdego \(\displaystyle s \in S \;\;\;f(s,1) = \{ s\},\)
dla każdego \(\displaystyle s \in S, \;\; a \in A\) oraz dowolnego \(\displaystyle w \in A^* \;\;\; f(s,wa)=f(f(s,w),a) .\)
Zwróćmy uwagę, że prawa strona ostatniej równości to obraz przez funkcję \(\displaystyle f\) zbioru \(\displaystyle f(s,w)\) i litery \(\displaystyle a\). Funkcję przejść automatu niedeterministycznego można także traktować jako relację
W związku z powyższą definicją automat wprowadzony wcześniej, w wykładzie 3, będziemy nazywać automatem deterministycznym.
Definicja 1.2.
Język \(\displaystyle L\subset A^{*}\) jest rozpoznawalny przez automat niedeterministyczny \(\displaystyle \mathcal{A}_{ND} \displaystyle =(S,f)\) wtedy i tylko wtedy, gdy istnieje \(\displaystyle I \subset S\) -- zbiór stanów początkowych oraz \(\displaystyle F \subset S\) - zbiór stanów końcowych taki, że
Niedeterministyczny automat rozpoznający język \(\displaystyle L\) będziemy oznaczać jako system \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,A,f,I,F)\) lub \(\displaystyle \mathcal{A}_{ND}=(S,f,I,F),\) jeśli wiadomo, nad jakim alfabetem określono automat.
Na pierwszy rzut oka mogłoby się wydawać, że wprowadzony automat istotnie rozszerza możliwości automatu deterministycznego, że jego moc obliczeniowa jest istotnie większa. Okazuje się jednak, że z punktu widzenia rozpoznawania języków, czyli właśnie z punktu widzenia mocy obliczeniowej, automaty deterministyczne i niedeterministyczne są równoważne.
Twierdzenie 1.1.
Język \(\displaystyle L \subset A^*\) jest rozpoznawany przez automat deterministyczny wtedy i tylko wtedy, gdy jest rozpoznawany przez automat niedeterministyczny.
Dowód
Rozpocznijmy dowód od oczywistej obserwacji. Zauważmy, iż każdy automat deterministyczny można przekształcić w niedeterministyczny, modyfikując funkcję przejść w ten sposób, że jej wartościami są zbiory jednoelementowe. Modyfikacja ta prowadzi w konsekwencji do równoważnego automatu niedeterministycznego.
Dla dowodu implikacji w stronę przeciwną załóżmy, że język \(\displaystyle L=L(\mathcal{A}_{ND})\) , gdzie \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,f,I,F)\), jest automatem niedeterministycznym. Określamy teraz równoważny, jak się okaże, automat deterministyczny. Jako zbiór stanów przyjmujemy \(\displaystyle \mathcal{P}(S)\) , czyli ogół podzbiorów zbioru \(\displaystyle S\). Funkcję przejść \(\displaystyle \overline{f}:\mathcal{P}(S)\times A^{*}\longrightarrow \mathcal{P}(S)\) określamy kładąc dla dowolnego stanu \(\displaystyle S_1 \in\displaystyle \mathcal{P}(S)\) oraz dowolnej litery \(\displaystyle a \in A\)
a następnie rozszerzamy ją do \(\displaystyle A^{*}\) . Łatwo sprawdzić, że funkcja \(\displaystyle \overline{f}\) spełnia warunki funkcji przejść. Przyjmując następnie zbiór \(\displaystyle I \in \displaystyle \mathcal{P}(S)\) jako stan początkowy oraz zbiór \(\displaystyle T=\left\{ \mathcal{S}_{1}\in \mathcal{P}(S)\, :\, S_{1}\cap F\neq \emptyset \right\}\) , jako zbiór stanów końcowych stwierdzamy, dla określonego automatu \(\displaystyle \mathcal{A}_{D}=\left( \mathcal{P}(S),\overline{f},I,T\right)\) , równość
Skonstruowany automat jest zatem deterministyczny i równoważny wyjściowemu, co kończy dowód twierdzenia.
Uwaga 1.1.
Dla określonego w dowodzie automatu \(\displaystyle \mathcal{A}_{D}\) na ogół nie wszystkie stany są osiągalne ze stanu \(\displaystyle I\). Aby uniknąć takich stanów, które są bezużyteczne, funkcję przejść należy zacząć definiować od stanu \(\displaystyle I\) i kolejno określać wartości dla już osiągniętych stanów.
Przykład 1.1.
Automat \(\displaystyle \mathcal{A}_{ND} \displaystyle = (Q,A,f,I,F)\) nad alfabetem \(\displaystyle A=\{a,b\}\) określony przez zbiory \(\displaystyle Q=\{q_{0},q_{1},q_{2},q_4\} , I=\{q_0\}, F=\{q_{3}\}\) i
zadany poniższym grafem jest przykładem automatu niedeterministycznego.
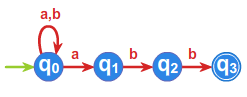
Automat ten, jak łatwo teraz zauważyć, rozpoznaje język \(\displaystyle L(\mathcal{A})=A^*abb\) .
Przedstawimy teraz algorytm, który mając na wejściu automat niedeterministyczny konstruuje równoważny automat deterministyczny.
Algorytm Determinizacja - buduje deterministyczny automat równoważny automatowi niedeterministycznemu
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat niedeterministyczny.
2 Wyjście: \(\displaystyle \mathcal{A}'=(S', A, f', s_0', T')\) - automat deterministyczny taki,
że \(\displaystyle L(\mathcal{A}')=L(\mathcal{A})\).
3 \(\displaystyle S' \leftarrow \{\{s_0\}\}\);
4 \(\displaystyle s_0' \leftarrow \{s_0\}\);
5 \(\displaystyle \mathcal{L} \leftarrow \{\{s_0\}\}\); \(\displaystyle \triangleright\displaystyle \mathcal{L}\) jest kolejką
6 while \(\displaystyle \mathcal{L} \not = \mbox{\O}\) do
7 \(\displaystyle M \leftarrow\) zdejmij \((\mathcal{L})\);
8 if \(\displaystyle T \cap M \not = \mbox{\O}\) then \(\displaystyle T' \leftarrow T' \cup \{M\}\);
9 for each \(\displaystyle a \in A\\) do
10 \(\displaystyle N \leftarrow \bigcup_{m \in M} f(m,a)\);
11 if \(\displaystyle N \not \in S'\\) then
12 \(\displaystyle S' \leftarrow S' \cup \{N\}\);
13 włóż \(\displaystyle (\mathcal{L},N)\);
14 end if
15 \(\displaystyle f'(M, a) \leftarrow N\);
16 end for
17 end while
18 return \(\displaystyle \mathcal{A}'\);
Funkcja zdejmij, występująca w linii 7., zdejmuje z kolejki element znajdujący się na jej początku i zwraca go jako swoją wartość. Procedura włóż\(\displaystyle (\mathcal{L},N)\) z linii 13. wstawia na koniec kolejki \(\displaystyle \mathcal{L}\) element \(\displaystyle N\).
Należy zauważyć, że algorytm determinizujący automat jest algorytmem eksponencjalnym. Stany wyjściowego automatu eterministycznego etykietowane są podzbiorami zbioru stanów \(\displaystyle Q\). Jeśli pewien stan \(\displaystyle q' \in Q'\) etykietowany jest zbiorem zawierającym stan końcowy z \(\displaystyle F\), to \(\displaystyle q'\) staje się stanem końcowym w automacie \(\displaystyle \mathcal{A}'\).
Z analizy algorytmu Determinacja wynika, że w ogólności zbiór stanów wyjściowego automatu deterministycznego może osiągać wartość rzędu \(\displaystyle O(2^n)\), gdzie \(\displaystyle n\) jest ilością stanów automatu niedeterministycznego.
Zastosujemy powyższy algorytm do uzyskania automatu deterministycznego równoważnego automatowi z przykładu 1.1. (patrz przykład 1.1.) Kolejne etapy działania ilustruje zamieszczona tu animacja 1.
Automaty niedeterministyczne z przejściami pustymi
Rozszerzenie definicji automatu skończenie stanowego do automatu niedeterministycznego nie spowodowało, jak wiemy, zwiększenia mocy obliczeniowej takich modeli. Nasuwać się może pytanie, czy dołączenie do tego ostatniego modelu możliwości wewnętrznej zmiany stanu, zmiany stanu bez ingerencji sygnału zewnetrznego, czyli bez czytania litery nie zwiększy rodziny jezyków rozpoznawanych.
Model taki, zwany automatem z pustymi przejściami (w skrócie: automat z p-przejściami), zdefiniujemy poniżej.
Definicja 2.1.
Automatem niedeterministycznym z pustymi przejściami nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,f),\) w którym \(\displaystyle S\) jest dowolnym zbiorem, zwanym zbiorem stanów, a \(\displaystyle f: S \times (A \cup \{1\}) \rightarrow \displaystyle \mathcal{P}(S)\) funkcją przejść.
Uwaga 2.1.
Słowo puste \(\displaystyle 1\) występuje w powyższej definicji w dwóch rolach. Pierwsza, to znana nam rola elementu neutralnego katenacji słów. Druga, to rola jakby "dodatkowej" litery, która może powodować zmianę aktualnego stanu automatu na inny. Ponieważ słowo puste może wystąpić przed i po każdej literze dowolnego słowa \(\displaystyle w \in A^*\) (i to wielokrotnie), dlatego też czytając słowo \(\displaystyle w\), automat zmienia stany zgodnie nie tylko z sekwencją liter tego słowa, ale także z uwzględnieniem tej drugiej roli słowa pustego.
Rozszerzając powyższą definicję poprzez dodanie zbioru stanów początkowych i zbioru stanów końcowych, uzyskamy niedeterministyczny automat z pustymi przejściami \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,A,f,I,F),\) dla którego będziemy mogli zdefiniować język rozpoznawany. W tym celu określimy najpierw działanie takiego automatu pod wpływem dowolnego słowa \(\displaystyle w \in A^*\). Jeśli \(\displaystyle s \in S\) oraz \(\displaystyle w=a \in A\), to
Zwróćmy uwagę, iż zbiór określający wartość rozszerzonej funkcji jest skończony i efektywnie obliczalny, bo zbiór stanów automatu jest skończony. Jeśli teraz \(\displaystyle s \in S\) oraz \(\displaystyle w=ua \in A\), to
Stany ze zbioru \(\displaystyle f(s,w)\) będziemy nazywać stanami osiągalnymi z \(\displaystyle s\) pod wpływem słowa \(\displaystyle w\). Prawdziwe jest następujące twierdzenie, które orzeka, iż z punktu widzenia rozpoznawania automaty niedeterministyczne z pustymi przejściami rozpoznają dokładnie te same języki, co automaty niedeterministyczne.
Twierdzenie 2.1.
Język \(\displaystyle L \subset A^*\) jest rozpoznawany przez automat niedeterministyczny z pustymi przejściami wtedy i tylko wtedy, gdy jest rozpoznawany przez automat niedeterministyczny.
Dowód
(szkic) Fakt, że język \(\displaystyle L\) rozpoznawany przez automat niedeterministyczny jest rozpoznawany przez automat niedeterministyczny z pustymi przejściami jest oczywisty.
Dowód implikacji w drugą stronę polega na takiej modyfikacji automatu niedeterministycznego z pustymi przejściami rozpoznającego jezyk \(\displaystyle L\), by uzyskać automat bez pustych przejść i nie ograniczyć ani nie zwiększyć jego możliwości rozpoznawania. Zarysujemy ideę tej konstrukcji. Niech \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,A,f,I,F),\) będzie automatem niedeterministycznym z pustymi przejściami akceptującym język \(\displaystyle L\). W konstruowanym automacie pozostawiamy zbiór stanów i zbiór stanów początkowych \(\displaystyle I\) bez zmian. Jeśli z któregoś ze stanów początkowych z \(\displaystyle I\) jest możliwość osiągnięcia jakiegoś stanu końcowego z \(\displaystyle F\), to dodajemy stan początkowy do zbioru stanów końcowych, czyli zbiór stanów końcowych w konstruowanym automacie ma postać \(\displaystyle F \cup I\). Jeśli nie ma takiej możliwości, to zbiór stanów końcowych pozostaje niezmieniony. Określamy wartość funkcji przejść dla dowolnego stanu \(\displaystyle s \in S\) i litery \(\displaystyle a \in A\) jako zbiór wszystkich stanów osiągalnych ze stanu \(\displaystyle s\) pod wpływem \(\displaystyle a\). Tak skonstruowany automat niedeterministyczny nie ma pustych przejść i jak można wykazać, indukcyjnie ze względu na długość słowa, rozpoznaje dokładnie język \(\displaystyle L\).
Algorytm usuwania przejść pustych i prowadzący do równoważnego automatu niedeterministycznego przedstawiony jest w ćwiczeniach do tego wykładu.
Lemat o pompowaniu
Jedną z wielu własności języków rozpoznawanych przez automaty skończone, i chyba jedną z najważniejszych, przedstawia prezentowane poniżej twierdzenie, zwane tradycyjnie w literaturze lematem o pompowaniu. Istota własności "pompowania" polega na tym, iż automat, mając skończoną ilość stanów, czytając i rozpoznając słowa dostatecznie długie, wykorzystuje w swoim działaniu pętlę, czyli powraca do stanu, w którym znajdował się wcześniej. Przez taką pętlę automat może przechodzić wielokrotnie, a co za tym idzie, "pompować" rozpoznawane słowo, prowadzając do niego wielokrotnie powtarzane podsłowo odpowiadające tej pętli.
Twierdzenie 3.1. (Lemat o pompowaniu)
Niech \(\displaystyle L \subset A^*\) będzie językiem rozpoznawalnym. Istnieje liczba naturalna \(\displaystyle N \geq 1\) taka, że dowolne słowo \(\displaystyle { w} \in L\) o długości \(\displaystyle \mid { w} \mid \geq N\) można rozłożyć na katenację \(\displaystyle { w} = { v}_1 { u v}_2,\) gdzie \(\displaystyle { v}_1 , { v}_2 \in A^*, { u}\in A^+\), \(\displaystyle \mid {v_{1}u} \mid \leq N\) oraz
Dowód
Niech \(\displaystyle L=L(\mathcal{A})\) , gdzie \(\displaystyle \mathcal{A} \displaystyle =(S,A, f,s_0,T)\) jest deterministycznym automatem skończenie stanowym. Niech \(\displaystyle N = \#S\) i rozważmy dowolne słowo \(\displaystyle { w } = a_1....a_k \in L\) takie, że \(\displaystyle \mid { w} \mid \geq N\). Oznaczmy:
Słowo \(\displaystyle w\) jest akceptowane przez automat \(\displaystyle \mathcal{A}\) , więc \(\displaystyle s_k \in T.\) Ponieważ \(\displaystyle \#S = N\) oraz \(\displaystyle k = \mid { w} \mid \geq N\), to istnieją \(\displaystyle i,j\in \{1,...,N\}\), \(\displaystyle i< j\) takie, że \(\displaystyle s_i =s_j\).
Przyjmując teraz \(\displaystyle { v}_1 = a_1...a_i ,\;\;\; { v}_2 = a_{j+1}...a_k , \;\;\; { u} =a_{i+1}...a_j,\) dochodzimy do nastepującej konkluzji:
A to oznacza, że słowo \(\displaystyle v_{1}u^{k}v_{2}\) jest rozpoznawane przez automat \(\displaystyle \mathcal{A}\) dla dowolnej liczby \(\displaystyle k\geq 0\) , co kończy dowód. Nierówność \(\displaystyle \mid {v_{1}u} \mid \leq N\) wynika w oczywisty sposób z przyjętego na początku dowodu założenia, że \(\displaystyle N = \#S\).
Istotę dowodu przedstawia następująca animacja 2.
Wniosek 3.1.
Jeśli rozpoznawalny język \(\displaystyle L \subset A^*\) jest nieskończony, to istnieją słowa \(\displaystyle { v}_1 , { u}, { v}_2 \in A^*\) takie, że
Wniosek 3.2.
Jeśli rozpoznawalny język \(\displaystyle L \subset A^*\) nie jest zbiorem pustym, to istnieje słowo \(\displaystyle w\in L\) takie, że \(\displaystyle \mid w\mid <N\) , gdzie \(\displaystyle N\) jest stałą występującą w lemacie o pompowaniu.
Jeśli słowo \(\displaystyle w\in L\) i \(\displaystyle \mid w\mid \geq N\) , to zgodnie z lematem o pompowaniu możemy przedstawić słowo \(\displaystyle w\) jako \(\displaystyle w=v_{1}uv_{2}\) , gdzie \(\displaystyle u\neq 1\) oraz \(\displaystyle v_{1}u^{i}v_{2}\in L\) dla \(\displaystyle i=0,1,2\ldots\) . Przyjmując \(\displaystyle i=0\) , mamy \(\displaystyle v_{1}v_{2}\in L\) i \(\displaystyle \mid v_{1}v_{2}\mid <\mid w\mid\) . Powtarzając powyższy rozkład skończoną ilość razy, otrzymamy słowo należące do języka \(\displaystyle L\) , o długości mniejszej od \(\displaystyle N\) .
Lemat o pompowaniu wykorzystuje się najczęściej do uzasadnienia faktu, iż pewne języki nie są rozpoznawane przez automaty skończone. Przyjrzyjmy się bliżej technice takiego uzasadnienia.
Przykład 3.1.
Rozważmy język \(\displaystyle L = \{ a^n b^n : n \geq 0 \}\) nad alfabetem \(\displaystyle A = \{ a,b\}\). W oparciu o lemat o pompowaniu wykażemy, że język \(\displaystyle L\) nie jest rozpoznawany. Dla dowodu nie wprost, przypuszczamy, że \(\displaystyle L\) jest rozpoznawany. Na podstawie udowodnionego lematu istnieją zatem słowa \(\displaystyle { v}_1 , { u}, { v}_2 \in A^*\) takie, że \(\displaystyle { v}_1 u^* { v}_2 \subset L\) oraz \(\displaystyle { u} \neq 1.\) Biorąc pod uwagę formę słów języka \(\displaystyle L\) , wnioskujemy, że
- słowo \(\displaystyle { u}\) nie może składać się tylko z liter \(\displaystyle a\), gdyż słowo \(\displaystyle { v}_1 { u}^2 { v}_2\) zawierałoby więcej liter \(\displaystyle a\) niż \(\displaystyle b\),
- słowo \(\displaystyle { u}\) nie może składać się tylko z liter \(\displaystyle b\), gdyż słowo \(\displaystyle { v}_1 { u}^2 { v}_2\) zawierałoby więcej liter \(\displaystyle b\) niż \(\displaystyle a\),
- słowo \(\displaystyle { u}\) nie może składać się z liter \(\displaystyle a \; i \; b\), gdyż w słowie \(\displaystyle { v}_1 { u}^2 { v}_2\) litera \(\displaystyle b\) poprzedzałaby literę \(\displaystyle a\).
Ponieważ słowo \(\displaystyle { v}_1 { u}^2 { v}_2,\) należy do języka \(\displaystyle L\) , więc każdy z wyprowadzonych powyżej wniosków prowadzi do sprzeczności.
Twierdzenie Kleene'ego. Własności języków i gramatyk regularnych
W wykładzie udowodnimy twierdzenie Kleene'ego, które orzeka, że rodzina języków regularnych jest identyczna z rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Przedstawimy własności języków regularnych i gramatyk typu (3). Na koniec uzasadnimy, że rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3), są tożsame.
Twierdzenie Kleene
Wiemy już, z poprzednich wykładów, że rodzina wyrażeń regularnych określa rodzinę języków regularnych. Celem pierwszej części tego wykładu jest ustalenie związku pomiędzy rodziną języków regularnych a rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Twierdzenie, udowodnione przez S.C.Kleene'ego w roku 1956, orzeka, iż te dwie rodziny języków są identyczne.
Twierdzenie 1.1.
Dla dowolnego skończonego alfabetu \(\displaystyle A\)
Dowód
Dowód pierwszej części twierdzenia, czyli inkluzja \(\displaystyle \mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})\) , będzie
prowadzony zgodnie ze strukturą definicji rodziny języków regularnych \(\displaystyle \mathcal{REG}(A^{*})\) .
1. Język pusty \(\displaystyle \emptyset\) jest rozpoznawany przez dowolny automat \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,s_0,T),\) w którym zbiór stanów końcowych \(\displaystyle T\) jest pusty.
2. Język a złożony z dowolnej litery \(\displaystyle a \in A\) jest rozpoznawany przez automat

Dla dalszej części dowodu ustalmy, iż dane są języki \(\displaystyle L_1, L_2\) rozpoznawane odpowiednio przez automaty deterministyczne \(\displaystyle \mathcal{A}_{i} \displaystyle = (S_i,f_i,{s_0}^i,T_i)\), gdzie \(\displaystyle i=1,2.\)
3. Sumę mnogościową języków \(\displaystyle L_1, L_2\), czyli język \(\displaystyle L = L_1 \cup L_2\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,{s_0},T)\), dla którego \(\displaystyle S = S_1 \times S_2\), \(\displaystyle s_0 = ({s_0}^1,{s_0}^2)\), \(\displaystyle \: \displaystyle T = T_1 \times S_2\; \cup \;S_1 \times T_2\) oraz dla dowolnego stanu \(\displaystyle (s_{1},s_{2})\in S\) i litery \(\displaystyle a\in A\) funkcja przejść określona jest równością
4. Katenację języków \(\displaystyle L_1, L_2\), czyli język \(\displaystyle L = L_1 \cdot L_2\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,{s_0},T)\), dla którego \(\displaystyle S=S_{1}\times \mathcal{P}(S_{2}),\quad s_{0}=\left( s_{0}^{1},\emptyset \right)\) oraz dla dowolnego stanu \(\displaystyle (s_1,S'_2) \in S\) i litery \(\displaystyle a\in A\) funkcja przejść określona jest następująco:
a zbiorem stanów końcowych jest
5. Załóżmy, że język \(\displaystyle L\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\). Określimy automat niedeterministyczny, który będzie rozpoznawał gwiazdkę Kleene języka \(\displaystyle L\), czyli \(\displaystyle L^*.\) Automat niedeterministyczny \(\displaystyle \mathcal{A}' \displaystyle =(S,f',\{ s_0\},T)\), w którym
rozpoznaje język język \(\displaystyle L^+.\) Dowód tego faktu jest indukcyjny i pozostawiamy go na ćwiczenia. Zauważmy teraz, że język \(\displaystyle \{1\}\) rozpoznaje automat

Ponieważ \(\displaystyle L^{*}=L^{+}\cup \left\{ 1\right\}\) , to korzystając z udowodnionej już zamkniętości języków rozpoznawanych
ze względu na sumę mnogościową, stwierdzamy, że istnieje automat rozpoznający język \(\displaystyle L^*\).
Zatem dowód inkluzji \(\displaystyle \mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})\) jest zakończony.
Przejdziemy teraz do dowodu inkluzji \(\displaystyle \mathcal{REG}(A^{*})\supseteq \mathcal{RE}C(A^{*})\) .
Niech \(\displaystyle L\) oznacza dowolny język rozpoznawany przez automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,s_0,T).\) Dowód polega na rozbiciu języka \(\displaystyle L\) na fragmenty, dla których stwierdzenie, że są to języki regularne będzie dość oczywiste. Natomiast sam język \(\displaystyle L\) będzie wynikiem operacji regularnych określonych na tych właśnie fragmentach. Poniżej przeprowadzamy defragmentację języka \(\displaystyle L.\)
Dla \(\displaystyle s,t \in S\) niech
Jest to język złożony ze słów, które przeprowadzają stan \(\displaystyle s\) automatu \(\displaystyle \mathcal{A}\) w stan \(\displaystyle t\) . Ogół liter alfabetu \(\displaystyle A\) przeprowadzających stan \(\displaystyle s\) w \(\displaystyle t\) oznaczymy przez
Dla stanów \(\displaystyle s,t \in S\) i zbioru \(\displaystyle S_1 \subseteq S\) niech
Jest to język, który można przedstawić graficznie następująco:

Na koniec przyjmijmy
określony dla \(\displaystyle S_2 \subseteq S\) i \(\displaystyle s,t \in S - S_2\)
Język ten jest graficznie interpretowany poniżej.

Wprost z określeń wynika, że wszystkie wprowadzone powyżej języki są regularne, czyli należą do rodziny \(\displaystyle \mathcal{REG}(A^{*})\) . Dowód tego faktu przebiega indukcyjnie ze względu na liczbę elementów zbiorów \(\displaystyle S_1\) i \(\displaystyle S_2\). Szczegóły tego dowodu pominiemy. Natomiast warto wskazać rolę, jaką spełniają w dowodzie wprowadzone wyżej języki. A mianowicie:
Tę ostatnią równość przedstawia poniższy rysunek.

co graficznie można przedstawić następująco:

Dochodzimy więc do konkluzji, iż jezyki \(\displaystyle L(s,S_{1},t)\) oraz \(\displaystyle \overline{L}(s,S_{2},t)\) są regularne.
W szczególności zatem regularny jest język \(\displaystyle L(s_{0},S,t)=L(s_{0},t)\).
Język \(\displaystyle L\) możemy przedstawić w następującej postaci:
co w połączeniu z ustaleniami punktu 3 z poprzedniej części dowodu uzasadnia tezę, że język \(\displaystyle L\) należy do rodziny \(\displaystyle \mathcal{REG}(A^{*})\).
Własności języków regularnych i gramatyk regularnych
W tej części wykładu omówimy własności rodziny języków i gramatyk regularnych, czyli typu (3) w hierarchii Chomsky'ego. Ustalimy też
związek pomiędzy językami a gramatykami regularnymi. Zbadamy zamkniętość rodziny języków regularnych ze względu na operacje mnogościowe, czyli ze względu na sumę, przecięcie, różnicę i uzupełnienie. Rozpoczniemy jednak tę część wykładu od wprowadzenia jednoargumentowego działania na słowach zwanego odbiciem zwierciadlanym.
Definicja 2.1.
Odbiciem zwierciadlanym słowa \(\displaystyle w = a_1 \ldots a_n \in A^*\) nazywamy słowo \(\displaystyle \stackrel{\leftarrow}{w} = a_n \ldots a_1\). Odbiciem zwierciadlanym języka \(\displaystyle L \subset A^*\) nazywamy język \(\displaystyle \stackrel{\leftarrow}{L} = \{ \stackrel{\leftarrow}{w} \in A^* \; : \; w \in L \}.\)
Twierdzenie 2.1.
Rodzina \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})\) jest zamknięta ze względu na:
- (1) sumę mnogościową, przecięcie, różnicę i uzupełnienie,
- (2) katenację i operację iteracji \(\displaystyle "*" ,\)
- (3) obraz homomorficzny,
- (4) podstawienie regularne,
- (5) przeciwobraz homomorficzny,
- (6) odbicie zwierciadlane.
Dowód
1. Zamkniętość rodziny języków \(\displaystyle \mathcal{REG}(A^{*})\) ze względu na sumę mnogościową wynika z twierdzenia Kleene'ego. Automat akceptujący iloczyn języków otrzymujemy, zmieniając odpowiednio zbiór stanów końcowych w automacie rozpoznającym sumę. Bowiem pozostając przy oznaczeniach punktu 3 z dowodu twierdzenia Kleene'ego, automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,{s_0},F),\) gdzie \(\displaystyle F = T_1 \times T_2\), rozpoznaje język \(\displaystyle L_1 \cap L_2.\) Jeśli automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\) akceptuje język \(\displaystyle L\), to automat \(\displaystyle \overline{\mathcal{A}} \displaystyle =(S,f,s_0,S\backslash T)\) akceptuje język \(\displaystyle \overline{L}=A^{*}\setminus L.\) Ostatnia własność implikuje zamkniętość ze względu na uzupełnienie.
2 Z twierdzenia Kleene'ego, punkt 4 i 5, wynika zamkniętość ze względu na katenację i operację iteracji \(\displaystyle "*"\).
3. Niech \(\displaystyle h: A^* \longrightarrow B^*\) będzie homomorfizmem. Dowód implikacji
przeprowadzimy zgodnie ze strukturą definicji rodziny języków regularnych. Dla \(\displaystyle L=\emptyset\) i dla \(\displaystyle L=\{a\}\)
gdzie \(\displaystyle a\) jest dowolną literą alfabetu \(\displaystyle A\) , implikacja jest oczywista. W pierwszym przypadku obrazem homomorficznym jest język pusty, a w drugim język \(\displaystyle \{w\}\) , gdzie \(\displaystyle w\) jest pewnym słowem nad alfabetem \(\displaystyle B\) . Dla dowolnych języków regularnych \(\displaystyle X, Y \in\displaystyle \mathcal{REG}(A^{*})\) prawdziwe są równości:
- \(\displaystyle h( X \cup Y)=h(X) \cup h(Y) \in\displaystyle \mathcal{REG}(B^{*})\) ,
- \(\displaystyle h( X \cdot Y) = h(X) \cdot h(Y) \in\displaystyle \mathcal{REG}(B^{*})\) ,
- \(\displaystyle {\displaystyle h(X^*)=h( \bigcup_{n=0} ^\infty X^n) = \bigcup_{n=0} ^\infty (h(X))^n = (h(X))^* \in}\displaystyle \mathcal{REG}(B^{*}),\)
co kończy dowód tego punktu.
4. Uzasadnienie jest podobne jak dla homomorfizmu. Jedyna różnica tkwi w tym, że dla podstawienia regularnego \(\displaystyle s:A^{*}\longrightarrow \mathcal{P}(B^{*})\) i dla dowolnej litery \(\displaystyle a \in A\) wartość podstawienia na literze jest pewnym językiem regularnym \(\displaystyle s(a)=L\in \mathcal{REG}(B^{*})\) , a nie słowem jak w przypadku homomorfizmu.
5. Niech \(\displaystyle h: A^* \longrightarrow B^*\) będzie homomorfizmem. Aby udowodnić implikację
odwołamy się do własności, że dla języka \(\displaystyle L \in\displaystyle \mathcal{REG}(B^{*})\) istnieje skończony monoid \(\displaystyle \; M \;\) i homomorfizm \(\displaystyle \varphi : B^* \longrightarrow M\) taki, że \(\displaystyle L = \varphi^{-1}(\varphi (L)).\) Dla
homomorfizmu \(\displaystyle \varphi \circ h : A^* \longrightarrow M\) mamy równość:
Korzystając teraz z punktu 4 twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2. wykład 3), wnioskujemy, że
\(\displaystyle h^{-1}(L) \in\displaystyle \mathcal{REG}(A^{*})\) .
6. Wykorzystamy tutaj zapis języka regularnego przez wyrażenie regularne. Niech dla języka \(\displaystyle L \in\displaystyle \mathcal{REG}(A^{*})\) wyrażenie regularne \(\displaystyle \alpha \in \mathcal{WR}\) będzie takie, że \(\displaystyle L = \mid {\bf \alpha} \mid\). Wtedy język \(\displaystyle \stackrel{\leftarrow}{L}\) jest opisany przez wyrażenie regularne \(\displaystyle \stackrel{\leftarrow}{\bf \alpha}\), które uzyskujemy z \(\displaystyle {\bf \alpha}\) przez odbicie zwierciadlane, a dokładniej odwrócenie kolejności katenacji w każdej sekwencji tego działania występującej w wyrażeniu regularnym.
W wykładzie drugim wprowadziliśmy pojęcie gramatyki. Wracamy do tego pojęcia, a w szczególności do gramatyki typu (3), czyli regularnej. Przypomnijmy, że produkcje takiej gramatyki \(\displaystyle G=(V_N ,V_T ,v_0 ,P )\) mają postać:
gdzie \(\displaystyle v,v' \in V_N , \; x \in {V_T}^*\). Gramatykę typu (3), nazywamy inaczej lewostronną lub lewoliniową. Określa się też gramatykę regularną prawostronną (prawoliniową). Jest to gramatyka \(\displaystyle G=(V_N ,V_T ,v _0 ,P)\), której produkcje są postaci:
gdzie \(\displaystyle v,v' \in V_N , \; x \in {V_T}^*\). Jeśli język \(\displaystyle L=L(G)\) jest generowany przez gramatykę typu (3) (lewoliniową), to jego odbiciem zwierciadlanym jest \(\displaystyle \stackrel{\leftarrow}{L} =L ( \stackrel{\leftarrow}{G})\), gdzie \(\displaystyle \stackrel{\leftarrow}{G}\) jest gramatyką prawoliniową, którą uzyskuje się z gramatyki \(\displaystyle G\) przez odbicie zwierciadlane prawych stron produkcji. Oznacza to, iż zmieniamy produkcje według następujących zasad:
Oczywiście, jeśli \(\displaystyle L\) jest językiem generowanym przez gramatykę prawoliniową, to \(\displaystyle \stackrel{\leftarrow}{L}\) jest
generowany przez odpowiednią gramatykę lewoliniową.
Podamy teraz charakterystykę rodziny języków regularnych \(\displaystyle \mathcal{REG}(A^{*})\) przez rodzinę gramatyk prawoliniowych.
Twierdzenie 2.2.
Niech \(\displaystyle L \subset A^*\). Język \(\displaystyle L \in\displaystyle \mathcal{REG}(A^{*})\) wtedy i tylko wtedy,
gdy \(\displaystyle L =L(G)\) dla pewnej gramatyki prawoliniowej \(\displaystyle G\).
Dowód
Załóżmy, że automat \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,s_0,T)\) rozpoznaje język \(\displaystyle L\) .
Definiujemy gramatykę \(\displaystyle G = (V_N , V_T , v_0 ,P)\) przyjmując \(\displaystyle V_N = S,\;\; V_T = A, \;\; v_0 = s_0\) oraz określając w następujący sposób zbiór produkcji
Dla dowolnego stanu \(\displaystyle s \in S\) i słowa \(\displaystyle w \in A^+\) prawdziwa jest równoważność
Dowód przeprowadzimy indukcyjnie ze względu na długość słowa \(\displaystyle w\). Niech \(\displaystyle w = a,\) dla pewnego \(\displaystyle a \in A\).
Z definicji zbioru produkcji \(\displaystyle P\) wynika równoważność
Rozważmy teraz \(\displaystyle w = a_1 \ldots a_n\) oraz \(\displaystyle s_0 \mapsto^* ws\). Z założenia indukcyjnego
wynika, że
oraz, że \(\displaystyle s = f(s' ,a_n )\) wtedy i tylko wtedy, gdy \(\displaystyle s' \mapsto a_n s .\) A więc fakt, że
\(\displaystyle s=f(s_{0},w)=f(s_{0},a_{1}\ldots a_{n})=f(f(s_{0},a_{1}\ldots a_{n-1}),a_{n})\) jest równoważny temu,
że \(\displaystyle s'=f(s_{0},a_{1}\ldots a_{n-1})\mapsto a_{n}s\) . A to z kolei równoważne jest
i ostatecznie równoważne faktowi, że \(\displaystyle s_{0}\mapsto ^{*}a_{1}\ldots a_{n-1}a_{n}s\) .
A zatem dowodzona równoważność jest prawdziwa dla \(\displaystyle w \in A^+\), ponieważ
Dla \(\displaystyle w=1\) mamy \(\displaystyle 1\in L(\mathcal{A})\: \Longleftrightarrow \: s_{0}\rightarrow 1\in P\: \Longleftrightarrow \: 1\in L(G),\) co kończy dowód w jedną stronę.
Rozważmy teraz język \(\displaystyle L = L(G)\) generowany przez pewna gramatykę prawoliniową \(\displaystyle G = (V_N , V_T , v_0 ,P)\). Skonstruujemy gramatykę równoważną \(\displaystyle G\) i taką, w której wszystkie produkcje są postaci \(\displaystyle v \rightarrow a v'\) lub \(\displaystyle v \rightarrow 1\), gdzie \(\displaystyle v,v' \in V_N , a \in A\). Będziemy zamieniać produkcje występujące w gramatyce \(\displaystyle G\) na inne, o żądanej postaci, zgodnie z następująmi zasadami:
1. Produkcje typu \(\displaystyle v \rightarrow v'\), gdzie \(\displaystyle v,v' \in V_N\)
Z symbolem nieterminalnym \(\displaystyle v \in V_N\) kojarzymy określony poniżej zbiór
oraz zbiór produkcji
Dla każdego takiego symbolu \(\displaystyle v \in V_N\) usuwamy ze zbioru \(\displaystyle P\) wszystkie produkcje
\(\displaystyle v \rightarrow v'\) i wprowadzamy na to miejsce wszystkie produkcje ze zbioru \(\displaystyle P(v)\).
2. Produkcje typu \(\displaystyle v \rightarrow x\) dla \(\displaystyle x \neq 1\).
Jeśli produkcja taka występuje w \(\displaystyle P\) i \(\displaystyle x \neq 1\), to do alfabetu nieterminalnego \(\displaystyle V_N\) dodajemy nowy symbol \(\displaystyle v_x\). Następnie ze zbioru \(\displaystyle P\) usuwamy powyższą produkcję i dodajemy dwie nowe:
Zauważmy, że jeśli \(\displaystyle x\neq y\), to \(\displaystyle v_x \neq v_y\).
3. Produkcje typu \(\displaystyle v \rightarrow x v'\) dla \(\displaystyle \mid x \mid > 1.\)
Jeśli \(\displaystyle v \rightarrow a_1 \ldots a_n v' \in P\), przy czym \(\displaystyle n \geq 2\), to do alfabetu
nieterminalnego \(\displaystyle V_N\) dodajemy nowe symbole \(\displaystyle v_1 , \ldots v_n\), produkcję \(\displaystyle v \rightarrow a_1 \ldots a_n v'\) usuwamy ze zbioru \(\displaystyle P\) i
dodajemy produkcje:
Po opisanych powyżej trzech modyfikacjach gramatyki \(\displaystyle G\) generowany język, co łatwo zauważyć, nie ulega zmianie. Zatem
skonstruowana gramatyka jest równoważna wyjściowej. Dla otrzymanej gramatyki określamy teraz automat niedeterministyczny \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,\{s_0\},T)\), przyjmując \(\displaystyle S= V_N\), \(\displaystyle A= V_T\) oraz \(\displaystyle s_0 = v_0\) i definiując następująco funkcję przejść: \(\displaystyle f(v,a) = \{ v' \in V_N \; : \; v \rightarrow av' \in P \}.\) Przjmując \(\displaystyle T = \{ v \in V_N \; : \; v \rightarrow 1 \in P \}\) jako zbiór stanów końcowych, stwierdzamy, że automat \(\displaystyle \mathcal{A}\) rozpoznaje język
Uzyskany rezultat, w świetle równości \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{RE}C(A^{*})\) , kończy dowód twierdzenia.
Algorytmiczną stroną równoważności udowodnionej w powyższym twierdzeniu zajmiemy się w następnym wykładzie. Przykłady ilustrujące twierdzenie zamieszczamy poniżej.
Przykład 2.1.
1. Niech \(\displaystyle \mathcal{A}=(S,A,f,s_0,T)\) będzie automatem takim, że
\(\displaystyle S=\{ s_0,s_1, s_2 \}, A=\{a,b\}, T=\{s_1\}\), a graf przejść wygląda następująco:
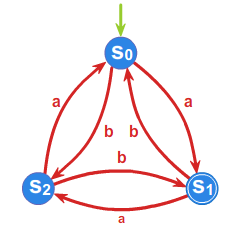
Gramatyka \(\displaystyle G=(S,A,s_0,P)\), gdzie
akceptuje język \(\displaystyle L(\mathcal{A})\).
Zauważmy, że język
2. Niech \(\displaystyle G=(\{v_0,v_1\},\{a,b\},v_0,P)\), gdzie
Gramatykę \(\displaystyle G\) przekształcamy w równoważną gramatykę
gdzie
Niedeterministyczny automat \(\displaystyle \mathcal{A}_{ND}=(\{v_0,v_1,v_2,v_b\},\{a,b\},f,v_0,\{v_1,v_b\})\), gdzie graf przejśc
wygląda następująco:

Wykorzystując udowodnione do tej pory własności rodziny języków generowanych przez gramatyki regularne, uzasadnimy teraz, iż ta
właśnie rodzina, czyli ogół języków typu (3) w hierarchii Chomsky'ego pokrywa się z rodziną \(\displaystyle \mathcal{REG}(A^{*})\) .
Twierdzenie 2.3.
Dla dowolnego alfabetu \(\displaystyle A\) rodziny języków regularnych \(\displaystyle A^{*}\) oraz języków generowanych przez gramatyki regularne są równe, czyli \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{L}_{3}\) .
Dowód
Odbicie zwierciadlane dowolnego języka \(\displaystyle L\in \mathcal{REG}(A^{*})\) , czyli język \(\displaystyle \overleftarrow{L}\) należy również do rodziny \(\displaystyle \mathcal{REG}(A^{*})\) , co oznacza, że \(\displaystyle \overleftarrow{L}\in \mathcal{RE}C(A^{*})\) .
Na podstawie twierdzenia 2.2. (patrz twierdzenie 2.2.) istnieje więc gramatyka prawoliniowa \(\displaystyle G\) taka, że \(\displaystyle \overleftarrow{L}=L(G)\) . A stąd wniosek, że \(\displaystyle L=\overleftarrow{\overleftarrow{L}}=L(\overline{G})\) dla pewnej gramatyki \(\displaystyle \overline{G}\) typu (3). Zatem \(\displaystyle L\in \mathcal{L}_{3}\) .
Rozważmy teraz język \(\displaystyle L\) typu (3), czyli \(\displaystyle L=L(G)\) dla pewnej gramatyki regularnej. A więc \(\displaystyle \overleftarrow{L}=L(\overline{G})\) dla pewnej gramatyki prawoliniowej i \(\displaystyle \overleftarrow{L}\in mathcal{RE}C(A^{*})\) . Z twierdzenia Kleene'ego wynika, że \(\displaystyle \overleftarrow{L}\in \mathcal{REG}(A^{*})\) i ostatecznie \(\displaystyle L=\overleftarrow{\overleftarrow{L}}\in \mathcal{REG}(A^{*})\) , co kończy dowód twierdzenia.
Zamkniemy rozważania następującą konkluzją podsumowującą główne rezultaty tego wykładu.
Dla dowolnego skończonego alfabetu \(\displaystyle A\) prawdziwe są równości:
czyli wprowadzone pojęcia rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3) są tożsame.
Dalsze algorytmy dla języków regularnych. Problemy rozstrzygalne
W tym wykładzie przedstawimy algorytmy konstrukcji gramatyki regularnej, automatu skończenie stanowego oraz wyrażeń regularnych opisujących ten sam język \(\displaystyle L\). Omówimy także problemy rozstrzygalne algorytmicznie w klasie języków regularnych.
Dalsze algorytmy języków regularnych
Dowód twierdzenia z ostatniego wykładu, w którym udowodniliśmy równoważność rozpoznawania języka \(\displaystyle L\) i generowania tego języka przez gramatykę regularną daje podstawę do określenia dwóch algorytmów. Algorytmu konstruującego automat skończony w oparciu o daną gramatykę regularną i oczywiście akceptujący język generowany przez tę gramatykę oraz algorytmu budowy gramatyki regularnej dla zadanego automatu. Bez utraty ogólności przyjmujemy, że automat jest deterministyczny.
Idea działania algorytmu Automat2GReg jest następująca: każdy symbol nieterminalny \(\displaystyle v\) tworzonej gramatyki odpowiada pewnemu stanowi \(\displaystyle s_v\) automatu. Jeśli w automacie pod wpływem litery \(\displaystyle a\) następuje przejście ze stanu \(\displaystyle s_v\) do stanu \(\displaystyle s_w\), to do zbioru praw gramatyki dodawane jest prawo \(\displaystyle s_v \rightarrow as_w\). Ponadto, jeśli stan \(\displaystyle s_w\) jest stanem końcowym, to dodajemy także prawo \(\displaystyle s_w \rightarrow 1\), aby w danym miejscu wywód słowa mógł zostać zakończony.
Algorytm Automat2GReg - buduje gramatykę regularną dla zadanego automatu skończonego.
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat niedeterministyczny.
2 Wyjście: \(\displaystyle G=(V_N, V_T, P, v_0)\) - gramatyka regularna taka, że \(\displaystyle L(G)=L(\mathcal{A})\).
3 \(\displaystyle V_N \leftarrow \{v_0,v_1,...,v_{|S|-1}\}\);
4 \(\displaystyle V_T \leftarrow A\);
5 \(\displaystyle v_0 \leftarrow s_0\);
6 \(\displaystyle P \leftarrow \emptyset\);
7 for each \(\displaystyle s_i\in S\) do
8 for each \(\displaystyle a\in A\) do
9 if \(\displaystyle f(s_i,a)\neq\)NULL then
10 \(\displaystyle s_j \leftarrow f(s_i,a)\); \(\displaystyle \triangleright\) funkcja \(\displaystyle f\) jest określona na \(\displaystyle (s_i,a)\)
11 \(\displaystyle P \leftarrow P \cup \{s_i \rightarrow as_j\}\);
12 if \(\displaystyle s_j \in T\) then
13 \(\displaystyle P \leftarrow P \cup \{s_j \rightarrow 1\}\);
14 end if
15 end if
16 end for
17 end for
18 return \(\displaystyle G\);
Oznaczmy przez \(\displaystyle E(\mathcal{A})\) ilość krawędzi w grafie \(\displaystyle n\)-stanowego automatu niedeterministycznego \(\displaystyle \mathcal{A}\). Złożoność czasowa liczona względem \(\displaystyle E(\mathcal{A})\) jest liniowa i równa \(\displaystyle O(E(\mathcal{A}))\). Również złożoność pamięciowa jest liniowa i wynosi \(\displaystyle O(|S|+E(\mathcal{A}))\).
Przykład 1.1
Niech dany będzie automat \(\displaystyle \mathcal{A}\) pokazany na rysunku 1. Zbudujemy gramatykę, która będzie generowała język akceptowany przez \(\displaystyle \mathcal{A}\).
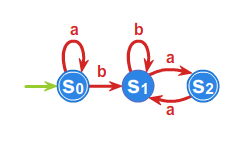
Ponieważ \(\displaystyle f(s_0,a)=s_0\), a ponadto \(\displaystyle s_0\) jest stanem końcowym, do \(\displaystyle P\) dodajemy produkcje \(\displaystyle v_0 \rightarrow av_0\) oraz \(\displaystyle v_0 \rightarrow 1\). Dodajemy także produkcję \(\displaystyle v_0 \rightarrow bv_1\), gdyż mamy \(\displaystyle f(s_0,b)=s_1\).
Fakt, że \(\displaystyle f(s_1,b)=s_1\) oraz \(\displaystyle f(s_1,a)=s_2\) sprawia, że do \(\displaystyle P\) dodajemy: \(\displaystyle v_1\ \rightarrow bv_1\), \(\displaystyle v_1 \rightarrow av_2\).
Ponieważ \(\displaystyle f(s_2, a)=s_1\) do \(\displaystyle P\) dodajemy: \(\displaystyle v_2 \rightarrow av_1\) oraz \(\displaystyle v_2 \rightarrow 1\), gdyż \(\displaystyle s_2 \in T\).
Symbolem początkowym nowej gramatyki jest symbol \(\displaystyle v_0\). Ostatecznie gramatyka ma postać:
Zwróćmy uwagę na wygodny zapis produkcji gramatyki, jaki został użyty powyżej. Produkcje o tej samej lewej stronie (wspólnym symbolu
nieterminalnym) zapisywane są razem, a prawe strony tych produkcji oddzielane są pionowymi kreskami.
Przedstawiony poniżej algorytm GReg2Automat konstruuje automat skończenie stanowy, akceptujący język generowany przez
zadaną gramatykę.
Zauważmy, że gramatyka podana na wejściu algorytmu nie może zawierać produkcji postaci \(\displaystyle v \rightarrow x\), gdzie \(\displaystyle v \in V_N\), \(\displaystyle x \in (V_N \cup V_T)\). Jeśli gramatyka zawiera takie produkcje, to możemy się ich łatwo pozbyć, zgodnie z Twierdzeniem 2.2 z Wykładu 7 (patrz twierdzenie 2.2 wykład 7), uzyskując oczywiście gramatykę równoważną.
Idea działania algorytmu jest podobna do poprzedniej - każdy tworzony stan automatu odpowiadać będzie pewnemu symbolowi nieterminalnemu gramatyki wejściowej. Zależnie od postaci produkcji gramatyki, niektóre stany będą stanami końcowymi.
Zapis \(\displaystyle f \leftarrow\displaystyle \emptyset\) w linii 7. symbolicznie oznacza, że funkcja przejść nie jest jeszcze określona.
W pętli 8.-15. pozbywamy się produkcji, w których występuje więcej niż jeden terminal; każdą taką produkcję "rozbijamy" na sekwencję
produkcji postaci \(\displaystyle v \rightarrow aw\), gdzie \(\displaystyle v,w \in V_N,\ a \in V_T\).
Algorytm GReg2Automat - buduje automat dla zadanej gramatyki regularnej.
1 Wejście: \(\displaystyle G=(V_N, V_T, P, v_0)\) - gramatyka regularna.
2 Wyjście: \(\displaystyle \mathcal{A}=(S, A, f, v_0, T)\) - automat taki, że \(\displaystyle L(\mathcal{A})=L(G)\).
3 \(\displaystyle S \leftarrow\displaystyle V_N\);
4 \(\displaystyle A \leftarrow V_T\);
5 \(\displaystyle T \leftarrow \emptyset\); \(\displaystyle \triangleright\) nie ma jeszcze stanów końcowych
6 \(\displaystyle s_0 \leftarrow v_0\);
7 \(\displaystyle f \leftarrow \emptyset\); \(\displaystyle \triangleright\) funkcja \(\displaystyle f\) nie jest określona dla żadnego argumentu
8 for each \(\displaystyle (v_i \rightarrow a_1a_2...a_nv_j) \in P\) do
9 if \(\displaystyle n>1\) then
10 \(\displaystyle V_N \leftarrow V_N \cup \{v^{a_1}, ..., v^{a_{n-1}}\}\); \(\displaystyle \triangleright\) rozbijamy produkcję na kilka prostszych
11 \(\displaystyle P \leftarrow P \backslash \{v_i \rightarrow a_1a_2...a_nv_j\}\); \(\displaystyle \triangleright\) w tym celu usuwamy produkcję z \(\displaystyle P\)
12 \(\displaystyle P \leftarrow P \cup \{v_i \rightarrow a_1v^{a_1}, v^{a_{n-1}} \rightarrow a_nv_j\}\); \(\displaystyle \triangleright\) w zamian dodając ciąg krótszych
13 \(\displaystyle P \leftarrow P \cup \{v^{a_1} \rightarrow a_2v^{a_2}, \ldots, v^{a_{n-2}} \rightarrow a_{n-1}v^{a_{n-1}} \}\);
14 end if
15 end for
16 \(\displaystyle \triangleright\) wszystkie produkcje są postaci \(\displaystyle u\rightarrow a v\) lub \(\displaystyle u\rightarrow 1\), gdzie \(\displaystyle u,v\in V_N\), \(\displaystyle a\in V_T\)
17 for each \(\displaystyle (s_i \rightarrow as_j) \in P\) do
18 \(\displaystyle f(s_i, a) \leftarrow s_j\);
19 end for
20 for each \(\displaystyle (v_i \rightarrow 1) \in P\) do
21 \(\displaystyle T \leftarrow T \cup \{v_i\}\);
22 end for
23 return \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\);
Przykład 1.2
Jako wejście algorytmu rozważmy gramatykę z przykładu 1.1 (patrz przykład 1.1.) Używając algorytmu Greg2Automat, zbudujemy dla niej automat akceptujący język przez nią generowany.
Mamy \(\displaystyle S=\{s_0, s_1, s_2\}\). W liniach 17. -- 19. określana jest funkcja przejścia: \(\displaystyle f(s_0, a)=s_0\), \(\displaystyle f(s_0, b)=s_1\), \(\displaystyle f(s_1, b)=s_1\), \(\displaystyle f(s_1, a)=s_2\) oraz \(\displaystyle f(s_2, a)=s_1\).
Pętla w liniach 20. - 22. przebiega po dwóch produkcjach: \(\displaystyle v_0 \rightarrow 1\) oraz \(\displaystyle v_2 \rightarrow 1\), dodaje zatem do zbioru \(\displaystyle T\) stanów końcowych stany \(\displaystyle s_0\) oraz \(\displaystyle s_2\). Szukany automat to automat z poprzedniego przykładu; przedstawiony jest na rysunku 1.
Automat powstały w wyniku działania algorytmu GReg2Automat nie musi być automatem deterministycznym (wystarczy, że w zbiorze
produkcji znajdą się dwie produkcje postaci \(\displaystyle v_i \rightarrow av_j\) oraz \(\displaystyle v_i \rightarrow av_k\) dla pewnego \(\displaystyle a \in A\)), jednak po jego determinizacji i minimalizacji otrzymujemy minimalny automat deterministyczny akceptujący język, który jest generowany przez gramatyke podaną na wejście algorytmu.
Złożoność czasowa jak i pamięciowa algorytmu wynosi \(\displaystyle O(p)\), gdzie \(\displaystyle p\) jest liczbą produkcji występujących w zbiorze praw \(\displaystyle P\) gramatyki.
Przedstawimy teraz algorytmy związane z wyrażeniami regularnymi. Pierwszy z nich prowadzi do konstrukcji automatu skończenie stanowego, rozpoznającego język opisany wyrażeniem regularnym. Drugi, mając na wejściu automat, konstruuje wyrażenie regularne opisujące język rozpoznawany przez ten automat.
Rozpoczynamy od algorytmu prowadzącego do konstrukcji automatu na podstawie wyrażenia regularnego.
Niech \(\displaystyle a \in A, r,s \in \mathcal{WR}\). Najpierw pokażemy, że językom odpowiadającym wyrażeniom regularnym , \(\displaystyle 1\), \(\displaystyle a\), \(\displaystyle r+s\), \(\displaystyle rs\) oraz \(\displaystyle r^*\) można przyporządkować automaty akceptujące te języki, a
następnie podamy algorytm konstruowania automatu rozpoznającego dowolne wyrażenie regularne.
Na rysunku 2 przedstawione są trzy automaty. Automat a) rozpoznaje język pusty, automat b) - język \(\displaystyle \{1\}\), a automat c) - język \(\displaystyle \{a\}\), dla \(\displaystyle a \in A\).
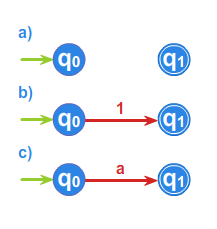
Niech dane będą automaty: \(\displaystyle M_1\), akceptujący język opisywany wyrażeniem \(\displaystyle r\) oraz \(\displaystyle M_2\), akceptujący język opisywany wyrażeniem \(\displaystyle s\). Na rysunku 3 przedstawiono konstrukcje automatów akceptujących wyrażenia regularne \(\displaystyle r+s\) (automat a)), \(\displaystyle (rs)\) (automat b)) oraz \(\displaystyle r^*\) (automat c)).

W automacie a) stan \(\displaystyle q_0\) jest stanem początkowym, stan \(\displaystyle f_0\) -stanem końcowym, stany \(\displaystyle q_1,q_2\) oraz \(\displaystyle f_1,f_2\) oznaczają odpowiednio stany początkowe automatów \(\displaystyle M_1\) i \(\displaystyle M_2\) oraz stany
końcowe automatów \(\displaystyle M_1\) i \(\displaystyle M_2\).
W automacie b) stan \(\displaystyle q_0\) jest jednocześnie jego stanem początkowym oraz stanem początkowym automatu \(\displaystyle M_1\), stan \(\displaystyle f_1\) jest stanem końcowym automatu b) i jednocześnie stanem końcowym automatu \(\displaystyle M_2\).
Stan \(\displaystyle f_0\) jest stanem końcowym w \(\displaystyle M_1\), a \(\displaystyle q_1\) - początkowym w \(\displaystyle M_2\).
W automacie c) stan \(\displaystyle q_0\) jest jego stanem początkowym a \(\displaystyle f_0\) końcowym. Stany \(\displaystyle q_1\) oraz \(\displaystyle f_1\) to odpowiednio początkowy i końcowy stan automatu \(\displaystyle M_1\).
Wyrażenia regularne można przedstawiać w postaci drzewa, w którym liśćmi są litery, słowo puste 1 lub zbiór pusty , a węzły symbolizują operacje na wyrażeniach regularnych, czyli sumę, konkatenację lub iterację, czyli gwiazdkę Kleene'ego.
Przykład 1.3
Rozważmy wyrażenie regularne \(\displaystyle r=(a^*b)(ab+c)\). Drzewo odpowiadające \(\displaystyle r\) przedstawione jest na rysunku 4. Korzeniem jest wierzchołek z małą wchodzącą strzałką.
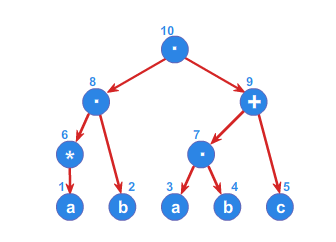
Powyższe konstrukcje będą stosowane podczas iteracyjnej budowy automatu. Algorytm do tego celu będzie wykorzystywał drzewo odpowiadające wyrażeniu regularnemu w następujący sposób: drzewo będzie przeszukiwane metodą post-order (zaczynając od korzenia),
tzn. najpierw rekurencyjnie przeszukiwane są poddrzewa danego węzła \(\displaystyle x\), a na końcu sam węzeł \(\displaystyle x\). Dzięki temu, wchodząc do węzła \(\displaystyle x\) drzewa etykietowanego daną operacją na wyrażeniu regularnym oba poddrzewa \(\displaystyle P\) i \(\displaystyle L\) wierzchołka \(\displaystyle x\) będą już reprezentowane przez automaty \(\displaystyle \mathcal{A}_P\) oraz \(\displaystyle \mathcal{A}_L\). Teraz wystarczy zastosować jedną z konstrukcji z rysunku 2 lub 3. Procedurę powtarzamy do momentu, aż przechodzenie drzewa zakończy się w korzeniu. Szukanym przez nas automatem będzie automat "odpowiadający" korzeniowi drzewa.
Poniżej przedstawiony jest algorytm konstrukcji automatu w oparciu o wyrażenie regularne. Jego istotną część składową stanowi procedura
PostOrder, której pseudo-kod jest przedstawiony poniżej. Wykorzystamy także dwie procedury, mianowicie CreateAutomata(type) oraz JoinAutomata(type,\(\displaystyle \mathcal{M}_1,\mathcal{M}_2\)). Zmienna type może przyjmować wartości '\(\displaystyle a\)', '\(\displaystyle b\)' lub '\(\displaystyle c\)'. Funkcja zwraca automat CreateAutomata(type)
przedstawiony (zależnie od zmiennej type) na rysunku 2. Procedura JoinAutomata(type,\(\displaystyle \mathcal{M}_1,\mathcal{M}_2\)) natomiast konstruuje na podstawie automatów \(\displaystyle \mathcal{M}_1\), \(\displaystyle \mathcal{M}_2\) automat z rysunku 2, przy czym dla przypadku type=\(\displaystyle c\) automat \(\displaystyle \mathcal{M}_2\) jest bez
znaczenia. Ostatnią wykorzystaną procedurą będzie BuildTree(r), tworząca drzewo (binarne) dla wyrażenia regularnego. Zakładamy, że studentowi doskonale jest znana Odwrotna Notacja Polska i budowa takiego drzewa nie będzie dla niego stanowiła problemu. Dla ustalenia uwagi zakładamy, że symbol \(\displaystyle *\) prowadzi zawsze do lewego dziecka.
Poniżej przedstawiamy oznaczenia standardowych funkcji operujących na drzewach. Funkcja \(\displaystyle \textsc{Root}(T)\) zwraca korzeń drzewa \(\displaystyle T\), funkcje \(\displaystyle \textsc{LeftChild}(T,v)\) oraz \(\displaystyle \textsc{RightChild}(T,v)\) zwracają lewe i prawe dziecko wierzchołka \(\displaystyle v\) (ew. NULL, gdy brak lewego lub prawego dziecka), natomiast funkcja \(\displaystyle \textsc{Label}(T,v)\) zwraca etykietę wierzchołka \(\displaystyle v\) drzewa \(\displaystyle T\). Funkcja \(\displaystyle \textsc{IsLeaf}(T,v)\) zwraca wartość \(\displaystyle \textbf{true}\), gdy \(\displaystyle v\) jest liściem w drzewie \(\displaystyle T\) oraz \(\displaystyle \textbf{false}\) w przypadku
przeciwnym.
Algorytm Wr2Automat -- buduje automat rozpoznający język
opisywany wyrażeniem regularnym
1 Wejście: \(\displaystyle r\) -- wyrażenie regularne.
2 Wyjście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) -- automat rozpoznający język opisywany wyrażeniem \(\displaystyle r\).
3 \(\displaystyle T\leftarrow \textsc{BuildTree}(r)\);
4 \(\displaystyle v_0 \leftarrow \textsc{Root}(T)\);
5 \(\displaystyle \mathcal{A} \leftarrow\) PostOrder(\(\displaystyle T,v_0\));
6 return \(\displaystyle \mathcal{A}\);
Przykład 1.4
Zastosujemy algorytm Wr2Automat do konstrukcji automatu dla wyrażenia regularnego \(\displaystyle w=(a^*b)(ab+c)\).
Automat \(\displaystyle \mathcal{A}_{10}\) jest zwrócony przez algorytm jako automat akceptujący język opisywany wyrażeniem \(\displaystyle r=(a^*b)(ab+c)\). Automat ten przedstawiony jest na rysunku 5.
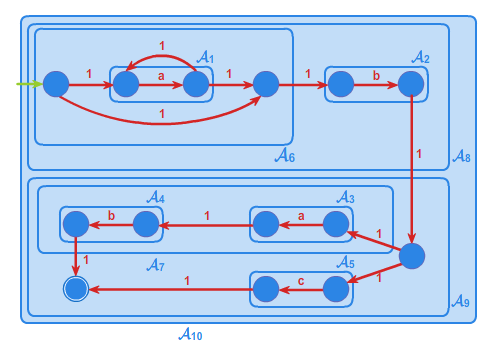
Ramkami zaznaczono i opisano automaty budowane w trakcie działania procedury PostOrder.
Rezultat działania algorytmu Wr2Automat może nie być zadawalający, gdyż wynikiem działania algorytmu nie jest automat deterministyczny, lecz automat z pustymi przejściami. Automat ten można więc poddać procesowi usunięcia przejść pustych oraz determinizacji, co można przeprowadzić przy pomocy omówionych wcześniej algorytmów UsuńPustePrzejścia oraz Determinizuj.
Algorytm Procedure PostOrder
1 procedure PostOrder (\(\displaystyle T\): drzewo, \(\displaystyle v\): wierzchołek)
2 if IsLeaf(\(\displaystyle T,v\)) then
3 if \(\displaystyle v\)=NULL then
4 \(\displaystyle \mathcal{A}_v \leftarrow\) CreateAutomata('\(\displaystyle a\)');
5 else
6 if Label(\(\displaystyle T,v\))='1' then
7 \(\displaystyle \mathcal{A}_v \leftarrow\) CreateAutomata('\(\displaystyle b\)');
8 else
9 \(\displaystyle \mathcal{A}_v \leftarrow\) CreateAutomata('\(\displaystyle c\)'); \(\displaystyle \triangleright\) Label\(\displaystyle (T,v)\in A\)
10 end if
11 end if
12 return \(\displaystyle \mathcal{A}_v\);
13 else
14 \(\displaystyle \mathcal{A}_L \leftarrow\) PostOrder(\(\displaystyle T\), LeftChild\(\displaystyle (T,v)\));
15 \(\displaystyle \mathcal{A}_P \leftarrow\) PostOrder(\(\displaystyle T\), RightChild\(\displaystyle (T,v)\));
16 if Label(\(\displaystyle T,v\))='\(\displaystyle +\)' then
17 \(\displaystyle \mathcal{A}_{LP}\leftarrow\)JoinAutomata('\(\displaystyle a\)'\(\displaystyle ,\mathcal{A}_L,\mathcal{A}_P\));
18 end if
19 if Label(\(\displaystyle T,v\))='\(\displaystyle \cdot\)' then
20 \(\displaystyle \mathcal{A}_{LP}\leftarrow\)JoinAutomata('\(\displaystyle b\)'\(\displaystyle ,\mathcal{A}_L,\mathcal{A}_P\));
21 end if
22 if Label(\(\displaystyle T,v\))='\(\displaystyle *\)' then
23 \(\displaystyle \mathcal{A}_{LP}\leftarrow\)JoinAutomata('\(\displaystyle c\)'\(\displaystyle ,\mathcal{A}_L,\mathcal{A}_P\));
24 end if
25 return \(\displaystyle \mathcal{A}_{LP}\);
26 end if
27 end procedure
Procedura tworzenia drzewa dla wyrażenia regularnego działa w czasie liniowym ze względu na długość napisu reprezentującego wyrażenie
regularne -- napis ten można najpierw przekształcić do równoważnego mu, zapisanego w Odwrotnej Notacji Polskiej, a następnie, przechodząc
od lewej strony do prawej, konstruować po kolei fragmenty drzewa.
Przechodzimy teraz do algorytmów konstruujących wyrażenie regularne na podstawie zadanego automatu. Pierwszą metodę, można owiedzieć
klasyczną i omawianą w większości podręczników, prezentujemy poniżej. Drugą, nieco prostszą i wygodniejszą w zastosowaniu, przedstawimy w ćwiczeniach do tego wykładu.
Niech dany będzie automat \(\displaystyle \mathcal{A}=(S, A, f, s_1, T)\). Zbudujemy wyrażenie regularne opisujące język akceptowany przez \(\displaystyle \mathcal{A}\).
Konstrukcja polega na obliczeniu zbiorów \(\displaystyle R_{ij}^k\) (definicja poniżej), gdzie \(\displaystyle i,j=1,...,|S|\), co jest równoważne konstrukcji pewnych wyrażeń regularnych \(\displaystyle r_{ij}^k\). Szukany język będzie odpowiadał sumie pewnych zbiorów \(\displaystyle R_{ij}^k\), a zatem opisywany będzie przez wyrażenie regularne postaci \(\displaystyle r_{ij_1}^k + ... + r_{ij_t}^k\) dla pewnych \(\displaystyle j_l\), \(\displaystyle i\) oraz \(\displaystyle k\).
Załóżmy, że zbiór stanów automatu jest postaci \(\displaystyle S=\{s_1, s_2, ..., s_n\}\). Wprowadźmy porządek na
zbiorze \(\displaystyle S\), przyjmując:
Zbiory \(\displaystyle R_{ij}^k\) definiujemy w następujący sposób:
\(\mbox{(1)}\)
Intuicyjnie, zbiór \(\displaystyle R_{ij}^k\) to ogół wszystkich słów \(\displaystyle w\) takich, że \(\displaystyle f(s_i, w)=s_j\), a ponadto jeśli \(\displaystyle w=a_1a_2...a_m\), to \(\displaystyle \forall 1 \leqslant j \leqslant m-1 f(s_i, a_1a_2...a_j) = s_l \wedge l \leqslant k\).
Zamiast obliczać zbiory \(\displaystyle R_{ij}^k\) wygodniej będzie od razu zapisywać odpowiadające im wyrażenia regularne, które oznaczać
będziemy poprzez \(\displaystyle r_{ij}^k\). Przez analogię mamy wzór rekurencyjny:
\(\mbox{(2)}\)
Pozostaje wyjaśnić jak wyglądają wyrażenia \(\displaystyle r_{ij}^0\). Jeśli \(\displaystyle R_{ij}^k=\{a_1,a_2,\dots,a_s\}\) to
\(\mbox{(3)}\)
Twierdzenie 1.1
Niech \(\displaystyle \mathcal{A}\) oraz \(\displaystyle R_{ij}^k\) będą zdefiniowane jak powyżej i niech zbiór stanów końcowych dla \(\displaystyle \mathcal{A}\) ma postać \(\displaystyle T=\{s_{j_1}, s_{j_2}, ..., s_{j_t}\}\). Wtedy
Powyższą metodę ujmiemy formalnie w ramy algorytmu (algorytm Automat2WR1).
Algorytm Automat2WR1 -- buduje wyrażenie regularne opisujące język akceptowany przez automat skończony.
1 Wejście: \(\displaystyle \mathcal{A}=(S=\{s_1, s_2, ..., s_n\}, A, f, s_1, T)\).
2 Wyjście: \(\displaystyle w\) - wyrażenie regularne opisujące język \(\displaystyle L=L(\mathcal{A})\).
3 for \(\displaystyle i\leftarrow 1\) to \(n\) do
4 for \(\displaystyle j\leftarrow 1\) to \(\displaystyle n\) do
5 oblicz \(\displaystyle r_{ij}^0\) \(\displaystyle \triangleright\) stosujemy wzór (3);
6 end for
7 end for
8 for \(\displaystyle k \leftarrow 1\) to \(\displaystyle n\) do
9 for \(\displaystyle i\leftarrow 1\) to \(\displaystyle n\) do
10 for \(\displaystyle j\leftarrow 1\) to \(\displaystyle n\) do
11 \(\displaystyle r_{ij}^k \leftarrow r_{ik}^{k-1}(r_{kk}^{k-1})^*r_{kj}^{k-1} + r_{ij}^{k-1}\); \(\displaystyle \triangleright\) dokonujemy katenacji słów
12 end for
13 end for
14 end for
15 \(\displaystyle r \leftarrow\) ""; \(\displaystyle \triangleright\) podstaw pod \(\displaystyle r\) słowo puste
16 for \(\displaystyle i\leftarrow 1\) to \(\displaystyle n\)
17 if \(\displaystyle \ s_i \in T\)
18 if r=""
19 \(\displaystyle r\leftarrow r_{1i}^{n}\); \(\displaystyle \triangleright\) stosujemy Twierdzenie 1.1
20 else
21 \(\displaystyle r \leftarrow r + r_{1i}^{n}\);
22 end if
23 end if
24 end for
25 return \(\displaystyle r\);
Podczas obliczania wyrażeń \(\displaystyle r_{ij}^k\) należy je w miarę możliwości upraszczać, gdyż, szczególnie przy dużej liczbie stanów,
nieskracane, mogą rozrastać się do bardzo dużych rozmiarów.
Przykład 1.5
Znajdziemy wyrażenie regularne opisujące język akceptowany przez automat z rysunku 6.

Mamy \(\displaystyle |S|=3\), \(\displaystyle i,j \in \{1, 2, 3\}\), \(\displaystyle k \in \{0, 1, 2, 3\}\), \(\displaystyle T=\{s_3\}\). Szukamy zatem wyrażenia regularnego \(\displaystyle r = r_{13}^3\).
Najpierw musimy obliczyć \(\displaystyle r_{ij}^0\) dla wszystich \(\displaystyle i,j \in \{1,2,3\}\). Mamy na przykład \(\displaystyle r_{31}^0=a+b\), gdyż z definicji zachodzi: \(\displaystyle R_{31}^0 = \{a \in A:\ f(s_3, a)=s_1\}=\{a, b\}\).
Gdy mamy wyliczone wszystkie \(\displaystyle r_{ij}^0\), przystępujemy do obliczeń dla \(\displaystyle k=1\).
Na przykład:
co po zredukowaniu daje
Obliczone wyrażenia \(\displaystyle r_{ij}^k\) dla \(\displaystyle k=0,1,2\) oraz dla wszystkich \(\displaystyle i,j\) przedstawione są w tabeli 1.
| \(\displaystyle k=0\) | \(\displaystyle k=1\) | \(\displaystyle k=2\) | |
| \(\displaystyle r_{11}^k\) | \(\displaystyle a+1\) | \(\displaystyle a^*\) | \(\displaystyle a^*b(a^+b)^*a^++a^*\) |
| \(\displaystyle r_{12}^k\) | \(\displaystyle b\) | \(\displaystyle a^*b\) | \(\displaystyle a^*b(a^+b)^*\) |
| \(\displaystyle r_{13}^k\) | \(\phi\) | \(\phi\) | \(\displaystyle a^*b(a^+b)^*b\) |
| \(\displaystyle r_{21}^k\) | \(\displaystyle a\) | \(\displaystyle a^+\) | \(\displaystyle (a^+b)^*a^+\) |
| \(\displaystyle r_{22}^k\) | \(\displaystyle 1\) | \(\displaystyle a^+b+1\) | \(\displaystyle (a^+b)^*\) |
| \(\displaystyle r_{23}^k\) | \(\displaystyle b\) | \(\displaystyle b\) | \(\displaystyle (a^+b)^*b\) |
| \(\displaystyle r_{31}^k\) | \(\displaystyle a+b\) | \(\displaystyle a^++ba^*\) | \(\displaystyle (1+(a^+b+ba^*b)(a^+b)^*)a^++ba^*\) |
| \(\displaystyle r_{32}^k\) | \(\phi\) | \(\displaystyle a^+b+ba^*b\) | \(\displaystyle (a^+b+ba^*b)(a^+b)^*\) |
| \(\displaystyle r_{33}^k\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle (a^+b+ba^*b)(a^+b)^*b+1\) |
Tabela 1. Obliczone wartości \(\displaystyle r_{ij}^k\) dla automatu z rys. 6
Ponieważ \(\displaystyle T=\{s_3\}\), szukanym wyrażeniem regularnym będzie \(\displaystyle r=r_{13}^3\). Obliczamy zatem:
Problemy rozstrzygalne algorytmicznie
Kończąc część wykładu prezentującą języki regularne, wskażemy problemy rozstrzygalne algorytmicznie w zakresie tej rodziny języków formalnych. Ponieważ pojęcia rozstrzygalności i nierozstrzygalności możemy uznać za znane (były wprowadzone na innych wykładach) nie
będziemy tutaj ich definiować ani kreślić tła teorii rozstrzygalności.
W obrębie rodziny języków regularnych wszystkie podstawowe problemy są algorytmicznie rozstrzygalne. Uzasadnienia są proste. Część z nich opiera się na lemacie o pompowaniu, a część wynika bezpośrednio z algorytmicznej struktury automatu skończenie stanowego, czy też gramatyki regularnej.
Twierdzenie 2.1
W klasie języków regularnych \(\displaystyle \mathcal{REG}(A^{*})\) następujące problemy są rozstrzygalne:
- problem niepustości języka, \(\displaystyle L\neq \emptyset,\)
- problem nieskończoności języka, \(\displaystyle card\, L=\aleph _{0},\)
- problem równości języków, \(\displaystyle L_{1}=L_{2},\)
- problem należenia słowa do języka, \(\displaystyle w\in L.\)
Dowód
1. Aby uzasadnić ten fakt zauważmy, że wystarczy sprawdzić niepustość skończonego podzbioru języka \(\displaystyle L,\) co wynika z równoważności:
gdzie \(\displaystyle N\) stała z lematu o pompowaniu. Implikacji \(\displaystyle \Leftarrow\) jest oczywista. Natomiast fakt, że do niepustego języka należy słowo o długości ograniczonej przez \(\displaystyle N\) , wynika z lematu o pompowaniu. Jeśli mianowicie \(\displaystyle w\in L\) i \(\displaystyle \mid w\mid \geqslant N\) , to rozkładamy słowo \(\displaystyle w\) następująco:
Przyjmując teraz wartość \(\displaystyle i=0\) , uzyskujemy:
Po skończonej ilości powtórzeń powyższego rozkładu uzyskamy słowo należące do języka, o długości ograniczonej przez \(\displaystyle N\) .
2. Wystarczy udowodnić nastepującą równoważność:
Jeśli \(\displaystyle L\) jest językiem nieskończonym, to znajdziemy w \(\displaystyle L\) słowo \(\displaystyle w\) dowolnie długie. Niech \(\displaystyle \mid w\mid \geqslant N\) . Jeśli słowo \(\displaystyle w\) nie spełnia ograniczenia \(\displaystyle \mid w\mid <2N\) , to podobnie jak poprzednio korzystamy z lematu o pompowaniu i po skończonej ilości kroków otrzymamy słowo krótsze od \(\displaystyle 2N\) . Istotne jest, że wykorzystując lemat o pompowaniu, możemy założyć, że usuwane słowo \(\displaystyle u\) ma długość ograniczoną przez \(\displaystyle N\) . Zatem oznacza to, że ze słowa dłuższego od \(\displaystyle 2N\) nie dostaniemy słowa krótszego od \(\displaystyle N\) .
Jeśli teraz do języka \(\displaystyle L\) należy słowo \(\displaystyle w\) o długości większej lub równej \(\displaystyle N\) , to znów z lematu o pompowaniu wnioskujemy, że
Istnieje więc nieskończony podzbiór języka \(\displaystyle L\) , a więc i sam język \(\displaystyle L\) jest nieskończony.
3. Rozważmy \(\displaystyle L=(L_{1}\cap \overline{L_{2}})\cup (\overline{L_{1}}\cap L_{2})\) . Język \(\displaystyle L\) jest regularny, co wynika z domkniętości klasy \(\displaystyle \mathcal{L}_{3}\) na operaje boolowskie. Równoważność
sprowadza problem równości języków do problemu niepustości omówionego powyżej.
4. Konstruujemy automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\) rozpoznający język \(\displaystyle L\) i sprawdzamy, czy \(\displaystyle f(s_{0},w)\in T.\)
Na podstawie dowodu powyższego twierdzenia nietrudno jest określić algorytmy rozstrzygające przedstawione problemy. Poniżej prezentujemy
algorytm rozstrzygający problem należenia słowa do języka regularnego zadanego automatem. Bez straty ogólności możemy założyć, że automat jest deterministyczny.
Algorytm NależenieDoJęzyka -- sprawdza, czy dane słowo należy do języka \(\displaystyle L\) akceptowanego przez zadany automat \(\displaystyle \mathcal{A}\)
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat akceptujący język \(\displaystyle L\) oraz \(\displaystyle w=w_1w_2\ldots w_n \in A^*\) - słowo.
2 Wyjście: Odpowiedź true (tak) lub false (nie).
3 \(\displaystyle k \leftarrow |w|\);
4 \(\displaystyle s \leftarrow s_0\);
5 for \(\displaystyle i\leftarrow 1\) to \(k\) do
6 \(\displaystyle s \leftarrow f(s,w_i)\);
7 end for
8 if \(\displaystyle s \in T\) then
9 return true;
10 else
11 return false;
12 end if
Algorytm działa w czasie \(\displaystyle O(|w|)\) i posiada złożoność pamięciową \(\displaystyle O(|A| \cdot |S|)\), co spowodowane jest koniecznością przechowywania funkcji przejść automatu \(\displaystyle \mathcal{A}\).
Jeśli język zadany jest nie automatem, a gramatyką regularną, to gramatykę można przekształcić na automat poznanym na początku wykładu algorytmem GReg2Automat, następnie zdeterminizować ten automat i podać go jako wejście dla algorytmu NależenieDoJęzyka.
Jeśli język zadany jest wyrażeniem regularnym, to mając wyrażenie regularne, można zbudować odpowiadający mu automat przy pomocy algorytmu WR2Automat. A zatem, na przykład, z powyższego twierdzenia wynika, iż problem równoważności wyrażeń regularnych jest rozstrzygalny.
Języki bezkontekstowe i ich gramatyki
W tym wykładzie rozpoczniemy omawianie drugiej w hierarchii Chomsky'ego rodziny języków formalnych, a mianowicie języków bezkontekstowych. Przedstawimy gramatyki bezkontekstowe i ich prostsze, a zarazem równoważne, postacie.
Gramatyki języków bezkontekstowych
Języki typu (2), zwane językami bezkontekstowymi, są rodziną szerszą niż omówione wcześniej języki regularne. Jak stwierdziliśmy w poprzednich wykładach gramatyki regularne generują poprawne napisy poprzez ciąg przepisywań metodą "od lewej do prawej". Natomiast gramatyki bezkontekstowe, zwane w lingwistyce gramatykami bezkontekstowych struktur frazowych, generują poprawne napisy poprzez sekwencję przepisywań, która ma strukturę drzewa. Ze względu na tę właśnie strukturę, gramatyki bezkontekstowe nadają się bardzo dobrze do opisu syntaktyki języków programowania. Z tego też powodu nastąpił szybki rozwój teorii gramatyk i języków bezkontekstowych.
Na wstępie przypomnijmy, że każda produkcja jakiejkolwiek gramatyki bezkontekstowej \(\displaystyle G = (V_N,V_T,v_0,P)\) ma postać \(\displaystyle v \rightarrow x_1\ldots.x_k\) lub \(\displaystyle v \rightarrow 1\), gdzie \(\displaystyle v \in V_N\;,\; x_i \in (V_N \cup V_T)\). Często korzystać będziemy z możliwości przedstawienia graficznego takiej produkcji. Mianowicie każdej produkcji odpowiada etykietowane drzewo z wyróżnionym wierzchołkiem początkowym.
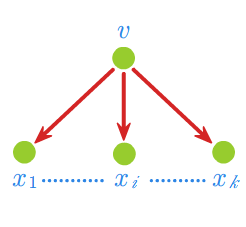
Drzewo odpowiadające pojedynczej produkcji z gramatyki \(\displaystyle G\) nazywane jest drzewem elementarnym. Mając dowolne yprowadzenie w gramatyce \(\displaystyle G\), można przedstawić je graficznie w postaci etykietowanego drzewa. Niech
będzie wyprowadzeniem słowa \(\displaystyle w\) w gramatyce \(\displaystyle G\). Drzewo reprezentujące to wyprowadzenie powstaje z połączenia drzew elementarnych odpowiadających pojedynczym produkcjom występującym w wyprowadzeniu słowa \(\displaystyle w\) w taki sposób, aby spełnić poniższe warunki:
- wierzchołek początkowy jest etykietowany przez \(\displaystyle v_0\),
- każdy wierzchołek nie będący liściem, czyli wierzchołkiem maksymalnym w drzewie, jest oznaczony przez elementy z \(\displaystyle V_N\),
- jeśli \(\displaystyle v \in V_N\) jest symbolem nieterminalnym występującym w słowie \(\displaystyle w_i\) w wyprowadzeniu \(\displaystyle w\), to bezpośrednie następniki wierzchołka etykietowanego przez \(\displaystyle v\) są oznaczone przez symbole \(\displaystyle x_1,\ldots, x_k\) (porządek od lewej do prawej), gdzie \(\displaystyle v \rightarrow x_1\ldots x_k \;\; \in \;\;P\) i ta
właśnie produkcja została wykorzystana w bezpośrednim wyprowadzeniu \(\displaystyle w_i\mapsto w_{i+1}\), to znaczy we fragmencie wyprowadzenia \(\displaystyle v_0 \mapsto^* w_n = w,\)
- wierzchołki maksymalne drzewa (ciąg liści "od lewej strony") to słowo \(\displaystyle w\), przy czym, jeśli wszystkie wierzchołki maksymalne są etykietowane przez 1, to \(\displaystyle w = 1\), a w przeciwnym razie wierzchołki oznaczone przez \(\displaystyle 1\) pomijamy.
Przykład 1.1
Niech \(\displaystyle G = (V_N,V_T,v_0,P)\), gdzie \(\displaystyle V_N = \{v_0, v_1\}, V_T = \{a,b,c\},\)
\(\displaystyle P = \{v_0 \rightarrow av_0c,\;\; v_0 \rightarrow bv_1c, v_1 \rightarrow bv_1c, v_1\rightarrow bc\}.\)
Wówczas wyprowadzeniu
odpowiada drzewo
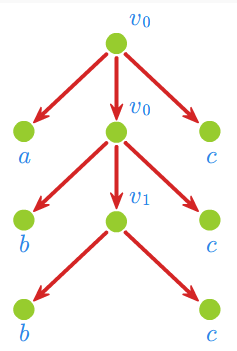
W poniższym przykładzie, jak i w dalszych wykładach symbolem \(\displaystyle \overline A\) oznaczamy kopię alfabetu \(\displaystyle A\), o której zakładać będziemy, że jest to zbiór rozłączny z oryginalnym alfabetem.
Przykład 1.2
- Język Dycka.
Określamy bezkontekstową gramatykę \(\displaystyle G = (V_N,V_T,v_0,P)\), w której \(\displaystyle V_N=\{v_0,v_1 \},\displaystyle V_T=A \cup \overline A,\displaystyle \; A=\left\{ a\right\} ,\; \overline{A}=\left\{ \overline{a}\right\} , \displaystyle P=\\)
\(\displaystyle{ v_0 \rightarrow 1,\; v_0 \rightarrow v_1v_0, \; v_1 \rightarrow av_0\overline{a} \}\).
Język generowany przez tę gramatykę, nazywany językiem Dycka, oznaczany jest przez \(\displaystyle D^*_A\). Język Dycka zwany jest też językiem "poprawnych nawiasów" przy interpretacji symboli \(\displaystyle a,\overline{a}\) jako lewego i prawego nawiasu.\(\displaystyle L(G)=\left\{ 1,a\overline{a},aa\overline{a}\overline{a},a\overline{a}a\overline{a},aa\overline{a}\overline{a}a\overline{a},\ldots \right\}.\) Język Dycka można zdefiniować także dla alfabetu \(\displaystyle A=\{a_{1},...,a_{n}\}\) mającego więcej niż dwa symbole. Do zbioru praw gramatyki \(\displaystyle G\) wprowadza się wszystkie możliwe prawa postaci \(\displaystyle v_1 \rightarrow a_iv_0\overline{a_i}\). W tym przypadku dla języka Dycka używa się oznaczenia \(\displaystyle D^*_n\), aby zaznaczyć liczbę elementów alfabetu \(\displaystyle A\). - Język Łukasiewicza.
Język Łukasiewicza jest generowany przez gramatykę bezkontekstową \(\displaystyle G = (V_N,V_T,v_0,P)\), gdzie \(\displaystyle V_N=\{v_0 \}\), \(\displaystyle V_{T}=\left\{ a,b,+,*\right\}\),\(\displaystyle v_{0}=v\) oraz \(\displaystyle P= \{v \rightarrow a, v \rightarrow b, v \rightarrow +vv, v \rightarrow *vv \}\). Język Łukasiewicza jest więc zbiorem\(\displaystyle L(G)=\left\{ a,\: b,+ab,*b+ab,*+ab+ab,\ldots \right\}\)
Używając tego języka, możemy zapisywać wyrażenia algebraiczne bez użycia nawiasów (notacja polska, prefiksowa), interpretując \(\displaystyle +\) jako operator dodawania, \(\displaystyle *\) jako operator mnożenia oraz \(\displaystyle a\) i \(\displaystyle b\) jako argumenty. Używając nawiasów, przy powyżej interpretacji, możemy ten język zapisać następująco:
Wprost z definicji gramatyk - regularnej i bezkontekstowej - wynika, że rodzina języków regularnych jest podrodziną rodziny języków bezkontekstowych. Z lematu o pompowaniu dla języków regularnych wiemy, że język \(\displaystyle L = \{a^n b^n \; : \; n= 1,2,\ldots \}\) nie jest regularny. Łatwo uzasadnić, że język ten jest bezkontekstowy, bo jest generowany przez gramatykę:
Zatem rodzina języków regularnych jest właściwą podrodziną rodziny języków bezkontekstowych, czyli \(\displaystyle mathcal{L}_{3}\subseteq \! \! \! \! \! _{/\; \, }\mathcal{L}_{2}.\)
Przejdziemy teraz do omówienia pewnych własności gramatyk bezkontekstowych, które prowadzą do ich uproszczenia. Występujące w poniższym twierdzeniu sformułowanie "produkcja wymazująca" oznacza produkcję \(\displaystyle v\rightarrow 1\) .
Twierdzenie 1.1
Niech \(\displaystyle G = (V_N,V_T,v_0,P)\) będzie dowolną gramatyką bezkontekstową.
- Istnieje gramatyka bezkontekstowa \(\displaystyle G'\) bez produkcji wymazującej taka, że
\(\displaystyle L(G') = L(G) \backslash \{ 1\}.\) - Jeśli \(\displaystyle 1 \in L(G)\), to istnieje równoważna \(\displaystyle G\) gramatyka bezkontekstowa \(\displaystyle G''=(V''_N ,V_T ,v_0'' , P'')\) taka,
że jedyną produkcją wymazującą w \(\displaystyle P''\) jest produkcja \(\displaystyle v_0'' \rightarrow 1\) i symbol \(\displaystyle v_0''\) nie występuje po prawej stronie żadnej produkcji z \(\displaystyle P''\).
Dowód
Dowód podaje konstrukcję odpowiednich gramatyk. Dla dowodu punktu 1 rozważmy ciąg zbiorów
określony dla \(\displaystyle i=1,2\ldots\) . Jest to ciąg podzbiorów \(\displaystyle V_{N}\) taki, że \(\displaystyle U_1 \subseteq U_2 \subseteq \ldots \subseteq V_N\). Ponieważ zbiór symboli nieterminalnych \(\displaystyle V_{N}\) jest skończony, więc istnieje indeks \(\displaystyle k\) taki, że \(\displaystyle U_k = U_{k+1}\). Zatem ciąg \(\displaystyle U_i\) jest skończony. Stąd równoważność
Zatem \(\displaystyle 1 \in L(G)\) wtedy i tylko wtedy, gdy \(\displaystyle v_0 \in U_k.\) Konstruujemy teraz gramatykę \(\displaystyle G' = (V_N,V_T,v_0,P')\), przyjmując \(\displaystyle V_N,V_T\) i \(\displaystyle v_0\) jak w gramatyce \(\displaystyle G\) . Natomiast nowy zbiór praw \(\displaystyle P'\) zawiera zmodyfikowane prawa gramatyki \(\displaystyle G\) . Jeśli prawo \(\displaystyle v\rightarrow x\in P\) , to do zbioru \(\displaystyle P'\) wprowadzamy prawa \(\displaystyle v\rightarrow x'\) , gdzie \(\displaystyle x'\neq 1\) i \(\displaystyle x'\) powstaje z \(\displaystyle x\) przez wymazanie dowolnej liczby (także \(\displaystyle 0\) ) symboli ze zbioru \(\displaystyle U_{k}\) . Pozostaje teraz uzasadnienie równości
Dowód inkluzji \(\displaystyle \; \subseteq\)
Zauważmy, że dla każdego prawa \(\displaystyle v\rightarrow x'\in P'\) istnieje prawo \(\displaystyle v\rightarrow x\in P\) takie, że \(\displaystyle x\) różni się od \(\displaystyle x'\) wyłącznie pewną ilością symboli z \(\displaystyle U_{k}\) . Z równoważności \(\displaystyle (*)\) wynika, że symbole ze zbioru \(\displaystyle U_{k}\) prowadzą w dalszym ciągu generowania do słowa pustego. A więc dla każdego wyprowadzenia
niepustego słowa w gramatyce \(\displaystyle G'\) istnieje w gramatyce \(\displaystyle G\) wyprowadzenie tego samego słowa. Wystarczy w wyprowadzeniu w gramatyce \(\displaystyle G'\) w miejsce praw postaci \(\displaystyle v\rightarrow x'\in P'\) wprowadzić prawa \(\displaystyle v\rightarrow x\in P,\) by otrzymać wyprowadzenie tego samego słowa w \(\displaystyle G\) .
Dowód inkluzji \(\displaystyle \; \supseteq\)
Określamy gramatykę pomocniczą \(\displaystyle \overline{G}=(V_{N},V_{T},v_{o},P\cup P')\) . Zbiór praw tej gramatyki rozszerza \(\displaystyle P'\) o wszystkie prawa wymazujące ze zbioru \(\displaystyle P\) . Z definicji wynika, że \(\displaystyle L(G)\subseteq L(\overline{G})\) , więc \(\displaystyle L(G)-\left\{ 1\right\} \subseteq L(\overline{G})-\left\{ 1\right\}\) . Dla dowodu wystarczy więc pokazać, że
Niech \(\displaystyle w\in L(\overline{G})-\left\{ 1\right\}\) i niech \(\displaystyle v_{0}\mapsto_{\overline{G}}....\mapsto_{\overline{G}}w\) będzie wyprowadzeniem słowa \(\displaystyle w\) w \(\displaystyle \overline{G}\) . Jeśli w tym wyprowadzeniu wszystkie prawa należą do \(\displaystyle P'\) , to oczywiście słowo \(\displaystyle w\in L(G')\) . Jeśli w wyprowadzeniu słowa \(\displaystyle w\) występuje prawo wymazujące, to oznacza, że dla pewnego \(\displaystyle y_{i}\in U_{k},\, \, \, x_{p}\rightarrow v_{1}v_{2}\in P'\) oraz \(\displaystyle x_{p}\rightarrow v_{1}y_{i}v_{2}\in P'\) wyprowadzenie ma postać
Jednak, jak łatwo zauważyć, słowo \(\displaystyle w\) można także wygenerować, pomijając to prawo wymazujące i wykorzystując wyłącznie prawa z \(\displaystyle P'\)
co kończy dowód punktu 1.
Przechodząc do dowodu punktu 2, załóżmy, że \(\displaystyle 1\in L(G)\) i niech \(\displaystyle G'\) będzie gramatyką taką jak w punkcie 1. Definiujemy teraz gramatykę
która spełnia żądane w twierdzeniu warunki i \(\displaystyle L(G)=L(G'')\) .
Z udowodnionego powyżej twierdzenia i z definicji gramatyk bezkontekstowych i kontekstowych (definicja 2.1. z wykładu 2) wynika następujące stwierdzenie
Wniosek 1.1
Rodzina języków bezkontekstowych (typu (2)) zawiera się w rodzinie jezyków kontekstowych (typu (1))
Przejdziemy teraz do zagadnienia upraszczania gramatyki bezkontekstowej. Wprowadzimy następującą definicję.
Definicja 1.1
Mówimy, że gramatyka bezkontekstowa \(\displaystyle G\) jest właściwa, jeśli zbiór praw nie zawiera produkcji wymazującej oraz produkcji typu \(\displaystyle v_1 \rightarrow v_2\), gdzie \(\displaystyle v_{1},v_{2}\in V_{N}\) .
Lemat 1.1
Dla każdej gramatyki bezkontekstowej \(\displaystyle G\) generującej język bez słowa pustego istnieje równoważna jej gramatyka bezkontekstowa \(\displaystyle H\) właściwa.
Dowód
W dowodzie przedstawimy konstrukcję gramatyki o żądanych własnościach. Na podstawie udowodnionego powyżej twierdzenia możemy przyjąć, że \(\displaystyle G = (V_N,V_T,v_0,P)\) jest bez produkcji wymazującej. Dla usunięcia produkcji w postaci \(\displaystyle v_1 \rightarrow v_2\) określamy ciąg zbiorów \(\displaystyle U_i(x)\) dla \(\displaystyle x \in V_N \cup V_T\), przyjmując \(\displaystyle U_{1}(x)=\left\{ x\right\}\) oraz dla \(\displaystyle i=1,2\ldots \displaystyle U_{i+1}(x)=U_{i}(x)\cup \left\{ y\in V_{N}\cup V_{T}\, :\, \exists u\in U_{i}(x),\, u\rightarrow y\in P\right\} .\)
Ciąg \(\displaystyle U_i(x)\) jest skończony (stabilizuje się), a więc \(\displaystyle U_k(x)=U_{k+1}(x)\) dla pewnego \(\displaystyle k\) i dla każdego \(\displaystyle l>k\) mamy równość \(\displaystyle U_l(x)=U_k(x)\). Dla dowolnego \(\displaystyle v \in V_N\) oraz \(\displaystyle z\in V_{N}\cup V_{T}\) prawdziwa jest równoważność
która w szczególności dla symbolu terminalnego \(\displaystyle a \in V_T\) oznacza, że \(\displaystyle a \in L(G)\) wtedy i tylko wtedy, gdy \(\displaystyle a \in U_k(v_0).\)
Określamy teraz gramatykę \(\displaystyle H= (V_N,V_T,v_0,\displaystyle \overline{P})\) , w której zbiór \(\displaystyle \overline{P}\) zawiera produkcje postaci:
- \(\displaystyle v_0 \rightarrow a\) dla każdego \(\displaystyle a \in V_T \cap U_k(v_0),\)
- \(\displaystyle v \rightarrow z_1... z_n\) dla \(\displaystyle v \in V_N\), \(\displaystyle n \geqslant 2\) oraz dla
każdego \(\displaystyle z_j \in V_N \cup V_T\), \(\displaystyle j=1,..., n\) takiego, że istnieje prawo \(\displaystyle \overline v \rightarrow x_1... x_n \in P\), \(\displaystyle \overline v \in U_k(v)\) i \(\displaystyle z_j \in U_k(x_j)\).
W gramatyce \(\displaystyle H\) nie występują prawa postaci \(\displaystyle v_1 \longrightarrow v_2\). Gramatyka \(\displaystyle H\) nie zawiera praw wymazujących oraz \(\displaystyle L(G)=L(H)\), co kończy dowód lematu.
Dalsze rozważania prezentują mozliwości upraszczania gramatyk bezkontekstowych poprzez usunięcie pewnych nieistotnych symboli nieterminalnych, a także poprzez zastąpienie danej gramatyki przez równoważną o prostszej strukturze.
Niech \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) będzie gramatyką bezkontekstową, generującą niepusty język. Mówimy, że symbol nieterminalny \(\displaystyle v\in V_{N}\) jest użyteczny, jeśli istnieje słowo \(\displaystyle w\in L(G)\) i wyprowadzenie tego słowa takie, że
dla pewnych \(\displaystyle x,y\in (V_{N}\cup V_{T})^{*}\) . W przeciwnym wypadku mówimy, że symbol \(\displaystyle v\) jest bezużyteczny. Symbole nieużyteczne można usunąć z gramatyki bez uszczerbku dla generowanego przez tę gramatykę języka. Przekonuje o tym następujące twierdzenie.
Twierdzenie 1.2
Dla dowolnego niepustego języka bezkontekstowego \(\displaystyle L\) istnieje gramatyka bezkontekstowa bez bezużytecznych symboli nieterminalnych, która generuje ten język.
Konstrukcja takiej gramatyki, a więc i dowód tego twierdzenia wynika bezpośrednio z następujących dwóch lematów.
Lemat 1.2
Dla każdej gramatyki bezkontekstowej \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje równoważna gramatyka bezkontekstowa \(\displaystyle \overline{G}=(\overline{V}_{N},V_{T},v_{0},\overline{P})\) taka, że dla dowolnego \(\displaystyle v\in \overline{V}_{N}\) istnieje \(\displaystyle w\in V_{T}^{*}\) oraz
Dowód
Określamy rekurencyjnie ciąg podzbiorów zbioru symboli nieterminalnych \(\displaystyle V_{N}\) :
\(\displaystyle U_{1}=\left\{ v\in V_{N}\: :\: v\rightarrow w\in P,\: w\in V_{T}^{*}\right\}\) oraz dla \(\displaystyle i=1,2,\ldots\)
\(\displaystyle U_{i+1}=U_{i}\cup \left\{ v\in V_{N}\: :\: \: v\rightarrow x\in P,\: x\in (U_{i}\cup V_{T})^{*}\right\}\) . Zbiory te tworzą ciąg wstępujący i stabilizujący się dla pewnego \(\displaystyle p\) . Oznacza to, że \(\displaystyle U_{1}\subseteq U_{2}\subseteq \ldots \subseteq U_{p}=U_{p+1}\) . Przyjmujemy z definicji \(\displaystyle \overline{V}_{N}=U_{p}\) oraz
Tak określona gramatyka \(\displaystyle \overline{G}=(\overline{V}_{N},V_{T},v_{0},\overline{P})\) ma własności gramatyki postulowanej w tezie lematu. Pozostaje udowodnić równoważność określonej gramatyki \(\displaystyle \overline{G}\) i gramatyki \(\displaystyle G\) . W tym celu wystarczy pokazać dla dowolnego \(\displaystyle v\in V_{N}\) i \(\displaystyle w\in V^{*}_{T}\) , że jeśli \(\displaystyle v\mapsto^{*}_{G}w\) , to \(\displaystyle v\in \overline{V}_{N}\) . Udowodnimy tę implikację indukcyjnie ze względu na długość wyprowadzenia. Dla \(\displaystyle n=1\) istnienie wyprowadzenia \(\displaystyle v\mapsto^{*}_{G}w\) oznacza, że \(\displaystyle v\rightarrow w\in P\) . Stąd zaś wynika, że \(\displaystyle v\in U_{1}\subset \overline{V}_{N}\) . Dla dalszej części rozumowania załóżmy, że implikacja jest prawdziwa dla wyprowadzenia o długości nie większej od \(\displaystyle n\) i niech
będzie wyprowadzeniem o długości \(\displaystyle n+1\) dla słowa \(\displaystyle w\in V_{T}^{*}\) . Niech \(\displaystyle z=y_{1}v_{1}y_{2}v_{2}\ldots v_{k}y_{k+1},\) dla pewnych \(\displaystyle v_{1},...,v_{k}\in V_{N}\) oraz \(\displaystyle y_{1},...,y_{k+1}\in V_{T}^{*}\) . Oznaczmy dla słowa \(\displaystyle z\) symbolem \(\displaystyle N(z)\) słowo otrzymane przez wymazanie wszystkich symboli terminalnych, a symbolem \(\displaystyle T(z)\) słowo otrzymane przez wymazanie wszystkich symboli nieterminalnych. Wtedy \(\displaystyle N(z)=v_{1}\ldots v_{k},\; T(z)=y_{1}\ldots y_{k+1}\) . Wówczas istnieją słowa \(\displaystyle w_{1},\ldots ,w_{k}\in V_{T}^{*}\) takie, że \(\displaystyle w=y_{1}w_{1}y_{2}\ldots y_{k}w_{k}y_{k+1}\) i dla każdego \(\displaystyle i=1,\ldots ,k\) istnieją wyprowadzenia \(\displaystyle v_{i}\mapsto^{*}_{G}w_{i}\) o długości mniejszej lub równej od \(\displaystyle n\) . Korzystając z założenia indukcyjnego, wnioskujemy, że dla każdego \(\displaystyle i=1,\ldots ,k,\: \: v_{i}\in \overline{V}_{N}\) , a to oznacza z definicji \(\displaystyle \overline{V}_{N}\) , że istnieje \(\displaystyle j\) takie, że dla każdego \(\displaystyle i=1,\ldots ,k,\: \: v_{i}\in U_{j}\) . Ostatecznie więc \(\displaystyle v\in \overline{V}_{N}\) .
Lemat 1.3
Dla każdej gramatyki bezkontekstowej \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje równoważna gramatyka bezkontekstowa \(\displaystyle \overline{\overline{G}}=(\overline{\overline{V}}_{N},\overline{\overline{V}}_{T},v_{0},\overline{\overline{P}})\) taka, że dla dowolnego \(\displaystyle x\in \overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T}\) istnieją słowa \(\displaystyle u_{1},u_{2}\in (\overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T})^{*}\) oraz
Dowód
Dla rekurencyjnego określenia ciągu podzbiorów zbioru \(\displaystyle V_{N}\cup V_{T}\) przyjmujemy:
\(\displaystyle U_{1}=\left\{ v_{0}\right\}\) oraz dla \(\displaystyle k=1,2,\ldots \displaystyle U_{k+1}=U_{k}\cup \left\{ x\in alph_{(V_{N}\cup V_{T})}y\: :\: v\rightarrow y\in P,\: v\in U_{k}\right\},\)
gdzie \(\displaystyle alph_{(V_{N}\cup V_{T})}y\) oznacza zbiór symboli terminalnych i nieterminalnych występujących w słowie \(\displaystyle y\) . Zbiory te tworzą stabilizujący się dla pewnego \(\displaystyle p\) ciąg wstępujący \(\displaystyle U_{1}\subseteq U_{2}\subseteq \ldots \subseteq U_{p}=U_{p+1}\) . Przyjmijmy
Zbiór \(\displaystyle \overline{\overline{P}}\) definiujemy jako zawierający te i tylko te prawa z \(\displaystyle P\) , w których wszystkie symbole tworzące słowa należą do \(\displaystyle \overline{\overline{V}}_{N}\cup \overline{\overline{V}}_{T}\) . Łatwo zauważyć, że tak określona gramatyka \(\displaystyle \overline{\overline{G}}= (\overline{\overline{V}}_{N},\overline{\overline{V}}_{T},v_{0},\overline{\overline{P}})\) spełnia tezę lematu.
W świetle uzyskanych rezultatów dowolną gramatykę bezkontekstową generującą niepusty język można przekształcić w oparciu o Lemat 1.2 na równoważną, a następnie raz jeszcze przekształcić uzyskaną gramatykę stosując konstrukcję opisaną w dowodzie Lematu 1.3, uzyskując ostatecznie gramatykę bez bezużytecznych symboli nieterminalnych, czyli spełniającą tezę powyższego twierdzenia.
Warto podkreślić, iż istotna jest kolejność przekształcania gramatyk. Zmiana kolejności może sprawić, iż nie uzyskamy pożądanego efektu. Załóżmy, dla ilustracji, że w gramatyce \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) istnieje wyprowadzenie \(\displaystyle v_{0}\mapsto^{*}_{G}u_{1}v_{1}u_{2}v_{2}u_{3}\) dla pewnych \(\displaystyle v_{1},v_{2}\in V_{N}\) oraz \(\displaystyle u_{1},u_{2},u_{3}\in (V_{N}\cup V_{T})^{*}\) i jest to jedyna możliwość wygenerowania z \(\displaystyle v_{0}\) słowa, w którym występuje \(\displaystyle v_{1}\) . Istnieje także słowo \(\displaystyle w\in V_{T}^{*}\) i wyprowadzenie \(\displaystyle v_{1}\mapsto^{*}_{G}w\) . Z symbolu \(\displaystyle v_{2}\) nie da się natomiast w gramatyce \(\displaystyle G\) wyprowadzić żadnego słowa terminalnego. Zastosowanie drugiego z powyższych lematów, uzasadniających twierdzenie, nie usunie symboli \(\displaystyle v_{1}\) i \(\displaystyle v_{2}\) z alfabetu nieterminalnego. Lemat pierwszy usunie tylko \(\displaystyle v_{2}\) . Symbol \(\displaystyle v_{1}\) pozostanie, pomimo iż jest bezużyteczny.
Gramatyki w postaci Chomsky'ego i Greibach
Wprowadzimy teraz określenia dwóch szczególnych postaci gramatyk bezkontekstowych, a mianowicie gramatyki w postaci normalnej Chomsky'ego oraz gramatyki w postaci normalnej Greibach.
Definicja 2.1
Gramatyka bezkontekstowa \(\displaystyle G = (V_N,V_T,v_0,P)\) jest
- w postaci normalnej Chomsky'ego, jeśli wszystkie prawa są w formie:
\(\displaystyle v \rightarrow v_1v_2 \;\) lub \(\displaystyle \; v \rightarrow a,\) gdzie \(\displaystyle v, v_1, v_2 \in V_N\), \(\displaystyle a \in V_T\). - w postaci normalnej Greibach, jeśli wszystkie prawa są w formie:
gdzie \(\displaystyle a\in V_{T},\: x\in V_{N}^{*}\) .
Łatwo zaobserwować, że gramatyka zarówno w postaci normalnej Chomsky'ego, jak i w postaci Greibach jest gramatyką właściwą oraz że język generowany przez te gramatyki nie zawiera słowa pustego. Ponadto drzewo wywodu dowolnego słowa w gramatyce w postaci normalnej Chomsky'ego jest binarne.
Twierdzenie 2.1
Dla każdej gramatyki bezkontekstowej \(\displaystyle G\), generującej język bez słowa pustego, istnieje równoważna gramatyka \(\displaystyle H\) w postaci normalnej Chomsky' ego.
Dowód
Zakładamy, że gramatyka \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) jest właściwa. Konstruujemy gramatykę \(\displaystyle H_{1}=\left( V_{N}\cup \overline{V}_{T},V_{T},v_{0},P_{1}\right)\) , gdzie \(\displaystyle \overline{V}_{T}=\left\{ v_{a}\, :\, a\in V_{T}\right\}\) jest kopią alfabetu terminalnego. Zbiór produkcji \(\displaystyle P_{1}\) powstaje z \(\displaystyle P\) przez zamianę w każdej produkcji, której prawa strona nie jest pojedynczą literą terminalną, symbolu \(\displaystyle a\) na \(\displaystyle v_a\) oraz dodaniu produkcji \(\displaystyle v_a \rightarrow a\) dla każdego \(\displaystyle a\in V_{T}\) . Prawdziwa jest równość \(\displaystyle L(G)=L(H_1)\) i w gramatyce \(\displaystyle H_1\) nie występują produkcje typu \(\displaystyle v \rightarrow \overline v\).
Aby uzyskać równoważną gramatykę \(\displaystyle H\) w postaci normalnej Chomsky' ego, produkcje typu \(\displaystyle v \rightarrow v_1... v_n\) dla \(\displaystyle n \geqslant 2\) i \(\displaystyle v_i \in V_N\) występujące ewentualnie w \(\displaystyle H_1\) zastępujemy
produkcjami:dodając do zbioru symboli nieterminalnych nowe elementy \(\displaystyle u_{1},\ldots ,u_{n-2}\) . Skonstruowana w ten sposób gramatyka \(\displaystyle H\) jest w normalnej postaci Chomsky'ego oraz \(\displaystyle L(G)=L(H)\) .
Przedstawiamy poniżej algorytm przekształcający gramatykę bezkontekstową właściwą w gramatykę mającą postać normalną Chomsky'ego.
Algorytm PostaćNormalnaChomsky'ego - buduje gramatykę bezkontekstową w postaci normalnej Chomsky'ego
1 Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa właściwa. 2 Wyjście: \(\displaystyle G'=(V_N', V_T', v_0', P')\) - gramatyka bezkontekstowa w postaci
normalnej Chomsky'ego. 3 \(\displaystyle P' \leftarrow \emtyset\); \(\displaystyle \triangleright\) nowy zbiór produkcji budujemy sukcesywnie 4 \(\displaystyle V_N' \leftarrow V_N\); \(\displaystyle \triangleright\) tak jak i nowe symbole nieterminalne 5 \(\displaystyle V_T' \leftarrow V_T\); \(\displaystyle \triangleright\) symbole terminalne pozostają takie same 6 \(\displaystyle v_0' \leftarrow v_0\); \(\displaystyle \triangleright\) podobnie jak symbol startowy 7 for each \(\displaystyle a \in V_T'\) do 8 \(\displaystyle V_N'\leftarrow V_N'\cup \{ v_a \}\) \(\displaystyle \triangleright\) dodaj nowy symbol nieterminalny 9 end for 10 \(\displaystyle k\leftarrow 1\) \(\displaystyle \triangleright\) licznik produkcji 11 for \(\displaystyle (v \rightarrow x_1x_2...x_m) \in P\) do 12 if \(\displaystyle m=1\) and \(\displaystyle x_1 \in V_T\) then 13 \(\displaystyle P' \leftarrow P' \cup \{v \rightarrow x_1\}\); \(\displaystyle \triangleright\) takie produkcje są dopuszczone 14 else 15 for \(\displaystyle i\leftarrow 1\) to \(\displaystyle m\) do 16 if \(\displaystyle x_i \in V_T'\) then 17 \(\displaystyle P' \leftarrow P' \cup \{v_{x_i} \rightarrow x_i\}\); 18 \(\displaystyle x_i \leftarrow v_{x_i}\); \(\displaystyle \triangleright\) zmień \(\displaystyle (v \rightarrow x_1x_2...x_m)\) na parę produkcji 19 end if 20 end for 21 \(\displaystyle V_N'\leftarrow V_N' \cup \{ u_1^k, u_2^k,\dots, u_{m-2}^k\}\); \(\displaystyle \triangleright\) nowe symbole nieterminalne 22 \(\displaystyle P'\leftarrow P' \cup \{v\rightarrow x_1 u^k_1\}\) \(\displaystyle \triangleright\) nowe produkcje w miejsce \(\displaystyle (v \rightarrow x_1x_2...x_m)\) 23 \(\displaystyle P'\leftarrow P' \cup \{u_{m-2}\rightarrow x_{m-1}x_m\}\) 24 for \(\displaystyle i\leftarrow 1\) to \(\displaystyle m-3\) do 25 \(\displaystyle P' \leftarrow P' \cup \{u_i \rightarrow x_{i+1}u_{i+1}\}\); 26 end for 27 end if 28 end for 29 return \(\displaystyle G'=(V_N', V_T', v_0', P')\);
Przykład 2.1
Gramatykę \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) , dla której \(\displaystyle V_{N}=\{v_0, u,w \}\), \(\displaystyle V_{T}=\{a,b\}\), a zbiór praw dany jest poniżej
sprowadzimy do postaci normalnej Chomsky'ego.
Do zbioru \(\displaystyle P'\) od razu włączamy produkcje \(\displaystyle u \rightarrow a\) oraz \(\displaystyle w \rightarrow b\). Poniżej, dla każdej z pozostałych produkcji wypisane są (po dwukropku) produkcje dodawane do \(\displaystyle P'\):
Ostatecznie gramtyka ma postać:
Uwaga 2.1
Rozumowanie z dowodu twierdzenia o postaci Chomsky'ego można zastosować do gramatyk regularnych prawoliniowych. W wyniku tego uzyskujemy łatwo fakt, że postać normalna Chomsky'ego oznacza tu gramatykę o prawach typu:
{ \(\displaystyle v \rightarrow av'\) lub \(\displaystyle v \rightarrow a\) lub \(\displaystyle v \rightarrow 1\). }
Podobne twierdzenie, w którym mowa o postaci normalnej Greibach podamy poniżej. Przypomnijmy następujące oznaczenie. Dla dowolnego symbolu nieterminalnego \(\displaystyle v\in V_{N}\) w gramatyce \(\displaystyle G\) przez \(\displaystyle P(v)\) oznaczamy podzbiór zbioru produkcji \(\displaystyle P\) zawierający wyłącznie takie produkcje, które po lewej stronie mają symbol \(\displaystyle v\) . Twierdzenie poprzedzimy dwoma lematami. Obserwacja sformułowana w pierwszym lemacie jest oczywista
Lemat 2.1
Niech \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) będzie gramatyką bezkontekstową, a \(\displaystyle v\rightarrow xuy\,\) prawem tej gramatyki dla pewnych \(\displaystyle v,u\in V_{N},\, x,y\in \left( V_{N}\cup V_{T}\right) ^{*}\) . Gramatyka \(\displaystyle \overline{G}=\left( V_{N},V_{T},v_{0},\overline{P}\right)\) , w której
< center>\(\displaystyle \overline{P}=(P - \left\{ v\rightarrow xuy\right\}) \cup \left\{ v\rightarrow xzy\, :\, u\rightarrow z\in P\right\}\)jest równoważna \(\displaystyle G\) .
Usuniętą produkcję \(\displaystyle v \rightarrow xuy\) nazywać będziemy niekońcową v-produkcją.
Definicja 2.2
Niech \(\displaystyle G=(V_N, V_T, v_0, P)\) będzie gramatyką bezkontekstową.
Produkcjęgdzie \(\displaystyle v \in V_N\), \(\displaystyle x \in (V_N \cup V_T)^*\) nazywamy lewostronnie rekursywną.
Kolejny lemat wskazuje możliwość wyeliminowania lewostronnej rekursji z gramatyki generującej język bezkontekstowy.
Lemat 2.2
Niech \(\displaystyle G=\left( V_{N},V_{T},v_{0},P\right)\) będzie gramatyką bezkontekstową oraz \(\displaystyle v\in V_{N}\) . Zakładając niepustość zbioru \(\displaystyle P_{1}(v)=\left\{ v\rightarrow vx\in P(v)\, :\, x\in \left( V_{N}\cup V_{T}\right) ^{*}\right\}\) niech
\(\displaystyle P_{2}(v)=P(v) - P_{1}(v)\) . Gramatyka \(\displaystyle \overline{G}=\left( V_{N}\cup \left\{ u\right\} ,V_{T},v_{0},\overline{P}\right)\) , gdzie \(\displaystyle u\notin V_{N}\) ,
\(\displaystyle \overline{P}= (P - P_{1}(v)) \cup \left\{ v\rightarrow xu\, :\, v\rightarrow x\in P_{2}(v)\right\} \displaystyle \cup \left\{ u\rightarrow x\, :\, v\rightarrow vx\in P_{1}(v)\right\} \displaystyle \cup \left\{ u\rightarrow xu\, :\, v\rightarrow vx\in P_{1}(v)\right\}\)
jest równoważna gramatyce \(\displaystyle G\) .
Dowód
Zaobserwujmy, że w gramatyce \(\displaystyle G\) każdy ciąg produkcji ze zbioru \(\displaystyle P_{1}(v)\) musi zakończyć produkcja z \(\displaystyle P_{2}(v)\) . Zatem wyprowadzenie
można w gramatyce \(\displaystyle \overline{G}\) przeprowadzić następująco:
W podobny sposób można każde wyprowadzenie w \(\displaystyle \overline{G}\) przeprowadzić w \(\displaystyle G\) .
Udowodnimy teraz twierdzenie o postaci normalnej Greibach.
Twierdzenie 2.2
Dla każdej gramatyki bezkontekstowej \(\displaystyle G\), generującej język bez słowa pustego, istnieje równoważna gramatyka bezkontekstowa \(\displaystyle H\) w postaci normalnej Greibach.
Dowód
Załóżmy, że gramatyka \(\displaystyle G\) jest w postaci normalnej Chomsky'ego. W alfabecie nieterminalnym \(\displaystyle V_{N}=\left\{ v_{0},\ldots ,v_{n}\right\}\) wprowadzamy porządek zadany przez indeksy symboli nieterminalnych. Gramatykę \(\displaystyle G\) przekształcimy teraz na równoważną taką, że jeśli \(\displaystyle v_{i}\rightarrow v_{j}x\) jest prawem nowej gramatyki, to \(\displaystyle j>i.\) Efekt taki uzyskamy, przekształcając prawa kolejno, zgodnie z porządkiem wprowadzonym w zbiorze \(\displaystyle V_{N}\) i symbolem nieterminalnym występującym po lewej stronie prawa. Załóżmy, że dla pewnego \(\displaystyle k\), wszystkich \(\displaystyle i=0,\ldots ,k-1\) , gdzie \(\displaystyle 1\leqslant k\leqslant n\) jest:
oraz istnieje \(\displaystyle j<k\) takie, że
W oparciu o lemat 2.1 prawo \(\displaystyle v_{k}\rightarrow v_{j}x\) zastępujemy prawami \(\displaystyle v_{k}\rightarrow v_{l}yx\) , gdzie \(\displaystyle v_{j}\rightarrow v_{l}y\in P\) lub \(\displaystyle v_{k}\rightarrow ayx\) , gdzie \(\displaystyle v_{j}\rightarrow ay\in P\) . Stąd, że \(\displaystyle j<k\) , to \(\displaystyle l>j\) . Powtarzamy to postępowanie (co najwyżej \(\displaystyle k-1\) razy), aż uzyskamy nierówność \(\displaystyle l\geqslant k\) lub prawo \(\displaystyle v_{k}\rightarrow ax\) , gdzie \(\displaystyle a\in V_{T}\) . W przypadku, gdy otrzymamy \(\displaystyle l=k\) , czyli lewą rekursję \(\displaystyle v_{k}\rightarrow v_{k}x\) , stosujemy Lemat 2.2, wprowadzając nowy symbol nieterminalny \(\displaystyle v_{n+k+1}\) . Analogicznie postępujemy, gdy w gramatyce \(\displaystyle G\) występuje lewa rekursja \(\displaystyle v_{k}\rightarrow v_{k}x\) dla \(\displaystyle k=0,...,n\).
W wyniku wprowadzonych przekształceń uzyskamy, równoważną wyjściowej, gramatykę ze zbiorem produkcji \(\displaystyle \overline{P}\) , w którym
gdzie pierwszą literą słowa \(\displaystyle x\), które występuje w trzecim typie produkcji, jest symbol nieterminalny różny od \(\displaystyle v_i\) (nie jest to lewa rekursja). Zauważmy, że każda produkcja z \(\displaystyle \overline{P}(v_{n})\) ma postać \(\displaystyle v_{n}\rightarrow ax\) oraz każda produkcja z \(\displaystyle \overline{P}(v_{n-1})\) ma postać \(\displaystyle v_{n-1}\rightarrow v_{n}x\) lub \(\displaystyle v_{n-1}\rightarrow ax\) . A więc dla \(\displaystyle i=0,...,n\) każda produkcja z \(\displaystyle \overline{P}(v_{i})\) jest postaci \(\displaystyle v_{i}\rightarrow v_{j}x,\: j>i\) lub \(\displaystyle v_{i}\rightarrow ax\) .
Stosujemy teraz Lemat 2.1 do praw ze zbioru \(\displaystyle \overline{P}(v_{n})\) i \(\displaystyle \overline{P}(v_{n-1})\) , tak by prawe strony otrzymanych produkcji zaczynały się symbolem terminalnym. Następnie stosujemy Lemat 2.1 do praw ze zbioru \(\displaystyle \overline{P}(v_{n-2}),\ldots ,\overline{P}(v_{1})\) . Po tych zmianach prawe strony produkcji zaczynają się symbolem terminalnym. Natomiast żadna z produkcji należących do \(\displaystyle \overline{P}(v_{i})\) dla \(\displaystyle i=n+1,\ldots ,2n +1\) nie jest lewą rekursją, co wynika z konstrukcji gramatyki \(\displaystyle \overline{G}\) i z Lematu 2.2. Produkcje te zaczynają się symbolem nieterminalnym i w związku z tym stosujemy kolejny raz Lemat 2.1. W rezultacie uzyskujemy bezkontekstową gramatykę \(\displaystyle H\) w postaci normalnej Greibach równoważną wyjściowej gramatyce \(\displaystyle G\) .
Prezentowany teraz algorytm PrzekształćDlaGreibach przekształca gramatykę bezkontekstową, realizując powyższe dwa lematy, czyli usuwając v-produkcje niekońcowe i eliminując lewostronną rekursję. Zakładamy, bez utraty ogólności, że na wejściu algorytm otrzymuje gramatykę w postaci normalnej Chomsky'ego.
Algorytm PrzekształćDlaGreibach - buduje gramatykę bezkontekstową taką, że każda produkcja jest postaci \(\displaystyle v_k \rightarrow v_jx\), \(\displaystyle k < j\) lub jej prawa strona zaczyna się od symbolu terminalnego
1 Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa w postaci Chomsky'ego. 2 Wyjście: \(\displaystyle G'=(V_N', V_T, v_0, P')\) - gramatyka bezkontekstowa
bez niekońcowych \(\displaystyle v\)-produkcji i bez lewostronnej rekursji. 3 \(\displaystyle V_N' \leftarrow V_N\); \(\displaystyle \triangleright\displaystyle V_N'=\{v_0,\dots, v_n\}\) 4 \(\displaystyle V_T' \leftarrow V_T\); 5 \(\displaystyle P' \leftarrow P\); 6 for \(\displaystyle k \leftarrow 1\) to \(\displaystyle n\) do 7 for \(\displaystyle r=1\) to \(\displaystyle k\) do 8 for \(\displaystyle j=0\) to \(\displaystyle k-1\) do 9 for each \(\displaystyle (v_k \rightarrow v_jx_1\dots x_s) \in P'\) do 10 \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_jx_1\dots x_s\}\); 11 for each \(\displaystyle (v_j \rightarrow y_1\dots y_l) \in P'\) do 12 \(\displaystyle P' \leftarrow P' \cup \{v_k \rightarrow y_1\dots y_lx_1\dots x_s\}\); 13 end for 14 end for 15 end for 16 end for 17 for \(\displaystyle j=0\) to \(\displaystyle k-1\) do 18 for each \(\displaystyle (v_k \rightarrow v_jx_1\dots x_s) \in P'\) do 19 \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_jx_1\dots x_s\}\); 20 end for 21 end for 22 end for 23 for \(\displaystyle k \leftarrow 0\) to \(\displaystyle n\) do 24 for each \(\displaystyle (v_k \rightarrow v_kx_1\dots x_s) \in P'\) do 25 \(\displaystyle V_N'\leftarrow V_N' \cup \{ v_{n+k+1} \}\); 26 \(\displaystyle P' \leftarrow P' \backslash \{v_k \rightarrow v_kx_1\dots x_s\}\); 27 \(\displaystyle P' \leftarrow P' \cup \{v_{n+k+1} \rightarrow x_1\dots x_s\}\); 28 \(\displaystyle P' \leftarrow P' \cup \{ v_{n+k+1} \rightarrow x_1\dots x_s v_{n+k+1}\}\); 29 end for 30 for each \(\displaystyle (v_k \rightarrow y_1 \dots y_s) \in P'\) do 31 if \(\displaystyle y_1 \neq v_k\) then 32 \(\displaystyle P' \leftarrow P' \cup \{v_k \rightarrow y_1 \dots y_s v_{n+k+1}\}\); 33 end if 34 end for 35 end for 36 return \(\displaystyle G'=(V_N', V_T, v_0, P')\);
Kolejny algorytm PostaćNormalnaGreibach przekształca gramatykę bezkontekstową do postaci normalnej Greibach. Zakładamy, że algorytm ten otrzymuje na wejściu gramatykę bezkontekstową właściwą.
Algorytm PostaćNormalnaGreibach - buduje gramatykę bezkontekstową w postaci normalnej Greibach
1 Wejście: \(\displaystyle G=(V_N, V_T, v_0, P)\) - gramatyka bezkontekstowa właściwa.
2 Wyjście: \(\displaystyle G'=(V_N', V_T', v_0', P')\) - gramatyka bezkontekstowa w postaci normalnej Greibach.
3 \(\displaystyle G \leftarrow\)PostaćNormalnaChomsky'ego\(\displaystyle (G)\); \(\displaystyle \triangleright\displaystyle V_N=\{v_0,...,v_n\}\)
4 \(\displaystyle G' \leftarrow\)PrzekształćDlaGreibach\(\displaystyle (G)\); \(\displaystyle \triangleright\displaystyle V_N' \subset \{v_0,...,v_{2n+1}\}\),\(\displaystyle V_T'=V_T\)
5 for \(\displaystyle i\leftarrow n-1\) downto \(\displaystyle 0\) do
6 for \(\displaystyle j\leftarrow 1\) to \(\displaystyle n-i\) do
7 for each \(\displaystyle (v_i \rightarrow v_{i+j}x_1\dots x_s)\in P'\) do
8 \(\displaystyle P'\leftarrow P' \setminus \{ v_i \rightarrow v_{i+j}x_1\dots x_s \}\)
9 for each \(\displaystyle (v_{i+j} \rightarrow z_1 \dots z_l)\in P'\) do
10 if \(\displaystyle z_1\in V_T\) then
11 \(\displaystyle P'\leftarrow P'\cup \{v_i \rightarrow z_1 \dots z_l x_1\dots x_s\}\);
12 end if
13 end for
14 end for
15 end for
16 end for
17 for \(\displaystyle i\leftarrow n+1\) to 2n+1 do
18 for each \(\displaystyle (v_i\rightarrow x_1\dots x_s)\in P'\) do
19 \(\displaystyle P' \leftarrow P' \setminus \{ v_i\rightarrow x_1\dots x_s \}\)
20 for each \(\displaystyle (x_1 \rightarrow z_1 \dots z_l)\in P'\) do
21 \(\displaystyle P'\leftarrow P' \cup \{ v_i \rightarrow z_1 \dots z_l x_2 \dots x_s \}\)
22 end for
23 end for
24 end for
25 \(\displaystyle v_0'\leftarrow v_0\);
26 return \(\displaystyle G'=(V_N', V_T', v_0', P')\);
Przykład 2.2
Gramatykę \(\displaystyle G=\left( V_{N},V_{T},v_{1},P\right)\) , dla której \(\displaystyle V_{N}=\{v_1, v_2, v_3 \}\), \(\displaystyle V_{T}=\{a,b\}\), a zbiór praw dany jest poniżej
sprowadzimy do postaci normalnej Greibach.
Stosujemy procedurę PrzekształćDlaGreibach, wykorzystującą lematy 2.1 oraz 2.2. Prawe strony produkcji rozpoczynających się od \(\displaystyle v_1\) i \(\displaystyle v_2\) rozpoczynają się symbolami terminalnymi lub nieterminalami o wyższych indeksach niż odpowiednio 1 i 2, zatem jedyna produkcja, do której zastosujemy lemat 2.1, to \(\displaystyle v_3 \rightarrow v_1v_2\). Usuwamy ją, a ponieważ prawa jej strona rozpoczyna się nieterminalem \(\displaystyle v_1\), zastępujemy ten nieterminal prawą stroną produkcji \(\displaystyle v_1 \rightarrow v_2v_3\) i nowo otrzymaną produkcję \(\displaystyle v_3 \rightarrow v_2v_3v_2\) dodajemy do \(\displaystyle P\). Ponieważ pierwszy nieterminal po prawej stronie ma niższy indeks niż 3, znowu stosujemy tę samą operację: usuwamy produkcję \(\displaystyle v_3 \rightarrow v_2v_3v_2\) i na jej miejsce wstawiamy produkcje powstałe w wyniku zastąpienia pierwszego \(\displaystyle v_2\) z prawej jej strony łańcuchami \(\displaystyle v_3v_1\) oraz \(\displaystyle b\), czyli prawymi stronami produkcji, po których lewej stronie jest \(\displaystyle v_2\). Otrzymujemy zatem dwie nowe produkcje: \(\displaystyle v_3 \rightarrow v_3v_1v_3v_2\) oraz \(\displaystyle v_3 \rightarrow bv_3v_2\). Teraz każda produkcja jest następującej postaci: albo prawa jej strona zaczyna się terminalem, albo nieterminalem o indeksie większym lub równym indeksowi nieterminala stojącego z lewej strony.
Następny krok to wyeliminowanie lewostronnej rekursji. Stosujemy lemat 2.2 do produkcji \(\displaystyle v_3 \rightarrow v_3v_1v_3v_2\). Usuwamy ją z \(\displaystyle P\) i w jej miejsce wstawiamy produkcje \(\displaystyle v_3 \rightarrow bv_3v_2w_3\), \(\displaystyle v_3 \rightarrow aw_3\), \(\displaystyle w_3 \rightarrow v_1v_3v_2w_3\).
Po zakończeniu działania procedury PrzekształćDlaGreibach otrzymujemy następującą gramatykę:
Wszystkie prawe strony produkcji mających po lewej stronie \(\displaystyle v_3\) zaczynają się od terminala. W pętli (linie 5. - 16.) zastępujemy tymi prawymi stronami nieterminale \(\displaystyle v_3\) stojące jako pierwsze nieterminale po prawej stronie produkcji postaci \(\displaystyle v_2 \rightarrow v_3 x\); w naszym przypadku jedyną taką produkcją jest produkcja \(\displaystyle v_2 \rightarrow v_3v_1\); teraz zarówno produkcje postaci \(\displaystyle v_3 \rightarrow x\) jak i \(\displaystyle v_2 \rightarrow x\) rozpoczynają się terminalami. Po tym przekształceniu gramatyka ma postać:
Prawymi stronami produkcji postaci \(\displaystyle v_2 \rightarrow x\) zastępujemy teraz nieterminale \(\displaystyle v_2\) stojące jako pierwsze nieterminale po prawej stronie produkcji postaci \(\displaystyle v_1 \rightarrow v_2x\). W naszym przypadku jedyną taką produkcją jest produkcja \(\displaystyle v_1 \rightarrow v_2v_3\). Gramatyka wygląda teraz tak:
Ostatecznie, po ukończeniu pętli, każda produkcja mająca po lewej stronie \(\displaystyle v_1\), \(\displaystyle v_2\) lub \(\displaystyle v_3\) zaczyna się terminalem, po którym następuje ciąg nieterminali. Te produkcje są więc w postaci normalnej Greibach.
W ostatnim kroku sprowadzamy do żądanej postaci nieterminale \(\displaystyle w_i\). Obie \(\displaystyle w_3\)-produkcje przekształcamy, zastępując pierwszy nieterminal stojący po ich prawych stronach (czyli \(\displaystyle v_1\)) prawymi stronami produkcji postaci \(\displaystyle v_1 \rightarrow x\). Obie \(\displaystyle w_3\)-produkcje zostaną z \(\displaystyle P\) usunięte, a na ich miejsce dodane zostaną produkcje
oraz
Ostatecznie, gramatyka w postaci Greibach ma postać:
Lemat o pompowaniu dla języków bezkontekstowych. Własności języków bezkontekstowych. Problemy rozstrzygalne
Wprowadzimy i udowodnimy najprostszą wersję lematu o pompowaniu dla języków bezkontekstowych.
Lemat o pompowaniu
Istotną cechą języków regularnych jest własność pompowania, którą ustaliliśmy w lemacie o pompowaniu. Podobną, ale nie taką samą, cechę posiadają języki bezkontekstowe. O ile dla języków regularnych własność pompowania wynikała z istnienia pętli w grafie opisującym automat, to dla języków bezkontekstowych pompowanie jest wynikiem powtarzającego się symbolu nieterminalnego w wyprowadzeniu dostatecznie długiego słowa w gramatyce.
Lemat 1.1
(o pompowaniu) Dla dowolnego języka bezkontekstowego \(\displaystyle L \subset A^*\) istnieją liczby naturalne \(\displaystyle N,M \geqslant 1\) takie, że każde słowo \(\displaystyle w \in L\) o długości \(\displaystyle |w| > N\) można przedstawić w formie \(\displaystyle w=u_1w_1uw_2u_2\), gdzie \(\displaystyle w_{1,}w_{2},v_{1},v_{2},u\in A^{*}\) oraz
- \(\displaystyle |w_1uw_2| \leqslant M\)
- \(\displaystyle w_1w_2 \neq 1\)
- \(\displaystyle u_1w_1^iuw_2^iu_2 \in L\) dla \(\displaystyle i=0,1,...\)
Zanim przeprowadzimy dowód lematu, zobaczmy jak stosuje się ten lemat do języka generowanego przez gramatykę \(\displaystyle (\{v_0,v_1,v_2 \},\{a,b\},v_0,P)\),
gdzie \(\displaystyle P: v_0 \rightarrow v_1v_2, \;v_1 \rightarrow av_2 b , v_2 \rightarrow b\;|\;v_0b.\)
Dowód
Załóżmy, bez utraty ogólności rozważań (dlaczego?), że język bezkontekstowy \(\displaystyle L\) nie zawiera słowa pustego i jest generowany przez gramatykę \(\displaystyle G=(V_N,V_T,v_0,P)\) w normalnej postaci Chomsky'ego. Rozważmy dowolne wyprowadzenie w \(\displaystyle G\)
o długości \(\displaystyle r \geqslant 1\) i \(\displaystyle w_0 \in V_N\). Niech najdłuższa ścieżka w drzewie binarnym \(\displaystyle T\) tego wyprowadzenia ma długość \(\displaystyle k\) (jako długość przyjmujemy tutaj liczbę wierzchołków, przez które przechodzi ścieżka). Indukcyjne ze względu na \(\displaystyle k\) łatwo jest uzasadnić, że
Załóżmy teraz, że zbiór \(\displaystyle V_N\) ma \(\displaystyle p\) elementów i przyjmijmy \(\displaystyle N=2^p\) oraz \(\displaystyle M=2^{p+1}\). Niech \(\displaystyle w \in L(G)\) będzie słowem, którego długość jest większa od \(\displaystyle N\). Zatem najdłuższa ścieżka \(\displaystyle S\) w drzewie wyprowadzenia \(\displaystyle T\) będącego wyprowadzeniem słowa \(\displaystyle w\) w gramatyce \(\displaystyle G\) ma długość co najmniej \(\displaystyle p+2\). A więc przechodzi przez co najmniej \(\displaystyle p+2\) wierzchołków. Stąd, że wierzchołki maksymalne drzewa wyprowadzenia mają etykiety terminalne, wnioskujemy, że w \(\displaystyle S\) występują dwa różne wierzchołki \(\displaystyle s_1, s_2\) etykietowane przez ten sam symbol nieterminalny \(\displaystyle v\). Przyjmijmy, że wierzchołek \(\displaystyle s_1\) jest bliższy wierzchołka początkowego drzewa wyprowadzenia niż \(\displaystyle s_2\). Wierzchołki \(\displaystyle s_1, s_2\) można tak dobrać, aby podścieżka ścieżki \(\displaystyle S\) o początku w wierzchołku \(\displaystyle s_1\) miała długość równą co najwyżej \(\displaystyle p+2\). Zauważmy teraz, że żadna ścieżka poddrzewa \(\displaystyle T_1\), którego wierzchołkiem początkowym jest \(\displaystyle s_1\), nie ma długości większej niż \(\displaystyle p+2\). Jeśli więc \(\displaystyle \overline w\) jest słowem określonym przez liście \(\displaystyle T_1\), to
\(\mbox{(1)}\)
Rozważmy teraz poddrzewo \(\displaystyle T_2\) drzewa \(\displaystyle T\) o wierzchołku początkowym w \(\displaystyle s_2\) i niech \(\displaystyle u\) będzie słowem określonym przez liście \(\displaystyle T_2\). Wtedy \(\displaystyle \overline w= w_1uw_2\) dla pewnych \(\displaystyle w_1, w_2 \in V_T^*\). W połączeniu z nierównością \(\mbox{(1)}\) uzyskujemy pierwszą własność postulowaną w lemacie. Co więcej, \(\displaystyle w_1w_2 \neq 1,\) ponieważ pierwsza produkcja wyprowadzenia \(\displaystyle v\mapsto^{*}\overline{w}\) jest postaci \(\displaystyle v \rightarrow v_1v_2\) dla pewnych \(\displaystyle v_{1},\, v_{2}\in V_{N}\) , a w gramatyce nie ma produkcji wymazującej. Zatem dla pewnych \(\displaystyle u_1, u_2 \in V^*_T\) jest
lub
lub
dla \(\displaystyle i=1,2,\ldots\)
W konsekwencji \(\displaystyle u_1w_1^iuw_2^iu_2 \in L\) dla dowolnego \(\displaystyle i=0,1,...\). Lemat zatem został udowodniony.
Analogicznie jak w przypadku języków regularnych, lemat o pompowaniu dla języków bezkontekstowych stosuje się najczęściej do zasadnienia,
że pewne języki nie należą do rodziny \(\displaystyle \mathcal{L}_{2}.\) Takie właśnie zastosowanie przedstawione jest poniżej, na przykładzie
języka, o którym pó{z}niej udowodnimy, że jest kontekstowy, czyli należy do rodziny języków \(\displaystyle \mathcal{L}_{1}.\)
Przykład 1.1
Niech \(\displaystyle L=\{a^nb^nc^n : n \geqslant 1 \}\). Przeprowadzając rozumowanie nie wprost, a więc zakładając bezkontekstowość tego języka, z lematu o pompowaniu uzyskujemy odpowiednie stałe \(\displaystyle M, N\). Niech \(\displaystyle k > \frac{N}{3}\) i rozważmy słowo \(\displaystyle x_1=a^kb^kc^k\). Zatem istnieje rozkład \(\displaystyle x_1=u_1w_1uw_2u_2\), \(\displaystyle w_1w_2 \neq 1\) oraz \(\displaystyle x_i=u_1w_1^iuw_2^iu_2 \in L\) dla \(\displaystyle i=0,1,...\) Z postaci słów języka \(\displaystyle L\) oraz z faktu \(\displaystyle w_1w_2 \neq 1\) wnioskujemy, że słowa \(\displaystyle w_1, w_2\) są potęgami jednej z liter \(\displaystyle a,b,c\) oraz że \(\displaystyle |x_i| \longrightarrow \infty\), o ile \(\displaystyle i \longrightarrow \infty\). A to wyklucza możliwość zachowania własności określającej język \(\displaystyle L\). Otrzymana sprzeczność prowadzi do wniosku, iż język \(\displaystyle \{a^nb^nc^n: n \geqslant 1 \}\) nie jest bezkontekstowy.
Lemat o pompowaniu wykorzystywany bywa również w dowodach rozstrzygalności pewnych problemów w rodzinie języków rozpoznawalnych. Zagadnieniem tym zajmiemy się w dalszej części tego wykładu.
Własności rodziny języków bezkontekstowych
Przedstawimy teraz podstawowe własności rodziny języków bezkontekstowych związane z zamkniętością ze względu na działania oraz
z problemami jednoznaczności.
Twierdzenie 2.1
Rodzina języków bezkontekstowych \(\displaystyle \mathcal{L}_{2}\) jest zamknięta ze względu na następujące działania:
- sumę mnogościową,
- katenację i operację iteracji \(\displaystyle *\),
- przecięcie (iloczyn mnogościowy) z językiem regularnym,
- homomorfizm.
Dowód
1. Niech \(\displaystyle G_i = (V^i_N ,V_T,v^i_0,P_i)\) będą gramatykami bezkontekstowymi dla \(\displaystyle i=1,2\) takimi, że \(\displaystyle V^1_N \cap V^2_N = \emptyset\) oraz \(\displaystyle L_i = L(G_i)\). Język \(\displaystyle L = L_1 \cup L_2\) jest generowany przez gramatykę bezkontekstową określoną w następujący sposób:
2. Przy powyższych oznaczeniach, język \(\displaystyle L = L_1 \cdot L_2\) jest generowany przez gramatykę bezkontekstową:
Jeśli \(\displaystyle L = L(G)\), dla \(\displaystyle G = (V_N ,V_T,v_0,P)\) gramatyki bezkontekstowej, to \(\displaystyle L^* = L(\overline{G})\) dla gramatyki
która jest również gramatyką bezkontekstową.
3. Niech \(\displaystyle R\) będzie dowolonym językiem rozpoznawanym przez pewien automat skończenie stanowy \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\). Język ten możemy przedstawić w postaci sumy \(\displaystyle R=\bigcup_{i=1}^k R_i\), w której każdy język \(\displaystyle R_i\) jest rozpoznawany przez automat \(\displaystyle \mathcal{A}\) , w którym jako stan końcowy przyjmujemy \(\displaystyle t_i \in T\). Rodzina języków bezkontekstowych jest zamknięta ze względu na sumę mnogościową i oczywista jest równość \(\displaystyle L \cap R= \bigcup _{i=1}^k (L \cap R_i)\). Wystarczy zatem udowodnić, że język \(\displaystyle L \cap R_i\) jest bezkontekstowy. Załóżmy, że \(\displaystyle T=\{t \}\) oraz \(\displaystyle L\) jest językiem generowanym przez gramatykę bezkontekstową \(\displaystyle G = (V_N ,V_T,v_0,P)\) w normalnej postaci Chomsky'ego. Bez utraty ogólności rozważań można także założyć, że \(\displaystyle 1\notin L\). Konstruujemy gramatykę
dla której \(\displaystyle P_H\) zawiera następujące produkcje:
- \(\displaystyle (s_1,v_1,s_2) \rightarrow (s_1,v_2,s_3)(s_3,v_3,s_2)\) dla \(\displaystyle s_i \in S\), \(\displaystyle v_i \in V_N\) jeśli \(\displaystyle v_1\rightarrow v_2v_3 \in P,\)
- \(\displaystyle (s_1,v_1,s_2) \rightarrow (s_1,a,s_2)\) dla \(\displaystyle s_i \in S\), \(\displaystyle a \in V_T\) jeśli \(\displaystyle v_1\rightarrow a \in P,\)
- \(\displaystyle (s_1,a,s_2)\rightarrow a\) dla \(\displaystyle s_i \in S\), \(\displaystyle a \in V_T\) jeśli \(\displaystyle f(s_1,a)=s_2.\)
Bezpośrednio z konstrukcji wynika, że gramatyka \(\displaystyle H\) jest bezkontekstowa. Łatwo również zauważyć, że język generowany przez gramatykę \(\displaystyle H\) jest równy \(\displaystyle L \cap R\).
4. Niech \(\displaystyle h: A^* \longrightarrow B^*\) oznacza dowolny homomorfizm, a \(\displaystyle L \subset A^*\) językiem bezkontekstowym generowanym przez gramatykę \(\displaystyle G = (V_N ,A,v_0,P)\). Rozszerzamy homomorfizm \(\displaystyle h\) do wolnych monoidów \(\displaystyle (A \cup V_N)^*\) i \(\displaystyle (B \cup V_N)^*\), przyjmując, że \(\displaystyle h\) na zbiorze \(\displaystyle V_N\) jest równe identyczności. Łatwo zauważyć, że język \(\displaystyle h(L)\) jest generowany przez gramatykę bezkontekstową \(\displaystyle G = (V_N, B, v_0, P_h)\), w której
Z równości \(\displaystyle L\setminus R=L\cap \overline{R}\) , zamkniętości klasy \(\displaystyle \mathcal{L}_{3}\) ze względu na zupełnienie
oraz z punktu 3 udowodnionego powyżej twierdzenia wynika następujący wniosek.
Wniosek 2.1
Niech \(\displaystyle L \subset A^*\) będzie dowolonym językiem bezkontekstowym, a \(\displaystyle R \subset A^*\) regularnym. Wtedy \(\displaystyle L \setminus R\) jest językiem bezkontekstowym.
Bez dowodu podajemy dwie dalsze własności związane z zamkniętością rodziny języków bezkontekstowych.
Fakt 2.1
Rodzina języków bezkontekstowych \(\displaystyle \mathcal{L}_{2}\) jest zamknięta ze względu na podstawienie regularne i przeciwobraz przez homomorfizm.
Rodzina języków bezkontekstowych nie jest zamknięta na wszystkie działania boolowskie. Jak wynika z poniższego twierdzenia, jedynym działaniem boolowskim nie wyprowadzającym poza rodzinę języków bezkontekstowych jest suma mnogościowa.
Twierdzenie 2.2
Rodzina języków bezkontekstowych \(\displaystyle \mathcal{L}_{2}\) nie jest zamknięta ze względu na:
- iloczyn mnogościowy,
- uzupełnienie.
Dowód
Dla \(\displaystyle i=1,2\) niech \(\displaystyle G_i = (\{ v_0 , v_1\},\{ a,b,c\},{v_0},P_i)\) będą gramatykami o następujących zbiorach praw:
Gramatyki te są bezkontekstowe i generują, odpowiednio, następujące języki:
Języki te są bezkontekstowe, lecz ich przecięcie
jest językiem istotnie kontekstowym.
Z udowodnionej właśnie własności oraz z praw de'Morgana wynika, że rodzina \(\displaystyle \mathcal{L}_{2}\) nie jest też domknięta ze względu na uzupełnienie.
Jednoznaczność języków bezkontekstowych
Omówimy teraz, dość ogólnie zresztą, problem występujący w niektórych gramatykach bezkontekstowych, a polegający na wielokrotnym wyprowadzeniu tego samego słowa. Z punktu widzenia języków programowania, których syntaktykę opisują, w pewnym zakresie, gramatyki bezkontekstowe, taka nadmiarowość (niejednoznaczność parsingu) jest cechą wysoce niepożądaną. Gramatyki, które nie będą mieć takiej własności nazwiemy jednoznacznymi. Jednoznacznym nazwiemy też język, dla którego istnieje gramatyka jednoznaczna.
Definicja 3.1
Niech \(\displaystyle G = (V_N,V_T,v_0,P)\) będzie gramatyką bezkontekstową. Lewostronnym (prawostronnym) wyprowadzeniem słowa \(\displaystyle w \in {V_T}^*\) w gramatyce \(\displaystyle G\) nazywamy wyprowadzenie
Jeśli chcemy zaznaczyć, że wyprowadzenie jest lewostronne lub prawostronne, to posługujemy się zapisem
Każde wyprowadzenie słowa w gramatyce bezkontekstowej można tak uporządkować, by sekwencja produkcji tworzyła prawostronne lub lewostronne wyprowadzenie. Stąd wynika też fakt, że dowolne słowo generowane przez gramatykę bezkontekstową ma tyle samo wyprowadzeń lewostronnych, co prawostronnych. Ilość różnych wyprowadzeń danego słowa jest w niektórych zastosowaniach gramatyk bezkontekstowych dość istotna, choćby w problemach parsingu, czyli poszukiwania w gramatyce wyprowadzenia dla danego słowa. Ilość różnych wyprowadzeń słów w gramatyce stanowi pewną informację na temat nadmiarowości tej gramatyki. Bardzo istotną rolę odgrywają zarówno w teorii, jak i zastosowaniach - gramatyki bezkontekstowe jednoznaczne, których definicję podajemy poniżej.
Definicja 3.2
Gramatyka bezkontekstowa \(\displaystyle G\) jest jednoznaczna wtedy i tylko wtedy, gdy każde słowo generowane przez tę gramatykę ma dokładnie jedno wyprowadzenie lewostronne (prawostronne). Język bezkontekstowy \(\displaystyle L\) nazywamy jednoznacznym, jeśli istnieje jednoznaczna gramatyka bezkontekstowa generująca ten język.
Jednoznaczność gramatyki oznacza istnienie dokładnie jednego drzewa wywodu dla każdego generowanego słowa. W klasie gramatyk bezkontekstowych problem jednoznaczności jest nierozstrzygalny. W rozdziale poświęconym algorytmicznej rozstrzygalności wrócimy do tego zagadnienia. Oczywiście wobec powyższego nierozstrzygalny jest też problem jednoznaczności języka. Problem jednoznaczności gramatyki i języka jest rozstrzygalny w podklasach języków bezkontekstowych, na przykład dla klasy języków ograniczonych, to znaczy takich
\(\displaystyle L\subset A^{*}\) , że \(\displaystyle L\subset w_{1}^{*}...w_{n}^{*}\) dla pewnych słów \(\displaystyle w_{1},...,w_{n}\in A^{*}\) .
Przykład 3.1
Język \(\displaystyle \left\{ a^{n}b^{n+m}c^m\, :\, n,m>0\right\}\) generowany przez gramatykę \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) , gdzie \(\displaystyle V_{N}=\{v_{0},v_{1}\}\) , \(\displaystyle V_{T}=\{a,b,c\}\) oraz
\(\displaystyle P= v_{0}\rightarrow v_1 v_2 , \;\; v_1 \rightarrow av_{1}b\;|ab, \;\; v_2 \rightarrow bv_2c, \;|bc\)
jest, jak łatwo sprawdzić, językiem jednoznacznym.
Mówimy, że język \(\displaystyle L\in \mathcal{L}_{2}\) jest niejednoznaczny, jeśli nie jest jednoznaczny, czyli nie istnieje gramatyka jednoznaczna generująca ten język. Przykładem języka niejednoznacznego jest
Uzasadnienie tego faktu jest dosyć żmudne i dlatego zostało tutaj pominięte.
Zauważmy na koniec tego krótkiego omówienia problematyki jednoznaczności gramatyk, że każdy język regularny (ale nie każda gramatyka regularna) jest jednoznaczny. Jednoznaczna jest bowiem gramatyka otrzymana z automatu deterministycznego generującego ten język.
Jednoznaczny jest również język bezkontekstowy, który jest iloczynem \(\displaystyle L\cap R\) , gdzie \(\displaystyle L\in \mathcal{L}_{2}\) i jest językiem jednoznacznym, a \(\displaystyle R\in \mathcal{L}_{3}\) . Gramatyka tego języka, skonstruowana w punkcie 3 w twierdzeniu 2.1 jest jednoznaczna, co wynika stąd, że automat rozpoznający \(\displaystyle R\) jest deterministyczny.
Problemy rozstrzygalne algorytmicznie
Podobnie jak dla języków regularnych tak i w przypadku bezkontekstowych lemat o pompowaniu wykorzystuje się do uzasadnienia rozstrzygalności pewnych problemów. Dla rodziny języków bezkontekstowych mamy następujące twierdzenie.
Twierdzenie 4.1
W rodzinie języków bezkontekstowych \(\displaystyle \mathcal{L}_{2}\) następujące problemy są rozstrzygalne:
- problem niepustości języka, \(\displaystyle L\neq \emptyset,\)
- problem nieskończoności języka, \(\displaystyle card\, L=\aleph _{0},\)
- problem należenia słowa \(\displaystyle w\) do języka \(\displaystyle L.\)
Dowód
Aby udowodnić punkt 1, wykorzystamy następującą równoważność:
Uzasadnienie tej równoważności polega na rozkładzie słowa \(\displaystyle w\) spełniającego warunek \(\displaystyle N<|w|\) (zgodnie z oznaczeniami i tezą lematu o pompowaniu) i zastąpieniu go słowem \(\displaystyle u_{1}uu_{2}\) , które jest istotnie krótsze. Po skończonej ilości takich skracających kroków dostaniemy słowo należące do języka \(\displaystyle L\) i spełniające warunek \(\displaystyle |w|\leqslant N\) .
W uzasadnieniu punktu 2 wykorzystamy równoważność
gdzie \(\displaystyle M,N\) są stałymi z lematu o pompowaniu.
Przyjmując, iż język \(\displaystyle L\) jest nieskończony, wnioskujemy, że istnieją w tym języku słowa dowolnie długie. Niech \(\displaystyle w\in L\) i \(\displaystyle |w|>N\) . Jeśli \(\displaystyle w\) nie spełnia warunku \(\displaystyle |w|\leqslant N+M\) , to stosujemy lemat o pompowaniu dla \(\displaystyle i=0\) , uzyskując słowo \(\displaystyle u_{1}uu_{2}\) należące do języka i istotnie krótsze od \(\displaystyle w\) . Z warunku \(\displaystyle |w_{1}w_{2}|\leqslant |w_{1}uw_{2}|\leqslant M\) (punkt 1 tezy lematu o pompowaniu) wynika, iż różnica długości tych słów nie może być wieksza niż stała \(\displaystyle M\) . Zatem po skończonej ilości kroków uzyskujemy słowo należące do języka i spełniające żądany warunek.
Implikacja w przeciwną stronę ( \(\displaystyle \Leftarrow\) ) wynika bezpośrednio z lematu o pompowaniu. Istnieje mianowicie nieskończony zbiór słów w postaci
dla \(\displaystyle i=0,1,2,....\)
Punkt 3 twierdzenia wymaga podania odpowiedniego algorytmu. Jego prezentacją i omówieniem zajmujemy się poniżej.
Algorytm CYK - przynależność słowa do języka.
Rozważmy problem przynależności słowa \(\displaystyle w\) do danego języka, generowanego przez gramatykę bezkontekstową \(\displaystyle G\). Jest to problem rozstrzygalny. Bardzo łatwo podać algorytm, wykorzystujący postać normalną Greibach. Po sprowadzeniu gramatyki \(\displaystyle G\) do postaci normalnej Greibach prawa strona każdej produkcji rozpoczyna się symbolem terminalnym i jest to jedyny symbol terminalny. Zatem jeśli \(\displaystyle w=a_1a_2...a_n\), to należy zbadać wszystkie wywody w \(\displaystyle G\), z symbolu początkowego \(\displaystyle S\), o długości dokładnie \(\displaystyle |w|\), to znaczy wywody złożone z dokładnie \(\displaystyle |w|\) kroków. Jeśli dla każdego symbolu nieterminalnego istnieje co
najwyżej \(\displaystyle k\) produkcji w gramatyce \(\displaystyle G\), w których pojawia się on po lewej stronie, to algorytm będzie działał w czasie \(\displaystyle O(k^{|w|})\). Metoda ta jest jednak bardzo nieefektywna. Czasochłonne jest też samo sprowadzenie gramatyki \(\displaystyle G\)
do postaci normalnej Greibach.
Istnieje szybszy algorytm rozwiązujący problem przynależności do języka. Jest to algorytm Cocke'a-Youngera-Kasamiego, w skrócie CYK.
Algorytm CYK działa w oparciu o ideę programowania dynamicznego . Rozważmy słowo \(\displaystyle w=a_1a_2...a_n\) oraz gramatykę \(\displaystyle G\). Niech zbiór \(\displaystyle V_i^j\) zawiera wyłącznie te symbole nieterminalne, z których można wywieść słowo \(\displaystyle a_ia_{i+1}...a_{i+j-1}\), czyli
Mamy zatem następującą równoważność:
Algorytm Cocke-Younger-Kasami - sprawdza, czy dane słowo
należy do języka generowanego przez gramatykę bezkontekstową
1 Wejście: \(\displaystyle G=(V_N, V_T, P, v_0)\), \(\displaystyle w \in V_T^*\) - gramatyka bezkontekstowa i słowo
\(\displaystyle w=a_1a_2...a_n\) o długości \(\displaystyle n\).
2 Wyjście: TAK lub NIE - odpowiedź na pytanie, czy \(\displaystyle w \in L(G)\).
3 \(\displaystyle G \leftarrow\)PostaćNormalnaChomsky'ego\(\displaystyle (G)\);
4 for \(\displaystyle i=1,...,n\) do
5 \(\displaystyle V_i^1 \leftarrow \{v \in V_N:\ (v \rightarrow a) \in P, a \in V_T\ \wedge\ a_i=a \}\);
6 end for
7 for \(\displaystyle j=2,...,n\) do
8 for \(\displaystyle i=1,...,n-j+1\) do
9 \(\displaystyle V_i^j \leftarrow\);
10 for \(\displaystyle k=1,...,j-1\) do
11 \(\displaystyle V_i^j \leftarrow V_i^j \cup \{v \in V_N:\ (v \rightarrow wy) \in P,\ w \in V_i^k,\ y \in V_{i+k}^{j-k}\}\);
12 end for
13 end for
14 end for
15 if \(\displaystyle v_0 \in V_1^n\)
16 return TAK, \(\displaystyle w \in L(G)\);
17 else
18 return NIE, \(\displaystyle w \not \in L(G)\);
19 end if
Algorytm CYK działa w czasie \(\displaystyle |w|^3\), gdzie \(\displaystyle |w|\) jest długością słowa, o którego przynależność do języka pytamy.
Przykład 4.1
Zbadamy, czy słowo \(\displaystyle w=bbaaaa\) należy do języka generowanego gramatyką:
gdzie \(\displaystyle v\) jest symbolem początkowym.
Poniższa animacja ilustruje działanie algorytmu CYK.
Automat ze stosem
W tym wykładzie określimy automat ze stosem rozpoznający języki bezkontekstowe. Wprowadzimy dwie definicje rozpoznawania języków przez automat ze stosem oraz omówimy ważną podklasę języków bezkontekstowych, mianowicie języków rozpoznawanych przez deterministyczne automaty ze stosem. Uzasadnimy też fakt, iż rodzina języków rozpoznawana przez automaty ze stosem pokrywa się z rodziną jezyków bezkontekstowych.
Automaty ze stosem to systemy rozpoznające języki bezkontekstowe. Ich działanie jest nieco bardziej skomplikowane niż działanie automatu skończenie stanowego. Poza możliwością zmiany stanu pod wpływem czytanego symbolu umieszczonego na taśmie wejściowej automat ten posiada także taśmę stosu, na którą może wpisywać słowa, jak i odczytywać pojedynczy symbol znajdujący się na wierzchu stosu.
Definicja 1.1
Automatem ze stosem nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{AS}=(A,A_{S},Q,f,s_{0},z_{0},Q_{F})\) , w którym:
\(\displaystyle A\) - jest alfabetem,
\(\displaystyle A_{S}\) - jest dowolnym skończonym i niepustym zbiorem zwanym alfabetem stosu (niekoniecznie rozłącznym z \(\displaystyle A\) ),
\(\displaystyle Q\) - jest dowolnym, skończonym i niepustym zbiorem zwanym zbiorem stanów,
\(\displaystyle f:A_{S}\times Q\times (A\cup \left\{ 1\right\} )\longrightarrow \mathcal{P}_{sk}(A_{S}^{*}\times Q)\) jest funkcją przejść, której wartościami są skończone podzbiory \(\displaystyle A_{S}^{*}\times Q\) (także zbiór pusty),
\(\displaystyle q_{0}\in Q\) jest stanem początkowym,
\(\displaystyle z_{0}\in A_{S}\) symbolem początkowym stosu,
\(\displaystyle Q_{F}\subset Q\) zbiorem stanów końcowych.
Badając działanie automatu ze stosem, wygodniej jest, zamiast funkcji przejść \(\displaystyle f\), rozważać skończoną relację \(\displaystyle P\subset (A_{S}\times Q\times (A\cup \left\{ 1\right\} ))\times (A_{S}^{*}\times Q)\) zwaną relacją przejść. Elementy tej relacji nazywane są prawami. Relacja \(\displaystyle P\) jest zatem skończonym zbiorem praw o następującej postaci:
- \(\displaystyle zq_i \longrightarrow uq_j\) dla \(\displaystyle z \in A_S, \;\; u \in A_S^*, \;\; q_i ,q_j \in Q\),
- \(\displaystyle zq_i a \longrightarrow uq_j\) dla \(\displaystyle z \in A_S, \;\; u \in A_S^*, \;\; a \in A, \;\;q_i ,q_j \in Q\).
Często, używając relacji przejść, oznaczamy automat ze stosem jako układ:
Prawo \(\displaystyle zq_{i}a\longrightarrow uq_{j}\) będziemy reprezentować grafem:
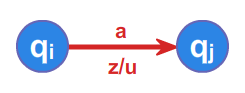
Napis \(\displaystyle z/u\) oznacza, iż symbol \(\displaystyle z\) pobrany ze stosu wymieniany jest na słowo \(\displaystyle u\) utworzone nad alfabetem stosu \(\displaystyle A_S\).
Natomiast prawo \(\displaystyle zq_{i}\rightarrow uq_{j}\) interpretowane jest graficznie jako:
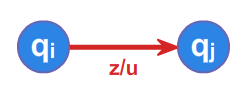
Działanie automatu ze stosem \(\displaystyle \mathcal{AS}\) zależne jest, jak wspomnieliśmy we wstępie wykładu, nie tylko od czytanego przez automat słowa, ale także od symbolu znajdującego się na wierzchu stosu. Poniżej przedstawiamy graficznie te zależności.
Prawo \(\displaystyle zq_{i}a\longrightarrow uq_{j}\) dla słowa \(\displaystyle u=z_{1}\ldots z_{m}\) określające działanie automatu \(\displaystyle \mathcal{AS}\) interpretujemy w ten sposób, że automat, będąc w stanie \(\displaystyle q_{i}\) po przeczytaniu litery \(\displaystyle a\) (ze słowa wejściowego) i symbolu \(\displaystyle z\) ze stosu, zmienia stan na \(\displaystyle q_{j}\) oraz zastępuje na stosie literę \(\displaystyle z\) słowem \(\displaystyle u\) w ten sposób, że ostatnia litera tego słowa, symbol \(\displaystyle z_{m}\) , jest na wierzchu stosu. Ten właśnie symbol będzie pobrany ze stosu przy kolejnym "ruchu" automatu, zgodnie z zasadą last in, first out. Ilustruje tę zasadę animacja, która jest zamieszczona będzie w dalszej części tego wykładu.
Dla precyzyjnego opisu działania automatu ze stosem wprowadza się pojęcie konfiguracji automatu, poprzedzając to pojęcie określeniem konfiguracji wewnętrznej.
Definicja 1.2
Konfiguracją wewnętrzną automatu ze stosem \(\displaystyle AS\) nazywamy dowolną parę \(\displaystyle (u,q)\in A_{S}^{*}\times Q\) taką, że \(\displaystyle q\) jest stanem, w którym automat znajduje się aktualnie, a \(\displaystyle u\) słowem zapisanym na stosie tak, że litera będąca na wierzchu stosu jest ostatnią literą tego słowa.
Konfiguracją automatu ze stosem \(\displaystyle AS\) nazywamy trójkę
gdzie \(\displaystyle (u,q)\) jest konfiguracją wewnętrzną, a \(\displaystyle w\) słowem wejściowym.
Wprowadzone pojęcia wykorzystamy do określenia działania automatu ze stosem dla dowolnych słów wejściowych i dowolnych słów znajdujących się na stosie. W tym celu rozszerzymy odpowiednio relację przejść \(\displaystyle P\) , określając ją na zbiorze konfiguracji i oznaczając symbolem \(\displaystyle |\! \! \! \Longrightarrow\) . Przyjmujemy dla dowolnych słów \(\displaystyle u_{1},u_{2}\in A_{S}^{*}\) i litery \(\displaystyle z\in A_{S}\) , dla dowolnego słowa \(\displaystyle w\in A^{*}\) i \(\displaystyle a\in A\cup \left\{ 1\right\}\) oraz dla dowolnych stanów \(\displaystyle q_{1},q_{2}\in Q\) , że zachodzi relacja
wtedy i tylko wtedy, gdy \(\displaystyle zq_{1}a\longrightarrow u_{2}q_{2}\in P\) .
Zwrotne i przechodnie domknięcie tej relacji nazywamy przejściem lub poprawnym obliczeniem automatu \(\displaystyle AS\) i oznaczamy symbolem \(\displaystyle |\! \! \! \Longrightarrow ^{*}\) .
Dla dowolnego słowa \(\displaystyle w\in A^{*}\) przyjmujemy oznaczenie \(\displaystyle (u,q)\, \mid \! \Longrightarrow ^{w}\, (u_{1},q_{1})\) , jeśli ma miejsce \(\displaystyle (u,q,w)|\! \! \! \Longrightarrow ^{*}(u_{1},q_{1},1)\) . Prawdziwa jest wówczas następująca równość:
Mówimy, że konfiguracja wewnętrzna \(\displaystyle (u,q)\) automatu ze stosem \(\displaystyle AS\) jest osiągalna z konfiguracji wewnętrznej \(\displaystyle (u_{1},q_{1})\), jeśli istnieje takie słowo \(\displaystyle w\in A^{*}\), że
Zdefiniujemy teraz język rozpoznawany przez automat ze stosem. W literaturze spotkać można kilka równoważnych definicji rozpoznawania. W naszym wykładzie wprowadzimy dwie, używane najczęściej:
- rozpoznawanie poprzez stany końcowe (wyróżniony zbiór stanów końcowych \(\displaystyle Q_{F}\) ),
- rozpoznawanie poprzez pusty stos.
Definicja 1.3
Niech \(\displaystyle \mathcal{AS}=(A,A_{S},Q,P,s_{0},z_{0},Q_{F})\) będzie automatem ze stosem. Językiem rozpoznawanym przez automat \(\displaystyle \mathcal{AS}\) poprzez stany końcowe nazywamy zbiór
Językiem rozpoznawanym przez automat \(\displaystyle \mathcal{AS}\) poprzez pusty stos nazywamy zbiór
Używając drugiego określenia rozpoznawania, w definicji automatu ze stosem pomija się zbiór stanów końcowych \(\displaystyle Q_{F}\) .
Przykład 1.1
Poniższa animacja ilustruje działanie automatu ze stosem. Przedstawiony grafem automat ze stosem \(\displaystyle \mathcal{AS}=(A,A_{S},\{q_0,q_F\},P,q_{0},z_{0},\{q_{F}\})\), w którym alfabet stosu \(\displaystyle A_{S}=\{z_{0},a,b\}\) rozpoznaje język bezkontekstowy
Animacja 2
Zauważmy, że automat ten rozpoznaje ten sam język zarówno zarówno przez stany końcowe ( \(\displaystyle Q_{F}=\{q_{F}\}\) ), jak i w sensie rozpoznawania przez pusty stos.
W ogólności dla ustalonego automatu ze stosem \(\displaystyle \mathcal{AS}\) wprowadzone wyżej dwa sposoby rozpoznawania niekoniecznie prowadzą do tego samego języka. Jednak są one równoważne, o czym przekonuje następujące twierdzenie, w dowodzie którego konstruujemy odpowiednie automaty ze stosem.
Twierdzenie 1.1
Język \(\displaystyle L\subset A^{*}\) jest rozpoznawany przez automat ze stosem przez stany końcowe wtedy i tylko wtedy, gdy jest rozpoznawany przez automat ze stosem poprzez pusty stos.
Dowód
Załóżmy, że automat \(\displaystyle \mathcal{AS}=(A,A_{S},Q,P,s_{0},z_{0},Q_{F})\) rozpoznaje przez stany końcowe język \(\displaystyle L=L_{F}(\mathcal{AS})\) . Wówczas automat
w którym symbol \(\displaystyle x_{0}\) jest spoza alfabetu \(\displaystyle A_{S}\) , stany \(\displaystyle q_{0}',q_{e}\) nie należą do \(\displaystyle Q\) , a relacja przejść \(\displaystyle P'\) określona jest poniżej
rozpoznaje język \(\displaystyle L\) przez pusty stos.
Na odwrót, jeśli automat ze stosem \(\displaystyle \mathcal{AS}=(A,A_{S},Q,P,q_{0},z_{0})\) rozpoznaje poprzez pusty stos język \(\displaystyle L=L_{e}(\mathcal{AS})\) , to automat
w którym symbol \(\displaystyle x_{0}\) jest spoza alfabetu \(\displaystyle A_{S}\) , stany \(\displaystyle q_{0}',q_{F}\) nie należą do \(\displaystyle Q\) , a relacja przejść \(\displaystyle P'\) określona jest poniżej
rozpoznaje język \(\displaystyle L\) poprzez stany końcowe.
Zdefiniujemy i omówimy teraz deterministyczne automaty ze stosem. W odróżnieniu od automatów skończenie stanowych deterministyczne automaty ze stosem posiadają mniejsze możliwości rozpoznawania języków niż automaty, które dopuszczają przejścia niedeterministyczne.
Definicja 1.4
Automat ze stosem \(\displaystyle \mathcal{AS}=(A,A_{S},Q,f,s_{0},z_{0},Q_{F})\) nazywamy deterministycznym, jeśli dla każdej konfiguracji \(\displaystyle (z,q,a)\in A_{S}\times Q\times (A\cup \left\{ 1\right\} )\) wartość funkcji \(\displaystyle f(z,q,a)\) jest zbiorem co najwyżej jednoelementowym, czyli \(\displaystyle \sharp f(z,q,a)\leqslant 1\) oraz jeśli \(\displaystyle f(z,q,1)\neq \emptyset\) , to \(\displaystyle f(z,q,a)=\emptyset,\) dla każdego \(\displaystyle a\in A\) .
A więc deterministyczny automat ze stosem ma możliwość co najwyżej jednego przejścia z dowolnej konfiguracji \(\displaystyle (z,q,a)\in A_{S}\times Q\times (A\cup \left\{ 1\right\} )\) oraz jeśli istnieje przejście dla określonego stanu i symbolu ze stosu pod wpływem słowa pustego, to jest ono jedynym możliwym dla tego układu w tym automacie.
Język rozpoznawany przez deterministyczny automat ze stosem nazywamy językiem deterministycznym.
O tym, że, w przeciwieństwie do klasy języków regularnych, języki rozpoznawane przez deterministyczne automaty ze stosem stanowią właściwą podklasę wszystkich języków akceptowanych przez automaty ze stosem, przekonuje przykład.
Przykład 1.2
Język \(\displaystyle L=\{a^{n}b^{n}:\: n\geqslant 1\}\cup \{a^{n}b^{2n}:\: n\geqslant 1\}\) rozpoznawany przez automat ze stosem opisany grafem
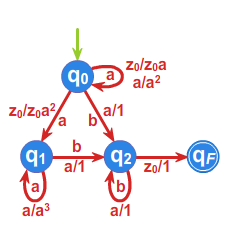
nie jest językiem deterministycznym. Zauważmy bowiem, że deterministyczny automat ze stosem, aby zaakceptować słowo \(\displaystyle a^{n}b^{n}\) , dla kontrolowania ilości liter \(\displaystyle a\) i \(\displaystyle b\) wykorzystuje stos, wprowadzając przy czytaniu każdej litery \(\displaystyle a\) ustalony symbol na stos, na przykład \(\displaystyle "a"\) i usuwając sekwencyjnie te symbole przy czytaniu liter \(\displaystyle b\) . Dla zaakceptowania słowa \(\displaystyle a^{n}b^{2n}\) podobne postępowanie prowadzi do wpisywania na stos słowa \(\displaystyle "aa"\) z alfabetu stosu dla każdej litery \(\displaystyle a\) i usuwaniu pojedynczego symbolu przy czytaniu \(\displaystyle b\) . Jest to jedyny sposób kontroli ilości liter, a opisane działanie automatu jest źródłem jego istotnej niedeterministyczności. Bez trudu można zauważyć, że każdy automat ze stosem rozpoznający język \(\displaystyle L\) będzie zawierać ten niedeterministyczny układ w swojej strukturze.
Aby lepiej uchwycić istotę tego niedeterminizmu, zauważmy, że automat ze stosem określony grafem
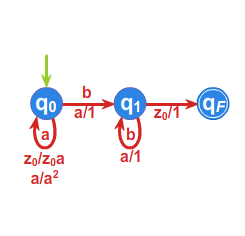
rozpoznaje język \(\displaystyle L=\{a^{n}b^{n}:\: n\geqslant 1\}\) i jest deterministyczny.
Każdy język rozpoznawany przez deterministyczny automat ze stosem
jest oczywiście (dlaczego?) jednoznaczny. Jednoznaczność języka nie implikuje jednak jego deterministyczności, o czym przekonuje zamieszczony poniżej przykład.
Przykład 1.3
Język \(\displaystyle L=\{a^{n}b^{n}:\: n\geqslant 1\}\cup \{a^{n}b^{2n}:\: n\geqslant 1\}\) , który jest rozpoznawany przez automat ze stosem z poprzedniego przykładu, nie jest, jak wiemy, deterministyczny, ale jest jednoznaczny.
Gramatyki bezkontekstowe i automaty ze stosem
Automaty ze stosem charakteryzują rodzinę języków bezkontekstowych w tym samym sensie, w jakim automaty skończenie stanowe charakteryzują języki regularne.
Twierdzenie 2.1
Rodzina języków rozpoznawanych przez automaty ze stosem jest równa rodzinie języków bezkontekstowych \(\displaystyle \mathcal{L}_{2}\) .
Dowód
(szkic)
Dla dowodu, że każdy język bezkontekstowy jest rozpoznawany przez odpowiedni automat ze stosem, rozważmy gramatykę \(\displaystyle G=(V_{N},V_{T},v_{0},P_{G})\) bezkontekstową w postaci normalnej Greibach i załóżmy, że słowo puste \(\displaystyle 1\) nie należy do języka \(\displaystyle L(G)\) generowanego przez tę gramatykę. Podamy konstrukcję automatu ze stosem \(\displaystyle AS\) , który, jak można wykazać, akceptuje poprzez pusty stos język \(\displaystyle L(G)\) . Niech
gdzie funkcja \(\displaystyle f:(V_{N}\cup V_{T})\times \{q\}\times (V_{T}\cup \left\{ 1\right\} )\longrightarrow \mathcal{P}_{sk}((V_{N}\cup V_{T})^{*}\times \{q\})\) określona jest następująco. Dla dowolnych \(\displaystyle v\in V_{N},\: a\in V_{T}\)
oraz ma wartość równą zbiorowi pustemu \(\displaystyle \emptyset\) we wszystkich pozostałych przypadkach.
Jest to więc automat o jednym stanie \(\displaystyle q\) , alfabetem wejściowym jest alfabet terminalny \(\displaystyle V_{T}\) , alfabetem stosu jest suma mnogościowa alfabetu symboli nieterminalnych \(\displaystyle V_{N}\) i terminalnych \(\displaystyle V_{T}\) , a symbol początkowy stosu jest symbolem startowym gramatyki. Istotą działania automatu \(\displaystyle AS\) jest symulacja lewostronnego wyprowadzenia w gramatyce \(\displaystyle G.\) Pełne uzasadnienie podanej konstrukcji znajduje sie na końcu tego wykładu, w części "dla zainteresowanych".
Załóżmy teraz, że automat \(\displaystyle \mathcal{AS}=(A,A_{S},Q,f,q_{0},z_{0})\) akceptuje poprzez pusty stos język \(\displaystyle L(\mathcal{AS})\) . Konstrukcja gramatyki bezkontekstowej \(\displaystyle G\) , która generuje ten sam język przebiega następująco. Niech \(\displaystyle G=((Q\times A_{S}\times Q)\cup \left\{ v_{0}\right\} ,A,v_{0},P_{G})\) , gdzie \(\displaystyle v_{0}\notin Q\cup A_{S}\cup A\) . Wprowadzamy do zbioru praw \(\displaystyle P_{G}\) wyłącznie następujące prawa:
- \(\displaystyle v_{0}\rightarrow (q_{0},z_{0},q)\) dla wszystkich stanów \(\displaystyle q\in Q\) ,
- \(\displaystyle (q,z,q_{1})\rightarrow a(q_{k+1},z_{k},q_{k})(q_{k},z_{k-1},q_{k-1})\ldots (q_{2},z_{1},q_{1})\) dla dowolnych stanów \(\displaystyle q,q_{1},\ldots ,q_{k+1}\in Q, \displaystyle \, a\in A\cup \left\{ 1\right\} ,\, z,z_{1},\ldots z_{k}\in A_{S}\) jeśli \(\displaystyle (z_{1}...z_{k},q_{k+1})\in f(z,q,a)\) ,
- \(\displaystyle (q,z,q_{1})\rightarrow a\in P_{G}\) jeśli \(\displaystyle (1,q_{1})\in f(z,q,a)\) .
Mamy więc następującą równoważność:
\(\mbox{(1)}\)
która w szczególności dla \(\displaystyle k=0\) przyjmuje postać
i oznacza dla gramatyki wymazywanie symboli nieterminalnych, a dla automatu wymazywanie symboli stosu.
Skonstruowana gramatyka \(\displaystyle G\) odtwarza działanie automatu \(\displaystyle AS\) działającego pod wpływem słowa wejściowego \(\displaystyle w\) . Pełne uzasadnienie podanej konstrukcji znajduje się na końcu tego wykładu, w części "dla zainteresowanych".
Z konstrukcji przedstawionej w szkicu dowodu twierdzenia wynika, że każdy język bezkontekstowy może być rozpoznawany poprzez pusty stos przez automat ze stosem o jednym stanie. Określenie algorytmów na podstawie powyższego twierdzenia proponujemy jako ćwiczenie.
Powróćmy na moment do języka Łukasiewicza. Język ten oraz jego gramatyka zostały wprowadzone podczas pierwszego wykładu poświęconego językom bezkontekstowym. Każde słowo, generowane przez tę gramatykę, jest pewnym wyrażeniem algebraicznym zapisanym w notacji polskiej, prefiksowej, bez użycia nawiasów. Bez trudności można określić gramatykę bezkontekstową, która generuje język Łukasiewicza, w którym słowa zapisywane są w wersji postfiksowej. Wystarczy bowiem przyjąć: \(\displaystyle G = (V_N,V_T,v_0,P)\), gdzie \(\displaystyle V_N=\{v_0 \}\), \(\displaystyle V_{T}=\left\{ a,b,+,*\right\}\) , \(\displaystyle v_{0}=v\) oraz \(\displaystyle P= \{v \rightarrow a, v \rightarrow b, v \rightarrow vv+, v \rightarrow vv* \}\). Język Łukasiewicza jest więc teraz zbiorem
Oczywiście język ten jest rozpoznawany przez odpowiedni automat ze stosem. Określeniem takiego automatu zajmiemy się podczas ćwiczeń. Warto zauważyć, że rozpoznając słowa języka Łukasiewicza w postfiksowej postaci, automat ze stosem działa dokładnie tak, jak obliczane są wartości wyrażeń arytmetycznych we współczesnych procesorach. Automat ze stosem, czytając wyrażenie od lewej do prawej, zapisuje wyniki częściowe na stosie, a operacje wykonywane są zawsze na ostatnich elementach stosu.
Dla bardziej dociekliwych studentów proponujemy poniżej pełny dowód twierdzenia 2.1 orzekajacego, że języki rozpoznawane przez automaty ze stosem to dokładnie języki bezkontekstowe.
Dowod
Dla dowodu, że każdy język bezkontekstowy jest rozpoznawany przez odpowiedni automat ze stosem, rozważmy gramatykę \(\displaystyle G=(V_{N},V_{T},v_{0},P_{G})\) bezkontekstową, w postaci normalnej Greibach i załóżmy, że słowo puste \(\displaystyle 1\) nie należy do języka \(\displaystyle L(G)\) generowanego przez tę gramatykę. Konstruujemy teraz automat ze stosem \(\displaystyle AS\) , który, jak udowodnimy, akceptuje poprzez pusty stos język \(\displaystyle L(G)\) . Niech
gdzie funkcja \(\displaystyle f:(V_{N}\cup V_{T})\times \{q\}\times (V_{T}\cup \left\{ 1\right\} )\longrightarrow \mathcal{P}_{sk}((V_{N}\cup V_{T})^{*}\times \{q\})\) określona jest następujaco. Dla dowolnych \(\displaystyle v\in V_{N},\: a\in V_{T}\)
oraz równa jest zbiorowi pustemu \(\displaystyle \emptyset\) we wszystkich pozostałych przypadkach.
A zatem jest to automat o jednym stanie \(\displaystyle q\) , alfabetem wejściowym jest alfabet terminalny \(\displaystyle V_{T}\) , alfabetem stosu jest suma mnogościowa alfabetu symboli nieterminalnych \(\displaystyle V_{N}\) i terminalnych \(\displaystyle V_{T}\) , a symbol początkowy stosu jest symbolem startowym gramatyki. Działanie automatu \(\displaystyle AS\) symuluje lewostronne wyprowadzenie w gramatyce \(\displaystyle G.\)
Dla dowolnego słowa \(\displaystyle w\in L(G)\) istnieje lewostronne wyprowadzenie
gdzie \(\displaystyle a_{i}\in V_{T}\) , \(\displaystyle v_{i}\in V_{N}\) oraz \(\displaystyle y_{i}\in V_{N}^{*}\) , gdyż gramatyka jest w postaci Greibach. Odpowiada temu wyprowadzeniu następujące działanie automatu \(\displaystyle \mathcal{AS}\) :
A to oznacza zaakceptowanie słowa \(\displaystyle w\) poprzez pusty stos. Zatem \(\displaystyle L(G)\subset L(\mathcal{AS})\) . Dla dowodu inkluzji w przeciwną stronę wykorzystamy implikację
która ma miejsce dla dowolnego \(\displaystyle w\in V_{T}^{*}\) . Implikację tę udowodnimy indukcyjnie ze względu na długość słowa \(\displaystyle w\) . Dla słowa pustego \(\displaystyle 1\) oraz dla \(\displaystyle w=a\in V_{T}\) powyższa implikacja wynika bezpośrednio z definicji automatu ze stosem. Załóżmy teraz, że \(\displaystyle (v_{0},q)\mid \! \Longrightarrow ^{w}(\overleftarrow{x},q)\) w \(\displaystyle \mathcal{AS}\) i niech \(\displaystyle w=w_{1}a\) dla \(\displaystyle a\in V_{T}\) i \(\displaystyle w_{1}\in V_{T}^{*}\) . Mamy więc \(\displaystyle (v_{0},q)\mid \! \Longrightarrow ^{w_{1}}(\overleftarrow{y},q)\) i \(\displaystyle (\overleftarrow{y},q)\mid \! \Longrightarrow ^{a}(\overleftarrow{x},q)\) w automacie \(\displaystyle \mathcal{AS}\) . Z założenia indukcyjnego wnioskujemy, że \(\displaystyle v_{0}\mapsto_{L}^{*}w_{1}y\) w \(\displaystyle G\) . W przypadku, gdy \(\displaystyle y=a\) , wnioskujemy z określenia automatu ze stosem, że \(\displaystyle x=1\) i wtedy \(\displaystyle v_{0}\mapsto_{L}^{*}w_{1}a=w\) w \(\displaystyle G\) . Jeśli natomiast \(\displaystyle y=vy'\) dla \(\displaystyle v\in V_{N}\) i \(\displaystyle y'\in V_{N}^{*}\) , to w automacie \(\displaystyle \mathcal{AS}\) ma miejsce wyprowadzenie
gdzie \(\displaystyle x'=az,\; \displaystyle a\in V_{T}\) i \(\displaystyle z\in V_{N}^{*}\) i prawo \(\displaystyle v\rightarrow x'\in P_{G}\) . W dalszym ciągu działania automatu następuje krok \(\displaystyle (\overleftarrow{y'}\overleftarrow{x',}q)\mid \! \Longrightarrow ^{a}(\overleftarrow{x},q)\) , a to w konsekwencji oznacza, że w gramatyce \(\displaystyle G\) ma miejsce wyprowadzenie
Załóżmy teraz, że automat \(\displaystyle \mathcal{AS}=(A,A_{S},Q,f,q_{0},z_{0})\) rozpoznaje z pustym stosem język \(\displaystyle L(\mathcal{AS})\) . Skonstruujemy gramatykę bezkontekstową \(\displaystyle G\) , generującą ten sam język. Niech \(\displaystyle G=((Q\times A_{S}\times Q)\cup \left\{ v_{0}\right\} ,A,v_{0},P_{G})\) , gdzie \(\displaystyle v_{0}\notin Q\cup A_{S}\cup A\) . Do zbioru praw \(\displaystyle P_{G}\) zaliczymy wyłącznie następujące prawa:
- \(\displaystyle v_{0}\rightarrow (q_{0},z_{0},q)\) dla wszystkich stanów \(\displaystyle q\in Q\) ,
- \(\displaystyle (q,z,q_{1})\rightarrow a(q_{k+1},z_{k},q_{k})(q_{k},z_{k-1},q_{k-1})\ldots (q_{2},z_{1},q_{1})\) dla dowolnych stanów \(\displaystyle q,q_{1},\ldots ,q_{k+1}\in Q, \displaystyle \, a\in A\cup \left\{ 1\right\} ,\, z,z_{1},\ldots z_{k}\in A_{S}\) jeśli \(\displaystyle (z_{1}...z_{k},q_{k+1})\in f(z,q,a)\) ,
- \(\displaystyle (q,z,q_{1})\rightarrow a\in P_{G}\) jeśli \(\displaystyle (1,q_{1})\in f(z,q,a)\) .
Mamy więc następującą równoważność:
\(\mbox{(2)}\)
która w szczególności dla \(\displaystyle k=0\) przyjmuje postać
i oznacza dla gramatyki wymazywanie symboli nieterminalnych, a dla automatu wymazywanie symboli stosu.
Skonstruowana gramatyka \(\displaystyle G\) odtwarza działanie automatu \(\displaystyle AS\) działającego pod wpływem słowa wejściowego \(\displaystyle w,\) co udowodnimy poniżej. W tym celu wykażemy indukcyjnie ze względu na długość słowa \(\displaystyle w\in A^{*}\) następującą równoważność:
Dla \(\displaystyle w=a\in A\) równoważność redukuje się do obserwacji (2). Załóżmy teraz, że słowo \(\displaystyle w=w_{1}a\) oraz że w gramatyce \(\displaystyle G\) mamy wyprowadzenie \(\displaystyle (q,z,q_{1})\Rightarrow _{G}^{*}w_{1}a(q_{k+1},z_{k},q_{k})\ldots (q_{2},z_{1},q_{1})\) . Z postaci gramatyki \(\displaystyle G\) wynika, że to wyprowadzenie można przedstawić nastepująco:
dla pewnego \(\displaystyle p\leqslant k\) i odpowiednich \(\displaystyle q,q',q_{1},\ldots ,q_{k+1}\in Q,\, z,z',z_{1},\ldots z_{k}\in A_{S}\) .
Z założenia indukcyjnego wynika, iż pierwszy fragment wyprowadzenia jest w automacie \(\displaystyle AS\) zastąpiony równoważnie poprawnym obliczeniem
a drugi
A to oznacza, że w automacie \(\displaystyle AS\) mamy poprawne obliczenie
co kończy dowód indukcyjny równoważności. Na jej podstawie, przyjmując \(\displaystyle q=q_{0},\: z=z_{0}\) , otrzymujemy:
Uwzględniając, iż dla dowolnego stanu \(\displaystyle q\) mamy w gramatyce \(\displaystyle G\) prawo \(\displaystyle v_{0}\rightarrow (q_{0},z_{0},q)\) oraz że automat \(\displaystyle AS\) akceptuje słowa przez pusty stos (stan \(\displaystyle q'\) jest nieistotny), ostatnia równoważność kończy dowód twierdzenia.
Języki kontekstowe i automat liniowo ograniczony. Maszyna Turinga
W tym wykładzie omówimy języki i gramatyki kontekstowe oraz ich własności. Wprowadzimy automat liniowo ograniczony i uzasadnimy równość rodziny języków kontekstowych i rodziny języków rozpoznawanych przez automaty liniowo ograniczone. Zdefiniujemy maszynę Turinga i pokażemy równoważność tego modelu z wybranymi innymi modelami obliczeń.
W tym wykładzie omówimy kolejną rodzinę języków hierarchii Chomsky'ego, a mianowicie języki kontekstowe. Przedstawimy kilka własnosci gramatyk kontekstowych, czyli typu (1) oraz wprowadzimy pojęcie automatu liniowo ograniczonego. Wprowadzimy też najogólniejszy model obliczeń, a mianowicie maszynę Turinga.
Języki kontekstowe
Języki kontekstowe to kolejna rodzina języków w hierarchii Chomsky'ego. Rozszerza ona istotnie rodzinę języków bezkontekstowych. Wykorzystanie tej rodziny języków formalnych jest dość ograniczone. Brak jest bowiem praktycznych metod konstrukcji parserów dla tych gramatyk.
Ta część wykładu prezentuje gramatyki równoważne gramatykom kontekstowym, posiadające pewne określone własności. Te własności wykorzystuje się przy uzasadnieniu faktu, że rodzina języków kontekstowych pokrywa się z rodziną języków rozpoznawanych przez automaty liniowo ograniczone. Biorąc pod uwagę to, że zastosowania tej rodziny języków formalnych nie są powszechne oraz to, że dowody dla przedstawionych poniżej twierdzeń są mocno techniczne, postanowiliśmy zrezygnować z rygorystycznej prezentacji tego materiału i pominąć dowody. Zainteresowany Student może je znaleźć w literaturze wskazanej do tego przedmiotu.
Definicja 1.1
Gramatykę \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) nazywamy rozszerzającą, jeśli każde prawo jest postaci \(\displaystyle x\rightarrow y\) , gdzie \(\displaystyle x,y\in (V_{N}\cup V_{T})^{*}\) i spełniona jest nierówność \(\displaystyle \mid x\mid \leqslant \mid y\mid\) lub jest to prawo \(\displaystyle v_{0}\rightarrow 1\) i wtedy \(\displaystyle v_{0}\) nie występuje po prawej stronie w żadnej produkcji z \(\displaystyle P\) .
Wprost z definicji wynika, że gramatyka kontekstowa jest gramatyką rozszerzającą. Prawdziwe jest również następujące twierdzenie.
Twierdzenie 1.1
Dla dowolnej gramatyki \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) rozszerzającej istnieje równoważna gramatyka kontekstowa.
Wprowadzimy teraz gramatyki z markerem końca.
Definicja 1.2
Gramatyką z markerem końca \(\displaystyle \sharp\) nazywamy gramatykę \(\displaystyle G_{\sharp }=(V_{N}\cup \{\sharp \},V_{T},v_{0},P)\) taką, że \(\displaystyle \sharp \notin V_{N}\cup V_{T}\) oraz prawa są postaci: \(\displaystyle u\rightarrow v\) , \(\displaystyle \sharp u\rightarrow \sharp v\) lub \(\displaystyle u\sharp \rightarrow v\sharp\) , gdzie \(\displaystyle u,v\in (V_{N}\cup V_{T})^{*}\) i w słowie \(\displaystyle u\) występuje co najmniej jeden symbol nieterminalny z \(\displaystyle V_{N}\) . Językiem generowanym przez tę gramatykę nazywamy zbiór
Gramatyka z markerem końca \(\displaystyle G_{\sharp }\) jest kontekstowa (typu \(\displaystyle 1\) ), jeśli jej prawa po wymazaniu markera \(\displaystyle \sharp\) spełniają warunki gramatyki rozszerzającej. Oczywiście dla dowolnej gramatyki kontekstowej istnieje równoważna gramatyka kontekstowa z markerem końca. Prawdziwe jest również następujące twierdzenie:
Twierdzenie 1.2
Dla dowolnej gramatyki kontekstowej z markerem końca istnieje równoważna gramatyka kontekstowa.
Dowód
Niech \(\displaystyle G_{\sharp }=(V_{N}\cup \{\sharp \},V_{T},v_{0},P)\) będzie dowolną gramatyką kontekstową z markerem końca. Zakładamy, bez ograniczania ogólności rozważań, że w zbiorze \(\displaystyle P\) nie występuje prawo \(\displaystyle v_{0}\rightarrow 1\) (po wymazaniu markera \(\displaystyle \sharp\) ). Dla każdego symbolu \(\displaystyle x\) ze zbioru \(\displaystyle V=V_{N}\cup V_{T}\) określamy trzy symbole \(\displaystyle \, ^{\sharp }x,x^{\sharp },^{\: \sharp }x^{\sharp }\) oraz oznaczamy odpowiednio przez \(\displaystyle \, ^{\sharp }V,V^{\sharp },^{\sharp }V^{\sharp }\) zbiory tych symboli. Dla \(\displaystyle u=u_{1}...u_{k}\) takiego, że \(\displaystyle k\geqslant 1\) i \(\displaystyle u_{i}\in V\) dla \(\displaystyle i=1,...,k\) wprowadzamy także następujące oznaczenia:
\(\displaystyle \, ^{\sharp }u=\, ^{\sharp }u_{1}u_{2}...u_{k}\) , \(\displaystyle u^{\sharp }=u_{1}...u_{k-1}u_{k}^{\sharp }\) oraz \(\displaystyle \, ^{\sharp }u^{\sharp }=\, ^{\sharp }u_{1}u_{2}...u_{k-1}u_{k}^{\sharp }\) gdy \(\displaystyle k>1\) .
Przy takich oznaczeniach definiujemy gramatykę
w której zbiór praw \(\displaystyle P_{1}\) składa się ze wszystkich praw uzyskanych zgodnie z poniższymi warunkami:
- jeśli \(\displaystyle u\rightarrow w\in P\) , to \(\displaystyle u\rightarrow w,\: ^{\#}u\rightarrow \, ^{\#}w,\: u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},\)
- jeśli \(\displaystyle \, ^{\#}u\rightarrow \, ^{\#}w\in P\) , to \(\displaystyle \: u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},\)
- jeśli \(\displaystyle u^{\#}\rightarrow w^{\#}\in P\) , to \(\displaystyle u^{\#}\rightarrow w^{\#},\: ^{\#}u^{\#}\rightarrow \, ^{\#}w^{\#}\in P_{1},\)
- \(\displaystyle \, ^{\#}x\rightarrow x,\: x^{\#}\rightarrow x,\: ^{\#}x^{\#}\rightarrow x\in P_{1}\)
dla wszystkich \(\displaystyle x\in V\) .
Określona w ten sposób gramatyka \(\displaystyle G_{1}\) jest gramatyką rozszerzającą i równoważną wyjściowej. Dla gramatyki \(\displaystyle G_{1}\) istnieje, zgodnie z poprzednim twierdzeniem, równoważna gramatyka kontekstowa, co kończy dowód twierdzenia.
Prawdziwe jest także następujące twierdzenie (porównaj z 1.1).
Twierdzenie 1.3
Dla dowolnej gramatyki kontekstowej (rozszerzającej) istnieje równoważna gramatyka kontekstowa (rozszerzająca) o tej własności, że każde prawo, w którym występuje symbol terminalny, jest postaci \(\displaystyle v\rightarrow a\) , gdzie \(\displaystyle v\in V_{N},\: a\in V_{T}\) .
Mówimy, że gramatyka \(\displaystyle G\) jest rzędu \(\displaystyle n>0\) , jeśli dla każdego prawa \(\displaystyle x\rightarrow y\) tej gramatyki spełniony jest warunek \(\displaystyle \mid x\mid \leqslant n\) i \(\displaystyle \mid y\mid \leqslant n\) . Kolejne twierdzenie stwierdza możliwość dalszego uproszczenia praw gramatyki rozszerzającej.
Twierdzenie 1.4
Dla każdej gramatyki rozszerzającej istnieje równoważna gramatyka rozszerzająca rzędu \(\displaystyle 2\) .
Na koniec wprowadzimy jeszcze jeden rodzaj gramatyk równoważnych gramatykom kontekstowym. Są to mianowicie gramatyki liniowo ograniczone.
Definicja 1.3
Gramatyka \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) jest liniowo ograniczona, jeśli każde prawo jest jednej z następujących postaci:
gdzie \(\displaystyle x\in V_{N}\cup V_{T},\: v,v_{1},v_{2},z_{1},z_{2}\in V_{N}\) oraz \(\displaystyle v_{0}\notin \{x,z_{1},z_{2},v\}\) .
Twierdzenie 1.5
Dla dowolnej gramatyki kontekstowej \(\displaystyle G\) istnieje gramatyka liniowo ograniczona \(\displaystyle G_{1}\) , która jest równoważna \(\displaystyle G\) lub też generuje język \(\displaystyle L(G)\setminus \{1\}\) .
Dowód
W świetle poprzednich twierdzeń możemy przyjąć, że gramatyka kontekstowa \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) ma prawa wyłącznie w następujących postaciach:
- \(\displaystyle v_{0}\rightarrow 1,\)
- \(\displaystyle v\rightarrow x\) gdzie \(\displaystyle v\in V_{N},\: x\in V_{N}\cup V_{T},\)
- \(\displaystyle v\rightarrow v_{1}v_{2}\) gdzie \(\displaystyle v,v_{1},v_{2}\in V_{N},\)
- \(\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\) gdzie \(\displaystyle v_{1},v_{2},v_{3},v_{4}\in V_{N}.\)
Określamy gramatykę \(\displaystyle G_{1}=(V_{N}\cup \{z_{0},z_{1}\},V_{T},z_{0},P_{1})\) , gdzie \(\displaystyle z_{1},z_{2}\) są nowymi symbolami nieterminalnymi, a więc nie należą do \(\displaystyle V_{N}\) . Natomiast zbiór praw \(\displaystyle P_{1}\) składa się ze wszystkich praw ze zbioru \(\displaystyle P\) postaci 2 i 4 oraz \(\displaystyle z_{0}\rightarrow z_{0}z_{1},\: z_{0}\rightarrow v_{0},\:\) praw \(\displaystyle z_{1}v\rightarrow vz_{1},\: vz_{1}\rightarrow z_{1}v\) dla \(\displaystyle v\in V_{N}\) i praw \(\displaystyle v_{1}z_{1}\rightarrow v_{3}v_{4}\) dla każdego prawa postaci 4 w gramatyce \(\displaystyle G\) . Skonstruowana gramatyka jest liniowo ograniczona i spełnia tezę twierdzenia.
Automat liniowo ograniczony
Określimy teraz systemy, zwane automatami liniowo ograniczonymi, który rozpoznają języki kontekstowe.
Definicja 2.1
Automatem liniowo ograniczonym nazywamy system \(\displaystyle \mathcal{A}_{LO}=(\Sigma _{T},S,P,s_{0},S_{F})\) , w którym \(\displaystyle \Sigma _{T}\) jest skończonym alfabetem, \(\displaystyle S\) skończonym zbiorem stanów, \(\displaystyle S\cap \Sigma _{T}=\emptyset\) oraz wyróżniony jest podzbiór \(\displaystyle \Sigma _{I}\subset \Sigma _{T}\) . Zbiór \(\displaystyle \Sigma _{T}\) zwany jest alfabetem taśmy, a \(\displaystyle \Sigma _{I}\) - alfabetem wejściowym. Wyróżnione są także: element \(\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}\) zwany markerem końca, stan początkowy \(\displaystyle s_{0}\in S\) oraz \(\displaystyle S_{F}\subset S\) - zbiór stanów końcowych. Natomiast relacja przejść \(\displaystyle P\subset (S\times \Sigma _{T})\times (S\times \Sigma _{T}\times \{-1,0,1\})\) spełnia następujące warunki:
- jeśli \(\displaystyle (s_{1},\#)P(s_{2},a,k)\) , to \(\displaystyle a=\#,\)
- jeśli \(\displaystyle (s_{1},a)P(s_{2},\#,k)\) , to \(\displaystyle a=\#.\)
Fakt, że \(\displaystyle (s_{1},a)P(s_{2},b,k)\) , zapisujemy zazwyczaj jako \(\displaystyle (s_{1},a)\rightarrow (s_{2},b,k)\) . Do opisu działania automatu liniowo ograniczonego wygodnie jest wprowadzić pojęcie konfiguracji (podobnie jak dla automatów ze stosem).
Konfiguracją automatu liniowo ograniczonego jest słowo \(\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}\) , w którym \(\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}\) . Pomiędzy dwoma konfiguracjami \(\displaystyle d_{1},d_{2}\) zachodzi relacja bezpośredniego następstwa \(\displaystyle d_{1}\mapsto d_{2}\) wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie \(\displaystyle s_{1},s_{2}\in S\) , \(\displaystyle a,b,c\in \Sigma _{T}\) oraz \(\displaystyle v,w\in \Sigma _{T}^{*}:\)
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}bw\) oraz \(\displaystyle (s_{1},a)P(s_{2},b,0),\)
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vbs_{2}w\) oraz \(\displaystyle (s_{1},a)P(s_{2},b,1),\)
- \(\displaystyle d_{1}=vcs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}cbw\) oraz \(\displaystyle (s_{1},a)P(s_{2},b,-1).\)
Przechodnie domknięcie relacji \(\displaystyle \mapsto\) oznaczać będziemy symbolem \(\displaystyle \mapsto^{*}\) i określać mianem obliczenia wykonanego przez automat liniowo ograniczony.
Język rozpoznawany przez automat liniowo ograniczony \(\displaystyle \mathcal{A}_{LO}\) to zbiór słów nad alfabetem \(\displaystyle \Sigma _{I}\) , pod działaniem których automat wykonuje obliczenie prowadzące do stanu końcowego, czyli
Język \(\displaystyle L\subset \Sigma _{I}^{*}\) jest rozpoznawany (akceptowany) przez automat liniowo ograniczony, jeśli istnieje automat \(\displaystyle \mathcal{A}_{LO}\) taki, że \(\displaystyle \mathcal{L}(\mathcal{A}_{LO})=L.\)

Opiszemy teraz możliwe ruchy automatu liniowo ograniczonego. Automat ten może czytać słowo wejściowe w dwóch kierunkach. Jego głowica może poruszać się w lewo lub w prawo. Automat może wymieniać czytaną literę na inną, ale nie rozszerza miejsca zajętego na taśmie przez czytane słowo.
Działa niedeterministycznie. Czytając literę \(\displaystyle a\), będąc w stanie \(\displaystyle s\), automat ma kilka możliwości działania. Może mianowicie:
- zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 1. Głowica czytająca automatu pozostaje w poprzedniej pozycji,
- zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 2. Głowica czytająca automatu przesuwa się w prawo,
- zamienić literę na inną literę i/lub zmienić stan na inny - zgodnie z warunkiem 3. Głowica czytająca automatu przesuwa się w lewo.
Związek pomiędzy rodziną języków kontekstowych a wprowadzoną rodziną automatów liniowo ograniczonych ustalają poniższe twierdzenia.
Twierdzenie 2.1
Dla dowolnego języka kontekstowego \(\displaystyle L\) istnieje automat liniowo ograniczony \(\displaystyle \mathcal{A}_{LO}\) taki, że \(\displaystyle \mathcal{L}(\mathcal{A}_{LO})=L\) .
Dowód
Można założyć, bez ograniczenia ogólności naszych rozważań, że gramatyka \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) generująca język \(\displaystyle L\) ma prawa wyłącznie następujących postaci:
- (G) \(\displaystyle v\rightarrow x\) , gdzie \(\displaystyle v\in V_{N},x\in V_{N}\cup V_{T},x\neq v_{0},\)
- (G) \(\displaystyle v_{0}\rightarrow v_{0}v_{1}\) , gdzie \(\displaystyle v_{1}\in V_{N},v_{1}\neq v_{0},\)
- (G) \(\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\) , gdzie \(\displaystyle v_{1},...,v_{4}\in V_{N},v_{3},v_{4}\neq v_{0},\)
- (G) \(\displaystyle v_{0}\rightarrow 1,\) jeśli \(\displaystyle 1\in L\) .
Określamy automat liniowo ograniczony \(\displaystyle \mathcal{A}_{LO}=(\Sigma _{T},S,P,s_{0},S_{F})\) , przyjmując \(\displaystyle \Sigma _{T}=V_{N}\cup V_{T}\cup \{\#,\flat \}\) , \(\displaystyle S=\{s_{0},s_{1},s_{2},s_{3},s_{4}\}\cup \{s_{v_{1}}: \displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\in P\}\) , \(\displaystyle \Sigma _{I}=V_{N}\cup V_{T}\) , \(\displaystyle S_{F}=\{s_{3}\}\) , \(\displaystyle s_{0}\) - stan początkowy. Relacja przejść automatu \(\displaystyle \mathcal{A}_{LO}\) zdefiniowana jest poniżej:
- (A) \(\displaystyle (s_{0},\#)\rightarrow (s_{0},\#,1),\)
- (A) \(\displaystyle (s_{0},\#)\rightarrow (s_{4},\#,1)\) jeśli \(\displaystyle 1\in L,\)
- (A) \(\displaystyle (s_{0},x)\rightarrow (s_{0},x,1)\) , \(\displaystyle (s_{0},x)\rightarrow (s_{0},x,-1)\) dla każdego \(\displaystyle x\in V_{N}\cup V_{T},\)
- (A) \(\displaystyle (s_{0},x)\rightarrow (s_{0},v,0)\) jeśli \(\displaystyle v\rightarrow x\in P\) i \(\displaystyle x\neq v_{0},\)
- (A) \(\displaystyle (s_{0},v_{3})\rightarrow (s_{v_{1}},v_{1},1),\; (s_{v_{1}},v_{4})\rightarrow (s_{0},v_{2},0)\) jeśli \(\displaystyle v_{1}v_{2}\rightarrow v_{3}v_{4}\in P,\)
- (A) \(\displaystyle (s_{0},v_{0})\rightarrow (s_{1},v_{0},-1),\)
- (A) \(\displaystyle (s_{1},\#)\rightarrow (s_{2},\#,1),\)
- (A) \(\displaystyle (s_{1},\flat )\rightarrow (s_{2},\flat ,1),\)
- (A) \(\displaystyle (s_{2},v_{0})\rightarrow (s_{3},\flat ,1),\)
- (A) \(\displaystyle (s_{3},v_{1})\rightarrow (s_{0},v_{0},0)\) , gdy \(\displaystyle v_{0}\rightarrow v_{0}v_{1}\in P,\)
- (A) \(\displaystyle (s_{3},\#)\rightarrow s_{3},\#,1),\; (s_{4},\#)\rightarrow (s_{3},\#,1).\)
Określony automat \(\displaystyle \mathcal{A}_{LO}\) rozpoznaje tylko te słowa, które są generowane przez gramatykę \(\displaystyle G\) , symulując wstecz każde wyprowadzenie gramatyki \(\displaystyle G\) .
Prawdziwe jest również następujące twierdzenie.
Twierdzenie 2.2
Dla dowolnego języka \(\displaystyle L\) rozpoznawanego przez automat liniowo ograniczony \(\displaystyle \mathcal{A}_{LO}\) istnieje gramatyka kontekstowa \(\displaystyle G\) taka, że \(\displaystyle L(G)=L\) .
W dowodzie konstruuje się odpowiednią gramatykę.Zasada tej konstrukcji jest następująca. Z symbolu startowego gramatyka generuje dowolne słowa, ustawiając zawsze na prawym końcu symbol nieterminalny związany z przejściem automatu do stanu końcowego. Następnie korzysta się z możliwości zamiany takiego symbolu nieterminalnego na inne. W ten sposób gramatyka symuluje wstecz działanie automatu, wprowadzając symbole nieterminalne odpowiadające stanom automatu. Dojście do stanu początkowego automatu w tej symulacji jest równoznaczne z usunięciem ostatniego symbolu nieterminalnego i wygenerowaniem słowa dokładnie tego samego, które rozpoznaje automat.
Udowownimy teraz zamkniętość rodziny języków kontekstowych ze względu na iloczyn mnogościowy.
Twierdzenie 2.3
Dla dowolnych języków kontekstowych \(\displaystyle L_{1},L_{2}\subset A^{*}\) iloczyn mnogościowy tych języków \(\displaystyle L_{1}\cap L_{2}\) jest językiem kontekstowym.
Dowód
(szkic) Załóżmy, że języki \(\displaystyle L_{1},L_{2}\) są rozpoznawane przez automaty liniowo ograniczone, \(\displaystyle \mathcal{A}^{1}_{LO}\) i \(\displaystyle \mathcal{A}_{LO}^{2}\) . Opiszemy konstrukcję automatu liniowo ograniczonego \(\displaystyle \mathcal{A}_{LO}\) , który rozpoznawać będzie wyłącznie słowa akceptowane równocześnie przez oba automaty. Działanie tego automatu jest następujące. Każde słowo będzie czytane trzy razy. Przy pierwszym czytaniu automat \(\displaystyle \mathcal{A}_{LO}\) dubluje litery, to znaczy w miejsce litery \(\displaystyle a\) wprowadza parę \(\displaystyle (a,a)\) . Po zakończeniu tej procedury automat wraca do skrajnej lewej pozycji i rozpoczyna symulację automatu \(\displaystyle \mathcal{A}^{1}_{LO}\) . Jeśli ta symulacja doprowadzi do zaakceptowania czytanego słowa przez automat \(\displaystyle \mathcal{A}^{1}_{LO}\) , to automat \(\displaystyle \mathcal{A}_{LO}\) rozpoczyna obliczenie od początku, symulując teraz pracę automatu \(\displaystyle \mathcal{A}_{LO}^{2}\) . Jeśli i ta symulacja zakończy się zaakceptowaniem czytanego słowa, to automat przechodzi do ustalonego stanu końcowego, a to oznacza akceptację tego słowa. Działając w opisany sposób, automat \(\displaystyle \mathcal{A}_{LO}\) rozpoznaje język \(\displaystyle L_{1}\cap L_{2}\) , a to w świetle udowodnionego powyżej twierdzenia oznacza, że przecięcie języków kontekstowych \(\displaystyle L_{1}\cap L_{2}\) jest językiem kontekstowym.
Ponieważ dalsze własności domkniętości rodziny języków kontekstowych pokrywają się z własnościami języków typu (0), więc omówimy te własności wspólnie, co będzie mieć miejsce w następnym wykładzie.
Maszyna Turinga
Przejdziemy teraz do prezentacji ogólnego modelu maszyny liczącej, który został wprowadzony w 1936 roku przez Alana M. Turinga. Na cześć swego autora został on nazwany (jednotaśmową) maszyną Turinga. Model ten jest podobny w swojej idei do rozważanych wcześniej automatów liniowo ograniczonych, przy czym jednym z podstawowych założeń (i różnic względem automatów) jest nieskończony dostęp do pamięci. Maszyna Turinga może wydawać się na początku pojęciem bardzo abstrakcyjnym. Jednak, jak później zobaczymy, stanowi ona jedną z podstawowych koncepcji współczesnej informatyki. Pozwala na formalne zdefiniowanie pojęcia algorytmu oraz jego złożoności obliczeniowej. Jako model obliczeń pozwala odpowiedzieć także na bardzo ważne pytanie: czy każdy problem można rozwiązać algorytmicznie?
Jednotaśmowa maszyna Turinga jest podobna w swej idei do automatu liniowo ograniczonego, pominięte jednak zostaje, jak wspomnieliśmy, ograniczenie dostępu do pamięci. Omawiana maszyna jest abstrakcyjnym tworem w skład którego wchodzą:
- dwustronnie nieskończona taśma zbudowana z komórek zawierających symbole z pewnego zadanego alfabetu,
- głowica, która może czytać i zapisywać symbole w komórkach taśmy oraz poruszać się w prawo lub lewo o jedną komórkę lub pozostawać na tej samej pozycji podczas jednego kroku czasowego,
- działający sekwencyjnie mechanizm odpowiedzialny za sterowanie maszyną; mechanizm ten na podstawie symbolu odczytanego z komórki pod głowicą oraz stanu, w którym aktualnie znajduje się maszyna, dokonuje zapisu symbolu w tejże komórce, przechodzi do kolejnego stanu i przesuwa głowicę w prawo, lewo lub też nie zmienia pozycji głowicy.
Podamy teraz formalną definicję maszyny Turinga. Aby zachować analogię do poprzednich wykładów, zdefiniujemy maszynę w języku konfiguracji.
Definicja 3.1
(Jednotaśmowa deterministyczna) maszyna Turinga jest to system \(\displaystyle \mathbf{MT}=(\Sigma _{T},S,f,s_{0},S_{F})\) , w którym \(\displaystyle \Sigma _{T}\) jest skończonym alfabetem, \(\displaystyle S\) skończonym zbiorem stanów, \(\displaystyle S\cap \Sigma _{T}=\emptyset\) oraz wyróżniony jest podzbiór \(\displaystyle \Sigma _{I}\subset \Sigma _{T}\) . Zbiór \(\displaystyle \Sigma _{T}\) zwany jest alfabetem taśmy, a \(\displaystyle \Sigma _{I}\) - alfabetem wejściowym. Wyróżnione są także: element \(\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}\) zwany markerem końca, stan początkowy \(\displaystyle s_{0}\in S\) oraz \(\displaystyle S_{F}\subset S\) - zbiór stanów końcowych. Natomiast funkcja przejść jest funkcją częściową \(\displaystyle f:\: (S\times \Sigma _{T})\rightarrow (S\times \Sigma _{T}\times \{-1,0,1\}\) .
Konfiguracją maszyny Turinga jest słowo \(\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}\) , w którym \(\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}\) . Pomiędzy dwiema konfiguracjami \(\displaystyle d_{1},d_{2}\) zachodzi relacja bezpośredniego następstwa \(\displaystyle d_{1}\mapsto d_{2}\) wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie \(\displaystyle s_{1},s_{2}\in S\) , \(\displaystyle a,b,c\in \Sigma _{T}\) oraz \(\displaystyle v,w\in \Sigma _{T}^{*}\):
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}bw\) oraz \(\displaystyle f(s_{1},a)=(s_{2},b,0),\)
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vbs_{2}w\) oraz \(\displaystyle f(s_{1},a)=(s_{2},b,1)\) i \(\displaystyle w\neq 1,\)
- \(\displaystyle d_{1}=vs_{1}\#\) , \(\displaystyle d_{2}=vbs_{2}\#\) oraz \(\displaystyle f(s_{1},\#)=(s_{2},b,1),\)
- \(\displaystyle d_{1}=vcs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}cbw\) oraz \(\displaystyle f(s_{1},a)=(s_{2},b,-1),\)
- \(\displaystyle d_{1}=s_{1}\#w\) , \(\displaystyle d_{2}=s_{2}\#bw\) oraz \(\displaystyle f(s_{1},\#)=(s_{2},b,-1).\)
Przechodnie domknięcie relacji \(\displaystyle \mapsto\) oznaczać będziemy symbolem \(\displaystyle \mapsto^{*}\) i określać mianem obliczenia wykonanego przez maszynę Turinga. Konfiguracja \(\displaystyle d_{1}\in (\Sigma _{T}\cup S)^{*}\) jest końcowa, jeśli stąd, że \(\displaystyle d_{1}\mapsto d_{2}\) , wynika \(\displaystyle d_{2}=d_{1}.\) Mówimy, że maszyna Turinga zatrzymuje się w \(\displaystyle d_{1}\) wtedy i tylko wtedy, gdy \(\displaystyle d_{1}\) jest konfiguracją końcową.
Zauważmy, że wprowadzenie markera końca jest zabiegiem czysto formalnym. Pozwala on z jednej strony na oznaczenie słowa wejściowego, a z drugiej strony wskazuje na elementy taśmy, które były zmieniane (czy to przez wprowadzenie słowa wejściowego, czy też poprzez ruch głowicy).
Definicja 3.2
Język rozpoznawany przez maszynę Turinga \(\displaystyle MT\) jest to zbiór
Język \(\displaystyle L\subset \Sigma _{I}^{*}\) jest rozpoznawany (akceptowany) przez maszynę Turinga, jeśli istnieje \(\displaystyle MT\) taka, że \(\displaystyle L(\mathcal{MT})=L.\) Klasę języków rozpoznawanych przez maszynę Turinga oznaczamy \(\displaystyle \mathcal{L}(MT)\) .
We wprowadzonym przez nas ujęciu formalnym, działanie maszyny Turinga należy wyobrażać sobie następująco. W pierwszym etapie na taśmę zostają zapisane symbole słowa wejściowego (z alfabetu \(\displaystyle \Sigma_I\)), a następnie komórki przyległe zostają oznaczone symbolami \(\displaystyle \sharp\). Jednocześnie maszyna jest sprowadzana do stanu \(\displaystyle s_0\), a głowica zostaje ustawiona nad pierwszym symbolem słowa wejściowego. W tym momencie rozpoczyna się sekwencyjne przetwarzanie zawartości taśmy przez maszynę. Jeśli maszyna "zatrzyma się", tzn. w dwóch kolejnych chwilach czasowych nie wykona ruchu i jednocześnie nie zmieni stanu i symbolu taśmy, sprawdzany jest jej aktualny stan. Jeśli stan był akceptujący (czyli należał do zbioru \(\displaystyle S_F\)), to maszyna zaakceptowała słowo, w przeciwnym razie - słowo odrzuciła (gdyż nie może już osiągnąć stanu ze zbioru \(\displaystyle S_F\)). Należy zwrócić uwagę na to, że dla niektórych konfiguracji początkowych maszyna może nigdy się nie zatrzymać, a mimo to słowo zostanie przez nią zaakceptowane. To samo tyczy się odrzucania słów, jednak w tej sytuacji dowód, że słowo nie zostanie zaakceptowane, może być problematyczny. Zaprezentowane podejście ma na celu uproszczenie i tak już dość technicznych dowodów twierdzeń pojawiających się w tym wykładzie. Związki pomiędzy akceptowaniem a zatrzymywaniem maszyny Turinga zostaną skomentowane później (zob. Wniosek 4.1). W pierwszej kolejności przedstawiamy dwa przykłady:
Przykład 3.1
Skonstruujemy maszynę Turinga \(\displaystyle MT_1\), która rozpoznaje język postaci \(\displaystyle L=\left\{0^{2^n}\; : \; n\geqslant 0\right\}\). Zamierzone działanie maszyny \(\displaystyle MT_1\) można opisać następująco:
- Przejdź od lewego markera do prawego, zaznaczając symbolem \(\displaystyle \diamondsuit\) co drugie \(\displaystyle 0\).
- Jeśli było tylko jedno \(\displaystyle 0\), to akceptuj.
- Jeśli w kroku 1. obszar pomiędzy markerami zawierał nieparzystą ilość \(\displaystyle 0\), to odrzuć.
- Powróć do lewego markera.
- Powtórz działanie od 1.
Zwróćmy uwagę, że o ile jasne jest, w jaki sposób maszyna ma akceptować słowa wejściowe, odrzucanie tych słów nie zostało zdefiniowane. Aby ominąć ten problem, wprowadzimy jeden dodatkowy stan (nie należący do stanów końcowych), po osiągnięciu którego maszyna się zatrzymuje (tzn. nie wykonuje ruchów i przepisuje na taśmie wciąż ten sam symbol).
Określamy kolejno elementy składowe maszyny \(\displaystyle MT_1\):
Pozostaje jeszcze zdefiniować funkcję przejść:
W miejsce tabeli wygodniej jest zobrazować funkcję przejść maszyny Turinga na etykietowanym grafie skierowanym. Zostało to zrobione na poniższym rysunku:

Łatwo zauważyć, że wprowadzona funkcja przejścia określa maszynę spełniającą postawione przez nas warunki. Symbol \(\displaystyle \clubsuit\) został wprowadzony dla odróżnienia wystąpienia pojedynczego zera od sytuacji, gdy liczba zer jest nieparzysta i większa od \(\displaystyle 1\).
Aby lepiej zrozumieć działanie maszyny \(\displaystyle MT_1\), zasymulujemy jej działanie na dwóch słowach wejściowych, przy czym pierwsze z nich będzie należało do języka \(\displaystyle L\), a drugie nie:
Wykazaliśmy więc, że \(\displaystyle \sharp s_0 0000 \sharp \mapsto^* \sharp \clubsuit \diamondsuit \diamondsuit \diamondsuit s_A \sharp\). Zatem \(\displaystyle 0^4 \in L(MT_1)\).
Dla porównania:
Czyli zgodnie z naszym założeniem \(\displaystyle 0^3\not \in L(MT_1)\).
Przykład 3.2
Przedstawimy maszynę Turinga \(\displaystyle MT_2\) akceptującą język
gdzie \(\displaystyle \overleftarrow{w}\) oznacza lustrzane odbicie słowa \(\displaystyle w\). Elementy języka \(\displaystyle L\) nazywamy palindromami. Definiujemy alfabet maszyny:
oraz zbiory stanów
Funkcję przejść maszyny \(\displaystyle MT_2\) określa tabela:
co dla przejrzystości zobrazowano na Rysunku 3.
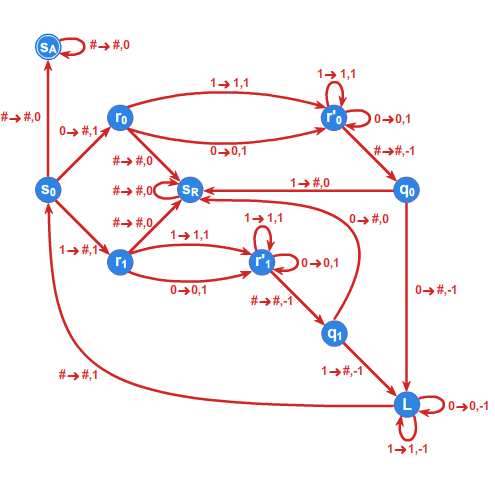
Inne możliwe definicje maszyn Turinga
Istnieje kilka możliwych definicji maszyny Turinga, które jak się okazuje są równoważne pod względem możliwości obliczeniowych (tzn. rozpoznają dokładnie tę samą klasę języków). Naszkicujemy kilka wybranych podejść.
Maszyna wielotaśmowa
W tym modelu zakłada się, że głowica ma do dyspozycji nie tylko jedną, ale wiele taśm, na których może zapisywać i odczytywać symbole. Zakłada się przy tym, że słowo wejściowe znajduje się na pierwszej taśmie. Aby symulować maszynę wielotaśmową na jednej taśmie, należy zamienić alfabet taśmy na alfabet \(\displaystyle (\Sigma_T)^k\), gdzie \(\displaystyle k\) oznacza ilość taśm. W tym momencie zapis na taśmie \(\displaystyle i\)-tej jest realizowany przez zmianę odpowiedniej współrzędnej litery z nowego alfabetu (zob. Rys. 4.a). Czyli w opisywanym przypadku funkcja przejść będzie operowała na następujących zbiorach:
Taśma jednostronnie nieskończona
Model ten zakłada, że taśma jest ograniczona z jednej ze stron. Różnica w porównaniu z rozważaną przez nas maszyną Turinga polega na tym, że nie jest dozwolone przesuwanie lewego markera (tzn. funkcja przejść nie może zawierać przejść typu punkt 5 definicji 3.1. W tej sytuacji, aby symulować maszynę z taśmą obustronnie nieskończoną na maszynie z taśmą ograniczoną z jednej strony, wystarczy zasymulować taśmę obustronnie nieskończoną poprzez rozszerzenie alfabetu (zob. Rys. 4.b).
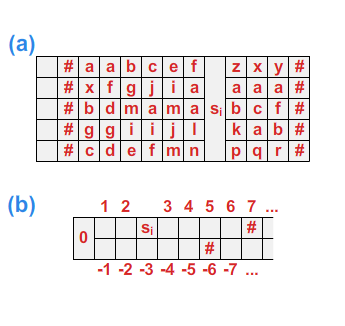
Wielogłowicowa maszyna wielotaśmowa
W tym podejściu zakłada się dodatkowo, że każda z taśm posiada swoją głowicę. Inaczej mówiąc, mamy do czynienia z iloczynem kartezjańskim \(\displaystyle k\) niezależnych maszyn jednotaśmowych. Akceptowany język jest w tym momencie \(\displaystyle k\)-wymiarowy. Oczywiście, słowo postaci \(\displaystyle (w,1,\dots,1)\in (\Sigma_T^*)^k\) można w naturalny sposób utożsamiać z \(\displaystyle w\in \Sigma_T\). Z drugiej strony maszynę wielogłowicową można symulować na jednotaśmowej w następujący sposób:
- Jako zbiór stanów bierzemy \(\displaystyle S^k\).
- Słowa startowe \(\displaystyle w_1,\dots, w_k\) zapisujemy jako konfigurację początkową maszyny jednotaśmowej w postaci:
\(\displaystyle \sharp (s_0)^k \$ \dot{1} w_1 \$ \dot{2} w_2 \$ \dots \$ \dot{k} w_k \$.\) Symbole \(\displaystyle \$\) mają za zadanie wirtualnego rozdzielenia taśm. Symbole \(\displaystyle \dot{i}\) wskazują na położenie \(\displaystyle i\)-tej głowicy na taśmie. - W trakcie symulacji przechodzimy pomiędzy markerami i wykonujemy przejścia dla kolejnych głowic.
Widać już, że formalne podanie funkcji przejść jest w omawianym przypadku bardzo techniczne. Musimy zapewnić możliwość poszerzania obszaru zapisu na poszczególnych taśmach, co jest realizowane poprzez dopisanie nowego symbolu i przepisywanie przyległych symboli, aż do markera włącznie. Następnie należy wrócić do poprzedniego miejsca zapisu i symulować działanie kolejnych głowic. Wymaga to wprowadzenia sporej liczby stanów pomocniczych. Nie będziemy zagłębiać się w te techniczne szczegóły. Mamy nadzieję że sama idea konstrukcji jest w tym momencie zrozumiała.
Najbardziej ogólna definicja maszyny tego typu dopuszcza dodatkowo, aby głowice mogły przeglądać pozostałe taśmy, dzięki czemu zapewnia się komunikację między głowicami. Symulacja takiej maszyny na jednej taśmie jest podobna w swej idei do metody przedstawionej wcześniej.
Maszyna niedeterministyczna
Ten typ maszyn ma ogromne znaczenie dla teorii złożoności. Z tego powodu przyglądniemy mu się dokładniej. Różnica pomiędzy niedeterministyczną maszyną Turinga a maszyną deterministyczną polega na tym, że funkcja przejść może pozwalać na kilka różnych przejść na skutek tego samego symbolu czytanego (gdyż funkcja przejść w tym przypadku będzie multi-funkcją).
Definicja 4.1
(Jednotaśmowa) niedeterministyczna maszyna Turinga jest to system \(\displaystyle \mathbf{NMT}=(\Sigma _{T},S,f,s_{0},S_{F})\), w którym \(\displaystyle \Sigma _{T}\) jest skończonym alfabetem, \(\displaystyle S\) skończonym zbiorem stanów, \(\displaystyle S\cap \Sigma _{T}=\emptyset\) oraz wyróżniony jest podzbiór \(\displaystyle \Sigma _{I}\subset \Sigma _{T}\) . Podobnie jak poprzednio zbiór \(\displaystyle \Sigma _{T}\) zwany jest alfabetem taśmy, a \(\displaystyle \Sigma _{I}\) - alfabetem wejściowym. Wyróżnione są także: element \(\displaystyle \#\in \Sigma _{T}\setminus \Sigma _{I}\) zwany markerem końca, stan początkowy \(\displaystyle s_{0}\in S\) oraz \(\displaystyle S_{F}\subset S\) - zbiór stanów końcowych. Natomiast funkcja przejść jest funkcją częściową \(\displaystyle f:\: (S\times \Sigma _{T})\rightarrow \mathcal{P}(S\times \Sigma _{T}\times \{-1,0,1\})\) gdzie \(\displaystyle \mathcal{P}(A)\) oznacza zbiór podzbiorów zbioru \(\displaystyle A\).
Konfiguracją maszyny Turinga jest słowo \(\displaystyle vsw\in (\Sigma _{T}\cup S)^{*}\) , w którym \(\displaystyle s\in S,\; v,w\in \Sigma _{T}^{*}\) , przy czym pomiędzy dwiema konfiguracjami \(\displaystyle d_{1},d_{2}\) zachodzi relacja bezpośredniego następstwa \(\displaystyle d_{1}\mapsto d_{2}\) wtedy i tylko wtedy, gdy spełniony jest jeden z niżej wypisanych warunków, gdzie \(\displaystyle s_{1},s_{2}\in S\) , \(\displaystyle a,b,c\in \Sigma _{T}\) oraz \(\displaystyle v,w\in \Sigma _{T}^{*}\):
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}bw\) oraz \(\displaystyle f(s_{1},a)\ni(s_{2},b,0),\)
- \(\displaystyle d_{1}=vs_{1}aw\) , \(\displaystyle d_{2}=vbs_{2}w\) oraz \(\displaystyle f(s_{1},a)\ni(s_{2},b,1)\) i \(\displaystyle w\neq 1,\)
- \(\displaystyle d_{1}=vs_{1}\#\) , \(\displaystyle d_{2}=vbs_{2}\#\) oraz \(\displaystyle f(s_{1},\#)\ni(s_{2},b,1),\)
- \(\displaystyle d_{1}=vcs_{1}aw\) , \(\displaystyle d_{2}=vs_{2}cbw\) oraz \(\displaystyle f(s_{1},a)\ni(s_{2},b,-1),\)
- \(\displaystyle d_{1}=s_{1}\#w\) , \(\displaystyle d_{2}=s_{2}\#bw\) oraz \(\displaystyle f(s_{1},\#)\ni(s_{2},b,-1).\)
Tak jak poprzednio, przechodnie domknięcie relacji \(\displaystyle \mapsto\) oznaczać będziemy symbolem \(\displaystyle \mapsto^{*}\) i określać mianem obliczenia wykonanego przez maszynę Turinga. Konfiguracja \(\displaystyle d_{1}\in (\Sigma _{T}\cup S)^{*}\) jest końcowa, jeśli stąd, że \(\displaystyle d_{1}\mapsto d_{2}\) , wynika \(\displaystyle d_{2}=d_{1}.\)
Pomimo tego, że postawiona definicja maszyny niedeterministycznej jest bardzo podobna do maszyny deterministycznej, występuje tutaj jedna bardzo istotna różnica. Słowo wejściowe może prowadzić do wielu różnych obliczeń wykonanych, w szczególności jedno z obliczeń może doprowadzać do zatrzymania maszyny, a inne nie.
Przykład maszyny niedeterministycznej podamy później, przy okazji omawiania klas złożoności obliczeniowej.
Definicja 4.2
Język rozpoznawany przez niedeterministyczną maszynę Turinga \(\displaystyle NMT\) jest to zbiór
Język \(\displaystyle L\subset \Sigma _{I}^{*}\) jest rozpoznawany (akceptowany) przez niedeterministyczną maszynę Turinga, jeśli istnieje \(\displaystyle \mathcal{NMT}\) taka, że \(\displaystyle L(\mathcal{NMT})=L.\)
Podkreślamy fakt, że aby maszyna niedeterministyczna zaakceptowała słowo wejściowe, wystarczy, aby wśród wszystkich możliwych obliczeń znalazło się co najmniej jedno akceptujące.
Wprost z definicji wynika że każda maszyna deterministyczna jest także maszyną niedeterministyczną, co oznacza, że języki rozpoznawane przez maszyny deterministyczne są zawarte w klasie języków rozpoznawanych przez maszyny niedeterministyczne. Przeciwna inkluzja jest gwarantowana przez następujące twierdzenie.
Twierdzenie 4.1
Dla każdej niedeterministycznej maszyny Turinga \(\displaystyle \mathcal{NMT}\) istnieje maszyna deterministyczna \(\displaystyle \mathcal{MT}\) taka, że
Dowód
(Szkic). Aby sprawdzić, czy maszyna niedeterministyczna akceptuje dane słowo wejściowe, należy przejrzeć wszystkie możliwe obliczenia wykonywane, tworzące drzewo obliczeń. Poziomy drzewa tworzone są przez kroki czasowe, wierzchołki stanowią obliczenia wykonane w danym kroku czasowym, a gałęzie zadane są przez relację bezpośredniego następstwa. W celu sprawdzenia, czy maszyna akceptuje dane słowo, przeglądamy drzewo obliczeń poziomami (por. algorytm BFS) i akceptujemy, gdy przeglądana konfiguracja była akceptująca. Tą techniką przeglądamy wszystkie możliwe obliczenia wykonane w \(\displaystyle 1,2,3,\dots\) krokach.
Do dokonania symulacji najwygodniej jest użyć maszyny \(\displaystyle 3\)-głowicowej z możliwością czytania na wszystkich taśmach. Wprowadzamy te taśmy kolejno do przechowywania słowa wejściowego, symulacji działania maszyny niedeterministycznej i adresowania wyboru przejść ze zbioru przejść danego przez funkcję przejść. Symulacja przebiega w czterech krokach:
- Rozpocznij ze słowem wejściowym \(\displaystyle w\) na taśmie \(\displaystyle 1\) oraz pustymi taśmami \(\displaystyle 2\) i \(\displaystyle 3\).
- Przekopiuj taśmę \(\displaystyle 1\) na taśmę \(\displaystyle 2\).
- Użyj taśmy \(\displaystyle 2\) do symulacji \(\displaystyle w\), wykorzystując taśmę \(\displaystyle 3\) do wyboru przejść funkcji przejść \(\displaystyle f\). Jeśli po wykonaniu skończonego zbioru instrukcji według adresowania z taśmy \(\displaystyle 3\) otrzymano konfigurację akceptującą, to akceptuj. W przeciwnym razie, przejdź do następnego punktu.
- Zamień ciąg adresowy na następny w kolejności leksykograficznej. Jeśli zapisany ciąg jest ostatnim możliwym ciągiem adresowym o długości \(\displaystyle N\), zapisz na taśmie \(\displaystyle 3\) pierwszy w kolejności leksykograficznej ciąg adresowy o długości \(\displaystyle N+1\) oraz przejdź do \(\displaystyle 2\).
Wniosek 4.1
Dla każdej maszyny Turinga \(\displaystyle \mathcal{MT}\) istnieje maszyna Turinga \(\displaystyle \mathcal{MT}'\) taka, że
oraz dla każdego \(\displaystyle w\in L(\mathcal{MT}')\) maszyna \(\displaystyle \mathcal{MT}'\) zatrzymuje się na \(\displaystyle w\).
Dowód
Wystarczy przerobić maszynę \(\displaystyle \mathcal{MT}\) na maszynę niedeterministyczną \(\displaystyle \mathcal{NMT}\) posiadającą dodatkowy stan \(\displaystyle s_A\) oraz taką, że dla każdego stanu ze zbioru \(\displaystyle S_F\) pod wpływem dowolnego symbolu z \(\displaystyle \Sigma_T\) maszyna \(\displaystyle \mathcal{NMT}\) posiada dodatkowe przejście do \(\displaystyle s_A\), w którym już pozostaje i nic nie zmienia. Stąd widać, że \(\displaystyle L(\mathcal{MT})=L(\mathcal{NMT})\).
Twierdzenie 4.1 pozwala na otrzymanie maszyny \(\displaystyle \mathcal{MT}'\) akceptującej ten sam język co \(\displaystyle \mathcal{NMT}\) z dodatkowym założeniem, że gdy \(\displaystyle \mathcal{NMT}\) osiąga stan \(\displaystyle s_A\), maszyna \(\displaystyle \mathcal{MT}'\) się zatrzymuje. Zauważmy, że stan \(\displaystyle s_A\) można osiągnąć tylko dla słów akceptowanych prze \(\displaystyle \mathcal{NMT}\), a z drugiej strony, każde słowo akceptowane przez \(\displaystyle \mathcal{NMT}\) prowadzi do co najmniej jednego obliczenia kończącego się w \(\displaystyle s_A\).
Złożoność obliczeniowa.
Sformułujemy definicje podstawowych klas złożoności w języku maszyn Turinga oraz metodę ich porównywania. Przeanalizujemy związki między rodziną języków określonych przez maszyny Turinga a rodziną języków typu (0) z hierarchii Chomsky'ego. Podamy dalsze własności języków kontekstowych i typu (0). Wprowadzimy pojęcie języka rekurencyjnie przeliczalnego oraz przedstawimy tezę Churcha. Następnie omówimy teoretyczne podstawy teorii rozstrzygalności oraz przeanalizujemy kilka problemów nierozstrzygalnych w teorii języków.
Klasy złożoności obliczeniowej
Jednym z podstawowych celów wprowadzania maszyn Turinga jest dążenie do formalnej definicji złożoności obliczeniowej. Na podstawie wcześniejszych uwag możemy utożsamiać akceptację słowa przez maszynę Turinga z jej zatrzymaniem się. Intuicyjnie, można takie zachowanie maszyny Turinga utożsamić z wykonaniem programu, który zwraca odpowiedź "Tak" na postawione przez nas pytanie.
Definicja 1.1
Ustalmy funkcje \(\displaystyle t,s:\mathbb{N}\rightarrow \mathbb{N}\). Mówimy, że maszyna Turinga \(\displaystyle \mathcal{MT}\) (deterministyczna lub niedeterministyczna) akceptuje słowo \(\displaystyle w\in \Sigma_I^*\) w czasie \(\displaystyle t(|w|)\), jeśli istnieje ciąg \(\displaystyle k\leqslant t(|w|)\) konfiguracji \(\displaystyle d_1,d_2,\dots, d_k\) takich, że \(\displaystyle d_1=\sharp s_0 w \sharp\), \(\displaystyle d_k= \sharp w_{1}s_{F}w_{2}\sharp\) dla pewnych \(\displaystyle w_{1},w_{2}\in \Sigma _{T}^{*},s_{F}\in S_{F}\) oraz \(\displaystyle d_i \mapsto d_{i+1}\) dla \(\displaystyle i=1,\dots,k-1\).
Jeśli istnieje ciąg konfiguracji \(\displaystyle d_1 \mapsto d_2 \mapsto \dots \mapsto d_m\), gdzie \(\displaystyle d_1=\sharp s_0 w \sharp\), \(\displaystyle d_m\) jest konfiguracją akceptującą (tzn. \(\displaystyle d_m= \sharp w_{1}s_{F}w_{2}\sharp\) dla pewnych \(\displaystyle w_{1},w_{2}\in \Sigma _{T}^{*},s_{F}\in S_{F}\)) oraz dodatkowo \(\displaystyle |d_i|\leqslant s(|w|)+2\), to mówimy, że maszyna \(\displaystyle \mathcal{MT}\) akceptuje słowo \(\displaystyle w\in \Sigma_I^*\) w pamięci \(\displaystyle s(|w|)\).
Mówimy, że język \(\displaystyle L\) jest akceptowany w czasie \(\displaystyle t(n)\) (pamięci \(\displaystyle s(n)\)), jeśli istnieje maszyna Turinga \(\displaystyle \mathcal{MT}\), dla której \(\displaystyle L(\mathcal{MT})=L\) oraz każde słowo \(\displaystyle w\in L\) jest akceptowane w czasie \(\displaystyle t(|w|)\) (pamięci \(\displaystyle s(|w|)\) odpowiednio).
Uwaga 1.1
W niektórych podejściach wykorzystuje się, do definicji złożoności pamięciowej, tak zwanych maszyn Turinga off-line. Pomysł polega na tym, aby nie uwzględniać komórek taśmy, z których maszyna czytała informacje, a jedynie te, do których następował zapis. Dzięki temu zabiegowi można w sposób "rozsądny" mówić o akceptacji słowa w pamięci \(\displaystyle \log n\) itp. W ujęciu prezentowanym w tym wykładzie zajmujemy się akceptacją w pamięci \(\displaystyle n^k\), dla \(\displaystyle k\geqslant 1\), zatem nie ma potrzeby dodatkowego definiowania maszyn Turinga off-line.
Definicja 1.2
Oznaczmy przez \(\displaystyle Dtime(t(n))\) oraz \(\displaystyle Dspace(s(n))\) rodzinę języków akceptowanych w czasie \(\displaystyle t(n)\) i odpowiednio pamięci \(\displaystyle s(n)\) przez deterministyczną maszynę Turinga. Dla maszyn niedeterministycznych wprowadzamy w identyczny sposób klasy \(\displaystyle Ntime(t(n))\) oraz \(\displaystyle Nspace(s(n))\).
Określamy następujące klasy złożoności (klasy języków):
Wprost z definicji otrzymujemy zależności P \(\displaystyle \subset\) NP oraz PSPACE \(\displaystyle \subset\) NPSPACE . W dalszej części wykładu udowodnimy kilka mniej oczywistych zależności.
Przykład 1.1
Rozważmy język:
Język \(\displaystyle L\in\) P . Deterministyczna maszyna Turinga \(\displaystyle MT_3\) akceptująca taki język może wyglądać następująco (zaczynamy od konfiguracji \(\displaystyle \sharp s_0 w \sharp\)):
- Jeśli symbol pod głowicą, to \(\displaystyle 1\) zamień go na \(\displaystyle\sharp\). Inaczej odrzuć.
- Przejdź od lewego ogranicznika do prawego, sprawdzając, czy po \(\displaystyle 1\) występuje \(\displaystyle 1\) lub \(\displaystyle 2\), po \(\displaystyle 2\) tylko \(\displaystyle 2\) lub \(\displaystyle 3\), a po \(\displaystyle 3\) kolejny symbol \(\displaystyle 3\) lub ogranicznik. Jeśli ta zależność nie jest spełniona, odrzuć. Gdy osiągniesz ogranicznik wykonaj następny krok.
- Gdy przed ogranicznikiem nie znajduje się symbol \(\displaystyle 3\), odrzuć. W przeciwnym razie zamień symbol \(\displaystyle 3\) na \(\displaystyle \sharp\), a następnie poruszaj się w lewo, aż dotrzesz do symbolu innego niż \(\displaystyle 3\) i \(\displaystyle \diamondsuit\).
- Jeśli symbol do którego dotarłeś to \(\displaystyle 2\), zamień go na \(\displaystyle \diamondsuit\). Sprawdź symbol po lewej. Jeśli to \(\displaystyle 2\), poruszaj się w prawo aż do ogranicznika. Następnie przejdź do kroku 3.
- Jeśli dotarłeś do symbolu \(\displaystyle 1\), poruszaj się w lewo aż do ogranicznika. Zamień symbol \(\displaystyle 1\) przy ograniczniku na \(\displaystyle \sharp\), a następnie idź w prawo, zamieniając wszystkie symbole \(\displaystyle \diamondsuit\) na \(\displaystyle 2\). Gdy dojdziesz do ogranicznika, przejdź do kroku \(\displaystyle 3\).
- Jeśli dotarłeś do ogranicznika, oznacza to, że skasowano już wszystkie symbole \(\displaystyle 1\). Przejdź w prawo aż do ogranicznika. Jeśli natrafisz na symbol \(\displaystyle 3\), odrzuć. W przeciwnym przypadku, akceptuj.
Nietrudno zaobserwować, że maszyna \(\displaystyle MT_3\) przechodzi przez taśmę w prawo i w lewo tyle razy, ile symboli \(\displaystyle 3\) zawiera taśma oraz wykonuje jeden dodatkowy przebieg na starcie. Zatem słowa z \(\displaystyle L\) są akceptowane w czasie ograniczonym wielomianowo.
Przykład 1.2
Rozważmy teraz język
Najprostszą metodą uzasadnienia, że \(\displaystyle L\in\) NP jest konstrukcja tak zwanej wyroczni. Polega ona na następującej dwuetapowej procedurze:
- Skonstruuj niedeterministyczną maszynę Turinga (wyrocznia) generującą pewne słowo (certyfikat).
- Zweryfikuj w sposób deterministyczny spełnienie założeń przez certyfikat.
W naszym przykładzie Etap 1 wygląda następująco:
- Użyj dwóch taśm. Na pierwszej z nich znajduje się \(\displaystyle 3^k\).
- Idź po pierwszej taśmie, wykorzystując niedeterministyczną funkcję przejść. Napotykając \(\displaystyle 3\), możesz wypisać \(\displaystyle 1\) na taśmie drugiej i przejść o jedną komórkę w prawo na taśmie pierwszej lub przejść do następnego kroku. Jeśli dotarłeś do prawego ogranicznika taśmy pierwszej, przejdź do kroku 3.
- Powróć do początku pierwszej taśmy. Wykonaj sekwencję jak w kroku \(\displaystyle 2\), z tą różnicą, że teraz na drugiej taśmie wypisuj symbole \(\displaystyle 2\).
- Jako ostatnią część tego etapu przekopiuj symbole \(\displaystyle 3\) z pierwszej taśmy na drugą (po symbolach \(\displaystyle 1\) i \(\displaystyle 2\)).
W konstrukcji wykorzystaliśmy dwie taśmy, ale oczywiście w nawiązaniu do wcześniejszych uwag, całą konstrukcję można wykonać na jednej taśmie (z odpowiednio rozszerzonym alfabetem i bardziej skomplikowaną funkcją przejść).
Etap 2 polega na weryfikacji, czy na taśmie drugiej znajduje się słowo postaci \(\displaystyle 1^i 2^j 3^k\), gdzie \(\displaystyle i,j>1\) oraz \(\displaystyle k=i\cdot j\). Jeśli tak, to słowo wejściowe \(\displaystyle 3^k\) pochodziło z języka \(\displaystyle L\) i akceptujemy. Można do tego wykorzystać deterministyczną maszynę Turinga, niemal identyczną z opisaną w przykładzie poprzednim.
Jeśli słowo wejściowe pochodzi z języka \(\displaystyle L\), to jedno z obliczeń maszyny niedeterministycznej z Etapu 1. prowadzi do konstrukcji odpowiedniego słowa na drugiej taśmie. Nie wiemy, jaka dokładnie ścieżka obliczeń ma być wykorzystana, ale dla akceptacji języka \(\displaystyle L\) nie ma to znaczenia.
Zastanów się, czy da się wykazać, że także \(\displaystyle L\in\) P (Ćwiczenie 1.3, do tego wykładu).
Definicja 1.3
Funkcja \(\displaystyle s(n)\) jest konstruowalna pamięciowo, jeśli istnieje maszyna Turinga \(\displaystyle \mathcal{MT}=(\Sigma _{T},S,f,s_{0},S_{F})\), dla której \(\displaystyle d_1 \mapsto^* d_2\), gdzie \(\displaystyle d_1=\sharp s_0 1^n \sharp\), \(\displaystyle d_2=\sharp s_1 1^{s(n)} w \sharp\) dla \(\displaystyle s_1\in S_F\), \(\displaystyle w\in (\Sigma_T\setminus \left\{1\right\})^*\) oraz dodatkowo \(\displaystyle d_2\) jest konfiguracją końcową.
Inaczej mówiąc, funkcję \(\displaystyle s(n)\) nazywamy konstruowalną pamięciowo, jeśli istnieje maszyna Turinga \(\displaystyle \mathcal{MT}\), otrzymując na wejściu słowo \(\displaystyle w\) długości \(\displaystyle |w|=n\), zaznacza na taśmie roboczej \(\displaystyle s(n)\) klatek i zatrzymuje się (akceptując słowo \(\displaystyle w\)).
Przykład 1.3
Funkcja \(\displaystyle s(n)=2n\) jest konstruowalna pamięciowo. Maszyna \(\displaystyle MT_4\), która konstruuje \(\displaystyle s(n)\) działa według schematu:
- Przejdź do prawego markera. Jeśli napotkano symbol inny niż \(\displaystyle 1\), to odrzuć.
- Idź w lewo aż do pierwszego symbolu \(\displaystyle 1\) lub markera \(\displaystyle \sharp\)
- Jeśli napotkałeś symbol \(\displaystyle 1\), zamień go na \(\displaystyle \clubsuit\) i przejdź do prawego markera. Dopisz do słowa symbol \(\displaystyle \clubsuit\) (zwiększając tym samym długość słowa na taśmie o \(\displaystyle 1\)). Następnie powtórz cykl od \(\displaystyle 2\).
- Jeśli napotkałeś marker, idź w prawo, zamieniając wszystkie wystąpienia \(\displaystyle \clubsuit\) na \(\displaystyle 1\). Następnie wracaj do lewego markera i zatrzymaj się, akceptując.
Twierdzenie 1.1 liniowa kompresja pamięci
Niech będzie dany język \(\displaystyle L\) oraz maszyna Turinga \(\displaystyle \mathcal{TM}\) akceptująca \(\displaystyle L\) w pamięci \(\displaystyle s(n)\). Dla dowolnego \(\displaystyle \varepsilon>0\) istnieje maszyna Turinga \(\displaystyle \mathcal{TM}'\) akceptująca \(\displaystyle L\) w pamięci \(\displaystyle \max\left\{n,\varepsilon s(n)\right\}\).
Dowód
(Szkic) Ustalamy liczbę naturalną \(\displaystyle k\), dla której \(\displaystyle \varepsilon k\geqslant 2\). Maszynę \(\displaystyle \mathcal{TM}'\) definiujemy następująco:
- Przekoduj słowo wejściowe, łącząc po \(\displaystyle r\) kolejnych symboli w jeden blok stanowiący nowy symbol na taśmie.
- Symuluj maszynę \(\displaystyle \mathcal{MT}\) na skompresowanej taśmie. Położenie głowicy wewnątrz bloku zakoduj w stanach maszyny \(\displaystyle \mathcal{MT}'\).
Zauważmy, że w kroku \(\displaystyle 1\). maszyna \(\displaystyle \mathcal{MT}'\) wykorzystuje \(\displaystyle n\) komórek pamięci do odczytania słowa wejściowego. Kompresja taśmy zapewnia, że podczas symulowania maszyny \(\displaystyle \mathcal{MT}\) nie wykorzystamy więcej niż \(\displaystyle \lceil \frac{s(n)}{k}\rceil \leqslant \varepsilon s(n)\) komórek. Jednocześnie można założyć, że \(\displaystyle \mathcal{MT}'\) akceptuje słowa wejściowe z języka \(\displaystyle L\) o długości mniejszej niż \(\displaystyle k\) bez symulowania \(\displaystyle \mathcal{MT}\).
Twierdzenie 1.2 Savitch
Dla dowolnej funkcji \(\displaystyle s(n)\) konstruowalnej pamięciowo spełniającej warunek \(\displaystyle s(n)\geqslant \log_2 n\) prawdziwa jest inkluzja \(\displaystyle Nspace(s(n))\subset DSpace(s^2(n))\).
Dowód
Niech \(\displaystyle \mathcal{NMT}\) będzie niedeterministyczną maszyną Turinga akceptującą język \(\displaystyle L=L(\mathcal{NMT})\) w pamięci \(\displaystyle s(n)\). Niech \(\displaystyle k(n)\) oznacza liczbę konfiguracji potrzebną do zaakceptowania słowa o długości \(\displaystyle n\). Istnieje liczba \(\displaystyle c>1\), dla której \(\displaystyle k(n)\leqslant c^{s(n)}\), co z kolei oznacza, że każde słowo o długości \(\displaystyle n\) jest akceptowane w \(\displaystyle c^{s(n)}\) krokach czasowych.
Rozważmy algorytm:
Algorytm
1 Wejście: słowo \(\displaystyle w\) długości \(\displaystyle |w|=n\) 2 oblicz \(\displaystyle s(n)\) 3 for każda konfiguracja akceptująca \(\displaystyle d_A\) dla której \(\displaystyle |d_A|\leqslant s(n)\) 4 do if Test(\(\displaystyle \sharp s_0 w \sharp\), \(\displaystyle d_A\), \(\displaystyle s(n) \log_2 c\)) then akceptuj
gdzie procedura Test ma następującą postać:
Algorytm Procedure Test(\(\displaystyle d\),\(\displaystyle d'\),\(\displaystyle i\))
1 if \(\displaystyle i=0\) and [ (\(\displaystyle d=d'\)) or (\(\displaystyle d\mapsto d'\))] then return true 2 else for każda konfiguracja \(\displaystyle d''\) dla której \(\displaystyle |d''|\leqslant s(n)\) 3 do if Test(\(\displaystyle d\),\(\displaystyle d''\),\(\displaystyle i-1\)) and Test \(\displaystyle d''\),\(\displaystyle d'\),\(\displaystyle i-1\)) 4 then return true; 5 return false
Przedstawiony algorytm można zrealizować za pomocą wielotaśmowej maszyny Turinga. Założenie dotyczące konstruowalności pamięciowej jest istotnie wykorzystywane w tej konstrukcji przy implementacji linii 3 algorytmu i linii 2 procedury Test. Musimy zaznaczyć \(\displaystyle s(n)\) komórek taśmy, aby móc konstruować konfiguracje o długości ograniczonej przez \(\displaystyle s(n)\) i móc następnie wykonywać na nich symulację maszyny \(\displaystyle \mathcal{NMT}\).
Zauważmy, że ilość konfiguracji jest ograniczona przez \(\displaystyle s(n)\), a głębokość rekursji przez \(\displaystyle \log c^{s(n)}\). Oznacza to, że jesteśmy w stanie skonstruować maszynę Turinga, która wymaga \(\displaystyle c' s^2(n)\) pamięci, gdzie \(\displaystyle c'\) jest pewną stałą. Na mocy Twierdzenia 1.1 jesteśmy w stanie określić maszynę \(\displaystyle \mathcal{MT}\) działającą w pamięci \(\displaystyle s^2(n)\).
Wniosek 1.1
Lemat 1.1
Jeśli \(\displaystyle g(n)\geqslant n\), to \(\displaystyle Dtime(g(n))\subset Dspace(g(n))\) oraz \(\displaystyle Ntime(g(n))\subset Nspace(g(n))\).
Dowód
Niech będzie dana maszyna deterministyczna \(\displaystyle \mathcal{MT}\) akceptująca dany język \(\displaystyle L\) w czasie \(\displaystyle g(n)\). Do akceptacji słowa \(\displaystyle w\) o długości \(\displaystyle n\) maszyna wykorzystuje co najwyżej \(\displaystyle g(n)\) kroków czasowych, czyli odwiedza co najwyżej \(\displaystyle g(n)+1\) komórek taśmy.
Na podstawie Twierdzenia 1.1 istnieje maszyna Turinga \(\displaystyle \mathcal{MT}'\) wykorzystująca
komórek pamięci. Dla niedeterministycznych maszyn Turinga argumentacja jest identyczna.
Wniosek 1.2
Uwaga 1.2
Nie jest znany przykład wykazujący silną inkluzję P \(\displaystyle \varsubsetneq\) NP ani dowód wykluczający istnienie takiego przykładu. Powszechnie uznawana hipoteza głosi:
Rozstrzygnięcie jej prawdziwości lub fałszywości stanowi jeden z najważniejszych, a zarazem najtrudniejszych problemów współczesnej informatyki. Jak widzieliśmy w Przykładzie 1.2, nawet w przypadku konkretnego języka \(\displaystyle L\in\) NP, problem uzasadnienia, że także \(\displaystyle L\in\) P, jest nietrywialny, gdyż wymaga zazwyczaj konstrukcji całkiem nowej maszyny Turinga niż ta do weryfikacji \(\displaystyle L\in\) NP .
Redukcja i problemy zupełne
Definicja 2.1 transformacja wielomianowa
Niech \(\displaystyle L_1,L_2\) będą dowolnymi językami nad pewnym alfabetem \(\displaystyle \Sigma_I\). Mówimy, że \(\displaystyle L_1\) redukuje się do \(\displaystyle L_2\) w czasie wielomianowym, co oznaczamy \(\displaystyle L_1 \propto L_2\), gdy istnieje deterministyczna maszyna Turinga \(\displaystyle \mathcal{MT}=(\Sigma _{T},S,f,s_{0},S_{F})\) taka, że dla dowolnego \(\displaystyle w\in \Sigma_I^*\) istnieje \(\displaystyle w'\in \Sigma_I^*\) i stan \(\displaystyle s_1\in S_F\) o własności
oraz
Lemat 2.1
Załóżmy, że \(\displaystyle L_1 \propto L_2\). Wtedy zachodzą implikacje:
- \(\displaystyle L_2 \in\) P \(\displaystyle \quad \Longrightarrow \quad L_1 \in\) P,
- \(\displaystyle L_2 \in\) NP \(\displaystyle \quad \Longrightarrow \quad L_1 \in\) NP,
- \(\displaystyle L_2 \in\) PSPACE \(\displaystyle \quad \Longrightarrow \quad L_1 \in\) PSPACE.
Dowód
Dane słowo \(\displaystyle w\) transformujemy do \(\displaystyle w'\) w czasie wielomianowym, co gwarantuje założenie \(\displaystyle L_1 \propto L_2\). Dzięki założeniu \(\displaystyle L_2 \in\) P możemy rozstrzygnąć, czy \(\displaystyle w'\in L_2\) (tzn. jeśli akceptujemy \(\displaystyle w'\), to robimy to w czasie wielomianowym). Tym sposobem (korzystając z definicji transformacji wielomianowej) akceptujemy \(\displaystyle w\) w czasie wielomianowym, o ile tylko \(\displaystyle w\in L_1\). Dowód dla pozostałych implikacji jest identyczny.
Definicja 2.2
Niech \(\displaystyle \mathcal{C}\) oznacza pewną klasę języków. Język \(\displaystyle L\) nazywamy \(\displaystyle \mathcal{C}\)-trudnym, jeśli spełniony jest warunek:
Jeżeli dodatkowo spełniony jest warunek \(\displaystyle L\in \mathcal{C}\), to język \(\displaystyle L\) nazywamy \(\displaystyle \mathcal{C}\)-zupełnym.
Intuicyjnie, fakt, że język jest \(\displaystyle \mathcal{C}\)-zupełny, oznacza, że jest on najbardziej skomplikowany (pod względem obliczeniowym) wśród języków z klasy \(\displaystyle \mathcal{C}\), natomiast język \(\displaystyle \mathcal{C}\)-trudny jest bardziej skomplikowany niż każdy z klasy \(\displaystyle \mathcal{C}\), choć sam nie musi do niej należeć.
Uwaga 2.1
Rozważając klasę P , NP i PSPACE, możemy mówić o językach (problemach) P -zupełnych, NP -zupełnych, czy też PSPACE -zupełnych. To samo odnosi się do języków trudnych (tzn. klasa języków P -trudnych, itd.).
Przykład 2.1
Rozważmy języki:
Języki: \(\displaystyle L_1\) oraz \(\displaystyle L_2\) wyglądają na bardzo podobne, zatem wydaje się, że \(\displaystyle L_1 \propto L_2\) oraz \(\displaystyle L_2 \propto L_1\). Uzasadnienie tego faktu jest prawie natychmiastowe.
Konstruujemy deterministyczną maszynę Turinga która działa w następujący sposób:
- Jeśli słowo wejściowe jest puste, to stop.
- Przejdź do prawego ogranicznika. Jeśli przy ograniczniku nie występuje symbol \(\displaystyle 4\), to wykonaj krok 1.
- Jeśli w słowie wejściowym występuje symbol \(\displaystyle 4\), to sprawdź, czy słowo przetwarzane jest postaci \(\displaystyle \sharp w 4^s \sharp\), gdzie \(\displaystyle s\geqslant 1\) oraz \(\displaystyle w\in (\Sigma_I\setminus \left\{4\right\})^*\) oraz czy dodatkowo \(\displaystyle s\) jest liczbą parzystą. Jeśli nie, to wykonaj krok 1.
- Zamień słowo \(\displaystyle 4^s\) na słowo \(\displaystyle 3^{\frac{s}{2}}\sharp^{\frac{s}{2}}\) i wykonaj krok 1.
- Przejdź nad pierwszy symbol po lewym ograniczniku i zatrzymaj się.
W ten sposób zawsze przeprowadzamy konfigurację \(\displaystyle \sharp s_0 w \sharp\) na konfigurację \(\displaystyle \sharp s_1 w' \sharp\), przy czym \(\displaystyle w'=1^i 2^j 3^k\) tylko, gdy \(\displaystyle w=1^i 2^j 4^{2k}\). Zatem \(\displaystyle w\in L_2\) wtedy i tylko wtedy, gdy \(\displaystyle w'\in L_1\). Wykazaliśmy, że \(\displaystyle L_2 \propto L_1\).
Warunek \(\displaystyle L_1 \propto L_2\) otrzymujemy w sposób identyczny. Trzeba tylko wypisać odpowiednią ilość symboli \(\displaystyle 4\) (a wiemy już, jak konstruować liczbę \(\displaystyle 2n\), mając dane \(\displaystyle n\)).
Języki maszyn Turinga i typu (0). Rozstrzygalność
Języki maszyn Turinga i rodzina \(\displaystyle \mathcal{L}_{0}\)
Powstaje naturalne pytanie o związki pomiędzy klasą języków rozpoznawanych przez maszyny Turinga a klasami zadanymi poprzez gramatyki. Odpowiemy na to pytanie w tej części wykładu.
Twierdzenie 1.1
Każdy język akceptowany przez maszynę Turinga jest typu(0).
Dowód
Niech \(\displaystyle L\) będzie językiem akceptowanym przez maszynę Turinga \(\displaystyle \mathbf{MT}=(\Sigma _{T},S,f,s_{0},S_{F})\) , o której założymy, że \(\displaystyle f(s_{0},\#)=(s',\#,1)\) , jeśli para \(\displaystyle (s_{0},\#)\) należy do dziedziny funkcji przejść \(\displaystyle f\) maszyny Turinga. Założenie to nie ogranicza ogólności rozważań. Wyróżnimy pewien podzbiór \(\displaystyle \overline{S}_{F}\) zbioru stanów \(\displaystyle S\) , którego elementy, jak wskazuje oznaczenie, skojarzone są ze stanami końcowymi. Do zbioru \(\displaystyle \overline{S}_{F}\) należy każdy stan \(\displaystyle \overline{s}\in S\) , dla którego istnieje ciąg stanów \(\displaystyle s_{1}=\overline{s},...,s_{k}\) dla \(\displaystyle k\geqslant 1\) taki, że \(\displaystyle (s_{i},\#)\rightarrow (s_{i+1},\#,0)\) dla \(\displaystyle k=1,...,k-1\) oraz \(\displaystyle (s_{k},\#)\rightarrow (s,\#,1)\) , gdzie \(\displaystyle s\in S_{F}\) . Zauważmy, iż wraz ze stanem \(\displaystyle \overline{s}\) do zbioru \(\displaystyle \overline{S}_{F}\) należą wszystkie elementy ciągu \(\displaystyle s_{1}=\overline{s},...,s_{k}\) .
Określamy teraz gramatykę \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) . Zbiór symboli nieterminalnych \(\displaystyle V_{N}\) zawiera wyłącznie następujące symbole:
- dla każdego stanu \(\displaystyle s\in S\) i \(\displaystyle a\in \Sigma _{T}\setminus \{\#\}\) symbole \(\displaystyle v_{sa},\: ^{\#}v_{sa},\: v_{sa}^{\#},\: ^{\#}v_{sa}^{\#},\)
- dla każdej litery \(\displaystyle a\in \Sigma _{T}\setminus \{\#\}\) symbole \(\displaystyle \, ^{\#}a\) i \(\displaystyle a^{\#},\)
- wszystkie elementy zbioru \(\displaystyle \Sigma _{T}\setminus (\Sigma _{I}\cup \{\#\}),\)
- symbole \(\displaystyle v_{0},\: v_{1}\) nie należące do \(\displaystyle \Sigma _{T}.\)
Zbiór praw \(\displaystyle P\) składa się z praw wymienionych poniżej:
- \(\displaystyle v_{0}\rightarrow \, ^{\#}v_{sa}^{\#}\) , \(\displaystyle v_{0}\rightarrow v_{1}v_{sa}^{\#}\), jeśli \(\displaystyle f(s,a)=(\overline{s},b,1)\) dla pewnego \(\displaystyle b\in \Sigma _{T}\setminus \{\#\}\) , \(\displaystyle \overline{s}\in \overline{S}_{F}\) ,
- \(\displaystyle v_{1}\rightarrow \, ^{\#}a\) , \(\displaystyle v_{1}\rightarrow v_{1}a\) dla każdego \(\displaystyle a\in \Sigma _{T}\setminus \{\#\}\) ,
- \(\displaystyle v_{s_{1}c}b\rightarrow cv_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}c}b\rightarrow \, ^{\#}cv_{sa}\) , \(\displaystyle v_{s_{1}c}b^{\#}\rightarrow cv^{\#}_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}c}b^{\#}\rightarrow \, ^{\#}cv^{\#}_{sa}\), jeśli \(\displaystyle f(s,a)=(s_{1},b,-1)\) i \(\displaystyle c\in \Sigma _{T}\setminus \{\#\}\) ,
- \(\displaystyle bv_{s_{1}c}\rightarrow v_{sa}c\) , \(\displaystyle \, ^{\#}bv_{s_{1}c}\rightarrow \, ^{\#}v_{sa}c\) , \(\displaystyle bv_{s_{1}c}^{\#}\rightarrow v_{sa}c^{\#}\) , \(\displaystyle \, ^{\#}bv_{s_{1}c}^{\#}\rightarrow \, ^{\#}v_{sa}c^{\#}\), jeśli \(\displaystyle f(s,a)=(s_{1},b,1)\) i \(\displaystyle c\in \Sigma _{T}\setminus \{\#\}\) ,
- \(\displaystyle v_{s_{1}b}\rightarrow v_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}b}\rightarrow \, ^{\#}v_{sa}\) , \(\displaystyle v_{s_{1}b}^{\#}\rightarrow v^{\#}_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}b}^{\#}\rightarrow \, ^{\#}v^{\#}_{sa}\), jeśli \(\displaystyle f(s,a)=(s_{1},b,0)\) ,
- \(\displaystyle v_{s_{1}b}^{\#}\rightarrow v^{\#}_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}b}^{\#}\rightarrow \, ^{\#}v^{\#}_{sa}\) , jeśli istnieją \(\displaystyle s_{1}',...,s_{k}'\in S\) dla \(\displaystyle k\geqslant 1\), takie że \(\displaystyle f(s,a)=(s_{1}',b,1)\) , \(\displaystyle f(s_{i}',\#)=(s_{i+1}',\#,0)\) dla \(\displaystyle i=1,...,k-1\) oraz \(\displaystyle f(s_{k}',\#)=(s_{1},\#,-1)\) ,
- \(\displaystyle \, ^{\#}v_{s_{1}b}\rightarrow \, ^{\#}v_{sa}\) , \(\displaystyle \, ^{\#}v_{s_{1}b}^{\#}\rightarrow \, ^{\#}v^{\#}_{sa}\) , jeśli istnieją \(\displaystyle s_{1}',...,s_{k}'\in S\) dla \(\displaystyle k\geqslant 1\) takie, że \(\displaystyle f(s,a)=(s_{1}',b,-1)\) , \(\displaystyle f(s_{i}',\#)=(s_{i+1}',\#,0)\) dla \(\displaystyle i=1,...,k-1\) oraz \(\displaystyle f(s_{k}',\#)=(s_{1},\#,1)\) ,
- \(\displaystyle a^{\#}\rightarrow a\) dla wszystkich \(\displaystyle a\in \Sigma _{T}\setminus \{\#\}\) ,
- \(\displaystyle \, ^{\#}v_{sa}\rightarrow a\) , \(\displaystyle \, ^{\#}v_{sa}^{\#}\rightarrow a\) , jeśli \(\displaystyle f(s_{0},\#)=(s,\#,1)\) (porównaj założenie na początku dowodu),
- \(\displaystyle v_{0}\Rightarrow 1\), jeśli \(\displaystyle 1\in L\) .
Określona powyżej gramatyka \(\displaystyle G\) jest gramatyką typu (0). Rozważmy teraz dowolne słowo \(\displaystyle w\) , dla którego istnieje wyprowadzenie w gramatyce \(\displaystyle G\) ze stanu początkowego \(\displaystyle v_{0}\) przy użyciu praw 1-7. Słowo \(\displaystyle w\) zawiera dokładnie jeden z następujących symboli \(\displaystyle v_{sa},\, ^{\#}v_{sa},v_{sa}^{\#}\) lub \(\displaystyle \, ^{\#}v_{sa}^{\#}\) . Pierwsza litera słowa \(\displaystyle w\) oznaczona jest markerem \(\displaystyle \#\) z lewej strony, a ostatnia litera słowa \(\displaystyle w\) oznaczona jest markerem \(\displaystyle \#\) ze strony prawej. Ponadto żadna z liter występujących pomiędzy pierwszą a ostatnią nie jest oznaczona markerem \(\displaystyle \#\) . Z każdym takim słowem kojarzymy konfigurację poprzez zastąpienie symbolu \(\displaystyle v_{sa}\) przez \(\displaystyle sa\) oraz przez dopisanie symbolu \(\displaystyle \#\) po lewej lub prawej stronie znaczonej przez ten marker litery, zgodnie z jego występowaniem. Jeśli np. \(\displaystyle w=\, ^{\#}v_{sa}^{\#}\) , to skojarzona konfiguracja jest postaci \(\displaystyle \#sa\#\) . Zauważmy, że jeśli słowa \(\displaystyle u\) i \(\displaystyle w\) są w powyższej formie, to fakt, iż \(\displaystyle u\mapsto^{*}w\) , jest równoważny stwierdzeniu, że z konfiguracji skojarzonej ze słowem \(\displaystyle w\) maszyna Turinga \(\displaystyle MT\) może przejść (bezpośrednie następstwo) do konfiguracji skojarzonej ze słowem \(\displaystyle u\) . Każdy krok obliczenia realizowanego przez \(\displaystyle MT\) ma swój odpowiednik - krok w wyprowadzeniu w gramatyce \(\displaystyle G\) . Z tym, że wobec praw 6 i 7 sekwencja obliczeń
jest traktowana jako jeden krok w obliczeniu prowadzonym przez maszynę Turinga. Analogicznie traktujemy sekwencję z markerem \(\displaystyle \#\) występującym po lewej stronie. Ze stanu początkowego \(\displaystyle v_{0}\) gramatyki \(\displaystyle G\) można wyprowadzić wszystkie słowa \(\displaystyle w\) , dla których konfiguracja jest równa \(\displaystyle \#vsa\#\), dla pewnego \(\displaystyle v\in (\Sigma _{I}\setminus \{\#\})^{*}\) oraz maszyna Turinga realizuje obliczenie:
Wynika to z praw 1 i 2 skonstruowanej gramatyki \(\displaystyle G\) . Z kolei prawa typu 9 służą do zastąpienia symboli nieterminalnych typu \(\displaystyle \, ^{\#}v_{sa},\, ^{\#}v_{sa}^{\#}\) przez litery terminalne, a prawa typu 8 eliminują symbole nieterminalne typu \(\displaystyle a^{\#}\) . A zatem dla niepustego słowa \(\displaystyle w\in (\Sigma _{I}\setminus \{\#\})^{*}\) spełniona jest równoważność
gdzie \(\displaystyle u\in (\Sigma _{I}\setminus \{\#\})^{*}\) oraz \(\displaystyle s_{1}\in S_{F}\) . Prawo 10. zapewnia, że powyższa równoważność prawdziwa jest także dla słowa pustego \(\displaystyle 1\) . A to kończy dowód tego twierdzenia.
Język \(\displaystyle L\) nazywamy rekurencyjnie przeliczalnym, jeśli istnieje efektywny algorytm wyliczający wyłącznie słowa z \(\displaystyle L\) . Przez efektywny algorytm rozumiemy skończony zbiór instrukcji, który w jednoznaczny sposób opisuje działanie tego algorytmu. Klasę języków rekurencyjnie przeliczalnych oznaczamy symbolem \(\displaystyle \mathcal{RP}\) .
Zauważmy, że każda gramatyka \(\displaystyle G\) typu (0) jest algorytmem wyliczającym wyłącznie słowa z \(\displaystyle L=L(G)\) . Dla każdej liczby naturalnej \(\displaystyle k\) można bowiem rozważyć skończony zbiór wyprowadzeń w \(\displaystyle G\), rozpoczynających się od symbolu początkowego \(\displaystyle v_{0}\) i o długości równej \(\displaystyle k\) . Z tego zbioru można z kolei wybrać wyłącznie te wyprowadzenia, które kończą się słowem nad alfabetem terminalnym gramatyki \(\displaystyle G\) i tylko te słowa dodawać do listy składającej się na język \(\displaystyle L\) . Są to, jak łatwo zauważyć, wszystkie słowa języka \(\displaystyle L\) i nic ponadto. A zatem
Twierdzenie 1.2
Każdy język typu (0) jest językiem rekurencyjnie przeliczalnym, czyli \(\displaystyle \mathcal{L}_{0}\subset \mathcal{RP}\) .
Język \(\displaystyle L\) nazywamy rekurencyjnym, jeśli istnieje efektywny algorytm rozstrzygający dla każdego słowa \(\displaystyle w\in A^{*}\) jego przynależność do języka \(\displaystyle L\) . Klasę języków rekurencyjnych oznaczamy symbolem \(\displaystyle \mathcal{R}\) .
Klasa języków kontekstowych zawiera się istotnie w klasie języków rekurencyjnych, o czym przekonuje poniższe twierdzenie.
Twierdzenie 1.3
Każdy język kontekstowy jest językiem rekurencyjnym, czyli \(\displaystyle \mathcal{L}_{1}\subset \mathcal{R}.\)
Dowód
Niech \(\displaystyle L\) będzie dowolnym językiem kontekstowym. Istnieje więc gramatyka kontekstowa \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) taka, że \(\displaystyle L=L(G)\) . Bezpośrednio z definicji gramatyki kontekstowej wynika, iż słowo puste \(\displaystyle 1\in L\) wtedy i tylko wtedy, gdy \(\displaystyle v_{0}\rightarrow 1\in P\) . Załóżmy teraz, że dane jest słowo \(\displaystyle w\in V^{*}_{T}\) , o którym mamy zadecydować, czy należy do języka \(\displaystyle L\) . W tym celu rozważmy wszystkie ciągi słów
o tej własności, że \(\displaystyle y_{i}\in (V_{N}\cup V_{T})^{*}\) są parami różne, dla \(\displaystyle i=0,...,n\) , \(\displaystyle n\geqslant 1\) oraz \(\displaystyle \mid y_{i}\mid \leqslant \mid y_{i+1}\mid\) . Ilość takich ciągów jest skończona i słowo \(\displaystyle w\in L\) wtedy i tylko wtedy, gdy wśród powyższych ciągów znajdziemy choć jeden taki, że tworzy wyprowadzenie w gramatyce \(\displaystyle G\) . Czyli
Ponieważ ilość ciągów podlegających rozważaniom jest skończona oraz ponieważ stwierdzenie, czy pomiędzy dowolnymi słowami zachodzi relacja \(\displaystyle \rightarrow\) , sprowadza się do przeszukania skończonego zbioru praw \(\displaystyle P\) , efektywnie rozstrzygniemy, czy \(\displaystyle w\) należy do języka \(\displaystyle L\), czy też nie.
Uzyskane dotąd rezultaty możemy podsumować następująco:
W określeniu języka rekurencyjnie przeliczalnego oraz języka rekurencyjnego wystąpiło pojęcie efektywnego algorytmu, efektywnej procedury. Pojęcie to, intuicyjnie dość jasne, nie zostało precyzyjnie określone. Co za tym idzie, dla matematycznie poprawnych definicji języka rekurencyjnie przeliczalnego i języka rekurencyjnego należałoby sformalizować pojęcie algorytmu. W dotychczasowych rozważaniach intuicja efektywnej procedury była o tyle wystarczająca, że naszym celem było wskazanie istnienia takiej procedury. W sytuacji, gdyby naszym celem było wykazanie, że taka procedura nie istnieje, formalizacja tego pojęcia byłaby wręcz konieczna. We wszystkich takich przypadkach powszechnie przyjmuje się, że maszyna Turinga jest właśnie taką formalizacją. Na zdefiniowaną w poprzednim wykładzie maszynę Turinga można spojrzeć jako na algorytm, efektywną procedurę dającą odpowiedź pozytywną lub negatywną w zależności od akceptacji lub nieakceptowania słowa wejściowego. Proces obliczenia prowadzony przez maszynę Turinga zgadza się z intuicyjnym rozumieniem algorytmu. O tym, że każda efektywna procedura jest reprezentowana przez pewną maszynę Turinga, mówi, powszechnie przyjęta jako prawdziwa, teza Churcha.
Teza Churcha
Każda efektywna procedura (algorytm) da się opisać przez maszynę Turinga.
Konsekwencją przyjęcia tezy Churcha jest inkluzja \(\displaystyle \mathcal{RP}\subset \mathcal{L}(MT)\) . Biorąc pod uwagę udowodnione powyżej twierdzenia, mamy:
co ostatecznie prowadzi do równości \(\displaystyle \mathcal{L}_{0}=\mathcal{L}(MT)\) .
Rodziny \(\displaystyle \mathcal{L}_{1}\) i \(\displaystyle \mathcal{L}_{0}\) - zamkniętość na działania
Dla kompletności tej części wykładu przedstawimy własności zamkniętości rodziny języków kontekstowych \(\displaystyle \mathcal{L}_{1}\) i języków typu (0) \(\displaystyle \mathcal{L}_{0}\) ze względu na najczęściej używane operacje. W niektórych przypadkach dowody dotyczące obu klas są takie same. W dowodach posłużymy się specjalną postacią gramatyk, a mianowicie taką, w której symbole terminalne występują tylko po prawej stronie. Prawdziwe bowiem jest twierdzenie
Twierdzenie 2.1
Dla każdej gramatyki istnieje równoważna gramatyka tego samego typu taka, że każda produkcja, w której występuje symbol terminalny \(\displaystyle a\) , jest postaci \(\displaystyle v\longrightarrow a\) .
Elementarny dowód tej własności pozostawiamy jako zadanie domowe.
Twierdzenie 2.2
Rodziny \(\displaystyle \mathcal{L}_{0}\) i \(\displaystyle \mathcal{L}_{1}\) są zamknięte ze względu na:
- sumę mnogościową,
- iloczyn mnogościowy,
- katenację,
- iterację \(\displaystyle *\),
- odbicie zwierciadlane.
Dowód
1. Niech dla \(\displaystyle i=1,2 \displaystyle G_{i}=(V_{N}^{i},V_{T},v_{0}^{i},P_{i})\) będą gramatykami typu \(\displaystyle (1)\) (odpowiednio typu \(\displaystyle (0)\) ) takimi, że \(\displaystyle V_{N}^{1}\cap V_{N}^{2}=\emptyset\) . I niech \(\displaystyle L_{i}=L(G_{i})\) . Określamy gramatykę \(\displaystyle G\) typu \(\displaystyle (1)\) (typu \(\displaystyle (0)\) ) generującą język \(\displaystyle L_{1}\cup L_{2}\) .
Jeśli \(\displaystyle 1\notin L_{1}\cup L_{2}\) , to przyjmujemy:
Zauważmy, że wówczas w żadnej z gramatyk nie ma prawa wymazującego. Jeśli natomiast \(\displaystyle 1\in L_{1}\cup L_{2}\) , to konstruujemy gramatykę \(\displaystyle G\) dla języków \(\displaystyle L_{1}\setminus \left\{ 1\right\}\) i \(\displaystyle L_{2}\setminus \left\{ 1\right\}\) , jak powyżej, a następnie dodajemy nowy symbol początkowy \(\displaystyle \overline{v}_{0}\) i prawa \(\displaystyle \overline{v}_{0}\rightarrow v_{0},\, \overline{v}_{0}\rightarrow 1\) .
2. Przecięcie udowodnimy tylko dla języków typu \(\displaystyle (0)\) . Dowód dla języków kontekstowych został przeprowadzony wcześniej.
Niech dla \(\displaystyle i=1,2 \displaystyle G_{i}=(V_{N}^{i},V_{T},v_{0}^{i},P_{i})\) będą gramatykami typu \(\displaystyle (0)\) takimi, że \(\displaystyle V_{N}^{1}\cap V_{N}^{2}=\emptyset\) . Niech \(\displaystyle L_{i}=L(G_{i})\) . Określamy gramatykę \(\displaystyle G\) typu \(\displaystyle (0)\) generującą język \(\displaystyle L_{1}\cap L_{2}\), przyjmując:
gdzie: \(\displaystyle V_{N}=\left\{ v_{a}\, :\, a\in V_{T}\right\} \cup \left\{ v_{0},\overline{v}_{1},\overline{v}_{2}\right\}\) ,
a do zbioru \(\displaystyle P\) należą prawa:
(1) \(\displaystyle v_{0}\rightarrow \overline{v}_{1}v_{0}^{1}\overline{v}_{2}v_{0}^{2}\overline{v}_{1},\)
(2) \(\displaystyle \overline{v}_{2}a\rightarrow v_{a}\overline{v}_{2}\) dla \(\displaystyle \forall a\in V_{T},\)
(3) \(\displaystyle bv_{a}\rightarrow v_{a}b\) dla \(\displaystyle \forall a,b\in V_{T},\)
(4) \(\displaystyle \overline{v}_{1}v_{a}a\rightarrow a\overline{v}_{1}\) dla \(\displaystyle \forall a\in V_{T},\)
(5) \(\displaystyle \overline{v}_{1}\overline{v}_{2}\overline{v}_{1}\rightarrow 1.\)
Przy pomocy prawa (1) i wszystkich praw ze zbioru \(\displaystyle P_{1}\cup P_{2}\) można wygenerować zbiór słów:
Z dowolnego słowa należącego do tego zbioru, korzystając z praw (2)-(4), można wyprowadzić słowo \(\displaystyle w_{1}\overline{v}_{1}\overline{v}_{2}\overline{v}_{1}\) wtedy i tylko wtedy, gdy \(\displaystyle w_{1}=w_{2}\) . Korzystając z prawa (5), dostajemy słowo \(\displaystyle w_{1}\) . A więc \(\displaystyle L(\overline{G})=L_{1}\cap L_{2}\) .
3. Niech dla \(\displaystyle i=1,2 \displaystyle G_{i}=(V_{N}^{i},V_{T},v_{0}^{i},P_{i})\) będą tak jak poprzednio gramatykami typu \(\displaystyle (1)\) ( \(\displaystyle (0)\) ) takimi, że \(\displaystyle V_{N}^{1}\cap V_{N}^{2}=\emptyset\) oraz spełniającymi warunki powyższego twierdzenia. Niech \(\displaystyle L_{i}=L(G_{i})\) . Określamy gramatykę \(\displaystyle G\) odpowiednio typu \(\displaystyle (1)\) ( \(\displaystyle (0)\) ) generującą język \(\displaystyle L_{1}L_{2}\) .
Jeśli \(\displaystyle 1\notin L_{1}\cup L_{2}\) , to przyjmujemy:
Jeśli \(\displaystyle 1\in L_{1}\cup L_{2}\) , to oznaczamy \(\displaystyle L_{1}'=L_{1}\setminus \left\{ 1\right\} ,\; \; L_{2}'=L_{2}\setminus \left\{ 1\right\}\) . Wówczas:
Wykorzystując poprzednią konstrukcję i zamkniętość ze względu na sumę w każdym z tych przypadków, otrzymujemy gramatykę generującą katenację języków \(\displaystyle L_{1}\) i \(\displaystyle L_{2}\) .
4. Niech \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) będzie gramatyką typu \(\displaystyle (1)\) (typu \(\displaystyle (0)\) ) taką, że symbole terminalne nie występują po lewej stronie żadnej produkcji z \(\displaystyle P\) . Załóżmy też, że \(\displaystyle 1\notin L=L(G)\) . Gramatyka
gdzie
generuje język \(\displaystyle L^{*}\) . Jeśli \(\displaystyle 1\in L\) , to usuwamy prawo wymazujące \(\displaystyle v_{0}\rightarrow 1\) i dla języka \(\displaystyle L\setminus \left\{ 1\right\}\) konstruujemy gramatykę \(\displaystyle \overline{G}\) . Z faktu, że \(\displaystyle (L\cup \left\{ 1\right\} )^{*}=L^{*}\) , wynika, że również \(\displaystyle L(\overline{G})=L^{*}\) .
5. Jeśli \(\displaystyle G=(V_{N},V_{T},v_{0},P)\) jest gramatyką typu \(\displaystyle (1)\) (typu \(\displaystyle (0)\) ) taką, że \(\displaystyle L(G)=L\) , to gramatyka \(\displaystyle \overleftarrow{G}=(V_{N},V_{T},v_{0},\overleftarrow{P})\) , gdzie \(\displaystyle \overleftarrow{P}=\left\{ \overleftarrow{x}\rightarrow \overleftarrow{y}\, :\, x\rightarrow y\in P\right\}\) generuje język \(\displaystyle \overleftarrow{L}\) .
Zauważmy na koniec, że rodzina \(\displaystyle \mathcal{L}_{0}\) nie jest zamknięta ze względu na uzupełnienie. Stwierdzenie to wynika z przyjęcia jako obowiązujacej tezy Churcha, która w tym wypadku implikuje równość rodziny języków \(\displaystyle \mathcal{L}_{0}\) i rodziny języków rekurencyjnie przeliczalnych oraz z faktu, iż istnieje język rekurencyjnie przeliczalny, którego uzupełnienie nie jest rekurencyjnie przeliczalne. Ten ostatni fakt podajemy bez dowodu. Dodajmy, że własność zamkniętości ze względu na uzupełnienie dla rodziny \(\displaystyle \mathcal{L}_{1}\) przez długi czas pozostawała problemem otwartym. Dopiero w roku 1987 udowodniono, iż własność ta jest spełniona dla języków kontekstowych. Podsumowanie własności zamkniętości ze względu na działania dla różnych klas języków hierarchii Chomsky'ego zawarte jest w poniższej tabeli:
| 3 | 2 | 1 | 0 | |
| \(\displaystyle\cup\) | T | T | T | T |
| \(\displaystyle\cdot\) | T | T | T | T |
| \(\displaystyle\star\) | T | T | T | T |
| \(\displaystyle\setminus\) | T | N | T | N |
| \(\displaystyle\cap\) | T | N | T | T |
Na koniec podamy twierdzenie o wzajemnych relacjach pomiędzy rodzinami języków z hierarchii Chomsky'ego. Dowód tego twierdzenia wynika w części z definicji typów gramatyk wprowadzonych na wykładzie 2, a w części z udowodnionych własności poszczególnych rodzin języków z hierarchii Chomsky'ego (zakładając obowiązywanie tezy Churcha).
Twierdzenie 2.3
Rodziny języków hierarchii Chomsky'ego spełniają następujące relacje:
Problemy rozstrzygalne
W poprzednim wykładzie uzasadniliśmy, że dla każdej deterministycznej maszyny Turinga jesteśmy w stanie wskazać taką, która akceptuje dany język i jednocześnie zatrzymuje się tylko na słowach akceptowanych. Wymagało to przejścia przez maszynę niedeterministyczną, a następnie jej symulację na maszynie deterministycznej. Z tego powodu ograniczamy się w dalszej części wykładu tylko do tego typu maszyn Turinga (akceptacja=stop). Jak to uzasadniono wcześniej, przy założeniu tezy Churcha, maszyna Turinga może być rozpatrywana jako matematycznie ścisła definicja algorytmu.
Pojęcie rozstrzygalnego problemu zostało wprowadzone wcześniej, na innym wykładzie, i jest ono znane. Przypomnijmy więc tylko, że rozstrzygalność, czy też nierozstrzygalność, odnosi się do pewnej klasy, którą tworzą określone przypadki ustalonego problemu. Jeśli istnieje algorytm, który rozwiązuje taki problem dla wszystkich przypadków w tej klasy, to mówimy, że problem jest rozstrzygalny (w tej klasie). Zatem taki algorytm jest uniwersalnym sposobem rozwiązywania problemu dla wszystkich danych wejściowych określających poszczególne przypadki w tej klasie. Jak łatwo zauważyć dla ustalenia rozstrzygalności problemu wystarczy się opierać na intuicyjnym pojęciu algorytmu. Są jednak takie problemy, dla których nie istnieje, w rozważanej klasie przypadków, uniwersalny sposób ich rozwiazywania. Takie problemy nazywamy nierozstrzygalnymi w danej klasie. Aby wykazać nierozstrzygalność jakiegoś problemu, nieodzownym jest sformalizowanie pojęcia algorytmu. Standardowo taką formalizacją jest, o czym wspomniano już wcześniej, maszyna Turinga.
Zwróćmy uwagę, że maszyna Turinga akceptuje języki, gdy tymczasem przyzwyczajeni jesteśmy, że algorytmy (programy) rozwiązują pewne, niekiedy bardzo skomplikowane, problemy (określone przy pomocy list, kolejek, grafów itp.). Zwracamy zatem uwagę na fakt, że w przypadku maszyny Turinga musimy wykonać wstępne umowne kodowanie naszego problemu. W tym przypadku rozważany język określa te spośród "sensownych" kodowań, które stanowią rozwiązanie postawionego problemu. Z drugiej strony maszyna, akceptując słowo \(\displaystyle \sharp w_1 \$ w_2 \sharp\), może informować nas o tym, że wynikiem obliczeń numerycznych na danych zakodowanych w \(\displaystyle w_1\) rzeczywiście jest liczba zakodowana w \(\displaystyle w_2\) itp.
Dla ilustracji powyższych dywagacji rozważmy problem skończoności w klasie jezyków regularnych. Problem ten jest rozstrzygalny, bo w oparciu o lemat o pompowaniu można skonstruować algorytm, który dla dowolnego języka regularnego rozstrzygnie, czyli odpowie twierdząco lub przecząco na pytanie o jego skończoność. W tym przypadku można np. przyjąć, że jako słowo wejściowe podajemy zakodowany opis gramatyki generującej język.
Nierozstrzygalność algorytmiczna problemu w ustalonej klasie nie oznacza, podkreślmy, niemożliwości rozwiązania konkretnego zadania z tej klasy. Nierostrzygalność oznacza niemożliwość rozwiązania za pomocą tego samego algorytmu, tej samej metody, wszystkich przypadków tego problemu należących do danej klasy.
W zamieszczonej poniżej tabeli przedstawiamy najczęściej rozważane pod kątem rozstrzygalności problemy z dziedziny języków formalnych w ramach hierarchii Chomsky'ego. Litera R oznacza rozstrzygalność problemu, N nierostrzygalność, a znak - pojawiający się przy problemie jednoznaczności oznacza, że problemu tego nie formułuje się dla gramatyk kontekstowych i typu (0):
| własność | (3) | (2) | (1) | (0) |
| należenie \(\displaystyle w\in L\) | R | R | R | N |
| inkluzja \(\displaystyle L_{1}\subset L_{2}\) | R | N | N | N |
| równoważność | R | N | N | N |
| pustość \(\displaystyle L=\emptyset\) | R | R | N | N |
| nieskończoność \(\displaystyle card\, L=\aleph _{0}\) | R | R | N | N |
| jednoznaczność gramatyki | R | N | - | - |
Najczęściej używaną metodą dowodzenia nierozstrzygalności problemu \(\displaystyle P\) jest redukcja tego problemu do innego, powiedzmy \(\displaystyle P'\) , dla którego nierozstrzygalność została ustalona wcześniej. Redukcja taka prowadzi do sformułowania implikacji:
jeśli \(\displaystyle P\) byłby rozstrzygalny, to i \(\displaystyle P'\) byłby rozstrzygalny.
A ponieważ to ostatnie (następnik implikacji) nie jest prawdą, więc problem \(\displaystyle P\) nie jest rozstrzygalny.
Należy w tym miejscu podkreślić fakt, że dowody nierozstrzygalności problemów uniwersalnych (takich jak problem Posta rozważany dalej) wiążą się z konstrukcją odpowiednich maszyn Turinga, kodowaniem problemu, a następnie dowodem uzasadniającym, że problem jest rzeczywiście nierozstrzygalny. Tematyka ta wykracza poza ramy wykładu. Z tego też powodu ograniczymy się tutaj do zaprezentowania jednego ze znanych problemów nierozstrzygalnych bez dowodu nierozstrzygalności.
Najczęściej występującym w literaturze problemem nierozstrzygalnym jest, bez wątpienia, problem Posta przedstawiony poniżej.
Problem Posta
Dla dowolnego alfabetu \(\displaystyle A\) , o co najmniej dwóch elementach ( \(\displaystyle \sharp A\geqslant 2\) ), załóżmy, iż dana jest, tak zwana, lista słów, a dokładniej: par słów \(\displaystyle \left( u_{1},w_{1}\right) \: \left( u_{2},w_{2}\right) \: \ldots \left( u_{n},w_{n}\right),\) gdzie \(\displaystyle u_{i},w_{i}\in A^{+}\) , \(\displaystyle n\in \Bbb N\) . Mówimy, że taka lista ma własność Posta (problem Posta ma rozwiązanie), jeśli istnieje ciąg indeksów \(\displaystyle i_{1},\ldots ,i_{k}\in \{1,...,n\}\) taki, że
Jest to w ogólnym przypadku problem nierozstrzygalny.
Problem ten można sformułować równoważnie następująco. Niech \(\displaystyle A\) będzie alfabetem interpretowanym jako zbiór indeksów, a \(\displaystyle B\) dowolnym alfabetem. Niech \(\displaystyle h:A^{*}\longrightarrow B^{*},\: g:A^{*}\longrightarrow B^{*}\) będą dowolnymi homomorfizmami. Problem Posta, inaczej sformułowany, polega na odpowiedzi na pytanie, czy istnieje słowo \(\displaystyle x\in A^{+}\) takie, że \(\displaystyle h(x)=g(x)\) .
Dwa kolejne przykłady ilustrują technikę redukcji pewnych problemów do problemu Posta. W efekcie uzyskujemy nierozstrzygalność w sposób opisany powyżej.
Twierdzenie 3.1
W klasie gramatyk bezkontekstowych problem niejednoznaczności jest nierozstrzygalny.
Dowód
Udowodnimy, że problem jest nierozstrzygalny dla gramatyk bezkontekstowych generujących języki nad alfabetem dwuelementowym \(\displaystyle A=\{a,b\}\) . Oznaczmy \(\displaystyle B=\{d,e\}\) i określmy homomorfizm \(\displaystyle h:B^{*}\longrightarrow A^{*}\) , przyjmując \(\displaystyle h(d)=ba^{2}\) oraz \(\displaystyle h(e)=ba^{3}\) . Niech \(\displaystyle u\) będzie ciągiem \(\displaystyle u_{1},...,u_{n}\in B^{+}\) dowolnie wybranych i ustalonych słów. Dla dowolnej liczby naturalnej \(\displaystyle i>0\) niech \(\displaystyle \overline{i}=de^{i}\) . Określony poniżej język
jest językiem bezkontekstowym, jako generowany przez gramatykę \(\displaystyle G_{u}=(V_{N},V_{T},v_{0},P_{u})\) , dla której
\(\displaystyle V_{N}=\{v_{u}\},\: V_{T}=\{a,b\},\: v_{0}=v_{u}\) oraz \(\displaystyle P_{x}=\{v_{u}\rightarrow h(\overline{i})v_{u}h(u_{i}),\: v_{u}\rightarrow h(\overline{i})bah(u_{i})\}\) .
Niech teraz \(\displaystyle u\) i \(\displaystyle w\) oznaczają ciągi dowolnie wybranych i ustalonych słów \(\displaystyle u_{1},...,u_{n}\in B^{+}\) i \(\displaystyle w_{1},...,w_{n}\in B^{+}\) . Tworzą one listę słów \(\displaystyle \left( u_{1},w_{1}\right) \: \left( u_{2},w_{2}\right) \: \ldots \left( u_{n},w_{n}\right),\) . Zatem zasadne jest postawienie pytania, czy lista ta ma własność Posta. Niech \(\displaystyle G_{u}\) oraz \(\displaystyle G_{w}\) będą gramatykami bezkontekstowymi określonymi tak jak powyżej. Gramatyka \(\displaystyle G=(\{v_{0},v_{u},v_{w}\},\{a,b\},v_{0},P)\) , gdzie \(\displaystyle P=\{v_{0}\rightarrow v_{u},\: v_{0}\rightarrow v_{w}\}\cup P_{u}\cup P_{w}\) jest bezkontekstowa. Gramatyka ta jest niejednoznaczna wtedy i tylko wtedy, gdy \(\displaystyle L_{u}\cap L_{y}\neq \emptyset\) . Ten ostatni warunek równoważny jest istnieniu liczb \(\displaystyle i_{1},...,i_{k}\in \Bbb N\) takich, że \(\displaystyle u_{i_{1}}.....u_{i_{k}}=w_{i_{1}}.....w_{i_{k}}\), czyli własności Posta listy \(\displaystyle \left( u_{1},w_{1}\right) \: \left( u_{2},w_{2}\right) \: \ldots \left( u_{n},w_{n}\right)\) .Ostatecznie więc rozstrzygalność problemu niejednoznaczności w klasie gramatyk bezkontekstowych prowadziłaby do rozstrzygalności własności Posta.
Dla drugiego przykładu przyjmijmy jako alfabety \(\displaystyle A_{2}=\left\{ a,b\right\} ,\: A_{3}=\left\{ a,b,c\right\}\) oraz określmy język
Ustalmy listę Posta \(\displaystyle \left( u_{1},w_{1}\right) \: \left( u_{2},w_{2}\right) \: \ldots \left( u_{n},w_{n}\right)\) nad alfabetem \(\displaystyle A_{2}\) , gdzie \(\displaystyle u_{i},w_{i}\in A_{2}^{+}\) . Wprowadzamy teraz języki \(\displaystyle L_{u},\: L_{w}\: L_{PP}\) nad alfabetem \(\displaystyle A_{3}\), przyjmując:
oraz definiujemy język
Określone powyżej języki nad alfabetem \(\displaystyle A_{3}\) mają własności konieczne do zastosowania lematu, który przytoczymy bez dowodu.
Lemat 3.1
Języki \(\displaystyle L,\: L_{PP},\: A_{3}^{*}\setminus L,\: A_{3}^{*}\setminus L_{PP}\) są bezkontekstowe.
Dla języków \(\displaystyle L\) i \(\displaystyle L_{PP}\) uzasadnienie ich bezkontekstowości jest proste poprzez konstrukcję odpowiednich gramatyk. Aby uzyskać bezkontekstowość ich uzupełnień, należy podzielić rozważane języki na rozłączne podzbiory i konstruować gramatyki bezkontekstowe dla tych wyróżnionych podzbiorów, a w końcu wykorzystać fakt, że suma języków bezkontekstowych jest językiem bezkontekstowym.
Zauważmy teraz, że istnienie rozwiązania problemu Posta nad alfabetem \(\displaystyle A_{3}\) jest równoważne temu, że \(\displaystyle L_{PP}\cap L\neq \emptyset\) .
Jeśli bowiem \(\displaystyle L_{PP}\cap L\ni ba^{i_{k}}\ldots ba^{i_{1}}cu_{i_{1}}\ldots u_{i_{k}}c\overleftarrow{w_{i_{1}}\ldots w_{i_{k}}}ca^{i_{1}}b\ldots a^{i_{k}}b\) , gdzie \(\displaystyle k\geqslant 1,1\leqslant i_{j}\leqslant n\) , to oczywiście \(\displaystyle u_{i_{1}}\ldots u_{i_{k}}=w_{i_{1}}\ldots w_{i_{k}}\) . Jeśli ciąg \(\displaystyle i_{1},\ldots ,i_{k}\) jest rozwiązaniem problemu Posta, to \(\displaystyle (i_{1},\ldots ,i_{k})(i_{1},\ldots ,i_{k})\) też. Zatem jeśli \(\displaystyle L_{PP}\cap L\neq \emptyset\) , to język \(\displaystyle L_{PP}\cap L\) jest nieskończony.
Wobec nierozstrzygalności problemu Posta wnioskujemy, że nierozstrzygalny jest problem pustości i problem nieskończoności przecięcia \(\displaystyle L_{1}\cap L_{2}\) w klasie języków bezkontekstowych.