Języki, automaty i obliczenia - zbiór zadań

Słowa, liczby, grafy

Do tej części zadań może podejść Czytelnik bez żadnej znajomości teorii automatów.

Słowa pierwotne.Słowo $w\in\Sigma^{*}$ nazywamy pierwotnym (ang. primitive),jeśli nie da się go przedstawić $w=v^{n}$, inaczej niż dla $n=1$ i $v=w$.
1. Dowieść, że dla każdego słowa niepustego $w$, istnieje dokładnie jedno słowo pierwotne $v$, takie że $w=v^{n}$, dla pewnego $n\geq 1$.
  Liczbę $n$ nazywamy wykładnikiem słowa $w$.
2. O słowach $wv$ i $vw$ mówimy, że są w relacji koniugacji. Dowieść, że jest to relacja równoważności.
  Dowieść, że dwa słowa będące w relacji koniugacji mają ten sam wykładnik. Jaka jest moc klasy abstrakcji relacji koniugacji dla słowa o długości $m$ i wykładniku $n$?
Język nawiasowy. Wykazać, że zbiór poprawnie uformowanych ciągów nawiasów może być zdefiniowany na dwa równoważne sposoby:
1. Jako najmniejszy zbiór $L$ zawierający ciąg pusty oraz taki, że jeśli $w,v\in L$, to również $(w),wv\in L$.
2. Zbiór słów nad alfabetem $\{(,)\}$, w których ilość “)” jest taka sama jak ilość “(”, a w każdym prefiksie ilość “)” jest niewiększa niż ilość “(” .
Zbiory semi–liniowe. Zbiór liczb naturalnych postaci $\{ a+bn\,:\, n\in{\bf N}\}$, dla ustalonych $a,b\in{\bf N}$ nazywamy liniowym. Zbiór bedący sumą skończonej liczby zbiorów liniowych nazywamy semiliniowym. (Gdy sumowana rodzina jest pusta, otrzymujemy zbiór pusty.)
1. Dowieść, że każdy zbiór postaci $\{ a+b_{1}n_{1}+\ldots+b_{k}n_{k}\,:\, n_{1},\ldots,n_{k}\in{\bf N}\}$, dla ustalonych $k$ i $a,b_{1},\ldots,b_{k}\in{\bf N}$, jest semi–liniowy.
  Wskazówka. Wykorzystać podziały zbioru liczb naturalnych na klasy abstrakcji relacji przystawania modulo $m$, dla odpowiednio dobranych liczb $m$.
2. Dowieść, że zbiór liczb naturalnych $A$ jest semi–liniowy wtedy i tylko wtedy, gdy jest prawie periodyczny tzn. gdy istnieją
  $c\in{\bf N}$ i $d\in{\bf N}-\{ 0\}$ takie, że dla każdego $x>c$, $x\in A\,\Leftrightarrow\, x+d\in A$.
3. W grafie zorientowanym ustalamy dwa wierzchołki. Interesuje nas zbiór długości wszystkich możliwych ścieżek pomiędzy tymi wierzchołkami. Dowieść, że jest to zbiór semi–liniowy.
4. Dowieść, że rodzina zbiorów semi–liniowych jest zamknięta na skończone sumy, przecięcia oraz na uzupełnienie względem $N$.
Graf gry (J. P. Jouannaud). Rozważamy następującą grę pomiędzy Barmanem i Klientem. Przed Barmanem na obrotowym talerzu stoją cztery szklanki tworząc wierzchołki kwadratu. Szklanka może być ustawiona normalnie lub dnem do góry, jednak Barman ma przepaskę na oczach i rękawiczki na rękach, tak że nie może tego zobaczyć ani wyczuć. Ruch Barmana polega na odwróceniu jednej lub dwóch dowolnie wybranych szklanek. Ruch Klienta polega na obróceniu talerza (o wielokrotność ćwierć-obrotu). Barman wygrywa, jeśli w jakimś momencie gry wszystkie szklanki ustawione są w tej samej pozycji (zostanie o tym lojalnie poinformowany).
Czy Barman noże wygrać startując z nieznanej konfiguracji początkowej, a jeśli tak, to w jakiej liczbie ruchów?

Czy graliby Państwo o pieniądze z Barmanem ? A gdyby zamiast kwadratu były 3 szklanki ustawione w trójkąt lub 5 w pięciokąt ?
Kody. Zbiór $C\subseteq\Sigma^{+}$ nazywamy kodem, jeśli każde słowo $w\in\Sigma^{*}$ dopuszcza co najwyżej jedną faktoryzację względem $C$ (tzn., da się “odkodować”).
Niech $\Sigma=\{ a,b\}$. Dowieść, że zbiór $\{ aa,baa,ba\}$ jest kodem, a zbiór $\{ a,ab,ba\}$ nie jest.

Jeśli skończony zbiór $C$ nie jest kodem, oszacować z góry długość najkrótszego słowa, które o tym świadczy (tzn. dopuszcza dwie różne faktoryzacje).
Oznaczmy: $x\preceq y$ jeśli słowo $x$ jest podciągiem $y$, np. $ab\preceq aabb$. Jest to częściowy porządek.
Udowodnić następujący fakt znany jako Lemat Higmana.

Jeśli $|\Sigma|<\infty$ to dla każdego $X\subseteq\Sigma^{*}$ zbiór jego słów minimalnych w sensie $\preceq$ jest skończny.

Wskazówka. Przypuśćmy, że teza jest fałszywa. Wtedy istnieje w $\Sigma^*$ nieskończony ciąg słów $x_{1},x_{2},..$ taki że $i < j\ \rightarrow\ not\ (x_{i}\preceq x_{j})$ (ale może być $x_{j}\preceq x_{i}$). Wybierzmy taki ”minimalny” ciąg w sensie długości, tzn. $|x_{1}|$ minimalne, jeśli $x_{1}$ ustalone to $|x_{2}|$ minimalne itd. Wybierzmy podciąg nieskończony $x_{{i_{1}}},x_{{i_{2}}}..$ wszystkich słów z tego ciągu zaczynających się na pewną taką samą literę $a$. Usuńmy tę literę z początku każdego z tych słów otrzymując ciąg $x^{{\prime}}_{{i_{1}}},x^{{\prime}}_{{i_{2}}}..$. Wtedy ciąg $x_{1},x_{2},\ldots,x_{{i_{1}-1}},x^{{\prime}}_{{i_{1}}},x^{{\prime}}_{{i_{2}}},x^{{\prime}}_{{i_{3}}}\ldots$ spełnia te same warunki co początkowy ciąg i jest ”mniejszy”, sprzeczność.
Niech $sup(L)$ oznacza zbiór nadciągów słów z języka $L$. Udowodnić, że dla dowolnego $L$ nad skończonym alfabetem $sup(L)$ jest językiem regularnym.
Wskazówka. Skorzystaj z lematu Higmana (poprzednie zadanie)..
Niech $subs(L)$ oznacza zbiór podciągów słów z języka $L$. Udowodnić, że dla dowolnego $L$ nad skończonym alfabetem $subs(L)$ jest językiem regularnym.
Wskazówka. Skorzystać z poprzedniego zadania.

Automaty skończone i wyrażenia regularne

Dowieść, że dla dowolnych języków $L,M$, $(L^{*}M^{*})^{*}=(L\cup M)^{*}$.
Dowieść, że wyrażenie regularne $(00+11+(01+10)(00+11)^{*}(10+10))^{*}$ reprezentuje zbiór wszystkich słów nad alfabetem $\{ 0,1\}$, w których zarówno liczba wystąpień 0 jak i liczba wystąpień 1 są parzyste.

Jak najkrócej reprezentować zbiór słów, w których te liczby są tej samej parzystości?
Zbudować automat nad alfabetem $\{ 0,1\}$, rozpoznający słowa, w których liczba jedynek na pozycjach parzystych jest parzysta, a liczba jedynek na pozycjach nieparzystych jest nieparzysta.
Dodawanie. Rozważamy słowa nad alfabetem $\{ 0,1\}^{3}$. Powiemy, że słowo $\langle a_{1},b_{1},c_{1}\rangle$ …$\langle a_{n},b_{n},c_{n}\rangle$ długości $n$ reprezentuje dodawanie, jeśli liczba reprezentowana binarnie przez słowo $c_{1}\ldots c_{n}$ jest sumą liczb reprezentowanych przez $a_{1}\ldots a_{n}$ i $b_{1}\ldots b_{n}$. Na przykład, ciąg $\langle 0,0,1\rangle\langle 1,1,1\rangle\langle 0,1,0\rangle\langle 1,1,0\rangle$ reprezentuje dodawanie (5+7=12). Podać wyrażenie regularne opisujące zbiór wszystkich słów nad alfabetem $\{ 0,1\}^{3}$ reprezentujących dodawanie w powyższym sensie.
Podzielność.
1. Skonstruować skończony automat deterministyczny nad alfabetem $\{ 0,1,\ldots,8,9\}$ rozpoznający zbiór dziesiętnych reprezentacji wielokrotności liczby 7.
2. Jak wyżej, ale przy reprezentacji odwrotnej, tj. poczynając od cyfr najmniej znaczących.
3. Uogólnić niniejsze zadanie.
Alfabet jednoliterowy. Dowieść, że język $L\subseteq\{ a\}^{*}$ jest regularny wtedy i tylko wtedy, gdy zbiór liczb naturalnych $\{ n:a^{n}\in L\}$ jest semi–liniowy w sensie rozdziału. Dowieść, że dla dowolnego zbioru
$X\subseteq\{ a\}^{*}$, język $X^{*}$ jest regularny.
Zbiory semi–liniowe (por. zadanie z rozdziału ).
1. Dowieść, że dla dowolnego języka regularnego $L$ zbiór $\{|w|:w\in L\}$ jest semi–liniowy.
  W szczególności, języki regularne nad jednoliterowym alfabetem mogą być utożsamiane ze zbiorami semi–liniowymi poprzez bijekcję $w\mapsto|w|$.
2. Dowieść, że jeśli $M\subseteq{\bf N}$ jest zbiorem semi–liniowym, to język $\{\mbox{bin}(m):$ $m\in M\}$ jest regularny, gdzie $\mbox{bin}(m)$ oznacza binarną reprezentację liczby $m$.
Uwaga. Fakt analogiczny do ?? można udowodnić dla dowolnej reprezentacji, a zatem zbiór semi–liniowy jest regularny w reprezentacji o podstawie $k$, dla $k\geq 1$. W przeciwnym kierunku wiadomo, że jeśli zbiór jest regularny w reprezentacjach o względnie pierwszych podstawach $p$ i $q$, to jest semi–liniowy — jest to wniosek z głębokiego Twierdzenia Cobhama.
Dowieść, że dla danych liczb $a,b,p,r\in{\bf N}$, następujący język jest regularny
$L\,=\,\{\,\mbox{bin}(x)\,\$\,\mbox{bin}(y)\,:(a\cdot x+b\cdot y)\equiv r\;\;(\textrm{mod} p)\}$

Lemat o pompowaniu

Dowieść, że następujące języki nie są regularne:
1. $\{ a^{n}b^{n}\,:\, n\in N\}$
2. $\{ a^{{2^{n}}}\,:\, n\in N\}$
3. $\{ a^{{p}}\,:\, p\mbox{ jest liczb"a pierwsz"a}\}$
4. $\{ a^{{i}}b^{j}\,:\,\mbox{nwd}(i,j)=1\}$
5. $\{ a^{m}b^{n}\,:\, m\neq n\}$
6. $\{\mbox{bin}(p)\,:\, p\mbox{ jest liczb"a pierwsz"a}\}.$
Dowieść, że zbiór palindromów nad alfabetem o co najmniej dwóch elementach nie jest regularny.
Dowieść, że zbiór wyrażeń regularnych nie jest regularny.
Dowieść, że jeśli w Zadaniu ?? z punktu ?? zamienimy dodawanie przez mnożenie, to otrzymany język (nad alfabetem $\{ 0,1\}^{3}$) jest wprawdzie dobrze określony, ale nie jest regularny.
Udowodnić nieco silniejszy wariant Lematu o pompowaniu:

Jeśli $L$ jest regularny, to

(*) Istnieje stała $n_{0}$, że dla każdych słów $v,w,u$ takich że $|w|\geq n_{0}$ i $vwu\in L$, istnieją $x,y,z$ takie, że $w=xyz$, $0< |y|\leq n_{0}$, oraz $\forall n\in{\bf N},\, vxy^{n}zu\in L$.

Podać przykład języka $L$, który spełnia (*), choć nie jest regularny.

Wskazówka. $\sum _{p}\underbrace{cb^{*}cb^{*}\ldots cb^{*}}_{p}+(b+c)^{*}cc(b+c)^{*}$, gdzie $p$ przebiega liczby pierwsze.
Czy jest regularny język:

$\{ w\in(a+b)^{*}:\ \# _{a}(u)>2009\cdot\# _{b}(u)\textrm{\quad dla ka"rdego niepustego prefiksu $u$ s"lowa $w$}\}$$u$ słowa $w$

$\# _{s}$ oznacza liczbę wystąpień symbolu $s$ w słowie.
Słowo binarne $x$ jest antypalindromem gdy dla pewnego niepustego słowa $z$, oraz $s\in\{ 0,1\}$ zachodzi:

$x\ =\ z\;\bar{z}^{R}$ lub $x\ =\ z\; s\;\bar{z}^{R}$,

gdzie $\bar{z}$ oznacza negację (logiczną) elementów w $z$. Np. 0010011, 0011 są antypalindromami, a słowo puste i pojedyńczy symbol nie są. Niech $L$ będzie zbiorem słów binarnych nie zawierających jako podsłowa antypalindromu o długości większej niż 3 zaczynającego się od zera. Czy $L$ jest regularny ?

Własności domknięcia języków regularnych

Dowieść, że dla języka regularnego $L\subseteq\Sigma^{*}$ i dowolnego zbioru $X\subseteq\Sigma^{*}$ języki

$\displaystyle X^{{-1}}L = \{ w:\,(\exists v\in X)\, vw\in L\}$

$\displaystyle LX^{{-1}} = \{ w:\,(\exists u\in X)\, wu\in L\}$
są regularne.
Dowieść, że język $L$ jest regularny wtedy i tylko wtedy, gdy język $L^{R}$ słów stanowiących lustrzane odbicia słów z $L$ jest regularny.
Uwaga. Lustrzane odbicie $w^{R}$ słowa $w$ możemy w ścisły sposób zdefiniować rekurencyjnie: $\epsilon^{R}=\epsilon$ i $(w\sigma)^{R}=\sigma w^{R}$, dla $w\in\Sigma^{*}$, $\sigma\in\Sigma$.
Dla danego automatu $A$ rozpoznającego język $L$, skonstruować automat rozpoznający język
$\mbox{Cycle}(L)=\{ vu\,:\, uv\in L\}$

Czy z faktu, że język $\mbox{ Cycle}(L)=\{ vu\,:\, uv\in L\}$ jest regularny, można wnioskować, że język $L$ jest regularny?
Niech $L$ bedzie językiem regularnym nad alfabetem $\{ 0,1\}$. Dowieść, że następujący język jest regularny:
$\{ w\,:\, w\in L\wedge\mbox{ spośróod słów o dlugości $|w|$, $w$ jest najmniejsze w porządku leksykograficznym}\}$$|w|$, $w$ jest najmniejsze w porządku leksykograficznym
Przyjmujemy, że każde niepuste słowo binarne $w\in\{ 0,1\}^{*}$, $w=w_{1}\ldots w_{k}$, reprezentuje pewien ułamek w przedziale $[0,1)$,
$\mbox{bin}(w)=w_{1}\frac{1}{2}+w_{2}\frac{1}{2^{{2}}}+\ldots+w_{k}\frac{1}{2^{{k}}}$

Dla liczby rzeczywistej $r\in[0,1]$, niech

$L_{r}=\{ w\,:\,\mbox{bin}(w)\leq r\}$

Dowieść, że język $L_{r}$ jest regularny wtedy i tylko wtedy, gdy liczba $r$ jest wymierna.
Podać przykład nieskończonego języka zamkniętego na branie podsłów, który nie zawiera nieskończonego języka regularnego.
Niech $L$ będzie językiem regularnym. Dowieść, że następujące języki są również regularne:
1. $\frac{1}{2}L=_{{df}}\{ w\,:\,(\exists u)\,|u|=|w|\wedge wu\in L\}$
2. $\sqrt{L}=_{{df}}\{ w\,:\, ww\in L\}$
Niech $L$ będzie językiem regularnym. Dowieść, że następujące języki są również regularne:
1. $\mbox{Root}(L)=\{ w\,:\,(\exists n\in N)\, w^{n}\in L\}$
2. $\mbox{Sqrt}(L)=\{ w\,:\,(\exists u)|u|=|w|^{2}\wedge wu\in L\}$
  Wskazówka. $n^{2}=1+3+\ldots(2n-1)$.
3. $\mbox{Log}(L)=\{ w\,:\,(\exists u)|u|=2^{{|w|}}\wedge wu\in L\}$
  Wskazówka. $2^{n}=1+2+2^{2}+2^{{n-1}}+1$.
4. $\mbox{Fibb}(L)=\{ w\,:\,(\exists u)|u|=F_{{|w|}}\wedge wu\in L\}$
  gdzie $F_{n}$ jest $n$-tą liczbą Fibonacciego tzn.
  
  $F_{1}=F_{2}=1$
  
  $F_{{n+2}}=F_{n}+F_{{n+1}}$
Dowieść, że dla dowolnego języka regularnego $L$, regularny jest również język

$\{ w\,:\, w^{{|w|}}\in L\}.$
Niech będzie dany język regularny $L$ i dowolne, niekoniecznie regularne, języki $L_{1}$, …, $L_{m}$. Skonstruować skończony automat deterministyczny rozpoznający język nad alfabetem $\{ 1,\ldots,m\}$
$L\,=\,\{ i_{1}i_{2}\ldots i_{k}:L_{{i_{1}}}L_{{i_{2}}}\ldots L_{{i_{k}}}\subseteq L\}$
Nietrywialnym palindromem nazwiemy każdy palindrom o długości co najmniej 2. Niech $\mbox{Pal\,}^{{>1}}_{{\Sigma}}$ oznacza zbiór nietrywialnych palindromów nad alfabetem $\Sigma$. Dowieść, że język $(\mbox{Pal\,}^{{>1}}_{{\Sigma}})^{*}$ jest regularny wtedy i tylko wtedy, gdy $|\Sigma|=1$.
Czy język $(\{ ww^{R}:w\in(0+1)^{*}\})^{*}$ jest regularny?
Które z następujących języków nad alfabetem $\{ 0,1\}$ są regularne?
1. Zbiór słów posiadających nietrywialny palindrom jako prefiks.
2. Zbiór słów posiadających palindrom długości parzystej jako prefiks.
3. Zbiór słów posiadających nietrywialny palindrom długości nieparzystej jako prefiks.
Oznaczmy przez $\mathit{Ile}(w,x)$ liczbę wystąpień słowa $w$ jako podsłowo $x$ (wystąpienia nie muszą być rozłączne). Czy następujący język nad alfabetem $\{ a,b\}$ jest regularny? Jeśli tak, to podać wyrażenie regularne. Jeśli nie, to udowodnić, że nie jest.
1. $L_{1}=\{ x\ :\ \mathit{Ile}(ab,x)=\mathit{Ile}(ba,x)+1\}$
2. $L_{2}=\{ x\ :\ \mathit{Ile}(aba,x)=\mathit{Ile}(bab,x)\}$
Niech $L$ będzie językiem regularnym. Dowieść, że języki:
1. $L_{{+--}}=\{ w\,:\,(\exists u)\,|u|=2|w|\wedge wu\in L\}$
2. $L_{{++-}}=\{ w\,:(\exists u)\, 2|u|=|w|\wedge wu\in L\}$
3. $L_{{-+-}}=\{ w\,:(\exists u,v)\,|u|=|v|=|w|\wedge uwv\in L\}$
są językami regularnymi, a język
1. $L_{{+-+}}=\{ uv\,:(\exists w)\,|u|=|v|=|w|\wedge uwv\in L\}$
może nie być regularny.
Czy zachodzi fakt: jeśli $L$ jest regularny to istnieja dwa niepuste słowa $u,v$ takie, że zachodzi równość ilorazów $L\{ uv\}^{{-1}}=L\{ vu\}^{{-1}}$ ?
Podać przykład języka nieregularnego $L$, takiego że $L^{2}$ jest językiem regularnym.
Dla słów $u,v$ o tej samej długości, określamy odległość Hamminga
$d(u,w)=|\{ i:w_{i}\neq v_{i}\}|.$

Udowodnić, że dla dowolnego języka regularnego $L$ i stałej $K$, następujący język jest również regularny:

$\{\ w\ :\ (\exists\ u\in L)\ |u|=|w|\ \textrm{oraz}\ d(u,w)\le K\ \}$
Przeplotem słów $w$ i $v$ nazwiemy dowolne słowo długości $|w|+|v|$, które można rozbić na rozłączne podciągi $w$ i $v$. Na przykład, przeplotami słów $ab$ i $acb$ są słowa $abacb$, $aabcb$, $acabb$, $acbab$, $aacbb$. Przeplotem języków $L$ i $M$ jest zbiór wszystkich możliwych przeplotów słów $w\in L$, $v\in M$. Język ten oznaczamy $L\parallel M$.

Dowieść, że jeśli $L$ i $M$ są językami regularnymi, to $L\parallel M$ jest również regularny.
Określamy $L^{{\sharp}}=L\,\cup\,(L\parallel L)\,\cup\,(L\parallel L\parallel L)\,\cup\ldots$. Podać przykład języka regularnego $L$ nad dwuelementowym alfabetem, dla którego $L^{{\sharp}}$ nie jest językiem regularnym.
Niech $L_{1}\subset L_{2}$ reularne języki, gdzue $L_{2}-L_{1}$ jest nieskończony. Pokazać, że istenieje język regularny $L$, t.że $L_{1}\subset L\subset L_{2}$, oraz $L_{2}-L$, $L-L_{1}$ są nieskończone.
Definiujemy operację, która dla słowa $xyz$ generuje słowo $xyyz$. Niech $L$ będzie najmniejszym zbiorem zawierającym słowo $abc$ i domkniętym ze względu na wprowadzoną operację. Czy $L$ jest regularny ?
Dla wektora $\alpha\ =\ (i_{1},i_{2},\ldots i_{n})$ definiujmy słowo $w(\alpha)$ z języka $1^{*}2^{*}..n^{*}$ które zawiera dokładnie $i_{k}$ liter $k$. Niech $X_{n}$ będzie zbiorem ciągów $(i_{1},i_{2},\ldots i_{n})$ o współrzędnych z przedziału $[1..n-2]$ , takich że $i_{n}=i_{k},\ k=i_{{n-1}}$.
Udowodnić, że skończony język $L_{n}\ =\ \{ w(\alpha)\ :\ \alpha\in X_{n}\}$ jest akceptowany przez dwukierunkowy det. automat skończony mający $O(n)$ stanów, ale jednokierunkowy automat deterministyczny musi mieć wykładniczą liczbę stanów.
Niech $Per_{n}$ będzie zbiorem wszystkich permutacji zbioru $\{ 1,2..n\}$, permutacje traktujemy tu jako słowa nad alfabetem $\{ 1,2..n\}$. Czy istnieje niedterministyczny automat skończony mający wielomianową liczbę stanów i akceptujący $Per_{n}$, ile stanów musi mieć (co najmniej) deterministyczny automat ?
Czy istnaieje automat deterministyczny wielomianowego rozmiaru dla nieskończoengo języka $\{ 1,2..n\}^{*}-Per_{n}$ ?
Niech $w$ będzie słowem długości $n$, udowodnij, że istnieje wyrażenie regularne rozmiaru $O(n)$ opisujące zbiór wszystkich prefisków $w$ (włącznie z $w$).
Niech $w$ będzie słowem długości $n$, udowodnij, że istnieje wyrażenie regularne rozmiaru $O(n)$ opisujące zbiór $\Sigma^{*}-w$.
Język jest palindromiczny gdy wszystkie jego słowa są palindromami. Niech $A$ będzie niedet. automatem skończonym o $n$ stanach. Udowodnij, że $L(A)$ jest palindromiczny wtedy i tylko wtedy gdy język $w\in L(A)\ :\ |w|< 3n\}$ jest palindromiczny.
Udowdnij, że istnieje niedet. automat skończony rozmiaru $O(n)$ akceptujący tylko słowa niesymetryczne oraz dla słów $w$ długości mniejszej niż $n$ akceptuje $w$ wtedy i tylko wtedy gdy $w$ nie jest palindromem. Dla słów większej długości automat może nie akceptować pewnych słów niesymetrycznych.
Jako wniosek z dwu poprzednich zadań podaj efektywny algorytm sprawdzający czy język regularny jest palindromiczny.

Automaty minimalne

Niech $w\in\Sigma^{*}$ będzie słowem o długości $|w|=n>0$. Dowieść, że minimalny automat deterministyczny rozpoznający wszystkie słowa nad $\Sigma$, których sufiksem jest $w$, ma dokładnie $n+1$ stanów.
Niech $w\in\Sigma^{*}$ będzie słowem o długości $|w|=n>0$. Dowieść, że minimalny automat deterministyczny rozpoznający wszystkie podsłowa słowa $w$ ma nie więcej niż $2n$ stanów.
Narysować diagramy automatów minimalnych rozpoznających odpowiednio
1. wszystkie podsłowa
2. wszystkie sufiksy
słowa $abbababa$ (dla przejrzystości rysunków pominąć stan ,,śmietnik”).
Ile stanów maja analogiczne automaty dla $w_{n}=ab(ba)^{n}$ (licząc stan ,,śmietnik”) ?
Skonstruować minimalny deterministyczny automat skończony dla języka$L\ =\ \{ a^{i}bb^{*}a^{j}\ :\ 2\ |\ (i+j)\}$.
Skonstruować minimalny deterministyczny automat skończony dla języka
$L\ =\ \{\ a_{1}a_{2}\ldots a_{n}\ :\ n>0,\ a_{i}\in\{ 0,1,2,3,4\},\ MAX_{{i,j}}(a_{i}-a_{j})\le 2\}.$
Opisać strukturę i narysować diagram minimalnego deterministycznego automatu skończonego akceptującego wszystkie skończone ciągi zerojedynkowe takie, że każde $k$ kolejnych symboli zawiera dokładnie 2 jedynki i każde kolejnych $j< k$ symboli zawiera co najwyżej dwie jedynki:
1. Dla $k=3$;
2. dla $k=4$.
(W szczególności słowo puste należy do obu języków, a słowo 111 do żadnego z nich.)
Dowieść, że minimalny automat deterministyczny równoważny podanemu automatowi niedeterministycznemu o $n$ stanach ($n\geq 2$) ma dokładnie
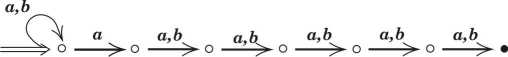
1. $2^{{n-1}}$ stanów,
2. (*)
  
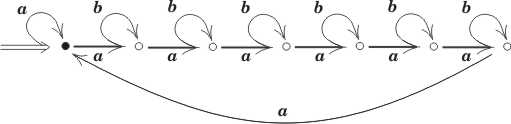
  $2^{n}$ stanów.
Na powyższych rysunkach $n=7$, stan początkowy jest wskazany przez $\Rightarrow$, a stan akceptujący jest oznaczony przez $\bullet$.

Uwaga. Właność słów rozpoznawaną przez automat z punktu można łatwo opisać w języku polskim, w przypadku punktu jest to trudniejsze.
Oznaczmy przez $\Sigma _{k}$ alfabet $\{ 0,1,\ldots k\}$. Niech $\mathit{NPAL}_{k}$ oznacza zbiór słów nad alfabetem $\Sigma _{k}$ nie zawierających, jako podsłowa, palindromu (symetrycznego słowa długości co najmniej 2). Ile stanów ma minimalny automat deterministyczny akceptujący $\mathit{NPAL}_{{99}}$ ? Podać rozwiązanie ogólne dla $k=0,1,2,\ldots$
Trzy drużyny piłkarskie $A$, $B$ i $C$ rozgrywają między sobą serię spotkań towarzyskich, przy czym umówiły się, że każdy kolejny mecz jest rozgrywany pomiędzy drużyną, która wygrała poprzedni mecz i drużynę, która nie brała udziału w tym spotkaniu (tzn. jeśli drużyna $X$ wygrała z drużyną $Y$, to następny mecz rozegrają $X$ i $Z$). Zakładając, że nie ma remisów, rozważamy zbiór słów nad alfabetem $\{ A,B,C\}$, stanowiących ciągi możliwych wyników spotkań. Dowieść, że jest to język regularny. Zbudować minimalny automat deterministyczny, który go rozpoznaje.
Pan $X$ zakupił pakiety trzech różnych akcji: $A,B$ i $C$. Każdego dnia bada wzajemne położenie wartości swoich akcji, które może być reprezentowane jako uporządkowanie zbioru $\{ A,B,C\}$, w kierunku od najmniej do najbardziej wartościowej. (Przyjmujemy założenie, że dwie różne akcje mają zawsze różne wartości.) Pan $X$ postanowił, że jeśli w ciągu dwóch kolejnych dni któraś z akcji dwukrotnie spadnie na niższą pozycję, to sprzeda tę akcję. Np. jeśli kolejne notowania (w tym wypadku: uporządkowania) są $(A,B,C),(B,C,A),(C,B,A)$ to pan $X$ sprzeda pakiet akcji $C$. Rozważamy zbiór $G$ wszystkich uporządkowań liniowych zbioru $\{ A,B,C\}$. Dowieść, że zbiór tych ciągów nad alfabetem $G$, które opisują takie wyniki notowań giełdowych, przy których pan $X$ nie pozbędzie się żadnego pakietu akcji, jest językiem regularnym. Znale”zć liczbę stanów automatu minimalnego akceptującego ten język.
Pan $X$ postanowił, że każdego dnia będzie pracował lub nie, przestrzegając przy tym zasady, by na żadne siedem kolejnych dni nie przypadało więcej niż cztery dni pracy. Możliwy rozkład dni pracy pana $X$ w ciągu $n$ kolejnych dni możemy przedstawić jako $n$-bitowe słowo, gdzie 1 odpowiada dniowi pracy, a 0 dniowi odpoczynku. Dowieść, że zbiór wszystkich tak otrzymanych słów jest językiem regularnym (nad alfabetem $\{ 0,1\}$). Znale”zć minimalny automat deterministyczny.
Wskazówka. Jako stany minimalnego automatu weżmy ciągi binarne długości 7 zawierające dokłądnie 4 jedynki,
plus stan typu śmietnik.

Naturalny automat pamięta historie (ciąg binarny) ostatnich siedmiu dni.
Każdy taki ciąg jest równoważny ciągowi dopełnionemu: zamieniamy kolejne zera od lewej na jedynke tak aby w sumie
były 4 jedynki.

Zatem ostatecznie automat ma tyle stanów ile jest ciągów binarnych długości 7 mających 4 jedynki, plus stan smietnik.
W sumie 35+1=36.
Dowieść, że istnieje nieskończenie wiele słów $w\in(a+b)^{*}$ takich, że jeśli zastosujemy homomorfizm $a\mapsto 0$, $b\mapsto 1$, to otrzymamy zapis binarny liczby podzielnej przez 3, a kiedy zastosujemy homomorfizm $a\mapsto 1$, $b\mapsto 0$, to również otrzymamy zapis binarny liczby podzielnej przez 3 (oczywiście ignorujemy początkowe zera).
Rozważamy automat wydający napoje, działający na następujących zasadach.
— Każdy napój kosztuje 1 złoty.

— W chwili początkowej automat nie zawiera żadnych monet.

— Automat przyjmuje monety: 1 złoty lub 1 euro; w tym ostatnim przypadku wydaje 3 złote reszty po warunkiem, oczywiście, że ma dostateczną ilość monet jednozłotowych (zakładamy, że €1 = 4 zł).

— Jeśli automat nie jest w stanie wydać reszty — sygnalizuje błąd.

— Jeśli po wrzuceniu monety i ewentualnym wydaniu reszty wartość wszystkich monet zgromadzonych w automacie osiągnie równowartość 8 zł, wszystkie monety są wyjmowane (reset).

Historią działania jest ciąg wrzuconych monet (złoty lub euro). Historia jest udana, jeśli w trakcie jej realizacji ani razu nie wystąpił błąd.

Skonstruować minimalny automat deterministyczny rozpoznajacy zbiór wszystkich udanych historii.
Narysować minimalny deterministyczny automat skończony rozpoznający zbiór $L$ słów nad alfabetem $\{ a,b\}$, zawierający słowo puste oraz słowa rozpoczynające się od $a$, które nie zawierają jako podsłowa palindromu o długości większej niż 3. (Na rysunku stan “śmietnik” pomijamy.) Jaka jest liczność języka $L$ ?
Narysować minimalny deterministyczny automat skończony rozpoznający język $L_{1}$ składający się ze wszystkich słów binarnych nie zawierających antypalindromu o długości większej niż 2 (zob. zadanie ??.??).
Dla automatu niedet. A przez $det(A)$ oznaczmy deterministyczną wersję $A$ (poprzez konstrukcję ”potęgową”, stanami są zbiory $A$) w której są tylko stany osiągalne ze stanu początkowego. Przez $A^{R}$ oznaczmy naturlany automat (z reguly niedeterministyczny) dla odwróconego języka $L(A)^{R}$ (powstały przez odwrócenie strzałek (tranzycji), oraz zamianę zbiorów stanów akceptujących i początkowych).
Prof. J. Brzozowski zauważył, następującą własność

$(*)$ jeśli $A$ jest deterministyczny to $det(A^{R})$ jest minimalnym automatem deterministycznym dla języka $L(A)^{R}$.

Udowodnić własność $(*)$.

Automaty związane z rozpoznawaniem wzorca

Deterministyczny automat z zadania ?? z punktu ?? rozpoznający język $\Sigma^{*}w$ można skonstruować biorąc za stany wszystkie prefiksy słowa $w$ (a zatem $|w|+1$ stanów) oraz przejścia $v\stackrel{a}{\rightarrow}u$, gdzie $u$ jest maksymalnym sufiksem słowa $va$ będącym jednocześnie prefiksem $w$. (Efektywna konstrukcja tegoż automatu, patrz zadanie w punkcie .) Dowieść, że liczba nietrywialnych przejść ,,wstecznych”, tj. przejść postaci $v\stackrel{a}{\rightarrow}u$, gdzie $|v|>|u|>0$, jest nie większa niż $|w|$. Zauważmy, że daje to możliwość reprezentacji automatu o rozmiarze proporcjonalnym do $|w|$ (przejścia postaci $v\stackrel{a}{\rightarrow}\epsilon$ możemy
pominąć).

Wskazówka. Wykazać, że dla każdej liczby $k$ istnieje co najwyżej jedno nietrywialne przejście wsteczne, takie, że $|va|-|u|=k$.
Rozpoznawanie podsłów.
1. Dla danego słowa $w$ o długości $|w|=n$ skonstruować automat deterministyczny o $\leq 2n+1$ stanach rozpoznający dokładnie zbiór sufiksów słowa $w$.
  
  Wskazówka. Jako stany automatu można wziąć zbiory pozycji $S_{x}$ ($S_{x}\subseteq\{ 0,1,\ldots,n\}$) kończących wystąpienie $x$ jako podsłowa słowa $w$. Oszacowanie na liczbę stanów wynika ze spostrzeżenia, że różne zbiory $S_{x}$, $S_{y}$ są albo w relacji inkluzji albo rozłączne, a zatem, ze względu na inkluzję, tworzą drzewo o nie więcej niż $n$ liściach.
2. Powyższy automat zawiera stan typu ,,czarna dziura”, mianowicie stan $\emptyset=S_{x}$, gdzie $x$ nie jest podsłowem $w$. Dowieść, że liczbę przejść nie prowadzących do stanu $\emptyset$ można oszacować z góry przez $3n$.
  
  Wskazówka. Wziąć drzewo rozpinające grafu automatu i oszacować liczbę pozostałych krawędzi przez liczbę sufiksów $w$.
3. Opisany wyżej automat jest minimalny dla zbioru sufiksów. Tę samą konstrukcję można zastosować również do rozpoznawania zbioru wszystkich podsłów słowa $w$, ale otrzymany automat nie musi być minimalny. Podać przykład.

Warianty automatów skończonych

Automaty z $\epsilon$-przejściami. Niedeterministyczny automat z $\epsilon$-przejściami $A=(\Sigma,Q,I,\delta,F)$ jest określony jak zwykły automat skończony z tym, że $\delta\subseteq Q\times(\Sigma\cup\{\epsilon\})\times Q$. Relacja $q\stackrel{w}{\rightarrow}p$ (gdzie $p,q\in Q$ i $w\in\Sigma^{*}$) jest określona jak poprzednio, tzn. $q\stackrel{\epsilon}{\rightarrow}q$ i $q\stackrel{va}{\rightarrow}p$ o ile $q\stackrel{v}{\rightarrow}q_{1}$ i $(q_{1},a,p)\in\delta$ z tym, że teraz $a$ może być literą w $\Sigma$ lub $\epsilon$.

Dowieść, że dla dowolnego automatu z $\epsilon$-przejściami istnieje zwykły automat skończony, który akceptuje ten sam język.
Automat z wyjściem wg Mealy'ego. Automat Mealy'ego można przedstawić jako deterministyczny automata skończony, powiedzmy $A=(\Sigma,Q,q_{I},\delta,F)$ dany razem z funkcją $\gamma:Q\times\Sigma\to\Delta$. Intuicyjnie, dany stan $q$ i litera $\sigma\in\Sigma$ determinują nie tylko kolejny stan, powiedzmy $p$, ale także sygnał wyjściowy (output), $\gamma(q,\sigma)$. Dokładniej, słowo $w=w_{1}w_{2}\ldots w_{n}$ nad $\Sigma$, takie, że $\hat{\delta}(q_{I},w_{1}\ldots w_{{i-1}})=p_{i}$, dla $i=1,\ldots,n$, wyznacza $n$-literowe słowo nad alfabetem $\Delta$,
$\hat{\gamma}(w)=_{{def}}\gamma(q_{I},w_{1})\gamma(p_{2},w_{2})\ldots\gamma(p_{n},w_{n})$

Powiemy, że automat Mealy'ego redukuje język $L_{1}$ do $L_{2}$ jeśli ($\forall w$) $w\in L_{1}\Leftrightarrow\hat{\gamma}(w)\in L_{2}$. Skonstruować automat, który redukuje $a^{*}b(a^{*}ba^{*}ba^{*})^{*}$ do $(a^{*}ba^{*}ba^{*})^{*}$.
Automat z wyjściem wg Moore'a. Automat Moore'a można przedstawić jako deterministyczny automata skończony wraz z funkcją $\gamma:Q\to\Delta$. Tym razem, słowo $w=w_{1}w_{2}\ldots w_{n}$ wyznacza
$\hat{\gamma}(w)=_{{def}}\gamma(\hat{\delta}(q_{I},w_{1}))\gamma(\hat{\delta}(q_{I},w_{1}w_{2}))\ldots\gamma(\hat{\delta}(q_{I},w_{1}w_{2}\ldots w_{n}))$

Dowieść, że automaty Mealy'ego i Moore'a są równoważne w tym sensie, że dla każdego automatu jednego typu można znale”zć automat drugiego typu realizujący tę samą funkcję $\hat{\gamma}$.
Automaty dwukierunkowe. Funkcja przejścia deterministycznego automatu dwukierunkowego jest postaci $\delta:Q\times\Sigma\to Q\times\{ L,R\}$, co interpretujemy, że automat może przesunąć czytnik zarówno w prawo jak i w lewo. Dowieść, że deterministyczne automaty dwukierunkowe mogą być symulowane przez zwykłe automaty skończone
Wskazówka. Znane rozwiązanie oparte na idei ciągów skrzyżowań (ang. crossing sequences) można znale”zć w rozdziale 2.6 książki J.E.Hopcroft, J.D.Ullman, Wprowadzenie do teorii automatów, języków i obliczeń, Wydawnictwo Naukowe PWN, Warszawa 1994. Innym, być może prostszym rozwiązaniem – zaproponowanym przez Mikołaja Bojańczyka – jest uwzględnienie w stanie symulującego automatu jednokierunkowego funkcji $h:Q\to Q\cup\{\bot\}$ o następującej interpretacji: jeśli automat (dwukierunkowy) pójdzie w lewo w stanie $q$, to wróci w stanie $h(q)$ (być może wcale nie wróci, gdy $h(q)=\bot$). (Rezultat zachodzi również dla automatów niedeterministycznych.)

Uwaga. W dalszej części wykładu spotkamy się z mocniejszym stwierdzeniem, a mianowicie, że maszyny Turinga pracujące na jednej taśmie w czasie liniowym akceptują jedynie języki regularne.
Dla ustalonego $k$, rozważmy język nad alfabetem $\{ a,b,c\}$ opisany wyrażeniem
$\left((a+b)^{*}c\right)^{{k-1}}\,(a+b)^{*}a(a+b)^{{k-1}}c\,\left((a+b)^{*}c\right)^{*}$

Intuicyjnie: język składa się z ,,bloków” liter $a,b$, zakończonych ,,znacznikiem” $c$, przy czym $k$-ty (od początku) blok ma tę własność, że jego $k$-ty symbol od końca jest $a$.
1. Wykazać, że deterministyczny ,,jednokierunkowy” automat rozpoznający ten język ma $\geq 2^{k}$ stanów.
2. Skonstruować 2-kierunkowy automat o liniowej (${\cal O}(k)$) liczbie stanów, rozpoznający ten język.
3. (*) Jak wyżej, ale automat ma prawo wykonać tylko jeden nawrót. (Bez zmniejszenia ogólności, możemy założyć, że automat idzie do końca słowa, po czym wraca i kończy obliczenie na początku słowa.)

Gramatyki bezkontekstowe

Podać gramatyki bezkontekstowe generujące następujące języki:
1. zbiór słów nad alfabetem $\{ a,b\}$, które zawierają tyle samo $a$ co $b$;
2. zbiór słów nad alfabetem $\{ a,b\}$, które zawierają dwa razy więcej $a$ niż $b$;
3. zbiór słów nad alfabetem $\{ a,b\}$ o długości parzystej, w których liczba wystąpień litery $b$ na pozycjach parzystych jest równa liczbie wystąpień tej litery na pozycjach nieparzystych;
4. zbiór wyrażeń arytmetycznych nad alfabetem $\{ 0,1,(,),+,\cdot\}$, które, przy zwykłej interpretacji działań dla liczb naturalnych, mają wartość 3;
5. zbiór wyrażeń arytmetycznych w notacji polskiej (nad alfabetem $\{ 0,1,+,\cdot\}$) o wartości 4;
6. zbiór poprawnie zbudowanych formuł rachunku zdań ze zmienną zdaniową $p$ i stałymi logicznymi true, false (alfabet: $\{ p,\mbox{true},\mbox{false},\wedge,\vee,\neg,(,)\}$);
7. zbiór tych formuł z poprzedniego punktu, które przy każdym wartościowaniu zmiennej $p$ mają wartość logiczną prawda (tzn. tautologii);
8. $\{ a^{i}b^{j}c^{k}\,:\, i\neq j\,\vee\, j\neq k\}$;
9. $\{ a^{i}b^{j}a^{k}\,:\, i+k=j\}$;
10. $\{ a^{i}b^{j}c^{p}d^{q}:\ i,j,p,q>0,\ i+j=p+q\ \}$.
Dla danych gramatyk bezkontekstowych $G,H$, skonstruować gramatyki generujące języki $L(G)\cup L(H)$, $L(G)L(H)$, $(L(G))^{*}$, $(L(G))^{R}$ (=lustrzane odbicie).
Wykazać, że zbiór palindromów nad ustalonym alfabetem jak również jego dopełnienie są językami bezkontekstowymi.
Napisać gramatykę bezkontekstową (jak najkrótszą) generującą język:
$L\ =\ \{\ a^{i}b^{j}\ :\ i,j\ge 1;\ i< 2j-1\ \}$
Skonstruować gramatykę bezkontekstową z jednym symbolem nieterminalnym generującą zbiór $\{ x\in(a+b)^{*}\ :\ \# _{a}(x)=\# _{b}(x)\ \}$, gdzie $\# _{s}(w)$ oznacza liczbę wystąpień symbolu $s$ w słowie $w$.
Skonstruować gramatykę bezkontekstową jednoznaczną generującą język $\mathbf{D_{1}}$ poprawnie uformowanych wyrażeń nawiasowych (por. Rozdział ??, Zadanie ?? ).
Napisać gramatyki bezkontekstowe generujace zbiór tych słów z języka $\mathbf{D_{1}}$, które
1. zawierają parzystą liczbę (np. 0) nawiasów otwierających,
2. nie zawierają podsłowa (()).
Skonstruować gramatykę bezkontekstową jednoznaczną generującą język z Zadania ??.

Wskazówka. Rozważyć gramatykę

$\displaystyle Z \rightarrow ZaZ^{+}b\,|\, ZbZ^{-}a\,|\,\varepsilon$

$\displaystyle Z^{+} \rightarrow Z^{+}aZ^{+}b\,|\,\varepsilon$

$\displaystyle Z^{-} \rightarrow Z^{-}bZ^{-}a\,|\,\varepsilon$

Zauważyć związek miedzy produkcjami dla $Z^{+}$ a poprzednim zadaniem (podobnie dla $Z^{-}$).
Dowieść, że następujące warunki są równoważne dla języka $L\subseteq\Sigma^{*}$:
1. $L$ jest regularny,
2. $L$ jest generowany przez gramatykę bezkontekstową, w której każda reguła jest postaci $X\rightarrow\epsilon$, $X\rightarrow Y$, lub $X\rightarrow\sigma Y$, $\sigma\in\Sigma$,
3. $L$ jest generowany przez gramatykę bezkontekstową, w której każda reguła jest postaci $X\rightarrow\epsilon$, $X\rightarrow Y$, lub $X\rightarrow Y\sigma$, $\sigma\in\Sigma$,
4. $L$ jest generowany przez gramatykę bezkontekstową, w której każda reguła jest postaci $X\rightarrow\alpha$ lub $X\rightarrow\beta Y$, $\alpha,\beta\in\Sigma^{*}$.
Podać przykład gramatyki bezkontekstowej w której każda reguła jest postaci $X\rightarrow\epsilon$, $X\rightarrow Y$, $X\rightarrow\sigma Y$ lub $X\rightarrow Y\sigma$, $\sigma\in\Sigma$, ale język generowany przez gramatykę nie jest regularny.
Czy każdy język bezkontekstowy jest generowany przez gramatykę w postaci z poprzedniego zadania?
Powiemy, że gramatyka $G$ ma własność właściwego samozapętlenia, jeśli dla pewnej zmiennej $X$ zachodzi $X\stackrel{G}{\rightarrow}^{*}\alpha X\beta$, gdzie $\alpha,\beta\neq\epsilon$. Udowodnij, że gramatyka bezkontekstowa nie mająca własności właściwego samozapętlenia generuje język regularny.
Udowodnij, że każdy język bezkontekstowy nad jednoliterowym alfabetem jest regularny.
Udowodnij, że jeśli $L$ jest bezkontekstowy to język $\{ a^{{|w|}}\ :\ w\in L\}$ jest regularny.
Niech $G$ będzie gramatyką bezkontekstową, z $m$ zmiennymi i niech, dla każdej reguły $Y\stackrel{G}{\rightarrow}w$, $|w|\leq\ell$. Dowieść, że jeśli $X^{I}\stackrel{G*}{\rightarrow}\epsilon$, to istnieje wyprowadzenie o długości $1+\ell+\ell^{2}+\ldots+\ell^{{m-1}}$. Czy to oszacowanie jest optymalne?
Dowieść, że dla każdej gramatyki $G$ istnieje stała $C$, taka, że dla dowolnego $w\neq\epsilon$, jeśli $X_{I}\stackrel{G*}{\rightarrow}w$, to istnieje wyprowadzenie o długości $\leq C\cdot|w|$.
Załóżmy, że mamy pewną skończoną liczbę reguł wymazujących postaci $\alpha\rightarrow\epsilon$. Stosując takie reguły możemy w danym słowie zastępować słowo $\alpha$ przez słowo puste. Niech $L$ będzie zbiorem słów, które możemy przekształcić na słowo puste stosując reguły wymazywania.

Czy zawsze istnieje gramatyka bezkontekstowa generująca $L$ i mająca tylko jeden symbol nieterminalny ?
Zaprojektować algorytm, który, dla danej gramatyki $G$, odpowiada na pytanie, czy język $L(G)$ jest nieskończony.
Udowodnij, że każdy język bezkontekstowy może być generowany przez gramatykę w której każdy symbol nieterminalny (poza być może symbolem początkowym) generuje nieskończenie wiele słów terminalnych.

Złożoność problemów automatowych

Zaprojektować algorytm, który dla wyrażenia regularnego $\beta$ i słowa $w\in\Sigma^{*}$ odpowiada na pytanie, czy $w$ należy do języka opisywanego przez $\beta$
1. w czasie ${\cal O}(|\Sigma|\cdot|\beta|^{2}\cdot|w|)$,
2. w czasie ${\cal O}(|\beta|\cdot|w|)$,
Wskazówka. Skonstruować automat niedeterministyczny równoważny wyrażeniu $\beta$ i obliczyć zbiór stanów osiągalnych po słowie $w$. Dla oszacowania w punkcie ?? użyć automatu z $\epsilon$-przejściami (por. zadanie ??.?? ), w grafie którego z każdego stanu wychodzą co najwyżej dwie krawędzie.
Rozważamy pytanie ,,$w\in L[\beta]$ ?” jak w zadaniu ??, ale dla uogólnionego wyrażenia regularnego, tj. takiego, w którym dopuszczamy również operacje teorio–mnogościowe $\cap$ i $-$. Zaprojektować algorytm, który rozstrzyga to pytanie w czasie wielomianowym od $|\beta|+|w|$.

Wskazówka. Zastosować metodę programowania dynamicznego:

dla $1\leq i\leq j\leq|w|$ sukcesywnie obliczać zbiór podwyrażeń

$\alpha$ wyrażenia $\beta$ takich, że $w[i..j]\in L[\alpha]$.
Konstrukcję automatu z zadań ??.?? i ??.?? , który dla danego $w$ rozpoznaje język $\Sigma^{*}w$, można przeprowadzić za pomocą następującego algorytmu. Niech $m=|w|$.

Najpierw obliczamy pomocniczą tablicę $F[0..m]$, taką, że $F[0]=0$ oraz $F[i]$ jest długością najdłuższego prefiksu właściwego $w[1..i]$ będącego jednocześnie sufiksem $w[1..i]$, dla $i=1,\ldots,m$.

$F[0]:=F[1]:=0$; $i:=0$;

for $j:=2$ to $m$ do

begin $(*\, i=F[j-1]\,*)$

while $w_{j}\neq w_{{i+1}}$ $\wedge$ $i>0$ do $i:=F[i]$;

if $w_{j}=w_{{i+1}}$ then $i:=i+1$;

$F[j]:=i$

end

W konstrukcji automatu przyjmujemy, że stany są liczbami $0,1,\ldots,m$ (które można utożsamić z prefiksami $w$ o odpowiednich długościach). Funkcję przejścia $\delta$ określamy przez
1. $\delta(0,w_{1})=1$, $\delta(0,a)=0$, dla $a\neq w_{1}$,
2. $\delta(j,w_{{j+1}})=j+1$, $\delta(j,a)=\delta(F[j],a)$, dla $a\neq w_{{j+1}}$
Dowieść, że powyższy algorytm oblicza żądany automat w czasie liniowym względem długości $w$ (zależnym od alafabetu).
Niech $A$ będzie ustalonym automatem deterministycznym. Zaprojektować algorytm, który dla danej liczby $n$ znajduje w czasie ${\cal O}(n)$ liczbę słów długości $n$ akceptowanych przez $A$.
Podać przykład świadczący o tym, że najkrótsze słowo, jakiego nie akceptuje automat niedeterministyczny o $n$ stanach może mieć długość $2^{{\Omega(n)}}$.

Wskazówka. Rozważyć automat akceptujący wszystko za wyjątkiem słowa

$(\ldots((a_{0}^{2}a_{1})^{2}a_{2})^{2}a_{3}\ldots a_{{n-1}})^{2}a_{n}.$
Dowieść, że jeśli dwa stany $n$–stanowego automatu deterministycznego nie są równoważne (tzn. $L(A,q)\neq L(A,p)$), to istnieje słowo długości nie większej niż $n$ akceptowane z dokładnie jednego z nich.

Wskazówka. Rozważyć zstępujący ciąg relacji równoważności na zbiorze stanów: $R_{i}(p,q)$ o ile stany $p$ i $q$ są nierozróżnialne słowami długości $\leq i$.
Podać algorytm rozstrzygający równoważność dwóch automatów deterministycznych.

Uwaga. Zastosowanie idei zadania prowadzi do efektywniejszego algorytmu niż testowanie niepustości automatu produktowego.
Czy dla słów $u,v$ takich, że $|u|< |v|=n$ istnieje automat deterministyczny spełniający: $u\in L(A)\ \wedge v\notin L(A)$ i mający ${\cal O}(\log n)$ stanów?
1. Wykazać, że dla dowolnego automatu niedeterministycznego o $n$ stanach można skonstruować równoważne wyrażenie regularne długości $2^{{{\cal O}(n)}}$.
2. (**) Podać przykład świadczący o tym, że najkrótsze wyrażenie regularne równoważne danemu automatowi deterministycznemu o $n$ stanach może mieć długość $2^{{\Omega(n)}}$.
  
  Wskazówka. Rozważyć automat, którego graf jest pełnym grafem o $n$ wierzchołkach, a każda krawęd”z ma inną etykietę. Stosując indukcję po $n$, skonstruować pętlę, która ,,wymusza” eksponencjalną długość wyrażenia regularnego.
Eksplozja stanów w produkcie automatów. Niech $\Sigma=\{ 0,1,\ldots,k\}$ i niech dla $i=1,\ldots,k$, $L_{i}$ będzie zbiorem słów $v$ nad $\Sigma$ o następującej własności:
$i$ występuje w $v$, ale przed pierwszym i pomiędzy kaźdymi dwoma kolejnymi wystąpieniami $i$, $i-1$ występuje co najmniej dwa razy.

Nietrudno jest skonstruować deterministyczny automat o 4 stanach rozpoznający $L_{i}$. Dowieść, że każdy (nawet niedeterministyczny) automat rozpoznający język $L_{1}\cap\ldots\cap L_{k}$ musi mieć co najmniej $2^{{k+1}}-1$ stanów.

Wskazówka. Oszacować od dołu długość najkrótszego słowa w tym języku.
Dowieść, że jakikolwiek automat niedeterministyczny rozpoznający język $\{ xcy:\, x,y\in\{ a,b\}^{*}\,\wedge\, x[1..k]=y[1..k]\}$ ma $2^{{\Omega(k)}}$ stanów.
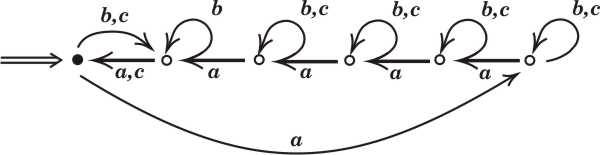
Zakładając, że następujący automat deterministyczny $A_{n}$ ma $n$ stanów ($n\geq 2$, na rysunku $n=6$), dowieść, że jakikolwiek automat deterministyczny rozpoznający lustrzane odbicie języka $L(A_{n})$ ma co najmniej $2^{n}$ stanów (por. zadanie ?? na str. ?? ).
Słowo synchronizujące. Mówimy, że słowo $w$ synchronizuje stany automatu deterministycznego, jeśli istnieje taki stan $q_{0}$, że startując z dowolnego stanu i czytając słowo $w$, automat dojdzie zawsze do stanu $q_{0}$, tzn.
$(\forall q\in Q)\, q\stackrel{w}{\rightarrow}q_{0}$.
1. Znaleźć słowo synchronizujące dla automatu nad alfabetem $\{ a,b\}$ o zbiorze stanów $\{ 0,1,\ldots,k-1\}$ i funkcji przejścia
  
  $i\stackrel{a}{\rightarrow}i+1\;\;(\textrm{mod}k)$
  dla $i=0,1,\ldots,k-1$
  
  $i\stackrel{b}{\rightarrow}i$
  dla i = 0,1, …, k-2
  
  $k-1\stackrel{b}{\rightarrow}0$
  
  Wskazówka. Dla k=5 słowem synchronizującym (najkrótszym) jest $w=\left(ba^{4}\right)^{3}b$
2. Zaprojektować algorytm, który dla automatu o $n$ stanach rozstrzyga w czasie ${\cal O}(n^{3})$, czy istnieje słowo synchronizujące i w pozytywnym przypadku znajduje takie słowo (długości $\leq(n-1)^{3}$).
  
  Wskazówka. Dla każdej pary stanów sprawdzamy, czy istnieje słowo synchronizujące dla tej pary. Szukamy ścieżki w grafie
  par od danej pary do pary o identycznych składowych. Wystarczy jeden taki graf dla wszystkich par.
  Graf ma rozmiar kwadratowy. Zatem pare można zsynchronizować słowem długości kwadratowej.
  Zaczynamy od zbioru wszystkich stanów. Stosując słowo do jednej pary sklejamy je w jeden stan. Teraz mamy juz tylko n-1
  stanów. Znowu bierzemy parę róznych słów. Dla niej liczymy słowo synchronizujące
  (w czasie kwadratowym) i sklejamy te stany. Kontynuujemy aż skleimy wszystkie stany do jednego stanu.
3. (*) Znaleźć najkrótsze słowo synchronizujące dla automatu z punktu ().
Uwaga. Licząca już 40 lat hipoteza Černego, zobacz www.liafa.jussieu.fr/$\sim$jep/Problemes/Cerny.html , głosi, że najkrótsze słowo synchronizujące, o ile istnieje, ma długość $(n-1)^{2}$.
Podać wielomianowy algorytm sprawdzania, czy dany skończony zbiór słów $C\subseteq\Sigma^{*}$ jest kodem (por. rozdz. ?? , ?? zadanie ).
Wskazówka. Skonstruować automat skończony, rozpoznający hipotetyczne słowa posiadające dwie różne faktoryzacje.
Podać algorytmy rozwiązujace następujące dwa problemy (złożoność moze być duża).
1. Dany jest (poprzez automat skończony) język regularny $L$ nad skończonym alfabetem $\Sigma$, sprawdzić czy zachodzi
  
  $\forall\ (x\in L)\ \forall\ (r,\ s\in\Sigma\ )\ \# _{{r}}(x)=\# _{{s}}(x).$
2. Dany jest (poprzez automat skończony) język regularny $L$ nad skończonym alfabetem $\Sigma$, sprawdzić czy dla wszystkich słów $x\in L$ poza skończoną ilością zachodzi
  
  $\forall\ (r,\ s\in\Sigma\ )\ r\ne s\ \Rightarrow\ \# _{{r}}(x)\ \ne\ \# _{{s}}(x).$

Bezkontekstowy czy nie?

Udowodnić, że żaden nieskończony podzbiór języka $L\ =\ \{ a^{n}b^{n}c^{n}\ :\ n\ge 1\}$ nie jest językiem bezkontekstowym.
Udowodnić, że dopełnienie języka z poprzedniego zadania jest językiem bezkontekstowym.
Udowodnić, że jeśli alfabet $\Sigma$ ma co najmniej dwie litery, to język $L=\{ ww:w\in\Sigma^{*}\}$ nie jest bezkontekstowy, natomiast jego dopełnienie $\Sigma^{*}-L$ jest językiem bezkontekstowym.
Dowieść, że dla każdego ustalonego $k$ dopełnienie języka $\{ w^{k}:w\in\Sigma^{*}\}$ jest językiem bezkontekstowym.
Udowodnić, że język $L\ =\ \{ xcx\ :\ x\in(a+b)^{*}\ \}$ nie jest językiem bezkontekstowym.
Udowodnić, że dopełnienie języka z poprzedniego zadania jest językiem bezkontekstowym.
Niech $\mbox{Subwords\/}(x)$ oznacza zbiór wszystkich podsłów słowa $x$, $\mbox{\em Subwords\/}(L)=\bigcup _{{x\in L}}\mbox{\em Subwords\/}(x)$.
1. Udowodnić, że dla języka bezkontekstowego $L$, $\mbox{\em Subwords\/}(L)$ jest językiem bezkontekstowym.
2. Podać przykład języka bezkontekstowego nieregularnego $L$, dla którego $\mbox{\em Subwords\/}(L)$ jest językiem regularnym.
3. Podać przykład języka bezkontekstowego $L$, dla którego $\mbox{\em Subwords\/}(L)$ nie jest językiem regularnym.
Pokazać, że język dopasowywania wzorca $L\ =\ \{ xcy\ :\ x,y\in(a+b)^{*},\ y\in\mbox{\em Subwords\/}(x)\}$ nie jest bezkontekstowy. Czy dopelnienie tego języka jest bezkontekstowe ?
Pokazać, że język $L\ =\ \{ xcy^{R}\ :\ x,y\in(a+b)^{*},\ y\in\mbox{\em Subwords\/}(x)\}$ jest bezkontekstowy.
(*) Pokazać, że dopełnienie języka z poprzedniego zadania nie jest językiem bezkontekstowym.
Rozstrzygnać, czy następujący język jest bezkontekstowy:

$L\ =\ \{ u\$ w^{R}\ :\ u,w\in\{ a,b\}^{+},\ w\textrm{ jest prefiksem i sufiksem }u\ \}$

To samo pytanie dla dopełnienia tego jezyka.
Udowodnić, że język $L\ =\ \{ a^{i}b^{j}c^{k}\ :i\ne j,\ i\ne k,\ j\ne k\ \}$ nie jest bezkontekstowy.

Czy jego dopełnienie jest bezkontekstowe ?
Czy język $L\ =\ \{ a^{i}b^{j}a^{i}b^{j}\ :i,j\ge 1\ \}$ jest bezkontekstowy ?
Czy jego dopełnienie jest językiem bezkontekstowym ?
Udowodnić, że język $L\ =\ \{ ww^{R}w:w\in(a+b)^{*}\}$ nie jest bezkontekstowy.

Czy jego dopełnienie jest bezkontekstowe ?
Pokaż, że język $\{ x\# y^{R}\ :\ x,y\in\{ 0,1\}^{+},\ [x]_{2}+1=[y]_{2}\}$ jest bezkontekstowy.
Pokaż, że język $\{ x\# y\ :\ x,y\in\{ 0,1\}^{+},\ [x]_{2}+1=[y]_{2}\}$ nie jest bezkontekstowy.
Które z następujących języków są bezkontekstowe ?
1. $\{ a^{m}b^{n}:m< n< 2m\}$
2. $(a+b)^{*}-\{(a^{n}b^{n})^{n}:n\geq 1\}$
3. $\{ ww^{R}w:w\in(a+b)^{*}\}$
4. $\{ a^{x}ba^{y}ba^{z}:x+y=z\}$
5. $\{ a^{x}ba^{y}ba^{z}:x\cdot y=z\}$
Dowiedź, że następujące języki nie są bezkontekstowe:
1. $\{ a^{i}b^{j}a^{k}:j=\mbox{ max }\{ i,k\}\}$
2. $\{ a^{i}b^{i}c^{k}:k\neq i\}$.
Czy jest bezkontekstowy język $\{ a^{i}b^{j}c^{p}d^{q}:\ i,j,p,q>0,\ i*j=p+q\ \}$ ?
Czy język

$\{\mbox{bin}(n)\,\$\,\mbox{bin}(n^{2})^{R}\,:\, n\in N\},$

gdzie $\mbox{bin}(n)\in\{ 0,1\}^{*}$ jest binarnym przedstawieniem liczby $n$, jest bezkontekstowy?
Niech $[n]_{2}$ oznacza zapis binarny liczby naturalnej $n\ge 1$, pierwszą cyfrą jest jedynka (najbardziej znacząca). Czy następujący język jest bezkontekstowy:

$\ L_{4}\ =\ \{\ [n]_{2}\;[2n]_{2}\ :\ n\ge 1\ \}$
1. Udowodnij, że zbiór tautologii nad ustalonym skończonym zbiorem zmiennych jest bezkontekstowy (stanowi to uogólnienie zadania (??) z sekcji ??).
2. Formuły nad przeliczalnym zbiorem zmiennych można przedstawić jako język nad skończonym alfabetem, przyjmując indeksowanie zmiennych. Dokładniej, przyjmijmy, że zbiór wszystkich formuł jest generowany przez gramatykę
  
  $\displaystyle F \to \mbox{\bf true}\,|\,\mbox{\bf false}\,|\, V\,|\,(F\vee F)\,|\,(F\wedge F)\,|\,(\neg F)$
  
  $\displaystyle V \to xI$
  
  $\displaystyle I \to 0\,|\, 1J$
  
  $\displaystyle J \to J0\,|\, J1\,|\,\epsilon$
  
  Np. $((x101\vee(\neg x0))\wedge(\neg(\mbox{\bf false}\vee x101)))$ jest formułą.
  
  Udowodnij, że zbiór wszystkich tautologii nie jest bezkontekstowy. Stwierdzenie to wynika łatwo z hipotezy P $\neq$ NP, ale należy je dowieść bez tej hipotezy..
Niech alfabetem będzie $\{ 0,1\}$. Słowo Lyndona to słowo pierwotne (nie będące potęgą mniejszego słowa, por. rozdz. , zad. ), które jest leksykograficznie najmniesze spośród swoich przesunięć cyklicznych.

Czy zbiór słów Lyndona jest bezkontekstowy ?

Wskazówka: we”zmy $a^{{n+1}}ba^{n}ba^{n}$ i zastosujmy lemat Ogdena, ,,markując” środkową grupę $a^{n}$.
Niech $PAL$ onacza zbiór palindromów. Czy zachodzi implikacja:

L bezkontekstowy $\Longrightarrow$ $L\cap PAL$ bezkontekstowy ?
Sformuluj $uvwxy$-lemat o pompowaniu dla języków liniowych w którym $|uvxy|=O(1)$.

Dowied”z, że język $\{ a^{i}b^{i}c^{j}d^{j}:i,j\in{\bf N}\}$ nie jest liniowy.
Dowied”z, że $L\ =\ \{ x\in(a+b)^{*},\# _{a}(x)=\# _{b}(x)\}$ nie jest liniowym językiem bezkontekstowym.
Udowodnij, że zbiór słów $w$ nad alfabetem $\{ a,b\}$ mających tę samą liczbę liter $a$ co $b$ nie jest liniowym językiem bezkontekstowym.
Który z następujących języków jest bezkontekstowy. W przypadku gdy język jest bezkontekstowy wypisać gramatykę bezkontekstową. W zadaniu $[x]_{2}$ oznacza binarny zapis liczby $x$, oraz $w^{R}$ oznacza odwrócenie słowa $w$.
1. $L_{1}\ =\ \{[x]_{2}\ \&\ [y]_{2}\ :\ 1\le x\le y\ \}$.
2. $L_{2}\ =\ \{[x]_{2}\ \&\ [y]_{2}^{R}\ :\ 1\le x\le y\ \}$.
Niech $\mathbf{D_{1},D_{2}}$ oznacza zbiór poprawnych ciągów nawiasowych jednego typu (okrągłe ) i dwóch typów nawiasów (okrągłe i kwadratowe), odpowiednio, włącznie ze słowem pustym. Czy następujące języki są bezkontekstowe
1. $\{\ u\# v^{R}\ :\ uv\in\mathbf{D_{1}}\ \}$,
2. $\{\ u\# v^{R}\ :\ uv\in\mathbf{D_{2}}\ \}$ ?
Niech $L$ będzie zbiorem słów w alfabecie trzyelementowym, które nie zawierają słowa postaci $xx$, dla $x\ne\epsilon$. Udowodnić, że $L$ nie jest bezkontekstowy.
Podać przykład języka bezkontekstowego nad alfabetem trzyelemnentowym, którego dopełnienie jest nieskończone i nie zawiera słów postaci $xx$, dla $x\ne\epsilon$.

Automaty ze stosem

Skonstruować automaty ze stosem rozpoznające poznane wcześniej języki bezkontekstowe: zbiór palindromów, zbiór poprawnie uformowanych ciągów nawiasów, zbiór słów, które mają dwa razy więcej $b$ niż $a$, zbiór ciągów, które nie są postaci $ww$.
Dla liczby naturalnej $n$, niech $\mbox{bin}(n)\in\{ 0,1\}^{*}$ będzie binarnym przedstawieniem liczby $n$. Skonstruować automat ze stosem rozpoznający język

$\{\mbox{bin}(n)\,\$\,\mbox{bin}(n+1)^{R}\,:\, n\in N\}$
Skonstruować automat ze stosem rozpoznający język

$\{\mbox{bin}(n)\,\$\,\mbox{bin}(3*n)^{R}\,:\, n\in N\}$

Uogólnić tezę zadania.
Dowieść, że dla każdego automatu ze stosem $A$, można skonstruować automat ze stosem o dwóch stanach $A^{{\prime}}$, taki że $L(A)=L(A^{{\prime}})$.
Dowieść, że automatowi $A^{{\prime}}$ z poprzedniego zadania można postawić dalszy wymóg, że każde przejście jest postaci

$q,a,Z\,\rightarrow _{{A^{{\prime}}}}\, q^{{\prime}},\alpha$

gdzie $|\alpha|\leq 2$ ($q,q^{{\prime}}$ dowolne).
Dowieść, że dla każdego automatu ze stosem $A$, można skonstruować równoważny mu automat ze stosem $A^{{\prime\prime}}$, w którym każde przejście jest postaci push lub pop, tzn.

$q,a,Z\,\rightarrow _{{A^{{\prime\prime}}}}\, q^{{\prime}},YZ$

lub

$q,a,Z\,\rightarrow _{{A^{{\prime\prime}}}}\, q^{{\prime}},\epsilon$

Czy dla takich automatów można nadal ograniczyć liczbę stanów?
Mając dany automat ze stosem akceptujący język $L$, skonstruować automaty ze stosem akceptujące następujące języki:
1. $\mbox{Prefix}(L)=\{ w\,:\,(\exists v)wv\in L\}$
2. $\mbox{Suffix}(L)=\{ w\,:\,(\exists u)uw\in L\}$
3. $\mbox{Subword}(L)=\{ w\,:\,(\exists u,v)uwv\in L\}$
4. $L^{R}=\{ w^{R}\,:\, w\in L\}$
5. (*) $\mbox{Cycle}(L)=\{ vw\,:\, wv\in L\}$
Mając dany automat ze stosem akceptujący język $L$ i automat skończony akceptujący język $R$, skonstruować automaty ze stosem akceptujące następujące języki:
1. $LR^{{-1}}$
2. $R^{{-1}}L$
3. $L\cap R$
Niech $\# _{s}(w)$ oznacza liczbę symboli $s$ w słowie $w$, oraz $PREF(u)$ oznacza zbiór prefiksów słowa $u$. Ponadto oznaczmy przez $max(w),\ min(w),\ med(w)$ opowiednio maksimum, minimum i medianę liczb $\# _{a}(w),\# _{b}(w),\# _{c}(w)$.

Który z następujących języków jest regularny, a który bezkontekstowy?
1. $L_{1}\ =\ \{ u\in(a\cup b\cup c)^{*}\ :\ \forall\ w\in PREF(u)\ max(w)-min(w)\le 13\ \}$.
2. $L_{2}\ =\ \{ u\in(a\cup b\cup c)^{*}\ :\ \forall\ w\in PREF(u)\ max(w)-med(w)\le 13\ \}$.
Dla danych językow regularnych $L$ i $M$, skonstruować automat ze stosem rozpoznający język $\bigcup _{{i\in N}}(L^{i}\cap M^{i})$. Uwaga: ten zbiór nie musi być regularny.
Dowieść, że dla każdego automatu ze stosem $A$ istnieje stała $C$ (zależna od automatu), taka, że dla każdego słowa $w\in Z(A)$, istnieje obliczenie akceptujące (przez pusty stos) o długości $\leq C|w|$. Wskazówka: oszacować wysokość stosu w obliczeniu akceptującym.
Niech $A$ będzie automatem ze stosem. Dowieść, że zbiór słów, które są możliwymi zawartościami stosu automatu $A$, jest językiem regularnym. Formalnie, mamy na myśli zbiór

$\{\alpha\in\Gamma^{*}\,:\,(\exists w,v\in\Sigma^{*})(\exists q\in Q)\, q_{I},w,Z_{I}\,\vdash _{{A}}\, q,v,\alpha\}$

Wywnioskować stąd, że zbiór słów, które są możliwymi zawartościami stosu automatu $A$ w jakimś obliczeniu akceptującym, jest językiem bezkontekstowym.
Automat ze stosem $A=(\Sigma,\Gamma,Q,q_{I},Z_{I},\delta,F)$ nazywamy deterministycznym, jeśli w każdej sytuacji możliwy jest co najwyżej jeden ruch. Dokładniej:
1. jeśli, dla pewnej pary $q,Z$, zachodzi $q,\epsilon,Z\rightarrow _{A}p,\alpha$ przy pewnych $p,\alpha$, to dla żadnego $\sigma\in\Sigma$, nie zachodzi $q,\sigma,Z\rightarrow _{A}p^{{\prime}},\alpha^{{\prime}}$, dla żadnych
  $p^{{\prime}},\alpha^{{\prime}}$;
2. dla każdych $q,\sigma,Z$, istnieje co najwyżej jedna para $p,\alpha$, taka że $q,\sigma,Z\rightarrow _{A}p,\alpha$.
Język bezkontekstowy jest deterministyczny jeśli jest rozpoznawany przez pewien deterministyczny automat ze stosem (w sensie stanów akceptujących, tzn. $L=L(A)$).

Dowieść, że język $\{ a^{n}b^{n}:n\in{\bf N}\}$ $\cup$ $\{ a^{n}b^{{2n}}:n\in{\bf N}\}$ nie jest deterministycznym językiem bezkontekstowym.

Wskazówka. Zakładając, że istnieje deterministyczny automat $A$ rozpoznający ten język, rozważyć automat $A^{{\prime}}$, który różni się od $A$ tylko tym, że zamienia rolami $a$ i $b$. Przy pomocy tych dwóch automatów można łatwo skonstruować automat ze stosem rozpoznający język $\{ a^{n}b^{n}a^{n}:n\in{\bf N}\}$.
Wykazać, że zbiór palindromów nad alfabetem dwuelementowym nie jest deterministycznym językiem bezkontekstowym.

Wskazówka. Zastosować metodę z poprzedniego zadania. Przy pomocy hipotetycznego automatu deterministycznego rozpoznającego palindromy można np. skonstruować automat rozpoznający język $\{ ca^{n}ba^{n}ca^{n}ba^{n}c:n\in{\bf N}\}$.

Własności języków bezkontekstowych

Podaj przykład języka bezkontekstowego $L$ t.że język $L\ =\ \{ x\ :\ (\exists y)\,|x|=|y|\,\wedge\, xy\in L\}$ nie jest bezkontekstowy.
Udowodnić, że przecięcie języka (deterministycznego) bezkontekstowego z regularnym jest też językiem (deterministycznym) bezkontekstowym.
Przeplotem słów $w$ i $v$ nazwiemy dowolne słowo długości $|w|+|v|$, które można rozbić na rozłączne podciągi $w$ i $v$. $L$ i $M$ jest zbiór wszystkich możliwych przeplotów słów $w\in L$, $v\in M$. Język ten oznaczamy $L\parallel M$. Udowodnij, ze przeplot języka bezkontekstowego i regularnego jest językiem bezkontekstowym. Podaj przykład języków bezkontekstowych $L$ i $M$, dla których $L\parallel M$ nie jest językiem bezkontekstowym.
Domknięcie przeplotne języka $L$ określamy przez $L^{{\sharp}}=L\,\cup\,(L\parallel L)\,\cup\,(L\parallel L\parallel L)\,\cup\ldots$. Wykazać, że operacja domknięcia przeplotnego języka skończonego może dać w wyniku język który nie jest bezkontekstowy.
Udowodnić, że jeśli $X$, $Y$ są językami regularnymi to język
$L\ =\ \sum _{{n\ge 1}}X^{n}\cap Y^{n}$
jest bezkontekstowy.
Podać przykład języków regularnych $X,\ Y$ t.że
$\sum _{{n\ge 1}}(X^{n}\cap Y^{n})\ =\ \{ w\in(a^{+}b^{+})^{+}:\# _{a}(w)=\# _{b}(w)\}$
Podaj języki regularne $X,\ Y,Z$ t.że język
$\sum _{{n\ge 1}}(X^{n}\cap Y^{n}\cap Z^{n})$
nie jest bezkontekstowy.
Wskaż język bezkontekstowy $L$, dla którego $\sqrt{L}=\{ w:ww\in L\}$ nie jest językiem bezkontekstowym.
Podaj przykład języka bezkontekstowego takiego. że $\{ x\ :\ x^{k}\in L$ dla pewnego $k\}$ nie jest bezkontekstowy.
Rozważmy następujący morfizm:

$h(a)=a,\ h(b)=b,\ h(a^{{\prime}})=a,\ h(b^{{\prime}})=b$

oraz $h(x)=\epsilon$ dla symboli $x\in\{ a,b,a^{{\prime}},b^{{\prime}}\}$ dla których morfizm nie został zdefiniowany powyżej. Wykazać, że język $EQ(h,g)=\{ w:h(w)=g(w)\}$ nie jest bezkontekstowy.
Udowodnij, że jeśli $U$ jest regularny to następujący język jest bezkontekstowy
$\{ xy^{R}\ :\ x\ne y,\ xy\in U\}$
Język ma własność prefiksową, gdy dla każdych dwóch słow z tego języka jedno z nich jest prefiksem drugiego. Wykaż, że jeśli język bezkontekstowy ma własność prefiksową to jest on regularny.
Niech $L\subseteq\{ a,b\}^{*}$ będzie językiem regularnym oraz $h,g$ będą morfizmami. Udowodnić, że następujący język jest liniowym językiem bezkontekstowym

$\{ h(u)c(g(u))^{R}\ :\ u\in L\}$
Udowodnij, że przecięcie liniowego języka bezkontekstowego z regularnym jest językiem liniowym.
Dla języka $L$ określamy $\mbox{Min}(L)$ jako zbiór słów w $L$ minimalnych ze względu na porządek bycia prefiksem. (Zatem $u\in\mbox{Min}(L)$ $\Leftrightarrow$ nie istnieją $v\in L$ oraz $w\neq\epsilon$ takie, że $v w\in L$.) Udowodnij, że dla deterministycznego języka bezkontekstowego $L$ język $\mbox{Min}(L)$ jest również deterministycznym językiem bezkontekstowym.
Niech $L\ =\ \{ a^{i}b^{j}c^{k}\ :\ k\ge i\ lub\ k\ge j\}$. Pokaż, że $Min(L)$ nie jest językiem bezkontekstowym.
Zbiór $\mbox{Max}(L)$ określamy analogicznie jak zbiór $\mbox{Min}(L)$ w zadaniu ??. Podaj przykład języka bezkontekstowego $L$, dla którego $\mbox{Max}(L)$ nie jest językiem bezkontekstowym.
Niech $h_{1},h_{2}$ będą morfizmami takimi, że alfabet wyjściowy nie zawiera $. Wykaż, że języki $\{ x\$ y^{R}\ :\ h_{1}(x)=h_{2}(x)\}$ i $\{ x\$ y^{R}\ :\ h_{1}(x)\ne h_{2}(x)\}$ są liniowymi językami bezkontekstowymi.
Podzbiór $M\subseteq{\bf N}^{k}$ nazywamy liniowym jeśli można go przedstawić $M=\{\vec{a}+n\cdot\vec{b}:n\in{\bf N}\}$, dla pewnych wektorów $\vec{a},\vec{b}\in{\bf N}^{k}$, a semi-liniowym, jeśli jest sumą skończenie wielu zbiorów semi-lniowych.
1. Udowodnij, że zbiór długości słów języka bezkontekstowego jest semi-liniowy.
2. (*) Udowodnij twierdzenie Parikha głoszące, że dla języka bezkontekstowego $L\subseteq\Sigma^{*}$ zbiór ($\subseteq{\bf N}^{{|\Sigma|}}$) wektorów liczby wystąpień liter z $\Sigma$ w słowach z $L$ jest semiliniowy.
Przypomnijmy pojęcie odległości Hamminga, określonej dla słów tej samej długości (zadanie ??.??)

$d(u,w)=|\{ i:w_{i}\neq v_{i}\}|.$

Udowodnić, że dla języka regularnego $L$, język

$\{\ w\ :\ (\exists\ u\in L)\ |u|=|w|\ \textrm{oraz}\ d(u,w)\le\frac{|u|}{2}\ \}$

jest bezkontekstowy. Czy język ten jest zawsze regularny ?
Czy następujące stwierdzenia są prawdziwe:
1. Istnieje nieskończony zbiór słów $L$ nad skończonym alfabetem taki, że ani $L$ ani dopełnienie $L$ nie zawierają nieskończonego języka regularnego.
2. To samo, ale wymagamy dodatkowo, aby $L$ był bezkontekstowy.

Maszyny Turinga

Skonstruować maszynę Turinga obliczającą funkcję $2^{n}$ reprezentowaną unarnie. Bardziej dokładnie, zakładamy, że alfabet wejściowy składa się z jednego symbolu, powiedzmy $\{ 1\}$. Jeśli na wejściu dany jest ciąg $n$ jedynek, (tzn. konfiguracja wejściowa jest $q_{0}1^{n}$), to po wykonaniu obliczenia konfiguracja powinna być $q_{f}1^{{2^{n}}}$.
Skonstruować maszynę Turinga obliczającą funkcję $\lceil\log n\rceil$ reprezentowaną unarnie.
Przyjmijmy $\Sigma=\{ 0,1\}$. Skonstruować maszyny Turinga rozpoznające następujące języki:
1. zbiór palindromów
2. $\{ w\$ w\,:\, w\in\Sigma^{*}\}$
3. $\{ ww\,:\, w\in\Sigma^{*}\}$
4. zbiór ciągów reprezentujących binarnie liczby pierwsze.
Graf zorientowany o $n$ wierzchołkach ponumerowanych $0,1,\ldots,n-1$, reprezentujemy ciągiem zer i jedynek długości $n^{2}$, takim, że $k$-ty bit jest 1 o ile istnieje krawędź z wierzchołka o numerze $i$ do wierzchołka o numerze $j$, gdzie $k=i\cdot n+j+1$.
1. Skonstruować niedeterministyczną maszynę Turinga rozpoznającą zbiór słów zero-jedynkowych, które w powyższy sposób reprezentują te grafy, w których istnieje ścieżka z wierzchołka o numerze $0$ do wierzchołka o numerze $n-1$.
2. Skonstruować maszynę deterministyczną realizującą to samo zadanie.
Przypomnijmy, że dwie maszyny Turinga o tym samym alfabecie wejściowym uważamy za równoważne o ile akceptują ten sam język. Udowodnić, że dla każdej maszyny Turinga istnieje równoważna jej maszyna posiadająca dokładnie jeden stan akceptujący i taka, że w konfiguracji akceptującej głowica znajduje się nad pierwszą komórką taśmy (tzn. konfiguracja akceptująca jest postaci $q_{f}\mbox{ co"s}$).
Dla danej niedeterministycznej maszyny Turinga skonstruować równoważną maszynę deterministyczną.
Dla danych deterministycznych maszyn Turinga $M_{1}$ i $M_{2}$ skonstruować deterministyczne maszyny rozpoznające języki
1. $L(M_{1})\cup L(M_{2})$
2. $L(M_{1})\cap L(M_{2})$
3. $L(M_{1})L(M_{2})$
4. $L(M_{1})^{{*}}$.
Udowodnić, że dla każdej maszyny Turinga nad alfabetem wejściowym $\{ 0,1\}$, istnieje równoważna jej maszyna, której alfabet wszystkich symboli roboczych obejmuje jedynie symbole 0,1,$B$.
Powiemy, że maszyna Turinga jest write-once jeśli może pisać tylko w pustych komórkach taśmy, a symbol raz napisany nie może być zastąpiony żadnym innym symbolem (w szczególności nie może być “zmazany” tj. zastąpiony przez “blank”). Dla dowolnej maszyny Turinga z jedną taśmą, skonstruować maszynę write-once z dwiema taśmami, która akceptuje ten sam język.

(*) Dowieść, że maszyny typu write-once z jedną taśmą akceptują jedynie języki regularne.
Dla dowolnej maszyny Turinga (nad dowolnym alfabetem), skonstruować równoważną maszyne o jednej taśmie i czterech stanach. (Wolno powiększyć alfabet roboczy.)
Pojęcie automatu ze stosem można rozszerzyć do automatu z $k$ stosami, $k\geq 2$. Dowieść, że dla każdej maszyny Turinga istnieje równoważny jej deterministyczny automat z dwoma stosami. Wywnioskować stąd, że automat z $k$ stosami, $k>2$ może być symulowany przez automat z 2 stosami (symulację tę można również opisać bezpośrednio).
Udowodnić, że jeśli automat skończony wyposażyć dodatkowo w kolejkę, to otrzymany model ma siłe obliczeniową maszyny Turinga, tzn. dla dowolnej maszyny istnieje automat z kolejką, który rozpoznaje ten sam język.
Automat z $k$ licznikami $c_{1},\ldots,c_{k}$, określamy podobnie jak automat z $k$ stosami, z tym, że liczniki zawierają liczby naturalne, a dostępne operacje na licznikach są postaci $c_{i}:=c_{i}+1$, $c_{i}:=c_{i}\dot{-}1$ (gdzie $0\dot{-}1=0$), oraz test $c_{i}\stackrel{?}{=}0$. Tzn. przejścia takiego automatu są postaci $q\rightarrow p$, $q,c_{i}\stackrel{?}{=}0\rightarrow p$, $q,c_{i}\stackrel{?}{\neq}0\rightarrow p$, $q\rightarrow p,c_{i}:=c_{i}+1$, $q\rightarrow p,c_{i}:=c_{i}\dot{-}1$. Nie ma taśmy, lecz zakładamy, że w chwili początkowej dana wejściowa jest wartością licznika $c_{1}$, a pozostałe liczniki mają wartość 0. Dowieść najpierw, że dla każdej maszyny Turinga nad alfabetem $\{ 1\}$ istnieje równoważny jej automat z 4 licznikami. Następnie wykazać, że liczba liczników może być dalej zredukowana do trzech. (Ograniczenie alfabetu maszyny Turinga nie jest istotne, bo słowa nad alfabetem $n$–literowym można również łatwo “przerobić” na liczby naturalne w systemie unarnym.)

Obliczalność i nierozstrzygalność

Udowodnić równoważność następujących warunków
1. język $L$ jest częściowo obliczalny,
2. język $L$ jest dziedziną pewnej funkcji częściowo obliczalnej,
3. język $L$ jest zbiorem wartości pewnej funkcji częściowo obliczalnej,
4. język $L$ jest zbiorem wartości pewnej funkcji obliczalnej.
Udowodnić, że język $L$ jest obliczalny, wtedy i tylko wtedy, gdy jest skończony lub jest zbiorem wartości pewnej funkcji obliczalnej rosnącej.
Udowodnić następujące twierdzenie Turinga–Posta : jeśli zarówno język jak i jego uzupełnienie są częściowo obliczalne, to są również obliczalne.
Udowodnić, że istnieje zbiór częściowo obliczalny, którego uzupełnienie nie zawiera żadnego nieskończonego zbioru częściowo obliczalnego.
Udowodnić, że istnieje automat z dwoma (sic !) licznikami $A$ taki, że nie jest rozstrzygalne, czy $A$ zatrzymuje się dla danej wejściowej $n$. Wskazówka : wykorzystać zadanie ??.
Udowodnić nierozstrzygalność następującego problemu Posta.

Dane są dwie listy słów : $u_{1},\ldots,u_{n}\in\Sigma^{*}$ i $w_{1},\ldots,w_{n}\in\Sigma^{*}$. Pytanie, czy istnieje ciąg indeksów $i_{1},\ldots,i_{m}\in\{ 1,\ldots,n\}$, taki, że $u_{{i_{1}}}\ldots u_{{i_{n}}}=w_{{i_{1}}}\ldots w_{{i_{n}}}$ ? Jeśli taki ciąg istnieje, to słowo $u_{{i_{1}}}\ldots u_{{i_{n}}}$ ($=w_{{i_{1}}}\ldots w_{{i_{n}}}$) nazywamy rozwiązaniem danej instancji problemu Posta.

Wskazówka : Rozważyć zmodyfikowany problem Posta, w którym dodatkowo wymaga się, by pierwszymi słowami w rozwiązaniu były $u_{1}$ i $w_{1}$ (tzn. $i_{1}=1$). Redukcja zmodyfikowanego problemu do oryginalnego problemu Posta nie jest trudna. Z kolei przedstawić algoerytm, który dla dowolnej maszyny Turinga $M$ i jej wejścia $w$ konstruuje instancję $P$ zmodyfikowanego problemu Posta w ten sposób, że $P$ ma rozwiązanie wtedy i tylko wtedy, gdy $M$ akceptuje $w$. Rozwiązaniem $P$ (o ile istnieje) będzie właśnie akceptujące obliczenie $M$ na $w$.
Dowieść, że następujące problemy są nierozstrzygalne :
1. Dana gramatyka bezkontekstowa $G$ nad alfabetem $\Sigma$. Pytanie : czy $L(G)=\Sigma^{*}$ ? (Tzw. problem uniwersalności.) Wskazówka : Dla maszyny Turinga $M$, udane obliczenie jest ciągiem $c_{0}\# c_{1}\#\ldots\# c_{f}$, gdzie $c_{i}$ są konfiguracjami $M$, $c_{0}$ jest konfiguracją początkową, $c_{f}$ akceptującą, oraz $c_{i}\vdash _{M}c_{{i+1}}$. Należy przedstawić algorytm, który dla dowolnej maszyny $M$ konstruuje gramatykę $G_{M}$ generującą wszystkie ciągi, które nie są udanymi obliczeniami. A zatem, gdybyśmy potrafili rozstrzygać problem uniwersalności, moglibyśmy również rozstrzygać problem niepustości ($L(M)\neq\emptyset$ ?) dla maszyn Turinga, co jest niemożliwe (na mocy twierdzenia Rice'a).
2. Dane dwie gramatyki bezkontekstowe $G_{1},G_{2}$. Pytanie : czy $L(G_{1})\cap (G_{2})\neq\emptyset$ ? Wskazówka : Podobnie jak poprzednie zadanie, ale należy wykorzystać operację lustrzanego odbicia.
3. Dana gramatyka bezkontekstowa $G$. Pytanie : czy $G$ jest jednoznaczna (tzn. dla każedego słowa w $L(G)$ istnieje dokładnie jedno drzewo wyprowadzenia).
  Wskazówka : wykorzystać problem Posta.
Czy następuący problem $X$ jest rozstrzygalny:
Dana gramatyka bezkontekstowa $G$, sprawdzić czy $L(G)$ zawiera palindrom.
Załóżmy, że wiemy że jednotasmowa deterministyczna maszyna Turinga $M$ wykonuje zawsze co najwyzej jeden ńawrót” (to znaczy glowica przesuwa sie w prawo a od pewnego momentu już tylko w lewo). Czy problem “$w\in L(M)$” jest rozstrzygalny, gdzie $w$ jest słowem wejściowym a $L(M)$ oznacza zbiór słów akceptowanych przez $M$ stanem akceptującym.
Czy następujący problem jest rozstrzygalny. Dane są dwa słowa $u,w\in\Sigma^{*}$ oraz liczba $k$, sprawdzić czy

$\left(\exists\ x\in\Sigma^{*}\right)\ \left(\ |x|>k\ \&\ \mathit{Ile}(w,x)=\mathit{Ile}(u,x)\ \right)$

gdzie $\mathit{Ile}(w,x)$ oznacza liczbę wystąpień słowa $w$ jako podsłowo $x$ (wystąpienia nie muszą być rozłączne).
Niech $\mathit{bin}(n)$ oznacza zapis binarny liczby naturalnej $n$. Mamy $|\mathit{bin}(n)|=\lfloor\log _{2}n\rfloor+1$ z wyjątkiem liczby 0, dla której $|\mathit{bin}(0)|=1$. Określić obliczalną różnowartościową funkcję pary $\{ 0,1\}^{*}\times\{ 0,1\}^{*}$, tak by

$|(x,y)|=|x|+|y|+\min\{|\mathit{bin}(|x|)|,|\mathit{bin}(|y|)|\}+{\cal O}(1)$
Ustalamy pewne kodowanie maszyn Turinga, które pozwala nam utożsamiać maszynę $M$ z pewnym słowem nad $\{ 0,1\}$. Rozważmy funkcję $C$, która parze $\left(M,v\right)$ przyporządkowuje minimalną długość słowa $x$, takiego że

$M(x)=v$

lub specjalny symbol $\infty$, gdy nie ma takiego $x$.
1. Dowieść, że funkcja $C$ nie jest obliczalna.
  
  Wskazówka. W przeciwnym razie obliczalna byłaby również funkcja, która liczbie $n$ danej w postaci binarnej przyporządkowuje pewne słowo $w\in(0+1)^{n}$, takie że
  
  $\min\{|(M,x)|:M(x)=w\}\geq n$
  
  (długość pary w rozumieniu za zadania ??). Biorąc za $M$ maszynę obliczajacą tę funkcję oraz $\mathit{bin}(n)$ za $x$, otrzymujemy sprzeczność.
2. Dowieść, że funkcja $C$ z punktu ?? moze być przybliżana w następującym sensie. Istnieje maszyna Turinga, która dla wejścia $\left(M,v\right)$ produkuje nieskończony ciąg liczb, który od pewnego miejsca ustala się na wartości $C\left(M,v\right)$.
  Uwaga. Nie ma sprzeczności pomiędzy punktami ?? i ?? , ponieważ odbiorca powyższego ciągu nigdy nie wie, czy jest on już ustalony.

Hierarchia Chomsky’ego

Dowieść, że każdą gramatykę monotoniczną, czyli o regułach $\alpha\to\beta$, gdzie $|\beta|\geq|\alpha|$, można sprowadzić do postaci, w której każda reguła ma formę
$\alpha X\beta\to\alpha\gamma\beta$

gdzie $X\in V$, $\alpha,\beta,\gamma\in(\Sigma\cup V)^{*}$, $\gamma\neq\varepsilon$ ($V$ – zbiór symboli nieterminalnych, $\Sigma$ – zbiór symboli terminalnych).

Uwaga. Przy powyższym sprowadzeniu trzeba na ogół powiększyć zbiór symboli nieterminalnych.
Dowieść, że języki kontekstowe, to dokładnie języki rozpoznawane przez niedeterministyczne automaty liniowo ograniczone.

Uwaga. Automaty liniowo ograniczone są określone podobnie jak maszyny Turinga, z tym, że jedyną dostępną pamięcią są komórki taśmy zajęte na początku przez słowo wejściowe (przy czym koniec słowa jest zaznaczony specjalnym markerem).
Dowieść, że iloraz języka kontekstowego przez język regularny może nie być językiem obliczalnym.

Wskazówka. Wykorzystać język obliczeń maszyny Turinga, która akceptuje język nieobliczalny.

Wywnioskować dalej, że ani języki kontekstowe, ani języki obliczalne nie są zamknięte na ilorazy przez języki regularne.
Dowieść, że języki częściowo obliczalne są zamknięte na ilorazy przez języki częściowo obliczalne.
Które z czterech klas hierarchii Chomsky'ego są zamknięte na operacje $\cup,\cap,-$ ?

Złożoność obliczeniowa

Konstruowalność pamięciowa. Skonstruować maszynę Turinga off-line, która dla wejścia $w$ o długości $n$ zużywa dokładnie $f(n)$ komórek pamięci roboczej, gdzie

$f(n)=2n,n^{2},n^{k},2^{n},\log n,\ldots$
Konstruowalność czasowa. Skonstruować maszynę Turinga, która dla wejścia $w$ o długości $n$ wykonuje dokładnie $f(n)$ kroków, gdzie $f(n)=2n,3n,n^{2},n^{k},2^{n},2^{{2^{n}}},\ldots$.
Dowieść, że klasy $P$, NP i PSPACE są zamknięte na operację *.
Problem domina. Instancja problemu domina obejmuje liczbę naturalną $M$ daną unarnie oraz skończony zbiór wzorców kostek domina, tzn. wektorów postaci (up, down, left, right ), gdzie up, down, left i right są binarnie zadanymi liczbami, które w tym kontekście nazywamy kolorami. (Liczba kolorów nie jest ograniczona, a więc zależy od danej instancji problemu.) Pytanie brzmi: czy kwadrat $M\times M$ można pokryć kostkami domina w ten sposób, że sąsiednie kostki stykają się bokami o tym samym kolorze, a na bokach kwadratu jest kolor 0 (“biały”). Zakładamy przy tym, że każdy wzorzec można wykorzystać dowolnie wiele razy, ale nie można go “obracać” (tzn. up jest zawsze górną krawędzią itd.).

Należy udowodnić, że problem domina jest NP-zupełny. Wskazówka : zastosować redukcję generyczną, tzn. wychodząc od dowolnej niedeterministycznej maszyny Turinga działającej w czasie wielomianowym.
Udowodnić, że następujący problem dokładnego pokrycia (ang. exact cover) jest NP-zupełny. Dana rodzina podzbiorów $\{ 1,2,\ldots,n\}$ (liczby dane binarnie). Pytanie: czy istnieje podrodzina podzbiorów rozłącznych, które w sumie dają $\{ 1,2,\ldots,n\}$.

Wskazówka : wykorzystać zadanie ??.
Udowodnić, że następujący problem plecakowy (ang. knapsack problem) jest NP-zupełny. Dane: liczby $n,m_{1},\ldots,m_{k}$ (binarnie). Pytanie: czy istnieje podzbiór zbioru $\{ m_{1},\ldots,m_{k}\}$ taki, że $m_{1}+\ldots+m_{k}=n$.

Wskazówka : wykorzystać zadanie ??.
Dowieść, że złożenie dwóch funkcji obliczalnych w pamięci (przestrzeni) logarytmicznej jest funkcją obliczalną w pamięci logarytmicznej.
Dowieść, że każdy problem z klasy NP redukuje się do problemu 3-CNF SAT w pamięci logarytmicznej.