













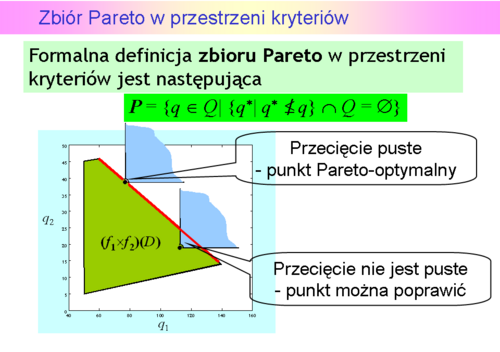



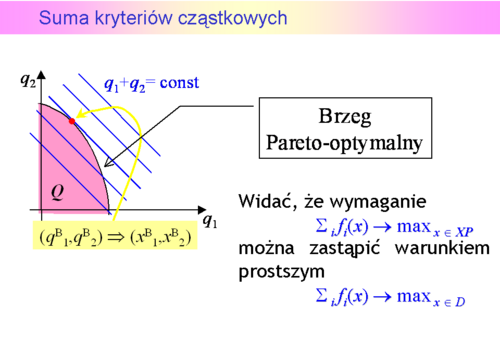
![\boldsymbol{P} = \{(q_1,q_2) \in [60,140] \times [14,46] |\, q_2 =70 - {2 \over 5}q_1 \}](images/EXTERN_0000.png) ,
,
to podejście utylitarianistyczne oparte na maksymalizacji sumy

jako rozwiązanie da  oraz decyzję
oraz decyzję  – tylko pracować. (Dobrze jest wykonać stosowny rysunek.)
– tylko pracować. (Dobrze jest wykonać stosowny rysunek.)

 ,
,
gdzie współczynnik  można interpretować jako cenę jednostki zadowolenia. Zauważmy, że dla
można interpretować jako cenę jednostki zadowolenia. Zauważmy, że dla  , każdy punkt ze zbioru Pareto daje tą samą wartość funkcji
, każdy punkt ze zbioru Pareto daje tą samą wartość funkcji 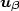 .
.
Dla  rozwiązaniem będzie
rozwiązaniem będzie  i
i  – punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów.
– punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów.
Dla  jako rozwiązanie otrzymamy
jako rozwiązanie otrzymamy  oraz
oraz  – punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie. (Dobrze jest wykonać stosowne rysunki.)
– punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie. (Dobrze jest wykonać stosowne rysunki.)

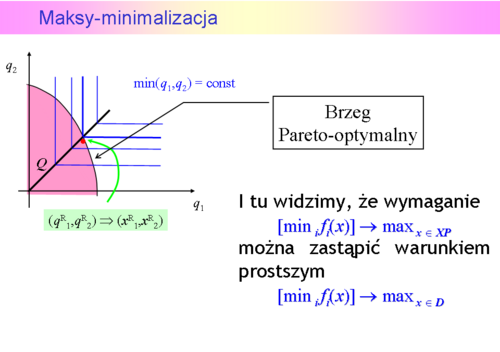
 oraz jako wybrany wariant
oraz jako wybrany wariant  .
.
Nie zawsze prosta o nachyleniu 45° przecina zbiór Pareto !



 , punkt nadiru
, punkt nadiru  . Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt
. Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt  czyli wybranymi wariantami powinna być para
czyli wybranymi wariantami powinna być para  . Oczywiście pan X zaokragli ten wynik i przy takim sposobie wyboru decyzji bedzie pracował przez 13 godzin a tylko godzinę czytał, co da mu 130 zł i 18 jednostek zadowolenia.
. Oczywiście pan X zaokragli ten wynik i przy takim sposobie wyboru decyzji bedzie pracował przez 13 godzin a tylko godzinę czytał, co da mu 130 zł i 18 jednostek zadowolenia.
Dla tej samej metryki, punktem najdalej położonym w stosunku do nadiru jest punkt określony przez warianty
określony przez warianty  (tylko pracować). (Dobrze jest wykonać stosowne rysunki.)
(tylko pracować). (Dobrze jest wykonać stosowne rysunki.)

