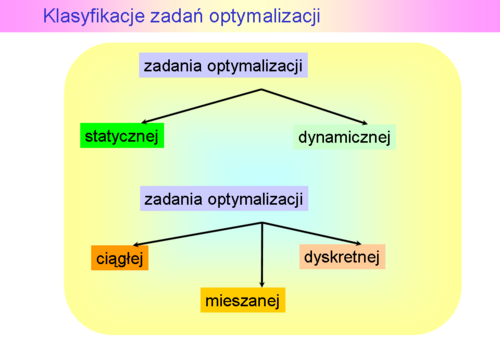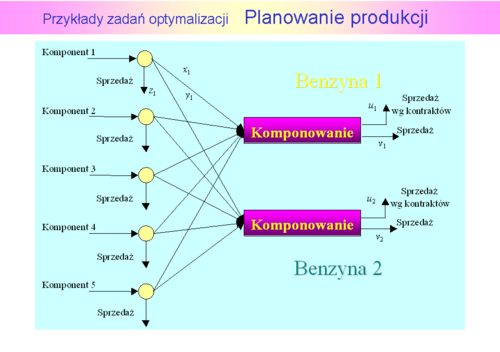




 – cena jednostki
– cena jednostki  -tej benzyny w kontrakcie,
-tej benzyny w kontrakcie,
 – cena jednostki
– cena jednostki  -tej benzyny w wolnej sprzedaży,
-tej benzyny w wolnej sprzedaży,
 – cena jednostki
– cena jednostki  -tego komponentu w wolnej sprzedaży,
-tego komponentu w wolnej sprzedaży,
 – koszt wytworzenia jednostki komponentu
– koszt wytworzenia jednostki komponentu  ,
,
 – koszty komponowania przeliczone na jednostkę komponentu
– koszty komponowania przeliczone na jednostkę komponentu  .
.




 i
i  można traktować dla benzyn np. jako liczbę oktanową.
można traktować dla benzyn np. jako liczbę oktanową.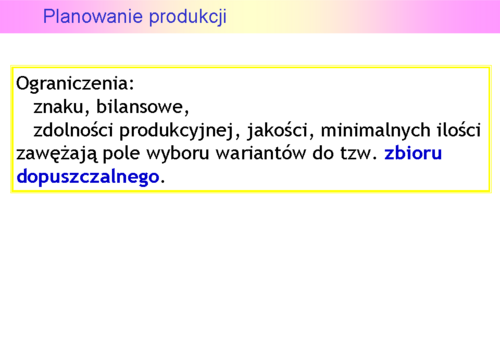




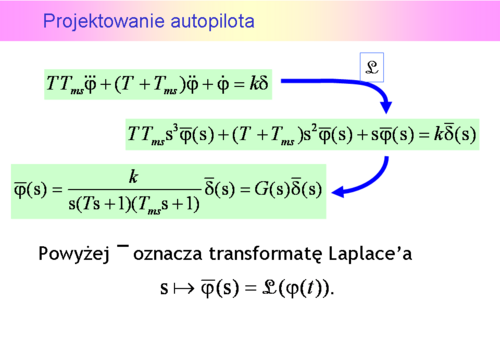
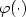 będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący
będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący  mają transformaty Laplace’a.
mają transformaty Laplace’a.
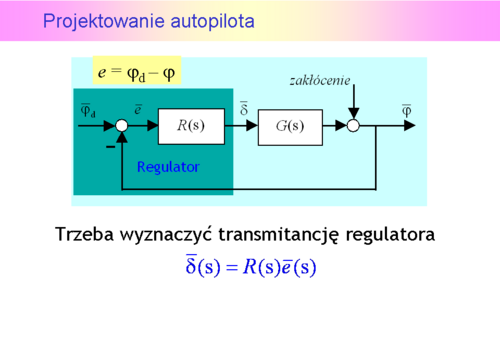




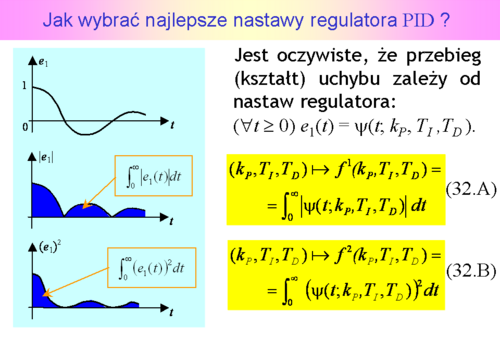







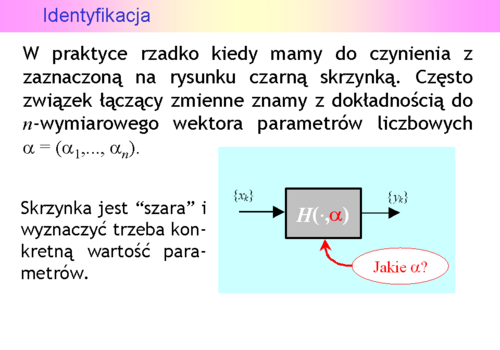








 albo
albo  , nie wykluczamy.
, nie wykluczamy.

























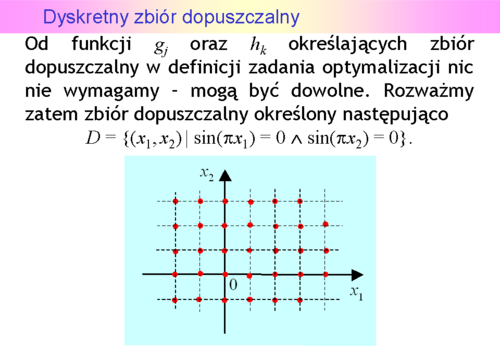
Jest to nieskończony przeliczalny zbiór izolowanych punktów płaszczyzny, a warianty są opisywane wektorami całkowitoliczbowymi. Zbiory tego typu nazywamy zbiorami dyskretnymi.
Zauważmy, że przedstawiony przykład ograniczeń definiujących zbiór całkowitoliczbowy jest przykładem teoretycznym i ma głównie na celu pokazanie bogactwa "różności” jakie kryje w sobie przyjęta definicja zbioru dopuszczalnego.






 zmiennych. Przy czterech miejscach lokalizacji,
zmiennych. Przy czterech miejscach lokalizacji,  , i dwudziestu pięciu odbiorcach,
, i dwudziestu pięciu odbiorcach,  , daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego bo trzeba uwzględnić różne produkty a także różne ich rodzaje), jest to niewiele.
, daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego bo trzeba uwzględnić różne produkty a także różne ich rodzaje), jest to niewiele.
 nie zostanie wybudowana nowa fabryka to,
nie zostanie wybudowana nowa fabryka to,  , zatem na mocy (85.A) i (85.B), dla każdego
, zatem na mocy (85.A) i (85.B), dla każdego  wielkość przewozu
wielkość przewozu  .
.



 oznaczono zbiór liczb całkowitych tj. zbiór
oznaczono zbiór liczb całkowitych tj. zbiór 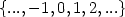 .
.