
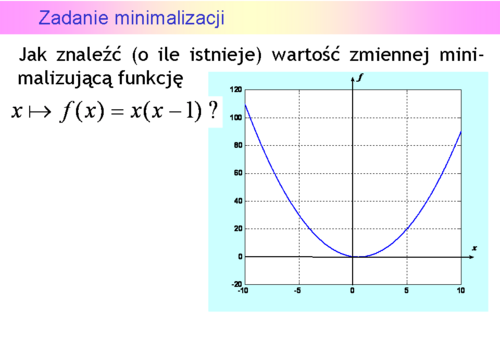
Zadanie minimalizacji
Ale matematyka nie dostarcza nam narzędzi pozwalających bezpośrednio to polecenie wypełnić. Brak bezpośrednich narzędzi pozwalających wprost znaleźć rozwiązanie zadania optymalizacji oznacza, że wtedy gdy chcemy je znaleźć drogą rachunkową musimy oryginalne sformułowanie przekształcićdo postaci pozwalającej na wykonanie stosownych rachunków. Jak się o tym przekonamy w wykładach następnych jest to najczęściej odpowiednio określonyukład równań i nierówności (obecność nierówności jest kłopotliwa), którego rozwiązanie jest (lub może być, warunek konieczny!) rozwiązaniem wyjściowego zadania optymalizacji.
Rozwiązywanie zadania minimalizacji

Algorytm poszukujący rozwiązania



I ja też przyjmę taką konwencję.
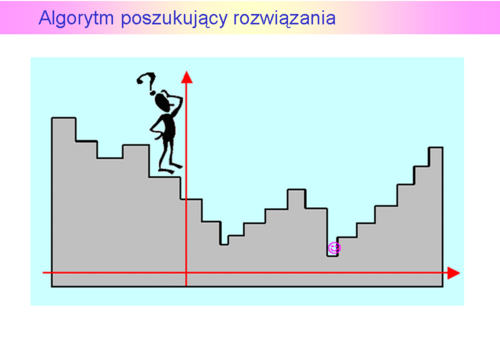
Przyjmujemy, że Algorytm całych schodów nie widzi, natomiast potrafi ocenić położenie każdego stopnia w stosunku do ustalonego poziomu odniesienia, nazwiemy je wysokością (dla każdego wariantu potrafi obliczyć wartość funkcji celu).
Algorytm na schodach
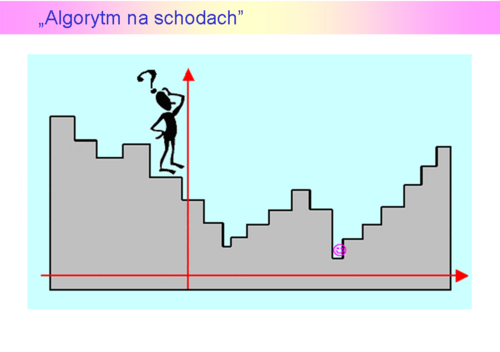
Algorytm wie, że stoi na jakimś stopniu i może się ruszać w jedną ze stron, przyjmijmy, że prawą i lewą. Jeżeli założymy, że jest “sprawny fizycznie” to może przeskakiwać kilka stopni na raz. Stopnie na schodach, nawet nieskończonych, można policzyć, każdy stopień to wariant, a więc zbiór wariantów jest przeliczalny. Jeżeli liczba stopni jestskończona (zbiór dopuszczalny jest skończony, a więc ograniczony) i nie jest zbyt duża w stosunku do szybkości poruszania się po nich Algorytmu, to przy założeniu, że jest on w stanie powiązać w pary stopień i jego wysokość i zapamiętać te pary, postępowanie jest oczywiste: być na wszystkich stopniach, określić ich wysokość i wybrać ten o wysokości najmniejszej (przeszukać wszystkie warianty). Gdy stopni jest bardzo dużo, Algorytm może odwiedzać np. co dziesiąty stopień (przeszukanie wybranych punktów węzłowych), albo wybierać je w sposób przypadkowy zgodnie z rozkładem równomiernym (równomierne przeszukanie przypadkowe). Takie postępowanie nie gwarantuje jednak znalezienia rozwiązania – Algorytm może przeskoczyć nad stopniem najniższym. Powstaje więcproblem dokładności znalezionego rozwiązania, ściśle związany z ilością odwiedzonych stopni (ilością punktów próbnych) ale też i ze sposobem wybierania stopni do odwiedzenia.
Algorytm na schodach nieskończonych
Algorytm leniwy
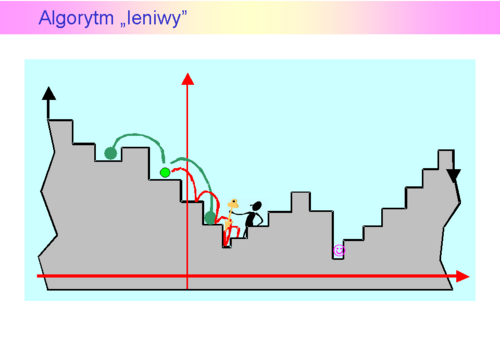

Algorytm na zbiorach nieprzeliczalnych
- Jak Algorytm ma zabrać się za poszukiwania aby znaleźć minimum globalne ?
- Algorytm wie że musi się ruszyć w prawo, ale jak długi skok ma wykonać ?
Naukowcy i praktycy pracują nad odpowiedzią na to pytanie od mniej więcejpięćdziesięciu lat, i dalsza część tych wykładów jest poświecona zwięzłemu przedstawieniu najistotniejszych, zdaniem ich autora, dokonań w tej dziedzinie.
Algorytm poszukiwania rozwiązania



Proste przeszukiwanie


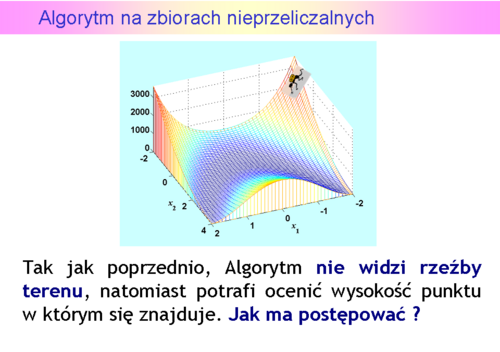
Różne siatki
 węzłach i
węzłach i  węzłach.
węzłach.
Tam gdzie było minimum – pojawiło się lokalne maksimum !


 węzłach i zgodnie z teorią pokazuje właściwe przybliżenie tej funkcji.
węzłach i zgodnie z teorią pokazuje właściwe przybliżenie tej funkcji.
Zauważmy tu, że dokładna analiza pokazała, że minimalna wartość funkcji oceniającej określona dla tych trzech siatek różni się nieznacznie. Oczywiście nie można tego powiedzieć o punktach w których ta wartość jest osiągana.
Co zamiast brutalnej siły?

