Lokalny a globalny
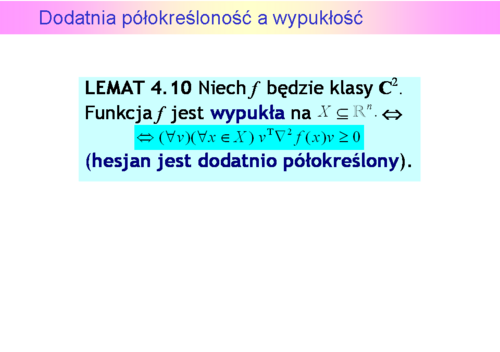
Warunki optymalności dla funkcji wypukłych
Piękny rezultat teoretyczny, sprowadzający procedurę redukcji do układu równań wyłącznie do rachunków: liczenia pochodnych i rozwiązywania równań, czyli do takiego postępowania, które zastosowaliśmy z ochotą lecz błędnie w przykładzie. Trzeba tylko policzyć macierz Hessego by stwierdzić wypukłość funkcji celu i zastanowić się nad sposobem rozwiązania stosownych równań, ale odpadają zagadnienia związane z dowodem istnienia rozwiązania.
Ocena procedury redukcji....
Napisaliśmy, w zasadzie, ponieważ opracowano procedury automatycznego różniczkowania (nie mylić z proceduramisymbolicznego różniczkowania), które przetwarzają kod wyliczający funkcję wyboru na kod wyliczający jej pochodne. Zatem wymaganie znajomości wzoru nie jest już takie kategoryczne.
Zauważmy, że jednym z plusów tej metody jest to, że idealnie nadaje się do, nazwijmy to tak, sprawdzania wiadomości i zdolności rachunkowych studentów.
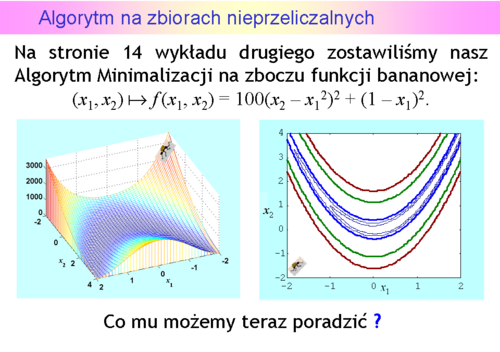
Algorytm na zbiorach nieprzeliczalnych

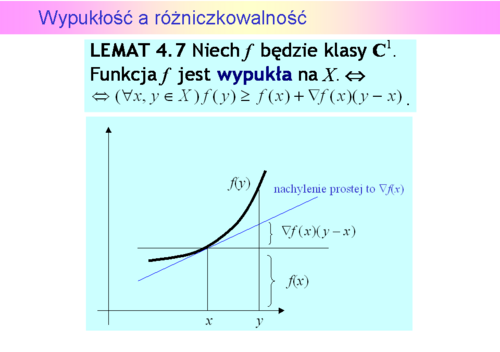
Warunki optymalizacji dla funkcji wypukłych
Gładkie zadania optymalizacji
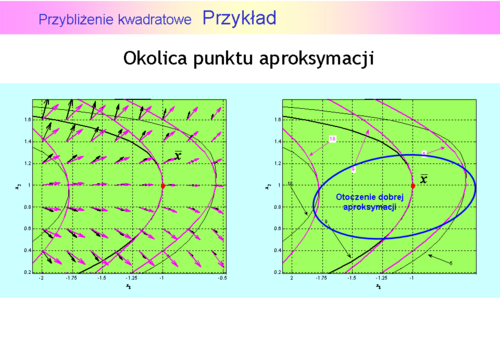
Przybliżenie kwadratowe

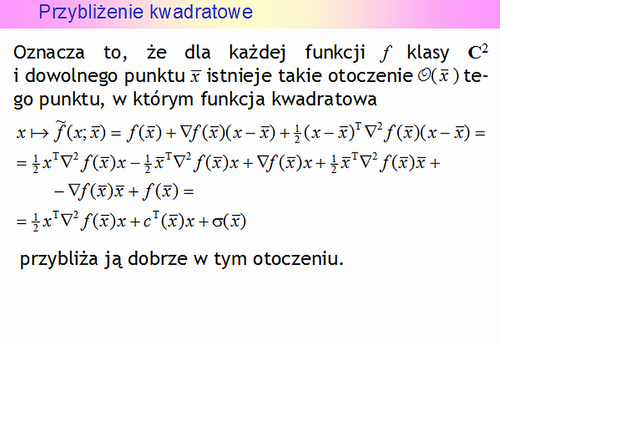



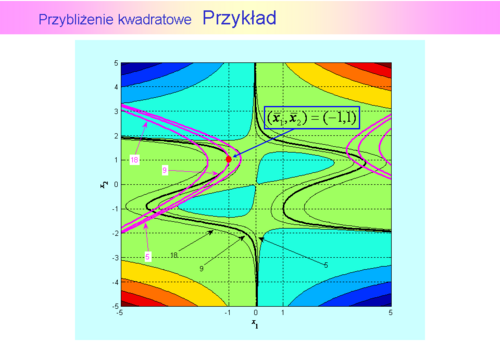
Widać, że otoczenie, w którym aproksymację uznalibyśmy za dobrą nie jest duże i jego kształt jest zbliżony do elipsy o osiach nierównoległych do osi współrzędnych kartezjańskich.
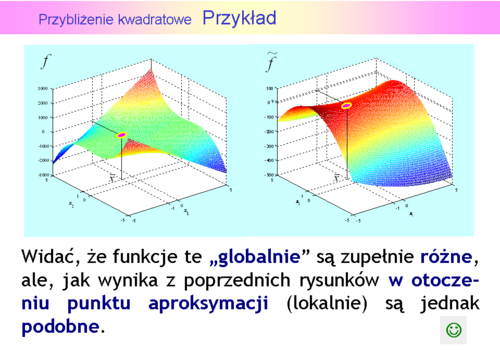

Korzystać z aproksymacji – nie korzystać ?
Tego rodzaju dylemat jest typowy dla sytuacji, w której znajduje się twórca nowych rozwiązań konstrukcyjnych – magister, a więc mistrz – a także twórca nowych teorii naukowych. Za podejściem optymisty opowiedział się Albert Einstein, który stwierdził, że "God is subtle but he is not malicious". Co w naszym przypadku przekłada się na przeświadczenie, że nieliniowe zadania optymalizacji związane z rozwiązywaniem zagadnień praktycznych, są takie, że zręczne wykorzystanie możliwości jakie daje posługiwanie się aproksymacją (APR)pozwoli opracować skuteczne algorytmy ich rozwiązywania. Współcześni optymiści mają sławnego poprzednika – Izaaka Newtona, który wymyślił metodę stycznych rozwiązywania równań nieliniowych opartą o jeszcze prostszą aproksymację, bo ograniczoną tylko do składnika afinicznego.
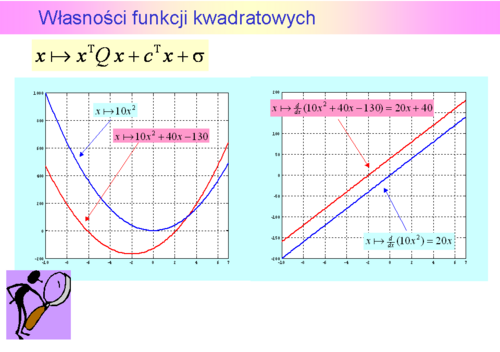
Własności funkcji kwadratowych

Intuicyjnie – dodanie członu afinicznego “przesuwa” formę kwadratową nie zmieniając jej kształtu, tzn. nie zmienia jej podstawowych własności.
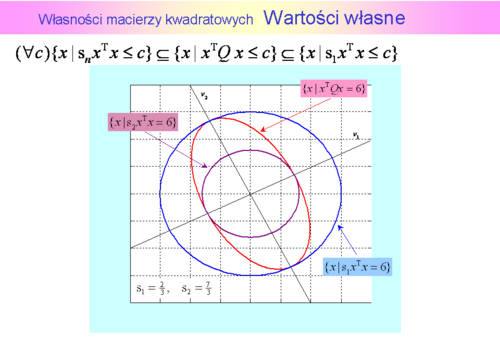
Własności macierzy kwadratowych
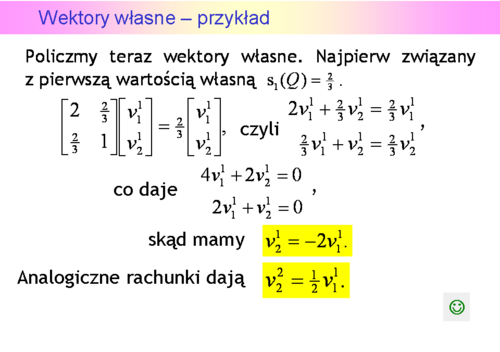
Wektory własne
Wektory własne nie są wyznaczone jednoznacznie, i nie jest to przypadek. W terminologii używanej w teorii metod optymalizacji wektory własne wyznaczają tylko kierunki (proste).
Uwarunkowanie macierzy kwadratowych
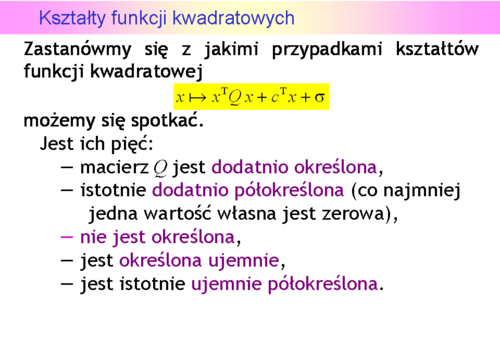
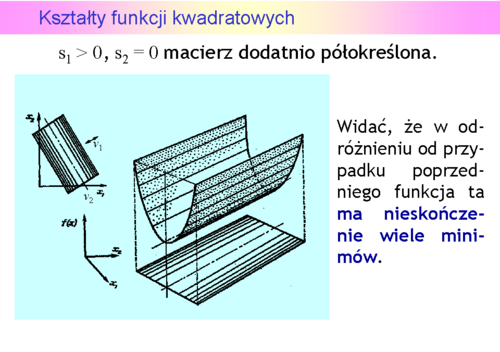
Kształty funkcji kwadratowych
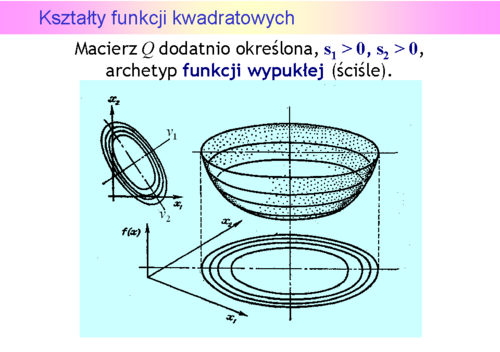
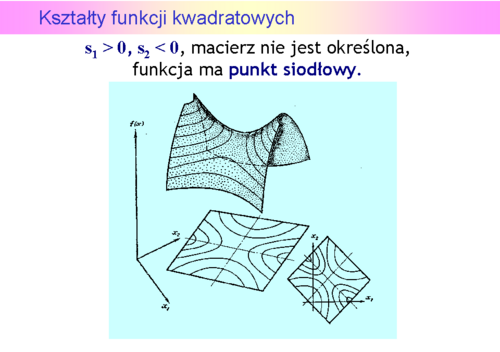
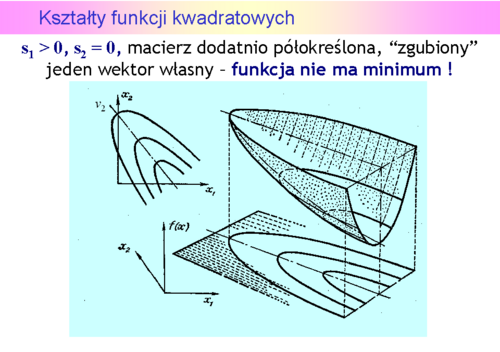
Niestety, możemy narysować tylko funkcję dwu zmiennych (jak często mówimy, na płaszczyźnie). Przedstawmy zatem wykresy trójwymiarowe i poziomicowe dla pierwszych trzech przypadków, ponieważ funkcje określone ujemnie to “odwrócone w dół” funkcje określone dodatnio.
Forma kwadratowa a funkcja kwadratowa
Algorytm na zbiorach nieprzeliczalnych
Aproksymujemy kwadratowo funkcję celu
Uwarunkowanie funkcji
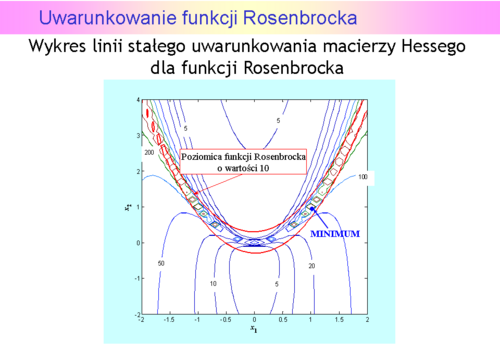
Uwarunkowanie funkcji Rosenbrocka
Widać, ze funkcja Rosenbrocka jest dobrze dobrana jako “tor badania sprawności” dla różnych algorytmów. Tylko w centralnej części (tam gdzie nie ma minimum) jej uwarunkowanie jest mniejsze od pięciu, a w okolicy minimum jest większe od 500.









 .
.


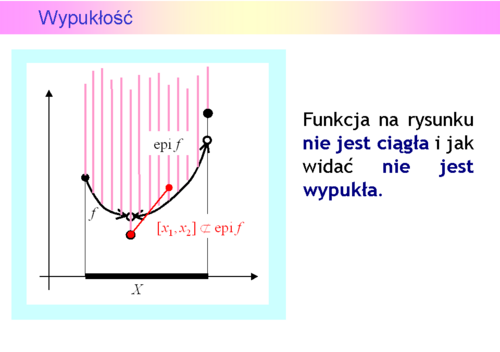






 , zatem macierz ta jest dodatnio (i ujemnie też!) półokreślona.
, zatem macierz ta jest dodatnio (i ujemnie też!) półokreślona.