


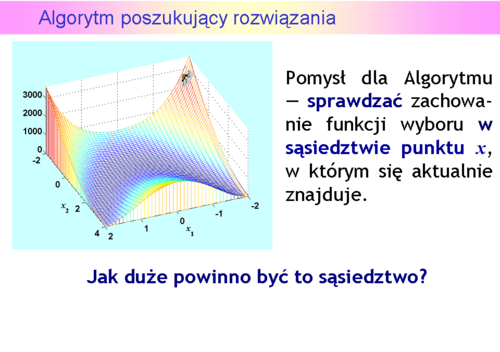
Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboruw sąsiedztwie punktu  , w którym się aktualnie znajduje. Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej).
, w którym się aktualnie znajduje. Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej).


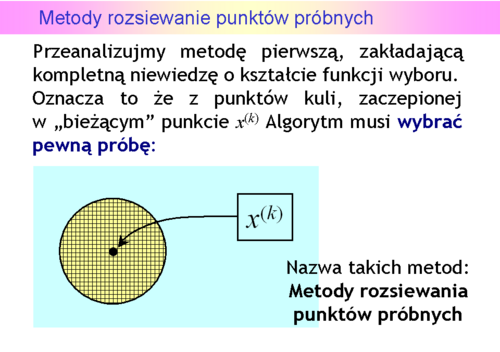
 Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne).
Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne).
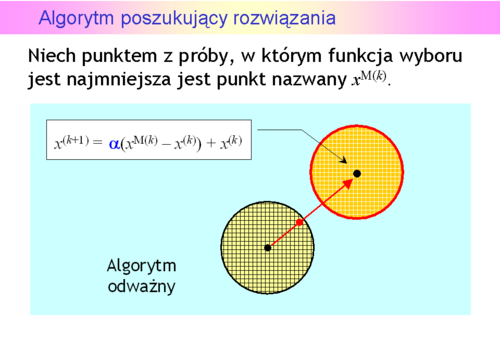
 za środek nowego otoczenia
za środek nowego otoczenia , a następnie przeszukiwać je tak jak poprzednio.
, a następnie przeszukiwać je tak jak poprzednio.
 , tzn. ustalić środek nowej kuli w punkcie
, tzn. ustalić środek nowej kuli w punkcie



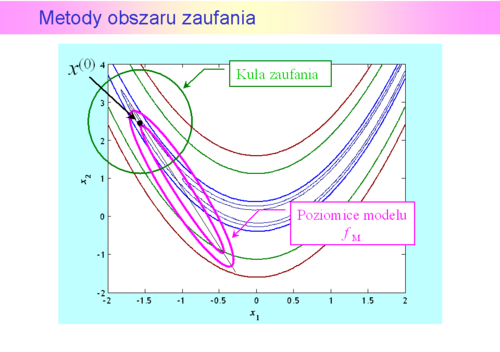
 została określona kula
została określona kula  i funkcja
i funkcja 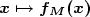 będąca modelem zachowania się funkcji wyboru
będąca modelem zachowania się funkcji wyboru  w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową
w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową  (APR)
(APR)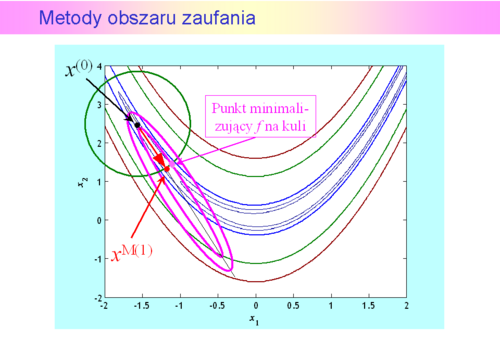
 , minimalizującego funkcję modelującą na kuli. Punkt ten oczywiście będzie się różnił od rzeczywistego minimum funkcji celu
, minimalizującego funkcję modelującą na kuli. Punkt ten oczywiście będzie się różnił od rzeczywistego minimum funkcji celu  na kuli zaufania, ale mamy nadzieję, żeniewiele, a co ważniejsze będzie spełniona nierówność
na kuli zaufania, ale mamy nadzieję, żeniewiele, a co ważniejsze będzie spełniona nierówność  oznaczająca, że funkcja celu z kroku na krok maleje.
oznaczająca, że funkcja celu z kroku na krok maleje.
 został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy — wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru — kwadratową funkcją aproksymującą.
został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy — wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru — kwadratową funkcją aproksymującą. 
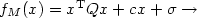 min p.o.
min p.o. 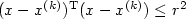 , co nastąpiło w połowie lat siedemdziesiątych ubiegłego wieku.
, co nastąpiło w połowie lat siedemdziesiątych ubiegłego wieku.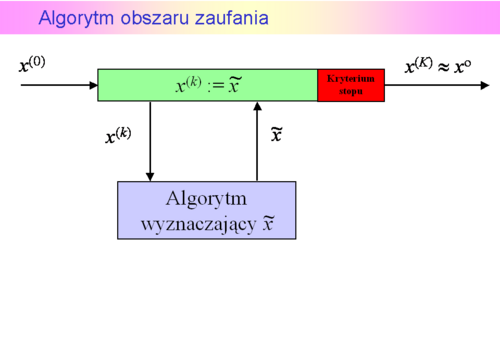
Inicjalizacja
Wybierz punkt początkowy  .
.
Ustal początkowy obszar zaufania 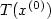 .
.
Podstaw  .
.
Kroki algorytmu
 wyznacz model
wyznacz model  funkcji celu w jego otoczeniu.
funkcji celu w jego otoczeniu.
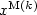
 punktu
punktu  = arg min
= arg min .
.
 , idź do 5. W przeciwnym przypadku idź do 4.
, idź do 5. W przeciwnym przypadku idź do 4.
 , podstaw
, podstaw 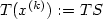 , idź do 2.
, idź do 2.
 przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6.
przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6.
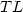 . Jeżeli tak, podstaw
. Jeżeli tak, podstaw 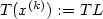 , idź do 7. W przeciwnym przypadku idź do 7.
, idź do 7. W przeciwnym przypadku idź do 7.
 , idź do 1.
, idź do 1.
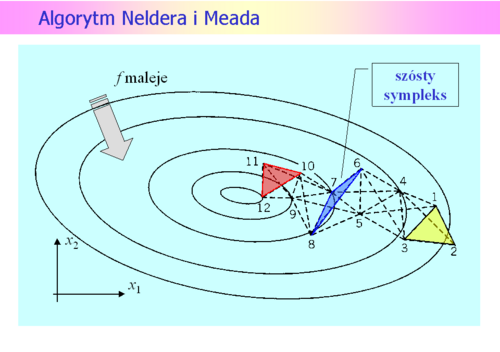
Wyjaśnień wymagają kroki 2, 3, 6 i oczywiście kryterium stopu.



 }
} Naturalne pytanie które postawiliśmy, to kiedy go uciąć – które
Naturalne pytanie które postawiliśmy, to kiedy go uciąć – które  uznać za ostatnie, dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – czy wygenerowany ciąg w ogólejest zbieżny, a gdy jest, to czy jego granica jest rozwiązaniem zadania optymalizacji ? Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym.
uznać za ostatnie, dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – czy wygenerowany ciąg w ogólejest zbieżny, a gdy jest, to czy jego granica jest rozwiązaniem zadania optymalizacji ? Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym.

 jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu.
jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu.
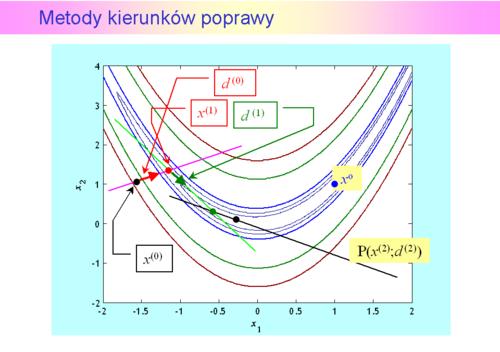
 jest równoważne ustaleniu pewnego
jest równoważne ustaleniu pewnego  . Zatemzmieniając
. Zatemzmieniając  od zera do plus nieskończoności ruszamy się wzdłuż prostej
od zera do plus nieskończoności ruszamy się wzdłuż prostej  w kierunku malenia funkcji celu. Konkretną wartość
w kierunku malenia funkcji celu. Konkretną wartość  –długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze
–długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze  trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak:
trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak:
wybieramy duży krok początkowy  ,
,
gdy 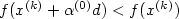 to
to  uznajemy za długość kroku,
uznajemy za długość kroku,
gdy przeciwnie – zmniejszamy  do
do 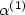 ),
),
powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę.

 (
( i
i  są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny
są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny  jest określony jednym ograniczeniem równościowym.
jest określony jednym ograniczeniem równościowym.
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu.


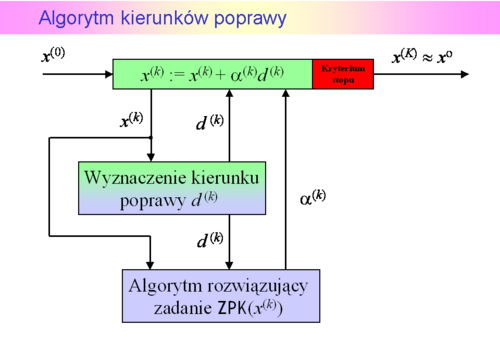
Podstawowy algorytm kierunków poprawy
Inicjalizacja
Wybierz punkt początkowy  .
.
Podstaw  .
.
Kroki algorytmu
 wyznacz kierunek poprawy
wyznacz kierunek poprawy  .
.
 .
.
 .
.
 przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5.
przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5.
 , idź do 1.
, idź do 1.





 dla której
dla której  . Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm SIMPLEX rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym
. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm SIMPLEX rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym  może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania.
może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania.
 , albo dla funkcji gładkich –zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora
, albo dla funkcji gładkich –zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora  , że
, że
 .
.
 może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie.
może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie.
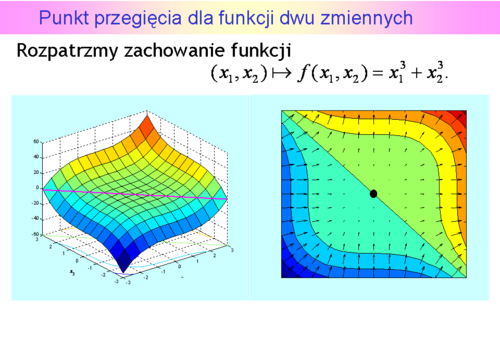
 jest
jest 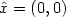 , a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie.
, a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie.

 otrzymany w kolejnych krokach algorytmu, jest zbieżny
otrzymany w kolejnych krokach algorytmu, jest zbieżny
a) liniowo, gdy dodatkowo
lim ,
,
b) superliniowo, gdy dodatkowo
lim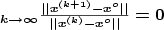 ,
,
c) kwadratowo, gdy dodatkowo
lim .
.
Definicje szybkości związane są z szybkością zbiegania do zera:
postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. danego wzorem
 , bo
, bo  –zbieżność liniowa, np. ciągu danego wzorem
–zbieżność liniowa, np. ciągu danego wzorem
 , bo
, bo – zbieżność superliniowa, np. ciągu danego wzorem
– zbieżność superliniowa, np. ciągu danego wzorem
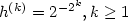 , bo
, bo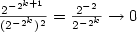 – zbieżność kwadratowa.
– zbieżność kwadratowa.
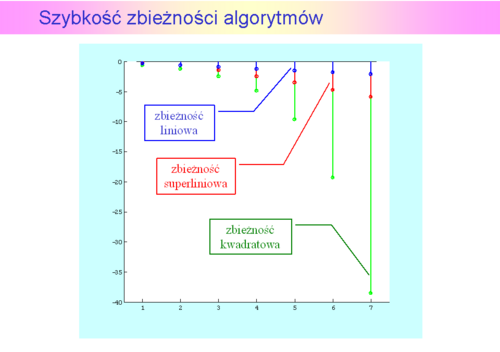
Widać że zbieżność liniowa jest najwolniejsza, a kwadratowa - najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych szybkość liniowa jest do zaakceptowania gdy granica  jest dostatecznie mała, nie większa niż
jest dostatecznie mała, nie większa niż  .
.



