jest wektorem wierszowym. Jego transpozycję do wektora kolumnowego oznacza się
jest wektorem wierszowym. Jego transpozycję do wektora kolumnowego oznacza się 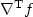 .
.








 w którym
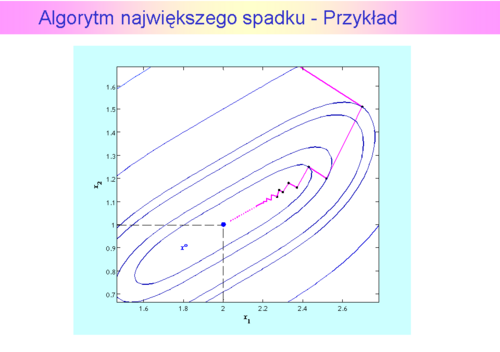
w którym . Wartość funkcji celu
. Wartość funkcji celu  , a odległość
, a odległość  .
.



 wynosi 0.09!). W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu.
wynosi 0.09!). W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu.



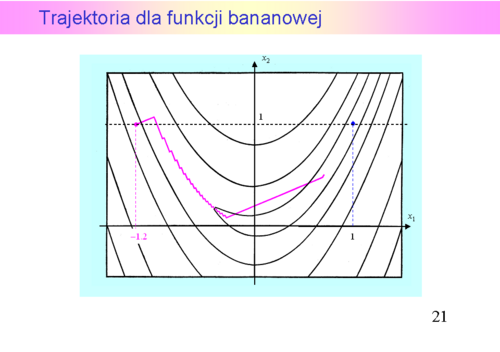
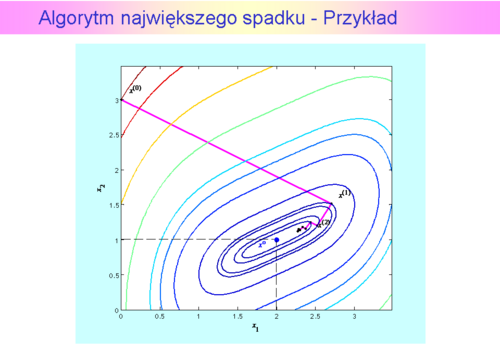
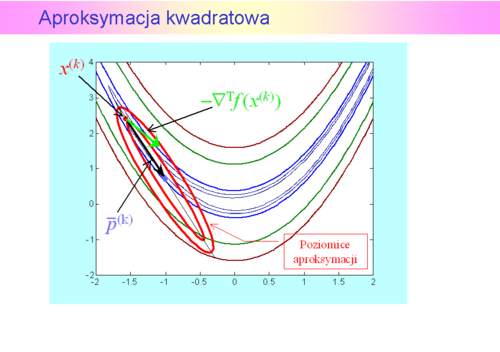
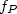 ma dwa minima lokalne, z których „dalsze” jest globalne. Do czterdziestej iteracji zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum, w czterdziestej pierwszej – „przeskoczyła” to minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania".
ma dwa minima lokalne, z których „dalsze” jest globalne. Do czterdziestej iteracji zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum, w czterdziestej pierwszej – „przeskoczyła” to minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania".










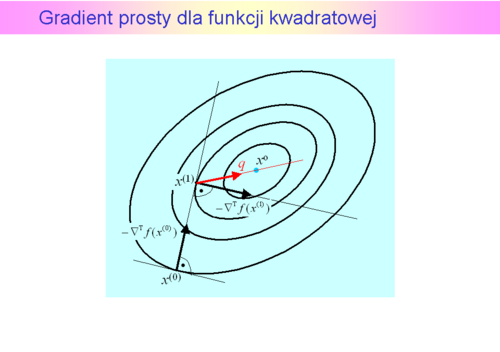











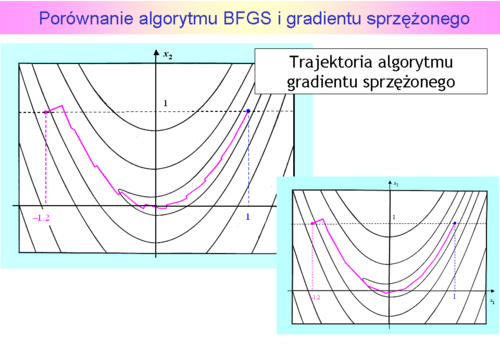
 , posługując się tylko gradientami, kierunek sprzężony względem
, posługując się tylko gradientami, kierunek sprzężony względem  z początkowym kierunkiem antygradientu.
z początkowym kierunkiem antygradientu.


















 lub co
lub co 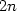 kroków, ponieważ z odnową co
kroków, ponieważ z odnową co  kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku.
kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku.





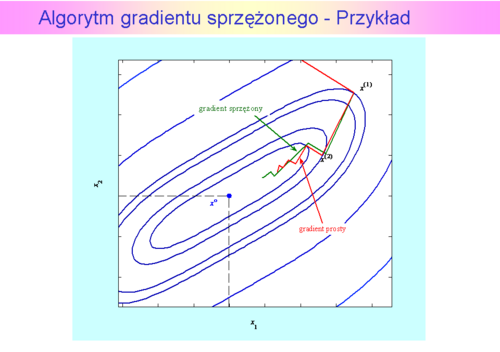
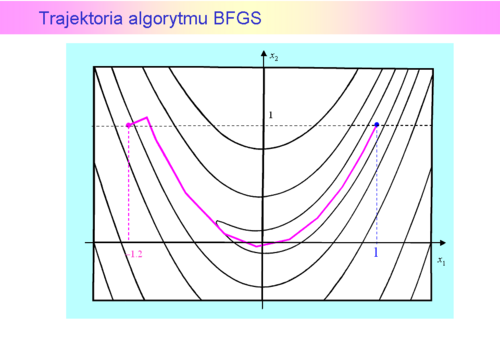
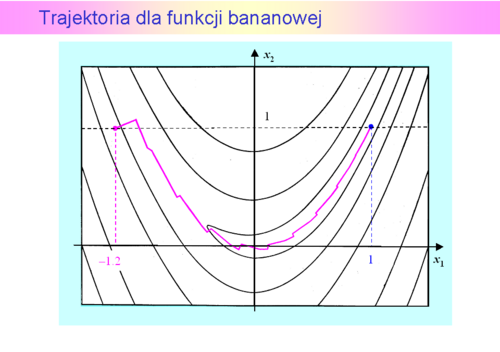
 i miał znaleźć rozwiązanie z dokładnością
i miał znaleźć rozwiązanie z dokładnością  (przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono.
(przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono. w którym
w którym  . Wartość funkcji celu
. Wartość funkcji celu 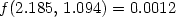 , a odległość proponowanego rozwiązania od punktu optymalnego jest równa
, a odległość proponowanego rozwiązania od punktu optymalnego jest równa
 .
.
Krok pierwszy z  do
do był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ
był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ  . Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty
. Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty  wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty
wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty  , które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie
, które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie  wyliczonym przez algorytm najszybszego spadku jest równy
wyliczonym przez algorytm najszybszego spadku jest równy ![[-0.18\,\vdots -0.28]](images/EXTERN_0022.png) , a kierunek poprawy wyznaczony w swoim punkcie
, a kierunek poprawy wyznaczony w swoim punkcie  przez algorytm gradientu sprzężonego jest równy
przez algorytm gradientu sprzężonego jest równy ![[-0.30\,\vdots -0.25]](images/EXTERN_0023.png) . Ta różnica spowodowała, że algorytm gradientu sprzężonego wyznaczył jako punkt
. Ta różnica spowodowała, że algorytm gradientu sprzężonego wyznaczył jako punkt 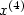 punkt o współrzędnych
punkt o współrzędnych  , co dało wartość funkcji celu
, co dało wartość funkcji celu  , a algorytm gradientu prostego – punkt o współrzędnych
, a algorytm gradientu prostego – punkt o współrzędnych  z wartością funkcji celu
z wartością funkcji celu  . W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt
. W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt  dający wartość funkcji celu
dający wartość funkcji celu  i wartość normy gradientu
i wartość normy gradientu  , a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt
, a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt  w którym
w którym  , oraz
, oraz  .
.



















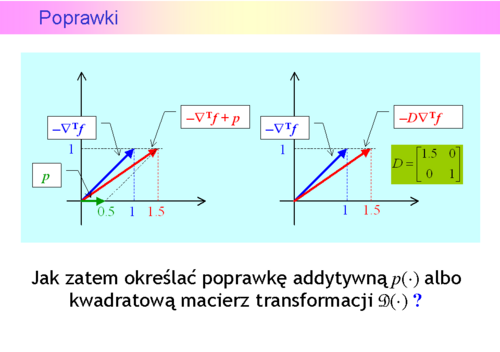
 nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw.rodzina poprawek Broydena.
nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw.rodzina poprawek Broydena.



 obliczone według wzorów (96.A) są przy użyciu dowolnej z nich takie same.
obliczone według wzorów (96.A) są przy użyciu dowolnej z nich takie same.