Witam serdecznie na kolejnym wykładzie z „Inżynierii oprogramowania”!
Tematem dzisiejszego wykładu są metody formalne, czyli metody oparte na matematyce. Metody matematyczne (np. widoczne na slajdzie funkcje trygonometryczne) są szeroko wykorzystywane w wielu obszarach nauk technicznych, więc nic dziwnego, że próbuje się je stosować również w inżynierii oprogramowania.

Wykład ten można traktować jako rozwinięcie poprzedniego wykładu dotyczącego języka UML. Zarówno język UML, jak i metody formalne służą do opisu systemów informatycznych i różnych ich aspektów.
Jedną z osób, której informatyka zawdzięcza bardzo wiele jest brytyjski profesor Tony Hoare. Urodził się w 1934 roku.
Najpierw interesował się filologią klasyczną, potem językiem rosyjskim.
W 1959 roku zainteresował się statystyką matematyczną i programowaniem komputerów. Zainteresowania te rozwijał w Moskwie, gdzie badał głównie problemy automatycznej translacji.
Po powrocie do Wielkiej Brytanii w 1960 roku wymyślił algorytm sortowania znany jako Quicksort i opracował w firmie Elliott Brothers jeden z pierwszych kompilatorów języka Algol 60, który właśnie został opracowany i którego rozwinięciem był później język Pascal.
W 1968 roku został profesorem w Belfaście w Irlandii Północnej, a w 1977 roku przeszedł na Uniwersytet w Oxfordzie.
W 1980 roku został uhonorowany nagrodą Turinga, która jest w informatyce odpowiednikiem nagrody Nobla.


Profesor Hoare zaproponował także podejście do specyfikowania i dowodzenia poprawności programów zwane często logiką Hoare’a. Właściwości programu (lub fragmentu programu) Q opisuje się za pomocą pary predykatów P i R. Predykat P opisuje tzw. warunek wstępny, natomiast R jest warunkiem końcowym. Wyrażenie, które widzimy na slajdzie można przeczytać w następujący sposób: jeżeli jest spełniony warunek P, to po wykonaniu instrukcji Q spełniony będzie warunek R.
Oto bardzo prosty przykład. Jeżeli zmienna X ma wartość n, to po wykonaniu instrukcji przypisania zmiennej Y wyniku funkcji silnia od X, zmienna Y będzie miała wartość n!.
To podejście zostało wykorzystane w praktyce przy definicji języka ANNA służącego do specyfikowania programów zapisanych w języku Ada.
Potem przedstawię związane z nimi tzw. implementacje niestandardowe. Jest to dość ciekawe zjawisko o charakterze anomalii, z którego trzeba sobie zdawać sprawę.
Ostatnią część wykładu chciałbym poświęcić sieciom Petriego, bardzo ciekawej metodzie specyfikowania programów i systemów współbieżnych.
Zaczynamy od specyfikacji aksjomatycznych.

Załóżmy, że chcemy opracować elektroniczną książkę telefoniczną. Książka, jak to w przykładach akademickich bywa, będzie bardzo prosta: z każdym nazwiskiem będzie związany numer telefonu.
Przechodząc do oprogramowania będziemy potrzebowali trzy typy danych:
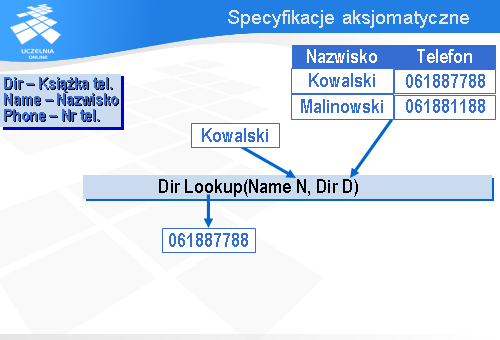
Nasza książka będzie oferować cztery operacje i każda z nich będzie funkcją. Najważniejszą operacją jest operacja Lookup (po angielsku „poszukaj”) odszukująca w książce telefonicznej numer telefonu podanego abonenta.
Operacja ta ma dwa parametry wejściowe: nazwisko abonenta N i książkę telefoniczną D, w której należy poszukać numer telefonu.
Wynikiem jest numer telefonu podanego abonenta.
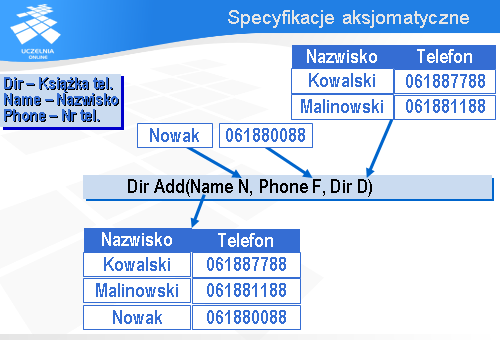
Aby móc dodawać nowych abonentów do książki telefonicznej wprowadzimy operację Add (po angielsku „dodaj”).
Operacja ta ma trzy parametry wejściowe: nazwisko abonenta N, numer telefonu F i książkę telefoniczną D, do której chcemy dodać informacje o tym abonencie.
Jako wynik dostajemy nową książkę telefoniczną z dopisaną informacją o nowym abonencie.

Skoro możemy dodawać nowych abonentów, to powinniśmy także móc usuwać abonentów. W tym celu wprowadzimy operację Delete (po angielsku „usuń”).
Parametrami wejściowymi dla tej operacji są:
W rezultacie dostajemy książkę telefoniczną, z której informacja o danym abonencie została usunięta.

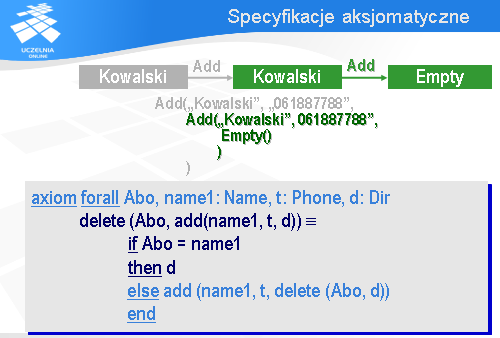
Zauważmy, że taką książkę telefoniczną, jak ją widzimy na slajdzie można otrzymać na bardzo wiele sposobów.
Na przykład można do pustej książki telefonicznej dodać informację o Kowalskim, a potem o Malinowskim.
W zapisie funkcyjnym można to przedstawić jako złożenie trzech operacji pokazanych na slajdzie.
Można też do pustej książki najpierw dodać informację o Malinowskim, a potem o Kowalskim.
W zapisie funkcyjnym wyglądałoby to tak, jak na slajdzie w prawym dolnym rogu.




Jeśli funkcja ma parametry wejściowe, to w sygnaturze opisuje się je na zasadzie iloczynu kartezjańskiego. Podaje się nazwy typów kolejnych parametrów oddzielając je między sobą symbolem „x ”. Sposób opisu 3-parametrowej funkcji Add jest przedstawiony na slajdzie.
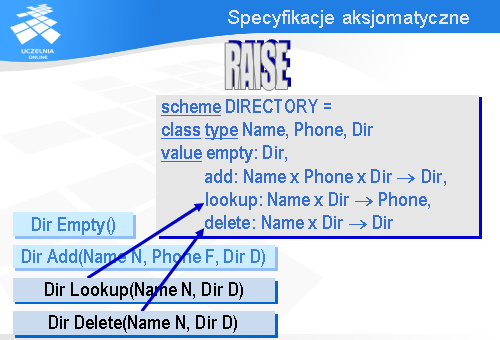

Przejdźmy teraz do sformułowania aksjomatów opisujących działanie tych funkcji. Jeżeli szukamy numeru telefonu abonenta Abo w pewnej książce telefonicznej
która powstała z książki d przez dodanie do niej informacji, że Abo ma numer telefonu t,
to oczywiście szukany numer telefonu jest równy t.
Formalnie można to zapisać jak na slajdzie.

Jeżeli szukamy numeru telefonu Abo w książce, która powstała z książki d przez dodanie informacji o innym abonencie niż Abo,
to musimy szukać dalej, czyli szukać informacji o abonencie Abo w „starej” książce d.
Formalnie, w notacji RAISE, można to zapisać za pomocą frazy ELSE pokazanej na slajdzie.

Kolejny aksjomat można sformułować następująco: usunięcie czegokolwiek z pustej książki telefonicznej daje pustą książkę telefoniczną.
Formalnie można to zapisać jak na slajdzie

Kolejny aksjomat, dotyczący usuwania, można by sformułować następująco: jeżeli jakaś książka powstała z książki d przez dodanie do niej informacji o numerze telefonu t abonenta Abo,
to usunięcie abonenta Abo z tej książki daje starą książkę d.
Za pomocą notacji RAISE można to zapisać w sposób pokazany na slajdzie.

Jeżeli dana książka telefoniczna powstała z książki d przez dodanie informacji o innym abonencie niż Abo, a my chcemy usunąć z książki Abo, to tego innego należy w książce pozostawić, a usunąć Abo ze starej książki d. Innymi słowy, należy ze starej książki d usnąć abonenta Abo i dodać do wyniku informację o tym innym abonencie.
Korzystając z notacji RAISE można to zapisać w sposób pokazany na slajdzie.


Załóżmy, że nasza książka telefoniczna ma dwa zapisy dotyczące abonenta Kowalskiego.

Ze specyfikacjami aksjomatycznymi wiąże się zjawisko o charakterze anomalii zwane implementacjami niestandardowymi. Postaram się to wyjaśnić na bardzo prostym przykładzie.
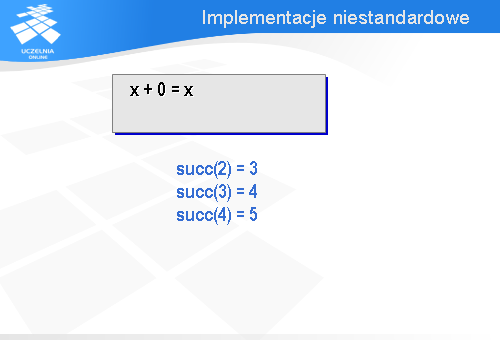
Załóżmy, że chcemy napisać specyfikację prostego pakietu wykonującego elementarne operacje arytmetyczne na liczbach naturalnych. Punktem wyjścia będzie dla nas aksjomatyczna definicja operacji arytmetycznych, którą można znaleźć w wielu książkach. Zawiera ona dwa aksjomaty. Po pierwsze, dodanie zera do dowolnej liczby x daje liczbę x.
W drugim aksjomacie występuje pojęcie następnika. Następnik jest to kolejna liczba naturalna względem podanej, np. następnikiem 2 jest 3, a następnikiem 3 jest 4. Niech funkcja succ(y) (od angielskiego „successor”, czyli następnik) podaje następnik liczby y.

Zgodnie z drugim aksjomatem dodanie do liczby x następnika liczby y daje następnik sumy liczb x i y.
Na przykład 2 + 4 można traktować jako sumę 2 i następnika 3. Zgodnie z tym aksjomatem 2 + 4 jest równe następnikowi 2 + 3. Jak wiemy, 2 + 3 = 5 i następnikiem 5 jest 6. Zatem faktycznie zgadza się: 2 + 4 jest równe 6.

Załóżmy, że stałą 0 będziemy realizować jako bezargumentową funkcję zero.
Funkcja succ będzie miała jeden argument będący liczbą naturalną i jej wynikiem też będzie liczba naturalna.
Operacja dodawania będzie realizowana jako funkcja plus, która będzie miała dwa argumenty będące liczbami naturalnymi i wynikiem będzie też liczba naturalna (dla uproszczenia posłużyłem się tutaj typem int, który obejmuje również liczby ujemne, ale z punktu widzenia problemu, o którym chcę powiedzieć nie ma to znaczenia).
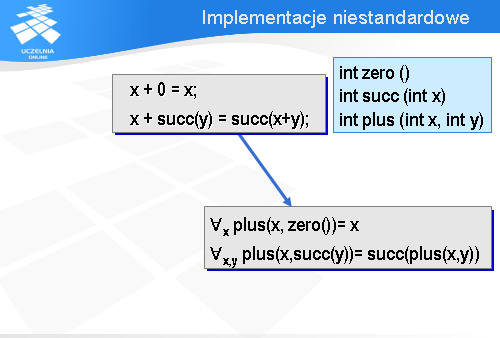
Uwzględniając przyjęty interfejs dla naszego mikro-modułu, przepisujemy oba nasze aksjomaty zastępując operator dodawania funkcją plus a stałą 0 funkcją zero.

Nasze oczekiwania są oczywiście takie, że funkcja plus zwróci dla argumentów 2 i 3 wartość 5. Ale czy na pewno zawsze tak będzie?
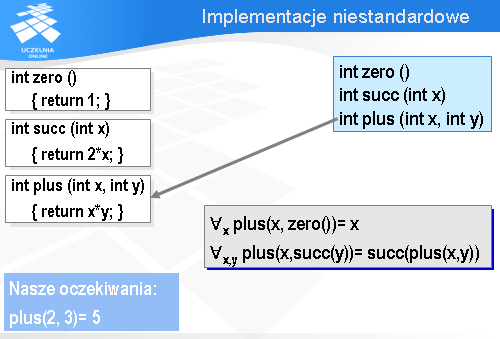
Załóżmy, że ktoś postanowił zrealizować nasz mikro-moduł w sposób niestandardowy. Funkcja zero zwraca zawsze wartość 1.
Funkcja następnika, succ, zwraca liczbę dwa razy większą od podanej.
Natomiast funkcja plus zwraca iloczyn podanych liczb.





Autor tego pomysłu, Carl Adam Petri, urodził się w 1926 roku w Lipsku.
W wieku 36 lat obronił rozprawę doktorską pt. „Komunikacja z automatami”, w której przedstawił pomysł opisu procesów współbieżnych za pomocą notacji graficznej, opartej na solidnych podstawach matematycznych. Koncepcja, nazwana sieciami Petri’ego, bardzo szybko uzyskała wręcz niesamowitą popularność i była stosowana nie tylko do opisu procesów obliczeniowych, ale także systemów transportowych, produkcyjnych i innych.
Od 1988 roku Carl Petri jest honorowym profesorem Uniwersytetu w Hamburgu.
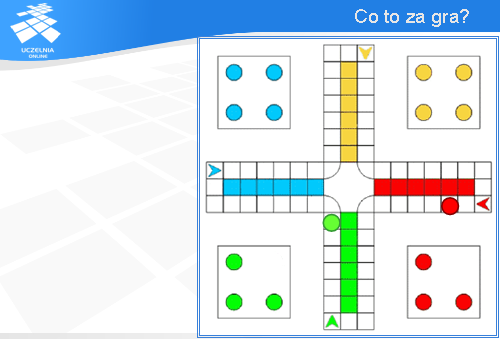
Być może inspiracją dla profesora Petri’ego były gry planszowe. Wiele z nich jest, w istocie, opartych na procesach współbieżnych. Na slajdzie mamy planszę do jednej z bardzo popularnych gier.
W grze tej może brać udział do czterech graczy. Każdy z nich ma po cztery pionki: jeden czerwone, drugi zielone itd.
Każdy pionek ma z góry wyznaczoną drogę do przebycia.
Jeden ruch odpowiada przesunięciu się na tej drodze o tyle pozycji, ile oczek pokazuje rzucona kostka. W przypadku zilustrowanym na slajdzie rzucona kostka pokazała dwa oczka.
Teraz do gry włączył się pionek zielony.
On ma swoją drogę do przebycia po tej planszy.
Jeśli rzucona kostka będzie miała 6 oczek,
to na planszy pojawi się następująca konfiguracja. Mamy zatem na jednej planszy jakby dwa procesy: czerwony, który jest o dwa miejsca bliżej celu, i zielony, który jest o sześć miejsc bliżej swojego celu. Pewnie Państwo już rozpoznaliście tę grę. Tak, to gra zwana chińczykiem.
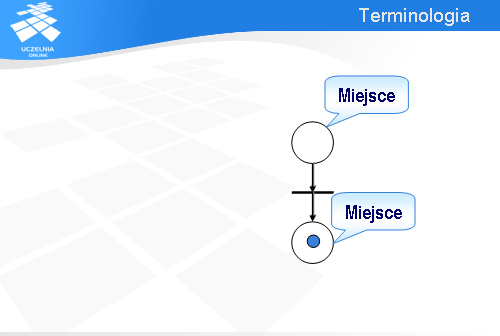
Oto najmniejsza sieć Petri’ego. Jak się za chwilę przekonamy, jest ona pod kilkoma względami bardzo podobna do planszy gry w chińczyka.
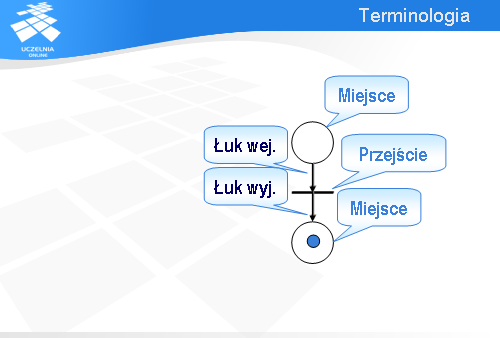
Po pierwsze, w sieci Petri’ego mamy miejsca oznaczane kółkami.
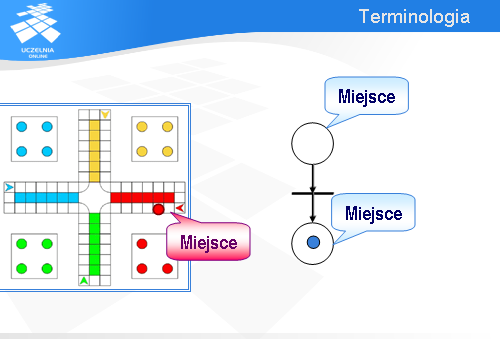
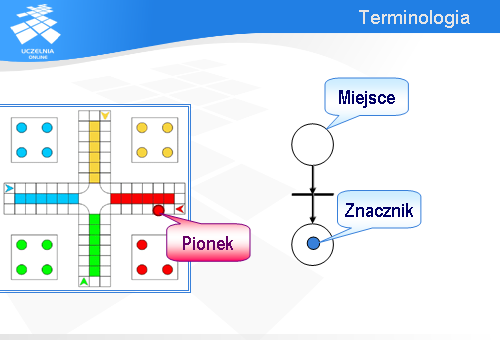
W sieci Petriego mamy znaczniki, które mogą przechodzić z miejsca do miejsca.
Są one odpowiednikami pionków w chińczyku.
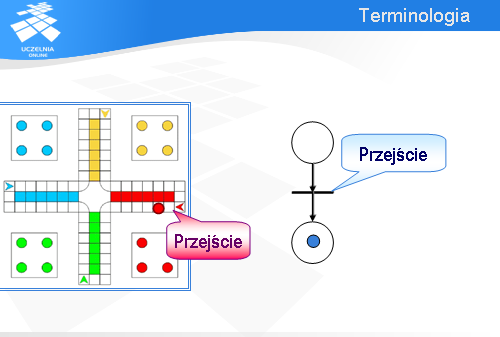
Znacznik przemieszczając się z jednego miejsca w drugie przechodzi przez tzw. przejście (niektórzy nazywają to tranzycją od ang. transition).
W chińczyku odpowiednikiem przejścia jest granica między dwoma miejscami. Nie ma ona w tej grze żadnego znaczenia, więc jest niezauważalna. W sieciach Petriego z przejściami mogą być związane różnego rodzaju akcje. Gdy znacznik przechodzi przez przejście, z którym związano akcję, to ta akcja jest wtedy wykonywana.
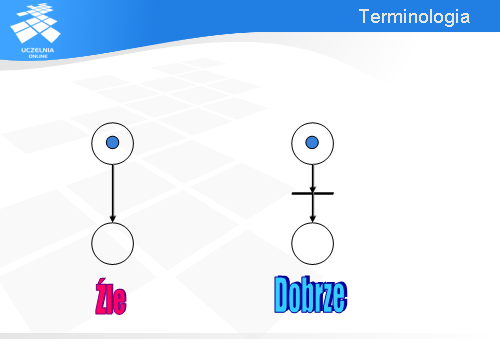
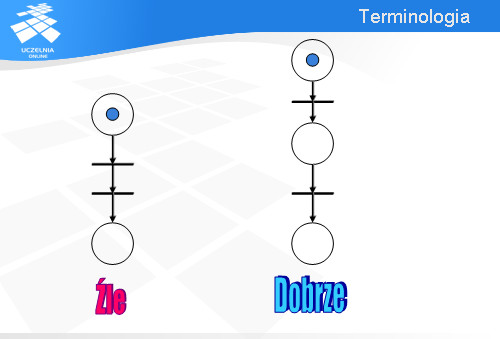
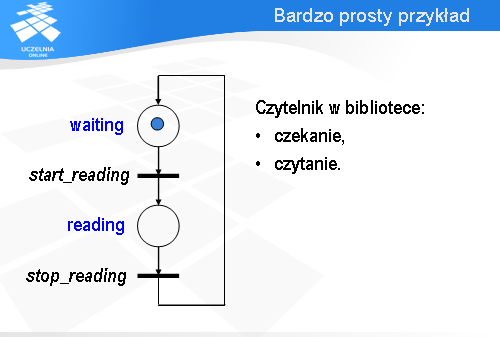
Rozważmy w charakterze przykładu proces opisujący zachowanie się czytelnika w bibliotece. Upraszczając możemy przyjąć, że czytelnik znajduje się w dwóch stanach: albo czeka na książkę, albo ją czyta. Możemy to zamodelować za pomocą następującej sieci Petriego.
Każdemu stanowi odpowiada jedno miejsce: z czekaniem związane jest miejsce waiting (czyli po angielsku „oczekujący”), natomiast z czytaniem - reading (po angielsku „czytający”). Czytanie jest poprzedzone wykonaniem akcji start_reading (zacznij czytanie), a kończy się wykonaniem akcji stop_reading (zakończ czytanie). Znacznik znajduje się w miejscu waiting , czyli nasz czytelnik teraz czeka.
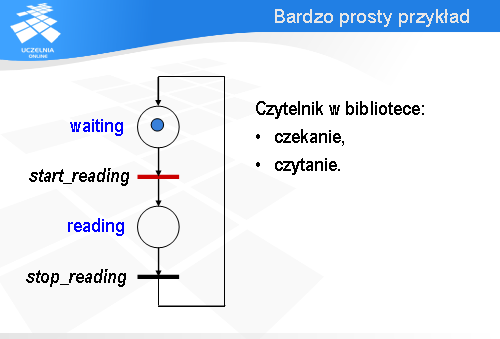
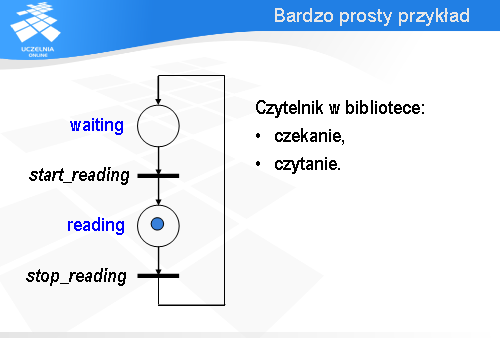
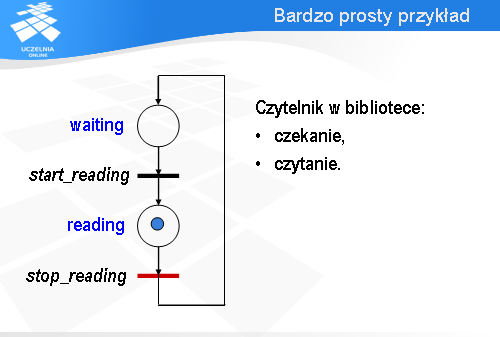
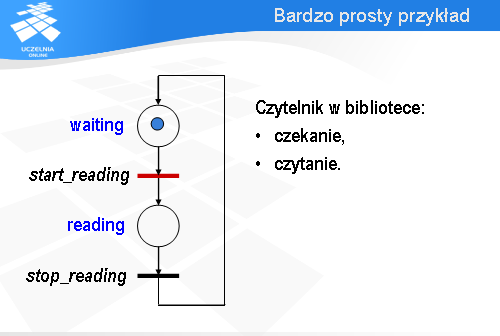
Po odpaleniu przejścia stop_reading znacznik przechodzi do miejsca waiting i przejście start_reading staje się gotowe do odpalenia. Zatem wróciliśmy do konfiguracji sieci, która była na samym początku.

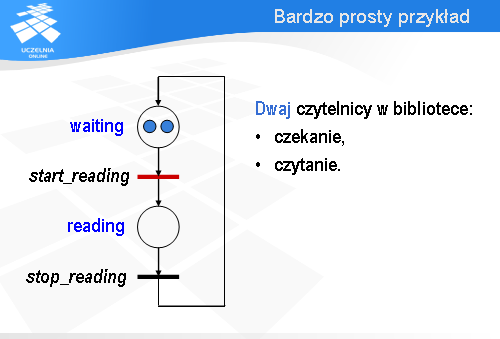
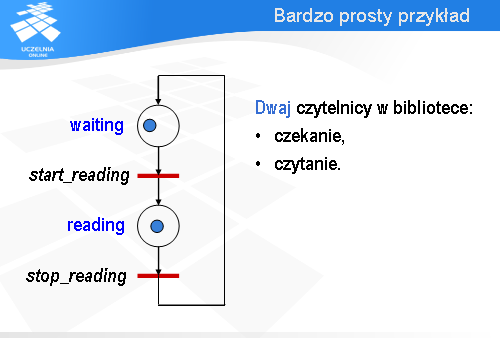
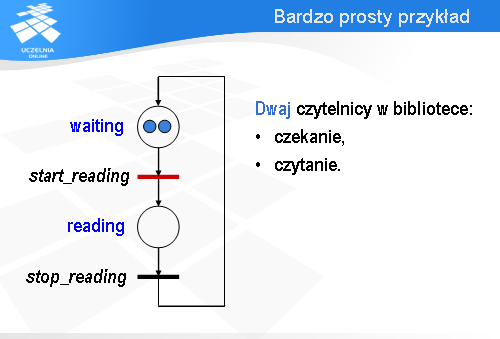
i wrócić do waiting .
Możliwy jest też inny wariant.
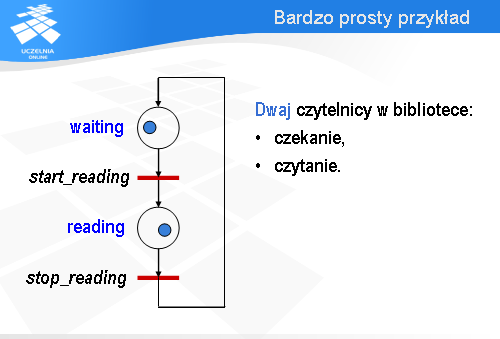
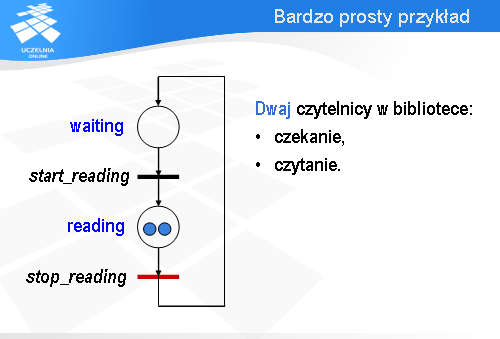
A drugi zaraz podąży za nim.
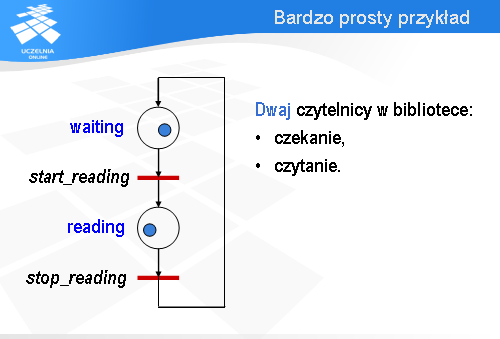
Potem znów jeden przechodzi przez stop_reading do waiting .
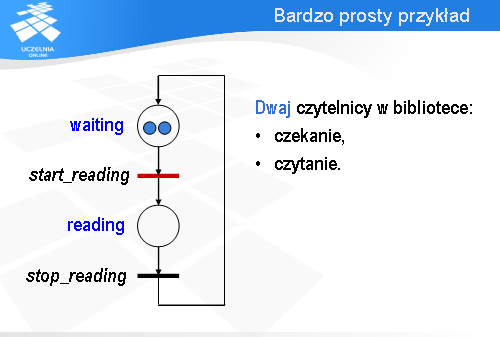
I po pewnym czasie drugi podąży za nim. Ta wielość możliwych zachowań (czyli indeterminizm) jest cechą charakterystyczną systemów współbieżnych i sieci Petri’ego, które takie systemy modelują.
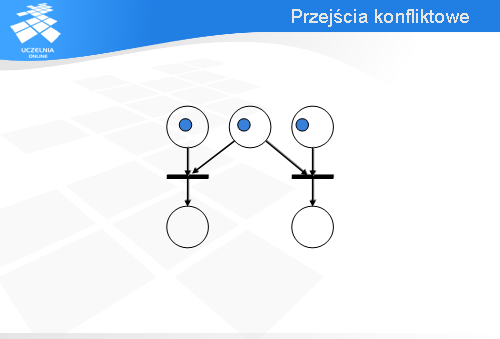
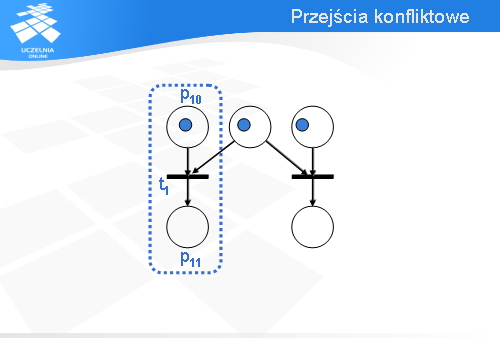
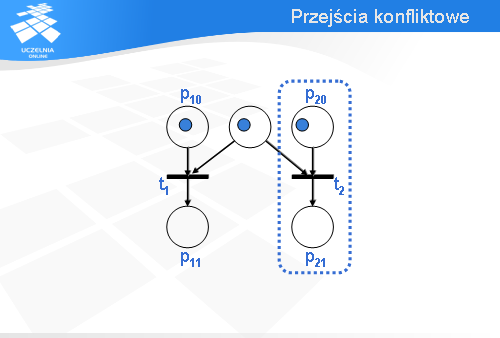
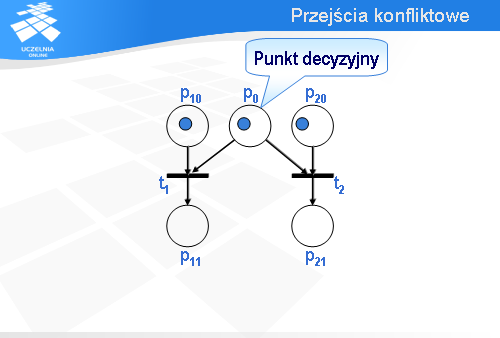
Miejsce p0 jest tzw. punktem decyzyjnym.
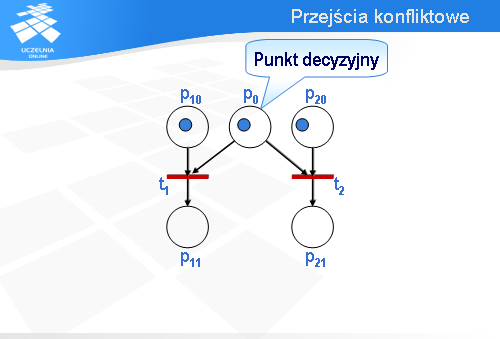
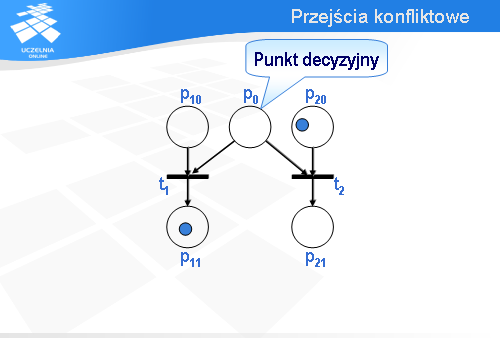
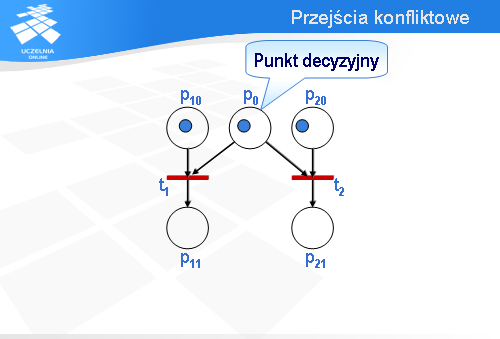
Wróćmy na chwilę do konfiguracji początkowej. Oczywiście, jest możliwe zachowanie alternatywne. Zamiast przejścia t1 może być odpalone przejście t2.
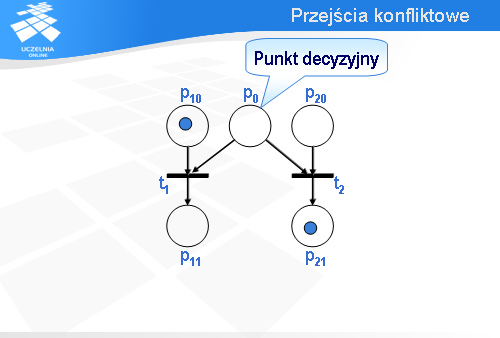
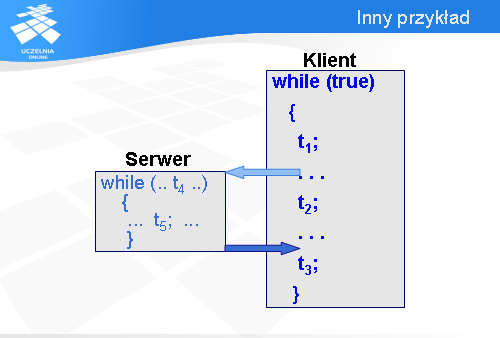
Spróbujmy teraz naszkicować, tytułem przykładu, model systemu pracującego w układzie klient-serwer.
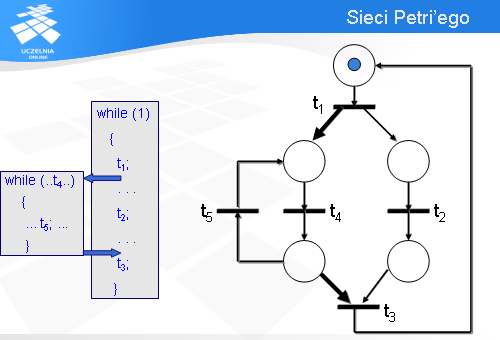
Klient pracuje w pętli nieskończonej. Wykonuje operację t1, potem jakieś nieistotne operacje pomocnicze, operację t2, znów nieistotne operacje pomocnicze i na końcu operację t3.
Serwer jest wywoływany przez klienta między operacjami t1 a t2. Po wywołaniu serwera klient niezależnie dalej prowadzi swoje obliczenia łącznie z operacją t2.
Obsługa wywołania jest realizowana przez serwer za pomocą pętli typu while. Aby sprawdzić, czy kontynuować obliczenia serwer wywołuje funkcję t4 (może to być np. sprawdzenie stanu bazy danych). Jeśli obliczenia mają być kontynuowane, to najpierw są wykonywane jakieś mało istotne operacje pomocnicze, potem operacja t5 i znów nieistotne operacje pomocnicze.
Po wyjściu z pętli while serwer kończy swoje obliczenia i przekazuje sterowanie do klienta, który nie wykona operacji t3 dopóki nie otrzyma wyników pracy serwera
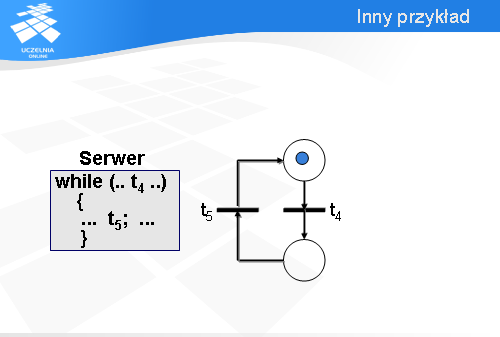
Zamodelowanie pracy serwera jest proste. Mamy do wykonania w pętli dwie operacje, zatem tworzymy sieć składającą się z dwóch przejść t1 i t2, dodajemy dwa miejsca i łączymy wszystko łukami tak, aby znacznik mógł krążyć po sieci w sposób zgodny z programem serwera.
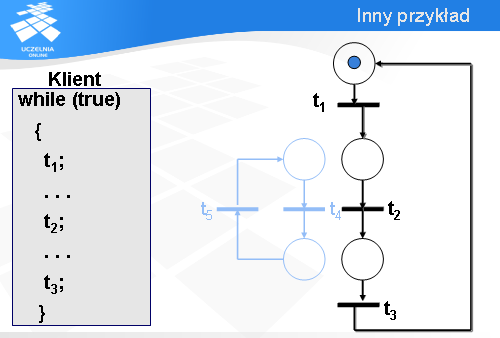
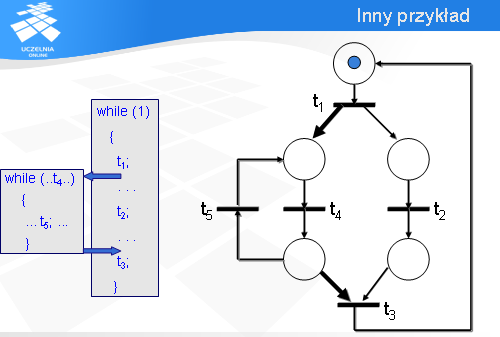
Jak teraz połączyć te dwa modele częściowe, aby dostać model całości? Jak się okazuje, nie jest to trudne.
Wystarczy dodać dwa łuki: łuk wyjściowy z tranzycji t1 i łuk wejściowy do tranzycji t3.
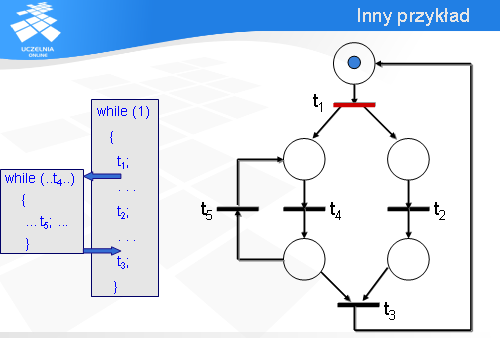
Na początku tranzycja t1 jest gotowa do odpalenia, czyli klient jest gotowy do wykonania operacji t1.
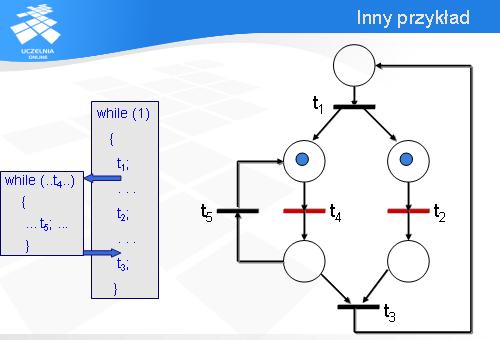
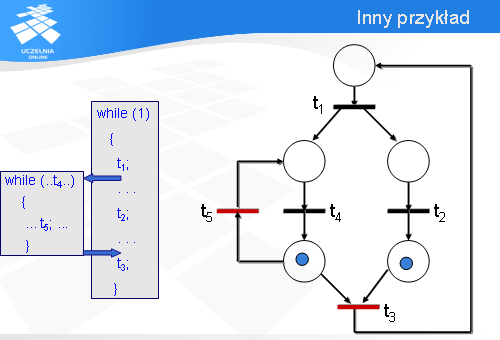
Wówczas znaczniki przemieszczają się i gotowe są do odpalenia tranzycje t5 oraz t3. Zauważmy, że lewe dolne miejsce pełni rolę punktu decyzyjnego: albo zostanie odpalona tranzycja t5 albo t3. Załóżmy, że serwer musi wykonać operację t5.
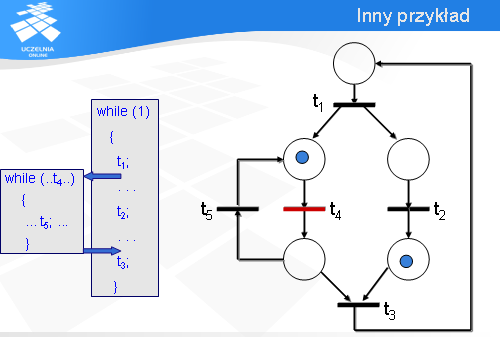
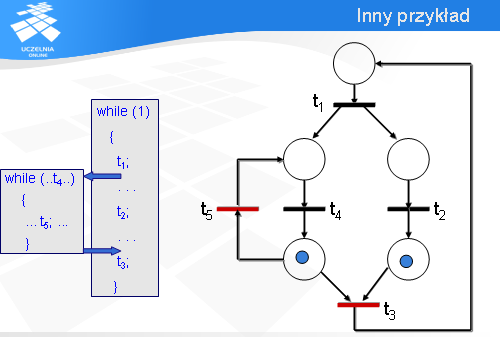
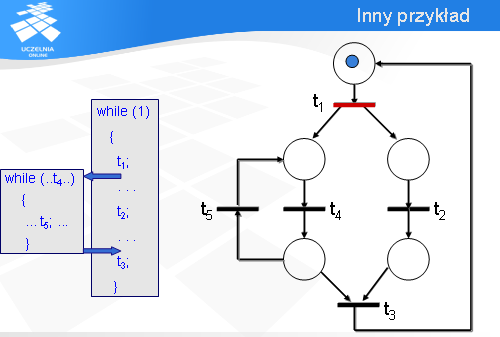
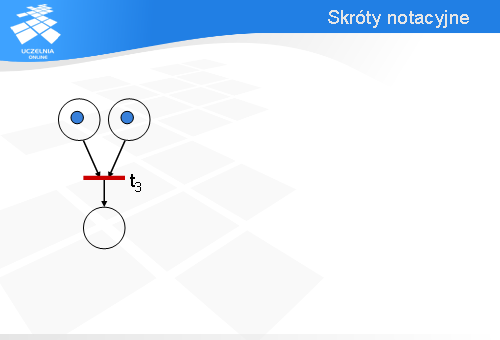
W sieci Petri’ego z ostatniego przykładu występował fragment z przejściem t3 przedstawiony na slajdzie.
Aby przejście t3 było gotowe do odpalenia znaczniki muszą być we wszystkich miejscach związanych z łukami wejściowymi.
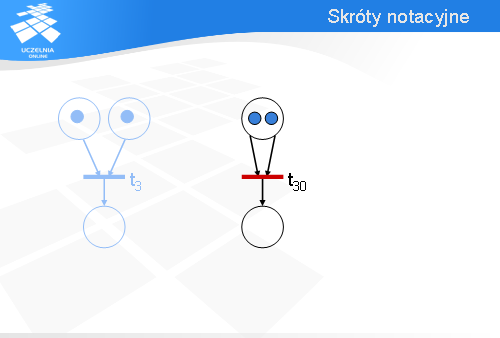
Rozważmy sieć Petri’ego z dwoma łukami wejściowymi wychodzącymi z tego samego miejsca. Ile (przynajmniej) znaczników musi być w górnym miejscu, aby tranzycja t30 była gotowa do odpalenia?
Tak jest – potrzeba przynajmniej dwóch znaczników, bo każdy łuk wejściowy „konsumuje” jeden znacznik.
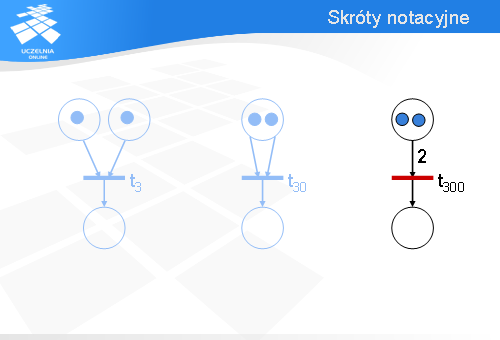
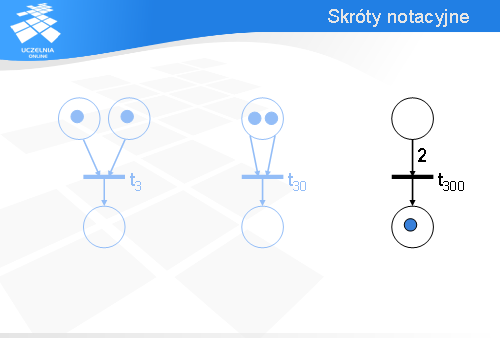
Zamiast rysować dwa łuki wejściowe wychodzące z tego samego miejsca można narysować jeden łuk wejściowy i dopisać przy nim liczbę dwa – tak jak na slajdzie.
Wówczas, aby tranzycja t300 była gotowa do odpalenia, w górnym miejscu muszą być przynajmniej dwa znaczniki.
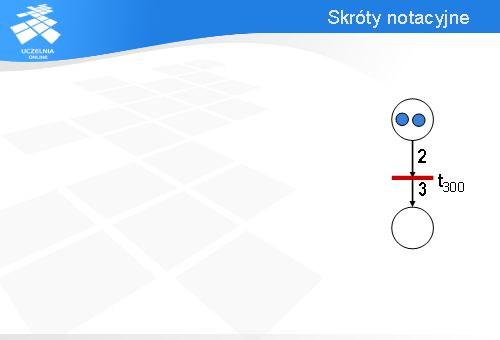
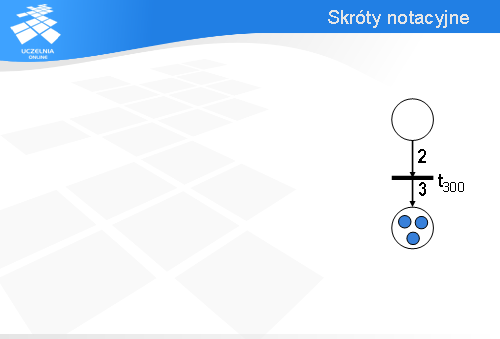

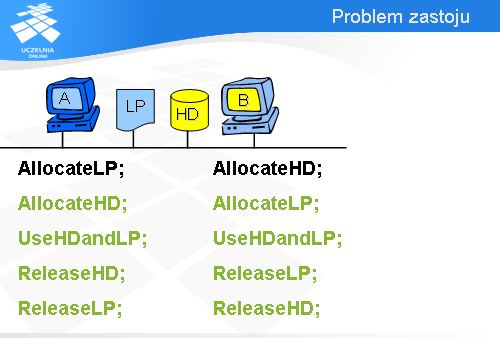
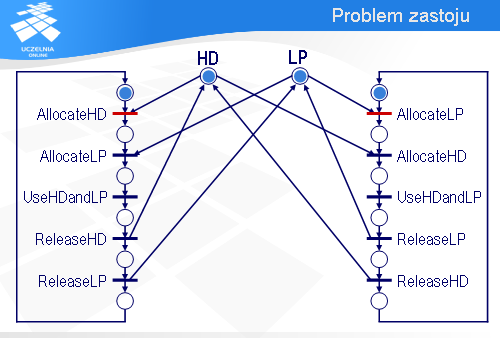
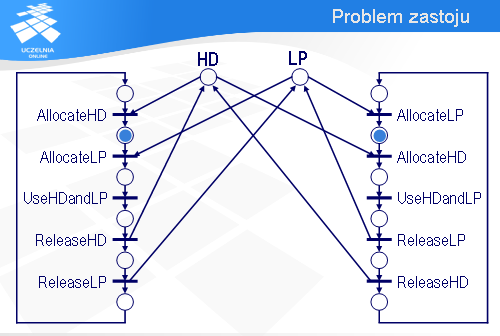
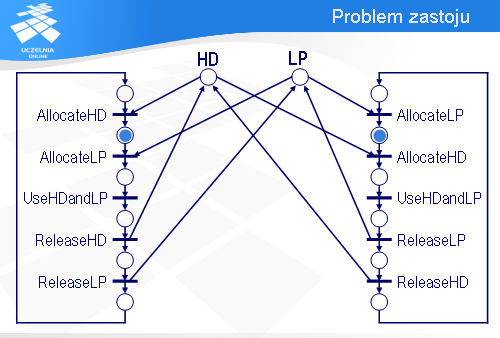
Spróbujemy teraz wykorzystać sieci Petri’ego do analizy systemu informatycznego pod kątem zastoju. Załóżmy, że w pewnym biurze są dwa komputery, A i B, które współdzielą drukarkę LP i dysk HD.
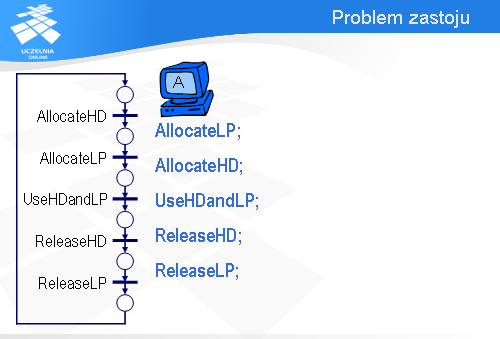
Najistotniejszy, z punktu widzenia naszej analizy, fragment oprogramowania komputera A można sprowadzić do sekwencji pięciu instrukcji.
Najpierw komputer A wykonuje operację AllocateLP, za pomocą której przydzielona zostaje mu drukarka LP (jeśli drukarka będzie zajęta, to wykonanie operacji AllocateLP będzie się przedłużało).
Potem komputer A wykonuje operację AllocateHD, w efekcie której zostaje mu przydzielony dysk HD.
Mając przydzieloną drukarkę LP i dysk HD, komputer A przysyła dane z dysku na drukarkę – jest to reprezentowane za pomocą operacji UseHDandLP.
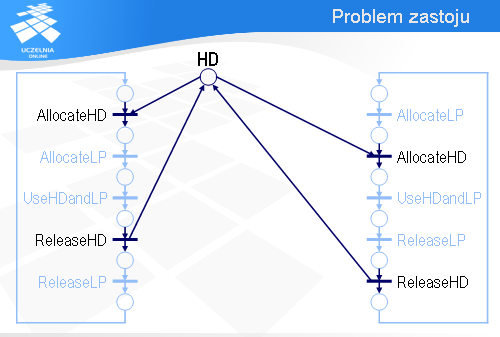
Po wykorzystaniu tych urządzeń komputer A najpierw zwalnia dysk HD,
a następnie drukarkę LP.
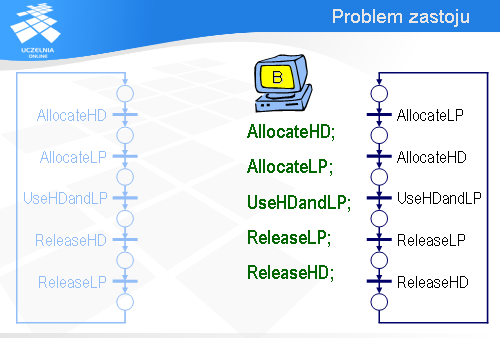
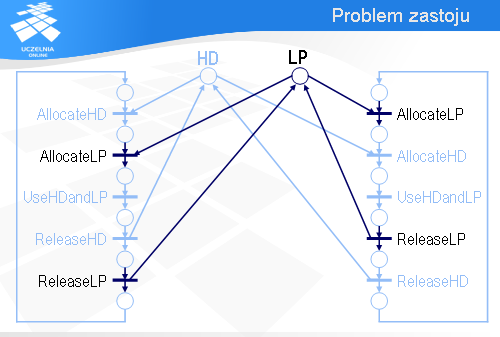
Program komputera B jest podobny. Najpierw jest sekwencja operacji przydzielających dysk HD i drukarkę LP.
Potem następuje wykorzystanie obu tych urządzeń.
A na końcu urządzenia zostają zwolnione.
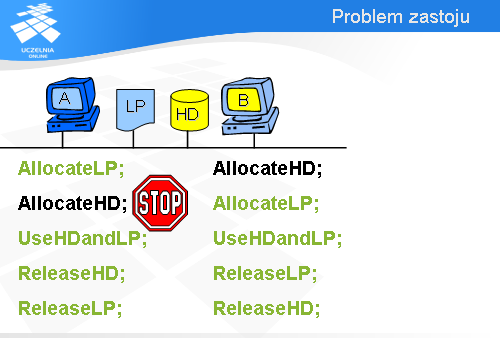
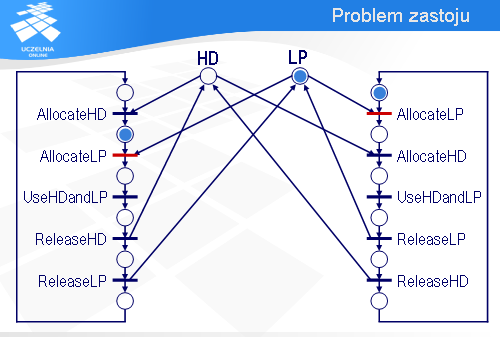
Jak nie trudno zauważyć, przedstawione rozwiązanie ma pewną wadę.