


Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia.
Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową. Jeżeli dany jest ciąg parami różnych liczb 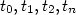 – węzłów interpolacyjnych i odpowiadających im punktom
– węzłów interpolacyjnych i odpowiadających im punktom 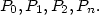 To poszukujemy krzywej wielomianowej
To poszukujemy krzywej wielomianowej takiej, że jest ona stopnia co najwyżej
takiej, że jest ona stopnia co najwyżej  oraz
oraz dla każdego
dla każdego  . Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:
. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:
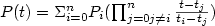
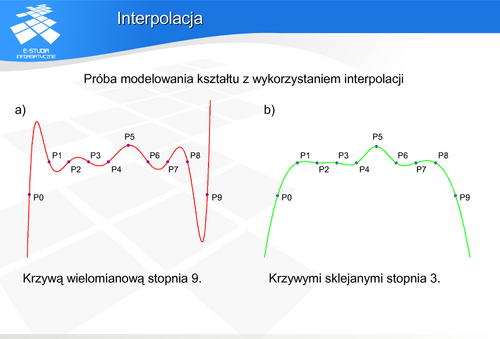
Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek a). Dodatkowo każdy fragment krzywej zależy od wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola nad kształtem krzywej pomiędzy węzłami jest trudna. Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne.

Wygodnym sposobem opisu krzywych i powierzchni jest opis parametryczny. W tym przypadku za pomocą doboru wartości parametru można zdefiniować dowolny fragment krzywej, a kierunek wzrostu parametru jednoznacznie określa np. kierunki stycznych połączonych fragmentów. Przykładowa czterolistna koniczynka jest narysowana na rysunku a) w postaci rozety czterolistnej :


dla

Na rysunku b) w postaci hipotrochoidy:
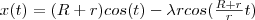
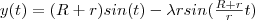
dla
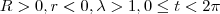
Często wykorzystywanymi powierzchniami są powierzchnie drugiego stopnia. Ich równanie uwikłane ma postać:
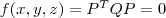
gdzie Q jest macierzą współczynników postaci
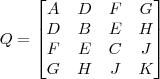
oraz

Przy czym dla każdej powierzchni drugiego stopnia jest znana reprezentacja parametryczna. Dla przykładowej hiperboloidy jednopowłokowej z prezentowanego rysunku:
Zalety stosowania powierzchni drugiego stopnia: Możliwość łatwego wyznaczenia wektora normalnego
![\cec N= [\frac{\delta f}{\delta x} \frac{\delta f}{\delta y} \frac{\delta f}{\delta z}]](images/EXTERN_0016.png)
Możliwość szybkiego wyznaczenia przecięcia powierzchni z prostą – efektywność stosowania w algorytmach związanych z metodą śledzenia promieni.
Możliwość szybkiego wyznaczenia  na podstawie
na podstawie  i
i 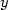 – przydatne w algorytmach eliminacji elementów zasłoniętych.
– przydatne w algorytmach eliminacji elementów zasłoniętych.
Wielomiany Bernsteina

Rysunek przedstawia wykresy wielomianów Bernsteina 2, 3, 4 i 5 stopnia. Najczęściej mamy do czynienia z wielomianami stopnia 3. W tym przypadku:

Ostatnia właściwość (zależność rekurencyjna) prowadzi do algorytmu wyznaczania punktów na krzywej bazującej na wielomianach Bernsteina.
 jest definiowana przez
jest definiowana przez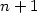 punktów
punktów 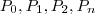 w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. Użytkownicy komputerów spotykają się z nią na co dzień w postaci fontów, których kształt jest projektowany właśnie z jej wykorzystaniem
w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. Użytkownicy komputerów spotykają się z nią na co dzień w postaci fontów, których kształt jest projektowany właśnie z jej wykorzystaniem

Wady:
- Brak możliwości reprezentacji krzywych stożkowych.
- Zmiana reprezentacji krzywej po rzutowaniu perspektywicznym.
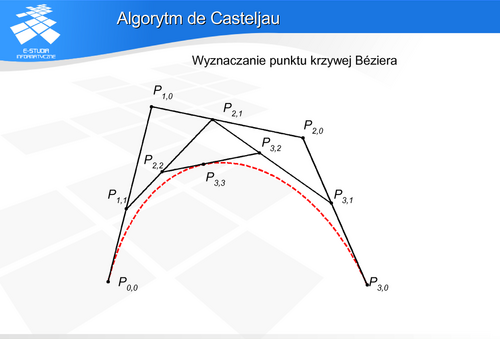
Algorytm de Casteljau wyznaczania punktu leżącego na krzywej Béziera na podstawie ciągu punktów kontrolnych 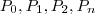
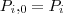 ;
;
 :=
:=  ;
;
Jeśli zadaniem jest wyznaczenie dużej liczby punktów leżących na krzywej Béziera to tańszym obliczeniowo rozwiązaniem będzie przejście w wielomianach Bernsteina do postaci naturalnej wielomianu i obliczanie jego wartości algorytmem Hornera.
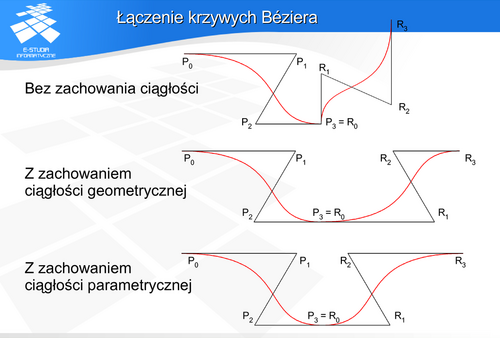
Rozpatrzmy dwa segmenty krzywych 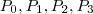 i
i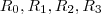 , połączone w punkcie
, połączone w punkcie  . Jeżeli punkty
. Jeżeli punkty  są współliniowe mówimy o ciągłości geometrycznej G1 krzywej (rysunek a). Jeżeli punkty
są współliniowe mówimy o ciągłości geometrycznej G1 krzywej (rysunek a). Jeżeli punkty  są współliniowe i sąsiednie odcinki łamanej są równej długości
są współliniowe i sąsiednie odcinki łamanej są równej długości  to mówimy o ciągłości parametrycznej C1 krzywej (rysunek b).
to mówimy o ciągłości parametrycznej C1 krzywej (rysunek b).

 , natomiast krzywe trójwymiarowe będą opisane w przestrzeni
, natomiast krzywe trójwymiarowe będą opisane w przestrzeni  .
.
Krzywa taka ma następujące cechy: Dana krzywa może mieć nieskończenie wiele reprezentacji we współrzędnych jednorodnych. Pomnożenie wszystkich wag przez tę samą stałą różną od zera nie zmienia krzywej. Krzywa wymierna jest uogólnieniem krzywej wielomianowej. Dla równej wartości wszystkich wag otrzymujemy krzywą wielomianową Béziera. Konstrukcja krzywej wymiernej jest niezmiennicza afinicznie. Krzywa wyznaczona na podstawie ciągu punktów kontrolnych jest taka sama jak krzywa wyznaczona na podstawie ciągu punktów kontrolnych poddanych przekształceniom afinicznym. Zmieniając odpowiednio wagi można uzyskać wszystkie krzywe stożkowe. Ta cecha była nieosiągalna w przypadku krzywych wielomianowych Béziera.

 o współczynnikach odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są przedziałami stopnia
o współczynnikach odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są przedziałami stopnia  , co nie jest związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście przedziałami w tym przypadku) od liczby punktów kontrolnych.
, co nie jest związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście przedziałami w tym przypadku) od liczby punktów kontrolnych.
Zakłada się, że węzły  są uporządkowane niemalejąco tzn.
są uporządkowane niemalejąco tzn. 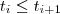 co oznacza, że mogą istnieć równe węzły (wielokrotne). Przyjmuje się wtedy, że 0/0=0. Takie założenia generalnie definiują krzywą dla węzłów które nie musza być równoodległe. Jednocześnie możliwość dodania (wstawienie) węzła pomiędzy dwa już istniejące, lub zwielokrotnienia węzła daje dodatkowe możliwości wpływania na kształt krzywej. Czasami jednak rozpatruje się krzywe o węzłach równoodległych. Istnieje algorytm de Boora i Coxa wyznaczania punktów krzywej B-sklejanej (analogiczny do algorytmu de Casteljau krzywej Béziera). Jeśli wyznaczanych jest wiele punktów krzywej to tańszym rozwiązaniem będzie obliczenie współczynników postaci naturalnej wielomianu w kolejnych podprzedziałach i skorzystanie z algorytmu Hornera.
co oznacza, że mogą istnieć równe węzły (wielokrotne). Przyjmuje się wtedy, że 0/0=0. Takie założenia generalnie definiują krzywą dla węzłów które nie musza być równoodległe. Jednocześnie możliwość dodania (wstawienie) węzła pomiędzy dwa już istniejące, lub zwielokrotnienia węzła daje dodatkowe możliwości wpływania na kształt krzywej. Czasami jednak rozpatruje się krzywe o węzłach równoodległych. Istnieje algorytm de Boora i Coxa wyznaczania punktów krzywej B-sklejanej (analogiczny do algorytmu de Casteljau krzywej Béziera). Jeśli wyznaczanych jest wiele punktów krzywej to tańszym rozwiązaniem będzie obliczenie współczynników postaci naturalnej wielomianu w kolejnych podprzedziałach i skorzystanie z algorytmu Hornera.
Właściwości krzywych B-sklejanych

Pierwsza właściwość – zerowanie funkcji sklejanej poza przedziałem
 jest bardzo istotna dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów. Rozpatrzmy podprzedział
jest bardzo istotna dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów. Rozpatrzmy podprzedział  dla
dla  niezerowe są tylko funkcje
niezerowe są tylko funkcje  o indeksach
o indeksach  . W takim przedziale wartość
. W takim przedziale wartość 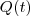 , a tym samym kształt krzywej, zależy tylko od punktów kontrolnych
, a tym samym kształt krzywej, zależy tylko od punktów kontrolnych  . Z drugiej strony punkt kontrolny
. Z drugiej strony punkt kontrolny 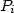 wpływa jedynie na fragment krzywej odpowiadający
wpływa jedynie na fragment krzywej odpowiadający  .
.
Indeks  zmienia się od 0 do
zmienia się od 0 do  , natomiast
, natomiast  od 0 do
od 0 do  . Cały zakres takiej krzywej definiują więc węzły:
. Cały zakres takiej krzywej definiują więc węzły:  . Ale danych jest
. Ale danych jest punktów kontrolnych (de Boora). Punkty
punktów kontrolnych (de Boora). Punkty  definiują krzywą dla
definiują krzywą dla  , natomiast punkty
, natomiast punkty  definiują krzywą dla
definiują krzywą dla  . Węzły
. Węzły  oraz
oraz nazywane są węzłami brzegowymi. Jeśli krzywa jest otwarta, to znaczy
nazywane są węzłami brzegowymi. Jeśli krzywa jest otwarta, to znaczy 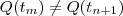 , i
, i  oraz
oraz to krzywa przechodzi przez końcowe punkty kontrolne, czyli
to krzywa przechodzi przez końcowe punkty kontrolne, czyli  oraz
oraz  . Podobnie jak było w przypadku krzywych Béziera, styczne do krzywej w punktach końcowych mają kierunek końcowych odcinków łamanej kontrolnej. Dla krzywej zamkniętej przyjmuje się, że punkty de Boora i węzły kontrolne są cykliczne
. Podobnie jak było w przypadku krzywych Béziera, styczne do krzywej w punktach końcowych mają kierunek końcowych odcinków łamanej kontrolnej. Dla krzywej zamkniętej przyjmuje się, że punkty de Boora i węzły kontrolne są cykliczne  .
.

Krzywe wymierne dają możliwość wykreślenia dowolnej krzywej stożkowej. .Konstrukcja wykorzystująca funkcje sklejane pozwala opisywać krzywą wielomianami, których stopień jest niezależny od liczby punktów kontrolnych. Wpływ punktu kontrolnego na kształt krzywej istnieje tylko w zakresie lokalnym. Dodatkowo wagi każdego punktu kontrolnego pozwalają na precyzyjne zmiany kształtu krzywej (też lokalnie). Krzywe wymierne są niezmiennicze względem przekształceń obrotu, skalowania i przesunięcia oraz przekształcenia perspektywicznego punktów kontrolnych.


Wykorzystując bazę wielomianów Hermite’a otrzymamy krzywe i powierzchnie Hermite’a. Płaty Coonsa są definiowane za pomocą czterech krzywych brzegowych mających wspólne punkty narożne oraz interpolacji między nimi. Powierzchnie Gordona są uogólnieniem płatów Coonsa,. definiują powierzchnię za pomocą dwóch wzajemnie przecinających się rodzin krzywych. Stosowane jest również modelowanie kształtu powierzchni w oparciu o fragmenty trójkątne. Zarówno w postaci powierzchni Béziera jak i B-sklejanej.


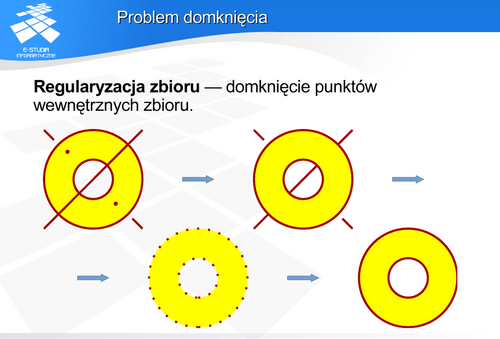
Zaproponowany zestaw właściwości bryły jest pewnym kompromisem między swobodą projektowania a zastosowaniami praktycznymi, kompromisem, który daje przy tym możliwość efektywnego wspomagania projektowania. Przykładem jak należy rozumieć ten kompromis jest jednorodność topologiczna. Z jednej strony nie ma w zasadzie żadnych przeciwwskazań w grafice komputerowej aby tworzyć obiekty niejednorodne (np. krzesło w postaci trójwymiarowego sześciennego siedziska połączonego z dwuwymiarowym prostokątnym oparciem). Ale jednocześnie ujednolicenie opisu może uprościć podejście do różnie definiowanych elementów. Natomiast jeśli popatrzymy na problem od strony praktycznej ; technologicznie realizacyjnej, to okaże się, że problem w zasadzie nie istnieje ponieważ żyjemy wśród obiektów trójwymiarowych jednorodnych topologicznie i praktyczne wykonanie prostokątnego oparcie dla rozpatrywanego krzesła i tak będzie wymagało określenia trzeciego wymiaru – jego grubości. Jeśli już nawet dla spełnienia wizji projektanta jest niezbędne istnienie niejednorodności topologicznej to prościej jest założyć, że w ramach jednej bryły zachowujemy jednorodność i w ostateczności dopuszczamy zestawienie różnych brył w ramach jednego procesu. Chociaż i tak w efekcie końcowym na etapie technologii zostanie to ujednolicone. Drugim elementem opisu właściwości bryły na który warto zwrócić uwagę jest domknięcie bryły. To co widzimy obserwując dowolny przedmiot jest efektem odbicia światła od powierzchni tego przedmiotu. Jeśli zostanie on przekrojony to zobaczymy powierzchnię przekroju – to znaczy będzie to nowy brzeg powstały przecięcia. Powierzchnia brzegu obiektu jest więc bardzo istotna w procesie rysowania – wizualizacji obiektu.

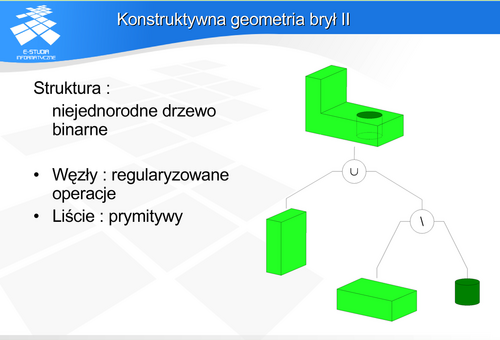

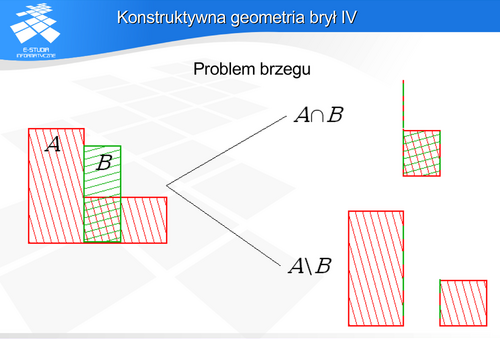
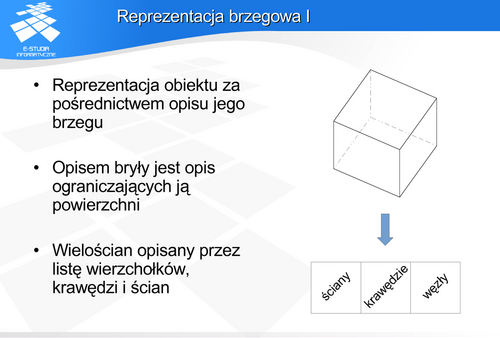
Dla modelu wielościennego istotnym problemem jest organizacja struktury danych zapamiętującej obiekt. Realizowane jest to w postaci list lub tablic ścian, krawędzi i wierzchołków. Pamiętanie powiązań między elementami obiektów prowadzi do struktur redundantnych. Wiąże się to oczywiście ze wzrostem kosztu pamięciowego. Czasami celowo wprowadzane są struktury redundantne w celu przyspieszenia wyszukania elementów. Takimi strukturami są na przykład DCEL (double connected edg list) i struktura krawędziowa Baumgarta. Są to struktury, w których deskryptory krawędzi zawierają wskazania na sąsiednie krawędzie, węzły i ściany.
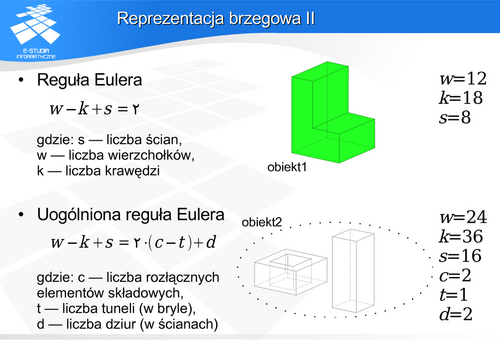
Dla każdego wielościanu zwykłego spełniona jest reguła Eulera. Rozszerzoną klasę obiektów - rozmaitości dwuwymiarowych obowiązuje uogólniona (rozszerzona) reguła Eulera. Należy jednak pamiętać że spełnienie tych warunków jest warunkiem koniecznym ale niewystarczającym przynależności do odpowiedniej klasy. Na przykład sześcian, do którego krawędzi doczepiono jeszcze jeden prostokąt nie jest już wielościanem zwykłym ale regułę Eulera (podstawową) spełnia.
Reprezentacja brzegowa jest czasem łączona w systemach modelowania z konstrukcyjną geometrią brył.
Reprezentacja z przesunięciem

Reprezentacja z przesunięciem nie stanowi samodzielnego sposobu opisu. Najczęściej jest łączona z reprezentacją powierzchniową i służy do definicji położenia węzłów siatki wielokątów. Ewentualnie (rzadziej) jest łączona z konstrukcyjną geometrią brył.
Podział przestrzeni

Woksel jest najmniejszym elementem przestrzeni analogicznym do piksela na płaszczyźnie. Można zdefiniować obiekt wskazując, które woksele on zajmuje. Taka reprezentacja jest dekompozycją na komórki, które tworzą regularną siatkę w przestrzeni. Podstawową cechą reprezentacji tego typu jest aproksymacja kształtu z zadana rozdzielczością. Struktura danych opisująca tak dekomponowaną bryłę będzie listą zajętych komórek. Podobny efekt można uzyskać strukturą hierarchiczną – drzewem ósemkowym wskazując w przestrzeni kolejne prostopadłościenne elementy będąca wielokrotnością woksela. W tym przypadku jednak struktura danych (drzewo ósemkowe) da efektywniejszy sposób zapisu (mniejszy koszt pamięciowy). Natomiast aproksymacja kształty z zadana rozdzielczością wokselową będzie identyczna. Alternatywą dla drzewa ósemkowego mogłoby być drzewo podziału binarnego (ang. BSP tree – binary space partitioning tree), w którym na każdym etapie podziału można wskazać którą półprzestrzeń reprezentuje dany fragment obiektu. Drzewa tego typu nie są jednak stosowane jako samodzielne systemy modelowania. SA natomiast wykorzystywane w algorytmach eliminacji elementów zasłoniętych.
Porównanie reprezentacji

Dokładność. Jeśli na scenie znajdują się obiekty wielościenne to reprezentacje wielościenne mogą dać dokładny opis obiektu. W pozostałych przypadkach tylko reprezentacja powierzchniowa z opisem kształtu za pomocą powierzchni Béziera, B-sklejanych, lub funkcji wymiernych może dać dokładny opis. Z reguły mamy do czynienia z pewną aproksymacją zależną np. od rozdzielczości siatki wokseli.
Dziedzina (zakres stosowania). Podział przestrzeni może być stosowany do dowolnych obiektów, przy czym zawsze będzie istniał problem aproksymacji zależny od siatki wokselowej. Pozostałe metody reprezentacji mogą być stosowane do określonej klasy obiektów. Na przykład w konstrukcyjnej geometrii brył klasa reprezentowanych obiektów bardzo silnie zależy od zastosowanego zestawu prymitywów.
Jednoznaczność/unikatowość. W zasadzie tylko podział przestrzeni za pomocą drzewa ósemkowego i reprezentacja wokselowa zapewniają unikatowośc reprezentacji w tym sensie, że istnieje tylko jeden zestaw wokseli reprezentujący dany obiekt. W pozostałych systemach modelowania istnieje wiele możliwości opisu tego samego obiektu. Szczególnym przypadkiem jest konstruktywna geometria brył gdzie dany obiekt można uzyskać nie tylko korzystając z różnych drzew, ale także z różnych zestawów prymitywów.
Poprawność. Podział przestrzeni jest zawsze poprawny – zawsze uzyskamy poprawny fragment przestrzeni. Pytanie oczywiście czy jest to ten fragment o który chodziło konstruktorowi. W pozostałych przypadkach wymagane jest sprawdzenie czy wynik definiowania/operacji jest poprawnym obiektem w danej klasie. Najtrudniejsze do sprawdzenia są opisy reprezentacji powierzchniowej.
Efektywność. Najprostsze w reprezentacji są metody wokselowe, gdyż pozwalają na szybkie manipulowanie takimi obiektami. Również konstruktywna geometria brył daje prosty nieprzetworzony (wymagający przetworzenia w trakcie np. rysowania) mechanizm, pozwalający dodatkowo na szybką modyfikacje obiektów.
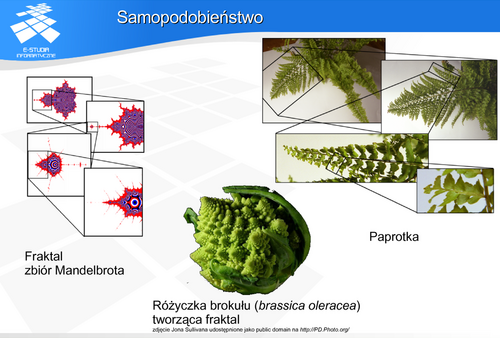
Często klasyfikuje się to pojęcie jako:
Samopodobieństwo dokładne – mówimy o nim wtedy, kiedy występuje wierna kopia powiększonego lub pomniejszonego fragmentu. Taką cechę mają fraktale IFS.
Quasi-samopodobieństwo – gdy występuje przybliżona kopia powiększonego lub pomniejszonego fragmentu. Charakterystyczne dla wielu fraktali definiowanych pewną zależnością rekurencyjną definiującą położenie punktów w przestrzeni.
Samopodobieństwo statystyczne – tę cechę mają fraktale losowe.
Rysunek z lewej strony pokazuje jeden z najbardziej znanych fraktali - tak zwany zbiór Mandelbrota. Zbiór ten powstaje przez interpretację barwami właściwości ciągu liczb zespolonych postaci  .
.
Modelowanie fraktalne
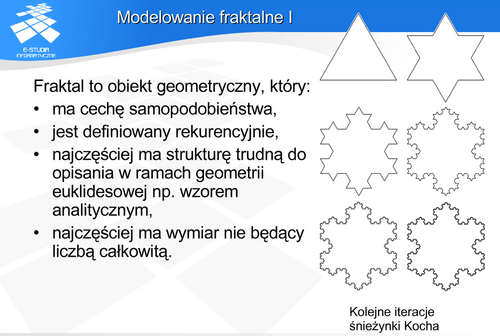
Problemem pozostaje wymiar takiej krzywej. Dla fraktali określa się wymiar Hausdorffa. F.Hausdorf – matematyk niemiecki zaproponował pojęcie wymiaru jako miarę wzrostu liczby kul (lub kół na płaszczyźnie) o promieniu  potrzebnych do pokrycia danego zbioru przy
potrzebnych do pokrycia danego zbioru przy  dążącym do zera. Wymiar Hausdorffa nigdy nie jest mniejszy niż wymiar topologiczny danego zbioru. Dla fraktali jest liczbą ułamkową. Sniezynka Kocha ma wymiar d=log4/log3=1,2618…
dążącym do zera. Wymiar Hausdorffa nigdy nie jest mniejszy niż wymiar topologiczny danego zbioru. Dla fraktali jest liczbą ułamkową. Sniezynka Kocha ma wymiar d=log4/log3=1,2618…
Fraktale stosuje się w grafice komputerowej do modelowania kształtu obiektów naturalnych wykazujących samopodobieństwo. Przykładem może być modelowanie krajobrazu. Fourier, Fussel i Carpenter zaproponowali zastosowanie iteracyjnego podziału do generowania fraktalnej góry. Jeśli podstawę góry będziemy dzielić systematycznie na pół, to po odpowiedniej liczbie iteracji uzyskamy punkty o zadanej dokładności. Wysokość dla każdego punktu podziału określa się na podstawie wysokości punktów poprzedniego kroku iteracji oraz pewnej funkcji zaburzenia. W zależności od przyjętej funkcji zaburzenia można w ten sposób otrzymać odpowiedni charakter zmian wysokości (łagodne pagórki lub ostre szczyty).
Innym zastosowaniem fraktali w grafice i przetwarzaniu obrazów jest kompresja fraktalna.
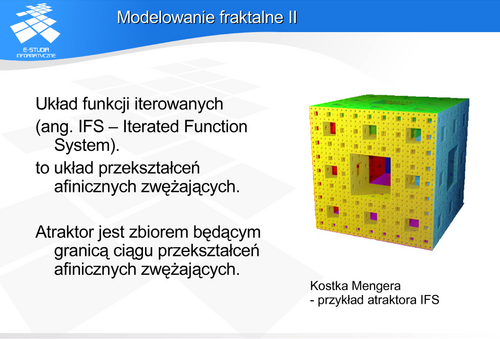
Metryka Hausdorffa określa odległości między zbiorami. Jeśli rozpatrzymy dwa zbiory A i B, to odległością d(A,B) punktu a ze zbioru A od zbioru B jest najmniejsza odległość spośród odległości tego punktu od wszystkich punktów zbioru B. Odległością d(A,B) zbioru A od zbioru B jest to największa odległośc spośród odległości punktu zbioru A od zbioru B. Metryka Hausdorfa h(A,B) jest określona wyrażeniem: h(A,B)=max(d(A,B), d(B,A))
Atraktory rozpatrywane są w przestrzeni metrycznej zupełnej, w której obowiązuje metryka Hausdorffa.
Modelowanie z wykorzystaniem gramatyk
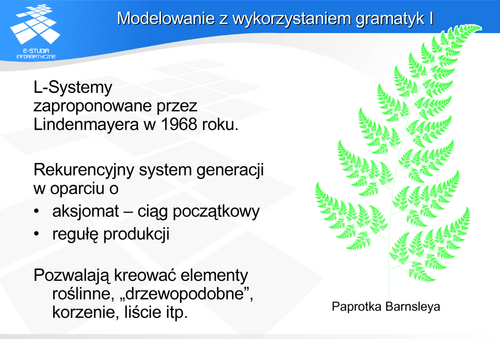
Na tej samej zasadzie można opisać grafikę żółwia rozkładając ruch pióra na proste reguły sterowania. Warto zwrócić uwagą na fakt, że również fraktale takie jak śnieżynka Kocha czy dywan Sierpińskiego można wygenerować za pomoca L-systemu.
Na przykład dla śnieżynki Kocha (dla pojedynczego boku startowego trójkąta !)
aksjomat: F
reguła produkcji: F -> F-F++F-F
gdzie F oznacza ruch do przodu z rysowaniem, - oznacza obrót w lewo o zadany kąt  , + oznacza obrót w prawo o zadany kąt
, + oznacza obrót w prawo o zadany kąt  . Dla śnieżynki Kocha
. Dla śnieżynki Kocha  wynosi 60 stopni.
wynosi 60 stopni.
Paprotka Barnsleya jest chyba najbardziej znanym przykładem wykorzystania gramatyk do modelowania roślin.
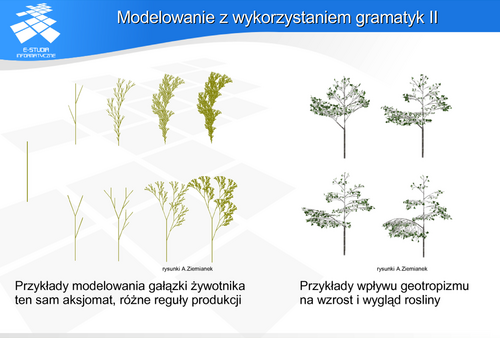
W opisie reguł produkcji wykorzystuje się takie symbole atrybutów jak długość i szerokość odcinka czy barwę. Pozwala to dość swobodnie definiować reguły wzrostu.
L-system można niezależnie uzupełnić o dodatkowe zasady „obowiązujące” roślinę w trakcie wzrostu. Pozwala to symulować naturalne zjawiska takie jak tropizm (naturalne kierowanie się rośliny w kierunku słońca) i geotropizm (reakcja wzrostowa roślin na siłę ciężkości).
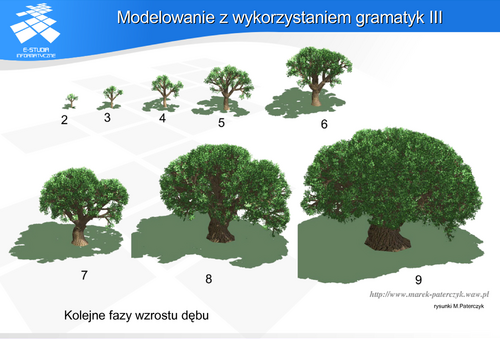
Samopodobieństwo roślin jest wynikiem ich wzrostu – w procesie wzrostu rośliny łatwo pokazać powtarzalność odpowiednich struktur. Projektując opis wzrostu (gramatykę) dla danego organizmu należy uwzględnić naturalne cechy tego organizmu. Na przykład dla drzewa byłyby to przede wszystkim: liczba rozgałęzień, wysokość drzewa i długości przyrostów między rozgałęzieniami, grubości konarów i gałęzi, kąty jakie tworzą młode gałęzie ze starymi. Oczywiście wizualizacje powinny także uwzględniać kształty, barwy i faktury poszczególnych elementów – liści, kory, i to na różnych etapach wzrostu. Ponieważ proces symulacji wzrostu organizmu jest dość skomplikowany można wykorzystać zarówno zdjęcia jak i reguły biologiczne, a także porównania uzyskanych efektów z obiektami rzeczywistymi.
Warto zwrócić uwagę na sposób realizacji wzrostu. Naturalny wzrost rzeczywistych roślin jest procesem ciągłym; płynnym. Natomiast symulacja z wykorzystaniem gramatyk jest procesem „skokowym” – realizowane są określone stany odpowiadające kolejnym iteracjom. Prezentowane rysunki pokazują stany wzrostu drzewa w określonych iteracjach. Liczby pod drzewami pokazują liczbę użytych iteracji.


Podobne efekty mogą powstawać przy przechodzeniu światła przez niejednorodne ośrodki półprzezroczyste np. powierzchnię morza. Analogicznie modeluje się przekroje na potrzeby prześwietleń w medycynie. W przypadku takich badań jak tomografia komputerowa (CT) czy rezonans magnetyczny (MRI) jest to związane z wizualizacją trójwymiarowej funkcji pochłaniania promieniowania. Funkcja ta określona jest dla każdego punktu przestrzeni pokazując właściwości badanej tkanki.
Stosuje się następujące metody:
• Metody uproszczone. Wizualizacja za pomocą tekstur (dwuwymiarowych rzadziej trójwymiarowych). Wizualizacja za pomocą półprzepuszczalnych płaszczyzn (jednej lub kilku) z nałożonymi obrazami zjawiska. Metody te dają dobre efekty i są efektywnie obliczeniowo, ale związane są tylko z określonym kierunkiem patrzenia. Metody takie stosuje się do uproszczonego modelowania mgły i chmur oraz podobnych zjawisk (np. w grach komputerowych).
Warto zwrócić uwagę na funkcję szumu opracowaną przez K.Perlina w 1985 roku (uzupełniona w 2002). Funkcja ta jest gładką interpolacją wektora gradientu między węzłami siatki. Jest ona prosta w implementacji i daje zaskakująco dobre efekty. Z tego powodu szum Perlina jest często dodawany do tekstur różnych powierzchni aby podkreślić drobne niejednorodności rzeczywistych obiektów i nadać naturalny wygląd.
