

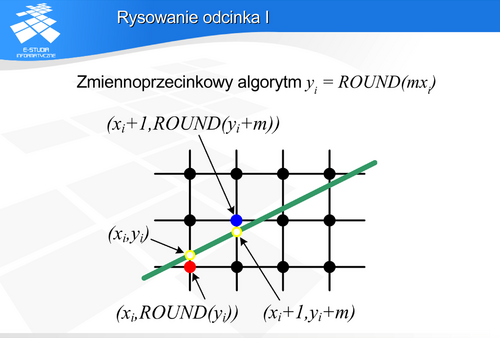
 . Następnie wyznaczenie wartości
. Następnie wyznaczenie wartości  dla całkowitych wartości
dla całkowitych wartości  odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne
odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne  do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn.
do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn.  , gdzie
, gdzie  jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania).
jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania).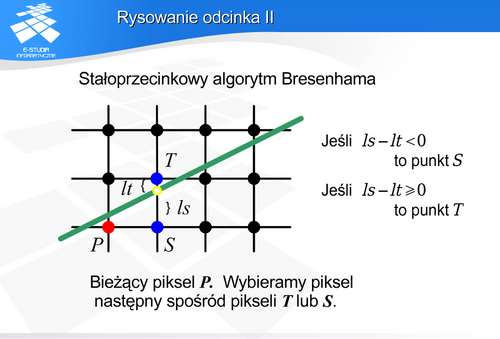
 . Bez zmniejszania ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka od 0 do 1. (Jest to 1/8 układu współrzędnych. Dla innych wartości można bowiem odpowiednio zamienić zmienne lub znaki przed nimi.) Wzrost y w takim przypadku zależy od wyboru piksela (S lub T), który jest bliżej teoretycznej prostej. O wyborze decyduje zmienna kontrolna d, która jest uaktualniana w każdym kroku.
. Bez zmniejszania ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka od 0 do 1. (Jest to 1/8 układu współrzędnych. Dla innych wartości można bowiem odpowiednio zamienić zmienne lub znaki przed nimi.) Wzrost y w takim przypadku zależy od wyboru piksela (S lub T), który jest bliżej teoretycznej prostej. O wyborze decyduje zmienna kontrolna d, która jest uaktualniana w każdym kroku.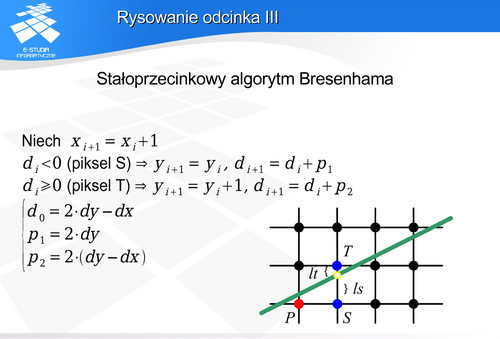
procedure Bresline (x1,x2, y2,y2,)
begin
end
Algorytm taki wykorzystujący tylko operacje całkowite jest również użyteczny w rozwiązaniach sprzętowych.

Pierwszym jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych.
Poważniejszym problemem jest zmiana jasności. Oba odcinki na rysunku składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest  razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i podobnie jak usuwanie wrażenia schodków odcinka rozwiązuje się go zmieniając barwy pikseli sąsiednich.
razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i podobnie jak usuwanie wrażenia schodków odcinka rozwiązuje się go zmieniając barwy pikseli sąsiednich.
Rysowanie łuku okręgu
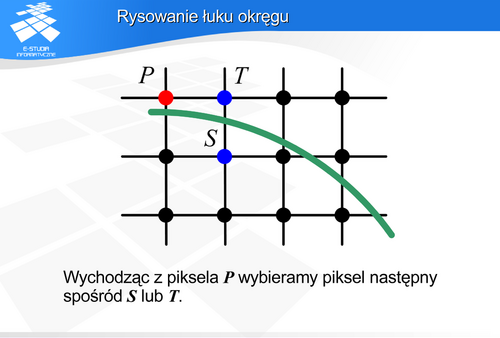
Przy okazji rysowania okręgu warto zwrócić uwagę na parametr charakteryzujący proporcje boków rastra pikseli w pionie i w poziomie, czyli aspekt. Jeśli proporcje rozdzielczości dla kart graficznych 1024x768 wynoszą 4:3, natomiast 1280x1024 wynoszą 5:4, to jeśli chcemy wyświetlić takie obrazy na tym samym monitorze, to proporcje trzeba przeliczyć także w odległości między pikselami. Inaczej narysowany okrąg albo w jednym albo w drugim przypadku będzie miał kształt elipsy.
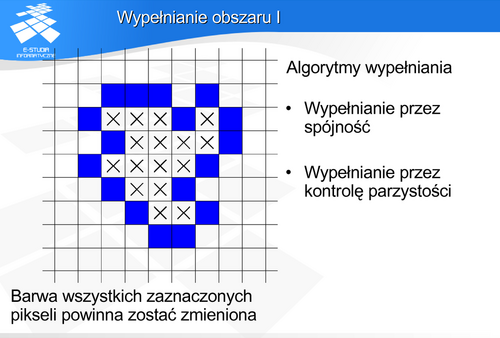
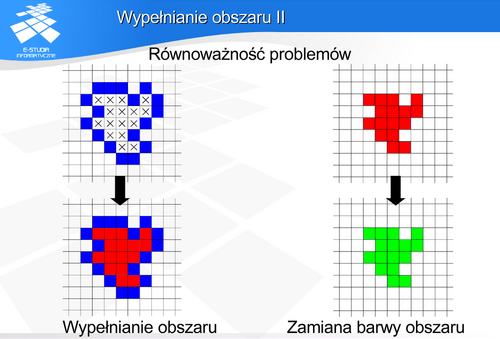
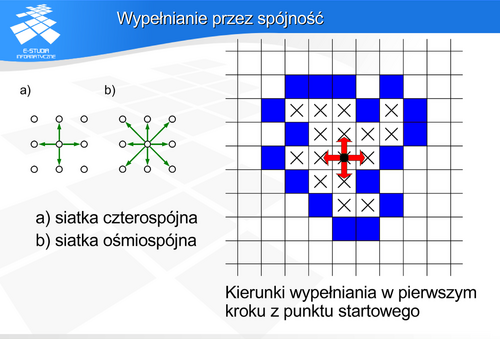
Wypełnianie przez spójność zakłada znajomość punktu startowego (tzw. „ziarna”) wewnątrz obszaru. Punkt ten jest wypełniany, a następnie startując z niego wypełniamy punkty sąsiednie (jeśli oczywiście istnieją – jeśli nie są już wypełnione, ani nie są punktami granicznymi obszaru). Jednocześnie punkty sąsiednie stają się wyjściowymi dla wypełniania w następnym kroku. Procedura ta jest powtarzana dopóki można wskazać punkty wyjściowe (niewypełnione) wewnątrz obszaru.
Warto zwrócić tutaj uwagę na problem sąsiedztwa i konieczność dostosowania do niego kształtu brzegu. Można wyróżnić dwa przypadki. Gdy ruchy po mapie pikseli mogą odbywać się analogicznie do ruchów wieży po szachownicy – wtedy piksel ma 4 sąsiadów – siatka jest czterospójna. Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to kierunkom ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna. Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli brzegu dla obu przypadków aby stanowił on figurę zamkniętą z punktu widzenia możliwości ruchu.
Algorytm wypełniania przez spójność dla siatki czterospójnej.
Przyjęto: c_b – barwa brzegu, c_f – barwa wypełnienia
procedure wypełnij1(x,y)
begin
end
Czytelnik może zaproponować korektę obejmującą siatkę ośmiospójną.
Zaproponowana postać algorytmu wypełniania przez spójność jest algorytmem rekurencyjnym. Daje to łatwość opisu ale także problemy realizacyjne. Z tego powodu znane są wersje niniejszego algorytmu w postaci nierekurencyjnej.
Algorytm wypełniania przez spójność jest czasem nazywany algorytmem przez sianie (punkt startowy jest „ziarnem”).
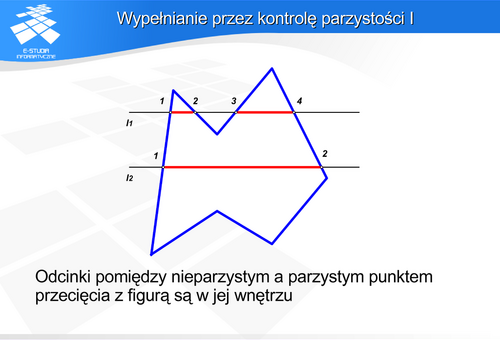
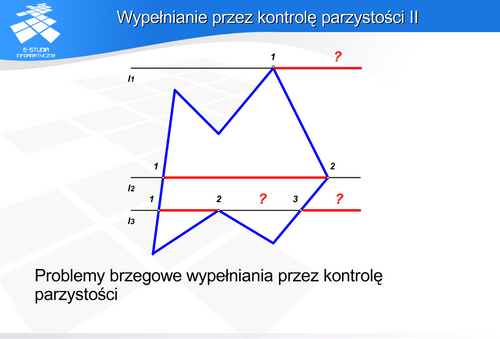
Na rysunku prosta l2 przecina wielokąt w wierzchołku (punkt 2) ale jest to przecięcie zwykłe – pozostałe końce przecinanych boków są po przeciwległych stronach prostej l2. Prosta l3 również przecina wielokąt w wierzchołku (punkt 2) ale jest to ekstremum lokalne – pozostałe końce boków są po tej samej stronie prostej l3.
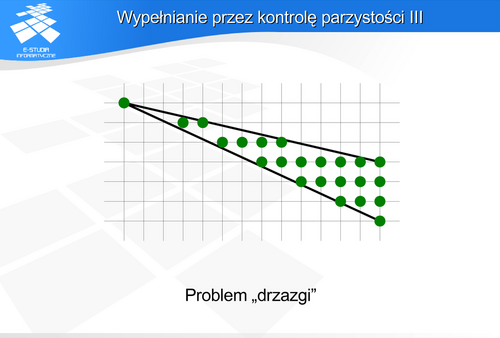

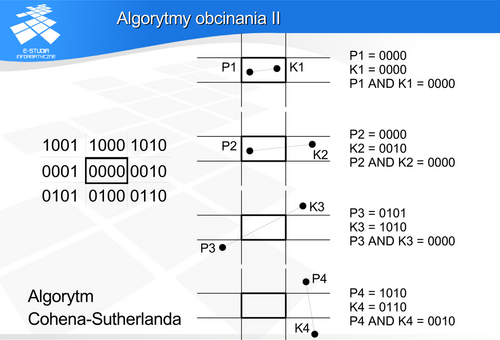
Płaszczyzna została podzielona na 9 obszarów . Prostokąt centralny odpowiada obszarowi okna. Jednocześnie krawędzie okna wyznaczają cztery proste: prawą, lewą, górna i dolną. Każdemu obszarowi został przypisany czterobitowy kod. Kolejne bity kodu określają poziome i pionowe pasy. Operacja AND przeprowadzona na kodach końców odcinka pozwala odrzucić te odcinki, które na pewno są poza oknem. Spośród pozostałych odcinków należy wybrać te, które rzeczywiście mają wspólne punkty z oknem oraz przyciąć do jego rozmiaru. Operacja AND pozwala w tym przypadku wybrać prostą obcinającą.
Jeśli wynik operacji AND jest różny od zera – należy odrzucić odcinek jako nie mający na pewno punktów wspólnych z oknem.
Jeśli wynik operacji AND jest zerowy – odcinek może przecinać okno. W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna.
Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy przyciąć odcinek. Odcinek 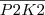 należy przyciąć prostą prawą (K2=0010). Odcinek
należy przyciąć prostą prawą (K2=0010). Odcinek 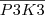 prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010).
prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010).
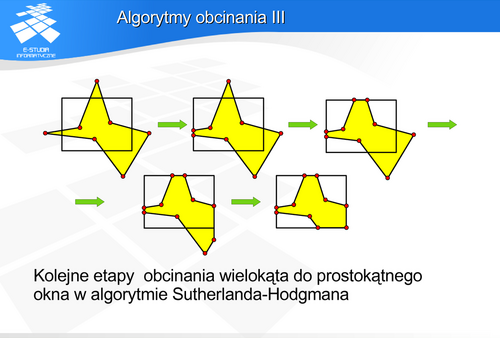
Przykładem algorytmu rozwiązującego ten problem jest algorytm Sutherlanda-Hodgmana obcinania wielokąta.
Niech kolejne wierzchołki wielokąta tworzą listę cykliczną
Obcinanie odbywa się kolejno dla prostych zawierających boki okna w ustalonym porządku – np. tak jak na rysunku zgodnie z ruchem wskazówek zegara poczynając od krawędzi lewej. W każdym kroku algorytmu rozpatrywany jest jeden wierzchołek leżący poza oknem przycinania. Wierzchołek taki jest usuwany z listy ale w jego miejsce wstawiane są wierzchołki „odpowiadające mu” na brzegu okna. Oczywiście należy wziąć pod uwagę również i takie przypadki, w których dodany wierzchołek będzie leżał na prostej zawierającej bok okna ale będzie to wierzchołek, który zostanie również usunięty np. w następnym kroku. Z drugiej strony możliwy jest także przypadek, kiedy kolejne wierzchołki wielokąta leżą na zewnątrz okna i wtedy kilka z nich może zostać zastąpionych jednym punktem na brzegu okna.
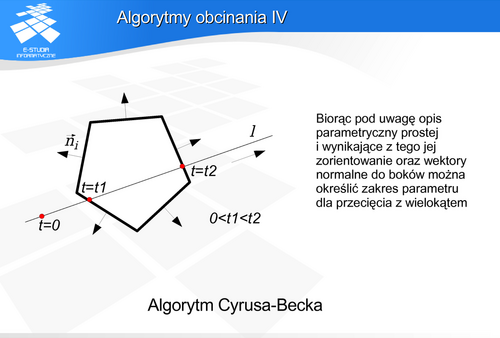
Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania.
Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor 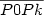 określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego (skierowanego na zewnątrz) do boku wielokąta.
określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego (skierowanego na zewnątrz) do boku wielokąta.
Jeśli  to parametr tk określa punkt Pk.który może być „maksymalnym” punktem przecięcia z wielokątem (np. punkt dla t=t2 na rysunku).
to parametr tk określa punkt Pk.który może być „maksymalnym” punktem przecięcia z wielokątem (np. punkt dla t=t2 na rysunku).
Jeśli  to parametr tk określa punkt Pk.który może być „minimalnym” punktem przecięcia z wielokątem (np. punkt dla t=t1 na rysunku).
to parametr tk określa punkt Pk.który może być „minimalnym” punktem przecięcia z wielokątem (np. punkt dla t=t1 na rysunku).
Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych.


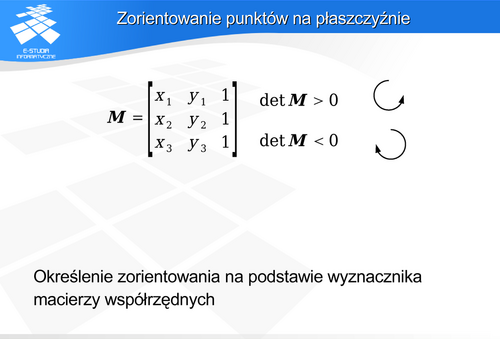
Zastosowanie macierzy współrzędnych (przez analogię do macierzy określającej iloczyn wektorowy) upraszcza obliczenia.
Jeśli det M > 0 mówimy o dodatnim zorientowaniu (lewoskrętnym lub przeciwnym do ruchu wskazówek zegara).
Jeśli det M < 0 mówimy o ujemnym zorientowaniu (prawoskrętnym lub zgodnym z ruchem wskazówek zegara).
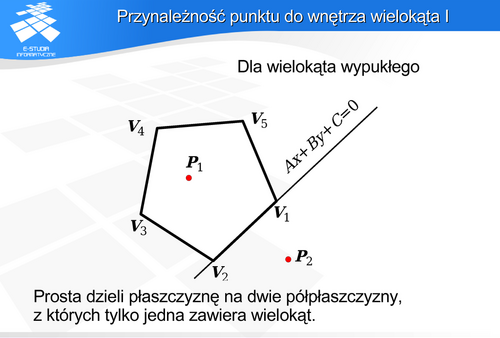
Algorytm sprawdzania przynależności punktu do wnętrza wielokąta wypukłego jest następujący.
Opisany algorytm należy w zależności od potrzeb uzupełnić o analizę samego wielokąta (przynależność lub nie do odpowiednich odcinków co jest zabiegiem technicznym i nie stanowi problemu).
Podstawową wadą zaprezentowanego algorytmu jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych będą proste wyznaczone przez kolejne wierzchołki, które będą przecinały wielokąt. Dla wielokątów dowolnych problem rozwiązuje się algorytmem kontroli parzystości lub algorytmem analizy sumy katów zorientowanych.
Warto przy tym zwrócić uwagę, że rozpatrywane są tylko wielokąty zwykłe, to znaczy takie, których krawędzie nie mają punktów wspólnych poza wierzchołkami.
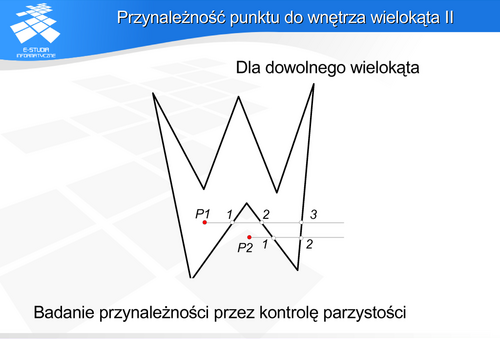
Algorytm jest bardzo prosty, jednak pamiętając o problemach ze szczególnymi przypadkami w algorytmie wypełniania przez kontrolę parzystości, należy przypuszczać, że podobne sytuacje wystąpią i tutaj.
Oczywiście rozwiązanie jest również analogiczne .Do algorytmu należy dodać dwa warunki.
Jeśli punkt przecięcia jest ekstremum lokalnym, to liczymy go podwójnie.
Jeśli półprosta zawiera cały bok wielokąta, to traktujemy to jako jeden pseudo-wierzchołek.
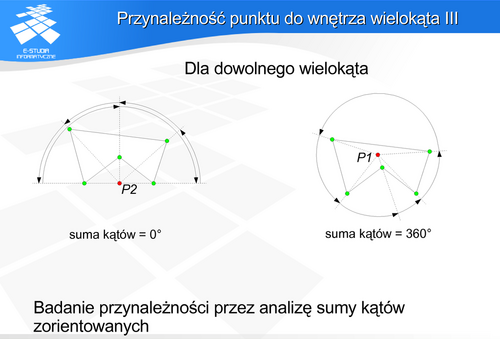
Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli  to punkt jest wewnątrz wielokąta. Jeśli
to punkt jest wewnątrz wielokąta. Jeśli  to na zewnątrz.
to na zewnątrz.
Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni że w implementacji nie ma błędu, to warunki można postawić jako:  i
i  .
.
Literatura
