

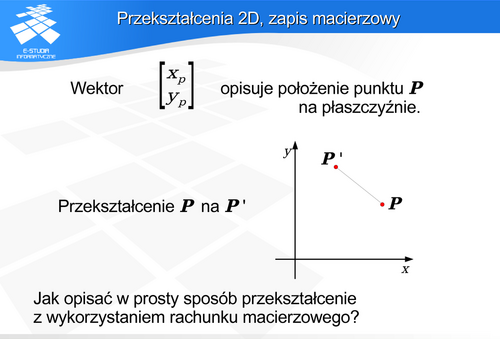
Niech  opisuje położenie punktu na płaszczyźnie.
opisuje położenie punktu na płaszczyźnie.
Najprostszym rozwiązaniem byłoby przyjęcie, że macierz  opisuje przekształcenie punktu
opisuje przekształcenie punktu 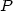 na
na 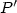 i że
i że 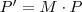
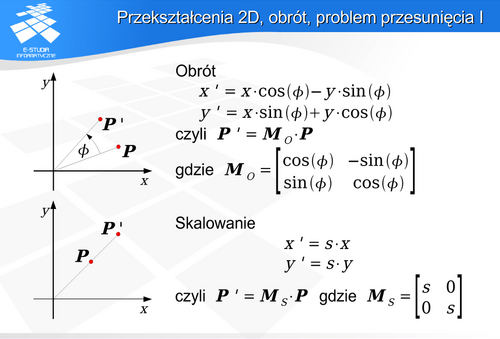
Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację).
Można zaproponować macierz 2x2, która, opisuje obrót punktu wokół początku układu współrzędnych.
Analogiczny opis można zaproponować dla operacji skalowania.
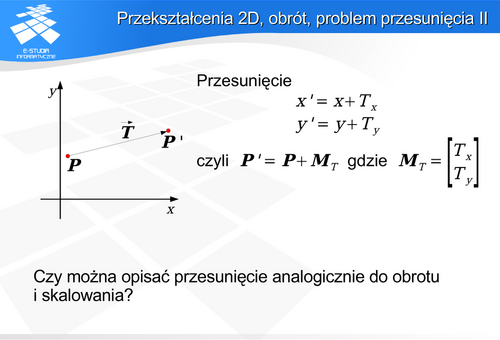
 . Niech wektor
. Niech wektor  opisuje translację punktu na płaszczyźnie.
opisuje translację punktu na płaszczyźnie.
Czy można znaleźć takie a, b, c, d, aby  dla
dla  i
i  .
.
Widać że nie jest to możliwe dla współrzędnych dowolnego punktu. Na dodatek punkt 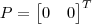 byłby punktem stałym takiego przekształcenia.
byłby punktem stałym takiego przekształcenia.
Jak zatem opisać translację na płaszczyźnie?
Operację tę można opisać macierzą 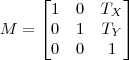
Między współrzędnymi zachodzi następujący związek:

i jest to równoważne opisowi translacji o wektor w postaci układu równań:

Tak wykonana operacja wymaga użycia współrzędnych jednorodnych.
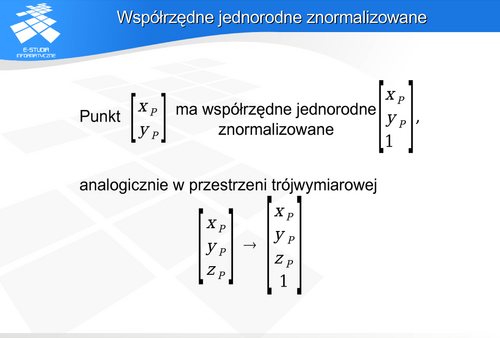
 , opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany układ współrzędnych jednorodnych znormalizowanych. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne
, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany układ współrzędnych jednorodnych znormalizowanych. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne  opisują położenie punktu, to odpowiada temu wektor
opisują położenie punktu, to odpowiada temu wektor
 we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać
we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać  dla
dla  .
.
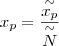 ,
, 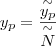 ,
, 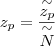 , co nosi nazwę operacji normalizacji.
, co nosi nazwę operacji normalizacji.
Zastosowanie w przypadku przesunięcia na płaszczyźnie współrzędnych jednorodnych można sobie wyobrazić jako umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu (tzn. dla  ). Wtedy analogiczne opisanie operacji translacji na płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt stały – początek układu współrzędnych jest poza płaszczyzną, na której jest wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych, czyli pracować na płaszczyźnie
). Wtedy analogiczne opisanie operacji translacji na płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt stały – początek układu współrzędnych jest poza płaszczyzną, na której jest wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych, czyli pracować na płaszczyźnie 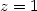 .
.
Gdyby operacja normalizacji nie została wykonana mogłoby się zdarzyć, że wynik operacji leżałby na innej płaszczyźnie – a to nie miałoby sensu
A zatem zawsze jeśli wynik operacji będzie nieznormalizowany zostanie przeprowadzona operacja normalizacji.
Analogicznie dla przekształceń trójwymiarowych można wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on początku układu współrzędnych.
Przekształcenia
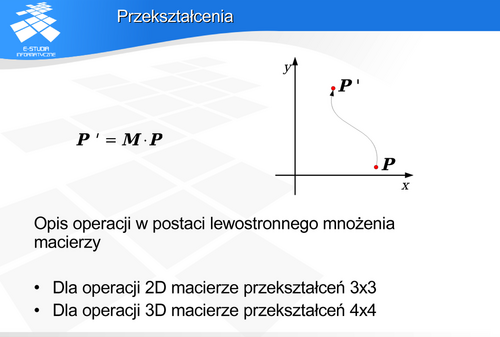
 na płaszczyźnie reprezentuje wektor P
na płaszczyźnie reprezentuje wektor P

Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco:
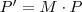
czyli:
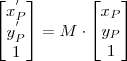
gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
W grafice komputerowej operacje na płaszczyźnie opisuje macierz 3x3.
Można powiedzieć, że macierz M definiuje liniowe funkcje określające każdą ze współrzędnych punktu tzn.:

Wykorzystując rachunek macierzowy przekształcenia punktu można opisać również za pomocą prawostronnego mnożenia macierzy. Wtedy, dla przyjętych wyżej danych operacja wyglądałaby tak.:

Jak widać tę samą operację można zapisać jako mnożenie lewostronne lub prawostronne przez macierz przekształcenia.
Tak naprawdę trudno byłoby wskazać uzasadnienie dla wyboru jednej lub drugiej formy zapisu. W książkach dotyczących grafiki komputerowej w ostatnich latach częściej stosowany jest zapis lewostronnego mnożenia, chociaż są autorzy, którzy nadal konsekwentnie trzymają się mnożenia prawostronnego. Natomiast sposób używania zależy od przyzwyczajeń i upodobań użytkownika. Jedno jest jednak bardzo istotne – konsekwencja. Nie można mieszać postaci opisu.
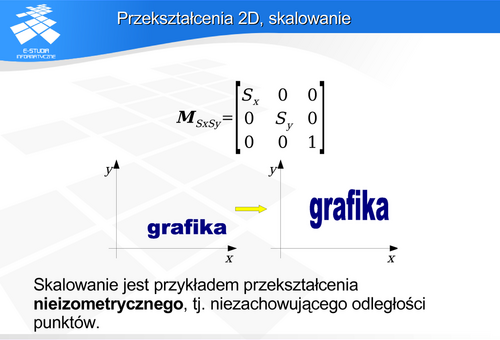
Przekształcenia 2D
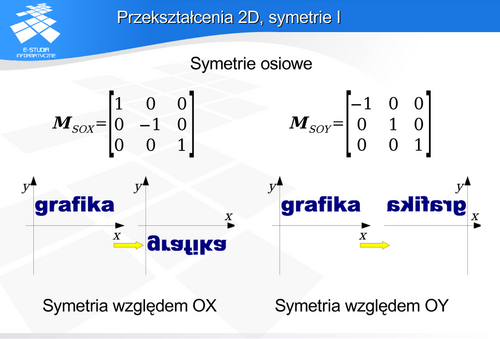
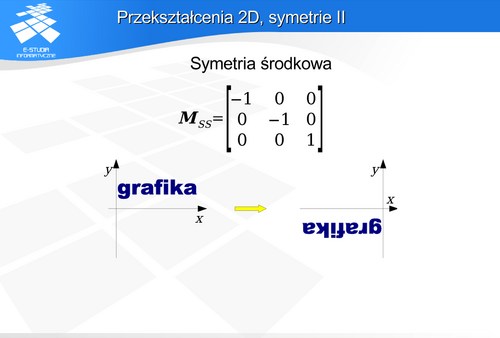
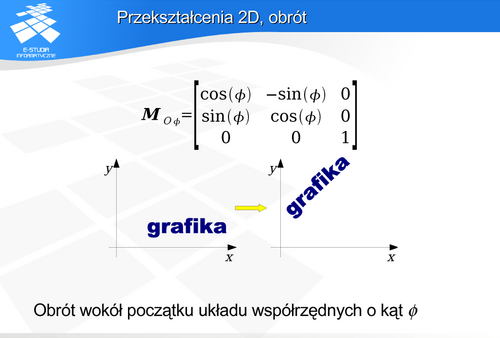
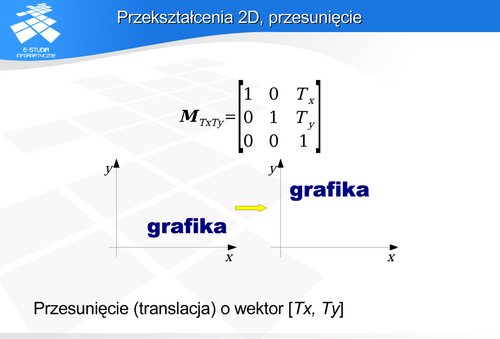
Niech położenie punktu o współrzędnych  w przestrzeni trójwymiarowej reprezentuje wektor P :
w przestrzeni trójwymiarowej reprezentuje wektor P :

Jeśli macierz M opisuje pewną transformację geometryczną w przestrzeni 3D, to operację tę można opisać następująco:
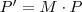
czyli:

gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D
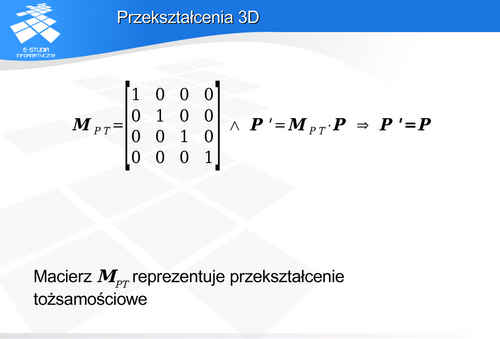
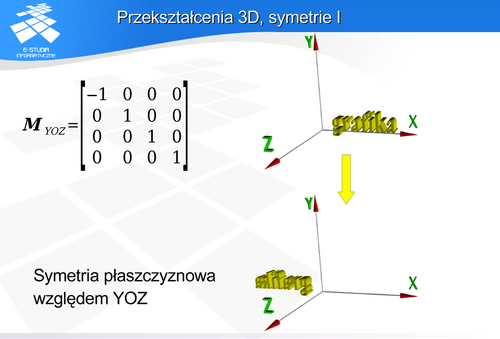
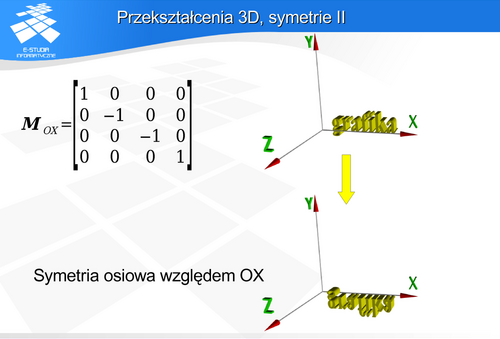
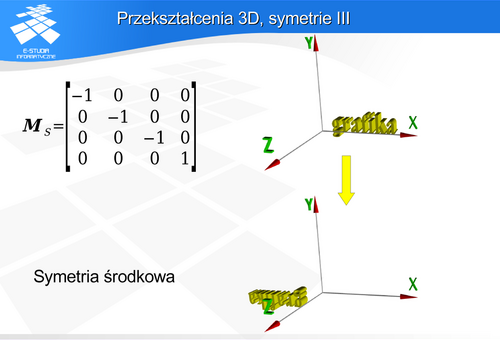
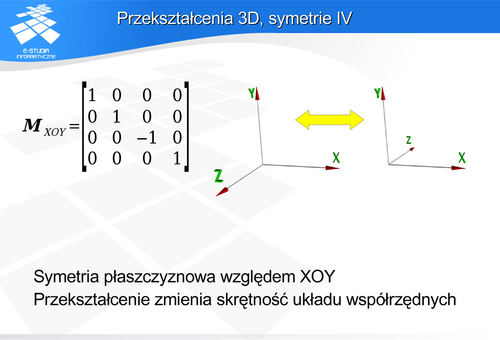
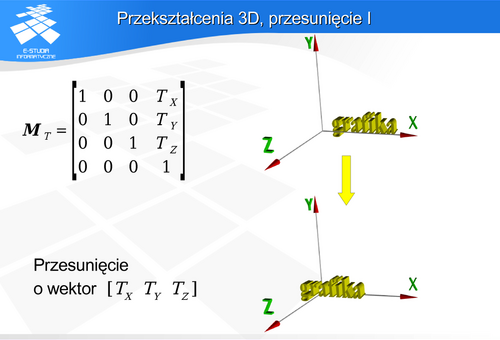

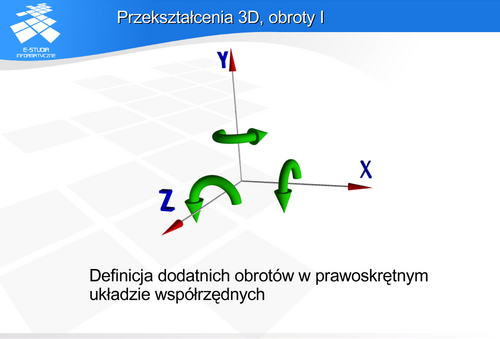
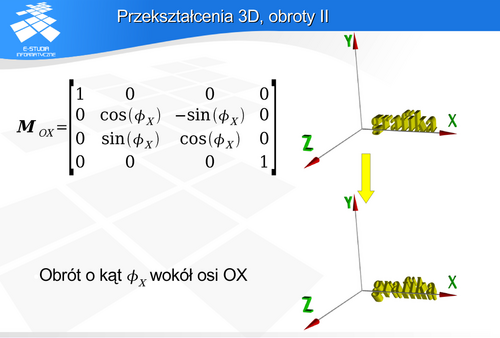
 wokół osi OX.
wokół osi OX.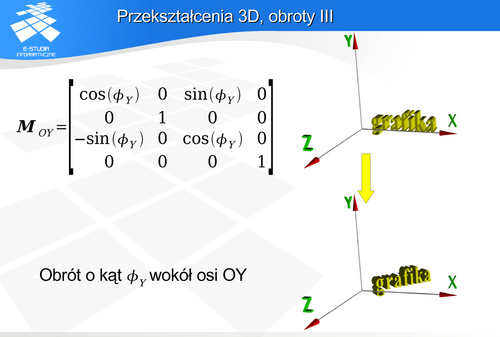
 wokół osi OY.
wokół osi OY.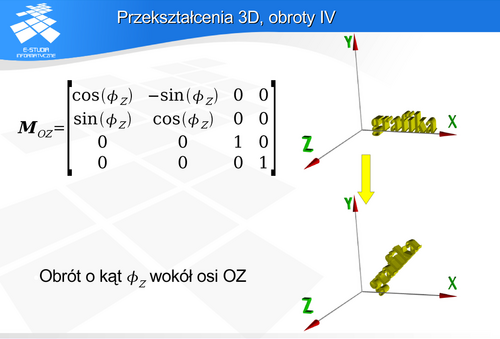
 wokół osi OZ.
wokół osi OZ.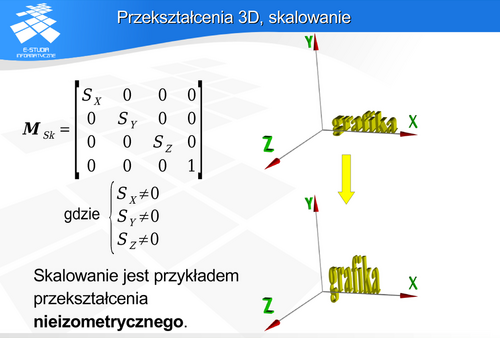
 to skalowanie można opisać macierzą:
to skalowanie można opisać macierzą:
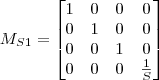
wtedy

Ale wynik tej operacji nie jest znormalizowany. Zgodnie z przyjętymi wcześniej zasadami posługiwania się współrzędnymi jednorodnymi taka operacja jest w tym przypadku niezbędna.
Zatem 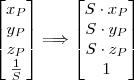 co odpowiada skalowaniu ze współczynnikiem S.
co odpowiada skalowaniu ze współczynnikiem S.
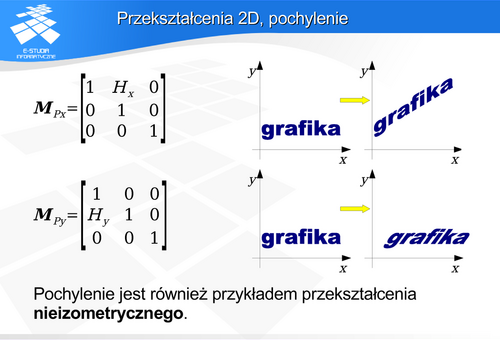
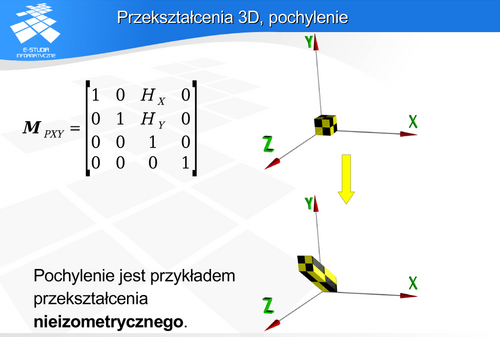
Przekształcenia 3D, pochylenie

Jeśli zatem  opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych
opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych 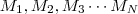 (w takiej kolejności) to :
(w takiej kolejności) to :

Oczywiście mnożenie macierzy i składanie przekształceń geometrycznych, jest operacją łączną ale nie jest operacją przemienną – złożenie najpierw translacji a potem obrotu jest innym przekształceniem niż złożenie najpierw obrotu a potem translacji.
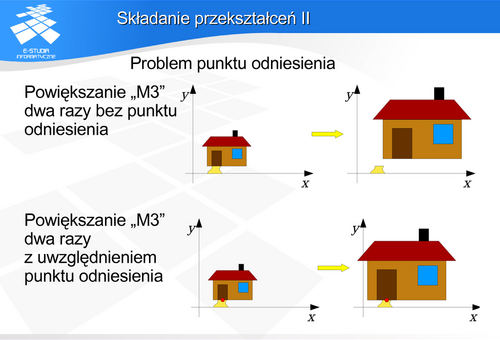
Skalowanie jest operacją zmieniającą proporcje wymiarów względem początku układu współrzędnych. Punkt [0,0,0] jest punktem stałym tego przekształcenia. Wyobraźmy sobie dwukrotne powiększenie pewnego obiektu (np. powiększenie domu jak na rysunku). Powiększenie dwukrotne oznacza nie tylko, że zwiększą się wymiary obiektu. Oznacza również, że każdy punkt obiektu zwiększy dwukrotnie odległość od początku układu współrzędnych. A przecież obiekt jest „osadzony” w pewnych realiach sceny – np. wejście do domu jest w określonym miejscu. Prosta realizacja skalowania prowadzi do pewnych konfliktów. Aby tego uniknąć należy wybrać punkt obiektu, który powinien zachować współrzędne – punkt odniesienia. A następnie zrealizować skalowanie względem tego punktu odniesienia.
To jednak wymaga złożenia operacji:

 opisuje pewną transformację geometryczną, przekształcenie współrzędnych jest opisane równaniem
opisuje pewną transformację geometryczną, przekształcenie współrzędnych jest opisane równaniem 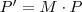 i jeśli istnieje przekształcenie odwrotne opisane macierzą
i jeśli istnieje przekształcenie odwrotne opisane macierzą  to
to 
Oczywiście nie zawsze konieczne jest wyznaczanie macierzy odwrotnej, np. dla translacji o dany wektor przekształceniem odwrotnym będzie translacja o wektor przeciwny, dla obrotu o zadany kąt obrót wokół tej samej osi o kąt przeciwny itp.
Ponieważ symetrie, translacja, obroty i skalowanie opisane odpowiednimi macierzami są operacjami odwracalnymi, to w bardzo prosty sposób można pokazać, że dowolna operacja będąca złożeniem dowolnego zestawu tych operacji, jest też operacją odwracalną.
Jeśli zatem  opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych
opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych  i jeśli każde z nich jest odwracalne to :
i jeśli każde z nich jest odwracalne to :

 na rysunku) pokryła się z wybraną osią układu współrzędnych. Przy czym przyjęty zwrot osi obrotu powinien być zgodny ze zwrotem osi okładu. Takie warunki pozwolą obrót o kąt
na rysunku) pokryła się z wybraną osią układu współrzędnych. Przy czym przyjęty zwrot osi obrotu powinien być zgodny ze zwrotem osi okładu. Takie warunki pozwolą obrót o kąt  wokół zadanej osi zrealizować bezpośrednio jako obrót o kąt
wokół zadanej osi zrealizować bezpośrednio jako obrót o kąt  wokół osi układu.
wokół osi układu.
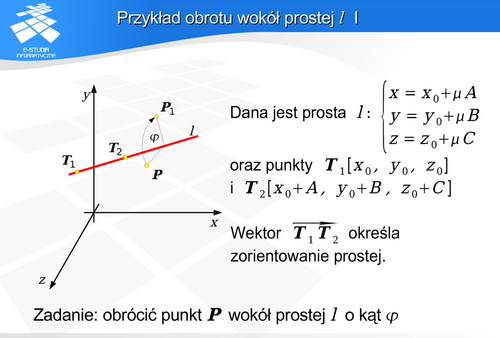
Zadanie można rozwiązać na wiele sposobów. Przyjęto następujący zestaw operacji:
 znalazł się w początku układu współrzędnych.
znalazł się w początku układu współrzędnych.
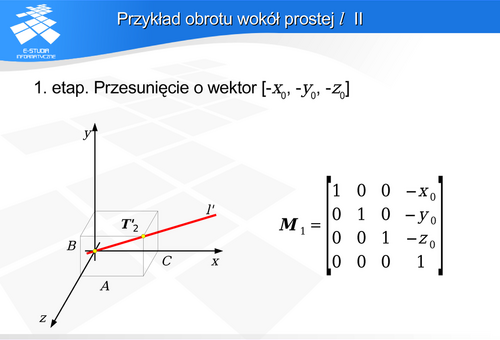
 ) pokryje się (z uwzględnieniem zwrotów) z osią OX układu współrzędnych.
) pokryje się (z uwzględnieniem zwrotów) z osią OX układu współrzędnych.
 wokół osi OX.
wokół osi OX.
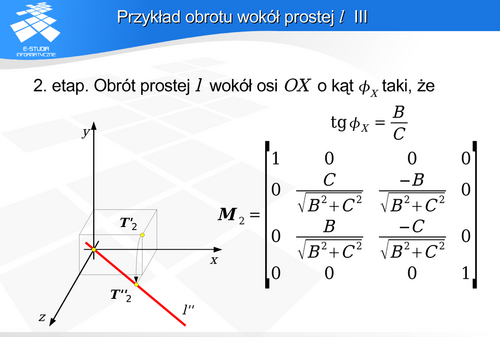
 znalazła się na płaszczyźnie XOZ.
znalazła się na płaszczyźnie XOZ.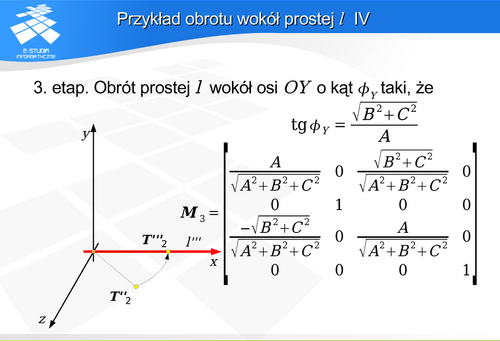
 pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi.
pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi.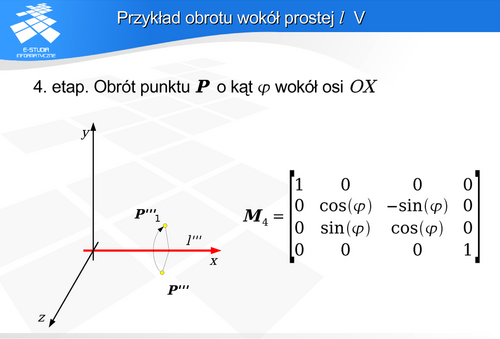
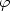 wokół prostej
wokół prostej  co, dzięki odpowiednim operacjom wstępnym, odpowiada obrotowi o kąt
co, dzięki odpowiednim operacjom wstępnym, odpowiada obrotowi o kąt 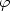 wokół osi OX układu współrzędnych.
wokół osi OX układu współrzędnych.
Macierz przekształcenia całkowitego jest iloczynem macierzy opisujących przekształcenia odpowiadające kolejnym przedstawionym etapom.

Rozpatrzmy przykład zegara, dla którego należy wyznaczyć położenie wskazówek.
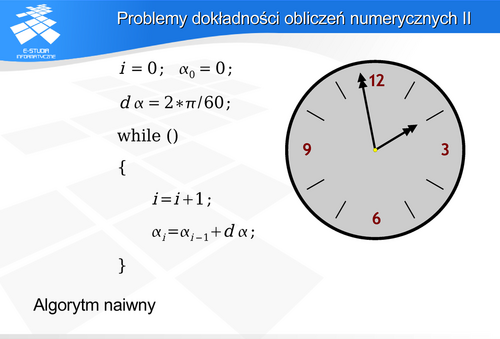


Realizując algorytm graficzny należy zawsze zwrócić uwagę na dokładność obliczeń numerycznych. Aby błąd zaokrągleń nie wpłynął na efekt obliczeń i nie zniweczył naszej pracy psując efekt końcowy.


Dla dowolnego kwaternionu istnieje kwaternion przeciwny.
Dla dowolnego kwaternionu różnego od zera istnieje kwaternion odwrotny.
Suma dwóch kwaternionów jest kwaternionem.
Iloczyn dwóch kwaternionów jest kwaternionem.

Dodawanie kwaternionów jest operacją łączną i przemienną.
Mnożenie kwaternionów jest operacją łączną i nie jest operacją przemienną

 reprezentujący oś obrotu w przestrzeni.
reprezentujący oś obrotu w przestrzeni.
Biorąc pod uwagę kwaternion jednostkowy  związany z tym wektorem jednostkowym, można wyznaczyć kwaternion
związany z tym wektorem jednostkowym, można wyznaczyć kwaternion  zgodnie z zaproponowanym wzorem. Kwaternion ten reprezentuje punkt będący obrazem w obrocie wokół osi wyznaczonej przez wektor
zgodnie z zaproponowanym wzorem. Kwaternion ten reprezentuje punkt będący obrazem w obrocie wokół osi wyznaczonej przez wektor  o kąt
o kąt 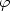 .
.
Porównując to rozwiązanie z zadaniem opisanym wcześniej widać prostotę operacji obrotu wykonywanej z wykorzystaniem kwaternionów.
Większość obrotów realizowanych w grach komputerowych jest wykonywana w taki sposób.
