Układ odmierzający czas jest standardowym wyposażeniem większości dzisiejszych komputerów. Od jego prawidłowego działania zależy często bardzo wiele innych elementów całego systemu komputerowego. Z zegarem związane są zazwyczaj dwa rejestry: rejestr licznika (ang. counter ) oraz rejestr podtrzymujący (ang. holding register ). Wraz z wybijaniem taktów przez czasomierz systemowy zmniejszana jest wartość rejestru licznika. W momencie kiedy jego wartość dojdzie do zera wywoływane jest przerwanie i ładowana jest do niego wartość rejestru podtrzymującego. Zauważmy, że zmieniając wartość rejestru podtrzymującego możemy sterować częstotliwością wywoływania przerwań, a tym samym częstotliwością tzw. impulsów zegara (ang clock tick ).
Dopóki zegar jest używany lokalnie na jednej maszynie kwestia jego niedokładności nie jest aż taka istotna. Procesy korzystają w tym wypadku z jednego zegara, a więc w ramach danej maszyny jego wskazania będą spójne. Problem pojawia się gdy dostępnych mamy kilka maszyn, z których każda posiada swój własny zegar. Ponieważ fizyczne zegary nie są idealne i ich częstotliwości będą się w jakimś stopniu różniły, po pewnym czasie zaczną wskazywać różne wartości. Innymi słowy pojawią się tzw. odchylenia wskazań zegara (ang. clock skew ). W takim przypadku założenie, że zegary fizyczne w danym momencie wskazują identyczny czas jest obarczone pewnym błędem.
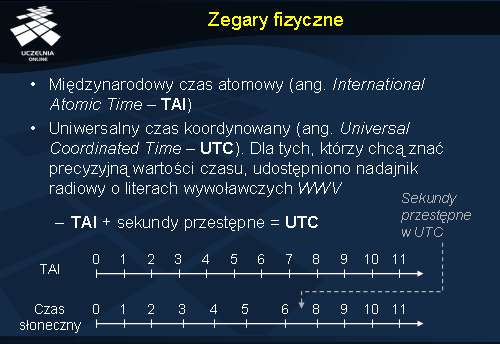
Do pomiaru upływu rzeczywistego czasu stosowano wiele różnych metod. Jednym z bardziej przełomowych momentów w tej dziedzinie było wynalezienie zegara atomowego. Wtedy też na nowo zdefiniowano pojęcie sekundy jako liczbę przejść w atomie cezu 133. Przy użyciu takich zegarów liczony jest międzynarodowy czas atomowy (ang. International Atomic Time – TAI ), który ustanawiany jest poprzez uśrednienie pomiarów z różnych laboratoriów. Okazało się, że mimo swoich zalet podejście to nie jest pozbawione błędu. Ponieważ średni dzień słoneczny trwa coraz dłużej pojawia się rozbieżność z międzynarodowym czasem atomowym. W celu rozwiązania tego problemu wprowadzono sekundy przestępne. System pomiaru czasu, który uwzględnia to ulepszenie nazywamy uniwersalnym czasem koordynowanym (ang. Universal Coordinated Time – UTC ). UTC jest podstawą dzisiejszego pomiaru czasu wśród cywilnych zastosowań. Wskazania UTC udostępniono również osobom, które chcą znać dokładny czas. W tym celu Narodowy Instytut Czasu Standardowego (ang. National Institute of Standard Time – NIST ) posiada nadajnik radiowy o literach wywoławczych WWV, który co sekundę wysyła impuls.
Algorytmy synchronizacji zegarów

W przypadku synchronizacji zegarów możemy wyróżnić różne cele. Jednym z nich może być potrzeba zsynchronizowania grupy maszyn z jedną dedykowaną stacją, która ma np. odbiornik WWV. Potrzeba synchronizacji może zaistnieć również, gdy nie ma wyróżnionej pewnej stacji pomiarowej, ale musimy skoordynować działanie grupy maszyn.
Do rozwiązania tych problemów istnieje wiele algorytmów, z których część zaprezentujemy w dalszej części wykładu. W tym momencie omówimy pewien wspólny dla tych algorytmów model systemu związanego z pomiarem czasu. W modelu tym zakładamy istnienie pewnego idealnego zegara. Oznaczmy dla wygody jego wartość jako t . Każda maszyna, która posiada czasomierz wyznacza czas o wartości C . Jeżeli maszyna p ma za zadanie wyznaczać czas t , wartość jej czasu oznaczamy jako Cp(t ). W tym momencie może wystąpić kilka przypadków. W wypadku kiedy Cp(t ) = t mamy do czynienia z sytuacją, w której zegar w maszynie jest zegarem doskonałym (dC/dt = 1 ). W praktyce występuje jednak sytuacja, w której zegary są szybsze lub wolniejsze w stosunku do zegara doskonałego t (dC/dt różne od 1). Takie zegary powinny być poddawane okresowej resynchronizacji.
Algorytm Cristiana

Algorytm ten jest przeznaczenie głównie dla środowisk rozproszonych w których jeden z węzłów jest serwerm czasu (ang. time server ) (np. posiada odbiornik WWV). W algorytmie tym zakłada się, że każda maszyna co pewien określony czas (wartość tego czasu zależy m.in. od maksymalnego odchylenia zegarów jakie będziemy tolerować) wysyła do serwera czasu zapytanie o podanie aktualnego czasu. Po otrzymaniu tego zapytania, serwer odpowiada prędko jak tylko może i przesyła aktualny czas UTC . Nadawca z kolei, po otrzymaniu informacji o czasie od serwera, zanim ustawi wartość swojego zegara, musi uwzględnić parę kwestii. Mianowicie, zwykłe przepisanie czasu nadesłanego z serwera mogłoby spowodować, że czas płynie wstecz. Może się tak zdarzyć jeżeli zegar nadawcy wymierza czas zbyt szybko. Opcja prostego przepisania czasu więc odpada. Poza tym istnieje pewien koszt w postaci czasu komunikacji. Taki koszt powoduje oczywiście, że wartość czasu UTC wysłana przez serwer jest nieaktualna po nadejściu do nadawcy zapytania. Aby rozwiązać ten problem nadawca może np. zapamiętać przedział czasowy zawarty pomiędzy momentem T0 , w którym wysłano zapytanie do serwera i momentem T1 , kiedy przyszła odpowiedź z serwera. W najprostszym przypadku przyjmuje się, że połowa tego przedziału jest czasem komunikacji od serwera do klienta (( T1 – T0 ) / 2 ). Jeśli dodatkowo znamy czas (T2 ) przetwarzania zapytania przez serwer, możemy poprawić oszacowanie czasu przez nadawcę i jako czas przesyłania komunikatu bierzemy wtedy połowę wartości ( T1 - T0 - T2).
W przypadku, gdy wiemy, że czas przesyłania komunikatu może się różnić przy każdym przesłaniu wiadomości z i do serwera, zaproponowano wykonywanie kilku pomiarów i odpowiednie ich uśrednianie.
Ilustracja algorytmu Cristiana
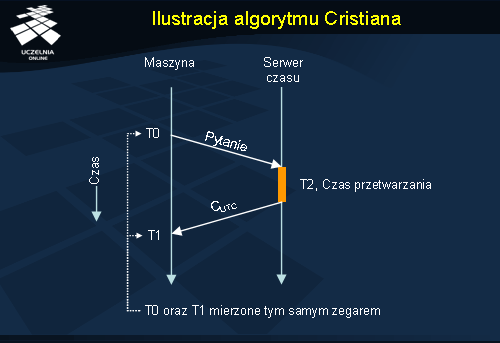
W przykładzie zaprezentowanym na powyższej ilustracji pewna maszyna chce zsynchronizować swój lokalny zegar z zegarem serwera czasu. W tym celu wysyła komunikat z pytaniem o czas do serwera czasu. Ten gdy tylko może, odsyła do maszyny wiadomość zawierającą jego lokalny czas oraz ew. czas przetwarzania zapytania. Po otrzymaniu danych o czasie, maszyna oblicza nowy czas i ustawia odpowiednio swój zegar.
Algorytm z Berkeley

W przeciwieństwie do algorytmu Cristiana w przypadku algorytmu z Berkeley serwer czasu jest aktywny i co pewien okres czasu wypytuje każdą maszynę o jej aktualny czas. Po zebraniu odpowiedzi od grupy maszyn serwer uśrednia ich czasy. Na podstawie takiej wyliczonej wartości czasu, serwer każe odpowiednim maszynom ustawić nową wartość czasu lub zwolnić działanie do chwili kiedy osiągną odpowiednią wartość.
Takie podejście do synchronizacji zegarów fizycznych może być użyte m.in. w systemie, w którym nie ma specjalnych serwerów czasu, a jedynie chodzi o wspólne ustalenie jednej podstawy czasu.
Algorytm uśrednienia

Algorytm uśredniania jest algorytmem zdecentralizowanym. W podejściu tym czas dzieli się na przedziały o określonym i stałym rozmiarze. Na początku każdego przedziału następuje resynchronizacja wszystkich zegarów. Polega to na tym, że każda maszyna rozgłasza wtedy aktualny czas swojego zegara. W momencie wysłania maszyna uruchamia lokalny czasomierz i rozpoczyna zbieranie komunikatów od innych maszyn. Komunikaty rozgłoszeniowe mogą przychodzić w różnych chwilach od różnych nadawców. Gdy zostaną zebrane wszystkie odpowiedzi obliczana jest na ich podstawia nowa wartość czasu. W najprostszym przypadku wykorzystuje się uśrednianie. W zmodyfikowanej wersji odrzuca się dodatkowo przed uśrednianiem skrajne wartości, aby nie zaburzały zbytnio wyniku. W jeszcze bardziej rozbudowanej wersji są brane pod uwagę m.in. czasy przesyłania komunikatów.
Algorytm Marzullo

Ogólna koncepcja algorytmu polega na znalezieniu najmniejszego przedziału czasu spójnego z jak największą liczbą źródeł czasu. Poprzez pojęcie spójnych przedziałów rozumieć tu należy przedziały, które na siebie zachodzą, czyli mają pewna część wspólną.
Po odnalezieniu szukanego przedziału czasowego do wyznaczenia konkretnej wartości czasu mogą być wykorzystane różne metody. Najprostsza z nich bierze po prostu środek przedziału. Bardziej wyrafinowane metody wykorzystują metody probabilistyczne do wyznaczenia czasu.
Jak już wspomniano w algorytmie używa się przedziałów do opisania czasu mierzonego przez zegary z różnych źródeł. Każdy przedział w postaci [t-d, t+d] w algorytmie reprezentowany jest przez dwie pary w formie <znacznik czasowy, typ>: <t-d; -1> oraz <t+d; +1>. Wartość -1 oznacza tutaj parę zawierającą wartość początku przedziału, natomiast +1 oznacza jego koniec.
W momencie kiedy dana maszyna otrzyma informacje o czasie na innych maszynach, algorytm może rozpocząć swoje działanie. W pierwszej kolejności pary, które reprezentują końce przedziałów czasowych są sortowane na liście według ich znaczników czasowych. Jeżeli pewne pary mają ten sam znacznik czasowy, jednym z rozwiązań jest umieszczenie par z typem +1 przed parami z typem -1 (robi się tak w celu uniknięcia problemu z przedziałami nakładającymi się tylko swoimi końcami). Po posortowaniu listy, brane są kolejne pary i sprawdzane w wyniku porównania z dotychczasowym najlepszym rozwiązaniem. Porównanie polega na sprawdzeniu czy oba przedziały się nakładają. Jeżeli tak, to wartość ich części wspólnej staje się ewentualnie nowym najlepszym rozwiązaniem (zależy to od tego czy wcześniej nie został już znaleziony przedział, który zawiera się w większej liczbie innych przedziałów).
Na slajdzie przedstawiono szczegóły algorytmu, a tutaj opiszemy znaczenie poszczególnych zmiennych użytych w algorytmie: best – największa dotychczasowa liczba nakładających się przedziałów; current – bieżąca liczba nakładających się przedziałów; [ beststart , bestend ] – najlepszy znaleziony do tej pory przedział; i – pewien indeks; offset[i ] – znacznik czasowy pary o indeksie i ; type[i ] – typ pary o indeksie i .
Algorytm Marzullo - przykład

Aby zaprezentować przykład wykonania algorytmu Marzullo załóżmy, że mamy podane pewne przedziały czasowe, zaprezentowane na slajdzie jako dane wejściowe. Po zebraniu takich przedziałów, maszyna przystępuje do obliczania nowego czasu. W pierwszej kolejności, zgodnie z algorytmem, wyliczane są odpowiednie pary dla każdego przedziału (na slajdzie sekcja: Tworzenie par ). Pary te są następnie sortowane według algorytmu podanego wcześniej.
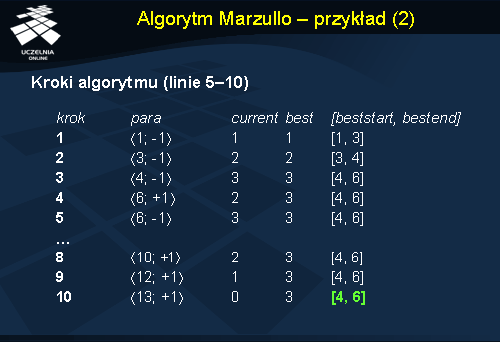
Zgodnie z posortowaną wcześniej listą par, bierzemy kolejne pary i obliczamy przedział wynikowy. Kolejne etapy wykonywania algorytmu przedstawione zostały na slajdzie. Wyliczonym przedziałem jest w tym przypadku [4, 6].
Algorytm przycięcia

Algorytm przecięcia (ang. intersection algorithm ) jest zmodyfikowaną wersją algorytmu Marzullo. Celem tego algorytmu jest znalezienie największego pojedynczego przecięcia przedziałów, które będzie zawierało czas mierzony przez zegary o określonej dokładności (ang. truechimer ). Podobnie jak w przypadku algorytmu Marzullo, mamy danych m przedziałów w postaci [ t-d , t+d ].
Główna różnica pomiędzy algorytmem Marzullo, a jego modyfikacją jest fakt, iż wynik uzyskiwany w przypadku tego pierwszego niekoniecznie zawiera środek sumy wszystkich przedziałów. W wypadku algorytmu przecięcia przedział wynikowy zawiera: przedział, który daje w wyniku algorytm Marzullo, a poza tym wspomniany wcześniej środek sumy przedziałów. Taki przedział jest większy, od tego uzyskanego poprzednią wersją algorytmu. To z kolei pozwala na zastosowanie pewnych danych statystycznych w celu wybrania punktu wynikowego z tego przedziału.
Algorytm szuka przedziału, który pokrywałby się z przedziałami m-f źródeł czasu, gdzie f jest liczbą źródeł z wartością czasu poza przedziałem ufności (błędne źródła). Aby otrzymać najlepszy wynik, zakłada się, że f powinno być tak małe jak to tylko możliwe, a wynik jest sensowny gdy f < m/2 (liczba błędnych źródeł nie powinna stanowić więcej niż połowę liczby wszystkich źródeł).
W porównaniu z algorytmem Marzullo w przypadku tego algorytmu każdy przedział jest reprezentowany przez trzy pary: początek przedziału <t-d; -1>, środek przedziału <t; 0> oraz koniec przedziału <t+d; +1>.
Oprócz wcześniej wspomnianych struktur danych, algorytm używa zmiennych: endcount – bieżąca liczba końców przedziałów, midcount – bieżąca liczba środków przedziałów, low – wartość dolnego końca przedziału wynikowego, high – wartość górnego końca przedziału.
Jak wspomniano działanie algorytmu polega na próbie znalezienia przedziału spójnego z m-f źródłami czasu. Przed rozpoczęciem głównej części algorytmu jest tworzona posortowana lista wszystkich dostępnych par, które reprezentują dostępne przedziały czasowe. Sortowanie odbywa się analogicznie jak w algorytmie Murzallo. Algorytm wykonuję się w pętli z rosnącą wartością f . Na początku zakłada się, że nie ma błędnych źródeł czasu, czyli f = 0 . Pętla wykonuje się do momentu kiedy zostanie znaleziony zadowalający przedział lub wartość f będzie równa bądź większa od m/2 . Wewnątrz głównej pętli wykonywane są dwie mniejsze pętle, z których jedna szuka dolnego końca przedziału wynikowego, a druga górnego końca przedziału wynikowego. W skrócie można napisać, iż jedna pętla przegląda na liście pary <znacznik czasowy, typ> w kolejności rosnącej, a druga pętla robi to w kolejności malejącej. Każda z pętli kończy się w momencie, gdy liczba rozpatrzonych przez nie przedziałów mających wspólną część będzie równa lub większa od wartość m-f . Pod koniec obu pętli sprawdzane jest czy liczba środków przedziałów znajdujących się poza przedziałem wynikowym nie przekracza liczby f błędnych źródeł czasu. Jeżeli nie przekracza główna pętla jest kończona i otrzymujemy odpowiedni wynik.

Dalsza część algorytmu przedstawionego na poprzednim slajdzie.
Algorytm przycięcia - przykład

Podobnie jak w przypadku oryginalnego algorytmu Marzullo, dana jest lista przedziałów na podstawie, których powstaje posortowana odpowiednio lista par. W przypadku tego algorytmu dla każdego przedziału wejściowego są konstruowane 3 pary, a nie 2 jak to miało miejsce w poprzednim algorytmie. Analizując w kilku krokach (ze zmieniającym się wartością f ) daną listę par od początku i od końca, otrzymujemy przedział wynikowy [4, 10].
Relacja uprzedniości zdarzeń

Analizując zagadnienie synchronizacji należy wspomnieć o relacji uprzedniości zdarzeń (ang. happened before relation ) często omawianej w kontekście systemów rozproszonych.
Relacja ta określa, kiedy pewne zdarzenie a poprzedza inne zdarzenie b . Jeżeli między zdarzeniami zachodzi taka relacja, oznacza to że jest ona prawdziwa dla wszystkich procesów.
Niech zdarzenie a poprzedza zdarzenie b . Relacja uprzedniości zdarzeń zachodzi w następujących przypadkach. Zdarzenia a i b działają wewnątrz tego samego procesu oraz a występuje przed b . W drugim przypadku a jest zdarzeniem wysłania komunikatu przez pewien proces, a b jest zdarzeniem odebrania tego komunikatu przez inny proces. Trzeci przypadek opisuje domknięcie przechodnie relacji uprzedniości. Mówimy, że zdarzenie a poprzedza zdarzenie b gdy istnieje sekwencja zdarzeń rozpoczynająca się od zdarzenia a i kończąca zdarzeniem b , taka że dla każdej pary kolejnych zdarzeń zachodzi jedna z dwóch wcześniej opisanych sytuacji.
Jeżeli między dwoma zdarzeniami nie zachodzi relacja uprzedniości, mówimy o nich, że są współbieżne (ang. concurrent ).
Relacja uprzedniości zdarzeń jest relacją antysymetryczną oraz przechodnią, a tym samym jest relacją częściowego porządku.
Diagramy przestrzenno-czasowe
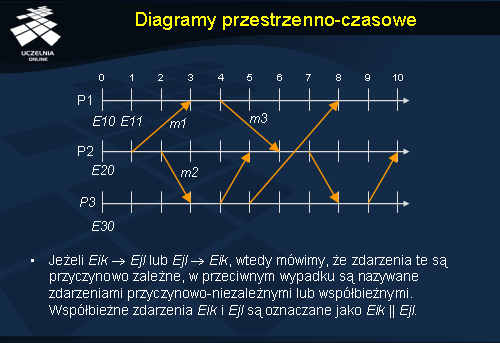
Diagramy przestrzenno-czasowe (ang. space-time diagram ) służą do graficznego zapisu realizacji przetwarzania rozproszonego. Osie diagramu reprezentują globalny upływ czasu, natomiast punkty na osiach oznaczają zdarzenia.
Zegary logiczne

Można wykazać, że synchronizacja zegarów nie musi być bezwzględna. W przypadku dwóch procesów, które się ze sobą nie komunikują w żaden sposób, nie ma potrzeby aby ich zegary były zsynchronizowane, ponieważ brak takiej synchronizacji będzie niezauważalny, a tym samym nie spowoduje żadnych problemów. Dla pewnej klasy algorytmów liczy się tylko spójność wewnętrzna zegarów, a niekoniecznie to że odzwierciedlają czas rzeczywisty. Dzieje się tak na przykład w wypadku kiedy istotna staję się kolejność występowania zdarzeń, a nie dokładny czas ich wystąpienia.
W dalszej części wykładu zostaną omówione algorytmy synchronizacji zegarów logicznych za pomocą znaczników czasu Lamporta i wektorowych znaczników czasu.
Znaczniki czasu Lamporta

Znaczniki czasu Lamporta zostały opracowane jako sposób pomiaru czasu logicznego. Każdemu zdarzeniu a przypisana jest pewna wartość czasu C(a ). Jeżeli weźmiemy dwa zdarzenia a i b , przy czym a poprzedza zdarzenie b , to powinna zachodzić nierówność C(a )< C(b ).
W podejściu Lamporta wykorzystano bezpośrednio koncepcję relacji uprzedniości zdarzeń. Każdy wysłany komunikat zawiera czas swojego nadania. Odbiorca, który odbierze wiadomość porównuje czas jej nadania z własnym czasem. Jeśli zegar odbiorcy wskazuje czas mniejszy od czasu nadania komunikatu, przesuwa swój zegar w przód do wartości równej czasowi nadania powiększonej o pewną wartość d . Dodanie d wymusza postęp czasu pomiędzy każdą parą zdarzeń.
Rozszerzeniem tego algorytmu jest dodanie po przecinku do każdej wartości zegara np. numeru procesu. Robi się tak, gdyż w normalnych warunkach dwa zdarzenia mogłyby posiadać znaczniki czasowe o tej samej wartości. Dodatkowa informacja pozwala na rozróżnienie zdarzeń. Na przykład zdarzenie, które wystąpiło w procesie 4 w chwili gdy wartość jego zegara logicznego wynosiła 120, będzie oznaczone znacznikiem (120, 4).
Zegar Lamporta spełnia kilka ważnych warunków. Jeżeli a poprzedza b , to C(a )< C(b ). Należy pamiętać, że implikacja taka nie zachodzi w odwrotną stronę. Algorytm Lamporta całkowicie porządkuje wszystkie zdarzenia w systemie.
Znaczniki Lamporta a relacja uprzedniości
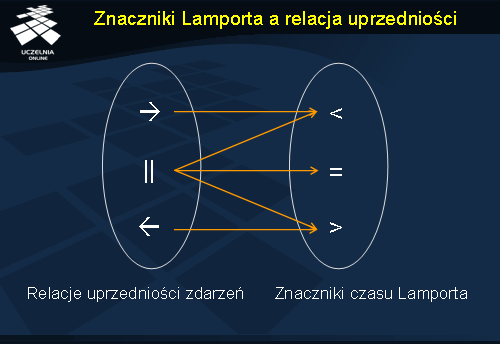
Na ilustracji przedstawiono w prosty sposób zależności między relacją uprzedniości zdarzeń a znacznikami czasu Lamporta. Zauważmy, że znając znaczniki czasu Lamporta nie jesteśmy w stanie określić relacji uprzedniości między zdarzeniami. Natomiast w przypadku, gdy jedno zdarzenie poprzedza drugie, znajduje to również swoje odzwierciedlenie w wartościach znaczników czasu Lamporta.
Wektorowe znaczniki czasu

Wektorowe znaczniki czasu (ang. vector timestamps ) są rozwinięciem koncepcji znaczników czasu Lamporta. Znaczniki czasu Lamporta pozwalają na całkowite uporządkowanie zdarzeń w systemie rozproszonym, ale na ich podstawie nie możemy stwierdzić jaki był związek między zdarzeniami. Na uchwycenie przyczynowości (ang. casuality ) pozwalają za to wektorowe znaczniki czasu.
Każdy proces jest wyposażony w zegar Vi , który jest wektorem liczb całkowitych i ma długość n , równą liczbie procesów w systemie. Zegar taki może być rozpatrywany w kategoriach funkcji, która przypisuje pewien wektor Vi(a ) każdemu zdarzeniu a . Vi(a ) jest określane jako znacznik czasowy zdarzenia a w procesie Pi . Wartość Vi[i ] (znana przez proces Pi ) jest równa liczbie zdarzeń jakie zaszły do tej pory w procesie Pi . Vi[j ] dla j różnego od i jest wartością zegara procesu Pj , jaką zna proces Pi . Innymi słowy, w dowolnym momencie czasu, j-ty element Vi wskazuje czas pojawienia się ostatniego zdarzenia procesu Pj , które poprzedza (w sensie relacji uprzedniości zdarzeń) bieżący moment czasu w procesie Pi .
Wartość zegara Vi jest zwiększana pomiędzy dowolnymi dwoma kolejnymi zdarzeniami w procesie Pi . Wektorowe znaczniki czasu przekazywane są razem z komunikatami. W ten sposób odbiorca jest powiadamiany o liczbie zdarzeń, które wystąpiły u nadawcy oraz u innych procesów, o których wiedział nadawca zanim wysłał komunikat. Po tym jak proces Pi otrzymuje od innego procesu Pj wektor v , aktualizuje własny ustawiając każdy wpis Vi[k ] na wartość maksimum{Vi[k ], v[k ]}.
Znaczniki wektorowe mają kilka istotnych cech. W każdym momencie czasu wartość Vi[i ] jest niemniejsza niż wartość Vj[i ]. Ponadto jeżeli w systemie wykorzystującym zegary wektorowe zdarzenie a poprzedza przyczynowo zdarzenie b , to zachodzi własność V(a )< V(b ). Co ważniejsze implikacja ta jest również prawdziwa w odwrotnym wypadku, czyli jeżeli wartość znacznika wektorowego dla zdarzenia a jest większa od znacznika zdarzenia b , to prawdą jest to, iż a poprzedza b .
Transakcje
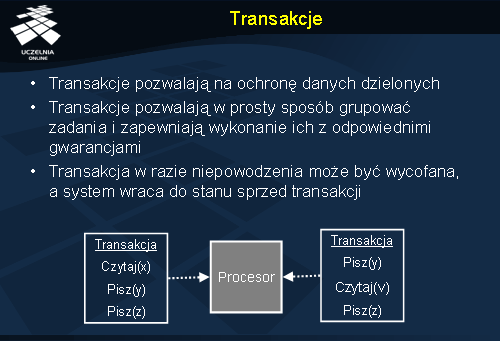
Pojęcie transakcji (ang. transaction ) wprowadza pewne zasady dotyczące operacji na współdzielonych zasobach. Transakcja określa m.in. kolejność w jakiej wykonywane są operacje. Ważną cechą transakcji jest ochrona dzielonych zasobów przed jednoczesnym dostępem współbieżnych procesów. Dają one również możliwość wykonywania pewnych operacji w sposób niepodzielny, mimo że tak naprawdę może to być grupa wielu mniejszych operacji na różnych danych. Poza tym jeśli taka transakcja jest wycofywana z pewnych powodów, stan systemu może być przywrócony do momentu sprzed rozpoczęcia wykonywania transakcji.
Transakcje były wykorzystywane głównie do tej pory w systemach bazodanowych, jednakże coraz szerzej stosowane są w systemach operacyjnych, również tych rozproszonych.
Model transakcji

Mówiąc o transakcjach, często odnosimy się do transakcji występujących w biznesie. Nieprzypadkowa jest tu zbieżność nazw np. transakcje bankowe. Weźmy operację przelewu, która składa się z dwóch mniejszych operacji: pobranie pieniędzy z jednego konta i dodanie ich do drugiego konta. Nietrudno sobie wyobrazić, co by było gdyby jedna z tych operacji się nie powiodła (pojawienie się nadmiaru pieniędzy lub ich zniknięcie).
Podobne sytuacje występują również w systemach komputerowych. Załóżmy, że istnieje proces, który współpracując z innymi procesami wykonuje jakieś operacje. Po ukończeniu tych operacji chce je zatwierdzić i pyta w tym celu inne procesy, czy się zgadzają. Gdy jeden z procesów nie wyrazi zgody, wszystkie operacje i ich skutki muszą być cofnięte.
Systemy plików również, mogą wykorzystywać zalety transakcji do grupowania operacji na plikach. Z pewnością pozwala to na łatwiejsze utrzymanie spójności całego systemu.
Do sterowania transakcjami istnieje zestaw kilku podstawowych funkcji elementarnych. Zasięg transakcji wskazywany jest odpowiednio przez dwie funkcje: początek_transakcji oraz koniec_transakcji. W celu zatrzymania i wycofania transakcji możemy użyć funkcji zaniechaj_transakcję . Do nadzorowania operacji wewnątrz transakcji służą z kolei np. funkcje czytaj i pisz .
Klasyfikacja transakcji
Transakcje można podzielić na: transakcje płaskie (najprostsze), transakcje zagnieżdżone oraz transakcje rozproszone. Kolejne slajdy omawiają poszczególne typy transakcji.
Cechy transakcji płaskich

Transakcje płaskie (ang. flat transactions ), definiowane jako ciąg operacji, są najczęściej używaną klasą transakcji. Posiadają one jednak cechy, które uniemożliwiają wykonanie pewnych przydatnych w praktyce czynności. Przeszkodą okazuje się głównie niemożność zatwierdzenia lub wycofania wyników częściowych.
Rozpatrzmy transakcję zakupu pewnej liczby książek za pomocą serwisu internetowego. Po wybraniu kilku interesujących nas książek składamy zamówienie (rozpoczynamy transakcję). Okazuje się jednak, że w rzeczywistości oferowane przez serwis internetowy książki znajdują się w odległych od siebie geograficznie magazynach. W tym momencie do każdego z magazynów musi spłynąć odpowiednie zamówienie na dostępne tam książki. W jakimś momencie transakcji może się okazać, że nie ma jednej z książek. Pojawia się pytanie co zrobić jeżeli niektóre magazyny przetworzyły już część globalnego zamówienia. Czy dać użytkownikowi możliwość zamówienia części książek? Jeżeli wszystkie zamówienia musiałyby być cofnięte, zostałby zmarnowany pewien być może niemały nakład pracy, a tymczasem użytkownik mimo braku książki chce kupić pozostałe. Jak łatwo zauważyć częściowe zatwierdzanie transakcji w tym wypadku byłby bardzo przydatne.
Drugą kwestią, jaka się pojawia w tym przykładzie, jest czas przetwarzania zamówień, który może się znacznie różnić w zależności od magazynu. Żeby nie tracić czasu, można by wysłać część książek do klienta wcześniej.
Transakcje zagnieżdżone
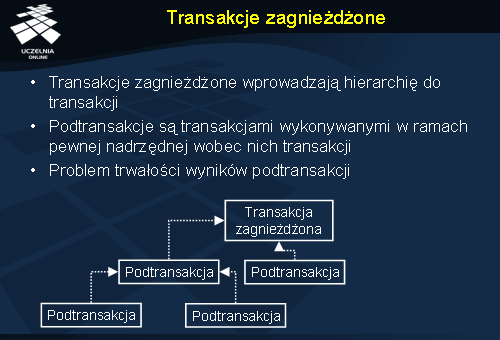
Niektórych problemów, które pojawiają się przy wykorzystywaniu transakcji płaskich, można się pozbyć korzystając z transakcji zagnieżdżonych (ang. nested transaction ).
Transakcja zagnieżdżona jest złożona z pewnej liczby podtransakcji (ang. subtransaction ). Każda transakcja w ramach transakcji zagnieżdżonej może również zawierać swoje podtransakcje itd. Podtransakcje mogą być wykonywane na różnych maszynach, jeżeli pozwoli to np. na zwiększenie efektywność przetwarzania.
Użycie podtransakcji implikuje pewien problem w postaci braku ich trwałości. Weźmy transakcja zagnieżdżoną, która składa się z pewnej liczby zatwierdzonych podtransakcji. Jeżeli taka transakcja zostanie teraz wycofana, jej skutki muszą być usunięte. Tym samym do wycofania zmuszone są zatwierdzone wcześniej podtransakcje.
W chwili rozpoczęcia, podtransakcja dysponuje stanem zasobów, jakie udostępniła jej transakcja nadrzędna. Kiedy podtransakcja zostaje zatwierdzona, wyniki jej działania stają się widoczne dla jej transakcji nadrzędnej, a tym samym dla wszystkich następujących po niej podtransakcji.
Transakcje rozproszone
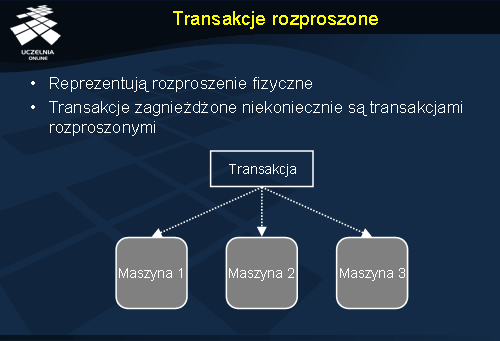
W powyższym przykładzie pojawił się jednak jeszcze jeden istotny element, którego nie analizowaliśmy: rozproszenie całego systemu. Transakcje zagnieżdżone nie stanowią od razu o tym, że dana transakcja działa w środowisku rozproszonym. Stanowi ona jedynie pewien sposób organizacji pracy systemu. W celu wyróżnienia transakcji, które działają na różnych maszynach, wprowadzono pojęcie transakcji rozproszonych (ang. distributed transactions).
Zdarzają się sytuacje, w których jedna transakcja musi mieć dostęp do danych w kilku miejscach jednocześnie. Mamy wtedy oczywiście do czynienia z transakcją rozproszoną, ale niekoniecznie zagnieżdżoną. Dla uwypuklenia głównej różnicy: transakcje zagnieżdżone stosuje się ze względu na logikę ich pracy, natomiast transakcje rozproszone ze względu na rozproszenie danych, na których operują.
Prywatna przestrzeń robocza
Transakcje są bardzo wygodnym sposobem organizowania pracy. Jednak, aby móc się o tym przekonać w praktyce, należy najpierw je jakoś zaimplementować. Do tego celu służą m.in. dwie metody. Jedną z nich zaprezentujemy poniżej, a drugą trochę później w dalszej części wykładu.
Pierwsze podejście polega na przypisaniu każdej transakcji, w momencie kiedy jest uruchamiana, prywatnej przestrzeni roboczej. W przestrzeni tej znajdują się wszystkie dane, do których transakcja ma dostęp. W trakcie działania transakcja operuje tylko na swojej prywatnej przestrzeni, a nie bezpośrednio na oryginalnych danych.
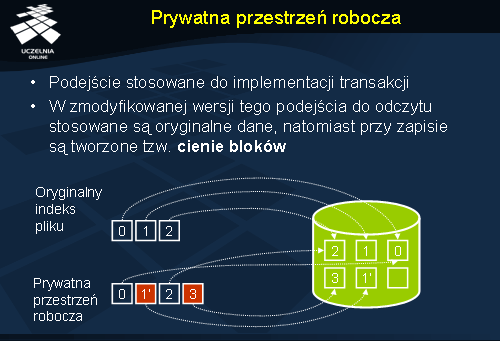
Istnieje kilka sposobów realizacji takiego pomysłu. Najprostszy z nich zakłada skopiowanie całości oryginalnych danych do przestrzeni roboczej transakcji. Ze względu na koszt kopiowania nie będziemy się dalej zajmować tą realizacją i przejdziemy do następnej zmodyfikowanej wersji. Przy realizacji drugiego sposobu wykorzystano spostrzeżenie, iż nie ma potrzeby tworzenia kopii danych, które są tylko odczytywane przez transakcję. Można tu wykorzystać oryginalne dane. Kolejna realizacja podejmuje problem zapisu. W tym celu transakcja kopiuje do swojej przestrzeni roboczej tylko tablicę odnośników do bloków potrzebnych plików z danymi. Podczas odczytu odczytywane są po prostu oryginalne dane, natomiast przy zapisie tworzona jest kopia modyfikowanego bloku (tzw. cienie bloków – ang. shadow blocks ) i dopiero do niego zapisywane są nowe dane. Po zatwierdzeniu takiej transakcji odnośniki do zmodyfikowanych bloków zastępują oryginalne bloki.
Ilustracja na slajdzie prezentuje przykład realizacji transakcji w systemie plików. Na potrzeby transakcji zapamiętywane są w jej przestrzeni roboczej indeksy bloków pliku, na których działa. Gdy transakcja modyfikuje blok 1, zostaje on skopiowany i powstaje cień bloku, 1’. Dodatkowo transakcja dodała nowy blok, do którego indeks pamiętany jest w prywatnej przestrzeni adresowej do czasu zatwierdzenia transakcji.
Rejestrowanie z wyprzedzeniem

Rejestrowanie z wyprzedzeniem (ang. writeahead log ) jest metodą realizacji transakcji, która pozwala na modyfikowanie oryginalnych plików, z których korzysta transakcja. Zanim jednak następuje sama operacja zapisu, fakt ten odnotowywany jest w specjalnym rejestrze w postaci rekordu z informacjami o transakcji, modyfikowanym przez nią pliku i bloku oraz nową i starą wartością bloku.
W momencie gdy transakcja zostaje zatwierdzona, do wspomnianego rejestru wpisywany jest tylko fakt samego zatwierdzania, gdyż dane zostały już wcześniej zaktualizowane. Kiedy jednak transakcja zostaje anulowana, przydatny okazuje się rejestr, który służy do przywrócenia stanu sprzed transakcji. Operacja przywracania polega w skrócie na odczytaniu od końca rekordów rejestru i wycofaniu (ang. rollback ) zapisanych w nim zmian.
Sterowanie współbieżnością

W celu zachowania spójnych danych, na których operują współbieżne procesy potrzebna jest specjalna kontrola. Za taką kontrolę odpowiedzialne jest sterowanie współbieżnością. Sterowanie to polega m.in. na udostępnianiu transakcjom odpowiednich danych w odpowiedniej kolejności. Wynik transakcji powinien być taki sam, jakby transakcje były uruchamiane szeregowo według pewnego porządku.
W celu lepszego zrozumienia metod sterowania współbieżnością, można wyróżnić w nim trzy elementy składowe w postaci zarządcy danych (ang. data manager ), planisty (ang. scheduler ) oraz zarządcy transakcji (ang. transaction manager ). Zarządca danych znajduje się na najniższym poziomie i zajmuje się rzeczywistymi operacjami odczytu i zapisu. Wyżej znajduje się planista, który odpowiada za właściwą politykę sterowania współbieżnością. Określa on kolejność operacji wykonywanych przez poszczególne transakcje. Zapewni również spójność i izolację transakcji. Zarządca transakcji odpowiada głównie za zapewnienie niepodzielności transakcji i wysyłanie zleceń do planisty.
Sterowanie współbieżnością - problemy

Sterowanie współbieżnością transakcji napotyka na dwa zasadnicze problemy: problem utraconej aktualizacji oraz problem niespójnych odzyskań .
Zilustrujmy teraz problem utraconej aktualizacji na przykładzie dwóch współbieżnych transakcji, dokonujących operacji na wspólnej danej. Przypuśćmy, że istnieje pewna dana x równa 5, do której transakcja T1 chce dodać wartość 3, a transakcja T2 chce dodać wartość 2. Załóżmy, że scenariusz wykonania obu transakcji wygląda następująco: transakcja T1 odczytuje wartość x , chwilę później wartość x odczytuje transakcja T2 , transakcja T1 dodaje do x wartość 3, transakcja T2 dodaje do x 2. Ostatecznie wszystkie te operacje sprawiły, że x jest równy 7, mimo że powinien wynieść 10. Stało się tak dlatego, iż wartości x jaką modyfikowała transakcja T2 była nieaktualna w momencie zapisu. Innymi słowy transakcja T2 polegała na odczycie, który był nieaktualny.
Prześledźmy drugi przykład, w którym występuje z kolei problem niespójnych odzyskań. Znowu załóżmy, że mamy dwie współbieżne transakcje T1 i T2 , które operują na zmiennych x i y , które początkowo przyjmują odpowiednio wartości 5 i 4. Transakcja T1 odejmuje wartość 2 od x , a następnie dodaje ją do y . Transakcja T2 ma za zadanie zsumowanie wartości x i y . Scenariusz wykonania transakcji niech wygląda następująco: transakcja T1 odczytuje wartość x , transakcja T1 zmniejsza odczytaną wartość x o 2, transakcja T2 odczytuje wartość x , transakcja T2 odczytuje wartość y i sumuje z wcześniej odczytaną wartością, transakcja T1 odczytuje wartość y i dodaje do niej wartość 2. Suma uzyskana przez transakcję T2 wyniosła ostatecznie 7, a powinna oczywiście 9. Błąd, który został tu popełniony, to zsumowanie przez transakcję T2 wartości x i y , podczas gdy transakcja T1 wykonała się tylko częściowo.
Szeregowalność

Antidotum na niektóre problemy związane ze sterowaniem współbieżnością jest tzw. szeregowalność (ang. serializability ). Szeregowalność pozwala na zachowanie izolacji transakcji. Sprawia, że wynik kilku współbieżnych transakcji, jest identyczny z wynikiem, który uzyskalibyśmy gdyby te transakcje uszeregować w pewien sposób jedna po drugiej.
W ogólności transakcję można przedstawić jako ciąg operacji czytania i zapisywania danych. Sterowanie współbieżnością polega na właściwej obsłudze operacji konfliktowych, czyli takich które działają na wspólnych danych, z czego co najmniej jedna jest operacją zapisu.
W przypadku algorytmów sterowania współbieżnością istnieją dwie główne metody używane do synchronizacji zapisów i odczytów. Pierwsza z nich to metoda wzajemnego wykluczania przy dostępie do wspólnych danych. Druga to użycie znaczników czasowych do porządkowania operacji.
Oprócz tego rozróżnia się pesymistyczne i optymistyczne sterowanie współbieżnością. W przypadku metod pesymistycznych konflikty są usuwane zanim do nich dojdzie. Metody optymistyczne zakładają natomiast, że konflikty raczej nie wystąpią i odkładają synchronizacje na koniec, co grozi zaniechaniem transakcji.
Szeregowalność - przykład

Aby współbieżne transakcje mogły być wykonane prawidłowo ich plan wykonania (uporządkowanie operacji) musi uwzględniać szeregowalność. Jeżeli plan nie jest szeregowy, mówimy o nim, że jest planem niedopuszczalnym, a jego wykonanie daje błędne wyniki transakcji. W przeciwnym wypadku mamy do czynienia z planem dopuszczalnym, który tworzy wyniki zgodne z szeregowym wykonaniem transakcji.
Blokowanie dwufazowe

Algorytm blokowania dwufazowego (ang. two-phase locking – 2PL ) jest jedną z najpopularniejszych metod implementacji transakcji. Algorytm ten należy do ogólniejszej klasy algorytmów sterowania współbieżnością, które stosują blokowanie. Działanie takich algorytmów w najprostszym przypadku polega na założeniu blokady na danej, która ma być zapisana lub odczytana, a po wykonaniu operacji blokada jest zwalniana.
Algorytm blokowania dwufazowego składa się z dwóch faz: fazy wzrostu (ang. growing phase ) oraz fazy zmniejszania (ang. shrinking phase ). W pierwszej fazie transakcja może blokować zasoby, ale nie wolno jej zwalniać zasobów, które wcześniej już zablokowała. W drugiej fazie transakcja może zwalniać zasoby, lecz nie wolno jej blokować żadnych nowych zasobów. Jeżeli proces nie chce modyfikować danych dopóki nie osiągnie momentu przed fazą zmniejszania, to w razie niepowodzenia przy zakładaniu jakiejś blokady może on zwolnić wszystkie blokady i rozpocząć ponownie algorytm.
Kluczową własnością tego algorytmu jest fakt, że jeżeli wszystkie transakcje działają według schematu blokowania dwufazowego, to ich scenariusze utworzone na skutek przeplotu są uszeregowalne.
Istnieje kilka odmian tego algorytmu. Np. ścisłe blokowanie dwufazowe (ang. strict two-phase locking ) jest realizowane w systemach, gdzie faza zmniejszania nie występuje dopóki transakcja nie zostanie zakończona. Atutem takiego rozwiązania jest to, że transakcja zawsze czyta wartości zapisane tylko przez zatwierdzone transakcje. Ponadto operacjami blokowania i zwalniania może zająć się system, żeby nie angażować w tym celu transakcji.
Należy zwrócić uwagę na jeden istotny fakt, że algorytm blokowania dwufazowego nie uwalnia nas od problemu zakleszczenia, w wypadku gdy dwie transakcje ubiegają się o te same zasoby tylko w odwrotnej kolejności. Można tutaj wykorzystać pewien z góry ustalony porządek przydzielania zasobów. Inna metodą jest tworzenie i przechowywanie grafu procesów, które posiadają blokady. Jeszcze inne podejście bazuje, na znanym maksymalnym czasie przez jaki może być założona blokada, tak że po wykryciu blokady przez inny proces może on stwierdzić po pewnym czasie, że wystąpiło zakleszczenie.
Ilustracja blokowania dwufazowego
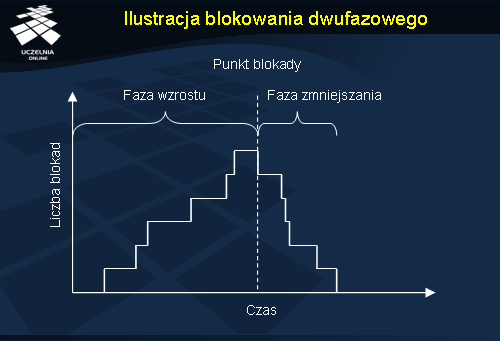
Na wykresie przedstawiono etapy działania algorytmu blokowania dwufazowego. Można zauważyć, że wraz z upływem czasu rośnie liczba założonych blokad. Gdy zostaną założone wszystkie blokady, następuje tzw. punkt blokady i może rozpocząć się przetwarzanie odpowiednich danych. Po zakończeniu operacji blokady są zwalniane, co ilustruje faza zmniejszania na wykresie.
Pesymistyczne porządkowanie według znaczników czasu

W wypadku wystąpienia konfliktu między operacjami, w pierwszej kolejności obsługiwana jest ta, która ma mniejszy znacznik czasowy.
Zobaczmy teraz co się dzieje w przypadku, kiedy planista otrzyma od transakcji T zlecenie na operację odczytu lub zapisu zmiennej x . Jeżeli transakcja zleca odczyt, planista porównuje wartości znacznika t transakcji z wartością tz(x ). Jeżeli wystąpił zapis na zmiennej x w momencie, kiedy transakcja T była już wykonywana, czyli gdy t < tz(x ), T musi zostać zaniechana. W przeciwnym wypadku T wykonuje operację, a wartość tc(x ) zostaje ustawiona na max[t , tc(x )].
Podobna sytuacja występuje dla operacji zapisu. Po nadejściu zlecenia zapisu, porównujemy wartości t oraz tc(x ). Jeśli t < tc(x ), transakcja zostaje zaniechana, gdyż zmienna x została w tym przypadku odczytana po rozpoczęciu transakcji T . Gdy zachodzi natomiast sytuacja odwrotna operacja może być wykonana, a wartość tz(x ) odpowiednio ustawiona na max[t , tz(x )].
Porównując ten algorytm do algorytmu blokowania dwufazowego, można zauważyć, że przeploty operacji, które są akceptowalne dla jednego algorytmu, niekoniecznie są akceptowalne dla drugiego i odwrotnie.
Zaletą tego algorytmu jest to, że uwalnia nas od problemu zakleszczania.
Porządkowanie pesymistyczne - przykłady
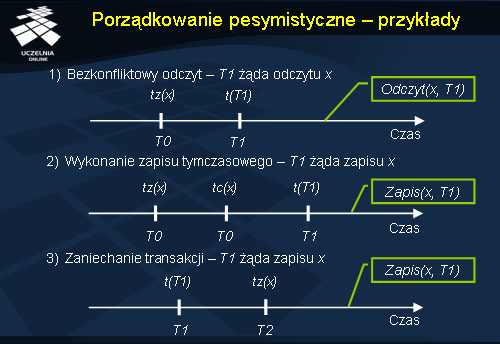
W prezentowanych przykładach zakładamy istnienie trzech transakcji T0 , T1 oraz T2 . Dodatkowo zakładamy, że transakcja T0 wykonywała się jako pierwsza przed rozpoczęciem pozostałych transakcji i korzystała z wszystkich danych, na których operują transakcje T1 oraz T2 . Oznacza to, że operacje zapisu i odczytu dla zmiennych są oznaczone na początku znacznikiem czasu transakcji T0 . Ponadto niech t(T1 ) < t(T2 ), czyli transakcja T1 rozpoczęła się przed transakcją T2.
Na początku rozpatrzmy odczyt zmiennej x przez transakcję T1 dla scenariusza przedstawionego w przykładzie 1. Transakcja T0 , która działała od dłuższego czasu wykonała zapis. Po tej operacji zapisu widzimy, że rozpoczęła się transakcja T1 i na tym kończy się sekwencja operacji. Nie występuje dalej żadna operacja zapisu na zmiennej x , która mogłaby powodować konflikt z operacją odczytu x . W związku z tym odczyt zmiennej x może być wykonany bezkonfliktowo.
Zajmijmy się teraz przykładem 2., gdzie transakcja T1 żąda zapisu zmiennej x . Są tu dwie kolejne operacje zapisu i odczytu x wykonane przez transakcję T0 . Po nich rozpoczyna się transakcja T1 , która chce następnie pisać do zmiennej x . Ponieważ transakcja T1 nie została jeszcze zatwierdzona, zapis wykonywany jest tymczasowo do momentu zatwierdzenia transakcji.
W ostatnim wypadku transakcja T1 również żąda zapisu x , ale w trakcie jej trwania, a przed żądanym przez nią zapisem, wystąpił zapis wykonany przez inną transakcję T2 . Transakcja T1 musi zostać zaniechana.
Optymistyczne porządkowanie według znaczników czasu

Ostatni algorytm to optymistyczne porządkowanie według znaczników czasu (ang. optimistic timestamp ordering ). Optymistyczne sterowanie współbieżnością transakcji jest kolejnym podejściem do jednoczesnego wykonywania kilku transakcji. Ogólna idea polega na tym, że transakcja jest wykonywana nawet w przypadku, kiedy występują konflikty. Ich rozwiązanie jest odkładane do czasu ewentualnego zatwierdzania. Jeżeli okaże się, że jakaś inna transakcja T1 zmieniła dane od czasu rozpoczęcia naszej transakcji T2 , to T2 zostaje zaniechana. W przeciwnym razie T2 zostaje zatwierdzona.
Zwróćmy uwagę, że wraz z zastosowaniem takiego podejścia do sterowania współbieżnością, można wykorzystać w transakcjach prywatną przestrzeń roboczą. W ten sposób każda transakcja może działać lokalnie bez przejmowania się innymi transakcjami.
Inną ważną cechą optymistycznego algorytmu jest brak zakleszczeń, gdyż transakcje w trakcie działania nie zajmują się konfliktami i działają dalej.