Wykład obejmuje wybrane zagadnienia z synchronizacji i jest kontynuacją poprzedniego wykładu, głównie zagadnień odnoszących się do synchronizacji zegarów fizycznych i logicznych, a także transakcji. Tematy poruszane w tym wykładzie są równie ważne i przydatne w kontekście synchronizacji w systemach rozproszonych.
Wykład składa się z trzech głównych części. W pierwszej części zajmiemy się algorytmami elekcji, które są bardzo istotne z punktu widzenia systemów rozproszonych, ponieważ są wykorzystywane w ramach innych algorytmów. Następnie przejdziemy do problematyki wzajemnego wykluczania. W trzeciej i ostatniej części wykładu poruszymy temat zakleszczeń w systemach rozproszonych.
Algorytmy elekcji

Algorytmy rozproszone wymagają często specjalnego procesu, który będzie koordynatorem działań innych procesów. Do wyboru koordynatora stosuje się tzw. algorytmy elekcji (ang. election algorithms).
Do ustalenia koordynatora niezbędna jest możliwość rozróżnienia procesów, które biorą udział w elekcji. W tym celu założymy, również na potrzeby prezentowanych algorytmów, że każdy proces ma przypisaną pewną unikalną liczbę, pewnego rodzaju identyfikator. Liczba taka pozwala w najprostszym przypadku znaleźć koordynatora np. poprzez wybór największej wartości liczbowej. Ponadto przyjmujemy, że każdy proces zna identyfikatory pozostałych procesów.
Prezentowane dalej algorytmy zasadniczo różnią się jedynie sposobem lokalizacji koordynatora. Poprawny algorytm elekcji powinien zapewnić, że jeżeli został wybrany proces-koordynator, to zgodziły się na to wszystkie inne procesy.
Algorytm tyrana

Algorytm tyrana (ang. bully algorithm ) jest pierwszym z dwóch algorytmów elekcji, które zaprezentujemy.
Kiedy proces zauważa, że koordynator nie odpowiada już na żądania, rozpoczyna elekcję.
Proces P wysyła wiadomość ELEKCJA do wszystkich procesów z wyższą liczbą. Jeżeli nikt nie odpowiada, P wygrywa elekcję i staje się koordynatorem. Jeżeli natomiast odpowie jeden z procesów o wyższej liczbie, to ten proces przejmuje zadanie.
W dowolnym momencie proces może otrzymać wiadomość ELEKCJA od jednego z procesów o niższej liczbie. Kiedy taka wiadomość dotrze, odbiorca odsyła z powrotem do nadawcy wiadomość potwierdzającą, że działa i przejmuje kontrolę. Odbiorca podtrzymuje wtedy proces elekcji, jeżeli jej nie przeprowadzał do tej pory.
W końcu wszystkie procesy za wyjątkiem jednego zaprzestają elekcji i właśnie ten jedyny proces staje się koordynatorem. Ogłasza on następnie swoje zwycięstwo poprzez rozesłanie do wszystkich procesów wiadomości z informacją, że jest nowym koordynatorem.
Algorytm tyrana - przykład

Na powyższej ilustracji znajduje się przykład wykonania algorytmu elekcji dla 8 procesów. Procesy oznaczone są kolejno numerami od 1 do 8.
Proces 8., który był do tej pory koordynatorem ulega awarii. Zauważył to proces 5., który rozpoczyna w tym momencie algorytm elekcji. Robi to rozsyłając do procesów o wyższych numerach (6, 7, 8) wiadomość ELEKCJA . Te odsyłają mu ODPOWIEDŹ , w celu powiadomienia go, że przejmują kontrolę nad algorytmem elekcji (za wyjątkiem 8., który nie działa). Następnie proces 6. i 7. wysyłają zapytanie do procesów o wyższych od siebie numerach. W ten sposób proces 7. nie otrzymuje żadnej odpowiedzi i zostaje koordynatorem, o czym informuje pozostałe procesy rozsyłając wiadomość KOORDYNATOR .
Algorytm pierścieniowy

Kolejnym prezentowanym algorytmem elekcji jest algorytm pierścieniowy.
Algorytm używa pierścienia, ale bez żetonu, który często występuje w algorytmach tego typu.
Gdy jakiś proces zauważy, że koordynator nie funkcjonuje, konstruuje wiadomość ELEKCJA zawierającą jego własny numer i wysyła ją do swojego następcy. Ten z kolei dodaje do listy w otrzymanej wiadomości swój numer i wysyła do swojego następcy itd. Dodanie numeru przez proces oznacza, że bierze on udział w wyborach, jako jeden z kandydatów na koordynatora.
Ostatecznie wiadomość dociera z powrotem do procesu który ją zapoczątkował. Typ wiadomości jest zmieniany na KOORDYNATOR i wiadomość puszczana jest w obieg jeszcze raz. Tym razem jednak w celu powiadomienia wszystkich procesów, kto jest koordynatorem (proces na liście o największym numerze).
Algorytm pierścieniowy - przykład
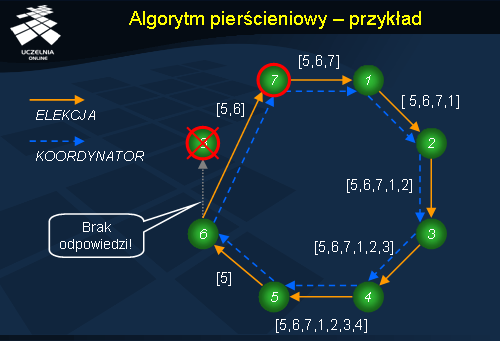
Prześledzimy teraz wykonanie pierścieniowego algorytmu elekcji dla 8 procesów. Załóżmy, że proces 8. był koordynatorem i uległ nagle awarii. Zauważył to proces 5., który rozpoczyna algorytm elekcji i wysyła wiadomość ELEKCJA , z dołączonym swoim numerem, do następnego procesu w pierścieniu. Proces, który odbierze wiadomość elekcja dołącza swój numer i przesyła dalej wiadomość do sąsiedniego procesu w pierścieniu. Wiadomość ELEKCJA jest przesyłana do momentu, aż nie dotrze do procesu 5. Ten oblicza ze wszystkich otrzymanych numerów największy dostępny i wysyła wiadomość KOORDYNATOR , która okrąża pierścień i powiadamia pozostałe procesy, że proces 7. zostaje nowym koordynatorem.
Wzajemne wykluczanie

Kolejnym problemem jakim się zajmiemy jest wzajemne wykluczanie. Temat wzajemnego wykluczania wywodzi się ze sposobu programowania systemów z wieloma procesami. Do tego celu wykorzystuje się sekcje krytyczne, które na czas wykonywania operacji na pewnych zasobach, zapewniają procesom wzajemne wykluczanie. Gdy proces wchodzi do sekcji krytycznej, może mieć pewność, że jakiś inny proces nie wejdzie do niej w tym samym czasie.
Wzajemne wykluczanie jest ważne także w systemach jednoprocesorowych, jednakże dalej zajmiemy się algorytmami, które są częściej stosowane w systemach rozproszonych.
Podejście scentralizowane

Spośród dostępnych procesów jeden wybierany jest jako koordynator. Kiedykolwiek proces chce wejść do sekcji krytycznej wysyła informację z żądaniem do koordynatora, określając do której sekcji krytycznej chce wejść i pytając zarazem o pozwolenie. Jeżeli w danej chwili żaden z procesów nie jest w tej sekcji krytycznej, koordynator odsyła odpowiedź udzielającą pozwolenia. Kiedy odpowiedź dotrze, proces, który ubiegał się o wejście do sekcji krytycznej, uruchamia ją. Natomiast gdy inny proces zapyta o pozwolenie na wejście do tej samej sekcji krytycznej, koordynator po prostu wstrzymuje się z odpowiedzią, blokując w ten sposób proces, który czeka na odpowiedź. Ewentualnie może np. odesłać odpowiedź z odmową wejścia do sekcji krytycznej.
Algorytm ten posiada kilka istotnych własności.
Jest sprawiedliwy w tym sensie, że procesy są obsługiwane są zgodnie z kolejnością żądań. Dodatkowo każdy z procesów w końcu, będzie mógł uruchomić swoją sekcję krytyczną. Innymi słowy algorytm nie powoduje zagłodzenia. Jest prosty w implementacji. Proces wejścia do sekcji krytycznej wymaga tylko trzech wiadomości.
Wadą algorytmu jest scentralizowany koordynator, który może ulec awarii.
Podejście scentralizowane - przykład
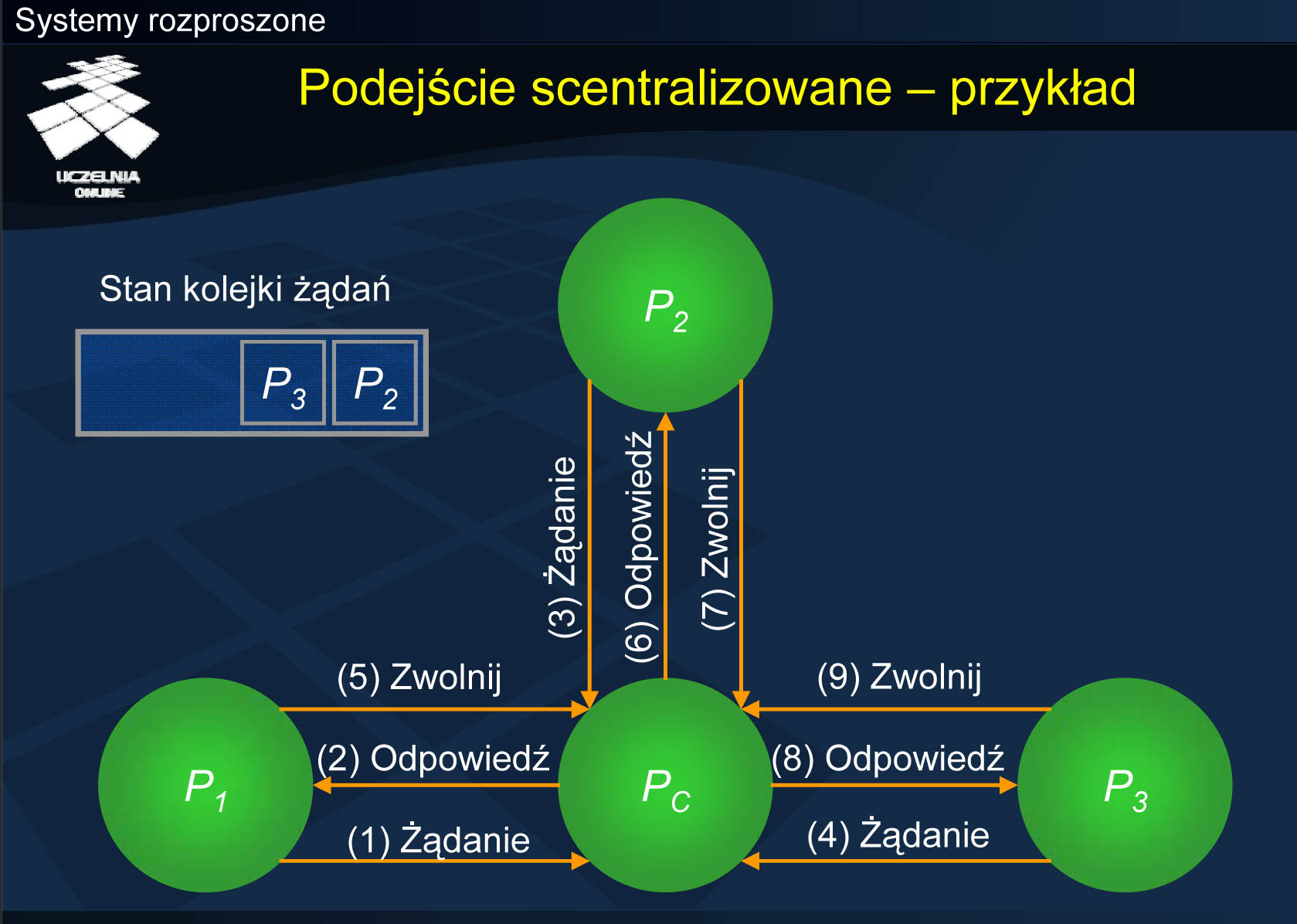
Niech proces Pc będzie koordynatorem, który kontroluje sekcje krytyczne. Załóżmy, że proces P1 chce wejść do sekcji krytycznej i wysyła żądanie do Pc . Ponieważ w danej sekcji krytycznej nikogo aktualnie nie ma, Pc odsyła odpowiedź z pozwoleniem na wejście do sekcji krytycznej do P1 . Następnie okazuje się, że procesy P2 i P3 również zgłaszają zapotrzebowanie na sekcję krytyczną, która jest aktualnie zajęta przez P1 . W związku z tym P2 i P3 zostają umieszczone w kolejce do późniejszego rozpatrzenia po zwolnieniu sekcji krytycznej przez P1 . Gdy P1 zakończyło wykonywanie sekcji krytycznej odsyła do Pc wiadomość zwalniającą, po czym Pc odsyła pozwolenie kolejnemu procesowi w kolejce oczekujących na sekcje krytyczną (proces P2 ). Po zwolnieniu sekcji przez P2 , dostęp do niej uzyskuje P3 .
Algorytm Lamporta - wprowadzenie

Lamport był pierwszym, który podał rozproszony algorytm wzajemnego wykluczania, jako przykład zastosowania wymyślonego przez siebie schematu synchronizacji zegarów.
Jako Ri oznaczmy zbiór żądań (ang. request set ) procesu Pi , tzn. zbiór procesów, od których Pi wymaga pozwolenia, kiedy chce się dostać do sekcji krytycznej. W algorytmie Lamporta zbiór żądań każdego procesu jest zbiorem wszystkich innych procesów. Każdy proces Pi utrzymuje kolejkę kolejka_żądań(i ), która zawiera żądania wejścia do sekcji krytycznej uszeregowane według ich znaczników czasowych. Algorytm ten wymaga, aby wiadomości dostarczane były pomiędzy każdą parą procesów w kolejności FIFO (ang. First In , First Out – pierwszy na wejściu, pierwszy na wyjściu).
Algorytm Lamporta

Gdy proces Pi zamierza wejść do sekcji krytycznej, wysyła wiadomość z żądaniem do wszystkich procesów, które znajdują się wewnątrz jego zbioru żądań Ri . Następnie umieszcza żądanie w swojej kolejce żądań (ts(i ) jest znacznikiem czasowym żądania procesu Pi ). Gdy proces Pj otrzyma żądanie od procesu Pi , odsyła ODPOWIEDŹ oznaczoną znacznikiem czasowym do procesu Pi i umieszcza żądanie procesu Pi w swojej kolejce żądań. Proces Pi rozpoczyna wykonywanie sekcji krytycznej, gdy spełnione są dwa następujące warunki: 1) proces Pi otrzymał wiadomość ze znacznikiem czasowym większym niż ( ts(i ), i ) od wszystkich innych procesów oraz 2) żądanie procesu Pi jest na początku jego własnej kolejki żądań
Po wyjściu z sekcji krytycznej proces Pi usuwa żądanie ze swojej kolejki żądań i wysyła wiadomości ZWOLNIJ oznaczoną znacznikiem czasowym do wszystkich procesów, znajdujących się w jego zbiorze żądań. Jeżeli proces Pj otrzyma wiadomość zwolnij od procesu Pi , usuwa żądanie Pi ze swojej kolejki żądań.
Kiedy proces usuwa pewne żądanie ze swojej kolejki żądań, jego własne żądanie może pojawić się na początku kolejki, umożliwiając mu wejście do sekcji krytycznej. Algorytm wykonuje żądania wejścia do sekcji krytycznej w rosnącym porządku i zgodnie z ich znacznikami czasowymi.
Algorytm Lamporta - przykład
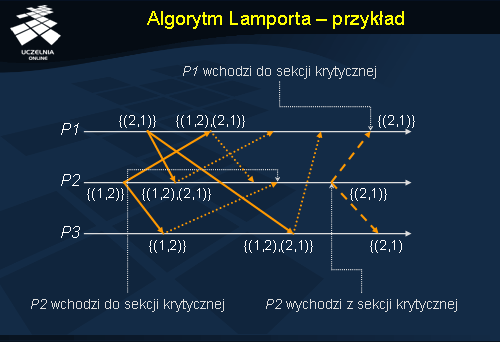
Prześledzimy teraz działanie algorytmu Lamporta na przykładzie 3 procesów. Proces P2 chce wykonać sekcję krytyczną i wysyła żądanie oznaczone znacznikiem czasu (1, 2) do procesów P1 oraz P2 . W międzyczasie do sekcji krytycznej chce wejść również proces P1 i również wysyła żądania ze znacznikiem (2, 1) do pozostałych procesów P2 oraz P3 . Odpowiednie procesy odsyłają odpowiedzi opatrzone znacznikami czasowymi tzn. P1 i P3 do P2 , a P2 i P3 do P1 . W tym momencie procesy P1 i P2 otrzymały wszystkie niezbędne odpowiedzi, ale to proces P2 otrzymuje pozwolenie na wejście do sekcji krytycznej, ponieważ znacznik czasu jego żądania jest najmniejszy, a samo żądanie znalazło się na początku kolejki. Po wyjściu z sekcji krytycznej P2 wysyła wiadomość zwalniającą do P1 oraz P3 . Po otrzymaniu tej wiadomości żądanie P1 znajduje się na szczycie jego kolejki i P1 może wejść do sekcji krytycznej.
Algorytm Ricarta i Agrawali

Algorytm Ricarta i Agrawali jest zoptymalizowana wersją algorytmu Lamporta, która obywa się bez wiadomości ZWOLNIJ (sekcję krytyczną) poprzez sprytne połączenie ich z wiadomościami typu ODPOWIEDŹ.
Gdy proces Pi chce wejść do sekcji krytycznej, wysyła wiadomość z żądaniem oznaczoną znacznikiem czasowym do wszystkich procesów, które znajdują się w jego zbiorze żądań. W momencie gdy proces Pj otrzyma żądanie od procesu Pi , wysyła odpowiedź do procesu Pi pod warunkiem, że nie zachodzi jedna z następujących sytuacji: 1) proces Pj wykonuje sekcję krytyczną, 2) proces Pj żąda wykonania sekcji krytycznej, a znacznik czasowy jego żądania jest mniejszy niż znacznik czasowy żądania procesu Pi . Jeżeli zachodzi, któraś z tych dwóch sytuacji, żądanie procesu Pi jest odkładane i trafia do kolejki żądań w procesie Pj.
Proces Pi wchodzi do sekcji krytycznej po otrzymaniu wiadomości ODPOWIEDŹ od wszystkich procesów, które są w jego zbiorze Ri . W chwili kiedy proces Pi kończy wykonywanie sekcji krytycznej wysyła odpowiedzi na wszystkie odłożone wcześniej żądania, a następnie usuwa je z kolejki.
Odpowiedzi na żądania procesu blokowane są tylko przez procesy, które ubiegają się o wejście do sekcji krytycznej i mają wyższy priorytet tzn. mniejszy znacznik czasowy. W ten sposób, gdy proces odsyła wiadomość typu odpowiedź na wszystkie odroczone żądania, proces, który ma kolejny najwyższy priorytet żądania, otrzymuje ostatnią niezbędną odpowiedź i wchodzi do sekcji krytycznej. Innymi słowy sekcje krytyczne w algorytmie Ricarta i Agrawali wykonywane są w kolejności zgodnej z wartościami znaczników czasowych ich żądań.
Algorytm Ricarta i Agrawali - przykład
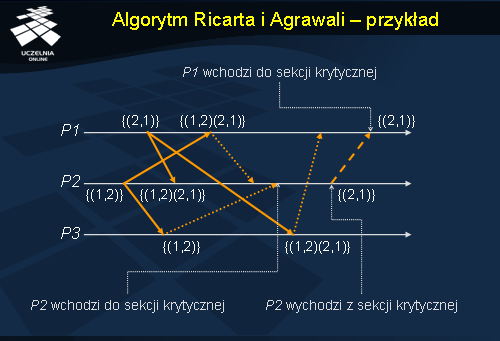
Rozpatrzmy przykład wykonania algorytmu Ricarta i Agrawali dla 3 procesów. Algorytm początkowo przebiega podobnie jak w przypadku przykłady dla algorytmu Lamporta. Dwa procesy P1 oraz P2 wysyłają żądania na wejście do sekcji krytycznej. P3 odsyła odpowiedzi do P1 i P2 , P1 odsyła odpowiedź do P2 . W międzyczasie P2 , otrzymało wszystkie niezbędne odpowiedzi i jego własne żądanie znalazło się z najmniejszym znacznikiem na szczycie lokalnej kolejki, wchodzi do sekcji krytycznej. Dopiero po wyjściu z sekcji krytycznej P2 odsyła odpowiedź do P1 , które może wtedy wejść do sekcji krytycznej.
Algorytm Maekawy - wprowadzenie

Algorytm Maekawy różni się od typowych algorytmów wzajemnego wykluczania. Świadczą o tym głównie dwie jego własności.
Po pierwsze proces, który chce wejść do sekcji krytycznej, nie żąda pozwolenia od wszystkich procesów, ale tylko od pewnego ich podzbioru. Jest to znacząco różne podejście w stosunku do algorytmu Lamporta i algorytmu Ricarta i Agrawali, gdzie wszystkie procesy uczestniczą w rozwiązywaniu konfliktu. W algorytmie Meakawy zbiory procesów, do których wysyłane są żądania, wybierane są w taki sposób, aby iloczyn dowolnych dwóch różnych zbiorów był zbiorem niepustym. W rezultacie tego każda para procesów, posiada proces, który pośredniczy między nimi w rozwiązywaniu ewentualnych konfliktów.
Po drugie w algorytmie Maekawy dowolny proces może wysłać naraz tylko jedną odpowiedź. Ponadto procesowi wolno wysłać odpowiedź tylko po otrzymaniu wiadomości typu ZWOLNIJ , która dotyczy poprzedniej wiadomości ODPOWIEDŹ . Z tego powodu proces Pi , zanim wejdzie do sekcji krytycznej, blokuje wszystkie pozostałe procesy, które razem z nim należą do pewnego podzbioru procesów oznaczonego przez Ri (zwanego dalej również podzbiorem żądań procesu Pi ).
Konstrukcja zbioru żądań w alg. Maekawy

Konstrukcja zbioru żądań w algorytmie Maekawy wymaga, aby spełnionych było kilka warunków.
Ponieważ istnieje co najmniej jeden wspólny proces pomiędzy podzbiorami żądań dowolnych dwóch procesów (warunek M1 ), każda para procesów posiada wspólny proces, który pośredniczy w rozwiązywaniu konfliktów pomiędzy nimi. W danej chwili proces może posiadać co najwyżej jedną zaległą wiadomość typu ODPOWIEDŹ . Oznacza to, że gdy przychodzi żądanie wejścia do sekcji krytycznej, proces udziela pozwolenia na jej wykonanie, jeżeli nie udzielił go wcześniej jakiemuś innemu procesowi. W ten sposób zapewnione jest wzajemne wykluczanie.
Warunki M1 i M2 są niezbędne dla poprawności, podczas gdy warunki M3 i M4 wprowadzają inne pożądane cechy algorytmu. Warunek M3 określa równy rozmiar podzbiorów żądań wszystkich procesów. Oznacza to, że wszystkie procesy powinny wykonywać, równą ilość pracy, w celu wzajemnego wykluczania. Warunek M4 wymusza, aby dokładanie ta sama liczba procesów żądała pozwolenia od dowolnego procesu. Innymi słowy wszystkie procesy ponoszą odpowiedzialność za udzielania pozwolenia innym procesom.
Algorytm Maekawy

W pierwszym kroku algorytmu wzajemnego wykluczania Maekawy proces Pi , który ubiega się o wejście do sekcji krytycznej, rozsyła ŻĄDANIE(i ) do wszystkich procesów, od których wymaga pozwolenia (procesy ze zbioru żądań Ri procesu Pi ).
Kiedy proces Pj otrzyma komunikat ŻĄDANIE(i ), wysyła ODPOWIEDŹ(j ) do procesu Pi pod warunkiem, że nie wysłał już komunikatu z odpowiedzią od czasu otrzymania ostatniej wiadomości ZWOLNIJ . W przeciwnym wypadku komunikat z żądaniem trafia do kolejki, w celu jego późniejszego rozpatrzenia.
W momencie kiedy proces Pi otrzyma komunikaty typu ODPOWIEDŹ od wszystkich procesów ze zbioru Ri , może uruchomić swoją sekcję krytyczną.
Po wykonaniu sekcji krytycznej, proces Pi wysyła wiadomości ZWOLNIJ(i ) do wszystkich procesów w Ri . W wypadku kiedy proces Pj otrzyma komunikat ZWOLNIJ(i ) od procesu Pi , wysyła ODPOWIEDŹ do następnego oczekującego procesu, który jest w jego kolejce i usuwa go z niej. Jeżeli kolejka jest pusta, wtedy proces aktualizuje swój stan, tak aby odzwierciedlał fakt, iż proces nie wysłał żadnego komunikatu ODPOWIEDŹ.
Algorytm Maekawy - przykład
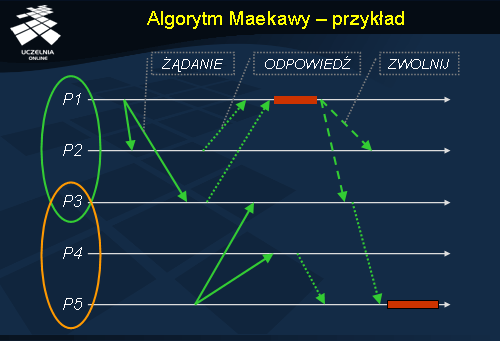
Na ilustracji przedstawiono działanie algorytmu Maekawy dla 5 procesów. Mamy tu dwie grupy procesów: {P1 , P2 , P3 } oraz {P3 , P4 , P5 }. Wspólnym procesem dla obu zbiorów jest proces P3.
Proces P1 żąda wejście do sekcji krytycznej i wysyła do wszystkich procesów {P2 , P3 } wewnątrz swojego zbioru żądań ŻĄDANIE . Procesy P2 i P3 , ponieważ nikomu wcześniej nie przydzieliły pozwolenia na wejście do sekcji krytycznej, odsyłają do P1 pozwolenie na wejście do sekcji krytycznej (ODPOWIEDŹ ). P1 wchodzi do sekcji krytycznej. W tym czasie do sekcji krytycznej chce się również dostać proces P5 i wysyła ŻĄDANIE do procesów ze swojego zbioru żądań {P3 , P4 }. Ponieważ P3 przydzieliło wcześniej już pozwolenie na wejście do sekcji krytycznej P1 , w danym momencie nie może odesłać odpowiedzi do P5 . Natomiast P4 wysyła odpowiedź do P5.
Po zakończeniu sekcji krytycznej P1 , wysyła wiadomość ZWOLNIJ do procesów P2 oraz P3 . P3 z kolei może już odesłać odpowiedź do P5. P5 wchodzi do sekcji krytycznej.
Algorytm Suzuki-Kasami - wprowadzenie

W algorytmie, który zaproponowali Suzuki i Kasami, jeżeli proces próbuje się dostać do sekcji krytycznej i nie ma żetonu, rozsyła wiadomość z żądaniem o żeton do wszystkich inny procesów. Proces, który posiada żeton, wysyła go do procesu, który go żądał po otrzymaniu wiadomości ŻĄDANIE . Jeżeli proces otrzyma wiadomość z żądaniem w trakcie wykonywania sekcji krytycznej, wysyła żeton chwilę po tym jak wyjdzie z sekcji krytycznej. Proces, który posiada żeton może wchodzić do sekcji krytycznej dopóty dopóki nie odeśle żetonu innemu procesowi.
Głównymi problemami projektowymi w tym algorytmie są: rozróżnianie przedawnionych żądań od bieżących oraz określenie, który proces ma zaległe żądanie sekcji krytycznej.

Przedawnione żądania są rozróżniane od bieżących w następujący sposób. Wiadomość typu ŻĄDANIE procesu Pj ma postać ŻĄDANIE(j , n ), gdzie n = 1,2 ,… jest liczbą porządkową, która wskazuje, że proces Pj żąda n-tego wykonania sekcji krytycznej. Proces Pi przechowuje tablicę liczb całkowitych RNi[1 .. N ], gdzie RNi[j ] jest największą liczbą porządkową otrzymaną do tej pory w żądaniu od procesu Pj . ŻĄDANIE(j , n ) otrzymane przez proces Pi jest przedawnione jeżeli RNi[j ]> n . Kiedy proces Pi otrzymuje ŻĄDANIE(j , n ), to zmienia RNi[j ]:= max(RNi[j ], n ).

Procesy z zaległymi żądaniami sekcji krytycznej są określane przy użyciu zawartości żetonu. Żeton składa się z kolejki żetonu Q oraz tablicy żetonu LN , gdzie Q jest kolejką procesów żądających, natomiast LN jest tablicą o rozmiarze N , taką że LN[j ] jest liczbą porządkową żądania, które proces Pj wykonał jako ostatnie. Po wykonaniu swojej sekcji krytycznej, proces Pi aktualizuje LN[i ]:= RNi[i ], aby wskazywało, że żądanie odpowiadające liczbie porządkowej RNi[i ] zostało spełnione. Tablica żetonu LN[1 .. N ] pozwala procesowi ustalić czy jakiś inny proces ma zaległe żądanie sekcji krytycznej. Zauważmy, że jeżeli dla procesu Pi mamy RNi[j ]= LN[j ]+ 1 , wtedy proces Pj jest w stanie żądania żetonu. Po wykonaniu sekcji krytycznej, proces sprawdza ten warunek dla wszystkich wartości j , żeby określić wszystkie procesy, które żądają żetonu oraz umieszcza ich identyfikatory w kolejce Q , jeżeli do tej pory ich tam nie ma. Następnie proces ten wysyła żeton do procesu, który znajduje się na początku kolejki Q .
Algorytm Suzuki-Kasami

Algorytm składa się z następujących kroków. Jeżeli proces który żąda wejścia do sekcji krytycznej, nie posiada żetonu, zwiększa swoja liczbę porządkową, RNi[i ], i wysyła ŻĄDANIE(i , sn ) do wszystkich innych procesów (sn jest zaktualizowaną wartością RNi[i ]).
Gdy proces Pj odbierze tę wiadomość, zmienia RNj[i ] na max(RNj[i ], sn ). W wypadku kiedy Pj ma bezczynny żeton, wysyła go do procesu Pi pod warunkiem, że RNj[i ]= LN[i ]+ 1 .
Kiedy proces Pi otrzymuje żeton, uruchamia sekcję krytyczną.
Po ukończeniu sekcji krytycznej, proces Pi wykonuje niniejsze czynności. Zmienia wartość elementu tablicy żetonu LN[i ] na RNi[i ]. Dla każdego procesu Pj , którego identyfikatora nie ma w kolejce żetonu, dodaje jego identyfikator do tej kolejki, jeśli spełniony jest warunek RNi[j ]= LN[j ]+ 1 . Jeżeli kolejka żetonu nie jest pusta po powyższych aktualizacjach, to proces Pi usuwa identyfikator z początku kolejki i wysyła żeton do procesu oznaczonego tym identyfikatorem.
W ten sposób, po wykonaniu sekcji krytycznej, proces nadaje priorytet innym procesom z zaległymi żądaniami sekcji krytycznej (priorytet, który przewyższa jego bieżące żądania w toku).
Algorytm ten nie jest symetryczny, ponieważ proces zachowuje żeton nawet, jeśli sam nie żąda wejścia do sekcji krytycznej. Jest to przeciwieństwem koncepcji algorytmu symetrycznego autorstwa Ricarta i Agrawali, gdzie „żaden proces nie posiada prawa dostępu do swojej sekcji krytycznej, jeżeli nie było takiego żądania”.

W algorytmie Raymonda, który bazuje na drzewie, procesy są logicznie zorganizowane w postaci skierowanego drzewa, takiego, że jego krawędzie wskazują w kierunku procesu, posiadającego żeton (korzeń drzewa). Każdy proces ma lokalną zmienną posiadacz , która wskazuje na sąsiedni proces w skierowanej ścieżce do korzenia. Tym sposobem zmienna posiadacz , definiuje w procesach strukturę logicznego drzewa procesów. Jeśli podążymy za wartościami zmiennych posiadacz w procesach, zobaczymy że każdy proces znajduje się na skierowanej ścieżce prowadzącej do procesu z żetonem. Wartość posiadacz korzenia, wskazuje na niego samego.
Każdy proces P utrzymuje kolejkę FIFO, oznaczaną jako kolejka_żądań , która przechowuje żądania tych sąsiednich procesów, które wysłały żądanie do procesu P , ale nie wysłano do nich jeszcze żetonu.
Algorytm Raymonda

Kiedy proces Pi chce wejść do sekcji krytycznej, wysyła ŻĄDANIE do procesu (wskazywany przez posiadacza ), wzdłuż skierowanej ścieżki prowadzącej do korzenia, pod warunkiem że nie posiada żetonu i jego kolejka_żądań jest pusta. Następnie Pi dodaje swoje żądanie do swojej kolejki_żądań(i ). Należy zauważyć, że niepusta kolejka_żądań procesu oznacza, że wysłał on ŻĄDANIE do korzenia, które odnosi się do wpisu z początku kolejki.
Gdy proces Pj otrzyma ŻĄDANIE , umieszcza je w swojej kolejce i wysyła ŻĄDANIE wzdłuż skierowanej ścieżki do korzenia o ile nie wysłał jakiegoś innego ŻĄDANIA (które było następstwem otrzymanego wcześniej ŻĄDANIA i znalazło się w kolejce żądań).
W momencie gdy proces będący korzeniem drzewa (posiadacz żetonu), odbierze wiadomość z ŻĄDANIEM , wysyła żeton do procesu Pi , od którego otrzymał to ŻĄDANIE , a następnie zmienia zmienną posiadacz , tak aby wskazywała na proces Pi.
Kiedy proces Pk otrzyma żeton, usuwa wpis ze szczytu swojej kolejki_żądań , wysyła żeton do procesu Pj wskazywanego przez ten wpis oraz zmienia zmienną posiadacz na proces Pj . Jeśli w tym momencie kolejka_żądań jest niepusta , to proces wysyła ŻĄDANIE do procesu, który jest wskazany przez zmienną posiadacz .

Proces Pi wchodzi do sekcji krytycznej w chwili gdy dostaje żeton, a jego własny wpis jest na szczycie jego kolejki_żądań . W tym wypadku, proces Pi kasuje początkowy wpis ze swojej kolejki_żądań i wchodzi do sekcji krytycznej.
Po ukończeniu sekcji krytycznej proces Pi , jeżeli jego kolejka żądań jest niepusta, kasuje wpis z początku swojej kolejki, wysyła żeton do odpowiedniego procesu Pj i ustawia zmienną posiadacz na Pj . Jeśli kolejka procesu Pi jest wciąż niepusta, wtedy proces wysyła ŻĄDANIE do procesu, który jest wskazany przez zmienną posiadacz.
Algorytm Raymonda - przykład

Proces P5 żąda żetonu. Żądanie dociera do aktualnego korzenia, którym jest proces P1 . Korzeń po otrzymaniu żądania, przekazuje żeton do P5 . Należy zauważyć, że w trakcie działanie algorytmu zmieniają się zmienne posiadacz , a wraz z nimi struktura drzewa.
Zakleszczenia

W systemach rozproszonych często pojawia się sytuacja, gdy dwa lub więcej procesów rywalizuje o pewne zasoby. Jeżeli zasoby w danym momencie będą niedostępne, procesy mogą być zmuszone do przejścia na jakiś czas w stan oczekiwania. Może się jednak zdarzyć, że jakiś zasób zostanie zablokowany przez pewien proces na czas z góry nieokreślony. W zaistniałej sytuacji inne procesy muszą oczekiwać na zasób, do którego nigdy nie będą miały dostępu. W tym wypadku mamy do czynienia z tzw. zakleszczeniem (ang. deadlock ).
Zagadnienie zakleszczenia pojawia się często w kontekście środowisk wieloprogramowych. W dalszej części wykładu skupimy się na problematyce zakleszczeń w systemach rozproszonych, a tym samym nie będziemy zajmować się pewnymi kwestiami, które wynikają ze środowisk nierozproszonych.
Warunki konieczne zakleszczenia

Aby wystąpiło zakleszczenie muszą być spełnione pewne warunki.
Po pierwsze musi występować wzajemne wykluczanie . Oznacza to, że jeśli w danej chwili zasobu używa jeden proces, to nie może z niego równocześnie korzystać inny.
Kolejnym warunkiem koniecznym do wystąpienia zakleszczenia jest istnienie procesu, który korzysta z jakiegoś zasobu, a jednocześnie sam oczekuje na przydział zasobu blokowanego przez inny proces.
Zakleszczenie warunkuje również brak możliwości wywłaszczania zasobów . Jeżeli proces blokuje zasób, tylko on może go zwolnić po zakończeniu swojej działania.
Ostatnim warunkiem, który nakłada się z dwoma poprzednimi, jest czekanie cykliczne . Polega to na tym, że istnieje ciąg procesów, z których każdy czeka na pewien zasób przetrzymywany przez kolejny proces w ciągu, a dodatkowo ostatni proces w ciągu czeka na zasoby przetrzymywane przez pierwszy proces w ciągu.
Graf przydziału zasobów
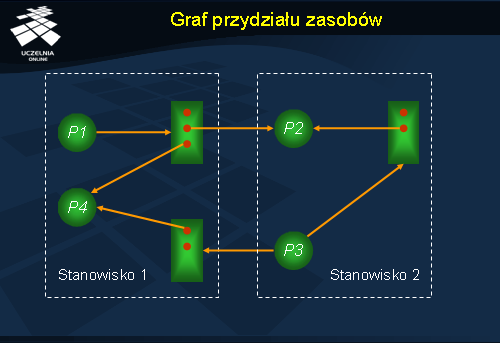
Do ilustracji i analizy zakleszczeń można posłużyć się tzw. grafami przydziału zasobów (ang. system resorce-allocation graph ). Zbiór wierzchołków takiego grafu podzielony jest na dwa zbiory: zbiór procesów oraz zbiór zasobów. Łuk, który biegnie od procesu Pi do zasobu Zj oznacza że proces chce użyć tego zasobu i czeka na niego. Jeżeli natomiast łuk biegnie od zasobu Zj do procesu Pi , oznacza to, że zasób został przydzielony procesowi. Stąd też krawędzie tego typu zwaną są odpowiednio: krawędzią zamówienia (ang. request edge ) oraz krawędzią przydziału (ang. assignment edge).
Na podstawie grafu przydziału zasobów można wykazać, że jeżeli w grafie nie występują cykle, to w systemie reprezentowanym przez ten graf nie ma zakleszczeń. W przeciwnym wypadku może pojawić się zakleszczenie.
W grafie przydziału zasobów na rysunku dla uproszczenia zasoby oznacza się prostokątami, a procesy kółkami. Egzemplarze zasobów rozróżnia się dodatkowo kropkami wewnątrz prostokątów (zasobów); gdy proces wysyła zamówienie na zasób, oznaczamy to krawędzią zamówienia dochodzącą do brzegu prostokąta, natomiast gdy proces otrzymuje przydział, to jest to konkretny egzemplarz zasobu i krawędź przydziału rozpoczyna się od kropki (egzemplarza zasobu).
Strategie postępowania z zakleszczeniami

W przypadku zakleszczeń można postępować na kilka sposobów. Po pierwsze można zapewnić, aby do zakleszczeń nigdy nie dochodziło. Po drugie można zezwalać na zakleszczenia, ale po ich wystąpieniu usuwać je. Można też zakleszczenia zupełnie ignorować.
W systemach, w których pojawienie się zakleszczenia nie jest pożądane, stosuje się m.in metody zapobiegania zakleszczeniom (ang. deadlock prevention ) i unikania zakleszczeń (ang. deadlock avoidance).
Zapobieganie zakleszczeniom polega w uproszczeniu na tym, aby nie dopuścić do zajścia któregoś z warunków koniecznych do wystąpienia zakleszczenia. Realizuje się to najczęściej poprzez nałożenie ograniczeń na porządek w jakim przydzielane są zasoby do procesów.
W metodach stosujących unikanie zakleszczeń, system stara się zebrać jak najwięcej informacji o zasobach z jakich będą korzystały procesy, tak aby podejmując później decyzje o przydziale zasobów mógł uniknąć zakleszczeń.
Zapobieganie zakleszczeniom w systemach rozproszonych

Wiele spośród algorytmów zapobiegania zakleszczeniom stosowanych w systemach nierozproszonych można zastosować również w środowiskach rozproszonych. Wymaga to oczywiście pewnych dodatkowych mechanizmów, jak m.in. odpowiedniego zastosowania globalnego porządku w systemie (np. wobec zasobów). Nieraz koszt takiego rozwiązania jest jednak nieopłacalny i trzeba zastosować inne rozproszone metody.
Poniżej prezentujemy zastosowanie znaczników czasowych, jako środek służący do zapobiegania zakleszczeń w systemach z wywłaszczaniem zasobów. Aby uprościć analizę, zakładamy istnienie jednego egzemplarza każdego zasobu.
W przedstawianym algorytmie każdy proces ma przypisany unikalny priorytet, który decyduje o tym, czy jeden proces powinien czekać na inny. Stosując informacje o priorytetach procesów, możemy nakazać, aby w razie konfliktu proces Pi o wyższym priorytecie mógł czekać na proces Pj o niższym priorytecie. W przeciwnym wypadku, gdy proces Pi ma niższy priorytet, usuwamy go z pamięci.
Stosując powyższy schemat pozbyliśmy się problemu zakleszczeń, ale pojawił się niestety problem w postaci możliwości zagłodzenia procesów o niskich priorytetach. Może się zdarzyć, że procesy takie będą wiecznie wywłaszczane przez procesy o wyższych priorytetach. W tym celu zaproponowano użycie znaczników czasowych i zaproponowano dwa podejścia do rozwiązania problemu. Unikalne znaczniki czasu nadaje się procesom raz, w trakcie ich utworzenia.
W pierwszej metodzie, zwanej czekanie albo śmierć (ang. wait-die ), nie używa się wywłaszczeń. Gdy proces Pi przetrzymuje zasób, którego chce użyć inny proces Pj , to Pj może poczekać aż zasób zostanie zwolniony tylko wtedy, gdy jego znacznik czasu jest mniejszy od znacznika czasu procesu Pi . W przeciwnym razie proces Pj jest usuwany z pamięci.
Zranienie albo czekanie (ang. wound-wait ) jest drugim zaproponowanym podejściem, które stosuje wywłaszczanie. W tym podejściu jeżeli proces Pj oczekuje zasobu używanego aktualnie przez Pi , to Pj może poczekać na zasób pod warunkiem, że znacznik czasu Pj jest większy. Inaczej Pj zostaje „zraniony”, czyli usunięty z pamięci.
Jak można zauważyć powyższe metody różnią się znacząco od siebie. Niemniej pozwalają na uniknięcie wcześniejszego problemu głodzenia, jeżeli usunięte procesy nie będą otrzymywały nowych znaczników.
Wadą obu schematów jest występowanie niepotrzebnych wywłaszczeń nawet, gdy nie ma zakleszczeń. W celu uniknięcia tego typu sytuacji można zastosować wykrywanie zakleszczeń.
Wykrywanie zakleszczeń
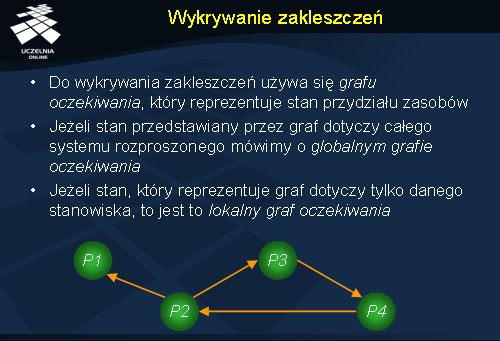
W algorytmach wykrywania zakleszczeń , konstruuje się tzw. graf oczekiwania (ang. wait-for graph ), który jest grafem skierowanym. Łuki w takim grafie reprezentują stan przydziału zasobów. Mając graf oczekiwania i wiedząc, czy istnieje w nim cykl możemy stwierdzić, czy mamy do czynienia z zakleszczeniem.
Wraz z pojęciem grafu oczekiwania w systemach rozproszonych, pojawiają się również pojęcia lokalnego i globalnego grafu oczekiwania.
Lokalny graf oczekiwania związany jest z danym stanowiskiem przetwarzania. Węzły w takim grafie odpowiadają procesom lokalnym lub zdalnym, które aktualnie utrzymują lub zamawiają zasoby lokalne na określonym komputerze. Zauważmy, że w ramach poszczególnych stanowisk, procesy mogą się powtarzać.
Globalny graf oczekiwania odnosi się do wszystkich stanowisk i otrzymywany jest w wyniku zsumowania lokalnych grafów oczekiwania.
Fakt, że lokalne grafy nie posiadają cykli nie oznacza, że nie występuje zakleszczenie. Może ono być widoczne dopiero w globalnym grafie. Zatem aby stwierdzić że w systemie rozproszonym występuje zakleszczenie, musimy znać globalny graf oczekiwania.
Na rysunku zilustrowano przykład zakleszczenie trzech procesów P2 , P3 oraz P4 .
Podejście scentralizowane

Centralnym elementem podejścia scentralizowanego jest koordynator wykrywania zakleszczeń (ang. deadlock-detection coordinator ). Jest to pojedynczy proces, którego głównym zadaniem jest utrzymanie globalnego grafu oczekiwania poprzez sumowanie lokalnych grafów. Ze względu na charakterystykę i opóźnienia panujące w systemie rozproszonym wiedza koordynatora o globalnym grafie oczekiwania nie zawsze jest kompletna i aktualna. Dlatego wprowadzono kolejne rozróżnienie między grafami oczekiwania: graf rzeczywisty odzwierciedlający rzeczywisty stan systemu oraz graf konstruowany , czyli taki jakim widzi go koordynator. Innymi słowy graf konstruowany jest pewnym przybliżeniem grafu rzeczywistego. Aby graf konstruowany był przydatny musi dać możliwość poprawnego wykrycia zakleszczeń.
Graf oczekiwania może być konstruowany na kilka sposobów. Informacje o globalnym grafie oczekiwania można aktualizować przy okazji każdej zmiany grafów lokalnych lub po uzbieraniu określonej liczby zmian. Istnieje także możliwość konstrukcji grafu w momencie gdy wywoływany jest algorytm wykrywania zakleszczeń.
W wypadku zastosowaniu pierwszego schematu aktualizacji grafu, gdy usuwany lub dodawany jest jakiś łuk do któregoś z lokalnych grafów, powiadamiany jest o tym koordynator, a następnie aktualizowany jest globalny graf oczekiwania. Na podstawie tego grafu koordynator wykrywa zakleszczenia i powiadamia odpowiednie stanowiska o swojej decyzji co do usunięcia lub wstrzymania niektórych procesów.
Graf oczekiwania konstruowany według powyższego schematu nie jest wolny od pewnych niedogodności w postaci np. fałszywych cykli (ang. false cycles ). Fałszywe cykle pojawiają się na skutek niedoinformowania koordynatora o aktualnie zwolnionych i przydzielonych zasobach. W ten sposób w grafie oczekiwania istnieje czasami łuk, którego nie ma w rzeczywistym grafie oczekiwania, a który to powoduje wykrycie nieistniejącego zakleszczenia. Niepotrzebne wycofania mogą się również pojawić, gdy procesy, które wcześniej powodowały zakleszczenie, są nagle usuwane bez wiedzy koordynatora.
Kolejna wersja algorytmu scentralizowanego zakłada, że aktualizacje grafu oczekiwania następują w trakcie wywoływania algorytmu wykrywania zakleszczeń. Przewagą tego algorytmu nad poprzednim jest brak wykrywania fałszywych zakleszczeń. Gdy proces Pi zamawia zasób od Pj , a oba procesy są na różnych stanowiskach, zamówienie opatrywane jest unikalnym znacznikiem czasu t . Tym samym krawędź zamówienia od Pi do Pj również posiada znacznik t . Ponadto krawędź ta wstawiana jest tylko do lokalnego grafu na stanowisku, gdzie przebywa proces Pi . W przypadku drugiego stanowiska wspomniana krawędź zamówienia jest wstawiana tylko wtedy, jeżeli stanowisko to otrzymało nowe zamówienie na zasób i nie może go od razu spełnić. Lokalne zamówienia nie są opatrywane znacznikami.
W momencie kiedy koordynator chce zbudować globalny graf oczekiwania, rozsyła do wszystkich stanowisk prośbę o dostarczenie grafów lokalnych. Po otrzymaniu wszystkich lokalnych grafów, składany jest graf globalny. Wierzchołkami globalnego grafu są wszystkie procesy w systemie, a do zbioru krawędzi trafiają te krawędzie z lokalnych grafów, które albo nie są oznaczone znacznikami czasu, albo posiadają znacznik i pojawiają się w więcej niż jednym lokalnym grafie oczekiwania. Jeżeli w tak skonstruowanym grafie występuje cykl, to w systemie jest zakleszczenie.
Podejście scentralizowane - przykład
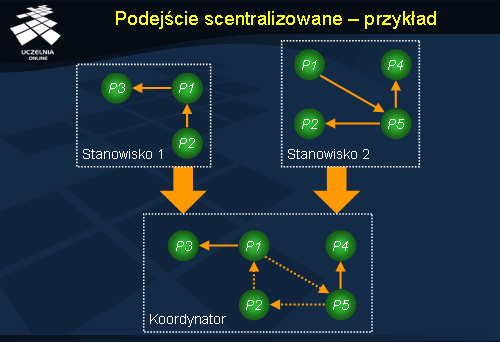
W podejściu scentralizowanym koordynator wykrywania zakleszczeń zbiera od różnych stanowisk lokalne grafy oczekiwania, a następnie konstruuje globalny graf oczekiwania. Na załączonej ilustracji możemy zobaczyć u koordynatora sumę dwóch grafów lokalnych ze stanowisk 1 i 2. Przerywaną linią oznaczono strzałki, które wspólnie tworzą wykryty cykl w globalnym grafie oczekiwania, a tym samym reprezentują zakleszczenie.
Podejście rozproszone

W przeciwieństwie do algorytmu scentralizowanego w podejściu rozproszonym konstrukcją globalnego grafu oczekiwania, a dokładniej jego części, zajmuje się wiele procesów. Odpowiedzialność za wykrywanie zakleszczeń jest więc podzielona pomiędzy tych kilka procesów. Jeżeli, któryś z takich procesów wykryje cykl w swojej części globalnego grafu, oznacza to, że wystąpiło zakleszczenie.
Graf lokalny każdego procesu różni się nieco od tego w algorytmie scentralizowanym, gdyż dodano do niego specjalny wierzchołek Pzew . Jeżeli istnieje łuk z pewnego procesu Pi do Pzew , to Pi czeka na zasób z innego stanowiska przetrzymywany przez dowolny proces. Jeżeli zachodzi sytuacja odwrotna tzn. pojawia się łuk od Pzew do Pi , znaczy to, że jakiś zdalny proces czeka na zasoby, do których dostęp ma w danej chwili lokalny proces.
Schemat działania algorytmu wygląda następująco. Jeżeli stanowisko wykryło w swoim grafie oczekiwania cykl, który nie zawiera Pzew , to w systemie jest zakleszczenie. Jeżeli cykl zawiera wierzchołek Pzew , to wykonywany jest algorytm rozproszony.
Jeżeli stanowisko Si wykryło cykl w grafie z wierzchołkiem Pzew , wysyła informacje o wystąpieniu zakleszczenia oraz dane o cyklu do stanowiska Sj , na którym znajduje się proces przetrzymujący aktualnie zasoby potrzebne procesowi czekającemu na Pzew . Stanowisko Sj po otrzymaniu informacji o wykryciu zakleszczenia, aktualizuje swój graf oczekiwania i szuka cyklu nie zawierającego Pzew . Jeżeli znajdzie, to jest zakleszczenie. Jeżeli w cyklu występuje natomiast Pzew , to informacje o wykryciu zakleszczenie wędrują do kolejnego stanowiska. Cała procedura powtarzana jest skończoną liczbę razy do momentu zakończenia algorytmu lub wykrycia zakleszczenia.
Do algorytmu wprowadzono pewną optymalizację komunikacji, tak aby w sytuacji, gdy kilka procesów wykryje zakleszczenie, nie wszystkie wysyłały o nim informację. Każdy proces oznaczono unikalnym identyfikatorem. Gdy stanowisko wykryje cykl, na który składa się ciąg procesów ( Pzew , P1 , P2 , …, PN , Pzew ), sprawdza czy zachodzi warunek identyfikator(PN ) < identyfikator(P1 ). Jeżeli warunek jest spełniony, informacja o zakleszczeniu jest wysyłana, w przeciwnym wypadku inicjatywę musi przejąć inne stanowisko.
Podejście rozproszone - przykład
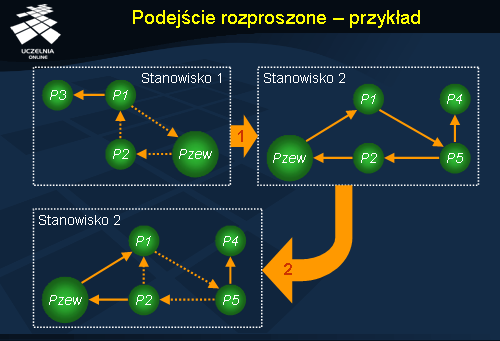
Na ilustracji przedstawiono przykładowy schemat działania rozproszonego algorytmu wykrywania zakleszczeń. Załóżmy, że stanowisko 1. wykryło cykl w swoim grafie oczekiwania Pzew ? P2 ? P1 ? Pzew. Cykl ten zawiera wierzchołek Pzew połączony z procesami P1 oraz P2 , co oznacza, że P1 oczekuje na zasoby przetrzymywane przez jakiś zdalny proces, natomiast P2 używa zasobów, których żąda również zdalny proces. Ponieważ stanowisko 2. zawiera proces P1 , który to na stanowisku 1. oczekuje na zwolnienie zasobów, graf ze stanowiska 1. przesyłany jest do stanowiska 2. Na stanowisku 2. lokalny graf oczekiwania sumowany jest z grafem otrzymanym ze stanowiska 1. W wyniku operacji sumowania okazało się, że uzyskany graf oczekiwania zawiera cykl P1 ? P5 ? P2 ? P1 , czyli zostało wykryte zakleszczenie.