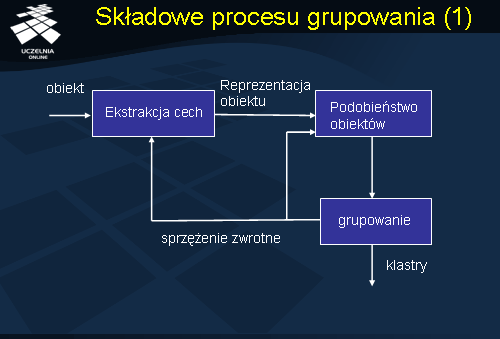
Proces grupowania jest procesem wieloetapowym i iteracyjnym. Punktem wyjścia jest charakterystyka zbioru grupowanych obiektów. Najczęściej, obiekt jest opisany licznym zbiorem bardzo heterogenicznych atrybutów o różnym stopniu znaczenia. Stąd, pierwszym etapem procesu jest wybór cech (atrybutów), które najlepiej charakteryzują dany typ obiektu. Wybór cech zależy również od celu grupowania. Przykładowo, grupując dokumenty tekstowe, informacja o dacie utworzenia dokumentu może być istotna, jeżeli proces grupowania ma uwzględniać datę, lub nie, jeżeli grupowanie ma na celu jedynie pogrupowanie tematyczne dokumentów. W wyniku selekcji cech otrzymujemy pewną abstrakcyjną reprezentację dokumentów. Kolejnym etapem procesu grupowania jest określenie miary podobieństwa pomiędzy grupowanymi obiektami. Miara ta silnie zależy od typu obiektów oraz od wybranej grupy cech opisujących obiekty – cechy mogą być opisane atrybutami kategorycznymi, liczbowymi, zbiorami danych, atrybutami sekwencyjnymi, czy wreszcie, atrybutami o charakterze multimedialnym.

Kolejnym etapem jest wybór metody grupowania, zależnej o reprezentacji obiektów, oraz konkretnego algorytmu grupowania. Po uruchomieniu algorytmu otrzymujemy zbiór klastrów. Może się okazać, że wybrana miara podobieństwa jest niewłaściwa powodując zniekształcenie wyniku grupowania (np. przyjęcie zwykłej miary odległości euklidesowej, ze względu na różnice zakresów atrybutów, może prowadzić do zniekształcenia wyniku na skutek dominacji pewnych cech nad innymi). Zachodzi wówczas potrzeba bądź transformacji zbioru obiektów (np. normalizacji atrybutów) lub przedefiniowania miary podobieństwa. Może się również okazać, że wynik grupowania jest niezadowalający ze względu na niewłaściwy wybór cech opisujących obiekty - zachodzi wówczas potrzeba ponownej redefinicji cech (selekcji cech) atrybutów – usunięcie pewnych atrybutów i dołączenie innych. Ostatnim etapem procesu grupowania jest analiza otrzymanych klastrów i próba znalezienia ogólnej charakterystyki klastrów. Przykładowo, analizując otrzymane klastry sekwencji dostępów do stron WWW, możemy je scharakteryzować jako sekwencje „muzyków” (użytkownicy poszukujący stron muzycznych), „turyści” (przeszukujący serwer poszukiwaniu informacji o hotelach, campingach, itd.
Miary odległości

Jak wynika z przedstawionego opisu składowych procesu grupowania, pierwszym etapem procesu jest ekstrakcja cech obiektów. Z braku miejsca i czasu, pominiemy ten etap procesu. Informacje na temat metod ekstrakcji cech można znaleźć w wielu podręcznikach dotyczących eksploracji i analizy danych. Kolejnym etapem jest etap wyboru miary podobieństwa pomiędzy obiektami. Najczęściej, podobieństwo dwóch obiektów, w procesie grupowania, definiujemy jako odległość dwóch obiektów zgodnie z pewną przyjęta miarą odległości. Przyjęta miara odległości, zależna od typu i charakterystyki grupowanych obiektów, powinna spełniać trzy podstawowe aksjomaty miary odległości (tzw. aksjomaty metryki). Po pierwsze, odległość obiektu x od obiektu y, D(x, y) = 0, wtedy i tylko tedy, gdy x=y. Miara odległości powinna być symetryczna, tj. D(x, y) = D(y, x). Wreszcie, miara odległości powinna spełniać nierówność trójkąta, tj D(x, y) ? D(x, z) + D(z, y). Przejdziemy obecnie do krótkiego przedstawienia i omówienia wybranych miar odległości.

Jeżeli grupowane obiekty można przedstawić w postaci k-wymiarowych wektorów liczbowych, wówczas każdy obiekt można traktować jako punkt w k-wymiarowej przestrzeni euklidesowej i za miarę odległości można przyjąć dowolną z tradycyjnych miar stosowanych dla tej przestrzeni. Najpopularniejsze miary odległości punktów w przestrzeni euklidesowej to odległość euklidesowa (tzw. norma L2), odległość Manhattan (tzw. norma L1), maksimum z wymiarów (tzw. norma L?), czy odległość Minkowskiego. Łatwo zauważyć, że wszystkie z podanych miar spełniają aksjomaty metryki odległości. Niestety, w przypadku, gdy obiekty nie poddają się transformacji do przestrzeni euklidesowej, proces grupowania wymaga zdefiniowania innych miar odległości (podobieństwa). Dotyczy to takich obiektów jak: sekwencje dostępów do stron WWW, sekwencje DNA, sekwencje zbiorów, zbiory atrybutów kategorycznych, dokumenty tekstowe, XML, grafy, itp. Przedstawimy obecnie kilka wybranych miar odległości stosowanych do grupowania wymienionych wyżej typów obiektów.

Inne miary odległości

Wróćmy do problemu grupowania dokumentów tekstowych (np. stron WWW), o którym wspominaliśmy już wcześniej. Założyliśmy, że każdy dokument jest opisany w postaci wektora słów pochodzących z pewnego słownika, nazywanego tezaurusem. Każdy dokument, w tej reprezentacji, można interpretować jako punkt w przestrzeni wielowymiarowej, w której pojedynczy wymiar odpowiada jednemu słowu z przyjętego słownika. Współrzędne dokumentu w tej przestrzeni są zdefiniowane względną częstością występowania słów ze słownika. Podobieństwo (lub inaczej mówiąc, odległość) D(x, y) dokumentów x i y można zdefiniować jako znormalizowany iloczyn skalarny wektorów reprezentujących x i y, tj. jako iloczyn skalarny obu wektorów podzielony przez iloczyn ich rozmiarów. Tak zdefiniowaną miarę nazywamy miarą kosinusową. Rozważmy następujący przykład. Załóżmy, że tezaurus składa się z 4 słów. Dokumenty x i y są opisane następującymi wektorami słów: x=[2, 0, 3, 1] i y=[5, 3, 2, 0]. Iloczyn skalarny dokumentów x i y wynosi 16.

Zauważmy, że tak zdefiniowana miara kosinusowa nie spełnia pierwszego z aksjomatów metryki. Jednakże, można łatwo zmodyfikować tą miarę, tak aby spełniała wszystkie aksjomaty metryki. Wystarczy przyjąć, że miarą odległości dwóch wektorów opisujących dokumenty x i y jest miara postaci D(x, y) = 1 – (x ? y)/|x| * |y|. Łatwo zauważyć, że teraz odległość dokumentu x i dokumentu y, gdzie y jest podwójna kopią x, wynosi 0.
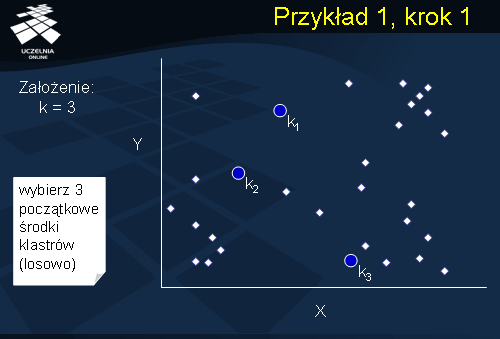
Przykład 1, krok 1
Rozważmy ponownie problem grupowania sekwencji dostępów do stron WWW, o którym wspominaliśmy już wcześniej. Definicja odległości (podobieństwa) sekwencji symboli powinna uwzględniać fakt, że sekwencje mogą mieć różną długość oraz różne symbole na tych samych pozycjach, np.: sekwencja x= abcde oraz sekwencja y= bcdxye. Popularną miarą odległości stosowaną do oceny podobieństwa sekwencji symboli jest tzw. miara LCS (ang. ang. longest common subsequence) – najdłuższej wspólnej podsekwencji. Odległość pomiędzy sekwencjami x i y definiujemy następująco: D(x, y) = |x| + |y| - 2 |LCS(x, y)|. Przykładowo, odległość pomiędzy sekwencją x= abcde a sekwencją y= bcdxye wynosi:
D(x, y) = 5 + 6 – 2* 4 = 3, gdyż LCS(x, y) = bcde. Łatwo zauważyć, że przedstawiona miara spełnia wszystkie aksjomaty metryki odległości.
Zmienne binarne

Przejdziemy obecnie do przedstawienia miar podobieństwa (lub niepodobieństwa) dla obiektów opisanych zmiennymi binarnymi. Dane są dwa obiekty „obiekt i” i „obiekt j”, oba opisane zbiorem p zmiennych binarnych. Konstruujemy macierz niepodobieństwa, przedstawioną na slajdzie, gdzie: q oznacza liczbę zmiennych przyjmujących wartość 1 dla obu obiektów, r oznacza liczbę zmiennych przyjmujących wartość 1 dla obiektu i, i wartość 0 dla obiektu j, s oznacza liczbę zmiennych przyjmujących wartość 0 dla obiektu i, i wartość 1 dla obiektu j, i t oznacza liczbę zmiennych przyjmujących wartość 0 dla obu obiektów.
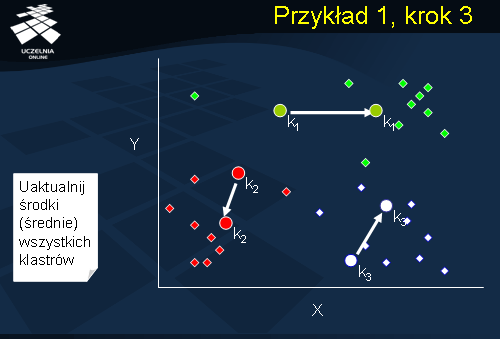
Przykład 1, krok 3
Definicja miary podobieństwa (lub niepodobieństwa), dla obiektów opisanych zmiennymi binarnymi, zależy od typu zmiennych binarnych. Wyróżniamy dwa typy zmiennych binarnych: zmienne binarne symetryczne i zmienne binarne asymetryczne. Zmienną binarną nazywamy symetryczną, jeżeli obie wartości tej zmiennej posiadają tą samą wagę (np. płeć). Tradycyjną miarą niepodobieństwa dwóch obiektów i i j, opisanych zmiennymi binarnymi symetrycznymi, jest stosunek (r + s)/p. Innymi słowy, niepodobieństwo dwóch obiektów i i j, opisanych zmiennymi binarnymi symetrycznymi, definiujemy jako stosunek liczby zmiennych, dla których oba obiekty posiadają różną wartość (r+s) do sumarycznej liczby wszystkich zmiennych p. Łatwo można się domyśleć, że miarą podobieństwa dwóch obiektów i i j, opisanych zmiennymi binarnymi symetrycznymi, będzie stosunek (q+t)/p, tj. stosunek liczby zmiennych, dla których oba obiekty posiadają identyczną wartość (q+t) do sumarycznej liczby wszystkich zmiennych p.
Zmienne binarne

Zmienną binarną nazywamy asymetryczną, jeżeli obie wartości tej zmiennej posiadają różne wagi (np. wynik badania EKG). Tradycyjną miarą niepodobieństwa dwóch obiektów i i j, opisanych zmiennymi binarnymi asymetrycznymi, jest stosunek (r + s)/(q+ r + s). Innymi słowy, niepodobieństwo dwóch obiektów i i j, opisanych zmiennymi binarnymi asymetrycznymi, definiujemy jako stosunek liczby zmiennych, dla których oba obiekty posiadają różną wartość (r+s) do liczby wszystkich zmiennych p umniejszonej o liczbę zmiennych t przyjmujących wartość 0 dla obu obiektów. Podobnie jak w przypadku zmiennych binarnych symetrycznych, miarą podobieństwa dwóch obiektów i i j, opisanych zmiennymi binarnymi asymetrycznymi, będzie stosunek q/(q+r+s), tj. stosunek liczby zmiennych, dla których oba obiekty posiadają wartość 1 (q) do liczby wszystkich zmiennych p umniejszonej o liczbę zmiennych t przyjmujących wartość 0 dla obu obiektów.
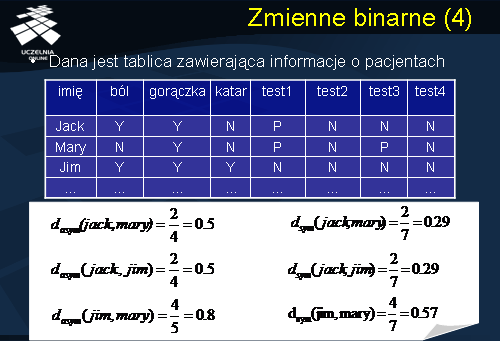
Rozważmy następujący przykład ilustrujący wprowadzone miary niepodobieństwa dokumentów opisanych zmiennymi binarnymi. Dana jest tablica zawierająca informacje o pacjentach. Obiektami są: Jack, Mary i Jim. Atrybuty: ból, gorączka, katar, test1, test2, test3 i test4 są zmiennymi binarnymi. Niepodobieństwo obiektów, przy założeniu, że wszystkie zmienne binarne, opisujące obiekty, są asymetryczne, wynosi: dasym(jack, mary) = 2/4, dasym(jack, jim) = 2/4, i dasym(jim, mary) = 4/5. Najbardziej niepodobni są zatem pacjenci jim i mary. Niepodobieństwo obiektów, przy założeniu, że wszystkie zmienne binarne, opisujące obiekty, są symetryczne, wynosi: dsym(jack, mary) = 2/7, dsym(jack, jim) = 2/7, i dsym(jim, mary) = 4/7. Podobnie, najbardziej niepodobni są pacjenci jim i mary.
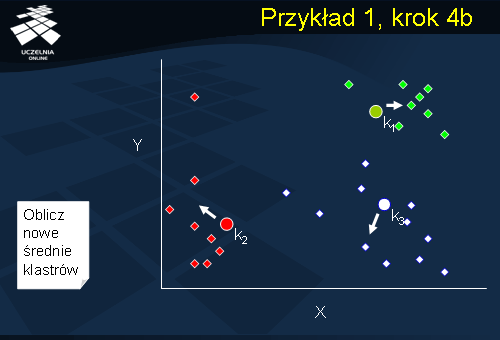
Przykład 1, krok 4b
Definicja miary podobieństwa (lub niepodobieństwa), dla obiektów opisanych zmiennymi kategorycznymi, jest analogiczna do miary zdefiniowanej dla zmiennych binarnych, w tym sensie, że jest ona zdefiniowana jako stosunek liczby zmiennych dla których obiekty się różnią do sumarycznej liczby wszystkich zmiennych opisujących obiekty. Wynika to z faktu, że zmienna kategoryczna jest generalizacją zmiennej binarnej. Zmienna kategoryczna może przyjmować więcej niż dwie wartości (np. zmienna dochód: wysoki, średni, niski). Niepodobieństwo pomiędzy obiektami i i j, opisanymi zmiennymi kategorycznymi, definiujemy jako stosunek liczby zmiennych, dla których oba obiekty posiadają różną wartość (p - m) do sumarycznej liczby wszystkich zmiennych p. Podobnie jak poprzednio, podobieństwo pomiędzy obiektami i i j, opisanymi zmiennymi kategorycznymi, definiujemy jako stosunek liczby zmiennych, dla których oba obiekty posiadają identyczną wartość (p - n) do sumarycznej liczby wszystkich zmiennych p. Miara podobieństwa pomiędzy obiektami i i j, opisanymi zmiennymi kategorycznymi, zdefiniowana powyżej jest również znana jako tzw. miara (współczynnik) Jaccarda i jest często stosowana w komercyjnych produktach eksploracji danych.
Metody grupowania Typy metod

Istnieje wiele metod i algorytmów grupowania. Istnieje również wiele klasyfikacji algorytmów grupowania, które biorą pod uwagę różne aspekty procesy grupowania. Algorytmy grupowania możemy podzielić ze względu na grupowane typy danych. Stąd, mamy algorytmy grupowania danych liczbowych, danych symbolicznych, danych tekstowych, multimedialnych, itd. Inna klasyfikacja dzieli algorytmy grupowania ze względu na mechanizm generowania klastrów. Zgodnie z tą klasyfikacja algorytmy grupowania dzielimy na algorytmy deterministyczne oraz probabilistyczne. W algorytmach deterministycznych proces grupowania opiera się o mechanizm optymalizacji błędu średniokwadratowego realizowany metodą tradycyjną, w algorytmach probabilistycznych mechanizm ten opiera się na penetracji przestrzeni stanów wszystkich możliwych podziałów zbioru grupowanych obiektów. Algorytmy grupowania możemy podzielić, ze względu na charakterystykę wynikowych klastrów, na: algorytmy generujące klastry rozłączne i algorytmy generujące klastry przecinające się. Algorytmy grupowania możemy podzielić, ze względu na sposób otrzymywania klastrów, na algorytmy hierarchiczne oraz algorytmy płaskie. Algorytmy hierarchiczne generują sekwencję klastrów; w przypadku algorytmów płaskich, liczba klastrów nie ulega zmianie w kolejnych iteracjach algorytmu, zmienia się natomiast przydziałów obiektów do klastrów. Algorytmy grupowania można podzielić, ze względu na sposób, ściślej mówiąc, kolejność, wykorzystania cech obiektów w procesie grupowania, na algorytmy monoteiczne i politeiczne.
Metody grupowania
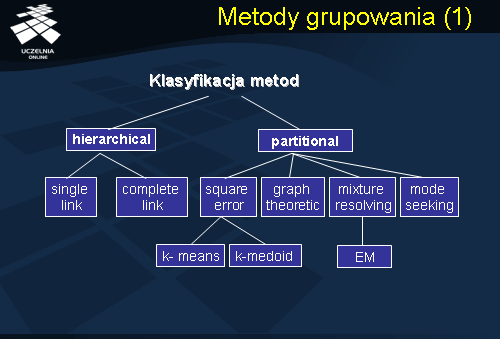
Pierwsza grupa algorytmów konstruuje klastry sekwencyjnie wykorzystując cechy obiektów, druga konstruuje klastry wykorzystując jednocześnie wszystkie cechy (atrybuty) obiektów. Wreszcie, algorytmy grupowania możemy podzielić, ze względu na sposób pielęgnacji klastrów, w przypadku rozszerzenia zbioru grupowanych obiektów o nowe obiekty, na metody przyrostowe i nie przyrostowe. W przypadku pierwszej grupy algorytmów, klastry są tworzone w sposób przyrostowy wraz ze wzrostem liczby obiektów do grupowania. W drugim przypadku, proces grupowania, w przypadku zmiany liczby grupowanych obiektów, jest realizowany zawsze od początku.

Podstawowa klasyfikacja algorytmów grupowania, do której najczęściej się odwołujemy i będziemy się odwoływać, to klasyfikacja, która dzieli algorytmy grupowania ze względu na przyjęty mechanizm grupowania. Wyróżniamy dwa zasadnicze podejścia do procesu grupowania obiektów: podejście hierarchiczne oraz podejście optymalizacyjno-iteracyjne. Algorytmy należące do pierwszej grupy metod generują zagnieżdżoną sekwencję podziałów zbiorów obiektów w procesie grupowania. Algorytmy należące do drugiej grupy metod generują tylko jeden podział (partycję) zbioru obiektów w dowolnym momencie procesu grupowania. Przejdziemy obecnie do przestawienia idei algorytmów grupowania hierarchicznego.
Metody grupowania hierarchicznego
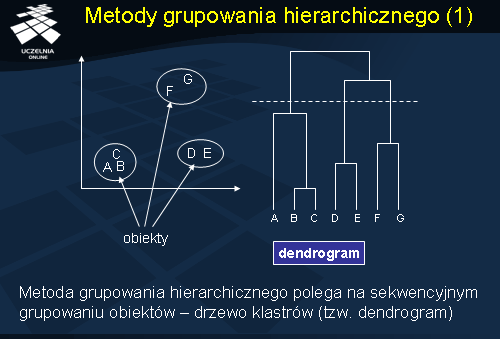
Jak wspomnieliśmy wcześniej, metoda grupowania hierarchicznego polega na sekwencyjnym grupowaniu obiektów. Sekwencja operacji grupowania tworzy tak zwane drzewo klastrów, nazywane dendrogramem. Dendrogram przedstawiony na slajdzie ilustruje działanie hierarchicznego aglomeracyjnego algorytmu grupowania. Początkowo, wszystkie obiekty A, B, ... G należą do osobnych klastrów. Następnie, w kolejnych krokach, klastry są łączone w większe klastry (łączymy B i C, D i E, oraz F i G, następnie, A łączymy z klastrem zawierającym obiekty B i C, itd.). Proces łączenia klastrów jest kontynuowany tak długo, aż liczba uzyskanych klastrów nie osiągnie zadanej liczby klastrów. Graficznie, na dendrogramie, warunek stopu (tj. zadana liczba klastrów) przedstawia linia pozioma przecinająca dendrogram. Na analizowanym slajdzie, zadana liczba klastrów wynosi 3. W wyniku grupowania otrzymujemy 3 klastry obiektów: C1, C2 i C3, gdzie klaster C1={A, B, C}, C2={D, E} oraz C3={F, G}.

Hierarchiczne algorytmy grupowania dzielimy, najogólniej, na dwie grupy algorytmów: algorytmy podziałowe (podejście top-down) oraz algorytmy aglomeracyjne (podejście bottom-up). Hierarchiczne algorytmy podziałowe działają następująco: początkowo, wszystkie obiekty są przypisywane do jednego klastra; następnie, w kolejnych iteracjach, klaster jest dzielony na mniejsze klastry, które, z kolei, dzielone są na kolejne mniejsze klastry aż do osiągnięcia zadanej liczby klastrów. Hierarchiczne algorytmy aglomeracyjne działają następująco: początkowo, każdy obiekt stanowi osobny klaster, następnie, w kolejnych iteracjach, klastry są łączone w większe klastry aż do osiągnięcia zadanej liczby klastrów.
Miary odległości

W obu podejściach, aglomeracyjnym i podziałowym, liczba klastrów jest ustalona z góry przez użytkownika i stanowi warunek stopu procesu grupowania. W praktyce, hierarchiczne algorytmy podziałowe nie są stosowane ze względu na problem podziału klastra. Problem ten można sformułować następująco. Dany jest klaster obiektów. w jaki sposób podzielić klaster na dwa klastry tak, aby optymalizować przyjętą funkcję kryterialną? Pamiętajmy, że w każdym kroku algorytmu podziałowego mamy M klastrów. Który z podziałów jest najlepszy? Stąd, najpopularniejszą i, de facto, jedyną grupą hierarchicznych algorytmów stosowaną w praktyce są algorytmy aglomeracyjne. W przypadku algorytmów aglomeracyjnych podstawowym problemem jest problem łączenia klastrów. Które klastry połączyć i utworzyć większy klaster? Odpowiedź wydaje się, na pierwszy rzut oka, oczywista – należy połączyć dwa „najbliższe” klastry. Co to znaczy „najbliższe”? W jaki sposób zdefiniować odległość pomiędzy klastrami?

Cztery podstawowe (najczęściej stosowane) miary odległości pomiędzy klastrami to: odległość minimalna, odległość maksymalna, odległość średnich oraz średnia odległość. Odległość minimalna pomiędzy klastrami C1 i C2 to minimalna z odległości pomiędzy dwoma dowolnymi obiektami p1 i p2, gdzie p1 należy do klastra C1 a p2 należy do klastra C2. Odległość maksymalna pomiędzy klastrami C1 i C2 to maksymalna z odległości pomiędzy dwoma dowolnymi obiektami p1 i p2, gdzie p1 należy do klastra C1 a p2 należy do klastra C2. W przypadku odległości średnich, odległość pomiędzy klastrem C1 a klastrem C2 definiujemy jako odległość ich średnich. W przypadku średniej odległości, odległość pomiędzy klastrem C1 a klastrem C2 definiujemy jako średnią odległość pomiędzy wszystkimi parami obiektów p1 i p2, gdzie p1 należy do klastra C1, natomiast p2 do klastra C2.
CLARA, CLARANS

Zauważmy, że miara odległości pomiędzy obiektami należącymi do klastrów może być zdefiniowana zależnie od typu grupowanych obiektów. Jeżeli grupowane obiekty można przedstawić w postaci k-wymiarowych wektorów w przestrzeni euklidesowej, to za miarę odległości pomiędzy obiektami można przyjąć dowolną z wcześniej wymienionych miar: odległość euklidesową, odległość Manhattan, itd. W przypadku, gdy mamy do czynienia z obiektami, których nie można przetransformować do przestrzeni euklidesowej, musimy przyjąć miary specyficzne dla typu grupowanych obiektów, np. miarę kosinusową dla dokumentów tekstowych, miarę LCS dla sekwencji symboli, itd. Pozwala to stosować algorytmy aglomeracyjne do grupowania najróżniejszych typów danych.
Ogólny hierarchiczny aglomeracyjny algorytm grupowania

Ogólny schemat hierarchicznego aglomeracyjnego algorytmu grupowania można zdefiniować następująco. Na wejściu algorytmu mamy bazę danych obiektów D. Wynikiem działania algorytmu jest dendrogram reprezentujący grupowanie obiektów. Algorytm składa się z 3 kroków. W kroku pierwszym, każdy obiekt jest umieszczany w osobnym klastrze. W kroku drugim jest konstruowana macierz odległości pomiędzy klastrami. Oczywiście, po kroku pierwszym, macierz ta reprezentuje, de facto, odległość pomiędzy obiektami bazy danych D. W kolejnym, trzecim kroku, dla zadanej wartości progowej niepodobieństwa dk, tworzony jest graf klastrów, w którym każda para klastrów, której wzajemna odległość jest mniejsza niż dk, jest połączona lukiem. Algorytm wraca do kroku drugiego – uaktualniana jest macierz odległości pomiędzy klastrami i ponownie, dla zadanej wartości progowej niepodobieństwa dk (wartość ta może się zmieniać w kolejnych iteracjach), którym każda para klastrów, której wzajemna odległość jest mniejsza niż dk, jest łączona łukiem w grafie klastrów. Proces ten powtarza się, aż wszystkie klastry utworzą graf spójny. Jak wspomnieliśmy wcześniej, wynikiem działania algorytmu jest dendrogram reprezentujący grupowanie obiektów. Jeżeli chcemy określić wynik grupowania obiektów dla zadanej wartości k (zadana liczba klastrów), to w dendrogramie należy ustawić warunek stopu w postaci linii przecinającej dendrogram w odpowiednim miejscu. Zauważmy, że przedstawiony ogólny algorytm aglomeracyjny pozwala zmieniać, w kolejnych iteracjach, wartość progową niepodobieństwa, co wpływa na wynik grupowania.
Hierarchiczny aglomeracyjny algorytm grupowania

Przedstawiony na slajdzie algorytm reprezentuje uproszczoną wersję ogólnego hierarchicznego aglomeracyjnego algorytmu grupowania. Podobnie jak w przypadku ogólnego algorytmu grupowania, w kroku pierwszym, każdy obiekt jest umieszczany w osobnym klastrze. Następnie, konstruowana jest macierz odległości pomiędzy klastrami. Znajdowana jest para najbliższych klastrów, zgodnie z przyjętą miara odległości. Znalezione klastry są łączone tworząc nowy klaster. Aktualizowana jest macierz odległości pomiędzy klastrami i poszukiwana jest kolejna para najbliższych klastrów. Proces łączenia klastrów powtarza się, aż do osiągnięcia zadanej liczby klastrów. W przedstawionym algorytmie można wykorzystać dowolną z omówionych uprzednio miar odległości. Jeżeli miarą odległości pomiędzy klastrami jest „minimalna odległość”, to mówimy o algorytmie grupowania typu „single link” lub „single linkage”. Jeżeli miarą odległości jest „maksymalna odległość”, to mówimy o algorytmie grupowania typu „complete link” lub „complete linkage”. W przypadku przyjęcia miary „średniej odległość” mówimy o algorytmie typu „average link” lub „average linkage”. W zależności od przyjętej miary odległości uzyskujemy klastry o różnym kształcie.


























