Grupowanie II
Tematem wykładu są iteracyjno-optymalizacyjne algorytmy grupowania. Przedstawimy i omówimy ideę podejścia iteracyjno-optymalizacyjnego oraz przedstawimy dwa podstawowe algorytmy reprezentujące to podejście: algorytm k-średnich oraz algorytm k-medoidów. Na zakończenie wykładu, krótko, scharakteryzujemy inne metody grupowania.
Metody iteracyjno-optymalizacyjne

Na poprzednim wykładzie przedstawiliśmy hierarchiczne algorytmy grupowania. Obecnie przejdziemy do przedstawienia drugiego z zasadniczych podejść do problemu grupowania, tj. podejścia iteracyjno-optymalizacyjnego. Metody iteracyjno-optymalizacyjne grupowania tworzą jeden podział zbioru obiektów (partycję) w miejsce hierarchicznej struktury podziałów, jak ma to miejsce w przypadku algorytmów hierarchicznych. Idea podejścia jest następująca: tworzony jest początkowy podział obiektów (zbiór klastrów k), a następnie, stosując technikę iteracyjnej realokacji obiektów pomiędzy klastrami, podział ten jest modyfikowany w taki sposób, aby uzyskać poprawę podziału zbioru obiektów pomiędzy klastry. Niestety, problem znalezienia najlepszego podziału zbioru obiektów pomiędzy k klastrów jest problemem trudnym. Łatwo zauważyć, że osiągnięcie „optimum” globalnego podziału obiektów wymaga przeanalizowania wszystkich możliwych podziałów zbioru n obiektów pomiędzy k klastrów. Zauważmy również, że w przypadku metod iteracyjno-optymalizacyjnych, liczba zadanych klastrów jest parametrem wejściowym procedury grupowania.

W jaki sposób początkowy podział obiektów pomiędzy k klastrów jest modyfikowany przez algorytmy iteracyjno-optymalizacyjne? Odpowiedź jest następująca. Metody iteracyjno-optymalizacyjne realokują obiekty pomiędzy klastrami optymalizując pewną funkcję kryterialną. Przy czym funkcja kryterialna może być zdefiniowana lokalnie (na podzbiorze obiektów) lub globalnie (na całym zbiorze obiektów).
Jak wspomnieliśmy wcześniej, problem znalezienia optymalnego podziału zbioru obiektów pomiędzy k klastrów jest problemem trudnym. Dla dużej liczby obiektów, rzędu tysięcy obiektów, przeszukanie całej przestrzeni wszystkich możliwych podziałów zbioru obiektów pomiędzy k klastrów jest, praktycznie, nie realizowalne. Ponieważ znalezienie optimum funkcji kryterialnej, praktycznie, jest niemożliwe, zachodzi potrzeba zdefiniowania heurystyki, która będzie znajdowała „najlepszy”, możliwy do osiągnięcia, podział obiektów pomiędzy k klastrów. Okazuje się, że w przypadku algorytmów iteracyjno-optymalizacyjnych wynik grupowania silnie zależy od początkowego podziału obiektów (do tego zagadnienia wrócimy jeszcze później w ramach wykładu), stąd, w celu poprawy wyniku grupowania stosuje się, dodatkowo, prosty mechanizm dywersyfikacji - algorytm grupowanie jest uruchamiany kilkakrotnie, dla różnych podziałów początkowych, a następnie, najlepszy z uzyskanych podziałów jest przyjmowany jako wynik procesu grupowania.

Zanim przejdziemy do przedstawienia ogólnego iteracyjno-optymalizacyjnego algorytmu grupowania, rozważmy problem grupowania jako klasyczny problem optymalizacyjny. Dowolny problem optymalizacyjny, a do takiej klasy należą problemy eksploracji danych, można zdefiniować w kontekście następujących 5 elementów: zadanie, model, funkcja kryterialna metoda przeszukiwania przestrzeni rozwiązań, oraz algorytmy i struktury danych wspierające proces eksploracji. W przypadku problemu grupowania zadaniem jest podział zbioru n obiektów na k rozłącznych zbiorów (klastrów, skupień). Modelem jest charakterystyka (definicja) wynikowych klastrów – np. możemy założyć, że poszukujemy wyłącznie klastrów wypukłych, że klaster musi zawierać co najmniej m obiektów, itd. Istnieje wiele możliwych rozwiązań danego zadania: które z rozwiązań jest najlepsze? W tym celu wprowadzamy funkcję kryterialną, która pozwala ocenić jakość przyjętego rozwiązania. W przypadku, gdy liczba możliwych rozwiązań danego problemu jest niewielka, to można zastosować metodę przeszukiwania pełnego – znaleźć wartość funkcji kryterialnej dla każdego z rozwiązań i, następnie, wybrać rozwiązanie, które jest optymalne z punktu widzenia przyjętej funkcji kryterialnej.

Niestety, większość problemów praktycznych nie można rozwiązać metodą pełnego przeszukiwania przestrzeni możliwych rozwiązań – po prostu rozmiar tej przestrzeni jest zbyt duży. Stąd, należy wybrać jakąś metodę przeszukiwania przestrzeni rozwiązań, co w konsekwencji prowadzi do rozwiązań, generalnie, nieoptymalnych. Jeżeli chodzi o metody przeszukiwania przestrzeni rozwiązań, to mamy, najogólniej mówiąc, trzy możliwe alternatywy: przeszukiwanie pełne (o którym już wspominaliśmy), podejście heurystyczne, które generuje, najczęściej, jedno rozwiązanie, oraz podejście kombinatoryczne (tzw. metaheurystyki). To ostatnie podejście polega na analizie pewnego fragmentu przestrzeni rozwiązań. Wreszcie ostatnim elementem problemu optymalizacyjnego są algorytmy i struktury danych wspierające procedurę rozwiązania problemu optymalizacyjnego. Wybór określonych struktur danych i odpowiednich algorytmów operujących na tych strukturach pozwala, często, poprawić efektywność znajdowania rozwiązania.
Funkcje kryterialne

Zasadniczym problemem procesu optymalizacyjnego jest wybór funkcji kryterialnej. Rozważmy prosty przykład problemu optymalizacyjnego: należy znaleźć trasę dojazdową z punktu A do punktu B. Zadaniem – dojazd z punktu A do punktu B. Model – ograniczenia tras, np. nie interesują nas żadne rozwiązania polegające na wykorzystaniu helikoptera, paralotni, samolotu, i innych sprzętów latających. Ograniczmy się do poszukiwania rozwiązań w zakresie dojazdu samochodem. Niemniej, rozwiązań, tj. możliwych dróg jest, praktycznie, nieskończenie wiele (np. z Poznania do Warszawy przez Hiszpanię). Czego zatem szukamy? Najszybszej trasy dojazdowej? W takim przypadku nasza funkcja kryterialna to czas dojazdu a my chcemy minimalizować wartość funkcji kryterialnej. Nie zawsze interesuje nas czas dojazdu. Możemy poszukiwać drogi, która, np. minimalizuje liczbę manewrów skrętu w lewo. Funkcji kryterialnych może być zatem bardzo wiele. Wracając do problemu grupowania – również w tym przypadku możemy zdefiniować bardzo wiele różnych funkcji kryterialnych.

Przedstawimy obecnie pewną filozofię stojącą za wyborem funkcji kryterialnej dla problemu grupowania metodą iteracyjno-optymalizacyjną oraz przedstawimy przykładową funkcję kryterialną, którą można wykorzystać w procesie grupowania. Po pierwsze, zauważmy, że w procesie grupowania rozłącznego (tj. zakładamy, że wynikowe klastry mają być rozłączne) oczekujemy, że: klastry będą maksymalnie zwarte i będą maksymalnie rozłączne. W związku z tym wprowadzamy dwie miary pomocnicze, służące do oceny wyniku grupowania: odchylenie wewnątrzklastrowe (wc(C)) oraz odchylenie międzyklastrowe (bc(C)), gdzie C oznacza podział (grupowanie) obiektów pomiędzy k klastrów. Miarę odchylenia (wc(C)) wewnątrzklastrowego definiujemy jako sumę odległości obiektów od środków klastrów, do których obiekty należą. Odchylenie międzyklastrowe (bc(C)) definiujemy jako sumę odległości środków wszystkich par klastrów.

Funkcję kryterialną problemu grupowania metoda iteracyjno-optymalizacyjną, która pozwala na ocenę jakości grupowania, można zdefiniować jako kombinację miar wc(C) i bc(C), np. jako stosunek bc(C)/wc(C). Proces grupowania jest tym lepszy, im większa jest wartość funkcji kryterialnej. maksymalizację funkcji kryterialnej można uzyskać bądź minimalizując wartość odchylenia wewnątrzklastrowego lub maksymalizując wartość odchylenia międzyklastrowego. Przyjęcie miary odchylenia wewnątrzklastrowego wc(C) zdefiniowanej na slajdzie, jako miary zwartości klastrów, prowadzi do generowania klastrów sferycznych (algorytm k-średnich).
Jak złożony jest obliczeniowo proces obliczania wartości funkcji kryterialnej? Złożoność procesu obliczania odchylenia wewnątrzklastrowego jest rzędu n, gdzie n oznacza liczbę grupowanych obiektów. Z kolei złożoność procesu obliczania odchylenia międzyklastrowego wymaga k do potęgi 2, gdzie k oznacza zadaną liczbę klastrów. Reasumując, obliczenie wartości funkcji kryterialnej dla pojedynczego grupowania (pojedynczego podziału) wymaga przejrzenia całego zbioru obiektów D. W przypadku analizy m podziałów, obliczenie wartości funkcji kryterialnej będzie wymagało m-krotnego przejrzenia zbioru obiektów D

Oczywiście, przedstawiona powyżej funkcja kryterialna nie jest jedyną funkcją kryterialną, którą można wykorzystać w procesie grupowania. Inna popularna definicja odchylenia wewnątrzklastrowego, które można wykorzystać do konstrukcji funkcji kryterialnej, jest następująca: dla każdego obiektu należącego do klastra obliczamy odległość tego punktu do najbliższego obiektu w tym klastrze, i bierzemy maksimum z tych odległości: Przyjęcie miary odchylenia wewnątrzklastrowego wc(C), jako miary zwartości klastrów, zdefiniowanej w taki sposób, prowadzi z kolei do generowania klastrów podłużnych. Często stosowaną funkcją kryterialną jest sama miara odchylenia wewnątrzklastrowego, z pominięciem odchylenia międzyklastrowego. Ta funkcja kryterialna jest również często nazywana funkcją błędu średniokwadratowego.
Grupowanie iteracyjno-optymalizacyjne

Po zdefiniowaniu funkcji kryterialnej pojawia się problem wyboru algorytmu grupowania, który optymalizowałby przyjętą funkcję kryterialną. Jak już wspominaliśmy kilkakrotnie, w celu znalezienia optimum globalnego funkcji kryterialnej należałoby przejrzeć wszystkie możliwe podziały C obiektów na k klastrów i wybrać ten podział, który jest „optymalny”. Można łatwo pokazać, że liczba możliwych podziałów n obiektów na k klastrów wynosi w przybliżeniu k do potęgi n. Stąd, znalezienie „optimum globalnego” funkcji kryterialnej metodą pełnego przeglądu przestrzeni możliwych rozwiązań jest obliczeniowo zbyt kosztowne. Innym rozwiązaniem, o którym już wspominaliśmy, jest zastosowanie, do penetracji przestrzeni rozwiązań, jednej z wielu technik optymalizacji kombinatorycznej: iterative improvement, tabu search, simulating annealing, genetic algorithms, itp. Niestety, efektywność metod optymalizacji kombinatorycznej silnie zależy od charakterystyki penetrowanej przestrzeni rozwiązań.

Popularnym podejściem, stosowanym do rozwiązywania wielu problemów optymalizacyjnych w informatyce, jest zastosowanie algorytmu zachłannego (ang.
greedy algorithm ). Ogólną ideę algorytmu zachłannego, w odniesieniu do problemu grupowania, można przedstawić następująco: losowo wybierany jest początkowy podział zbioru obiektów na k klastrów, a następnie, stosując technikę iteracyjnej realokacji obiektów pomiędzy klastrami, początkowy podział jest modyfikowany w taki sposób, aby uzyskać poprawę funkcji kryterialnej aż do osiągnięcia warunku stopu. Przykładem takiego podejścia jest jeden z najpopularniejszych algorytmów grupowania, zaimplementowany praktycznie we wszystkich komercyjnych systemach eksploracji danych, algorytm k-średnich.
Algorytm k-średnich

Ogólny schemat algorytmu grupowania k-średnich ma następująca postać. Danymi wejściowymi algorytmu są: baza danych obiektów D oraz zadana liczba klastrów k. Wynikiem działania algorytmu jest zbiór k klastrów minimalizujący kryterium odchylenia wewnątrzklastrowego (błędu średniokwadratowego). Algorytm składa się z 3 kroków. W kroku pierwszym, wybieranych jest losowo k obiektów jako początkowe środki k klastrów.
W kroku drugim, obiekty alokowane są do klastrów. Każdy obiekt jest przydzielany do tego klastra, dla którego odległość obiektu od środka klastra jest najmniejsza. Następnie, po alokacji obiektów do klastrów, uaktualniane są wartości średnie klastrów (środki klastrów) i ponownie wracamy do kroku alokacji obiektów do klastrów. Może się bowiem okazać, że na skutek aktualizacji średnich klastrów zachodzi konieczność realokacji obiektów. Proces realokacji obiektów i uaktualniania średnich klastrów jest powtarzany tak długo, jak długo występują zmiany przydziału obiektów do klastrów. Warunek stopu może być zdefiniowany również w inny sposób, np. warunek time-out’u, zadana liczba iteracji, itp.
Przykład 1, krok 1
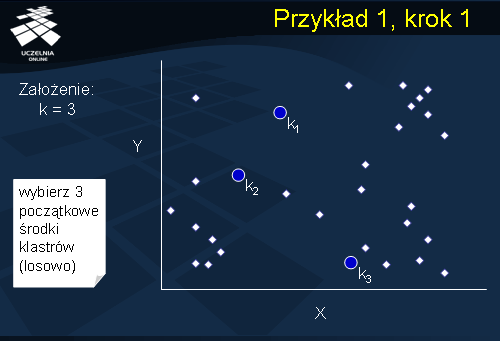
Dla ilustracji działania algorytmu k-średnich rozważmy następujący przykład przedstawiony na slajdzie. Dany jest zbiór obiektów reprezentowanych przez zbiór punktów w 2-wymiarowej przestrzeni euklidesowej. Załóżmy, że zadana liczba klastrów k wynosi 3. W pierwszym kroku, algorytm wybiera losowo 3 punktyk1, k2, i k3, spośród zbioru obiektów, które, początkowo, stanowią środki trzech klastrów C1, C2, i C3.
Przykład 1, krok 2
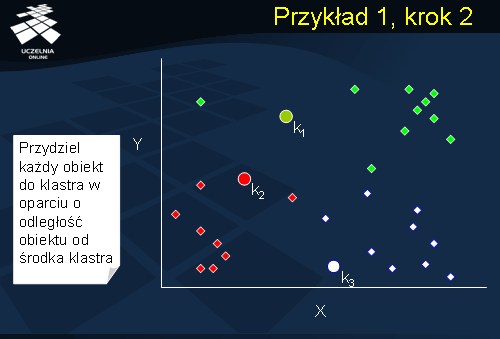
W kroku drugim, algorytm alokuje obiekty do klastrów. Każdy obiekt jest przydzielany do tego klastra, dla którego odległość obiektu od środka klastra jest najmniejsza. Przydział obiektów do klastrów jest zaznaczony na slajdzie kolorami. Obiekty o tym samym kolorze zostały przydzielone do tego samego klastra.
Przykład 1, krok 3
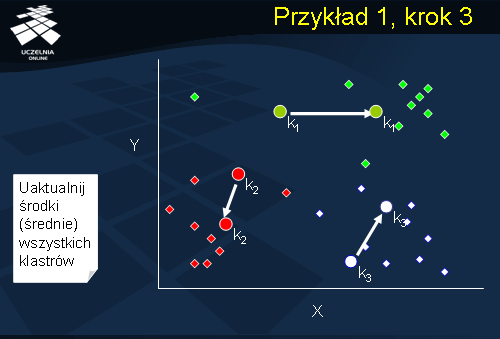
W kolejnym kroku algorytmu następuje uaktualnienie średnich (środków) wszystkich klastrów. Środki klastrów C1, C2 i C3 ulegają zmianie – na slajdzie zmiana lokalizacji środków klastrów została zaznaczona strzałkami.
Przykład 1, krok 4
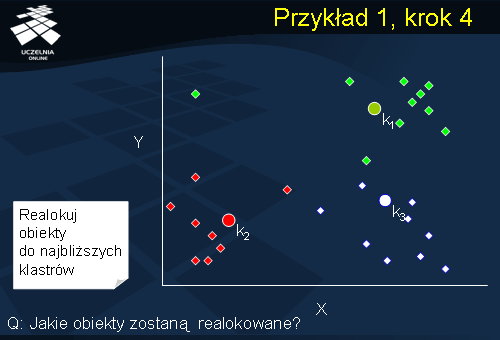
Po uaktualnieniu średnich wszystkich klastrów następuje powrót do kroku drugiego – realokacji obiektów. Łatwo zauważyć, że po aktualizacji średnich klastrów, niektóre z obiektów znajdują się obecnie bliżej innych klastrów aniżeli tych, do których zostały przydzielone. Niemniej, weryfikacja, które z obiektów wymagają realokacji wymaga odczytu całej bazy danych D.
Przykład 1, krok 4a
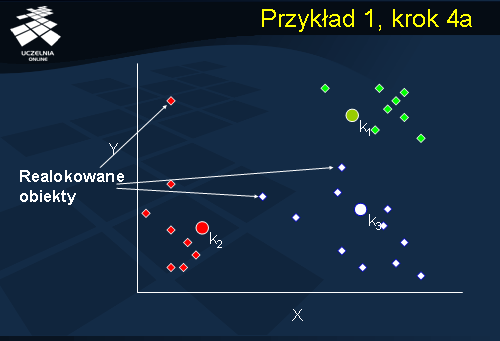
Konieczność realokacji dotyczy trzech obiektów. Pierwszy został przydzielony do klastra C1. Po aktualizacji środków klastrów C1 i C2, aktualnie obiekt ten znajduje się bliżej klastra C2. Drugi z obiektów został również przydzielony do klastra C1, natomiast po aktualizacji środków klastrów, obiekt ten znajduje się bliżej klastra C3. Wreszcie, ostatni ze wskazanych obiektów, początkowo przydzielony do C1, znajduje się obecnie bliżej klastra C3. Realokujemy obiekty do najbliższych klastrów i, ponownie, przechodzimy do kolejnego kroku aktualizacji środków klastrów.
Przykład 1, krok 4b
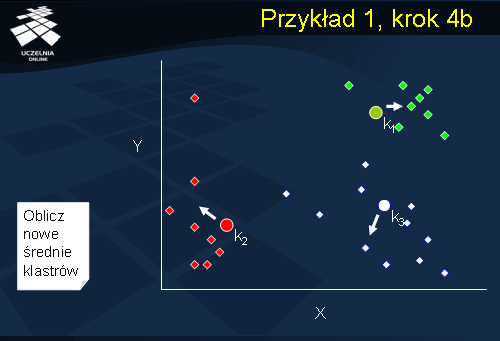
Ponownie aktualizujemy średnie wszystkich klastrów i wracamy do kroku realokacji obiektów. Dla każdego obiektu następuje weryfikacja, czy obiekt ten podlega realokacji. Jeżeli żaden z obiektów nie wymaga realokacji następuje zakończenie działania algorytmu.
Przykład 1, krok 5
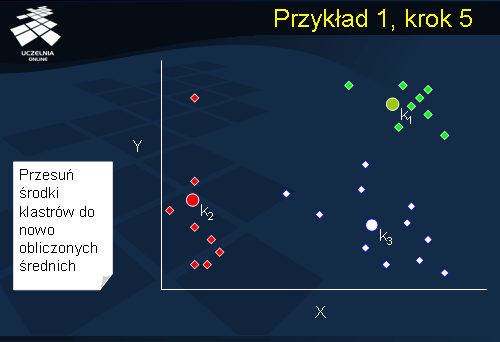
W jego wyniku uzyskujemy trzy klastry C1, C2 i C3 przedstawione na slajdzie. Łatwo zauważyć na slajdzie, że odchylenie wewnątrzklastrowe klastra C1 jest mniejsze aniżeli odchylenie wewnątrzklastrowe klastra C2 i odchylenie wewnątrzklastrowe klastra C3 – klaster C1 jest bardziej zwarty aniżeli klastry C2 i C3. Zauważmy również, że środek klastra C2 jest przesunięty w stosunku do środka „masy” tego klastra ze względu na jeden z punktów, który istotnie odbiega od pozostałych. Taki punkt nazywamy punktem osobliwym – ang. outlier .
Algorytm k-średnich

Złożoność algorytmu k-średnich jest rzędu O(knI), gdzie I oznacza liczbę iteracji algorytmu, n liczbę grupowanych obiektów, natomiast k oznacza zadaną liczbę klastrów. Wynika ona z następującego spostrzeżenia. Dla danego zbioru środków klastrów rk, w ramach jednokrotnego przeglądu bazy danych D, można obliczyć wszystkie k*n odległości d(rk, x) i dla każdego obiektu x wybrać minimalną odległość tego punktu do środka klastra. Obliczenie nowych środków klastrów można wykonać w czasie O(n).

Algorytm cechuje się stosunkowo wysoka efektywnością. Niestety, algorytm ten posiada dwie istotne wady. Po pierwsze, algorytm ten jest bardzo czuły na dane zaszumione lub dane zawierające punkty osobliwe, gdyż punkty takie w istotny sposób wpływają na średnie klastrów powodując ich zniekształcenie. Po drugie, wynik działania algorytmu (tj. ostateczny podział obiektów pomiędzy klastrami) silnie zależy od początkowego podziału obiektów, co za chwile pokażemy. Po trzecie, co wynika z charakteru algorytmu (przypomnijmy, że algorytm k-średnich jest algorytmem zachłannym), algorytm może „wpaść” w optimum lokalne, które może odbiegać od optimum globalnego. W celu zwiększenia szansy znalezienia optimum globalnego, lub przynajmniej, „wyrwania” się z optimum lokalnego, należy kilkakrotnie uruchomić algorytm dla różnych podziałów początkowych.
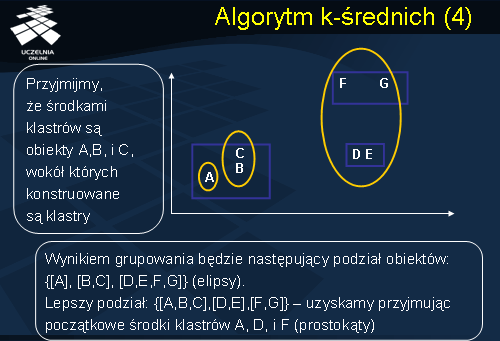
Jak wspomnieliśmy, wynik działania algorytmu k-średnich (tj. ostateczny podział obiektów pomiędzy klastrami) zależy od początkowego podziału obiektów. Dla ilustracji tego faktu rozważmy następujący przykład przedstawiony na slajdzie. Danych jest 7 obiektów reprezentowanych, podobnie jak w poprzednim przykładzie, przez zbiór punktów A, B, C, D, E, F, i G. Załóżmy, że zadana liczba klastrów k wynosi 3. Załóżmy również, że w pierwszym kroku algorytmu, środkami klastrów wybrano punkty A, B i C, wokół których konstruowane są klastry. W wyniku działania algorytmu k-średnich otrzymamy następujący podział zbioru obiektów pomiędzy 3 klastry: C1={A}, C2 ={B, C} i C3={D, E, F, G}. Jako ćwiczenie domowe zalecamy weryfikację w jaki sposób algorytm wygeneruje ten podział. Gdyby przyjąć, że początkowymi środkami klastrów C1, C2 i C3 są, odpowiednio, punkty A, D i F, wówczas wynikiem grupowania będzie następujący podział obiektów: C1 ={A,B,C}, C2={D,E}, i C3={F,G}. Łatwo zauważyć, że drugi z podziałów charakteryzuje się mniejszym odchyleniem wewnątrzklastrowym (mniejszym błędem średniokwadratowym).
Algorytm k-medoidów

Jedną z zasadniczych wad algorytmu k-średnich jest jego czułość na dane zaszumione i występowanie punktów osobliwych. W celu uodpornienia algorytmu k-średnich na występowanie punktów osobliwych, zamiast średnich klastrów jako środków tych klastrów, można przyjąć medoidy – najbardziej centralnie ulokowane punkty klastrów. Wystąpienie punktu osobliwego w klastrze nie spowoduje wówczas tak dramatycznej zmiany wartości średniej klastra. Ile wynosi średnia zbioru składającego się z elementów o następujących wartościach: 1, 3, 5, 7, i 9? Średnia wynosi (1+3+5+7+9)/5 = 5. Ile wynosi średnia zbioru składającego się z następujących elementów: 1, 3, 5, 7, i 1009? Punkt 1009 jest tutaj punktem osobliwym, którego wartość istotnie odbiega od pozostałych punktów. Średnia wynosi (1+3+5+7+1009)/5 = 205. Widzimy, że średnia wyraźnie uległa zmianie przesuwając się w kierunku punktu osobliwego. Zastępując średnią zbioru medoidem tego zbioru otrzymujemy następujący wynik – medoidem zbioru 1, 3, 5, 7, i 1009 jest punkt 5. Zastąpienie w algorytmie k-średnich wartości średniej klastra medoidem klastra prowadzi do algorytmu, który w literaturze nosi nazwę algorytmu k-medoidów.

Ogólny schemat algorytm k-medoidów jest analogiczny do schematu algorytmu k-średnich, w którym średnią klastra zastąpiono medoidem klastra. Jednakże, zastąpienie średniej klastra jego medoidem ma istotną konsekwencję z punktu widzenia efektywności działania algorytmu. Aktualizacja średniej klastra w algorytmie k-średnich jest prostą operacją arytmetyczną. W algorytmie k-medoidów aktualizujemy medoid klastra, tj. wybieramy nowy punkt centralny klastra. Wybór nowego punktu centralnego polega na zastąpieniu aktualnego medoidu klastra obiektem nie będącym medoidem, jeżeli ta operacja poprawi wartość funkcji kryterialnej. Sprawdzenie, czy obiekt y (nie będący medoidem) może zastąpić aktualny medoid m wymaga analizy 4 przypadków dla każdego obiektu p (p również nie jest medoidem). Przypadek 1: p należy do klastra medoidu m. Jeżeli zastąpimy medoid m obiektem y i p znajduje się bliżej medoidu n, to przydziel p do klastra medoidu n. Przypadek 2: p należy do klastra medoidu m. Jeżeli zastąpimy medoid m obiektem y i p znajduje się bliżej obiektu y, to przydziel p do klastra nowego medoidu y. Przypadek 3: p należy do klastra medoidu n. Jeżeli zastąpimy medoid m obiektem y i p znajduje się bliżej medoidu n, to nie zmieniaj przydziału obiektu p. Przypadek 4: p należy do klastra medoidu n. Jeżeli zastąpimy medoid m obiektem y i p znajduje się bliżej obiektu y, to przydziel p do klastra nowego medoidu y. Po przeanalizowaniu wszystkich punktów oblicz wartośc funkcji kryterialnej. Jeżeli operacja zastąpienia medoidu m obiektem y poprawia wartość tej funkcji to dokonaj zastąpienia medoidu m obiektem y. Łatwo zauważyć, że operacja znajdowania nowego medoidu klastra jest znacznie bardziej złożona aniżeli operacja znajdowania średniej klastra.
Algorytm PAM

Algorytm PAM jest wersją algorytmu k-medoidów. Po początkowym losowym wybraniu k medoidów, w kolejnych iteracjach, algorytm próbuje poprawić wybór medoidów. Analizowane są wszystkie możliwe pary obiektów, takich, że jeden z obiektów jest medoidem, natomiast drugi z obiektów nie jest medoidem. Jakość grupowania, dla każdej kombinacji par, jest szacowana, zgodnie z przyjętą funkcją kryterialną, i wybierany jest najlepszy zbiór medoidów. Otrzymany zbiór medoidów stanowi punkt wyjścia do obliczeń w kolejnej iteracji algorytmu.
CLARA, CLARANS

Łatwo zauważyć, że algorytmy typu k-medoidów są słabo skalowalne – są bardzo kosztowne obliczeniowo dla dużych wartości n i k. Złożoność algorytmu wynika z kosztownej analizy aktualizacji medoidów. Próbą rozwiązania tego problemu była propozycja algorytmu CLARA. Idea algorytmu CLARA sprowadza się do następującego pomysłu: zamiast rozważać cały dostępny zbiór obiektów do grupowania, wybieramy reprezentatywny podzbiór obiektów metodą próbkowania. Rozwinięciem idei algorytmu CLARA i połączenia go z algorytmem PAM jest popularny algorytm CLARANS. Podobnie jak w przypadku algorytmu CLARA, zamiast rozważać cały dostępny zbiór obiektów do grupowania, wybieramy reprezentatywny podzbiór obiektów metodą próbkowania. Następnie, z wybranej próbki, stosując algorytm PAM, wybieramy zbiór medoidów będących środkami klastrów. Jeżeli mechanizm próbkowania obiektów zapewnia losowość próbki, to próbka będzie dobrze odzwierciedlała rozkład obiektów w oryginalnym zbiorze obiektów. Wybrany zbiór medoidów będzie, natomiast, w miarę wiernie odpowiadał wyborowi medoidów przez algorytm PAM z całego zbioru obiektów. Algorytmy CLARA i CLARANS cechują się lepszą efektywnością aniżeli klasyczny algorytm k-medoidów, jednakże nie zmieniają zasadniczą wysokiej złożoności metody k-medoidów. Poprawa efektywności jest skutkiem lepszego wyboru początkowego medoidów, a co za tym idzie, najczęściej, mniejszą liczbą iteracji.
Inne metody grupowania

Przedstawione metody grupowania nie wyczerpują, oczywiście, wszystkich algorytmów grupowania. Jest jeszcze cały szereg algorytmów, których nie można zaklasyfikować ani do grupy algorytmów hierarchicznych ani tez algorytmów iteracyjno-optymalizacyjnych. J. Han wymienia w swoim podręczniku jeszcze 3 grupy metod grupowania: metody oparte o analizę gęstości, metody oparte o analizę struktury gridowej, oraz metody oparte o konstrukcję modelu. Idea metod opartych o analizę gęstości polega na tym, że dany klaster, w kolejnych iteracjach, jest rozszerzany o obiekty należące do jego sąsiedztwa, pod warunkiem, że gęstość obiektów w danym sąsiedztwie przekracza zadaną wartość progową. Do tej grupy metod należą znane algorytmy DBSCAN, OPTICS, DENCLUE. Ta grupa metod była rozwijana, głównie, w odniesieniu do zastosowań w dziedzinie rozpoznawania obrazów. Druga z wymienionych grup, tj. metody oparte o analizę struktury gridowej, zakłada, że przestrzeń obiektów jest dzielona na skończoną liczbę komórek, które tworzą strukturę gridu - cały proces grupowania jest wykonywany na tej strukturze. Do tej grupy metod należą znane algorytmy STING i CLIQUE. Cechą i zasadniczą zaletą tej grupy metod jest skalowalność i możliwość analizy dużych wolumenów danych wielowymiarowych. Ostatnia z wymienionych grup, tj. metody oparte o konstrukcję modelu, zakłada pewien model dla każdego z klastrów, a następnie, przypisuje obiekty do klastrów zgodnie z przyjętymi modelami klastrów.

Poza wymienionymi grupami metod, istnieje wiele algorytmów grupowania, specyficznych dla danych określonego typu. Istnieje szereg algorytmów przeznaczonych do grupowania obiektów opisanych danymi kategorycznymi (algorytmy ROCK, STIRR, CACTUS). Specyficzną grupą algorytmów są algorytmy grupowania sekwencji, zarówno liczbowych jak i sekwencji danych symbolicznych, czy wreszcie, sekwencji zbiorów liczbowych i/lub sekwencji zbiorów danych kategorycznych. Grupa metod, bardzo intensywnie rozwijanych w ostatnim czasie, są metody grupowania dokumentów tekstowych, stron WWW, dokumentów XML, oraz innych niestandardowych danych (szczególnie danych multimedialnych).

Na zakończenie należy wspomnieć o jeszcze jednym zastosowaniu algorytmów grupowania, a mianowicie, o ich wykorzystaniu do odkrywania punktów osobliwych. Problematyka odkrywania punktów osobliwych (ang.
outlier detection ) stała się, w ostatnim czasie, ważnym zagadnieniem o dużym znaczeniu praktycznym. Znajduje ona, głównie, zastosowanie w takich dziedzinach jak bańkowość, ubezpieczenia, aukcje internetowe, itp., i związana jest z hasłem bezpieczeństwo i wykrywanie oszustw (ang.
fraud detection ). Przykładowo, korzystanie z karty kredytowej przez klienta banku można opisać jako sekwencję danych liczbowych, w której pojedynczy element sekwencji opisuje pojedynczą transakcje klienta. Sekwencje opisujące zachowanie klienta w poszczególnych miesiącach można pogrupować, próbując określić typowy profil korzystania z karty przez danego klienta. Nienaturalny sposób korzystania z karty kredytowej, znacząco odbiegający od dotychczasowej historii (profilu klienta), może świadczyć o kradzieży karty. Do wykrywania takich niestandardowych, osobliwych transakcji wykorzystuje się często zmodyfikowane algorytmy grupowania.



























