Optymalizacja zapytań część I

Wykład jest poświęcony problemom wykonywania i optymalizacji zapytań w systemach baz danych. Rozpoczniemy od krótkiego wprowadzenia do wykonywania zapytań. Przedstawimy poszczególne fazy przetwarzania zapytań, takie jak analiza zapytań, normalizacja zapytań, analiza semantyczna zapytań upraszczanie zapytań oraz restrukturyzacja zapytań. Następnie, przejdziemy do omówienia problemów związanych z optymalizacją zapytań. W kolejnej części wykładu, przedstawimy i omówimy algebraiczne reguły transformacji zapytań. Na zakończenie wykładu powiemy o technice przepisywania zapytań jako ważnym mechanizmie optymalizacji wykonywania zapytań.


Fazy przetwarzania zapytania



Proces wykonywania zapytania składa się, najogólniej mówiąc, z kilku faz: fazy dekompozycji, fazy optymalizacji zapytania, fazy generacji kodu, oraz fazy wykonania. Zapytanie wyrażone w języku SQL, w fazie dekompozycji, jest transformowane do postaci wyrażenia algebry relacji, umożliwiającej dalsze przetwarzania zapytania. Transformacja zapytania do postaci wyrażenia algebraicznego wymaga dostępu do katalogu bazy danych. W kolejnej fazie, wyrażenie reprezentujące zapytanie jest optymalizowane za pomocą dwóch mechanizmów. Pierwszym jest mechanizm reguł transformacji, który wykorzystując pewien zbiór reguł stara się uprościć zapytanie. Drugim, jest mechanizm optymalizacji kosztowej, który, dla danego wyrażenia, stara się określić optymalny plan wykonania zapytania (m.in. stara się określić optymalne drzewo połączeń). Moduł optymalizatora wykorzystuje w procesie optymalizacji zapytania statystyki, przechowywane w systemie bazy danych, dotyczące relacji, atrybutów i indeksów (rozmiary relacji, liczba stron relacji, liczba różnych wartości atrybutu, itp.). W kolejnym kroku, dla znalezionego planu wykonania zapytania, generowany jest kod zapytania, który jest, następnie, uruchamiany przez tak zwany silnik zapytań (ang. query engine).


Dynamiczna vs statyczna optymalizacja zapytań



Zanim przejdziemy do przedstawienia i omówienia poszczególnych faz przetwarzania zapytania, wprowadzimy i omówimy krótko klasyfikację metod optymalizacji zapytań. Istnieje wiele klasyfikacji metod optymalizacji zapytań. Pierwsza z podanych klasyfikacji wyróżnia optymalizację statyczną i optymalizację dynamiczną. Optymalizacja statyczna polega na znalezieniu „najlepszego” planu wykonania zapytania, przed rozpoczęciem wykonywania zapytania. W trakcie realizacji zapytania plan wykonania zapytania nie ulega już zmianie – stąd nazwa optymalizacja statyczna. Optymalizacja dynamiczna polega na znalezieniu „najlepszego” planu wykonania zapytania, przed rozpoczęciem wykonywania zapytania, ale później, w trakcie wykonywania zapytania jego plan wykonania może ulęgać zmianie. Aktualnie, komercyjne systemy baz danych zapewniają jedynie optymalizację statyczna, choć efektywność takiej optymalizacji jest najczęściej niższa aniżeli efektywność optymalizacji dynamicznej. Optymalizacja dynamiczna jest jednak znacznie bardziej kosztowna.

Druga z podanych klasyfikacji wyróżnia optymalizację pojedynczego zapytania oraz jednoczesną optymalizację wielu zapytań. W przypadku optymalizacji pojedynczego zapytania, optymalizacji podlega tylko jedno zapytanie. W przypadku jednoczesnej optymalizacji wielu zapytań, częściowe wyniki wykonania jednego zapytania mogą być wykorzystane przez wiele innych zapytań, co prowadzi do minimalizacji czasu wykonania zbioru zapytań. W chwili obecnej systemy komercyjnych baz danych zapewniają jedynie optymalizację pojedynczego zapytania.



Proces optymalizacji zapytań



Jak już wspomnieliśmy, pierwszą fazą przetwarzania zapytań jest faza transformacji zapytania SQL do postaci drzewa wyrażenia logicznego: Celem tej fazy jest również identyfikacja bloków zapytania (odpowiadających zagnieżdżonym zapytaniom lub perspektywom). W kolejnym kroku realizowana jest faza przepisywania zapytania za pomocą transformacji algebraicznych w celu uzyskania tańszego planu wykonania zapytania. W konsekwencji uzyskujemy zbiór najlepszych planów wykonania pojedynczych bloków zapytania. Pozostaje jeszcze problem połączenia bloków, w szczególności, problem zdefiniowania porządku wykonywania operacji połączenia. Wybór kolejności wykonywania operacji połączenia, tzn. wybór uszeregowania operacji połączenia, kończy proces optymalizacji zapytania. Obecnie, przejdziemy do przedstawienia poszczególnych faz przetwarzania zapytań.


Dekompozycja zapytania



Pierwszą fazą przetwarzania zapytania jest faza dekompozycji zapytania. Celem procesu dekompozycji zapytania jest transformacja zapytania wyrażonego w języku wysokiego poziomu na wyrażenie algebry relacji i weryfikacja syntaktycznej i semantycznej poprawności zapytania. Proces dekompozycji składa się z następujących etapów:


–analiza zapytania,


–normalizacja zapytania,


–analiza semantyczna zapytania,


–upraszczanie zapytania,


–restrukturyzacja zapytania.



Analiza zapytania



Celem etapu analizy jest analiza syntaktyczna poprawności zapytania. W skład tej analizy wchodzi weryfikacja poprawności atrybutów i relacji (czy w bazie danych występują wyspecyfikowane w zapytaniu relacje i atrybuty, czy zapytanie poprawnie specyfikuje typy danych). Następnie, zapytanie wyrażone w języku SQL jest transformowane do postaci reprezentacji wewnętrznej (wyrażenia algebry relacji), bardziej adekwatnej do procesu dalszego przetwarzania zapytania. Przedstawione na slajdzie drzewo algebry relacji, reprezentujące postać wewnętrzną zapytania, reprezentuje zapytanie, którego postać w języku SQL jest nastepująca:

Select *


From Employee E, Department D


Where E. deptId = D. DeptId


And E.position = ‘manger” and D.location = ‘London”;



Normalizacja zapytania



Kolejnym etapem fazy dekompozycji jest normalizacja zapytania. Celem etapu normalizacji zapytania jest przekształcenie wewnętrznej reprezentacji zapytania do znormalizowanej postaci koniunkcyjnej lub dysjunkcyjnej. W fazie tej sekwencja predykatów selekcji jest przekształcana do normalnej postaci koniunkcyjnej lub normalnej postaci dysjunkcyjnej. Postać dysjunkcyjna jest, najczęściej, mniej efektywna, gdyż wymaga niezależnego wartościowania poszczególnych składowych wyrażenia. Przykłady postaci koniunkcyjnej i dysjunkcyjnej wyrażenia zapytania przedstawiono na slajdzie.


Analiza semantyczna zapytania



Kolejnym, ważnym, etapem dekompozycji zapytania jest etap analizy semantycznej zapytania. Celem analizy semantycznej zapytania jest odrzucenie niepoprawnie sformułowanych lub sprzecznych zapytań. Zapytanie jest niepoprawnie sformułowane, jeżeli jego elementy składowe nie prowadzą do generacji wyniku. Zapytanie jest sprzeczne, jeżeli jego predykaty nie mogą być spełnione przez żadną krotkę w bazie danych. Przykładem klauzuli, która jest sprzeczna jest wyrażenie: position = ‘manager’ and position = ‘assistant’.

Zakładając, że baza danych jest w 1NF, nie istnieje w bazie danych żadna krotka, któraby jednocześnie spełniała oba predykaty. Wartość sprzecznej klauzuli interpretujemy jako wartość FALSE. W związku z tym, wyrażenie zawierające sprzeczna klauzulę można uprościć. Przykładowo, wyrażenie


(position = ‘manager’ and position = ‘assistant’) or salary > 1000;


ze względu na sprzeczność klauzuli : „position = ‘manager’ and position = ‘assistant’” można uprościć do postaci „salary > 1000”





Niestety, algorytmy oceny poprawności semantycznej zapytań istnieją tylko dla pewnej klasy zapytań, nie zawierających dysjunkcji i negacji. W jaki sposób rozwiązywany jest problem zapytań niepoprawnie sformułowanych oraz zapytań sprzecznych? Rozwiązanie problemu zapytań niepoprawnie sformułowanych opiera się na konstrukcji tak zwanego grafu połączenia relacji. W grafie tym, wierzchołki odpowiadają relacjom, natomiast luki odpowiadają operacjom połączenia wyspecyfikowanych w zapytaniu. Dodatkowo, graf połączenia relacji zawiera wierzchołek reprezentujący wynik zapytania. Jeżeli graf połączenia relacji nie jest spójny, to zapytanie jest niepoprawnie sformułowane.




Rozwiązanie problemu zapytań niepoprawnie sformułowanych opiera się na konstrukcji tak zwanego grafu połączeń atrybutów. Graf połączeń atrybutów konstruujemy następująco. Dla każdej referencji do atrybutu tworzymy w grafie wierzchołek atrybutu lub wierzchołek 0. Następnie, tworzymy luk skierowany pomiędzy wierzchołkami reprezentującymi operację połączenia, oraz łuk skierowany pomiędzy wierzchołkiem atrybutu a wierzchołkiem 0, reprezentujący warunek selekcji. W kolejnym kroku nadajemy wagi lukom:

łuk: a -> b posiada wagę c, jeżeli luk reprezentuje warunek nierównościowy (a<= b+c),


łuk: 0 -> a posiada wagę -c, jeżeli luk reprezentuje warunek nierównościowy (a >= c).


łuki reprezentujące połączenia posiadają wagę 0.


Jeżeli graf połączeń atrybutów zawiera cykl, którego suma wag jest ujemna, zapytanie jest sprzeczne.





Dla ilustracji problemu zapytań niepoprawnie sformułowanych rozważmy przykładowe zapytanie przedstawione na slajdzie. Skonstruujmy dla podanego zapytania graf połączenia relacji. W grafie tym, przypomnijmy, wierzchołki odpowiadają relacjom, natomiast luki odpowiadają operacjom połączenia wyspecyfikowanym w zapytaniu. Zapytanie zawiera trzy relacje. Zatem, graf połączenia relacji będzie zawierał 4 wierzchołki. Po uzupełnieniu grafu lukami reprezentującymi operacje połączenia wyspecyfikowane w zapytaniu, otrzymujemy graf przedstawiony na slajdzie. Łatwo zauważyć, że podane zapytanie jest źle sformułowane, gdyż graf nie jest spójny. W zapytaniu brakuje warunku połączeniowego v.propertyNo = p.propertyNo.





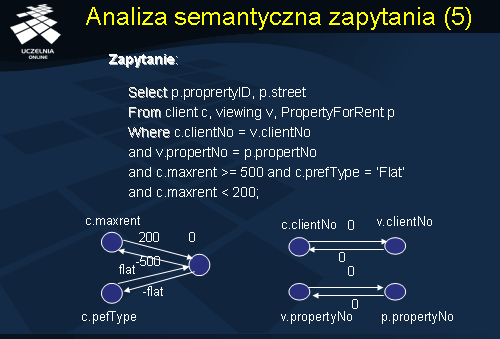
Dla ilustracji problemu zapytań sprzecznych rozważmy przykładowe zapytanie przedstawione na slajdzie. Skonstruujmy dla podanego zapytania graf połączeń atrybutów. Przypomnijmy, że graf połączeń atrybutów konstruujemy następująco. Dla każdej referencji do atrybutu tworzymy w grafie wierzchołek atrybutu lub wierzchołek 0. Następnie, tworzymy luk skierowany pomiędzy wierzchołkami reprezentującymi operację połączenia, oraz łuk skierowany pomiędzy wierzchołkiem atrybutu a wierzchołkiem 0, reprezentujący warunek selekcji. W kolejnym kroku nadajemy wagi lukom. Zauważmy, że zapytanie zawiera dwa warunki połączeniowe:

(1) c.clientNo = v.clientNo


(2) v.propertNo = p.propertNo


reprezentowane przez wierzchołki atrybutów: c.clientNo, v.clientNo, v.propertNo, p.propertNo. Wierzchołki te połączone są wzajemnie lukami o wagach 0. Podane zapytanie zawiera 3 predykaty selekcji (referencje do atrybutów):


c.maxrent >= 500


c.prefType = ‘Flat’


c.maxrent < 200


reprezentowane przez wierzchołki atrybutów: c.maxrent, c.prefType, i c.maxrent. Wierzchołki te połączone są wzajemnie lukami o wagach, odpowiednio, 200, -500, flat oraz –flat. Jak łatwo zauważyć, przedstawiony graf połączeń atrybutów zawiera cykl, którego suma wag jest ujemna (-300). Zatem, podane zapytanie jest sprzeczne.



Uproszczanie zapytania



Kolejnym etapem fazy dekompozycji jest upraszczanie zapytań. Celem tego etapu jest identyfikacja wyrażeń redundantnych, eliminacja wspólnych podwyrażeń, i transformacja zapytania do równoważnej postaci, ułatwiającej dalsze przekształcanie zapytania. Transformacja zapytania do postaci równoważnej polega na zastosowaniu znanych reguł algebry relacji podanych na slajdzie.


Budowa bloków



Kolejnym etapem fazy dekompozycji jest etap restrukturyzacji, czy tez transformacji zapytania. Zanim jednak przejdziemy do przedstawienia podstawowych reguł transformacji, wróćmy na chwilę do problemu konstrukcji podstawowych bloków zapytania. Tradycyjne podejście do konstrukcji bloków zapytania opera się na zastosowaniu transformacji algebraicznych, które zostaną przedstawione w dalszej części wykładu. jednakże, zbiór stosowanych transformacji różni się zasadniczo dla różnych systemów komercyjnych. Co więcej, nie wszystkie transformacje gwarantują minimalizację czasu wykonania danego bloku. W ostatnim czasie, coraz częściej, konstrukcja bloków opiera się na optymalizacji kosztowej, w której, dla każdego bloku, konstruujemy możliwe plany wykonania danego bloku i szacujemy koszt i rozmiar wykonania każdego planu. Ostatecznie wybierany jest plan wykonania o najniższym szacowanym koszcie. Do zakończenia procesu optymalizacji pozostaje jeszcze znalezienie najlepszego drzewa operacji połączenia, łączącego wyniki wykonania bloków zapytania. Tradycyjne podejście do problemu znajdowania najlepszego drzewa operacji połączenia (nazywane często podejściem w stylu systemu R) polega na zastosowaniu algorytmu programowania dynamicznego.


Problemy z optymalizacją



Generalnie, problem optymalizacji zapytań jest problemem bardzo trudnym. Istnie bardzo wiele podejść do optymalizacji. De facto, istnieje tyle podejść ile jest na rynku systemów zarządzania bazami danych. Złożoność problemu optymalizacji wynika z konieczności uwzględniania w procesie optymalizacji bardzo wielu czynników, które, dodatkowo, w trakcie wykonywani zapytania mogą ulegać modyfikacjom i zmianom (np. charakterystyka relacji i atrybutów, obciążenie stanowisk w systemie, fluktuacja obciążenia sieci, itp.). Należy stwierdzić, że problem optymalizacji zapytań nie został tak naprawdę jeszcze rozwiązany. Jest to szczególnie widoczne w przypadku dużych zapytań i aplikacji występujących w systemach wspomagania podejmowania decyzji. Ciągle trwają prace badawcze nad dalszą poprawą efektywności metod optymalizacji wykonywania zapytań, szczególnie, dla nowych typów danych (zbiory, sekwencje, grafy, dokumenty XML). Możliwe kierunki poprawy efektywności obejmują: opracowanie nowych reguł algebraicznej transformacji złożonych zapytań, opracowanie nowych metod znajdowanie kolejności wykonywania operacji binarnych ( w tym szczególnie, operacji połączenia), oraz opracowanie nowych metod szacowania kosztów i rozmiarów wyników pośrednich zapytania. Po tym krótkim przedstawieniu problemów związanych z optymalizacją zapytań, wróćmy do reguł transformacji wyrażeń reprezentujących zapytania.


Operacje



Każdy plan wykonania zapytania jest częściowo uporządkowanym zbiorem operacji. W skład tego zbioru operacji wchodzą: operacja skanowania, selekcji, projekcji, połączenia, produktu kartezjańskiego, operacje grupowania i agregacji. Problem znalezienia najlepszego planu wykonania zapytania obejmuje, z jednej strony, określenie kolejności wykonania operacji wchodzących w skład zapytania, z drugiej, określenia metody wykonania poszczególnych operacji. Przykładowo, mamy dwie metody dostępu do relacji: bezpośrednie skanowanie (odczyt) relacji lub dostęp do relacji poprzez skanowanie indeksu założonego na relacji. Podstawowa reguła optymalizacji mówi, że wszystkie operacje unarne (projekcja i selekcja) należy przesunąć w dół drzewa zapytania, tzn. wykonywać w pierwszej kolejności. Operacje te charakteryzują się silną własnością redukcji (filtrowania) przetwarzanych danych. Redukując rozmiar przetwarzanych danych, operacje unarne prowadzą do poprawy efektywności wykonywania operacji binarnych. Dlatego, operacje binarne (połączenie, produkt kartezjański) należy przesunąć w kierunku korzenia drzewa zapytania. Dla operacji binarnych, np. połączenia, poza określeniem kolejności ich wykonywania, należy wybrać również metodę ich wykonania (dla połączenia - nested loop, sort-merge, hash-join). Najczęściej, na końcu planu wykonania zapytania znajdują się operacje grupowania i agregacji.


Prawa algebry relacji



Podstawowe reguły transformacji wyrażeń reprezentujących zapytania wynikają z praw algebry relacji i obejmują, m. in. reguły przemienności i łączności operacji oraz reguły dystrybutywności. Przykładowe reguły przemienności i łączności operacji oraz reguły dystrybutywności operacji przedstawiono na slajdzie. Zgodnie z przedstawioną regułą dystrybutywności, wyrażenie będące połączeniem relacji R oraz relacji, będącej sumą relacji S i T, transformujemy do sumy relacji będących połączeniem relacji R z S i R z T. Reguła ta pozwala przesunąć operator sumy za operator połączenia. Ponieważ koszt operacji połączenia silnie zależy od rozmiarów łączonych relacji, zastosowanie transformacji, opartej o regułę dystrybutywności, transformuje wyjściowe wyrażenie do sumy relacji będących połączeniem mniejszych relacji, co powinno skutkować niższym kosztem wykonania całego wyrażenia. Reguła łączności operacji połączenia pozwala zmienić kolejność łączonych relacji. Łącząc, w pierwszej kolejności, mniejsze relacje, zmniejszamy rozmiary częściowych wyników operacji połączenia, co również powinno prowadzić do zmniejszenia kosztu wykonania całego wyrażenia.




Kolejny slajd przedstawia reguły transformacji dla operacji selekcji. Szczególne znaczenie ma pierwsza reguła dotycząca koniunkcji predykatów selekcji:

selekcja C AND C’(R) = selekcja C(selekcja C’(R))


Reguła ta wynika z komutatywności operatora selekcji i pozwala zmienić kolejność wykonywania operacji selekcji. W pierwszej kolejności zawsze wykonywana jest operacja selekcji o większym współczynniku selektywności, bardziej redukująca rozmiar relacji R. Zwróćmy uwagę na regułę nr 3:


selekcja C (R połączenie S) = selekcja C (R) połączenie S (jeżeli C zawiera tylko atrybuty relacji R)


oraz regułę nr 4:


selekcja C (R połączenie S) = (selekcja C (R)) połączenie (selekcja C (S)) (jeżeli C zawiera atrybuty obu relacji R i S)

Transformacja oparta o te reguły pozwala przesunąć operator selekcji przed operator połączenia, redukując rozmiary łączonych relacji, co prowadzi do zmniejszenia kosztu wykonania zapytania. Podobna uwaga dotyczy ostatnich trzech przedstawionych reguł, które pozwalają przesunąć operator selekcji przed operatory binarne sumy, iloczynu i różnicy.





Kolejny slajd przedstawia podstawową regułę transformacji wykorzystującą własność komutatywności operacji selekcji i projekcji. Przesuwając operator projekcji przed operator selekcji zmniejszamy rozmiar argumentu operatora selekcji.

Rozważmy dwa przykłady ilustrujące działanie przedstawionych dotychczas reguł transformacji. Dane są relacje R(A, B, C, D) i S(E, F, G).

Jaką regułę transformacji należy zastosować w odniesieniu do pierwszego wyrażenia?


Odpowiedź – regułę: selekcja z relacji R przed połączeniem z relacją S, tj. „selekcja C (R połączenie S) = selekcja C (R) połączenie S” (jeżeli C zawiera tylko atrybuty relacji R). Po zastosowaniu powyższej reguły, przedstawione wyrażenie zostanie przetransformowane do postaci: „selekcja F=3 (S) połączenie R”.


Rozważmy drugie z podanych wyrażeń. Jaką regułę transformacji należy zastosować w odniesieniu do tego wyrażenia? Odpowiedź – złożenie dwóch reguł: reguły dotyczącej kaskady selekcji oraz reguły dotyczącej dystrybutywności selekcji i połączenia. Po zastosowaniu powyższych reguł, przedstawione wyrażenie zostanie przetransformowane do postaci: „(selekcja G=9 (S)) połączenie (selekcja A=5 (R))”.





Kolejny slajd przedstawia podstawowe reguły transformacji wyrażeń zawierających projekcje. Pierwsza reguła transformacji wynika z reguły dystrybutywności operacji połączenia względem projekcji. Przesuwając operator projekcji przed operator połączenia zmniejszamy rozmiar argumentu operatora połączenia. Druga reguła transformacji dotyczy kaskady projekcji, które mogą być łączone w jedną operację projekcji. Rozważmy przykład ilustrujący działanie przedstawionych reguł transformacji. Dane są relacje R(A, B, C, D) i S(E, F, G). W jaki sposób można uzyskać przedstawioną na slajdzie transformację? Jakie będą predykaty projekcji w wynikowym wyrażeniu? Z przedstawionych powyżej reguł wynika, że predykaty projekcji w wynikowym wyrażeniu mają następującą postać:

projekcjaA,B,G(R połączenie S) = projekcja A, B, G ((projekcja A,B,D (R)) połączenie D=E (projekcja E,G(S)))



Przepisywanie zapytań: podzapytania



Przejdziemy obecnie do przedstawienia bardziej specyficznych reguł transformacji zapytań. Dane jest zapytanie przedstawione na slajdzie. Jak łatwo zauważyć, przedstawione zapytanie zawiera skorelowane podzapytanie zagnieżdżone. Zapytania zawierające skorelowane podzapytania zagnieżdżone są kosztowne w realizacji, gdyż wymagają sprawdzenia, dla każdej krotki zapytania zewnętrznego, czy spełniony jest dla tej krotki warunek podzapytania skorelowanego. Klasyczna metoda transformacji takich zapytań polega na przepisaniu zapytania w taki sposób, aby usunąć zagnieżdżenie (ang. unnesting). Usunięcie zagnieżdżenia polega na zastąpieniu zagnieżdżenia operacją połączenia.




Kolejny slajd przedstawia przepisanie zapytania ze slajdu nr 21, w którym zastąpiono podzapytanie zagnieżdżone operacją połączenia. Pozostałe warunki selekcji podzapytania zagnieżdżonego zostały przeniesione o zapytania zewnętrznego. Usunięcie zagnieżdżenia zdecydowanie poprawia czas realizacji zapytania.


Transformacja zapytań zagnieżdżonych



Rozważmy inny przykład zapytania zawierającego skorelowane podzapytanie zagnieżdżone przedstawiony na slajdzie. Przykład ten ilustruje, że nie zawsze jest możliwe przetransformowanie zapytania do postaci bez zagnieżdżenia, i że, de facto, dla każdego typu zapytania, zawierającego skorelowane podzapytanie zagnieżdżone, należałoby zdefiniować specyficzne reguły transformacji. Celem zapytania przedstawionego na slajdzie jest znalezienie nazwy najdroższego produktu w kolorze niebieskim, i nazwy jego producenta.




Na kolejnych slajdach przedstawiono transformację zapytania ze slajdu nr 23 do postaci nie zawierającej skorelowanego podzapytania zagnieżdżonego. Pierwszym krokiem transformacji jest znalezienie uzupełnienia zapytania ze slajdu 23. Przedstawione na slajdzie zapytanie znajduje nazwy niebieskich produktów, i nazwy ich producentów, dla których istnieją produkty niebieskie o wyższej cenie. Zauważmy, że zapytanie cały czas jest zapytaniem zawierającym skorelowane podzapytanie zagnieżdżone. Transformujemy podane zapytanie do postaci, w której podzapytanie zastąpiono operacją połączenia.




Transformujemy podane zapytanie do postaci, w której podzapytanie zastąpiono operacją połączenia. Jak już wspominaliśmy, operacja usunięcia podzapytania prowadzi do istotnej minimalizacji czasu wykonania zapytania. Przedstawione na slajdzie zapytanie zwraca w wyniku dokładnie to czego nie szukamy.




Ostatnim krokiem transformacji jest odjęcie od zbioru wszystkich niebieskich produktów tych niebieskich produktów, dla których istnieją produkty niebieskie o wyższej cenie. W wyniku wykonania operacji EXCEPT znajdujemy poszukiwany zbiór najdroższych niebieskich produktów. Zauważmy, że wynikowe zapytanie nie zawiera skorelowanego podzapytania i jego koszt będzie niższy niż oryginalnego zapytania ze slajdu 23. Zauważmy, jednakże, że przedstawiona transformacja nie jest trywialna.


Redukcja rozmiarów relacji



Jak już wspomnieliśmy, zagadnienie optymalizacji jest zagadnieniem trudnym i istnieje bardzo wiele, specyficznych, reguł transformacji dla różnych typów zapytań. Co więcej, nie zawsze jest możliwe przetransformowanie zapytań w taki sposób, aby nie zawierało podzapytań (szczególnie dla podzapytań skorelowanych). W szczególnych przypadkach, gdy czas realizacji zapytania jest nieakceptowany, można zastosować technikę redukcji rozmiarów relacji uczestniczących w zapytaniu opartą o sekwencję operacji półpołączenia. Technika ta jest wykorzystywana do optymalizacji zapytań rozproszonych w systemach rozproszonych baz danych.