Macierzą typu strecher nazywamy macierz, której niezerowymi elementami mogą być tylko elementy, mające obie współrzędne równe. Innymi słowy, macierz typu strecher to macierz diagonalna. Przykłady macierzy typu strecher zamieszczono na slajdzie. Macierz typu stretcher jest macierzą diagonalną i działa rozciągająco wzdłuż osi współrzędnych. Dwuwymiarowa macierz diagonalna o elementach a i b działa rozciągająco wzdłuż osi x ze współczynnikiem a oraz wzdłuż osi y ze współczynnikiem b, co łatwo pokazać. Jeżeli pomnożymy wektor jednostkowy [1, 1] przez macierz o elementach 3 i 2, przedstawioną na slajdzie, to otrzymamy w wyniku wektor o elementach 3 i 2.

Po wprowadzeniu macierzy aligner, hanger i strecher możemy obecnie wprowadzić pojęcie rozkładu macierzy A względem wartości szczególnych.

Rozkładem macierzy A (o rozmiarze m x n) względem wartości szczególne nazywamy rozkład postaci: A = U S V (transponowane).

W rozkładzie macierzy A względem wartości szczególnych, macierze U, S i transponowana macierz V, to następujące macierze. Macierz U jest macierzą typu hanger kolumnami ortonormalną o rozmiarze m x m, macierz V jest macierzą typu aligner wierszami ortonormalną o rozmiarze n x n, wreszcie, macierz S jest macierzą typu strecher, jest macierzą diagonalną o rozmiarze m x n, której elementy leżące na przekątnej są nieujemne. Kolumny macierzy hanger to prawe wektory szczególne macierzy A, natomiast wiersze macierzy aligner to lewe wektory szczególne macierzy A.

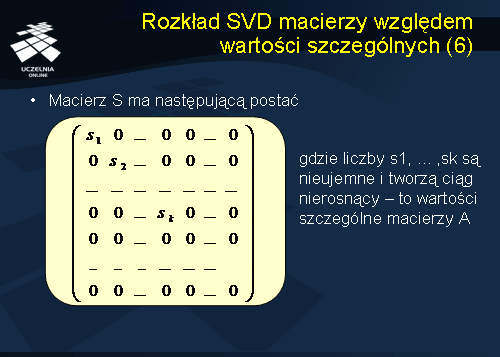
Macierz S jest macierzą diagonalną o elementach s1, s2, ..., sk, gdzie liczby s1, ... ,sk są nieujemne i tworzą ciąg nierosnący. Liczby te to wartości szczególne macierzy A.

Pytanie jakie można postawić jest następujące: czy rozkład macierzy A względem wartości szczególnych jest jednoznaczny. Odpowiedzią na to pytanie jest następujące twierdzenie: Każda macierz posiada rozkład na wartości szczególne i wartości te są wyznaczone jednoznacznie. Rozkład SVD macierzy względem wartości szczególnych posiada szereg ciekawych własności. Przypomnijmy pojęcie normy macierzy. Normę euklidesową macierzy A definiujemy jako max { || A x || / ||x|| }. Okazuje się, że norma Euklidesowa macierzy A jest równa największej jej wartości szczególnej (s1). Rząd macierzy A to liczba liniowo niezależnych kolumn macierzy A. Rząd macierzy A jest równy rzędowi macierzy diagonalnej S w rozkładzie SVD, który, z kolei, jest równy liczbie niezerowych wartości szczególnych macierzy S w rozkładzie SVD. Mając rozkład SVD łatwo obliczyć rząd macierzy: jest on równy liczbie niezerowych wartości szczególnych macierzy. Podobnie, wymiar przestrzeni zer macierzy A równy jest liczbie zerowych wartości szczególnych macierzy S.

Miarą liniowej niezależności pomiędzy kolumnami macierzy A jest tak zwana liczba warunkowa macierzy A (oznaczona cond(A)). Jest to ważna miara, z punktu widzenia analizy macierzy wektorów dokumentów, która mówi o tym w jakim stopniu słowa kluczowe macierzy TF są niezależne. Liczba warunkowa macierzy A, cond(A) = stosunkowi maksymalnej wartości szczególnej macierzy S (smax) do minimalnej wartości szczególnej macierzy S (smin), tj. smax/smin.

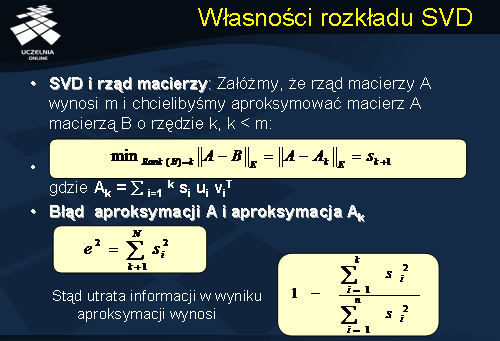
Szczególne znaczenie, z punktu widzenia problemu wymiarowości macierzy TF, ma własność dekompozycji macierzy A na macierze rzędu 1. Niech rząd macierzy A wynos m. Rozkład macierzy A względem wartości szczególnych oznacza, że macierz A można przedstawić w postaci zredukowanej jako sumę iloczynów si * ui * vi (transponowane), po i od 1 do m, gdzie każdy ze składników si *hi*ai jest macierzą rzędu 1. Załóżmy, że rząd macierzy A wynosi m i chcielibyśmy aproksymować macierz A macierzą B o rzędzie k, k < m. Załóżmy, że macierz B jest sumą iloczynów si * ui * vi (transponowane), po i od 1 do k. Błąd aproksymacji macierzy A macierzą B, równą sumie iloczynów si * ui * vi (transponowane), po i od 1 do k, jest równy sumie wartości szczególnych sk+1, sk+2, ..., sm macierzy S w rozkładzie SVD, podniesionych do kwadratu. Stąd, można obliczyć utratę informacji w wyniku aproksymacji.

Aproksymacja macierzy A macierzą Ak pozwala na znaczącą kompresję danych z niewielką utratą informacji. Rozważmy przykład zdjęcia przedstawionego na slajdzie. Reprezentacją zdjęcia jest macierz M o rozmiarze 254 x 264. Rząd macierzy M wynosi 256. Macierz M można przedstawić jako sumę iloczynów si * ui * vi (transponowane), po i od 1 do 256, gdzie każdy ze składników jest macierzą rzędu 1.

Jeżeli ograniczymy się do pierwszych k wartości szczególnych macierzy M uzyskamy macierz będącą aproksymacją macierzy M. Okazuje się, wizualnie, że już od k=40 aproksymacja macierzy M jest akceptowalna i jej przybliżenie wygląda całkiem dobrze.

Zauważmy, że wyjściowa macierz M wymaga zapamiętania 256 x 264 = 67584 liczb. Aby zapamiętać macierz skompresowaną (dla k=40) wystarczy zapamiętać: 40 wartości szczególnych macierzy M, 40 lewych wektorów szczególnych macierzy M (każdy ma 256 elementów), oraz 40 prawych wektorów szczególnych macierzy M (każdy ma 264 elementy). Razem: 40(1+256+264)=20840 liczb. Zysk z tytułu kompresji wynosi w przybliżeniu 70 %.

Wróćmy do przykładowej macierzy M, przedstawionej na slajdzie nr 15, na poprzednim wykładzie. Macierz diagonalna S w rozkładzie SVD macierzy M posiada następujące wartości szczególne: ( 77,4 69,5 22,9 13,5 12,1 4,8). Załóżmy, że aproksymujemy macierz M macierzą Mk, k=1, 2, tj. ograniczymy się do dwóch pierwszych wartości szczególnych macierzy S. Jak wynika z rozważań przedstawionych na slajdzie nr 14, błąd aproksymacji wyniesie w tym przypadku tylko 7, 5%. Wydaje się, że utrata informacji semantycznej na poziomie 7,5% jest akceptowalna. Ile wyniesie redukcja wymiarowości macierzy M? Macierz M o rozmiarze 10 x 6 zastępujemy macierzą B o rozmiarze 10 x 2. Zysk z tytułu aproksymacji macierzy M macierzą B wyniesie zatem w przybliżeniu 66 %.

Wagi dokumentów w nowej reprezentacji (macierz B), odpowiadającej 2-wymiarowej przestrzeni składowych głównych (2 pierwsze wartości szczególne macierzy S), odpowiadają dwóm pierwszym kolumnom macierzy U w rozkładzie SVD macierzy M.

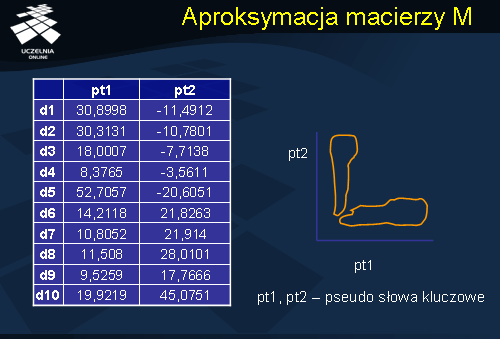
Niniejszy slajd przedstawia nową reprezentację macierzy M (macierz B), która odpowiada dwóm pierwszym kolumnom macierzy U w rozkładzie SVD macierzy M. Kolumny nowej reprezentacji odpowiadają nowym pseudo-słowom powstałym jako ważona kombinacja oryginalnych słów kluczowych. Zauważmy, że w nowej dwu-wymiarowej przestrzeni dokumenty wyraźnie grupują się w dwóch klastrach, co przedstawia schematyczny rysunek zamieszczony na slajdzie. Okazuje się, analizując składowe główne nowej przestrzeni, że pierwsze pseudo-słowo uwzględnia w większym stopniu (nadaje im największe wagi) dwa pierwsze słowa kluczowe: bazy_danych i SQL, natomiast drugie uwzględnia w większym stopniu słowa kluczowe regresja, wiarygodność i liniowa. Stąd, pierwszy klaster jest utworzony przez dokumenty związane z problematyką bazodanową, natomiast drugi z klastrów zawiera głównie dokumenty związane z analizą danych. Zaletą zastosowanej aproksymacji jest znalezienie, stąd nazwa techniki – ukryte indeksowanie semantyczne, niejawnego związku pomiędzy dokumentami, które w oryginalnej reprezentacji są mało podobne do siebie. Rozważmy dwa dokumenty d11 i d12, z których dokument d11 zawiera słowo kluczowe bazy_danych (niech częstość wynosi 10), natomiast dokument d12 zawiera słowo kluczowe SQl (niech częstość wynosi również 10). W oryginalnej reprezentacji TF, oba dokumenty będą mało podobne do siebie, ponieważ nie zawierają żadnych wspólnych słów. W nowej reprezentacji, oba dokumenty znacznie się do siebie zbliżą, gdyż oba dotyczą tej samej problematyki bazodanowej. Ta zaleta ukrytego indeksowania semantycznego przejawia się również w odniesieniu do zapytań. Gdybyśmy zdefiniowali zapytanie o dokumenty dotyczące baz danych w odniesieniu do oryginalnej reprezentacji, to dokument d12, jako nie zawierający słowa kluczowego nie pojawiłby się w wyniku zapytania. W przypadku nowej reprezentacji, jako dokument odnoszący się do problematyki baz danych, dokument d12 znalazłby się w wyniku zapytania.

Przejdziemy obecnie do przedstawienia wybranych struktur danych wspierających przechowywanie i wyszukiwanie dokumentów. W literaturze zaproponowano szereg struktur danych wspierających przechowywanie i wyszukiwanie dokumentów tekstowych. Najbardziej popularne, w chwili obecnej, są dwie struktury danych: pliki odwrócone i pliki sygnaturowe. Idea pliku odwróconego jest przedstawiona na następnym slajdzie. Najczęściej, dokumenty tekstowe przechowujemy z wykorzystaniem dwóch poindeksowanych tablic: TermTable i DocTable. Podstawową tablicą przechowująca dokumenty jest tablica TermTable, której rekordy składają się z par lub <słowo-lista_wskaźników>. Słowa są kluczami wyszukiwania, natomiast wskaźnik wskazuje na blok zawierający wskaźniki do dokumentów zawierających dane słowo (rozwiązanie przedstawione na slajdzie). W przypadku pary słowo-lista_wskaźników, lista wskaźników wskazuje bezpośrednio na dokumenty zawierające dane słowo. Tablica DicTable jest uzupełnieniem tablicy TermTable. Rekordy tablicy DocTable składają się z par <doc_id, lista słów kluczowych> lub lista wskaźników do słów kluczowych występujących w dokumencie doc_id, uporządkowana zgodnie z ich ważnością. W bloku zawierającym, dla danego słowa, wskaźniki do dokumentów zawierających dane słowo, umieszcza się również pewne dodatkowe dane o samym wystąpieniu słowa (np. częstość występowania słowa danym dokumencie, waga TF-IDF slowa). Wyszukiwanie jest realizowane w oparciu o słowa.

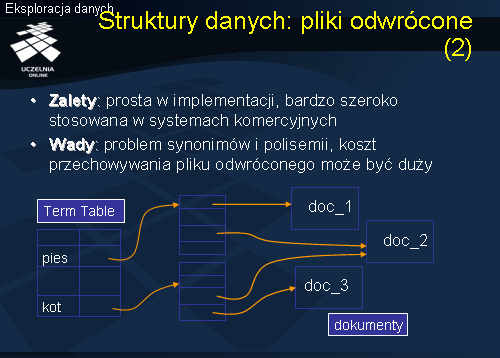
Korzystając z indeksu tablicy TermTable, założony na atrybucie , wyszukiwany jest odpowiedni rekord tej tablicy zawierający wskaźnik do bloku wskaźników. Jeżeli szukamy dokumentów zawierających słowa kluczowe <pies> i <kot>, znajdujemy wskaźniki do dokumentów zawierających, odpowiednio, słowa kluczowe. Dokumenty, które zawierają oba wymienione słowa kluczowe są wskazywane przez wskaźniki należące do obu zbiorów wskaźników. Główną zaletą omawianej struktury jest prostota implementacji pliku odwróconego. Struktura ta jest bardzo szeroko stosowana w systemach komercyjnych, zarówno systemów tekstowych baz danych jak i systemów wyszukiwania informacji. Wadą tej struktury jest problem synonimów i polisemii oraz koszt przechowywania pliku odwróconego.

Drugą, popularną strukturą danych wspierającą przechowywanie i wyszukiwanie dokumentów tekstowych jest struktura pliku sygnaturowego. Idea tej organizacji danych opiera się na sygnaturowej reprezentacji dokumentu jako zbioru słów kluczowych. Czym jest sygnatura dokumentu? Sygnatura dokumentu reprezentuje zbiór słów kluczowych opisujących dany dokument. Sygnatura dokumentu jest złożeniem (superpozycją) sygnatur słów opisujących dany dokument. Taki sposób tworzenia sygnatury dokumentu nazywamy kodowaniem z nakładaniem (ang. superimposed coding). Czym jest sygnatura słowa? Jest to ciąg bitów o stałej długości (np. b). Pojedyncze słowo jest reprezentowane przez k bitów ustawionych na 1. Oczywiście, dwa różne słowa mogą być reprezentowane przez te samą sygnaturę. Przykładowo, niech b=6. Niech <1 1 0 0 0 0> oznacza sygnaturę słowa <pies>, natomiast <1 0 0 0 0 1> niech oznacza sygnaturę słowa <kot>. Sygnatura dokumentu zawierającego oba słowa jest złożeniem (superpozycją) sygnatur słów opisujących dany dokument i ma postać: <1 1 0 0 0 1>. Plik sygnaturowy jest plikiem sygnatur dokumentów tekstowych.

W jaki sposób realizowane jest zapytanie do pliku sygnaturowego? Załóżmy, że dane jest zapytanie Q o dokumenty zawierające zbiór słów t1, t2, .., tk. Realizacja zapytania Q przebiega następująco. Dla każdego słowa t1, t2, .., tk generowana jest sygnatura słowa, a następnie, generowana jest sygnatura zapytanie poprzez złożenie sygnatur słów. Kolejnym krokiem jest faza wyszukiwania. W tej fazie, system znajduje dokumenty, których sygnatury pokrywają sygnaturę zapytania. Jak należy rozumieć pokrywanie się sygnatur? Mówimy, że sygnatura S1 pokrywa sygnaturę S2, jeżeli wszystkie bity ustawione na 1 w sygnaturze S2 są również ustawione na 1 w sygnaturze S1. Po zakończeniu fazy wyszukiwania przechodzimy do fazy filtracji. W fazie filtracji, ze względu na niejednoznaczność konstrukcji sygnatury, system odfiltrowuje te dokumenty, które nie zawierają słów kluczowych podanych w zapytaniu.

Faza filtracji wymaga bezpośredniego odczytu dokumentów (tj. dostępu bazy danych), w celu weryfikacji czy wyszukany dokument zawiera podane słowa kluczowe. W większości przypadków praktycznych, plik sygnaturowy zapewnia stosunkowo wysoką selektywność dokumentów i w fazie filtracji sprawdzeniu podlega, najczęściej, niewielki zbiór dokumentów. Przedstawiony schemat wyszukiwania ma charakter ogólny, Istnieje wiele różnych implementacji plików sygnaturowych, różniących się mechanizmem generowana sygnatur słów i ich superpozycją.

Wróćmy na zakończenie wykładu do pewnych ogólnych rozważań związanych z eksploracją tekstu. Poważnym problemem praktycznym jest problemem inflacja informacji. Generowanych są codziennie miliony dokumentów tekstowych. Problemem jest nie tylko wyszukanie odpowiednich dokumentów, ale, mówiąc, ogólniej, „wydobycie” odpowiedniej informacji z tych dokumentów. Łatwo zauważyć, że wyszukiwanie dokumentów nie rozwiązuje jeszcze problemu. Dla ilustracji, przytoczymy historię, która przytrafiła się Autorowi niniejszych slajdów. Autor poszukiwał w Internecie polskiego tłumaczenia angielskiego określenia „partitioning algorithms”. Po podaniu określenia „partitioning algorithms”, wyszukiwarka Google zwróciła 13 700 000 dokumentów! Niestety, pierwsze strony wyniku wyszukiwania nie zwróciły ani jednej polskiej publikacji. Nota bene, Google zwrócił, na wysokiej pozycji, slajdy Autora dotyczące grupowanie, ale również w języku angielskim. Kolejna próba polegała na zdefiniowaniu określenia „algorytmy grupowania”. Tym razem wynik wyszukiwania wynosił 11 900 dokumentów. Sprawdzenie pierwszych dokumentów również niewiele pomogło. Część Autorów używała określenia „algorytmy iteracyjno-optymalizacyjne”, część „algorytmy z podziałem”, z kolei inni Autorzy używali określenia „algorytmy podziałowe”. Reasumując, wiele (czasami bardzo wiele) dokumentów może zawierać pożyteczną (szukaną) informację, ale dokument to jeszcze nie informacja. Przydatność dokumentu można, często, określić dopiero po przejrzeniu jego zawartości (lepsze procedury wyszukiwania niewiele tu pomogą). Wreszcie, często problemem nie jest znajdowanie dokumentów, lecz wzorców/trendów]informacji w tych dokumentach

Jak wspomnieliśmy, wyszukiwanie relewantnych dokumentów tekstowych, mimo swojej ważności, nie wyczerpuje problemu eksploracji dokumentów tekstowych. Inne, typowe, zadania eksploracji tekstu to: analiza połączeń (asocjacje) pomiędzy dokumentami, wykrywanie podobieństw i anomalii w dokumentach, klasyfikacja dokumentów, kategoryzacja dokumentów, grupowanie dokumentów, czy ekstrakcja cech dokumentów.

Analiza asocjacji (nazywane odkrywaniem asocjacji) polega na wykrywaniu niespodziewanych korelacji pomiędzy dokumentami lub słowami kluczowymi.

Metody analizy asocjacji są wykorzystywane m.in. we wstępnym przetwarzaniu tekstu:

parsing, stemming, usuwanie słów ze stop listy, itp.

Podstawowym zadaniem algorytmów odkrywania asocjacji w dokumentach tekstowych jest znajdowanie słów często występujących w wielu dokumentach. Każdy dokument traktujemy jako pojedynczą transakcję klienta (document_id, zbiór słów kluczowych), a następnie, stosując znane algorytmy odkrywania asocjacji (np. algorytm Apriori) odkrywamy słowa/frazy/zdania często występujące w dokumentach.

Innym ważnym zadaniem eksploracji tekstu jest klasyfikacja dokumentów tekstowych. Metody klasyfikacji dokumentów tekstowych można wykorzystać do automatycznej klasyfikacji stron WWW, wiadomości e-mail, lub plików tekstowych. Proces konstrukcji klasyfikatora dokumentów tekstowych, w ogólności, wygląda następująco. W kroku pierwszym generowany (konstruowany) jest zbiór treningowy dokumentów, który, następnie, podlega klasyfikacji przez eksperta (ekspertów). Klasyfikacja dokumentów, w odróżnieniu od omawianych wcześniej metod klasyfikacji innych typów danych, wymaga bezpośredniego udziału ekspertów w procedurze klasyfikacji zbioru treningowego. Następnie, system eksploracji generuje zbiór reguł klasyfikacyjnych. dkryte reguły można zastosować do klasyfikacji nowych dokumentów tekstowych i ich podziału na klasy.

Ważnym i ciekawym zadaniem eksploracji tekstu jest ekstrakcja cech dokumentów. Metody ekstrakcji cech pozwalają na: automatyczne odkrywanie języka, w jakim został przygotowany dokument, rozpoznawanie słownika (zbioru słów), który został wykorzystany do przygotowania tekstu, rozpoznawanie typu dokumentu (artykuł gazetowy, ulotka, strona WWW, itd..), ekstrakcja nazwisk osób i ich afiliacji wymienionych w tekście, znajdowanie skrótów wprowadzonych w tekście i łączenie tych skrótów z ich pełnym brzmieniem.

Bardzo popularnym zadaniem eksploracji tekstu jest grupowanie dokumentów tekstowych w oparciu o ich zawartość (a ściślej mówiąc, w oparciu o ich reprezentację). Temu zagadnieniu poświęciliśmy już sporo uwagi przy omawianiu algorytmów grupowania. Najczęstszą metodą grupowania dokumentów tekstowych jest hierarchiczny algorytm aglomeracyjny, który jako miarę odległości dwóch dokumentów wykorzystuje zmodyfikowaną miarę kosinusową. Ciekawym problemem związanym z grupowaniem dokumentów tekstowych jest znajdowanie charakterystyki otrzymanych klastrów. Jest to szczególnie widoczne w przypadku grupowania wyników uzyskiwanych z wyszukiwarek internetowych. Dla ilustracji rozważmy popularny i często przytaczany przykład z podaniem terminu „lampart” do wyszukiwarki Google. Wyszukiwarka zwraca ponad 3 mln dokumentów, z czego zdecydowana większość dotyczy piłkarza F. Lamparta, cześć dotyczy czołgu, itd.

W ostatnim czasie pojawiło się szereg narzędzi, które grupują wyniki uzyskiwane z wyszukiwarek (np. Carrot 2). Problem w tym, aby każdemu z klastrów dokumentów przypisać określoną, czytelną charakterystykę.

W odniesieniu do dokumentów tekstowych definiuje się jeszcze jedno zadanie eksploracji, a mianowicie, kategoryzację dokumentów tekstowych. Termin ten jest, często, używany w różnych znaczeniach – czasami jest używany jako synonim terminu grupowanie, czasami, jako synonim terminu klasyfikacja. Kategoryzacja dokumentu tekstowego jest pewna forma klasyfikacji. Grupowanie dokumentów polega na tym, że dokumenty są przetwarzane i grupowane w dynamicznie generowane klastry. Kategoryzacja dokumentów polega na grupowaniu dokumentów w zbiór predefiniowanych klas (kategorii) w oparciu o taksonomię generowaną przez zbiór treningowy. Taksonomia klas pozwala na grupowanie dokumentów według haseł (tematów). Klasy (kategorie) dokumentów są definiowane przez użytkowników.

Kategoryzacja dokumentów, ze względu na niejednoznaczność (czy raczej wieloznaczność), wymaga rankingu dokumentów z punktu widzenia przypisania danego dokumentu do określonej kategorii. Przykładowo, dokument x należy do kategorii: „Frank Lampart”, „Piłkarze”, „Piłka nożna”, „Sport”. Kategorie te tworzą taksonomie specjalizacji/generalizacji.