Optymalizacja zapytań część II
Niniejszy wykład jest kontynuacją wykładu poświęconego problemom wykonywania i optymalizacji zapytań w systemach baz danych. Rozpoczniemy od dokończenia prezentacji technik przepisywania złożonych zapytań. Następnie, przejdziemy do przedstawienia zagadnień związanych z optymalizacją kosztową zapytań. Skoncentrujemy się na zagadnieniu szacowania rozmiarów wyników pośrednich wykonania podstawowych operacji w systemie bazy danych, takich jak: selekcja, projekcja, połączenie, agregacja. Przedstawimy, następnie, koncepcję histogramów i pokażemy w jaki sposób histogramy pozwalają dokładniej oszacować wynik wykonania operacji. Na zakończenie wykładu powiemy o typach drzew zapytań i zagadnieniu określania porządku wykonywania operacji połączenia.
Przepisywanie zapytań: agregacja i połączenie

Prezentowany slajd przedstawia podstawową regułę transformacji wyrażeń zawierających operację połączenia i operację agregacji danych. Dane jest drzewo zapytania, przedstawione na slajdzie, które, dla każdego produktu, znajduje łączną liczbę sprzedanych produktów. Zapytanie może zawierać pewne dodatkowe predykaty selekcji. Podstawowa reguła transformacji takich drzew polega na przesunięciu operatora agregacji przed operator połączenia. W konsekwencji, jeden z argumentów operatora połączenia posiada znacznie mniejszy rozmiar, co prowadzi do minimalizacji czasu wykonywania zapytania.
Przykładowy schemat

Zanim przejdziemy do prezentacji dalszych reguł transformacji, wprowadzimy obecnie przykładową bazę danych, do której będziemy się odwoływać w dalszej części wykładu. baza danych składa się z dwóch relacji: Wykładowca i Wykład. Kluczami relacji są atrybuty podkreślone linią ciągłą. Na slajdzie podane są rozmiary obu relacji.
Przypisywanie zapytań: wstawianie operacji

Kolejny slajd przedstawia zmodyfikowaną regułę transformacji wyrażeń zawierających operację połączenia i operację agregacji danych. Dane jest drzewo zapytania, przedstawione na slajdzie, które, dla każdej kategorii produktów, znajduje łączną liczbę sprzedanych produktów danej kategorii. Zauważmy, że przedstawiona na slajdzie transformacja, polegająca na przesunięciu operatora agregacji przed operator połączenia, nie może być bezpośrednio zastosowana, gdyż operator agregacji jest zdefiniowany na atrybucie, który nie występuje w relacji Sprzedaż. Przedstawiona na slajdzie modyfikacja reguły ze slajdu 2 polega na wprowadzeniu do drzewa zapytania dodatkowej operacji – w tym wypadku operacji agregacji. Wprowadzając operator agregacji GroupBy(p_id) zmniejszamy w istotny sposób rozmiar argumentu operacji połączenia. Operator GroupBy(c_id) pozostaje na swoim miejscu.
Przypisywanie zapytań: przesuwanie predykatów
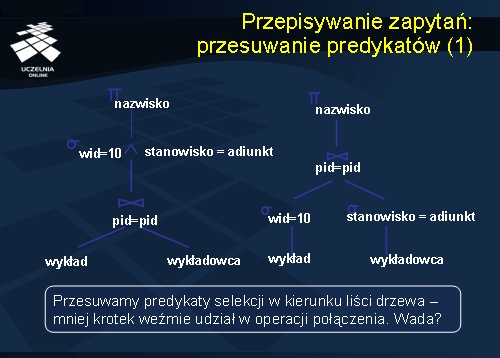
Kolejny slajd przedstawia regułę transformacji wykorzystującą własność dystrybutywności operacji selekcji i połączenia (transformacja przesuwania predykatów). Przesuwając operatory selekcji przed operator połączenia zmniejszamy rozmiary argumentów operatora połączenia. Oszacowanie opłacalności tej reguły jest trudne. Po pierwsze, jest to trudne ze względu na konieczność materializacji wyników wykonania operacji selekcji. Po drugie, automatycznie tracimy możliwość wykorzystania indeksów do wykonania operacji połączenia. Łączymy relacje o mniejszej liczbie krotek, ale musimy zastosować nieefektywne metody wykonania operacji połączenia.
Do kwestii opłacalności mechanizmu przepisywania zapytań (transformacji zapytań) wrócimy jeszcze w dalszej części wykładu.

Prezentowany slajd również przedstawia regułę transformacji wykorzystującą technikę przesuwania predykatów selekcji przed operator połączenia. Rozważmy zapytanie przedstawione na slajdzie, którego celem jest znalezienie, dla każdego wykładu (wid), wieku najstarszego wykładowcy, który prowadzi ten wykład. Zapytanie przedstawione po lewej stronie zawiera klauzulę „HAVING max(wiek) > 40”. W oryginalnym drzewie zapytania, ten predykat jest weryfikowany po wykonaniu operacji połączenia relacji Wykładowca i relacji Wykład. Przesuwając predykat selekcji, wyspecyfikowany przez tę klauzulę, przed operator połączenia, minimalizujemy rozmiar jednego z argumentów operacji połączenia. W tym przypadku, minimalizujemy, prawdopodobnie, również rozmiar wyniku wykonania operacji połączenia. Niestety, przedstawiona reguła jest specyficzna i pozwala przesunąć predykat selekcji, zdefiniowany klauzulą HAVING, ze względu na typ operatora agregacji. Czy można zastosować tą regułę w przypadku, gdy operatorem agregacji jest operator MIN?
Przypisywanie zapytań: podsumowanie

Podsumowując przedstawione reguły transformacji i przepisywania zapytań, można stwierdzić, że istnieje bardzo wiele poprawnych semantycznie reguł przepisywania zapytań. Co więcej, można opracować bardzo wiele, bardzo specyficznych reguł przepisywania zapytań. Pytanie, na które, często jest trudno odpowiedzieć brzmi - czy każda reguła transformacji minimalizuje koszt wykonania zapytania? Przykładem tutaj może być nasza wcześniejsza dyskusja na temat przesuwania predykatów selekcji przed operator połączenia.
Niemniej, technika transformacji i przepisywania zapytań jest ważnym elementem procesu optymalizacji zapytań. Jest ona szczególnie istotna dla dużych złożonych zapytań, dla których optymalizacja kosztowa, o której powiemy za chwilę, jest zbyt „kosztowna” i , najczęściej, mało efektywna.
W poprzednich latach, proces optymalizacji zapytań ograniczał się do optymalizacji regułowej, nazywanej czasami syntaktyczną. Optymalizacja regułowa okazała się mało skuteczna. W późniejszym okresie, optymalizacja regułowa została uzupełniona o mechanizm optymalizacji kosztowej. Należy jeszcze wspomnieć, w odniesieniu do optymalizacji regułowej, o problemie wyboru reguł. Dane jest zapytanie i zbiór reguł transformacji, który można zastosować w stosunku do zapytania. Jakie reguły zastosować?
Szacowanie kosztu wykonania planu zapytania

Jak już wspomnieliśmy, zdecydowana większość komercyjnych systemów zarządzania bazami danych stosuje zarówno optymalizację regułową jak i optymalizację kosztową. Optymalizacja kosztowa polega, najogólniej mówiąc, na wygenerowaniu wszystkich możliwych planów wykonania zapytania, oszacowaniu kosztu wykonania tych planów i wyborze planu o „najmniejszym” koszcie. Najczęściej, wygenerowanie wszystkich możliwych planów wykonania jest niemożliwe, stąd, optymalizator ogranicza się do pewnego podzbioru planów wykonania zapytania.
Kluczowe znacznie ma w przypadku optymalizacji kosztowej oszacowanie kosztu wykonania danego planu. Dla każdego planu wykonania zapytania optymalizator musi oszacować:
–Szacunkowy koszt wykonania każdego operatora w planie zapytania (zależny od rozmiarów argumentów wejściowych operatora)
–Szacunkowy rozmiar wyniku wykonania każdego operatora w planie zapytania (dane znajdują się w katalogu bazy danych, dla operacji selekcji i projekcji zakładamy niezależność atrybutów).
Katalog bazy danych

Podstawowym źródłem informacji o relacjach, ich rozmiarach, itp. jest katalog bazy danych.
Katalog bazy danych zawiera informacje o:
– liczbie krotek każdej relacji R (card(R)) i liczbie stron (Pcard(R)) dla każdej relacji, czasami katalog przechowuje również informacje o liczbie różnych wartości każdego atrybutu relacji (val(A[R]),
– liczbie różnych wartości atrybutu (NKeys) i liczbie stron dla każdego indeksu,
– wysokości indeksu, minimalnej i maksymalnej wartości klucza indeksu (Low/High).
Katalog jest odświeżany periodycznie. Bieżąca, ciągła, aktualizacja katalogu, w przypadku każdej zmiany parametrów systemu, jest zbyt kosztowna. W ostatnim czasie, coraz częściej, systemy zarządzania bazami danych przechowują histogramy dla atrybutów relacji.
Szacowanie rozmiarów i współczynnik selektywności

Proces szacowania kosztu wykonania danego planu zapytania opiera się o oszacowanie rozmiarów wyników wykonania operatorów wchodzących w skład danego planu. Przedstawimy obecnie, na kolejnych slajdach, metody szacowania rozmiarów wyników wykonania poszczególnych operatorów. Rozpoczniemy od wprowadzenia współczynnika selektywności. Rozważmy ogólną postać zapytania, wyrażonego w języku SQL, przedstawioną na slajdzie. Górne oszacowanie rozmiaru wyniku zapytania będzie równe iloczynowi rozmiarów relacji wyspecyfikowanych w klauzuli FROM. Oczywiście, to oszacowanie jest oszacowaniem maksymalnym, które, najczęściej, znacznie odbiega od rzeczywistego rozmiaru wykonania zapytania. Szacowanie wyniku wykonania zapytania bazuje głównie na wykorzystaniu w procesie szacowania tak zwanego współczynnika selektywności, który jest związany z każdym predykatem term i odzwierciedla wpływ predykatu
na redukcję rozmiaru wyniku.

Oszacowanie wyniku wykonania zapytania, przedstawionego na poprzednim slajdzie, z którym związany jest zbiór predykatów selekcji (term1, term2, ..., term k), jest zdefiniowane następującym wzorem:
rozmiar wyniku jest równy maksymalnej liczbie krotek * iloczyn wszystkich współczynników selektywności związanych z poszczególnymi predykatami selekcji. Podane powyżej oszacowanie wyniku zapytania zakłada, że predykaty są niezależne, co najczęściej nie jest spełnione w praktyce, ale istotnie ułatwia oszacowanie wyniku.
W jaki sposób obliczana jest wartość współczynnika selektywności dla danego predykatu?
Wartości współczynnika selektywności, dla poszczególnych typów predykatów przedstawiono na slajdzie. Przykładowo, jeżeli predykat term posiada postać „atrybut = wartość”, wówczas wartość współczynnika selektywności wynosi 1/val(atrybut), gdzie val(atrybut) oznacza liczbę różnych wartości danego atrybutu. Załóżmy, że predykat posiada postać „miasto = ‘Konin’ i val(miasto) = 5 (atrybut miasto przyjmuje 5 różnych wartości). Wówczas, szacunkowa liczba krotek spełniających dany predykat wynosi 1/5 liczby krotek. Przykładowo, jeżeli dana relacja Pracownicy posiada 1000 krotek i zapytanie do relacji jest sformułowane następująco:
Select nazwisko
From Pracownicy
Where miasto=’Konin’
Wówczas optymalizator szacuje, że w wyniku zapytania otrzymamy 1/5 * 1000 = 200 krotek.
Oczywiście, ze względu na rozkład wartości atrybutu miasto , podane oszacowanie może się istotnie różnić od rzeczywistego rozmiaru wyniku.
Szacowanie rozmiarów selection

Obecnie przejdziemy do bardziej szczegółowego przedstawienia szacowania rozmiarów wyników wykonania poszczególnych operatorów. Rozpoczniemy od operatora selekcji.
Niech S oznacza wynik wykonania operacji selekcji na relacji R. Niech card oznacza rozmiar relacji. Wówczas, dla prostego predykatu selekcji (Atrybut = wartość),
sf definiujemy następująco:
sf = 1/val(A[R ])
Przy założeniu równomiernego rozkładu wartości krotek:
card(S ) = sf * card(R )
(patrz przykład relacji Pracownicy przedstawiony na poprzednim slajdzie).
Zauważmy, że selekcja nie wpływa na szerokość wynikowej relacji, stąd
size(S ) = size(R )
(gdzie size(R) oznacza szerokość relacji R).

Liczba różnych wartości (val) wyniku zależy, oczywiście, od predykatu selekcji. Jeżeli szacujemy liczbę rożnych wartości atrybutu miasto w wyniku operacji selekcji, w przytaczanym przykładzie „miasto=’Konin”, to oczywiście, wynik selekcji będzie zawierał krotki odnoszące się tylko i wyłącznie do jednego miasta– stąd, val(miasto[S]) =1.
Rozważmy atrybut B, który nie uczestniczy w warunku selekcji. Określenie wartości val(B[S]) jest następujące: dane n=card(R) (zakładamy, że krotki relacji R są równomiernie rozłożone pomiędzy m = val(B[R]) kolorów). Ile różnych kolorów c= val(B[S]) wybierzemy, jeżeli losowo wybierzemy r krotek z relacji R?

Do oszacowania rozmiaru liczby różnych wartości atrybut B w wyniku selekcji S (c= val(B[S])) stosuje się tak zwaną aproksymację Yao przedstawioną na slajdzie. Dla ilustracji rozważmy ponownie rozważany wcześniej przykład relacji Pracownicy. Niech card(Pracownicy) = 1000. Relacja Pracownicy zawiera, m. in. atrybuty
miasto i
stanowisko . Załóżmy, że liczba różnych wartości atrybut miasto w relacji Pracownicy wynosi 5 (val(miasto[Pracownicy]) = 5) i val(stanowisko[Pracownicy]) = 10. Ile różnych wartości atrybutu stanowisko znajdzie się w wyniku zapytania S:
Select nazwisko, stanowisko
From Pracownicy
Where miasto=’Konin’
Dane: n=1000 (krotek relacji Pracownicy), m=10 (różnych stanowisk), r =200 = card(S) (rozmiar wyniku zapytania). Stąd, zgodnie z aproksymacją Yao, val(stanowisko[S]) = m = 10.
Szacowanie rozmiarów Projection

Przejdziemy obecnie do przedstawienia oszacowania wyniku rozmiaru wykonania operacji projekcji. Podobnie jak poprzednio, niech S oznacza wynik wykonania operacji projekcji na relacji R. Jeżeli założymy, że operator projekcji usuwa duplikaty z wynikowej relacji, to oszacowanie rozmiaru relacji S jest trudne. Stosuje się trzy reguły oszacowania:
- Projekcja na pojedynczym atrybucie A: rozmiar wyniku zapytania S (card(S) = val(A[R])) jest równy liczbie różnych wartości atrybutu A w relacji R.
- Jeżeli iloczyn różnych wartości atrybutów wyspecyfikowanych w wyniku projekcji jest mniejszy niż card(R), wówczas card(S) = iloczyn różnych wartości atrybutów wyspecyfikowanych w wyniku projekcji.
- Jeżeli projekcja zawiera klucz relacji R, wówczas card(S) = card(R).

Jeżeli założymy, że operator projekcji nie usuwa duplikatów z wynikowej relacji, to oszacowanie rozmiaru relacji S wynosi:
card(S) = card(R)
Szerokość wyniku projekcji jest równa sumie rozmiarów atrybutów wyspecyfikowanych w projekcji. Liczba różnych wartości atrybutów należących do wyniku projekcji S jest identyczna z liczbą różnych wartości tych samych atrybutów w relacji R.
Szacowanie rozmiarów GROUP BY

Przejdziemy obecnie do przedstawienia oszacowania wyniku rozmiaru wykonania operacji agregacji GROUP BY. Niech G oznacza zbiór atrybutów, na którym wykonywana jest operacja grupowania. Oszacowanie rozmiaru wynikowej relacji jest trudne. Stąd, system szacuje górne ograniczenia rozmiaru relacji S, które wynosi: card(S) <= iloczyn różnych wartości atrybutów należących do zbioru G.
Dla wszystkich atrybutów A należących do G: size(R.A) = size (S.A).
Podobnie, dla wszystkich atrybutów A należących do G: val(A[S]) = val(A[R]).
Szacowanie rozmiarów UNION

Oszacowanie rozmiaru wykonania operacji sumy. Niech T oznacza wynik wykonania operacji sumy na relacjach R i S.
Górne ograniczenie rozmiaru relacji T wynosi: card(T) <= card(R) + card(S). Równość zachodzi w przypadku, gdy nie eliminujemy duplikatów. Szerokość relacji T wynosi: size(T) = size(R) = size(S).
Górna granica liczby różnych wartości atrybutu A w relacji T wynosi: val(A[T]) < val(A[R]) + val(A[S]).
Szacowanie rozmiarów JOIN

Przejdziemy obecnie do przedstawienia oszacowania wyniku rozmiaru wykonania operacji połączenia. Podobnie jak poprzednio, niech T oznacza wynik wykonania operacji połączenia relacji R i S.
Oszacowanie rozmiaru relacji T, będącej wynikiem połączenia relacji R i S, jest bardzo trudne. Można łatwo podać górne ograniczenie rozmiaru relacji T, które wynosi: card(T) < card(R) * card(S), ale jest to bardzo duże przybliżenie. Najczęściej podaje się następujące przybliżenie rozmiaru relacji T:
card(T) = (card(R) * card(S))/max{val(A[R]), val(A[S])}, gdzie A oznacza atrybut połączeniowy relacji R i S.

Szerokość relacji T jest równa sumie szerokości relacji R i S: size(T) = size(R) + size(S).
W przypadku połączenia naturalnego, od szerokości wyniku odejmujemy szerokość atrybutu połączeniowego.
Niech A oznacza atrybut połączeniowy, wówczas górne ograniczenie liczby różnych wartości atrybutu A wynosi: val(A[T]) < min(val(A[R]), val(B[S])).
Jeżeli A nie jest atrybutem połączeniowym, wówczas liczba różnych wartości atrybutu A wynosi: val(A[T]) < val(A[R]) + val(B[S]).
Histogram

Jak już wspominaliśmy, szacowanie wyników wykonania operacji składających się na dany plan zapytania w oparciu o współczynniki selektywności charakteryzuje się dużą niedokładnością. Zaletą tego podejścia jest prostota i łatwość obliczania współczynników selektywności. W ostatnim czasie, coraz częściej, wykorzystuje się do szacowania rozmiarów wyników histogramy.
Histogramy umożliwiają uzyskanie znacznie dokładniejszych oszacowań rozmiarów wyników wykonania operacji. Histogramy występują w różnych wersjach:
- Histogram typu equi-depth (o równej głębokości) oznacza histogram, w którym dla każdego pojedynczego interwalu histogramu występuje równa liczba wartości atrybutu;
- Histogram typu equi-width (o równej szerokości) oznacza histogram, w którym wszystkie interwały posiadają równą szerokość.
Ze względu na znaczenie operacji połączenia w systemach relacyjnych baz danych i trudności w oszacowaniu rozmiaru tej operacji, histogramy są szczególnie przydatne do oszacowania wyniku operacji połączenia.
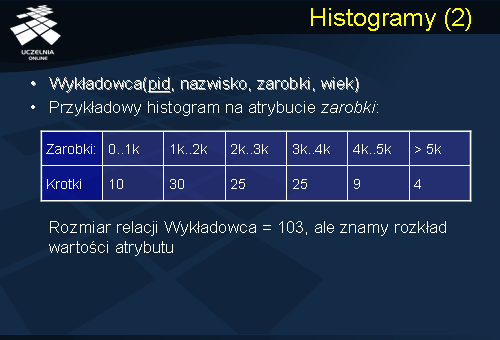
Niniejszy slajd przedstawia przykładowy histogram dla atrybutu
zarobki przedstawionej relacji
Wykładowca . Przedstawiony histogram jest histogramem typu equi-with (o równej szerokości). Jak łatwo zauważyć, histogram można interpretować jako aproksymację rozkładu wartości atrybutu
zarobki . Przykładowo, z histogramu można odczytać, że 30 krotek relacji
Wykładowca posiada wartość atrybutu zarobki z przedziału wartości (1000, 2000), natomiast 4 krotki posiadają wartość atrybutu zarobki powyżej 5000.
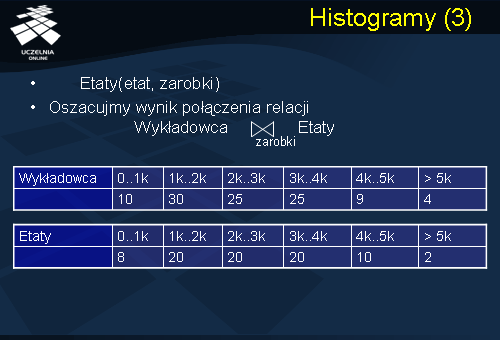
Jak już powiedzieliśmy wcześniej, histogramy są szczególnie przydatne do oszacowania wyniku operacji połączenia. Rozważmy przykład przedstawiony na slajdzie. Dana jest relacja
Wykładowca , przedstawiona na poprzednim slajdzie, oraz relacja
Etaty . Oszacujmy wynik połączenia obu relacji, zakładając, że dane są histogramy dla atrybutu połączeniowego
zarobki , przedstawione na slajdzie.
Operacje połączenia

Oszacowanie rozmiaru wyniku wykonania operacji połączenia relacji
Wykładowca i
Etaty , w oparciu o oszacowanie selektywności przedstawione na slajdzie 19, daje 330 krotek, przy założeniu, że liczba różnych wartości atrybutu
zarobki relacji
Wykładowca wynosi 25, natomiast liczba różnych wartości atrybutu
zarobki relacji
Etaty wynosi 20. Oszacowanie to wynika z przedstawionego na slajdzie wzoru. Rozmiar relacji
Wykładowca wynosi 103, rozmiar relacji
Etaty wynosi 80, maksymalna liczba różnych wartości atrybutu zarobki w relacji Etaty i Wykładowca wynosi 25 (max{val(zarobki[Etaty]), val(zarobki[Wykładowca])}). Stąd, rozmiar wyniku operacji połączenia wynosi: 103*80/25 = 330.
Operacje połączenia: (histogram)

Oszacowanie rozmiaru wyniku wykonania operacji połączenia relacji Wykładowca i Etaty , z wykorzystaniem przedstawionych wcześniej histogramów, daje 72 krotki. Zauważmy, że błąd oszacowania poprzednią metodą jest ponad 400 razy większy! Ten przykład ilustruje przydatność histogramów do szacowania wyniku wykonania operacji połączenia.
Plany wykonania zapytań

Jak już wspominaliśmy wcześniej, optymalizator zapytań konstruuje plan wykonania zapytania dla każdego bloku typu select-projection-group-by. Następnie, wyniki poszczególnych bloków są łączone operatorami binarnymi (sumy, iloczynu, połączenia lub iloczynu kartezjańskiego). W przypadku pojedynczego bloku, optymalizator poszukuje najlepszego planu wykonania tego bloku. Punktem wyjścia jest znalezienie najlepszych ścieżek dostępu do relacji wyspecyfikowanych w zapytaniu. Optymalizator analizuje wszystkie możliwe ścieżki dostępu do krotek relacji i wybiera „najtańszą” ścieżkę dostępu.
W większości komercyjnych systemów zarządzania bazami danych, stosuje się tak zwany model operatorowy, w którym operacje leżące na pojedynczej ścieżce planu wykonania zapytania są wykonywane łącznie. Ma to na celu umożliwienie przetwarzania potokowego krotek (np., jeżeli wykorzystujemy indeks w celu selekcji krotek relacji, operacja projekcji jest wykonywana dla każdej wybranej krotki, która następnie przesyłana jest do operatora agregacji). W konsekwencji nie zachodzi potrzeba materializowania (tj. zapisywania na dysk do osobnego pliku temporalnego) częściowych wyników wykonania operacji danego planu.
Przykład

Prezentowany slajd przedstawia przykładowe zapytanie, składające się z pojedynczego bloku.
Optymalizator rozpoczyna analizę możliwych ścieżek dostępu do relacji Wykładowca . Jeżeli w systemie został zdefiniowany indeks (I) na atrybucie stanowisko relacji Wykładowca , to wówczas jedną z możliwych ścieżek dostępu do tej relacji jest dostęp poprzez zdefiniowany indeks. Oszacowanie kosztu dostępu do relacji za pomocą indeksu zależy od typu indeksu. Jeżeli jest to indeks gęsty, wówczas, zgodnie ze wzorem przedstawionym na slajdzie 11, wynikowy rozmiar selekcji wynosi 1/10 * 40000 (liczba krotek relacji Wykładowca ) = 4000 krotek. Liczba operacji odczytu stron bazy danych zależy od typu indeksu – czy jest to indeks zgrupowany czy tez indeks nie zgrupowany. Oszacowanie liczby odczytywanych stron, dla tych dwóch typów indeksów, przedstawiono na slajdzie. W przypadku, gdy w systemie został zdefiniowany indeks (I) na kluczu relacji Wykładowca (sid), ale brak indeksu na atrybucie stanowisko , wówczas należy odczytać wszystkie strony indeksu i relacji. Liczba odczytanych stron wynosi wówczas 550 stron. W przypadku, gdy nie dysponujemy indeksem na relacji Wykładowca , pozostaje operacja skanowani relacji, której koszt wynosi 500 stron. Po przeanalizowaniu wszystkich możliwych ścieżek dostępu, optymalizator wybiera ścieżkę o „najmniejszym” koszcie.
Określenie porządku operacji połączenia
Po zakończeniu procesu optymalizacji bloków zapytania, optymalizator rozpoczyna poszukiwanie najlepszego planu połączenia wyników wykonania bloków. Problem ten można zdefiniować jako problem znalezienia najlepszej kolejności wykonania operacji połączenia (w ogólnym przypadku). Problemu znalezienia najlepszej kolejności wykonania operacji sumy lub produktu kartezjańskiego, jest znacznie łatwiejszy – wystarczy łączyć relacje w kolejności rosnących rozmiarów łączonych relacji (zaczynamy od relacji o najmniejszym rozmiarze i łączymy, kolejno, z relacjami o coraz większych rozmiarach). Kolejność porządku wykonania operacji połączenia można przedstawić w postaci tak zwanego drzewa połączeń (ang. join tree). Drzewo połączeń reprezentuje plan wykonania zapytania, którego wierzchołkami są wyniki wykonania bloków zapytania (relacje).
Typy drzew
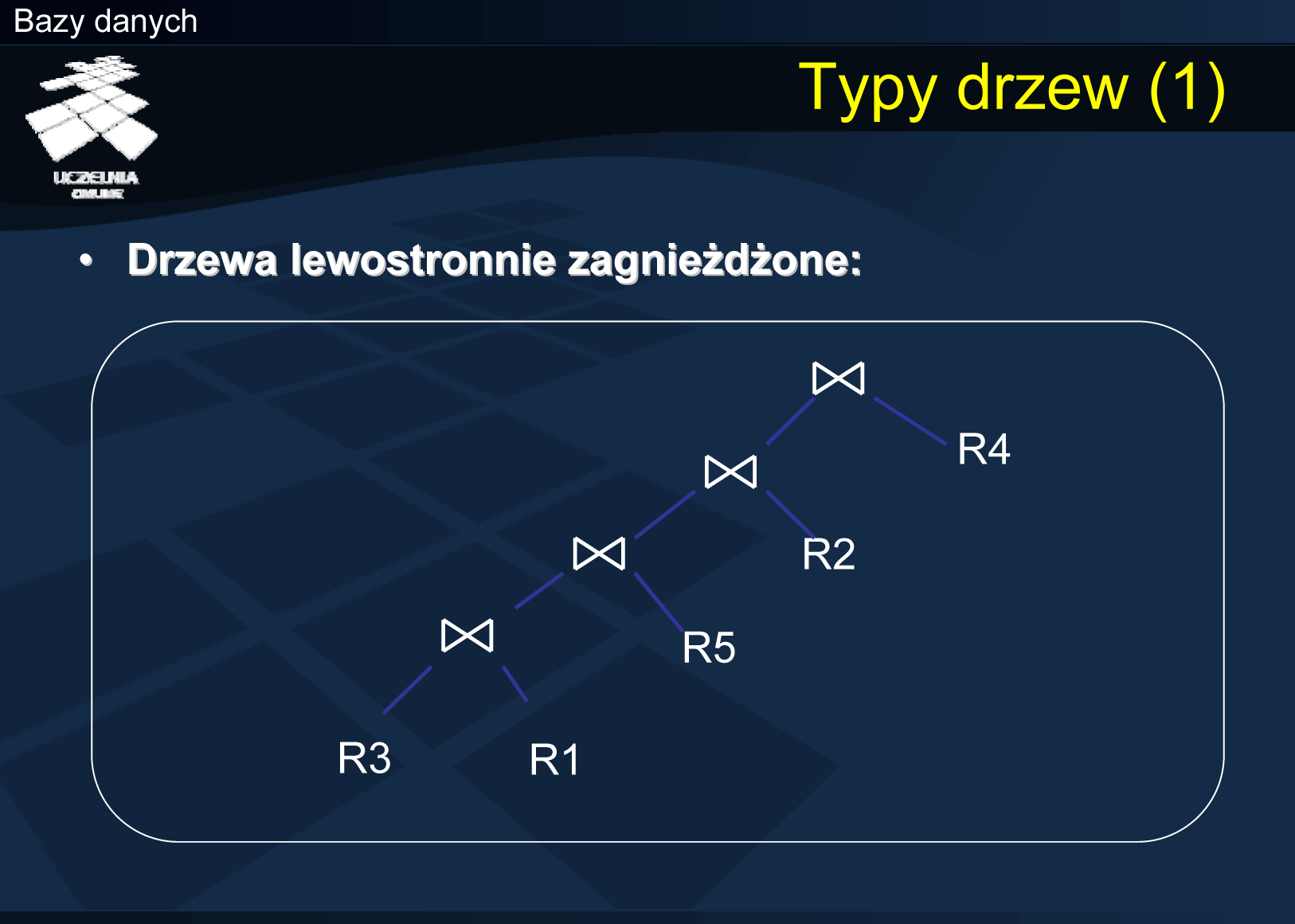
Istnieje wiele struktur drzew połączeń. Większość komercyjnych systemów baz danych dopuszcza tylko niektóre z nich. Krótko przedstawimy możliwe i stosowane drzewa połączeń. Podstawowym typem drzew połączeń, stosowanym przez większość optymalizatorów zapytań, są tak zwane drzewa lewostronnie zagnieżdżone (ang. left deep join tree). Cechą charakterystyczną tych drzew jest to, że sekwencja operacji połączenia jest wykonywana w sposób potokowy. Relacje (lub wyniki wykonania bloków zapytania) są zmaterializowane (relacje R3, R1, R5, R2, R4). Po połączeniu relacji R3 z R1, krotki tego połączenia mogą być przetwarzane potokowo – są one łączone z krotkami relacji, będącymi prawymi argumentami operacji połączenia. Zauważmy, że krotki otrzymywane w wyniku połączenia nie muszą być materializowane! Są one natychmiast konsumowane przez następny operator połączenia. Co więcej, w procesie łączenia relacji można wykorzystać indeksy na relacjach będących prawymi argumentami operacji połączenia. Większość systemów zarządzania bazami danych opuszcza tylko i wyłącznie drzewa tego typu. Dlaczego? Liczba możliwych drzew połączeń dla n relacji może być bardzo duża, natomiast liczba drzew lewostronnie zagnieżdżonych jest znacznie mniejsza. W przypadku n relacji istnieje tylko jeden kształt drzewa zagnieżdżonego, do którego można dopasować relacje na n silnia sposobów.

Kolejnym typem drzew połączeń są tak zwane drzewa krzaczaste (ang. bushy tree). Plany zapytań reprezentowane w postaci drzew krzaczastych, z reguły, charakteryzują się krótszym czasem wykonania zapytania. Niestety, ich zasadniczą wadą jest konieczność materializacji wyników wykonania operacji połączenia. Materializacja wiąże się, z jednej strony, z koniecznością rezerwacji pamięci dyskowej, z drugiej, zwiększa narzut czasowy na wykonanie planu zapytania. Łącząc relacje R1 i R5, wynik połączenia materializujemy na dysku, a następnie, ponownie odczytujemy ten wynik po to, aby wykonać połączenie z relacją R3. W przypadku systemów scentralizowanych baz danych, większość optymalizatorów nie analizuje i nie generuje drzew krzaczastych, ze względu na materializację wyników częściowych, jak również, ze względu na fakt, że liczba możliwych drzew krzaczastych dla n łączonych relacji jest znacznie większa, aniżeli drzew zagnieżdżonych.

Kolejnym typem drzew połączeń są tak zwane drzewa prawostronnie zagnieżdżone. Drzewa prawostronnie zagnieżdżone są drzewami binarnymi, w których wynik wykonania poprzedniego połączenia jest prawym argumentem kolejnej operacji połączenia. Drzewa prawostronnie zagnieżdżone charakteryzują się, najczęściej, niższą efektywnością, co wynika z implementacji algorytmów wykonywania operacji połączenia, stosowanych w systemach komercyjnych baz danych (dotyczy to głównie metody nested loop).
Problem znajdowania optymalnego drzewa połączeń
Wróćmy do problemu ustalenia optymalnej kolejności wykonywania operacji połączenia, lub inaczej mówiąc, do problemu znalezienia „najlepszego” drzewa połączenia. Załóżmy, że dana jest funkcja kosztu cost(), określająca koszt wykonania każdego drzewa połączeń. Zadaniem optymalizatora jest znalezienie drzewa połączeń o najniższym koszcie.
Zauważmy, że, de facto, problem znajdowania optymalnego drzewa połączeń można traktować jako problem optymalizacyjny - problem poszukiwania optymalnego stanu w przestrzeni stanów zawierającej wszystkie możliwe drzewa połączeń dla danego zapytania. Stan optymalny jest to stan o najmniejszej wartości funkcji kosztu.
Z tego punktu widzenia, można rozpatrywać działanie optymalizatora zapytań w trzech aspektach:
- Modelu planu wykonywania zapytania (struktura drzewa połączeń),
- Algorytmu przeszukiwania przestrzeni stanów,
- Funkcji kosztów.
Jak już wspominaliśmy, większość komercyjnych systemów zarządzania bazami danych ogranicza się do analizy drzew lewostronnie zagnieżdżonych. Mimo przyjęcia określonego kształtu drzewa połączeń, nadal liczba możliwych drzew, które należy przeanalizować, i których koszt należy oszacować, może być bardzo duża. Pozostaje zatem problem wyboru strategii przeszukiwania przestrzeni możliwych drzew połączeń. Funkcja kosztu, stosowana przez optymalizatory, opiera się na oszacowaniach rozmiarów wyników operatorów, które przedstawiliśmy ma poprzednich slajdach.
Algorytmy przeszukiwania

Jeżeli chodzi o algorytmy przeszukiwania przestrzeni możliwych drzew połączeń, to stosuje się trzy podstawowe podejścia:
- algorytmy dokładne,
- algorytmy przybliżone,
- metaheurystyki - algorytmy kombinatoryczne.
Algorytmy dokładne, stosowane, w praktyce, analizują wszystkie możliwe drzewa połączeń (tzw. pełne przeszukiwanie) lub ograniczają się do przejrzenia tylko niektórych podzbiorów. Najpopularniejszym algorytmem, stosowanym przez większość systemów komercyjnych, jest algorytm programowania dynamicznego. Koncepcja programowania dynamicznego polega na wypełnieniu tabeli kosztów wykonania połączeń tak, aby przechowywać tylko minimum danych potrzebnych do analizy. Tabela ta jest konstruowana, kolejno, dla pojedynczych relacji, par relacji, trojek relacji, itd. Wadą tych algorytmów jest zależność czasu optymalizacji od liczby operacji połączenia.
Algorytmy przybliżone, do znalezienia „najlepszego” planu stosują bądź heurystyki lub ograniczają się do optymalizacji regułowej, o której już mówiliśmy. Zasadniczą wadą tych algorytmów jest to, że, najczęściej, plan znaleziony przez algorytm przybliżony znacząco odbiega od „najlepszego” możliwego planu wykonania zapytania.
Trzecie z możliwych podejść do znajdowania najlepszego drzewa połączeń polega na zastosowaniu algorytmów kombinatorycznych takich jak: Iterative Improvement, Simulated Annealing, Tabu Search, algorytmy genetyczne. Algorytmy te pozwalają na znaczną penetrację przestrzeni możliwych drzew połączeń, a jednocześnie, czas optymalizacji nie zależy od liczby operacji połączenia. Jak pokazują badania, algorytmy, mimo, że nie znajdują optymalnych drzew połączeń, znajdują jednak plany znacznie efektywniejsze niż w przypadku stosowania prostych heurystyk. Jednak ich zasadniczą zaletą, w stosunku do algorytmów dokładnych, jest to, że pozwalają one optymalizować nawet bardzo duże zapytania ( o liczbie połączeń dochodzących do 100 operacji).
Problem optymalizacji zapytań jest ciągle obszarem aktywnych badań naukowych. Wiąże się to, z jednej strony, z problemem coraz bardziej złożonych zapytań i nowych typów danych, z drugiej, z nowymi potrzebami wynikającymi z popularności Internetu.
































