Eksploracja sieci Web
Tematem wykładu są zagadnienia związane z eksploracją sieci Web. Rozpoczniemy od krótkiego wprowadzenia do problematyki eksploracji sieci Web i przedstawimy przykłady zastosowań metod eksploracji sieci Web w praktyce. Krótko scharakteryzujemy specyfikę sieci Web, która odróżnia sieć Web od innych typów zasobów. Następnie, przejdziemy do przedstawienia taksonomii metod eksploracji Web-u. Prezentację metod eksploracji Web rozpoczniemy od przedstawienia problemu eksploracji zawartości sieci Web. W kolejnej części wykładu skoncentrujemy się na zagadnieniu i algorytmach eksploracji połączeń sieci Web. Przedstawimy i omówimy dwa podstawowe algorytmy rankingu stron: Page Rank i H&A. Na zakończenie wykładu, przejdziemy do omówienia zagadnienia eksploracji korzystania z sieci, lub, inaczej mówiąc, eksploracji logów.
Czym jest eksploracja Web?

Czym jest eksploracja sieci Web? Eksploracja sieci Web to odkrywanie interesującej, potencjalnie użytecznej, dotychczas nieznanej wiedzy (reguł, wzorców, zależności) ukrytej w zawartości sieci Web, sieci jej połączeń i sposobie korzystania z niej. Sieć Web jest olbrzymim repozytorium różnorodnej wiedzy. Klasyfikacja wszystkich metod stosowanych do eksploracji Web-u jest trudna i ryzykowna, niemniej, wyróżnia się trzy podstawowe grupy metod eksploracji sieci Web: eksploracja zawartości sieci Web (Web content mining), eksploracja połączeń sieci Web (Web linkage mining), wreszcie, eksploracja korzystania z sieci Web (Web usage mining).
Przykłady zastosowania metod eksploracji

Jak już powiedzieliśmy, siec Web jest olbrzymim repozytorium różnorodnej wiedzy, które może być eksplorowane najróżniejszymi metodami. Szereg z tych metod było i jest szeroko stosowane w praktyce od wielu lat , niektóre z tych metod zyskały na znaczeniu w ostatnim czasie. Metody eksploracji znalazły zastosowanie w wyszukiwarkach – głównie algorytmy rankingu stron (Google, Yahoo, Ask). Wiele różnych metod, począwszy od algorytmów odkrywania asocjacji, poprzez grupowanie, klasyfikację, ocenę wiarygodności klientów, znalazło zastosowanie w handlu elektronicznym (Netflix, Amazon). Ciekawe algorytmy zostały zaproponowane w ostatnim czasie dla potrzeb reklamy internetowej (Google). Bardzo intensywnie rozwijaną grupą algorytmów są algorytmy oceny reputacji stosowane do oceny wiarygodności sprzedających i kupujących na aukcjach internetowych, wykorzystywane również w tak zwanych systemach rekomendacyjnych. Algorytmy eksploracji logów są wykorzystywane do projektowania serwerów WWW (menu), do personalizacji usług (adaptatywne serwery WWW), do poprawy efektywności działania systemów (analiza logów serwerów baz danych w celu automatycznego generowania indeksów i algorytmów wymiany stron). Algorytmy eksploracji sieci socjalnych, należące do grupy algorytmów eksploracji sieci powiązań, są stosowane w praktyce przez policję i nauki społeczne. Algorytmy eksploracji logów wykorzystuje się szeroko do analizy efektywności poczty elektronicznej, opracowania adaptatywnych strategii buforowania danych, czyszczenia danych w systemach hurtowni danych, itp.
Specyfika sieci Web

Na czym polega specyfika sieci Web jako specyficznego zasobu podlegającego eksploracji? Sieć Web można interpretować jako dużą, heterogeniczną, rozproszoną bazę danych, ale: dane (strony WWW) są nieustrukturalizowane, złożoność danych jest znacznie większa aniżeli złożoność tradycyjnych dokumentów tekstowych, wreszcie Web to dane tekstowe + multimedia + struktura połączeń. Tym co jeszcze wyróżnia sieć Web jest bardzo duża dynamika zmian zachodzących w tym środowisku – dynamicznie pojawiają się nowe zasoby i znikają istniejące. Zmiany te nigdzie nie są rejestrowane. Tylko niewielka część informacji zawartej w Web jest istotna dla pojedynczego użytkownika – Web obsługuje różne środowiska i różne grupy zainteresowań. Z punktu widzenia analizy korzystania z zasobów sieci Web, to, z jednej strony, dane dotyczące korzystania z sieci mają bardzo duże rozmiary i bardzo dynamiczny przyrost, z drugiej, informacja opisująca użytkowanie sieci, zawarta w logach serwerów Web, jest bardzo uboga ( stąd prace nad nowym standardem logów serwerów WWW prowadzone przez konsorcjum W3C (standard Extended Logs). Jak podaje Google, dzienna porcja danych generowanych do plików logów jest porównywalna z rozmiarami największych konwencjonalnych hurtowni danych. To wszystko powoduje, że eksploracja sieci Web jest trudna i wymaga opracowania specyficznych algorytmów eksploracji.
Taksowanie metod eksploracji Web

Jak już wspomnieliśmy, praktycznie wszystkie metody eksploracji danych znajdują zastosowanie w odniesieniu do sieci Web i jej zawartości informacyjnej. Niemniej, w literaturze wyróżnia się trzy podstawowe grupy metod eksploracji sieci Web: eksploracja zawartości sieci Web (Web content mining), eksploracja połączeń sieci Web (Web linkage mining), wreszcie, eksploracja korzystania z sieci Web (Web usage mining).
Eksploracja zawartości

Eksploracja zawartości sieci Web w dużej mierze przypomina eksplorację dokumentów tekstowych, z tą różnicą, że zamiast dokumentów tekstowych mamy tutaj do czynienia ze stronami WWW. Stąd, w zakresie eksploracji zawartości sieci Web, wyróżniamy takie typowe zadania eksploracji jak: wyszukiwanie stron WWW (opracowano szereg języków zapytań do sieci Web takich jak: WebSQL, WebOQL, WebML, WebLog, W3QL), grupowanie stron WWW (w ostatnim czasie opracowano szereg algorytmów grupowania ukierunkowanych na grupowanie dokumentów XML), klasyfikacja stron WWW (podobnie jak w przypadku grupowania, w ostatnim czasie opracowano szereg algorytmów klasyfikacji dokumentów XML). Dwie ostatnie grupy algorytmów eksploracji dokumentów XML-owych swoje źródło mają w pracach nad eksploracją struktur grafowych. Istotnym problemem, o którym warto wspomnieć w kontekście omawianych wcześniej na tych wykładach algorytmów grupowania i klasyfikacji jest problem specyficznych miar podobieństwa (odległości) pomiędzy dokumentami XML.
Eksploracja połączeń

Druga grupa metod eksploracji Web wiąże się z eksploracją struktury połączeń sieci Web. Początkowo, celem badań w zakresie eksploracji połączeń sieci Web było opracowanie algorytmów umożliwiających przeprowadzenie rankingu wyników wyszukiwania stron WWW. Okazało się jednak, że opracowane techniki są przydatne również w innych dziedzinach zastosowań. Algorytmy eksploracji sieci połączeń można wykorzystać do znajdowania lustrzanych serwerów Web, co pozwala na implementację bardziej elastycznych optymalizatorów zapytań dla sieci rozległych, do oceny wiarygodności uczestników aukcji internetowych czy też do konstrukcji systemów rekomendacyjnych.
Algorytmy eksploracji struktury połączeń sieci Web zilustrujemy dwoma najpopularniejszymi algorytmami (Page Rank i H&A), których podstawowym zadaniem jest ranking (inaczej mówiąc, ocena ważności) stron WWW. Problem rankingu jest znany od wielu lat i występuje w wielu dziedzinach zastosowań. Punktem wyjścia dla obu wspomnianych algorytmów rankingu stron były prace prowadzone w ramach systemów IR nad rankingiem publikacji naukowych. W ramach systemów IR, na początku lat 70-tych zaproponowano metody oceny (rankingu) artykułów naukowych w oparciu o cytowania. Podobna strategię rankingu produktów stosują klienci kupujący produkty AGD. Ocena jakości produktu, jak i ocena jakości publikacji naukowej, opiera się nie na samoocenie dokonywanej przez producenta (lub autora publikacji), lecz w oparciu o opinie innych klientów (innych autorów).
Ranking stron

Wyróżniamy trzy zasadnicze podejścia do rankingu stron WWW: bezkontekstowy ranking stron WWW (algorytm Page Rank - PR), kontekstowy ranking stron (algorytm Topic Specific Page Rank - TSPR), oraz szczegółowa ocena ważności stron z wyróżnieniem stron typu „hub” i stron typu „authorities” (algorytrm Hubs & Authorities - H&A). Ze względu na ograniczenia czasowe, ograniczymy się na tym wykładzie do prezentacji dwóch z wymienionych wyżej algorytmów, a mianowicie, algorytmu Page Rank i algorytmu Hubs & Authorities.
Zaczniemy od prezentacji algorytmu Page Rank. Punktem wyjścia algorytmu rankingu stron Page Rank jest przyjęta w algorytmie definicja ważności strony: Strona jest ważna, jeżeli inne ważne strony posiadają wskazania (linki) na tą stronę. Łatwo zauważyć w tej definicji analogie do definicji ważności publikacji naukowej: publikacja naukowa jest ważna, jeżeli inne ważne publikacje posiadają referencje do tej publikacji.
Page Rank

Schemat działania algorytmu Page Rank jest następujący. Utwórz stochastyczną macierz Web oznaczoną przez M: Ponumeruj wszystkie strony. Strona i odpowiada i-tej kolumnie i i-temu wierszowi macierzy M. Element M[i, j] = 1/n, jeżeli strona j posiada linki do n stron (w tym do strony i), w przeciwnym razie M[i, j] = 0. Zauważmy, że wartość elementu M [i,j ] określa prawdopodobieństwo, że w następnym kroku przejdziemy ze strony j do strony i. Obliczanie ważności stron ma charakter iteracyjny i polega na wymnażaniu wektora ważności stron przez macierz M.

Jaka jest interpretacja praktyczna macierzy M?
Załóżmy, że, początkowo, ważność każdej strony wynosi 1. W każdej kolejnej iteracji algorytmu, strona i przekazuje swoją ważność następnikom (tj. stronom, do których posiada linki), a jednocześnie, otrzymuje nową ważność od swoich poprzedników (stron, które posiadają linki do strony i). Stąd, ważność strony można interpretować jako prawdopodobieństwo, że startując od dowolnej strony, i losowo wędrując wzdłuż linków wychodzących, dojdziemy do danej strony.

Niech v oznacza wektor ważności stron.
i-ta składowa wektora określa prawdopodobieństwo, że w danej chwili znajdujemy się na stronie i. Startując ze strony
i , prawdopodobieństwo przejścia do innych stron, w kolejnym kroku, jest określone przez wektor
M v . Redefiniując pojęcie ważności strony przedstawione uprzednio, możemy powiedzieć, że strona jest ważna proporcjonalnie do prawdopodobieństwa odwiedzenia tej strony. Formalnie, wektor ważności stron v jest wektorem własnym macierzy M i jest nazywany wektorem Page Rank.
Przykład 1
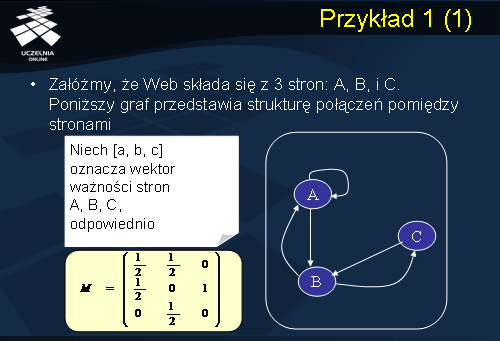
Dla ilustracji działania algorytmu Page Rank rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Niech v=[a, b, c] oznacza wektor ważności stron, odpowiednio, A, B, C. Macierz M naszej uproszczonej sieci Web przedstawiono na slajdzie. Przykładowo, kolumna 1 macierzy zawiera następujące elementy: 1/2, 1/2 i 0. Elementy M[1, 1] = 1/2 i M[2, 1]=1/2, gdyż strona A (z numerem 1) posiada link do siebie i link do strony B (o numerze 2). Element M[3, 1] = 0 , gdyż nie ma linku od strony A do strony C (o numerze 3). Kolumna 2 macierzy M zawiera elementy: 1/2, 0 i 1/2, gdyż strona B posiada link do strony A i strony C. Zatem 1/2 ważności strony B jest przekazywane stronie A i 1/2 ważności strony B wędruje do strony C. Kolumna 3 macierzy M zawiera elementy: 0, 1 i 0, gdyż strona C posiada jedynie link do strony B. Zatem cała ważność strony C jest przekazywana stronie B.

Jak już wiadomo, równanie opisujące ważność stron A, B, C ma postać: v = M v. Rozwiązanie powyższego równania można znaleźć metodą relaksacyjną (iteracyjną) (zakładając początkową ważność stron a=b=c=1), poprzez wymnażanie macierzą M kolejnych estymat ważności stron M (M (…M (M
v ) …)). Oszacowanie ważności stron uzyskane po 4 pierwszych iteracjach wynosi:
a = 1 1 5/4 9/8 5/4
b = 1 3/2 1 11/8 17/16
c = 1 1/2 3/4 1/2 11/16
W granicy, rozwiązanie posiada następujące wartości a=b=6/5, c=3/5, tj. ważność stron A i B jest dwukrotnie większa niż ważność strony C
Problemy

W przypadku modelowania rzeczywistych struktur sieci Web, w rzeczywistych sieciach Web występują dwa problemy, które mogą prowadzić do zniekształcenia oszacowań ważności stron i które wymagające rozwiązania. Jest to problem tak zwanej „ślepej uliczki” i problem „pułapki pajęczej”. „Ślepą uliczką” (DE- dead end) nazywamy stronę, która nie posiada następników, a tym samym nie ma gdzie przekazać swojej ważności. W takim przypadku ważność wszystkich stron dąży do 0. „Pułapką pajęczą” (ST – spider trap) nazywamy grupę stron, która nie posiada linków wychodzących, a tym samym, przechwytuje ważność całej sieci Web. Przykłady przedstawione na kolejnych slajdach ilustrują zjawisko ślepej uliczki i pułapki pajęczej.
Przykład 2
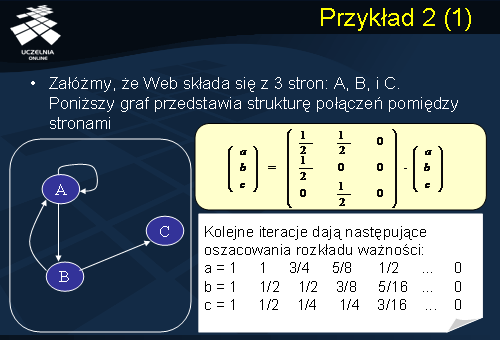
Rozważmy przykład 2 przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Zauważmy, że strona C nie posiada, tym razem, linków wychodzących, jest zatem typowym przykładem „ślepej uliczki”. Niech v=[a, b, c] oznacza wektor ważności stron, odpowiednio, A, B, C. Macierz M naszej sieci Web przedstawiono na slajdzie. Jak łatwo zauważyć, ponieważ strona C nie posiada następników, ostatnia kolumna macierzy M składa się z samych zer. W konsekwencji, kolejne iteracje dają następujące oszacowania rozkładu ważności:
a = 1 1 3/4 5/8 1/2 ...0
b = 1 1/2 1/2 3/8 5/16 ...0
c = 1 1/2 1/4 1/4 3/16 ...0
Jak widać, ważność wszystkich stron dąży do 0.
Przykład 3
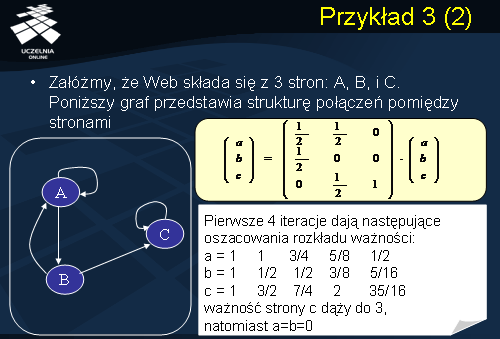
Kolejny przykład ilustruje zjawisko pułapki pajęczej. Załóżmy, podobnie jak poprzednio, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Zauważmy, że strona C tym razem posiada link wychodzący, ale jest to link do strony C. Strona C jest zatem typowym przykładem „pułapki pajęczej”. Niech v = [a, b, c] oznacza wektor ważności stron, odpowiednio, A, B, C. Macierz M naszej sieci Web przedstawiono na slajdzie. Jak łatwo zauważyć, ponieważ strona C posiada tylko jeden link wychodzący do siebie, ostatnim elementem kolumny 3 macierzy M jest 1. W konsekwencji, kolejne iteracje dają następujące oszacowania rozkładu ważności:
a = 1 1 3/4 5/8 1/2
b = 1 1/2 1/2 3/8 5/16
c = 1 3/2 7/4 2 35/16
Ważność strony C dąży do 3, natomiast ważność stron A i B wynosi a=b=0. Strona C przechwyciła ważność całej sieci Web.
Rozwiązanie problemów DE i ST

Rozwiązanie problemów „ślepej uliczki” i „pułapki pajęczej”, przyjęte przez Google, polega na „opodatkowaniu” każdej strony pewnym procentem jej ważności i rozdystrybuowanie łącznego podatku pomiędzy wszystkie strony w równym procencie. Przykładowo, wprowadzając podatek w wysokości 20%, równania ważności stron z poprzedniego przykładu (przykład nr 3 – slajd nr 16) przyjmą następującą postać:
a = 0.8 * (1/2*a + 1/2*b +0*c) + 0,2
b = 0.8 * (1/2*a + 0*b + 0*c) + 0,2
c = 0.8 * (0*a + 1/2*b + 1*c) + 0,2
Rozwiązaniem tych równań są następujące wartości ważności stron: a=7/11, b=5/11, c=21/11. Zauważmy, że obecnie, w przeciwieństwie do wartości ważności stron podanych w Przykładzie nr 3, ważność stron A i B jest różna od zera.
Hubs & Authorities

Przejdziemy obecnie do przedstawienia drugiego ze wspomnianych wcześniej algorytmów rankingu stron, a mianowicie, algorytmu H & A (oryginalna nazwa algorytmu – algorytm HITS - skrót od Hyperlink-Induced Topic Search). Algorytm H & A składa się z dwóch modułów: modułu próbkowania oraz modułu propagacji. Moduł próbkowania konstruuje zbiór kilku tysięcy stron WWW, zawierający relewantne, z punktu widzenia wyszukiwania, strony WWW. Z kolei moduł propagacji określa oszacowanie ważności stron. Algorytm wyróżnia dwa typy stron: strony autorytatywne (tzw. authorities) – stanowią one źródło ważnej informacji na zadany temat, oraz strony koncentratory (tzw. hubs) - zawierają one linki do autorytatywnych (tj. ważnych) stron.

Definicja typów stron w algorytmie H & A ma charakter rekursywny. Stronę typu koncentrator definiujemy jako stronę zawierającą linki do wielu autorytatywnych stron, natomiast stronę autorytatywną definiujemy jako stronę, do której linki posiada wiele stron koncentratorów. Algorytm jest realizowany w trzech fazach: fazie konstrukcji zbioru początkowego, fazie ekspansji oraz fazie propagacji wag. Do konstrukcji zbioru początkowego wykorzystuje się indeks przeglądarki, który, w oparciu o zbiór slow kluczowych, znajduje początkowy zbiór ważnych stron (zarówno autorytatywnych jak i koncentratorów). Następnie, w fazie ekspansji, początkowy zbiór stron jest rozszerzony do tzw. zbioru bazowego (ang.
base set ) poprzez włączenie do zbioru początkowego wszystkich stron, do których strony zbioru początkowego zawiera linki, oraz stron, które zawierają linki do stron zbioru początkowego. Warunkiem stopu procesu ekspansji jest osiągnięcie określonej liczby stron (kilka tysięcy). Wreszcie, w fazie trzeciej, fazie propagacji wag, moduł propagacji, iteracyjnie, oblicza wartości oszacowania prawdopodobieństwa, że dana strona jest autorytatywna lub jest koncentratorem. Linki pomiędzy stronami, które należą do tej samej domeny, najczęściej, są linkami nawigacyjnymi, stąd, linki te są eliminowane z analizy.

W fazie propagacji wag, algorytm H & A korzysta z macierzowego opisu sieci Web, podobnie jak algorytm Page Rank, ale w przypadku algorytmu H & A macierz Web (oznaczona A) nie jest macierzą stochastyczną. W macierzy A, każdy link posiada wagę 1, niezależnie od tego, ile następników lub poprzedników posiada dana strona. Ze względu na brak ograniczenia dotyczącego stochastyczności macierzy Web, algorytm H & A wprowadza dwa współczynniki skalujące, alfa i beta, tak, aby wartości wag nie przekroczyły górnego ograniczenia wartości wag. Definicja macierzy A ma następującą postać: element A[i, j] = 1, jeżeli strona i posiada link do strony j, w przeciwnym razie, A[i, j] = 0.

Niech wektory
a i
h oznaczają, odpowiednio, wektory autorytatywności i koncentratywności stron, których i-ty element odpowiada wartości stopnia autorytatywności i koncentratywności strony i. Niech alfa i beta oznaczają odpowiednie współczynniki skalujące. Z definicji typów stron, przedstawionych poprzednio, otrzymujemy, że
h =
alfa*A*a . Innymi słowy, koncentratywność danej strony jest sumą autorytatywności wszystkich stron, do których dana strona posiada linki, pomnożoną przez współczynnik skalujący alfa. Podobnie, definiujemy autorytatywność stron:
a = beta*A(transponowane)*
h . Autorytatywność danej strony jest sumą koncentratywności wszystkich stron, które posiadają linki do danej strony, pomnożoną przez współczynnik skalujący beta.

Podstawiając do wzoru na koncentratywność stron definicję wektora a, oraz, podstawiając do wzoru na autorytatywność stron definicję wektora h, otrzymujemy następujące wzory:
h = beta * alfa* A*A(transponowane)*h
a = beta * alfa* A(transponowane)*A*a
Rozwiązanie powyższych równań można znaleźć metodą relaksacyjną (iteracyjną) (analogicznie jak w przypadku algorytmu Page Rank), zakładając, że początkowe wartości autorytatywności i koncentratywności każdej strony wynoszą 1. Pozostaje jeszcze problem wyboru odpowiednich wartości współczynników skalujących alfa i beta. Wartości tych współczynników dobiera się doświadczalnie. Celem tych współczynników jest zagwarantowanie, że wartości autorytatywności i koncentratywności stron nie przekroczą górnych ograniczeń przyjętych dla tych wartości.
Przykład 4
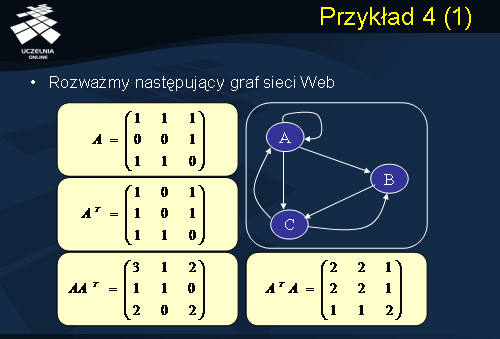
Dla ilustracji działania algorytmu H & A rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Macierz A naszej uproszczonej sieci Web przedstawiono na slajdzie. Przykładowo, wiersz 1 macierzy A zawiera następujące elementy: 1, 1 i 1. Elementy A[1, 1] = A[1, 2] = A[1, 3] = 1, gdyż strona A (z numerem 1) posiada linki wychodzące do stron A, B (z numerem 2) i C (z numerem 3). Wiersz 2 macierzy A zawiera następujące elementy: 0, 0, i 1. Elementy A[2, 1] = A[2, 2] = 0, gdyż strona B nie posiada linków wychodzących do stron A i B, natomiast element A[2, 3] = 1, gdyż strona B posiada link wychodzący do strony C. Wreszcie, wiersz 3 macierzy A zawiera elementy: 1, 1, i 0. Elementy A[3, 1] = A[3, 2] = 1, gdyż strona C posiada linki wychodzące do stron A i B, natomiast element A[3, 3] = 0, gdyż strona C nie posiada linku do siebie. Na slajdzie przedstawiono również macierze: A(transponowane) oraz iloczyny macierzy A * A(transponowane) oraz A(transponowane)* A.

Przyjmując, że współczynniki skalujące alfa = beta = 1 i zakładając, że początkowe wartości autorytatywności i koncentratywności każdej strony wynoszą 1,
h = [ ha=1, hb=1, hc=1] i
a = aa=1, ab=1, ac=1], po trzech pierwszych iteracjach otrzymujemy następujące wartości autorytatywności i koncentratywności stron:
aa = 1 5 24 114
ab = 1 5 24 114
ac = 1 4 18 84
ha = 1 6 28 132
hb = 1 2 8 36
hc = 1 4 20 96
Łatwo zauważyć, że strona a jest typowym koncentratorem, natomiast strona B jest strona autorytatywną.
Eksploracja korzystania z sieci

Przejdziemy obecnie do omówienia problemów i metod eksploracji danych opisujących korzystanie z sieci Web. Celem eksploracji danych opisujących korzystanie z zasobów sieci Web jest odkrywanie ogólnych wzorców zachowań użytkowników sieci Web, w szczególności, wzorców dostępu do stron (istnieje szereg narzędzi komercyjnych jak i ogólnodostępnych eksploracji logów serwerów WWW - WUM, WEBMiner, WAP, WebLogMiner). Odkryta wiedza pozwala na: budowę adaptatywnych serwerów WWW (personalizacja usług serwerów WWW – przykładem serwer firmy Amazon), optymalizację struktury serwera i poprawę nawigacji (stosowana w Yahoo), czy wreszcie, znajdowanie potencjalnie najlepszych miejsc reklamowych (znając wzorce zachowań klientów i ich preferencje konsumenckie).
Czym jest eksploracja logów?
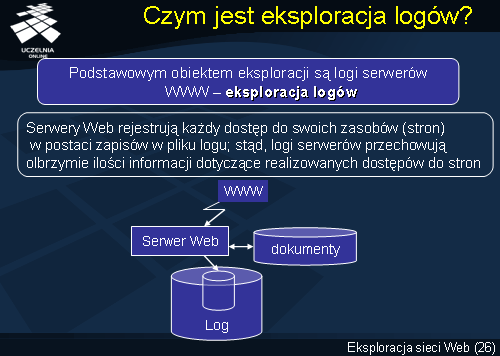
Eksploracji danych opisujących korzystanie z sieci Web, najczęściej, polega na eksploracji logów serwerów WWW. Serwery Web rejestrują każdy dostęp do swoich zasobów (stron) w postaci zapisów w pliku logu. Stąd, logi serwerów przechowują olbrzymie ilości informacji dotyczące realizowanych dostępów do stron i stanowią potencjalnie ważne źródło opisu zachowań użytkowników serwera.
Metody eksploracji logów

Eksploracja logów serwerów pozwala odkrywać wiedzę o różnym charakterze. Stąd, istnieje wiele metod eksploracji logów: odkrywanie charakterystyki danych (próba określenia charakterystyki użytkowników), porównywanie różnych klas (grup) użytkowników ( w oparciu o ich adresy IP), odkrywanie asocjacji (np. zależności pomiędzy przynależnością do określonej grupy użytkowników a stronami WWW, do których ci użytkownicy realizują dostęp), predykcja (predykcja kolejnych stron, do których dany użytkownik będzie żądał dostępu), klasyfikacja użytkowników, analiza przebiegów czasowych opisujących zdarzenia dostępu do stron WWW i analiza ruchu w sieci, pozwalające na odkrywanie wzorców sekwencji opisujących preferencje użytkowników, oraz aktualna analizę trendów.
Odkrywanie wzorców dostępu do stron

Najpopularniejsza metodą eksploracji logów serwerów WWW jest odkrywanie częstych sekwencji dostępu do stron WWW, które opisują wzorce zachowań i preferencje użytkowników w zakresie tematyki stron WWW. Dla ilustracji idei eksploracji logów, przedstawimy ogólny schemat algorytmu odkrywania częstych sekwencji dostępu do stron WWW, który nosi nazwę algorytmu WAP (od angielskiego Web Access Pattern mining). Algorytm WAP jest algorytmem odkrywania wzorców sekwencji w oparciu o strukturę WAP-drzewa. Czym jest WAP-drzewo? WAP-drzewo jest ukorzenionym grafem skierowanym, który reprezentuje sekwencję dostępu do stron WWW realizowaną przez użytkownika.
Wierzchołki drzewa reprezentują zdarzenia należące do sekwencji (pojedyncze zdarzenie – dostęp do strony), natomiast łuki drzewa reprezentują kolejność zachodzenia zdarzeń w ramach sekwencji. WAP-drzewo jest skojarzone z grafem reprezentującym organizację stron na serwerze WWW.
Odkrywanie częstych wzorców ścieżek nawigacyjnych

Odkrywanie częstych sekwencji dostępu do stron WWW sprowadza się do problemu odkrywanie częstych wzorców ścieżek nawigacyjnych (ang. mining path traversal patterns). Algorytm WAP odkrywa częste wzorce ścieżek nawigacyjnych dwukrokowo. W kroku 1 następuje przekształcenie oryginalnej ścieżki nawigacyjnej użytkownika, pobranej z logu serwera, w zbiór maksymalnych ścieżek nawigacyjnych „w przód” (ang. maximal forward reference). Ma to na celu wyeliminowanie operacji dostępu o charakterze ściśle nawigacyjnym (tj. wyeliminowanie linków powrotnych).

W kroku 2, odkrywane są częste wzorce ścieżek nawigacyjnych (ang. large reference sequences). Do znajdowania częstych wzorców ścieżek można zastosować dowolny algorytm odkrywania wzorców sekwencji omówiony na jednym ze wcześniejszych wykładów poświęconych odkrywaniu wzorców sekwencji. Należy tutaj podkreślić, że algorytm WAP nie jest konkretnym algorytmem, lecz ma charakter ogólny i reprezentuje pewien schemat działania algorytmów odkrywania częstych ścieżek nawigacyjnych.
Przykład 5
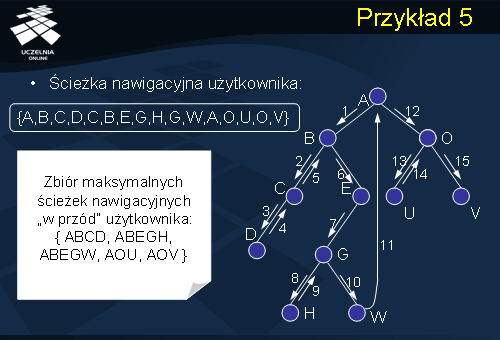
Dla ilustracji działania algorytmu WAP rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że ścieżka nawigacyjna użytkownika ma następującą postać. {A, B, C, D, C, B, E, G, H, G, W, A, O, U, O, V}. WAP–drzewo reprezentujące podaną ścieżkę przedstawiono na slajdzie. W kroku 1 algorytm przekształca podaną ścieżkę w zbiór maksymalnych ścieżek nawigacyjnych „w przód”. W tym przypadku, zbiór maksymalnych ścieżek nawigacyjnych „w przód” użytkownika ma następującą postać: {A B C D, A B E G H, A B E G W, A O U, A O V}.
W wyniku 1 kroku algorytmu, otrzymujemy zbiór sekwencji, a ściślej mówiąc, zbiór maksymalnych ścieżek nawigacyjnych „w przód” (dla wszystkich użytkowników). Stosując dowolny algorytm odkrywania wzorców sekwencji możemy znaleźć najczęstsze ścieżki nawigacyjne. Przykładowo: taką ścieżka może być ścieżka {A B E G}. Fakt ten można wykorzystać, na przykład, do wstępnego ściągania stron – jeżeli użytkownik, aktualnie, realizuje dostęp do strony B, to w celu minimalizacji opóźnienia, system może już wstępnie wczytać do bufora stronę E.
Problemy

Jak już wspomnieliśmy, przedstawiony algorytm ma charakter ogólny i celem przedstawienia algorytmu było zilustrowanie mechanizmu eksploracji logu. Szczegółowa implementacja algorytmów eksploracji logów wymaga rozwiązania szeregu trudnych problemów. Pierwszym problemem wymagającym rozwiązania jest problem identyfikacji pojedynczej ścieżki nawigacyjnej użytkownika. Otóż, w ramach pojedynczej sesji, użytkownik może realizować, de facto, wiele ścieżek nawigacyjnych: np. poszukuje książek poświęconych eksploracji danych, a następnie, w ramach tej samej sesji, rozpoczyna poszukiwanie książek dotyczących sieci komputerowych. Problem identyfikacji pojedynczej ścieżki nawigacyjnej wiąże się z problemem identyfikacji dostępów nawigacyjnych, np. ścieżka D, C, B. Reasumując, transformacja sesji użytkownika w zbiór maksymalnych ścieżek nawigacyjnych „w przód” jest problemem trudnym, który, dodatkowo, wymaga znajomości struktury serwera. Ograniczenia algorytmów eksploracji logów wynikają, również, z ograniczonej informacji dostępnej w pliku logu. Rekordu logu zawierają bardzo skąpą informację, stąd, brak możliwości głębszej analizy operacji dostępu.
Na zakończenie, należy stwierdzić, że analiza eksploracyjna logów powinna być uzupełniona analizą OLAP, pozwalającą na generację raportów podsumowujących (log serwera musi być przetransformowany do postaci hurtowni danych).






























