W2_Odkrywanie_asocjacji

Odkrywanie asocjacji

Wykład jest poświęcony wprowadzeniu i zaznajomieniu się z problemem odkrywania reguł asocjacyjnych. Przybliżymy problem analizy koszyka zakupów (MBA) oraz pokażemy jak zamodelować różne przypadki świata rzeczywistego w postaci tablicy informacji. Dokonamy klasyfikacji reguł oraz objaśnimy każdy z typów reguł asocjacyjnych. Na koniec przedstawimy algorytmy: algorytm naiwny oraz ogólny algorytm odkrywania reguł asocjacyjnych.

Odkrywanie asocjacji jest jedną z najciekawszych i najbardziej popularnych technik eksploracji danych. Celem procesu odkrywania asocjacji jest znalezienie interesujących zależności lub korelacji, nazwanych ogólnie asocjacjami, pomiędzy danymi w dużych zbiorach danych. Wynikiem procesu odkrywania asocjacji jest zbiór reguł asocjacyjnych opisujących znalezione zależności lub korelacje pomiędzy danymi. Geneza problemu odkrywania reguł asocjacyjnych sięga problemu odkrywania asocjacji rozważanego w kontekście tak zwanej analizy koszyka zakupów (MBA - Market Basket Analysis). Klasyczny problem analizy koszyka zakupów polega na analizie danych zawierających informacje o zakupach zrealizowanych przez klientów supermarketu. Celem takiej analizy jest znalezienie naturalnych wzorców zachowań konsumenckich klientów poprzez analizę produktów (grup produktów), najczęściej kupowanych razem przez klientów supermarketu.

Celem tej analizy jest znalezienie naturalnych wzorców zachowań konsumenckich klientów poprzez analizę produktów, które są przez klientów supermarketu kupowane najczęściej wspólnie (tj. określenie grup produktów, które klienci najczęściej umieszczają w swoich koszykach – stąd nazwa problemu). Znalezione wzorce zachowań klientów mogą być, następnie, wykorzystane do opracowania akcji promocyjnych, organizacji półek w supermarkecie, opracowania koncepcji katalogu oferowanych produktów itd.

Załóżmy, przykładowo, że znaleziono w bazie danych regułę asocjacyjną (wzorzec) postaci „ ktoś kto kupuje pieluszki , najczęściej kupuje również piwo ”. Wiedza, jaką niesie powyższa reguła, może być wykorzystana wielorako, np.: organizując akcję promocyjną można zastosować typowy trick pod hasłem 10% obniżki ceny pieluszek. Naturalną konsekwencją akcji powinno być zwiększenie liczy klientów kupujących pieluszki i tym samym, zrekompensowanie straty wynikającej z oferowanej obniżki ceny pieluszek. Jednakże, dodatkowym źródłem dochodu może być również zwiększony zysk z tytułu dodatkowej sprzedaży piwa kupowanej najczęściej z pieluszkami. Innym przykładem wykorzystania zdobytej wiedzy może być reorganizacja półek sklepowych w taki sposób aby umieścić produkty kupowane wspólnie obok siebie na półkach co może wpłynąć na zwiększenie sprzedaży obu produktów odwołując się do naturalnych preferencji konsumenckich klientów. Można również wykorzystać sytuację odwrotną umieszczając produkty kupowanych wspólnie w przeciwległych końcach sklepu, zmuszając klientów do przejścia przez cały sklep.

Market Basket Analysis znajduje zastosowanie wszędzie tam, gdzie „klienci” nabywają łącznie pewien zbiór dóbr lub usług:

może to być analiza pogody, w której koszykiem będzie zbiór zdarzeń pogodowych, występujących w danym przedziale czasu. Telekomunikacja, gdzie koszykiem będzie zbiór rozmów telefonicznych, oraz wiele innych dziedzin życia np.: diagnostyka medyczna czy też bankowość.

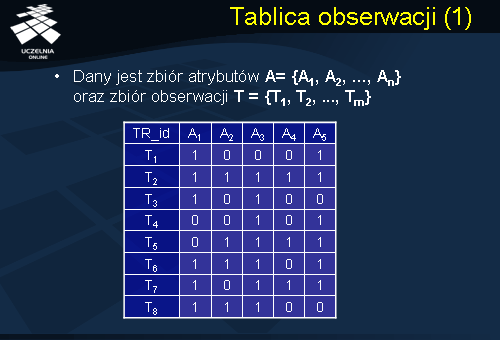
Dany jest zbiór atrybutów A= {A1, A2, ..., An}. Przykładowa tablica obserwacji D dla zbioru atrybutów A, zawierająca 8 obserwacji {T1,…,T8}. Przedstawiona tablica obserwacji dla celów ilustracyjnych, poza zbiorem atrybutów A, zawiera dodatkową kolumnę TR_id, której wartościami są identyfikatory poszczególnych obserwacji. Za pomocą tablicy obserwacji można zamodelować różne przypadki świata rzeczywistego.

Tablicę obserwacji można wykorzystać również do analizy koszyka zakupów. Zbiór atrybutów tablicy obserwacji odpowiada liście produktów oferowanych przez supermarket, natomiast wiersze tablicy reprezentują klientów i ich koszyki zakupów. Dodatkowy atrybut Tr_id przedstawia identyfikatory poszczególnych obserwacji. Pozycja Ti[Aj] = 1 tablicy wskazuje, że i-ta obserwacja zawiera wystąpienie j-tego atrybutu.

Tablica obserwacji może posłużyć na przykład, do opisu wyboru przedmiotów obieralnych przez studentów. W takim przypadku zbiór atrybutów będzie odpowiadał liście przedmiotów obieralnych oferowanych studentom przez uczelnię, natomiast wiersze tablicy obserwacji będą reprezentowały studentów i ich wybory przedmiotów. Weźmy pod uwagę inny przykład, w którym koszykiem będą strony WWW natomiast produktami – słowa kluczowe, dla takiej reprezentacji możemy sformułować problem MBA jako poszukiwanie stron WWW opisanych takimi samymi, lub podobnymi, zbiorami słów kluczowych. Możemy przypuszczać iż prawdopodobnie znalezione strony będą dotyczyły podobnej tematyki.

Skala problemu

Analizując problem MBA, podając jego rozwiązanie musimy pamiętać o jego skalowalności. Dane, które podane są analizie często osiągają olbrzymie rozmiary. Np. supermarket sprzedaj ponad 150 000 produktów i przechowuje informacje o miliardach wykonanych transakcji rocznie, albo biorąc pod uwagę Web gdzie mamy do czynienia z kilkoma miliardami stron zawierającymi ponad 100 milionów słów.

Wynik analizy koszyka zakupów przedstawiany jest w formie zbioru reguł asocjacyjnych postaci relacji przedstawionej na powyższym slajdzie oznaczonej (1). Taką regułę można interpretować w następujący sposób: „jeżeli klient kupił produkty Ai1, Ai2, ..., Aik, to prawdopodobnie kupił również produkty Aik+1, Aik+2, ..., Aik+l”.

Regułę asocjacyjna można przedstawić jednoznacznie w równoważnej postaci ? ? ?: (Ai1, Ai2, ..., Aik) ? (Aik+1, Aik+2, ..., Aik+l).

Z każdą binarną regułą asocjacyjną ? ? ?, są związane dwie miary określające statystyczną ważność i siłę

reguły: {wsparcie} reguły (ang. support) oraz {ufność} reguły (ang. confidence).

{Wsparciem} (sup) reguły asocjacyjnej ? ? ? nazywać będziemy stosunek liczby obserwacji, które spełniają warunek ? ? ?, do liczby wszystkich obserwacji, przy czym wsparcie reguły jest równe prawdopodobieństwu zajścia zdarzenia ? ? ?.

Ufnością conf reguły asocjacyjnej ? ? ? nazywać będziemy stosunek liczby obserwacji, które spełniają warunek ? ? ?, do liczby obserwacji, które spełniają warunek ? (ufność reguły = warunkowemu prawdopodobieństwu p(? | ?) . Łatwo zauważyć, że ufność reguły jest równa warunkowemu prawdopodobieństwu zajścia zdarzenia ? pod warunkiem zajścia zdarzenia p(? | ?)

W literaturze poświęconej eksploracji danych można znaleźć wiele rodzajów reguł asocjacyjnych. Reguły te można sklasyfikować według szeregu kryteriów. Wśród tych kryteriów podstawowe znaczenie mają trzy kryteria:

typ przetwarzanych danych, wymiarowość przetwarzanych danych oraz stopień abstrakcji przetwarzanych danych.

W dalszej części wykładu, krótko scharakteryzujemy poszczególne kryteria klasyfikacji i przedstawimy rodzaje reguł asocjacyjnych wynikające z tych klasyfikacji.

Typ przetwarzanych danych

Z punktu widzenia typu przetwarzanych danych wyróżniamy dwa rodzaje reguł asocjacyjnych: (1) {binarne reguły asocjacyjne} (ang. binary lub Boolean association rules) oraz (2) {ilościowe reguły asocjacyjne} (ang. quantitative association rules). Regułę asocjacyjną nazywamy {binarną regułą asocjacyjną}, jeżeli dane występujące w regule są danymi (zmiennymi) binarnymi, to znaczy, danymi, które mogą przyjmować tylko dwie wartości: '1' ({true}) lub '0' ({false}). Regułę asocjacyjną nazywamy {ilościową regułą asocjacyjną}, jeżeli dane występujące w regule są danymi ciągłymi i\lub kategorycznymi. Ilościowe reguły asocjacyjne reprezentują, najogólniej mówiąc, współwystępowanie wartości niektórych danych.

Binarne reguły asocjacyjne reprezentują, najogólniej mówiąc, współwystępowanie danych. Przykładem binarnej reguły asocjacyjnej może być reguła: „pieluszki=1 -> piwo=1”; Reguła ta wywiedziona w ramach analizy koszyka zakupów klientów supermarketu, stwierdza, że produkt 'pieluszki' często występuje w koszykach klientów łącznie z produktem 'piwo'. Przykładem ilościowej reguły asocjacyjnej jest reguła: „wiek =’30…40’ ? wykształcenie = ‘wyższe’ -> opcja_polityczna = ‘demokrata’. Ilościowe reguły asocjacyjne reprezentują, najogólniej mówiąc, współwystępowanie wartości niektórych danych. Reguła wywiedziona z analizy danych osobowych, stwierdza, że jeżeli wiek pracownika należy do przedziału wartości '30...40' i pracownik posiada wykształcenie wyższe, to, często, jego poglądy polityczne zwrócone są w kierunku demokracji. Atrybut {wiek} jest atrybutem ciągłymi, natomiast atrybuty {wykształcenie oraz opcja_polityczna} są atrybutami kategorycznym. W procesie odkrywania ilościowych reguł asocjacyjnych, atrybuty ciągłe podlegają dyskretyzacji. Stąd, w regule wartością atrybutu {wiek} jest pewien przedział wartości.

Z punktu widzenia wymiarowości przetwarzanych danych wyróżniamy dwa rodzaje reguł asocjacyjnych: (1) {jednowymiarowe reguły asocjacyjne} (ang. single-dimensional association rules) oraz (2) {wielowymiarowe reguły asocjacyjne} (ang. multidimensional association rules). Regułę asocjacyjną nazywamy {jednowymiarową regułą asocjacyjną}, jeżeli dane występujące w regule reprezentują tę samą dziedzinę wartości. Regułę asocjacyjną nazywamy {wielowymiarową regułą asocjacyjną}, jeżeli dane występujące w regule reprezentują różne dziedziny wartości. Pojęcie {wymiaru} wywodzi się z terminologii magazynów danych, gdzie pojawia się w kontekście pojęcia {analiza wielowymiarowa danych}.

Przykładem reguły jednowymiarowej będzie reguła asocjacyjna „pieluszki = 1 -> piwo = 1”, natomiast reguła „wiek =’30…40’ ? wykształcenie = ‘wyższe’ -> opcja_polityczna = ‘demokrata’ ” - jest wielowymiarową regułą asocjacyjną, gdyż występują w niej trzy wymiary: {wiek}, {wykształcenie}, oraz {opcja_polityczna}. Każdy z wymiarów jest reprezentowany jako osobny predykat reguły.

Z punktu widzenia stopnia abstrakcji przetwarzanych danych wyróżniamy dwa rodzaje reguł asocjacyjnych: (1) {jednopoziomowe reguły asocjacyjne} (ang. single-level association rules) oraz (2) {wielopoziomowe} lub {uogólnione reguły asocjacyjne} (ang. multilevel lub generalized association rules). Regułę asocjacyjną nazywamy {jednopoziomową regułą asocjacyjną}, jeżeli dane występujące w regule reprezentują ten sam poziom abstrakcji. Przykładem takich danych są konkretne produkty zakupione w supermarkecie, wykłady, na które zarejestrowali się studenci na studiach, słowa kluczowe występujące w dokumentach tekstowych, itd. Czasami dane występujące w bazie danych tworzą pewną hierarchię poziomów abstrakcji. Przykładowo, produkty w supermarkecie można poklasyfikować według kategorii produktu: produkt 'pieluszki_Pampers' należy do kategorii 'pieluszki', która, z kolei, należy do kategorii 'środki_czystości'; produkt 'piwo_żywiec' należy do kategorii 'piwo', która, z kolei, należy do kategorii ‘napoje_alkoholowe' i, dalej, do kategorii 'napoje'; wreszcie, produkt 'czekolada_milka' należy do kategorii 'słodycze'. Reguły, które opisują asocjacje występujące pomiędzy danymi reprezentującymi różne poziomy abstrakcji, nazywamy {wielopoziomowymi regułami asocjacyjnymi}.

Przykładem jednopoziomowej reguły asocjacyjnej jest reguła: „pieluszki_Pampers = 1 -> piwo_Żywiec = 1”.

Przykładem wielopoziomowej reguły asocjacyjnej jest reguła: „pieluszki_Pampers = 1 ? piwo_Żywiec = 1 -> napoje = 1”. Zauważmy, że dane występujące w regule reprezentują różne poziomy abstrakcji: dana ‘napoje' reprezentuje wyższy poziom abstrakcji aniżeli dana opisująca konkretny produkt ‘piwo_Żywiec'. Produkt napoje reprezentuje pewną abstrakcję, będącą generalizacją określonych produktów.

Odkrywanie binarnych reguł asocjacyjnych

Sformułowanie problemu odkrywania silnych jednopoziomowych jednowymiarowych binarnych reguł asocjacyjnych, przedstawione wcześniej abstrahuje od rzeczywistych metod przechowywania danych. Założenie, że obiektem eksploracji danych jest zerojedynkowa tablica obserwacji jest mało realistyczne w praktyce. Stąd, w literaturze, znacznie częściej spotykamy alternatywne sformułowanie problemu odkrywania binarnych reguł asocjacyjnych.

Wsparcie jest istotną miarą wartościującą daną regułę asocjacyjną, gdyż określa liczbę transakcji w analizowanym zbiorze D, które potwierdzają daną regułę. Odwołując się do przykładu supermarketu, wsparcie reguły określa liczbę klientów, którzy zachowują się zgodnie z daną regułą. Łatwo zauważyć, że miara wsparcia jest symetryczna względem zbiorów stanowiących poprzednik i następnik reguły, to znaczy, jeżeli reguła asocjacyjna posiada w zbiorze D wsparcie s, to takie samo wsparcie w zbiorze D posiada reguła asocjacyjna. Reguły o niewielkim wsparciu są mało reprezentatywne, gdyż opisują zachowanie niewielkiej grupy klientów. Z drugiej strony, reguły o wysokim wsparciu są, najczęściej, mało interesujące dla użytkowników, gdyż ze względu na swoją powszechność są użytkownikom dobrze znane i nie wnoszą niczego nowego do ich wiedzy o świecie. Ufność reguły określa na ile odkryta reguła asocjacyjna jest "pewna"'. Reguły o niskiej ufności są mało wiarygodne, natomiast reguły charakteryzujące się wysoką ufnością są "prawie pewne"'. Miara ufności, w przeciwieństwie do wsparcia, jest asymetryczna względem zbiorów stanowiących poprzednik i następnik reguły w tym sensie, że ufność(X -> Y) <> ufność(Y->X).

W przypadku analizy dużych wolumenów danych liczba znajdowanych (odkrywanych) reguł asocjacyjnych jest być bardzo duża i, oczywiście, nie wszystkie znalezione reguły są równie interesujące i ważne z punktu widzenia użytkownika systemu eksploracji danych. Najczęściej, reguła asocjacyjna jest uważana za interesującą i ważną, jeżeli wartości wsparcia i ufności reguły przekraczają pewne zadane wartości progowe: minimalny próg wsparcia (ang. minimum support threshold) i minimalny próg ufności(ang. minimum confidence threshold). Wartości tych progów są definiowane przez użytkownika, lub eksperta dziedzinowego, i stanowią parametry wejściowe procesu odkrywania reguł asocjacyjnych dla danego zbioru analizowanych danych. Mówimy, że reguła jest silna, jeżeli wartość współczynnika wsparcia (sup(X->Y)) jest większa lub równa minimalnemu progowi wsparcia (minsup) oraz wartość ufności reguły (conf(X->Y)) jest większa lub równa minimalnemu progowi ufności. Celem odkrywania reguł asocjacyjnych jest znalezienie wszystkich silnych binarnych reguł asocjacyjnych.

Rozważmy powyższy przykład. Mamy dana tabelę informacji zawierająca identyfikator transakcji oraz produkty jakie w ramach tej transakcji zostały zakupione. Przyjmujemy, że interesują nas tylko reguły z 50% wsparciem minsup = 50% i jednocześnie z co najmniej 50% ufnością minconf=50%. W przedstawionej bazie danych możemy znaleźć następujące reguły asocjacyjne:

A -> C dla której możemy obliczyć sup = 50% (liczba transakcji, które potwierdzają daną regułę czyli 2/4), conf=66,6% (stosunek liczby transakcji zawierających A -> C do liczby transakcji zawierających A czyli 2/3 ), analogicznie obliczamy dla reguły C -> A sup = 50% oraz conf=100%.

Naiwny algorytm odkrywania zbiorów częstych składa się z trzech głównych kroków.

Dany jest zbiór elementów I i baza danych D.
Wygeneruj wszystkie możliwe podzbiory zbioru I i następnie, dla każdego podzbioru oblicz wsparcie tego zbioru w bazie danych D.
Dla każdego zbioru, którego wsparcie jest większe/równe minsup, wygeneruj regułę asocjacyjną – dla każdej otrzymanej reguły oblicz ufność reguły.

Trywialna metoda znajdowania zbiorów częstych mogłaby polegać na wygenerowaniu wszystkich podzbiorów zbioru I i, następnie, na obliczeniu, dla każdego podzbioru Li wartości wsparcia tego podzbioru. W praktyce takie rozwiązanie jest nieakceptowalne ze względu na ilość potencjalnych zbiorów częstych. Liczba wszystkich możliwych podzbiorów zbioru I wynosi 2^|I| - 1, gdzie |I|, w zastosowaniach praktycznych (np. analizie koszyka), może sięgać nawet 300 000 elementów.

Pierwszy algorytm odkrywania silnych binarnych reguł asocjacyjnych przedstawiono w roku 1993. W tym samym roku, przedstawiono też algorytm SETM, który w procesie odkrywania silnych binarnych reguł asocjacyjnych wykorzystuje operatory relacyjne. W roku 1994 pojawiła się fundamentalna praca Agrawala i Srikanta, w której przedstawiono dwa nowe algorytmy odkrywania silnych binarnych reguł

asocjacyjnych: Apriori i AprioriTID. Algorytmy te stały się, w późniejszym czasie, podstawą wielu nowych algorytmów odkrywania binarnych reguł asocjacyjnych. Cechą wspólną wszystkich algorytmów odkrywania silnych binarnych reguł asocjacyjnych jest identyczny ogólny schemat działania algorytmu. Schemat ten, został umieszczony na slajdzie. Schemat został nazwany "ogólnym algorytmem odkrywania silnych binarnych reguł asocjacyjnych"'.

Algorytm 1.1 składa się z dwóch kroków. W pierwszym kroku znajdowane są wszystkie zbiory częste, które reprezentują zbiory elementów

występujących wspólnie w transakcjach. W kroku drugim, na podstawie znalezionych zbiorów częstych, generowane są wszystkie silne

binarne reguły asocjacyjne, których ufność jest nie mniejsza niż zadany próg minimalnej ufności minconf.

Kluczowe znaczenie, z punktu widzenia efektywności algorytmu odkrywania silnych binarnych reguł asocjacyjnych, ma pierwszy krok algorytmu - znajdowanie zbiorów częstych, to jest, podzbiorów zbioru I, których wsparcie jest większe lub równe minimalnej wartości wsparcia minsup. W ostatnim kroku algorytmu wygenerowane reguły są poddawane analizie. W zbiorze wynikowym pozostaną tylko te reguły , których współczynnik ufności będzie co najmniej tak dobry jak minimalny próg wsparcia. W ten sposób otrzymujemy tylko silne reguły asocjacyjne.

Jak już wspomnieliśmy wcześniej, problem odkrywania binarnych reguł asocjacyjnych był bardzo intensywnie analizowany od roku 1993 i zaproponowano szereg algorytmów odkrywania binarnych reguł asocjacyjnych różniących się, głównie, dwoma elementami: metodą odkrywania zbiorów częstych oraz metodą obliczania wsparcia zbiorów elementów.